Spatial and Temporal Variability in Positive Degree-Day in Western China under Climate Change
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
3. Results
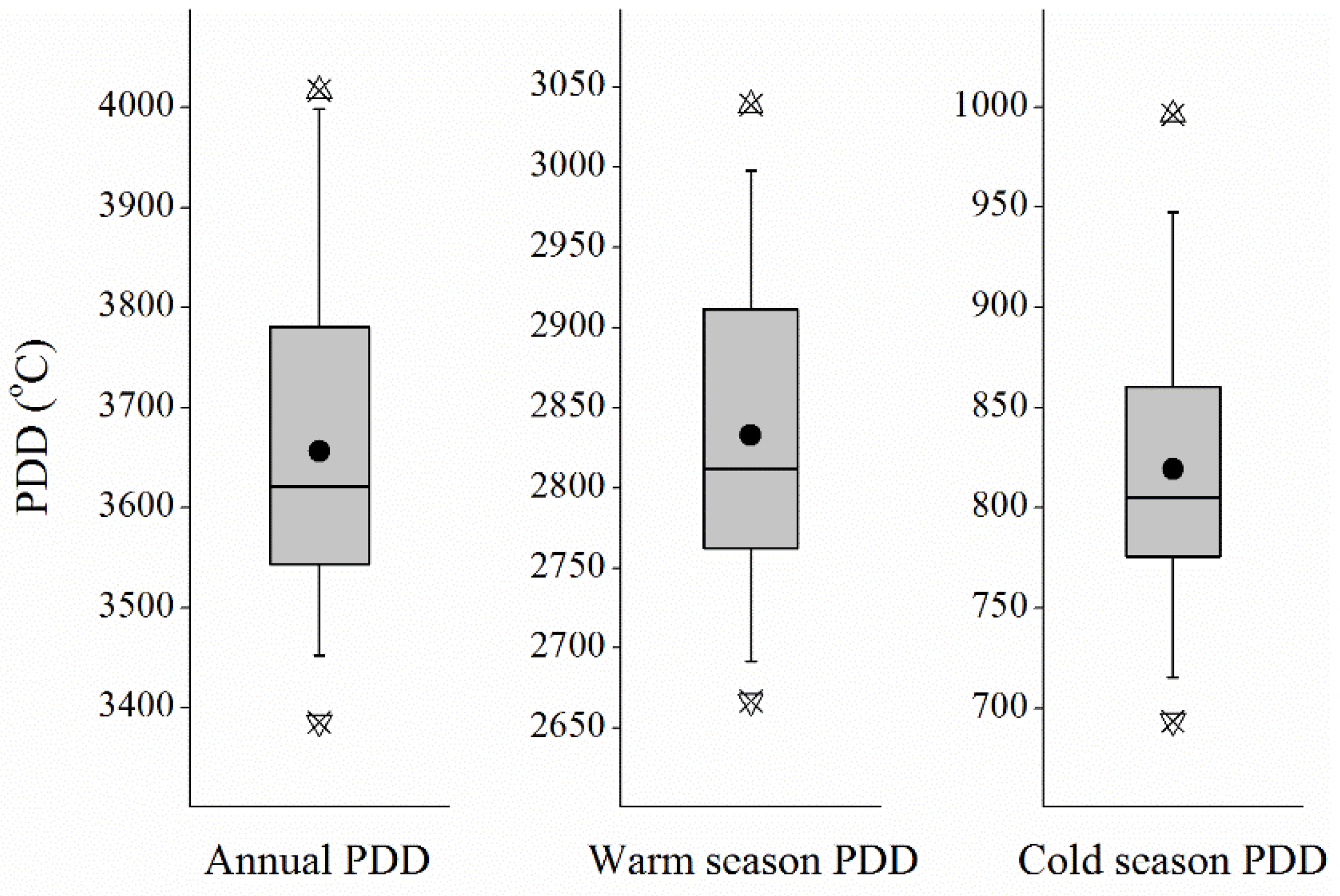
3.1. PDD Distribution in WC from the 1960s to 2018
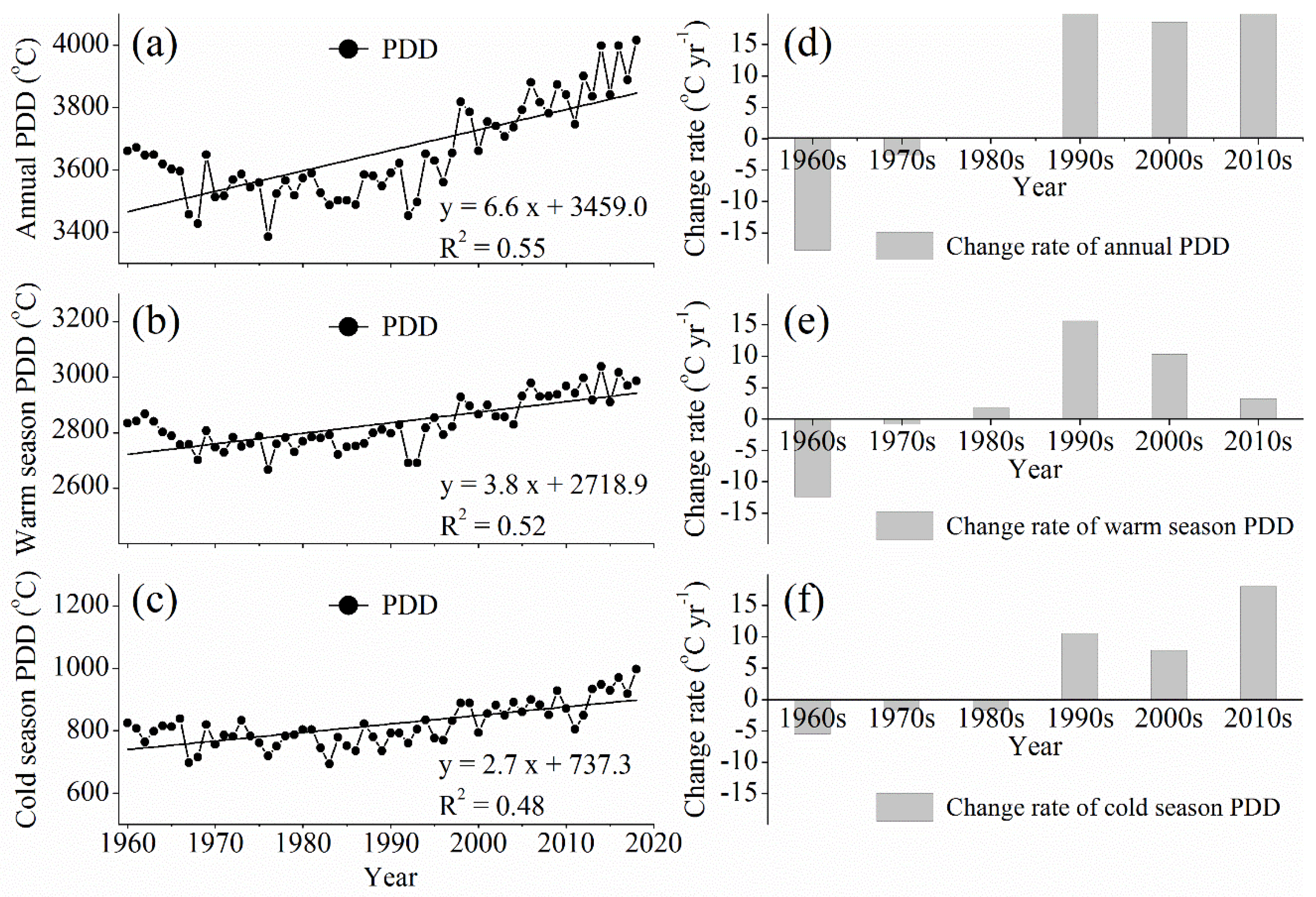
3.2. Temporal Characteristics of PDD Change in WC
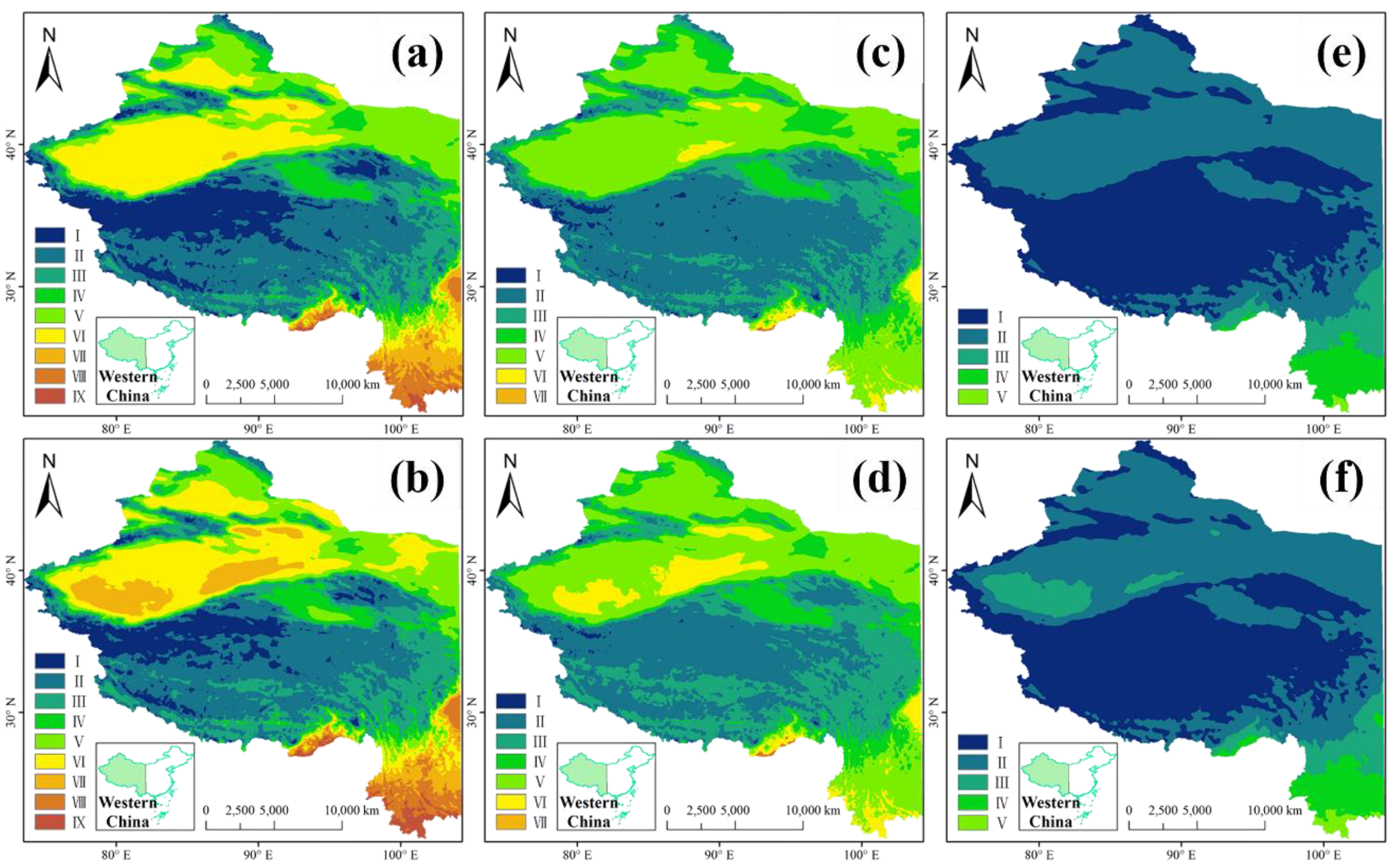
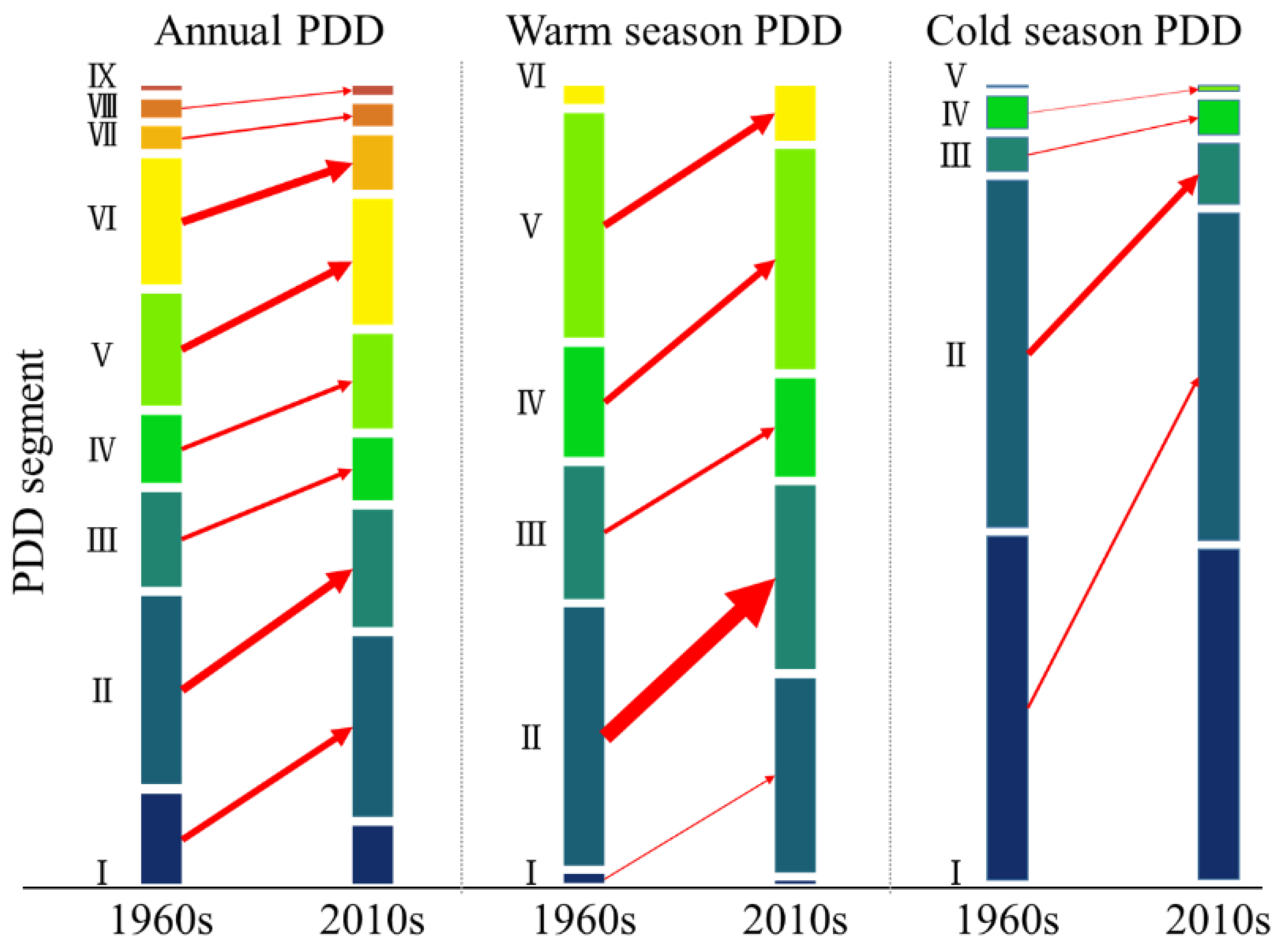
3.3. Spatial Characteristic of PDD Change in WC
4. Discussion
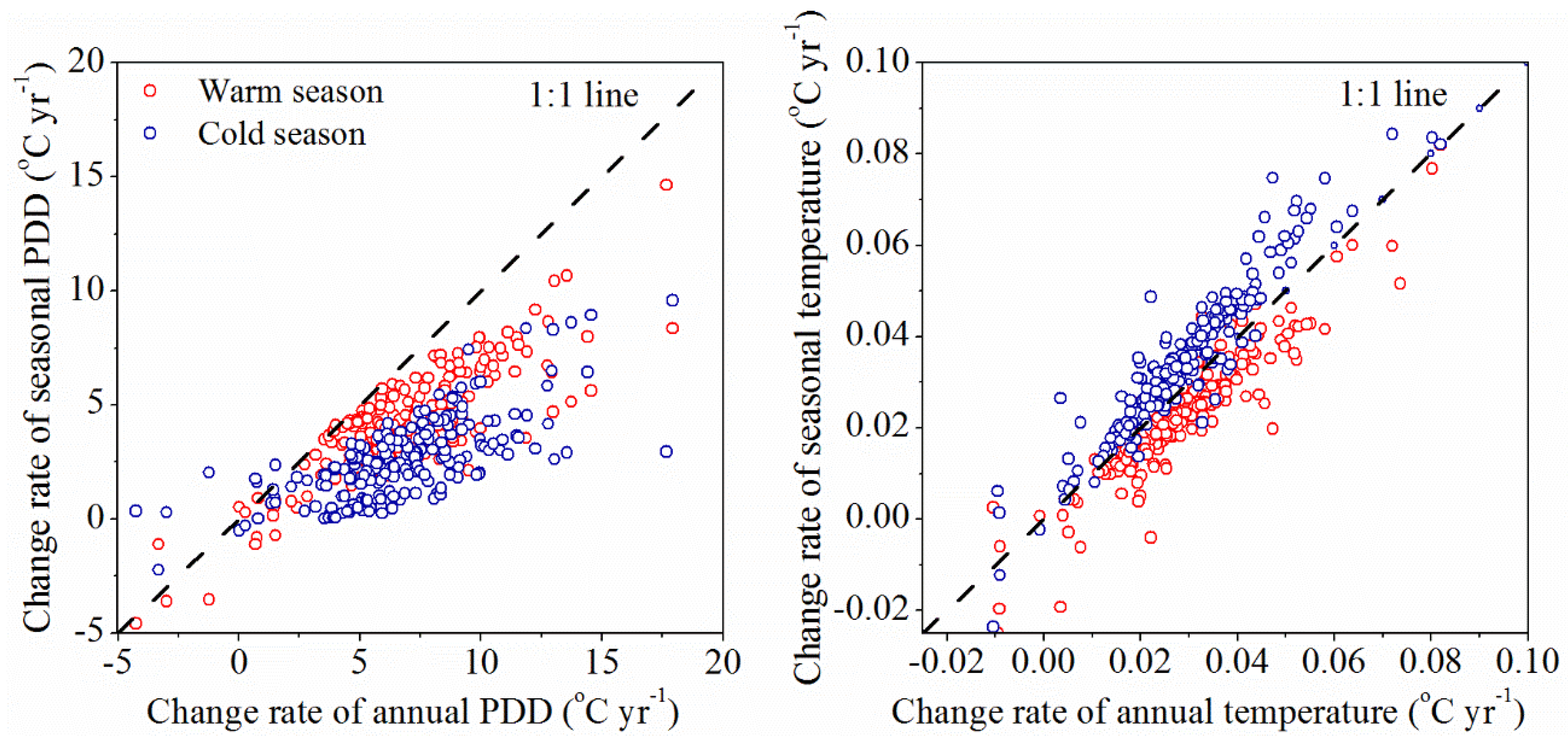
4.1. Difference in Time Trend between PDD and Air Temperature
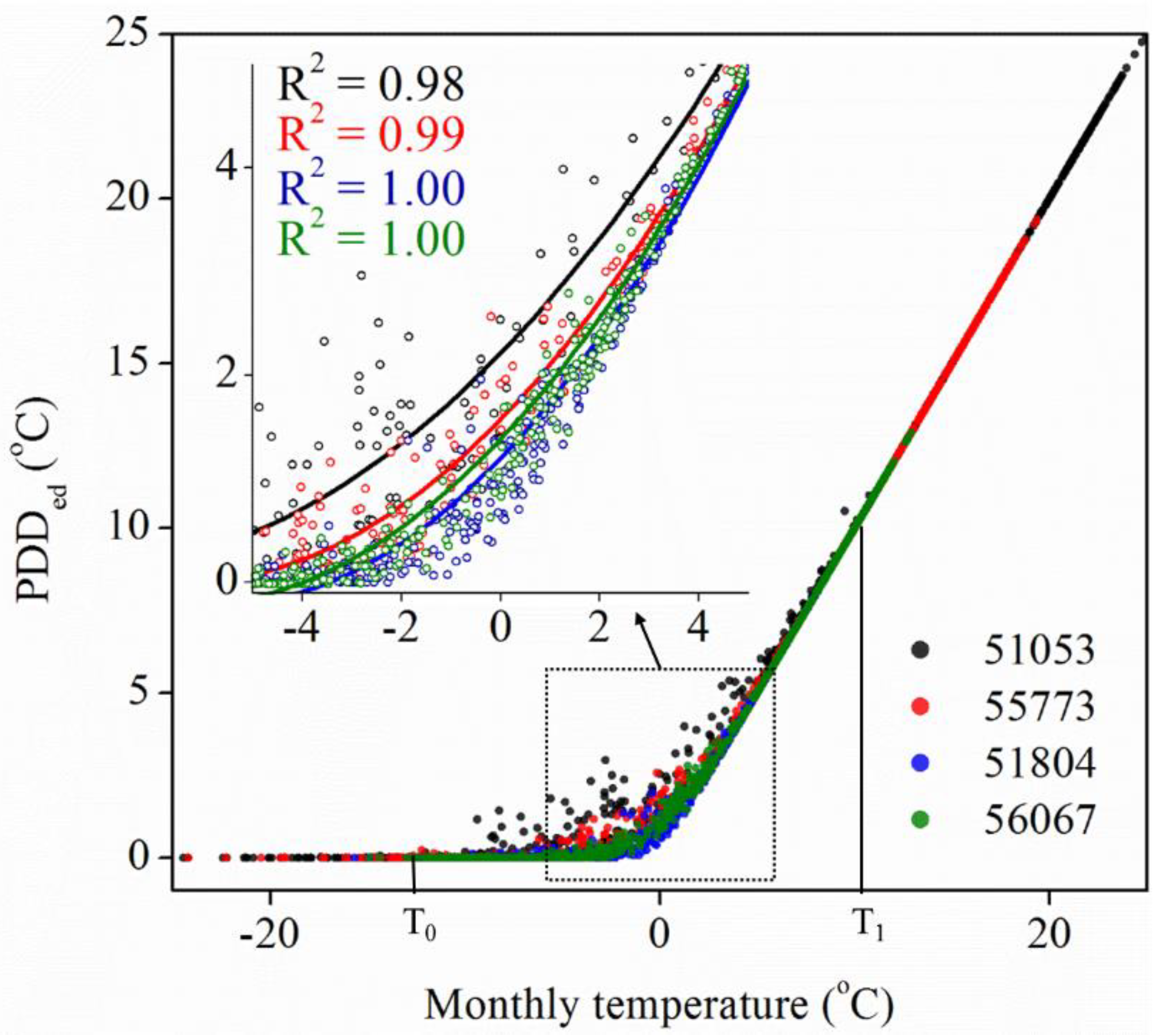
4.2. Sources of Time Trend Differences: The Relationship between PDD and Air Temperature
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change: The Physical Science Basis: Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA; Cambridge, UK, 2007. [Google Scholar]
- IPCC. Climate change: The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA; Cambridge, UK, 2013. [Google Scholar]
- Ji, F.; Wu, Z.; Huang, J.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Ren, G.; Ding, Y.; Tang, G. An overview of mainland China temperature change research. J. Hydrometeorol. 2017, 31, 3–16. [Google Scholar] [CrossRef]
- Tang, H.; Zhai, P. Comparison of variations of surface air temperatures in eastern and western China during 1951~2002. Chin. J. Geophys. 2005, 48, 526–534. (In Chinese) [Google Scholar] [CrossRef]
- Huang, J.; Guan, X.; Ji, F. Enhanced cold-season warming in semi-arid regions. Atmos. Chem. Phys. 2012, 12, 5391–5398. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Shi, X. Why does the temperature rise faster in the arid region of northwest China? J. Geophys. Res. 2012, 117, 1–7. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Shi, X.; Chen, Z.; Li, Q. Temperature and precipitation changes in different environments in the arid region of northwest China. Theor. Appl. Climatol. 2013, 112, 589–596. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, H.; Li, B.; Li, Z.; Xu, C. Abrupt change of temperature and precipitation extremes in the arid region of Northwest China. Quatern. Int. 2014, 336, 35–43. [Google Scholar] [CrossRef]
- Shi, Y.; Shen, Y.; Hu, R. Preliminary study on siginal, impact and foreground of climatic shift from warm-dry to warm-humid in northwest China. J. Glaciol. Geocryol. 2002, 24, 219–226. (In Chinese) [Google Scholar]
- Shi, Y.; Shen, Y.; Li, D.; Zhang, G.; Ding, Y.; Hu, R.; Kang, E. Discussion on the present climate change from warm-dry to warm-wet in northwest China. Quat. Sci. 2003, 23, 153–164. [Google Scholar]
- Ohmura, A. Physical Basis for the temperature-based melt-index method. J. Appl. Meteorol. 2001, 40, 753–761. [Google Scholar] [CrossRef]
- Rangwala, I.; Miller, J. Climate change in moutains: A review of elevation-dependent warming and its possible cause. Clim. Chang. 2012, 114, 527–547. [Google Scholar] [CrossRef]
- Palazzi, E.; Mortarini, L.; Terzago, S.; Hardenberg, J. Elevation-dependent warming in global climate simulations at high spatial resolution. Clim. Dynam. 2018, 52, 2685–2702. [Google Scholar] [CrossRef]
- Ren, G.; Xu, M.; Chu, Z. Changes of surface air temperature in China during 1951–2004. Clim. Environ. Res. 2005, 10, 717–727. (In Chinese) [Google Scholar]
- Liu, X.; Cheng, G.; Yan, L.; Yin, J. Elevation dependency of recent and future minimum surface air temperature trends in the Tibetan Plateau and its surroundings. Global. Planet. Chang. 2009, 68, 164–174. [Google Scholar] [CrossRef]
- Gong, D.; Zhou, T.; Wang, S. Advance in the studies on north atlantic oscillation (NAO). Adv. Earth. Sci. 2001, 16, 413–420. (In Chinese) [Google Scholar]
- Duan, A.; Wu, G. Change of cloud amount and the climate warming on the Tibetan Plateau. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Hua, S.; Liu, Y.; Jia, R.; Chang, S.; Wu, C.; Zhu, Q.; Shao, T.; Wang, B. Role of clouds in accelerating cold-season warming during 2000–2015 over the Tibetan Plateau. Int. J. Climatol. 2017, 38, 4950–4966. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Hu, T.; Qin, D.; Song, L. Attribution of temperature changes in Western China. Int. J. Climatol. 2017, 38, 1–9. [Google Scholar] [CrossRef]
- Duan, A.; Xiao, Z. Does the climate warming hiatus exist over the Tibetan Plateau? Sci. Rep. UK 2015, 5, 13711. [Google Scholar] [CrossRef]
- Monjur, M. Relationship between annual mean temperature and degree-days. Energ. Build. 2012, 54, 418–425. [Google Scholar]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geog. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Ding, Y. Observed degree-day factors and their spatial variation on glaciers in western China. Ann. Glaciol. 2006, 43, 301–306. [Google Scholar] [CrossRef]
- Chen, G.; Jiang, H.; Wang, K. Thawing index and freezing index in the embankment surface in permafrost regions. J. Glaciol. Geocryol. 2003, 25, 603–607. (In Chinese) [Google Scholar]
- Anisimov, O.A.; Lobanov, V.; Reneva, S.; Shiklomanov, N.; Zhang, T.; Nelson, F. Uncertainties in gridded air temperature fields and effects on predictive active layer modeling. J. Geophys. Res. 2007, 112, 1–12. [Google Scholar] [CrossRef]
- Beltaos, S. Climate impacts on the ice regime of an Atlantic river. Nordic Hydrol. 2003, 35, 81–99. [Google Scholar] [CrossRef]
- Braithwaite, R. Calculation of degree-days for glacier-climate research. Z. Gletsch. Glazialgeol. 1985, 20, 1–8. [Google Scholar]
- Reeh, N. Parameterization of melt rate and surface temperature on the Greenland ice sheet. Polarforschung 1989, 5913, 113–128. [Google Scholar]
- Carlov, R.; Greve, R. A semi-analytical solution or the positive degree-day model with stochastic temperature variations. J. Glaciol. 2005, 51, 173–175. [Google Scholar] [CrossRef]
- Wake, L.; Marshall, S. Assessment of current methods of positive degree-day calculation using in situ observations from glaciated regions. J. Glaciol. 2015, 61, 329–334. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Qin, D. Assessment Report on Environment Evolutions in Western China; Science Press: Beijing, China, 2002; p. 242. [Google Scholar]
- Qin, D.; Ding, Y. Cryospheric Changes and their impacts: Present, trends and key issues. Adv. Clim. Chang. Res. 2009, 5, 187–195. (In Chinese) [Google Scholar] [CrossRef]
- Kang, S.; Xu, Y.; You, Q.; Flügel, W.A.; Pepin, N.; Yao, T. Review of climate and cryospheric change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 1–8. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Y.; Shangguang, D.; Wang, R. Regional differences in global glacier retreat from 1980 to 2015. Adv. Clim. Chang. Res. 2019, 10, 203–213. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Jin, H.; Kang, E.; Che, T.; Jin, R.; Wu, L.; Nan, Z.; Wang, J.; Shen, Y. Cryospheric change in China. Glob. Planet. Chang. 2008, 62, 210–218. [Google Scholar] [CrossRef]
- Guo, W.; Liu, S.; Xu, J.; Wu, L.; Shangguan, D.; Yao, X.; Wei, J.; Bao, W.; Yu, P.; Liu, Q.; et al. The second Chinese glacier inventory: Data, methods and results. J. Glaciol. 2015, 61, 357–372. [Google Scholar] [CrossRef]
- Wang, X.; Chen, R.; Liu, J. Spatial and temporal variation characteristice of accumulated negative temperature in Qilian Mountains under Climate. Plateau Meteorol. 2017, 36, 1267–1275. (In Chinese) [Google Scholar]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Li, X.; Jin, R.; Pan, X.; Zhang, T.; Guo, J. Changes in the near-surface soil freeze–thaw cycle on the Qinghai-Tibetan Plateau. Int. J. Appl. Earth. Obs. 2012, 17, 33–42. [Google Scholar] [CrossRef]
- Wang, X.; Chen, R.; Liu, G.; Yang, Y.; Song, Y.; Liu, J.; Liu, Z.; Han, C.; Liu, X.; Guo, S.; et al. Spatial distributions and temporal variations of the near-surface soil freeze state across China under climate change. Glob. Planet. Chang. 2018, 172, 150–158. [Google Scholar] [CrossRef]
- Liu, X.; Chen, R.; Liu, J.; Wang, X.; Zhang, B.; Han, C.; Liu, G.; Guo, S.; Liu, Z.; Song, Y.; et al. Effects of snow-depth change on spring runoff in cryosphere areas of China. Hydrol. Sci. J. 2019, 64, 1–9. [Google Scholar] [CrossRef]
- Xu, F.; Jia, Y.; Peng, H.; Niu, C.; Liu, J. Temperature and precipitation trends and their links with elevation in the Hengduan Mountain region, China. Clim. Res. 2018, 75, 163–180. [Google Scholar] [CrossRef]
- Wang, L.; Chen, R.; Han, C.; Wang, X.; Liu, G.; Song, Y.; Yang, Y.; Liu, J.; Liu, Z.; Liu, X.; et al. Change characteristics of precipitation and temperature in the Qilian Mountains and Hexi Oasis, Northwestern China. Environ. Earth. Sci. 2019, 78, 284. [Google Scholar] [CrossRef]
- Shah, F.; Xu, J.; Fazli, H.; Anis, U.; Wei, Q.; Cai, S.; Bai, W.; Yousef, A. Spaciotemporal deviation in growing degree days and season under increasing temperature in Heilongjiang province. Pak. J. Agr. Sci. 2019, 56, 1075–1086. [Google Scholar]
- Mountain Research Initiative EDW Working Group. Elevation-dependent warming in moutain regions of the word. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar] [CrossRef]
- Wang, Y. Evolvement of the cumulative temperatures in China loess plateau. J. Glaciol. Geocryol. 2007, 29, 119–125. (In Chinese) [Google Scholar]
- Seguinot, J. Spatial and seasonal effects of temperature variability in a positive degree-day glacier surface mass-balance model. J. Glaciol. 2013, 59, 1202–1204. [Google Scholar] [CrossRef]
- Li, F. Impact of Climate Change to Water Resource on the Upper Reach of Kaidu River Basin. Master’s Thesis, Lanzhou University, Lanzhou, China, 2017. (In Chinese). [Google Scholar]



| R2 | 1960s | 1970s | 1980s | 1990s | 2000s | 2010s |
|---|---|---|---|---|---|---|
| Annual PDD | 0.96 | 0.96 | 0.95 | 0.96 | 0.96 | 0.96 |
| Warm season PDD | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.94 |
| Cold season PDD | 0.92 | 0.92 | 0.92 | 0.93 | 0.93 | 0.93 |
| Time Segment | MRE | MAE | RMSE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| OK | IDW | SPLINE | OK | IDW | SPLINE | OK | IDW | SPLINE | |
| 1960s | −165 | −207 | −293 | 212 | 214 | 376 | 53 | 59 | 110 |
| 1970s | −181 | −222 | −303 | 221 | 228 | 380 | 56 | 63 | 112 |
| 1980s | −167 | −211 | −284 | 200 | 213 | 377 | 51 | 58 | 109 |
| 1990s | −134 | −178 | −246 | 170 | 181 | 354 | 47 | 54 | 104 |
| 2000s | −28 | −76 | −117 | 109 | 103 | 299 | 38 | 41 | 91 |
| 2010s | 11 | −35 | −117 | 87 | 71 | 299 | 33 | 33 | 91 |
| mean | −111 | −155 | −227 | 166 | 169 | 348 | 46 | 51 | 103 |
| PDD Segment | Annual PDD | Warm Season PDD | Cold Season PDD |
|---|---|---|---|
| I (0 °C) | 10.6% | 0.8% | 44.4% |
| II (0~1000 °C) | 26.0% | 31.5% | 45.9% |
| III (1000~2000 °C) | 14.2% | 19.6% | 5.1% |
| IV (2000~3000 °C) | 9.2% | 14.1% | 4.4% |
| V (3000~4000 °C) | 14.9% | 30.3% | 0.2% |
| VI (4000~5000 °C) | 18.2% | 3.6% | -- |
| VII (5000~6000 °C) | 3.6% | 0.1% | -- |
| VIII (6000~7000 °C) | 2.7% | -- | -- |
| IX (>7000 °C) | 0.6% | -- | -- |
| Significance Level | Initial Date of PDD | Terminal Date of PDD | Duration | |||
|---|---|---|---|---|---|---|
| Number of Stations | Mean CR (Day 10y−1) | Number of Stations | Mean CR (Day 10y−1) | Number of Stations | Mean CR (Day 10y−1) | |
| p < 0.01 | 27 | 0.14 | 18 | 0.25 | 9 | 0.015 |
| p < 0.05 | 49 | 0.86 | 44 | 0.83 | 19 | 1.21 |
| p < 0.1 | 48 | 1.65 | 44 | 1.40 | 50 | 2.17 |
| p > 0.1 | 45 | 2.53 | 63 | 2.10 | 91 | 3.78 |
| NA | 40 | 40 | 40 | |||
| Sum and Mean | 209 | 1.41 | 209 | 1.39 | 209 | 2.82 |
| PDD Segment | Annual PDD | Warm Season PDD | Cold Season PDD | |||
|---|---|---|---|---|---|---|
| 1960s | 2010s | 1960s | 2010s | 1960s | 2010s | |
| I | 12.5% | 8.2% | 1.20% | 0.40% | 45.3% | 43.50% |
| II | 26.1% | 25.2% | 34.20% | 25.70% | 45.80% | 43.30% |
| III | 13.2% | 15.7% | 17.60% | 24.40% | 4.50% | 8.00% |
| IV | 9.2% | 8.9% | 14.60% | 13.00% | 4.20% | 4.50% |
| V | 15.3% | 13.3% | 29.90% | 29.20% | 0.20% | 0.70% |
| VI | 17.3% | 17.0% | 2.40% | 7.20% | -- | -- |
| VII | 3.4% | 7.5% | 0.10% | 0.10% | -- | -- |
| VIII | 2.6% | 3.0% | -- | -- | -- | -- |
| IX | 0.4% | 1.2% | -- | -- | -- | -- |
| sum | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Chen, R.; Wang, X. Spatial and Temporal Variability in Positive Degree-Day in Western China under Climate Change. Atmosphere 2021, 12, 443. https://doi.org/10.3390/atmos12040443
Liu G, Chen R, Wang X. Spatial and Temporal Variability in Positive Degree-Day in Western China under Climate Change. Atmosphere. 2021; 12(4):443. https://doi.org/10.3390/atmos12040443
Chicago/Turabian StyleLiu, Guohua, Rensheng Chen, and Xiqiang Wang. 2021. "Spatial and Temporal Variability in Positive Degree-Day in Western China under Climate Change" Atmosphere 12, no. 4: 443. https://doi.org/10.3390/atmos12040443
APA StyleLiu, G., Chen, R., & Wang, X. (2021). Spatial and Temporal Variability in Positive Degree-Day in Western China under Climate Change. Atmosphere, 12(4), 443. https://doi.org/10.3390/atmos12040443





