Abstract
Electrification represents a fundamental process in planetary atmospheres, widespread in the Solar System. The atmospheres of the terrestrial planets (Venus, Earth, and Mars) range from thin to thick are rich in heavier gases and gaseous compounds, such as carbon dioxide, nitrogen, oxygen, argon, sodium, sulfur dioxide, and carbon monoxide. The Jovian planets (Jupiter, Saturn, Uranus, and Neptune) have thick atmospheres mainly composed of hydrogen and helium involving. The electrical discharge processes occur in the planetary atmospheres leading to potential hazards due to arcing on landers and rovers. Lightning does not only affect the atmospheric chemical composition but also has been involved in the origin of life in the terrestrial atmosphere. This paper is dealing with the transport parameters and the breakdown voltage curves of the gas compositions representing atmospheres of the planets of the Solar System. Ionization coefficients, electron energy distribution functions, and the mean energy of the atmospheric gas mixtures have been calculated by BOLSIG+. Transport parameters of the carbon dioxide rich atmospheric compositions are similar but differ from those of the Earth’s atmosphere. Small differences between parameters of the Solar System’s outer planets can be explained by a small abundance of their constituent gases as compared to the abundance of hydrogen. Based on the fit of the reduced effective ionization coefficient, the breakdown voltage curves for atmospheric mixtures have been plotted. It was found that the breakdown voltage curves corresponding to the atmospheres of Solar System planets follow the standard scaling law. Results of calculations satisfactorily agree with the available data from the literature. The minimal and the maximal value of the voltage required to trigger electric breakdown is obtained for the Martian and Jupiter atmospheres, respectively.
1. Introduction
Space missions brought new insights into the atmospheres of the Solar System planets representing an active field of research [1,2,3,4,5,6,7]. One of the major risks to instrumentation of rovers and landers is electrification in planetary atmospheres causing failure of numerous landing attempts [8,9,10]. To prevent the impact of electrical discharges, designs of electrical components on spacecrafts should be relied on breakdown voltage curves of the gas mixture representing atmospheric compositions [11,12]. Thus, studies of the electrical phenomena that occur in the planetary atmospheres are essential for designing space-flight hardware.
In spite of the fact that lightning played a crucial role in the origin of life [13,14], understanding lightning strikes in the solar system are still incomplete [15]. Since the first detection of lightning in the Earth’s atmosphere. [16,17], proofs of lightning and lightning-related transient luminous events in the atmospheres of Jupiter, Saturn, Uranus, and Neptune have been reported and modeled [18,19,20,21,22,23,24]. Electrical activities in the Martian and Venusian atmospheres are also recorded, but there are not completely confirmed [25,26]. Based on opposite evidence about lightning detection in Venus atmosphere [27,28,29,30,31] it was suggested that plasma instabilities could be the cause of whistler wave observed by Venus orbiter rather than lightning.
Despite numerous papers devoted to calculations of the electric breakdown threshold in Venus, Earth, Mars, Jupiter, and Saturn [32,33,34], some aspects still remain unclear. Atmospheric electricity present in all Solar System gaseous giants can be also detected in extrasolar planets [33]. Observation of extraterrestrial lightning is limited primarily by existing detection techniques [34]. For triggering electrical discharge an electron field is required to accelerate free electrons throughout the atmosphere gas composition. In collisions with other gas particles, electrons gain enough energy to produce an electron avalanche. The critical electric field necessary for this depends on the gas composition of the atmosphere. Lightning is detected or indirectly inferred on most of the cloud-carrying solar system planets. It was found that cloud particles or droplets trigger such transient discharges in planetary atmospheres [35]. The Venusian and Martian atmospheres are predominantly rich in carbon dioxide, while nitrogen and oxygen comprise the majority of Earth’s atmosphere. The atmospheres of Jupiter and Saturn are mainly formed by hydrogen and helium with clouds formed of ammonia, ice particles, ammonium hydrosulfide, and water droplets. The energy that sustains atmospheric convection on gaseous giant planets comes from the inner part of the planet instead of from the Sun leading to differences between lightning produced in giant gaseous planets and terrestrial lightning. It was estimated that Jovian and Saturnian lightning strokes could be 4 orders of magnitude stronger as compared to the terrestrial atmospheric discharges [36,37,38,39,40,41]. Some new findings suggest that there are also flashes with lower energy [42].
In this paper, we study the breakdown voltage curves and transport parameters for gas mixtures representing the compositions of the atmospheres of the terrestrial and the Jovian planets. Calculations were performed by using BOLSIG+ code [43,44,45] to calculate Townsend coefficients for the atmospheres of all the Solar System planets, except for Mercury whose atmosphere is extremely thin and unstable. The ionization coefficients, mean energies, and electron energy distribution functions are calculated for the reduced field in the range from 10 to 1000 Td. Based on the fit of the reduced effective ionization coefficients, the breakdown voltage curves have been plotted. and the minimum breakdown voltage values have been estimated. Coefficients derived from the exponential fit accurately predict the minimum voltages for each atmospheric gas mixture.
2. Method
For this study, calculations were carried out by using BOLSIG+, a user-friendly computer program for solving the Boltzmann equation (BE) of electrons in weakly ionized gases in a uniform electric field [43,44,45]. The electron energy distribution functions (EEDF) and the transport coefficients for all planetary atmosphere mixtures were calculated by solving BE [43]:
with the electron distribution f, the velocity coordinates v, the electric field E and the velocity-gradient operator ∇v. C on the right-hand side of the Equation (1) corresponds to the rate of change in f due to collisions, while e and m represent the elementary charge and the electron mass, respectively. Under assumptions of the spatial uniformity of the electric field and the collision probabilities, the electron distribution f is symmetric in velocity space around the electric field direction. Equation (1) can be rewritten in the form [43]:
where electron distribution f depends on four coordinates: the magnitude of the velocity v, the angle θ between the velocity and the field direction, the position along this direction z, and t. The θ-dependence can be simplified by the classical two-term approximation (TTA).
In TTA the electron distribution f is represented by the first two terms of an expansion in spherical harmonics in velocity space [43]:
with the isotropic f0 and anisotropic f1 parts. In the case of a constant electric field, the solution for the electron distribution function (EEDF) can be expressed as a function of the reduced electric field E/N (the ratio of electric field strength to gas particle number density expressed in units of 1Td =10−21 Vm2).
Transport coefficients in the BOLSIG+ output have been multiplied or divided by the total gas density N. The Townsend ionization coefficient is defined as the total number of electrons created per unit length. On the other hand, the Townsend attachment coefficient represents the total number of electrons lost per unit length. The ionization α/N and attachment η/Ν coefficients to the total gas density ratio (both expressed in m2) are given by the relations [46]:
where the total ionization frequency νiz and the total attachment frequency νat are defined as the number of electrons created and lost per unit time, respectively. P represents energy per unit time absorbed by the electrons from the electric field.
The mean energy (in eV) is calculated as [46]:
where ε is the electron energy and f0 is the isotropic part of electron distribution function (expressed in eV−3/2), corresponding to zeroth-order term of spherical harmonics expansion in velocity space [46].
In this study, TTA calculations were performed for the atmospheres of the Solar System planets. In our calculations, we assumed the atmosphere compositions of three innermost planets in the solar system as follows [47]: Venus (96.5% CO2, 3.5% N2, 0.015% SO2, 0.0017% CO), Earth (78% N2, 21% O2, 0.93% Ar, 0.04% CO2), and Mars (95.3% CO2, 2.7% N2, 1.6% Ar, 0.13% O2, 0.07% CO). The atmospheres of the outermost planet in the solar system are made of: Jupiter (92.5% H2, 7.3% He, 0.1% C, 0.03% N), Saturn (96.3% H2, 3.25% He, 0.45% CH4), Uranus (82.5% H2, 15.2% He, 2.3% CH4), and Neptune (79.5% H2, 19% He, 1.5% CH4). The sets of cross-sections for carbon dioxide, nitrogen, oxygen, argon, sulfur dioxide, carbon monoxide, hydrogen, helium, methan, and carbon include 13, 25, 17, 3, 6, 18, 17, 3, 11, and 4 processes, respectively. Cross-section data are taken from an open-access website for collecting, displaying, and downloading electron and ion scattering cross-sections, swarm parameters, reaction rates, energy distribution functions, etc. [48]. The available databases have been contributed by members of the community. The ionization coefficients, electron energy distribution functions, mean energy, the reduced ionization coefficient, and the breakdown voltage curves have been calculated for the planetary atmospheres, for the reduced electric fields ranging from 10 to 1000 Td.
3. Results and Discussion
Figure 1 shows the results of the TTA calculations for the dependence of the ionization coefficients α/N on the reduced electric field E/N for the gas mixture representing atmospheres of the: (a) innermost and (b) outermost planets. The ionization coefficients of Venus and Mars are similar since their atmospheres are carbon dioxide-rich. The ionization coefficients of the Earth’s atmosphere are lower due to different ionization energy of N2 as compared to CO2. The ionization coefficients of the gas mixtures of the outermost planets are similar since hydrogen is the most abundant constituent in their atmospheres. For all planets, the dash curves represent the fit to a semi-empirical formula for the ionization coefficient for the gas mixture [49]:
where xz is the fraction of the gas z in the mixture. The ionization coefficient for the individual gas can be expresses as a sum [49]:
where E/N is the reduced field, while Ai and Bi are constants [49]. For the atmospheric compositions of all Solar System planets calculated results (symbols) agree well with the theoretical predictions obtained by Equation (6) (dash curves). The consistency among data calculated by BOLSIG+ on α/N and those obtained by semi-empirical formula (6) was checked by plotting the logarithm of α/N as a function of N/E. Figure 2 displays linearized representation of ln(α/N) versus N/E of the: (a) innermost and (b) outermost planets. As expected, behaviors of the data points for all planets are almost linear [50]. Additionally, all results can be fitted with the Korff parameterization to determine parameters Ai and Bi in Korff’s expressions α/N=Ai exp(−Bi·N/E) [50].
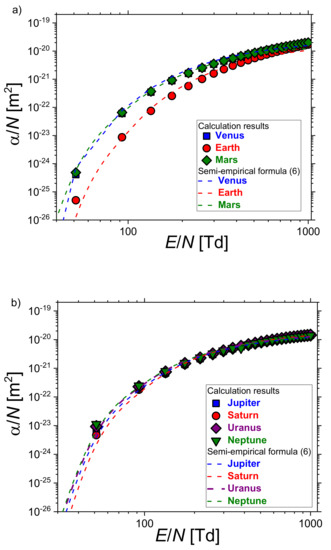
Figure 1.
The density-normalized first ionization coefficient as a function of the reduced electric field corresponding to the atmospheres of the: (a) terrestrial and (b) Jovian planets. Dash curves represent fit according to Equation (6).
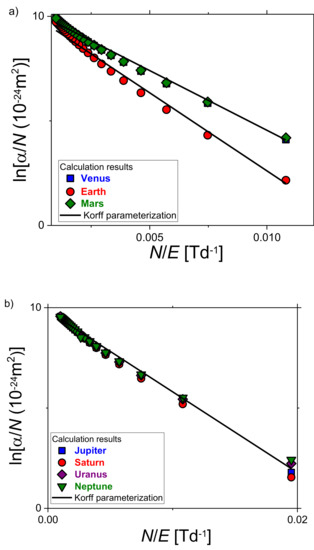
Figure 2.
Linearized representation of ln(α/N) versus N/E for the atmosphere gas mixture of the: (a) terrestrial and (b) Jovian planets. Korff parameterization is represented by solid line.
Figure 3 shows the slope of the electron energy distribution functions (EEDFs) calculated for the: (a) terrestrial and (b) Jovinian planets at the reduced field of 90 Td. Electron kinetics is strongly affected by the electric field so the EEDFs at the same reduced field E/N for individual atmosphere mixtures rich in carbon dioxide (Venus and Mars) are similar, while the Earth’s atmoshere is lower. Additionally, there is no large difference between the EDDFs of the atmospheres rich in hydrogen (Jovian planets).
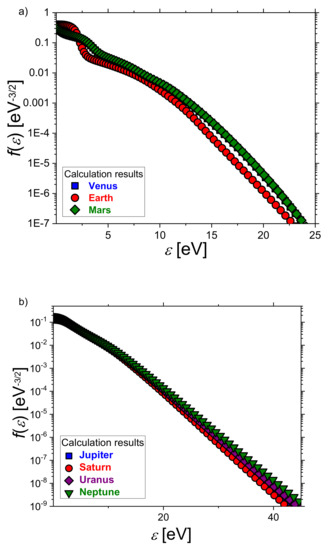
Figure 3.
The TTA calculation results for the electron energy distribution functions of the atmospheres of the: (a) innermost and (b) outermost planets at the reduced electric field of 90 Td.
The dependence of the mean electron energies on the reduced electric field of the terrestrial planetary atmospheres can be observed from Figure 4a. The results are similar for the CO2-rich atmospheres (Venus and Mars). Due to gas compositions, the mean energy corresponding to the Earth’s atmosphere differs from those of the Martian and Venusian atmospheres at the low values of the reduced field. For higher E/N values, however, the results of the Earth’s atmosphere approach those of Venus and Mars. Since the atmospheric compositions of all outermost planets made up primarily of hydrogen, values of the mean energy are similar all over the range of E/N (see Figure 4b).
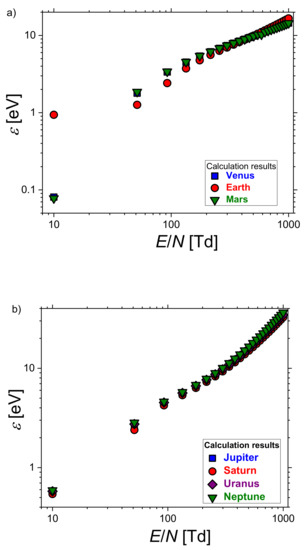
Figure 4.
The electron mean energy against the reduced electric field E/N for the gas mixture representing the atmospheric compositions of the: (a) terrestrial and (b) Jovian planets.
The ionization coefficients as a function of the mean energy for the atmospheres of the Solar System planets are depicted in Figure 5. The ionizations of the Martian and Venusian gas mixtures prevail over the ionization of the gas composition representing the Earth’s atmosphere due to different electron energy distributions. On the other hand, for the atmospheres of the outermost planets rich in hydrogen, there are no remarkable differences between the ionization coefficients.
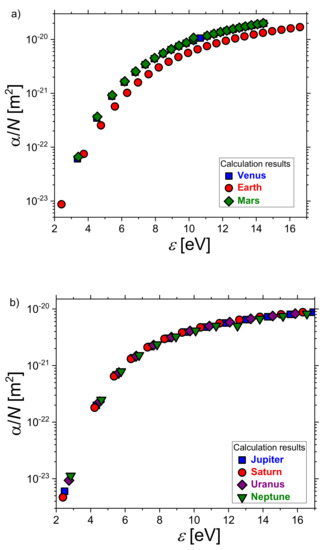
Figure 5.
The ionization coefficients versus the mean electron energy calculated for the atmospheres of the: (a) innermost and (b) outermost planets.
The effective ionization coefficient is defined as (α−η). The reduced effective ionization coefficient (α−η)/N is determined from the difference between the ionization α/N (Figure 1) and attachment η/N coefficients (insert small Figure) and shown in Figure 6. These coefficients given by (4) are calculated from the electron energy distributions based on the collision cross-section sets of ionization and attachment and number densities of all components in the gas mixtures. Calculated values of the reduced effective ionization coefficients are fitted according to the empirical expression to determine coefficients A and B taking into account conversion factors 1 Td = 10−17 Vcm2 and 1V/(cm·Torr) = 3.0341 Td. Such determined coefficients A and B (listed in Table 1) are then put in the expression for the breakdown voltage VB [51]:
where p is the pressure, d is the distance, while Q = 104 is estimated from the avalanche criteria [51].
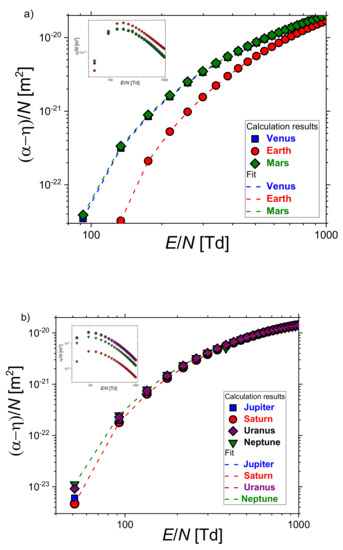
Figure 6.
The reduced effective ionization coefficients for the atmospheric gas mixture of the: (a) innermost and (b) outermost planets. Fit to the calculated data are shown by dash curves.

Table 1.
Calculated values of the coefficients A, B, the voltage and the pd value at the minimum of the breakdown curve are compared with corresponding data taken from [12].
The breakdown voltage curves for atmospheric compositions of the: (a) terrestrial and (b) Jovian planets are plotted in Figure 7. Breakdown voltages calculated by expression (8) with A and B determined in this study and from ref. [12] are shown by symbols and dash curves, respectively. All breakdown voltage curves follow the standard scaling law. The experimentally recorded Pachen curve for Mars [52] (crosses) agrees well with calculated values especially on the right-hand side of the curve.
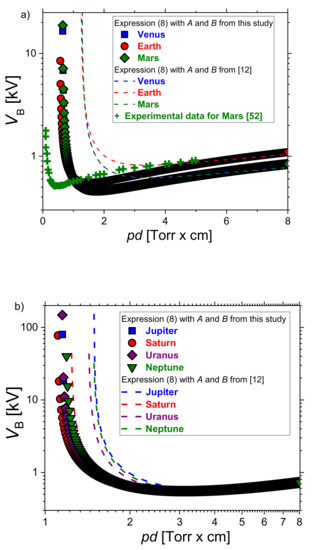
Figure 7.
The breakdown voltage curves for the atmosphere of the: (a) terrestrial and (b) Jovian planets. The results of measurements for the Martian atmosphere [52] are shown by crosses.
For each gas composition a minimum voltage required to achieve electric breakdown and corresponding pd value has been estimated from the condition dVB/d(pd) = 0 [51]:
and listed in Table 1. Calculated values are compared with the data from the literature [12]. A better agreement between our results and the data from the literature [12] for the minimum breakdown voltage is achieved for the terrestrial planets. For Venus and Mars, the divergence is less than 1%, while for the Earth is around 11%. The maximal discrepancy is obtained for Saturn, while for other Jovian planets varies between 23% and 27%. Since the breakdown voltage increases as the gas temperature decreases, larger values calculated for the outermost planets can be attributed to the lower atmospheric temperature. Unlike breakdown values, our calculations for the position of the pd at the minimum agree better with the literature [12] for the Jovian planets. For the innermost planets difference between our BOLSIG+ results and data from [12] ranges from 47% to 67. The large disagreement between calculated and theoretical values of the pd at the minimum can be explained by differences in the avalanche criteria used here [51] and in [12].
4. Conclusions
This paper contains the transport coefficients and the breakdown voltage curves of the atmospheres of the Solar System planets calculated by using BOLSIG+, a numerical solver for the Boltzmann equation. The ionization coefficients, the electron mean energy, and the electron energy distribution functions of the atmospheric compositions have been presented and analyzed. The results of two-term approximation (TTA) calculations for the ionization coefficients provide an insight into similarities and differences between the transport parameters that correspond to the gas mixtures representing the planetary atmospheres. For all energies, the ionizations of the innermost atmosphere gas mixtures are larger than those of the outermost planets. For the terrestrial planets, for all E/N values, the ionization coefficient of the Earth’s atmosphere is systematically lower than those of the Venusian and Martian atmospheres. Small differences between parameters of the Solar System’s outer planets can be explained by a small abundance of their constituent gases as compared to the abundances of hydrogen. Based on the dependence of the reduced effective ionization coefficient on the reduced electric field, the breakdown voltage curves have been determined. The results of calculations were validated using classic Paschen theory. The breakdown voltages required to create discharges in the atmospheres of the Jovian planets are higher than those in the innermost planet atmospheres. The lowest minimum breakdown voltage is obtained for the Martian atmosphere, while the highest value corresponds to Jupiter’s atmosphere. The difference between them is around 18%. The minimum breakdown voltage of the Martian atmosphere is lower about 16% than that of the Earth’s atmosphere. Values of the minimum breakdown voltage for all the solar system planets differ between 1% and 27%. The larger discrepancies between 2% up to 67% are obtained for the pd product at the minimum of the breakdown voltage curves. Since lightning is responsible for the failure of space launch vehicles, the obtained results could be useful for designs of electrical components on spacecraft. Enhanced computing capabilities evolved into a very powerful tool for extensive research of the planetary atmospheres [53]. Studies of atmospheric electricity are also motivated by a strong astrobiological context [54].
Author Contributions
Conceptualization, M.R.-R. and B.R.; methodology, M.R.-R.; software, B.R.; validation, M.R.-R., M.S. and B.R.; formal analysis, M.R.-R., M.S. and B.R.; investigation, M.R.-R., M.S. and B.R.; resources, M.R.-R.; data curation, M.R.-R.; writing—original draft preparation, M.R.-R.; writing—review and editing, M.R.-R.; visualization, B.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institute of Physics Belgrade, through the grant by the Ministry of Education, Science and Technological Development of the Republic of Serbia and Operational Programme Integrated Infrastructure for the project: Innovation through research into the integration of heterogeneous IoT systems using Smart Active Cloud technologies with high-level security (ITMS code: 313012Q938), co-funded by the European Regional Development Fund (ERDF).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge funding provided by the Institute of Physics Belgrade, through the grant by the Ministry of Education, Science and Technological Development of the Republic of Serbia. This publication has also been written thanks to the support of the Operational Programme Integrated Infrastructure for the project: Innovation through research into the integration of heterogeneous IoT systems using Smart Active Cloud technologies with high-level security (ITMS code: 313012Q938), co-funded by the European Regional Development Fund (ERDF).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Golombek, M.P. The Mars Pathfinder Mission. J. Geophys. Res. Planets 1997, 102, 3953–3965. [Google Scholar] [CrossRef]
- Squyres, S.W.; Arvidson, R.E.; Bell, J.F.; Brückner, J.; Cabrol, N.A.; Calvin, W.; Carr, M.H.; Christensen, P.R.; Clark, B.C.; Crumpler, L.; et al. The opportunity Rover’s Athena science investigation at Meridiani Planum, Mars. Science 2004, 306, 1698–1703. [Google Scholar] [CrossRef] [PubMed]
- Krapivin, V.F.; Varotsos, C.A.; Christodoulakis, J. Mission to Mars: Adaptive identifier for the solution of inverse optical metrology tasks. Earth Moon Planets 2016, 118, 1–14. [Google Scholar] [CrossRef]
- Chow, D. NASA’s Mars Rover Successfully Touches Down on the Red Planet. Available online: https://www.nbcnews.com/science/space/nasas-mars-rover-perseverance-touches-red-planet-rcna295 (accessed on 19 February 2021).
- Gibney, E. Rescued Japanese spacecraft delivers first results from Venus. Nature 2016, 532, 157–158. [Google Scholar] [CrossRef][Green Version]
- Barth, E. Planet CARMA: A new framework for studying the microphysics of planetary atmospheres. Atmosphere 2020, 11, 1064. [Google Scholar] [CrossRef]
- Inza, A.G.M.; Lopez-Reyes, G. Mars Exploration-A Step Forward; IntechOpen: London, UK, 2020. [Google Scholar]
- Mazur, V.; Moreau, J. Aircraft-triggered lightning: Processes following strike initiation that affect aircraft. J. Aircr. 1992, 29, 575–580. [Google Scholar] [CrossRef]
- Larsson, A. The interaction between a lightning flash and an aircraft in flight. Comptes Rendus Phys. 2002, 3, 1423–1444. [Google Scholar] [CrossRef]
- SKYbrary. Lightning. Available online: https://www.skybrary.aero/index.php/Lightning (accessed on 5 August 2019).
- Manning, H.; Kate, I.T.; Battel, S.; Mahaffy, P. Electric discharge in the Martian atmosphere, Paschen curves and implications for future missions. Adv. Space Res. 2010, 46, 1334–1340. [Google Scholar] [CrossRef]
- Helling, C.; Jardine, M.; Stark, C.R.; Diver, D.A. Ionization in atmospheres of brown dwarfs and extrasolar planets. III. breakdown conditions for mineral clouds. Astrophys. J. 2013, 767, 136. [Google Scholar] [CrossRef]
- Zahnle, K.; Schaefer, L.; Fegley, B. Earth’s earliest atmosphere. Cold Spring Harb. Perspect. Biol. 2010, 2, a004895. [Google Scholar] [CrossRef] [PubMed]
- Camprubí, E.; De Leeuw, J.W.; House, C.H.; Raulin, F.; Russell, M.J.; Spang, A.; Tirumalai, M.R.; Westall, F. The Emergence of Life. Space Sci. Rev. 2019, 215, 56. [Google Scholar] [CrossRef]
- Hodosán, G.; Helling, C.; Asensio-Torres, R.; Vorgul, I.; Rimmer, P.B. Lightning climatology of exoplanets and brown dwarfs guided by Solar system data. Mon. Not. R. Astron. Soc. 2016, 461, 3927–3947. [Google Scholar] [CrossRef]
- Pasko, V.P.; Yair, Y.; Kuo, C.L. Lighning related transient luminous events at high altitude in the Earth’s atmosphere: Phenomenology, mechanisms and effects. Space Sci. Rev. 2012, 168, 475–516. [Google Scholar] [CrossRef]
- Cooray, V. Interaction of lightning flashes with the Earth’s atmosphere. In An Introduction to Lightning; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Gurnett, D.A.; Shaw, R.R.; Anderson, R.R.; Kurth, W.S.; Scarf, F.L. Whistlers observed by Voyager 1: Detection of lightning on Jupiter. Geophys. Res. Lett. 1979, 6, 511–514. [Google Scholar] [CrossRef]
- Cook, A.F.; Duxbury, T.C.; Hunt, G.E. First results on Jovian lightning. Nature 1979, 280, 794. [Google Scholar] [CrossRef]
- Gurnett, D.A.; Kurth, W.S.; Cairns, I.H.; Granroth, L.J. Whistlers in Neptune’s magnetosphere: Evidence of atmospheric lightning. J. Geophys. Res. 1990, 95, 20967. [Google Scholar] [CrossRef]
- Yair, Y. New results on planetary lightning. Adv. Space Res. 2012, 50, 293–310. [Google Scholar] [CrossRef]
- Dubrovin, D.; Luque, A.; Gordillo-Vazquez, F.J.; Yair, Y.; Parra-Rojas, F.C.; Ebert, U.; Price, C. Impact of lightning on the lower ionosphere of Saturn and possible generation of halos and sprites. Icarus 2014, 241, 313–328. [Google Scholar] [CrossRef]
- Luque, A.; Gordillo-Vazquez, F.J.; Pallé, E. Ground-based search for lightning in Jupiter with GTC/OSIRIS fast photometry and tunable filters. Astron. Astrophys. 2015, 577, A94. [Google Scholar] [CrossRef]
- Giles, R.S.; Greathouse, T.K.; Bonfond, B.; Gladstone, G.R.; Kammer, J.A.; Hue, V.; Grodent, D.C.; Gérard, J.C.; Versteeg, M.H.; Wong, M.H.; et al. Possible transient luminous events observed in Jupiter’s upper atmosphere. J. Geophys. Res. Planets 2020, 125, e2020JE006659. [Google Scholar] [CrossRef]
- Scarf, F.L.; Taylor, W.W.L.; Russell, C.T.; Brace, L.H. Lightning on Venus: Orbiter detection of whistler signals. J. Geophys. Res. 1980, 85, 8158–8166. [Google Scholar] [CrossRef]
- Pérez-Invernón, F.J.; Luque, A.; Gordillo-Vázquez, F.J. Mesospheric optical signatures of possible lightning on Venus. J. Geophys. Res. Space Phys. 2016, 121, 7026–7048. [Google Scholar] [CrossRef]
- Brace, L.H.; Kliore, A.J. The structure of the Venus ionosphere. Space Sci. Rev. 1991, 55, 81–163. [Google Scholar] [CrossRef]
- Huba, J.D. Theory of small-scale density and electric field fluctuations in the nightside Venus ionosphere. J. Geophys. Res. Space Phys. 1992, 97, 43. [Google Scholar] [CrossRef]
- Moinelo, A.C.; Abildgaard, S.; Muñoz, A.G.; Piccioni, G.; Grassi, D. No statistical evidence of lightning in Venus night-side atmosphere from VIRTIS-Venus Express Visible observations. Icarus 2016, 277, 395–400. [Google Scholar] [CrossRef]
- Pérez-Invernón, F.J.; Lehtinen, N.G.; Gordillo-Vázquez, F.J.; Luque, A. Whistler wave propagation through the ionosphere of Venus. J. Geophys. Res. Space Phys. 2017, 122, 11633–11644. [Google Scholar] [CrossRef]
- Lorenz, R.D. Lightning detection on Venus: A critical review. Prog. Earth Planet. Sci. 2018, 5, 34. [Google Scholar] [CrossRef]
- Yair, Y.; Takahashi, Y.; Yaniv, R.; Ebert, U.; Goto, Y. A study of the possibility of sprites in the atmospheres of other planets. J. Geophys. Res. Planets 2009, 114, 09002. [Google Scholar] [CrossRef]
- Luque, A.; Dubrovin, D.; Vázquez, F.J.G.; Ebert, U.; Rojas, F.C.P.; Yair, Y.; Price, C. Coupling between atmospheric layers in gaseous giant planets due to lightning-generated electromagnetic pulses. J. Geophys. Res. Space Phys. 2014, 119, 8705–8720. [Google Scholar] [CrossRef]
- Riousset, J.A.; Nag, A.; Palotai, C. Scaling of conventional breakdown threshold: Impact for predictions of lightning and TLEs on Earth, Venus, and Mars. Icarus 2020, 338, 113506. [Google Scholar] [CrossRef]
- Yuan, T.; Remer, L.A.; Pickering, K.E.; Yu, H. Observational evidence of aerosol enhancement of lightning activity and convective invigoration. Geophys. Res. Lett. 2011, 38, 4701. [Google Scholar] [CrossRef]
- Borucki, W.J.; McKay, C.P. Optical efficiencies of lightning in planetary atmospheres. Nature 1987, 328, 509–510. [Google Scholar] [CrossRef] [PubMed]
- Yair, Y.; Levin, Z.; Tzivion, S. Lightning generation in a jovian thundercloud: Results from an axisymmetric numerical cloud model. Icarus 1995, 115, 421–434. [Google Scholar] [CrossRef]
- Fischer, G.; Kurth, W.S.; Dyudina, U.A.; Kaiser, M.L.; Zarka, P.; Lecacheux, A.; Ingersoll, A.P.; Gurnett, D.A. Analysis of a giant lightning storm on Saturn. Icarus 2007, 190, 528–544. [Google Scholar] [CrossRef]
- Fischer, G.; Gurnett, D.A.; Kurth, W.S.; Akalin, F.; Zarka, P.; Dyudina, U.A.; Farrell, W.M.; Kaiser, M.L. Atmospheric electricity at Saturn. Space Sci. Rev. 2008, 137, 271–285. [Google Scholar] [CrossRef]
- Dyudina, U.A.; Ingersoll, A.P.; Ewald, S.P.; Porco, C.C.; Fischer, G.; Kurth, W.S.; West, R.A. Detection of visible lightning on Saturn. Geophys. Res. Lett. 2010, 37, 09205. [Google Scholar] [CrossRef]
- Dyudina, U.A.; Ingersoll, A.P.; Ewald, S.P.; Porco, C.C.; Fischer, G.; Yair, Y. Saturn’s visible lightning, its radio emissions, and the structure of the 2009–2011 lightning storms. Icarus 2013, 226, 1020–1037. [Google Scholar] [CrossRef]
- Becker, H.N.; Alexander, J.W.; Atreya, S.K.; Bolton, S.J.; Brennan, M.J.; Brown, S.T.; Guillaume, A.; Guillot, T.; Ingersoll, A.P.; Levin, S.M.; et al. Small lightning flashes from shallow electrical storms on Jupiter. Nature 2020, 584, 55–58. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M. Coulomb collisions in the Boltzmann equation for electrons in low-temperature gas discharge plasmas. Plasma Sources Sci. Technol. 2016, 25, 015015. [Google Scholar] [CrossRef]
- Bolsig+. Electron Boltzmann Equation Solver Bolsig+. Available online: http://www.bolsig.laplace.univ-tlse.fr/download.html (accessed on 5 January 2021).
- Hagelaar, G.J.M. Brief Documentation of BOLSIG+ Version 03/2016. Available online: http://www.bolsig.laplace.univ-tlse.fr/wp-content/uploads/2016/03/bolsigdoc0316.pdf (accessed on 5 January 2021).
- The Atmospheres of the Solar System. Available online: https://www.compoundchem.com/2014/07/25/planetatmospheres/ (accessed on 25 July 2014).
- The Plasma Data Exchange Project. Available online: https://nl.lxcat.net/home/ (accessed on 5 January 2021).
- Marić, D.; Radmilović-Radjenović, M.; Petrović, Z.L. On parametrization and mixture laws for electron ionization Coefficients. Eur. Phys. J. D 2005, 35, 313–321. [Google Scholar] [CrossRef]
- Petri, A.; Goncalves, J.; Mangiarotti, A.; Botelho, S.; Bueno, C. Measurement of the first Townsend ionization coefficient in a methane-based tissue-equivalent gas. Nucl. Instrum. Methods Phys. Res. Sect. A 2017, 849, 31–40. [Google Scholar] [CrossRef]
- Engle, J.A.; Riousset, J.A. Numerical and analytical studies of critical radius in new geometries for corona discharge in air and CO2-rich environments. In Proceedings of the 2017 CEDAR Workshop, Workshop on Thunderstorm Coupling and Effects, Keystone, CO, USA, 22 June 2017; Available online: http://riousset.com/jeremy/wp-content/uploads/EngleCEDAR2017a.pdf (accessed on 4 February 2021).
- Calle, C.; Mackey, P.; Hogue, M.; Johansen, M.; Kelley, J.; Phillips, J.R., III; Clements, J.S. An electrostatic precipitator system for the Martian environment. J. Electrost. 2013, 71, 254–256. [Google Scholar] [CrossRef][Green Version]
- Rafkin, S.; Michaels, T. The Mars Regional Atmospheric Modeling System (MRAMS): Current status and future directions. Atmosphere 2019, 10, 747. [Google Scholar] [CrossRef]
- Fairén, A.G.; Parro, V.; Schulze-Makuch, D.; Whyte, L. Is Searching for Martian life a priority for the Mars community? Astrobiology 2018, 18, 101–107. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).