Abstract
CloudSat is often the only measurement of snowfall rate available at high latitudes, making it a valuable tool for understanding snow climatology. The capability of CloudSat to provide information on seasonal and subseasonal time scales, however, has yet to be explored. In this study, we use subsampled reanalysis estimates to predict the uncertainties of CloudSat snow water equivalent (SWE) accumulation measurements at various space and time resolutions. An idealized/simulated subsampling model predicts that CloudSat may provide seasonal SWE estimates with median percent errors below 50% at spatial scales as small as 2° × 2°. By converting these predictions to percent differences, we can evaluate CloudSat snowfall accumulations against a blend of gridded SWE measurements during frozen time periods. Our predictions are in good agreement with results. The 25th, 50th, and 75th percentiles of the percent differences between the two measurements all match predicted values within eight percentage points. We interpret these results to suggest that CloudSat snowfall estimates are in sufficient agreement with other, thoroughly vetted, gridded SWE products. This implies that CloudSat may provide useful estimates of snow accumulation over remote regions within seasonal time scales.
1. Introduction
Most snow that falls on the planet lands over remote and unpopulated terrain where few in situ measurements are available [1,2]. Understanding the amount of snow that falls in these regions is important since the Snow Water Equivalent (SWE) stored in remote snowpack can determine the freshwater supply for whole ecosystems and societies. Estimates of snow accumulation in remote regions are difficult to come by, however, and products that exist often carry large uncertainties. Reanalysis models or interpolated hydrological products rely on in situ SWE observations thousands of km apart, and SWE estimates between different methods can vary significantly [3]. Satellite measurements do not have a sampling discrepancy between inhabited and uninhabited terrain, so they are a logical choice for measuring snow in remote locations. Indeed, recent observations from the Gravity Recovery and Climate Experiment (GRACE-FO) have successfully been used to provide novel information on total snowpack in mountainous regions and high latitudes [4]. This measurement inherently combines all mass-change that occurs during a time period, however. If one is interested in total deposited snowfall, that information will be absorbed alongside any snowmelt, rain, evaporation, or blowing that occurs.
Integrated satellite precipitation estimates can theoretically be used to provide a purer measurement of the amount of snow that falls in a region over time. Passive microwave sensors provide the most frequent measurements of precipitation. These measurements have historically had errors over snow-covered surfaces, though recent algorithms are making strides in resolving this issue [5,6]. Satellite radar can provide estimates of surface precipitation rates over most kinds of terrain, as long as the topography is relatively smooth. CloudSat is the first satellite radar to provide global snowfall measurements [7]. The Dual Frequency Precipitation Radar (DPR [8]) on the GPM satellite has a maximum latitude that misses the highest latitudes where snow is most frequent, and it has a minimum detectability that prevents it from seeing over 90% of snowfall events on the planet [9,10]. CloudSat has been used to calculate the amount of snow falling across the entire planet [1,11] and to understand regional snowfall climatologies across mountain ranges [12], Antarctica [13], Greenland [14], Arctic Ice Sheets [15], and high latitude oceans [16,17,18]. CloudSat snowfall rates have also been used as a target for evaluations of snowfall in reanalyses [4,19] and climate models [20]. CloudSat retrievals have not yet been used to measure accumulations over discrete time periods, however. This may be due in part to perceived uncertainties from CloudSat’s infrequent coverage, but this uncertainty is currently ill-defined. If the uncertainty for CloudSat retrievals of monthly snowfall is within acceptable limits, it could open up new applications for satellite radar measurements of snowfall.
The purpose of this study is to determine the accuracy of CloudSat snow accumulation over discrete time periods at seasonal and subseasonal time scales. We predict this accuracy by drawing a distribution of percent errors in a modelled CloudSat global retrieval scenario. We evaluate our prediction by comparing real CloudSat snowfall accumulation estimates against a blend of best available estimates of SWE time-differences. CloudSat and surface SWE data sources are described in Section 2. The method to evaluate CloudSat products and SWE estimates is described in Section 3. Predictions of CloudSat accuracy are drawn in Section 4. CloudSat estimates of snow accumulation are evaluated in Section 5. The study is summarized in Section 6.
2. Data
2.1. CloudSat 2C-SNOW-PROFILE
CloudSat was launched on 28 April 2006. Only data from 2006–2015 are used in this study to be conterminous with the gridded SWE datasets (see Section 2.2). CloudSat has an orbital apogee of 81 degrees and repeats its orbital track roughly every 16 days. CloudSat carries the Cloud Profiling Radar (CPR), a W band (3.2 mm) radar with a minimum detectable reflectivity of −30 dBZ. CPR reflectivities are converted to snowfall rates via the 2C-SNOW-PROFILE [21]. This product relies on a Bayesian optimal estimation algorithm. The algorithm uses measurements of reflectivity and ECMWF analysis to update prior assumptions of microphysical properties and retrieve snowfall rates. The CloudSat snowfall rates are presented as lognormal snowfall probability distributions. The standard deviations of these distributions, herein referred to as the Bayesian uncertainty, tend to be between 150% and 250% of the mean value. CloudSat is still operating today, but observations have not been continuous. There are numerous gaps in the data record, particularly during 2009 and 2011 for winter snowfall. In 2012, CloudSat experienced a battery failure, and after the battery was repaired it operated in a “Daylight Only” mode that reduces the frequency of retrievals as a function of distance to the northern orbital peak. The loss of CloudSat snowfall measurements results in a bias of annual snowfall measurements from CloudSat after 2012 [22].
The Bayesian uncertainty is not the only source of error that can impact 2C-SNOW-PROFILE retrievals. If the ice crystals in a size distribution are not sufficiently small compared to the incident wavelength, non-Rayleigh scattering effects will dampen the relationship between W band reflectivity and snowfall rate, adding increasingly large uncertainties for snowfall rates at high reflectivity. Atmospheric gasses can attenuate W band reflectivity, but this effect is typically accounted for in the 2C-SNOW-PROFILE algorithm and can be safely ignored [23]. Attenuation due to liquid water may also be substantial in mixed phase clouds, and no attempt is made to identify or offset this attenuation. If there are an excessive number of snowflakes in a particle size distribution (PSD), multiple scattering effects may artificially increase the reflectivity of a PSD by introducing cross sections from snowflakes outside of the radar footprint. High snowflake concentration also increases W band attenuation in a fashion that tends to cancel out the increase due to multiple scattering [24]. Finally, the 2C-SNOW-PROFILE defines “surface precipitation rate” as the precipitation rate 1.25 km above the surface. This is done to remove the “blind zone” of spurious radar measurements that obfuscate precipitation reflectivity near the ground, but it will also remove information on any sublimation [25] or low-level precipitation development [26] that may occur within the boundary layer. The surface clutter will often spread beyond the 1.25 km threshold over mountains and cliffsides, and in these cases the 2C-SNOW-PROFILE flags a retrieval as unreliable.
2.2. Gridded SWE Products
Gridded SWE products are generated from forward models of SWE that are constrained by collocated observations at set time intervals. In this study, we use the Blended-4 (B4) gridded SWE product developed by the Canadian Sea Ice and Snow Evolution (CanSISE) network [3]. B4 contains daily northern hemisphere (NH) SWE on ground estimates from 2006 to 2015 at 0.5° resolution. The B4 product is the average (or blend) of four gridded SWE products: the Canadian Meteorological Center (CMC) gridded SWE product, CROCUS, GlobSnow (GS) and MERRA-2 (M2) datasets. The CMC dataset (updated by Ross Brown) provides daily estimates of gridded snow depth and SWE at ⅓ degree resolution [27]. Background field estimates are derived using a simple snowpack model as described in Brasnett [28] which is forced with six-hourly ECMWF two-meter air temperature and precipitation fields. The data are then interpolated to the grid using an optimal interpolation data assimilation scheme that ingests in situ data from approximately 8000 survey sites across North America (NA). CROCUS is a complex, physically based, energy and mass balance snow model developed by the National Centre for Meteorological Research (NCMR) at 1° resolution [29]. The CROCUS model operates as a replacement snow model in the Interactions between Soil, Biosphere, and Atmosphere (ISBA) land model, driven by ERA-Interim meteorology and provides daily estimates of SWE for multiple snow layers. The GS (version two) product developed by the European Space Agency (ESA) is the only satellite-based component of the B4 which provides daily estimates of SWE through a combination of in situ data and satellite temperature brightness (TB) measurements [30]. In situ snow depth observations are used to force a single layer snow emission model to simulate passive microwave estimates across the NH. Snow grain size is then estimated through the optimized agreement between simulated and observed satellite TB estimates, which are then kriged across the NH to produce a spatially contiguous map of assimilated SWE at 25 km resolution. This product is masked over alpine regions due to uncertainties related to microwave estimates over complex terrain. M2 is a reanalysis product developed by the National Aeronautics and Space Administration’s (NASA) Global Modeling and Assimilation Office (GMAO) [31]. M2 uses the Catchment land surface model and an intermediate complexity snow scheme to provide SWE estimates at 0.5° by 0.6° resolution. In situ data are ingested using a 3DVAR assimilation scheme of nearby surface observations, which is then used as forcing data for the Goddard Earth Observing System (GEOS) atmospheric model to derive gridded SWE estimates.
There are several sources of error in SWE data products. SWE can be underestimated at in situ stations due to “gauge undercatch”, whereby falling snow is not captured by the gauge opening during strong winds [32]. SWE products can have errors resulting from errors in modelled precipitation, especially for grid cells that are positioned further away from observation sites, since these have less information to constrain model estimates [29]. Various sources of error propagating from assumptions in forward models may also add uncertainty to final gridded SWE estimates [30]. The blending approach has been shown to reduce SWE uncertainty, however, as well as diminishing any overall bias from these effects [3,33,34,35,36,37,38].
2.3. Weather Observations and Reanlaysis
An hourly simulation of global precipitation is drawn from the NCAR Global Climate Four-Dimensional Data Assimilation (CFDDA) Hourly 40 km Reanalysis [39]. This Reanalysis provides estimates of total (combined water and liquid) precipitation at 0.4° increments. CFDDA incorporates hourly and six-hourly surface and upper air measurements. Land surface conditions such as surface temperature and soil moisture are initialized by the NASA Global Land Data Assimilation System and compiled using the Noah Land Surface Model (LSM). Sea surface temperatures are provided by the National Center for Environmental Prediction (NCEP) version 2.0 global and daily dataset. At the time of its creation, it was the highest temporally resolved reanalysis model. While newer reanalysis models such as ERA5 can now provide hourly reanalysis estimates with similar or higher resolution, the purpose of this reanalysis model is more to provide a realistic simulation of weather patterns than to account for the best approximation of real weather at any particular period in Earth’s history. CFDDA is sufficient for this purpose.
Daily maximum temperatures come from the Climate Prediction Center (CP) Global Daily Temperature dataset. This dataset is generated by National Oceanic and Atmospheric Administration/Ocean Atmospheric Research/Earth Science Research Laboratory (NOAA/OAR/ESRL) Physical Science Laboratory (PSL) in Boulder, Colorado. These temperatures represent a combination of weather station and satellite observations.
3. Method
As long as temperatures remain below freezing, the total snow that falls from the atmosphere during a time period should be comparable to the change in surface snow as measured at the beginning and end of that time period. We refer to both of these measurements as , assuming herein that ≥ 0. A B4 measurement of () is defined as the difference of SWE between any two consecutive days over the same grid cell,
with and referring to the final and initial B4 measurement of SWE. A Cloudsat measurement of () is defined as the average measured snowfall rate for a grid cell multiplied by the sample collection time,
with S representing a single snowfall rate retrieval, N representing the number of retrievals, and t representing the time period. Calculating and adds new uncertainties to the data sources. will have a Gaussian random error representing the different estimates from the constituent SWE products. In some measurements, had negative values. This could be due to sublimation/melting or random errors from the blending process. Either way, − cannot be evaluated against CloudSat, so these measurements are rejected from the study. The accuracy of relies on CloudSat gathering a representative average precipitation rate over a measurement time period. At finer spatiotemporal resolutions CloudSat snowfall estimates have larger disagreements with surface evaluations, since may be disproportionately impacted by non-precipitating periods or snowfall rates during individual storms that will often be stronger than average snowfall rates [34].
and are compared against each other at 20° × 5°, 10° × 5°, and 5° × 5° spatial resolutions, with the 10° × 5° and 5° × 5° nested inside of larger 20° × 5° grid cells, at 10-day, 20-day, and 30-day time periods. We draw comparison grid cells over relatively flat regions to prevent SWE and CloudSat errors that are linked with complex topography (Figure 1). In all of these regions, the average surface clutter within the range gates that determine CloudSat-retrieved surface snowfall rates are negligible.
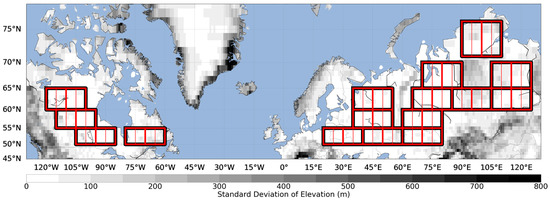
Figure 1.
Sample cells used to compare estimates from Cloudsat and B4. Black-bordered boxes represent to 20° × 5° cells, and red borders within black-bordered boxes represent 10° × 5° and 5° × 5° cells.
4. Estimated Accuracy of CloudSat Snow Accumulation Retrievals
Before evaluating CloudSat measurements using the method described in the previous section, we first generate predictions of CloudSat seasonal and subseasonal snow accumulation accuracy at varying resolutions. The process used to generate this prediction is visualized in Figure 2. CloudSat snowfall accumulation errors can be divided into two categories: sampling errors and retrieval errors. Retrieval errors can be further subdivided into Bayesian retrieval errors, which can be described by the probability distribution function accompanying retrievals in the 2C-SNOW-PROFILE, and non-Bayesian retrieval errors, which represent all other retrieval errors discussed in Section 2. Sampling errors are simulated by subsampling CloudSat orbit tracks from an arbitrary three-month period (January, February, and March of 2000) of hourly precipitation generated by CFDDA precipitation estimates (Figure 2a,b). Bayesian uncertainty is simulated by multiplying the measurements from each simulated satellite orbit with a random coefficient generated from a lognormal probability distribution function with a mean of 1 and a standard deviation of 200%. This corresponds to a typical Bayesian uncertainty from the 2C-SNOW-PROFILE. No attempt is made to simulate non-Bayesian retrieval errors, such as non-Rayleigh scattering or blind zone biases. This introduces some uncertainty, though such errors are expected to be infrequent over the sample grids used in this study–away from the mountains and water bodies typically responsible for snow storms with heavy precipitation or shallow cloud depths [2].
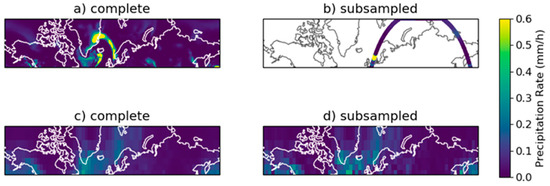
Figure 2.
Figure depicting the formation of monthly estimates of global precipitation through complete (a,c) and subsampled (b,d) CFDDA reanalysis. Subplots (a,b) represent a single hour, subplots (c,d) represents the average of all hours in a month.
In order to generate distributions of retrieval uncertainty, the CFDDA product and the simulated satellite retrievals are averaged at the same spatiotemporal resolutions (30 days and 10° × 5° as an example, in Figure 2c,d). The accuracy of can be estimated by calculating the distribution of percentage errors () at all grid cells for each space and time resolution,
with and referencing the full and subsampled grid cells from Figure 2c,d, respectively. These distributions are visualized as box-plot distributions for some example spatiotemporal resolutions in Figure 3. Note that the distributions in Figure 3 are presented without fliers (Figure 3 with fliers is presented in the Appendix A). This is done for visualization’s sake, as some fliers approach 10000%. The presence of these rare errors may be concerning, and they should be considered if CloudSat is to be used for seasonal or subseasonal measurements. However, these extreme errors did not exhibit any latitude dependence, indicating that they are more likely a result of the simulated Bayesian uncertainty rather than the sampling error. Since the simulated lognormal PDF is unbounded, it allows for the potential of extremely high errors that do not occur in CloudSat retrievals. This is an admitted flaw of the simulation. We do not believe it will strongly impact the quantitative results of this study, however, since it primarily affects outliers, and the results of this section will be evaluated in terms of percentiles.
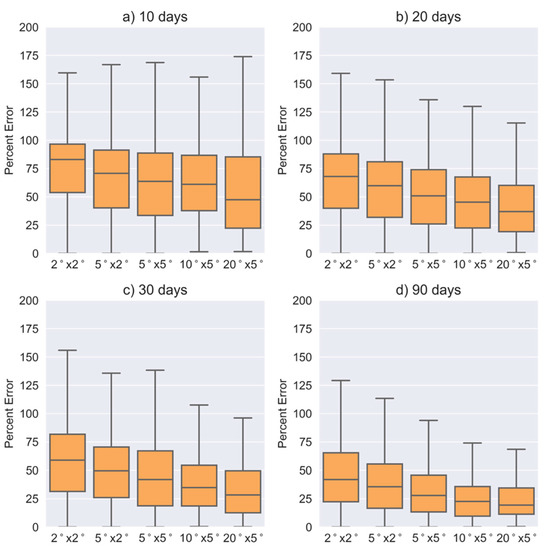
Figure 3.
Box and whisker plots describing the distributions between complete and subsampled CFDDA precipitation reanalysis estimates at different spatial resolutions for 10 (a), 20 (b), 30 (c) and 90 (d) day time periods. The middle line representing the median , the box edges represent the first and third quartile, and the edges of the “whiskers” are extended 1.5 times the interquartile range beyond the first and third quartiles. Data beyond the whisker boundaries are not visualized.
On seasonal time scales, is predicted to have median near 50% at the smallest spatial scale of 2° × 2°, and near 20% at the largest spatial scale of 20° × 5°. On monthly time scales, estimated median are still near 50% at spatial scales as small as 5° × 2°. These estimates are not weighted by sampling frequency, so they are likely larger or smaller depending on latitude. Whisker ranges are typically several times larger between the 75th and 95th percentiles than the 5th and 25th percentile, indicating again that errors may often be considerable even if median errors are relatively low. The overall picture is that theoretical accuracy improves, and the variation of errors decreases, with increasing spatial and temporal scale.
PE distributions cannot be directly evaluated, however, since the gridded B4 product carries too much uncertainty to be considered as a . An alternative measurement of uncertainty that can be evaluated against measured data is the percentage differences (),
with and here representing the full and subsampled grid cells from Figure 2c,d, respectively. Box plots of predicted distributions are provided in Figure 4. The 90-day distributions are not calculated since there are no 90-day frozen time periods that can be used to generate cells for evaluation. As an example, if a CloudSat measurement could retrieve a snowfall accumulation of 20 mm with a median percent difference error of 50%, the true snow accumulation would be between 12 and 33 mm half of the time.
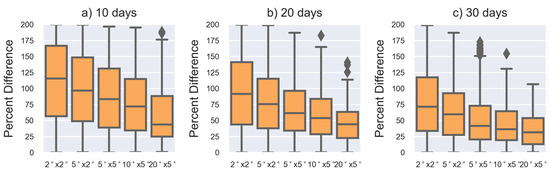
Figure 4.
As in Figure 3, but with for 10 (a), 20 (b), and 30 (c) day time periods. Fliers (measurements beyond the whisker range) are visualized.
It should be noted that the reanalysis model may not be capturing a natural distribution of snowfall rates. In particular, the heaviest snowfall rates that occur at the finest resolutions may not be well represented in an hourly gridded model. This discrepancy between natural and re-analysis estimated precipitation rates may adversely influence our simulations of CloudSat snowfall retrieval error distributions. Since the purpose of this simulation is just to recreate sampling and relative errors, it is also possible that heavier snowfall events would have no noticeable effect on results. Regardless, such extreme precipitation would be rare events, and they are not expected to impact the central distribution of the median, first, and third percentile in the displayed plots.
5. Evaluation of CloudSat Snow Accumulation Estimates
We evaluate our predicted CloudSat accuracy by comparing collocated ∆SWEC with . Evaluations are presented at all combinations of 5° × 5°, 10° × 5°, and 20° × 5° and 10-day, 20-day, and 30-day resolutions in Figure 5. can vary by two orders of magnitude and the differences between and are heteroscedastic, so results are presented on a log-log scale. There is a visible agreement between the two measurements of in all panels, though the correlation decreases with finer space and time resolutions. The strongest correlation coefficient of 0.8 occurs for 20° × 5° grid cells on 20 and 30 day time periods. The next highest correlation coefficient (0.7) comes for 10° × 5° grid cells on 30 day time periods. The lowest observed correlation coefficient is 0.4 at 5° × 5° grid cells over 10 day time periods.
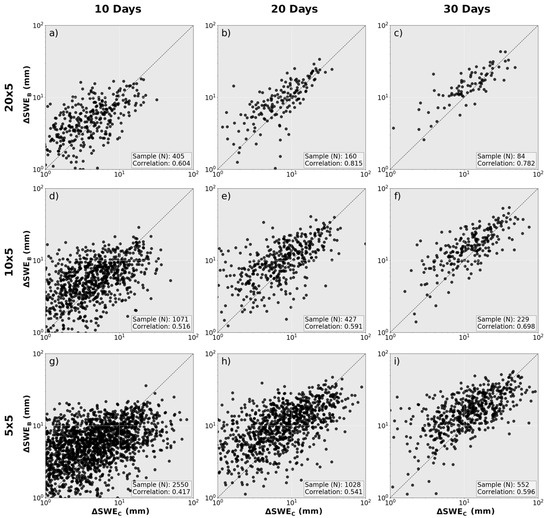
Figure 5.
Comparisons between B4 and CloudSat estimates of at different spatiotemporal resolutions. Subplots (a,d,g) have 10 day time periods. Subplots (b,e,h) have 20 day time periods. Subplots (c,f,i) have 30 day time periods, Subplots (a–c) have 20° × 5° spatial resolution. Subplots (d–f) have 10° × 5° spatial resolution. Subplots (g–i) have 5° × 5° spatial resolution.
At resolutions that provided relatively well correlated datasets, values tend to be larger when measured by B4. For 20° × 5° resolutions, this bias is fairly consistent along the domain. At finer resolutions, the relationship between and appears to be skewed; the maximum tends to be lower than the maximum while becomes disproportionately larger at low . This behavior is likely related to undersampled CloudSat measurements. If a grid cell is not adequately capturing the average precipitation rate during a sample period, a chance observation of a few storms may lead to an anomalously high . If significant storms are missed, it may lead to an anomalously low . A simpler interpretation may also be that becomes uncorrelated with when CloudSat measurements are too sparse to provide meaningful snow accumulation information. Indeed, within the finest spatiotemporal resolutions tested (10 days, 5° × 5°), the correlation coefficient increases with increasing sampling frequency at higher latitudes; the correlation coefficient between log-transformed and increases from 0.4, 0.5, and 0.6 as the along central grid latitudes increases from 62.5, 67.5, and 72.5.
The differences between biases and correlations in different datasets may also reflect conditional biases on CloudSat or B4 estimates. For example, one might expect a low-bias from CloudSat at warmer temperatures when retrieved snowfall rates would be largest [40]. To investigate this possibility, we consider three sensitivities in Figure 6: A regional sensitivity, a sampling sensitivity, and a temperature sensitivity. Regions represent different longitude spans. NA (North America) refers to any central longitude less than 0, EA (Eurasia) refers to any central longitude less between 0° and 60°, ES (East Siberia) refers to the region between 60° and 90°, and WS (West Siberia) refers to any longitude greater than 90°. Sampling sensitivity is measured in terms of an overpass ratio, representing the relative number of days during a sampling period that a Cloudsat Measurement was conducted. Overpass ratio is mostly a function of latitude, but it will also be impacted by the 2012 battery anomaly. Temperature is represented by the maximum temperature during a grid cell measurement.
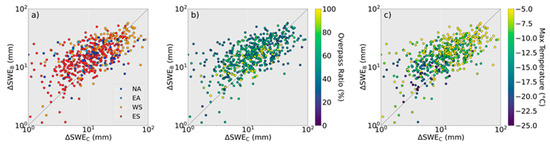
Figure 6.
Collocated measurements for 10° × 5° grid cells at one month resolution, as in Figure 5, but colored with respect to region (a), overpass ratio (b), and maximum temperature (c).
These sensitivity tests do not reveal any obvious biases that are not better described through decreased correlation. Warmer temperatures lead to larger snowfall accumulations, though this could be expected without looking at any data. From a climate standpoint, it is interesting that EA contains the largest wide-scale accumulations of snow and the warmest frozen 30-day time periods in our North-Hemispheric dataset. Looking at Figure 6b, it appears that grid cells with a higher overpass frequency also have a stronger correlation. This is predictable for the same reason that correlations generally increased with increasing spatiotemporal resolution, though it does motivate a new presentation of results that accounts for differences in spatiotemporal resolution and latitude. Figure 7 presents the correlation coefficient of the nine resolutions from Figure 5, with datasets subset by central latitude.
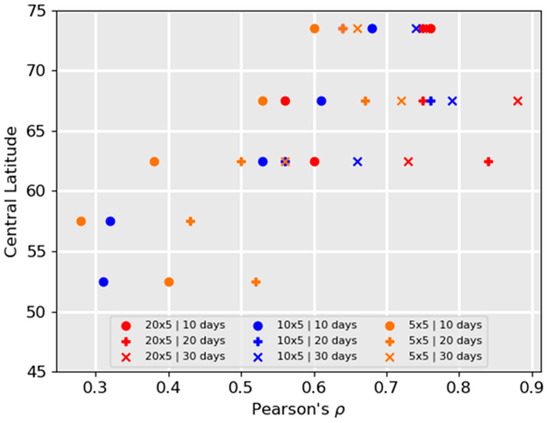
Figure 7.
Correlation coefficients of collocated and datasets at the nine spatiotemporal resolutions considered in this study, subset by latitude ranges. Data are plotted at the central latitude of a grid cell. Data points are only included at a given central latitude if measurements exist and if the p value corresponding to the correlation coefficient of the measurements is less than 0.01.
The correlation coefficients paint an expected picture: correlation increases with decreasing spatiotemporal resolution and higher latitudes. Of course, the two are not totally independent, since grid cells will decrease in physical area with increasing area. Note that there are great variations in the number of measurements and range of within datasets, and while data are only presented if they provide a p-value less than 0.01, these differences likely still influence the results for data subsets with particularly low volumes. Additionally, note that the different latitudes represent different numbers of grid cells that are providing data. The 70–75° N grid is entirely comprised of one 20° × 5° cell in northern Siberia (Figure 1) and there were no 20° × 5° grid cells that provided consistently freezing time periods below 60° N. Figure 7 does demonstrate, however, that the results from Figure 5 are likely more intricate than they appear. The 5° × 5° data 10-day data, which has the most data points and can be expected to be the most statistically robust measurement at all central latitudes, has a stronger correlation at 75° N than any represented dataset (5 × 5° 10 days, 10° × 5° 10 days, 5° × 5° to days) below 60° N, for example. Therefore, one can expect higher accuracy for finer spatiotemporal resolutions closer to the poles [38].
Finally, the collocated and are converted into percentage differences (Equation (4)) so that they can be used to evaluate the predicted CloudSat accuracy from Section 4. Measured distributions are presented alongside the simulated distributions from Section 4 in Figure 8. The measured accuracy (orange boxes) is in very good agreement with the simulated accuracy (blue boxes). Differences between the 25th, 50th, and 75th percentiles of measured and simulated distributions at all resolutions are less than 8%. This agreement is particularly remarkable considering that the initial predictions were based off two simulated precipitation products generated from the same model data, whereas the and products represent two independent datasets with their own biases and uncertainties.
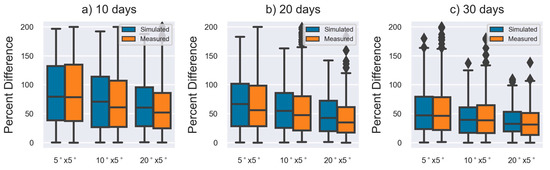
Figure 8.
Orange box and whisker plots represent the measured distributions between B4 and CloudSat estimates of for 10 day (a), 20 day (b), and 30 day (c) time periods. Simulated distributions from Figure 4 are provided for comparison in blue.
Since the PE predictions in Figure 2 are a reconfiguration of the same data in Figure 3, we interpret Figure 8 to suggest our subsampling method provides confident estimates of uncertainty for seasonal and subseasonal time scales. In other words, we conclude that CloudSat can provide measurements of snow accumulation over wide areas with a predictable accuracy.
6. Summary
Active satellite radars such as CloudSat’s CPR have a unique skill in providing radar profiles that can perform with similar accuracy over level ocean, land, ice, and snow-covered terrain. In this paper, we evaluated the potential of CloudSat to measure seasonal snowfall accumulation.
Using a simulation of global CloudSat snowfall rate retrievals, we generated a distribution of percentage errors at different spatial and temporal scales. We found that CloudSat seasonal snowfall accumulation measurements could have reasonable accuracy at different spatiotemporal resolutions, with median percent errors within 50% at 2° × 2° spatial scales as one example. To evaluate these predictions, we recast the uncertainty estimates into percentage differences so that CloudSat estimates could be compared against a best estimate of surface snowfall accumulation from the B4 gridded SWE model dataset. We also defined a common variable () that could be interpreted as the integration of the average snowfall rate from CloudSat or as the difference between gridded SWE at the beginning and end of a time period as long as temperatures remained below freezing.
We found 84 to 2550 collocated ∆SWE observations that were usable for evaluation, depending on resolution constraints. Correlation coefficients between CloudSat and B4 measured range between 0.4–0.8 from the finest (10 day, 5° × 5°) to the coarsest (30 day, 20° × 5°) resolution. Overall, the distribution of errors between CloudSat and B4 agreed very well with the predicted values; the 25th, 50th, and 75th percentile of percent-differences between measured and were within several percentage points of the predicted values at all resolutions. Based on the success of our percentage difference predictions, we infer that the predictions of percentage error from the same data are similarly reliable. While a direct evaluation of CloudSat accumulation estimates over large spatial scales is not possible with our method, we believe this study strongly supports the capability of CloudSat to measure snow accumulation with a quantifiable accuracy at arbitrary space and time scales. We aim to find ways to decrease the uncertainty of and increase the data available for evaluations in follow-up studies.
The results of this study can only be considered applicable in regions that are similar to our sample grids—flat terrain (land or ocean). This study makes no predictions on the ability of CloudSat to measure accumulations over mountainous terrain, which would must be properly validated before examining CloudSat-derived snow information over areas of high elevation, such as Antarctica. However, we note that Antarctica, in particular, presents a host of other issues for snow-accumulation measurements, including a greater effect of post-battery-anomaly CloudSat measurement losses [21,40] and a greater impact of blowing snow on regional accumulation totals [41].
Author Contributions
Conceptualization, G.D.; methodology, G.D.; coding, G.D., F.K.; data generation, G.D., F.K.; writing—original draft preparation, G.D.; writing—review and editing, G.D., F.K., R.B., C.G.F.; supervision, R.B., C.G.F. All authors have read and agreed to the published version of the manuscript.
Funding
George Duffy was supported by NASA Earth and Space Science Fellowship NNX14AK91H under Ming-Ying Wei and Claire McKauley. This work was supported by the NASA Modeling, Analysis, and Prediction program Grant NH16ZDA001N-MAP.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
NOAA temperature data is available from https://psl.noaa.gov. CFDDA reanalysis is available from https://rda.ucar.edu/datasets/ds604.0. CloudSat data is available from http://www.cloudsat.cira.colostate.edu/. All SWE products from the B4 dataset can be found in their respective citations.
Acknowledgments
The research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (80NM0018D0004).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
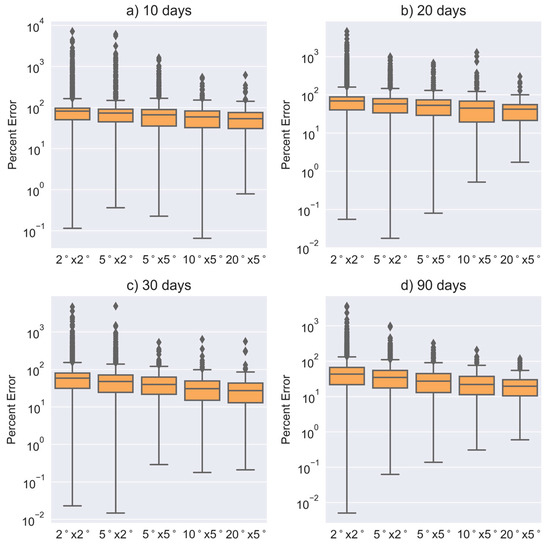
Figure A1.
Box and whisker plots describing the distributions between complete and subsampled CFDDA precipitation reanalysis estimates at different spatial resolutions for 10 (a), 20 (b), 30 (c) and 90 (d) day time periods The middle line representing the median , the box edges represent the first and third quartile, and the edges of the “whiskers” are extended 1.5 times the interquartile range beyond the first and third quartiles. Measurements beyond the whiskers are represented as “fliers”.
References
- Liu, G. Deriving snow cloud characteristics from CloudSat observations. J. Geophys. Res. Atmos. 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Behrangi, A.; Christensen, M.; Richardson, M.; Lebsock, M.; Stephens, G.; Huffman, G.J.; Bolvin, D.; Adler, R.F.; Gardner, A.; Lambrigtsen, B.; et al. Status of high-latitude precipitation estimates from observations and reanalyses. J. Geophys. Res. Atmos. 2016, 121, 4468–4486. [Google Scholar] [CrossRef] [PubMed]
- Mudryk, L.R.; Derksen, C.; Kushner, P.J.; Brown, R. Characterization of Northern Hemisphere snow water equivalent datasets, 1981–2010. J. Clim. 2015, 28, 8037–8051. [Google Scholar] [CrossRef]
- Behrangi, A.; Richardson, M. Observed High-Latitude Precipitation Amount and Pattern and CMIP5 Model Projections. Remote Sens. 2018, 10, 1583. [Google Scholar] [CrossRef]
- Rysman, J.-F.; Panegrossi, G.; Sanò, P.; Marra, A.C.; Dietrich, S.; Milani, L.; Kulie, M.S.; Casella, D.; Camplani, A.; Claud, C.; et al. Retrieving surface snowfall with the gpm microwave imager: A new module for the slalom algorithm. Geophys. Res. Lett. 2019, 46, 13593–13601. [Google Scholar] [CrossRef]
- Adhikari, A.; Ehsani, M.R.; Song, Y.; Behrangi, A. Comparative assessment of snowfall retrieval from Microwave Humidity Sounders using machine learning methods. Earth Space Sci. 2020, 7, e2020EA001357. [Google Scholar] [CrossRef]
- Stephens, G.L.; Vane, D.G.; Boain, R.J.; Mace, G.G.; Sassen, K.; Wang, Z.; Illingworth, A.J.; O’Connor, E.J.; Rossow, W.B.; Durden, S.; et al. The cloudsat mission and the A-Train: A new dimension of space-based observations of clouds and precipitation. Bull. Am. Meteorol. Soc. 2002, 83, 1771–1790. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kulie, M.; Milani, L.; Munchak, S.J.; Wood, N.B.; Levizzani, V. Satellite Estimation of Falling Snow: A Global Precipitation Measurement (GPM) Core Observatory Perspective. J. Appl. Meteorol. Climatol. 2019, 58, 1429–1448. Available online: https://journals.ametsoc.org/view/journals/apme/58/7/jamc-d-18-0124.1.xml (accessed on 31 January 2021). [CrossRef]
- Casella, D.; Panegrossi, G.; Sanò, P.; Marra, A.; Dietrich, S.; Johnson, B.; Kulie, M. Evaluation of the GPM-DPR snowfall detection capability: Comparison with CloudSatCPR. Atmos. Res. 2017, 197, 64–75. Available online: http://www.sciencedirect.com/science/article/pii/S0169809516304677 (accessed on 3 February 2021). [CrossRef]
- Daloz, A.; Mateling, M.; L’Ecuyer, T.; Kulie, M.S.; Wood, N.B.; Durand, M.; Wrzesien, M.; Stjern, C.W.; Dimri, A.P. How much snow falls in the world’s mountains? A first look at mountain snowfall estimates in A-train observations and reanalyses. Cryosphere 2020, 14, 3195–3207. [Google Scholar] [CrossRef]
- Palerme, C.; Kay, J.E.; Genthon, C.; L’Ecuyer, T.; Wood, N.B.; Claud, C. How much snow falls on the Antarctic ice sheet? Cryosphere 2014, 8, 1577–1587. [Google Scholar] [CrossRef]
- Bennartz, R.; Fell, F.; Pettersen, C.; Shupe, M.; Schuettemeyer, D. Spatial and temporal variability of snowfall over Greenland from CloudSat observations. Atmos. Chem. Phys. 2019, 19, 8101–8121. [Google Scholar] [CrossRef]
- Cabaj, A.; Kushner, P.J.; Fletcher, C.G.; Howell, S.; Petty, A.A. Constraining reanalysis snowfall over the Arctic Ocean using CloudSat observations. Geophys. Res. Lett. 2020, 47, e2019GL086426. [Google Scholar] [CrossRef]
- Duffy, G.; Bennartz, R. The Role of Melting Snow in the Ocean Surface Heat Budget. Geophys. Res. Lett. 2018, 9782–9789. [Google Scholar] [CrossRef]
- Kulie, M.S.; Milani, L.; Wood, N.B.; Tushaus, S.A.; Bennartz, R.; L’Ecuyer, T.S. A Shallow Cumuliform Snowfall Census Using Spaceborne Radar. J. Hydrometeorol. 2016, 17, 1261–1279. [Google Scholar] [CrossRef]
- Milani, L.; Kulie, M.S.; Casella, D.; Dietrich, S.; L’Ecuyer, T.S.; Panegrossi, G.; Porcù, F.; Sanò, P.; Wood, N.B. CloudSat snowfall estimates over Antarctica and the Southern Ocean: An assessment of independent retrieval methodologies and multi-year snowfall analysis. Atmos. Res. 2018, 213, 121–135. [Google Scholar] [CrossRef]
- Palerme, C.; Claud, C.; Dufour, A.; Genthon, C.; Wood, N.B.; L’Ecuyer, T. Evaluation of Antarctic snowfall in global meteorological reanalyses. Atmos. Res. 2017, 190, 104–112. [Google Scholar] [CrossRef]
- Palerme, C.; Genthon, C.; Claud, C.; Kay, J.E.; Wood, N.B.; L’Ecuyer, T. Evaluation of current and projected Antarctic precipitation in CMIP5 models. Clim. Dyn. 2017, 48, 225–239. [Google Scholar] [CrossRef]
- Wood, N.B.; L’Ecuyer, T.S.; Vane, D.G.; Stephens, G.L.; Partain, P. Level 2C Snow Profile Process Description and Interface Control Document,. CloudSat Project, (D). Available online: http://www.cloudsat.cira.colostate.edu/sites/default/files/products/files/2C-SNOW-PROFILE_PDICD.P1_R05.rev0_.pdf (accessed on 3 February 2021).
- Milani and Wood 2019: CloudSat Bias on Falling Snow Estimates over the Daylight Only Operational Period (2012–2019). AGU Fall Meeting 2019. Available online: https://core.ac.uk/download/pdf/286392927.pdf (accessed on 3 February 2021).
- Chen, S.; Hong, Y.; Kulie, M.; Behrangi, A.; Stepanian, P.M.; Cao, Q.; You, Y.; Zhang, J.; Hu, J.; Zhang, X. Comparison of snowfall estimates from the NASA CloudSat Cloud Profiling Radar and NOAA/NSSL Multi-Radar Multi-Sensor System. J. Hydrol. 2016, 541, 862–872. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Battaglia, A. Influence of multiple scattering on CloudSat measurements in snow: A model study. Geophys. Res. Lett. 2009, 36, 2–5. [Google Scholar] [CrossRef]
- Grazioli, J.; Madeleine, J.-B.; Gallée, H.; Forbes, R.M.; Genthon, C.; Krinner, G.; Berne, A. Katabatic winds diminish precipitation contribution to the Antarctic ice mass balance. Proc. Natl. Acad. Sci. USA 2017, 201707633. [Google Scholar] [CrossRef] [PubMed]
- Maahn, M.; Burgard, C.; Crewell, S.; Gorodetskaya, I.V.; Kneifel, S.; Lhermitte, S.; Tricht, K.V.; van Lipzig, N.P.M. How does the spaceborne radar blind zone affect derived surface snowfall statistics in polar regions? J. Geophys. Res. Atmos. 2014, 119, 13. [Google Scholar] [CrossRef]
- Brown, R.D.; Brasnett, B.; Robinson, D. Gridded North American monthly snow depth and snow water equivalent for GCM evaluation. Atmos.-Ocean 2003, 41, 1–14. [Google Scholar] [CrossRef]
- Brasnett, B. A Global Analysis of Snow Depth for Numerical Weather Prediction. J. Appl. Meteorol. 1999, 38, 726–740. [Google Scholar] [CrossRef]
- Brun, E.; Martin, E.; Simon, V.; Gendre, C.; Coleou, C. An Energy and Mass Model of Snow Cover Suitable for Operational Avalanche Forecasting. J. Glaciol. 1989, 35, 333–342. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.P.; Koskinen, J.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Rasmussen, R.; Wolff, M.; Baker, B.; Hall, M.E.; Meyers, T.; Landolt, S.; Jachcik, A.; Isaksen, K.; Brækkan, R.; et al. The quantification and correction of wind-induced precipitation measurement errors. Hydrol. Earth Syst. Sci. 2017, 21, 1973–1989. [Google Scholar] [CrossRef]
- Mekis, E.; Donaldson, N.; Reid, J.; Zucconi, A.; Hoover, J.; Li, Q.; Nitu, R.; Melo, S. An overview of surface-based precipitation observations at environment and climate change Canada. Atmos.-Ocean 2018, 56, 71–95. [Google Scholar] [CrossRef]
- Solman, S.A.; Sanchez, E.; Samuelsson, P.; da Rocha, R.P.; Li, L.; Marengo, J.; Pessacg, N.L.; Remedio, A.R.C.; Chou, S.C.; Berbery, H.; et al. Evaluation of an ensemble of regional climate model simulations over South America driven by the ERA-Interim reanalysis: Model performance and uncertainties. Clim. Dyn. 2013, 41, 1139–1157. [Google Scholar] [CrossRef]
- Orsolini, Y.J.; Senan, R.; Balsamo, G.; Doblas-Reyes, F.J.; Vitart, F.; Weisheimer, A.; Carrasco, A.; Benestad, R.E. Impact of snow initialization on sub-seasonal forecasts. Clim. Dyn. 2013, 41, 1969–1982. [Google Scholar] [CrossRef]
- Quets, J.; De Lannoy, G.J.; Al Yaari, A.; Chan, S.; Cosh, M.H.; Gruber, A.; Reichle, R.H.; Van der Schalie, R.; Wigneron, J.P. Uncertainty in soil moisture retrievals: An ensemble approach using SMOS L-band microwave data. Remote Sens. Environ. 2019, 229, 133–147. [Google Scholar] [CrossRef]
- Oozeer, Y.; Fletcher, C.G.; Champagne, C. Evaluation of Satellite-Derived Surface Soil Moisture Products over Agricultural Regions of Canada. Remote Sens. 2020, 12, 1455. [Google Scholar] [CrossRef]
- King, F.; Fletcher, C.G. Using CloudSat-CPR retrievals to estimate snow accumulation in the Canadian Arctic. Earth Space Sci. 2020, 7, e2019EA000776. [Google Scholar] [CrossRef]
- Rife, D.L.; Pinto, J.O.; Monaghan, A.J.; Davis, C.A.; Hannan, J.R. NCAR Global Climate Four-Dimensional Data Assimilation (CFDDA) Hourly 40 km Reanalysis; The National Center for Atmospheric Research, Computational and Information Systems Laboratory: Boulder, CO, USA, 2014. [Google Scholar] [CrossRef]
- Norin, L.; Devasthale, A.; L’Ecuyer, T.S.; Wood, N.B.; Smalley, M. Intercomparison of snowfall estimates derived from the CloudSat Cloud Profiling Radar and the ground-based weather radar network over Sweden. Atmos. Meas. Tech. 2015, 8, 5009–5021. [Google Scholar] [CrossRef]
- Souverijns, N.; Gossart, A.; Lhermitte, S.; Gorodetskaya, I.V.; Grazioli, J.; Berne, A.; Duran-Alarcon, C.; Boudevillain, B.; Genthon, C.; Scarchilli, C.; et al. Evaluation of the CloudSat surface snowfall product over Antarctica using ground-based precipitation radars. Cryosphere 2018, 12, 3775–3789. [Google Scholar] [CrossRef]
- Palerme, C.; Claud, C.; Wood, N.B.; L’Ecuyer, T.; Genthon, C. How Does Ground Clutter Affect CloudSat Snowfall Retrievals over Ice Sheets? IEEE Geosci. Remote Sensing Lett. 2019, 16, 342–346. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).