Snow Processes and Climate Sensitivity in an Arid Mountain Region, Northern Chile
Abstract
1. Introduction
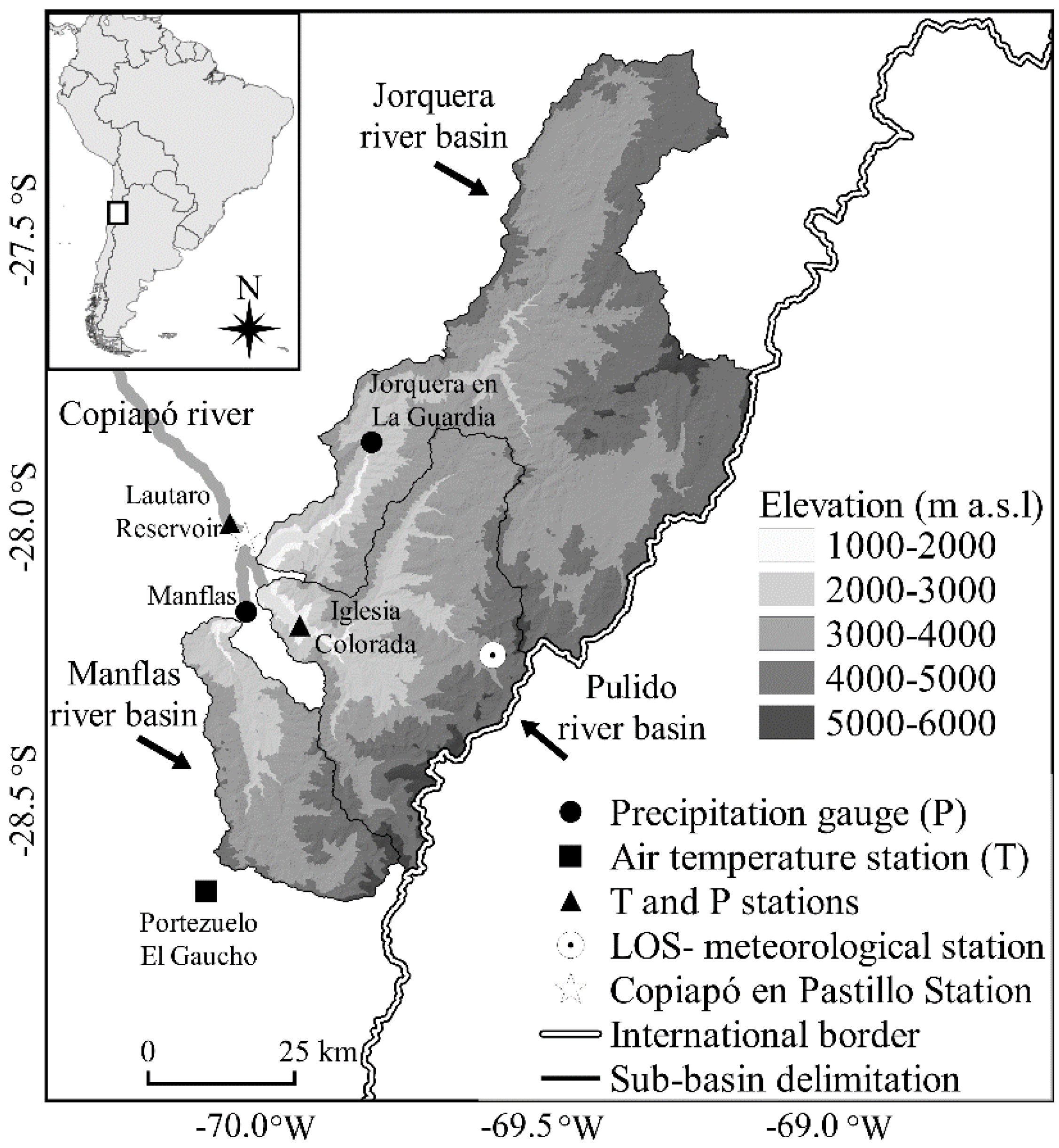
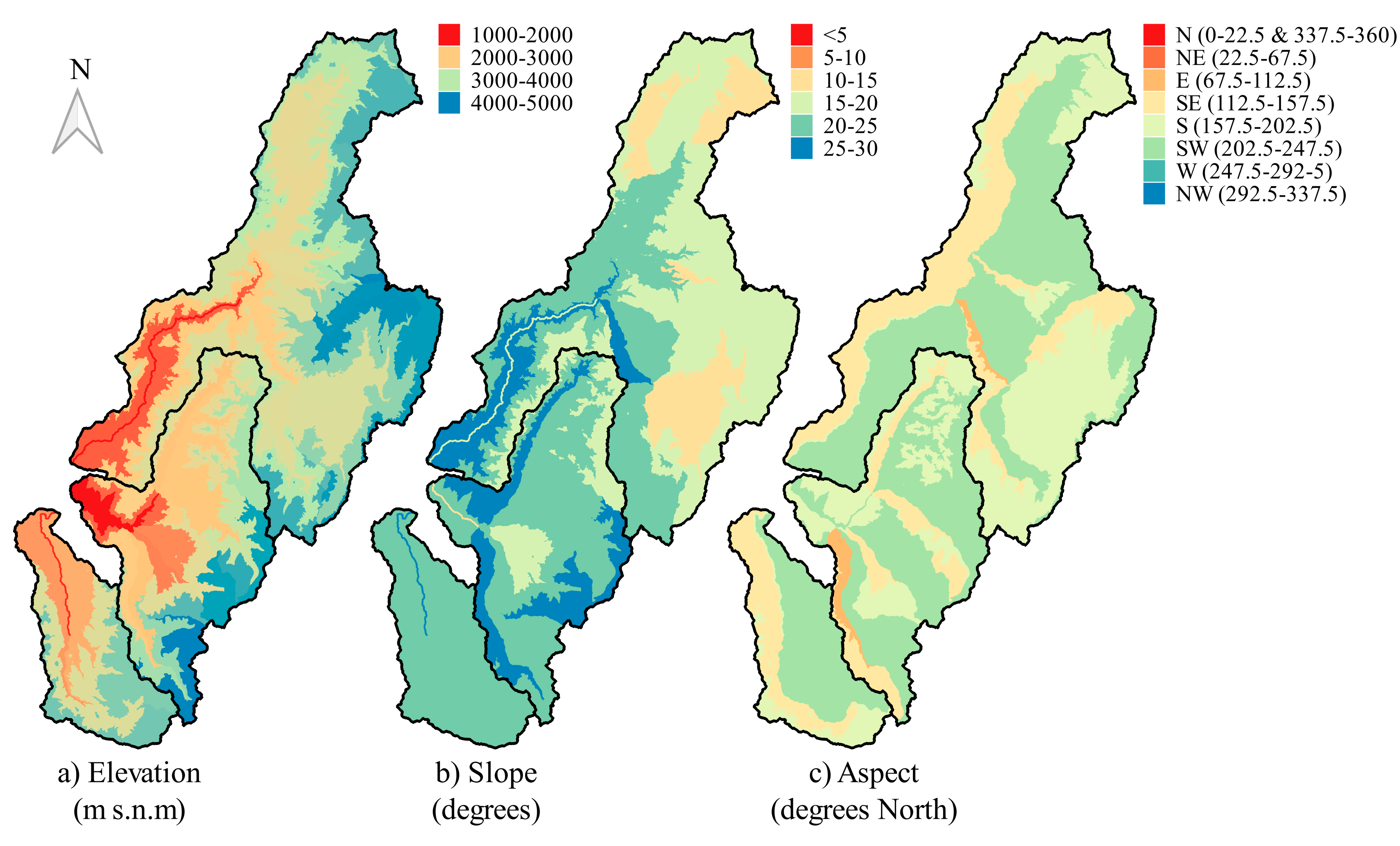
2. Study Area and Available Data
2.1. La Ollita Snow and Meteorological Station (LOS)
2.2. Hydrometeorological Network
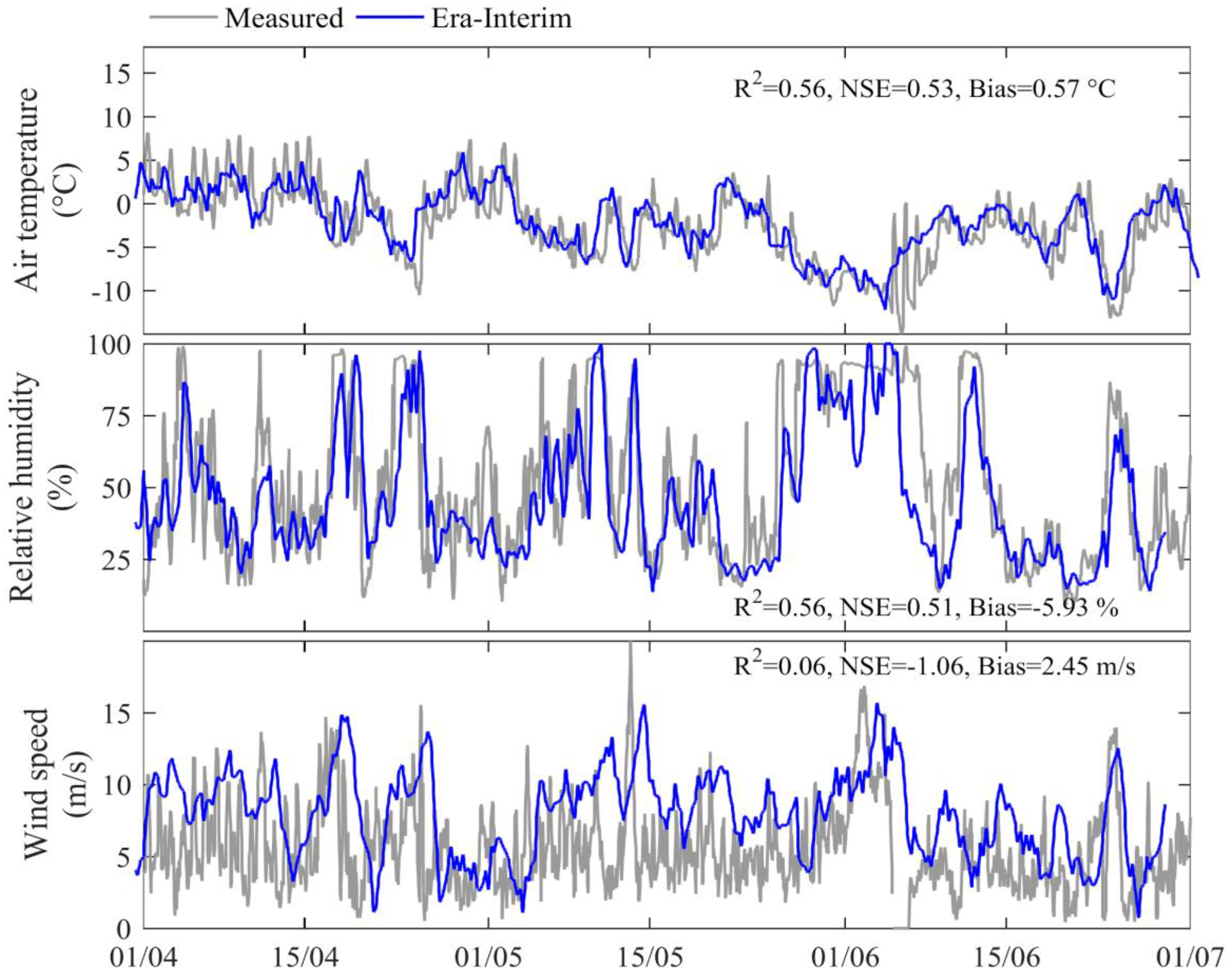
2.3. Reanalysis Data
3. Methodology
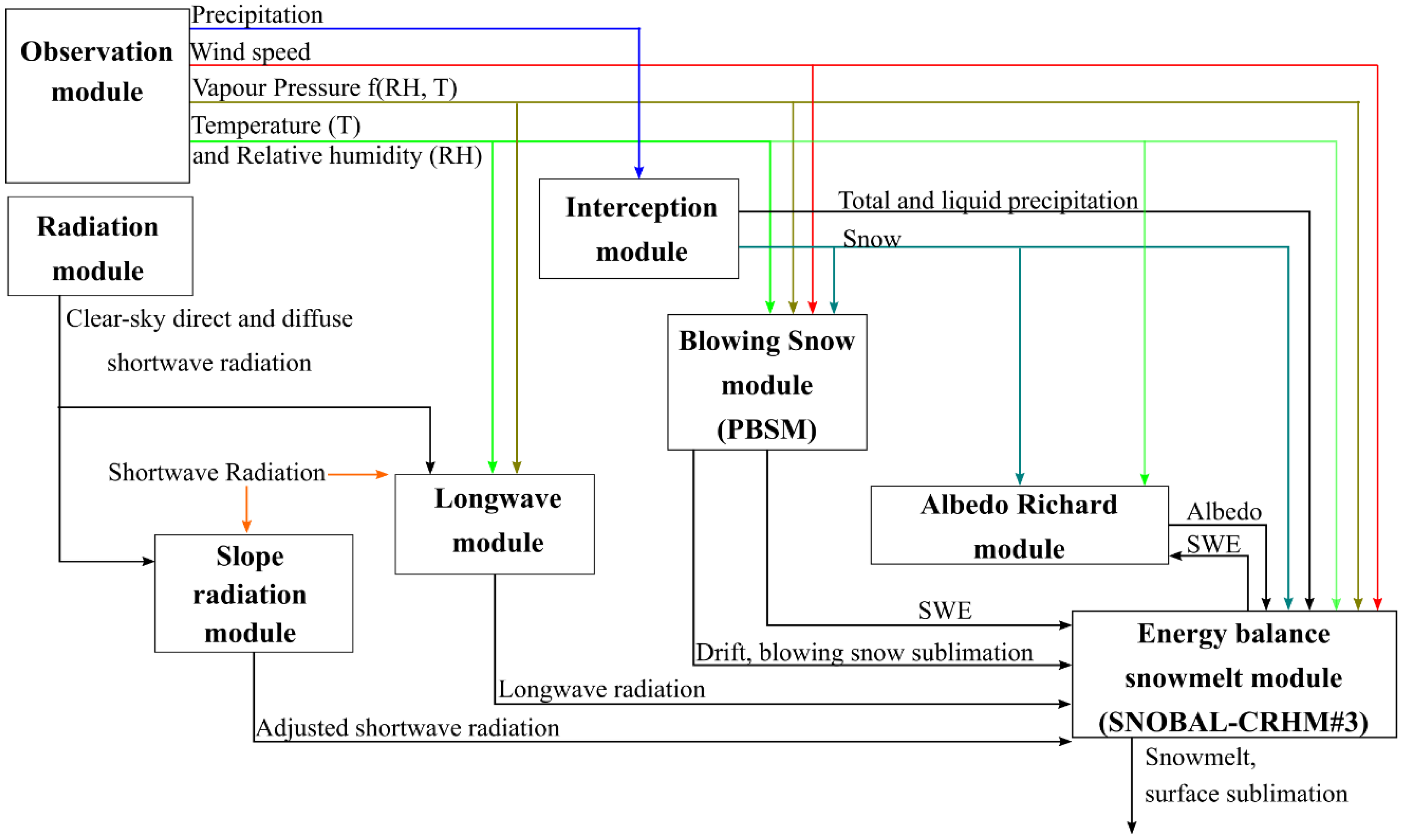
3.1. Snow Mass Balance Model
3.2. Distributed Hydrological Model
3.3. Climate Sensitivity Analysis
4. Results
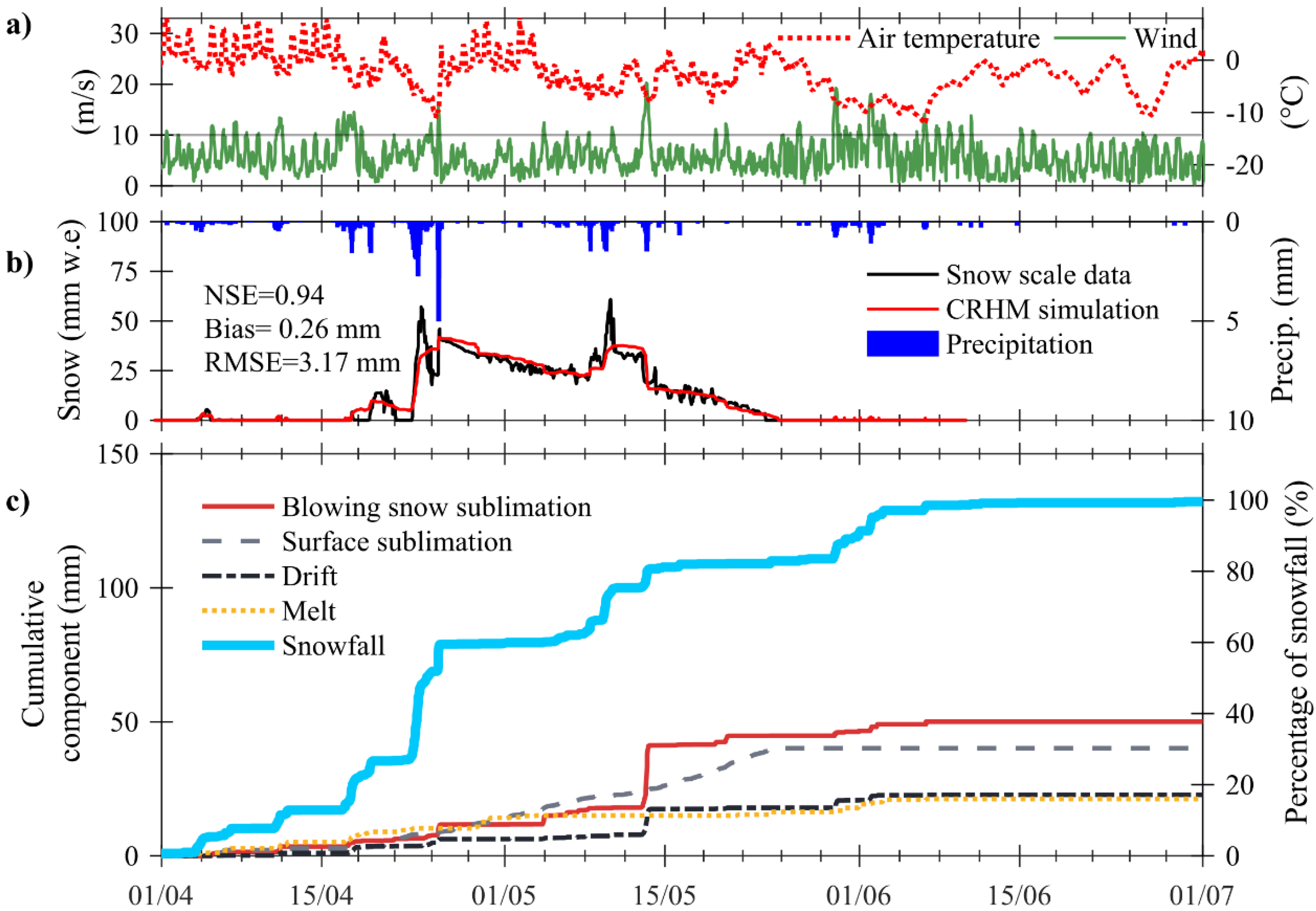
4.1. Simulations at LOS
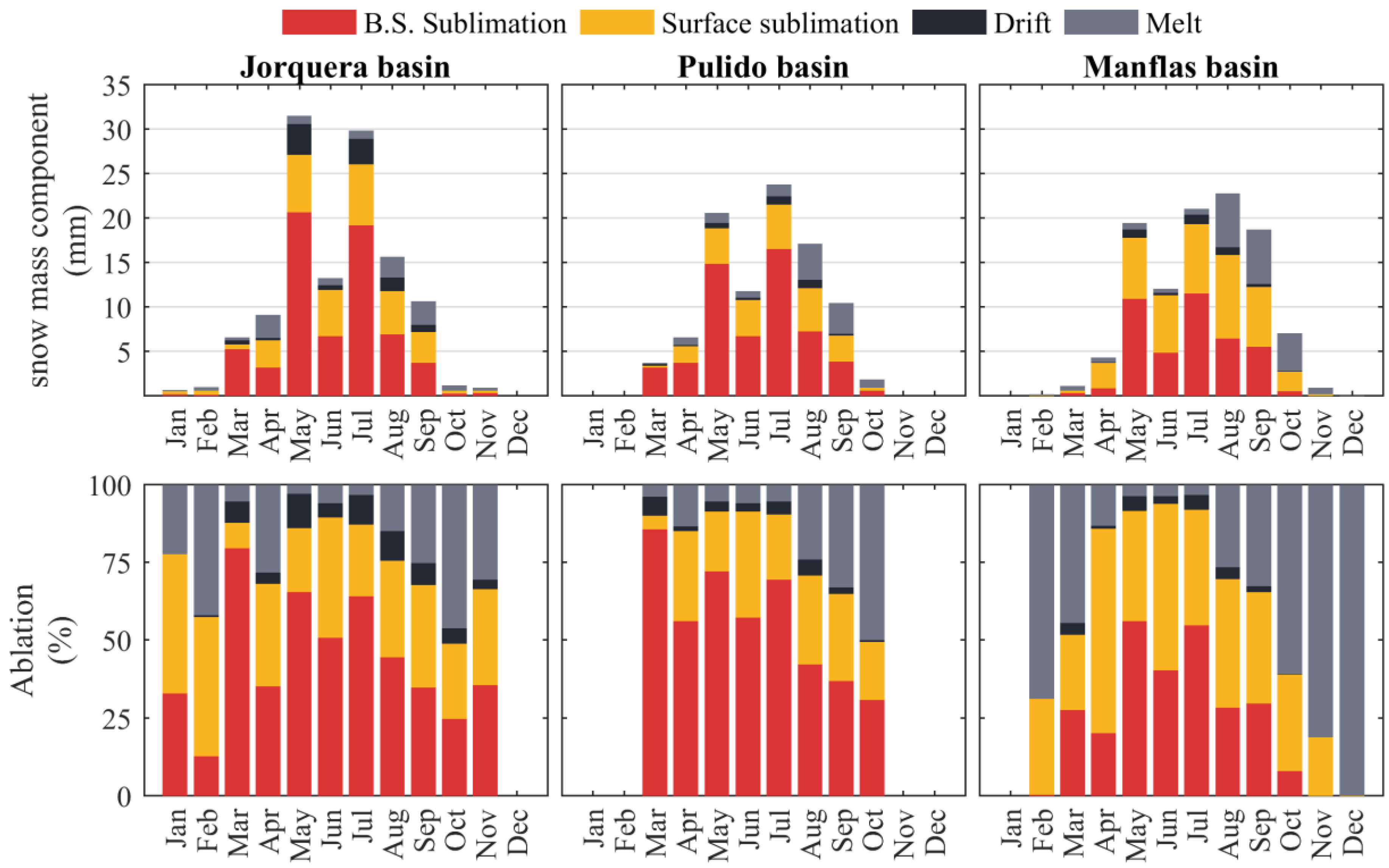
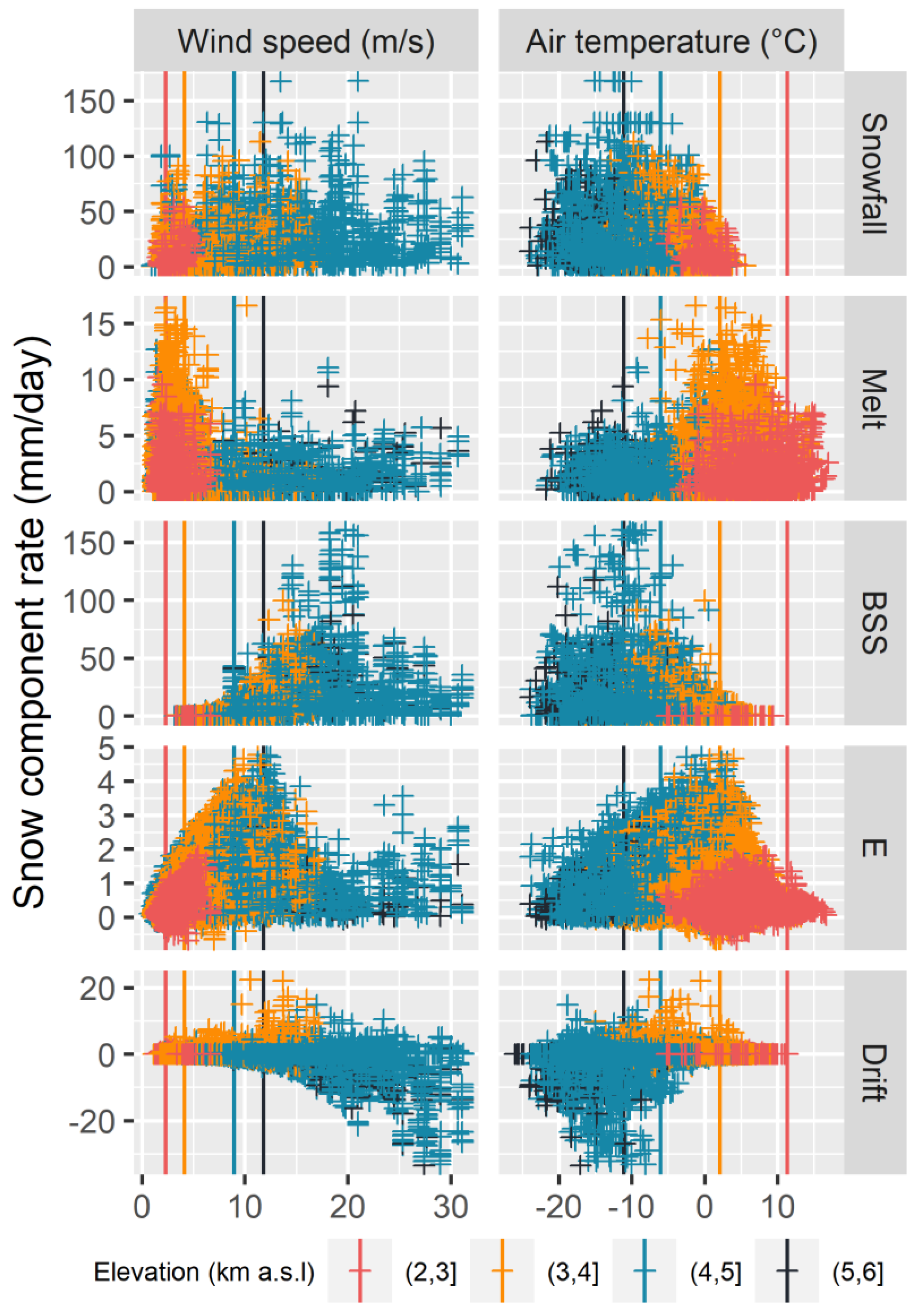
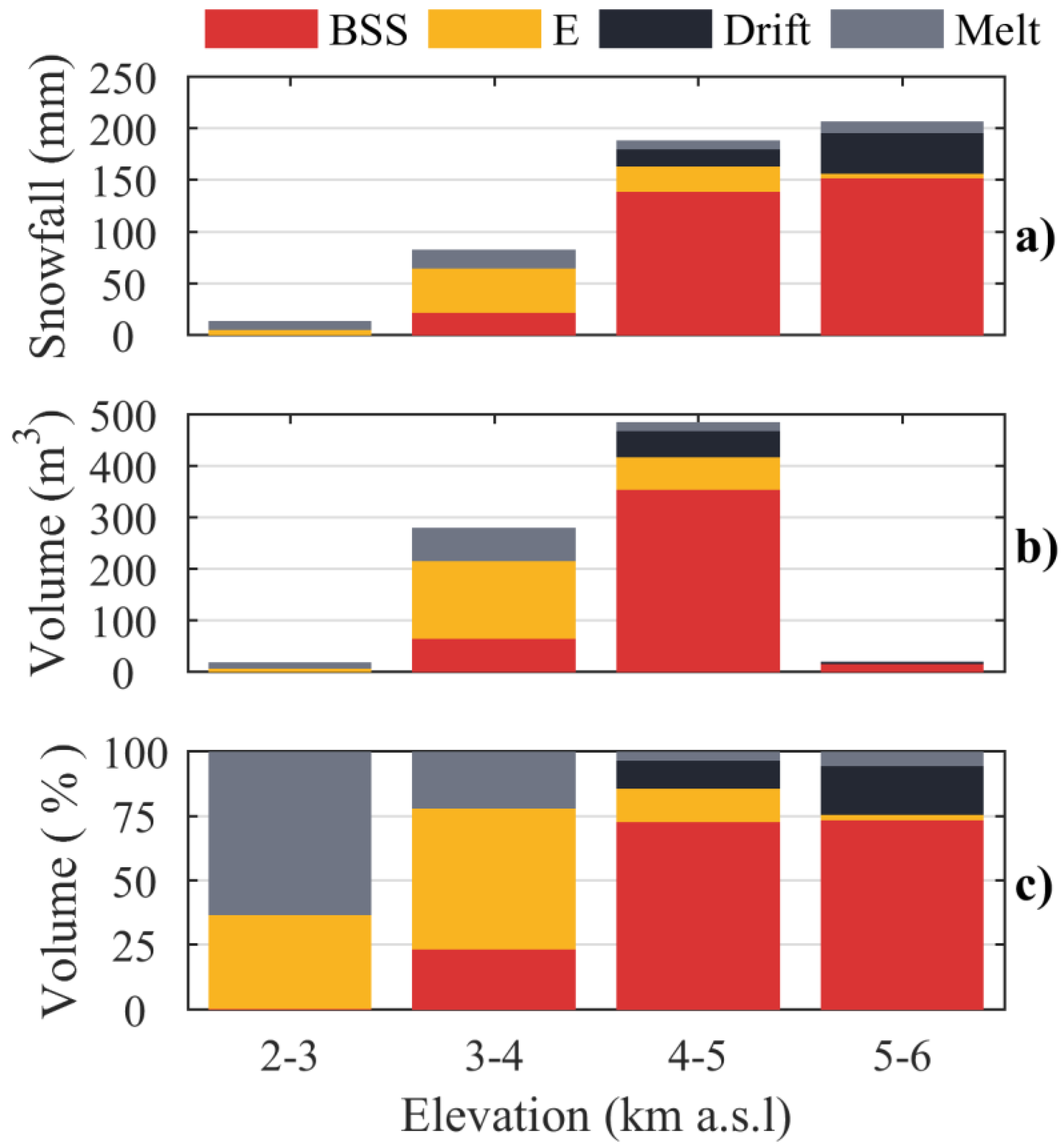
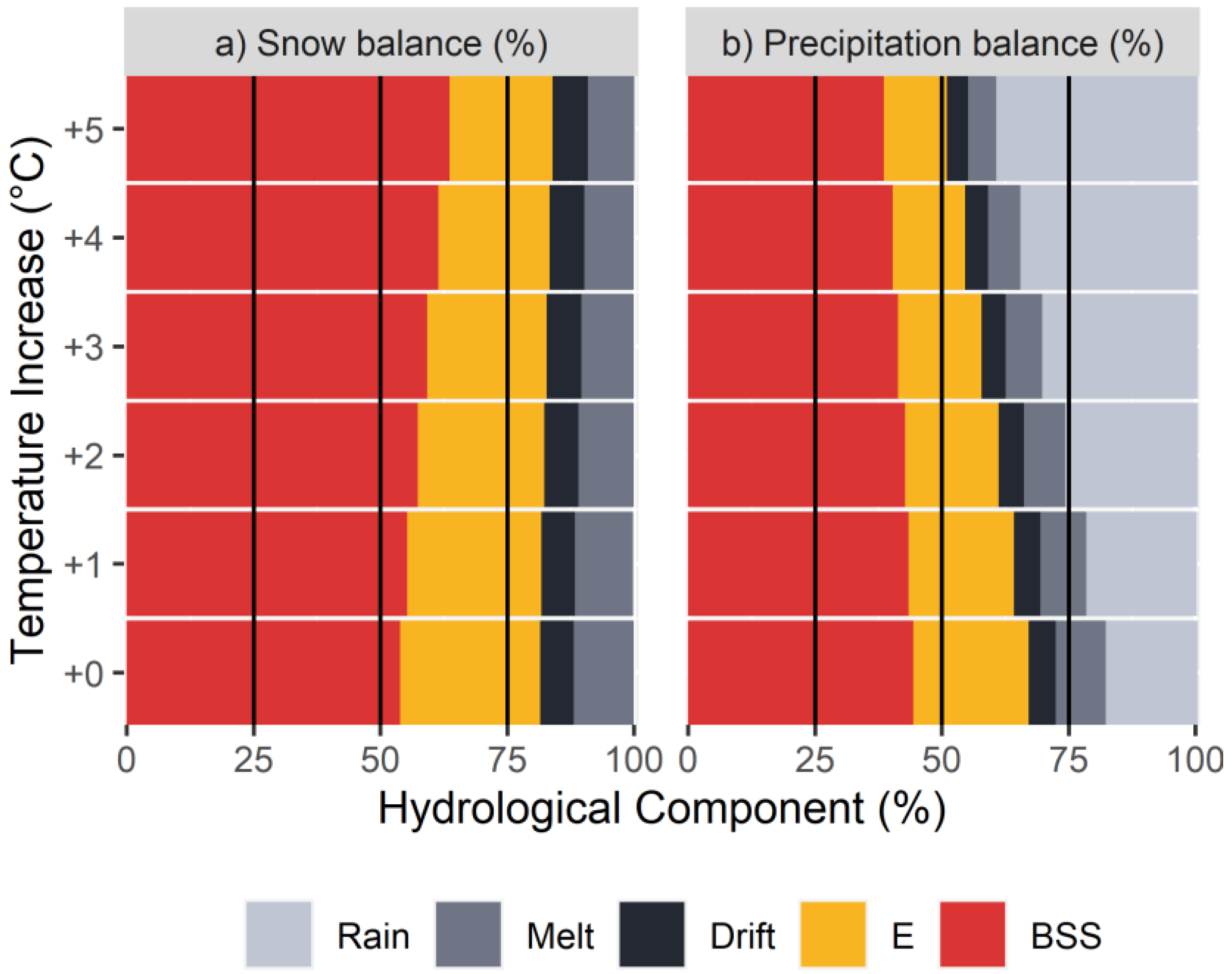
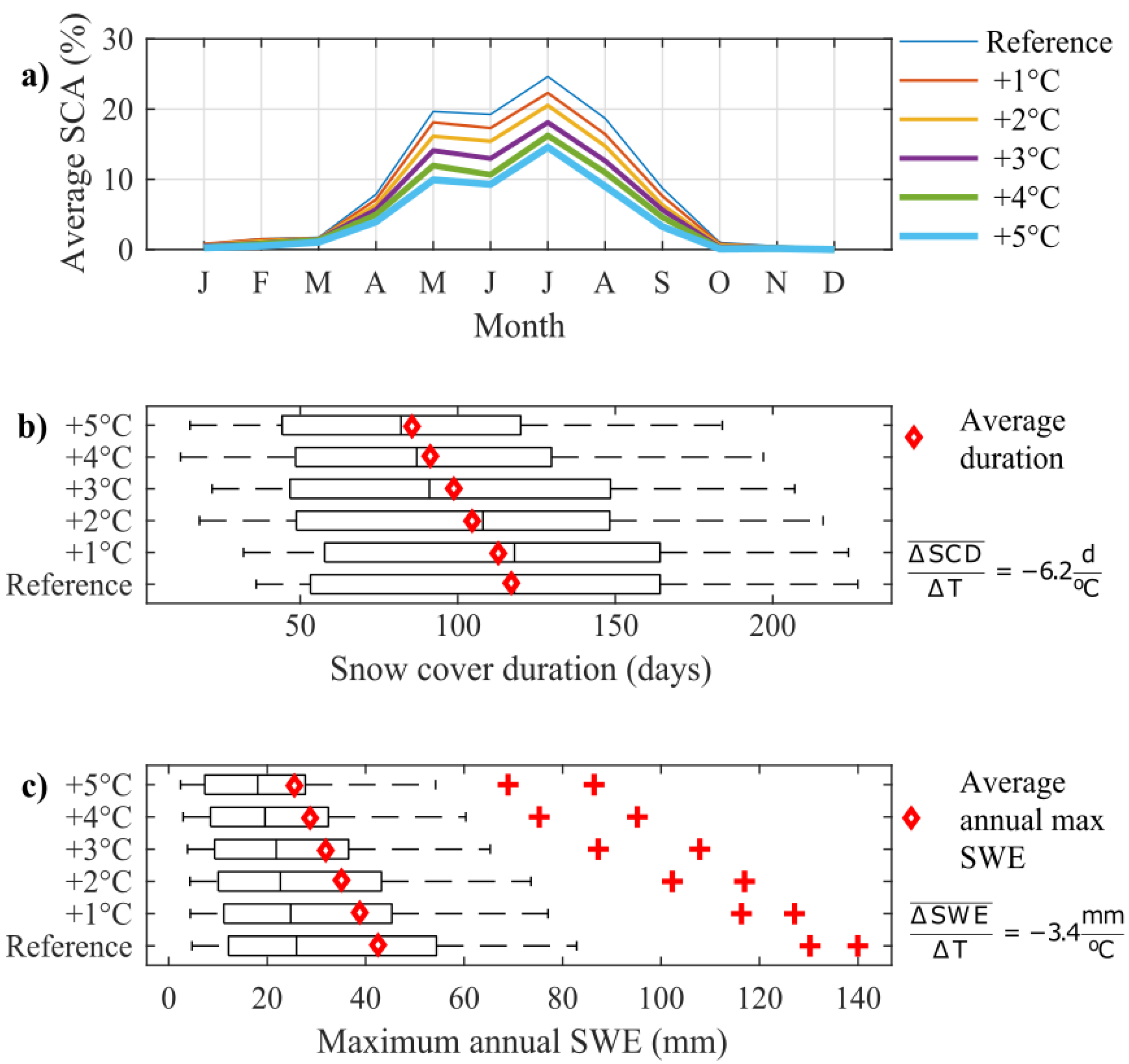
4.2. Simulations at Catchment-Scale
5. Discussion
5.1. Meteorological Uncertainties
5.2. Model Limitations
5.3. Potential Impact of Warmer Conditions
5.4. Snow Ablation Results in Other Studies
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303. [Google Scholar] [CrossRef]
- Hoffman, M.J.; Fountain, A.G.; Liston, G.E. Surface energy balance and melt thresholds over 11 years at Taylor Glacier, Antarctica. J. Geophys. Res. Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- MacDonell, S.; Kinnard, C.; Mölg, T.; Nicholson, L.; Abermann, J. Meteorological drivers of ablation processes on a cold glacier in the semi-arid Andes of Chile. Cryosphere 2013, 7, 1513. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Gray, D.M.; Landine, P.G. The prairie blowing snow model: Characteristics, validation, operation. J. Hydrol. 1993, 144, 165–192. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Li, L. Prairie and arctic areal snow cover mass balance using a blowing snow model. J. Geophys. Res. Atmos. 2000, 105, 26619–26634. [Google Scholar] [CrossRef]
- Reba, M.L.; Pomeroy, J.; Marks, D.; Link, T.E. Estimating surface sublimation losses from snowpacks in a mountain catchment using eddy covariance and turbulent transfer calculations. Hydrol. Processes 2012, 26, 3699–3711. [Google Scholar] [CrossRef]
- Strasser, U.; Bernhardt, M.; Weber, M.; Liston, G.E.; Mauser, W. Is snow sublimation important in the alpine water balance? Cryosphere 2008, 2, 53–66. [Google Scholar] [CrossRef]
- Gascoin, S.; Lhermitte, S.; Kinnard, C.; Bortels, K.; Liston, G.E. Wind effects on snow cover in Pascua-Lama, Dry Andes of Chile. Adv. Water Resour. 2013, 55, 25–39. [Google Scholar] [CrossRef]
- Réveillet, M.; MacDonell, S.; Gascoin, S.; Kinnard, C.; Lhermitte, S.; Schaffer, N. Impact of forcing on sublimation simulations for a high mountain catchment in the semiarid Andes. Cryosphere 2020, 14, 147–163. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Gray, D.M.; Brown, T.; Hedstrom, N.R.; Quinton, W.L.; Granger, R.J.; Carey, S.K. The cold regions hydrological model: A platform for basing process representation and model structure on physical evidence. Hydrol. Process. 2007, 21, 2650–2667. [Google Scholar] [CrossRef]
- Trefry, M.; McFarlane, D.; Moffat, K.; Littleboy, A.; Norgate, T. Copiapó River Basin Water Management: Terms of Reference for Future Governance and Research Activities; Report to AusAID and Chilean Stakeholders from the Minerals Down under Flagship; CSIRO: Canberra, Australia, 2012. [Google Scholar] [CrossRef]
- Olivera-Guerra, L.; Mattar, C.; Merlin, O.; Durán-Alarcón, C.; Santamaría-Artigas, A.; Fuster, R. An operational method for the disaggregation of land surface temperature to estimate actual evapotranspiration in the arid region of Chile. ISPRS J. Photogramm. Remote Sens. 2017, 128, 170–181. [Google Scholar] [CrossRef]
- Urrutia, R.; Vuille, M. Climate Change Projections for the Tropical Andes Using a Regional Climate Model: Temperature and Precipitation Simulations for the End of the 21st Century. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Ortega, C.; Vargas, G.; Rojas, M.; Rutllant, J.A.; Muñoz, P.; Lange, C.B.; Ortlieb, L. Extreme ENSO-driven torrential rainfalls at the southern edge of the Atacama Desert during the Late Holocene and their projection into the 21th century. Glob. Planet. Chang. 2019, 175, 226–237. [Google Scholar] [CrossRef]
- Araya-Osses, D.; Casanueva, A.; Román-Figueroa, C.; Uribe, J.M.; Paneque, M. Climate change projections of temperature and precipitation in Chile based on statistical downscaling. Clim. Dyn. 2020, 1–22. [Google Scholar] [CrossRef]
- Juliá, C.; Montecinos, S.; Maldonado, A. Características Climáticas de la Región de Atacama; Libro Rojo de la Flora Nativa y de los Sitios Prioritarios para su Conservación: Región de Atacama; Universitarias de La Serena: La Serena, Chile, 2008; pp. 25–42. [Google Scholar]
- DGA. Estadística Hidrológica en Línea. 2020. Available online: https://snia.mop.gob.cl/BNAConsultas/reportes (accessed on 20 August 2017).
- NASA. MODIS Imagery MOD10A and MYD10A database. Available online: https://nsidc.org/data/mod10a1 (accessed on 8 September 2016).
- Garreaud, R.D. The Andes climate and weather. Adv. Geosci. 2009, 22, 3. [Google Scholar] [CrossRef]
- Garreaud, R.; Fuenzalida, H.A. The Influence of the Andes on Cutoff Lows: A Modeling Study. Mon. Weather Rev. 2007, 135, 1596–1613. [Google Scholar] [CrossRef]
- Barrett, B.S.; Campos, D.A.; Veloso, J.V.; Rondanelli, R. Extreme temperature and precipitation events in March 2015 in central and northern Chile. J. Geophys. Res. Atmos. 2016, 121, 4563–4580. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.; Poli, P.; Brugge, R.; Fielding, K.; Fuentes, M.; Simmons, A. The ERA-Interim Archive, Version 2.0. European Centre for Medium-Range Weather Forecasts, Reading, U.K. 2011. Available online: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim (accessed on 8 November 2016).
- ECMWF. ERA Interim Dataset. 2020. Available online: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim (accessed on 8 November 2016).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Bechtold, P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- DeBeer, C.M.; Pomeroy, J.W. Simulation of the snowmelt runoff contributing area in a small alpine basin. Hydrol. Earth Syst. Sci. 2010, 14, 1205–1219. [Google Scholar] [CrossRef]
- Essery, R.; Etchevers, P. Parameter sensitivity in simulations of snowmelt. J. Geophys. Res. Atmos. 2004, 109, 1–15. [Google Scholar] [CrossRef]
- Marks, D.; Domingo, J.; Susong, D.; Link, T.; Garen, D. A spatially distributed energy balance snowmelt model for application in mountain basins. Hydrol. Processes 1999, 13, 1935–1959. [Google Scholar] [CrossRef]
- MacDonald, M.K.; Pomeroy, J.W.; Pietroniro, A. Parameterizing redistribution and sublimation of blowing snow for hydrological models: Tests in a mountainous subarctic catchment. Hydrol. Processes 2009, 23, 2570–2583. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; MacDonald, M.; DeBeer, C.; Brown, T. Modelling alpine snow hydrology in the Canadian Rocky Mountains. In Proceedings of the 77th Annual Meeting of the Western Snow Conference, Canmore, Canada, 20 April 2009. [Google Scholar]
- OTT HydroMet. OTT Pluvio Weighing Rain Gauge. 2021. Available online: https://www.otthydromet.com/en/Ott/p-ott-pluvio-weighing-rain-gauge/70.040.000.9.0 (accessed on 26 January 2021).
- Marks, D.; Winstral, A.; Flerchinger, G.; Reba, M.; Pomeroy, J.; Link, T.; Elder, K. Comparing simulated and measured sensible and latent heat fluxes over snow under a pine canopy to improve an energy balance snowmelt model. J. Hydrometeorol. 2008, 9, 1506–1522. [Google Scholar] [CrossRef]
- Harding, R.J. Exchanges of energy and mass associated with a melting snowpack. In Modelling Snowmelt-Induced Processes; Morris, E.M., Ed.; IAHS Publication: Wallingford, UK, 1986; Volume 155, pp. 3–15. [Google Scholar]
- DeWalle, D.; Rango, A. Principles of Snow Hydrology; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Paeschke, W. Experimentelle untersuchungen zum rauhigkeits-und stabilitatsproblem in der boden-nahen luftschicht. Beit. Phys. Freien Atmos. 1937, 24, 163–189. [Google Scholar]
- SINIA. National Service of Environmental Information. Soil Use Layer from the Atacama Region, Chile. Available online: http://ide.mma.gob.cl/ (accessed on 23 May 2016).
- Gao, L.; Bernhardt, M.; Schulz, K. Elevation correction of ERA-Interim temperature data in complex terrain. Hydrol. Earth Syst. Sci. 2012, 16, 4661–4673. [Google Scholar] [CrossRef]
- DGA. Balance Hídrico de Chile (Chilean Water Balance); Dirección General de Aguas, Ministerio de Obras Públicas: Santiago, Chile, 1987; 24p. [Google Scholar]
- Lagos-Zúñiga, M.A.; Vargas, M.X. PMP and PMF estimations in sparsely-gauged Andean basins and climate change projections. Hydrol. Sci. J. 2014, 59, 2027–2042. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Boike, J.; Sanchez-Lorenzo, A.; Pomeroy, J.W. Impact of climate warming on snow processes in Ny-Ålesund, a polar maritime site at Svalbard. Glob. Planet. Chang. 2016, 146, 10–21. [Google Scholar] [CrossRef]
- Beniston, M.; Keller, F.; Koffi, B.; Goyette, S. Estimates of snow accumulation and volume in the Swiss Alps under changing climatic conditions. Theor. Appl. Climatol. 2013, 76, 125–140. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Pomeroy, J.W.; Alonso-González, E.; Morán-Tejeda, E.; Revuelto, J. Decoupling of warming mountain snowpacks from hydrological regimes. Environ. Res. Lett. 2020, 15, 114006. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Gascoin, S.; Herrero, J.; Sproles, E.A.; Pons, M.; Alonso-González, E.; Sickman, J. Different sensitivities of snowpacks to warming in Mediterranean climate mountain areas. Environ. Res. Lett. 2017, 12. [Google Scholar] [CrossRef]
- Barrett, B.S.; Garreaud, R.; Falvey, M. Effect of the Andes Cordillera on precipitation from a midlatitude cold front. Mon. Weather Rev. 2009, 137, 3092–3109. [Google Scholar] [CrossRef]
- Viale, M.; Garreaud, R. Orographic effects of the subtropical and extratropical Andes on upwind precipitating clouds. J. Geophys. Res. Atmos. 2015, 120, 4962–4974. [Google Scholar] [CrossRef]
- Scaff, L.; Rutllant, J.A.; Rahn, D.; Gascoin, S.; Rondanelli, R. Meteorological interpretation of orographic precipitation gradients along an Andes west slope basin at 30 S (Elqui Valley, Chile). J. Hydrometeorol. 2017, 18, 713–727. [Google Scholar] [CrossRef]
- Mechoso, C.R.; Wood, R.; Weller, R.; Bretherton, C.S.; Clarke, A.D.; Coe, H.; Fairall, C.; Farrar, J.T.; Feingold, G.; Garreaud, R.; et al. Ocean–Cloud–Atmosphere–Land Interactions in the Southeastern Pacific: The VOCALS Program. Bull. Am. Meteorol. Soc. 2014, 95, 357–375. [Google Scholar] [CrossRef]
- Muñoz, R.C.; Garreaud, R. Dynamics of the Low-Level Jet off the West Coast of Subtropical South America. Mon. Weather Rev. 2005, 133, 3661–3677. [Google Scholar] [CrossRef]
- Rusticucci, M.; Zazulie, N.; Raga, G.B. Regional winter climate of the southern central Andes: Assessing the performance of ERA-Interim for climate studies. J. Geophys. Res. Atmos. 2014, 119, 8568–8582. [Google Scholar] [CrossRef]
- Schumacher, V.; Justino, F.; Fernández, A.; Meseguer-Ruiz, O.; Sarricolea, P.; Comin, A.; Comin, A.; Venancio, L.; Althoff, D. Comparison between observations and gridded data sets over complex terrain in the Chilean Andes: Precipitation and temperature. Int. J. Climatol. 2020, 40, 5266–5288. [Google Scholar] [CrossRef]
- Wolff, M.A.; Isaksen, K.; Petersen-Øverleir, A.; Ødemark, K.; Reitan, T.; Brækkan, R. Derivation of a new continuous adjustment function for correcting wind-induced loss of solid precipitation: Results of a Norwegian field study. Hydrol. Earth Syst. Sci. 2015, 19, 951–967. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Rasmussen, R.; Wolff, M.; Baker, B.; Hall, M.E.; Meyers, T.; Landolt, S.; Jachcik, A.; Isaksen, K.; Brækkan, R.; et al. The quantification and correction of wind-induced precipitation measurement errors. Hydrol. Earth Syst. Sci. 2017, 21, 1973–1989. [Google Scholar] [CrossRef]
- Torralba, V.; Doblas-Reyes, F.J.; Gonzalez-Reviriego, N. Uncertainty in recent near-surface wind speed trends: A global reanalysis intercomparison. Environ. Res. Lett. 2017, 12, 114019. [Google Scholar] [CrossRef]
- Mattar, C.; Borvarán, D. Offshore wind power simulation by using WRF in the central coast of Chile. Renew. Energy 2016, 94, 22–31. [Google Scholar] [CrossRef]
- Pomeroy, J.W. Wind Transport of Snow; University of Saskatchewan: Saskatoon, SK, Canada, 1988; p. 226. [Google Scholar]
- Fang, X.; Pomeroy, J.W.; Westbrook, C.J.; Guo, X.; Minke, A.G.; Brown, T. Prediction of snowmelt derived streamflow in a wetland dominated prairie basin. Hydrol. Earth Syst. Sci. 2010, 14, 991–1006. [Google Scholar] [CrossRef]
- Zhou, J.; Pomeroy, J.W.; Zhang, W.; Cheng, G.; Wang, G.; Chen, C. Simulating cold regions hydrological processes using a modular model in the west of China. J. Hydrol. 2014, 509, 13–24. [Google Scholar] [CrossRef]
- MacDonald, M.K.; Pomeroy, J.W.; Pietroniro, A. On the importance of sublimation to an alpine snow mass balance in the Canadian Rocky Mountains. Hydrol. Earth Syst. Sci. 2010, 14, 1401–1415. [Google Scholar] [CrossRef]
- Rasouli, K.; Pomeroy, J.W.; Janowicz, J.R.; Carey, S.K.; Williams, T.J. Hydrological sensitivity of a northern mountain basin to climate change. Hydrol. Processes 2014, 28, 4191–4208. [Google Scholar] [CrossRef]
- Krogh, S.A.; Pomeroy, J.W.; McPhee, J. Physically based mountain hydrological modeling using reanalysis data in Patagonia. J. Hydrometeorol. 2015, 16, 172–193. [Google Scholar] [CrossRef]
- Schneider, T.; O’Gorman, P.A.; Levine, X.J. Water vapor and the dynamics of climate changes. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Favier, V.; Falvey, M.; Rabatel, A.; Praderio, E.; López, D. Interpreting discrepancies between discharge and precipitation in high-altitude area of Chile’s Norte Chico region (26–32° S). Water Resour. Res. 2009, 45, 1–20. [Google Scholar] [CrossRef]
- Ginot, P.; Kull, C.; Schwikowski, M.; Schotterer, U.; Gäggeler, H.W. Effects of postdepositional processes on snow composition of a subtropical glacier (Cerro Tapado, Chilean Andes). J. Geophys. Res. Atmos. 2001, 106, 32375–32386. [Google Scholar] [CrossRef]

| Station | Latitude | Longitude | Elevation | Start–End | Measured |
|---|---|---|---|---|---|
| Name | (°) | (°) | (m a.s.l.) | date | variable |
| Iglesia Colorada | −28.1572 | −69.8808 | 1550 | 1988–2016 | P and T |
| Jorquera en La Guardia | −27.8364 | −69.7550 | 2000 | 1966–2016 | P |
| Lautaro Embalse | −27.9783 | −70.0033 | 1110 | 1930–2016 | P and T |
| Manflas | −28.1336 | −69.9750 | 1410 | 1966–2016 | P |
| Portezuelo El Gaucho | −28.6231 | −70.0450 | 4000 | 2003–2016 | T |
| Río Copiapó en Pastillo | −28.0003 | −69.9747 | 1300 | 2013–2016 | P |
| La Ollita | −28.2095 | −69.5425 | 4320 | December/15-July/16 | P, T, RH, ISR, U |
| Parameter | Description | Value | Units | Reference | Module |
|---|---|---|---|---|---|
| Maximum Albedo for fresh snow | 0.85 | - | [26] | Albedo | |
| Minimum Albedo for aged snow | 0.5 | - | [27] | ||
| Albedo decay for cold snow | s | [26] | |||
| Minimum snowfall amount required to refresh the albedo to | 1 | mm | Calibrated | ||
| Fetch length | LOS: 650 m UCRB: 1500 m | m | Calibrated | PBSM | |
| Snow density of falling snow | 100 | kg m−3 | [28] | SNOBAL | |
| Max liquid water content as volume ratio | 0.01 | - | |||
| Maximum active layer thickness | 0.1 | m | |||
| Roughness length | 0.001 | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jara, F.; Lagos-Zúñiga, M.; Fuster, R.; Mattar, C.; McPhee, J. Snow Processes and Climate Sensitivity in an Arid Mountain Region, Northern Chile. Atmosphere 2021, 12, 520. https://doi.org/10.3390/atmos12040520
Jara F, Lagos-Zúñiga M, Fuster R, Mattar C, McPhee J. Snow Processes and Climate Sensitivity in an Arid Mountain Region, Northern Chile. Atmosphere. 2021; 12(4):520. https://doi.org/10.3390/atmos12040520
Chicago/Turabian StyleJara, Francisco, Miguel Lagos-Zúñiga, Rodrigo Fuster, Cristian Mattar, and James McPhee. 2021. "Snow Processes and Climate Sensitivity in an Arid Mountain Region, Northern Chile" Atmosphere 12, no. 4: 520. https://doi.org/10.3390/atmos12040520
APA StyleJara, F., Lagos-Zúñiga, M., Fuster, R., Mattar, C., & McPhee, J. (2021). Snow Processes and Climate Sensitivity in an Arid Mountain Region, Northern Chile. Atmosphere, 12(4), 520. https://doi.org/10.3390/atmos12040520








