Abstract
The Haifa bay area (HBA), which includes Mount Carmel and the Zevulun valley is the third largest metropolitan area in Israel. It is also a centre of heavy industry and an important transportation hub which serve as sources of local anthropogenic pollution. Such sources are associated with adverse health effects. In order to estimate the possible exposure of the inhabitants in such heterogeneous orographic area, a detailed atmospheric transport and dispersion modelling study is required, which in turn must take into account the local micrometeorology. The aim of this study is to conduct a spatio-temporal analysis of the flow field in the HBA in order to identify the common patterns of the average wind and characterize the statistical parameters of turbulence in this area, essential for detailed pollutants dispersion modelling. This study analyses data collected during four months of summer in a network of 16 weather stations which extend across Mount Carmel and the Zevulun valley. It was found that, during the evening and night time on Mount Carmel, different flow patterns may develop on each side, separated by the watershed line. When such conditions do not develop, as well as during the daytime, the wind field, both on Mount Carmel and the Zevulun valley is approximately homogenous. The analysis of the Monin–Obukhov similarity theory functions for the velocity standard deviations show a distinct difference between Mount Carmel and the Zevulun valley, as well as between strong and weak winds. This difference can be clearly seen also in the diurnal hourly distribution of atmospheric stabilities which exhibit higher proportions of unstable conditions in the Zevulun valley during day time and higher proportion of stable stratifications at the Mount Carmel during night-time.
1. Introduction
The Haifa bay area (HBA) is a major area in Israel. It hosts the city of Haifa as well as the Krayot, a cluster of four small cities, Kiryat Bialik, Kiryat Yam, Kiryat Motzkin and Kiryat Atta. These compose an urbanized area with a population of 468,000 which makes it the third largest metropolitan area in Israel [1].
The Haifa bay area (HBA) is a heterogeneous area due to several aspects. Geographically, it includes Mount Carmel and the Zevulun valley (Figure 1). The highest peaks of Mount Carmel rise to a height of 500 m. The ridge of the mountain extends generally along the southeast-northwest axis (140°–320°). The total width of the ridge is about 15–25 km, where the horizontal distance from peak to mountain foot is 10–20 km in the western slope and 2–4 km in the eastern slope [2]. The Zevulun valley, is a plain area that borders the Mediterranean Sea, the eastern slopes of Mount Carmel and the Alonim range of hills [3].
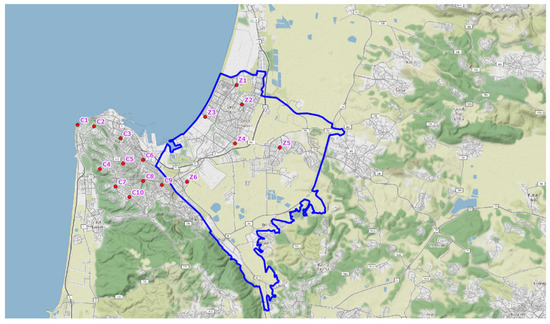
Figure 1.
The weather stations in the Zevulun valley area (with Z prefix) and Mount Carmel (with C prefix). The blue border signifies the borders of southern Zevulun valley, which contains the Haifa Bay area.
Diversity also exists in the land cover in HBA. It consists of densely populated residential areas as well as major industrial facilities such as the national oil refiners, an oil-fired power plant and several petrochemical, chemical and agrochemical industrial plants. In addition, several main roads pass through the HBA, especially the intercity roads that lead to Haifa, from the south (from Tel-Aviv), from the north-east (from the Krayot) and south-east (from Jezreel valley). These major industrial plants and the intercity roads serve as local anthropogenic sources of pollution, and especially particulate matter (PM) [4,5]. There are indications that increased PM concentrations may be associated with adverse health effects. Specifically, chronic exposure to ambient PM10 concentrations was found to be associated with lung cancer incidence among males in the Haifa bay area (HBA) [6].
In order to be able to examine the expected impact of different anthropogenic pollutant sources in the HBA on the health of people living in this area, a rigorous atmospheric transport and dispersion model should be used. Such a model should account for scenarios that correspond to the specific atmospheric conditions of this area [7]. Such scenarios should be based on comprehensive information on the average wind field, the statistical parameters of the turbulence as well as the influence of the heterogeneous canopy on these variables [8,9].
It was reported that the coastal plain of Israel is rather homogenous regarding dispersion of pollutants from power plants. However, this homogeneity excludes the HBA, due to presence of the complex topography of Mount Carmel [10]. Despite this fact, studies that dealt with the wind field in the HBA have based their analysis on very few weather stations, and did not include analysis of the time dependency of the wind [2,5,11].
Therefore, the aim of this study is to conduct a spatio-temporal analysis of the wind field in the HBA in order to identify and describe the common patterns of the average wind and turbulence in the HBA. It should be mentioned that the HBA is also affected by the regional semi-arid climate which is expressed by extreme natural dust events. As this study is supposed to provide information for models that will assess the effect of local emissions on the PM concentrations that people residing in this area are exposed to, this study will deal with the summer season, as during this season no natural dust outbreaks develop and anthropogenic sources dominate [12].
2. Materials and Methods
2.1. Weather Stations
The wind measurements analysed in this study originated from a combination of a dataset of a one-year wind measurement campaign conducted by the IIBR (Israel Institute for Biological Research) at the Haifa metropolitan area during 2014–2015. This dataset was supplemented by data from the ongoing monitoring network of Haifa metropolitan area which was installed and maintained by the HBUA (Haifa bay municipal association for environmental protection; http://www.envihaifa.net (accessed on 1 February 2021)). As this study deals with the summer season, the measurements that were made during the summer season were extracted from the dataset. As the summer season in the Eastern Mediterranean region spans from June to September, the data analysed in this study consist of the measurements collected during these four months in 2015 [13].
Overall, the weather stations’ network analysed in this study consists of 16 stations, 10 in Mount Carmel and 6 in the Zevulun valley (Figure 1). The wind measurements in the IIBR weather stations were equipped with ultrasonic anemometers (R.M. Young 81000), while the HBUA weather stations consisted of propeller-vane anemometers (R.M. Young 05103VM) (Table 1). The ultrasonic anemometer specifications (http://www.youngusa.com/products/6/3.html accessed on 16 February 2021) for wind speed are measuring range 0 to , resolution: , threshold: , accuracy: ±1% (, ±3% (40 m/s). Its specifications for wind direction are measuring range 0 to 360°, resolution: 0.1°, accuracy: ± 2° , ± 5° . The HBUA equipment specifications (http://www.envihaifa.org.il accessed on 16 February 2021) for wind speed are measuring range 0 to , resolution: , threshold: , accuracy: ±2% , ±3% . Its specifications for wind direction are measuring range 0 to 360°, resolution: 1°, accuracy: ± 2°.

Table 1.
The stations analysed in this study. Stations’ code with a C prefix are located on Mount Carmel, and those whose code begins with Z are located in the Zevulun valley. Stations owned by IIBR were installed during a one-year campaign during 2014–2015. Stations owned by HBUA are a part of the ongoing monitoring network of Haifa metropolitan area (http://www.envihaifa.net (accessed on 1 February 2021)).
Several field studies have compared co-located ultrasonic and mechanical anemometers, such as propeller-vane anemometers [14,15,16]. The main disadvantage of the later is over-speeding which occurs when an anemometer responds quicker to an increase in wind speed than to a decrease of the same magnitude [17,18]. An earlier study have estimated the over-speeding of a cup anemometer as 10% of the reference wind speed measured by a sonic anemometer, over a speed range of [16]. However, a more recent study that analysed a year of data have found that over a wider speed range of the differences were 2%. The over-speeding effect was noticeable in speeds up to , where the median bias was . Wind directions differences were within 80% of the time [15]. Based on these results, the time averaged horizontal wind data from the weather stations network were used for the spatio-temporal analysis of the flow field in the HBA. In order to extract surface layer turbulence parameters only stations equipped with ultrasonic anemometer were used.
Data quality control computer programs were applied on the data files, in order to remove erroneous records. The procedures included search for characters in numeric fields, examination of the time order of records, and examination whether the wind direction and speed were within the correct range, i.e., wind direction within and wind speed within . This maximal wind speed was set as the reported multiannual maximal wind speed in a representative station in Carmel coast was [11]. It should be noted that all reference to specific time is in LST (UTC + 2).
All stations were installed on the rooftop of buildings. The height of the measurement above ground level (AGL) was between 5 and 30 m. The elevation above sea level (ASL) of the locations of the weather stations was between 0 and 350 m (Table 1).
Since the canopy roughness sublayer is highly inhomogeneous, in order for a station to represent its surroundings it should be just above the roughness sublayer, which is above at least 1.5 H (H being the averaged building height at the area of the station) for turbulent parameters and a little less for averaged wind if the canopy is sparse [19]. All stations in Table 1 matched the stricter criterion being in the range of 1.5 H–2 H, with the exception of station Z1, being at 1.3 H. This station is mounted on a 3 m mast on the rooftop of a single floor shelter (small cubed 1 floor structure of about ) where the surrounding a sparse urban area where the buildings are 1 (3 m) or 2 (6 m) floors.
2.2. Wind Field Interpolation
In order to analyse the spatial wind field, the wind measurements of the 16 weather stations were interpolated using a horizontal- and vertical-weighted wind field interpolation scheme that takes into account conditions of complex topography.
Two of the most popular interpolation methods in geoscience and atmospheric science is the inverse-distance weighting (IDW) and kriging, as indicated by the fact that they were implemented in many GIS packages [20,21]. Both of these methods estimate a value to a given point based on its distance to measurement points in space [21]. The distance that these methods rely upon does not take into account the vertical variability which is characteristic to complex terrains, and under a low sampling density may fail to describe important small scale phenomena, such as the difference between sunny and shady slopes or the difference between a valley and a nearby top of a hill [21,22].
In order to account for the effect of topography, and in particular where surface wind observations are concerned, it was proposed to replace the horizontal distance with the topographical elevation distance [22]. This study uses a surface wind field spatial interpolation method that was developed in the context of a detailed high resolution atmospheric transport and dispersion model [23]. This method follows the suggestion regarding the topographical elevation distance but instead of replacing the horizontal distance with the vertical, it incorporated both these dimensions. It is based on the IDW framework, due to the fact that the kriging is computationally cumbersome [20]. The method uses two length scales: a characteristic horizontal length scale, , (“influence” scale) by which the topography varies, and a characteristic vertical length scale, , associated with the influence of vertical atmospheric turbulent mixing. Therefore, the approach presented in this study expand previous methods for wind field interpolation by taking into account the extent of influence dictated by the topography as well as the effect of turbulent mixing [22,24].
The interpolation was performed on a square metric grid whose coordinates were in ITM (Israeli Traverse Mercator, a geographic coordinates system optimized for Israel). The wind vector values on a square grid of were interpolated as a weighted mean of the values at the measurement sites (the weather stations’ locations):
where is the interpolated velocity at position on the grid; is the weight given to observation/measurement site for grid point ; is the observed velocity at site ; and the summation is performed over all measurement sites.
The weight factors are taken as a product of two functions:
First, a horizontal weight function , roughly based on the inverse square of , the horizontal distance between grid point and measurement site :
where , here taken as , is a characteristic horizontal length scale above which the topography starts varying considerably.
Then, a vertical weight function , roughly based on the inverse square of now , the difference between the elevation at grid point and measurement site :
where is the same as above and is a dimensionless constant which depends on the atmospheric stability, taken here for the near neutral case to be 5 (for stable and for convective atmosphere ). The resulting characteristic vertical length scale over which information in transferred between different topographical elevations (by turbulent mixing) is accordingly .
This above interpolation is used in this study for identifying the typical diurnal wind patterns. The robustness of this interpolation method was tested by removing one station at a time (from the stations in Table 1) and comparing the interpolated grid calculated with and without this particular station. The error was defined as the influence of the omitted station to the spatial wind field, i.e., as the averaged L2 norm distance between the two grids, normalized to the average measured wind speed:
where is the error obtained by removing station , is the interpolated velocity at grid point obtained using all measurement stations, is the interpolated velocity at the same grid point obtained without station , n is the number of grid points and is the average over all stations of the measured wind speed.
The median error was found to be 3.4%, with an interquartile range (IQR): 3%–5%. We also note that the basis for choosing stations for sub-areal climatological description is that their error is being well within the IQR, as manifested in the choice of stations C4, C9, Z2, Z4 in Section 3.
2.3. Nonparametric Bivariate Density
The diurnal time series of the wind speed and direction in a given weather station may change from day to day. However, it is possible to identify climatological patterns in these time series, if each pair of time and wind vector component observation (either the direction or speed) is defined as a realization of a bivariate distribution. In this study, all these realizations were grouped into a two dimensional histograms, which were later plotted in a form of density contours. This resulted in a nonparametric visualization of the bivariate (time-speed or time-direction) distribution. Each contour represents a boundary in which a given percentile of the nonparametric bivariate distribution is contained.
2.4. Surface Layer Turbulence Parameters
Turbulent structure in the surface layer is usually described in terms of Monin–Obukhov similarity theory (MOST) using the well-known logarithmic velocity profile law and the so called universal relationships between scaling parameters [25]; The applicability of this description was critically reviewed [26]. The basic reasoning to MOST lies in two main observations. The first is that above the roughness sub-layer which extends to 2–5 averaged canopy elements height, the (horizontally homogeneous steady state) turbulent kinetic energy (TKE) budget approximately reduces to a “local equilibrium” between shear production and dissipation [27]. The second is that many times in this layer there exists a “constant-flux layer” in which fluxes are approximately constant with height (typically between 10–20% [28]). Analysis of the standard deviations of the wind-velocity fluctuations over complex surfaces is essential to our understanding of the turbulence structure of the atmospheric surface layer. In our case the terrain is characterized by varying topography and roughness. We focus here on characteristics of atmospheric turbulence over coastal flat terrain and a neighboring complex terrain under various wind directions, and atmospheric stabilities. These two cases allow us to compare the influence of terrain and roughness changes on the properties of turbulence, and in particular on the dimensionless velocity standard deviations, ( being velocity terms, and being the friction velocity), which are central to the characterization of surface layer turbulence structure.
Turbulence data for the three wind components and the sonic temperature were measured at 30 Hz during the summer of 2015 (Table 1); data are analysed over 10 min intervals. For the sake of our analysis turbulent components (u’, v’, w’, T’) are extracted from the observations. The friction velocity , the standard deviation of each component of the wind () and the stability parameter z/L have been computed (z is the height from the ground and L is the Obukhov length scale , g is the gravitational acceleration and the von Karman constant). The fit to MOST normalized standard deviations functional form is described in the results section.
3. Results
The examination of two typical summer days shows that the night time in the Zevulun valley is characterized by low winds with easterly to south-easterly directions. During this time, two different regimes may develop in Mount Carmel (Figure 2a,b). One is characterized by south to south-south-west wind directions in the western slope of Mount Carmel and west to south-west winds in the eastern slopes of Mount Carmel (Figure 2a). The other is relatively uniform with south-westerly winds (Figure 2b). During the daytime, the wind directions measured on Mount Carmel are mostly west to west-south-west and in Zevelun valley west to north-west (Figure 2c,d). During the evening, the wind in Zevulun decreases in speed. The measured wind direction may exhibit a pattern similar to the daytime (Figure 2e), or a veering to the north-west (Figure 2f). During this time, the wind in Mount Carmel may be uniform, with south-westerly winds (Figure 2e) or a specific pattern in each slope, north-north-east directions in the western slope and north-north-west in the eastern slope (Figure 2f).
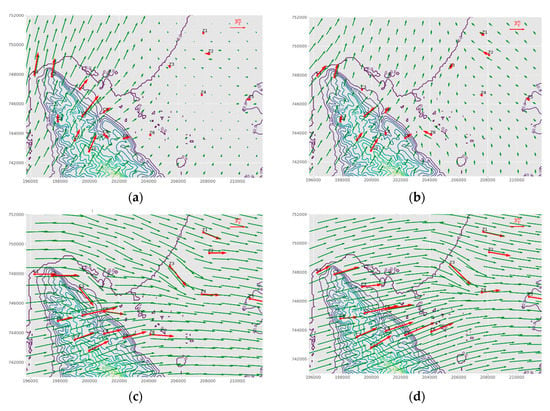
Figure 2.
Characteristic examples of the spatial wind field in the Carmel Mountain and Haifa bay area in two representative days (colored contours represent different topographical height). (a,c,e) 4 August 2015 (b,d,f) 15 August 2015. Panels (a,b) describe 0400 h as representing the night time; (c,d) describe 1400 h which represents the daytime and (e,f) describe 2000 h that represents the evening. All time points are in LST (UTC+2).
The wind speed at all weather stations at the three regions (Mount Carmel, Zevulun valley and the metropolitan area of Tel-Aviv) exhibit similar diurnal regime. The wind speed is weak during the night. It grows stronger during the morning, beginning around 0800 h, and begins to get weaker in the late afternoon, beginning around 1800 h. During the periods of time where the wind is weak, its distribution is centred around in the Zevulun valley stations (Figure 3a,b), in the stations at Mount Carmel and the metropolitan area of Tel-Aviv (Figure 3c–f).
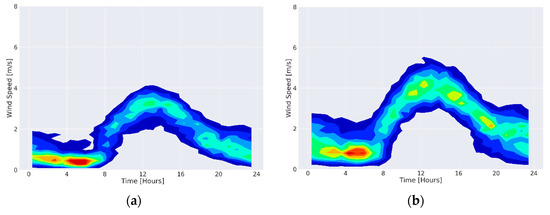
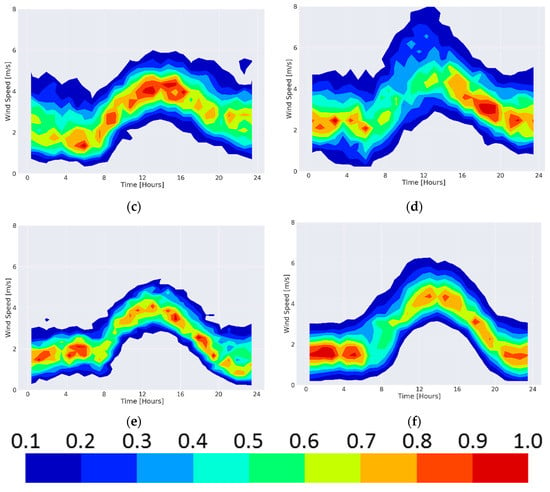
Figure 3.
Nonparametric bivariate density of the wind speed of representative weather stations (a) Z4–Kiryat Bialik (b) Z2–Kiryat Motzkin (c) C4–Leah street, Haifa (d) C9–Tel Hai elementary school, Haifa, (e) TI–The world Zionist. Organization house Tel-Aviv (f) TO-Israeli meteorological service Beit Dagan. All time points are in LST (UTC + 2).
The wind speed reaches a single maximum between 1230 h to 1330 h (Figure 3). The range of the maximum’s distribution width at the Zevulun valley stations is (Figure 3a,b), at Mount Carmel (Figure 3c,d) and at the metropolitan area of Tel-Aviv (Figure 3e,f). The upper limit of the maximum’s range is at the Mount Carmel weather stations (Figure 3c,d). At the Zevulun valley stations it reaches (Figure 3a,b) and in the metropolitan area of Tel-Aviv (Figure 3e,f).
The wind direction in the Zevulun valley stations exhibit a similar behaviour during the daytime and evening (0700 h–2200 h). The wind direction distribution is uni-modal where its centre is around westerly winds. It is spread over a relatively narrow sector of 90°. However, while the central tendency of the wind direction distribution in station Z4 is 270° (West; Figure 4a), station Z2 experience some wind veering from 270° during 0700 h–1400 h to 315° (south-west) from 1400 h–2200 h (Figure 4b).
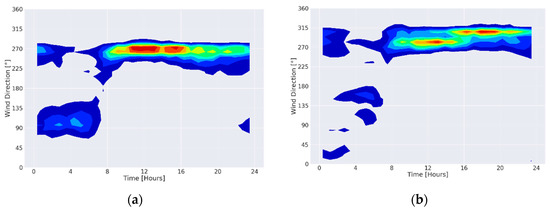
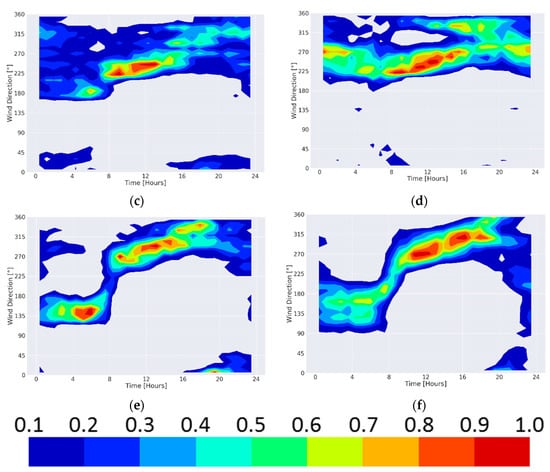
Figure 4.
Nonparametric bivariate density of the wind direction of representative weather stations (a) Z4–Kiryat Bialik (b) Z2–Kiryat Motzkin (c) C4–Leah street, Haifa (d) C9–Tel Hai elementary school, Haifa, (e) TI–The world Zionist Organization house Tel-Aviv (f) TO–Israeli meteorological service Beit Dagan. All time points are in LST (UTC+2).
The night time can be divided into two periods (2200 h–0300 h and 0300 h–0700 h). during the first night period, the wind direction distribution is multi-modal, where one mode continues around westerly directions (270°–315°) and the other is around 112.5° (East-South-East) in station Z4 (Figure 4a) and 22.5° (north-north-east) in station Z2 (Figure 4b). During the second night period the wind distribution in station Z4 is uni-modal around 112.5° while in station Z2 the wind direction is rather undefined, with modes around 112.5° (east-south-east), 157.5° (south-south-east) and 292.5° (west-north-west).
In the Mount Carmel stations, the central tendency of the wind direction distributions exhibit a clockwise veering from the south-east to the north-west (Figure 4c,d). This occurs during the daytime (0800 h–2000 h). During most of this period (until 1600 h) the wind direction distribution is uni-modal. From then on, the distribution is multi-modal, with modes in the west, north-west (270°, 315°, 337.5°).
During the night time, there is a distinct difference between the Mount Carmel stations. Station C4, which is located in western slopes of Mount Carmel, exhibit two separate periods. During the first (2000 h–0400 h) the wind direction distribution is multi-modal, with modes in the North-West, West and South-West (315°, 270°, 225°). The second period is characterized by a uni-modal south centred distribution (0400 h–0800 h; Figure 4c). Contrary to this wind regime, the night time wind distribution in station C9, on the eastern slopes of Mount Carmel is uni-modal during the whole period (2000 h–0800 h). First, the distribution is western centred (270°; 2000 h–0400 h) and then south-eastern centred (225°; 0400 h–0800 h; Figure 4d).
Compared to the wind direction regimes in Mount Carmel and Zevulun valley, the wind direction regime in the Tel-Aviv area exhibits four distinct periods. During the day, from 0800 h, winds that rotate clockwise from westerly to north-westerly winds. During the night, from 2200 h in TO and 2330 in TI, south-westerly winds. Between these periods there are transition periods (Figure 4e,f). During the transition periods the wind changes from the night to day regime and vise-versa. The rotation of the wind may occur either clockwise or anticlockwise [29].
The analysis of turbulence parameters was based on the data measured at station Z2 (Kiryat Motzkin) which represented the flat urban region that is the Zevulun valley, and C9 (Tel Hai elementary school) that represented the complex terrain ridge of Mount Carmel (Figure 1 and Table 1). The measurement sensors at both stations were stationed at about twice the mean height of canopy elements (), which for closely spaced (urban) canopies is assumed to be above the roughness sub-layer [30,31].
In Figure 5, Figure 6 and Figure 7 the dimensionless turbulence parameters for the vertical and horizontal standard deviations of wind- velocity fluctuations are plotted as functions of z/L. Similar to [32] we have evaluated turbulence parameters on the available data for the full range , which covers the largest interval generally considered in literature when evaluating the similarity functions. We divide our analysis taking into account that the mean wind speed is below the threshold indicated by (Mahrt et al., 2013; Sun et al., 2012) for the weakly turbulent regime. For each regime we present the data as points, the 25–75 percentiles as a shaded area and the median as a solid line of the same color. We fitted the observational data with solid lines represented by the commonly used general function:
where is the friction velocity calculated in all cases from formula , is the stability parameter, z is the height, is the Obukhov length (g being the gravitational acceleration, and the von Karman constant), and d is the zero-plane displacement height, taken here as [33]. As can be seen from the figures, the observations around the neutral stratification, within the range of , show constant value, after which it grows on both sides. The fit to the empirical coefficients is given in Table 2.
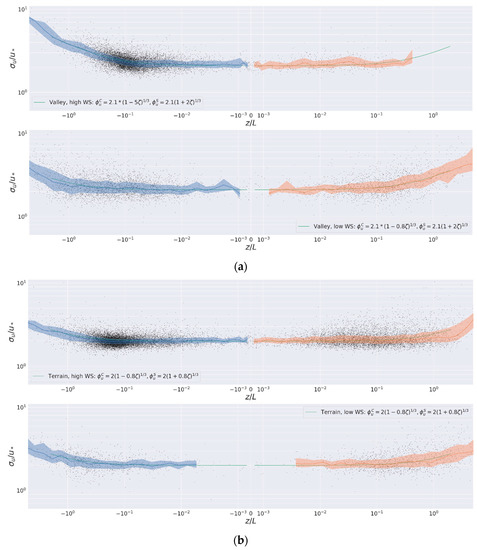
Figure 5.
The dimensionless turbulence parameters for , the along-wind horizontal standard deviation of the wind velocity fluctuations, plotted as functions of both for weak wind (; lower part for each station) and for strong wind (; upper part for each station); The Zevulun valley region, as represented by the Z2 (Kiryat Motzkin) weather station is shown in (a), while the Mount Carmel region, as represented by the C9 (Tel Hai elementary school, Haifa) weather station is shown in (b).
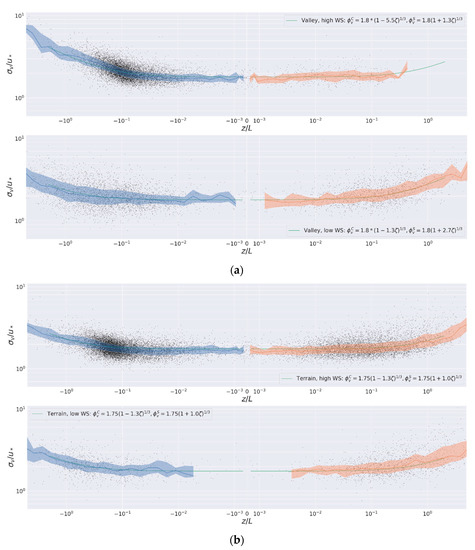
Figure 6.
The dimensionless turbulence parameters for , the cross-wind horizontal standard deviation of the wind velocity fluctuations, plotted as functions of both for weak wind (; lower part for each station) and for strong wind (; upper part for each station); The Zevulun valley region, as represented by the Z2 (Kiryat Motzkin) weather station is shown in (a), while the Mount Carmel region, as represented by the C9 (Tel Hai elementary school, Haifa) weather station is shown in (b).
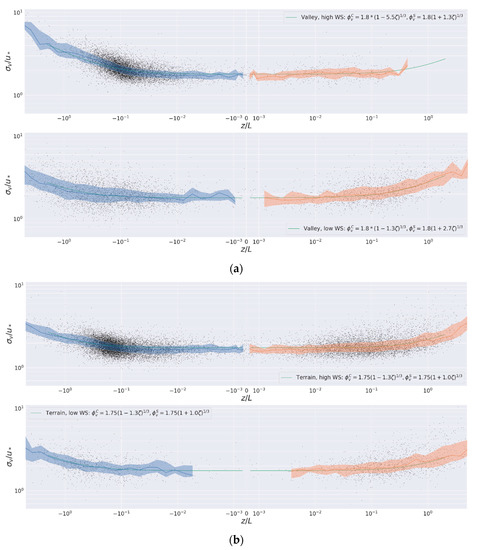
Figure 7.
The dimensionless turbulence parameters for , the vertical standard deviation of the wind velocity fluctuations, plotted as functions of both for weak wind (; lower part for each station) and for strong wind (; upper part for each station); The Zevulun valley region, as represented by the Z2 (Kiryat Motzkin) weather station is shown in (a), while the Mount Carmel region, as represented by the C9 (Tel Hai elementary school, Haifa) weather station is shown in (b).

Table 2.
The standard deviations of wind-velocity fluctuations in the Zevulun valley region, as represented by the Z2 (Kiryat Motzkin) weather station and the ridge of Mount Carmel, as represented by the C9 (Tel Hai elementary school, Haifa) weather station.
In Figure 8 the diurnal hourly distribution of stabilities for the summer season based on the stability parameter is presented. The five categories we chose are adopted from [34]: for the neutral , very stable/unstable stratification , and in between the stable/unstable regime. A very distinct difference can be seen as the station on Mount Carmel exhibits a more pronounced stable stratification and less convective stability compared to the station in the Zevulun valley.
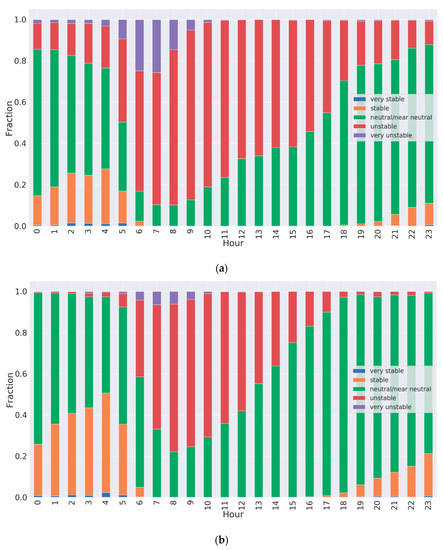
Figure 8.
The hourly distribution of the atmospheric stability at the (a) Z2–Kiryat Motzkin and (b) C9–Tel Hai elementary school, Haifa weather stations. All time points are in LST (UTC+2).
4. Discussion and Summary
This study has analysed the diurnal and spatial patterns of the wind field in the HBA, with its two distinct regions of Mount Carmel and Zevulun valley. It was found that the examined weather stations in this region exhibit similar wind speed diurnal regime. In this regime the wind speed is weak (~0.5–2 m/s) during the night and grows stronger during the morning until a maximum of around 3–6 m/s is reached around noon time. It was also found that this regime is similar to metropolitan area of Tel-Aviv. This result is in line with the wind speed regime farther to the south of Israel, the southern coastal plain [35]. As the HBA, metropolitan Tel-Aviv and the southern coastal plain are all regions that are adjacent to the Mediterranean Sea, it can be deduced that they are all affected by the land-sea temperature difference. This phenomenon is closely related to the sea breeze [35].
The spatial analysis of the wind field in this study has shown two different flow regimes that may develop during the night time in Mount Carmel. One regime is characterized by a relatively uniform south-westerly winds. The other manifests a divergence of the flow between the two slopes, where on the western slope south to south-south-west wind directions occur and on the eastern slope west to south-west winds. This phenomenon of two wind regimes, a uniform one and the other separated by the watershed line was also found in relation to wintery rain events in Mount Carmel. The uniform regime was characterized by southeastern winds, while during the separated regime, mainly south-western to western winds were measured on the western side of the mountain, and on the eastern side northwesterly or southeasterly winds [2]. The fact that this and the previously mentioned studies, although each deals with different seasons, and finds different typical winds, find flow patterns of either uniform or separated flow patterns on Mount Carmel, supports the insight that the topographical disturbance posed by Mount Carmel may occasionally lead to different flow patterns in each of the mountains’ sides.
The analysis of the diurnal regime of the wind directions in the HBA has shown periods of uni-modal wind direction distribution during the night time, although the wind speed is rather weak. During these periods, the wind distribution is centred around the south or south-east on Mount Carmel and mostly eastern or south-easterly in the Zevulun valley. These periods begin on 0400 h on Mount Carmel and 0300 h in the Zevulun valley. Compared to these, south-westerly winds develop in outskirts of Tel-Aviv from 2200 h and in inner Tel-Aviv from 2330 h. In the case of Tel-Aviv area, it is possible that this area is influenced by down slope flows from the Judean mountain range.
The night time periods of uni-modal wind directions’ distributions may be associated by the land breeze that develop due to katabatic winds and land-sea differential cooling. Interestingly, a numerical weather prediction (NWP) model with a space-time resolution of 2 km–6 h that was used to reconstruct the timing of the land breeze phenomenon in the Israeli summer was able to provide a rather accurate timing for the Tel-Aviv area (2100–0100 h), but predicted a too early beginning of this period (2300 h) in the HBA [36]. This suggests that the complex and heterogeneous topography of the HBA requires a specific modelling effort in order to be described accurately.
Figure 5, Figure 6 and Figure 7 show a fit to the semi-empirical MOST functions (Equation (5)) for the stable as well as the unstable regimes. We should note that the free convective regime is known to scale using mixed layer height [37]. According to [38], below the free convective layer there exists two more sublayers, a shallow dynamic sublayer up to and a convective-dynamic sublayer above up to . Both our measurements are at about twice the averaged canopy height, and therefor are expected to be mostly in the convective-dynamic sublayer (which scales with ).
The analysis of turbulent parameters in complex terrain, such as the respective standard deviations of the longitudinal, transverse and vertical components of the wind, might be affected, especially for developed winds, by an upwind change of surface roughness (e.g., [39,40]). This issue can be addressed by analysis according to wind direction sectors correlated with different upwind roughness (e.g., [39]). The wind characteristics in the HBA, as exhibited in Figure 4, are essentially confined in a single sector during night (with weak wind and stable to neutral stratification) and a single one during the day (with developed winds and unstable to neutral stratification). Therefore, there is no need to address sectors of difference surface roughness.
Regarding the values of our empirical fits (Table 2) to the parameters of Equation (6), these are well within the common range of values for these parameters documented the literature (e.g., [26,41]), although in the ridge station horizontal homogeneity is only approximate. We should note that in accordance with [39] we also find that there is a distinct difference between data points measured in the valley and the ridge stations. In the neutral stability limit () we obtain for valley and complex terrain, respectively. This value agrees with the mean value of given by [42], which is 1.25 over flat terrain and is lower than their 1.23 over complex terrain, and in accordance with the value of 1.2 of [39] for a station surrounded by different topography. Our valley values are lower than those of [43] which are around 1.3 and 1.4 for along- and cross- valley, respectively. Our interpretation to that is that the Zevulun valley’s station in this study resembles a flatter area than a typical valley.
In contrast to the values of , the first parameter of Equation (5), the estimates for the second parameter, , vary dramatically between strong () and weak () wind speeds and between the two sites (Table 2). The difference between strong and weak winds is especially pronounced in the valley station in convective conditions; due to the urban heat island phenomena however, the valley station recorded too little data in the stable regime for the difference between strong and weak winds to be statistically significant–and this is further corroborated by the low frequency of stable regimes in Figure 8 discussed below. In the ridge station, a difference between strong and weak winds was only found for the vertical standard deviations.
From the hourly distribution of stabilities for the summer season (Figure 8), both stations, the flat urban valley station and the complex terrain ridge station, display neutral and stable conditions during night-time, with neutral ones being more common. In the flat valley urban station, we also have a small contribution of unstable conditions. During the day both unstable (convective) and neutral condition are dominant, with the fraction of neutral conditions significantly increasing during the day, becoming pronounced from early afternoon till evening. However, it can be clearly seen that these two stations, exhibit pronounced differences. In the ridge station the unstable and certainly the very unstable day conditions are less pronounced. This can be attributed to the stronger winds typical to mountain top ridge areas. Regarding the night-time, the ridge station shows a higher proportion of stable stratifications, which can be attributed to two contributions: the heat island forming more effectively in flat areas, and the higher elevation or shallower atmospheric column for the ridge station leading to more efficient radiative cooling.
Author Contributions
Conceptualization, Z.K. and E.F.; Data curation, Z.K., M.B.-E., Y.A. and E.F.; Formal analysis, Z.K., M.B.-E. and E.F.; Funding acquisition, Z.K., E.T. and E.F.; Methodology, Z.K. and E.F.; Project administration, Z.K., E.T. and E.F.; Resources, Z.K., E.T. and E.F.; Software, M.B.-E., Y.A. and E.F.; Supervision, Z.K., E.T. and E.F.; Validation, Z.K. and E.F.; Visualization, Z.K., M.B.-E., Y.A. and E.F.; Writing–original draft, Z.K. and E.F.; Writing—Review and editing, Z.K., M.B-.E. and E.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Israeli Ministry of Environmental Protection, grant number 162-4-2.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data obtained from the ongoing monitoring network of the HBUA (Haifa bay municipal association for environmental protection) is available on http://www.envihaifa.net accessed on 29 September 2020.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- CBS. I.C.B. of S. Statistical Abstract of Israel—No.71. Available online: https://www.cbs.gov.il/he/publications/doclib/2020/2.shnatonpopulation/st02_25.pdf (accessed on 8 November 2020).
- Goldreich, Y.; Freundlich, A.; Alpert, P. Rainfall anomaly over the lee side of Mount Carmel (Israel) and the associated wind field. J. Appl. Meteorol. 1997, 36, 748–762. [Google Scholar] [CrossRef]
- Federman, R.; Mendelson, A.; Romem, E.; Mor-Federman, T.; Lahav, C.; Ron, M.; Ramon, U. Zevulun Survey—Survey, Analysis and Evaluation of Nature, Landscape and Human Heritage; Open Landscape Institute (OLI): Tel-Aviv, Israel, 2015. [Google Scholar]
- Freiman, M.T.; Hirshel, N.; Broday, D.M. Urban-Scale variability of ambient particulate matter attributes. Atmos. Environ. 2006, 40, 5670–5684. [Google Scholar] [CrossRef]
- Yuval; Broday, D.M. High-Resolution spatial patterns of long-term mean concentrations of air pollutants in Haifa Bay area. Atmos. Environ. 2006, 40, 3653–3664. [Google Scholar] [CrossRef]
- Eitan, O.; Yuval; Barchana, M.; Dubnov, J.; Linn, S.; Carmel, Y.; Broday, D.M. Spatial analysis of air pollution and cancer incidence rates in Haifa Bay, Israel. Sci. Total Environ. 2010, 408, 4429–4439. [Google Scholar] [CrossRef] [PubMed]
- Broday, D.; Dayan, U.; Aharonov, E.; Laufer, D.; Adel, M. Emissions from gas processing platforms to the atmosphere-case studies versus benchmarks. Environ. Impact Assess. Rev. 2020, 80, 106313. [Google Scholar] [CrossRef]
- Gavze, E.; Fattal, E. A semi-analytical model for short-range near-ground continuous dispersion. Bound. Layer Meteorol. 2018, 169, 297–326. [Google Scholar] [CrossRef]
- Shnapp, R.; Bohbot-Raviv, Y.; Liberzon, A.; Fattal, E. Turbulence-Obstacle interactions in the Lagrangian framework: Applications for stochastic modeling in canopy flows. Phys. Rev. Fluids 2020, 5, 094601. [Google Scholar] [CrossRef]
- Koch, J.; Dayan, U. A synoptic analysis of the meteorological conditions affecting dispersion of pollutants emitted from tall stacks in the coastal plain of Israel. Atmos. Environ. 1992, 26, 2537–2543. [Google Scholar] [CrossRef]
- Bitan, A.; Rubin, S. Climatic Atlas of Israel for Physical and Environmental Planning and Design; Ramot Publishing—Tel Aviv University: Tel-Aviv, Israel, 1991. [Google Scholar]
- Saaroni, H.; Levi, E.; Ziv, B. Particulate matter in the summer season and its relation to synoptic conditions and regional climatic stress—The case of Haifa, Israel. Water Air Soil Pollut. 2018, 229. [Google Scholar] [CrossRef]
- Alpert, P.; Osetinsky, I.; Ziv, B.; Shafir, H. A new seasons definition based on classified daily synoptic systems: An example for the eastern Mediterranean. Int. J. Climatol. 2004, 24, 1013–1021. [Google Scholar] [CrossRef]
- Finkelstein, P.L.; Kaimal, J.C.; Gaynor, J.E.; Graves, M.E.; Lockhart, T.J. Comparison of wind monitoring systems. Part I: In situ sensors. J. Atmos. Ocean. Technol. 1986, 3, 583–593. [Google Scholar] [CrossRef]
- Bowen, B.M. Improved wind and turbulence measurements using a low-cost 3-D sonic anemometer at a low-wind site. Open Atmos. Sci. J. 2008, 2, 131–138. [Google Scholar] [CrossRef]
- Izumi, Y.; Barad, M.L. Wind speeds as measured by cup and sonic anemometers and influenced by tower structure. J. Appl. Meteorol. 1970, 9, 851–856. [Google Scholar] [CrossRef]
- Busch, N.E.; Kristensen, L. Cup anemometer overspeeding. J. Appl. Meteorol. 1976, 15, 1328–1332. [Google Scholar] [CrossRef]
- Kristensen, L. Cup anemometer behavior in turbulent environments. J. Atmos. Ocean. Technol. 1998, 15, 5–17. [Google Scholar] [CrossRef]
- Louka, P.; Belcher, S.E.; Harrison, R.G. Coupling between air flow in streets and the well-developed boundary layer aloft. Atmos. Environ. 2000, 34, 2613–2621. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Yao, X.; Fu, B.; Lü, Y.; Sun, F.; Wang, S.; Liu, M. Comparison of four spatial interpolation methods for estimating soil moisture in a complex terrain catchment. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Palomino, I.; Martín, F. A simple method for spatial interpolation of the wind in complex terrain. J. Appl. Meteorol. 1995, 34, 1678–1693. [Google Scholar] [CrossRef]
- Fattal, E. A non-homogenous non-Gaussian Lagrangian stochastic model for pollutant dispersion in complex topography—Comparison to Haifa 2009 urban tracer campaign (in Hebrew); 2014/56/53/5614; Israel Institute for Biological Research: Ness-Ziona, Israel, 2014. [Google Scholar]
- Goodin, W.R.; McRa, G.J.; Seinfeld, J.H. A comparison of interpolation methods for sparse data: Application to wind and concentration Fields. J. Appl. Meteorol. 1979, 18, 761–771. [Google Scholar] [CrossRef][Green Version]
- Stull, R.B. (Ed.) An Introduction to Boundary Layer Meteorology; Springer Netherlands: Dordrecht, The Netherlands, 1988; ISBN 978-90-277-2769-5. [Google Scholar]
- Wilson, J.D. Monin-Obukhov functions for standard deviations of velocity. Bound. Layer Meteorol. 2008, 129, 353–369. [Google Scholar] [CrossRef]
- Charuchittipan, D.; Wilson, J.D. Turbulent kinetic energy dissipation in the surface layer. Bound. Layer Meteorol. 2009, 132, 193–204. [Google Scholar] [CrossRef]
- Hicks, B.B.; Pendergrass, W.R.; Vogel, C.A.; Keener, R.N.; Leyton, S.M. On the micrometeorology of the southern great plains 1: Legacy relationships revisited. Bound. Layer Meteorol. 2014, 151, 389–405. [Google Scholar] [CrossRef]
- Klausner, Z.; Fattal, E. An objective and automatic method for identification of pattern changes in wind direction time series. Int. J. Climatol. 2011, 31, 783–790. [Google Scholar] [CrossRef]
- Cheng, H.; Castro, I.P. Near wall flow over urban-like roughness. Bound. Layer Meteorol. 2002, 104, 229–259. [Google Scholar] [CrossRef]
- Raupach, M.R.; Antonia, R.A.; Rajagopalan, S. Rough-Wall turbulent boundary layers. Appl. Mech. Rev. 1991, 44, 1–25. [Google Scholar] [CrossRef]
- Trini Castelli, S.; Falabino, S. Analysis of the parameterization for the wind-velocity fluctuation standard deviations in the surface layer in low-wind conditions. Meteorol. Atmos. Phys. 2013, 119, 91–107. [Google Scholar] [CrossRef]
- Hanna, S.R.; Britter, R.E. Wind Flow and Vapor Cloud Dispersion at Industrial and Urban Sites; Center for Chemical Process Safety/AIChE: New York, NY, USA, 2002; ISBN 0-8169-0863-X. [Google Scholar]
- Irwin, J.S. A theoretical variation of the wind profile power-law exponent as a function of surface roughness and stability. Atmos. Environ. 1979, 13, 191–194. [Google Scholar] [CrossRef]
- Goldreich, Y. The Climate of Israel: Observation, Research and Application; Springer: New York, NY, USA, 2003; ISBN 978-1-4613-5200-6. [Google Scholar]
- Berkovic, S.; Feliks, Y. The land breeze characteristics in Israel during the summer by the MM5 model. In Proceedings of the World Weather Research Program Symposium on Nowcasting and Very Short Range Forecasting, Toulouse, France, 5 September 2005; p. 1.05. [Google Scholar]
- Deardorff, J.W. Convective velocity and temperature scales for the unstable planetary boundary layer and for rayleigh convection. J. Atmos. Sci. 1970, 27, 1211–1213. [Google Scholar] [CrossRef]
- Kader, B.A.; Yaglom, A.M. Mean fields and fluctuation moments in unstably stratified turbulent boundary layers. J. Fluid Mech. 1990, 212, 637. [Google Scholar] [CrossRef]
- Al-Jiboori, M.H.; Yumao, X.; Yongfu, Q. Turbulence characteristics over complex terrain in West China. Bound. Layer Meteorol. 2001, 101, 109–126. [Google Scholar] [CrossRef]
- Figueroa-Espinoza, B.; Salles, P. Local monin-obukhov similarity in heterogeneous terrain. Atmos. Sci. Lett. 2014, 15, 299–306. [Google Scholar] [CrossRef]
- Roth, M. Review of atmospheric turbulence over cities. Q. J. R. Meteorol. Soc. 2000, 126, 941–990. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Dutton, J.A. Atmospheric Turbulence: Models and Methods for Engineering Applications, 1st ed.; Wiley-Interscience: New York, NY, USA, 1984; ISBN 0471057142. [Google Scholar]
- de Franceschi, M.; Zardi, D.; Tagliazucca, M.; Tampieri, F. Analysis of second-order moments in surface layer turbulence in an Alpine valley. Q. J. R. Meteorol. Soc. 2009, 135, 1750–1765. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).