Abstract
The combined effect of the sea surface temperature (SST) and the North Atlantic subtropical high-pressure system (NASH) in the interannual variability of the genesis of tropical cyclones (TCs) and landfalling in the period 1980–2019 is explored in this study. The SST was extracted from the Centennial Time Scale dataset from the National Oceanic and Atmospheric Administration (NOAA), and TC records were obtained from the Atlantic Hurricane Database of the NOAA/National Hurricane Center. The genesis and landfalling regions were objectively clustered for this analysis. Seven regions of TC genesis and five for landfalling were identified. Intercluster differences were observed in the monthly frequency distribution and annual variability, both for genesis and landfalling. From the generalized least square multiple regression model, SST and NASH (intensity and position) covariates can explain 22.7% of the variance of the frequency of TC genesis, but it is only statistically significant (p < 0.1) for the NASH center latitude. The SST mostly modulates the frequency of TCs formed near the West African coast, and the NASH latitudinal variation affects those originated in the Lesser Antilles arc. For landfalling, both covariates explain 38.7% of the variance; however, significant differences are observed in the comparison between each region. With a statistical significance higher than 90%, SST and NASH explain 33.4% of the landfalling variability in the archipelago of the Bahamas and central–eastern region of Cuba. Besides, landfalls in the Gulf of Mexico and Central America seem to be modulated by SST. It was also found there was no statistically significant relationship between the frequency of genesis and landfalling with the NASH intensity. However, the NASH structure modulates the probability density of the TCs trajectory that make landfall once or several times in their lifetime. Thus, the NASH variability throughout a hurricane season affects the TCs trajectory in the North Atlantic basin. Moreover, we found that the landfalling frequency of TCs formed near the West Africa coast and the central North Atlantic is relatively low. Furthermore, the SST and NASH longitude center explains 31.6% (p < 0.05) of the variance of the landfalling intensity in the archipelago of the Bahamas, while the SST explains 26.4% (p < 0.05) in Central America. Furthermore, the 5-year moving average filter revealed decadal and multidecadal variability in both genesis and landfalling by region. Our findings confirm the complexity of the atmospheric processes involved in the TC genesis and landfalling.
1. Introduction
Tropical cyclones (TCs) can be defined as non-frontal synoptic low-pressure systems, which are formed over tropical or subtropical waters at a synoptic scale, with a warm core, organized deep convection, and a cyclonic circulation of wind on the surface. These systems mainly form from June to November (hereafter “TC season” or “hurricane season”). Besides, they are one of the most destructive natural phenomena in the world [1]. Therefore, any trend in TC activity is relevant to society, and particularly for coastal populations where the effects of TCs are most damaging. Historically, but particularly in recent years, the devastating impacts of TCs formed in the North Atlantic (NATL) basin have been a major concern for the economies and societies of affected countries [2]. In 2001, Goldenberg et al. [3] showed that the frequency of TCs did not exhibit a clear trend from 1971 to 2000, while TC intensity shows an increasing trend. Later, Trenberth [4] proposed that TC activity in the NATL basin had increased significantly by the end of the 20th century. Observations of TCs are considered to be more accurate since the introduction of meteorological satellites in the late 1970s, and since then, there has been no clear trend in the frequency of TCs on a global scale [5,6,7]. Nevertheless, the low quality of historical TC records prevents an accurate analysis of trends in intensity [8,9] and frequency [10,11,12]. Consequently, there are doubts as to whether changes in tropical cyclonic activity have exceeded the expected natural variability [13].
Several authors [14,15,16] have shown that enthalpy fluxes play an important role in the TCs evolution and are strongly modulated by sea surface temperature (SST). Surface fluxes of latent and sensible heat from the oceans provide the potential energy to TCs [14]. Rapid changes in SST are directly linked to changes in TCs intensity and trajectory [17]. Indeed, it has been related to the poleward migration in the average latitude at which TCs reach maximum intensity [7]. Furthermore, the changes in the cloud pattern and the rainfall associated with TCs are influenced by the SST through the atmospheric water vapor [13,18]. These relationships contribute to the air–sea enthalpy disequilibrium and therefore influence the TCs intensification and weakening process. The TCs over warm waters tend to intensify [19,20], while dissipating or weakening over cold waters [21].
The close relationship between TCs and SST has opened a debate on the possibility of an increase in the total number of TCs that form in a warmer ocean [22,23]. By 2006, Santer et al. [24] showed that SST in most regions of TC formation increased by several tenths of a degree Celsius during the past decades. Moreover, many scientists have found that increased SST [24,25] affects not only the hurricane frequency [26,27] but also hurricane intensity [28,29,30,31] and TC size [32]. Likewise, some studies have proposed that the increase in SST due to global warming has caused an increase in destructive TCs in recent decades [30,31,33]. Vecchi and Knutson [12] also showed that multidecadal variations in TC counts in the NATL basin appear to be strongly correlated with SST; however, the upward trend in NATL TCs counts since 1851 contains a spurious trend component due to missing storms before the satellite era [10,11,12].
One of the most important aspects to take into account in the analysis of TC activity is the landfalling events. When a TC makes landfall, it can produce high winds, storm surges, and severe flooding that can result in loss of life and widespread damage to coastal populations. The intensity of the North Atlantic subtropical high-pressure system (NASH) can also influence the TC activity in the NATL [34,35]. A westward extension and a strengthening of the NASH favors the non-curving moving tracks of TCs, while a weakening of the NASH leads to a recurving trajectory over the Atlantic Ocean, decreasing landfalling frequency [36]. Fudeyasu et al. [37] determined that most of the TCs landfalling on the United States (U.S.) form in the Caribbean Sea and the Gulf of Mexico and move north-westward toward the southern and eastern coasts. In agreement, previous findings of Kossin et al. [35] revealed that most landfalling storms form in the Gulf of Mexico, and have not experienced discernible trends.
Dailey et al. [38] examined the relationship between NATL SST and U.S. landfalling hurricanes, suggesting that landfall risk is sensitive to SST conditions, but that sensitivity varies by region and intensity. Some authors have even used a Poisson regression model to examine the relationship between U.S. landfalling hurricane events and principal climate variability modes, e.g., [38,39].
Despite the great number and variety of studies, most have evaluated individually the influence of the SST, wind shear, or teleconnection modes on the cyclonic activity in the NATL, while less attention has been given to landfall frequency and geographic distribution. However, this, beside the changes in their intensity, and frequency, are crucial factors to assess the human, environmental, and economic impacts of TCs. Indeed, a key question that has motivated the development of many research studies on this topic, e.g., [2,6,9,23,24,32], is whether the activity of TCs has changed and will change due to global warming. Additionally, previous works have shown a strengthening of the NASH in a warmer climate, but the cause of its long-term variability, as well as the impact of this variability on the TC activity, has been poorly investigated [36,40]. Thus, the goal of this study is to examine the influence of SST and NASH intensity and position on the interannual variability observed in TCs genesis and landfalling frequency from 1980 to 2018 in the whole NATL basin. To investigate further, the aim is also to consider different regions of the genesis of TCs and landfall.
This paper is organized into four sections. In Section 2 the hurricane data, the NASH, and the SST dataset are described. Additionally, it contains the methodology used, including the description of the generalized least square model and the Kernel density estimation. Section (Section 3.2). Section 4 contains conclusions.
2. Materials and Methods
2.1. Dataset
Historical records of TCs in the NATL basin from 1851 to 2019 were taken from the Atlantic hurricane database (HURDAT2) of the NOAA/National Hurricane Center. This dataset comprised a text format file of TC parameters, including location and intensity (maximum wind speed and minimum central pressure), taken every six hours [41,42,43]. The HURDAT2 database also includes the TCs landfall events.
The possibility of detecting TCs that did not approach land or ships during their trajectories was minimal before the beginning of the meteorological satellites era in the mid-1970s. Therefore, historical records in the HURDAT2 database may contain physically unsupported trends due to the uncertain storm detection at this time (e.g., [8,9,10,11,12]). Kossin et al. [8] point out that the intensity estimation methods based on satellite were improved with the introduction of the Dvorak technique [44,45].
Considering these limitations of TC records in the NATL basin, we followed the criteria of Kossin et al. [8] and Bathia et al. [46] for the selection of the study period. Several authors (e.g., [8,46,47,48]) pointed out that after 1980 the TCs records in the NATL present higher quality for climate analysis. Thus, we focus the following analysis on the period after 1980.
The June–November monthly mean SST data was obtained from the Centennial Time Scale (COBE SST2) dataset [49,50] of the National Oceanic and Atmospheric Administration (NOAA). Daily SST of this dataset was constructed as the sum of a trend, interannual variations, and daily changes, using in situ SST and sea ice concentration observations. The annual series of SST anomalies shown in Figure 1a was computed for the region confined between 5° N–50° N in latitude and 10° W–100° W in longitude. This region encompasses the genesis and peak of maximum intensity portions of all TCs formed from 1980 to 2019 in this area, as shown in Figure 1b.
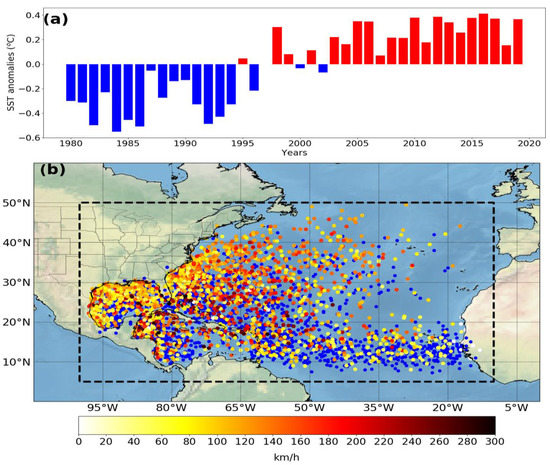
Figure 1.
(a) Centennial Time Scale (COBE) sea surface temperature (SST) anomalies time-series; (b) location of the genesis (blue points) and peak of maximum intensity (the color bar represents the maximum surface wind) of (tropical cyclones TCs) formed in the North Atlantic (NATL) basin. The genesis point is defined as the first reported location in the Atlantic hurricane database (HURDAT2) database. The black dashed line represents the interest area for the SST analysis. Period: June–November from 1980 to 2019.
To obtain a coherent physical insight of TCs activity in the NATL basin during the study period, we used the June–November monthly averages of the mean sea level pressure (MSLP) from the National Center for Environmental Prediction–National Center for Atmospheric Research (NCEP–NCAR) reanalysis fields on a 2.5° latitude by 2.5° longitude grid [51].
2.2. Methodology
To find inconsistencies in the HURDAT2 database records, we compared these datasets with the International Best Track Archive for Climate Stewardship database (IBTrACS) [52]. The IBTrCAS database collects the historical data of the best monitoring of tropical cyclones from all Regional Specialized Meteorological Centers and other agencies, and combines the different datasets in a single product. In our study period, both databases show similar records. Therefore, the analysis presented in this research is based on the HURDAT2 database.
The historical records of TC genesis (defined as the first reported location of the TC) and the landfalling events are separated into clusters applying statistical methods, which permitted to investigate the whole basin and each cluster separately. The cluster technique applied is similar to that described by Corporal-Lodangco et al. [53].
The center of the NASH was determined based on the nearest neighbor technique [54,55,56,57,58,59] to find the highest pressure value using the MSLP in the area between 15° N–60° N and 60° W–0°. Each grid point was compared to the 24 neighboring nodes. A grid point is a candidate to be the core of the NASH if its MSLP is higher than or equal to the eight near neighbors and higher than the other 16 nodes surrounding the eight neighbors around the single center grid point. In the case that several grid points have the same maximum pressure value, the grid point with the lowest latitude was considered as NASH center [54].
The Pearson’s correlation coefficient (hereafter r) was determined by applying a two-tailed test, using the effective number of degrees of freedom [60]. Furthermore, a t-test [61] was applied to determine the statistical significance of the correlations.
To understand the combined effect of the SST and NASH intensity and position on the interannual variability of cyclonic activity in the NATL basin, we applied the generalized least squares (GLS) estimation model. Similar to other multiple linear regression models, GLS allows us to estimate the unknown parameters of the linear relationship according to Equation (1):
where Y is the dependent variable, a is a vector containing the regression coefficients, X = [[Xij]] is a matrix (n_data x n_features) of the independent variables, and b is the intercept. Further information of the GLS model is provided by Safi and Saif [62] and Davidson and MacKinnon [63].
Kernel Density Estimation
To estimate the probability density of the TCs trajectory and intensity at landfall, the nonparametric kernel density estimation (KDE) was applied, following Equation (2):
where x is the independent variable of the kernel function K(x) and xi are the data points; f(x) is the smooth estimate; h is the selected bandwidth; and n is the length of the dataset. The KDE smooths each data point xi into a small density bumps and then sums all these small bumps together to obtain the final density estimate. The kernel function K(x) must commonly satisfy the condition , but may be considered arbitrary. The Gaussian kernel (Equation (3)) is a common choice [64]. Here, we used the classical KDE [65].
3. Results and Discussion
3.1. TC Genesis
From the cluster technique, seven regions, in which the genesis of TCs in the NATL frequently occurs, were identified. These are the tropical Central North Atlantic (G1, purple) that represents 14.9% of the total genesis counts in the study period, the Caribbean Sea (G2, red, 11.7%), the Lesser Antilles arc (G3, green, 13.1%), the coast of West Africa (G4, orange, 18.2%), the Central North Atlantic (G5, yellow, 6.2%), the northeast of the Bahamian archipelago (G6, brown, 21.3%), and the Gulf of Mexico (G7, blue, 14.6%), as shown in Figure 2 (top). The monthly seasonality of TCs formed on each cluster is represented in Figure 2 (bottom). Genesis at the beginning of the hurricane season generally occurs at high latitudes due to favorable thermodynamic conditions and in the Gulf of Mexico, while at the end of the season they are more frequent in the western Caribbean Sea and the central North Atlantic. The regions G1 and G4 exhibit the highest frequency of genesis in August and September, coinciding with the peak of the cyclonic season. These G1,4 TCs are frequently originated from African easterly waves.
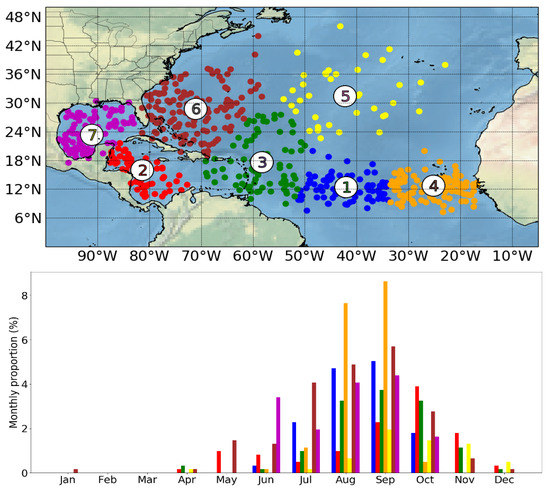
Figure 2.
Map representation of TC genesis clusters (top) and monthly proportion of genesis for each cluster (bottom). The monthly proportion was computed as the proportion of genesis count in a month for a cluster and the genesis counts in the whole basin in the study period (1980–2019).
The interannual variability of the cyclonic activity is deduced from Figure 3; however, the application of the 5-year moving average filter reveals the existence of a decadal time scale variability, more frequent in the TCs formed in G5 y G7 regions.
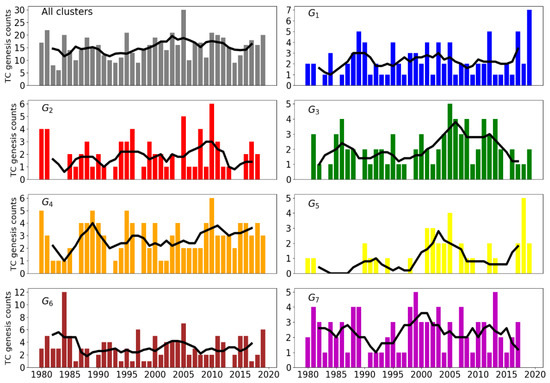
Figure 3.
Annual TC genesis counts for the whole NATL basin and for each cluster. The bold line shows the time series filtered with a centered 5-yr moving window. GN (N = 1, 2, 3, 4, 5, 6, 7) represents each genesis cluster.
The relationship between the mean annual SST during the TC season in the NATL basin and the number of genesis was first analyzed using Pearson’s correlation. A strong statistically significant correlation was observed at 95% significance level between SST and TC genesis throughout the basin, as well as in the G1 and G4 regions, as shown in Table 1. In G2, G3, and G5, the correlation coefficient ranged between 0.13 and 0.30, however, it was not statistically significant. The inverse correlation (p > 0.05) observed in the G6 and G7 clusters is curious, and constitutes a strong evidence of the complexity of the physical processes for TC genesis. In these two regions, the other preconditions described by Gray [66] seem to be more important. The NASH latitude center is significantly correlated with TC genesis frequency (r = 0.36) in the whole basin, while G3 (r = 0.36) is significantly correlated, too. No significant correlations were found between TC genesis and NASH intensity and NASH longitude center (Table 1).

Table 1.
Pearson’s correlation coefficients between annual time series of mean SST, the North Atlantic subtropical high-pressure system (NASH) intensity and NASH position (June to November) with the number of tropical cyclones (TCs) genesis in the whole NATL and each cluster. Statistical significance is marked with the bold text (p < 0.05). NASH latitude and NASH longitude represent the NASH center latitude and NASH center longitude, respectively.
When the frequency of genesis is modeled with the SST as a single covariate from the GLS linear regression model, both for the whole basin and for the GN regions (N = 1, 2, 3, 4, 5, 7), the genesis frequency increases with increasing SST, while an inverse pattern is observed in G6, as shown in Figure 4. However, SST only explains 12% (p < 0.05) of the genesis frequency variance throughout the basin and 9%, 15.1%, and 9.1% in G1, G4, and G5 regions, respectively. The northward latitudinal movement of the NASH center favors the genesis processes, explaining 12.9% (p < 0.05) of the variance in the entire basin. By regions, the latitude center of the NASH explains only the variability of the G3 region, with 13.1% (p < 0.05). It is notable that the intensity of NASH individually does not play an important role in the genesis of TCs. These results fully support the linear relationship obtained from Pearson’s correlation coefficient.
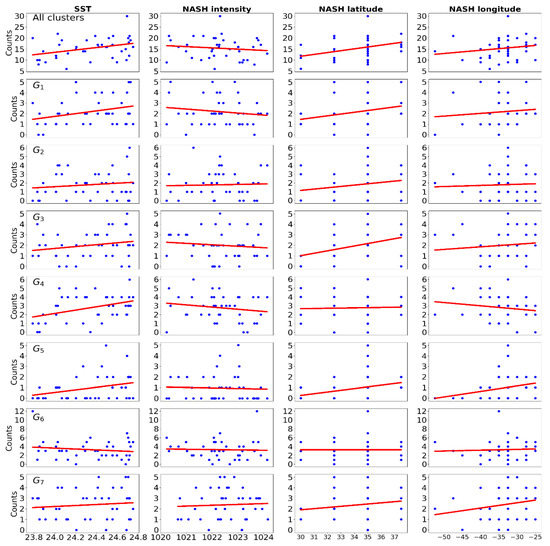
Figure 4.
Frequency of TC genesis adjusted from the generalized least squares (GLS) linear regression model using the SST, NASH intensity, and NASH position as single covariate. “All clusters” represents the whole basin and GN (N = 1, 2, 3, 4, 5, 6, 7) represents each genesis cluster.
As a logical next step, we consider how SST and NASH (intensity and position) modulate the frequency of genesis both throughout the basin and within each cluster (the four covariates do not contain significant linear trends over the study period). The results of the regression are shown in Table 2. The GLS multiple linear regression suggests that the SST and the NASH (intensity and position) covariates explain 22.7% of the genesis frequency variance over the whole basin; however, the relationship is only statistically significant (p < 0.05) for NASH center latitude. The GLS regression reveals that the G4 region is more dependent on the mean SST, while G3 is dependent on the latitudinal variation of the NASH center.

Table 2.
Generalized least squares (GLS) multiple linear regression of annual NATL genesis frequency (for the whole basin and for each cluster) onto the SST and NASH (intensity and position). The SST and NASH values are based on June–November. Statistical significance is marked with bold text (p < 0.05). SST is in °C and NASH intensity in hPa. NASH latitude and NASH longitude represent the NASH center latitude and NASH center longitude, respectively.
3.2. Landfall
An important key in the analysis of TC activity is the relationship between TC genesis and TC landfalling. Applying the cluster analysis technique, we identify the five most frequent regions for landfalling in the NATL basin: archipelago of the Bahamas, Jamaica, and the central−eastern region of Cuba and the western of La Española (L1, purple) with 15.1% of the recorded landfalling; the Florida Peninsula, the east coast of the United States up to 40°N latitude, and the coast of the Gulf of Mexico up to 87°W longitude (L2, red, 26.4%); the coasts of the Gulf of Mexico from longitude 87°W (L3, green, 24.4%); the western region of Cuba, the Yucatan Peninsula and Central America (L4, orange, 18.1%), and the arc of the Lesser Antilles and Puerto Rico (L5, blue, 15.8%), as shown in Figure 5. In this study, landfalling on the east coast of the United States from north of 40°N latitude and those that occurred on the islands located in the central North Atlantic were not considered.
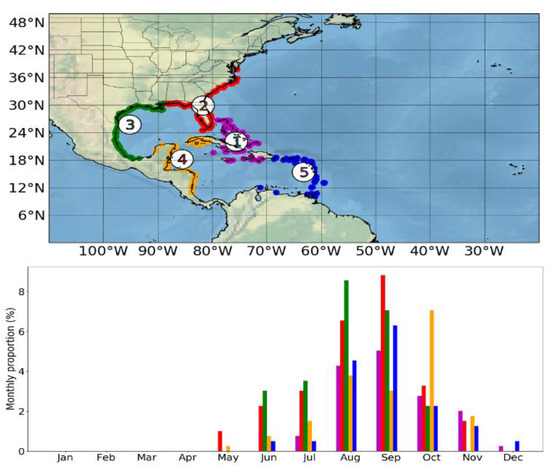
Figure 5.
Map representation of TC landfalling regions (top) and monthly proportion of landfalling for each cluster (bottom). The monthly proportion was computed as the proportion of landfalling count in a month for a cluster and the sum of total landfalling (L1 +…+ L5) (1980–2019). Note that landfalling on the east coast of the United States from 40°N latitude and those that occurred on the islands located in the central North Atlantic were not considered.
The landfalling monthly variation shows the maximum in August and September, although in regions L2 and L3, secondary maximums are observed in June and July. The secondary maximums are a consequence of the TCs genesis in the Gulf of Mexico at the beginning of the TC season, while in the region L4, a secondary maximum is observed in October, mainly because of the TCs that originate in the Western Caribbean Sea at the end of the hurricane season. For the entire NATL basin, the highest frequency of landfalling is observed in August and September. The landfalling frequency shows a similar monthly distribution to genesis frequency.
As appreciated in Figure 6, the annual evolution of landfalling events experienced a major frequency during the 2000 decade for all the clusters. A visual analysis of the time series filtered with a centered 5-year moving window reveals that great similarities exist between the landfall occurrence in L1 and L3, L2 and L4, and are greatly different in L5. The increase of annual landfalling in the latter part of the record is also evident, particularly in L1 and L2.
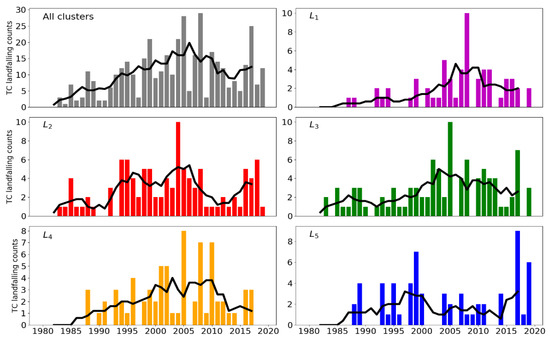
Figure 6.
Annual landfalling counts for the whole NATL basin and each cluster. The bold line shows the time series filtered with a centered 5-yr moving window. LN (N = 1, 2, 3, 4, 5) represents each landfalling cluster.
TC landfalling seems to have a direct relationship with the increase of SST. The Pearson correlation between the mean annual SST (June–November) and the NATL basin-wide (L1 +…+ L5) landfalling count of 0.52 is statistically significant at 95% of the significance level, as well as in regions L1, L3, and L4 with r = 0.44, r = 0.46, and r = 0.33, respectively. However, it is notable that the Pearson correlation between SST and landfalling is low in L2 and L5 (r = 0.30), but statistically significant at 90% of the significance level. For the whole basin, SST and landfalling counts exhibit a strong correlation (r = 0.52), statistically significant at 95% of the significance level. No statistically significant correlation was found between NASH intensity and TC landfalling counts. However, the correlation between the frequency of landfalling and the latitude NASH center in a whole basin is statistically significant (r = 0.42), as shown in Table 3. A significant correlation is also observed in L1 (r = 0.34) and L4 (r = 0.38) landfalling regions with the latitudinal variations of the NASH center. Moreover, L1 exhibits a strong Pearson correlation (0.40, p < 0.05) with the longitude of the NASH center.

Table 3.
Pearson’s correlation coefficients between annual time series of mean SST, the NASH intensity, and NASH position (center latitude and longitude) (June to November) with the landfalling counts in the whole NATL (L1 + ... + L5) and each cluster. Statistical significance is marked with bold text (p < 0.05). NASH latitude and NASH longitude represent the NASH center latitude and NASH center longitude, respectively.
From the GLS model, the SST and the NASH latitude covariates explain 38.7% of the variance of the landfalling events over the NATL basin with a statistically significant dependence (p < 0.05) on the SST. Similar results are obtained for cluster L1, but explaining only 33.4% of the variance. The SST mostly explains the variance (p < 0.05) of the L3 and L4 regions with 26.4% and 24.1%, respectively. In the case of the L2 and L5 regions, the landfalling events do not appear to have a significant modulation of the SST and the position of the NASH. In the same way, as for genesis, no dependence was observed between the landfalling events and the intensity of the NASH, as shown in Table 4.

Table 4.
Generalized least squares (GLS) multiple linear regression of annual NATL landfalling frequency (for the whole basin and each cluster) onto the SST and NASH (intensity and position). The SST and NASH values are based on June–November. Statistical significance is marked with the bold text (p < 0.05). SST is in °C and NASH intensity in hPa. NASH latitude and NASH longitude represent the NASH center latitude and NASH center longitude, respectively.
The landfalling of the TCs formed in G1 are distributed among all the LN regions (N = 1, 2, 3, 4, 5), although the highest frequency is observed in L5. Similarly, G3 and G4 also exhibit high frequencies of landfalling in L5, as shown in Figure 7. We assume that these distributions are mainly due to the wide range of trajectories for these TCs. Additionally, G3 has the highest frequency of landfalling in the central−eastern region of Cuba, the archipelago of the Bahamas, and the west of La Española (L1), and another secondary maximum in L2. TCs formed in the western Caribbean Sea frequently make landfall on the coasts of Central America, the Yucatan Peninsula, and the western region of Cuba (L4). In L2, TCs that form in G4 and G6 frequently make landfall, while those originating in the Gulf of Mexico (G7) generally struck the coastline in L3.
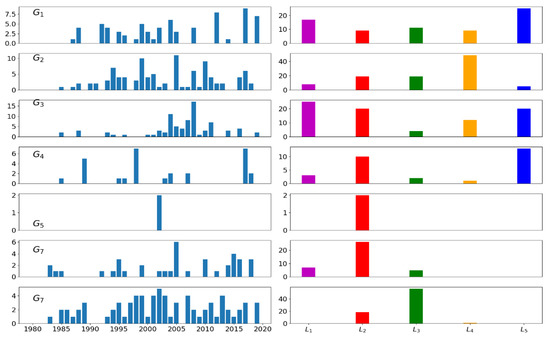
Figure 7.
Landfalling counts of TCs formed in each genesis region from 1980 to 2019 (left panel) and frequency of landfalling in each landfall region of each genesis region (right panel).
The landfalling events mostly depend on the TC trajectory, which is influenced by the large-scale steering flow. Changes in the NASH position and intensity induce large-scale flow changes that affect the TCs track and, consequently, the probability of landfalling. Figure 8 shows the TCs track density of TCs that made landfall in each region and the mean position of the NASH (composite using the specific month and specific year of landfalling event). As can be seen, there is no significant variation in the position of NASH center, however, there are appreciable differences in the NASH structure, which modulate the preferential trajectory followed by the TCs. For L1 and L2, the anticylonic ridge is less pronounced, while for L3 and L4, it penetrates to the Florida Peninsula. For the L5 region, the structure of the NASH shows a pattern similar to that observed for L1 and L2, although more contracted, suggesting that TCs that make landfall in L5 have a high probability to make landfall again in L1 or L2. The NASH structure directly influences the distribution of the probability density tracks of TC that make landfall. The effect is different depending on the genesis location. TCs that develop in the eastern part of the main development region (G4) tend to have a low probability of landfalling than those that develop in the western part (G1 and G3), due to the longer time over the tropical ocean. These results fully support the findings of Colbert and Soden [36], who pointed out that the evolution of NASH throughout a hurricane season affects the TCs trajectory in the NATL basin. When the NASH is strong and centered to the west, TCs are directed south toward the Gulf of Mexico, increasing the landfalling probability.
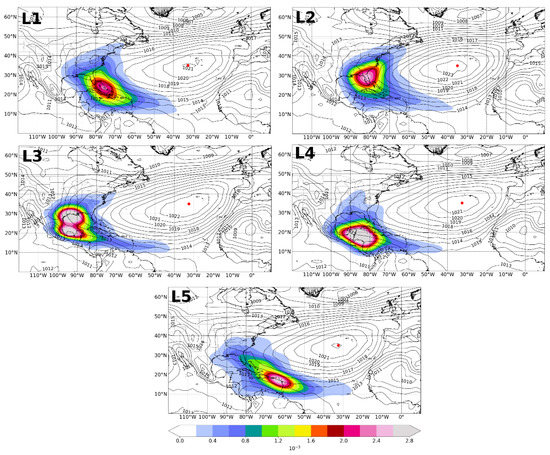
Figure 8.
Kernel density estimation (KDE) for the trajectory of TCs that make landfall in each region. Contour lines represent the composite of mean sea level pressure for a specific month and specific year that landfalling events occurred. The red point and LN (N = 1, 2, 3, 4, 5) represents the NASH center and each landfalling cluster, respectively.
These results are confirmed in Figure 9, which shows the position and mean structure of the NASH (considering only the months where landfalling occurred) for the year with the highest frequency of landfalling, both for the entire basin and each region. The steering flow imposed by the NASH circulation modulates the frequency of landfalling in the different regions. No significant variations are observed in the intensity of the NASH; however, the frequency of landfalling depends on the latitudinal variations of the NASH center. When the NASH center is shifted to the north, it favors that TCs make landfall in the L1, L2, and L5 regions, while an NASH center low in latitude modulates the movement of the TCs through the Caribbean Sea towards the Gulf of Mexico, favoring landfalling in Central America, the western region of Cuba, and the Mexican coast.
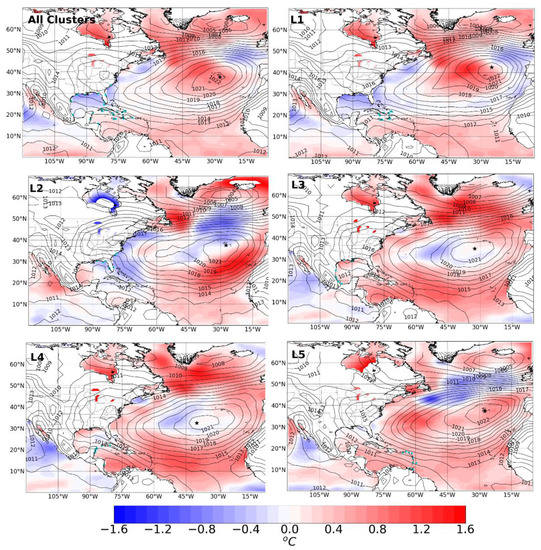
Figure 9.
Composite of NASH position and structure (contour) for months with landfalling events in the year of maximum landfalling frequency for the whole basin and each region. The shaded plots represent the mean SST anomalies for the same months and years of NASH position and structure composite. The black star point represents the NASH center, and cyan points represent landfalling events. “All clusters” represents the whole basin and LN (N = 1, 2, 3, 4, 5) represents each landfalling cluster.
From Figure 9, we can infer that landfalling occurs more frequently in regions where positive SST anomalies predominate in the surrounding waters. However, in L2 in 2004 (Table 5), there were 10 landfallings with negative SST anomalies in the northeast of the Gulf of Mexico, the Straits of Florida, and the seas surrounding the archipelago of the Bahamas, which is evidence of the strong modulating role of steering flow imposed by the NASH.

Table 5.
TC season of maximum landfalling frequency for whole basin and each region.
As shown in Figure 10, the probability density of TC landfalling intensity shows the most probable intensity ranging between 18 and 35 m/s. Despite the similarity of the patterns, the regions slightly differ from another in the probability density of the TC intensity spectrum at landfall. In all cases, the mean landfall intensity is approximately 35 m/s, although region L1 shows a mean intensity of 42.5 m/s, with two maximums of the probability density.
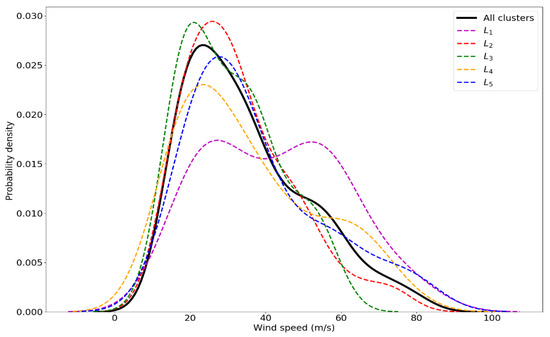
Figure 10.
Probability density of intensities at TC landfalling for the wide NATL (the sum of landfalling counts in all regions) and each cluster.
Moreover, the SST and NASH (intensity and position) covariates explain 31.6% of the variance of the intensity at which the TCs make landfall in the L1 region; however, the dependence is only significant (p < 0.05) for the SST and the NASH center longitude. In the case of region L4, the covariates explain 25.1%, but it is statistically significant for the NASH center latitude. No statistically significant relationships were found for the other regions.
4. Conclusions
The genesis of tropical cyclones (TCs) in the North Atlantic basin from 1980 to 2019 were objectively separated into groups and analyzed to identify the combined effects of sea surface temperature (SST) over the domain previously defined in Figure 1, and the North Atlantic subtropical high-pressure system (NASH) in its interannual variability. A strong Pearson correlation was identified between the frequency of genesis throughout the whole basin and the SST, as well as between the genesis frequency and NASH position. Nevertheless, the generalized least squares (GLS) multiple linear regression model showed that the SST and NASH covariates can only explain 22.7% of the variance in the genesis frequency, but the relationship is statistically significant with the NASH latitude center (p < 0.1). Furthermore, the multiple regression revealed that TC genesis near the coast of West Africa is more dependent on SST, while TCs formed near the Lesser Antilles arc are more influenced by the NASH position than by the SST. In the other genesis clusters, no statistically significant relationship was identified between SST and NASH. These findings show the complexity of the atmospheric processes involved in the TC genesis. Moreover, our results also reveal that the NATL TC genesis exhibits clear interbasin differences in frequency, but similar interannual variability.
Differences between each landfalling region, as well as the interannual variability of landfalling events, were also identified by Pearson’s correlation and multiple regression analysis. The frequency of landfalling in the Florida Peninsula and the east coast of the United States show a marked decadal variability, while the other regions exhibit a multidecadal variability. Similar to the frequency of genesis, the frequency of landfalling events throughout the basin shows a strong Pearson correlation with the SST and the NASH latitude center. However, the SST and NASH covariates only explain 38.7% (p < 0.05 for SST) of the variance in the study period. Regionally, both covariates explain 33.4% of the variance of the frequency of landfalling in the archipelago of the Bahamas and the central−eastern region of Cuba, while landfalling events in the coasts of the Gulf of Mexico and Central America seem to have a statistically significant dependence on SST. Similar to the frequency of genesis, no direct modulation of the NASH intensity and the landfalling frequency was found. However, the structure of NASH modulates the probability density of TC trajectories that made landfall one or more times in their lifetime. The TCs formed near the West Africa coasts and central North Atlantic show the lowest frequency of landfalls in the study period. The latitudinal shift of the NASH modulates the frequency of landfalling in each region. Furthermore, the SST explains only 24.4% of the variance of the intensity at which TCs make landfall in the Bahamas archipelago, while the NASH position explains 24.6% of those who make landfall in Central America and the western region of Cuba.
The results discussed above support the observation that it is not optimal to consider the genesis and landfalling regions as a whole when attempting to study the interannual variability of TC activity. The differences observed in both genesis and landfalling regions show that the TC activity is also dependent on local-scale factors and processes such as the SST, but also of the synoptic-scale influence of the NASH, which is an important feature to consider when making future projections of TC activity.
Author Contributions
A.P.-A., R.N., and L.G. conceived the idea of the study. A.P.-A., J.C.F.-A., and R.S. processed the data and created the figures. A.P.-A. analyzed the results and wrote the manuscript. All authors analyzed the results and revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The LAGRIMA project (grant no. RTI2018-095772-B-I00) was funded by the Ministerio de Ciencia, Innovación y Universidades, Spain. Partial support was also obtained from the Xunta de Galicia under the project “Programa de Consolidación e Estructuración de Unidades de Investigación Competitivas (Grupos de Referencia Competitiva)” (no. ED431C 2017/64-GRC).
Acknowledgments
The authors acknowledge the COBE SST2 data provided by the NOAA/OAR/ESRL (PSL, Boulder, CO, USA), obtained from their website at https://psl.noaa.gov/data/gridded/data.cobe2.html, and to the public HURDAT2 database (https://www.nhc.noaa.gov/data/hurdat/hurdat2-1851-2019-052520.txt) provided by the National Hurricane Center. A.P-A. acknowledges the support from UVigo PhD grants. J.C.F-A. and R.S. acknowledge the support from the Xunta de Galicia (Galician Regional Government) under the grants no. ED481A-2020/193 and ED481B 2019/070, respectively. We also thanks to Xunta de Galicia under Project ED431C 2017/64-GRC “Programa de Consolidación e Estructuración de Unidades de Investigación Competitivas (Grupos de Referencia Competitiva)”, co-funded by the European Regional Development Fund, European-Union (FEDER).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ankur, K.; Busireddy, N.K.R.; Osuri, K.K.; Niyogi, D. On the relationship between intensity changes and rainfall distribution in tropical cyclones over the North Indian Ocean. Int. J. Climatol. 2020, 40, 2015–2025. [Google Scholar] [CrossRef]
- Duan, H.; Chen, D.; Lie, J. The Impact of Global Warming on Hurricane Intensity. IOP Conf. Ser. Earth Environ. Sci. 2018, 199, 022045. [Google Scholar] [CrossRef]
- Goldenberg, S.B.; Landsea, C.W.; Mestas-Nuñez, A.M.; Gray, W.M. The Recent Increase in Atlantic Hurricane Activity: Causes and Implications. Science 2001, 293, 474–479. [Google Scholar] [CrossRef]
- Trenberth, K. Uncertainty in Hurricanes and Global Warming. Science 2005, 308, 1753–1754. [Google Scholar] [CrossRef]
- Frank, W.M.; Young, G.S. The interannual variability of tropical cyclones. Mon. Weather Rev. 2007, 135, 3587–3598. [Google Scholar] [CrossRef]
- Holland, G.; Bruyere, C.L. Recent intense hurricane response to global climate change. Clim. Dyn. 2014, 42, 617–627. [Google Scholar] [CrossRef]
- Kossin, J.; Emanuel, K.; Vecchi, G. The poleward migration of the location of tropical cyclone maximum intensity. Nature 2014, 509, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Kossin, J.P.; Olander, T.L.; Knapp, K.R. Trend Analysis with a New Global Record of Tropical Cyclone Intensity. J. Clim. 2013, 26, 9960–9976. [Google Scholar] [CrossRef]
- Landsea, C.W.; Harper, B.A.; Hoarau, K.; Knaff, J.A. Can we detect trends in extreme tropical cyclones? Science 2006, 313, 452–454. [Google Scholar] [CrossRef] [PubMed]
- Vecchi, G.A.; Knutson, T.R. Estimating annual numbers of Atlantic hurricanes missing from the HURDAT database (1878–1965) using ship track density. J. Clim. 2011, 24. [Google Scholar] [CrossRef]
- Landsea, C.W.; Vecchi, G.A.; Bengtsson, L.; Knutson, T.R. Impact of duration thresholds on Atlantic tropical cyclone counts. J. Clim. 2010, 23, 2508–2519. [Google Scholar] [CrossRef]
- Vecchi, G.A.; Knutson, T.R. On Estimates of Historical North Atlantic Tropical Cyclone Activity. J. Clim. 2008, 21, 3580–3600. [Google Scholar] [CrossRef]
- Knutson, T.R.; McBride, J.L.; Chan, J.; Emanuel, K.; Holland, G.; Landsea, C.; Held, I.; Kossin, J.P.; Srivastava, A.K.; Sugi, M. Tropical cyclones and climate change. Nat. Geosci. 2010, 3, 157–163. [Google Scholar] [CrossRef]
- Palmen, E. On the formation and structure of tropical hurricanes. Geophysica 1948, 3, 26–38. [Google Scholar]
- Miller, B.I. On the maximum intensity of hurricanes. J. Atmos. Sci. 1958, 15, 184–195. [Google Scholar] [CrossRef]
- Riehl, H. Tropical Meteorology; McGraw-Hill: New York, NY, USA, 1954; 392p. [Google Scholar]
- Kaplan, J.; DeMaria, M. Large-Scale Characteristics of Rapidly Intensifying Tropical Cyclones in the North Atlantic Basin. Weather Forecast. 2003, 18, 1093–1108. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Davis, C.A.; Fasullo, J. Water and energy budgets of hurricanes: Case studies of Ivan and Katrina. J. Geophys. Res. 2007, 112, D23106. [Google Scholar] [CrossRef]
- Shay, L.K.; Goni, G.J.; Black, P.G. Effects of a warm oceanic feature on Hurricane Opal. Mon. Weather Rev. 2000, 128, 1366–1383. [Google Scholar] [CrossRef]
- Goni, G.; Trinanes, J. Ocean thermal structure monitoring could aid in the intensity forecast of tropical cyclones. Eos. Trans. Am. Geophys. Union 2003, 84, 573–580. [Google Scholar] [CrossRef]
- Ma, Z.; Fei, J.; Liu, L.; Huang, X.; Cheng, X. Effects the cold core eddy on tropical cyclone intensity and structure under idealized air–sea interaction conditions. Mon. Weather Rev. 2013, 141, 1285–1303. [Google Scholar] [CrossRef]
- Trigo, R.M.; Gimeno, L. Observed Impacts on Planet Earth. In Weather Pattern Changes in Weather Mid-Latitudes the Tropics Pattern and Changes, Climate Change, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2016; Chapter 7; pp. 105–119. [Google Scholar]
- Sun, Y.; Zhong, Z.; Li, T.; Yijia, H.; Hu, Y.; Wan, H.; Chen, H.; Liao, Q.; Ma, C.; Li, Q. Impact of Ocean Warming on Tropical Cyclone Size and Its Destructiveness. Sci. Rep. 2017, 7, 8154. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Wen, Z.; Huang, R. Tropical cyclones in a warming climate. Sci. China Earth Sci. 2020, 63, 456–458. [Google Scholar] [CrossRef]
- Santer, B.D.; Wigley, T.M.L.; Gleckler, P.J.; Bonfils, C.; Wehner, M.F.; AchutaRao, K.; Barnett, T.P.; Boyle, J.S.; Brüggemann, W.; Fiorino, M.; et al. Forced and unforced ocean temperature changes in Atlantic and Pacific tropical cyclogenesis regions. Proc. Natl. Acad. Sci. USA 2006, 103, 13905–13910. [Google Scholar] [CrossRef]
- Knutson, T.R.; Delworth, T.L.; Dixon, K.W.; Held, I.M.; Lu, J.; Ramaswamy, V.; Schwarzkopf, M.D.; Stenchikov, G.; Stouffer, R.J. Assessment of Twentieth-Century Regional Surface Temperature Trends Using the GFDL CM2 Coupled Models. J. Clim. 2006, 19, 1624–1651. [Google Scholar] [CrossRef]
- Xie, L. The effect of Atlantic sea surface temperature dipole mode on hurricanes: Implications for the 2004 Atlantic hurricane season. Geophys. Res. Lett. 2005, 32, L03701. [Google Scholar] [CrossRef]
- Xie, K.; Liu, B. An ENSO-Forecast Independent Statistical Model for the Prediction of Annual Atlantic Tropical Cyclone Frequency in April. Adv. Meteorol. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Tan, Z. The Relationship between Sea Surface Temperature and Maximum Intensification Rate of Tropical Cyclones in the North Atlantic. J. Atmos. Sci. 2016, 73, 4979–4988. [Google Scholar] [CrossRef]
- Foltz, G.R.; Balaguru, K.; Hagos, S. Interbasin Differences in the Relationship between SST and Tropical Cyclone Intensification. Mon. Weather Rev. 2018, 146, 853–870. [Google Scholar] [CrossRef]
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.R. Changes in Tropical Cyclone Number, Duration, and Intensity in a Warming Environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Chen, D.; Qiu, B.; Wanget, W. Strengthening of the Kuroshio current by intensifying tropical cyclones. Science 2020, 368, 988. [Google Scholar] [CrossRef]
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Deser, C.; Alexander, M.A.; Xie, S.-P.; Phillips, A.S. Sea surface temperature variability: Patterns and mechanisms. Annu. Rev. Mar. Sci. 2010, 2, 115–143. [Google Scholar] [CrossRef] [PubMed]
- Kossin, J.P.; Camargo, S.J.; Sitkowski, M. Climate modulation of North Atlantic hurricane tracks. J. Clim. 2010, 23, 3057–3076. [Google Scholar] [CrossRef]
- Colbert, A.; Soden, B. Climatological variations in North Atlantic tropical cyclone tracks. J. Clim. 2012, 25, 657–673. [Google Scholar] [CrossRef]
- Fudeyasu, H.; Hirose, S.; Yoshioka, H.; Kumazawa, R.; Yamasaki, S. A Global View of the Landfall Characteristics of Tropical Cyclones. Trop Cyclone Res. Rev. 2014, 3, 178–192. [Google Scholar] [CrossRef]
- Dailey, P.S.; Zuba, G.; Ljung, G.; Dima, J.M.; Guin, J. On the Relationship between North Atlantic Sea Surface Temperatures and U.S. Hurricane Landfall Risk. J. Appl. Meteorol. Climatol. 2009, 48, 111–129. [Google Scholar] [CrossRef]
- Elsner, J.B.; Bossak, H.; Niu, H.F. Secular changes to the ENSO-U.S. hurricane relationship. Geophys. Res. Lett. 2012, 28, 4123–4126. [Google Scholar] [CrossRef]
- Li, W.; Li, L.; Ting, M.; Liu, Y. Intensification of Northern Hemisphere subtropical highs in a warming climate. Nat. Geosci. 2012, 5, 830–834. [Google Scholar] [CrossRef]
- Jarvinen, B.R.; Neumann, C.J.; Davis, M.A.S. A tropical cyclone data tape for the North Atlantic Basin, 1886–1983: Contents, limitations, and uses. NOAA Technical Memorandum 1984, NWS NHC 22, Coral Gables, FL, 24 p. Available online: http://www.nhc.noaa.gov/pdf/NWS-NHC-1988-22.pdf (accessed on 15 November 2020).
- Landsea, C.W.; Franklin, J.L. Atlantic Hurricane Database Uncertainty and Presentation of a New Database Format. Mon. Weather Rev. 2013, 141, 3576–3592. [Google Scholar] [CrossRef]
- Atlantic Hurricane Database (HURDAT2). Available online: https://www.nhc.noaa.gov/data/hurdat/hurdat2-1851-2019-052520.txt (accessed on 2 September 2020).
- Dvorak, V.F. Tropical cyclone intensity analysis and forecasting from satellite imagery. Mon. Wea. Rev. 1975, 103, 420–430. [Google Scholar] [CrossRef]
- Dvorak, V.F. Tropical Cyclone Intensity Analysis Using Satellite Data; NOAA Technical Report; NESDIS: Silver Spring, MD, USA, 1984; Volume 11, p. 47. [Google Scholar]
- Bhatia, K.T.; Vecchi, G.A.; Knutson, T.R.; Murakami, H.; Kossin, J.; Dixon, K.W.; Whitlock, C.E. Recent increases in tropical cyclone intensification rates. Nat. Commun. 2019, 10, 635. [Google Scholar] [CrossRef]
- Chang, E.K.M.; Guo, Y. Is the number of North Atlantic tropical cyclones significantly underestimated prior to the availability of satellite observations? Geophys. Res. Lett. 2007, 34, L14801. [Google Scholar] [CrossRef]
- Kang, N.; Elsner, J.B. Consensus on Climate Trends in Western North Pacific Tropical Cyclones. J. Clim. 2012, 25, 7564–7573. [Google Scholar] [CrossRef][Green Version]
- Centennial Time Scale (COBE SST2) Dataset. Available online: https://psl.noaa.gov/data/gridded/data.cobe2.html (accessed on 18 September 2020).
- Hirahara, S.; Ishii, M.; Fukuda, Y. Centennial-scale sea surface temperature analysis and its uncertainty. J. Clim. 2014, 27, 57–75. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying tropical cyclone best track data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Corporal-Lodangco, I.L.; Richman, M.B.; Leslie, L.M.; Lamb, P.J. Cluster Analysis of North Atlantic Tropical Cyclones. Procedia Comput. Sci. 2014, 36, 293–300. [Google Scholar] [CrossRef]
- Reboita, M.S.; Ambrizzi, T.; Silva, B.A.; Pinheiro, R.F.; da Rocha, R.P. The South Atlantic Subtropical Anticyclone: Present and Future Climate. Front. Earth Sci. 2019, 7, 8. [Google Scholar] [CrossRef]
- Degola, T.S.D. Impacts and Variability of the South Atlantic Subtropical Anticyclone on Brazil in the Present Climate and in Future Scenarios. Master’s Thesis, University of São Paulo, São Paulo, Brazil, 2013. [Google Scholar]
- Lambert, S.J. A cyclone climatology of the Canadian centre general circulation model. J. Clim. 1988, 1, 109–115. [Google Scholar] [CrossRef]
- Murray, R.J.; Simmonds, I. A numerical scheme for tracking cyclone centres from digital data. Austr. Meteorol. Mag. 1991, 39, 155–166. [Google Scholar]
- Sinclair, M.R. A diagnostic model for estimating orographic precipitation. J. Appl. Meteorol. Climatol. 1994, 33, 1163–1175. [Google Scholar] [CrossRef][Green Version]
- Sugahara, S. Annual Variation of the Frequency of Cyclones in the South Atlantic Ocean. In Proceedings of the XI Brazilian Congress of Meteorology, Rio de Janeiro, Brazil, 16–20 June 2000. [Google Scholar]
- Bretherton, C.S.; Widmann, M.; Dymnikov, V.P.; Wallace, J.M.; Bladé, I. The effective number of spatial degrees of freedom of a time-varying field. J. Clim. 1999, 12, 1990–2009. [Google Scholar] [CrossRef]
- Kim, T.K. T test as a parametric statistic. Korean J. Anesthesiol. 2015, 68, 540. [Google Scholar] [CrossRef] [PubMed]
- Safi, S.K.; Saif, E.A.A. Using GLS to Generate Forecasts in Regression Models with Auto-correlated Disturbances with simulation and Palestinian Market Index Data. Am. J. Theor. Appl. Stat. 2014, 3, 6–17. [Google Scholar] [CrossRef][Green Version]
- Davidson, R.; MacKinnon, J.G. Econometric Theory and Methods; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Wahiduzzaman, M.; Yeasmin, A. A kernel density estimation approach of North Indian Ocean tropical cyclone formation and the association with convective available potential energy and equivalent potential temperature. Meteorol. Atmos. Phys. 2020, 132, 603–612. [Google Scholar] [CrossRef]
- Loader, C.R. Bandwidth Selection: Classical or Plug-In? Ann. Stat. 1999, 27, 415–438. [Google Scholar] [CrossRef]
- Gray, W.M. Global view of the origin of tropical disturbances and storms. Mon. Weather Rev. 1968, 96, 669–700. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).