Reproducibility of the Quantification of Reversible Wall Interactions in VOC Sampling Lines
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Set-Up
- Configuration A: the detector receives the Zero Air flowing through the bypass while the VOC Mixture is sent to the vent (Ref. Figure 2); gas is entrapped in the test pipe.
- Configuration B: the detector receives the Zero Air flowing through the test pipe while the VOC Mixture is sent to the vent (Ref. Figure 2).
- Configuration C: the detector receives the VOC Mixture flowing through the bypass, while Zero Air is sent to the vent; Zero Air is entrapped in the test pipe.
- Configuration D: the detector receives the VOC Mixtures flowing through the test pipe while Zero Air is sent to the vent.
2.2. Materials
3. Methodology
3.1. Measurand Equation: Amount of VOC Adsorbed Per Unit Area of Wall at Equilibrium
3.2. Measurement Procedure
3.3. Bias Correction
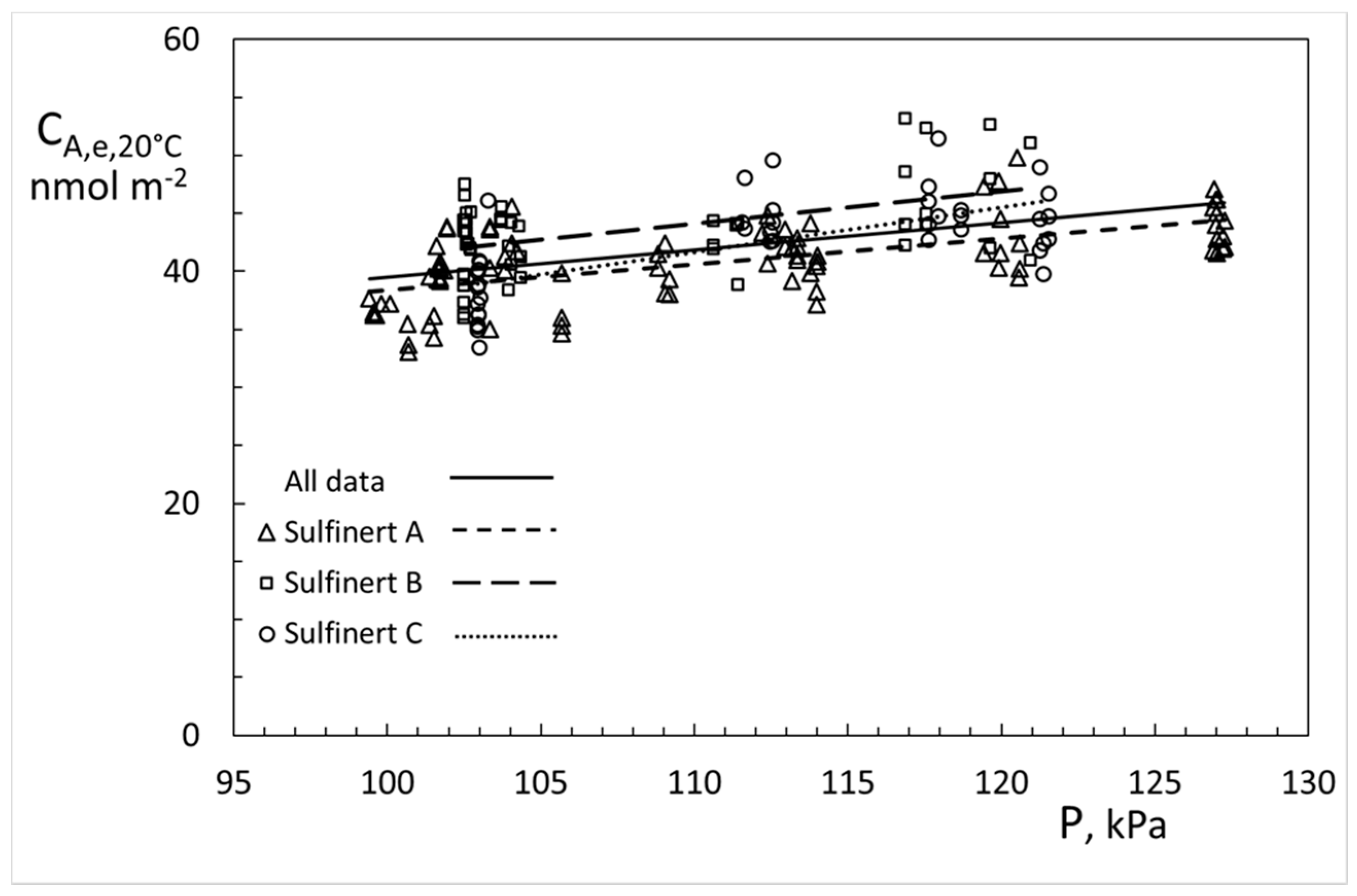
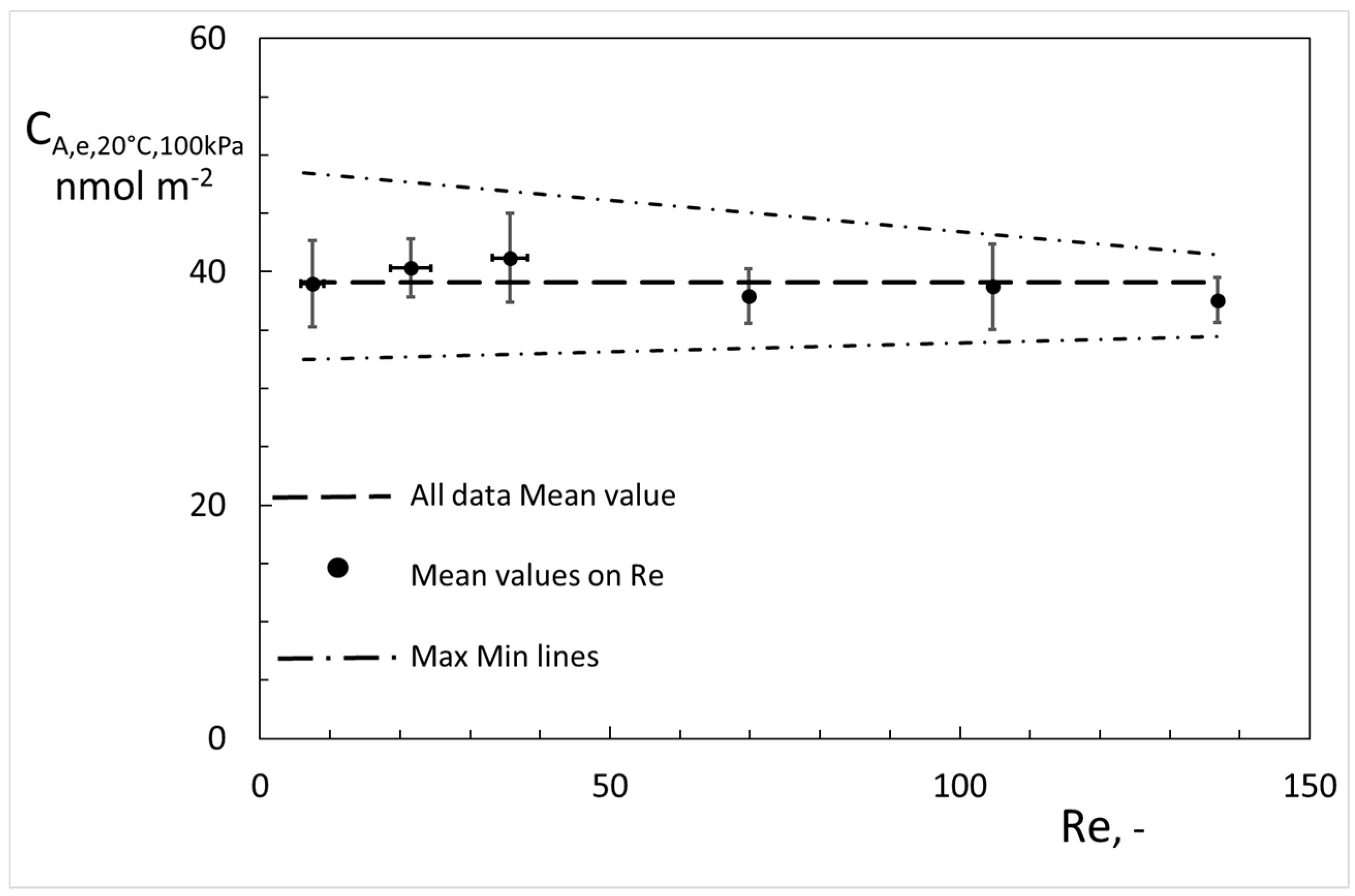
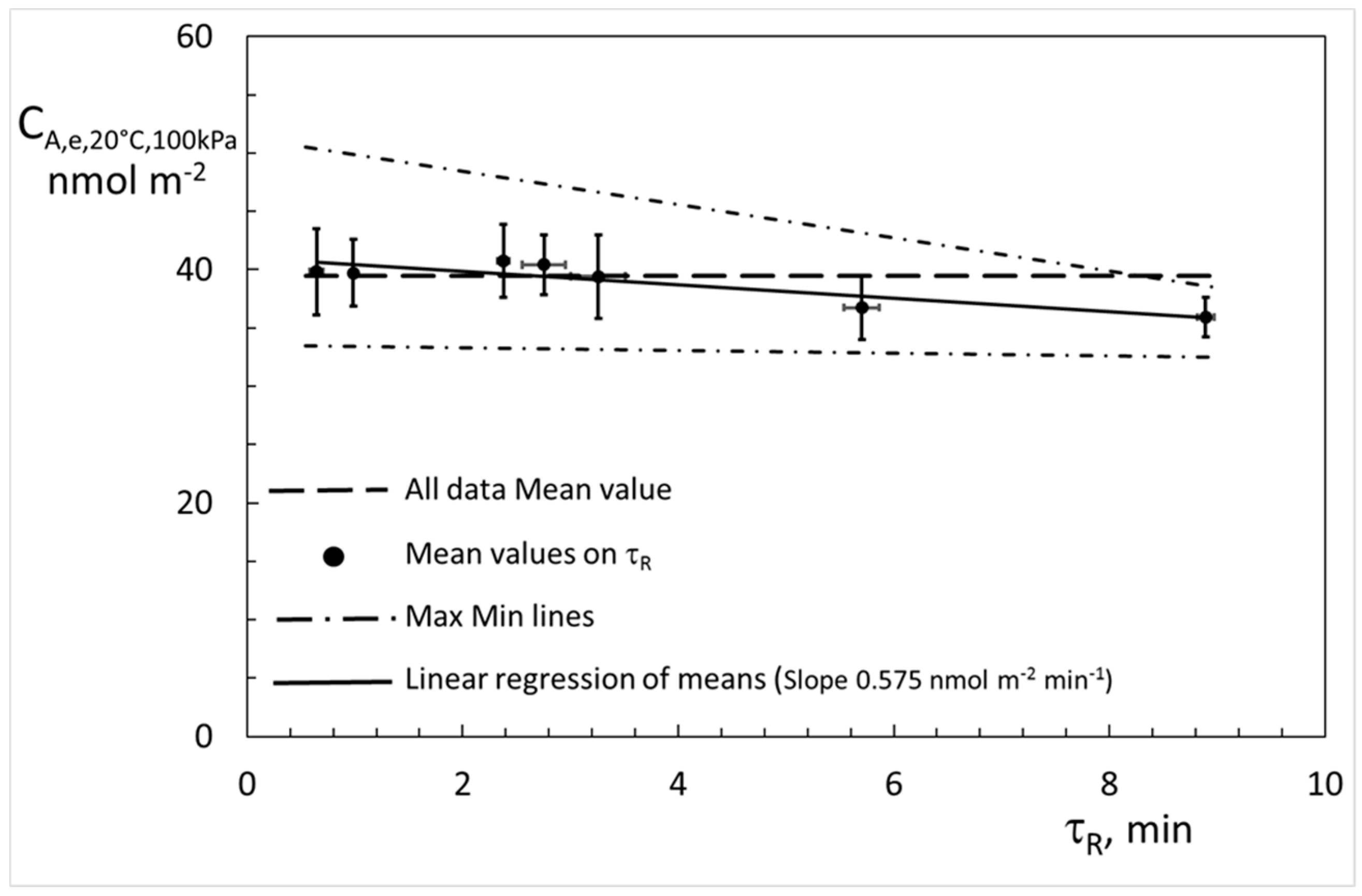
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sassi, G.; Demichelis, A.; Lecuna, M.; Sassi, M.P. Preparation of standard VOC mixtures for climate monitoring. Int. J. Environ. Anal. Chem. 2015, 95, 1195–1207. [Google Scholar] [CrossRef]
- Investigations for the Improvement of the Measurement of Volatile Organic Compounds from Floor Coverings within the Health-Related Evaluation of Construction Products. Available online: https://www.google.com.sg/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwj7wPb9wujuAhW5yYsBHSoFD_kQFjABegQIBBAC&url=https%3A%2F%2Fopus4.kobv.de%2Fopus4-bam%2Ffiles%2F19838%2FInvestigations%2Bfor%2Bthe%2Bimprovement%2Bof%2Bthe%2Bmeasurement%2Bof%2Bvolatile%2Borganic%2Bcompounds%2Bfrom%2Bfloor%2Bcoverings%2Bwithin%2Bthe%2Bhealth-related%2Bevaluation%2Bof%2Bconstruction%2Bproducts.pdf&usg=AOvVaw2zTZtBrY2SQkxJekU3Qu9r (accessed on 27 January 2021).
- Penkett, S. GAW Report No. 171: A WMO/GAW Expert Workshop on Global Long-Term Measurements of Volatile Organic Compounds (VOCs); World Meteorological Organization (WMO): Geneva, Switzerland, 2007. [Google Scholar]
- Rappengluck, B.; Apel, E.; Bauerfeind, M.; Bottenheim, J.; Brickell, P.; Cavolka, P.; Cech, J.; Gatti, L.; Hakola, H.; Honzak, J.; et al. The first VOC intercomparison exercise within the Global Atmosphere Watch (GAW). Atmos. Env. 2006, 20, 7508–7527. [Google Scholar] [CrossRef]
- Pascale, C. 19ENV06, MetClimVOC, Metrology for Climate Relevantvolatile Organic Compounds. European Metrology Programme for Innovation AndResearch (EMPIR). 2019. Available online: https://www.aramis-r.admin.ch/Kategorien/?ProjectID=47398&Sprache=en-US (accessed on 27 January 2021).
- Roberts, M.; Reiss, M.; Monger, G. Advanced Biology; Nelson Thornes: Cheltenham, UK, 2000. [Google Scholar]
- Rovelli, S.; Cattaneo, A.; Fazio, A.; Spinazzè, A.; Borghi, F.; Campagnolo, D.; Dossi, C.; Cavallo, D.M. VOCs Measurements in Residential Buildings: Quantification via Thermal Desorption and Assessment of Indoor Concentrations in a Case-Study. Atmosphere 2019, 10, 57. [Google Scholar] [CrossRef]
- De Gennaro, G.; Farella, G.; Marzocca, A.; Mazzone, A.; Tutino, M. Indoor and outdoor monitoring of volatile organic compounds in school buildings: Indicators based on health risk assessment to single out critical issues. Int. J. Environ. Res. Public Health 2013, 10, 6273–6291. [Google Scholar] [CrossRef] [PubMed]
- Adgate, J.; Church, T.; Ryan, A.; Ramachandran, G.; Fredrickson, A.; Stock, T.; Morandi, M.; Sexton, K. Outdoor, indoor, and personal exposure to VOCs in children. Environ. Health Perspect. 2004, 112, 1386–1392. [Google Scholar] [CrossRef] [PubMed]
- Demichelis, A.; Sassi, G.; Lecuna, M.; Sassi, M. Molar fraction stability in dynamic preparation of reference trace gas mixtures. IET Sci. Meas. Technol. 2016, 10, 414–419. [Google Scholar] [CrossRef]
- Vogt, S.R.; Landoni, C. Approaches to airborne molecular contamination assessment. In Metrology, Inspection, and Process Control for Microlithography XXV; SPIE: Washington, DC, USA, 2011. [Google Scholar]
- Hattori, T. Chemical Contamination Control in ULSI Wafer Processing. 2001. Available online: https://aip.scitation.org/doi/pdf/10.1063/1.1354411 (accessed on 27 January 2021).
- Gordon, S.M.; Szidon, J.P.; Krotoszynski, B.K.; Gibbons, R.D.; O’Neill, H.J. Volatile organic compounds in exhaled air from patients with lung cancer. Clin. Chem. 1985, 31, 1278–1282. [Google Scholar] [CrossRef] [PubMed]
- Peng, G.; Tisch, U.; Adams, O.; Hakim, M.; Shehada, N.; Broza, Y.Y.; Billan, S.; Abdah-Bortnyak, R.; Kuten, A.; Haick, H. Diagnosing lung cancer in exhaled breath using gold nanoparticles. Nat. Nanotechnol. 2009, 4, 669–673. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Dong, R.; Wang, X.; Lian, A.; Chi, C.; Ke, C.; Guo, L.; Liu, S.; Zhao, W.; Xu, G. Exhaled volatile organic 16ompound sas lung cancer biomarkers during one-lung ventilation. Sci. Rep. 2014, 4, 1–8. [Google Scholar]
- Adiguzel, Y.; Kulah, H. Breath sensors for lung cancer diagnosis. Biosens. Bioelectron. 2015, 65, 121–138. [Google Scholar] [CrossRef] [PubMed]
- Daneshkhah, A.; Siegel, A.P.; Agarwal, M. Volatile organic compounds: Potential biomarkers for improved diagnosis and monitoring of diabetic wounds. In Wound Healing, Tissue Repair, and Regeneration in Diabetes; Elsevier: Amsterdam, The Netherlands, 2020; pp. 491–512. [Google Scholar]
- Rhoderick, G.C.; Cecelski, C.E.; Miller, W.R.; Worton, D.R.; Moreno, S.; Brewer, P.J.; Viallon, J.; Idrees, F.; Moussay, P.; Kim, Y.D.; et al. Stability of gaseous volatile organic compounds contained in gas cylinders with different internal wall treatments. Elementa 2019, 7, 28. [Google Scholar] [CrossRef]
- Brewer, P.; Brown, R.; Mussell, E.; van Aswegen, S.; Ward, M.; Hill-Pearce, R.; Worton, D. Breakthrough in Negating the Impact of Adsorption in Gas Reference Materials. Anal. Chem. 2019, 91, 5310–5315. [Google Scholar] [CrossRef]
- Pagonis, D.; Krechmer, J.E.; De Gouw, J.; Jimenez, J.L.; Ziemann, P.J. Effects of gas–wall partitioning in Teflon tubing and instrumentation on time-resolved measurements of gas-phase organic compounds. Atmos. Meas. Tech. 2017, 10, 4687–4696. [Google Scholar] [CrossRef]
- Yeh, G.K.; Ziemann, P.J. Gas-wall partitioning of oxygenated organic compounds: Measurements, structure–activity relationships, and correlation with gas chromatographic retention factor. Aerosol Sci. Tech. 2015, 49, 727–738. [Google Scholar] [CrossRef]
- Krechmer, J.E.; Pagonis, D.; Ziemann, P.J.; Jimenez, J.L. Quantification of gas-wall partitioning in Teflon environmental chambers using rapid bursts of low-volatility oxidized species generated in situ. Environ. Sci. Tech. 2016, 50, 5757–5765. [Google Scholar] [CrossRef] [PubMed]
- Ye, P.; Ding, X.; Hakala, J.; Hofbauer, V.; Robinson, E.S.; Donahue, N.M. Vapor wall loss of semi-volatile organic compounds in a Teflon chamber. Aerosol Sci. Tech. 2016, 50, 822–834. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, R.; Charan, S.M.; Kenseth, C.M.; Zhang, X.; Seinfeld, J.H. Unified Theory of Vapor–Wall Mass Transport in Teflon-Walled Environmental Chambers. Environ. Sci. Tech. 2018, 52, 2134–2142. [Google Scholar] [CrossRef]
- Arrhenius, K.; Fischer, A.; Büker, O. Methods for sampling biogas and biomethane on adsorbent pipes after collection in gas bags. Appl. Sci. 2019, 9, 1171. [Google Scholar] [CrossRef]
- Liu, X.; Deming, B.; Pagonis, D.; Day, D.A.; Palm, B.B.; Talukdar, R.; Roberts, J.M.; Veres, P.R.; Krechmer, J.E.; Thornton, J.A.; et al. Effects of gas–wall interactions on measurements of semivolatile compounds and small polar molecules. Atmos. Meas. Tech. 2019, 12, 3137–3149. [Google Scholar] [CrossRef]
- McMurry, P.H.; Grosjean, D. Gas and aerosol wall losses in Teflon film smog chambers. Environ. Sci. Tech. 1985, 19, 1176–1182. [Google Scholar] [CrossRef]
- McCabe, W.; Smith, J.; Harriott, P. Unit Operations of Chemical Engineering; McGraw Hill: New York, NY, USA, 1956. [Google Scholar]
- Zhang, J.; Zhang, J.; Chen, Q.; Yang, X. A critical review on studies of volatile organic compound (VOC) sorption by building materials (RP-1097). Trans. Am. Soc. Heat. Refriger. Air Cond. Eng. 2001, 108, 162–174. [Google Scholar]
- Goss, K.-U. The air/surface adsorption equilibrium of organic compounds under ambient conditions. Crit. Rev. Environ. Sci. Tech. 2004, 34, 339–389. [Google Scholar] [CrossRef]
- Metrology for VOC Indicators in Air Pollution and Climate Change. Euramet European Metrology Research Programme (EMRP). 2013. Available online: https://www.era-learn.eu/network-information/networks/emrp/emrp-call-2013-energy-and-environment/metrology-for-voc-indicators-in-air-pollution-and-climate-change (accessed on 27 January 2021).
- Nowak, J.; Neuman, J.; Kozai, K.; Huey, L.; Tanner, D.; Holloway, J.; Ryerson, T.; Frost, G.; McKeen, S.; Fehsenfeld, F. A chemical ionization mass spectrometry technique for airborne measurements of ammonia. J. Geophys. Res Atmos. 2007, 112, D10. [Google Scholar] [CrossRef]
- Neuman, J.A.; Huey, L.G.; Ryerson, T.B.; Fahey, D.W. Study of inlet materials for sampling atmospheric nitric acid. Environ. Sci. Tech. 1999, 33, 1133–1136. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Standard Operating Procedures (SOPs) for Air Sampling in Stainless Steel Canisters for Non-Methane. 2012. Available online: https://library.wmo.int/index.php?lvl=notice_display&id=13702#.YCjHezLiuUk (accessed on 27 January 2021).
- Ma, C.; Haider, A.M.; Shadman, F. Atmospheric pressure ionization mass spectroscopy for the study of permeation in polymeric tubing. IEEE Trans. Semicond. Manuf. 1993, 6, 361–366. [Google Scholar] [CrossRef]
- Matsunaga, A.; Ziemann, P.J. Gas-wall partitioning of organic compounds in a Teflon film chamber and potential effects on reaction product and aerosol yield measurements. Aerosol Sci. Tech. 2010, 44, 881–892. [Google Scholar] [CrossRef]
- Lee, S.; Kim, M.E.; Oh, S.H.; Kim, J.S. Determination of physical adsorption loss of primary standard gas mixtures in cylinders using cylinder-to-cylinder division. Metrologia 2017, 54, L26. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Sassi, G.; Demichelis, A.; Sassi, M.P. Uncertainty analysis of the diffusion rate in the dynamic generation of volatile organic compound mixtures. Meas. Sci. Tech. 2011, 22, 105104. [Google Scholar] [CrossRef]
- Takahashi, C.; Kato, K.; Maruyama, M.; Kim, J.S.; Kao, M.-J.; Botha, A.; Dimashki, M. Final report on key comparison APMP. QM-K4 of ethanol in air. Metrologia 2003, 40, 08008. [Google Scholar] [CrossRef]
- Kato, K.; Maruyama, M.; Kim, J.S.; Hyub, O.S.; Woo, J.-C.; Kim, Y.; Bae, H.; Han, Q.; Zhou, Z. Final report on key comparison APMP. QM-K4. 1: Ethanol in nitrogen. Metrologia 2007, 45, 08007. [Google Scholar] [CrossRef]
- Guenther, F.R.; Miller, W.R.; Duewer, D.L.; Heo, G.S.; Kim, Y.-D.; van der Veen, A.M.H.; Konopelko, L.; Kustikov, Y.; Shor, N.; Brookes, C.; et al. International Comparison CCQM-K41: Hydrogen sulfide in nitrogen. Metrologia 2007, 44, 08004. [Google Scholar] [CrossRef]
- Kim, Y.-D.; Heo, G.-S.; Lee, S.; Han, Q.; Wu, H.; Konopelko, L.A.; Kustikov, Y.A.; Malginov, A.V.; Gromova, E.V.; Pankratov, V.V.; et al. Final report on international key comparison APMP. QM-K41: 10 μmol/mol hydrogen sulfide in nitrogen. Metrologia 2014, 51, 08012. [Google Scholar] [CrossRef]
- Van der Veen, M.H.; Nieuwenkamp, G.; Wessel, R.M.; Maruyama, M.; Heo, G.S.; Kim, Y.-D.; Moon, D.M.; Niederhauser, B.; Quintilii, M.; Milton, M.J.T.; et al. International comparison CCQM K46—Ammonia in nitrogen. Metrologia 2010, 47, 08023. [Google Scholar] [CrossRef]
- Brown, A.S.; Milton, M.; Brookes, C.; Vargha, G.; Downey, M.; Uehara, S.; Augusto, C.; de Lima Fioravante, A.; Sobrinho, D.; Dias, F.; et al. Final report on CCQM-K93: Preparative comparison of ethanol in nitrogen. Metrologia 2013, 50, 08025. [Google Scholar] [CrossRef]
- Lee, S.; Heo, G.S.; Kim, Y.; Oh, S.; Han, Q.; Wu, H.; Konopelko, L.A.; Kustikov, Y.A.; Kolobova, A.V.; Efremova, O.V.; et al. International key comparison CCQM-K94: 10 μmol/mol dimethyl sulfide in nitrogen. Metrologia 2016, 53, 08002. [Google Scholar] [CrossRef]
- Harris, P.; Pelligrini, M. Mass Transport in Sample Transport lines Adsorption Desorption Effects and their Influence on Process Analytical Measurements. Available online: https://www.silcotek.com/hubfs/Literature%20Catalog/White%20Papers/Externally%20Written/Sulfur%20and%20H2S/%23WP-EXT-SULF-002%20ISA%202011%20Sample%20Lines.pdf (accessed on 27 January 2021).
- Deming, L.; Pagonis, D.; Liu, X.; Day, D.A.; Talukdar, R.; Krechmer, J.E.; de Gouw, J.A.; Jimenez, J.L.; Ziemann, P.J. Measurements of delays of gas-phase compounds in a wide variety of tubing materials due to gas–wall interactions. Atmos. Meas. Tech. 2019, 12, 3453–3461. [Google Scholar] [CrossRef]
- Metrology for Airborne Molecular Contamination in Manufacturing Environments. European Metrology Research Programme (EMRP). 2012. Available online: https://www.euramet.org/index.php?eID=tx_securedownloads&p=588&u=0&g=0&t=1641528179&hash=31fb1f3ab963204de5ce80ba65fc8605b53c7edf&file=Media/docs/EMRP/JRP/JRP_Summaries_2012/Industry_SRTs/SRT-i17.pdf (accessed on 27 January 2021).
- Barwood, G. 17IND09, MetAMCII, Metrology for Airborne Molecular Contaminants II European. Metrology Programme for Innovation and Research (EMPIR). 2017. Available online: https://www.era-learn.eu/network-information/networks/empir/empir-call-2017/metrology-for-airborne-molecular-contaminants-ii (accessed on 27 January 2021).
- Szulejko, J.; Kim, Y.H.; Kim, K.H. Method to predict gas chromatographic response factors for the trace-level analysis of volatile organic compounds based on the effective carbon number concepts. J. Sep. Sci. 2013, 36, 3356–3365. [Google Scholar] [CrossRef]
- University of Torino. Meteorological Station of the Department of Physics. 2020. Available online: http://www.meteo.dfg.unito.it/tutti (accessed on 27 January 2021).
- Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement (GUM) JCGM 100:2008. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_100_2008_E.pdf (accessed on 27 January 2021).
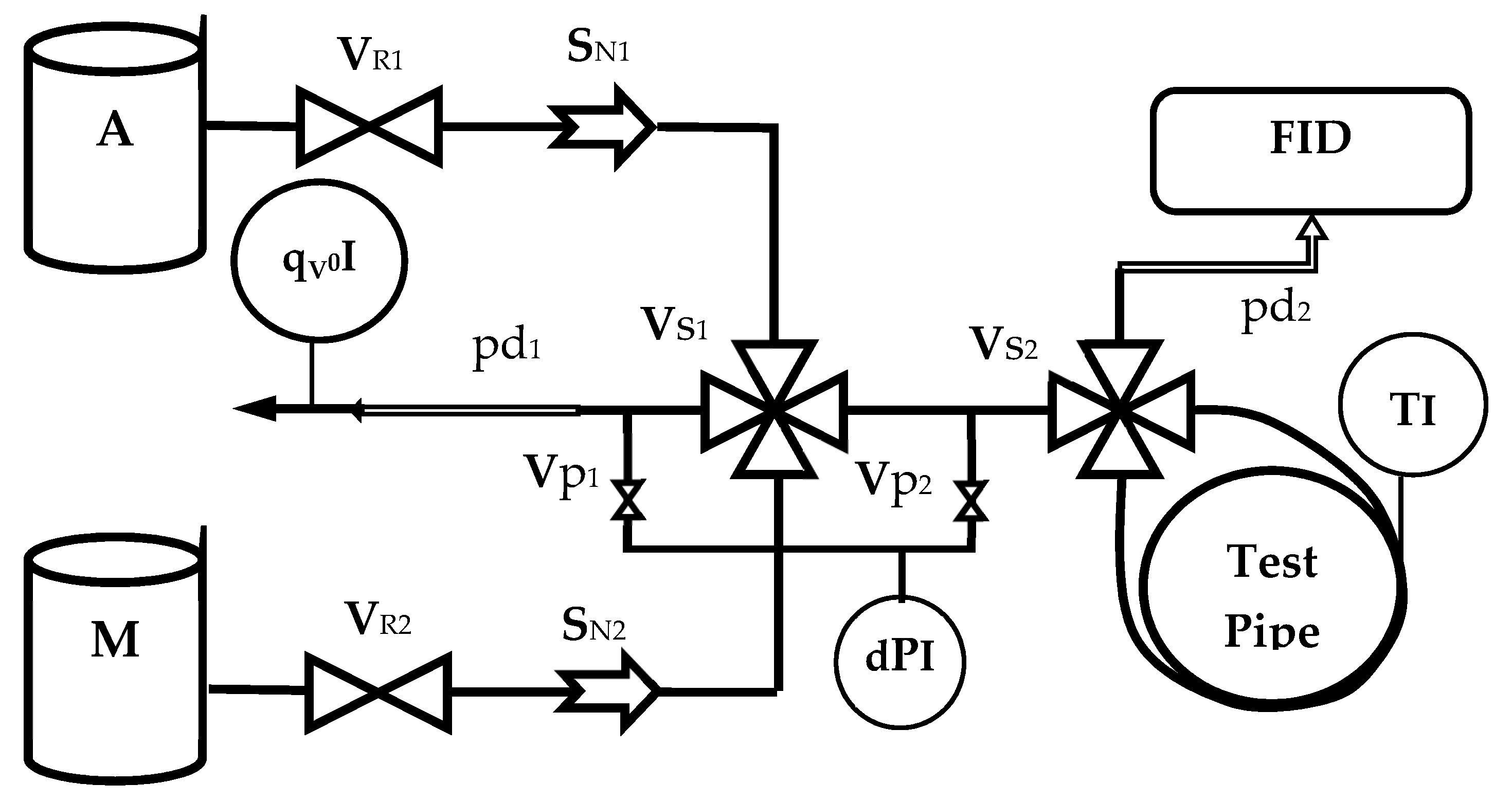
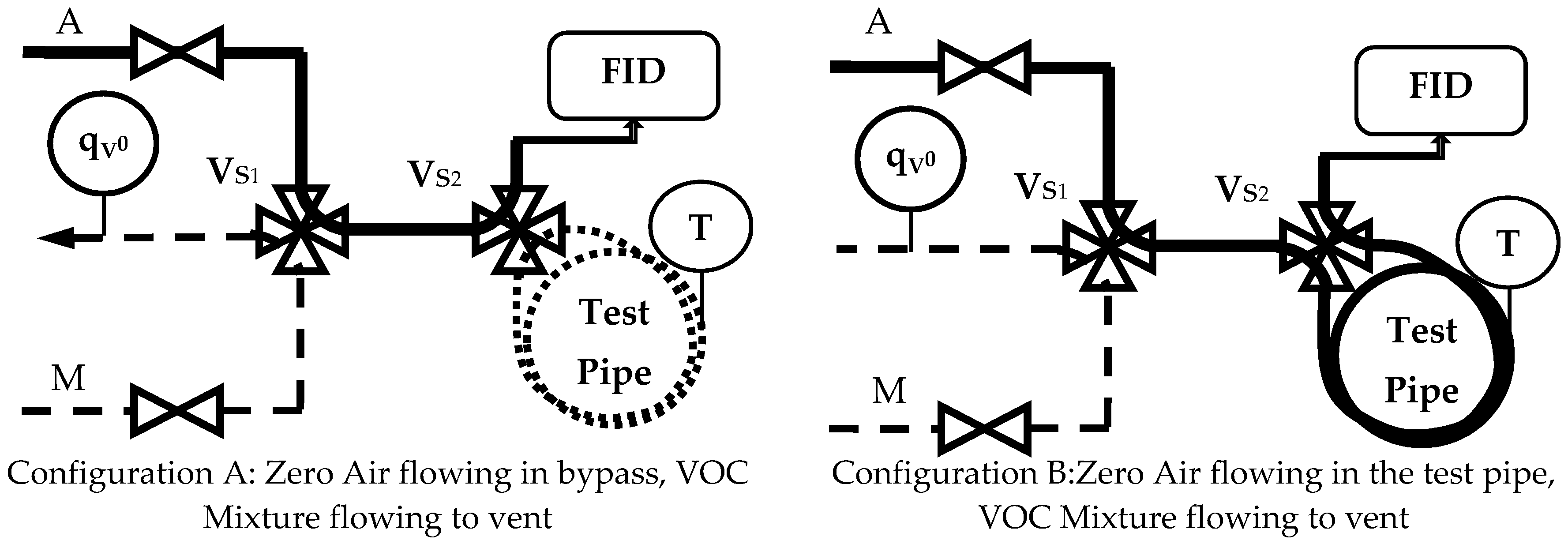
| Switch | Valve | S∞ | Test Pipe | Gas | Operation and Effects | |
|---|---|---|---|---|---|---|
| B | SAir | In | Clean | Zero | Cleaning device and test pipe till Flat signal | |
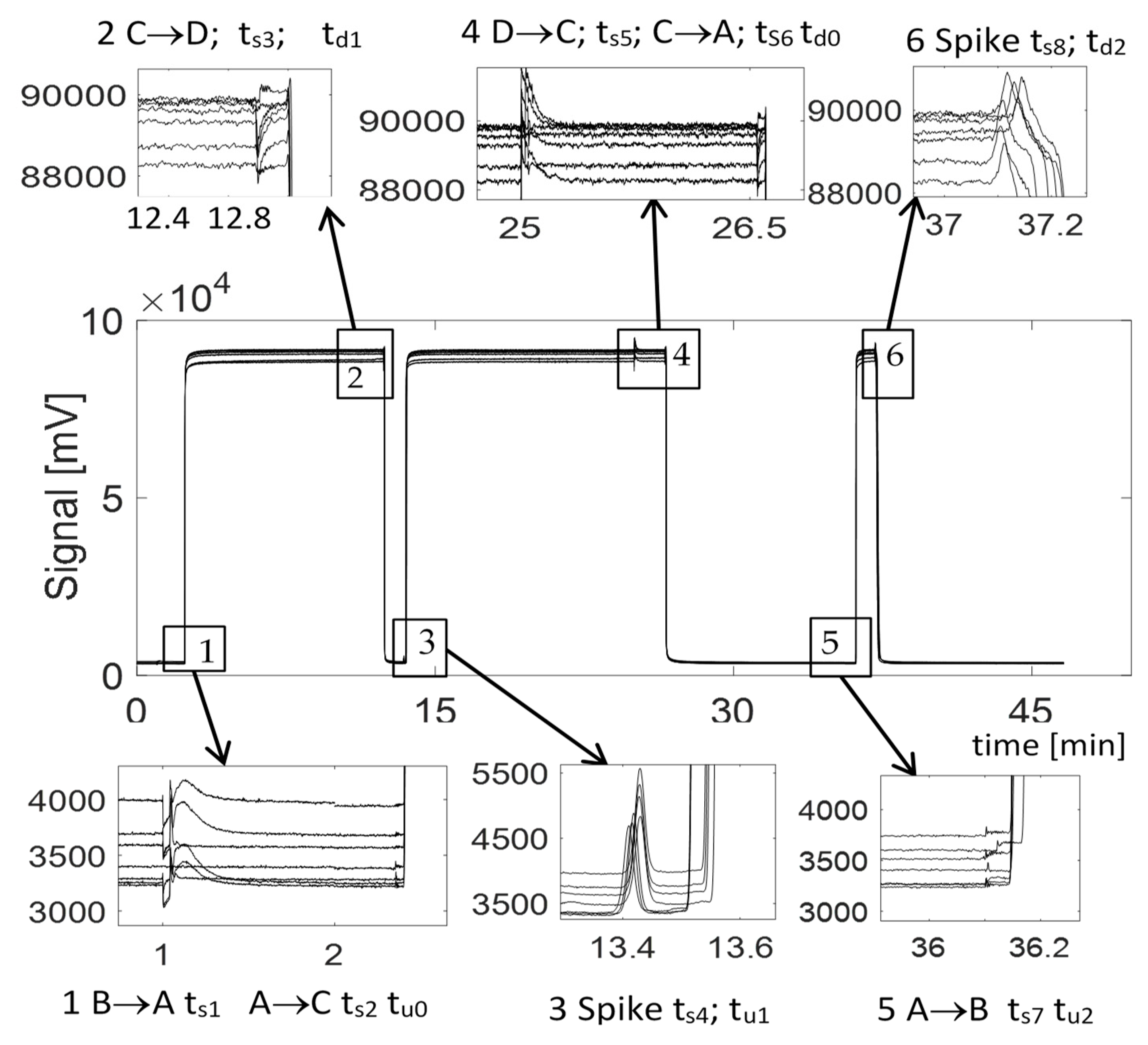
| B→A | Vs2 | SAir | Off | Clean | Zero | Spike (ts1) at switch |
| A→C | Vs1 | SMix | Off | Clean | VOC | Spike (ts2) at switch, tu0, Saturating device |
| C→D | Vs2 | SMix | In | Sat. | VOC | Spike (ts3) at switch Signal depletion (td1) after device residence time Spike (ts4) after test pipe residence times tu1 |
| D→C | Vs2 | SMix | Off | Sat. | VOC | Spike (ts5) at switch, Cleaning device |
| C→A | Vs1 | SAir | Off | Sat. | Zero | Spike (ts6) at switch td0 |
| A→B | Vs2 | SAir | In | Clean | Zero | Spike (ts7) at switch Signal increase (tu2) after device residence time Spike (ts8) after test pipe residence times, td1 |
| Time | Box | Event | Characteristic Time |
|---|---|---|---|
| Spike ts1 | 1 | B→A Switch | |
| Spike ts2 | 1 | A→C Switch | |
| tu0 | 1 | VOC Mixture reaches FID | tu0 − ts2 Residence time from Vs1 to detector no test pipe |
| Spike ts3 | 2 | C→D Switch | |
| td1 | 2 | Air entrapped reaches FID | td1 − ts3 Residence time from Vs2 to detector |
| Spike ts4 | 3 | VOC Mixture reaches FID without VOC (all adsorbed on wall) | τr = ts4 − td1 Residence time in test pipe |
| tu1 | 3 | VOC starts to overpass pipe | Delay of VOC appearance |
| Spike ts5 | 4 | D→C Switch | |
| Spike ts6 | 4 | C→A Switch | |
| td0 | 4 | Zero Air reaches the FID | td0 − ts6 Residence time in the device without test pipe |
| Spike ts7 | 5 | A→B Switch | |
| tu2 | 5 | VOC Mixture entrapped reaches FID | tu2 − ts7 Residence time from Vs2 to detector |
| Spike ts8 | 6 | Zero Air reaches FID | τR = ts8 − tu2 Residence time in test pipe |
| td1 | 6 | VOC starts to overpass pipe | Delay of VOC disappearance |
| Sample | N | L | qV0g | τr | T | P | Re |
|---|---|---|---|---|---|---|---|
| (m) | (SmL min−1) | (min) | (°C) | (kPa) | (-) | ||
| Sulfinert A | 53 | 26 | 9–195 | 0.5–9.5 | 22–27 | 100–130 | 5–150 |
| Sulfinert B | 29 | 8.5 | 9–55 | 0.6–3.2 | 17–30 | 100–120 | 5–40 |
| Sulfinert C | 18 | 8.5 | 9–55 | 0.6–3.2 | 20–22 | 100–120 | 5–40 |
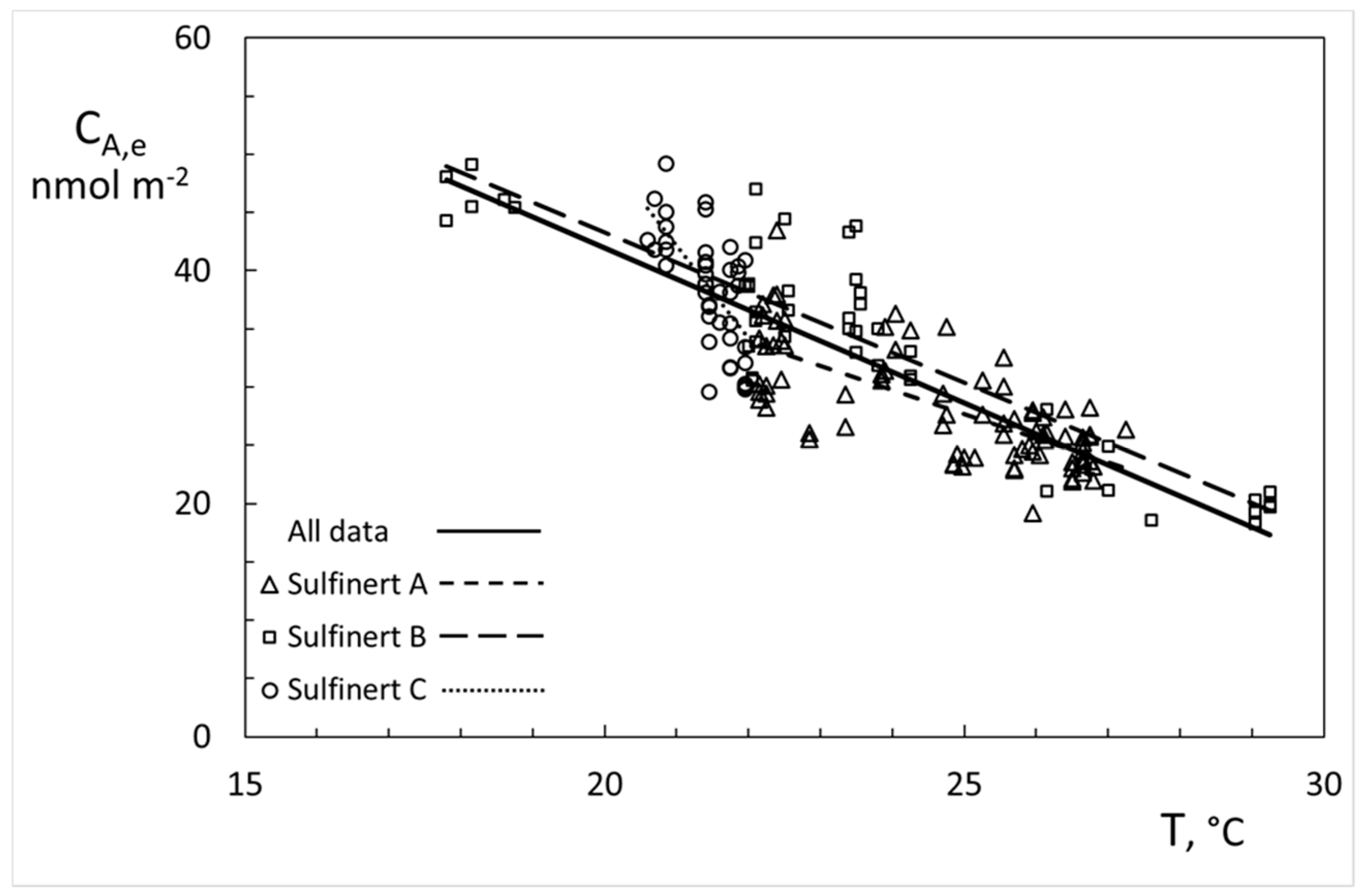
| Sample | CA,e | σ | σ% | CA,e, 20 °C, 1 bar | σ, 20 °C, 1 bar | σ%. 20 °C, 1 bar |
|---|---|---|---|---|---|---|
| (nmol m−2) | (nmol m−2) | σ/CA,e | (nmol m−2) | (nmol m−2) | σ/CA.e | |
| Sulfinert A | 28.2 | 4.8 | 17% | 38.2 | 2.8 | 7.3% |
| Sulfinert B | 34.0 | 9.1 | 27% | 41.7 | 3.3 | 8.0% |
| Sulfinert C | 38.5 | 4.9 | 13% | 39.6 | 3.4 | 8.5% |
| All data | 32.3 | 7.6 | 24% | 39.5 | 3.4 | 8.6% |
| Mean ABC | 33.5 | 5.2 | 15% | 39.8 | 1.7 | 4.4% |
| Sample | CA,e,20 °C,1 bar | σ20 °C,1 bar | σ%,20 °C,1 bar | Ke,20 °C,1 bar | σ,20 °C,1 bar | σ%,20 °C,1 bar |
|---|---|---|---|---|---|---|
| (nmol m−2) | (nmol m−2) | σ/CA,e | (m) | (m) | σ/Ke | |
| Sulfinert A | 38.2 | 0.3 | 0.8% | 0.173 | 0.002 | 1.0% |
| Sulfinert B | 41.7 | 0.5 | 1.2% | 0.185 | 0.003 | 1.5% |
| Sulfinert C | 39.6 | 0.5 | 1.3% | 0.171 | 0.002 | 1.4% |
| All data | 39.5 | 0.3 | 0.7% | 0.176 | 0.001 | 0.8% |
| Mean ABC | 39.8 | 1.0 | 2.5% | 0.176 | 0.005 | 2.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sassi, G.; Khan, B.A.; Lecuna, M. Reproducibility of the Quantification of Reversible Wall Interactions in VOC Sampling Lines. Atmosphere 2021, 12, 280. https://doi.org/10.3390/atmos12020280
Sassi G, Khan BA, Lecuna M. Reproducibility of the Quantification of Reversible Wall Interactions in VOC Sampling Lines. Atmosphere. 2021; 12(2):280. https://doi.org/10.3390/atmos12020280
Chicago/Turabian StyleSassi, Guido, Bilal Alam Khan, and Maricarmen Lecuna. 2021. "Reproducibility of the Quantification of Reversible Wall Interactions in VOC Sampling Lines" Atmosphere 12, no. 2: 280. https://doi.org/10.3390/atmos12020280
APA StyleSassi, G., Khan, B. A., & Lecuna, M. (2021). Reproducibility of the Quantification of Reversible Wall Interactions in VOC Sampling Lines. Atmosphere, 12(2), 280. https://doi.org/10.3390/atmos12020280







