Abstract
The increase in built surfaces constitutes the main reason for the formation of the Urban Heat Island (UHI), that is a metropolitan area significantly warmer than its surrounding rural areas. The urban heat islands and other urban-induced climate feedbacks may amplify heat stress and urban flooding under climate change and therefore to predict them correctly has become essential. Currently in the COSMO model, cities are represented by natural land surfaces with an increased surface roughness length and a reduced vegetation cover, but this approach is unable to correctly reproduce the UHI effect. By increasing the model resolution, a representation of the main physical processes that characterize the urban local meteorology should be addressed, in order to better forecast temperature, moisture and precipitation in urban environments. Within the COSMO Consortium a bulk parameterization scheme (TERRA_URB or TU) has been developed. It parametrizes the effects of buildings, streets and other man-made impervious surfaces on energy, moist and momentum exchanges between the surface and atmosphere, and additionally accounts for the anthropogenic heat flux as a heat source from the surface to the atmosphere. TU implements an impervious water-storage parameterization, and the Semi-empirical Urban canopy parametrization (SURY) that translates 3D urban canopy into bulk parameters. This paper presents evaluation results of the TU scheme in high-resolution simulations with a recent COSMO model version for selected European cities, namely Turin, Naples and Moscow. The key conclusion of the work is that the TU scheme in the COSMO model reasonably reproduces UHI effect and improves air temperature forecasts for all the investigated urban areas, despite each city has very different morphological characteristics. Our results highlight potential benefits of a new turbulence scheme and the representation of skin-layer temperature (for vegetation) in the model performance. Our model framework provides perspectives for enhancing urban climate modelling, although further investigations in improving model parametrizations, calibration and the use of more realistic urban canopy parameters are needed.
1. Introduction
Urban areas have a significant impact on atmospheric flow and meteorological processes and this field of study is growing within the scientific community. One of the most investigated phenomena is the Urban Heat Island (UHI from now on), which occurs when a city experiences much warmer temperatures than its nearby rural area. The topic is of great public and scientific interest because urbanized surfaces are expanding throughout the world [1] and the number of urban residents will increase in the following years, according to the 2018 Revision of World Urbanization Prospects produced by the Population Division of the UN Department of Economic and Social Affairs [2]. Because of this, the impact of the UHI phenomenon is becoming more relevant and, according to IPCC’s climate projections [3], this situation will aggravate in the next 80 years since a continued increase in number, intensity and duration of heat waves during the 21st century is expected [4]. Indeed, many studies have already documented that UHIs tend to intensify during the heat waves (e.g., [5,6]) leading to additional deterioration of the human thermal comfort [7,8], amplification of heat-stress hazards, and even increase of heat-related mortality in the cities [9,10]. Higher rates of climate warming and heat stress increase in the 21st century are expected for urban areas in comparison to rural background, according to regional [11,12] or global [13] urban climate projections. The correct representation of UHI in numerical models is then a crucial aspect for Numerical Weather Prediction (NWP) applications and regional climate simulations.
An adequate representation of urban areas in NWP models is essential to correctly forecast not only air temperature, UHI and human heat stress, but also dangerous weather events such as heavy rain and thunderstorms, which may be triggered or modified by urban-induced effects. There are studies [14,15] suggesting that urban heat island-induced circulation is able to modify the boundary layer over a city, affecting the precipitation pattern. The urban heat island effect could give rise to a more unstable atmosphere, producing an increase of extreme precipitation larger than in nearby rural areas [16]. This effect is more evident over the tropics. For instance, in Singapore, the urban area leads to the formation of a rainfall “hot spot” which is responsible for 20–30% of the afternoon/evening total precipitation [17]. On the other hand, the humidity could be lowered, creating an urban dry island over a city, during the day particularly, and the local circulation could be modified [18,19].
The standard classification separates the canopy layer UHI, measured by in-situ meteorological stations (using 2m temperature), and the surface UHI (SUHI), measured by means of remote sensors (using land surface temperature—LST). The UHI is more essential than SUHI when dealing with health impacts, since air temperature has a closer relationship with the urban environment and is essential for any assessment of urban heat reduction efficiency [20]. Nevertheless, given the progress in remote sensing and spatial science, more and more studies [21] consider SUHI which is able to provide a more detailed spatial pattern. In this work we deal with UHI only, but SUHI will be the subject of further studies.
The reproduction of urban climate features in NWP and regional climate studies is possible with the use of so-called urban canopy models (UCMs), which are needed to parameterize the interaction between the urbanized surface and the overlying atmosphere when individual buildings remain unresolved. A wide variety of UCMs have been developed over the last decades [22], and their use is getting more and more common in high-resolution climate simulations as well as in NWP. Nowadays, several widely used atmospheric models already include the selection of UCMs of different complexity in their basic versions. For example, Weather Research and Forecasting (WRF) model is coupled separately with three different UCMs, a slab (SB), which considers buildings as increased roughness, a single-layer representation of the canopy (SL), and an advanced multi-level Building Environment Parameterization (BEP) [23,24]. The three different types of UCMs are also available in the HIRLAM model [25,26]. Numerous studies have already demonstrated the advances of urban climate modelling with UCMs. Simulations of London’s meteorology using the Met Office Unified Model with a new surface energy-balance scheme to represent the urban surfaces, called MORUSES, show encouraging agreement with observations and identify the urban land-use fraction as the dominant factor [27]. Several studies with WRF model have been performed as well, using different UCMs. In Bucharest, the comparison of simulations with no urban parameterization scheme, a SL UCM (SLUCM) or a BEP demonstrated that the last better represents the UHI [28]. The same results were also found for Berlin in a recent work [29]. The further introduction of a Building Energy Model (BEM) coupled with BEP minimizes the RMSE for 2-m temperature and 2-m relative humidity in Barcelona [30].
In the basic version of the COSMO model [31], cities are represented as natural surfaces with an increased surface roughness length and a reduced vegetation cover. This representation is not very effective, since urban areas are still treated as water-permeable soil with aerodynamic, radiative and thermal parameters similar to the surrounding natural land. Different UCMs have been coupled to COSMO: the single layer urban canopy model TEB (Town Energy Balance), the most advanced multi-layer schemes Double-Canyon effect parameterization (DCEP) and BEP-Trees and the TERRA_URB (TU) bulk parameterization. TU offers an intrinsic representation of urban physics with modifications of the input data, soil module and land-atmosphere interactions. The effect of buildings on the surface-atmosphere interaction is described without resolving the energy budgets of the buildings themselves but parameterizing the impervious surface water balance, translating the 3D urban-canopy parameters into bulk parameters by Semi-empirical Urban canopy parameterization (SURY) [32] and using the externally calculated anthropogenic heat flux, which has been proved to be beneficial for the simulation of screen-level temperature [33]. TU scheme is the simplest one in comparison to other UCMs, however its simplicity and effectiveness make it suitable to urban climate application. Despite the TU scheme is rather new, it has been already tested for different cities. Recent studies over Moscow megacity demonstrated the ability of the TU parameterization to capture the UHI and other urban-induced meso-climatic effects and confirmed that it is a useful tool for urban climate research, especially if the city-descriptive parameters are improved [34,35]. Moreover, TU scheme has been already implemented in the high-resolution numerical weather forecasts for Moscow megacity with grid spacing of 1 km and 500 m within the framework of the COSMO-Ru system [36,37]. The TU scheme has been previously evaluated offline (forced with observations) for Basel, Toulouse and Singapore [38,39] and online (coupled to COSMO-CLM v5) for Berlin, Belgium and Kampala [12,40,41,42]. The other UCMs in COSMO were tested less extensively, e.g., TEB was tested only over Berlin [43], DCEP over Zürich [44] and Berlin [45], BEP-Trees over Basel [46] and BEP with a Building Energy Model (BEP-BEM) over Berlin [47].
Currently, all listed UCMs are not available within the official (operational) COSMO version, but exist as parallel branches of the model code development, which are not synchronized with recent updates in the operational version. Due to the computational efficiency of the TU scheme and its encouraging evaluation results, the COSMO and CLM consortia decided to select it as the default urban parameterization. It is planned to include TU into the official COSMO code in the forthcoming unified model version 6.0, and latter to implement it into ICON (Icosahedral Nonhydrostatic Weather and Climate), the future operational model of the COSMO Consortium. This work focuses on the improvement that TU could provide to urban climate modelling.
The aim of this paper is then an in-depth evaluation and verification of the performances of the recent COSMO version 5.05 with TU scheme [48] and new implemented physical parameterizations, such the ICON-like surface-layer turbulence scheme and the new formulation of the surface temperature. Since the goal of the urban scheme is to catch small-scale features, only high-resolution runs have been considered in order to verify its capabilities in reproducing the urban dynamics and specific phenomena, e.g., UHI. The validation was performed for 1- or 2-week selected periods over 3 European cities characterized by different environment and climate, namely the Moscow megacity in Russia and Turin and Naples in Italy.
This paper is organized as follows: Section 2 contains a description of the model, with emphasis on the surface-layer turbulent schemes, the skin temperature scheme and the urban parameterization TU. Section 3 contains a description of the performed experiments, while results are presented in Section 4 and conclusions in Section 5.
2. Model Description
The COSMO model [31,49] is a nonhydrostatic limited-area atmospheric prediction model, which is developed and maintained by the COSMO consortium [50]. It is designed for both operational NWP and various scientific applications on the meso-β and meso-γ scale. The COSMO model is based on the primitive equations describing compressible flow in a moist atmosphere. A variety of physical processes, such as radiation, convection, turbulence, and land surface processes, are taken into account by parameterization schemes. The governing equations are integrated using the mode-splitting approach to split up the equations into a longer model time step for the processes on larger time scales such as advection and the tendencies from the physical parameterizations, and into a short time step for the fast sound wave processes. Several options for a two time-level second and third order Runge–Kutta split-explicit scheme are available [51].
2.1. Surface-Layer Turbulence Scheme
2.1.1. Current Formulation
The COSMO model implements the next-generation TKE-based surface-layer transfer scheme [31,52]. The surface layer, which refers to the layer of air between the earth’s surface and the lowest model level, is divided into a laminar-turbulent sublayer, a roughness layer and a constant-flux (or Prandtl) layer. The surface layer scheme is also intimately related to the TKE-based closures of the COSMO model (see Sections 3.3 and 3.4 in [31]). As a result, the surface layer does not need the empirical Monin–Obukhov stability functions (as in [53,54]) for which the Obukhov stability parameter needs to be determined from an iterative procedure or a non-iterative approximation [55,56]. It rather generates these functions using the dimensionless coefficients of the turbulence closure ([57]; see Section 4.2 in [31]).
2.1.2. New Formulation
Since COSMO version 5.05, a new ICON-based physics has been implemented involving a different turbulence scheme [58]. One main extension of the vertical diffusion scheme is the formal separation of turbulence from a potential non-turbulent component of the sub-grid scale energy spectrum. This separation is related to additional scale interaction terms in the prognostic TKE equation which describe additional shear production of TKE by the action of other, non-turbulent, sub-grid scale flow patterns, such as wakes generated by sub-grid scale orography [59], convective currents or separated horizontal circulations. Through this formalism, the scheme describes separated turbulence interacting with non-turbulent circulations which allows for a consistent application of turbulence closure assumptions, even though other sub-grid scale processes may be dominant within the grid cell.
One of the significant shortcomings of the older turbulence scheme is related with constant values of minimum vertical diffusion coefficients for momentum and scalars (tkmmin and tkhmin parameters), which are introduced in the model to prevent the turbulence from decaying in stable conditions [60]. Such limitation results in artificial mixing in the model leading to warm nocturnal temperature biases [37,60,61]. The new turbulence scheme attempts to fix this problem by introducing a correction function for minimum values diffusion coefficients in dependence on Ri-number and height above the surface, together with a retuned value of tkmmin and tkhmin. Additionally, the new scheme is supplemented by fixed pattern-length scale pat_len (which is used in our additional TKE-source-term due to near surface heterogeneity) by an upper limit dependent on the standard deviation of sub-grid-orography height, together with a retuned value for pat_len. With these modifications there is less artificial mixing at stable stratification and hence a stronger drop of near-surface temperature during night, as well as a stronger and shallower nocturnal surface inversion (Matthias Raschendorfer, personal communication).
2.2. Land Surface Scheme TERRA
The physical parameterization schemes include the multi-layer land surface model TERRA [49,62]. It simulates the energy and water balance at the land surface and in the ground, providing the land surface temperature and humidity as lower boundary conditions for computing the energy and water fluxes between surface and atmosphere. In TERRA, all processes are modelled one-dimensionally in the vertical, no lateral interactions between adjacent soil columns are considered. The soil temperature is calculated by the heat conduction equation, while the soil water content is predicted by the Richards equation. Both equations are discretized by a multi-layer scheme.
At the interface between surface and atmosphere, the surface energy balance equation is solved, yielding the new surface temperature. The current representation of the surface temperature as well as the new skin temperature in TERRA are described in the following Subsections.
2.2.1. Current Formulation of Surface Temperature
In the current model version of TERRA, the surface temperature Ts is represented by the temperature of the uppermost soil layer [63]. The surface energy balance equation has the following form:
where Cs is the heat capacity per unit area, and t is the time. RSW and RLW are the net shortwave and longwave radiation flux, respectively, while LE and H denote the latent and sensible heat flux and G the ground heat flux.
Cs ∂Ts/∂t = RSW + RLW + LE + H + G,
2.2.2. New Formulation of Surface Temperature
The new description of the surface temperature in TERRA [63] is based on the skin temperature formulation by Viterbo and Beljaars [64]. They introduced an additional temperature of the canopy leaves, the skin temperature Tsk, as a representation of the vegetation in the surface energy balance:
Λsk (Tsk−Ts) = RSW + RLW + LE + H
The behavior of this equation is mainly determined by the new parameter Λsk, the skin layer conductivity. Large values represent a strong coupling between the skin temperature Tsk and the surface temperature Ts, so that their diurnal cycles stay similar. In contrast, small values of Λsk describe a weak coupling and the diurnal cycle of Tsk can become considerably larger than the one of Ts. The leaves can become warmer during day and cooler during night. This can improve the surface temperature simulated by the soil-vegetation system.
2.3. TERRA_URB
Urban–atmosphere interactions are taken into account with the urban canopy model TU [32,38]. The urban scheme considers the urban physics in terms of surface energy and moisture exchanges including the influence of street-canyon geometry. TU scheme provides the corrections of the surface parameters (roughness length, albedo, emissivity, heat capacity, etc.) within the framework of the TERRA module using the semi-empirical urban canopy dependencies. TU integrates road, roof and wall surfaces into a 2D horizontal surface for which radiative and thermodynamic properties are adapted according to the 3D structure of the urban canopy. This is done through the Semi-empirical Urban canopy parametrization (SURY), which translates 3D urban canopy into bulk surface parameters [32]. In order to describe the 3D urban canopy for urban tiles, TU requires the definition of several urban canopy parameters for each grid cell of the model, including impervious surface area fraction (ISA), building area fraction (BF), mean building height (H) and height-to-width ratio (H/W). The anthropogenic heat flux (AHF) is also taken into account according to Flanner [65], assuming annual-mean values together with the typical diurnal and annual variations and the dependence of its annual amplitude on the latitude. TU also represents the water puddles on impervious surfaces in the urban environment at which storage, run-off and evaporation of precipitated water occurs [38]. To describe the heterogeneity of the urban surface, TU implements the so-called tile approach, for which urbanized and natural parts can coexist in each grid cell of the model. The fraction of urban area in a tile is defined by the ISA parameter. Hence, (near-)surface temperature values, heat fluxes and other soil or surface variables are simulated separately for natural and urban tiles in each grid cell of the model. The average values for each grid cell are calculated according to the area fraction of urban and natural tiles, and to annual-mean anthropogenic heat flux (AHF).
2.4. External Parameters
The external input parameters for TERRA are provided by the external parameter pre-processor EXTPAR and are aggregated from various raw datasets describing land use, orography, soil, etc. [66]. For the urban surfaces, EXTPAR, by default, uses AHF data from Flanner [65], ISA from Elvidge et al. [67] for global cities and the ”degree of soil sealing product” from EEA [68] for European cities. However, the use of these datasets in combination with Globcover 2009 land use classes [69] leads to inconsistencies for the urban surfaces, which affect a number of time-invariant natural land cover parameters (root depth, stomatal resistance, roughness length, minimum and maximum land cover, skin conductivity, emissivity, and leaf area index). This so-called ‘urban double-counting effect’ requires an additional pre-processing step, explained in detail in Appendix A. Since the reported simulations in the current study use different data sources to describe the urban canopy parameters, this information is provided in more detail in Section 3 for each case study.
3. Experiments
The COSMO model has been used at high resolution to perform simulations in 3 different cities in Europe, namely Turin and Naples in Italy and Moscow in Russia, on selected periods characterized by heat waves or intense heat islands (Table 1). Even if the study weeks differ among the domains, due to different background and meteorological conditions, the model has been configured as consistently as possible across the various cities. Firstly, each area experienced high-pressure conditions and absence of rainfall and wind, favorable for UHI appearance. In addition, the final grid spacing adopted was 1 km for all the three domains and the lowest model level was equal to 10 m in each case. The model set up and the corresponding namelist switches were derived from the COSMO User’s Guide [58], which recommends values for both the conservative (old COSMO physics) and the advanced (new ICON physics) approach. The model set up for Moscow was close to other partners’ configurations with minor differences, determined by previous experience in COSMO simulations for this region. An additional scaling coefficient of 2.5 was introduced for the rooting depth to avoid dry and hot bias temperature bias, which is typical for hot summers in the European part of Russia [70]. In TERRA look-up tables the rooting depth does not exceed 1 m even for the forests, which is a significant underestimation in comparison to observations [71,72,73]. Previously, a positive effect from such engineering was found for tropical Africa [74] as well as for the Moscow region [34]. Additionally, the scale of subgrid thermal inhomogeneity (pat_len parameter) in the simulations adopting the ICON-like turbulence was set to 100 m instead of 750 m (as in the Italian domains), in order to better represent the nocturnal temperatures. It was verified that the adoption of pat_len = 100 m for Turin and Naples has no effect at all on the results (not shown here).

Table 1.
Setup of the simulations.
The information about the simulation workflow and resolution are summarized in Table 1 for the three domains.
As regards the city-descriptive external parameters for TU, they are provided by EXTPAR for the Piedmont and Campania domains. Even if a better characterization of the urban parameters could be done, and it will be the subject of further studies, they were the only available data when the present simulations were started. In any case we believe that they are acceptable approximations of reality for these areas. Morphological urban canopy parameters, thermal and radiative parameters of urban environment were set by the defaults from [32]. For Moscow, default EXTPAR output on ISA and AHF was found to be too coarse and unrealistic [75], which was a motivation for incorporating a more advanced GIS-based approach to derive the city-descriptive parameters. ISA and morphological urban canopy parameters for Moscow were obtained based on GIS-processed vector OpenStreetMap data on buildings and roads, vegetation mask derived from Sentinel-2 satellite imagery with 10-m resolution and the recent Copernicus Global Land Cover raster dataset with 100-m resolution. Anthropogenic heat flux was defined based on a literature estimate of its city-mean value from [76] and re-distributed over the area based on building area fraction and height. More details about this approach are given in [77], while its advantages over default EXTPAR output was already demonstrated for Moscow in model simulations for different seasons [75]. Specifically, in this study we used REF1 data set from [75]. Thermal and radiative parameters of urban environment were taken from [32], in line with the other two regions.
Different model configurations have been tested in order to assess the one that better reproduces the observed values. Specifically, the capabilities of TU scheme in reproducing the UHI effect was evaluated by comparing reference simulations without the urban parameterization (lterra_urb = FALSE) with simulations in which TU was activated (lterra_urb = TRUE). Additional sensitivity tests were then performed to evaluate the current and icon-like formulation of the turbulence scheme (loldtur = TRUE/FALSE) and the new skin temperature scheme compared to the current formulation of surface temperature (itype_canopy = 2/1). Summarizing, six configuration model settings have been tested over the three domains, which are described in Table 2.

Table 2.
Model configuration settings.
The model validation for Turin was carried out by using the hourly data provided by the ARPA Piemonte network (Figure 1a). The analysis focused on six stations, three urban and three rural, located at similar elevation above the sea level. The urban ones comprehend both the historical city center and suburbs, with an impervious surface area above 0.60 (for details see Table A1 in Appendix B). The rural stations are chosen in the southern surroundings of the urban area, since Turin is enclosed by mountains in the north-western sector and by hills in the eastern part. The modelled values used for validation purposes have been calculated for each station using a bilinear method and refer to the values interpolated from the values of the four nearest raster cells.

Figure 1.
(a) Piedmont domain, Italy: the black marks indicate the whole stations of the Arpa Piemonte network; (b) Campania domain, Italy. Observations are provided by the Civil Protection of Campania; (c) Moscow domain, Russia: the black marks indicate the Roshydromet network (WMO) that include 43 weather stations. For all three domains, the urban stations considered in the analysis are sketched in red markers, while the stations selected to calculate the mean rural temperature are sketched in yellow markers.
The model validation for Naples has been carried out by using the hourly observational data provided by the Civil Protection network of Campania. In this domain, five stations were considered, two urban and three rural (Figure 1b). The urban ones are located in Naples and S. Marco Evangelista. The second one has been chosen in order to reduce the effects of the proximity to the sea with respect to Naples. They are both characterized by an impervious surface area above 0.60 (Table A2, Appendix B). The rural stations are chosen respectively in Grazzanise, Rocca D’Evandro and Alife. The simulated values used for validation purposes have been obtained for each station with a bilinear method.
The model validation for Moscow was performed using observational data on 1-hourly intervals from the Roshydromet network that include 42 weather stations (Figure 1c). Stations from uncertified networks, used in previous studies for Moscow, are not used in this study. Most of the stations are in the countryside, in relatively small towns or in airports, so we further consider them as rural. Five stations are considered as urban, i.e., representing the urbanized area within Moscow megacity. These stations are located in different urban environments, e.g., Balchug station in a densely built area in the historical city center, Strogino and Dolgoprudny in residential areas with newer development at the periphery of the megacity, MSU and VDNKh in urban parks. According to the previous studies, all these stations experience higher temperatures than rural surroundings, with the most intense UHI observed for Balchug weather station in the city center [35,78]. Since many stations in Moscow are located in inhomogeneous environment (e.g., at the border between urban park and build areas, which is a case for MSU and VDNKh stations), the procedure of grid cell assignment for Moscow was a bit more complicated than for other study areas. For each station, one model grid cell was selected among 4 nearest ones taking into account real and modelled settings of the station’s environment (e.g., if the station is located in a park area, the grid cell with lower ISA is selected). If more than one among four nearest cells corresponds to the actual local settings of the station, the one with smallest temperature RMSE is selected.
More specific information about the stations used for validation purposes are provided in Appendix B for each of the three domains.
4. Results
In order to evaluate the configuration that better suits the observations and therefore which of the six parameterizations is able to better capture and reproduce the UHI phenomenon, the same statistical evaluations were performed over the different domains. The air temperature and how it evolves is the most effective parameter to detect the UHI effect. During the day, a city stores heat, which is then released at night, resulting in warmer urban temperatures than its rural surroundings. Then, the dynamics of observed and modelled 2-m temperature (T2m) was analyzed for urban and rural stations both over the entire study period and in their mean daily cycle. In a similar manner the dynamics of the UHI intensity, defined as the difference between urban and rural temperature, was investigated.
A unified set of statistical indices was calculated for all domains in order to evaluate the performance of the different model configurations. The mean daily evolution of Mean Bias (MB) and Root Mean Square Error (RMSE) of T2m, evaluated both over rural and urban stations, and of UHI intensity are plotted and allow to identify the configuration that better reproduces the urban features. Taylor diagrams are shown for T2m, referred to both rural and urban stations, and for UHI intensity and provide a concise statistical summary of how well patterns match each other in terms of their correlation, their root-mean-square difference and the ratio of their variances.
4.1. Turin, Piedmont Domain, Italy
The UHI intensity is calculated as the difference between the mean urban temperature, obtained averaging temperature of the three selected stations in the city, and the mean rural temperature, i.e., the average of the three selected stations surrounding Turin (Figure 1a).
The hourly values of T2m, both for rural and urban areas, have been analyzed for the considered period in October 2017 and evaluated in their mean daily cycle. Although minimum temperatures are rather overestimated and maximum temperatures are slightly underestimated, the characteristic oscillating pattern is well reproduced by all configurations (Figure 2a,b). Simulations with the current turbulence scheme experience the highest nocturnal bias, with values more than 4 °C, and worst diurnal and nocturnal RMSE (Figure 3a,d). The adoption of the ICON-like physics and skin-layer temperature scheme decreases nocturnal temperatures and partially reduces positive nocturnal bias up to 2 °C, improving also the RMSE (Figure 3d). The new formulation of turbulence scheme has also a minor impact on the maximum daily temperature, as highlighted by better scores. The activation of the TU scheme has no significant impact on rural temperatures, as expected, and the small differences could be attributed to the proximity of urban settlements. A major impact can be noted on urban temperatures, as the TU scheme induces warmer temperatures than reference simulations (black and green lines). It’s worth noting that there is an evident overestimation of the model of the nocturnal temperature, which is partially compensated in the urban stations due to the UHI effect: the reference simulations (without TU) get better scores during night, since the positive model bias fictitiously reproduces the effect of the heat island at night. For this reason, we analyzed the UHI intensity, which eliminates any possible bias or systematic error by being the difference between two temperatures. Figure 2c demonstrates the ability of the TU scheme in capturing the dynamics of the UHI intensity, since the results that come closest to the observations concern TU configurations. The fact that the TU scheme improves the representation of the UHI is also confirmed by the better scores obtained by the configurations using the urban scheme (Figure 3c,f). Among the runs with TU, significant improvements are provided by adopting the new turbulence scheme and the skin temperature scheme, as confirmed by the best scores for urban temperature and UHI intensity. Nevertheless, a significant overestimation of nocturnal temperatures remains also in the best configuration (TUnew2, yellow line), due to the positive model bias we discussed above. A possible explanation of this systematic error could be related to the 2-nesting domains or to the external urban parameters and it will be furtherly investigated.
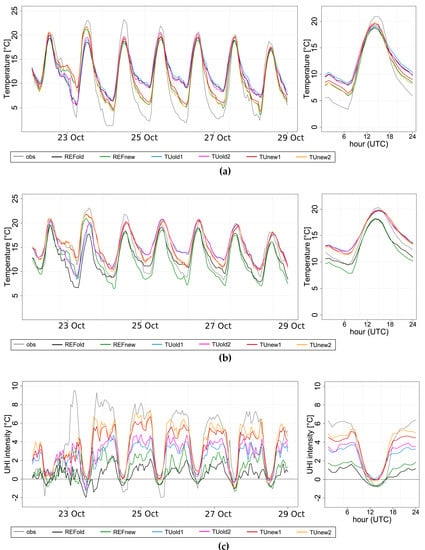
Figure 2.
(a) mean rural T2m, (b) mean urban T2m and (c) Urban Heat Island (UHI) intensity during the week 22-29 October 2017. Subplots on the right show the mean daily cycle of the rural temperature and UHI intensity.
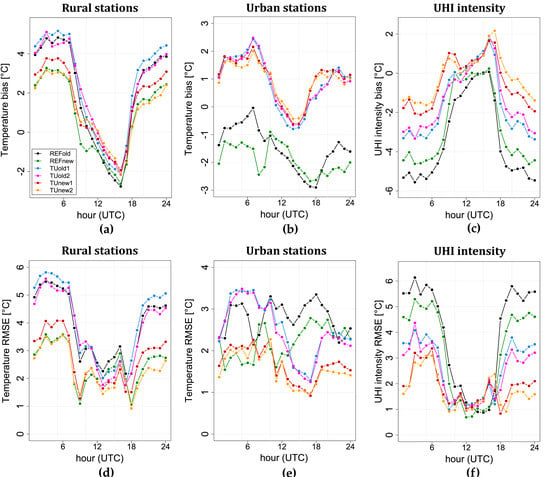
Figure 3.
Mean biases and root-mean square errors of T2m, evaluated over rural (a,d) and urban (b,e) stations in the Piedmont study area; mean biases and root-mean square errors of UHI intensity for urban stations (c,f).
The correlation between modelled and observed data is shown in the Taylor diagrams (Figure 4). These diagrams show the strong improvement provided by the new turbulence scheme in forecasting rural and urban temperatures. If we focalize on the UHI intensity, the correlation between model and observations increases from 0.6 to 0.83 and the RMS error gradually decreases by activating TU scheme, adopting the ICON-like physics and skin temperature scheme. This result confirms that the TUnew2 is the configuration that better captures and reproduces the UHI effect.
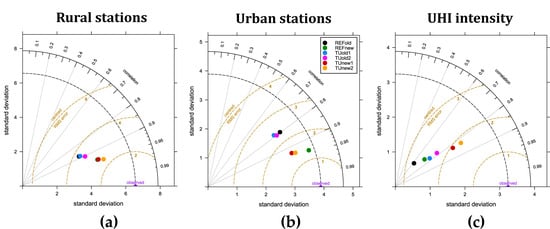
Figure 4.
Taylor diagrams for rural stations (a), urban stations (b) and UHI intensity (c).
4.2. Naples, Campania Domain, Italy
The T2m hourly values have been analyzed over the considered week and evaluated in their mean daily cycle. The behavior of the rural stations (average values among the three stations) is displayed in Figure 5a. The characteristic oscillating pattern reveals that, during daytime, peaks up to 38 °C are reached, while during the night the temperature decreases up to 18 °C. In general, this pattern is well captured by all the configurations, even if in the first three days maximum values are largely underestimated. The new turbulence scheme provides a sensible reduction of the minimum nocturnal values with significant performance improvement, as confirmed by MB and RMSE values for rural stations (Figure 6a,d). In rural sites, as expected, the activation of TU does not produce remarkable effects. On the other side, TU improves the representation of nocturnal values in urban stations, especially when the skin temperature scheme is activated. The hourly UHI intensity, calculated as the difference between the mean temperature urban value and the mean temperature rural value, is well reproduced when TU is activated (Figure 5), as confirmed by MB values less than 1.2 °C.
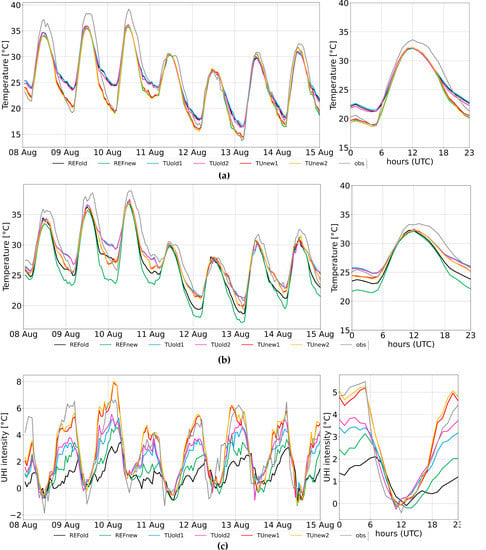
Figure 5.
(a) mean rural T2m, (b) mean urban T2m and (c) Urban Heat Island intensity during the week 8-14 August 2017. Subplots on the right show the mean daily cycles of the rural temperature and UHI intensity.
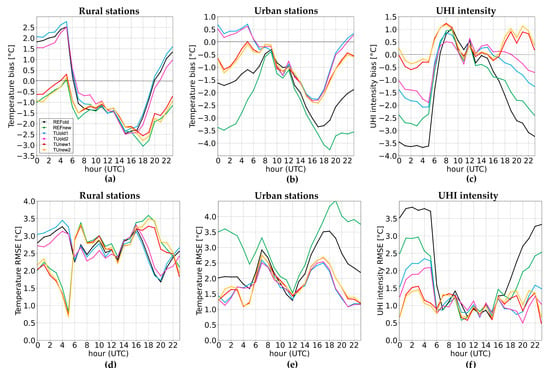
Figure 6.
Mean biases and root-mean square errors of T2m, evaluated over rural (a,d) and urban (b,e) stations in the Campania study area; mean biases and root-mean square errors of UHI intensity for urban stations (c,f).
Taylor diagrams (Figure 7) show a good correlation value (about 0.95) between the modelled and the observed data, both in urban and rural sites with all the configurations. Moreover, in urban stations all the simulations are characterized by a standard deviation generally lower than the observed one, with a better agreement achieved with the new turbulent scheme. The RMSE value is close to 1 for all the configurations. In rural stations the usage of TU causes an unexpected increase of the standard deviation and of RMSE values. The Taylor diagram related to UHI intensity provides interesting findings. In fact, the standard deviation gradually increases from the minimum value with the reference configuration to a value close to the observational one when TU is employed (TUnew1 and TUnew2). These configurations also provide the best values of correlation and RMSE.
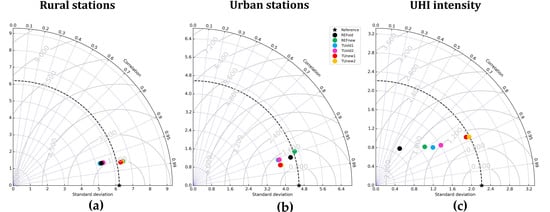
Figure 7.
Taylor diagrams for rural stations (a), urban stations (b) and UHI intensity (c).
4.3. Moscow Megacity, Russia
Model evaluation for Moscow domain was performed separately for 30 stations located outside urban environment at the distance of more than 25 km from the Moscow city center (further referred as rural neither they may be also affected by local anthropogenic effects due to their location near smaller cities or within sparsely built rural/suburban settlements), and for five urban stations, located within the megacity in the different types of urban environment. Among them, special attention is given to Balchug weather station in the city center, since it is the only one located within a relatively homogeneous dense urban environment and experiences higher temperatures than other urban stations. UHI intensity for Moscow is defined for each individual weather station as a temperature difference between this station and mean rural temperature, calculated for 9 selected stations surrounding Moscow. Same approach was used in previous studies for Moscow [34,35,37].
For the considered study period in June 2019, all model runs capture the basic patterns of the rural temperature dynamics, and a typical summer daily temperature cycle (Figure 8). As for other regions, the model overestimates nocturnal temperatures (at 0 and 21 UTC) in the runs with old physics, with worst MB more than 1.5 °C in TUold1 simulation (Figure 9). Simulations with old physics also demonstrate the highest daytime bias. The use of the new turbulence scheme and skin-layer temperature scheme decreases nocturnal temperatures and partially, but not fully eliminates positive nocturnal bias and improves RMSE (Figure 9a,c). It should be noted that model sensitivity to the change of physical schemes is smaller than for Turin and Naples, which may be associated with weather conditions or with flat terrain in the Moscow region, as well as with a larger number of rural weather stations used in analysis. Switching on TU scheme makes a small, but noticeable impact on rural temperatures since some rural stations are still affected by nearby settlements.
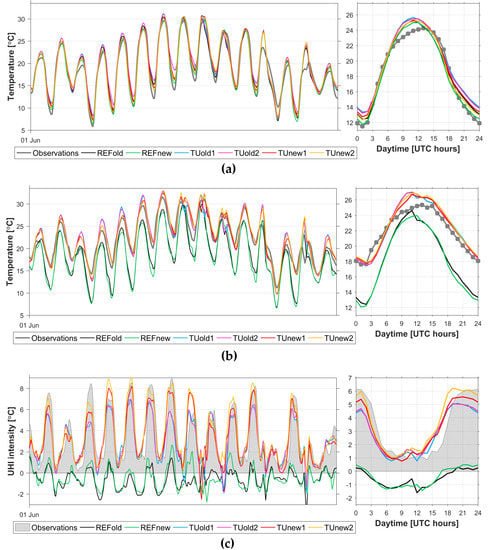
Figure 8.
Dynamics of observed and modelled values of the mean rural T2m, averaged over 9 selected rural stations in Moscow region (a), T2m at Balchug weather station at the city center (b) and urban heat island intensity for this station (c) during the considered period of 1-16 June 2019. Subplots on the right show the mean daily cycles of the rural temperature and UHI intensity. Observed and modelled time series in left subplots are smoothed by a running mean with 3-hourly window.
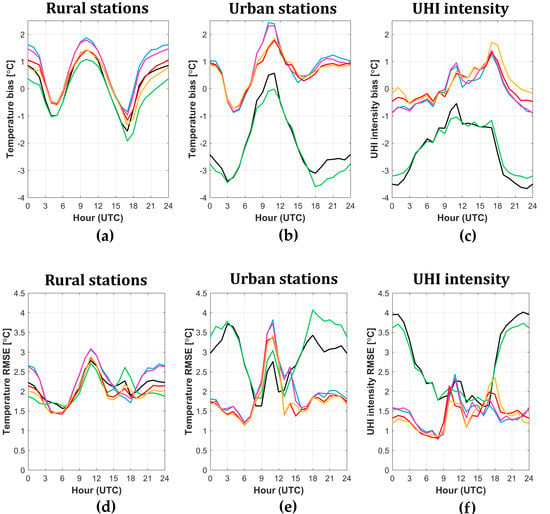
Figure 9.
Mean biases and root-mean square errors of T2m, evaluated over rural (a,d) and urban (b,e) Roshydromet weather stations in the Moscow study area; mean biases and root-mean square errors of UHI intensity for urban weather stations (c,f).
As in previous modelling studies for Moscow [34,35,37], the model runs with TU nicely captures the dynamics of the air temperature in the city center, UHI intensity and its daily turn (Figure 8b,c). On the contrary, simulations without TU do not reproduce even a part of urban-induced temperature anomaly. The differences between UHI intensity in the runs with TU and different physical schemes are consistent with other regions, although the model sensitivity is less than for other study regions: the strongest UHI is experienced in TUnew2 run and the weakest in TUold1/2 runs. Not surprisingly, runs without TU provide the worst evaluation scores for temperature and UHI intensity for urban stations (Figure 9). Among the runs with TU, simulations with new turbulence provide the best scores during the most part of the day. TUnew2 simulation provides the best scores for UHI intensity at night and morning, since it is the only one which fully captures nocturnal maximum of UHI intensity (Figure 8c). However, this run performs worse in the evening (at 15–20 UTC) due to the phase shift between modelled and observed UHI daily cycle (Figure 8b). Such phase shift is also observed for Turin and may be associated with specific microclimatic features within the urban canopy layer, which remain unresolved in TU, as well with shortcomings the ABL scheme in the model.
Taylor diagrams on Figure 10 confirm that there is only a minor difference between the model runs for rural temperature, with slightly better correlation for TUnew1/2 runs with new turbulence. The difference between the runs becomes more noticeable if considering urban stations (Figure 10b) or specifically Balchug station in the city center (Figure 10c) where TUnew1/2 runs are again the best in terms of the air temperature (Figure 10b,d). The difference between the model runs becomes even more noticeable when considering the UHI intensity for all urban weather stations and for the city center (Figure 10b,c). In both cases, TUnew2 run becomes the best one in terms of correlation coefficient and standard deviation.
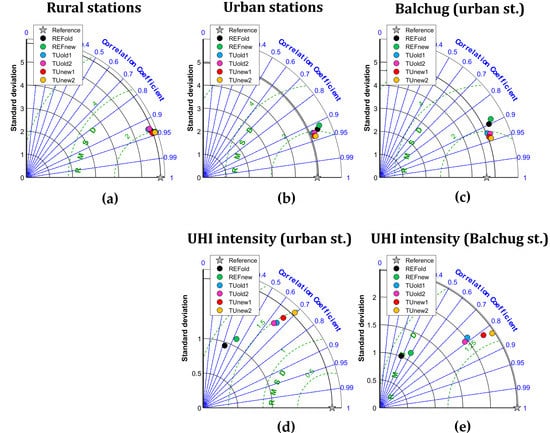
Figure 10.
Taylor diagrams for 2-m temperature for rural (a), urban (b) weather stations and Balchug weather station in the city center (c), and for UHI intensity for urban weather stations (d) and for Balchug weather station in the city center (e).
5. Discussion and Conclusions
This paper presents evaluation results of the TU scheme in high-resolution simulations with a recent COSMO model version for selected European cities, namely Turin, Naples and Moscow. Additional sensitivity tests have been performed in order to evaluate the ICON-like turbulence scheme developed in COSMO and the use of a new skin-layer temperature scheme. The novelty of the work in comparison with previous TU evaluation studies lies in the use of the recent model version, and in the uniform approach for setting up numerical experiments and their evaluation applied for all different cities.
Even if the three domains are morphologically different and the stations for data validation do not share the same properties in Turin, Naples and Moscow, the outcomes follow a common behavior. This similarity in such different morphological conditions points out that the finding is not due to specific model calibration but has a universal meaning. The effect of TU combined with the ICON-like turbulence and skin temperature schemes provides a substantial improvement in capturing the UHI intensity and improving air temperature forecasts for urban areas. It should be noted that model sensitivity to the change of physical schemes is smaller for Moscow than for Turin and Naples, which may be associated with weather conditions or with flat terrain in the Moscow domain, as well as with a larger number of rural weather stations used for the validation.
In comparison with other urban canopy schemes, TU is much simpler, but provides reasonable results for three cities considered in our study and for more cities in previous studies ([12,36,37,38,39,40,41,42]). Additionally, it realistically represents urban effects in the lower atmosphere by capturing the urban-induced modification of precipitation patters [34]. The scheme simplicity together with encouraging verification results for these three cities strongly supports the use of TU scheme in operational weather forecast, as it is already done for Moscow [37].
This study is limited to the canopy-layer UHI effect, while it would be better to have a more comprehensive view of other urban-induced climatic and atmospheric effects, including SUHI and urban effects on air humidity and wind. Further verification studies should involve satellite-retrieved land surface temperatures and urban/rural observations on other meteorological parameters. Moreover, a better evaluation of the PBL structure by means of temperature and wind stratification is needed. Among the case study cities, Moscow and Turin provides opportunities for further in-depth model verification due to the presence of temperature profiler networks. Moreover, sodar wind profilers are available in Moscow, Turin and Naples. The presence of necessary observations together with experience of effective collaborative work will allow to consider these three cities as a cross-border test bed for further deeper model evaluation studies.
The TU scheme will soon be implemented in the main branch of COSMO development under version 6.0, which will simplify its use in NWP and climate modelling tasks. Since in the COSMO Consortium it is planned the migration to ICON model, which will be the future operational model, a special attention will be devoted to the porting of the scheme into ICON. The authors have already formalized the steps in a new Priority Project inside the Consortium. The latter foresees further research on the urban canopy parameters and the potential use of Local Climate Zone [79,80,81] information, found to be promising for Moscow [75].
Author Contributions
Conceptualization, V.G. and P.M.; methodology, J.-P.S., H.W., V.G., M.V., M.M., P.M.; software, M.V., M.D, U.S., J.-P.S., H.W., D.B.; investigation: M.M., F.R., V.G., M.V., E.B.; validation, E.B., F.R., V.G., F.B., M.V.; formal analysis, E.B., P.M., M.M., V.G.; writing—original draft preparation, F.B., V.G., M.V., J.-P.S., H.W., M.D.; writing—review and editing, V.G., E.B., M.V., G.R., I.R., M.D., F.B., M.M.; visualization, F.R., F.B., M.V.; supervision, V.G.; project administration, P.M., I.R, G.R. All authors have read and agreed to the published version of the manuscript.
Funding
The contribution of the authors from Hydrometeorological Research Center of Russia was funded by the grant for the implementation of activities on the development of the system for monitoring, forecasting, and warning of severe and adverse weather events in Moscow city (the Resolution of the Government of Moscow No. 257-PP, April 3, 2018) and by the Federal Service for Hydrometeorology and Environmental Monitoring of Russia (topic AAAA-A20-120021490079-3. Work on the development of the external parameters for Moscow megacity, performed by M. Varentsov, was partially supported by the Russian Science Foundation under the project under grant No. 19-77-30012. M. Demuzere is funded by the ENLIGHT project, funded by the German Research Foundation (DFG) under grant No. 437467569. F. Bassani is funded by RISK-GEST Project—PITEM RISK, Interreg 2014–2020 Alcotra IT-FR, MISTRAL 2017-IT-IA-0144 Program Connecting Europe Facility (CEF) and the 2019–2021 Agreement between National Department of Civil Protection and Arpa Piemonte.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The simulations for Moscow region were carried out using Cray-XC40-LC supercomputer in Roshydromet Main Computing Center and partially on the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University. The authors are grateful to the administration and staff of Hydrometeorological Research Center of Russian Federation and Meteorological observatory of the Lomonosov Moscow State University for providing the data of meteorological observations used for Moscow domain. The simulations for Piedmont domain were carried out at ECMWF supercomputer in the framework of the Special Project “Implementation and test of an urban parameterization module in ICON Model”. A special thank goes to the RISK-GEST Project—PITEM RISK, the MISTRAL Program and the National Department of Civil Protection for supporting this kind of activities. M. Demuzere was supported by the ENLIGHT project, funded by the German Research Foundation (DFG) under grant No. 437467569
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
List of Abbreviations
| AHF | Anthropogenic Heat Flux |
| BEM | Building Energy Model |
| BEP | Building Environment Parameterization |
| CLM | Climate Limited-area Modelling Community |
| COSMO | Consortium for Small-scale Modelling |
| DCEP | Double-Canyon Effect Parameterization |
| EEA | European Environment Agency |
| ICON | Icosahedral Nonhydrostatic Weather and Climate Model |
| IFS | Integrated Forecast System |
| ISA | Impervious Surface Area fraction |
| LCZ | Local Climate Zones |
| LST | Land Surface Temperature |
| MB | Mean Bias |
| NWP | Numerical Weather Prediction |
| PBL | Planetary Boundary Layer |
| RMSE | Root Mean Square Error |
| SLUCM | Single Level Urban Canopy Model |
| SUHI | Surface Urban Heat Island |
| SURY | Semi-empirical URban canopY parameterization |
| TEB | Town Energy Balance |
| TKE | Turbulent Kinetic Energy |
| TU | TERRA_URB |
| UCM(s), | Urban Canopy Model(s) |
| UHI | Urban Heat Island |
| UTC | Coordinated Universal Time |
| WRF | Weather Research and Forecasting |
Appendix A: The “urban double-counting effect”
The output external parameters used by COSMO are generated by the EXTPAR software that aggregates various raw datasets to the target grid and performs general consistency checks [66]. Some external parameters are calculated as a function of land use classes and might therefore depend on urban fraction (artificial surfaces, class=19 in GLOBCOVER classification, which corresponds to URBAN parameter). The parameters affected by the presence of artificial surfaces are: roughness length (Z0 [m]), minimum / maximum ground fraction covered by plants in the vegetation period (PLCOV_MN / PLCOV_MX), ground fraction covered by deciduous / evergreen forest (FOR_D / FOR_E), skin conductivity (SKC [Wm−1K−1]), root depth (ROOTDP [m]), minimum / maximum leaf area index in the vegetation period (LAI_MN / LAI_MX), minimum plant resistance (RSMIN [sm-1]) and long wave surface emissivity (EMISS_RAD).
If TU is switched off, the effect of urban surfaces is then represented in increased roughness and reduced green vegetation fraction and characteristics, the so-called ‘zero-order urban model’, which is currently implemented in the operational COSMO model.
If TU is activated, a tile approach is implemented in which each cell is divided into two tiles, an urban tile and a natural tile. The fraction of the urban tile is defined by the impervious surface area (ISA) parameter. The SURY parameterization is used to calculate the model variables for the urban tile, whereas the zero-order urban description provides the model variables for the natural tile. However, the current external parameters associated with the natural tile are those provided by EXTPAR and are still calculated by considering the urban contribution: this is what we call the ‘urban double-counting effect’, as the presence of the city is counted twice, once by the TU scheme and once by the zero-order urban model that integrates urban characteristics into the natural tile. In order to avoid this double-counting effect, a new dataset for natural tile has been built from the one provided by EXTPAR, where the urban-based external parameters have been calculated according to the functions implemented in EXTPAR but re-weighted excluding GLOBCOVER’s URBAN class. A python routine that accounts for this double-counting is contained in the WUDAPT-to-COSMO converter [80] and it is publicly available on GitHub: https://github.com/matthiasdemuzere/WUDAPT-to-COSMO/blob/eb4d232dbb56f712dd2b486cb555b5e3c3c209fb/utils.py#L290 (accessed on 20 November 2020).
Appendix B: Characteristics of the stations used for model validation
The following Tables display the specifics of the weather stations, for Turin (Table A1), for Naples (Table A2) and for Moscow (Table A3) respectively. The modelled elevation is extracted from EXTPAR; ISA values are from EXTPAR for Turin and Naples as well, while for Moscow they were obtained with the GIS-based approach described in Section 3 [77]. Finally, the Local Climate Zone (LCZ) classes are extracted from the European LCZ map [80,82]. Both ISA and especially the LCZ class, allowed the classification of each station into urban or rural, thanks to its universality of application. A summary of the LCZ types involved is listed below, taken from Stewart and Oke’s study [79]:
- urban, LCZ 2: “compact midrise”; dense mix of midrise buildings (3-9 stories). Few or no trees, land cover mostly paved.
- urban, LCZ 4: “open high-rise”; open arrangement of tall buildings to tens of stories. Abundance of pervious land cover (low plants, scattered trees).
- urban, LCZ 5: “open midrise”; open arrangement of midrise buildings (3-9 stories). Abundance of pervious land cover.
- urban LCZ 6: “open low-rise”; open arrangement of low-rise buildings (1-3 stories). Abundance of pervious land cover.
- urban, LCZ 8: “large low-rise”; open arrangement of large low-rise buildings (1-3 stories). Few or no trees, land cover mostly paved.
- rural, LCZ A: “dense trees”; heavily wooded landscape of deciduous and/or evergreen trees. Land cover mostly pervious (low plants). Zone function: natural forest, tree cultivation, urban park.
- rural, LCZ B: “scattered trees”; same as LCZ A, but lightly wooded.
- rural, LCZ D: “low plants”; featureless landscape of grass or herbaceous plants/crops. Few or no trees. Zone function: natural grassland, agriculture, urban park.

Table A1.
Turin, Piedmont domain, Italy.
Table A1.
Turin, Piedmont domain, Italy.
| Station Name | Lat | Lon | Elevation, Actual (m a.s.l.) | Elevation, Model (m a.s.l.) | ISA (%) | LCZ | Classification |
|---|---|---|---|---|---|---|---|
| Reiss Romoli | 45.113 | 7.671 | 270 | 246 | 0.67 | 8 | urban |
| Alenia | 45.081 | 7.612 | 320 | 279 | 0.62 | 8 | urban |
| Consolata | 45.077 | 7.679 | 290 | 248 | 0.93 | 2 | urban |
| Bauducchi | 44.961 | 7.710 | 226 | 225 | 0.09 | D | rural |
| Santena-Banna | 44.946 | 7.783 | 238 | 234 | 0.14 | D | rural |
| Carmagnola | 44.887 | 7.688 | 232 | 232 | 0.02 | D | rural |

Table A2.
Naples, Campania domain, Italy.
Table A2.
Naples, Campania domain, Italy.
| Station Name | Lat | Lon | Elevation, Actual (m a.s.l.) | Elevation, Model (m a.s.l.) | ISA (%) | LCZ | Classification |
|---|---|---|---|---|---|---|---|
| Napoli | 40.9375 | 14.0759 | 13 | 61 | 0.80 | 8 | urban |
| S. Marco Evangelista | 41.0225 | 14.3358 | 31 | 22 | 0.72 | 8 | urban |
| Grazzanise | 41.0542 | 14.0913 | 6 | 9 | 0.02 | D | rural |
| Rocca d’Evandro | 41.4244 | 13.8800 | 62 | 55 | 0.09 | D | rural |
| Alife | 41.3391 | 14.3336 | 117 | 117 | 0.01 | D | rural |

Table A3.
Moscow megacity, Russia.
Table A3.
Moscow megacity, Russia.
| Station Name | Lat | Lon | Elevation, Actual (m a.s.l.) | Elevation, Model (m a.s.l.) | ISA (%) | LCZ | Classification |
|---|---|---|---|---|---|---|---|
| Dolgoprudnyy | 55.93027 | 37.51944 | 193 | 195 | 0.64 | 5 | urban |
| Strogino | 55.79694 | 37.39527 | 145 | 155 | 0.70 | 4 | urban |
| VDNKh | 55.83138 | 37.62194 | 148 | 145 | 0.00 | A/B/5 | urban |
| Balchug | 55.74555 | 37.63 | 123 | 129 | 0.88 | 2 | urban |
| MSU | 55.70694 | 37.5222 | 192 | 183 | 0.49 | 5/B | urban |
| Klin | 56.35 | 36.74972 | 165 | 171 | 0.08 | 6/8 | rural |
| Novo-Iyerusalim | 55.90638 | 36.825 | 159 | 161 | 0.00 | 6 | rural |
| Naro-Fominsk | 55.38722 | 36.70111 | 190 | 200 | 0.00 | D | rural |
| Maloyaroslavets | 55.01694 | 36.48583 | 195 | 203 | 0.26 | 6 | rural |
| Dmitrov | 56.3575 | 37.55722 | 178 | 180 | 0.43 | 6 | rural |
| Serpukhov | 54.9225 | 37.46556 | 164 | 165 | 0.19 | D | rural |
| Alexandrov | 56.4 | 38.75055 | 185 | 184 | 0.00 | 6 | rural |
| Pavlovsky Posad | 55.7716 | 38.6925 | 134 | 133 | 0.22 | 6 | rural |
| Kolomna | 55.1422 | 38.7325 | 112 | 111 | 0.03 | 6 | rural |
References
- Reba, M.; Seto, K.C. A Systematic Review and Assessment of Algorithms to Detect, Characterize, and Monitor Urban Land Change. Remote Sens. Environ. 2020, 242, 111739. [Google Scholar] [CrossRef]
- United Nations; Department of Economic and Social Affairs. Population Division World Urbanization Prospects: The 2018 Revision; United Nations: New York, NY, USA, 2019; ISBN 978-92-1-148319-2. [Google Scholar]
- IPCC Reports. Available online: https://www.ipcc.ch/report/ar5/syr/ (accessed on 30 November 2020).
- Koffi, B.; Koffi, E. Heat waves across Europe by the end of the 21st century: Multiregional climate simulations. Clim. Res. 2008, 36, 153–168. [Google Scholar] [CrossRef]
- Schatz, J.; Kucharik, C.J. Urban Climate Effects on Extreme Temperatures in Madison, Wisconsin, USA. Environ. Res. Lett. 2015, 10, 094024. [Google Scholar] [CrossRef]
- De Ridder, K.; Maiheu, B.; Lauwaet, D.; Daglis, I.A.; Keramitsoglou, I.; Kourtidis, K.; Manunta, P.; Paganini, M. Urban Heat Island Intensification during Hot Spells—The Case of Paris during the Summer of 2003. Urban Sci. 2017, 1, 3. [Google Scholar] [CrossRef]
- Konstantinov, P.I.; Varentsov, M.I.; Malinina, E.P. Modeling of Thermal Comfort Conditions inside the Urban Boundary Layer during Moscow’s 2010 Summer Heat Wave (Case-Study). Urban Clim. 2014, 10, 563–572. [Google Scholar] [CrossRef]
- Van Hove, L.W.A.; Jacobs, C.M.J.; Heusinkveld, B.G.; Elbers, J.A.; van Driel, B.L.; Holtslag, A.A.M. Temporal and Spatial Variability of Urban Heat Island and Thermal Comfort within the Rotterdam Agglomeration. Build. Environ. 2015, 83, 91–103. [Google Scholar] [CrossRef]
- Tan, J.; Zheng, Y.; Tang, X.; Guo, C.; Li, L.; Song, G.; Zhen, X.; Yuan, D.; Kalkstein, A.J.; Li, F.; et al. The Urban Heat Island and Its Impact on Heat Waves and Human Health in Shanghai. Int. J. Biometeorol. 2010, 54, 75–84. [Google Scholar] [CrossRef]
- Gabriel, K.M.A.; Endlicher, W.R. Urban and Rural Mortality Rates during Heat Waves in Berlin and Brandenburg, Germany. Environ. Pollut. 2011, 159, 2044–2050. [Google Scholar] [CrossRef]
- Lo, E.; Mitchell, D.; Bohnenstengel, S.; Collins, M.; Hawkins, E.; Hegerl, G.; Joshi, M.; Stott, P. U.K. Climate Projections: Summer Daytime and Nighttime Urban Heat Island Changes in England’s Major Cities. J. Clim. 2020, 33, 9015–9030. [Google Scholar] [CrossRef]
- Wouters, H.; De Ridder, K.; Poelmans, L.; Willems, P.; Brouwers, J.; Hosseinzadehtalaei, P.; Tabari, H.; Vanden Broucke, S.; van Lipzig, N.P.M.; Demuzere, M. Heat Stress Increase under Climate Change Twice as Large in Cities as in Rural Areas: A Study for a Densely Populated Midlatitude Maritime Region. Geophys. Res. Lett. 2017, 44, 8997–9007. [Google Scholar] [CrossRef]
- Zhao, L.; Oleson, K.; Bou-Zeid, E.; Krayenhoff, E.S.; Bray, A.; Zhu, Q.; Zheng, Z.; Chen, C.; Oppenheimer, M. Global Multi-Model Projections of Local Urban Climates. Nat. Clim. Chang. 2021. [Google Scholar] [CrossRef]
- Mote, T.L.; Lacke, M.C.; Shepherd, J.M. Radar Signatures of the Urban Effect on Precipitation Distribution: A Case Study for Atlanta, Georgia. Geophys. Res. Lett. 2007, 34, L20710. [Google Scholar] [CrossRef]
- Baik, J.-J.; Kim, Y.-H.; Kim, J.-J.; Han, J.-Y. Effects of Boundary-Layer Stability on Urban Heat Island-Induced Circulation. Theor. Appl. Climatol. 2007, 89, 73–81. [Google Scholar] [CrossRef]
- Li, Y.; Fowler, H.J.; Argüeso, D.; Blenkinsop, S.; Evans, J.P.; Lenderink, G.; Yan, X.; Guerreiro, S.B.; Lewis, E.; Li, X. Strong Intensification of Hourly Rainfall Extremes by Urbanization. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Doan, Q.-V.; Dipankar, A.; Simón-Moral, A.; Sanchez, C.; Venkatraman, P.; Roth, M.; Huang, X.-Y. Urban-Induced Modifications to the Diurnal Cycle of Rainfall over a Tropical City. Q. J. R. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Dou, J.; Wang, Y.; Bornstein, R.; Miao, S. Observed Spatial Characteristics of Beijing Urban Climate Impacts on Summer Thunderstorms. J. Appl. Meteorol. Climatol. 2015, 54, 12. [Google Scholar] [CrossRef]
- Dimitrova, R.; Danchovski, V.; Egova, E.; Vladimirov, E.; Sharma, A.; Gueorguiev, O.; Ivanov, D. Modeling the Impact of Urbanization on Local Meteorological Conditions in Sofia. Atmosphere 2019, 10, 366. [Google Scholar] [CrossRef]
- Martilli, A.; Roth, M.; Chow, W.T.L.; Demuzere, M.; Lipson, M.; Krayenhoff, E.S.; Sailor, D.; Nazarian, N.; Voogt, J.; Wouters, H.; et al. Summer Average Urban-Rural Surface Temperature Differences Do Not Indicate the Need for Urban Heat Reduction. Open Sci. Framew. 2020. [Google Scholar] [CrossRef]
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite Remote Sensing of Surface Urban Heat Islands: Progress, Challenges, and Perspectives. Remote Sens. 2019, 11, 48. [Google Scholar] [CrossRef]
- Garuma, G.F. Review of Urban Surface Parameterizations for Numerical Climate Models. Urban Clim. 2018, 24, 830–851. [Google Scholar] [CrossRef]
- Chen, F.; Kusaka, H.; Bornstein, R.; Ching, J.; Grimmond, C.S.B.; Grossman-Clarke, S.; Loridan, T.; Manning, K.W.; Martilli, A.; Miao, S.; et al. The Integrated WRF/Urban Modelling System: Development, Evaluation, and Applications to Urban Environmental Problems. Int. J. Climatol. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Sharma, A.; Fernando, H.J.S.; Hamlet, A.F.; Hellmann, J.J.; Barlage, M.; Chen, F. Urban Meteorological Modeling Using WRF: A Sensitivity Study. Int. J. Climatol. 2017, 37, 1885–1900. [Google Scholar] [CrossRef]
- Baklanov, A.; Mestayer, P.; Clappier, A.; Zilitinkevich, S.; Joffre, S.; Mahura, A.; Nielsen, N.W. On the Parameterisation of the Urban Atmospheric Sublayer in Meteorological Models. Atmos. Chem. Phys. Discuss. 2005, 5, 12119–12176. [Google Scholar]
- Baklanov, A.; Mestayer, P.G.; Clappier, A.; Zilitinkevich, S.; Joffre, S.; Mahura, A.; Nielsen, N.W. Towards Improving the Simulation of Meteorological Fields in Urban Areas through Updated/Advanced Surface Fluxes Description. Atmos. Chem. Phys. 2008, 8, 543. [Google Scholar] [CrossRef]
- Bohnenstengel, S.I.; Evans, S.; Clark, P.A.; Belcher, S.E. Simulations of the London Urban Heat Island. Q. J. R. Meteorol. Soc. 2011, 137, 1625–1640. [Google Scholar] [CrossRef]
- Iriza, A.; Dumitrache, R.; Stefan, S. Numerical Modelling of the Bucharest Urban Heat Island with the WRF-Urban System. Romanian J. Phys. 2017, 62, 1–14. [Google Scholar]
- Vogel, J.; Afshari, A. Comparison of Urban Heat Island Intensity Estimation Methods Using Urbanized WRF in Berlin, Germany. Atmosphere 2020, 11, 1338. [Google Scholar] [CrossRef]
- Ribeiro, I.; Martilli, A.; Falls, M.; Zonato, A.; Villalba, G. Highly Resolved WRF-BEP/BEM Simulations over Barcelona Urban Area with LCZ. Atmos. Res. 2021, 248, 105220. [Google Scholar] [CrossRef]
- Doms, G.; Förstner, J.; Heise, E.; Herzog, H.-J.; Mironov, D.; Raschendorfer, M.; Reinhardt, T.; Ritter, B.; Schrodin, R.; Schulz, J.-P. A Description of the Nonhydrostatic Regional COSMO Model. Part II: Physical Parameterization; Deutscher Wetterdienst: Offenbach, Germany, 2011. [Google Scholar]
- Wouters, H.; Demuzere, M.; Blahak, U.; Fortuniak, K.; Maiheu, B.; Camps, J.; Tielemans, D.; Van Lipzig, N. The Efficient Urban Canopy Dependency Parametrization (SURY) v1.0 for Atmospheric Modelling: Description and Application with the COSMO-CLM Model for a Belgian Summer. Geosci. Model Dev. 2016, 9, 3027–3054. [Google Scholar] [CrossRef]
- Bohnenstengel, S.I.; Hamilton, I.; Davies, M.; Belcher, S.E. Impact of Anthropogenic Heat Emissions on London’s Temperatures. Q. J. R. Meteorol. Soc. 2014, 140, 687–698. [Google Scholar] [CrossRef]
- Varentsov, M.; Wouters, H.; Platonov, V.; Konstantinov, P. Megacity-Induced Mesoclimatic Effects in the Lower Atmosphere: A Modeling Study for Multiple Summers over Moscow, Russia. Atmosphere 2018, 9, 50. [Google Scholar] [CrossRef]
- Varentsov, M.I.; Grishchenko, M.Y.; Wouters, H. Simultaneous Assessment of the Summer Urban Heat Island in Moscow Megacity Based on in Situ Observations, Thermal Satellite Images and Mesoscale Modeling. Available online: https://ges.rgo.ru/jour/article/view/903 (accessed on 27 November 2020).
- Rivin, G.S.; Vil’fand, R.M.; Kiktev, D.B.; Rozinkina, I.A.; Tudriy, K.O.; Blinov, D.V.; Varentsov, M.I.; Samsonov, T.E.; Bundel’, A.Y.; Kirsanov, A.A.; et al. The System for Numerical Prediction of Weather Events (Including Severe Ones) for Moscow Megacity: The Prototype Development. Russ. Meteorol. Hydrol. 2019, 44, 729–738. [Google Scholar] [CrossRef]
- Rivin, G.S.; Rozinkina, I.A.; Vil’fand, R.M.; Kiktev, D.B.; Tudrii, K.O.; Blinov, D.V.; Varentsov, M.I.; Zakharchenko, D.I.; Samsonov, T.E.; Repina, I.A.; et al. Development of the High-Resolution Operational Systemfor Numerical Prediction of Weather and Severe Weather Events for The Moscow Region. Russ. Meteorol. Hydrol. 2020, 45, 455–465. [Google Scholar] [CrossRef]
- Wouters, H.; Demuzere, M.; Ridder, K.D.; van Lipzig, N.P.M. The Impact of Impervious Water-Storage Parametrization on Urban Climate Modelling. Urban Clim. 2015, 11, 24–50. [Google Scholar] [CrossRef]
- Demuzere, M.; Harshan, S.; Järvi, L.; Roth, M.; Grimmond, C.S.B.; Masson, V.; Oleson, K.W.; Velasco, E.; Wouters, H. Impact of Urban Canopy Models and External Parameters on the Modelled Urban Energy Balance in a Tropical City. Q. J. R. Meteorol. Soc. 2017, 143, 1581–1596. [Google Scholar] [CrossRef]
- Trusilova, K.; Schubert, S.; Wouters, H.; Früh, B.; Grossman-Clarke, S.; Demuzere, M.; Becker, P. The Urban Land Use in the COSMO-CLM Model: A Comparison of Three Parameterizations for Berlin. Meteorol. Z. 2016, 25, 231–244. [Google Scholar] [CrossRef]
- Brousse, O.; Georganos, S.; Demuzere, M.; Vanhuysse, S.; Wouters, H.; Wolff, E.; Linard, C.; van Lipzig, N.P.-M.; Dujardin, S. Using Local Climate Zones in Sub-Saharan Africa to Tackle Urban Health Issues. Urban Clim. 2019, 27, 227–242. [Google Scholar] [CrossRef]
- Brousse, O.; Wouters, H.; Demuzere, M.; Thiery, W.; de Walle, J.V.; van Lipzig, N.P.M. The Local Climate Impact of an African City during Clear-Sky Conditions—Implications of the Recent Urbanization in Kampala (Uganda). Int. J. Climatol. 2020, 40, 4586–4608. [Google Scholar] [CrossRef]
- Trusilova, K.; Früh, B.; Brienen, S.; Walter, A.; Masson, V.; Pigeon, G.; Becker, P. Implementation of an Urban Parameterization Scheme into the Regional Climate Model COSMO-CLM. J. Appl. Meteorol. Climatol. 2013, 52, 2296–2311. [Google Scholar] [CrossRef]
- Mussetti, G.; Brunner, D.; Allegrini, J.; Wicki, A.; Schubert, S.; Carmeliet, J. Simulating Urban Climate at Sub-Kilometre Scale for Representing the Intra-Urban Variability of Zurich, Switzerland. Int. J. Climatol. 2020, 40, 458–476. [Google Scholar] [CrossRef]
- Li, Y.; Schubert, S.; Kropp, J.P.; Rybski, D. On the Influence of Density and Morphology on the Urban Heat Island Intensity. Nat. Commun. 2020, 11, 2647. [Google Scholar] [CrossRef] [PubMed]
- Mussetti, G.; Brunner, D.; Henne, S.; Allegrini, J.; Krayenhoff, E.S.; Schubert, S.; Feigenwinter, C.; Vogt, R.; Wicki, A.; Carmeliet, J. COSMO-BEP-Tree v1.0: A Coupled Urban Climate Model with Explicit Representation of Street Trees. Geosci. Model Dev. 2020, 13, 1685–1710. [Google Scholar] [CrossRef]
- Schubert, S.; Grossman-Clarke, S.; Martilli, A. A Double-Canyon Radiation Scheme for Multi-Layer Urban Canopy Models. Bound. Layer Meteorol. 2012, 145, 439–468. [Google Scholar] [CrossRef]
- Bucchignani, E.; Mercogliano, P.; Garbero, V.; Milelli, M.; Varentsov, M.; Rozinkina, I.; Rivin, G.; Blinov, D.; Kirsanov, A.; Wouters, H.; et al. Analysis and Evaluation of TERRA_URB Scheme: PT AEVUS Final Report. Technical Report No. 40. 2019. Available online: http://www.cosmo-model.org/content/model/documentation/techReports/docs/techReport40.pdf (accessed on 11 January 2021). [CrossRef]
- Steppeler, J.; Doms, G.; Schättler, U.; Bitzer, H.W.; Gassmann, A.; Damrath, U.; Gregoric, G. Meso-Gamma Scale Forecasts Using the Nonhydrostatic Model LM. Meteorol. Atmos. Phys. 2003, 82, 75–96. [Google Scholar] [CrossRef]
- Cosmo Public Area. Available online: http://www.cosmo-model.org/ (accessed on 30 November 2020).
- Baldauf, M.; Seifert, A.; Förstner, J.; Majewski, D.; Raschendorfer, M.; Reinhardt, T. Operational Convective-Scale Numerical Weather Prediction with the COSMO Model: Description and Sensitivities. Mon. Weather Rev. 2011, 139, 3887–3905. [Google Scholar] [CrossRef]
- Buzzi, M. Challenges in Operational Numerical Weather Prediction at High Resolution in Complex Terrain. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2008. [Google Scholar]
- Paulson, C.A. The Mathematical Representation of Wind Speed and Temperature Profiles in the Unstable Atmospheric Surface Layer. J. Appl. Meteorol. 1970, 9, 857–861. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H. A Performance Comparison between Nonlinear Similarity Functions in Bulk Parameterization for Very Stable Conditions. Environ. Fluid Mech. 2007, 7, 239–257. [Google Scholar] [CrossRef]
- Louis, J.-F. A Parametric Model of Vertical Eddy Fluxes in the Atmosphere. Bound. Layer Meteorol. 1979, 17, 187–202. [Google Scholar] [CrossRef]
- Wouters, H.; De Ridder, K.; van Lipzig, N.P.M. Comprehensive Parametrization of Surface-Layer Transfer Coefficients for Use in Atmospheric Numerical Models. Bound. Layer Meteorol. 2012, 145, 539–550. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a Turbulence Closure Model for Geophysical Fluid Problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Schattler, U.; Doms, G.; Schraff, C. A Description of the Nonhydrostatic Regional COSMO-Model. Part VII: User’s Guide. Dtsch. Wetterd. 2018, 226. [Google Scholar] [CrossRef]
- Schulz, J.-P. Introducing Sub-Grid Scale Orographic Effects in the COSMO Model. COSMO Newsl. 2008, 9, 29–36. [Google Scholar]
- Cerenzia, I.; Tampieri, F.; Tesini, M.S. Diagnosis of Turbulence Schema in Stable Atmospheric Conditions and Sensitivity Tests. COSMO Newsl. 2014, 14, 28–36. [Google Scholar]
- Varentsov, M.I.; Samsonov, T.E.; Kislov, A.V.; Konstantinov, P.I. Simulations of Moscow agglomeration heat island within framework of regional climate model COSMO-CLM. Moscow Univ. Vestnik. Ser. 5 Geogr. 2017, 6, 25–37. [Google Scholar]
- Schulz, J.-P.; Vogel, G.; Becker, C.; Kothe, S.; Ahrens, B. Evaluation of the Ground Heat Flux Simulated by a Multi-Layer Land Surface Scheme Using High-Quality Observations at Grass Land and Bare Soil. Meteorol. Z. 2016, 11, 607–620. [Google Scholar] [CrossRef]
- Schulz, J.-P.; Vogel, G. Improving the Processes in the Land Surface Scheme TERRA: Bare Soil Evaporation and Skin Temperature. Atmosphere 2020, 11, 513. [Google Scholar] [CrossRef]
- Viterbo, P.; Beljaars, A.C.M. An Improved Land Surface Parameterization Scheme in the ECMWF Model and Its Validation. J. Clim. 1995, 8, 2716–2748. [Google Scholar] [CrossRef]
- Flanner, M.G. Integrating Anthropogenic Heat Flux with Global Climate Models. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Asensio, H.; Messmer, M.; Luthi, D.; Osterried, K.; Jucker, J. External Parameters for Numerical Weather Prediction and Climate Application EXTPAR v5_4, User and Implementation Guide. 2020. Available online: http://www.cosmo-model.org/content/support/software/ethz/EXTPAR_user_and_implementation_manual.pdf (accessed on 15 October 2020).
- Elvidge, C.D.; Tuttle, B.T.; Sutton, P.C.; Baugh, K.E.; Howard, A.T.; Milesi, C.; Bhaduri, B.; Nemani, R. Global Distribution and Density of Constructed Impervious Surfaces. Sensors 2007, 7, 1962–1979. [Google Scholar] [CrossRef]
- EEA Fast Track Service Precursor on Land Monitoring—Degree of Soil Sealing—European Environment Agency. Available online: https://www.eea.europa.eu/data-and-maps/data/eea-fast-track-service-precursor-on-land-monitoring-degree-of-soil-sealing (accessed on 30 November 2020).
- Bicheron, P.; Defourny, P.; Brockmann, C.; Schouten, L.; Vancutsem, C.; Huc, M.; Ranera, F. GLOBCOVER: Products Description and Validation Report; Technical Report; MEDIAS-France: Levallois-Perret, France, 2008. [Google Scholar]
- Kislov, A.V.; Varentsov, M.I.; Tarasova, L.L. Role of Spring Soil Moisture in the Formation of Large-Scale Droughts in the East European Plain in 2002 and 2010. Izv. Atmos. Ocean. Phys. 2015, 51, 405–411. [Google Scholar] [CrossRef]
- Canadell, J.; Jackson, R.B.; Ehleringer, J.B.; Mooney, H.A.; Sala, O.E.; Schulze, E.-D. Maximum Rooting Depth of Vegetation Types at the Global Scale. Oecologia 1996, 108, 583–595. [Google Scholar] [CrossRef] [PubMed]
- Plant Root Systems and Natural Vegetation; Acta Phytogeographica Suecica; Persson, H., Baĭtulin, I.O., Eds.; Opulus Press AB: Uppsala, Sweden, 1996; ISBN 978-91-7210-481-5. [Google Scholar]
- Schenk, H.J.; Jackson, R.B. The Global Biogeography of Roots. Ecol. Monogr. 2002, 72, 311–328. [Google Scholar] [CrossRef]
- Akkermans, T.; Lauwaet, D.; Demuzere, M.; Vogel, G.; Nouvellon, Y.; Ardö, J.; Caquet, B.; Grandcourt, A.D.; Merbold, L.; Kutsch, W.; et al. Validation and Comparison of Two Soil-Vegetation-Atmosphere Transfer Models for Tropical Africa. J. Geophys. Res. Biogeosciences 2012, 117. [Google Scholar] [CrossRef]
- Varentsov, M.; Samsonov, T.E. Impact of Urban Canopy Parameters on a Megacity’s Modelled Thermal Environment. Atmosphere 2020, 11, 1349. [Google Scholar] [CrossRef]
- Stewart, I.D.; Kennedy, C.A. Metabolic Heat Production by Human and Animal Populations in Cities. Int. J. Biometeorol. 2017, 61, 1159–1171. [Google Scholar] [CrossRef] [PubMed]
- Samsonov, T.E.; Varentsov, M.I. Computation of City-Descriptive Parameters for High-Resolution Numerical Weather Prediction in Moscow Megacityin the Framework of the COSMO Model. Russ. Meteorol. Hydrol. 2020, 45, 515–521. [Google Scholar] [CrossRef]
- Lokoshchenko, M.A. Urban ‘Heat Island’ in Moscow. Urban Clim. 2014, 10, 550–562. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Demuzere, M.; Bechtel, B.; Middel, A.; Mills, G. Mapping Europe into Local Climate Zones. PLoS ONE 2019, 14, e0214474. [Google Scholar] [CrossRef]
- Demuzere, M.; Hankey, S.; Mills, G.; Zhang, W.; Lu, T.; Bechtel, B. Combining Expert and Crowd-Sourced Training Data to Map Urban Form and Functions for the Continental US. Sci. Data 2020, 7, 264. [Google Scholar] [CrossRef] [PubMed]
- Demuzere, M.; Bechtel, B.; Middel, A.; Mills, G. European LCZ Map. 2019. Available online: https://urlsand.esvalabs.com/?u=https%3A%2F%2Ffigshare.com%2Farticles%2Fdataset%2FEuropean_LCZ_map%2F13322450%2F1&e=78898b00&h=9a0f73a7&f=y&p=n (accessed on 11 January 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).