Abstract
This paper shall present a multifractal interpretation of turbulent atmospheric entities, considering them a complex system whose dynamics are manifested on continuous yet non-differentiable multifractal curves. By bringing forth theoretical considerations regarding multifractal structures through non-differentiable functions in the form of an adaptation of scale relativity theory, the minimal vortex of an instance of turbulent flow is considered. In this manner, the spontaneous breaking of scale invariance becomes a mechanism for atmospheric turbulence generation. This then leads to a general equation for the non-differentiable vortex itself, with its component velocity fields, and to a vortex turbulent energy dissipation—all of which are plotted and studied. Once the structure of the non-differentiable multifractal structure is mathematically described, an improved phenomenological turbulence model and relations between turbulent energy dissipation and the minimal vortex are employed together, exemplifying the codependency of such models. Using turbulent medium wave propagation theory, certain relations are then extrapolated which allow the obtaining of the inner and outer length scales of the turbulent flow using lidar data. Finally, these altitude profiles are compiled and assembled into timeseries to exemplify the theory and to compare the results with known literature. This model is a generalization of our recent results published under the title “On a Multifractal Approach of Turbulent Atmosphere Dynamics”.
1. Introduction
In many cases, models used to describe atmospheric dynamics are built using a combination of fundamental theories and simulations; whilst the description of atmosphere dynamics implies computational simulations based on specific algorithms, theoretical developments imply various classes of models. These classes of models can be divided into two fundamental types: a differentiable class of models based on the used conservation laws, developed on spaces with integer dimensions, or a non-differentiable class of models based on conservations laws, developed on spaces with non-integer dimensions and explicitly written through fractional derivations. Recently, a new class of models in the description of atmosphere dynamics has arisen, based on a multifractal paradigm of motion in the form of theories of motion dependent on scale resolution [1,2]. In this class of models, supposing that the atmosphere is assimilated, both structurally and functionally, to multifractal objects, its dynamics can be described through motions of the atmospheric entities on continuous and non-differentiable curves—which is to say multifractal curves.
Mathematically, this implies that, instead of “working” in atmosphere dynamics with a single variable described by a strict non-differentiable function, it is possible to “work” only with approximations of this mathematical function, obtained by averaging them on different scale resolutions. As a consequence, any variable proposed to describe atmosphere dynamics (velocity fields, density fields, and others) will perform as the limit of a family of mathematical functions, these being non-differentiable for null scale resolutions and differentiable otherwise [3,4]. Now, considering the stochastic and statistically predictable behavior of some quasi-fractal or multifractal phenomena being manifested in the atmosphere, many of them being equated to random walks of the type Levy flight [3], it stands to reason that non-differentiability becomes operational through stochasticity, with atmosphere dynamics being assimilated to various flow regimes at various scale resolutions of a stochastic fluid (multifractal fluid).
Using these notions regarding the multifractality of turbulent flow, coupled with correlations between turbulent energy dissipation and the initial and minimal turbulent length scales, it is possible to employ a modified version of the turbulent model to calculate various atmospheric parameters—this model has been validated using lidar data and comparison with relevant scientific articles [5,6]. However, in the present work, a much more general multifractal model, one that does not necessarily exclude simpler turbulence models but contains them as particular cases, is developed. By exploring conservation laws that explain multifractality through non-Markovian processes, it is possible to obtain a generalized expression of the velocity fields of turbulent vortices’ velocity fields—then, by proposing the spontaneous breaking of scale invariance as an evolution mechanism for the turbulent energy cascade, a much more general constant model is created which can be used to solve various turbulence parameters.
2. Conservation Laws at Various Scale Resolutions
Assuming that the atmosphere is a multifractal, its dynamics on the multifractal theory of motion are described through continuous but non-differentiable curves [5]. According to this theory, the following covariant derivative:
where
becomes operational in the writing of conservation laws.
In Equations (1)–(7), is the non-multifractal time with the role of the affine parameter of the motion curves, are the multifractal spatial coordinates, is the scale resolution, is the complex velocity field, is the differentiable part of the velocity field independent of scale resolution, is the non-differentiable part of the velocity field and dependent on the scale resolution; are constant coefficients associated with differential–non-differential transition, is the singularity spectrum of order , is the singularity index, and is the fractal dimension of the “movement curves” [7,8,9,10].
There are many modes and thus a varied selection of definitions of fractal dimensions: more precisely, the fractal dimension in the sense of Kolmogorov, the fractal dimension in the sense of Hausdorff–Besikovitch, etc. [3,10]. In the case of many standard stochastic atmospheric models, selecting one of these definitions and operating it in the context of atmosphere dynamics, the value of the fractal dimension must be constant and arbitrary for the entirety of the dynamical analysis: for example, we regularly find for atmospheric correlative processes, for atmospheric non-correlative processes, etc. [2,3]—it shall be seen shortly that this interpretation is not always favorable for atmospheric studies and that a variable-dimension model can be achieved.
Accepting the scale covariant principle in the description of atmosphere dynamics, the conservation law of the specific momentum (i.e., geodesic equations on a multifractal manifold) takes the form:
The explicit form of depends on the type of multifractalization used. It can be admitted that the multifractalization process can take place through stochastic, Markovian (thus, memoryless) processes; however, since natural processes exhibit memory-like qualities, it is then necessary to employ a non-Markovian multifractalization method. In this case, wherein it is possible to generalize many of our previous results [5], we admit the following equations:
where and are two constant coefficients associated with the differential–non-differential transition, and is Kronecker’s pseudotensor. Thus, Equations and yield:
After this expression, the separation of atmospheric dynamics on various scale resolutions implies either a conservation law for the specific momentum at differentiable scale resolutions:
or a conservation law for the specific momentum at non-differentiable scale resolutions:
Thus, any geodetic motion on multifractal manifolds (i.e., non-constrained free motions on multifractal manifolds—see Equation ) is found as correlated with non-geodetic motion on Euclidian manifolds (i.e., constrained motions on Euclidian manifolds—see Equations and ), induced either through a specific multifractal force at differentiable scale resolution:
or through a specific multifractal force at non-differentiable scale resolution:
In order to correlate the non-geodetic dynamics on Euclidian manifolds, constraints arising from the multifractal–non-multifractal transition must be exploited. In this case, the velocity field associated with the multifractal-non-multifractal interface dynamics:
satisfies, by subtracting Equations and , the conservation law of the relative specific momentum:
Now, according to the self-similarity property of the movement curves (through which also dynamics on Euclidian manifolds should be geodetic or free), the supplementary constraint:
correlated with the incompressibility of the multifractal fluid at non-differentiable scale resolution:
will function as an intrinsic property of the atmosphere (“non-manifest” at differentiable scale resolutions, yet “manifest” at the same scale through the spontaneous breaking of scale invariance). The differential Equations and are constituted as stationary Navier–Stokes-type systems at non-differentiable scale resolution. This system of differential equations in dimensionless plane coordinates, with adequate initial and boundary conditions, admits the following solutions [5]:
where and are non-dimensional spatial coordinates, and are the non-dimensional components of the velocity field along the and axes, and is the multifractality degree. Then, the multifractal minimal vortex is obtained [5,11]:
Thus, the multifractal soliton (Equation ) and the soliton-kink multifractal mixture (Equation ) are responsible, through the multifractal minimal vortex (Equation ), for turbulence management at non-differentiable scale resolutions [5]. Although they are non-manifested at differentiable scale resolution, these turbulences can become manifest at the same scale through the spontaneous breaking of scale invariance.
In Figure 1, Figure 2 and Figure 3, the dimensionless multifractal velocity fields and the vortex which they compose, along with their dependency on the multifractality degree, are presented.
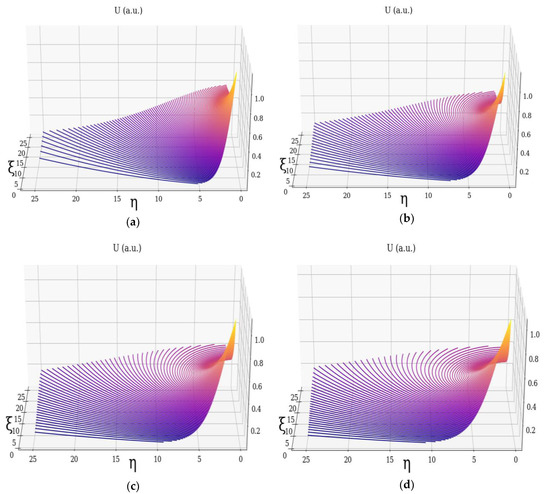
Figure 1.
Dimensionless velocity field U of non-differentiable atmospheric multifractal: (a) , (b) , (c) , (d) .
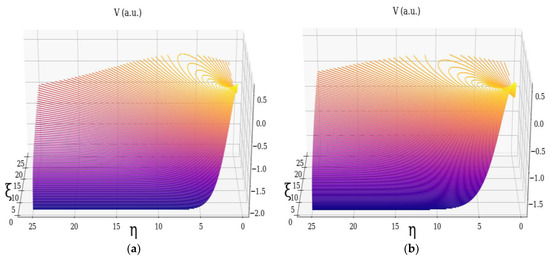
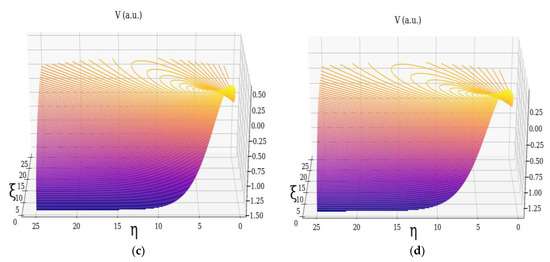
Figure 2.
Dimensionless velocity field V of non-differentiable atmospheric multifractal: (a) , (b) , (c) , (d) .
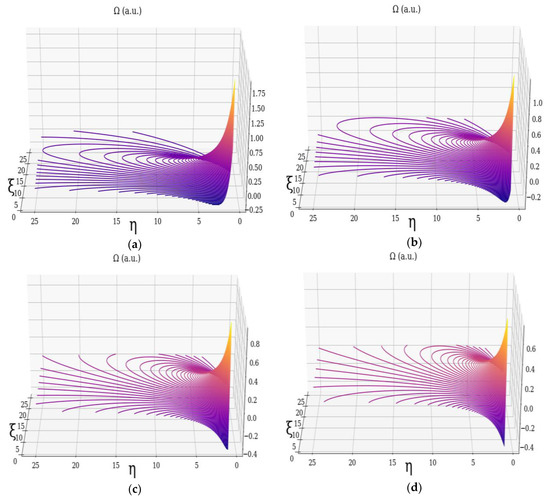
Figure 3.
Dimensionless vortex Ω of non-differentiable atmospheric multifractal: (a) , (b) , (c) , (d) .
3. Spontaneous Breaking of Scale Invariance as a Mechanism of Turbulence
In general, turbulent energy is injected through vortices of length , which triggers a “cascade” of intermediary vortices towards minimal vortices of dissipation scale . This process of scale evolution can be described through the series of discrete length scales:
given the wavenumbers:
This typical model assumes that the energy dissipation is uniformly distributed on homogenously dimensional fractal eddies; this assumption is also named “absolute curdling” [12].
By defining as the total number of stages in the given energy cascade:
This gives us:
The result is that the model assumes that each eddy has a characteristic length scale which is precisely half the size of that of the previous eddy. This places an artificial limit on the average number of bifurcations per every vortex corresponding to an energy cascade stage (or the number of “new eddies” appearing for each other previous eddy); in this typical model, the ratio of “volume reduction” from one stage to another is given by the equation:
Logically, is necessarily smaller than 1, given that a volume reduction must take place. However, from the definition of the eddy length scale evolution, we obtain:
In the following segment, we shall prove that the above results can be generalized through regularization by sets of functions of -approximation-type scale.
Let us consider a multifractal function with , a function which can be associated with any multifractal variable that describes atmospheric dynamics. We consider now the sequence of the values of the variable :
We shall denote by the fractured (broken) line connecting the points:
The broken line will be considered as an approximation which is different from the one used before. We shall say that is an -approximation scale. Let us consider now the -approximation scale of the same function. Since is self-similar almost everywhere, if and are small enough, then the two approximations and must lead to the same results when we study a multifractal atmospheric phenomenon by approximations. If we compare the two cases, then to an infinitesimal increase or decrease of , it corresponds to an increase or decrease for , if the scale is dilated or contracted. In this case, we have:
that is,
is the ratio of the scale and must be preserved. We can then consider the infinitesimal transformation of the scale as:
By such transformation, in the case of the function , it results:
respectively, if we stop after the first approximation:
that is:
Let us consider that, for an arbitrary but fixed :
so, Equation becomes:
Finally, we have:
The operator:
is a dilation or contraction operator. Equation shows us that the intrinsic variable of the resolution is not but . In this condition, the spontaneous breaking of scale invariance of any multifractal variable which shall describe atmospheric dynamics implies the functionality of the following equation:
where is a function for which the following is true:
By picking the simplest possible option, , in which is a constant, arbitrary coefficient, we obtain:
In this manner, the spontaneous breaking of scale invariance can become the mechanism through which the turbulent energy cascade operates from large to small scales.
4. Formulation of an Improved Multifractal Turbulence Model
Now, the fact that Equation is a general case of Equation for , , , and , let us visualize the standard model as a particular case of a general scale invariance-breaking model. Let us now admit a new form of the model in which , an unknown constant coefficient, and let us admit a relation between and such that:
Thus, we arrive at the modified model:
We find that is still a constant in this model; yet, regarding the initial model, generally speaking, there is no reason to assume that this exact halving of the length scale correctly represents reality; in fact, the nature of turbulent flow should point to the fact that such cases are either rare or outright impossible. Moreover, in the following segment, it shall be seen that the eddy dimension defined by the classic model is, indeed, constant throughout the stages of the energy cascade. Once again, it does not seem to be the case that the eddy dimension remains constant in this manner; this implies that the shape and complexity of the eddies remains more or less the same during the cascade, which might not be realistic. We would expect that the new model presents a more realistic eddy length scale evolution, a more flexible limit for , and an eddy dimension which is not constant throughout the stages.
Due to the fact that can be used to proceed, let us name the inverse of the volume reduction from one eddy to another:
In order for to be constant, this quantity must also be constant; thus, the following relation is true:
The next relations can then be iterated:
It is then possible to deduce that:
Which yields:
Meanwhile:
The fact that the volume reduction from one stage to another is governed by the initial and the immediately following scale instead of an arbitrary number seems to be a significant improvement.
In order to further obtain other parameters connected to the turbulent energy cascade, we start by considering definitions of the turbulent kinetic energy associated with . This energy can be generally defined:
where is the velocity difference across an eddy [13]. However, the average turbulent energy dissipation rate is also approximately defined as:
Thus, one can arrive at [13]:
Another definition of the turbulent kinetic energy can be connected to the scales themselves and [13]:
An equivalence can now be drawn between and the eddy dimension through the following relation [13]:
Thus:
Immediately, one notices that, for the equation to be valid, must be a function of , since the other terms excepting are constant for the given energy cascade. Proceeding:
We obtain:
It is implied that the term contained in the largest brackets is sub-unitary; one should not logically expect an eddy to have a dimension higher than . A much simpler definition is found in the case of the typical model:
It is possible for the eddy dimension to be replaced with a singularity index, in which case the typical model will no longer exhibit monofractality; however, it is unclear how one might extract the specific dimensions of the vortices in each stage with just this function. In any case, the new model does show that each stage of the energy cascade presents vortices of continuously increasing dimensions. This result is to be expected; it shows that, because of the quasi-chaotic nature of the flow, the trajectories that form the eddies themselves become so extremely convoluted as the eddies shrink that they are nearly completely space-filling. Another conclusion is also immediately obvious: the fact that the vortices in the energy cascade are characterized by a spectrum of dimensions implies that the energy cascade is a multifractal system.
With a modified (and arguably improved) phenomenological model, we can pursue other physical parameters of the turbulent flow. Given, for example, the fact that each stage we are presented with an average bifurcations, we define the number of eddies at a stage :
Thus, the number of eddies at the final stage of the energy cascade:
We define the turnover time quite literally as the time it takes for an eddy to spin once:
According to Kolmogorov:
Moreover:
This gives us:
If we then suppose an equation of in a similar vein to that of :
By using the popular approximation:
We obtain:
5. Multifractal Interpretation and Model Correlation
However, one aspect of this theory remains unanswered: is it possible to obtain directly, solely through the scales necessary to initialize this model and solve the equations? The answer is yes—starting from an equivalence of two different definitions of :
Seeing that this relation is true for any , we impose , and use the previously found new definition of and , obtaining:
which will then yield:
Thankfully, this cumbersome equation is not made more complex by expanding , thus obtaining:
Replacing this in :
and now, the number of eddies produced at the final stage of the energy cascade:
As expected, and are constant, and they are completely dependent on length scales. Then, finally, we can also arrive at:
and:
It becomes apparent that, in order to calculate turbulent energy per stage, and turbulent energy dissipation, we need to find the velocity difference . This, in practice, is a very difficult task: we require the real velocity field of the minimal vortex in order to obtain this velocity difference, but this is where the two main theoretical points of this paper are united. Using the previously described non-manifest non-differentiable velocity fields, it is possible to confidently estimate the real field, by assuming that , which is equivalent to the plausible assumption that the entire minimal vortex is characterized by a single Hölder exponent [5]. Then, by replacing the specific lengths and velocities with those corresponding with the minimal vortex and considering the relation between and , we obtain:
With these new velocity fields, we can specify an approximate real minimal vortex and take the velocity difference as:
Given the fact that this difference refers to two points in the velocity field separated by a distance of , it is fair to assume that the maximum possible difference will be obtained between the maxima and minima of the vortex. The vortex resulting from these new velocity fields is presented in Figure 4 in a rotating manner. It is found that the values of this vortex are in good accordance with the theory and that they are of the order of .
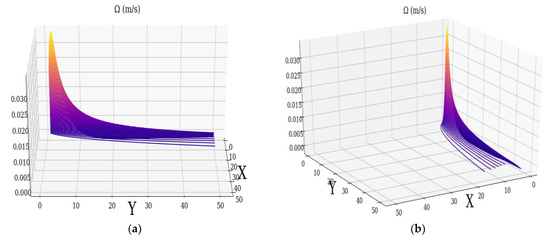
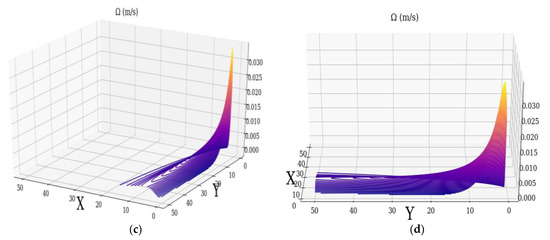
Figure 4.
Approximate minimal vortex of real atmospheric multifractal: (a) , (b) , (c) , (d) .
Returning to the definition of the average turbulent energy dissipation rate, Tatarski finds the following definition for stationary atmospheric turbulence [14]:
which will allow us to construct the field of the turbulent dissipation rate of the non-differentiable vortex (Figure 5).
Figure 5.
Turbulent dissipation field of minimal vortex of the non-differentiable atmospheric multifractal: (a) , (b) .
Now, having calculated the velocity difference , it is necessary to consult the bifurcation diagram of , , and in order to determine the full range of initial parameters that, once inputted, will produce realistic results from our improved model. Doing so in a comprehensive manner would require many such diagrams and their combined analysis; however, even from an initial attempt, it is possible to discern that there can be instances when reaches values smaller than and larger than . This is not realistic; thus, this inequality needs to be true for all possible values of :
If , then this implies that the vortex becomes a kind of “hypervolume”, which should be more or less impossible; furthermore, if , it is no longer clear that the attractor-like aspect of these vortices can even function properly, and it is shown by the Figure 6, Figure 7 and Figure 8 that if , then , which, once again, makes no physical sense.
Figure 6.
bifurcation maps: between and , with a fixed and .
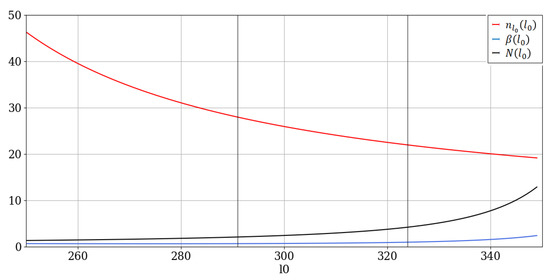
Figure 7.
as functions of : between and , with a fixed and .
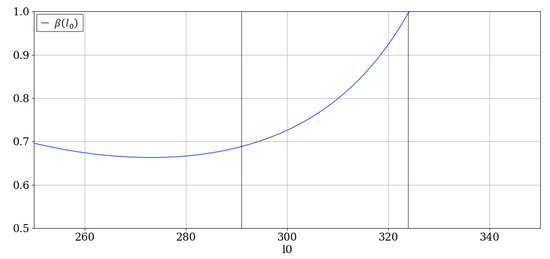
Figure 8.
as function of : between and , with a fixed and .
Thankfully, contains all three necessary scales to initiate the model—in this manner, we may use the above inequality as a method to verify whether or not our chosen parameters are realistically picked. Replacing with and for the left, respectively, the right inequality, we obtain:
Now, we have obtained an inequality which allows us to determine the range of possible realistic input values for our model.
6. Correspondences of the Model with Experimental Data
The introduction of this model in relation to the multifractal theory is performed in order to verify equations with experimental data, and, by using experimental data to solve a number of these equations, to investigate the results. In this segment of this paper, experimental data obtained via a lidar platform are introduced in order to apply the theory. For the sake of convenience, we shall name the method behind obtaining these data profiles with a lidar platform the “Roșu–Tatarski method”; the finer details of this method are contained in a previous study [15]. This comparison is mostly of qualitative nature; it is of interest to check if the various profiles yielded through theory in this study present realistic values in both evolution and order. Additionally, timeseries of , , and altitude profiles will be produced. The experimental data used to solve these equations are calculated by analyzing lidar RCS (Range Corrected Signal) data obtained from the lidar platform at the Optical Atmosphere Spectroscopy and Lasers Laboratory, part of the Faculty of Physics in the “Alexandru Ioan Cuza” University, at the coordinates and . The methodology for obtaining the injection and dissipation scale profiles is reliant on calculating the scintillation profiles of the lidar signal by observing the variation between multiple RCS profiles [15].
The technical specifications of the main components of the lidar platform utilized in the study are as follows: the laser component is a Nd:YAG, producing pulses of laser at a frequency of , with a wavelength of , laser beam diameter of , and a pulse energy of ; meanwhile, the optical component is a Newtonian LightBridge telescope with a primary mirror diameter of . The lidar platform utilized in the study has a spatial resolution of and both technical details and results from previous measurement campaigns were reported in the scientific literature in independent studies [16,17] and in our previous studies [5,15,18]. The profile is calculated by software written in Python 3.6 [15]. The signal overlap altitude in most cases is approximately 200.
As mentioned, the length scale profiles used in this study are obtained by first calculating scintillation profiles in order to compile the structure coefficient of the refraction index profile . This can be calculated in this manner:
with being the “scintillation" (or, in this case, the logarithm of the standard deviation of light intensity) of a source of light observed from a distance represented by the optical path [14]. The definition:
is given, with being the intensity of the range-corrected signal at the particular point in the optical path, which is analogous with the RCS intensity. Having determined the profile, it is now possible to calculate, with a degree of approximation, the length scales. The inner scale profile is linked to scintillation [14]:
while the outer scale is linked to the profile [14,15]:
With turbulent eddies within the inertial subrange, the refraction index profile can be approximated from the definition of the respective structure coefficient [14,19]:
which then gives us the means to extract the outer scale profile.
Regarding the potential influence of noise-related errors on the calculation of the scintillation profile used to obtain the length scales, the overall added signal uncertainty:
where is raw lidar signal, is background lidar signal, and is the so-called “noise scale factor”, which is equal to the standard deviation of the shot noise divided by the square root of average shot noise [20]. It is determined that the signal uncertainty, in the case of attenuated backscatter, has values of the order or lower [20], while a typical attenuated backscatter profile has values of the order or lower; thus, this uncertainty represents variations many times smaller than the actual values of the profile [15]. Since the model subtracts the “dark” signal (generated by photocathode thermionic emission, which is collected before the measurements begin [21]) from the raw signal, we can assume that such uncertainty is even lower. Furthermore, the fact that the photomultiplier component of the lidar platform utilized in this study was being operated in analogue mode removes the need to consider possible instances of “afterpulsing”, which only take place when a photomultiplier component is operated in a “pulse detection mode” [21]. Finally, the fact that the photomultiplier component of the lidar platform used in this study is a PMT (photomultiplier tube) presents an advantage, since excess noise decreases with an increase in the average photo-multiplication gain in PMTs [20].
In order to perform our calculations in the context of altitude profile timeseries, we require altitude profiles, which of course we cannot obtain solely from the lidar data. Thus, an approximation is needed; shall be taken as being approximately equal to . Given the conditions set by Equation (78), this seems to be a reasonable assumption. The following figure is a timeseries of the RCS lidar signal used to calculate the length scales according to the presented theory (Figure 9 and Figure 10); this figure is presented in order to ascertain with accuracy the location of the PBL (Planetary Boundary Layer) relative to values obtained in the rest of the timeseries.
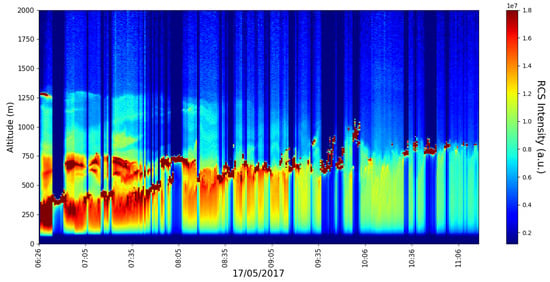
Figure 9.
RCS profile timeseries, profiling rate 1/min, 17 April 2017.
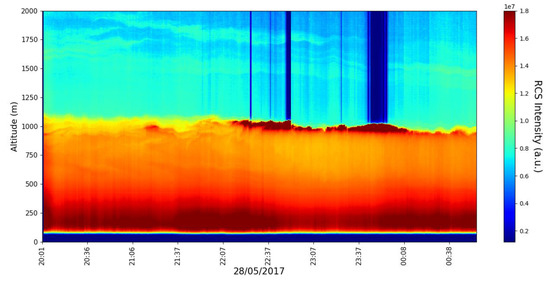
Figure 10.
RCS profile timeseries, profiling rate 1/min, 28 April 2017.
The timeseries associated with are shown next (Figure 11 and Figure 12); beyond its further uses in our calculations, this coefficient is associated with optical turbulence strength and thus with turbulence intensity in general.
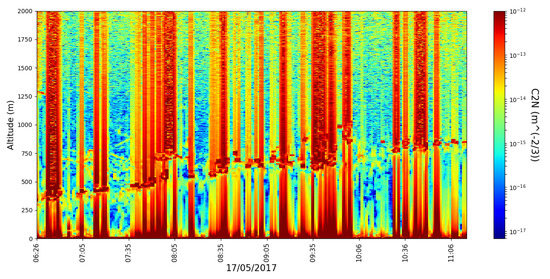
Figure 11.
profile timeseries, profiling rate 1/min, 17 April 2017.
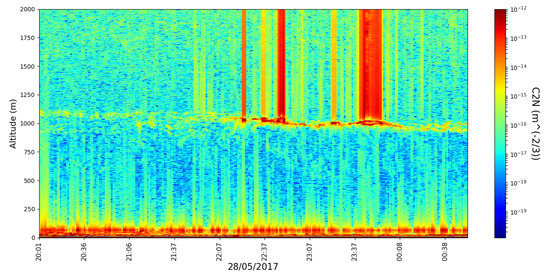
Figure 12.
profile timeseries, profiling rate 1/min, 28 April 2017.
Observing the rest of the timeseries, values seem to be lowest in or near the region of the PBL (Figure 13 and Figure 14); multiple studies seem to support the fact that turbulent dissipation is lowest at, or just above, the PBL, with both experimental and theoretical data [6,22].
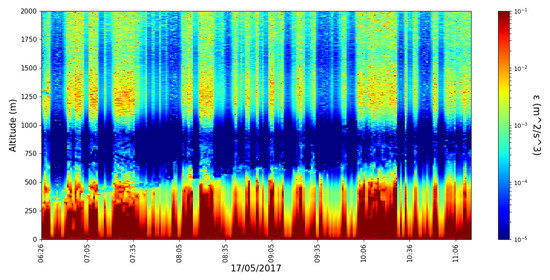
Figure 13.
profile timeseries, profiling rate 1/min, 17 April 2017.
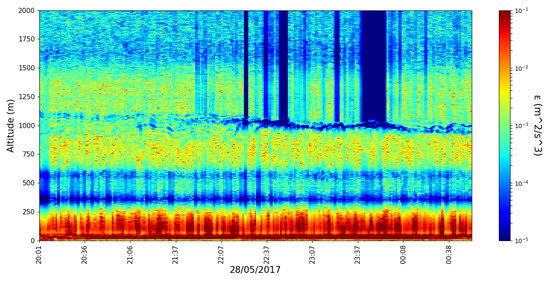
Figure 14.
profile timeseries, profiling rate 1/min, 28 April 2017.
Timeseries of the parameter do not show values larger than (Figure 15 and Figure 16); in fact, most of the time and at most altitudes, appears to remain close to the value of and this is more or less expected given the nature of such flows in general; mass and energy conservation dictates that, at each bifurcation stage in an ideal real flow, each vortex would split into two oppositely rotating, smaller vortices. However, once again, we have avoided restricting ourselves to any and all potentially limiting initial presuppositions and have instead obtained a result that seems to confirm our intuition of the process with a generalized model. It seems clear from Figure 7 that the phenomenological theory can predict flows with higher values of ; however, we can attribute this apparent inconsistency to the difference in scale between real values obtained via the Roșu–Tatarski method, whose timeseries are exemplified in Figure 17 and Figure 18, and the much smaller values used in Figure 7.
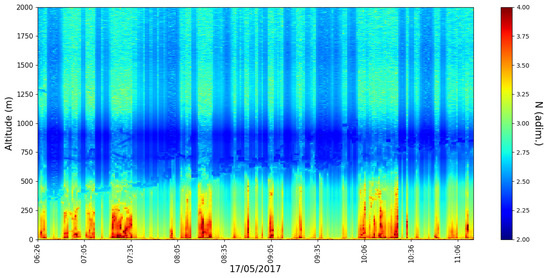
Figure 15.
profile timeseries, profiling rate 1/min, 17 April 2017.
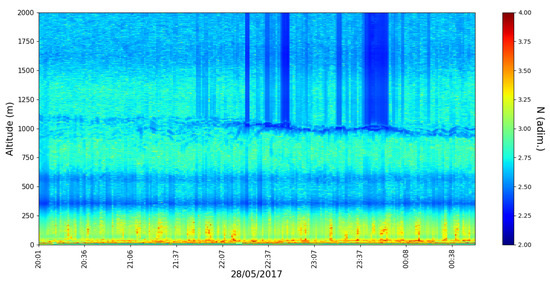
Figure 16.
profile timeseries, profiling rate 1/min, 28 April 2017.
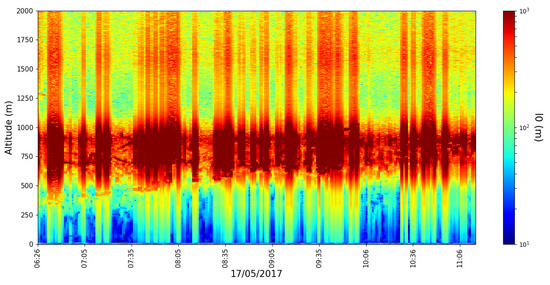
Figure 17.
profile timeseries, profiling rate 1/min, 17 April 2017.
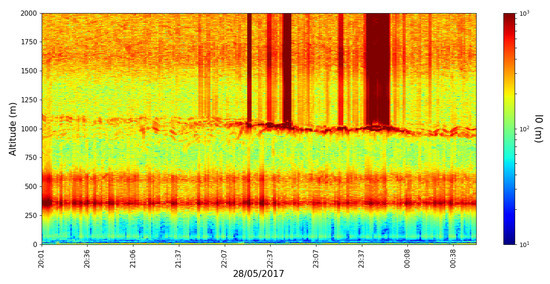
Figure 18.
profile timeseries, profiling rate 1/min, 28 April 2017.
Meanwhile, minimal scale timeseries have not been shown because this value appears to be quite homogenous, varying in very small amounts in both time and altitude. Even with a logarithmic colormap timeseries plot, the results are, at least from a visual perspective, not very useful.
The altitude variability of shown by the timeseries does not seem to be very high, roughly between and (Figure 19 and Figure 20); then again, we should not expect a higher variability given that this number is supposed to be relatively low. One must highlight the fact that values seem to be at their highest in the PBL region, while dissipation values and values seem to be at their lowest; of course, lower dissipation means that the energy cascade requires more stages with fewer potential bifurcations to manifest itself from to , so this difference in values is perfectly consistent with our theory. It is possible that this difference can also mean that the atmospheric PBL turbulent behavior is much more active and more “resilient” to the various dissipative effects, which does indeed justify why this layer is such a stable and easily recognizable feature of the atmosphere in most meteorological scenarios.
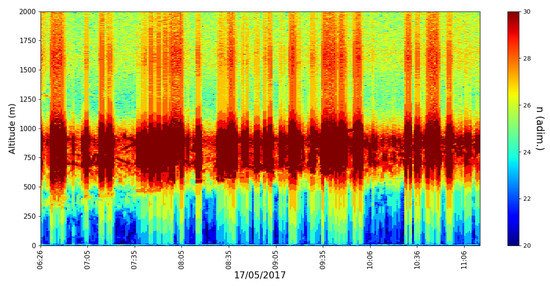
Figure 19.
profile timeseries, profiling rate 1/min, 17 April 2017.
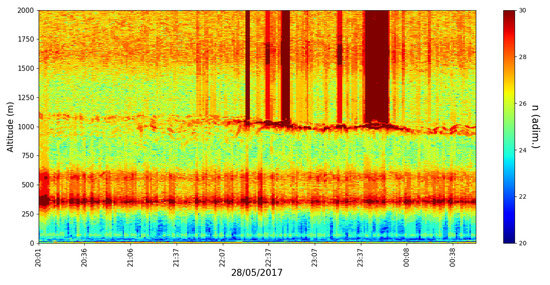
Figure 20.
profile timeseries, profiling rate 1/min, 28 April 2017.
In general, for all of the given timeseries, the horizontal stripes of either very high or very low values, starting from certain intervals above the PBL, are produced due to signal noise present in the RCS lidar data used to calculate the length scales; this noise appears because of the influence of clouds or other rapidly evolving aerosol masses in the vicinity of the PBL.
7. Conclusions
In this article, the non-linear behavior and functionality of the atmosphere has been placed under a multifractal approach, by supposing that it is a system whose structural and functional units support dynamics on continuous and non-differentiable curves. The formulation of a multifractal interpretation yields an analytic solution in the case of planar symmetry for the velocity fields of the system, whose rotor is interpreted as a generalized multifractal vortex. Employing an approximation contained in the continuity of the multifractal minimal vortex, it is then possible to extract an expression of turbulent energy dissipation in the atmospheric flow. Then, an improved and generalized phenomenological model of the turbulent energy cascade is assembled, which is used to describe the behavior of the vortices of the turbulent energy cascade in terms of their scales, the average number of vortex fragmentations per “stage”, and the total number of stages of fragmentation, from injection to dissipation. The evolution of this cascade is found to be dependent on a special case of a generalized spontaneous scale invariance break of the multifractal functions describing the turbulent vortex length scales. The expression of the multifractal minimal vortex is used to solve the equation system produced by the phenomenological model, and the applicability limits of this model are found through bifurcation mapping and inequalities.
In the derived equation system, from an atmospheric modeling and forecast point of view, the remaining unknown quantities are the injection and dissipation scales themselves, and the associated second stage to be approximated; but these quantities can be obtained as an atmospheric profile through a method detailed in one of our previous studies with a lidar platform. Employing these profiles, timeseries of some of the various parameters detailed in this study have been compiled, and it has been found that, especially regarding the known behavior of the PBL, they are in accordance with the presented theory and existing scientific literature. A future study might further implement these theories and reduce the number of known scales necessary to initiate the model, in order to produce forecasts of turbulent parameters—this, of course, using measured, ground-level, initial parameters. Currently, a research subject considered by the authors of this paper is the development of a fully stage-dependent phenomenological model, which would be a model wherein is longer constant for the given flow. A future study might also include multiple other methods of experimentation and validation using platforms that would contain both traditional measurement instruments and remote sensing instruments. Finally, if these theories, along with many others, would be implemented into a fully functional model, a comparison with other well-known models could be performed in a potential new study.
Author Contributions
Conceptualization, I.A.R., M.M.C. and M.A.; methodology, I.A.R., M.A.; software, I.A.R.; validation, I.A.R., M.M.C. and M.A.; formal analysis, I.A.R., M.M.C. and M.A.; investigation, I.A.R., M.M.C. and M.A.; resources, I.A.R. and M.M.C.; data curation, I.A.R., M.M.C. and M.A.; writing—original draft preparation, I.A.R., M.M.C. and M.A.; writing—review and editing, I.A.R., M.M.C. and M.A.; visualization, I.A.R., M.M.C. and M.A.; supervision, M.A.; project administration, I.A.R., M.M.C. and M.A.; funding acquisition, I.A.R. and M.M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant of the Romanian Ministry of Education and Research, CNCS - UEFISCDI, project number PN-III-P1-1.1-TE-2019-1921, within PNCDI III.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors acknowledge the Faculty of Physics of the “Alexandru Ioan Cuza” University of Iași for the financial support offered for the publication of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nottale, L. Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011; pp. 403–425. [Google Scholar]
- Cresson, J. Fractional embedding of differential operators and lagrangian systems. J. Math. Phys. 2007, 48, 033504. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: San Fracisco, CA, USA, 1982; pp. 80–103. [Google Scholar]
- Agop, M.; Paun, V.P. On the New Perspectives of Fractal Theory. Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2017. [Google Scholar]
- Roșu, I.A.; Cazacu, M.M.; Ghenadi, A.S.; Bibire, L.; Agop, M. On a multifractal approach of turbulent atmosphere dynamics. Front. Earth Sci. 2020, 8, 216. [Google Scholar] [CrossRef]
- Shupe, M.D.; Brooks, I.M.; Canut, G. Evaluation of turbulent dissipation rate retrievals from Doppler cloud radar. Atmos. Meas. Tech. 2012, 5, 1375–1385. [Google Scholar] [CrossRef]
- Baker, G.L.; Gollub, J.P. Chaotic Dynamics: An Introduction; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press; University of Maryland: College Park, MD, USA, 2002; pp. 160–182. [Google Scholar]
- van den Berg, J.C. Wavelets in Physics; Cambridge University Press: Cambridge, UK, 2004; pp. 143–147. [Google Scholar]
- Cristescu, C.P. Nonlinear Dynamics and Chaos. Theoretical Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2008. [Google Scholar]
- Rosu, I.A.; Cazacu, M.M. Further Developments of a Multifractal Model of Atmospheric Turbulence. Bull. Polytech. Inst. Jassy Sect. Math. Theor. Mech. Phys. 2020, 66, 77–91. [Google Scholar]
- Boffetta, G.; Mazzino, A.; Vulpiani, A. Twenty-five years of multifractals in fully developed turbulence: A tribute to Giovanni Paladin. J. Phys. A Math. Theor. 2008, 41, 363001. [Google Scholar] [CrossRef]
- Benzi, R.; Paladin, G.; Parisi, G.; Vulpiani, A. On the multifractal nature of fully developed turbulence and chaotic systems. J. Phys. A Math. Gen. 1984, 17, 3521. [Google Scholar] [CrossRef]
- Tatarski, V.I. Wave Propagation in a Turbulent Medium; Courier Dover Publications: Mineola, NY, USA, 2016. [Google Scholar]
- Rosu, I.A.; Cazacu, M.M.; Prelipceanu, O.S.; Agop, M. A Turbulence-Oriented Approach to Retrieve Various Atmospheric Parameters Using Advanced Lidar Data Processing Techniques. Atmosphere 2019, 10, 38. [Google Scholar] [CrossRef]
- Belegante, L.; Cazacu, M.M.; Timofte, A.; Toanca, F.; Vasilescu, J.; Rusu, M.I.; Ajtai, N.; Stefanie, H.I.; Vetres, I.; Ozunu, A.; et al. Case study of the first volcanic ash exercise in Romania using remote sensing techniques. Environ. Eng. Manag. J. 2015, 14, 2503–2504. [Google Scholar]
- Papayannis, A.; Nicolae, D.; Kokkalis, P.; Binietoglou, I.; Talianu, C.; Belegante, L.; Tsaknakis, G.; Cazacu, M.M.; Vetres, I.; Ilic, L. Optical, size and mass properties of mixed type aerosols in Greece and Romania as observed by synergy of lidar and sunphotometers in combination with model simulations: A case study. Sci. Total Environ. 2014, 500–501, 277–294. [Google Scholar] [CrossRef] [PubMed]
- Roșu, I.A.; Ferrarese, S.; Radinschi, I.; Ciocan, V.; Cazacu, M.M. Evaluation of Different WRF Parametrizations over the Region of Iași with Remote Sensing Techniques. Atmosphere 2019, 10, 559. [Google Scholar] [CrossRef]
- Yura, H.T. Signal-to-noise ratio of heterodyne LIDAR systems in the presence of atmospheric turbulence. Opt. Acta Int. J. Opt. 1979, 26, 627–644. [Google Scholar] [CrossRef]
- Liu, Z.; Hunt, W.; Vaughan, M.; Hostetler, C.; McGill, M.; Powell, K.; Winker, D.M.; Hu, Y. Estimating random errors due to shot noise in backscatter lidar observations. Appl. Opt. 2006, 45, 4437–4447. [Google Scholar] [CrossRef] [PubMed]
- Hamamatsu. Photomultiplier Tubes, and Photomultipliers Tubes Photonics “Basics and Applications”; Hamamatsu Photonics KK: Iwata City, Japan, 2007. [Google Scholar]
- Chen, W.Y. Energy dissipation rates of free atmospheric turbulence. J. Atmos. Sci. 1974, 31, 2222–2225. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).