Reconstruction of the Interannual to Millennial Scale Patterns of the Global Surface Temperature
Abstract
1. Introduction
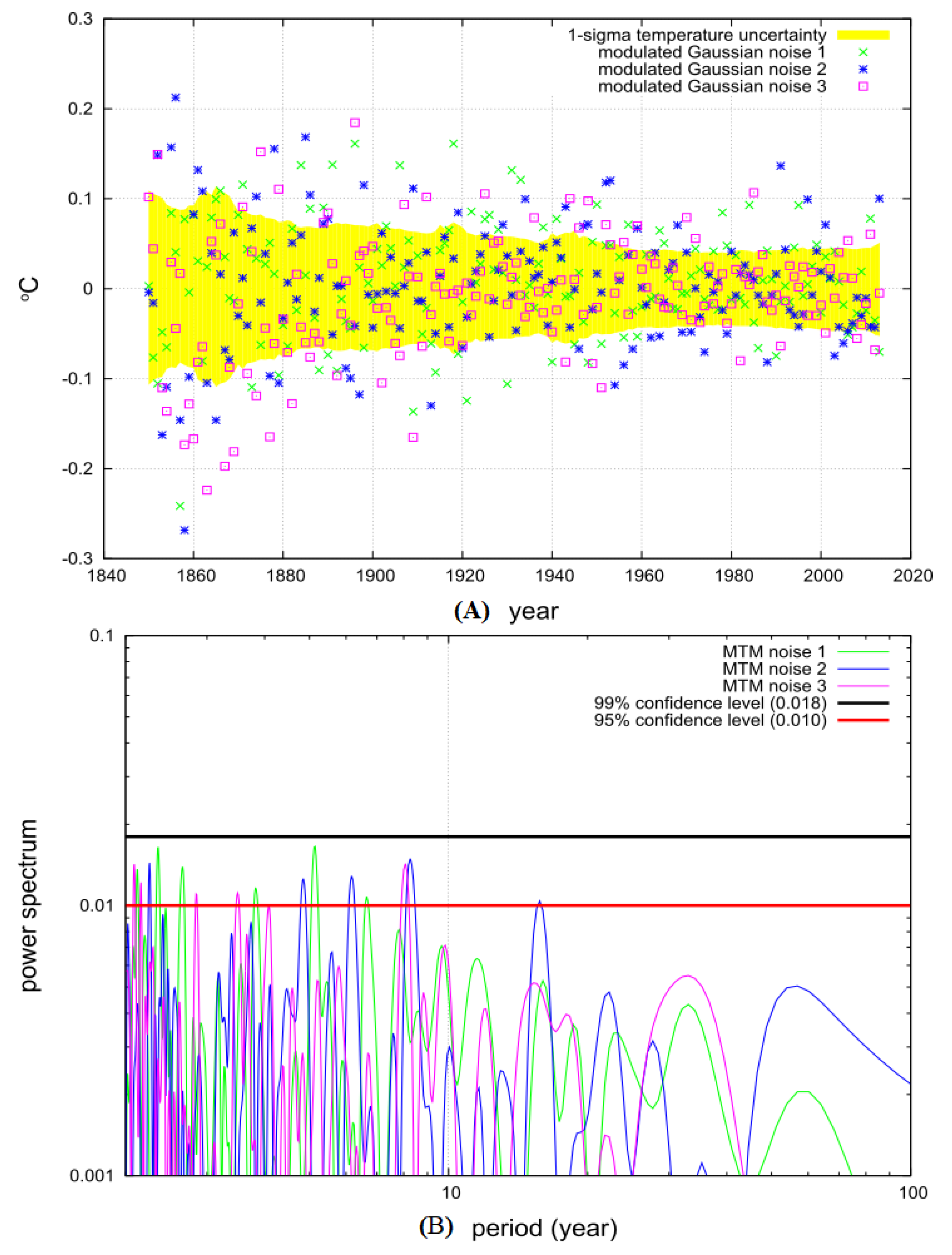
2. Evaluation of the Confidence Levels of the Spectral Analysis
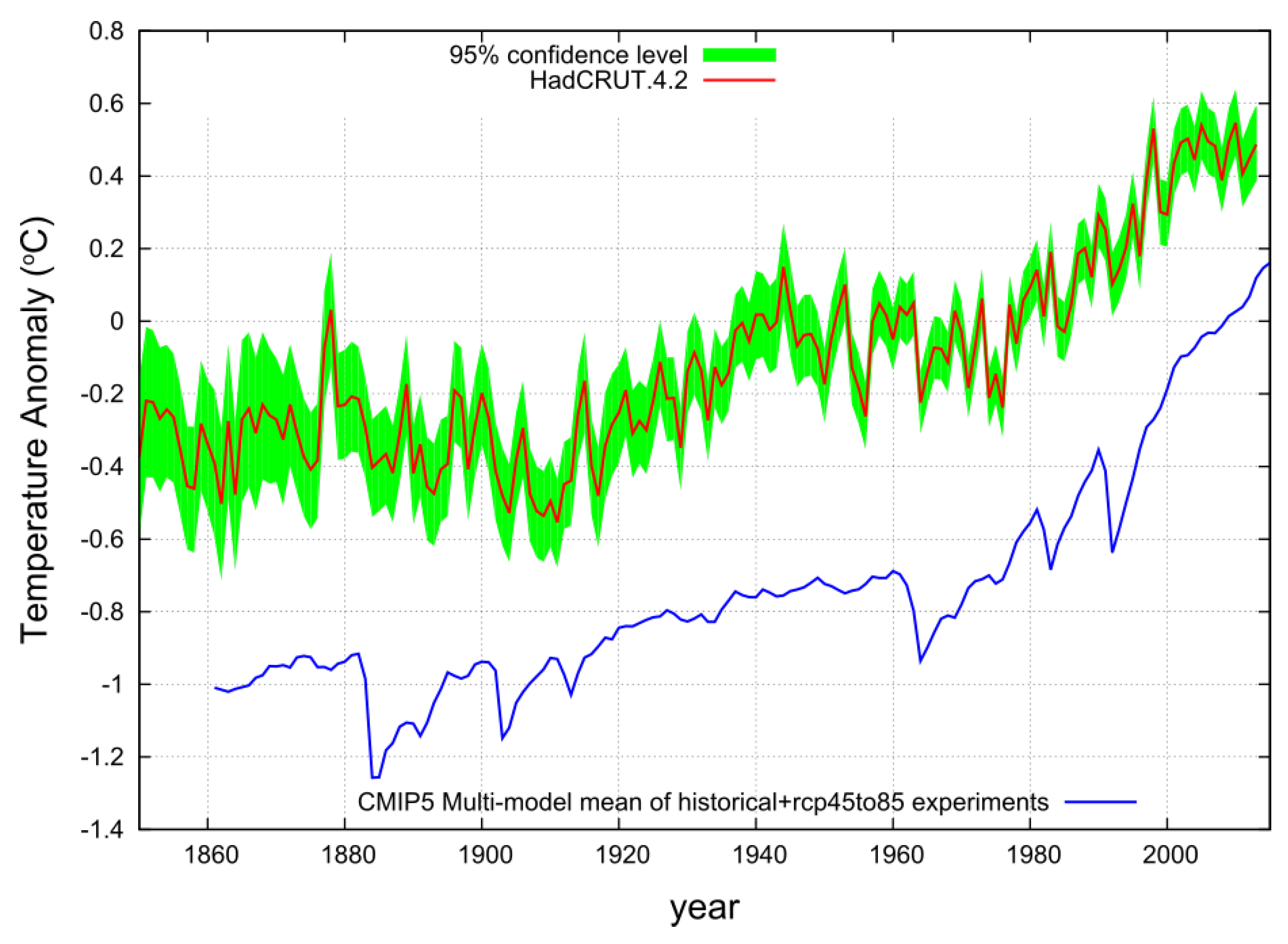
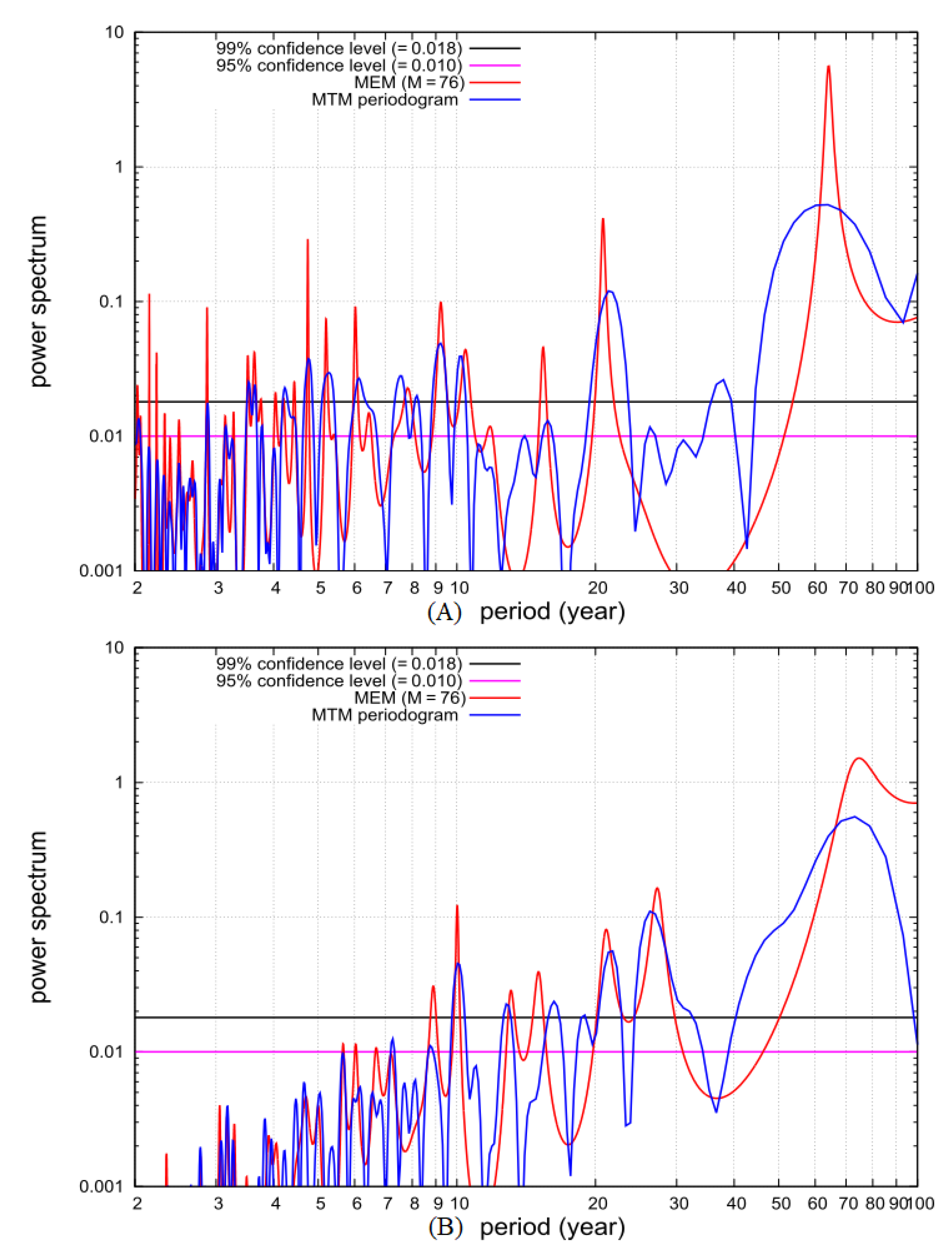
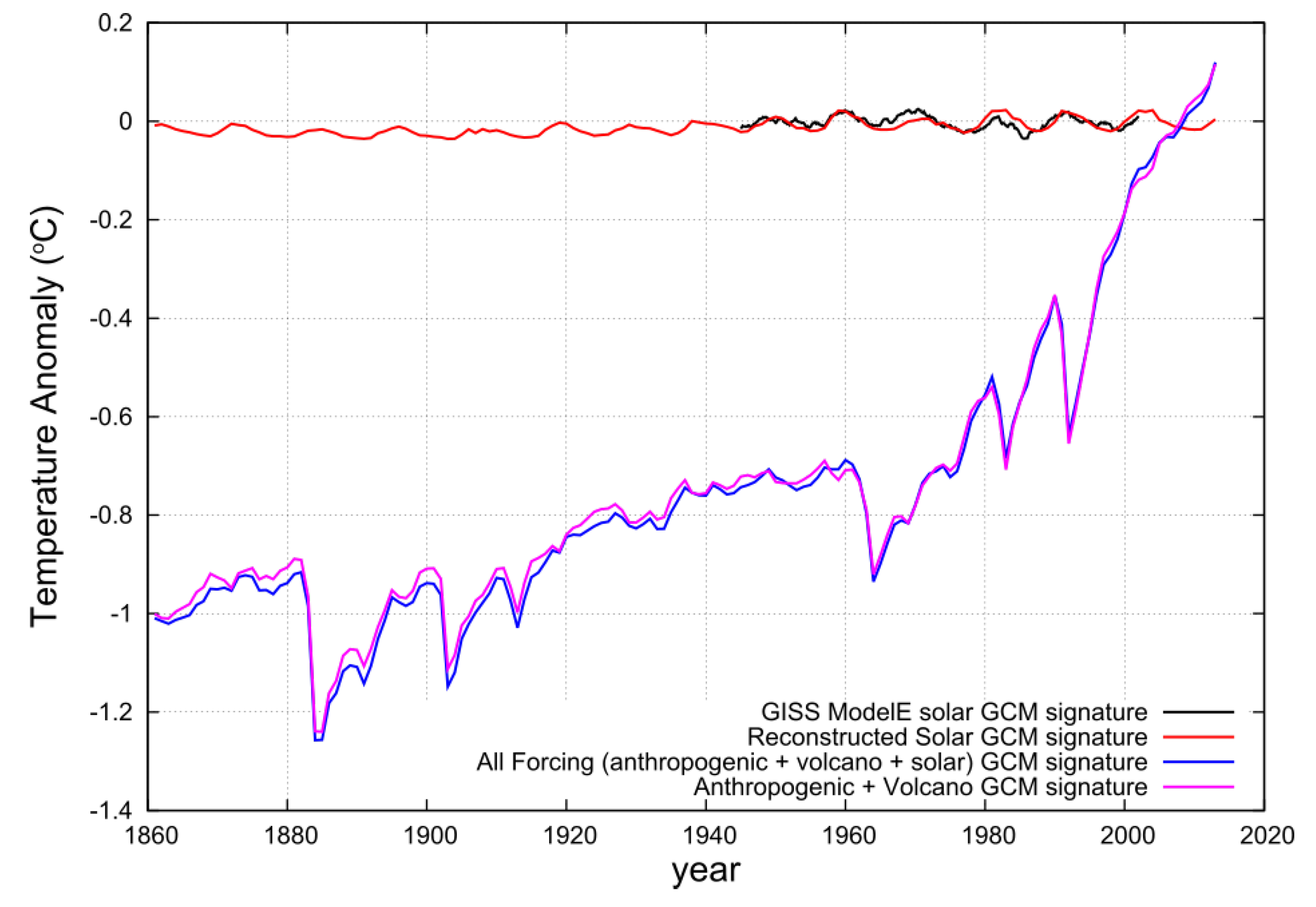
3. High-Resolution Spectral Analysis of the Global Surface Temperature Versus the CMIP5 Multi-Model Mean Function
4. Optimized Spectral Analysis and Harmonic Modeling
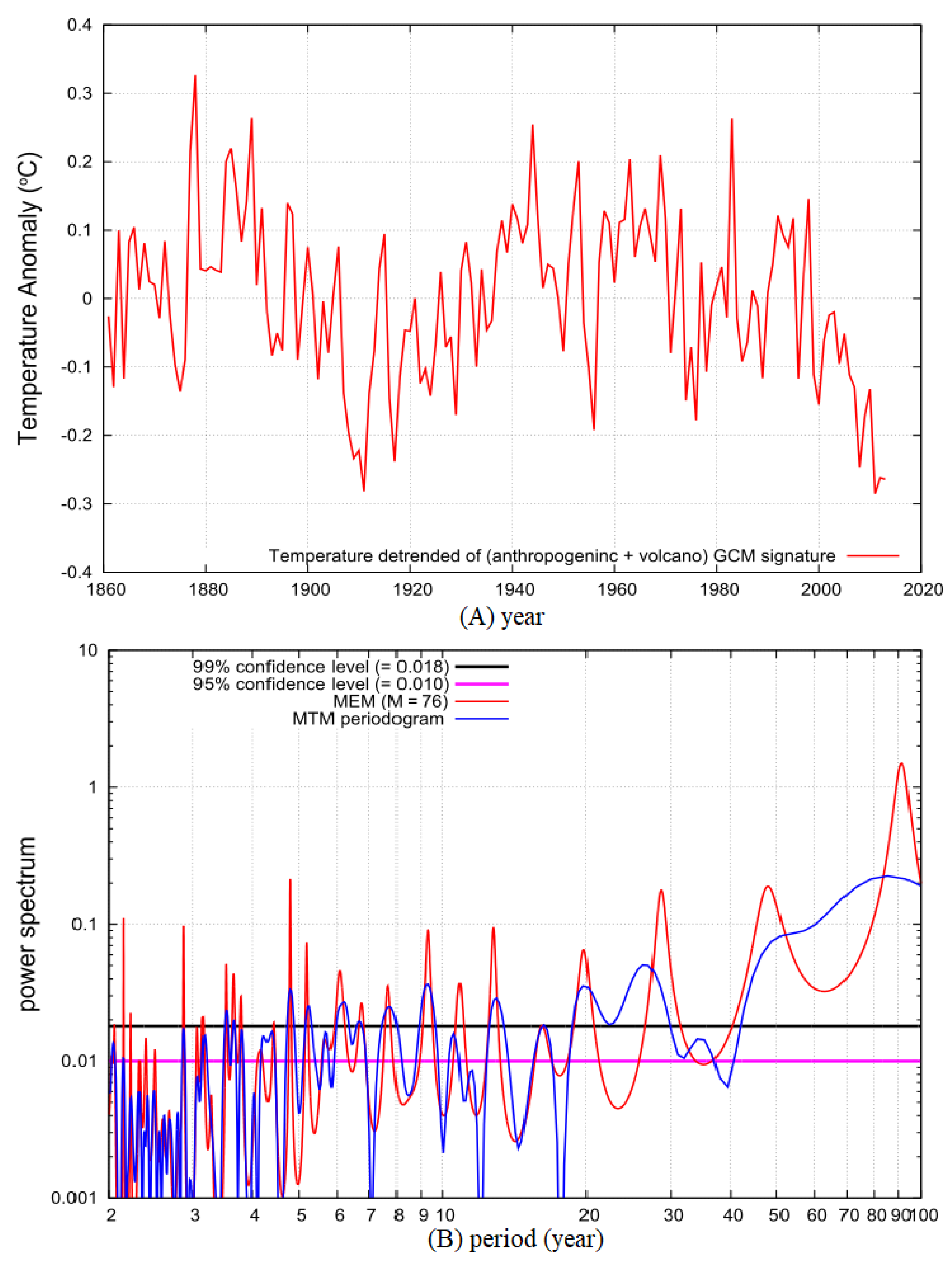
4.1. The Non-Harmonic Temperature Component is Assumed to be Simulated by the Anthropogenic + Volcano CMIP5 Multi-Model Mean Temperature Function
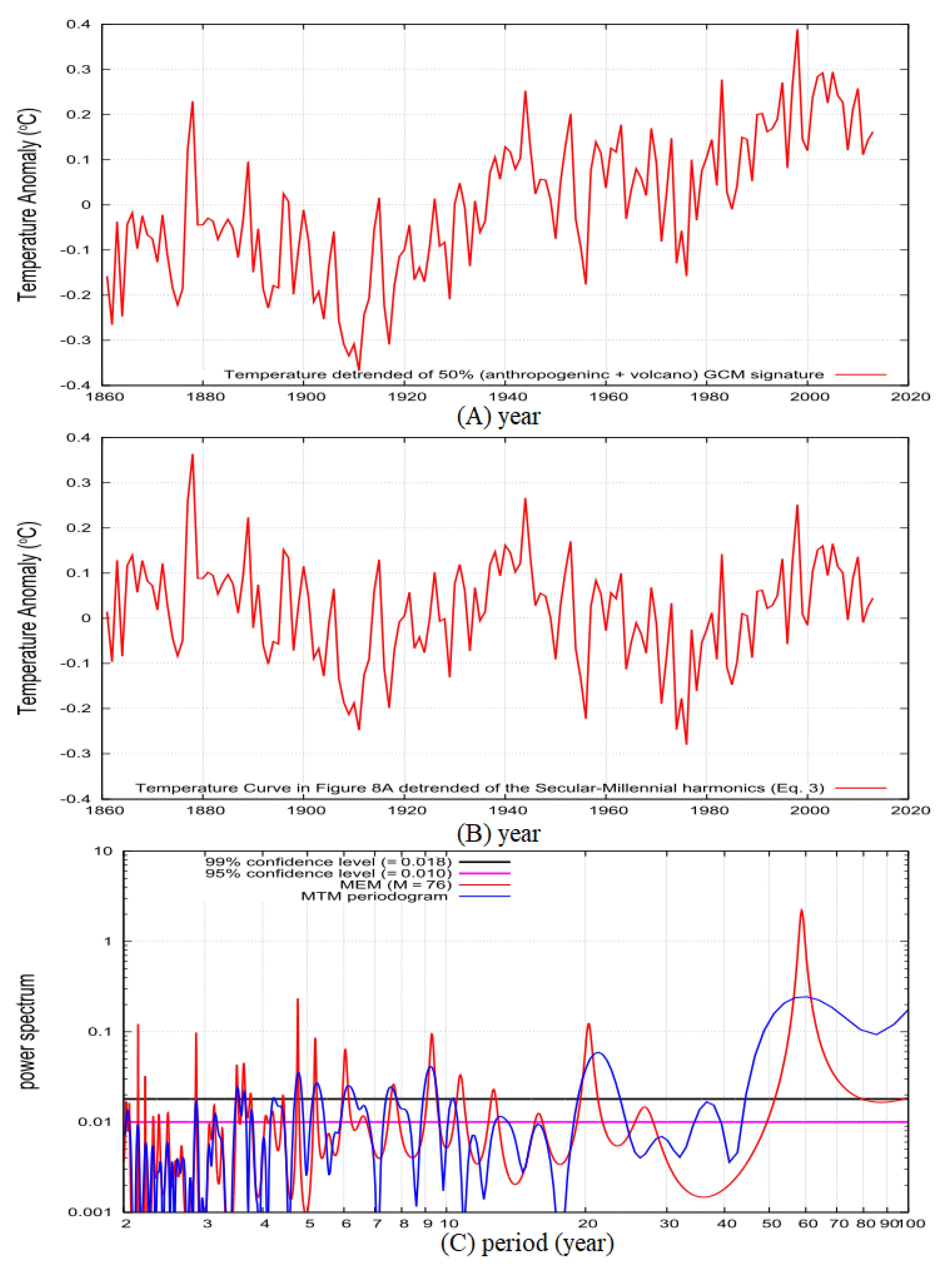
4.2. The Non-Harmonic Temperature Component is Assumed to be Simulated by 50% of the Anthropogenic + Volcano CMIP5 Multi-Model Mean Temperature Function
5. Secular and Millennial Temperature Reconstruction and a Discussion on the Physical Origin of the Climatic Oscillations
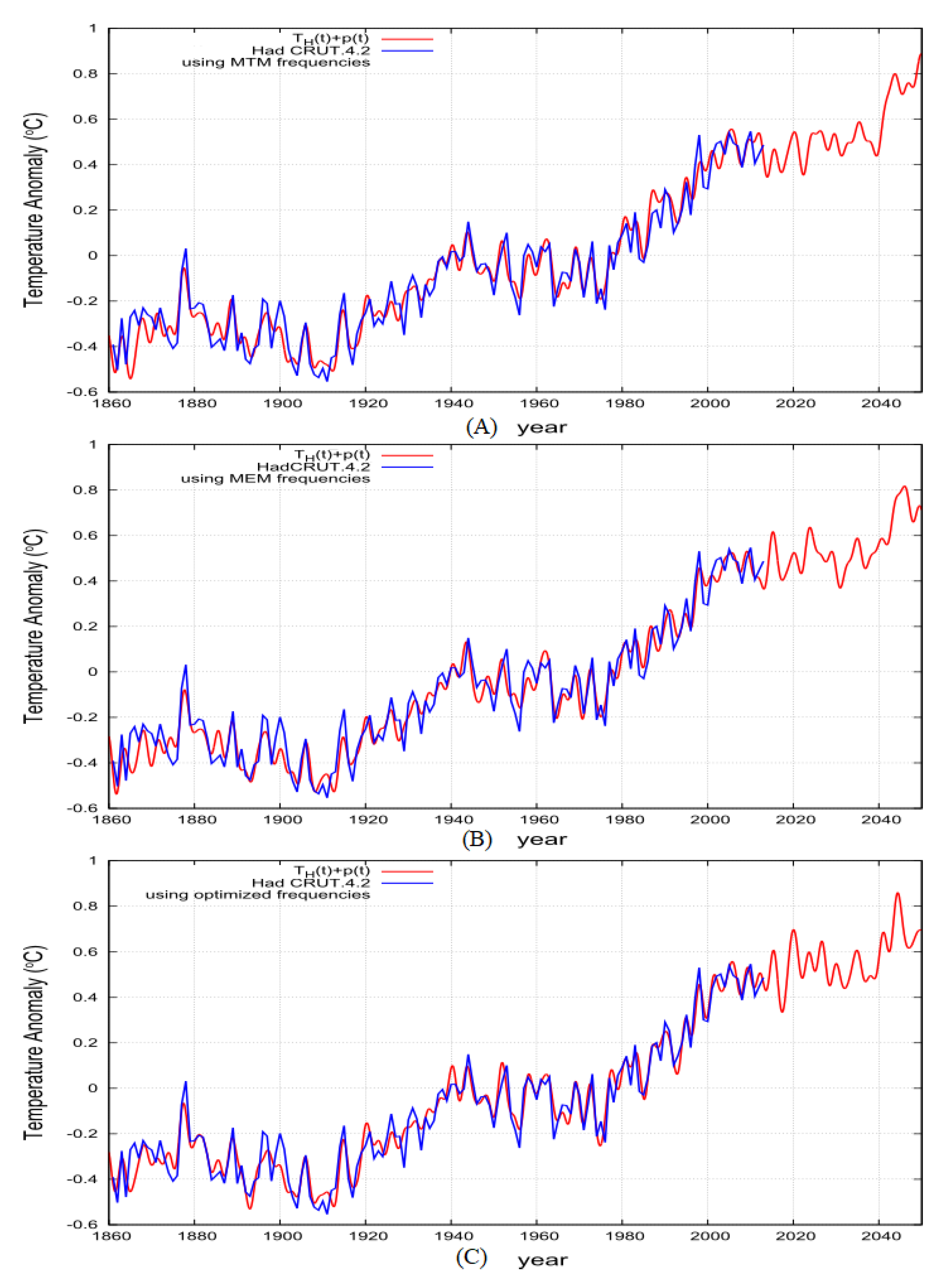
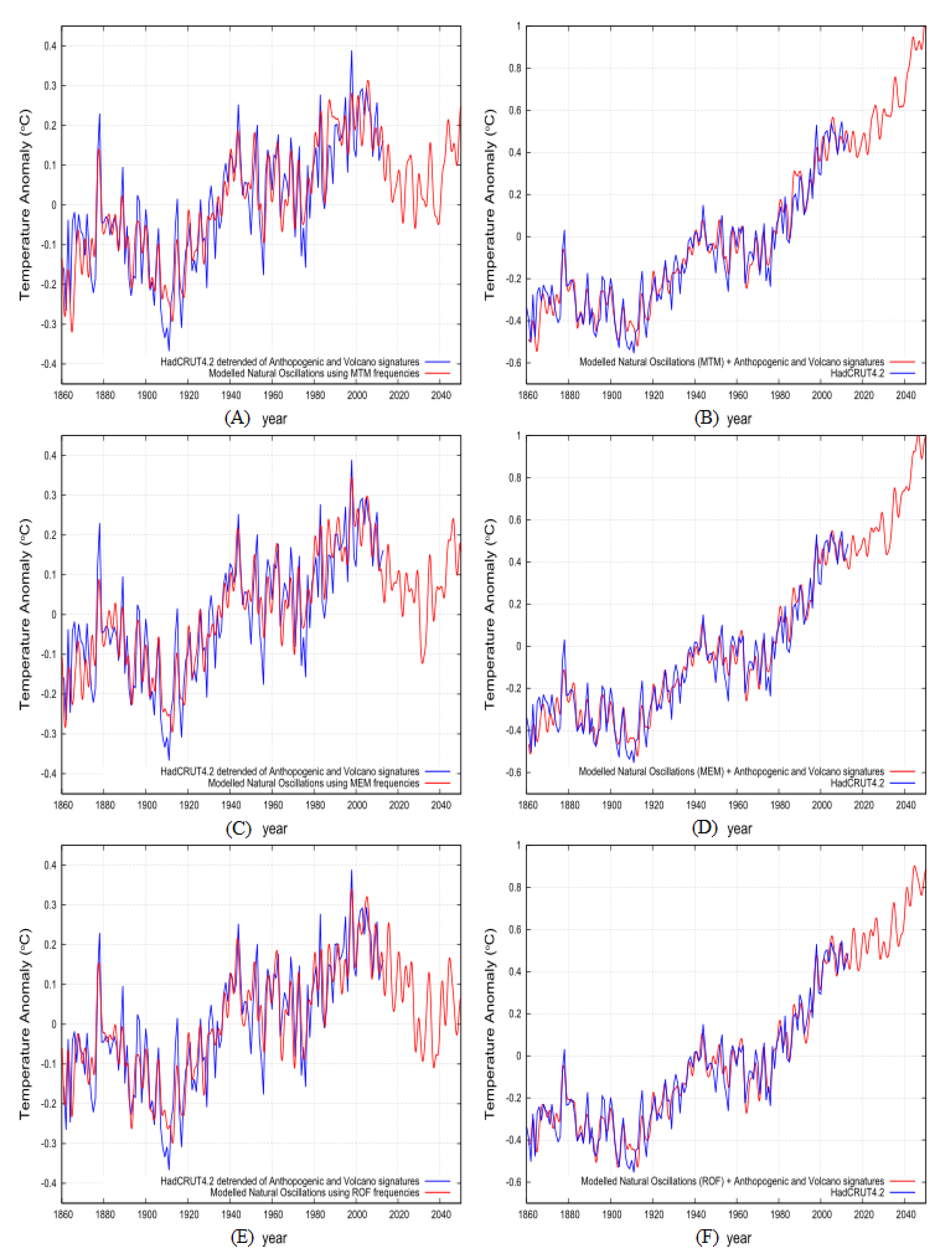
5.1. The Optimized Semi-Empirical Climate Regression Model
5.2. The Astronomically Optimized Semi-Empirical Climate Model
6. Validation of the Model Forecast
7. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- House, M.R. Orbital forcing timescales: An introduction. Geol. Soc. Lond. Spec. Publ. 1995, 85, 1–18. [Google Scholar] [CrossRef]
- Bond, G.; Kromer, B.; Beer, J.; Muscheler, R.; Evans, M.N.; Showers, W.; Hoffmann, S.; Lotti-Bond, R.; Hajdas, I.; Bonani, G. Persistent solar influence on North Atlantic climate during the Holocene. Science 2001, 294, 2130–2136. [Google Scholar] [CrossRef] [PubMed]
- Hoyt, D.V.; Schatten, K.H. The Role of the Sun in the Climate Change; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Kerr, R.A. A variable sun paces millennial climate. Science 2001, 294, 1431–1433. [Google Scholar] [CrossRef] [PubMed]
- Scafetta, N. Discussion on climate oscillations: CMIP5 general circulation models versus a semi-empirical harmonic model based on astronomical cycles. Earth-Sci. Rev. 2013, 126, 321–357. [Google Scholar] [CrossRef]
- Shaviv, N.J. Cosmic Ray Diffusion from the Galactic Spiral Arms, Iron Meteorites, and a Possible Climatic Connection. Phys. Rev. Lett. 2002, 89, 051102. [Google Scholar] [CrossRef] [PubMed]
- Soon, W.-H.; Herrera, V.M.V.; Selvaraj, K.; Traversi, R.; Usoskin, I.; Chen, C.-T.A.; Lou, J.-Y.; Kao, S.-J.-Y.; Carter, R.M.; Pipin, V.; et al. review of Holocene solar-linked climatic variation on centennial to millennial timescales: Physical processes, interpretative frameworks and a new multiple cross-wavelet transform algorithm. Earth-Sci. Rev. 2014, 134, 1–15. [Google Scholar] [CrossRef]
- Svensmark, H. Cosmoclimatology: A New Theory Emerges. Astron. Geophys. 2007, 48, 1.18–1.24. [Google Scholar] [CrossRef]
- Svensmark, H.; Enghoff, M.B.; Shaviv, N.J.; Svensmark, J. Increased ionization supports growth of aerosols into cloud condensation nuclei. Nat. Commun. 2017, 8, 2199. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, D.; Song, X.; Chen, X.; Nicholls, S. Sun–moon gravitation-induced wave characteristics and climate variation. J. Geophys. Res. 2012, 117, D07102. [Google Scholar] [CrossRef]
- Mörner, N.-A. Solar wind, Earth’s rotation and changes in terrestrial climate. Phys. Res. Int. 2013, 3, 117–136. [Google Scholar]
- Mörner, N.-A. Planetary beat and solar–terrestrial responses. Pattern Recogn. Phys. 2013, 1, 107–116. [Google Scholar] [CrossRef]
- Doodson, A.T. The Harmonic Development of the Tide-Generating Potential. Proc. R. Soc. London Ser. A 1921, 100, 305–329. [Google Scholar]
- Scafetta, N. Testing an astronomically based decadal-scale empirical harmonic climate model versus the IPCC (2007) general circulation climate models. J. Atmos. Sol. Terr. Phys. 2012, 80, 124–137. [Google Scholar] [CrossRef]
- Mann, M.E.; Steinman, B.A.; Miller, S.K. Absence of internal multidecadal and interdecadal oscillations in climate model simulations. Nat. Commun. 2020, 11, 49. [Google Scholar] [CrossRef]
- Müller-Plath, G. Internal Multidecadal and Interdecadal Climate Oscillations: Absence of Evidence is no Evidence of Absence. Front. Earth Sci. 2020. [Google Scholar] [CrossRef]
- Ljungqvist, F.C. A new reconstruction of temperature variability in the extratropical northern hemisphere during the last two millennia. Geogra-Fiska Ann. Ser. A 2010, 92, 339–351. [Google Scholar] [CrossRef]
- Alley, R.B. GISP2 Ice Core Temperature and Accumulation Data; IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series #2004-013; NOAA/NGDC Paleoclimatology Program: Boulder, CO, USA, 2004. [Google Scholar]
- Esper, J.; Frank, D.C.; Timonen, M.; Zorita, E.; Wilson, R.J.S.; Luterbacher, J.; Holzkämper, S.; Fischer, N.; Wagner, S.; Nievergelt, D.; et al. Orbital forcing of tree-ring data. Nat. Clim. Chang. 2012, 2, 862–866. [Google Scholar] [CrossRef]
- Esper, J.; Holzkämper, S.; Büntgen, U.; Schöne, B.; Keppler, F.; Hartl, C.; St. George, S.; Riechelmann, D.F.C.; Treydte, K. Site-specific climatic signals in stable isotope records from Swedish pine forests. Trees 2018, 32, 855–869. [Google Scholar] [CrossRef]
- Kutschera, W.; Patzelt, G.; Steier, P.; Wild, E.M. The tyrolean iceman and his glacial environment during the holocene. Radiocarbon 2017, 59, 395–405. [Google Scholar] [CrossRef]
- Hao, Z.; Wu, M.; Liu, Y.; Zhang, X.; Zheng, J. Multi-scale temperature variations and their regional differences in China during the Medieval Climate Anomaly. J. Geogr. Sci. 2020, 30, 119–130. [Google Scholar] [CrossRef]
- Margaritelli, G.; Cacho, I.; Català, A.; Barra, M.; Bellucci, L.G.; Lubritto, C.; Rettori, R.; Lirer, F. Persistent warm Mediterranean surface waters during the Roman period. Sci. Rep. 2020, 10, 10431. [Google Scholar] [CrossRef] [PubMed]
- Büntgen, U.; Arseneault, D.; Boucher, É.; Churakova (Sidorova), O.V.; Gennaretti, F.; Crivellaro, A.; Hughes, M.K.; Kirdyanov, A.V.; Klippel, L.; Krusic, P.J.; et al. New tree-ring evidence from the Pyrenees reveals western Mediterranean climate variability since medieval times. J. Clim. 2020, 30, 5295–5318. [Google Scholar] [CrossRef]
- Matskovsky, V.V.; Helama, S. Testing long-term summer temperature reconstruction based on maximum density chronologies obtained by reanalysis of tree-ring data sets from northernmost Sweden and Finland. Clim. Past 2014, 10, 1473–1487. [Google Scholar] [CrossRef]
- Wyatt, M.; Curry, J. Role of Eurasian Arctic shelf sea ice in a secularly varying hemispheric climate signal during the 20th century. Clim. Dyn. 2014, 42, 2763–2782. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; Available online: http://www.ipcc.ch/ (accessed on 22 January 2021).
- Scafetta, N.; Mirandola, A.; Bianchini, A. Natural climate variability, part 1: Observations versus the modeled predictions. Int. J. Heat And Technol. 2017, 35, S9–S17. [Google Scholar] [CrossRef]
- Scafetta, N.; Mirandola, A.; Bianchini, A. Natural climate variability, part 2: Interpretation of the post 2000 temperature standstill. Int. J. Heat Technol. 2017, 35, S18–S26. [Google Scholar] [CrossRef]
- Liua, Z.; Zhua, J.; Rosenthalc, Y.; Zhangd, X.; Otto-Bliesnere, B.L.; Timmermannf, A.; Smithg, R.S.; Lohmannd, G.; Zhengh, W.; Timmi, O.E. The Holocene temperature conundrum. PNAS 2014, 111, E3501–E3505. [Google Scholar] [CrossRef]
- Bohleber, P.; Schwikowski, M.; Stocker-Waldhuber, M.; Fang, L.; Fischer, A. New glacier evidence for ice-free summits during the life of the Tyrolean Iceman. Sci. Rep. 2020, 10, 20513. [Google Scholar] [CrossRef]
- Hays, J.D.; Imbrie, J.; Shackleton, N.J. Variations in the Earth’s Orbit: Pacemaker of the Ice Ages. Science 1976, 194, 1121–1132. [Google Scholar] [CrossRef]
- Guarino, M.V.; Sime, L.C.; Schröeder, D.; Malmierca-Vallet, I.; Rosenblum, E.; Ringer, M.; Ridley, J.; Feltham, D.; Bitz, C.; Steig, E.J.; et al. Sea-ice-free Arctic during the Last Interglacial supports fast future loss. Nat. Clim. Chang. 2020, 10, 928–932. [Google Scholar] [CrossRef]
- Rahmstorf, S. Anthropogenic Climate Change: Revisiting the Facts. In Global Warming: Looking Beyond Kyoto; Zedillo, E., Ed.; Brookings Institution Press: Washington, DC, USA, 2008; pp. 34–53. [Google Scholar]
- Lewis, N.; Curry, J. The Impact of Recent Forcing and Ocean Heat Uptake Data on Estimates of Climate Sensitivity. J. Clim. 2018, 31, 6051–6071. [Google Scholar] [CrossRef]
- Knutti, R.; Rugenstein, M.A.; Hegerl, G.C. Beyond equilibrium climate sensitivity. Nat. Geosci. 2017, 10, 727–736. [Google Scholar] [CrossRef]
- Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Jones, P.D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 dataset. J. Geophys. Res. 2012, 117, D08101. [Google Scholar] [CrossRef]
- Seip, K.L.; Grøn, Ø. On the statistical nature of distinct cycles in global warming variables. Clim. Dyn. 1990, 52, 7329–7337. [Google Scholar] [CrossRef]
- DelSole, T.; Tippett, M.K.; Shukla, J. A significant component of unforced multidecadal variability in the recent acceleration of global warming. J. Clim. 2011, 24, 909–926. [Google Scholar] [CrossRef]
- Tung, K.K.; Zhou, J. Using data to attribute episodes of warming and cooling in instrumental records. Proc. Natl. Acad. Sci. USA 2013, 110, 2058–2063. [Google Scholar] [CrossRef] [PubMed]
- Ogurtsov, M.G.; Nagovitsyn, Y.A.; Kocharov, G.E.; Jungner, H. Long-period cycles of the Sun’s activity recorded in direct solar data and proxies. Sol. Phys. 2002, 211, 371–394. [Google Scholar] [CrossRef]
- Scafetta, N. Empirical evidence for a celestial origin of the climate oscillations and its implications. J. Atmos. Sol. Terr. Phys. 2010, 72, 951–970. [Google Scholar] [CrossRef]
- Soon, W.-H.; Legates, D.L. Solar irradiance modulation of Equator-to Pole (Arctic) temperature gradients: Empirical evidence for climate variation on multi-decadal timescales. J. Atmos. Sol. Terr. Phys. 2013, 93, 45–56. [Google Scholar] [CrossRef]
- Thejll, P.; Lassen, K. Solar forcing of the northern hemisphere land air temperature: New data. J. Atmos. Sol. Terr. Phys. 2000, 62, 1207–1213. [Google Scholar] [CrossRef]
- Loehle, C.; Scafetta, N. Climate change attribution using empirical decomposition of climatic data. Open Atmos. Sci. J. 2011, 5, 74–86. [Google Scholar] [CrossRef]
- Akasofu, S.-I. On the recovery from the Little Ice Age. Nat. Sci. 2010, 2, 1211–1224. [Google Scholar] [CrossRef]
- Chylek, P.; Dubey, M.K.; Lesins, G.; Li, J.; Hengartner, N. Imprint of the Atlantic multidecadal oscillation and Pacific decadal oscillation on southwestern US climate: Past, present, and future. Clim. Dyn. 2013, 43, 119–129. [Google Scholar] [CrossRef]
- Chylek, P.; Hengartner, N.; Lesins, G.; Klett, J.D.; Humlum, O.; Wyatt, M.; Dubey, M.K. Isolating the anthropogenic component of Arctic warming. Geophys. Res. Lett. 2014, 41, 3569–3576. [Google Scholar] [CrossRef]
- Zhou, J.; Tung, K.K. Deducing multidecadal anthropogenic global warming trends using multiple regression analysis. J. Atmos. Sci. 2013, 70, 3–8. [Google Scholar] [CrossRef]
- Akasofu, S.-I. On the Present Halting of Global Warming. Climate 2013, 1, 4–11. [Google Scholar] [CrossRef]
- Klyashtorin, L.B.; Borisov, V.; Lyubushin, A. Cyclic changes of climate and major commercial stocks of the Barents Sea. Mar. Biol. Res. 2009, 5, 4–17. [Google Scholar] [CrossRef]
- Mörner, N.-A. The Earth’s differential rotation: Hydrospheric changes. Geophys. Monogr. 1990, 59, 27–32. [Google Scholar]
- Mörner, N.-A. Changes in the Earth’s rate of rotation on an El Nino to century basis. In Geomagnetism and Paleomagnetism; Lowes, F.J., Collinson, D.W., Parry, J.H., Puncorn, S.K., Eds.; Kluwer Acad. Publ.: Dordrecht, The Netherlands, 1989; pp. 45–53. [Google Scholar]
- Qian, W.-H.; Lu, B. Periodic oscillations in millennial global-mean temperature and their causes. Chin. Sci. Bull. 2010, 55, 4052–4057. [Google Scholar] [CrossRef]
- Parker, A. Sea level trends at locations of the United States with more than 100 years of recording. Nat. Hazards 2013, 65, 1011–1021. [Google Scholar] [CrossRef]
- Parker, A. Oscillations of sea level rise along the Atlantic coast of North America north of Cape Hatteras. Nat. Hazards 2013, 65, 991–997. [Google Scholar] [CrossRef]
- Semenov, V.A.; Latif, M.; Dommenget, D.; Keenlyside, N.S.; Strehz, A.; Martin, T.; Park, W. The Impact of North Atlantic–Arctic Multidecadal Variability on Northern Hemisphere Surface Air Temperature. J. Clim. 2010, 23, 5668–5677. [Google Scholar] [CrossRef]
- Wyatt, M.; Kravtsov, S.; Tsonis, A. Atlantic Multidecadal Oscillation and Northern Hemisphere’s climate variability. Clim. Dyn. 2012, 38, 929–941. [Google Scholar] [CrossRef]
- Yao, S.L.; Luo, J.J.; Huang, G.; Wang, P. Distinct global warming rates tied to multiple ocean surface temperature changes. Nat. Clim. Chang. 2017, 7, 486–491. [Google Scholar] [CrossRef]
- Chylek, P.; Lohmann, U. Aerosol radiative forcing and climate sensitivity deduced from the Last GlacialMaximum toHolocene transition. Geophys. Res. Lett. 2008, 35, L04804. [Google Scholar]
- Lewis, N. An objective Bayesian, improved approach for applying optimal fingerprint techniques to estimate climate sensitivity. J. Clim. 2013, 26, 7414–7429. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Choi, Y.-S. On the determination of climate feedbacks from erbe data. Geophys. Res. Lett. 2009, 36, L16705. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Choi, Y.-S. On the observational determination of climate sensitivity and its implications. Asia Pac. J. Atmos. Sci. 2011, 47, 377–390. [Google Scholar] [CrossRef]
- Spencer, R.W.; Braswell, W.D. On the diagnosis of radiative feedback in the presence of unknown radiative forcing. J. Geophys. Res. 2010, 115, D16109. [Google Scholar] [CrossRef]
- Spencer, R.W.; Braswell, W.D. On themisdiagnosis of surface temperature feedbacks from variations in earth’s radiant energy balance. Remote Sens. 2011, 3, 1603–1613. [Google Scholar] [CrossRef]
- Ring, M.J.; Lindner, D.; Cross, E.F.; Schlesinger, M.E. Causes of the global warming observed since the 19th century. Atmos. Clim. Sci. 2012, 2, 401–415. [Google Scholar] [CrossRef]
- Scafetta, N. Solar and planetary oscillation control on climate change: Hind-cast, forecast and a comparison with the CMIP5 GCMs. Energy Environ. 2013, 24, 455–496. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R.; Kharecha, P.; Lacis, A.; Miller, R.; Nazarenko, L.; Lo, K.; Schmidt, G.A.; Russell, G.; et al. Climate simulations for 1880–2003 with GISS modelE. Clim. Dynam. 2007, 29, 661–696. [Google Scholar] [CrossRef]
- Lean, J. Evolution of the Sun’s spectral irradiance since the Maunder Minimum. Geophys. Res. Lett. 2000, 27, 2425–2428. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Lean, J.L.; Sheeley, N.R., Jr. Modeling the sun’s magnetic field and irradiance since 1713. Astrophys. J. 2005, 625, 522–538. [Google Scholar] [CrossRef]
- Scafetta, N. Empirical analysis of the solar contribution to global mean air surface temperature change. J. Atmos. Sol. Terr. Phys. 2009, 71, 1916–1923. [Google Scholar] [CrossRef]
- Scafetta, N. Multi-scale harmonic model for solar and climate cyclical variation throughout the Holocene based on Jupiter–Saturn tidal frequencies plus the 11-year solar dynamo cycle. J. Atmos. Sol. Terr. Phys. 2012, 80, 296–311. [Google Scholar] [CrossRef]
- Scafetta, N. Global temperatures and sunspot numbers. Are they related? Yes, but non linearly. A reply to Gil-Alana et al. Phys. A Stat. Mech. Appl. 2014, 413, 329–342. [Google Scholar] [CrossRef]
- Soon, W.; Connolly, R.; Connolly, M. Re-evaluating 1157 the role of solar variability on Northern Hemisphere temperature trends since the 19th century. Earth-Sci. Rev. 2015, 150, 409–452. [Google Scholar] [CrossRef]
- Soon, W.W.-H.; Connolly, R.; Connolly, M.; O’Neill, P.; Zheng, J.; Ge, Q.; Hao, Z.; Yan, H. Comparing the current and early 20th century warm periods in China. Earth-Sci. Rev. 2018, 185, 80–101. [Google Scholar] [CrossRef]
- Fröhlich, C.; Lean, J. The Sun’s total irradiance: Cycles, trends and related climate change uncertainties since 1978. Geophys. Res. 1998, 25, 4377–4380. [Google Scholar]
- Willson, R.C. Total solar irradiance trend during solar cycles 21 and 22. Science 1997, 277, 1963–1965. [Google Scholar] [CrossRef]
- Willson, R.C.; Mordvinov, A.V. Secular total solar irradiance trend during solar cycles 21–23. Geophys. Res. Lett. 2003, 30, 1199. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C. ACRIM gap and TSI trend issue resolved using a surface magnetic flux TSI proxy model. Geophys. Res. Lett. 2009, 36, L05701. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C. ACRIM total solar irradiance satellite composite validation versus TSI proxy models. Astrophys. Space Sci. 2014, 350, 421–442. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C.; Lee, J.N.; Wu, D.L. Modeling quiet solar luminosity variability from TSI satellite measurements and proxy models during 1980–2018. Remote Sens. 2019, 11, 2569. [Google Scholar] [CrossRef]
- Scafetta, N.; West, B.J. Estimated solar contribution to the global surface warming using the ACRIM TSI satellite composite. Geophys. Res. Lett. 2005, 32, L18713. [Google Scholar] [CrossRef]
- Scafetta, N.; West, B.J. Phenomenological reconstruction of the solar signature in the NH surface temperature records since 1600. J. Geophys. 2007, 112, D24S03. [Google Scholar] [CrossRef]
- Scafetta, N.; Milani, F.; Bianchini, A.; Ortolani, S. On the astronomical origin of the Hallstatt oscillation found in radiocarbon and climate records throughout the Holocene. Earth-Sci. Rev. 2016, 162, 24–43. [Google Scholar] [CrossRef]
- Scafetta, N. Solar Oscillations and the Orbital Invariant Inequalities of the Solar System. Sol. Phys. 2020, 295, 33. [Google Scholar] [CrossRef]
- Scafetta, N.; Milani, F.; Bianchini, A. A 60-year cycle in the Meteorite fall frequency suggests a possible interplanetary dust forcing of the Earth’s climate driven by planetary oscillations. Geophys. Res. Lett. 2020, 47, e2020GL089954. [Google Scholar] [CrossRef]
- Kirkby, J. Cosmic rays and climate. Surv. Geophys. 2007, 28, 333–375. [Google Scholar] [CrossRef]
- Soon, W.-H. Variable solar irradiance as a plausible agent for multidecadal variations in the Arctic-wide surface air temperature record of the past 130 years. Geophys. Lett. 2005, 32, L16712. [Google Scholar] [CrossRef]
- Soon, W.-H. Solar arctic mediated climate variation on multidecadal to centennial timescales: Empirical evidence, mechanistic explanation and testable consequences. Phys. Geogr. 2009, 30, 144–148. [Google Scholar] [CrossRef]
- Steinhilber, F.; Abreu, J.A.; Beer, J.; Brunner, I.; Christl, M.; Fischer, H.; Heikkila, U.; Kubik, P.W.; Mann, M.; McCracken, K.G.; et al. 9400 years of cosmic radiation and solar activity from ice cores and tree rings. Proc. Natl. Acad. Sci. USA 2012, 109, 5967–5971. [Google Scholar] [CrossRef]
- Vahrenholt, F.; Lüning, S. Die kalte Sonne—Warum die Klimakatastrophe nicht stattfindet. In The Neglected Sun: How the Sun Precludes Climate Catastrophe; Hoffmann und Campe: Hamburg, Germany, 2013. [Google Scholar]
- Booth, B.B.B.; Dunstone, N.J.; Halloran, P.R.; Andrews, T.; Bellouin, N. Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability. Nature 2012, 263, 228–232. [Google Scholar] [CrossRef]
- Mann, M.E.; Steinman, B.A.; Miller, S.K. On forced temperature changes, internal variability, and the AMO. Geophys. Res. Lett. 2014, 41, 3211–3219. [Google Scholar] [CrossRef]
- Zhang, R.; Delworth, T.L.; Sutton, R.; Hodson, D.L.R.; Dixon, K.W.; Held, I.M.; Kushnir, Y.; Marshall, J.; Ming, Y.; Msadek, R.; et al. Have Aerosols Caused the Observed Atlantic Multidecadal Variability? J. Atmos. Sci. 2013, 70, 1135–1144. [Google Scholar] [CrossRef]
- Davis, J.C.; Bohling, G. The search for patterns in ice-core temperature curves. In Geological Perspectives of Global Climate Change; Gerhard, L.C., Harrison, W.E., Hanson, B.M., Eds.; AAPG: Tulsa, OK, USA, 2001; pp. 213–229. [Google Scholar]
- Jevrejeva, S.; Moore, J.C.; Grinsted, A.; Woodworth, P. Recent global sea level acceleration started over 200 years ago? Geophys. Res. Lett. 2008, 35, L08715. [Google Scholar] [CrossRef]
- Knudsen, M.F.; Seidenkrantz, M.-S.; Jacobsen, B.H.; Kuijpers, A. Tracking the Atlantic Multidecadal Oscillation through the last 8000 years. Nat. Commun. 2011, 2, 178. [Google Scholar] [CrossRef]
- Mazzarella, A.; Scafetta, N. Evidences for a quasi 60-year North Atlantic Oscillation since 1700 and its meaning for global climate change. Theor. Appl. Climatol. 2012, 107, 599–609. [Google Scholar] [CrossRef]
- Scafetta, N. Multi-scale dynamical analysis (MSDA) of sea level records versus PDO, AMO, and NAO indexes. Clim. Dyn. 2014, 43, 175–192. [Google Scholar] [CrossRef]
- Scafetta, N.; Humlum, O.; Solheim, J.-E.; Stordahl, K. Comment on “The influence of planetary attractions on the solar tachocline” by Callebaut, de Jager and Duhau. J. Atmos. Sol. Terr. Phys. 2013, 102, 368–371. [Google Scholar] [CrossRef][Green Version]
- Pustil’nik, L.A.; Din, G.Y. Influence of solar activity on the state of the wheat market in medieval England. Sol. Phys. 2004, 223, 335–356. [Google Scholar] [CrossRef]
- Chylek, P.; Folland, C.K.; Dijkstra, H.A.; Lesins, G.; Dubey, M.K. Ice-core data evidence for a prominent near 20 year time-scale of the Atlantic Multidecadal Oscillation. Geophys. Res. Lett. 2011, 38, L13704. [Google Scholar] [CrossRef]
- Puetz, S.J.; Prokoph, A.; Borchardt, G.; Mason, E.W. Evidence of synchronous, decadal to billion year cycles in geological, genetic, and astronomical events. Chaos Solitons Fractals 2014, 62–63, 55–75. [Google Scholar] [CrossRef]
- Neff, U.; Burns, S.J.; Mangini, A.; Mudelsee, M.; Fleitmann, D.; Matter, A. Strong coherence between solar variability and the monsoon in Oman between 9 and 6 kyr ago. Nature 2001, 411, 290. [Google Scholar] [CrossRef]
- Christiansen, B.; Ljungqvist, F.C. The extra-tropical Northern Hemisphere temperature in the last two millennia: Reconstructions of low-frequency variability. Clim. Past. 2012, 8, 765–786. [Google Scholar] [CrossRef]
- Scafetta, N. Discussion on the spectral coherence between planetary, solar and climate oscillations: A reply to some critiques. Astrophys. Space Sci. 2014, 354, 275–299. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C. Planetary harmonics in the historical Hungarian aurora record (1523–1960). Planet. Space Sci. 2013, 78, 38–44. [Google Scholar] [CrossRef]
- Gervais, F. Anthropogenic CO2 warming challenged by 60-year cycle. Earth-Sci. Rev. 2016, 155, 129–135. [Google Scholar] [CrossRef]
- Haigh, I.D.; Eliot, M.; Pattiaratchi, C. Global influences of the 18.61 year nodal cycle and 8.85 year cycle of lunar perigee on high tidal levels. J. Geophys. 2011, 116, C06025. [Google Scholar] [CrossRef]
- Scafetta, N. Does the Sun work as a nuclear fusion amplifier of planetary tidal forcing? A proposal for a physical mechanism based on the mass–luminosity relation. J. Atmos. Sol. Terr. Phys. 2012, 81–82, 27–40. [Google Scholar] [CrossRef]
- Abreu, J.A.; Beer, J.; Ferriz-Mas, A.; McCracken, K.G.; Steinhilber, F. Is there a planetary influence on solar activity? Astron. Astrophys. 2012, 548, A88. [Google Scholar] [CrossRef]
- Scafetta, N. A shared frequency set between the historical mid-latitude aurora records and the global surface temperature. J. Atmos. Sol. Terr. 2012, 74, 145–163. [Google Scholar] [CrossRef]
- Qu, W.-Z.; Huang, F.; Du, L.; Zhao, J.-P.; Deng, S.-G.; Cao, Y. The periodicity of volcano activity and its reflection in some climate factors. Chin. J. Geophys. 2011, 54, 135–149. [Google Scholar] [CrossRef]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin, Germany, 1984. [Google Scholar]
- Strogatz, S.H. Exploring complex networks. Nature 2009, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 1990, 344, 734–741. [Google Scholar] [CrossRef]
- Zielinski, G.A. Use of paleo-records in determining variability within the volcanism climate system. Quat. Sci. Rev. 2000, 19, 417–438. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, R.M.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 3.1–3.41. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D 1992, 58, 95–126, (SSA-MTM toolkit for spectral analysis). Available online: http://web.atmos.ucla.edu/tcd//ssa/ (accessed on 21 January 2021). [CrossRef]
- Hansen, J.; Sato, M.; Kharecha, P.; von Schuckmann, K. Earth’s energy imbalance and implications. Atmos. Chem. Phys. 2011, 11, 13421–13449. [Google Scholar] [CrossRef]
- Knight, J.; Kenned, J.J.; Folland, C.; Harris, G.; Jones, G.S.; Palmer, M.; Parke, D.; Scaife, A.; Stott, P. Do global temperature trends over the last decade falsify climate predictions? In “State of the Climate in 2008”. Bull. Am. Meteorol. Soc. 2009, 90, S1–S196. [Google Scholar]
- Scafetta, N. The complex planetary synchronization structure of the solar system. Pattern Recognit. Phys. 2014, 2, 1–19. [Google Scholar] [CrossRef]
- Mann, M.E.; Zhang, Z.; Hughes, M.K.; Bradley, R.S.; Miller, S.K.; Rutherford, S.; Ni, F. Proxy-based reconstructions of hemispheric and global surface temperature variations over the past two millennia. PNAS 2008, 105, 13252–13257. [Google Scholar] [CrossRef]
- Moberg, A.; Sonechkin, D.M.; Holmgren, K.; Datsenko, N.M.; Karlén, W. Highly variable Northern Hemisphere temperatures reconstructed from low- and highresolution proxy data. Nature 2005, 433, 613–617. [Google Scholar] [CrossRef]
- Crowley, T.J. Causes of climate change over the past 1000 years. Science 2000, 289, 270–277. [Google Scholar] [CrossRef]
- Lovejoy, S. Scaling fluctuation analysis and statistical hypothesis testing of anthropogenic warming. Clim. Dyn. 2014, 42, 2339–2351. [Google Scholar] [CrossRef]
- Mann, M.E.; Bradley, R.S.; Hughes, M.K. Northern hemisphere temperatures during the pastmillennium: Inferences, uncertainties, and limitations. Geophys. Res. Lett. 1999, 26, 759–762. [Google Scholar] [CrossRef]
- Mann, M.E.; Jones, P.D. Global surface temperature over the past two millennia. Geophys. Res. Lett. 2003, 30, 1820–1824. [Google Scholar] [CrossRef]
- Guidoboni, E.; Navarra, A.; Boschi, E. The Spiral of Climate: Civilizations of the Mediterranean and Climate Change in History; Bononia University Press: Bologna, Italy, 2011. [Google Scholar]
- Scafetta, N. On the reliability of computer-based climate models. Ital. J. Eng. Environ. 2019, 1, 50–70. [Google Scholar]
- Liu, J.; Wang, B.; Cane, M.A.; Yim, S.-Y.; Lee, J.-Y. Divergent global precipitation changes induced by natural versus anthropogenic forcing. Nature 2013, 493, 656–659. [Google Scholar] [CrossRef] [PubMed]
- Scafetta, N. Discussion on common errors in analyzing sea level accelerations, solar trends and global warming. Pattern Recognit. Phys. 2013, 1, 37–57. [Google Scholar] [CrossRef]
- Eddy, J.A. The Maunder minimum. Science 1976, 192, 1189–1202. [Google Scholar] [CrossRef] [PubMed]
- Humlum, O.; Solheim, J.-E.; Stordahl, K. Identifying natural contributions to late Holocene climate change. Glob. Planet. Chang. 2011, 79, 145–156. [Google Scholar] [CrossRef]
- Manzi, V.; Gennari, R.; Lugli, S.; Roveri, M.; Scafetta, N.; Schreiber, C. High-frequency cyclicity in the Mediterranean Messinian evaporites: Evidence for solar-lunar climate forcing. J. Sed. Res. 2012, 82, 991–1005. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. Estimation of the coherence function with the MVDR approach. Acoustics, Speech and Signal Processing. In Proceedings of the 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 14–19 May 2006; Volume 3, pp. 500–503. [Google Scholar]
- Wolf, R. Extract of a letter to Mr. Carrington. Mon. Not. R. Astron. Soc. 1859, 19, 85–86. [Google Scholar]
- Scafetta, N.; Willson, R.C. Empirical evidences for a planetary modulation of total solar irradiance and the TSI signature of the 1.09-year Earth-Jupiter conjunction cycle. Astrophys. Space Sci. 2013, 348, 25–39. [Google Scholar] [CrossRef]
- Charvátová, I. Long-term predictive assessments of solar and geomagnetic activities made on the basis of the close similarity between the solar inertial motions in the intervals 1840–1905 and 1980–2045. New Astron. 2009, 14, 25–30. [Google Scholar] [CrossRef]
- Fairbridge, R.W.; Shirley, J.H. Prolonged minima and the 179- year cycle of the solar inertial motion. Sol. Phys. 1987, 10, 191–210. [Google Scholar] [CrossRef]
- Hung, C.-C. Apparent Relations Between Solar Activity and Solar Tides Caused by the Planets. NASA report/TM-2007-214817. 2007. Available online: http://ntrs.nasa.gov/search.jsp?R=20070025111 (accessed on 21 January 2021).
- Jakubcová, I.; Pick, M. The planetary system and solarterrestrial phenomena. Stud. Geophys. Geod. 1986, 30, 224–235. [Google Scholar] [CrossRef]
- McCracken, K.G.; Beer, J.; Steinhilber, F.; Abreu, J. Evidence for Planetary Forcing of the Cosmic Ray Intensity and Solar Activity Throughout the Past 9400 Years. Sol. Phys. 2014, 286, 609–627. [Google Scholar] [CrossRef]
- Tan, B.; Cheng, Z. The mid-term and long-term solar quasiperiodic cycles and the possible relationship with planetary motions, Astrophys. Space Sci. 2013, 343, 511–521. [Google Scholar] [CrossRef][Green Version]
- Wilson, I.R.G. The Venus–Earth–Jupiter spin–orbit coupling model. Pattern Recogn. Phys. 2013, 1, 147–158. [Google Scholar] [CrossRef]
- Wolff, C.L.; Patrone, P.N. A new way that planets can affect the Sun. Sol. Phys. 2010, 266, 227–246. [Google Scholar] [CrossRef]
- Holm, S. On the alleged coherence between the global temperature and the Sun’s movement. J. Atmos. Solar-Terrestr. Phys. 2014, 110–111, 23–27. [Google Scholar] [CrossRef]
- Scafetta, N. High resolution coherence analysis between planetary and climate oscillations. Adv. Space Res. 2016, 57, 2121–2135. [Google Scholar] [CrossRef]
- Scafetta, N. Reply on Comment on “High resolution coherence analysis between planetary and climate oscillations” by S. Holm. Adv. Space Res. 2018, 62, 334–342. [Google Scholar] [CrossRef]
- Holm, S. Comment on “High resolution coherence analysis between planetary and climate oscillations”. Adv. Space Res. 2018, 62, 326–333. [Google Scholar] [CrossRef]
- Scafetta, N.; Milani, F.; Bianchini, A. Multiscale Analysis of the Instantaneous Eccentricity Oscillations of the Planets of the Solar System from 13,000 BC to 17,000 AD. Astron. Lett. 2019, 45, 778–790. [Google Scholar] [CrossRef]
- Scafetta, N.; Ouyang, S. Detection of UHI bias in China climate network using Tmin and Tmax surface temperature divergence. Glob. Planet. Chang. 2019, 181, 102989. [Google Scholar] [CrossRef]
- Scafetta, N. Detection of non-climatic biases in land surface temperature records by comparing climatic data and their model simulations. Clim. Dyn. 2021, in press. [Google Scholar] [CrossRef]
- Melott, A.L.; Bambach, R.K. A ubiquitous ~62-Myr periodic fluctuation superimposed on general trends in fossil biodiversity. Part I & Part II. Paleobiology 2011, 37, 92–112, 383–408; [Google Scholar]
- Rohde, R.; Muller, R. Cycles in fossil diversity. Nature 2005, 434, 208–210. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Global Warming of 1.5 °C. 2018. Available online: https://www.ipcc.ch/sr15/ (accessed on 21 January 2021).

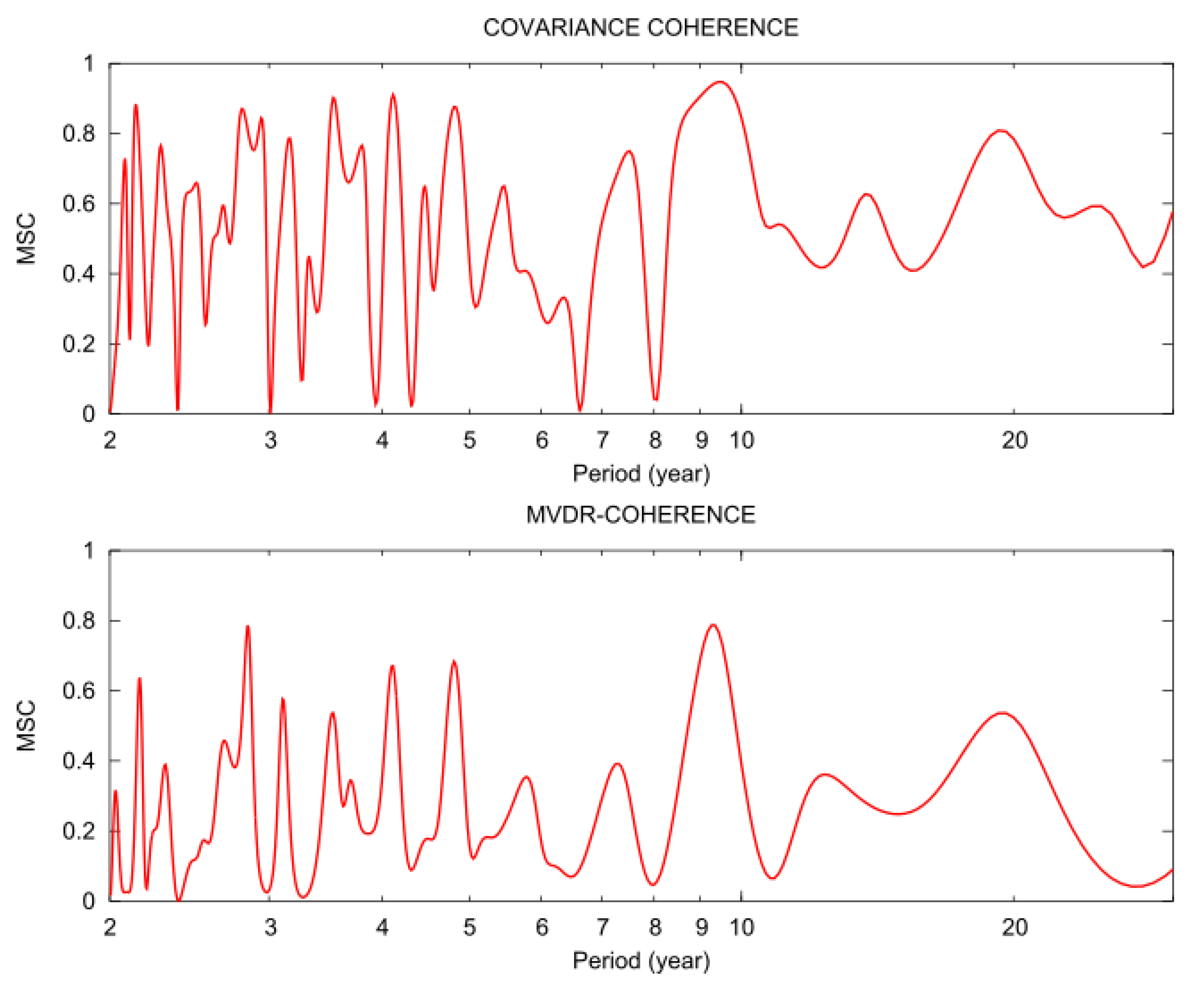

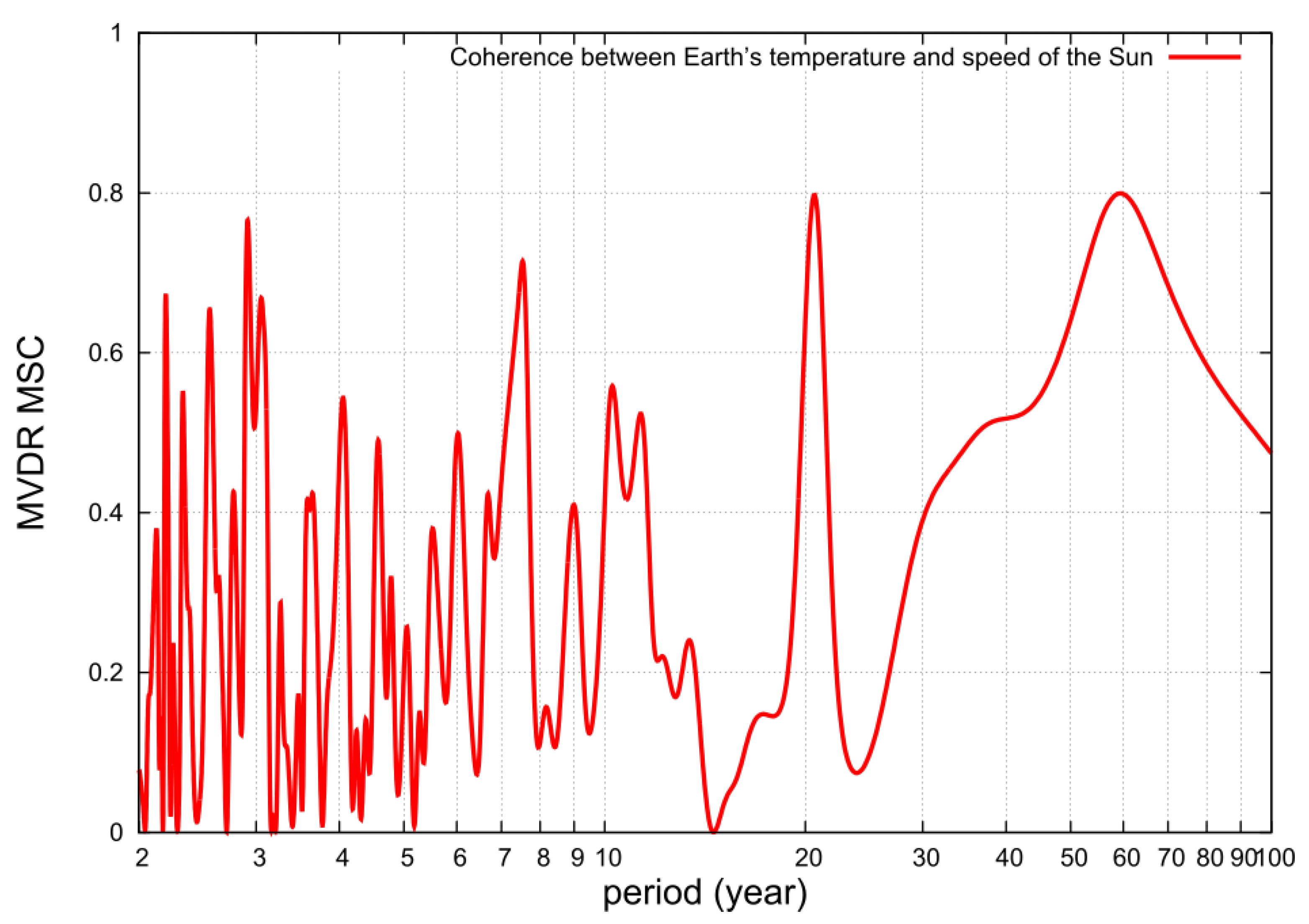
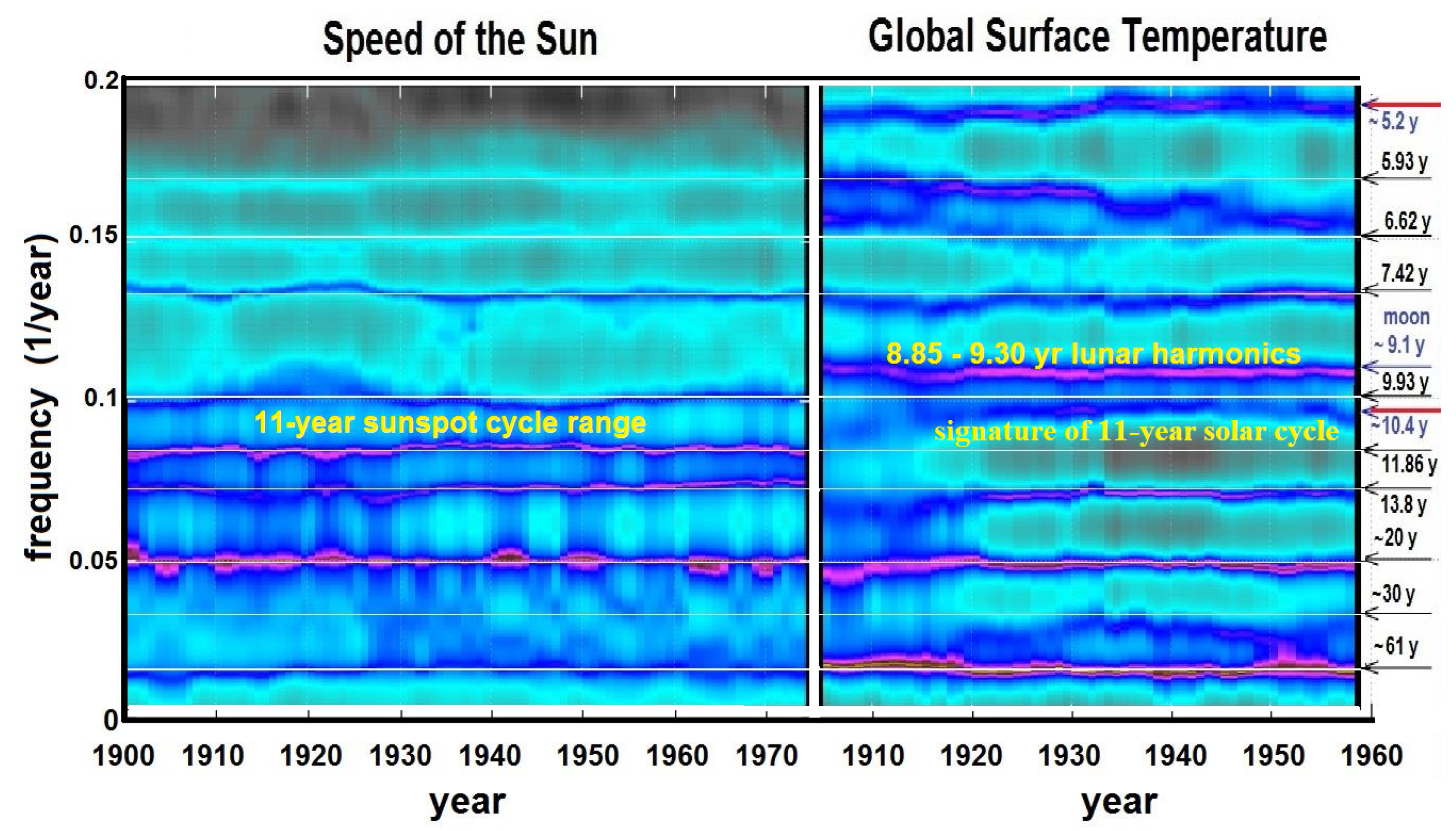
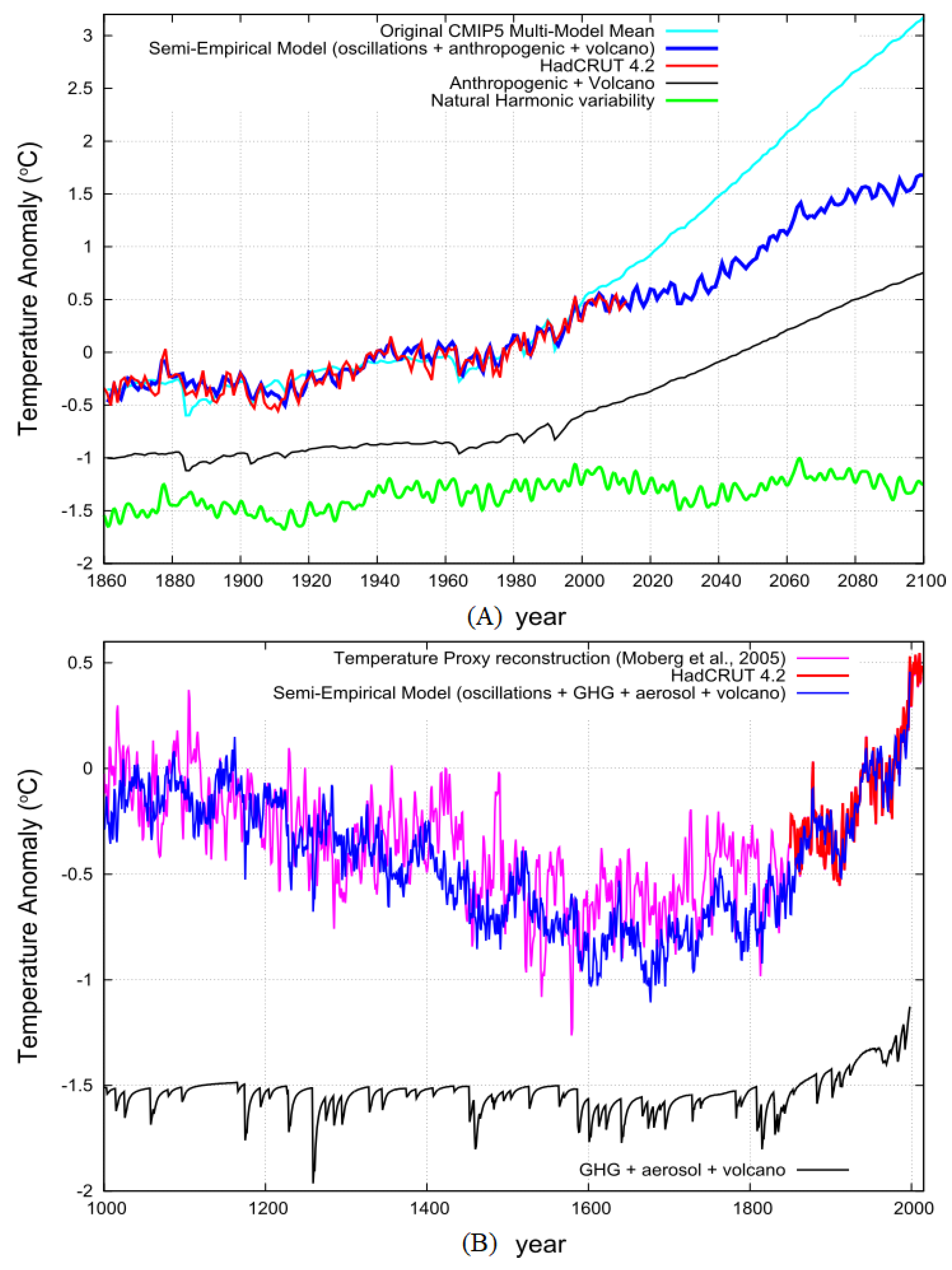

| MTM Spectral Peak Frequencies | MEM Spectral Peak Frequencies | Regression Optimized Frequencies | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| () | () | (°C) | () | () | (°C) | () | () | (°C) | |||
| 62.11 | 0.0161 | 0.118 | 0.20 | 64.10 | 0.0156 | 0.122 | 0.16 | 65.79 | 0.0152 | 0.121 | 0.14 |
| 21.33 | 0.0469 | 0.042 | 1.00 | 20.75 | 0.0482 | 0.044 | 0.08 | 20.70 | 0.0483 | 0.046 | 0.10 |
| 10.24 | 0.0977 | 0.027 | 0.13 | 10.44 | 0.0958 | 0.025 | 0.97 | 10.21 | 0.0979 | 0.031 | 0.13 |
| 9.225 | 0.1084 | 0.038 | 0.45 | 9.234 | 0.1083 | 0.041 | 0.44 | 9.183 | 0.1089 | 0.039 | 0.50 |
| 8.190 | 0.1221 | 0.024 | 0.82 | 7.831 | 0.1277 | 0.015 | 0.38 | 8.190 | 0.1221 | 0.021 | 0.80 |
| 7.530 | 0.1328 | 0.024 | 0.66 | 7.645 | 0.1308 | 0.024 | 0.57 | ||||
| 6.131 | 0.1631 | 0.021 | 0.27 | 6.020 | 0.1661 | 0.027 | 0.61 | 6.254 | 0.1599 | 0.027 | 0.94 |
| 5.277 | 0.1895 | 0.025 | 0.33 | 5.200 | 0.1923 | 0.025 | 0.49 | 5.236 | 0.1910 | 0.029 | 0.42 |
| 4.762 | 0.2100 | 0.031 | 0.04 | 4.746 | 0.2107 | 0.033 | 0.10 | 4.773 | 0.2095 | 0.034 | 0.01 |
| 4.232 | 0.2363 | 0.017 | 0.46 | 4.202 | 0.2380 | 0.022 | 0.58 | 4.179 | 0.2393 | 0.026 | 0.65 |
| 3.644 | 0.2744 | 0.025 | 0.70 | 3.635 | 0.2751 | 0.024 | 0.73 | 3.628 | 0.2756 | 0.029 | 0.79 |
| 3.531 | 0.2832 | 0.023 | 0.89 | 3.516 | 0.2844 | 0.021 | 0.95 | 3.556 | 0.2812 | 0.028 | 0.79 |
| 2.876 | 0.3477 | 0.025 | 0.95 | 2.869 | 0.3486 | 0.025 | 0.02 | 2.875 | 0.3478 | 0.025 | 0.97 |
| MTM Spectral Peak Frequencies | MEM Spectral Peak Frequencies | Regression Optimized Frequencies | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| () | () | (°C) | () | () | (°C) | () | () | (°C) | |||
| 760 | 1/760 | 0.350 | 0.171 | 760 | 1/760 | 0.350 | 0.171 | 760 | 1/760 | 0.33 | 0.171 |
| 115 | 1/115 | 0.050 | 0.424 | 115 | 1/115 | 0.050 | 0.424 | 115 | 1/115 | 0.055 | 0.424 |
| 58.50 | 0.0171 | 0.086 | 0.26 | 58.82 | 0.0170 | 0.088 | 0.25 | 63.29 | 0.0158 | 0.091 | 0.17 |
| 21.32 | 0.0469 | 0.029 | 0.94 | 20.33 | 0.0492 | 0.033 | 0.08 | 20.33 | 0.0492 | 0.034 | 0.10 |
| 10.34 | 0.0967 | 0.023 | 0.024 | 10.72 | 0.0933 | 0.012 | 0.85 | 10.37 | 0.0964 | 0.025 | 0.00 |
| 9.225 | 0.1084 | 0.032 | 0.46 | 9.302 | 0.1075 | 0.033 | 0.37 | 9.19 | 0.1088 | 0.034 | 0.49 |
| 7.587 | 0.1318 | 0.020 | 0.61 | 7.680 | 0.1302 | 0.020 | 0.52 | 7.536 | 0.1327 | 0.020 | 0.65 |
| 6.131 | 0.1631 | 0.024 | 0.25 | 6.039 | 0.1656 | 0.027 | 0.51 | 6.010 | 0.1664 | 0.029 | 0.61 |
| 5.252 | 0.1904 | 0.026 | 0.39 | 5.198 | 0.1924 | 0.024 | 0.51 | 5.219 | 0.1916 | 0.026 | 0.44 |
| 4.785 | 0.2090 | 0.031 | 0.96 | 4.762 | 0.2100 | 0.031 | 0.03 | 4.787 | 0.2089 | 0.033 | 0.95 |
| 3.644 | 0.2744 | 0.024 | 0.70 | 3.640 | 0.2747 | 0.024 | 0.72 | 3.636 | 0.2750 | 0.027 | 0.75 |
| 3.531 | 0.2832 | 0.023 | 0.91 | 3.516 | 0.2844 | 0.021 | 0.96 | 3.554 | 0.2814 | 0.025 | 0.81 |
| 2.876 | 0.3477 | 0.025 | 0.96 | 2.871 | 0.3483 | 0.026 | 1.00 | 2.874 | 0.3480 | 0.025 | 0.98 |
| Semi-Empirical Optimized Frequencies | ||||
|---|---|---|---|---|
| Possible Origin | () | () | (°C) | |
| Solar/Planetary | 760 | 760 | 0.3228 | 0.1711 |
| Solar/Planetary | 115 | 115 | 0.0585 | 0.4239 |
| Solar/Planetary | 61 | 61 | 0.0859 | 0.152 |
| Solar/Planetary | 20 | 20 | 0.0334 | 0.148 |
| Sun Spots | 10.4 | 10.4 | 0.0241 | 0.020 |
| Solar-Lunar tidal | 9.3 | 9.3 | 0.0265 | 0.497 |
| Solar/Planetary | 7.463 | 0.1340 | 0.0216 | 0.711 |
| Solar/Planetary | 6.003 | 0.1666 | 0.0272 | 0.617 |
| Solar/Planetary | 5.238 | 0.1909 | 0.0260 | 0.409 |
| Solar/Orbital | 4.795 | 0.2086 | 0.0326 | 0.931 |
| Solar/Orbital | 3.633 | 0.2752 | 0.0276 | 0.767 |
| Solar/Orbital | 3.556 | 0.2812 | 0.0254 | 0.792 |
| Solar/Orbital | 2.874 | 0.3480 | 0.0247 | 0.975 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scafetta, N. Reconstruction of the Interannual to Millennial Scale Patterns of the Global Surface Temperature. Atmosphere 2021, 12, 147. https://doi.org/10.3390/atmos12020147
Scafetta N. Reconstruction of the Interannual to Millennial Scale Patterns of the Global Surface Temperature. Atmosphere. 2021; 12(2):147. https://doi.org/10.3390/atmos12020147
Chicago/Turabian StyleScafetta, Nicola. 2021. "Reconstruction of the Interannual to Millennial Scale Patterns of the Global Surface Temperature" Atmosphere 12, no. 2: 147. https://doi.org/10.3390/atmos12020147
APA StyleScafetta, N. (2021). Reconstruction of the Interannual to Millennial Scale Patterns of the Global Surface Temperature. Atmosphere, 12(2), 147. https://doi.org/10.3390/atmos12020147





