Predicting the Effects of Solar Storms on the Ionosphere Based on a Comparison of Real-Time Solar Wind Data with the Best-Fitting Historical Storm Event
Abstract
:1. Introduction
2. Data
2.1. Solar Wind Measurements
2.2. Geomagnetic Indices
2.3. Global TEC Maps
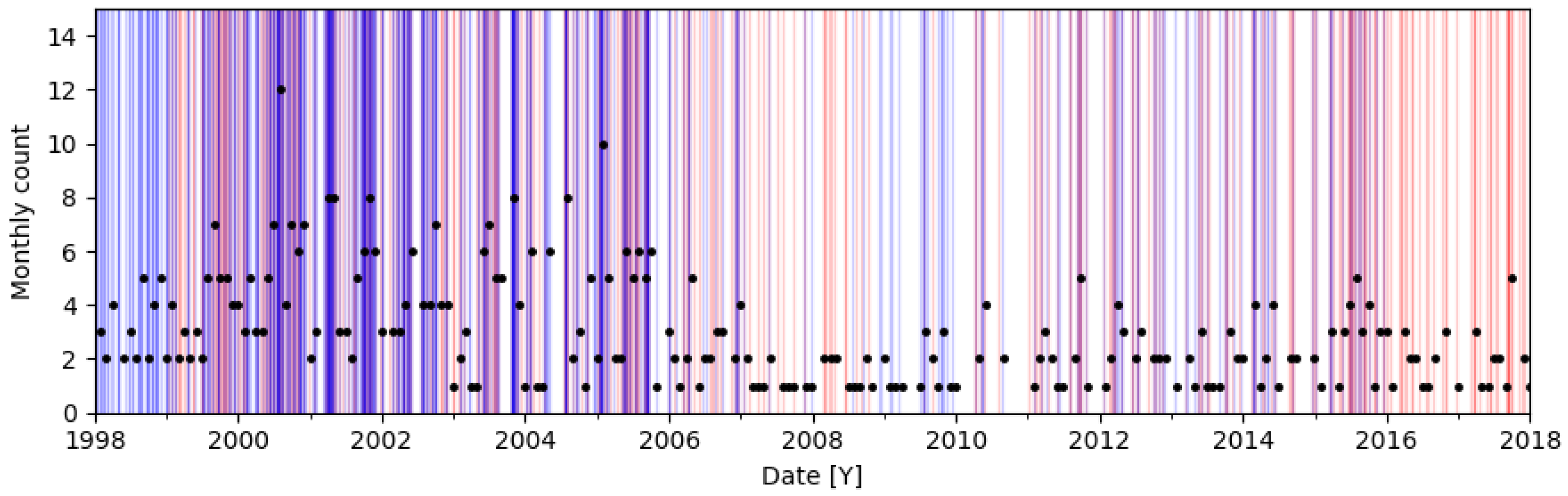
2.4. Reference Events
3. Modeling Approach
3.1. Solar Wind Monitoring
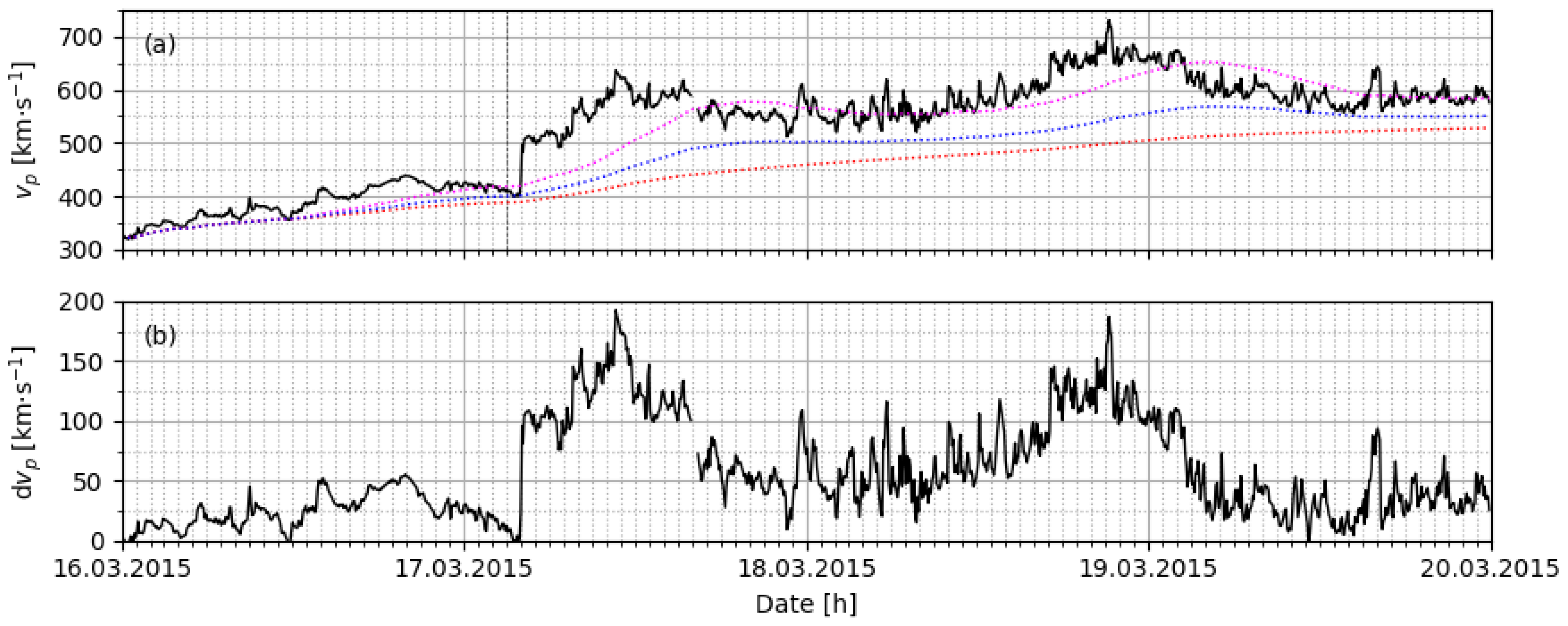
3.2. Event Reconstruction
3.3. dTEC Archive
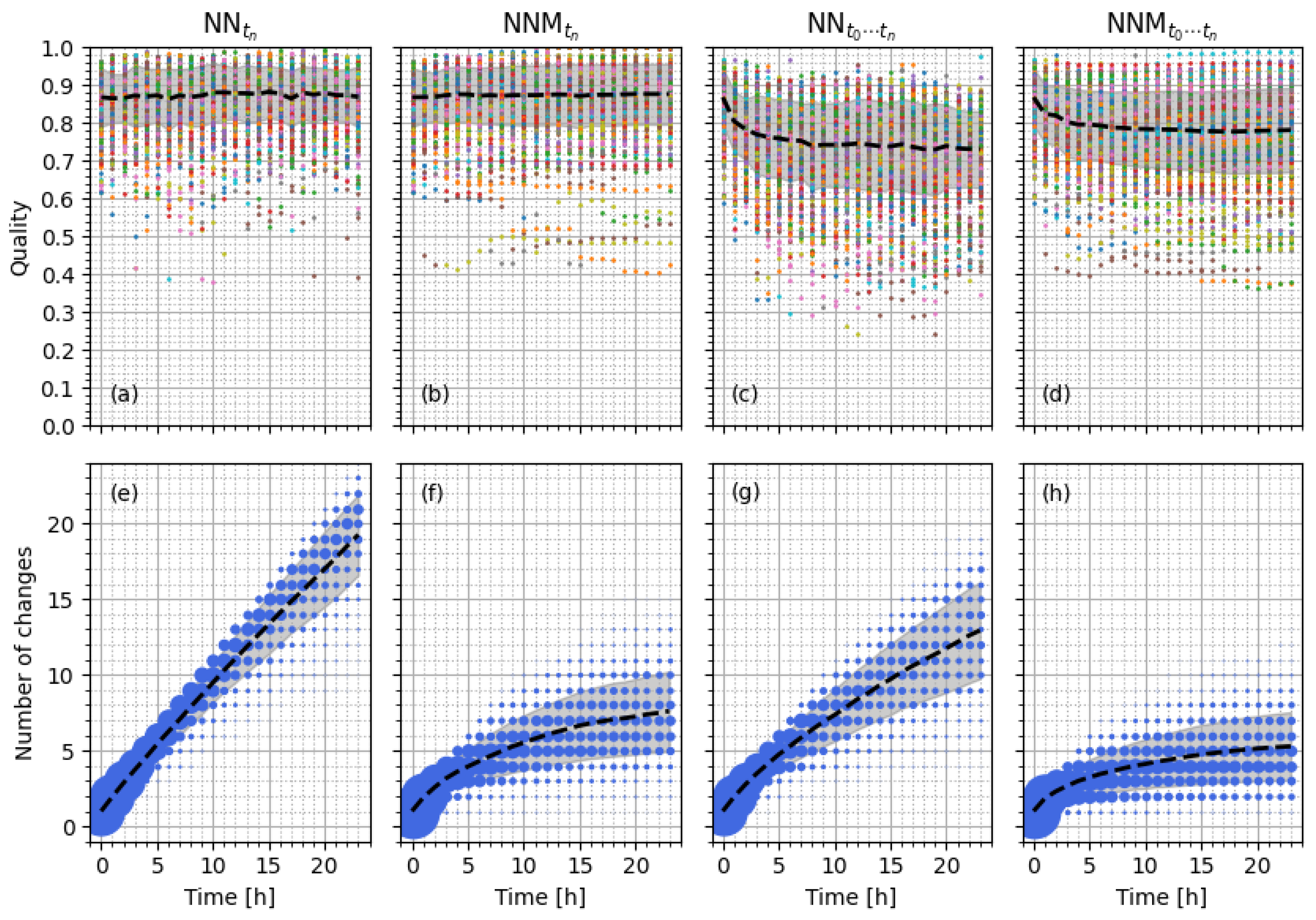
3.4. Quiet Condition Forecast
3.5. Storm Condition Forecast
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Milan, S.E.; Clausen, L.B.N.; Coxon, J.C.; Carter, J.A.; Walach, M.T.; Laundal, K.; Østgaard, N.; Tenfjord, P.; Reistad, J.; Snekvik, K.; et al. Overview of Solar Wind-Magnetosphere-Ionosphere-Atmosphere Coupling and the Generation of Magnetospheric Currents. Space Sci. Rev. 2017, 206, 547–573. [Google Scholar] [CrossRef]
- Borovsky, J.E.; Denton, M.H. Differences between CME-driven storms and CIR-driven storms. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Denton, M.H.; Borovsky, J.E.; Skoug, R.M.; Thomsen, M.F.; Lavraud, B.; Henderson, M.G.; McPherron, R.L.; Zhang, J.C.; Liemohn, M.W. Geomagnetic storms driven by ICME- and CIR-dominated solar wind. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Turner, N.E.; Cramer, W.D.; Earles, S.K.; Emery, B.A. Geoefficiency and energy partitioning in CIR-driven and CME-driven storms. J. Atmos. Sol.-Terr. Phys. 2009, 71, 1023–1031. [Google Scholar] [CrossRef]
- Yang, N.; Le, H.; Liu, L. Statistical analysis of the mid-latitude trough position during different categories of magnetic storms and different storm intensities. Earth Planets Space 2016, 68, 171–181. [Google Scholar] [CrossRef] [Green Version]
- Ogawa, Y.; Seki, K.; Keika, K.; Ebihara, Y. Characteristics of CME- and CIR-Driven Ion Upflows in the Polar Ionosphere. J. Geophys. Res. Space Phys. 2019, 124, 3637–3649. [Google Scholar] [CrossRef] [Green Version]
- Dugassa, T.; Habarulema, J.B.; Nigussie, M. Equatorial and low-latitude ionospheric TEC response to CIR-driven geomagnetic storms at different longitude sectors. Adv. Space Res. 2020, 66, 1947–1966. [Google Scholar] [CrossRef]
- Baker, D.N.; Daly, E.; Daglis, I.; Kappenman, J.G.; Panasyuk, M. Effects of Space Weather on Technology Infrastructure. Space Weather 2004, 2. [Google Scholar] [CrossRef]
- Balan, N.; Skoug, R.; Ram, S.T.; Rajesh, P.K.; Shiokawa, K.; Otsuka, Y.; Batista, I.S.; Ebihara, Y.; Nakamura, T. CME front and severe space weather. J. Geophys. Res. Space Phys. 2014, 119, 10041–10058. [Google Scholar] [CrossRef]
- Eastwood, J.P.; Biffis, E.; Hapgood, M.A.; Green, L.; Bisi, M.M.; Bentley, R.D.; Wicks, R.; McKinnell, L.A.; Gibbs, M.; Burnett, C. The Economic Impact of Space Weather: Where Do We Stand? Risk Anal. 2017, 37, 206–218. [Google Scholar] [CrossRef]
- Berdermann, J.; Borries, C.; Hoque, M.M.; Jakowski, N. Forecast of Total Electron Content over Europe for Disturbed Ionospheric Conditions. Available online: https://elib.dlr.de/80067/ (accessed on 14 December 2021).
- Borries, C.; Berdermann, J.; Jakowski, N.; Hoque, M.; Bothmer, V. Preparation of an advanced TEC forecast based on the statistical analysis of historical ionospheric storms. In Proceedings of the 4th International Galileo Science Colloquium, Prague, Czech Republic, 4–6 December 2013. [Google Scholar]
- Borries, C.; Berdermann, J.; Jakowski, N.; Wilken, V. Ionospheric storms-A challenge for empirical forecast of the total electron content. J. Geophys. Res. Space Phys. 2015, 120, 3175–3186. [Google Scholar] [CrossRef]
- Hoque, M.M.; Jakowski, N. A new global empirical NmF2 model for operational use in radio systems. Radio Sci. 2011, 46. [Google Scholar] [CrossRef]
- Jakowski, N.; Hoque, M.M.; Mayer, C. A new global TEC model for estimating transionospheric radio wave propagation errors. J. Geod. 2011, 85, 965–974. [Google Scholar] [CrossRef]
- Hoque, M.M.; Jakowski, N. A new global model for the ionospheric F2 peak height for radio wave propagation. Ann. Geophys. 2012, 30, 797–809. [Google Scholar] [CrossRef] [Green Version]
- Schrijver, C.J.; Kauristie, K.; Aylward, A.D.; Denardini, C.M.; Gibson, S.E.; Glover, A.; Gopalswamy, N.; Grande, M.; Hapgood, M.; Heynderickx, D.; et al. Understanding space weather to shield society: A global road map for 2015–2025 commissioned by COSPAR and ILWS. Adv. Space Res. 2015, 55, 2745–2807. [Google Scholar] [CrossRef]
- Heelis, R.A.; Maute, A. Challenges to Understanding the Earth’s Ionosphere and Thermosphere. J. Geophys. Res. Space Phys. 2020, 125. [Google Scholar] [CrossRef]
- Licata, R.J.; Tobiska, W.K.; Mehta, P.M. Benchmarking Forecasting Models for Space Weather Drivers. Space Weather 2020, 18, e2020SW002496. [Google Scholar] [CrossRef]
- Tsagouri, I.; Belehaki, A. A new empirical model of middle latitude ionospheric response for space weather applications. Adv. Space Res. 2006, 37, 420–425. [Google Scholar] [CrossRef]
- Tsagouri, I.; Belehaki, A. An upgrade of the solar-wind-driven empirical model for the middle latitude ionospheric storm-time response. J. Atmos. Sol.-Terr. Phys. 2008, 70, 2061–2076. [Google Scholar] [CrossRef]
- Tsagouri, I.; Belehaki, A. Ionospheric forecasts for the European region for space weather applications. J. Space Weather Space Clim. 2015, 5, A9. [Google Scholar] [CrossRef] [Green Version]
- Cesaroni, C.; Spogli, L.; Aragon-Angel, A.; Fiocca, M.; Dear, V.; Franceschi, G.D.; Romano, V. Neural network based model for global Total Electron Content forecasting. J. Space Weather Space Clim. 2020, 10, 11. [Google Scholar] [CrossRef]
- Liu, L.; Zou, S.; Yao, Y.; Wang, Z. Forecasting Global Ionospheric TEC Using Deep Learning Approach. Space Weather 2020, 18. [Google Scholar] [CrossRef]
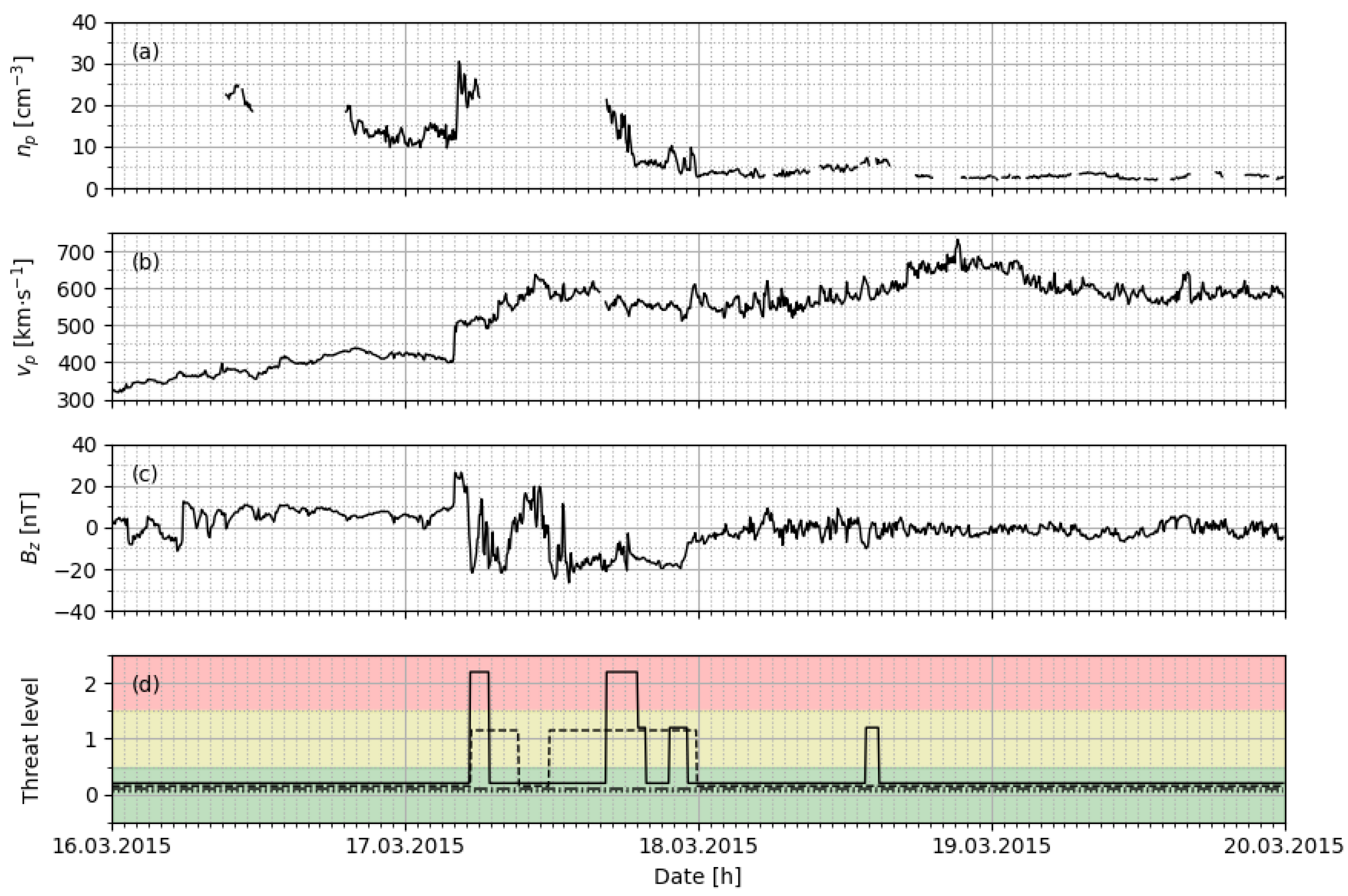
- Astafyeva, E.; Zakharenkova, I.; Förster, M. Ionospheric response to the 2015 St. Patrick’s Day storm: A global multi-instrumental overview. J. Geophys. Res. Space Phys. 2015, 120, 9023–9037. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.C.; Liou, K.; Lepping, R.P.; Hutting, L.; Plunkett, S.; Howard, R.A.; Socker, D. The first super geomagnetic storm of solar cycle 24: “The St. Patrick’s day event (17 March 2015) ”. Earth Planets Space 2016, 68, 151. [Google Scholar] [CrossRef] [Green Version]
- Krypiak-Gregorczyk, A. Ionosphere response to three extreme events occurring near spring equinox in 2012, 2013 and 2015, observed by regional GNSS-TEC model. J. Geod. 2018, 93, 931–951. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Kumar, V.V. Ionospheric Response to the St. Patrick’s Day Space Weather Events in March 2012, 2013, and 2015 at Southern Low and Middle Latitudes. J. Geophys. Res. Space Phys. 2019, 124, 584–602. [Google Scholar] [CrossRef] [Green Version]
- Stone, E.C.; Frandsen, A.M.; Mewaldt, R.A.; Christian, E.R.; Margolies, D.; Ormes, J.F.; Snow, F. The Advanced Composition Explorer. Space Sci. Rev. 1998, 86, 1–22. [Google Scholar] [CrossRef]
- Zwickl, R.D.; Doggett, K.A.; Sahm, S.; Barrett, W.P.; Grubb, R.N.; Detman, T.R.; Raben, V.J.; Smith, C.W.; Riley, P.; Gold, R.E.; et al. The NOAA Real-Time Solar-Wind (RTSW) System Using Ace Data. In The Advanced Composition Explorer Mission; Springer: Dordrecht, The Netherlands, 1998; pp. 633–648. [Google Scholar] [CrossRef]
- McComas, D.J.; Bame, S.J.; Barker, P.; Feldman, W.C.; Phillips, J.L.; Riley, P.; Griffee, J.W. Solar Wind Electron Proton Alpha Monitor (SWEPAM) for the Advanced Composition Explorer. In The Advanced Composition Explorer Mission; Springer: Dordrecht, The Netherlands, 1998; pp. 563–612. [Google Scholar] [CrossRef]
- Burt, J.; Smith, B. Deep Space Climate Observatory: The DSCOVR mission. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012. [Google Scholar] [CrossRef]
- Garrard, T.L.; Davis, A.J.; Hammond, J.S.; Sears, S.R. The ACE Science Center. Space Sci. Rev. 1998, 86, 649–663. [Google Scholar] [CrossRef]
- ASC. ACE Level 2 (Verified) Data. 2021. Available online: http://www.srl.caltech.edu/ACE/ASC/level2/index.html (accessed on 16 August 2021).
- NCEI. DSCOVR Space Weather Data Portal. 2021. Available online: https://www.ngdc.noaa.gov/dscovr/portal/index.html (accessed on 16 August 2021).
- Gonzalez, W.D.; de Gonzalez, A.L.C.; Lago, A.D.; Tsurutani, B.T.; Arballo, J.K.; Lakhina, G.K.; Buti, B.; Ho, C.M.; Wu, S.T. Magnetic cloud field intensities and solar wind velocities. Geophys. Res. Lett. 1998, 25, 963–966. [Google Scholar] [CrossRef] [Green Version]
- Verbanac, G.; Živković, S.; Vršnak, B.; Bandić, M.; Hojsak, T. Comparison of geoeffectiveness of coronal mass ejections and corotating interaction regions. Astron. Astrophys. 2013, 558, A85. [Google Scholar] [CrossRef] [Green Version]
- Adachi, H.; Sakurai, T.; Marubashi, K. Geomagnetic effects of high-density plasma with southward magnetic field in the interplanetary coronal mass ejection observed on 2–3 May 1998. Earth Planets Space 2006, 58, 315–322. [Google Scholar] [CrossRef] [Green Version]
- Mayaud, P.N. Derivation, Meaning, and Use of Geomagnetic Indices; American Geophysical Union: Washington, DC, USA, 1980. [Google Scholar] [CrossRef]
- Sugiura, M.; Kamei, T. Equatorial Dst index 1957–1986. In IAGA Bull. 40; Berthelier, A., Menvielle, M., Eds.; International Service of Geomagnetic Indices: Saint-Maur-des-Fosses, France, 1991. [Google Scholar]
- Nose, M.; Sugiura, M.; Kamei, T.; Iyemori, T.; Koyama, Y. Dst Index. 2015. Available online: https://isds-datadoi.nict.go.jp/wds/10.17593__14515-74000.html (accessed on 16 August 2021). [CrossRef]
- WDC. Geomagnetic Equatorial Dst Index. 2021. Available online: http://wdc.kugi.kyoto-u.ac.jp/dstdir/ (accessed on 16 August 2021).
- Valdivia, J.A.; Sharma, A.S.; Papadopoulos, K. Prediction of magnetic storms by nonlinear models. Geophys. Res. Lett. 1996, 23, 2899–2902. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.G.; Lundstedt, H. Prediction of geomagnetic storms from solar wind data using Elman Recurrent Neural Networks. Geophys. Res. Lett. 1996, 23, 319–322. [Google Scholar] [CrossRef]
- O’Brien, T.P.; McPherron, R.L. Forecasting the ring current index Dst in real time. J. Atmos. Sol.-Terr. Phys. 2000, 62, 1295–1299. [Google Scholar] [CrossRef]
- Temerin, M.; Li, X. A new model for the prediction of Dst on the basis of the solar wind. J. Geophys. Res. Space Phys. 2002, 107, SMP 31-1–SMP 31-8. [Google Scholar] [CrossRef]
- Kim, R.S.; Moon, Y.J.; Gopalswamy, N.; Park, Y.D.; Kim, Y.H. Two-step forecast of geomagnetic storm using coronal mass ejection and solar wind condition. Space Weather 2014, 12, 246–256. [Google Scholar] [CrossRef] [Green Version]
- Bartels, J. The standardized index Ks and the planetary index Kp. IATME Bulletin 12b. 1949. Available online: http://isgi.unistra.fr/IAGABulletins/IATME_Bulletin_12b_Herbert_Weisman_Bartels_1949.pdf (accessed on 14 December 2021).
- Bartels, J.; Veldkamp, J. International data on magnetic disturbances, fourth quarter, 1953. J. Geophys. Res. 1954, 59, 297–302. [Google Scholar] [CrossRef]
- Chambodut, A.; Marchaudon, A.; Menvielle, M.; Mazouz, F.E.L.; Lathuillére, C. The K -derived MLT sector geomagnetic indices. Geophys. Res. Lett. 2013, 40, 4808–4812. [Google Scholar] [CrossRef] [Green Version]
- GFZ. Geomagnetic Kp Index. 2021. Available online: https://www.gfz-potsdam.de/kp-index/ (accessed on 16 August 2021).
- Boberg, F.; Wintoft, P.; Lundstedt, H. Real time Kp predictions from solar wind data using neural networks. Phys. Chem. Earth Part C Solar Terr. Planet. Sci. 2000, 25, 275–280. [Google Scholar] [CrossRef]
- Wintoft, P.; Wik, M.; Matzka, J.; Shprits, Y. Forecasting Kp from solar wind data: Input parameter study using 3-hour averages and 3-hour range values. J. Space Weather Space Clim. 2017, 7, A29. [Google Scholar] [CrossRef] [Green Version]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- NASA. GNSS Atmospheric Products. 2021. Available online: https://cddis.nasa.gov/archive/gnss/products/ionex/ (accessed on 16 August 2021).
- Kriegel, M.; Berdermann, J. Ionosphere Monitoring and Prediction Center. In Proceedings of the 2020 European Navigation Conference (ENC), Dresden, Germany, 23–24 November 2020. [Google Scholar] [CrossRef]
- Jian, L.; Russell, C.T.; Luhmann, J.G.; Skoug, R.M. Properties of Interplanetary Coronal Mass Ejections at One AU During 1995 - 2004. Sol. Phys. 2006, 239, 393–436. [Google Scholar] [CrossRef] [Green Version]
- Jian, L.; Russell, C.T.; Luhmann, J.G.; Skoug, R.M. Properties of Stream Interactions at One AU during 1995–2004. Sol. Phys. 2006, 239, 337–392. [Google Scholar] [CrossRef] [Green Version]
- Jian, L.; Russell, C.T.; Luhmann, J.G. Comparing Solar Minimum 23/24 with Historical Solar Wind Records at 1 AU. Sol. Phys. 2011, 274, 321–344. [Google Scholar] [CrossRef] [Green Version]
- Pick, L.; Effenberger, F.; Zhelavskaya, I.; Korte, M. A Statistical Classifier for Historical Geomagnetic Storm Drivers Derived Solely From Ground-Based Magnetic Field Measurements. Earth Space Sci. 2019, 6, 2000–2015. [Google Scholar] [CrossRef] [Green Version]
- Codrescu, S.M.; Codrescu, M.V.; Fedrizzi, M. An Ensemble Kalman Filter for the Thermosphere-Ionosphere. Space Weather 2018, 16, 57–68. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Evensen, G. Data Assimilation; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Rand, D.; Young, L.S. (Eds.) Dynamical Systems and Turbulence, Warwick 1980; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar] [CrossRef]
- Hamilton, F.; Berry, T.; Sauer, T. Ensemble Kalman Filtering without a Model. Phys. Rev. X 2016, 6, 011021. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, F.; Berry, T.; Sauer, T. Kalman-Takens filtering in the presence of dynamical noise. Eur. Phys. J. Spec. Top. 2017, 226, 3239–3250. [Google Scholar] [CrossRef] [Green Version]
- Jankovičovà, D.; Vörös, Z.; Šimkanin, J. The influence of solar wind turbulence on geomagnetic activity. Nonlinear Process. Geophys. 2008, 15, 53–59. [Google Scholar] [CrossRef]
- Thomsen, M.F. Why Kp is such a good measure of magnetospheric convection. Space Weather 2004, 2. [Google Scholar] [CrossRef]
- Şentürk, E. Statistical Analysis of Storm-time TEC Variation during Ascending and Descending Solar Periods of 24th Solar Cycle. Geomagn. Aeron. 2021, 61, 277–286. [Google Scholar] [CrossRef]
- Schwenn, R. Heliospheric 3D structure and CME propagation as seen from SOHO: Recent lessons for space weather predictions. Adv. Space Res. 2000, 26, 43–53. [Google Scholar] [CrossRef]
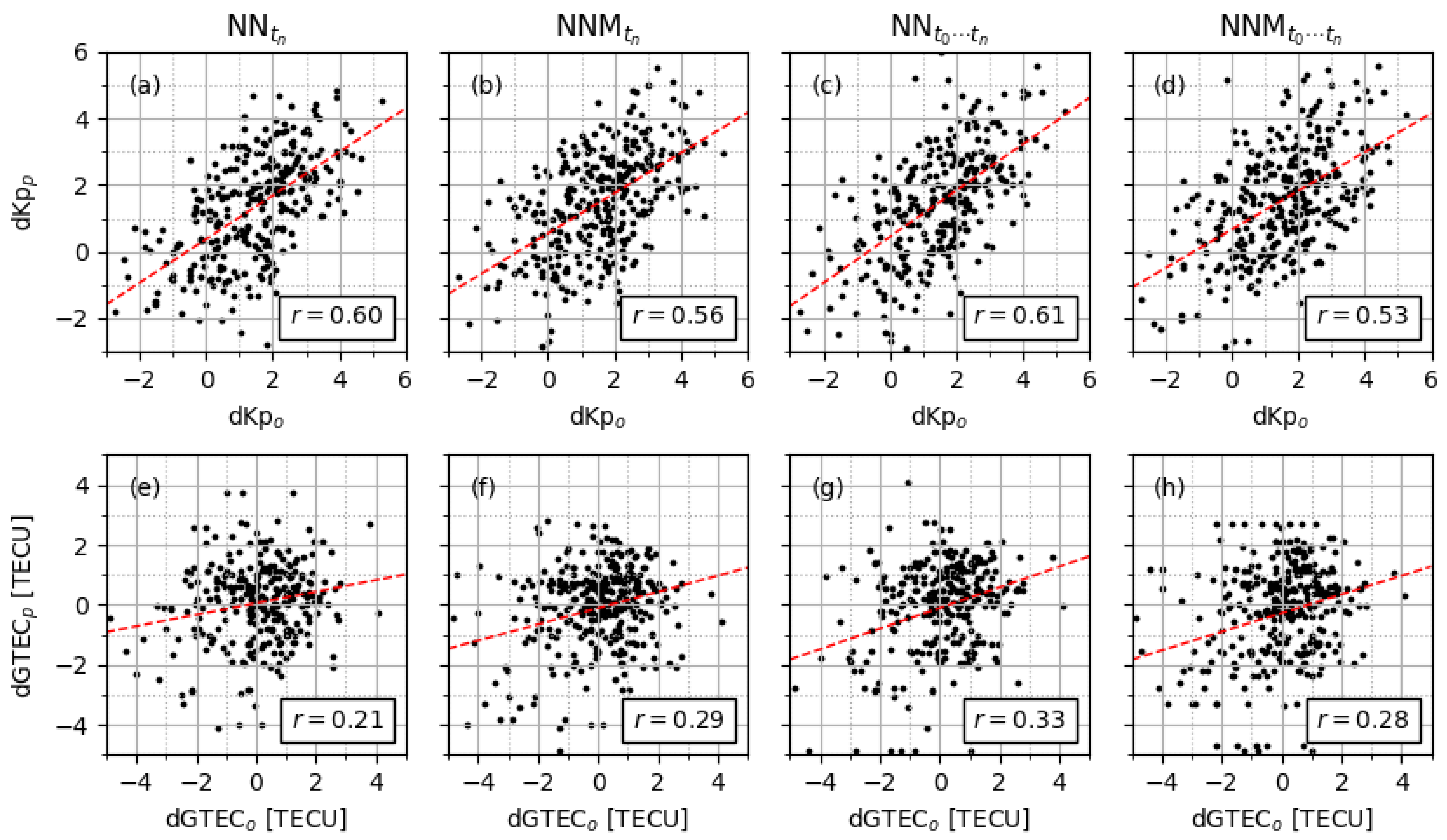
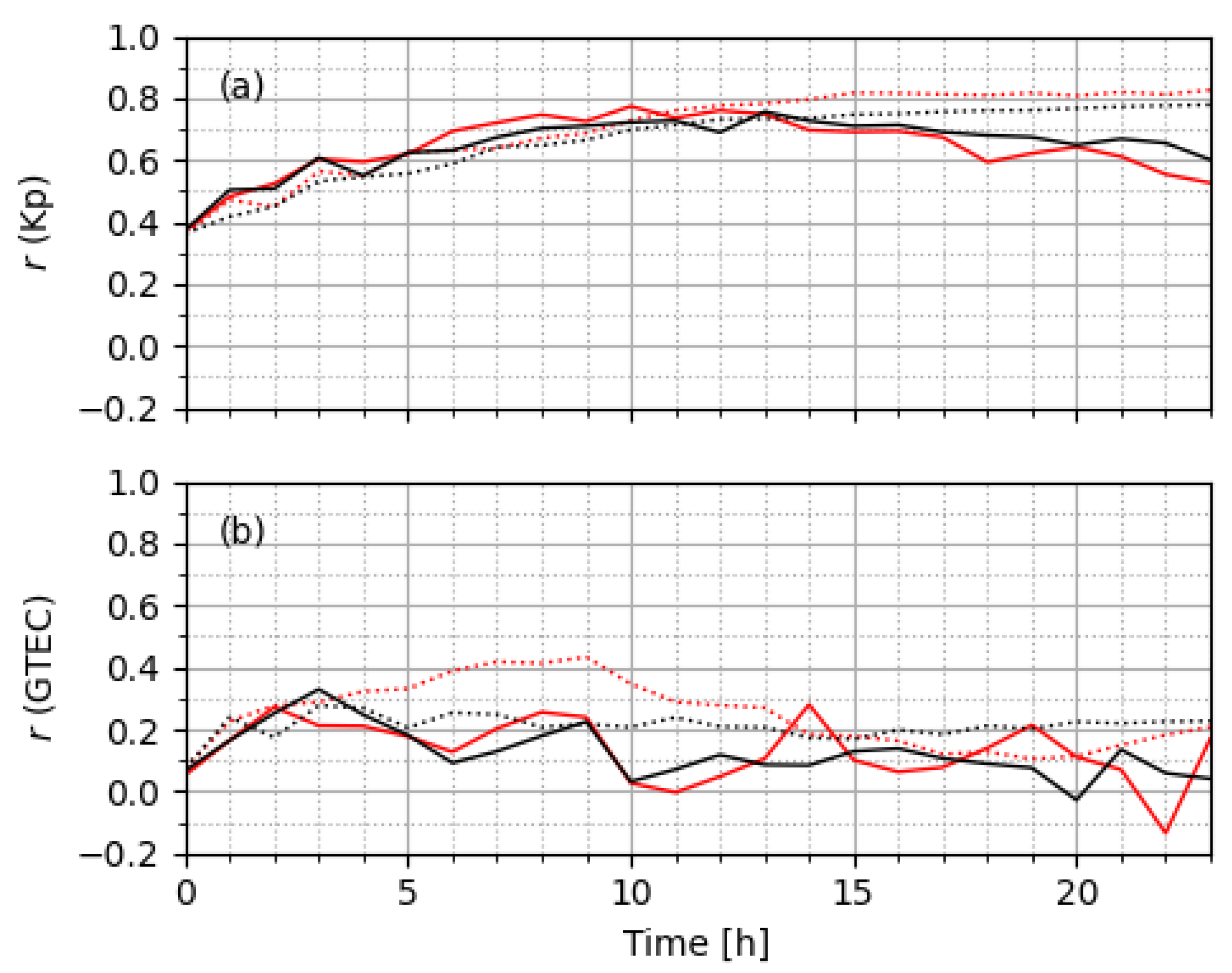


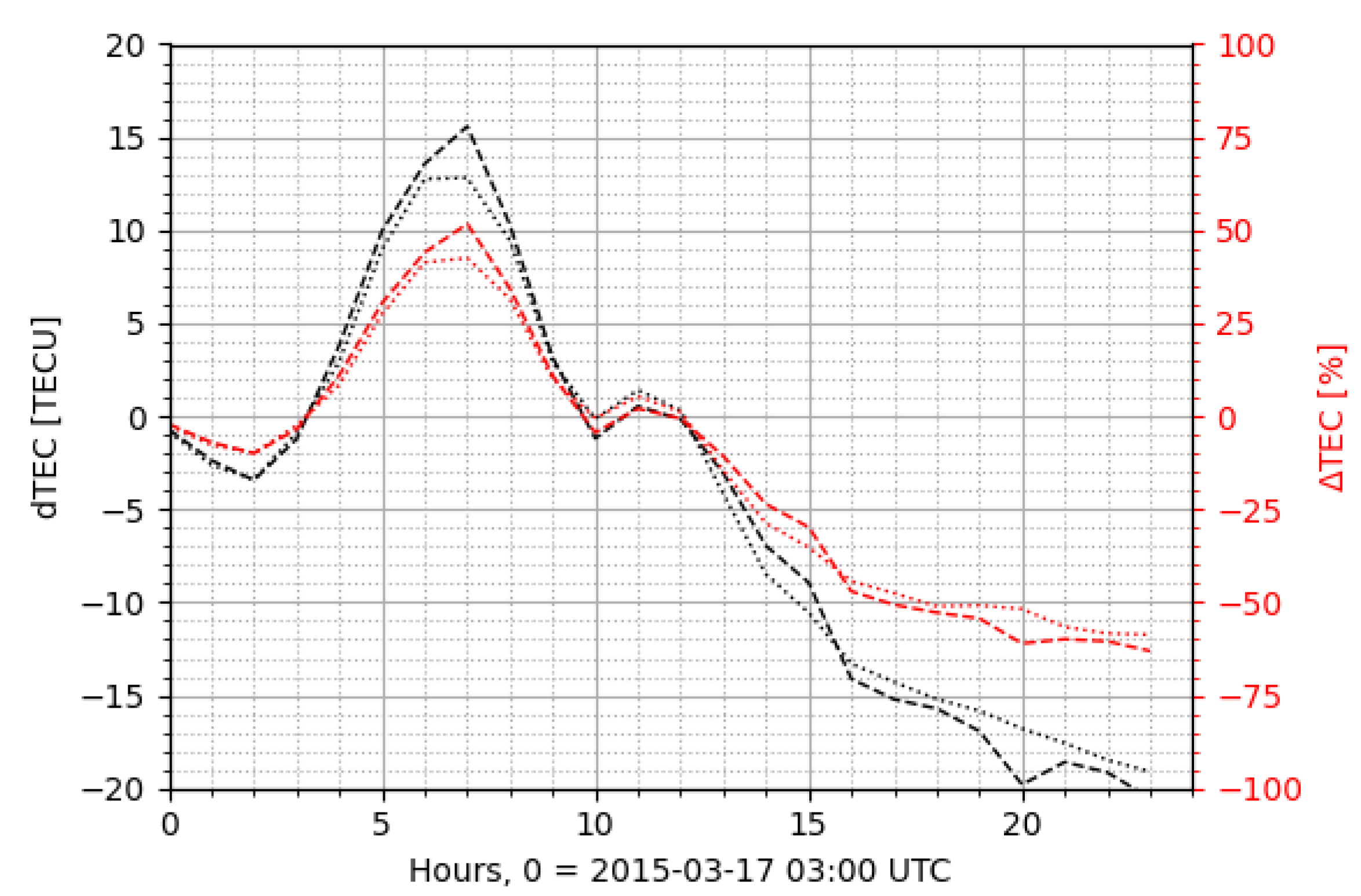
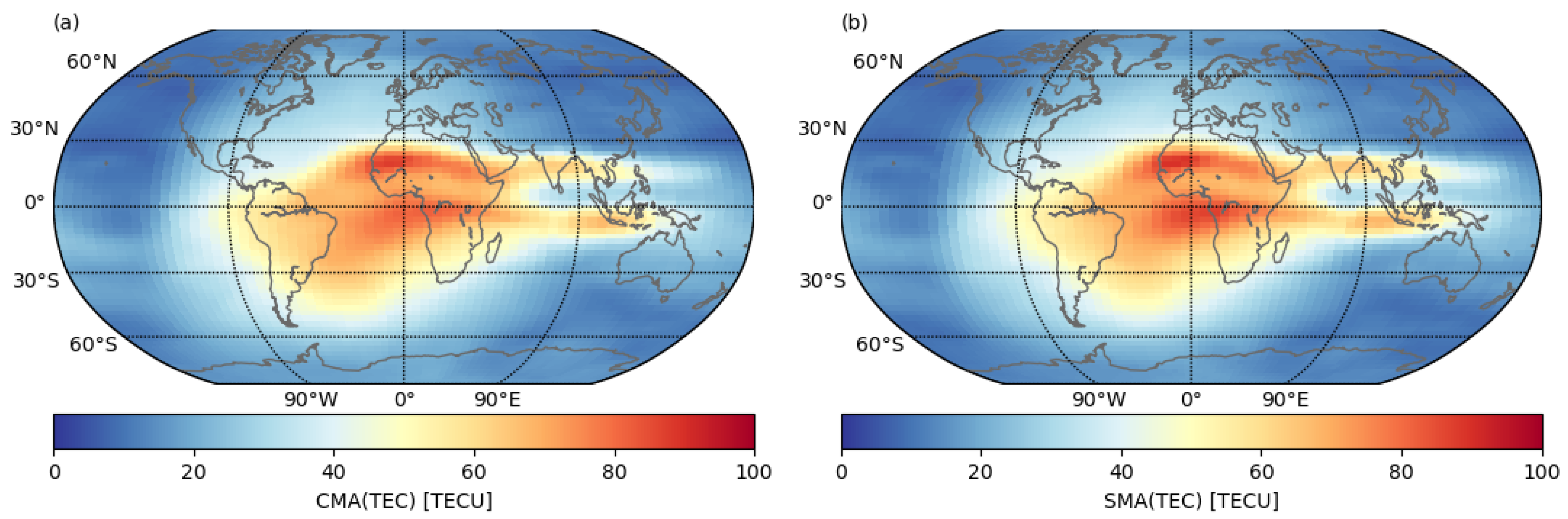
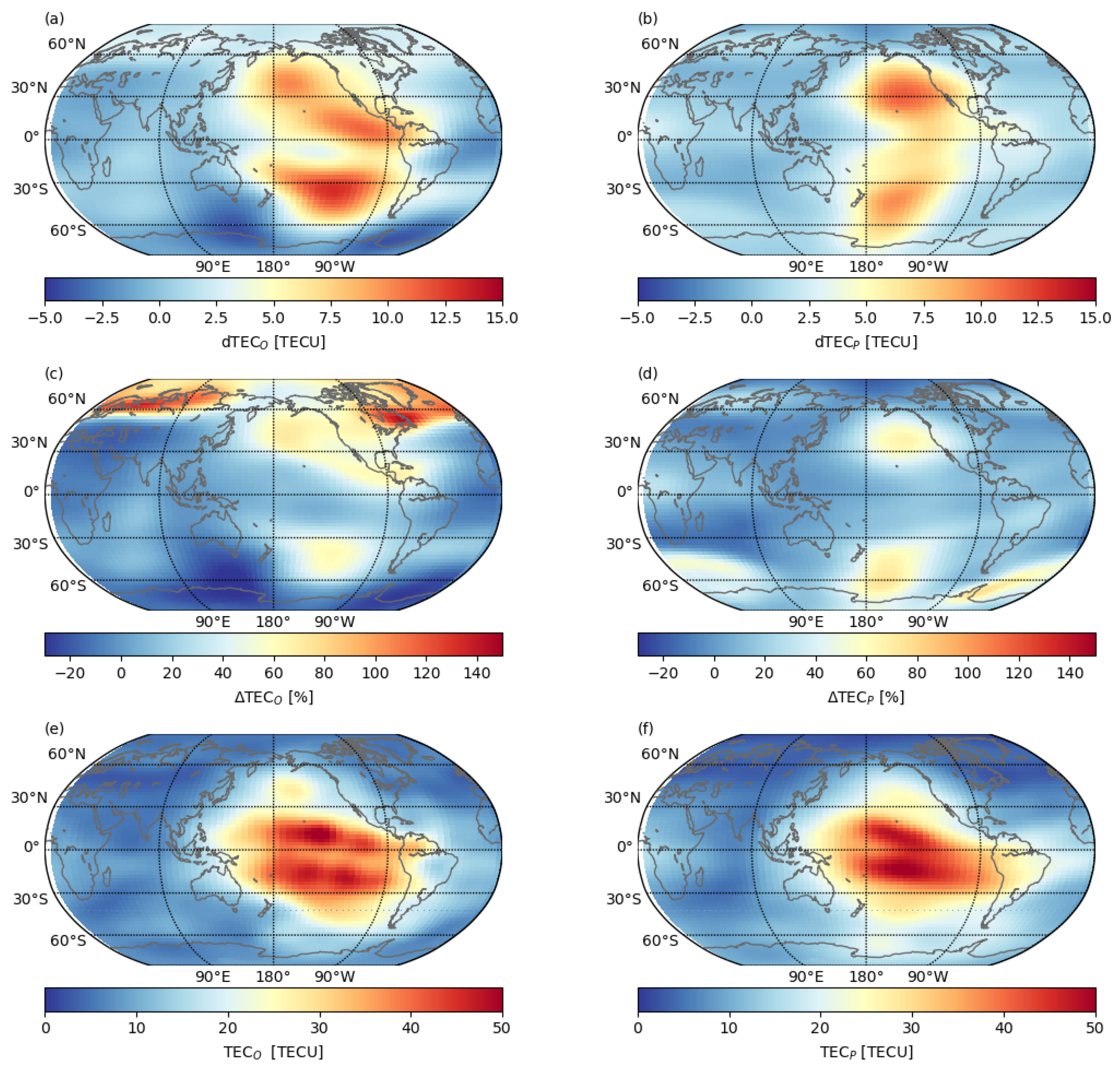
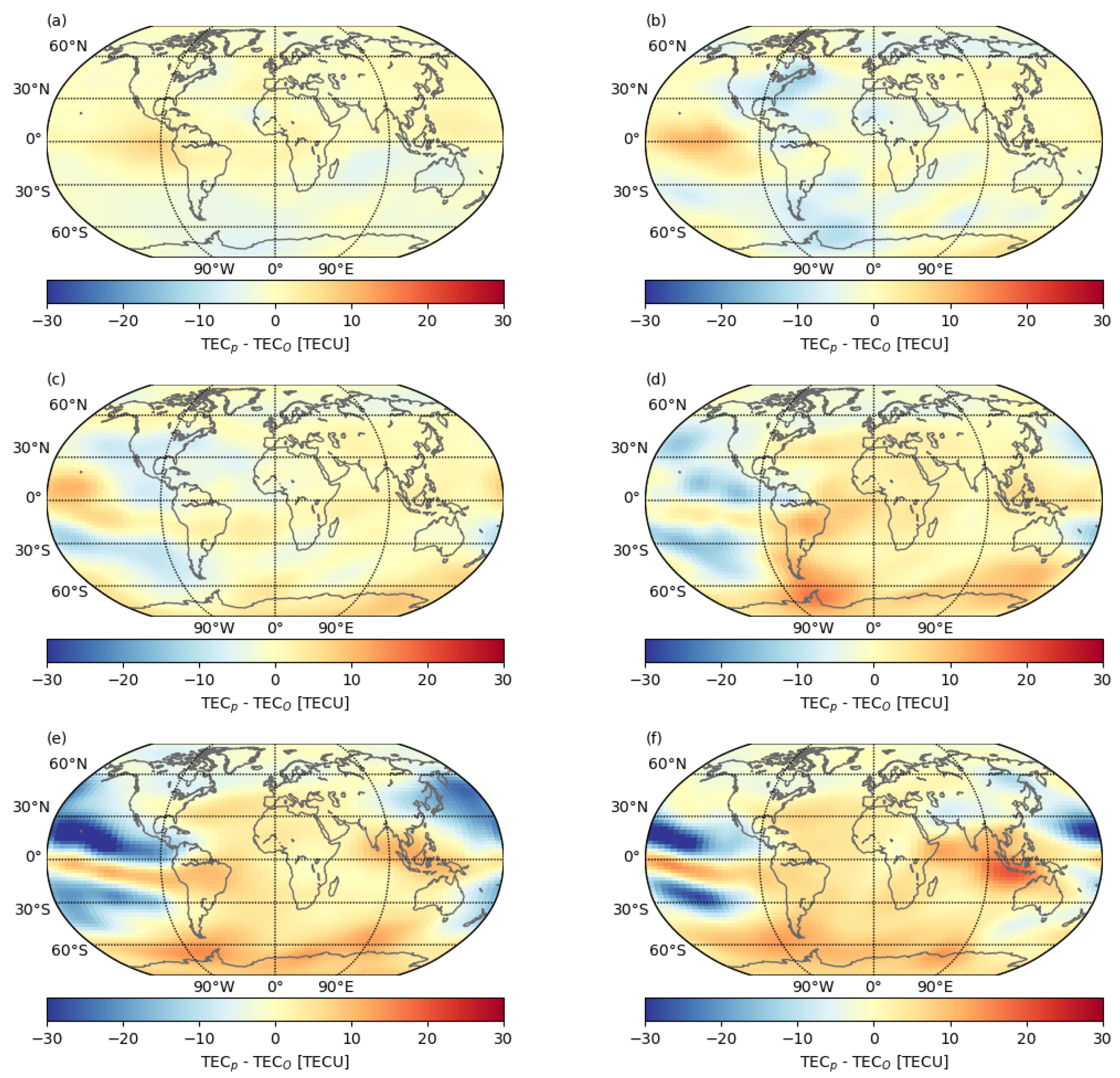
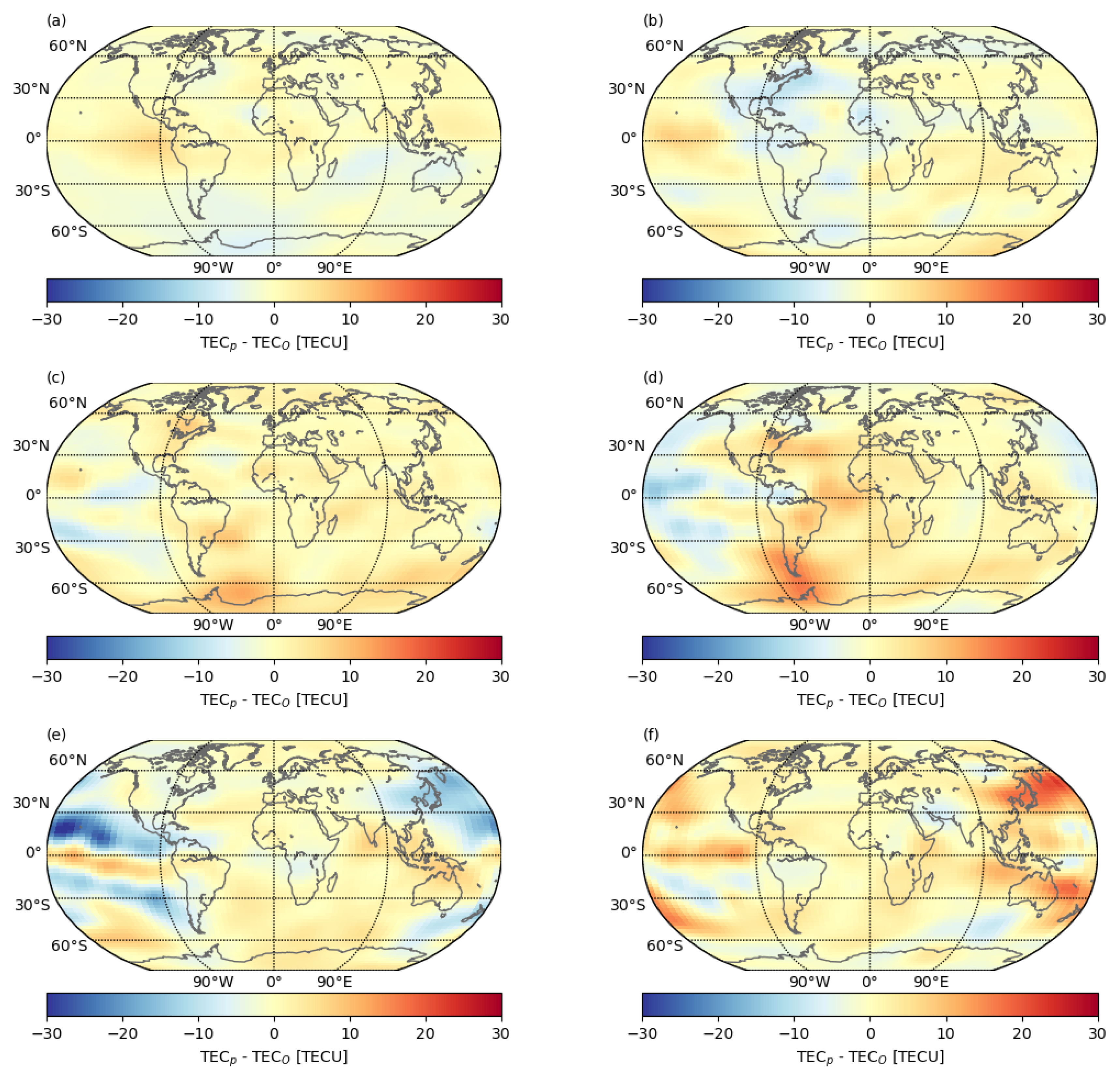
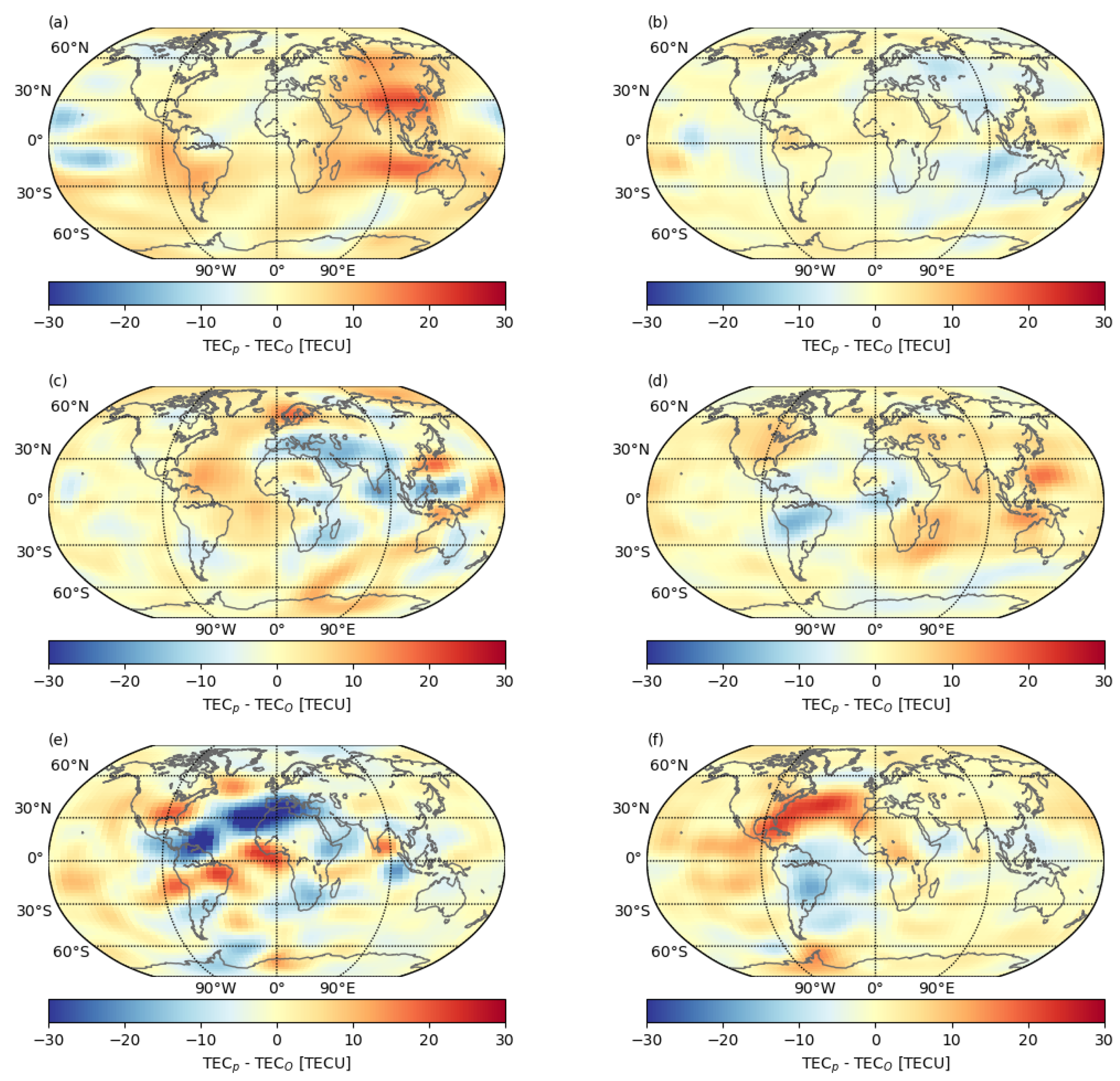
| Parameter | Threshold 1 | Threshold 2 |
|---|---|---|
| Proton density | 40 cm | 60 cm |
| Proton speed | 800 km·s | 1000 km·s |
| North-South IMF | −15 nT | −50 nT |
| Dynamic pressure | 10 nPa | 50 nPa |
| Effective pressure | 2 nPa | 3 nPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmölter, E.; Berdermann, J. Predicting the Effects of Solar Storms on the Ionosphere Based on a Comparison of Real-Time Solar Wind Data with the Best-Fitting Historical Storm Event. Atmosphere 2021, 12, 1684. https://doi.org/10.3390/atmos12121684
Schmölter E, Berdermann J. Predicting the Effects of Solar Storms on the Ionosphere Based on a Comparison of Real-Time Solar Wind Data with the Best-Fitting Historical Storm Event. Atmosphere. 2021; 12(12):1684. https://doi.org/10.3390/atmos12121684
Chicago/Turabian StyleSchmölter, Erik, and Jens Berdermann. 2021. "Predicting the Effects of Solar Storms on the Ionosphere Based on a Comparison of Real-Time Solar Wind Data with the Best-Fitting Historical Storm Event" Atmosphere 12, no. 12: 1684. https://doi.org/10.3390/atmos12121684
APA StyleSchmölter, E., & Berdermann, J. (2021). Predicting the Effects of Solar Storms on the Ionosphere Based on a Comparison of Real-Time Solar Wind Data with the Best-Fitting Historical Storm Event. Atmosphere, 12(12), 1684. https://doi.org/10.3390/atmos12121684






