Abstract
Ground based rainfall information is hardly available in most high mountain areas of the world due to the remoteness and complex topography. Thus, proper understanding of spatio-temporal rainfall dynamics still remains a challenge in those areas. Satellite-based rainfall products may help if their rainfall assessment are of high quality. In this paper, microwave-based integrated multi-satellite retrieval for the Global Precipitation Measurement (GPM) (IMERG) (MW-based IMERG) was assessed along with the random-forest-based rainfall (RF-based rainfall) and infrared-only IMERG (IR-only IMERG) products against the quality-controlled rain radar network and meteorological stations of high temporal resolution over the Pacific coast and the Andes of Ecuador. The rain area delineation and rain estimation of each product were evaluated at a spatial resolution of 11 km2 and at the time of MW overpass from IMERG. The regionally calibrated RF-based rainfall at 2 km2 and 30 min was also investigated. The validation results indicate different essential aspects: (i) the best performance is provided by MW-based IMERG in the region at the time of MW overpass; (ii) RF-based rainfall shows better accuracy rather than the IR-only IMERG rainfall product. This confirms that applying multispectral IR data in retrieval can improve the estimation of rainfall compared with single-spectrum IR retrieval algorithms. (iii) All of the products are prone to low-intensity false alarms. (iv) The downscaling of higher-resolution products leads to lower product performance, despite regional calibration. The results show that more caution is needed when developing new algorithms for satellite-based, high-spatiotemporal-resolution rainfall products. The radar data validation shows better performance than meteorological stations because gauge data cannot correctly represent spatial rainfall in complex topography under convective rainfall environments.
1. Introduction
Understanding precipitation amounts and patterns is essential for sustainable water management and monitoring the hydrological cycle [1]. In complex mountainous regions characterized by high spatiotemporal variability, coarse networks of operational precipitation gauge stations are often lacking. The spatiotemporal variability, combined with lack of gauge data, makes the time series and area-averaged rainfall analysis more complicated in these regions [2]. This also applies to the complex topography of the Andes in Ecuador.
Early satellite-based rainfall retrieval efforts estimated rainfall from geostationary infrared (IR) data, using the indirect relationship between precipitation rate and the temperature of cloud on top [3]. Hence, the algorithms and the product accuracy were limited to the top of the cloud’s characteristics. Unlike IR, microwave (MW) sensors measure thermal radiance from actual precipitation particles in the clouds; consequently, MW retrieval generally provides superior precipitation information [4].
A recent result of the continuous technological improvement of low-Earth-orbiting passive MW satellites and spaceborne radars in the MW band is the Global Precipitation Measurement (GPM) mission [5]. GPM was launched in 2014 as post Tropical Rainfall Measuring Mission (TRMM) [6]. Compared with TRMM, the GPM improved sensitivity to light precipitation and distribution of rain and snow. These improvements have achieved by a two-frequencies precipitation radar (Ku band (13.6 GHz) and Ka-band (35.5 GHz)) as well as the GPM multi-channel microwave imager (GMI) that accommodates higher spectral resolution at frequencies of 10.65, 18.7, 23.8, 26.5, 89, 165.5, and 183.3 GHz [5,7,8].
However, several studies showed that machine learning could improved the regionally calibrated retrievals using simply passive IR data from geostationary orbit (GEO) [3,8,9,10,11,12,13]. Compared to the passive MW and radar sensors, the GEO systems provide the high temporal (10–30 min) and spatial (2–4 km2) resolution. It is essential to capture the short-term characteristics of rainfall systems in the retrieval [8]
A few studies have investigated the performance of satellite-based rainfall products over Ecuadorian areas. The Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks (PERSIANN) [14] shows low agreement with rain gauge in daily resolution [2] in rain area detection. Manz et al. [15] investigated the performance of the integrated multi-satellite retrievals for GPM (IMERG) [5] and TRMM multi-satellite precipitation analysis (TMPA) [6] against gauge data with different temporal resolutions (hourly, 3 h, and daily). In their study, IMERG showed better agreement than TMPA, especially on the high elevation of Andes. Erazo et al. [16] reported that at high elevations in the Andes, TRMM 3B43 Version 7 retrievals showed a higher correlation (R2 = 0.82) on monthly compared with interpolated gauge data at a spatial resolution of 27.75 km2. The result of the validation of the regionally developed algorithm in Ecuador, the random forest-based rainfall (RF-based rainfall) of Turini et al. [3] with an 11 km2 resolution, obtained a median Heike skill score (HSS) around 0.35 for daily gauge stations, meanwhile the lower performance of the IR-only from the IMERG (IR-only IMERG) showed by HSS = 0.2. In their method, they used the Random forest algorithm to retrieve rainfall. In this text, the RF-based rainfall stands for the rainfall retrieval from random forest algorithm [3]. The RF-based rainfall retrieval performed in estimating the rainfall rate with correlation coefficient (r) values 0.34 [3].
To improve satellite-based products’ overall performance, understanding the sources of error on the highest possible temporal resolution is crucial [6,17]. Given the high spatiotemporal variability of rainfall in Ecuador, spatiotemporally high-resolution validation sources for rainfall are lacking. Therefore, as stated before, only a couple of studies have investigated the performance of satellite-based rainfall products at higher spatiotemporal resolution [15,18].
Different studies have found that, due to the variability of weather and climate in complex terrain, the satellite retrievals are posed to challenges both in IR and MW products [3,8,12,13,19]. Dinku et al. [19] evaluated the impact of topography on IR-based Tropical Applications of Meteorology using Satellite and ground-based observation (TAMSAT) [20] in East Africa for 1998–2012, comprising five different countries: Uganda, Kenya, Tanzania, Rwanda, and Burundi. In the study, the elevation varied between 1500 and 4500 m [19]. TAMSAT showed an underestimation. Dinku et al. [19] argued that the underestimation corresponded mainly to convective and orographic rainfall during the rainy season (March, April, and May), mostly in the windward exposition.
In this work, we aimed to validate different satellite-based rainfall products to identify and understand sources of errors in the complex elevation of the Andes in Ecuador on a sub-daily time scale. Our aim was not just to compare satellite-based rainfall products with ground measurements but also to identify the sources of the differences between the satellite-based rainfall products and ground measurements. Therefore, in this study, we evaluated the performance of MW-based IMERG in comparison with RF-based rainfall and IR-only IMERG against high-spatiotemporal-resolution data from ground based radar network and high temporal resolution of meteorological stations to characterize the impact of climatic and topographic conditions on satellite-based rainfall products at the time of MW overpass. We also assessed the performance of regionally trained RF-based rainfall in Ecuador on the subdaily time scale (30 min) and high spatial resolution (2 km2) with the aim of finding the source of possible errors for further development. Following a description of the climatology of the study area, the satellite-based rainfall products, ground based radar data and meteorological stations are described in Section 2.1. Section 2.2 introduces the evaluation methodology with a focus on rain area detection and rain estimation. The results are presented in Section 3 and discussed in Section 4. Finally, the important findings are summarized in Section 5.
2. Materials and Methods
2.1. Data
2.1.1. Radar
In the current study, the data from two rainfall radars, which are part of the Radarnet-Sur network in Southern Ecuador, were used. The westernmost radar system is located on Cerro Guachaurco (3100 m above sea level (m.a.s.l) (GUAXX radar)). Another radar system is located at 4450 m.a.s.l (to the best of our knowledge, this is the highest worldwide) on the Paragüillas peak on the north border of the Cajas National Park in Southern Ecuador (CAXX radar). The radars have a maximum range of 100 km2 and provide images with spatial resolutions of 500 m every 5 min. For more information about the Radarnet-Sur network (Figure 1a) infrastructure, please refer to Bendix et al. [21]. The coverage of radars in this study is shown in Figure 1a.
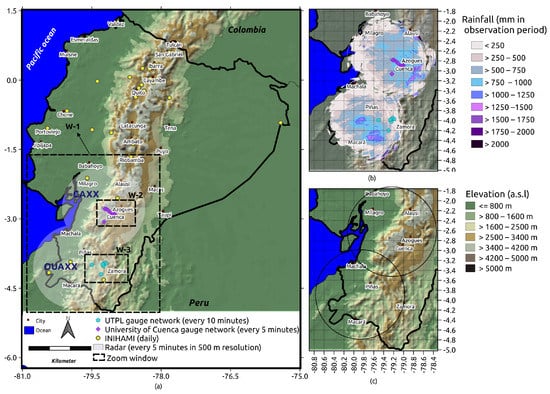
Figure 1.
The distribution of (a) meteorological stations (19 April 2017 to 28 February 2018) and spatial coverage of radars (GUAXX: 16 June 2017 to 1 February 2018; CAXX: 19th April 2017 to 1 July 2017) used in this study, (b) the radars in the study period (GUAXX: 16 June 2017 to 1 February 2018; CAXX: 19th April 2017 to 1 July 2017). For validation purposes, we excluded the radar data in the very near range (<10 km distance from the radar site) to avoid contamination through noise. We also excluded the far range >50 km due to possible attenuation errors. Nevertheless, we show the rainfall amount in the entire radar range for better illustration. The extent of study area is shown in windows (W)-1. (c) Spatial distribution of the elevation in the radar coverage area. W-2 and W-3 rectangles outline the extent of Figure 2a,b.
Radarnet-Sur calibration strategies have been continuously developed since 2006. The calibration strategy is based on a statistical procedure that uses the available rain gauge data. The data processing and correction algorithms in this empirical calibration consisted of four steps: (i) clutter and noise removal; (ii) atmospheric and geometric attenuation correction; (iii) interpolation of blind sectors; (vi) application of the empirically derived daily variable Z/R relationship. In this equation Z means radar reflectivity factor and R stands for rainfall intensity. For more information about the calibration algorithm, please refer to [22]. The final product from the radars used a blending technique for overlapping areas and temporal data gaps were completed using additional data from the rain gauges. For further information about the extended calibration strategy, please refer to [23].
The observed rainfall data from the radars were quality-controlled for detecting possible inconsistencies and selecting high-quality data. All the scenes from the radars were visually inspected. For this, the gauge data from the National Institute of Meteorology and Hydrology (INAMHI) (daily), the Universidad TécnicaParticular de Loja (UTPL) gauge network (10 min resolution), and the Cuenca University gauge network were used as references. The scenes in which there were no rain in the radar but rain in each of the gauges and vice versa were removed. Additionally, obviously failed recordings were manually removed. Furthermore, we used the infrared channel IR 3.9 from GOES-16 to detect the movement of cold clouds and radar rainfall rate. Although we have enough data available in our observation period, electronic technical problems and other issues caused data failure.
We delivered the final products of radar reflectivity and rainfall rate after attenuation and clutter correction for the time period between April 2017 and the end of January 2018 (GUAXX: 16 June 2017 to 1 February 2018; CAXX: 19 April 2017 to 1 July 2017). The reflectivity ranged from −31.5 to 91.5 dBZ with a total of 256 possible values.
The spatial distribution of the sum of the radar rainfall for the observation period is shown in Figure 1b. The rainfall sum, showing totals between 250 and 4492 mm. The rainfall pattern is different over the study region, covering a climatically diverse area. The spatiotemporal rainfall distribution in the radar coverage is generally affected by the Andes mountains, the El Niño–Southern Oscillation (ENSO), the biannual migration of the intertropical convergence zone (ITCZ), and also the cold von Humboldt current in the Pacific Ocean, [15,24,25]. On the eastern sides of the Andes, the strong topographic slopes and easterly winds result in orographic effects [26,27], which is causing the cyclical spatiotemporal rainfall behavior and deep convection [28].
2.1.2. Meteorological Stations
A meteorological station network, comprising 21 high-temporal-resolution rain stations, was used in this study. Meteorological station data were obtained from UTPL and University of Cuenca. Meteorological stations from UTPL and University of Cuenca provide rain data every 10 and 5 min, respectively. Daily rainfall information was acquired from INAMHI. Meteorological station data from 19 April 2017 to 28 February 2018 were used as validation information to examine radar quality. The high temporal resolution meteorological stations from UTPL and the University of Cuenca are used to validate the satellite-based products at the time of MW-overpasses. We obtained the data from all organizations after quality checks.
The quality check for the station data from the University of Cuenca is performed by drawing a cumulative precipitation curve that identifies abnormal records (outliers and wrong measurements). These measurements are disregarded from the time series. In addition, correlation to nearby stations is also performed as a double check if necessary. In order to maximize the quality of the measurements, regular maintenance of the stations in the field (every three weeks or fewer) is performed. For the INAMHI data, it is checked if daily values are between 0 and 250 mm, which is the maximum daily precipitation value registered at a national scale.
Figure 1a shows the distribution of the meteorological stations used in this study.
It should be noted that these data are not included in the Global Precipitation Climatology Center (GPCC) network and therefore not used for the gauge-calibrated final IMERG product.
2.1.3. Integrated Multi-Satellite Retrievals for GPM
IMERG is a level 3 product which integrates all MW sensors, MW-calibrated IR estimates, and rain gauge measurements on a global scale [29]. All MW estimates, after calibration, were subjected to the Climate Prediction Center MORPHing technique (CMORPH) [30] to calculate the motion vectors from the IR measurements and the different atmospheric variables from numerical models. In regions without direct PMW overpasses, the algorithm uses the retrieved rainfall from PERSIANN-CCS [14] and GEO IR (IR-only IMERG) to complete the gridded product. In the last step, the monthly rain data from the GPCC were used to as a bias correction of the rainfall estimate [29].
In this study, the latest available version of IMERG (IMERG-V06 [29]), which displayed an overall improvement in the precipitation estimation compared with version-05 [31], was used.
The IMERG provides rainfall estimates with the spatial resolution of 0.1° (11 km2) in every 30 min. We focused on the final product of IMERG Version 06 (IMERG-V06), gauge-adjusted retrievals for the study period. NASA also provided the quality index (QI) as a variable in 30 min resolution [32]. The QI indicates the relative quality of rainfall estimates in half-hourly IMERG products, fluctuating temporally between passive MW (PMW) and IR-based rainfall estimates. Additionally, the time of the overpass of each MW swath is provided in metadata with the name of ‘HQobservationTime’.
For our validation, the multi-satellite precipitation estimates with the gauge calibration subdata set of IMERG (precipitationCal), as well as “IRprecipitation” was used. In this study, IRprecipitation and IR-only IMERG are equivalent.
2.1.4. Random Forest-Based Rainfall
The random forest-based rainfall (RF-based rainfall) product is the regionally calibrated rainfall retrieval scheme developed Ecuador by Turini et al. [3]. The algorithm uses random forest (RF) to calculate rainfall rates in surface level by means of multi-spectral IR data from Geostationary Operational Environmental Satellite 16 (GOES-16). The algorithm is trained based on MW-only precipitation data from IMERG-V06. The RF-based rainfall product was implemented by (i) delineating the rain area, and (ii) assigning of the rainfall rate at 11 km2 spatial resolution and for the time of a MW overpass. As predictors, GOES IR bands, band combinations, geostatistical texture features calculated from the original GOES IR bands, and ancillary data were used. Turini et al. [3] used the geostatistical texture features to capture the clouds’ heterogeneity. They calculated the texture features using a 5 × 5 pixel moving window method. First, for each GOES IR band, variograms (VARs), madograms (MADs), and rodograms (RODs) and then, for each possible bands combination, cross-variograms (CVs) and pseudo cross-variograms (PCVs) were calculated. Please refer to Schulz et al. [33] for more information about definitions and equations of texture features. The most important features were obtained monthly for each of the steps (rain area delineation and rainfall rate assignment) separately. The model tuning and feature selection results showed that, in addition to the ancillary data, the information recorded in the geostatistical texture features was the most important for rain area delineation and rainfall rate assignment [3].
The PCV was the dominant texture feature selected in almost all months, both for rain area delineation and rain rate assignment [3].
After training the models, the RF-based rainfall at a high spatiotemporal resolution (2 km2, 15 min) was estimated. In this step, the models were applied to the GOES-16 scenes where MW-IMERG was available and the following scenes until the next model was present in Turini et al. [3]. The product is available from 19 April 2017 to 19 April 2018.
2.2. Methods
Three different validations were employed in this study to assess satellite-based rainfall product performance. Due to the different availabilities of the slots of the products, the period for this study ranged from 19 April 2017 to 1 February 2018 in the time slots where radar data are available.
- The performance of the satellite-based rainfall products are investigated against the X-band rain radar network at the time of MW overpass at a spatial resolution of 11 km2.
- The performance of the satellite-based rainfall products is investigated against the ground based meteorological station network at the time of MW overpass at a spatial resolution of 11 km2.
- The RF-based rainfall product is validated against the X-band rain radar network in the temporal resolution of 30 min and spatial resolution of 2 km2.
2.2.1. Validation of Satellite-Based Rainfall Products at the Time of MW Overpass from IMERG
The first validation was performed to investigate satellite-based rainfall products’ performance against X-band rain radar network when MW overpass sensors from IMERG are present. This is essential since the IMERG data set has been widely used to develop satellite-based rainfall products [8,12,13,34].
We used different subdata sets in the IMERG product. We first considered the pixels from “precipitationCal” when the PMWs swat was available (“HQobservation”). Then, the pixels with the “PrecipitationQualityIndex” >0.6 (which indicates the current half-hour microwave swath data) [32] were picked out. “IRprecipitation” were also selected in the same pixels from IMERG. This data set (IR only) was retrieved from the PERSIANN-CCS in IMERG, which are calibrated regionally to the PMW-only measures [29]. Therefore, in this study, we named this product “IR-only IMERG”.
To compile the most robust data set for the first validation of satellite-based rainfall products against the radars at the time of MW overpass in IMERG, we defined the following criteria: (i) For temporal matching, we used “HQobservationTime” for IMERG to determine the exact time of MW overpass in each pixel. Then, we rounded the WM overpass time to the closest 5 min to be compatible with the temporal resolution of the radar (every 5 min). In this step, we assumed that the RF-based rainfall and IR-only IMERG have the same timing as the time of MW overpass. (ii) To ensure the high-quality rainfall information from IMERG (merged MW-only precipitation estimates), we used the “PrecipitationQualityIndex”. (iii) Sensitivity to light rain continuously degrades with increasing distance from the radar. To only assess the near range, we applied a circular mask with a radius of 50 km from the center of each radar. (iv) A mask for filtering the radar data for plausibility was also applied. A value of 1 indicates reliable data from radars. (v) There was some noise in the center of the radar due to the cross-talk from the antenna’s side-lobes. Therefore, we omitted the inner pixels with a radius of 10 km from the center for the validation. (vi) Due to the different spatial resolutions of the RF-based rainfall (2 km2), radar (0.5 km2), radar quality index (0.5 km2), DEM (1 km2), and IMERG (11 km2), the average resampling techniques in gdal [35] were used to guarantee spatial matching between the different data sets. In our study, we used the WGS84 projection coordinate system and all dataset were resampled to the spatial resolution of IMERG (11 km2). (vi) The 0.5 mm/h was used as a threshold between rainy and non-rainy pixels for validation. (vii) The pixels in the radar considered rainy (>0.5 mm/h) but has a dBZ lower than −15 were considered false and filtered out from the validation data set.
By applying above criteria and withdraw the data pairs of the first validation against radar on a pixel basis, a total of 117,183 pixels of radar and MW-based IMERG, RF-based rainfall, and IR-only IMERG were made available at a half-hourly resolution for validation.
In the second validation, the overall performance of the rainfall area delineation and rainfall rate assignment was investigated for each product against data from ground based meteorological stations at the time of the MW overpass.
For comparison with the meteorological ground based station network, we only considered pixels with a minimum number of three gauges (see Figure 2). Tang et al. [36] underline that gauge networks with limited numbers of gauges in each pixel leads to underestimation of the performance of satellite-based rainfall products. This is because the point observations of gauges cannot represent pixel-based precipitation. Therefore, for this validation the stations from University of Cuenca with the temporal resolution of 5 min (Ana Davis, Zona Militar Davis and Balzay) and from UTPL (UTPL Militar, UTPL Tecnico and UTPL Villonaca) with the temporal resolution of 10 min are considered.
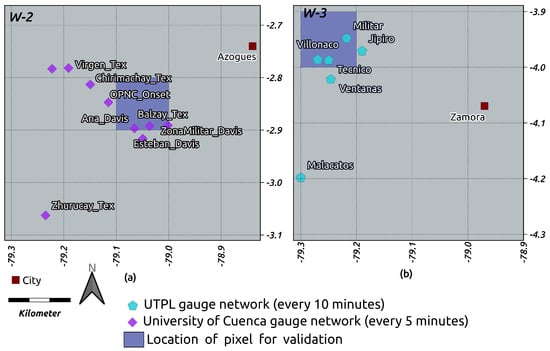
Figure 2.
Location of pixels with a minimum number of three gauges for (a) the University of Cuenca gauge network and (b) the UTPL gauge network. In Figure 1a, W-2 and W-3 rectangles outline the extent of (a) and (b), respectively.
To generate the dataset for ground truth validation of the three satellite-based products against the gauge network, we proceeded as follows: (i) for temporal matching, we used “HQobservationTime” for IMERG to determine the exact time of MW overpass in each pixel. Then, we rounded the WM overpass time to the closest 5 min to be compatible with the temporal resolution of the radar (every 5 min). In this step, we assumed that the RF-based rainfall and IR-only IMERG have the same timing as the time of MW overpass. (ii) To ensure the high-quality rainfall information from IMERG (merged MW-only precipitation estimates), we used the “PrecipitationQualityIndex”. In the next step (iii), the spatial matching were done using the average resampling techniques in gdal [35] to resample the products to the spatial resolution of IMERG (11 km2). (iv) The threshold of 0.5 mm/h was used to distinguish between rainy and non-rainy events. (v) After selecting pixels, the arithmetic mean rainfall from station data was computed in these pixels, given that every pixel includes three stations at minimum.
2.2.2. Validation of RF-Based Rainfall Products in Native Resolution
In the third validation, we investigated the general behavior RF-based rainfall in rainfall area delineation and rainfall estimation in the native spatial resolution (2 km2) and every 30 min in the entire study area for the study period. To prepare the data set for this validation strategy, we defined the following criteria: (i) In our study, area, subscale convective rainfall systems in the transition zones and valleys [37] are dominant. To understand satellite-based rainfall products’ capability to capture these events, we kept the original spatial resolutions of the RF-based rainfall, 2 km2; (ii) to minimize the uncertainties caused by the potential temporal offset between RF-based rainfall products, the radar and RF-based rainfall were aggregated in time to 30 min. For the temporal aggregation of the radar and the RF-based rainfall, we considered a unit conversion between mm/h and mm/30 min. (iii) We used a threshold of 0.2 mm/30 min to distinguish between rainy and non-rainy pixels for validation; (iv) equal to the first validation strategy, the pixels of the radar considered rainy (>0.2 mm/30 min) at a dBz lower than −15 dBz were considered false and were removed from the validation data set. (v) We omitted the inner pixels within a radius of 10 km2 from the center; (vi) a mask for filtering the radar data for plausibility was also applied. (vii) In the next step, the RF-based rainfall was aggregated for the observation period in 1 h, 3 h, and daily for evaluation against the radar.
2.2.3. Validation Metrics for Rainfall Area Delineation and Rainfall Estimate
We considered all pixels from the validation data set in each validation strategy for the validation of rainfall area delineation. First, we calculated the cross-table’s respective satellite-based rainfall products in comparison with the radar as a reference. Therefore we calculated the misses (M), hits (H), false alarms (F), and correct negatives (C). We define hit when the satellite-rainfall product and the radar are both raining in the same location. A miss occurs when the satellite-rainfall product is not raining but the radar shows rain, a false alarm holds when the satellite-rainfall product is raining but the radar is not and a correct negative is when both, the satellite-rainfall product and radar are showing cloudy but not rainy conditions (Figure 3).
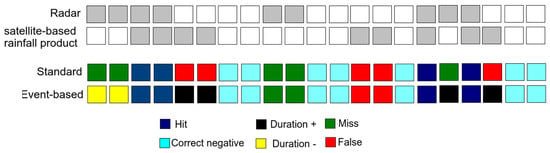
Figure 3.
Schematic view of how H, M, and F were designated in the rain area validation. The dry pixels are shown in white, and the rainy pixels are shown in grey. The standard approach defines M (F) when a rainy pixel in the radar (satellite-based rainfall product) is related to a dry pixel in the satellite-based rainfall product (radar) at the same time. In the temporal event-based approach (fourth row), the M (F) in the vicinity time of hits are defined as a reduction (continuous) in the event duration. Thus, the terms Duration+ (Duration-) are described. True misses and true false alarms are the errors occurring simultaneously or in the same pixel, respectively [17].
We also defined temporal and spatial events. Schematic images of temporal and spatial events are illustrated in Figure 3 and Figure 4, respectively.
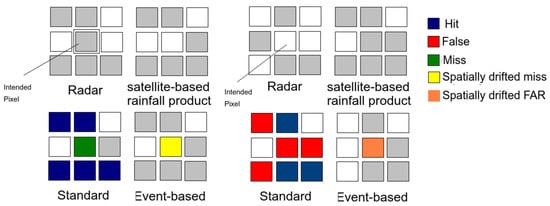
Figure 4.
Schematic view of how hits, misses, and false alarms are designated in the rain area validation. The dry pixels are shown in white, and the rainy pixels are shown in grey. The standard approach defines M (F) when a rainy pixel in the radar (satellite-based rainfall product) is related to a dry pixel in the satellite-based rainfall product (radar) at the same time. In the spatial event-based approach (second row), the M (F) in the neighboring pixels are defined as a spatially drifted miss (false alarm) of the event. The errors simultaneously and in the same pixel are called true misses and false alarms, respectively.
Temporal events were defined to check the time lag effect of satellite scanning. You et al. [38] stressed this aspect for PMW observation. Later, Maranan et al. [17] investigated the time lag effect in IMERG, where false alarms were reduced through the temporal shift in IMERG relative to surface observations.
We calculated the probability of detection (POD), false alarm ratio (FAR), and Heike skill score (HSS) as validation metrics from the H, M, F, and C.
To evaluate the accuracy of estimated rainfall from each satellite-based rainfall product, we used the mean absolute error (MAE), root mean square error (RMSE) and mean error (ME), and their normalized counterparts. These metrics were calculated when it was rainy for both radar and satellite-based rainfall products. Table 1 shows the detailed equations and the range of these metrics.

Table 1.
List of validation metrics used in this study for rain area delineation and rain estimate.
3. Results
3.1. Validation Metrics for Satellite-Based Rainfall Products at the Time of MW Overpass against X-Band Rain Radar Network
3.1.1. Rain Area Delineation
The frequency of occurrence of the cross-table components formed on all available MW overpass timing (n = 51,384) is presented in Figure 5. Less than 5% of the MW overpass times in either radar or satellite-based rainfall products contain rainfall and a total of 0.73%, 0.58%, and 0.39% are hits for MW-based IMERG, RF-based rainfall, and IR-only IMERG, respectively. Successively, false alarms dominated the error with a fraction of 2.53% for MW-based IMERG, 2.08% for RF-based rainfall, and 2.24% for IR-only IMERG. All three product show reasonable agreement with the radar at the time of MW overpass Table 2. All products have a high FAR (0.78 for MW-based IMERG and RF-based rainfall, and 0.85 for IR-only IMERG).
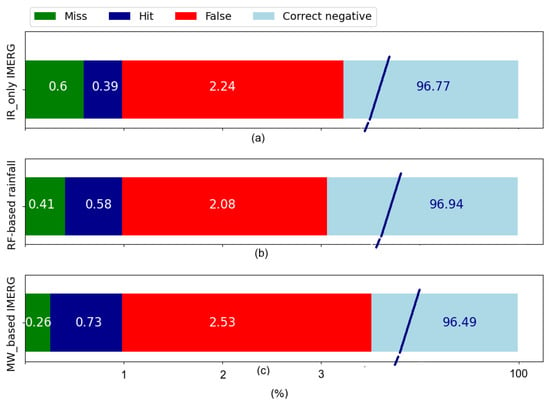
Figure 5.
Standard cross-table approach for all available MW overpass times for the validation of rain area delineation for (a) IR-only IMERG, (b) RF-based rainfall, and (c) MW-based IMERG. Note that the correct negative fraction extends to 100%.

Table 2.
The rain area delineation performance of satellite-based rainfall over the MW overpass time compared to ground radar network.
Overall, MW-based IMERG exhibits relatively better performance (HSS = 0.33), RF-based rainfall performs somewhat the same as MW-based IMERG (HSS = 0.3), whereas IR-only IMERG performs the worst (HSS = 0.2). This shows the higher potential of using multispectral GEO data (RF-based rainfall) compared with only one IR channel rainfall retrieval, as is the case for IR-only IMERG [3,8,12,13].
Figure 6 reveals the spatial performance of the satellite-based rainfall products at the time of MW overpass during the study period. Figure 6c,f,i shows the spatial distribution of HSS for MW-based IMERG, IR-only IMERG, and RF-based rainfall, respectively. The HSS share similarities in the spatial distribution for all products, with the maximum occurring at the north and northeast of the study region (0.4–0.7 for MW-based IMERG, and 0.4–0.8 for IR-only IMERG and RF-based rainfall). However, in the northwestern part of the region, the ability to capture precipitation is almost lost due to the lower POD and higher FAR (0.7–1 for MW-based IMERG, IR-only IMERG, and RF-based rainfall) in all the products. The GUAXX radar performs better in terms of POD in general but with a relatively higher FAR (0.6–1 for MW-based IMERG, and 0.7–1 for IR-only IMERG and RF-based rainfall), and this phenomenon illustrates that the products have difficulties in capturing the rainfall in these region (HSS of 0.1–0.6 for MW-based IMERG, 0.1–0.3 for IR-only IMERG, and 0.1–0.6 for RF-based rainfall). Please note that the time periods of available data for GUAXX and CAXX are different.
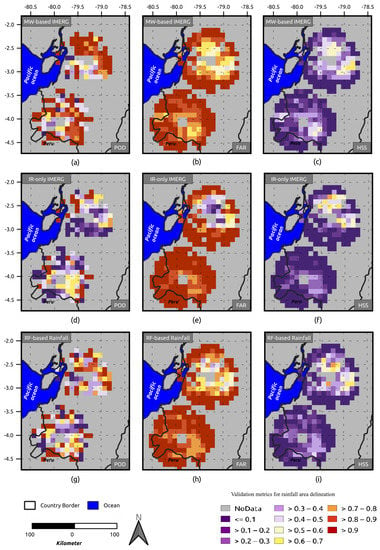
Figure 6.
Spatial distribution of the validation metrics for rain area delineation at the time of MW overpass. (a) POD, (b) FAR, and (c) HSS showing the matrics for MW. The variables were calculated for MW-based IMERG. (d) POD, (e) FAR, and (f) HSS illustrating the performance of IR-only IMERG. (g) POD, (h) FAR, and (i) HSS showing the RF-based rainfall performance. The variables were calculated for each grid point of the validation data set over the stated period. For better illustration, we show the results up to 75 km distance from the center of each radar.
Figure 7 provides an overview of the validation metrics of the three satellite-based rainfall products for rain area delineation, along with the altitude. All products have a high FAR and a convincing POD. The performance at a terrain elevation of approximately 0–1500 m.a.s.l is relatively lower for all of the three products with HSS of 0.2–0.29 for MW-based IMERG, 0.1–0.22 for IR-only IMERG, and 0.2–0.25 for RF-based rainfall. The rain area delineation performance increased until 3000 m.a.s.l. At 0–750 m.a.s.l, the RF-based rainfall (HSS = 0.25) performs the best of all products.
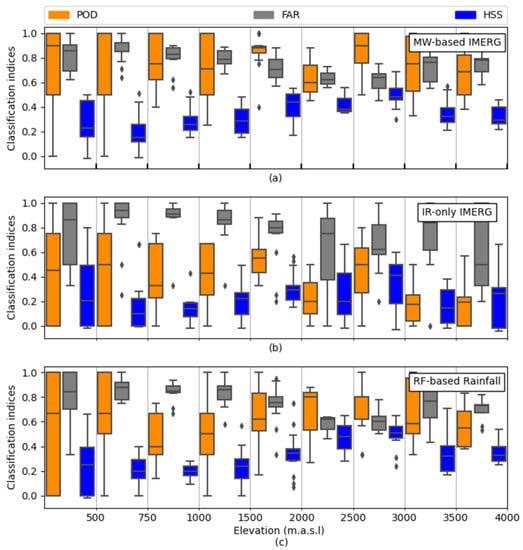
Figure 7.
Boxplot of the validation metrics for rain area delineation over the MW overpass time. The performance of (a) MW-based IMERG, (b) IR-only IMERG, and (c) RF-based rainfall along elevation. Boxes show the 25th, 50th, and 75th percentiles. Whiskers extensions are to the maximum data value between the 75th and 25th percentiles. Diamonds indicate outliers.
Figure 8 provides an overview of the rain area delineation performance, along with different rainfall rates. In all products, rainfall rates lower than 2 mm/h have the highest FAR. With increasing rainfall rate, the performance of all products increases until 6 mm/h. For a rain rate of more than 6 mm/h, the products perform steadily. Altogether, the graph confirms (i) the poor rain area delineation performance at lower rainfall rates in Ecuador, and (ii) the WM-based IMERG shows the best performance with different rain rates in Ecuador, followed by RF-based rainfall.
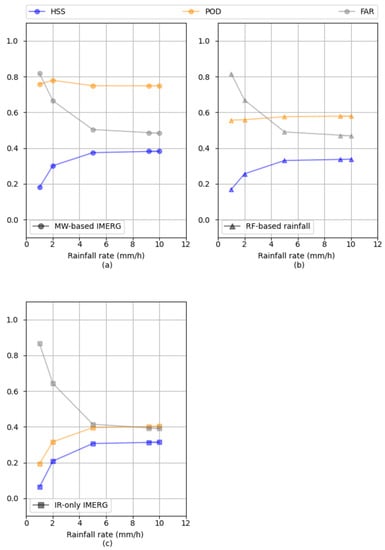
Figure 8.
The rain area delineation performance over the MW overpass time and at 11 km2 for different rainfall rates for (a) MW-based IMERG, (b) RF-based rainfall, and (c) IR-only IMERG.
3.1.2. Rainfall Estimation
Table 3 exhibits the ability of satellite-based rainfall products to estimate rainfall at the time of MW overpass. RF-based rainfall shows the best performance compared with the two other products. All three products underestimate rainfall, indicated by their negative ME and NME.

Table 3.
The rainfall estimation performance of satellite-based rainfall over the MW overpass time compared to the ground radar network.
The scatter plots in Figure 9 illustrate how the rainfall rate at the time of MW overpass is distributed for each of the satellite-based rainfall products against the radar. Only pixels with hits are considered, therefore the number of hits (n) differs for each product (Figure 9a,d,g). The overall variability in all the products is high, which might be due to issues in timing or/and rainfall estimation (Figure 9a,d,g) [17]. Overall, IR-only rainfall shows the best correlation line close to 1:1. The regression line also indicates the underestimation by RF-based rainfall. MW-based IMERG and IR-only rainfall overestimate the rainfall rate. Figure 9b,e,h shows the rainfall rate for each product against radar in quantile–quantile (Q–Q) plots.
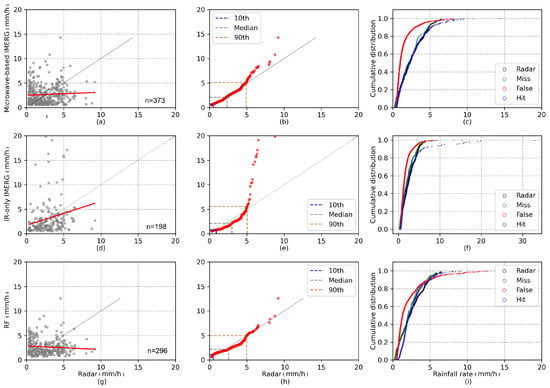
Figure 9.
Comparison of rainfall rates estimated by the radar and satellite-based products. (a,d,g) Scatter plot with radar rainfall rates (x-axis) and microwave-based IMERG, IR-only IMERG, and RF-based rainfall rates (y-axis), respectively. Only pixels with hits are considered. The parameters n show the total number of hits. (b,e,h) Quantile–quantile (Q–Q) plot of the radar (x-axis) and microwave-based IMERG (y-axis), IR-only IMERG (y-axis), and RF-based (y-axis) rainfall rates. The 10th, 50th, and 90th percentiles are illustrated. (c,f,i) The distribution of cumulative rainfall rate for the contingency table of each satellite-based product. The radar rain rate is displayed in black as a reference.
The Q–Q plot ignores the corresponding time steps in order to underline the differences between the radar and each product in a more comprehensive manner [17]. In MW-based IMERG (Figure 9b) the rainfall rate is almost evenly distributed up to 5 mm/h, the positive values for MW-based IMERG at higher rainfall rates are more evident. The distribution of the rainfall rate between radar and IR-only IMERG shows more discrepancies (Figure 9e). IR-only IMERG shows negative biases until the 90th percentile and shows high positive bias for the higher rainfall rates. RF-based rainfall is distributed relatively even for all rainfall rates, with a slight negative bias between 3 and 5 mm/h. Overall, IR-only IMERG and MW-based IMERG are unable to model the most extreme rainfall rates. For extreme rainfall rates, RF-based rainfall shows better performance. The cumulative distribution of the rainfall rates for hits and the other contingency table elements is compared in Figure 9c,f, i, for MW-based IMERG, IR-only IMERG, and RF-based rainfall, respectively. In MW-based IMERG (Figure 9c) and RF-based rainfall (Figure 9i), around 60% of the FARs is equal to or less than 1 mm/h. This is also true for IR-only IMERG (Figure 9f). The FAR is also shown for higher rainfall rates in the RF-based rainfall product. This underlines that the algorithm is flawed for low-intensity rainfall in these products [17]. The misses show the same distribution as the radar’s distribution for all three products.
Figure 10 provides an overview of the validation metrics of the three satellite-based rainfall products for rain estimation along with altitude. MW-based IMERG and IR-only IMERG have difficulty estimating rainfall at lower elevations (0–500 m.a.s.l), which is shown by the extension of the boxplot for NRMSE and NMAE in this elevation range. RF-based rainfall has relatively lower values of NRMSE, NMAE, and NME at an elevation of 0–500 m.a.s.l. With increasing elevation, the rain estimation performance is relatively moderate until 2500 m.a.s.l. For high terrain elevations of approximately 2500–4000 m.a.s.l, all products show a significant uncertainty, mainly in NME. All the products underestimate the rainfall rate at high elevation (2000–4000 m.a.s.l).
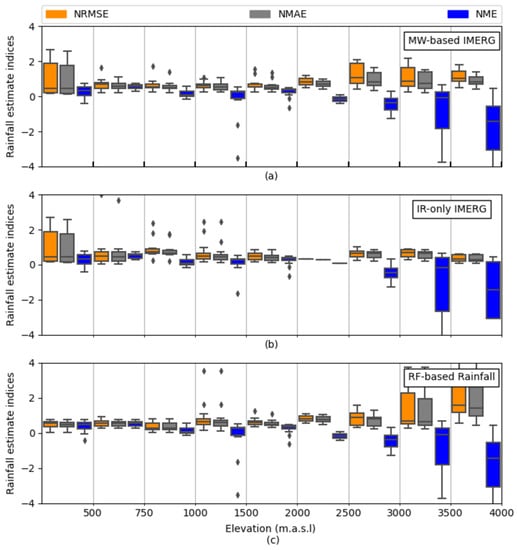
Figure 10.
Boxplot of the validation metrics for rain estimation at the MW overpass time. The performance of (a) MW-based IMERG, (b) IR-only IMERG, and (c) RF-based rainfall are shown along with elevation. Boxes show the 25th, 50th, and 75th percentiles. Whiskers extensions are to the maximum data value between the 75th and 25th percentiles. Diamonds indicate outliers.
3.2. Validation Metrics for Satellite-Based Rainfall Products at the Time of MW Overpass from IMERG against Meteorological Stations
Table 4 summarizes the performance of satellite-based rainfall products for rain area delineation against meteorological stations at the time of MW overpasses for the pixel in W-2 (Figure 2a) and W-3 (Figure 2b).

The validation scores show the superior performance of the IMERG-MW-based and RF-based rainfall products in comparison to IMERG-IR-only in W3. W2 shows a slightly better performance for RF-based rainfall while IR-only IMERG and MW-based IMERG are more or less the same. Still, all of the products overestimate precipitation area. These behaviors are similar to the validation of the rainfall products at the MW overpass time against the X-band rain radar network (Table 2). However, the validation scores indicate a lower performance of the satellite-based rainfall products by using the radar data compared to higher scores by using the station data. This is not surprising, since a low number of the gauges in a pixel (3 gauges in 11 km2) is not representative for the spatial distribution of rain. Therefore, the assessment of satellite-based rainfall products against a low number of gauges in each pixel underestimates their performance [36].
Table 5 shows the satellite-based rainfall products’ ability to estimate the rainfall at the time of MW overpass against ground truth data. The behavior of satellites is different in two pixels. In W-2, IR-only IMERG shows the best performance compared to the other two products. Meanwhile, in W-3, the RF-based rainfall capture the rain estimate more accurately compared to other products. In general, all of the products overestimate rainfall slightly (positive ME).

Table 5.
Rainfall estimation performance of satellite-based rainfall over the MW overpass time compared to ground radar network.
3.3. Validation Metrics for RF-Based Rainfall Products in Native Resolution
3.3.1. Rain Area Delineation
Using the analysis techniques described in Section 2.2.3, the ability of RF-based rainfall to estimate rainfall in comparison with the radar at 2 km2 spatial resolution and 30 min temporal resolution is shown in Figure 11 (n = 1,048,575). Less than 3% of the time steps in either radar or RF-based rainfall contain rainfall including 0.31% of hits (Figure 11a). The errors are dominated by false alarms at 1.57%. The decomposition of misses using the temporal event-based approach shows that almost 12% of the misses occur in the coincidental timing from radar precipitation (Figure 11b, Duration −, yellow bar; Duration +, black bar), whereas the spatially drifted misses are not recognizable (Figure 11d). Almost 4% of the overestimation occurs by overestimating event duration (Figure 11c), and 8.5% by overestimating events in the neighboring pixel (Figure 11e).
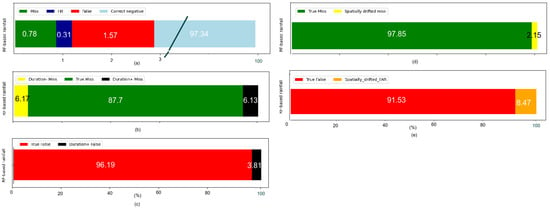
Figure 11.
(a) Standard contingency table approach for all available RF-based rainfall products for both radars at 2 km2 and 30 min. Note that the correct negative fraction extends to 100%. (b,c) The temporal event-based approach of the contingency table was evaluated in the M and F subsets, respectively. (d,e) The spatial event-based approach of the contingency table was evaluated in the M and F subsets, respectively. The numbers in the bars show the percentage.
The performance is summarized in Table 6. As expected, a noticeable result is the high FAR of 83%, showing that 83% of rainy events are false alarms. This is almost similar behaviour as for RF-based rainfall at the MW overpass in 11 km2 temporal resolution (Table 2). By applying the algorithm in 2 km2 spatial and 30 min temporal resolution, the ability of rain detection by RF-based rainfall has reduced compared to the RF-based rainfall in MW-overpasses and at 11 km2 spatial resolution (HSS = 0.31).

Table 6.
Performance evaluation of RF-based rainfall at rainfall area delineation for 2 km2 spatial and 30 min temporal resolution.
3.3.2. Rain Estimation
Table 7 summarizes the performance of RF-based rainfall in estimating rain at 2 km2 spatial and 30 min temporal resolution. The RF-based rainfall shows better performance in estimating rainfall at higher resolution compared with lower resolution (Table 3).

Table 7.
Performance evaluation of RF-based rainfall for rainfall estimation 2 km2 spatial and 30 min temporal resolution.
Focusing on hits, Figure 12 shows the rain estimation retrieval ability of RF-based rainfall in comparison with the radar. The scatter plot in Figure 12a shows the distribution of the half-hourly rain rates. The rain rates illustrates high variability, suggesting problems in rain estimation retrieval and/or timing. This is also shown in Figure 9g at the time of MW overpass. Figure 12b shows the Q–Q plot for RF-based rainfall. The overall estimation of the rainfall is placed along the 1:1 line to the 90th percentile. However, the curve deviates towards the left after the 90th percentile, showing an overestimation of rain intensities in the outliers. Figure 12c decomposes the results in more detail. Overall, RF-based rainfall is unable to detect the most extreme rainfall rates, as reported by Turini et al. [3]. The cumulative distribution of rainfall rates for hits, misses, radar, and false alarms are compared in Figure 12a. Around 60% of false alarms and misses are less than or equal to 1 mm/h. This is also true for 60% of event-based (temporally and spatially) false alarms Figure 12d. The event-based misses are evenly distributed over the different rainfall rates.
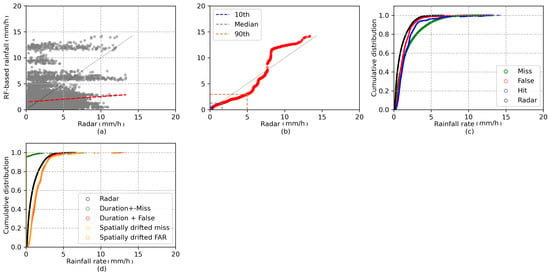
Figure 12.
Comparison of rain rates estimated by the radar and RF-based rainfall at 2 km2 and 30 min. (a) Scatter plot with radar rainfall (x-axis) and RF-based rainfall (y-axis). Only the pixels with hit are considered. (b) Q–Q plot of radar (x-axis) and RF-based rainfall rates (y-axis). The 10th, 50th, and 90th percentiles are illustrate. (c) The distribution of cumulative rainfall rate for the contingency table. (d) The distribution of cumulative rainfall rate based on the event-based (spatial and temporal) contingency table.
3.4. Validation Metrics for RF-Based Rainfall Products at Different Temporal Resolutions
To validate the results of rain area delineation and rain estimation in different temporal resolutions, Figure 13a,b presents the validation metrics with the radar for the whole study region and observation period. The results show the best agreements regarding rain area delineation in daily resolution (POD 0.68, HSS 0.4, and FAR 0.6).
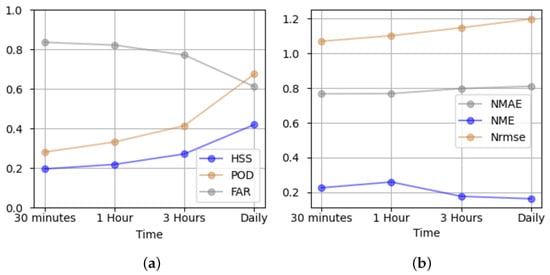
Figure 13.
Comparison of the validation metrics between the radar and RF-based rainfall at 2 km2 and 30 min, 1 h, 3 h, and daily. The performance of RF-based (a) rain area delineation and (b) rain estimation is shown for different temporal resolutions.
The rain estimation indices for RF-based rainfall do not show a significant improvement for the different temporal resolutions. The NME suggests the overestimation of precipitation by RF-based rainfall at lower resolution (after 3 h) and an underestimation at higher temporal resolutions. Note that in this step, we considered rainfall at a rate of more than 0.5 mm/h as rainy.
4. Discussion
In Section 3.1, satellite-based rainfall products at the time of MW overpasses from IMERG were assessed using radar data. We evaluated the satellite-based products in grid cells at the time of MW overpasses and a spatial resolution of 11 km2.
The verification scores for rain area delineation revealed that the MW-based IMERG has superior performance in estimating rain area (POD = 0.74, HSS = 0.33). RF-based rainfall, which is trained based on MW-based IMERG, has slightly lower performance compared to MW-based IMERG data (HSS = 0.31). IR-only IMERG performed the worst in Ecuador. This is in line with the findings of Kolbe et al. [12], Kolbe et al. [13], Turini et al. [8], and Turini et al. [3]. It shows that multispectral GEO data has more potential than using one IR channel only for rainfall retrieval.
The frequent false alarm is one of the most noticeable issues identified in the present study. This agrees well with the result of IMERG-V06 validation in the west African forest zone [17] and confirms the previous investigation of IMERG-v05 by Manz et al. [15] in the Andes region. In our study, around 60% of the false alarms were related to rain rates less than 1 mm/h for all products (Figure 9), which was found to be the dominant rainfall intensity in this region of the world [39]. We also note that the radar potentially underestimated rainfall [40,41,42,43]. This was also reported elsewhere for the radars in Ecuador [23]. In MW-based IMERG and RF-based rainfall, with increasing the rainfall rate, the FAR decreases while POD does not change (Figure 8).
The results of the topography-based evaluation indicated the high detection accuracy of MW-based IMERG and RF-based rainfall in different topographical regions. Moreover, the highest errors occurred for coastal areas and foothills (0–1500 m.a.s.l) and high mountains regions (>3000 m.a.s.l) compared to the other topographical regions. All the products experienced challenges in estimating rainfall at high elevation in the Andes (Figure 10). In Ecuador, high-elevation areas and volcanoes have two issues for rainfall retrieval algorithms: (i) They are regularly covered by ice, which generates errors in MW-based IMERG [29,44]; (ii) the drizzle on the high elevation is hard to be captured by MW and IR channels. This conclusion is in agreement with the findings of study conducted by Prakash et al. [45], who assessed the performance of IMERG products in monsoon-dominated regions in India. Their results showed that IMERG was affected by the orographic process, which leads to higher errors in mountainous areas. Another study by Kim et al. [46] revealed the disadvantage of IMERG products over mountainous and coastal regions. Similar results were obtained by Turini et al. [3] in Ecuador for RF-based rainfall. They argued that because of local topography, the subscale convective rainfall systems probably could not be captured by GOES data and IMERG [3,37]. Altogether, at the elevation of 0–750 m.a.s.l, RF-based rainfall showed the best performance of all products (Figure 7 and Figure 10).
Concerning rainfall rate validation, the overall variability in all the products is high, suggesting rainfall rate estimation and/or timing issues. Different studies discuss a possible time lag between the satellite-based rainfall products and the ground-based rainfall measurements as a source of degrading validation results [17,38,47,48,49]. The time lag is defined as the time shift when satellite observation and surface precipitation rate from ground data obtain to their optimum correlation. This time lag might be due to the time it takes for the precipitation detected by the satellite to reach the ground [17,47]. You et al. [38] related the precipitation time from GMI to the environmental temperature and storm top height. They found that when the storm is taller, the lag time increases to obtain the optimum correlation between the GMI and ground truth data. This is due to the long way of raindrops from the storm top to the gauge.
Ignoring the corresponding time steps in the Q–Q plots shows that the MW-based IMERG and RF-based (Figure 9b,h) rainfall rates are distributed up to 5 mm/h evenly. The positive values in MW-based IMERG at higher rainfall rates are more evident. Conversely, the rainfall rate distribution between the radar and IR-only IMERG shows more discrepancies (Figure 9e). The validation of satellite-based rainfall products against the gauges show lower consistency (Table 5). However, in the term of rain area delineation (Table 4), the RF-based rainfall product shows better performance than IMERG-IR-only, which confirms the potential to use multispectral GEO data.
The validation of satellite-based rainfall show a slight overestimation of rainfall totals for all products (Table 5).
It should be noted that the evaluation of satellite-based products against only a few gauges has high uncertainties [8,36], especially in areas with high small-scale precipitation variability in mainly convective environments, like the Ecuadorian Andes, where point based observations at weather stations cannot properly represent the spatial rainfall distribution.
The validation of RF-based rainfall retrieval at high spatiotemporal resolution for all the available rain events is shown in Table 6. The RF-based rainfall is calibrated locally for Ecuador. The importance of local calibration, which involves determining relevant climatic parameters, including the selection of appropriate temperature thresholds for clouds and a local correlation systematic biases that may not have been adjusted in global products, have been mentioned in different studies [50,51,52].
RF-based rainfall for 2 km2 and 30 min shows a lower HSS compared to the RF-based rainfall for 11 km2 at the time of MW overpass. This was expected because the errors at higher temporal resolutions may cancel each other out following the aggregation to a lower temporal resolution [50]. However, in terms of rainfall estimation, RF-based rainfall performs better at higher spatial resolution (Table 3). This result needs to be interpreted with caution, since the rainfall events at the time of MW overpasses differ from the validation of the RF-based rainfall at 2 km2 and 30 min.
An event-based analysis was then used to investigate the source of error in the RF-based rainfall product. Shifting the RF-based rainfall backward by one to two time steps (i.e., 30 min) resulted in the more accurate detection of rainfall around 10% (Figure 11b) by lowering the misses. RF-based rainfall rates are lower than their counterparts in radar, as shown in Figure 12d. We speculate that this lag appears due to the lag time between the time of MW overpass and the GOES-16 scan time. The RF-based rainfall algorithm relies on the precipitation information from MW-based IMERG and IR data from GOES-16.
However, RF-based rainfall also has a high FAR. The event-based spatial analysis reduced the FAR by 8.5% (Figure 11e), but the challenge remains the same. High FAR values occur for all the different types of rain with different intensities (Figure 12c,d). The reason for the high FAR in RF-based rainfall might be (i) the high amount of FAR from MW-based IMERG in Ecuador (Table 2), which is used as a reference for calibrating of RF-based rainfall; (ii) A bias in IR retrievals that classify cold cloud pixels as rainy. They experience difficulties in defining the correct rainfall cloud and profile, thus producing error in statistical-physical rainfall algorithms.
By increasing the temporal resolution of the RF-based rainfall product, the performance of the product increased. However, the FAR (60% in daily resolution) remains a main challenge.
5. Conclusions
In this study, we evaluated and compared the performance of different satellite-based rainfall products over the Pacific coast and Andes of Ecuador. A mesoscale quality-controlled rain radar network was used as the rainfall reference. Statistical comparison indices were used to analyze the performance and to describe different aspects of the satellite-based rainfall products. The first validation was performed at 11 km2 spatial resolution and at the time of MW overpass for MW-based IMERG, RF-based rainfall, and IR-only IMERG products. Based on the validation, MW-based IMERG and RF-based rainfall provided better rainfall estimates in Ecuador than IR-only IMERG during MW overpasses. The distribution of the evaluation metrics spatially shows the impact of topography and the complex climate zonations in the study region. High precipitation values were better captured by the MW-based IMERG and the RF-based rainfall algorithms. The frequent false alarms are one of the most important issues in all products; FAR decreases with an increasing rainfall rate. Future studies on the lag time are therefore required in order to elucidate the high FAR in the satellite-based products. In the third validation, we investigated regionally calibrated RF-based rainfall products for Ecuador. RF-based rainfall is trained by MW-based IMERG. Although the product shows convincing results at a MW overpass of 11 km2, the performance decreased by increasing the resolution to 2 km2 spatial and 30 min temporal resolution. Furthermore, RF-based rainfall is trained to the available microwave-only data from IMERG. Consequently, due to the low temporal resolution of the data from MW satellites, some rainfall events might not have been considered [8].
Author Contributions
N.T., B.T. and J.B. developed the theoretical methodology; N.T. performed the analytic calculations; N.T., B.T., J.B. and R.R. analyzed and discussed the results; N.T. wrote the manuscript; N.T., B.T., N.H., R.R., A.F., F.P.-C., J.O.-A. and J.B. reviewed the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Federal Ministry for Education and Research of Germany within the projects “Seasonal Water Resource Management in Semi-arid regions” (02WGR1421C: http://www.grow-sawam.org, accessed on 6 October 2021); DFG research unit “RESPECT” (BE1780/51-1) and DFG “High-resolution Radar analysis of precipitation extremes in Ecuador and North Peru and implications of the ENSO-dynamics” (RO3815/2-1).
Data Availability Statement
The RF-based rainfall data presented in this study are available online: http://lcrs.geographie.uni-marburg.de/lcrs/data_pre.do?citid=448 (accessed on 6 October 2021). Restriction applies for the availability of ground radar data and gauge data. Because the data were obtained from third parties.
Acknowledgments
This work was carried out within the “Seasonal Water Resource Management” (SaWaM) research program by the Federal Ministry for Education and Research of Germany’s (BMBF). The work was done in the subproject “Remote Sensing of Precipitation” (02WGR1421C). We gratefully acknowledge the DFG research unit FOR2730 RESPECT, subproject A1 (BE1780/51-1) and the research project “High-resolution Radar analysis of precipitation extremes in Ecuador and North Peru and implications of the ENSO-dynamics” (DFG RO3815/2-1). The authors also thank National Weather Service of Ecuador (INAMHI), Universidad TécnicaParticular de Loja (UTPL), and University of Cuenca (Proyecto “Desarrollo de modelos para pronóstico hidrológico a partir de datos de radar meteorológico en cuencas de montaña”) for providing their meteorological station data and NOAA for produce the GOES-16 satellite data used in this study. Additionally, the IMERG-V06 data were provided by the NASA/Goddard Space Flight Centers and PPS, which develop and compute IMERG as a contribution to GPM, archived at the NASA GES DISC.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seidel, J.; Trachte, K.; Orellana-Alvear, J.; Figueroa, R.; Célleri, R.; Bendix, J.; Fernandez, C.; Huggel, C. Precipitation characteristics at two locations in the tropical Andes by means of vertically pointing micro-rain radar observations. Remote Sens. 2019, 11, 2985. [Google Scholar] [CrossRef] [Green Version]
- Ward, E.; Buytaert, W.; Peaver, L.; Wheater, H. Evaluation of precipitation products over complex mountainous terrain: A water resources perspective. Adv. Water Resour. 2011, 34, 1222–1231. [Google Scholar] [CrossRef]
- Turini, N.; Thies, B.; Horna, N.; Bendix, J. Random forest-based rainfall retrieval for Ecuador using GOES-16 and IMERG-V06 data. Eur. J. Remote Sens. 2021, 54, 117–139. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Tokay, A. A novel approach to identify sources of errors in IMERG for GPM ground validation. J. Hydrometeorol. 2016, 17, 2477–2491. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.; Xie, P. NASA Global Precipitation Measurement Integrated Multi-satellitE Retrievals for GPM (IMERG). Algorithm Theoretical Basis Doc.; Version 4.5; National Aeronautics and Space Administration: Washington, DC, USA, 2015; 30p. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Olson, W.S.; Masunaga, H.; GPM, C.R.R.A.T. GPM Combined Radar-Radiometer Precipitation Algorithm Theoretical Basis Document (Version 4); NASA: Washington, DC, USA, 2016. [Google Scholar]
- Turini, N.; Thies, B.; Bendix, J. Estimating High Spatio-Temporal Resolution Rainfall from MSG1 and GPM IMERG Based on Machine Learning: Case Study of Iran. Remote Sens. 2019, 11, 2307. [Google Scholar] [CrossRef] [Green Version]
- Kimani, M.W.; Hoedjes, J.C.B.; Su, Z. An Assessment of Satellite-Derived Rainfall Products Relative to Ground Observations over East Africa. Remote Sens. 2017, 9, 430. [Google Scholar] [CrossRef] [Green Version]
- Kühnlein, M.; Appelhans, T.; Thies, B.; Nauss, T. Improving the accuracy of rainfall rates from optical satellite sensors with machine learning—A random forests-based approach applied to MSG SEVIRI. Remote Sens. Environ. 2014, 141, 129–143. [Google Scholar] [CrossRef] [Green Version]
- Kühnlein, M.; Appelhans, T.; Thies, B.; Nauß, T. Precipitation Estimates from MSG SEVIRI Daytime, Nighttime, and Twilight Data with Random Forests. J. Appl. Meteorol. Climatol. 2014, 53, 2457–2480. [Google Scholar] [CrossRef] [Green Version]
- Kolbe, C.; Thies, B.; Egli, S.; Lehnert, L.; Schulz, H.M.; Bendix, J. Precipitation Retrieval over the Tibetan Plateau from the Geostationary Orbit—Part 1: Precipitation Area Delineation with Elektro-L2 and Insat-3D. Remote Sens. 2019, 11, 2302. [Google Scholar] [CrossRef] [Green Version]
- Kolbe, C.; Thies, B.; Turini, N.; Liu, Z.; Bendix, J. Correction: Kolbe, C., et al. Precipitation Retrieval over the Tibetan Plateau from the Geostationary Orbit—Part 2: Precipitation Rates with Elektro-L2 and Insat-3D. Remote Sensing 2020, 12, 2114. Remote Sens. 2020, 12, 3594. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X. Precipitation estimation from remotely sensed imagery using an artificial neural network cloud classification system. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef] [Green Version]
- Manz, B.; Páez-Bimos, S.; Horna, N.; Buytaert, W.; Ochoa-Tocachi, B.; Lavado-Casimiro, W.; Willems, B. Comparative ground validation of IMERG and TMPA at variable spatiotemporal scales in the tropical Andes. J. Hydrometeorol. 2017, 18, 2469–2489. [Google Scholar] [CrossRef]
- Erazo, B.; Bourrel, L.; Frappart, F.; Chimborazo, O.; Labat, D.; Dominguez-Granda, L.; Matamoros, D.; Mejia, R. Validation of satellite estimates (Tropical Rainfall Measuring Mission, TRMM) for rainfall variability over the Pacific slope and Coast of Ecuador. Water 2018, 10, 213. [Google Scholar] [CrossRef] [Green Version]
- Maranan, M.; Fink, A.H.; Knippertz, P.; Amekudzi, L.K.; Atiah, W.A.; Stengel, M. A process-based validation of GPM IMERG and its sources using a mesoscale rain gauge network in the West African forest zone. J. Hydrometeorol. 2020, 21, 729–749. [Google Scholar] [CrossRef]
- Bulovic, N.; McIntyre, N.; Johnson, F. Evaluation of IMERG V05B 30-Minute Rainfall Estimates over the High Elevation Tropical Andes Mountains. J. Hydrometeorol. 2020, 21, 1–53. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.; Ropelewski, C. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef]
- Bendix, J.; Fries, A.; Zárate, J.; Trachte, K.; Rollenbeck, R.; Pucha-Cofrep, F.; Paladines, R.; Palacios, I.; Orellana, J.; Oñate-Valdivieso, F.; et al. RadarNet-Sur first weather radar network in tropical high mountains. Bull. Am. Meteorol. Soc. 2017, 98, 1235–1254. [Google Scholar] [CrossRef]
- Rollenbeck, R.; Bendix, J. Experimental calibration of a cost-effective X-band weather radar for climate ecological studies in southern Ecuador. Atmos. Res. 2006, 79, 296–316. [Google Scholar] [CrossRef]
- Rollenbeck, R.; Bendix, J. Rainfall distribution in the Andes of southern Ecuador derived from blending weather radar data and meteorological field observations. Atmos. Res. 2011, 99, 277–289. [Google Scholar] [CrossRef]
- Boers, N.; Bookhagen, B.; Marwan, N.; Kurths, J.; Marengo, J. Complex networks identify spatial patterns of extreme rainfall events of the South American Monsoon System. Geophys. Res. Lett. 2013, 40, 4386–4392. [Google Scholar] [CrossRef] [Green Version]
- Vuille, M.; Bradley, R.S.; Keimig, F. Climate variability in the Andes of Ecuador and its relation to tropical Pacific and Atlantic sea surface temperature anomalies. J. Clim. 2000, 13, 2520–2535. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Chavez, S.; Ronchail, J.; Junquas, C.; Takahashi, K.; Lavado, W. Rainfall hotspots over the southern tropical Andes: Spatial distribution, rainfall intensity, and relations with large-scale atmospheric circulation. Water Resour. Res. 2015, 51, 3459–3475. [Google Scholar] [CrossRef]
- Bookhagen, B.; Strecker, M.R. Orographic barriers, high-resolution TRMM rainfall, and relief variations along the eastern Andes. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Romatschke, U.; Houze, R.A., Jr. Extreme summer convection in South America. J. Clim. 2010, 23, 3761–3791. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.; Sorooshian, S.; Tan, J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG); Version 06; Algorithm Theoretical Basis Document (ATBD): Greenbelt, MD, USA, 2019. [Google Scholar]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. IMERG V06: Changes to the morphing algorithm. J. Atmos. Ocean. Technol. 2019, 36, 2471–2482. [Google Scholar] [CrossRef]
- Huffman, G. IMERG V06 Quality Index 2019. Available online: https://gpm.nasa.gov/resources/documents/imerg-v06-quality-index (accessed on 15 March 2019).
- Schulz, H.M.; Li, C.F.; Thies, B.; Chang, S.C.; Bendix, J. Mapping the montane cloud forest of Taiwan using 12 year MODIS-derived ground fog frequency data. PLoS ONE 2017, 12, e172663. [Google Scholar] [CrossRef]
- Min, M.; Bai, C.; Guo, J.; Sun, F.; Liu, C.; Wang, F.; Xu, H.; Tang, S.; Li, B.; Di, D.; et al. Estimating summertime precipitation from Himawari-8 and global forecast system based on machine learning. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2557–2570. [Google Scholar] [CrossRef]
- GDAL; OGR Contributors. Geospatial Data Abstraction Software Library 2020. Open Source Geospatial Foundation 2021. Available online: https://gdal.org (accessed on 6 October 2021).
- Tang, G.; Behrangi, A.; Long, D.; Li, C.; Hong, Y. Accounting for spatiotemporal errors of gauges: A critical step to evaluate gridded precipitation products. J. Hydrol. 2018, 559, 294–306. [Google Scholar] [CrossRef] [Green Version]
- Bendix, J.; Trachte, K.; Cermak, J.; Rollenbeck, R.; Nauß, T. Formation of convective clouds at the foothills of the tropical eastern Andes (South Ecuador). J. Appl. Meteorol. Climatol. 2009, 48, 1682–1695. [Google Scholar] [CrossRef]
- You, Y.; Meng, H.; Dong, J.; Rudlosky, S. Time-Lag Correlation Between Passive Microwave Measurements and Surface Precipitation and Its Impact on Precipitation Retrieval Evaluation. Geophys. Res. Lett. 2019, 46, 8415–8423. [Google Scholar] [CrossRef]
- Orellana-Alvear, J.; Célleri, R.; Rollenbeck, R.; Bendix, J. Analysis of rain types and their Z–R relationships at different locations in the high Andes of southern Ecuador. J. Appl. Meteorol. Climatol. 2017, 56, 3065–3080. [Google Scholar] [CrossRef]
- Hazenberg, P.; Leijnse, H.; Uijlenhoet, R. Radar rainfall estimation of stratiform winter precipitation in the Belgian Ardennes. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Generation and verification of rainfall estimates from 10-yr volumetric weather radar measurements. J. Hydrometeorol. 2016, 17, 1223–1242. [Google Scholar] [CrossRef]
- Fairman, J.G., Jr.; Schultz, D.M.; Kirshbaum, D.J.; Gray, S.L.; Barrett, A.I. A radar-based rainfall climatology of Great Britain and Ireland. Weather 2015, 70, 153–158. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.A.; Baeck, M.L.; Villarini, G.; Welty, C.; Miller, A.J.; Krajewski, W.F. Analyses of a long-term, high-resolution radar rainfall data set for the Baltimore metropolitan region. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Petkovi, V.; Kummerow, C.D. Understanding the sources of satellite passive microwave rainfall retrieval systematic errors over land. J. Appl. Meteorol. Climatol. 2017, 56, 597–614. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2017, 187, 95–105. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Kirchengast, G.; Goodrich, D.C.; Wolff, D.B. Evaluation of Global Precipitation Measurement Rainfall Estimates against Three Dense Gauge Networks. J. Hydrometeorol. 2018, 19, 517–532. [Google Scholar] [CrossRef]
- Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar]
- Villarini, G.; Krajewski, W.F. Evaluation of the research version TMPA three-hourly 0.25 rainfall estimates over Oklahoma. Geophys. Res. Lett. 2007, 34, 2007. [Google Scholar] [CrossRef]
- Ayehu, G.T.; Tadesse, T.; Gessesse, B.; Dinku, T. Validation of new satellite rainfall products over the Upper Blue Nile Basin, Ethiopia. Atmos. Meas. Tech. 2018, 11, 1921–1936. [Google Scholar] [CrossRef] [Green Version]
- Ghajarnia, N.; Liaghat, A.; Arasteh, P.D. Comparison and evaluation of high resolution precipitation estimation products in Urmia Basin-Iran. Atmos. Res. 2015, 158, 50–65. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.S.; Nasrollahi, N.; Hsu, K.l.; Sorooshian, S. Evaluation of satellite-based precipitation estimation over Iran. J. Arid. Environ. 2013, 97, 205–219. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).