Green’s Function for Static Klein–Gordon Equation Stated on a Rectangular Region and Its Application in Meteorology Data Assimilation
Abstract
1. Introduction
2. The Data Assimilation and Its Variational Problem
3. Retrieving the Weights by Formal Solution
- Step 1. Choose initial point , l = 0, precise requirement ;
- Step 2. Calculate . If , stop. Otherwise, let ;
- Step 3. Let , find from ;
- Step 4. Let , turn to Step 2.
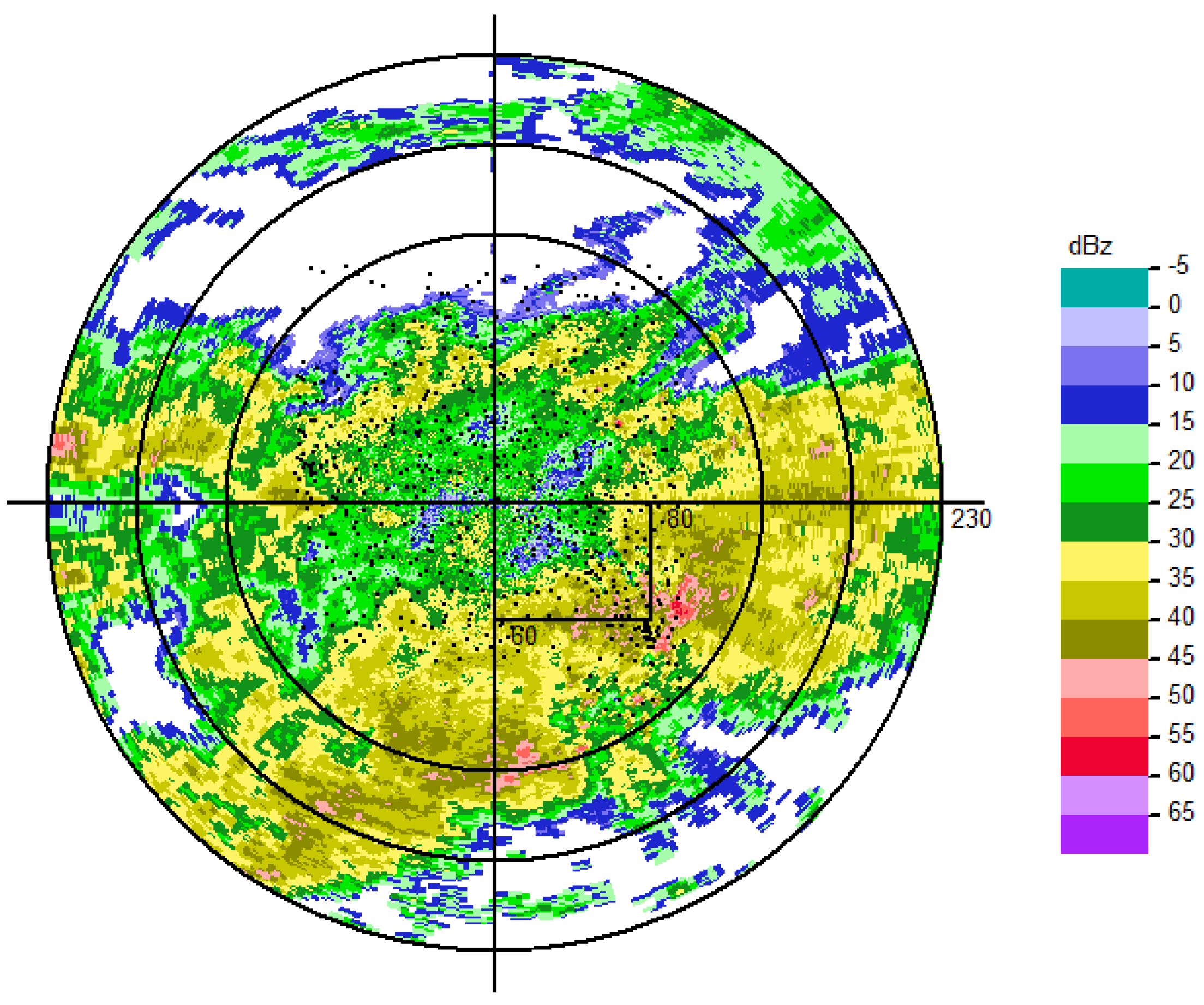
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Green’s Function for the SKGE Stated on a Rectangular Region
Appendix B. Convergence Analysis and Truncation Error Analysis
References
- Talagrand, O.; Courtier, P. Variational assimilation of meteorological observations with the adjoint vorticity equation. I: Theory. Q. J. R. Meteorol. Soc. 1987, 113, 1311–1328. [Google Scholar] [CrossRef]
- Al-Jamal, M.F. Numerical Solution of Elliptic Inverse Problems via the Equation Error Method. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2012. [Google Scholar]
- Mehraliyev, Y.T.; Kanca, F. An inverse boundary value problem for a second order elliptic equation in a rectangle. Math. Modeling Anal. 2014, 19, 241–256. [Google Scholar] [CrossRef][Green Version]
- Mehraliyev, Y.T. On solvability of an inverse boundary value problem for a fourth order elliptic equation. J. Math. Syst. Sci. 2013, 3, 560–566. [Google Scholar]
- Orlovsky, D.G. Inverse problem for elliptic equation in Banach space with Bitsadze—Samarsky boundary value conditions. J. Inverse ILL-Posed Probl. 2013, 21, 141–157. [Google Scholar] [CrossRef]
- Ming, W.; Renqing, D.; Wenzhong, G.; Takeda, T. Retrieval Single-Doppler Radar Wind with Variational Assimilation Method—Part I: Objective Selection of Functional Weighting Factors. Adv. Atmos. Sci. 1998, 15, 553–567. [Google Scholar] [CrossRef]
- Ming, W.; Guo-qing, L.; Cheng-gang, W.; Wen-zhong, G.; Qin, X. Optimal Selection for the Weighted Coefficients of the Constrained Variational Problems. Appl. Math. Mech. 2003, 24, 926–944. [Google Scholar] [CrossRef]
- Melnikov, Y.A. Construction of Green’s functions for the two-dimensional static Klein-Gordon equation. J. Part. Differ. Equ. 2011, 24, 114–139. [Google Scholar]
- Aseeri, S.; Batrašev, O.; Icardi, M.; Leu, B.; Liu, A.; Li, N.; Muite, B.K.; Müller, E.; Palen, B.; Quell, M. Solving the Klein-Gordon equation using Fourier spectral methods: A benchmark test for computer performance. In Proceedings of the Symposium on High Performance Computing (HPC’15), Montreal, QC, Canada, 17 June 2015; pp. 182–191. [Google Scholar]
- Gravel, P.; Cauthier, C. Classical applications of the Klein-Gordon equation. Am. J. Phys. Teach. 2011, 79, 447–453. [Google Scholar] [CrossRef]
- Muravey, D. The boundary value problem for a static 2D Klein-Gordon equation in the infinite strip and in the half-plane. Mathematics 2015, 40, 205–227. [Google Scholar]
- Cheng, H.; Mu, X.; Jiang, H.; Liu, G.; Wei, M. Green’s Function for the boundary value problem of thestatic Klein-Gordon equation stated on a rectangular region and its convergence analysis. Bound. Value Probl. 2017, 2017, 72. [Google Scholar] [CrossRef]
- Courant, R.; Hilbert, D. Methods of Mathematical Physics; Interscience Publishers Inc.: New York, NY, USA, 1953. [Google Scholar]
- Sasaki, Y.K. Some basic formulisms in numerical variational analysis. Mon. Weather Rev. 1970, 98, 875–883. [Google Scholar] [CrossRef]



| Pos | (17, 47) | (59, 21) | (62, 58) | (78, 36) | (67, 44) | (50, 28) | (28, 22) | (52, 25) |
|---|---|---|---|---|---|---|---|---|
| Obs | 1.2 | 0.7 | 1.8 | 2.7 | 2.3 | 0.9 | 0.2 | 0.6 |
| Rad | 30 | 27 | 47 | 35 | 38 | 31 | 11 | 30 |
| Rtr | 1.2322 | 0.9353 | 3.2013 | 1.6780 | 3.5835 | 0.9404 | 0.1644 | 0.7484 |
| Joi | 0.2224 | 0.1274 | 5.2259 | 0.5629 | 0.9826 | 0.2678 | 0.0065 | 0.2224 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Mu, X.; Jiang, H.; Wei, M.; Liu, G. Green’s Function for Static Klein–Gordon Equation Stated on a Rectangular Region and Its Application in Meteorology Data Assimilation. Atmosphere 2021, 12, 1602. https://doi.org/10.3390/atmos12121602
Cheng H, Mu X, Jiang H, Wei M, Liu G. Green’s Function for Static Klein–Gordon Equation Stated on a Rectangular Region and Its Application in Meteorology Data Assimilation. Atmosphere. 2021; 12(12):1602. https://doi.org/10.3390/atmos12121602
Chicago/Turabian StyleCheng, Hao, Xiyu Mu, Hua Jiang, Ming Wei, and Guoqing Liu. 2021. "Green’s Function for Static Klein–Gordon Equation Stated on a Rectangular Region and Its Application in Meteorology Data Assimilation" Atmosphere 12, no. 12: 1602. https://doi.org/10.3390/atmos12121602
APA StyleCheng, H., Mu, X., Jiang, H., Wei, M., & Liu, G. (2021). Green’s Function for Static Klein–Gordon Equation Stated on a Rectangular Region and Its Application in Meteorology Data Assimilation. Atmosphere, 12(12), 1602. https://doi.org/10.3390/atmos12121602






