Abstract
The drag coefficient is essential for calculating the aerodynamic friction between air and sea. In this study, we regress a set of relationships between the drag coefficient and the wind speed for different wind ranges using an observational dataset that consists of 5941 estimates of the mean flow and fluxes from 11 aircraft turbulent measurements over the sea surface. Results show that: (1) the drag coefficient is a power function of wind speed over smooth sea surface when it is no greater than 4.5 ms−1, and the drag coefficient decreases with the increase of wind speed; and (2) for rough sea surface, when the wind speed is greater than 4.5 ms−1 and less than or equal to 10.5 ms−1, the drag coefficient increases linearly with the increase of horizontal wind speed; when the wind speed is greater than 10.5 ms−1 and less than or equal to 33.5 ms−1, the drag coefficient changes parabolically with the increase of wind speed; when the wind speed is greater than 33.5 ms−1, the drag coefficient is constant. Additionally, regressed from drag coefficient, the saturated wind speed threshold is 23 ms−1. Parameterizations of turbulent heat transfer coefficient () and water vapor transfer coefficient () are also investigated.
1. Introduction
The wind stress acting on the sea surface is important for both the structure of the atmospheric boundary layer over the sea as well as the movements of ocean mixed layer and ocean currents [1]. The wind stress depends not only on the wind speed, but also on the drag coefficient () or the aerodynamic roughness length () [2,3]. Over the years, there has been great interest and effort in the community to parameterize for a wide range of wind conditions [4]. Traditionally, in very low wind environments, sea surface is aerodynamically smooth, and the roughness Reynolds number is approximately 0.11, so that is given by Equation (1).
where υ is the kinematic viscosity of air, and is the surface friction velocity, , where , , and are the perturbations in vertical velocity, meridional wind, and zonal wind. The roughness Reynolds number . When the 10-m wind speed is greater than 5.5 ms−1, correspondingly, is greater than 0.23 ms−1, and is greater than 2, and sea surface becomes fully rough flow while is given by Equation (2).
where is the Charnock’s constant, and = 0.012, and g is the acceleration due to gravity, which characterizes the equilibrium between wind and waves, with the spectrum of gravity waves acting as roughness elements. The transitional regime between smooth and fully rough sea surfaces corresponds to the 10-m wind speed ranging from 2.5 to 5.5 ms−1. Once is determined from , the neutral drag coefficient () can be obtained for smooth surface by
and for rough surface by
where k is the von Karman constant, and z is the measurement height.
Much effort has also gone into investigating the variation of with 10-m wind speed, particularly under high wind speed regime. Recently, it was found that drag coefficient increases with the 10-m wind speed under moderate wind speed and decreases with the 10-m wind speed under high wind speed (Table 1). However, the saturated wind speed thresholds obtained by different studies vary greatly, as summarized in Table 1. The lack of consensus on the magnitude of the saturated wind speed poses a challenge in modeling applications.

Table 1.
Values of the saturated 10-m wind speed (ms−1) from the literature.
Following Gao et al. [5], we directly used the wind speed measured by aircraft in Equations (3) and (4), and did not convert the wind speed measured by the aircraft to the wind speed at a height of 10 m, since the logarithmic wind profile hypothesis and the constant flux layer hypothesis over the layer may bring additional errors.
Previous studies usually used a single or fewer databases for regression tests where the wind speed usually could not cover the wind speed range from calm, light wind to high wind, and a limited number of samples usually reduce the representativeness of regression results. Unlike most of the prior studies, the motivation of this study is to use a large sample database to obtain more convincing regression results, and to provide a simple parameterization that is more representative and may be used in a fully coupled (atmosphere–wave–ocean) hurricane prediction model. To achieve this goal, we developed a new set of equations of the sea surface drag coefficient () that are solely dependent on wind speed and over a full range of wind speeds. We also used a large dataset of eddy-covariance turbulence flux measurements over the sea surfaces, which are collected from 11 different experiments from 1992 to 2008 on four different aircrafts. There are 5941 sample data in total.
2. Database
The Oregon State University aircraft marine boundary layer air-sea dataset described in detail by Vickers et al. [14] is used in this study, and the locations of the 11 aircraft experiments are shown in Figure 1. The horizontal averaging segment is 4 km at the typical aircraft speed, and the maximum (4 km average) aircraft altitude is 50 m. This dataset consists of turbulent wind speed, air temperature, and water vapor collected by the following:
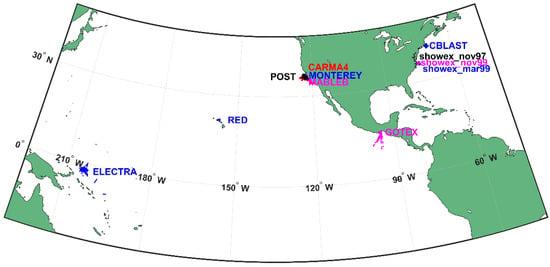
Figure 1.
The 11 aircraft experiments’ locations.
- (1)
- The Long-EZ aircraft of the National Oceanic and Atmospheric Administration (NOAA) during the four experiments: (1) the pilot program of the Coupled Boundary Layers and Air Sea Transfer experiment (CBLAST Weak Wind) conducted during July–August 2001 over the Atlantic Ocean south of Martha’s Vineyard Island, MA [15]; (2) the Shoaling Waves experiment (SHOWEX) over the Atlantic east of the Outer Banks near Duck, NC during November and December 1999 [16]; (3) the SHOWEX pilot study in November 1997; and (4) the SHOWEX pilot study in March 1999.
- (2)
- The Naval Postgraduate School’s Center for Interdisciplinary Remotely-Piloted Aircraft Studies (CIRPAS) Twin Otter aircraft in five experiments: (1) outside Monterey Bay off the coast of California during the Cloud-Aerosol Research in the Marine Atmosphere IV experiment (CARMAIV) in August 2007; (2) outside Monterey Bay (Monterey) during April 2008 [17]; (3) the Rough Evaporation Duct experiment (RED) during August–September of 2001 to the east (windward side) of Oahu in the Hawaiian Islands [18]; (4) the Marine Atmospheric Boundary Layer Energy Budget (MABLEB) experiment during April 2007; and (5) the Physics Of Stratocumulus Top during July–August 2008 (POST).
- (3)
- The C-130 Hercules aircraft of the National Center for Atmospheric Research (NCAR) in the Gulf of Tehuantepec Experiment (GOTEX) in February 2004 on the Pacific coast of the Isthmus of Tehuantepec, Mexico [19], and the data collected by the NCAR Electra aircraft in TOGA COARE during November 1992 to February 1993 in the Pacific warm pool [20].
3. Results
3.1. Variation of Friction Velocity () against Wind Speed
Figure 2 shows the friction velocity against the wind speed () for all 11 experiments. is derived from the fast measurements of three-dimensional wind speed. Overall, increased with increasing . Figure 2 shows that most of the data were collected with a wind speed of less than 17 ms−1 during the 11 experiments. Almost all of the data with wind speeds greater than 17 ms−1 were collected by the C-130 Hercules aircraft of National Center for Atmospheric Research (NCAR) in February 2004, in the Gulf of Tehuantepec Experiment (GOTEX) which took place near the coast area of Isthmus of Tehuantepec, Mexico [19]. The correlation coefficient between and is 0.90.
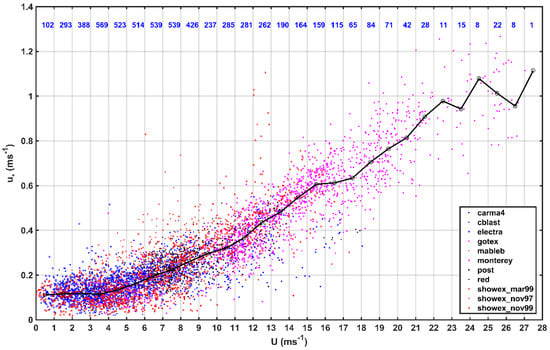
Figure 2.
The scattered plot of friction velocity () against wind speed () measured during the 11 aircraft experiments. The black line with circle is the median and the number of samples for each group of data is labeled in blue.
Statistically, the non-uniformity of the sample distribution affects the statistical results, which means that if the data in Figure 2 are directly used to regress the relationship between the friction velocity and the wind speed, the relationship should be more representative when the wind speed is less than 17 ms−1. Meanwhile, we found that the changes in frictional speed with the changes in wind speed from the 11 experiments were consistent, so we combined the observational data from those experiments. With an interval of 1 ms−1, these data were categorized into 28 bins, and the number of samples in each bin was shown at the top of Figure 2.
3.2. Parameterizations of Turbulent Drag Coefficient ()
Figure 3I shows the drag coefficient () against wind speed () for all of the 11 experiments. is obtained by taking the square of the ratio over . If the wind speed is less than 4.5 ms−1, the air–sea interaction is mainly achieved by viscous motion. We regressed the relationship between and for all of the 11 experiments in Equation (5). The standard error of the estimate (SEE) of is 1.4 × 10−7.
when the wind speed is higher than 4.5 ms−1, increased with increasing . By using the median numbers of these data bins, the relationship between the drag coefficient and is regressed as
where a, b, and c are regression coefficients. is found to have a parabolic relationship with using these 11 different regression tests:
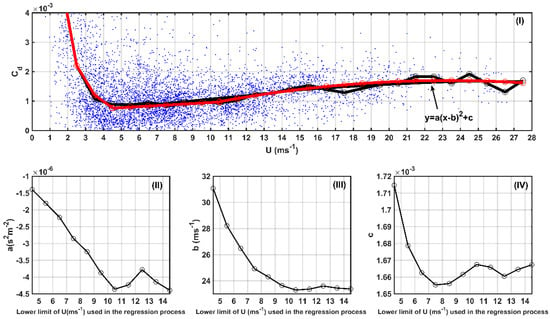
Figure 3.
(I) Similar to Figure 2, but for drag coefficient. The black line with circles is the median number line. The red lines are the parabolic regression lines for all for all 11 tests. (II–IV) are variations of parabolic regression coefficients (a, b, and c) against the lower limit of wind speed in the regression process. The red line with dots is regression line segments.
Test #1: are median numbers of bins: 4–5 ms−1, 5–6 ms−1,…, and 27–28 ms−1;
Test #2: are median numbers of bins: 5–6 ms−1, 6–7 ms−1,…, and 27–28 ms−1;
Test #11: are median numbers of bins: 14–15 ms−1, 16–17 ms−1,…, and 27–28 ms−1.
The regression coefficients (a, b, and c) obtained during 11 different tests are shown in Figure 3II–IV, respectively. The value of (a) reflects the nonlinearity of the parabola. While the critical (or saturated) wind speed is indicated by the value of b in Equation (6), and at the critical wind speed reaches its local maximum. Figure 3III shows that the values of b range from 31.07 to 23.30 ms−1 and gradually converge as the lower limit of the wind speed range corresponding to the regression data continues to increase. The results of b obtained here are not only consistent with the results of many previous studies, but they also explain the great difference in the critical wind speeds from previous studies. The maximum critical wind speed we obtained (corresponding to test #1) is 31.07 ms−1, which is slightly smaller than those from previous studies [6,7,8]. A possible reason is that the data in this work have wind speed generally smaller than 28 ms−1, while the relatively lower wind speed range may affect the regression and bring in uncertainty. In this study, we calculated the drag coefficient directly from the wind speed measured by aircrafts, and we did not convert the wind speed measured by the aircrafts to the wind speed at a height of 10 m, since the conversion may introduce additional errors. Recently, some studies also mentioned the height conversion of wind speed. For example, Mahrt et al. [21] used the data collected during two Floating Instrument Platform field campaigns and the data collected at the Air–Sea Interaction Tower site, to investigate the relationship between the wind and sea surface stress for contrasting conditions. They found that the sea surface wind stress decreased significantly with height near the surface under thin marine boundary layers and/or enhanced stress divergence close to the sea surface conditions. It is worth noting that b converges when the lower limit of the wind speed range corresponding to the regression process is about 10.5 ms−1. Therefore, 10.5 ms−1 may be a threshold value, that is, when the wind speed is less than 10.5 ms−1, is a linear function of wind speed; when the wind speed is greater than 10.5 ms−1, is a parabolic function of wind speed. Figure 3IV shows that the value of c ranges from 1.715 × 10−3 to 1.655 × 10−3. It is lower than previous values because we calculated the drag coefficient directly from the wind speed measured by the aircraft rather than using the 10-m wind speed. In summary, when the wind speed is less than 10.5 ms−1, we recommend using a linear equation to approximate the relationship between and . Following Garratt [1], we regressed the relationship between and for case: 4.5 ms−1< ≤10.5 ms−1 for all of the 11 experiments in Equation (6). The standard error of the estimate (SEE) of is 5.3 × 10−9. We plotted the values of estimated by Equations (5) and (7) onto Figure 3I (red line with circles).
For wind speeds greater than 10.5 ms−1, we recommend using the following equation to approximate it.
Equation (8) implies that will be negative when > 43 ms−1. Unfortunately, we have never observed such high wind speeds, so it is difficult to define the upper limit of the applicable wind speed scope of Equation (8). For the sake of brevity, and considering the symmetry of parabola, we recommend that modelers use the value (1.20 × 10−3) when the wind speed is 10.5 ms−1 as the value when the wind speed is greater than or equal to 33.5 ms−1. It is obvious that, since the maximum wind speed in the database we used is 27.05 ms−1, the Equation (8) under conditional wind speed greater than 27 ms−1 is purely mathematical, lacking the support of observational data.
3.3. Parameterizations of Turbulent Heat Transfer Coefficient () and Water Vapor Transfer Coefficient ()
We regressed the relationship between and for the wind speed less than or equal to 4.5 ms−1 for all of the 11 experiments in Equation (9). SEE of is 6.78 × 10−8.
and a linear relationship between and for the wind speed higher than 4.5 ms−1 and less than or equal to 10.5 ms−1 for all of the 11 experiments is expressed in Equation (10). SEE of is 6.36 × 10−8.
We plotted the values of estimated by Equations (9) and (10) onto Figure 4a (red line with circles). When 10.5 ms−1 < ≤ 23 ms−1, is almost a constant (9.39 × 10−4) and When > 23 ms−1, is almost a constant (3.25 × 10−4). We also plot these two values onto Figure 4a.
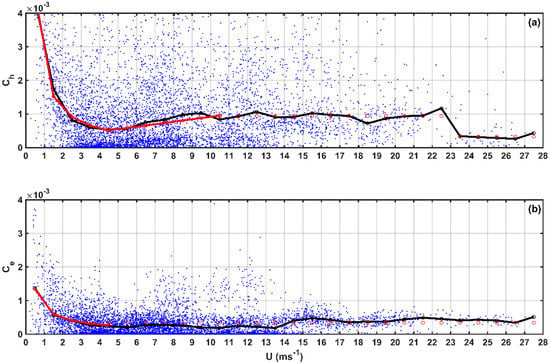
Figure 4.
Similar to Figure 3I, but for turbulent heat transfer coefficient (a) and turbulent water vapor transfer coefficient (b). The red line with circles is regression results.
The variation of turbulent heat transfer coefficient () and water vapor transfer coefficient () along with wind speed () are presented in Figure 4. It can be seen from Figure 3I and Figure 4a that is distributed more dispersedly than . This is because that not only the dynamic process but also the thermal process affect the turbulent heat transfer, which lead to more complexity and uncertainty. We plotted the values of estimated by Equation (9) onto Figure 4a (red line with circles). Unlike Figure 4a,b shows a more concentrated distribution of turbulent water vapor transport coefficients, which is also a result of the assumed saturated surface water vapor in the calculation. We also regressed the relationship between and for the wind speed less than 4.5 ms−1 for all of the 11 experiments in Equation (10). SEE of is 2.66 × 10−9. We plotted the values of estimated by Equation (11) onto Figure 4b (red line with circles)
When > 4.5 ms−1, is almost a constant (3.4 × 10−4), which is also shown in Figure 4b.
Alamaro et al. [6] concluded that the value of strongly affected hurricane intensity. Strictly speaking, is not the sum of and , but since we only have sensible heat flux and latent heat flux data, and lack turbulence original observation data, here, we roughly take as the sum of and . We illustrate enthalpy transfer coefficient (≡ + ) and in Figure 5a, and the variations of with wind speed are shown in Figure 5b. It can be seen from Figure 4 and Figure 5 that when reaches at 23 ms−1 suddenly decreases and keeps almost invariant after. However, variations of with wind speed (especially a sudden drop) under strong wind conditions are rarely shown in previous studies. Figure 5b shows > 1 under moderate wind speed and < 1 under low and high wind speed.
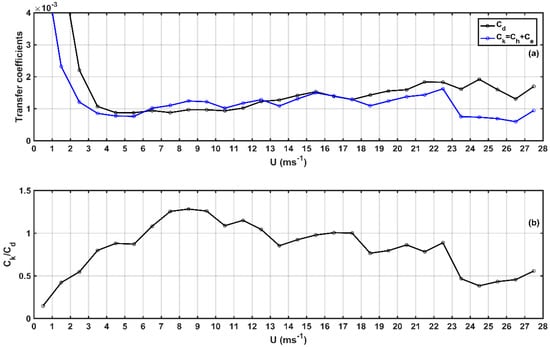
Figure 5.
(a) The median number variations of drag coefficient () and enthalpy transfer coefficient against wind speed () measured during the 11 aircraft experiments; (b) The value of against wind speed () measured during the 11 aircraft experiments.
4. Conclusions
We derived a suite of functions of drag coefficient, heat transfer coefficient, and water vapor transfer coefficient with respect to wind speed under all wind conditions as follows:
We also found a power relationship between heat and water vapor transfer coefficients and wind speed using the turbulent data collected from aircraft measurements conducted in 11 experiments. A saturated wind speed of 23 ms−1 is found based on the regression of wind speed and drag coefficient. Since the maximum wind speed in the database we used is 27.05 ms−1, the expression of under conditional wind speed greater than 27 ms−1 is only the product of mathematical derivation, lacking the support of observational data. Therefore, we provide the expression of for the full wind speed range for use in models. In this study, since these 11 experiments did not measure these parameters, we did not consider the dependence of on wave parameters (such as wave age and wave height). Therefore, the equations we have derived in this study are useful for atmospheric models, and they could be further improved in the future with advanced measurements of other parameters. Parameterizations of turbulent heat transfer coefficient () and water vapor transfer coefficient () are also investigated. It is found that they are almost independent of wind speed under strong wind conditions: is 9.39 × 10−4 when 10.5 ms−1 < ≤ 23 ms−1; while is 3.4 × 10−4 when > 4.5 ms−1.
Author Contributions
Conceptualization, methodology, investigation, data curation, S.Z., J.Z. and Z.Z.; Formal analysis and writing–review, X.B.; Editing and supervision, Z.G. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Key Research and Development Program of Ministry of Science and Technology of China (2018YFC1506405), and by National Natural Science Foundation of China (Grants 41275022 and 41975067).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding references in this paper.
Acknowledgments
All the dedicated scientists who collected and made available the fast response aircraft data are greatly appreciated. The database used in this work was created by the North West Research Associates under the U.S. Office of Naval Research (ONR) supports. We are very grateful to three anonymous reviewers for their careful review and valuable comments, which lead to substantial improvement of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: New York, NY, USA, 1992; p. 316. [Google Scholar]
- Nosov, V.V.; Lukin, V.P.; Nosov, E.V.; Torgaev, A.V. Turbulence Scales of the Monin-Obukhov Similarity Theory in the Anisotropic Mountain Boundary Layer. Russ. Phys. J. 2020, 63, 244–249. [Google Scholar] [CrossRef]
- Shikhovtsev, A.; Kovadlo, P.; Lukin, V. Temporal variations of the turbulence profiles at the Sayan solar observatory site. Atmosphere 2019, 10, 499. [Google Scholar] [CrossRef] [Green Version]
- Deskos, G.; Carre, A.; Palacios, R. Assessment of low-altitude atmospheric turbulence models for aircraft aeroelasticity. J. Fluids Struct. 2020, 95, 102981. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Peng, W.; Gao, C.Y.; Li, Y. Parabolic dependence of the drag coefficient on wind speed from aircraft eddy-covariance measurements over the tropical Eastern Pacific. Sci. Rep. 2020, 10, 1805. [Google Scholar] [CrossRef] [PubMed]
- Alamaro, M.; Emanuel, K.A.; McGillis, W.R. Experimental investigation of air-sea transfer of momentum and enthalpy at high wind speed. In Preprints, Proceedings of the 25th Conference on Hurricane and Tropical Meteorology, San Diego, CA, USA, 28 April–3 May 2002; American Meteorological Society: San Diego, CA, USA, 2002; pp. 667–668. [Google Scholar]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Donelan, M.A.; Haus, B.K.; Reul, N.; Plant, W.J.; Stiassnie, M.; Graber, H.C.; Brown, O.B.; Saltzman, E.S. On the limiting aerodynamic roughness of the ocean in very strong winds. Geophys. Res. Lett. 2004, 31, L18306. [Google Scholar] [CrossRef] [Green Version]
- Makin, V.K. A note on drag of the sea surface at Hurricane winds. Bound. Layer Meteorol. 2005, 115, 169–176. [Google Scholar] [CrossRef]
- Black, P.G.; Dasaro, E.A.; Drennan, W.M.; French, J.R.; Niiler, P.P.; Sanford, T.B.; Terrill, E.; Walsh, E.J.; Zhang, J.A. Air–Sea Exchange in Hurricanes: Synthesis of Observations from the Coupled Boundary Layer Air-Sea Transfer Experiment. Bull. Am. Meteorol. Soc. 2007, 88, 357–374. [Google Scholar] [CrossRef] [Green Version]
- Troitskaya, Y.I.; Sergeev, D.A.; Kandaurov, A.A.; Baidakov, G.A.; Vdovin, M.A.; Kazakov, V.I. Laboratory and theoretical modeling of air-sea momentum transfer under severe wind conditions. J. Geophys. Res. 2012, 117, C00J21. [Google Scholar] [CrossRef]
- Soloviev, A.V.; Lukas, R.; Donelan, M.A.; Haus, B.K.; Ginis, I. The air-sea interface and surface stress under tropical cyclones. Sci. Rep. 2014, 4, 5306. [Google Scholar] [CrossRef]
- Donelan, M.A. On the decrease of the oceanic drag coefficient in high winds. J. Geophys. Res. Ocean. 2018, 123, 1485–1501. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L.; Andreas, E.L. Estimates of the 10-m neutral sea surface drag coefficient from aircraft eddy-covariance measurements. J. Phys. Oceanogr. 2013, 43, 301–310. [Google Scholar] [CrossRef]
- Edson, J.B.; Crawford, T.; Crescenti, J.; Farrar, T.; Frew, N.; Gerbi, G.; Helmis, C.; Hristov, T.; Khelif, D.; Jessup, A.; et al. The coupled boundary layers and air-sea transfer experiment in low winds. Bull. Am. Meteorol. Soc. 2007, 88, 341–356. [Google Scholar] [CrossRef]
- Sun, J.; Vandemark, D.; Mahrt, L.; Vickers, D.; Crawford, T.; Vogel, C. Momentum transfer over the coastal zone. J. Geophys. Res. 2001, 106, 12437–12448. [Google Scholar] [CrossRef] [Green Version]
- Khelif, D.; Burns, S.P.; Friehe, C.A. Improved wind measurements on research aircraft. J. Atmos. Ocean. Technol. 1999, 16, 860–875. [Google Scholar] [CrossRef]
- Anderson, K.; Brooks, B.; Caffrey, P.; Clarke, A.; Cohen, L.; Crahan, K.; Davidson, K.; De Jong, A.; De Leeuw, G.; Dion, D.; et al. The RED Experiment: An assessment of boundary layer effects in a trade winds regime on microwave and infrared propagation over the sea. Bull. Am. Meteorol. Soc. 2014, 85, 1355–1366. [Google Scholar] [CrossRef]
- Raga, G.; Abarca, S. On the parameterization of turbulent fluxes over the tropical eastern Pacific. Amer. Chem. Phys. 2007, 7, 635–643. [Google Scholar] [CrossRef] [Green Version]
- Vickers, D.; Esbensen, S.K. Subgrid surface fluxes in fair weather conditions during TOGA COARE: Observational estimates and parameterization. Mon. Weather Rev. 1998, 126, 620–633. [Google Scholar] [CrossRef]
- Mahrt, L.; Scott, M.; Tihomir, H.; James, E. On Estimating the Surface Wind Stress over the Sea. J. Phys. Oceanogr. 2018, 48, 1533–1541. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).