Global Radiative Sky Cooling Potential Adjusted for Population Density and Cooling Demand
Abstract
:1. Introduction
2. Methodology
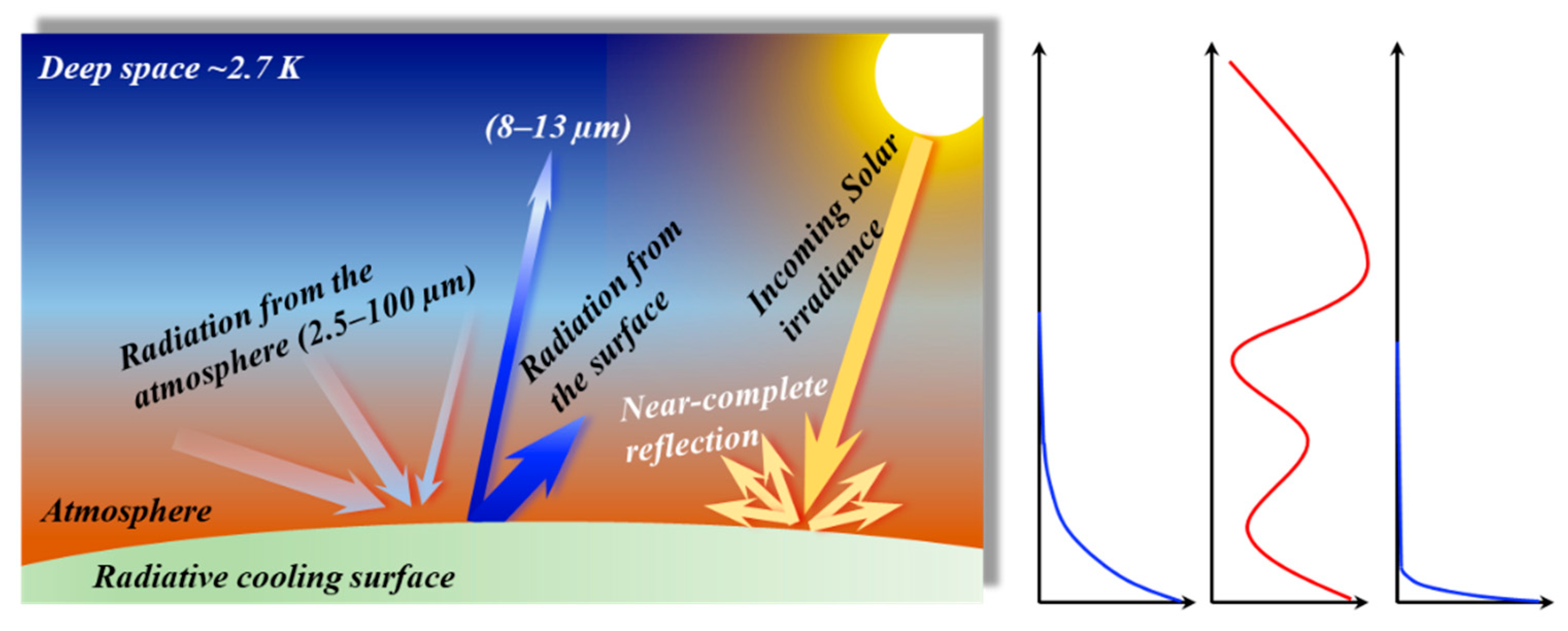
2.1. Radiative Cooling Model
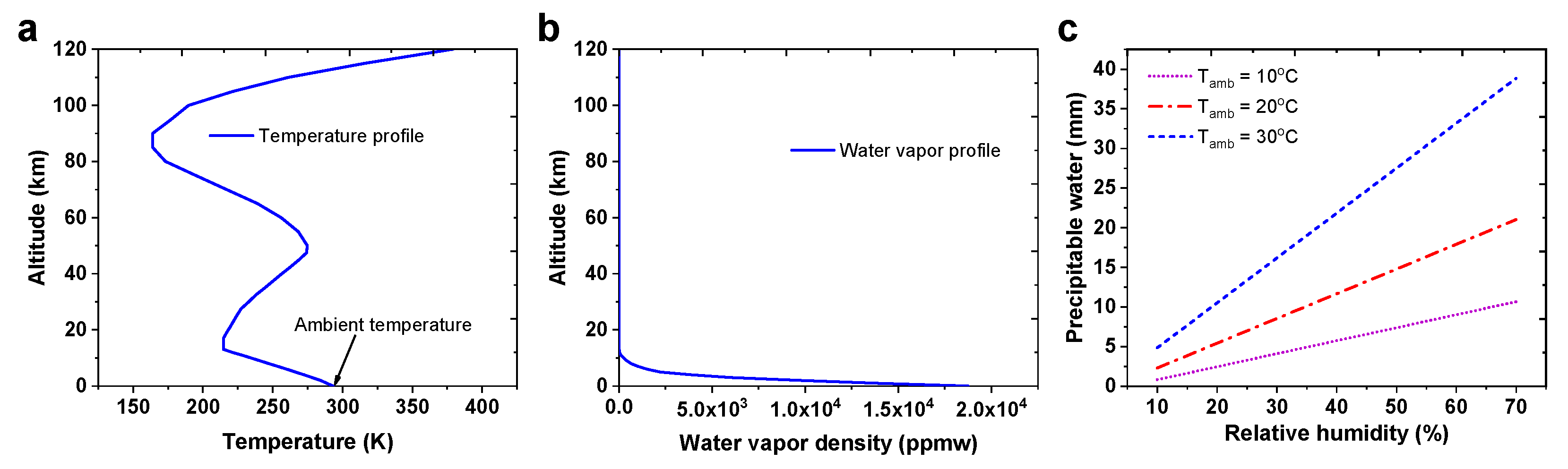
2.2. Effective Atmospheric Emissivity
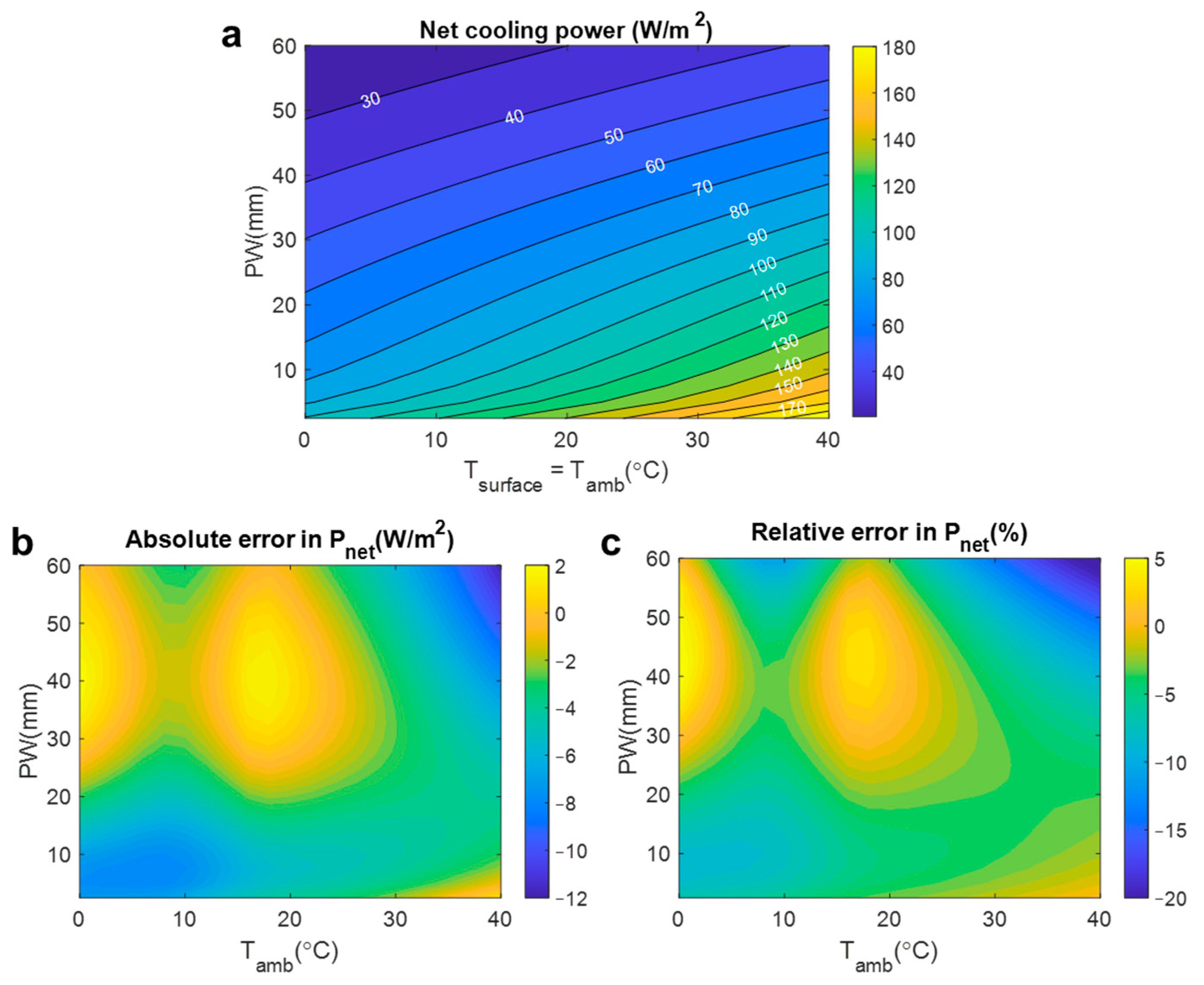
2.3. Radiative Cooling Potential
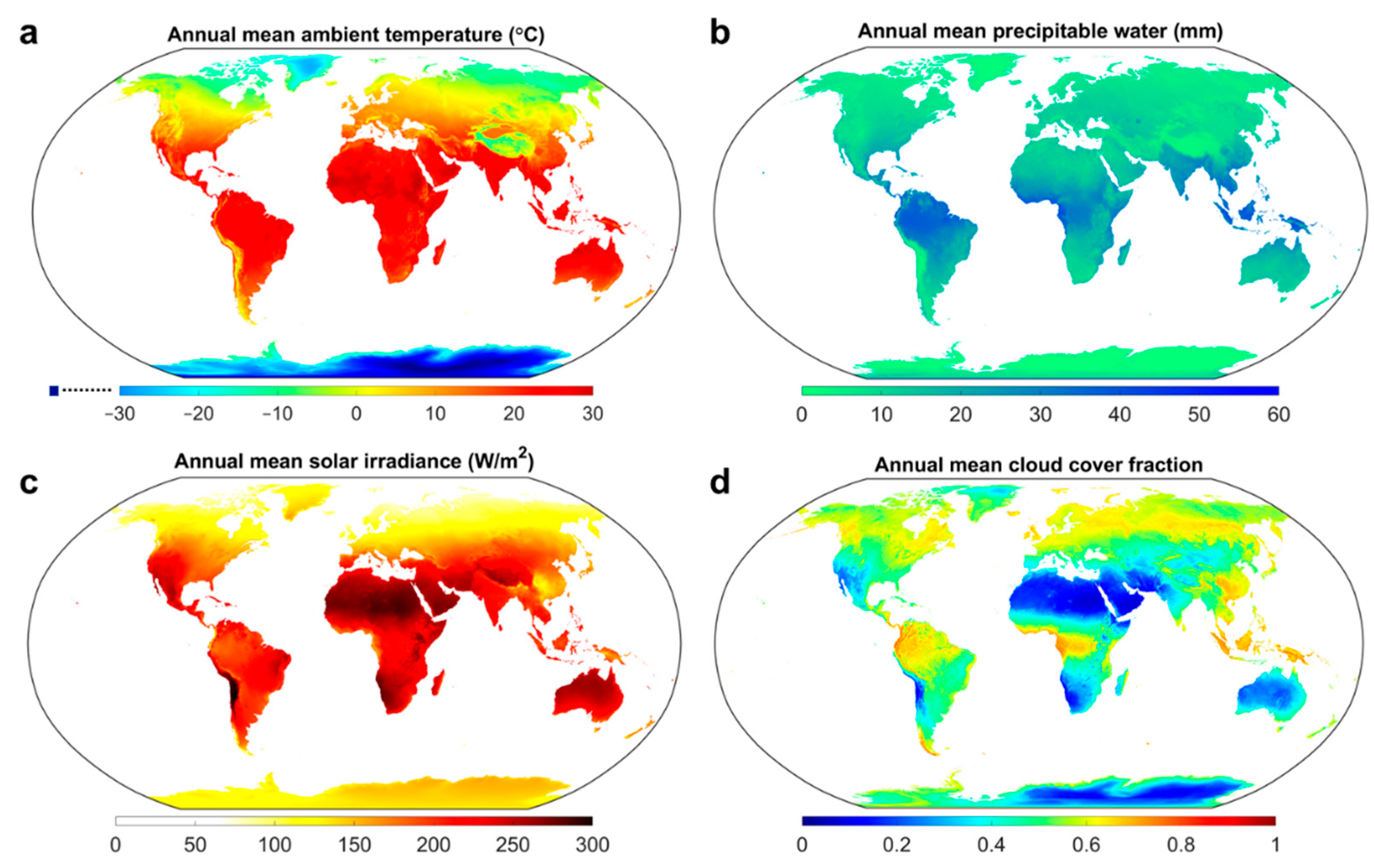
2.4. Global Datasets of Weather, Population Density, and Cooling Degree Days
3. Results
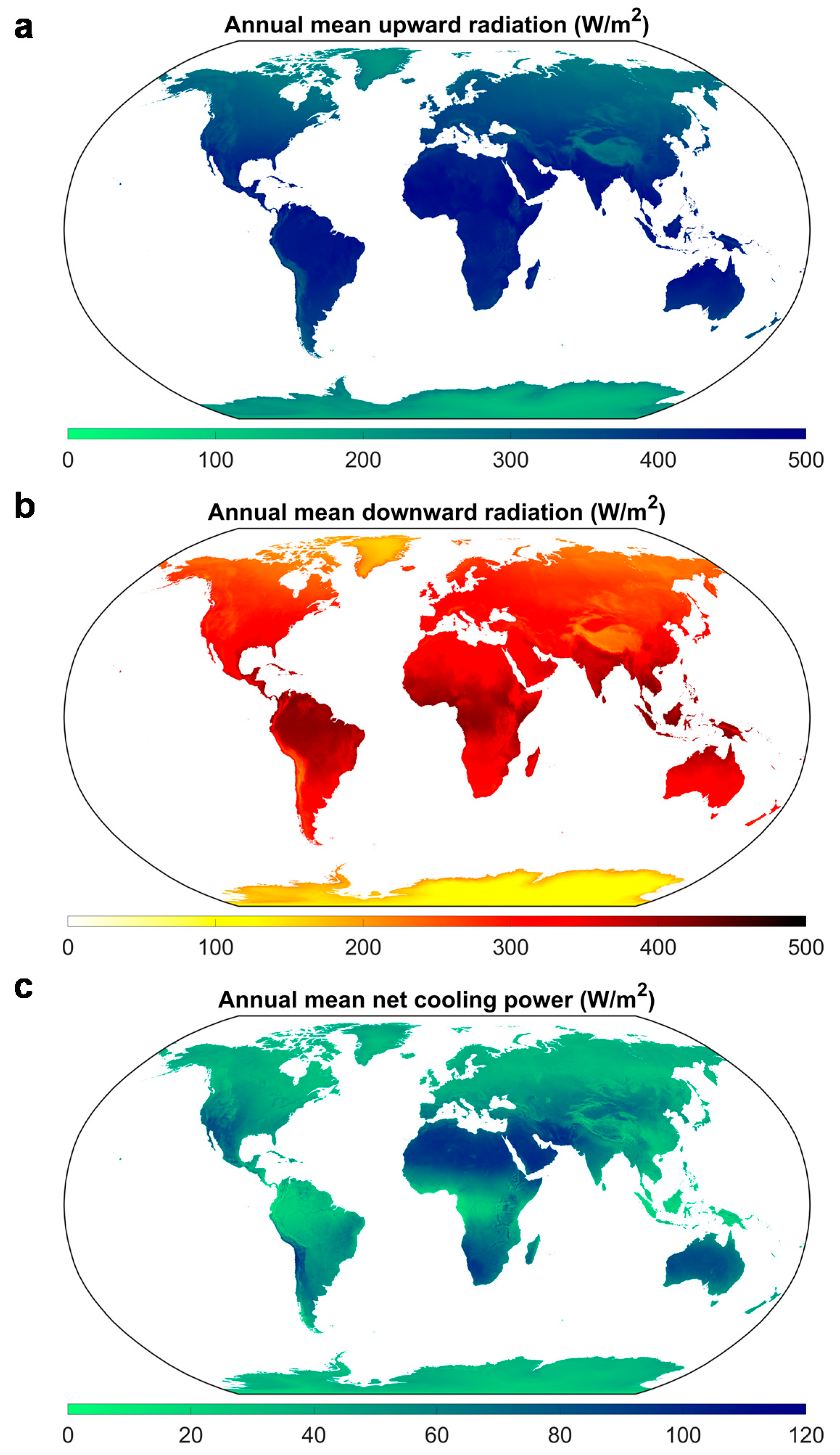
3.1. Global Radiative Cooling Potential
3.2. Global Radiative Cooling Potential Anomaly
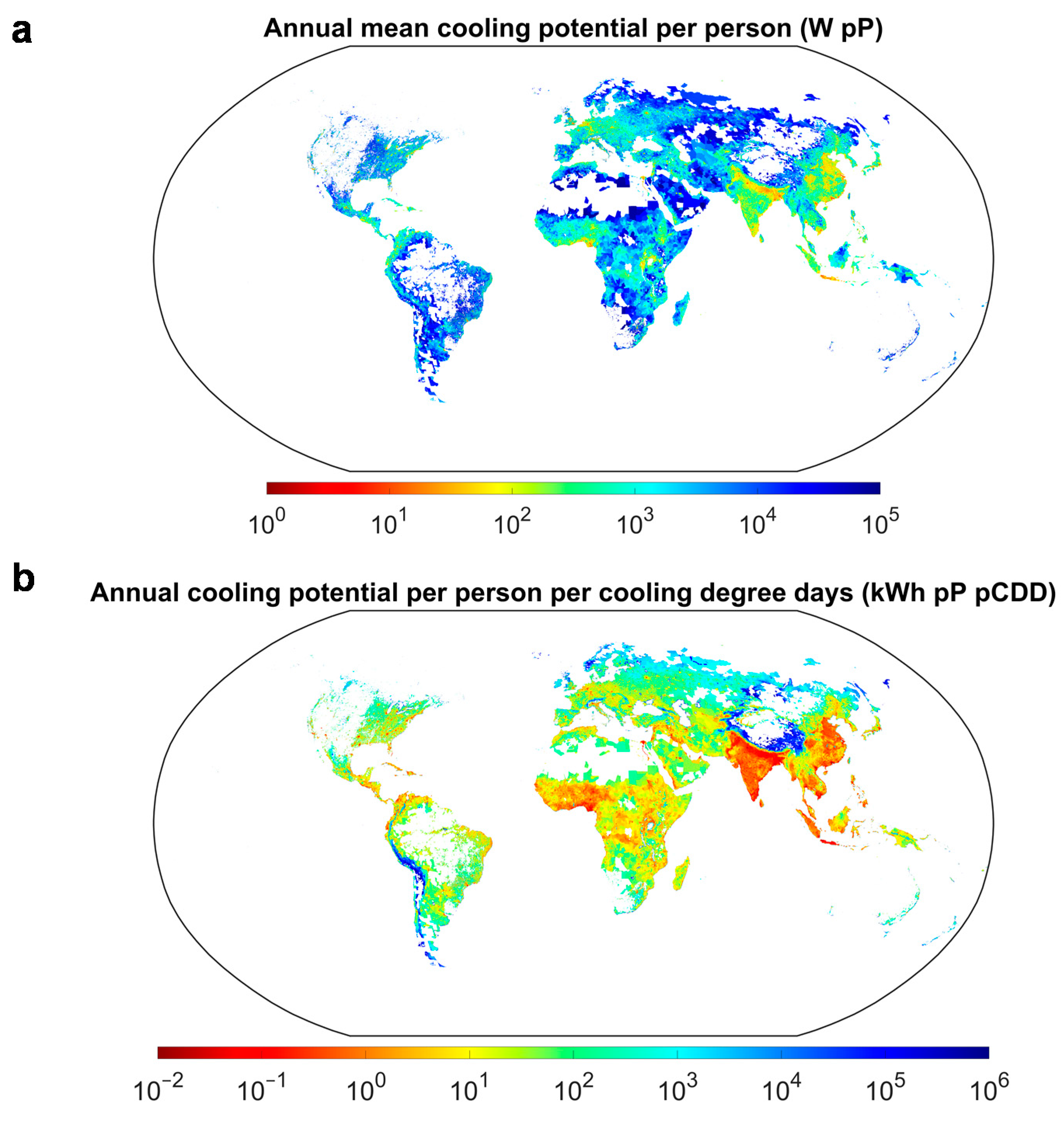
3.3. Global Radiative Cooling Potential Adjusted for Population Density and Cooling Demand
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kiehl, J.T.; Trenberth, K.E. Earth’s Annual Global Mean Energy Budget. Bull. Am. Meteorol. Soc. 1997, 78, 197–208. [Google Scholar] [CrossRef] [Green Version]
- Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, K.J. (Eds.) Fundamental Astronomy; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Zhao, D.; Aili, A.; Zhai, Y.; Xu, S.; Tan, G.; Yin, X.; Yang, R. Radiative sky cooling: Fundamental principles, materials, and applications. Appl. Phys. Rev. 2019, 6, 021306. [Google Scholar] [CrossRef]
- Haechler, I.; Park, H.; Schnoering, G.; Gulich, T.; Rohner, M.; Tripathy, A.; Milionis, A.; Schutzius, T.; Poulikakos, D. Exploiting radiative cooling for uninterrupted 24-hour water harvesting from the atmosphere. Sci. Adv. 2021, 7, 1–10. [Google Scholar] [CrossRef]
- Raman, A.; Anoma, M.A.; Zhu, L.; Rephaeli, E.; Fan, S. Passive radiative cooling below ambient air temperature under direct sunlight. Nature 2014, 515, 540–544. [Google Scholar] [CrossRef]
- Zhai, Y.; Ma, Y.; David, S.N.; Zhao, D.; Lou, R.; Tan, G.; Yang, R.; Yin, X. Scalable-manufactured randomized glass-polymer hybrid metamaterial for daytime radiative cooling. Science 2017, 355, 1062–1066. [Google Scholar] [CrossRef] [Green Version]
- Mandal, J.; Fu, Y.; Overvig, A.C.; Jia, M.; Sun, K.; Shi, N.N.; Zhou, H.; Xiao, X.; Yu, N.; Yang, Y. Hierarchically porous polymer coatings for highly efficient passive daytime radiative cooling. Science 2018, 362, 315–319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leroy, A.; Bhatia, B.; Kelsall, C.C.; Castillejo-Cuberos, A.; Di Capua H, M.; Zhao, L.; Zhang, L.; Guzman, A.M.; Wang, E.N. High-performance subambient radiative cooling enabled by optically selective and thermally insulating polyethylene aerogel. Sci. Adv. 2019, 5, eaat9480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, T.; Zhai, Y.; He, S.; Gan, W.; Wei, Z.; Heidarinejad, M.; Dalgo, D.; Mi, R.; Zhao, X.; Song, J.; et al. A radiative cooling structural material. Science 2019, 364, 760–763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aili, A.; Wei, Z.; Chen, Y.; Zhao, D.; Yang, R.; Yin, X. Selection of polymers with functional groups for daytime radiative cooling. Mater. Today Phys. 2019, 10, 100127. [Google Scholar] [CrossRef]
- Zhu, L.; Raman, A.; Fan, S. Color-preserving daytime radiative cooling. Appl. Phys. Lett. 2013, 103, 223902. [Google Scholar] [CrossRef]
- Goldstein, E.A.; Raman, A.P.; Fan, S. Sub-ambient non-evaporative fluid cooling with the sky. Nat. Energy 2017, 2, 17143. [Google Scholar] [CrossRef]
- Zhao, D.; Aili, A.; Zhai, Y.; Lu, J.; Kidd, D.; Tan, G.; Yin, X.; Yang, R. Subambient Cooling of Water: Toward Real-World Applications of Daytime Radiative Cooling. Joule 2018, 3, 111–123. [Google Scholar] [CrossRef] [Green Version]
- Aili, A.; Zhao, D.; Lu, J.; Zhai, Y.; Yin, X.; Tan, G.; Yang, R. A kW-scale, 24-hour continuously operational, radiative sky cooling system: Experimental demonstration and predictive modeling. Energy Convers. Manag. 2019, 186, 586–596. [Google Scholar] [CrossRef]
- Zhao, D.; Yin, X.; Xu, J.; Tan, G.; Yang, R. Radiative sky cooling-assisted thermoelectric cooling system for building applications. Energy 2019, 190, 116322. [Google Scholar] [CrossRef]
- Zhao, D.; Aili, A.; Yin, X.; Tan, G.; Yang, R. Roof-integrated radiative air-cooling system to achieve cooler attic for building energy saving. Energy Build. 2019, 203, 109453. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, D.; Yin, X.; Yang, R.; Tan, G. Energy saving and economic analysis of a new hybrid radiative cooling system for single-family houses in the USA. Appl. Energy 2018, 224, 371–381. [Google Scholar] [CrossRef]
- Fang, H.; Zhao, D.; Yuan, J.; Aili, A.; Yin, X.; Yang, R.; Tan, G. Performance evaluation of a metamaterial-based new cool roof using improved Roof Thermal Transfer Value model. Appl. Energy 2019, 248, 589–599. [Google Scholar] [CrossRef]
- Hanif, M.; Mahlia, T.; Zare, A.; Saksahdan, T.; Metselaar, H. Potential energy savings by radiative cooling system for a building in tropical climate. Renew. Sustain. Energy Rev. 2014, 32, 642–650. [Google Scholar] [CrossRef]
- Lu, X.; Xu, P.; Wang, H.; Yang, T.; Hou, J. Cooling potential and applications prospects of passive radiative cooling in buildings: The current state-of-the-art. Renew. Sustain. Energy Rev. 2016, 65, 1079–1097. [Google Scholar] [CrossRef]
- Dyreson, A.; Miller, F. Night sky cooling for concentrating solar power plants. Appl. Energy 2016, 180, 276–286. [Google Scholar] [CrossRef]
- Zhang, K.; Zhao, D.; Zhai, Y.; Yin, X.; Yang, R.; Tan, G. Modelling study of the low-pump-power demand constructal T-shaped pipe network for a large scale radiative cooled-cold storage system. Appl. Therm. Eng. 2017, 127, 1564–1573. [Google Scholar] [CrossRef]
- Stark, A.K.; Klausner, J.F. An R&D Strategy to Decouple Energy from Water. Joule 2017, 1, 416–420. [Google Scholar] [CrossRef]
- Zeyghami, M.; Khalili, F. Performance improvement of dry cooled advanced concentrating solar power plants using daytime radiative cooling. Energy Convers. Manag. 2015, 106, 10–20. [Google Scholar] [CrossRef]
- Aili, A.; Zhao, D.; Tan, G.; Yin, X.; Yang, R. Reduction of water consumption in thermal power plants with radiative sky cooling. Appl. Energy 2021, 302, 117515. [Google Scholar] [CrossRef]
- Zhu, L.; Raman, A.; Wang, K.X.; Anoma, M.A.; Fan, S. Radiative cooling of solar cells. Optica 2014, 1, 32–38. [Google Scholar] [CrossRef]
- Zhu, L.; Raman, A.P.; Fan, S. Radiative cooling of solar absorbers using a visibly transparent photonic crystal thermal blackbody. Proc. Natl. Acad. Sci. USA 2015, 112, 12282–12287. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Shi, Y.; Chen, K.; Zhu, L.; Fan, S. A Comprehensive Photonic Approach for Solar Cell Cooling. ACS Photon- 2017, 4, 774–782. [Google Scholar] [CrossRef]
- Zhan, Z.; ElKabbash, M.; Li, Z.; Li, X.; Zhang, J.; Rutledge, J.; Singh, S.; Guo, C. Enhancing thermoelectric output power via radiative cooling with nanoporous alumina. Nano Energy 2019, 65, 104060. [Google Scholar] [CrossRef]
- Ishii, S.; Dao, T.D.; Nagao, T. Radiative cooling for continuous thermoelectric power generation in day and night. Appl. Phys. Lett. 2020, 117, 013901. [Google Scholar] [CrossRef]
- Raman, A.P.; Li, W.; Fan, S. Generating Light from Darkness. Joule 2019, 3, 2679–2686. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, J.; Song, A.Y.; Catrysse, P.B.; Hsu, P.-C.; Cai, L.; Liu, B.; Zhu, Y.; Zhou, G.; Wu, D.S.; et al. Nanoporous polyethylene microfibres for large-scale radiative cooling fabric. Nat. Sustain. 2018, 1, 105–112. [Google Scholar] [CrossRef]
- Hsu, P.; Song, A.Y.; Catrysse, P.B.; Liu, C.; Peng, Y.; Xie, J.; Fan, S.; Cui, Y. Radiative human body cooling by nanoporous polyethylene textile. Science 2016, 353, 1019–1023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsu, P.-C.; Liu, C.; Song, A.Y.; Zhang, Z.; Peng, Y.; Xie, J.; Liu, K.; Wu, C.-L.; Catrysse, P.B.; Cai, L.; et al. A dual-mode textile for human body radiative heating and cooling. Sci. Adv. 2017, 3, e1700895. [Google Scholar] [CrossRef] [Green Version]
- Ono, M.; Chen, K.; Li, W.; Fan, S. Self-adaptive radiative cooling based on phase change materials. Opt. Express 2018, 26, A777–A787. [Google Scholar] [CrossRef]
- Chen, M.; Morsy, A.M.; Povinelli, M.L. Design of VO2-coated silicon microspheres for thermally-regulating paint. Opt. Express 2019, 27, 21787–21793. [Google Scholar] [CrossRef]
- Long, L.; Taylor, S.; Ying, X.; Wang, L. Thermally-switchable spectrally-selective infrared metamaterial absorber/emitter by tuning magnetic polariton with a phase-change VO2 layer. Mater. Today Energy 2019, 13, 214–220. [Google Scholar] [CrossRef]
- Li, W.; Shi, Y.; Chen, Z.; Fan, S. Photonic thermal management of coloured objects. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef]
- Chen, Y.; Mandal, J.; Li, W.; Smith-Washington, A.; Tsai, C.-C.; Huang, W.; Shrestha, S.; Yu, N.; Han, R.P.S.; Cao, A.; et al. Colored and paintable bilayer coatings with high solar-infrared reflectance for efficient cooling. Sci. Adv. 2020, 6, eaaz5413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sheng, C.; An, Y.; Du, J.; Li, X. Colored Radiative Cooler under Optical Tamm Resonance. ACS Photonics 2019, 6, 2545–2552. [Google Scholar] [CrossRef]
- Carlosena, L.; Ruiz-Pardo, Á.; Feng, J.; Irulegi, O.; Hernández-Minguillón, R.J.; Santamouris, M. On the energy potential of daytime radiative cooling for urban heat island mitigation. Sol. Energy 2020, 208, 430–444. [Google Scholar] [CrossRef]
- Wang, Z.-H.; Li, Q. Thermodynamic characterisation of urban nocturnal cooling. Heliyon 2017, 3, e00290. [Google Scholar] [CrossRef]
- Dong, M.; Chen, N.; Zhao, X.; Fan, S.; Chen, Z. Nighttime radiative cooling in hot and humid climates. Opt. Express 2019, 27, 31587–31598. [Google Scholar] [CrossRef]
- Liu, C.; Wu, Y.; Wang, B.; Zhao, C.; Bao, H. Effect of atmospheric water vapor on radiative cooling performance of different surfaces. Sol. Energy 2019, 183, 218–225. [Google Scholar] [CrossRef]
- Li, M.; Coimbra, C.F. On the effective spectral emissivity of clear skies and the radiative cooling potential of selectively designed materials. Int. J. Heat Mass Transf. 2019, 135, 1053–1062. [Google Scholar] [CrossRef]
- Li, M.; Peterson, H.B.; Coimbra, C.F.M. Radiative cooling resource maps for the contiguous United States. J. Renew. Sustain. Energy 2019, 11, 036501. [Google Scholar] [CrossRef]
- Yin, X.; Yang, R.; Tan, G.; Fan, S. Terrestrial radiative cooling: Using the cold universe as a renewable and sustainable energy source. Science 2020, 370, 786–791. [Google Scholar] [CrossRef] [PubMed]
- Zhao, B.; Hu, M.; Ao, X.; Chen, N.; Pei, G. Radiative cooling: A review of fundamentals, materials, applications, and prospects. Appl. Energy 2018, 236, 489–513. [Google Scholar] [CrossRef]
- Sun, X.; Sun, Y.; Zhou, Z.; Alam, M.A.; Bermel, P. Radiative sky cooling: Fundamental physics, materials, structures, and applications. Nanophotonics 2017, 6, 997–1015. [Google Scholar] [CrossRef]
- Vall, S.; Castell, A. Radiative cooling as low-grade energy source: A literature review. Renew. Sustain. Energy Rev. 2017, 77, 803–820. [Google Scholar] [CrossRef] [Green Version]
- Kondratyev, K.Y. Radiation in the Atmosphere; Academic Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Berk, A.; Hawes, F. Validation of MODTRAN®6 and its line-by-line algorithm. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 542–556. [Google Scholar] [CrossRef]
- MODTRAN®. Available online: http://modtran.spectral.com/modtran_order (accessed on 20 January 2021).
- Ruckstuhl, C.; Philipona, R.; Morland, J.; Ohmura, A. Observed relationship between surface specific humidity, integrated water vapor, and longwave downward radiation at different altitudes. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Yang, F.; Cheng, J. A framework for estimating cloudy sky surface downward longwave radiation from the derived active and passive cloud property parameters. Remote. Sens. Environ. 2020, 248, 111972. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. Global atmospheric downward longwave radiation over land surface under all-sky conditions from 1973 to 2008. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Martin, M.; Paul, B. Characteristics of infrared sky radiation in the United States. Sol. Energy 1984, 33, 321–336. [Google Scholar] [CrossRef] [Green Version]
- Allen, J.R.; Allen, J.R. Measurements of Cloud Emissivity in the 8–13 μ Waveband. J. Appl. Meteorol. Climatol. 1971, 10, 260–265. [Google Scholar] [CrossRef] [Green Version]
- World Wide Total Daily Precipitable Water Map. Available online: https://eldoradoweather.com/climate/world-maps/world-precipitable-water.html (accessed on 30 October 2020).
- Cloud Fraction & Water Vapor. Available online: https://neo.sci.gsfc.nasa.gov/view.php?datasetId=MODAL2_M_CLD_FR (accessed on 30 October 2020).
- Solomon, S.; Rosenlof, K.H.; Portmann, R.W.; Daniel, J.S.; Davis, S.M.; Sanford, T.J.; Plattner, G.-K. Contributions of Stratospheric Water Vapor to Decadal Changes in the Rate of Global Warming. Science 2010, 327, 1219–1223. [Google Scholar] [CrossRef] [Green Version]
- Perkins, S. Humidity holds the heat. Nat. Clim. Chang. 2010. [Google Scholar] [CrossRef]
- Kou, J.-L.; Jurado, Z.; Chen, Z.; Fan, S.; Minnich, A.J. Daytime Radiative Cooling Using Near-Black Infrared Emitters. ACS Photonics 2017, 4, 626–630. [Google Scholar] [CrossRef] [Green Version]
- Ye, C.; Li, M.; Hu, J.; Cheng, Q.; Jiang, L.; Song, Y. Highly reflective superhydrophobic white coating inspired by poplar leaf hairs toward an effective “cool roof”. Energy Environ. Sci. 2011, 4, 3364–3367. [Google Scholar] [CrossRef]
- ERA5-Land Monthly Averaged Data from 1981 to Present. Commission’s Copernicus Climate Change Service (2019). Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.68d2bb30?tab=overview (accessed on 6 October 2021).
- Water Vapor. Available online: https://neo.sci.gsfc.nasa.gov/view.php?datasetId=MYDAL2_M_SKY_WV (accessed on 18 January 2021).
- UN WPP-Adjusted Population Density, v4.11: Gridded Population of the World (GPW), v4; SEDAC. Center for International Earth Science Information Network—CIESIN—Columbia University: Palisades, NY, USA, 2018. [CrossRef]
- Mistry, M.N. A High-Resolution (0.25 Degree) Historical Global Gridded Dataset of Monthly and Annual Cooling and Heating Degree-Days (1970–2018) Based on GLDAS Data. 2019. Available online: https://doi.pangaea.de/10.1594/PANGAEA.903123?format=html#download (accessed on 18 January 2021).
- Mistry, M.N. Historical global gridded degree-days: A high-spatial resolution database of CDD and HDD. Geosci. Data J. 2019, 6, 214–221. [Google Scholar] [CrossRef] [Green Version]
- Davis, L.W.; Gertler, P.J. Contribution of air conditioning adoption to future energy use under global warming. Proc. Natl. Acad. Sci. USA 2015, 112, 5962–5967. [Google Scholar] [CrossRef] [Green Version]
- Trenberth, K.E.; Fasullo, J.; Kiehl, J. Earth’s Global Energy Budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–324. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. Global atmospheric downward longwave radiation at the surface from ground-based observations, satellite retrievals, and reanalyses. Rev. Geophys. 2013, 51, 150–185. [Google Scholar] [CrossRef]
- Stephens, G.L.; Wild, M.; Stackhouse, P.W.; L’Ecuyer, T.; Kato, S.; Henderson, D. The Global Character of the Flux of Downward Longwave Radiation. J. Clim. 2012, 25, 2329–2340. [Google Scholar] [CrossRef] [Green Version]
- Dehghan, A.; Dehghani, A. Experimental and theoretical investigation of thermal performance of underground cold-water reservoirs. Int. J. Therm. Sci. 2011, 50, 816–824. [Google Scholar] [CrossRef]
- Degree-Days—U.S. Energy Information Administration (EIA). Available online: https://www.eia.gov/energyexplained/units-and-calculators/degree-days.php (accessed on 2 September 2021).
- Mandal, J.; Yang, Y.; Yu, N.; Raman, A.P. Paints as a scalable and effective radiative cooling technology for buildings. Joule 2020, 15, 1350–1356. [Google Scholar] [CrossRef]
- Feng, J.; Khan, A.; Doan, Q.-V.; Gao, K.; Santamouris, M. The heat mitigation potential and climatic impact of super-cool broadband radiative coolers on a city scale. Cell Rep. Phys. Sci. 2021, 2, 100485. [Google Scholar] [CrossRef]
- Baniassadi, A.; Sailor, D.J.; Ban-Weiss, G.A. Potential energy and climate benefits of super-cool materials as a rooftop strategy. Urban Clim. 2019, 29, 100495. [Google Scholar] [CrossRef]
- Levinson, R.; Akbari, H. Potential benefits of cool roofs on commercial buildings: Conserving energy, saving money, and reducing emission of greenhouse gases and air pollutants. Energy Effic. 2009, 3, 53–109. [Google Scholar] [CrossRef] [Green Version]
- Gillingham, K.T.; Huang, P.; Buehler, C.; Peccia, J.; Gentner, D.R. The climate and health benefits from intensive building energy efficiency improvements. Sci. Adv. 2021, 7, eabg0947. [Google Scholar] [CrossRef]
- Akbari, H.; Menon, S.; Rosenfeld, A. Global cooling: Increasing world-wide urban albedos to offset CO2. Clim. Chang. 2008, 94, 275–286. [Google Scholar] [CrossRef]
- Suehrcke, H.; Peterson, E.L.; Selby, N. Effect of roof solar reflectance on the building heat gain in a hot climate. Energy Build. 2008, 40, 2224–2235. [Google Scholar] [CrossRef]
- Donohoe, A.; Battisti, D. Atmospheric and Surface Contributions to Planetary Albedo. J. Clim. 2011, 24, 4402–4418. [Google Scholar] [CrossRef]



| T (°C) | PW (mm) | 2.5 | 5.0 | 7.5 | 10.0 | 12.5 | 15.0 | 17.5 | 20.0 | 22.5 | 25.0 | 27.5 | 30.0 | 32.5 | 35.0 | 37.5 | 40.0 | 42.5 | 45.0 | 47.5 | 50.0 | 52.5 | 55.0 | 57.5 | 60.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 108 | 96 | 89 | 83 | 78 | 74 | 69 | 65 | 61 | 57 | 53 | 49 | 46 | 43 | 40 | 37 | 34 | 32 | 29 | 27 | 25 | 23 | 22 | 20 | |
| 2 | 112 | 100 | 92 | 87 | 82 | 77 | 72 | 68 | 64 | 60 | 56 | 52 | 49 | 45 | 42 | 39 | 36 | 34 | 31 | 29 | 27 | 25 | 23 | 22 | |
| 4 | 115 | 103 | 96 | 90 | 85 | 80 | 75 | 71 | 67 | 63 | 59 | 55 | 51 | 48 | 45 | 42 | 39 | 36 | 33 | 31 | 29 | 27 | 25 | 24 | |
| 6 | 119 | 107 | 99 | 93 | 88 | 83 | 79 | 74 | 70 | 66 | 62 | 58 | 54 | 51 | 47 | 44 | 41 | 38 | 36 | 33 | 31 | 29 | 27 | 25 | |
| 8 | 122 | 110 | 102 | 96 | 91 | 86 | 82 | 77 | 73 | 69 | 65 | 61 | 57 | 53 | 50 | 46 | 43 | 41 | 38 | 35 | 33 | 31 | 29 | 27 | |
| 10 | 126 | 113 | 105 | 99 | 94 | 89 | 84 | 80 | 75 | 71 | 67 | 63 | 59 | 55 | 51 | 48 | 45 | 42 | 39 | 37 | 34 | 32 | 30 | 28 | |
| 12 | 129 | 116 | 108 | 102 | 96 | 91 | 86 | 82 | 77 | 73 | 68 | 64 | 60 | 56 | 53 | 49 | 46 | 43 | 40 | 37 | 35 | 32 | 30 | 28 | |
| 14 | 133 | 119 | 111 | 104 | 99 | 93 | 88 | 84 | 79 | 74 | 70 | 65 | 61 | 57 | 53 | 50 | 46 | 43 | 40 | 38 | 35 | 33 | 30 | 28 | |
| 16 | 136 | 122 | 114 | 107 | 101 | 96 | 91 | 85 | 81 | 76 | 71 | 67 | 62 | 58 | 54 | 50 | 47 | 44 | 41 | 38 | 35 | 33 | 31 | 29 | |
| 18 | 140 | 126 | 117 | 110 | 104 | 99 | 93 | 88 | 83 | 78 | 73 | 69 | 64 | 60 | 56 | 52 | 49 | 45 | 42 | 39 | 36 | 34 | 31 | 29 | |
| 20 | 144 | 129 | 120 | 113 | 107 | 102 | 96 | 91 | 86 | 81 | 76 | 71 | 67 | 63 | 59 | 55 | 51 | 47 | 44 | 41 | 38 | 36 | 33 | 31 | |
| 22 | 148 | 133 | 124 | 117 | 111 | 105 | 100 | 94 | 89 | 84 | 79 | 74 | 70 | 65 | 61 | 57 | 54 | 50 | 47 | 43 | 41 | 38 | 35 | 33 | |
| 24 | 153 | 137 | 128 | 121 | 114 | 109 | 103 | 98 | 92 | 87 | 82 | 78 | 73 | 68 | 64 | 60 | 56 | 53 | 49 | 46 | 43 | 40 | 37 | 35 | |
| 26 | 157 | 141 | 132 | 124 | 118 | 112 | 106 | 101 | 96 | 91 | 86 | 81 | 76 | 71 | 67 | 63 | 59 | 55 | 52 | 48 | 45 | 42 | 39 | 37 | |
| 28 | 161 | 145 | 135 | 128 | 121 | 116 | 110 | 104 | 99 | 94 | 89 | 84 | 79 | 75 | 70 | 66 | 62 | 58 | 54 | 51 | 48 | 45 | 42 | 39 | |
| 30 | 165 | 149 | 139 | 132 | 125 | 119 | 113 | 108 | 103 | 97 | 92 | 87 | 82 | 78 | 73 | 69 | 65 | 61 | 57 | 53 | 50 | 47 | 44 | 41 | |
| 32 | 170 | 153 | 143 | 135 | 129 | 123 | 117 | 111 | 106 | 101 | 96 | 90 | 86 | 81 | 76 | 72 | 68 | 64 | 60 | 56 | 53 | 49 | 46 | 44 | |
| 34 | 174 | 157 | 147 | 139 | 132 | 126 | 121 | 115 | 110 | 104 | 99 | 94 | 89 | 84 | 79 | 75 | 71 | 66 | 63 | 59 | 55 | 52 | 49 | 46 | |
| 36 | 179 | 161 | 151 | 143 | 136 | 130 | 124 | 119 | 113 | 108 | 102 | 97 | 92 | 87 | 83 | 78 | 74 | 69 | 65 | 62 | 58 | 55 | 51 | 48 | |
| 38 | 183 | 165 | 155 | 147 | 140 | 134 | 128 | 122 | 117 | 111 | 106 | 101 | 96 | 91 | 86 | 81 | 77 | 73 | 68 | 65 | 61 | 57 | 54 | 51 | |
| 40 | 188 | 170 | 159 | 151 | 144 | 138 | 132 | 126 | 120 | 115 | 109 | 104 | 99 | 94 | 89 | 85 | 80 | 76 | 72 | 68 | 64 | 60 | 57 | 54 |
| Data Name | Source | Period | Temporal Resolution | Spatial Resolution |
|---|---|---|---|---|
| 2-m air temperature | cds.climate.copernicus.eu | 2015–2019 | Monthly | 0.1° |
| Solar irradiance | cds.climate.copernicus.eu | 2015–2019 | Monthly | 0.1° |
| Precipitable water | neo.sci.gsfc.nasa.gov | 2015–2019 | Monthly | 0.1° |
| Cloud cover | neo.sci.gsfc.nasa.gov | 2015–2019 | Monthly | 0.1° |
| ↓longwave radiation | cds.climate.copernicus.eu | 2015–2019 | Monthly | 0.1° |
| Population density | sedac.ciesin.columbia.edu | 2015 | 2.5 min | |
| Cooling degree days | doi.pangaea.de | 1970–2018 | Monthly | 0.25° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aili, A.; Yin, X.; Yang, R. Global Radiative Sky Cooling Potential Adjusted for Population Density and Cooling Demand. Atmosphere 2021, 12, 1379. https://doi.org/10.3390/atmos12111379
Aili A, Yin X, Yang R. Global Radiative Sky Cooling Potential Adjusted for Population Density and Cooling Demand. Atmosphere. 2021; 12(11):1379. https://doi.org/10.3390/atmos12111379
Chicago/Turabian StyleAili, Ablimit, Xiaobo Yin, and Ronggui Yang. 2021. "Global Radiative Sky Cooling Potential Adjusted for Population Density and Cooling Demand" Atmosphere 12, no. 11: 1379. https://doi.org/10.3390/atmos12111379
APA StyleAili, A., Yin, X., & Yang, R. (2021). Global Radiative Sky Cooling Potential Adjusted for Population Density and Cooling Demand. Atmosphere, 12(11), 1379. https://doi.org/10.3390/atmos12111379





