Next Article in Journal
Comparison of Top-Down and Bottom-Up Road Transport Emissions through High-Resolution Air Quality Modeling in a City of Complex Orography
Next Article in Special Issue
Snowpack Distribution Using Topographical, Climatological and Winter Season Index Inputs
Previous Article in Journal
An Application of the LCZ Approach in Surface Urban Heat Island Mapping in Sofia, Bulgaria
Previous Article in Special Issue
Characteristics of Subseasonal Winter Prediction Skill Assessment of GloSea5 for East Asia
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 12
Issue 11
10.3390/atmos12111371
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of a Short-Term and a Seasonal Precipitation Forecast over Kenya

by
Sara Miller
1,2,*,
Vikalp Mishra
1,2,
W. Lee Ellenburg
1,2,*,
Emily Adams
1,2,
Jason Roberts
1,3,
Ashutosh Limaye
1,3 and
Robert Griffin
1,2,4
1
NASA SERVIR Science Coordination Office, Marshall Space Flight Center, 320 Sparkman Dr., Huntsville, AL 35805, USA
2
Earth System Science Center, The University of Alabama in Huntsville, 320 Sparkman Dr., Huntsville, AL 35805, USA
3
Earth Science Branch, Marshall Space Flight Center, 320 Sparkman Dr., Huntsville, AL 35805, USA
4
Department of Atmospheric and Earth Science, The University of Alabama in Huntsville, 320 Sparkman Dr., Huntsville, AL 35805, USA
*
Authors to whom correspondence should be addressed.
Atmosphere 2021, 12(11), 1371; https://doi.org/10.3390/atmos12111371
Submission received: 4 September 2021 / Revised: 12 October 2021 / Accepted: 16 October 2021 / Published: 20 October 2021
(This article belongs to the Special Issue Recent Progress and Future Prospects of Subseasonal and Seasonal Climate Prediction)
Browse Figures
Versions Notes

Abstract

:
Kenya is highly dependent on precipitation for both food and water security. Farmers and pastoralists rely on rain to provide water for crops and vegetation to feed herds. As such, precipitation forecasts can be useful tools to inform decision makers and potentially allow the preparation for such events as drought. This study assessed the predictability of a seasonal forecast (CFSv2) and a short-term precipitation forecast (CHIRPS-GEFS) over Kenya. The short-term forecast was assessed on its ability to predict the onset date of the rainy season, and the skill of the seasonal forecast in predicting abnormal precipitation patterns. CHIRPS-GEFS provided a useful starting point to estimate the onset date, but during the long rains in the southwest, where agriculture is concentrated, differences between the predicted and actual onset dates were large (over 20 days). Assessments for CFSv2 generally displayed lower forecast skill over highlands and coastal regions at a seasonal scale. The CFSv2 forecast skill varied widely over individual months and lead times, but over whole rainy seasons, CFSv2 was more skillful than a random forecast at all lead times in the major agricultural areas of Kenya. This research fills a critical research and application gap in understanding the forecast precipitation skill for onset and sub-seasonal prediction.

1. Introduction

Agriculture in Kenya contributes to ∼26% of the Gross Domestic Product, and employs over 40% of the population [1]. However, there is a high prevalence of rainfed agriculture, and much of the country does not receive enough precipitation to support most crops [1]. Nearly 61% of the population depends on rainfed agriculture for income [2]. Pastoralists also depend on precipitation to sustain their herds. This makes food security in the region vulnerable to erratic precipitation patterns. Natural variability in precipitation patterns, further complicated by political conflicts, greatly impacts food and water security in Kenya and surrounding areas.
Kenya has two main rainy seasons: the long rains (March to June) and the short rains (October to December). The long rains are more reliable (show less inter-annual variability), and the short rains show more inter-annual variability, but less spatial variability over Kenya [3]. Accumulation patterns across the country are spatially variable, with the most precipitation in the highlands and southwest region around Lake Victoria (>2000 mm/year) and the least in the north (<200 mm/year). Precipitation is affected by the tropical circulation, as well as topography, lakes, and maritime influence [3]. East African precipitation is strongly connected to variations in the Walker cell with modifications on sub-seasonal to inter-annual time scale driven by Madden–Julian oscillation and El Niño–Southern oscillation variability. The slowly varying ENSO variability and remote response of the tropical circulation are able to provide some level of predictability at seasonal time scales. These types of connections, especially with East African rainfall, have been explored extensively [4,5,6].
While droughts generally occur about once every five years, the frequency of drought and flood events has been increasing in the past 30 years [7,8,9]. Combined with increasing temperatures, the long rain season has shown declining precipitation trends since the 1980s as indicated by decreasing trends in the total precipitation amount, number of precipitating days, number of consecutive wet days, and number of very heavy precipitating days [7,8,10,11,12]. In contrast, the short rains have increased in recent years as indicated by total precipitation amounts and number of precipitating days, but the overall yearly precipitation has been decreasing [3,12]. Drought events have also been spanning multiple rainy seasons, such as during the 2010 short rains and 2011 long rains [13,14].
Precipitation data have traditionally come from station or rain gauge observations. However, in many regions, observation networks are sparse, causing large spatial disparities in coverage [15]. In addition, many sites have incomplete or inconsistent historical records [16]. Gauge data are available through the Kenya Meteorological Department; however, rain-gauge data observed during the post-independence era of the 1970s in particular suffer from spatial and temporal discontinuities over large sections of eastern Africa [17]. To address these challenges, satellite observations from dedicated missions, such as the Tropical Rainfall Measuring Mission (TRMM) [18] or the Global Precipitation Measurement mission (GPM) [19], and models, such as SM2Rain [20], can be used to create more consistent precipitation data with greater coverage.
Precipitation forecasts at both seasonal and sub-seasonal scales are an important part of early warning systems. If forecasts predict poor precipitation for a season, measures can be taken to prepare aid, such as food and water distribution, reducing response time if government intervention is needed. Precipitation forecasts are one of the key inputs to land and cropping system models. Short-term forecasts can also be useful in such systems, particularly when more precise dates of precipitation events are needed, for example, to predict the onset of the rainy season. There are ongoing efforts to produce crop yield forecasts for Kenya, some of which require weather forecast data as inputs [21,22,23]. Agricultural models, such as the Decision Support System for Agro-Technology Transfer (DSSAT [24]), require sub-seasonal data in order to simulate crop growth. Therefore, evaluations of these weather forecast inputs are necessary to understand the skill and uncertainty associated with forecast data.
The onset date of the rainy season is an important first indicator for potential drought events. A delay of the onset date of the rainy season by at least 10 days can be a reliable predictor of drought in food insecure regions of East Africa [25]. Knowledge of the onset of the rainy season is also important for such applications as modeling crop yields, as the projected yields will be affected by the date of planting.
Several seasonal forecasts are available for the region, such as the European Center for Medium-Range Weather Forecasts seasonal forecasting system (SEAS5), IRI’s seasonal climate forecasts, and the NASA Global Modeling and Assimilation Office’s seasonal forecasts, using the Goddard Earth Observing System [26,27,28]. One such seasonal forecast is the Climate Forecast System version 2 (CFSv2). CFSv2 is one of the widely used forecast products in the region for applications such as drought, agriculture, and soil moisture prediction [29,30,31]. Moreover, it provides continuous data throughout the year (not just during the rainy seasons), and provides a 6 month forecast, which is useful since crop growth seasons last beyond the end of the rainy seasons. The CFSv2 product used here is a downscaled and bias-corrected version, available through ClimateSERV (https://climateserv.servirglobal.net/, accessed on 3 June 2021) at 0.5° resolution [32,33].
The Climate Hazards Group InfraRed Precipitation with Station data-Global Ensemble Forecast System (CHIRPS-GEFS) was evaluated for a short-term forecast. The CHIRPS-GEFS dataset combines the higher spatial resolution of CHIRPS (0.05°) and the advanced forecasting ability of GEFS to provide up to a 16-day forecast updated every five days at a spatial resolution of ∼5 km across the globe [33]. GEFS is a weather forecast model made up of 21 ensembles, started by the National Centers for Environmental Prediction (NCEP) to address the uncertainty in weather observations, which are used to initialize weather forecast models [34].
The purpose of this study was to evaluate both a short-term and a seasonal precipitation forecast over Kenya. The short-term forecast was evaluated for potential use at the beginning of rainy seasons to determine the onset date. Then, the overall skill of the seasonal forecast was analyzed to determine if and how far out the forecast would be useful. It is important for researchers and organizations to know the capabilities and limitations of forecasts in order to disseminate information and uncertainty in the most effective way. Therefore, this study conducted an evaluation of the CFSv2 and CHIRPS-GEFS precipitation forecasts. We analyzed the CFSv2 lead times from 0–6 months to determine how far out skillful precipitation forecasts can be made.
CHIRPS data were used as a reference dataset for precipitation to compare the forecast products. CHIRPS uses global 0.05° precipitation climatologies, time-varying grids of real-time satellite-based precipitation estimates, and in situ precipitation observations to create its precipitation data [35]. CHIRPS was used as a reference, as it has better skill than other gridded products, and is known to have almost negligible bias in the region [36]. Furthermore, the CHIRPS data ensure a consistent spatio-temporal continuity, due to their long period of record (over 40 years) and global coverage.
Several studies have assessed the forecast skill of seasonal forecasts in the region [29,37,38,39]. These studies have used methods such as analyzing the correlation of forecast precipitation with a reference, and translation of precipitation forecasts into categorical events for the calculation of skill scores [29,37,38,39]. However, few, if any, have assessed the skills of forecast data in onset date prediction, and none to our knowledge have assessed the downscaled and bias-corrected version of CFSv2 used here for the region. The results of these evaluations will be used to inform stakeholders in the region. This analysis will also be useful for organizations using the forecasts for applications such as drought or agriculture forecasting.

2. Materials and Methods

2.1. Study Area and Period

This study was conducted over Kenya at pixel level (0.5° for CFSv2, 0.05° for CHIRPS-GEFS). Kenya has a wide range of precipitation in different regions, varying from >2000 mm/yr in the southwest to <200 mm/yr in the most arid regions (Figure 1). The vast spatial variability in the precipitation patterns allows for a robust assessment of the forecast model under different climatic and ecological conditions. The highlands are concentrated in the southwest of Kenya, as is most of the agricultural land. There is also a swath of agricultural fields along the coast in the east. There are a range of ecological zones across the country, from humid in the southwest to arid in the east. This study covers the time frame of 1990–2020 to include enough years for statistical analysis at a monthly level.

2.2. Data

The CFSv2 product used here is a downscaled and bias-corrected version, available through ClimateSERV (https://climateserv.servirglobal.net/, accessed on 3 June 2021) at 0.5° resolution [32,33]. A bias correction and statistical downscaling (BCSD) algorithm was applied to CFSv2 as described in Sikder et al. [43] following the approach of Wood et al. [44]. Quantile–quantile mapping was used to bias correct lead-dependent model forecast distributions of precipitation and temperature to observation-based distributions of the Princeton surface global forcing dataset (SGF) for the years 1982–2012 Sheffield et al. [45]. To spatially downscale, a local scaling approach was applied to the bias-corrected forecasts to generate 0.5° estimates from the 1.0° CFSv2 forecasts obtained from the International Research Institute for Research and Society (IRI; https://iridl.ldeo.columbia.edu/SOURCES/.Models/.NMME/, accessed on 3 June 2021). The local scaling factor was equal to the ratio of the climatological high-resolution estimate against that obtained by resampling of the coarse-resolution climatology to the locations of the finer-resolution grid [43].
CHIRPS-GEFS is a bias-corrected and downscaled version of the National Centers for Environmental Prediction (NCEP) Global Ensemble Forecast System precipitation forecasts made to be spatially compatible with various CHIRPS products [46]. It provides a 16 day forecast updated every five days. It is available through the University of California, Santa Barbara (UCSB) at https://data.chc.ucsb.edu/products/EWX/data/forecasts/CHIRPS-GEFS_precip/ (accessed on 3 June 2021). Daily data at 0.05° were used for prediction of the rainy season onset date.
CHIRPS was used as the reference precipitation dataset for comparison with both forecast products. CHIRPS version 2.0 daily data were used, available from USCB at https://data.chc.ucsb.edu/products/CHIRPS-2.0/ (accessed on 3 June 2021) [35]. In order to compare it with CFSv2 data, CHIRPS was resampled to 0.5° using bilinear interpolation and aligned with CFSv2 grids.

2.3. Methods

2.3.1. Onset Date

Onset date is defined here as the first dekad with at least 25 mm of precipitation, followed by two dekads, which sum to at least 20 mm of rain. This definition was originally defined by AGRHYMET and is widely used in the region [47]. The first dekad of the three is considered the onset date when all conditions are met. CHIRPS-GEFS data were used to predict the onset date at pixel level. CHIRPS-GEFS forecasts are 16 days out, but the definition of onset date used here requires at least 30 days of data. Therefore, CHIRPS-GEFS forecasts would only be able to define the onset date in-season about 2 weeks after the onset date actually occurs in real time. However, this onset date estimate would still be available prior to an estimate from CHIRPS, which is available at about 3 weeks latency. The CHIRPS-GEFS onset predictions were compared to CHIRPS, and the average and absolute differences in onset date were analyzed.

2.3.2. Seasonal Forecast

The total monthly precipitation from CFSv2 was analyzed for the seasonal forecast. CFSv2 was assessed at the scale of the entire rainy season, and at each individual month. The forecast was translated into discrete events by classifying ‘anomaly events’ as the 20th and 80th percentiles of precipitation at the pixel level. The percentiles were calculated from data for all years for each particular month. Events below the 20th percentile were classified as dry anomaly events, and above the 80th percentile were classified as wet anomaly events. These percentiles were chosen, as droughts are recurrent about every 5 years, and livestock insurance efforts in the region use the 20th percentile as a threshold for insurance payouts [48,49]. Contingency Table 1 was created from the events, using CHIRPS to classify the `observed’ events.
There are several statistical matrices to compare and evaluate precipitation products. The probability of detection (POD) is one such metric that measures the proportion of events successfully forecast by the model. POD ranges from 0 to 1, with 1 being the best. It is calculated as follows:
POD = a a + c
Another metric is the false alarm ratio (FAR) that measures the proportion of ‘yes’ forecasts that fail to materialize. This score is important to report, as raising many false alarms will lessen people’s confidence in the forecasts. FAR ranges from 0 to 1, with the best possible value being 0. It is calculated as follows:
FAR = b a + b
The Heidke skill score (HSS) is based on the proportion correct in comparison to a reference forecast. The reference forecast is the correct proportion that would be achieved by random forecasts statistically, independent of the observations. Perfect forecasts would receive HSS = 1, forecasts equivalent to the reference would receive HSS = 0, and forecasts worse than the reference would receive negative scores [50]. HSS is calculated as follows:
HSS = 2 ( a d − b c ) ( a + c ) ( c + d ) + ( a + b ) ( b + d )
The relative operating characteristics (ROC) score (also known as the receiver operating characteristics score) shows the degree of correct probabilistic discrimination for a set of forecasts. ROC is plotted as a graph, with the hit rate shown on the x-axis and the false alarm rate shown on the y-axis. The ROC curve is created from a set of points: the first point indicates the hit rate and the associated false alarm rate only for forecasts in the highest bin of issued forecast probabilities. Subsequent points indicate the hit versus false alarm rates for cases with successively decreasing forecast probabilities. The area underneath the ROC curve is the ROC score. ROC scores above 0.5 reflect positive discrimination skill, with 1 being the best possible score [50,51].

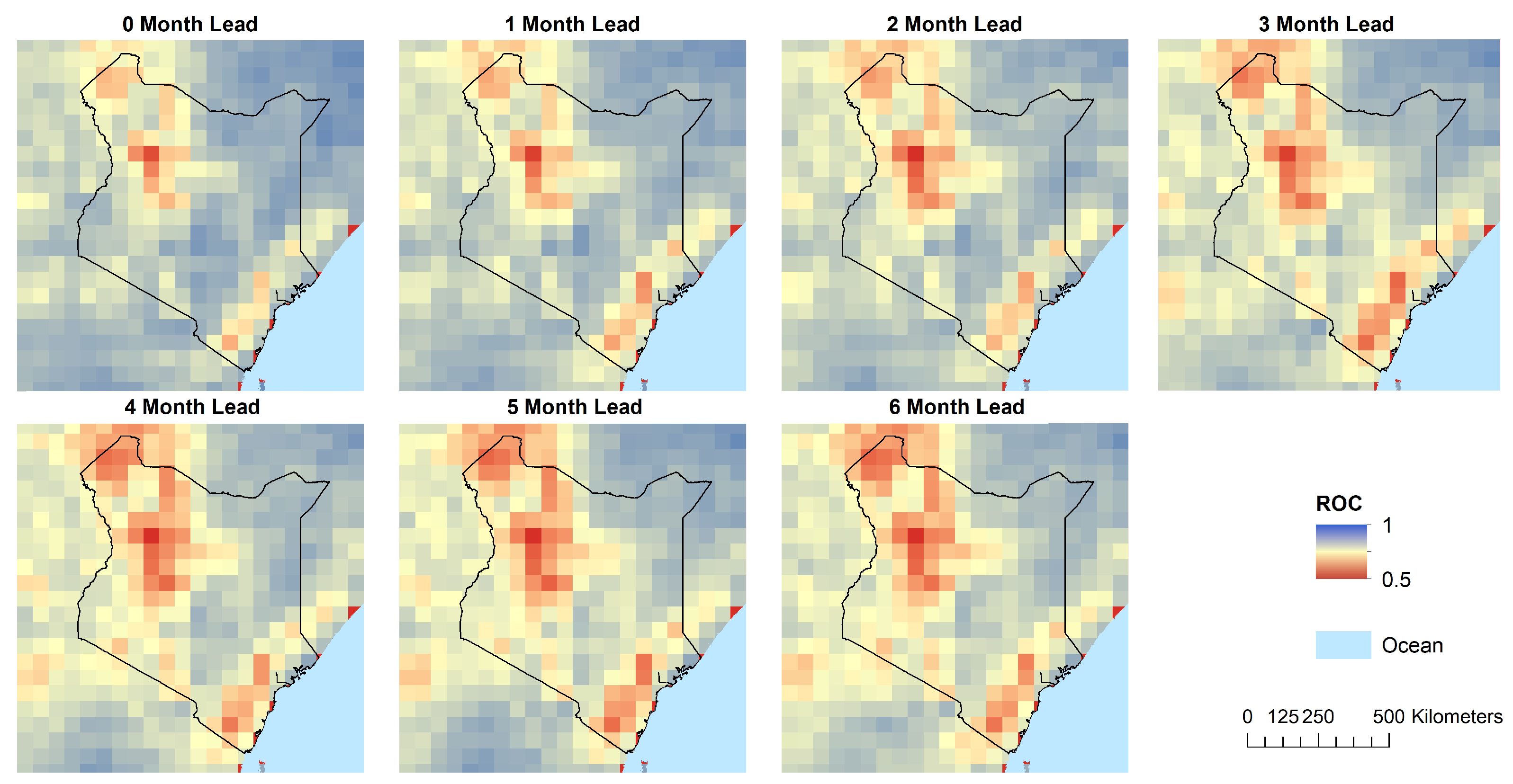
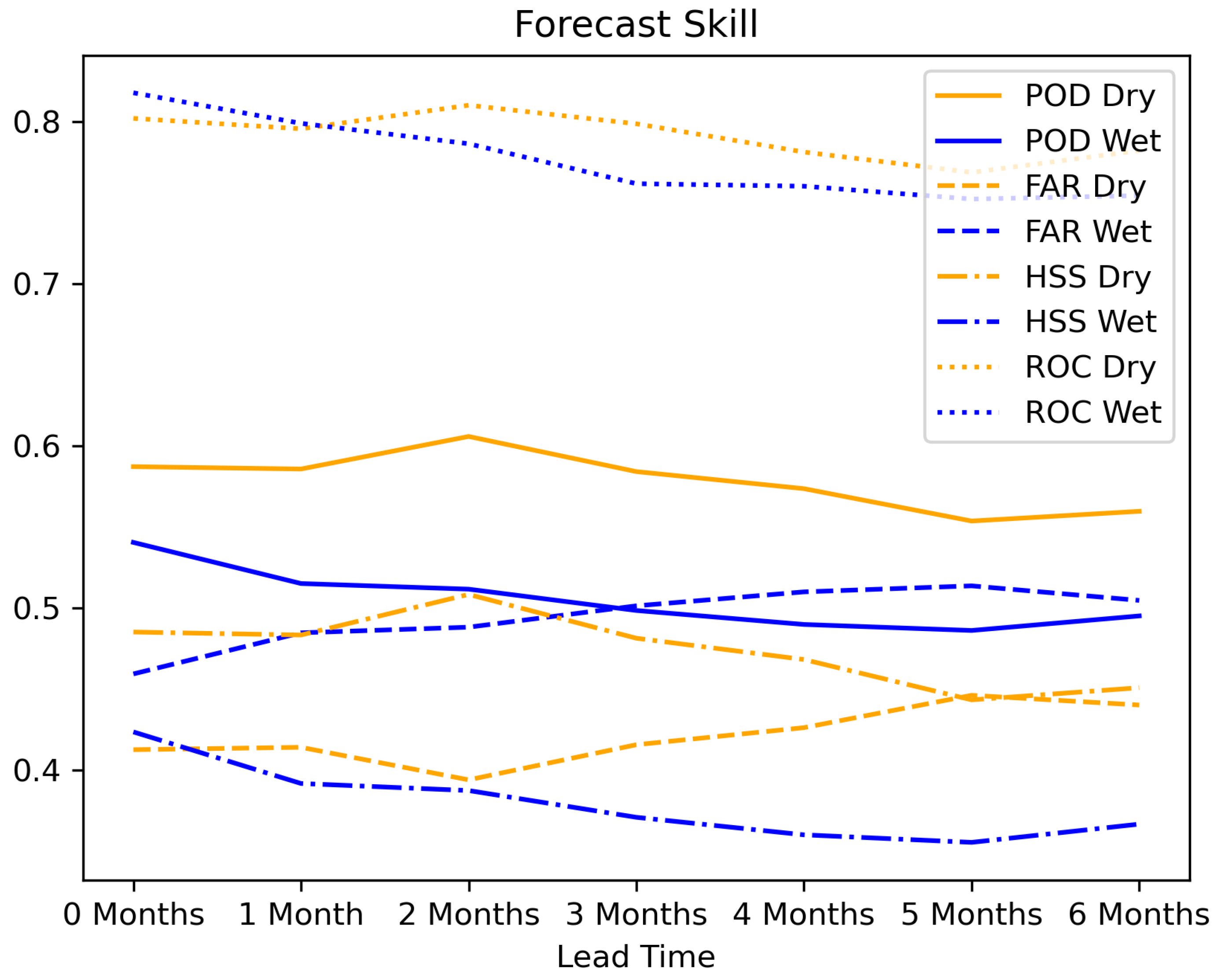
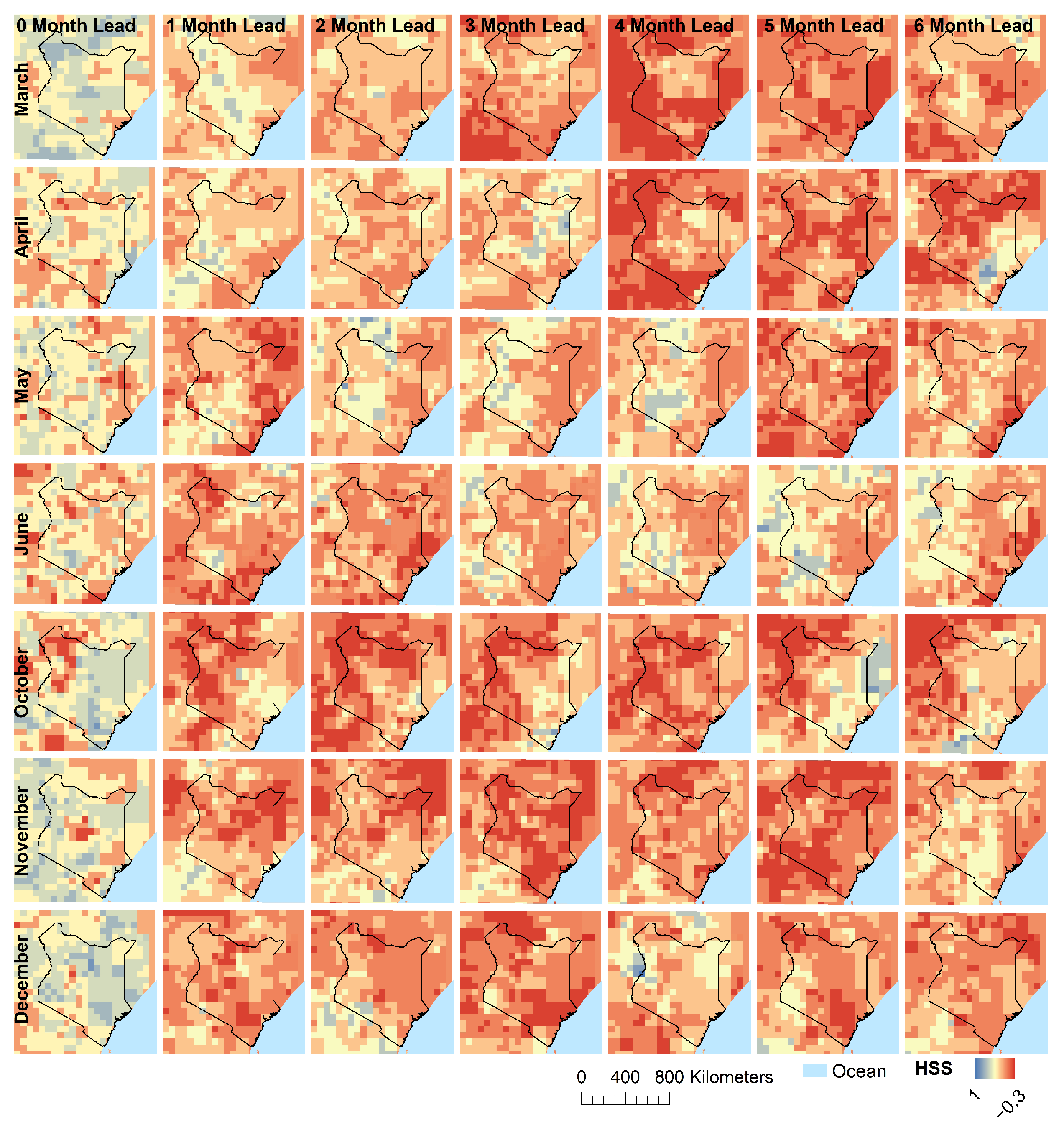
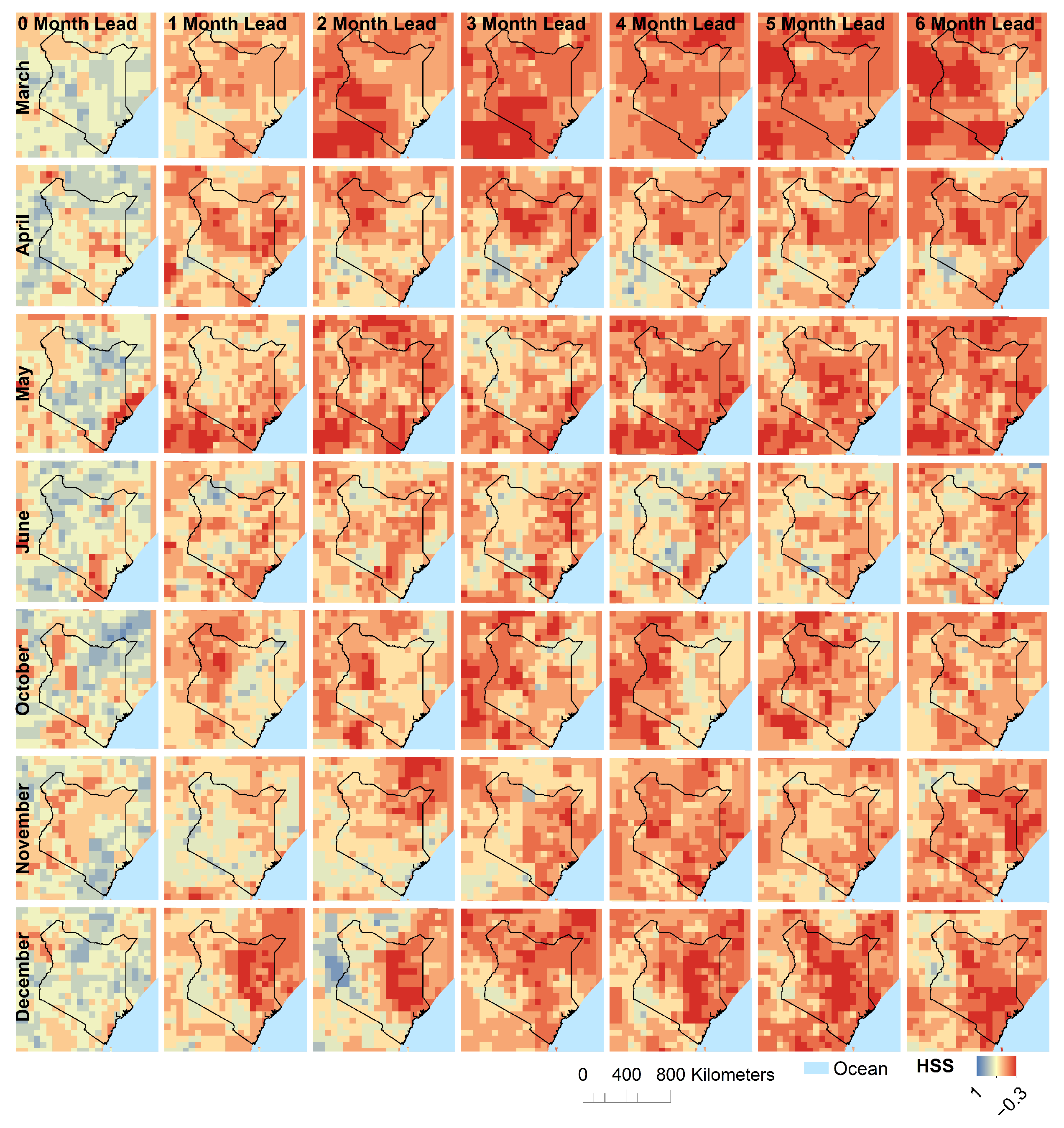
3. Results

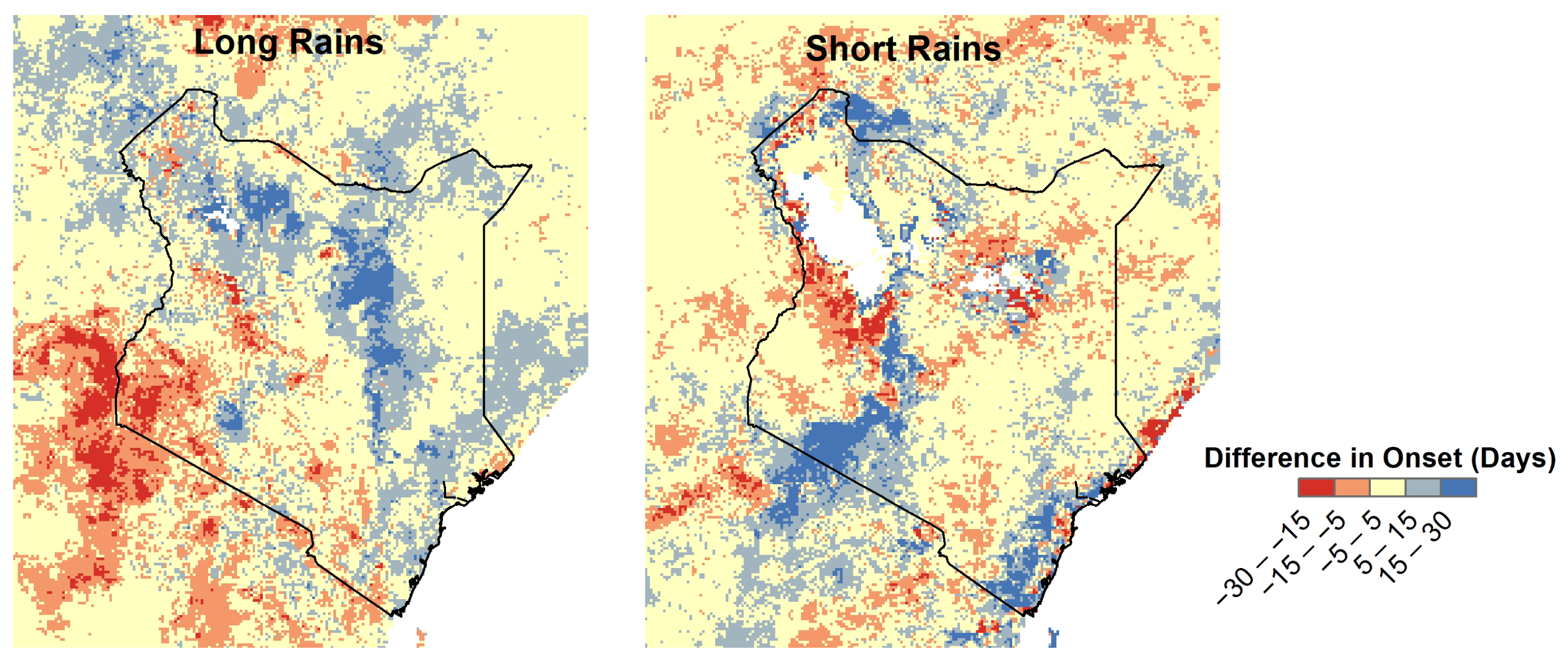
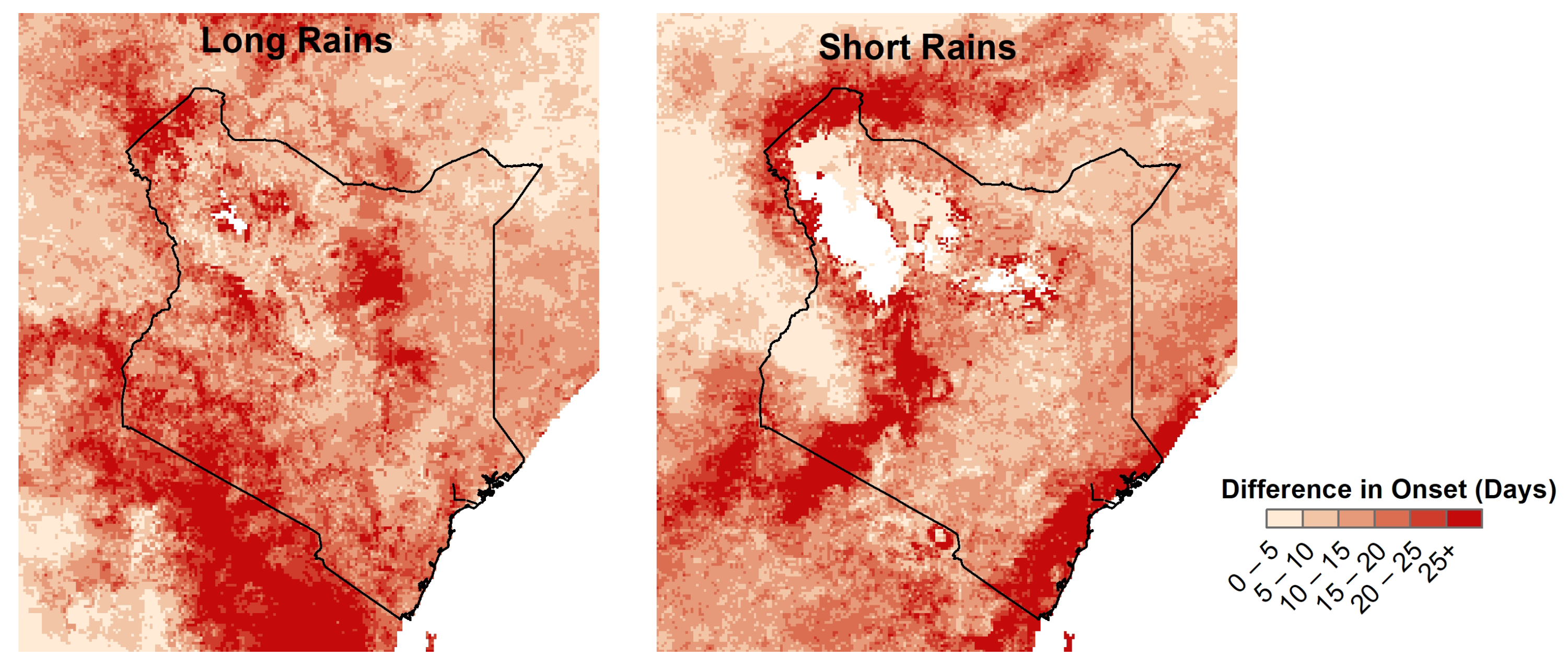
3.1. Onset Date

CHIRPS-GEFS predicted a later start date than observed for most of southwest Kenya during the long rains, where much of the agriculture is concentrated (Figure 2. In contrast, CHIRPS-GEFS predicted an earlier onset of the short rains in parts of the same region, mainly the highland areas. Through much of eastern Kenya, CHIRPS-GEFS predicted an early onset date. Along the coast during the short rains, there are both areas where CHIRPS-GEFS predicted much earlier and much later start dates than observed. In the most arid regions, no start dates were predicted or observed, as they did not receive enough precipitation over a period of three dekads to ever fit the onset definition used here. This is especially evident in the short rains in the northwest, shown by a large area of no data in the figure. This area is semi-arid to arid. This pattern was expected, as yearly precipitation in the area is very low.
The absolute difference in onset dates in Figure 3 show the largest differences in predicted long rains’ onset in the southwest and northeast. The short rains had the largest differences in the predicted onset date in the highlands and along the coast.

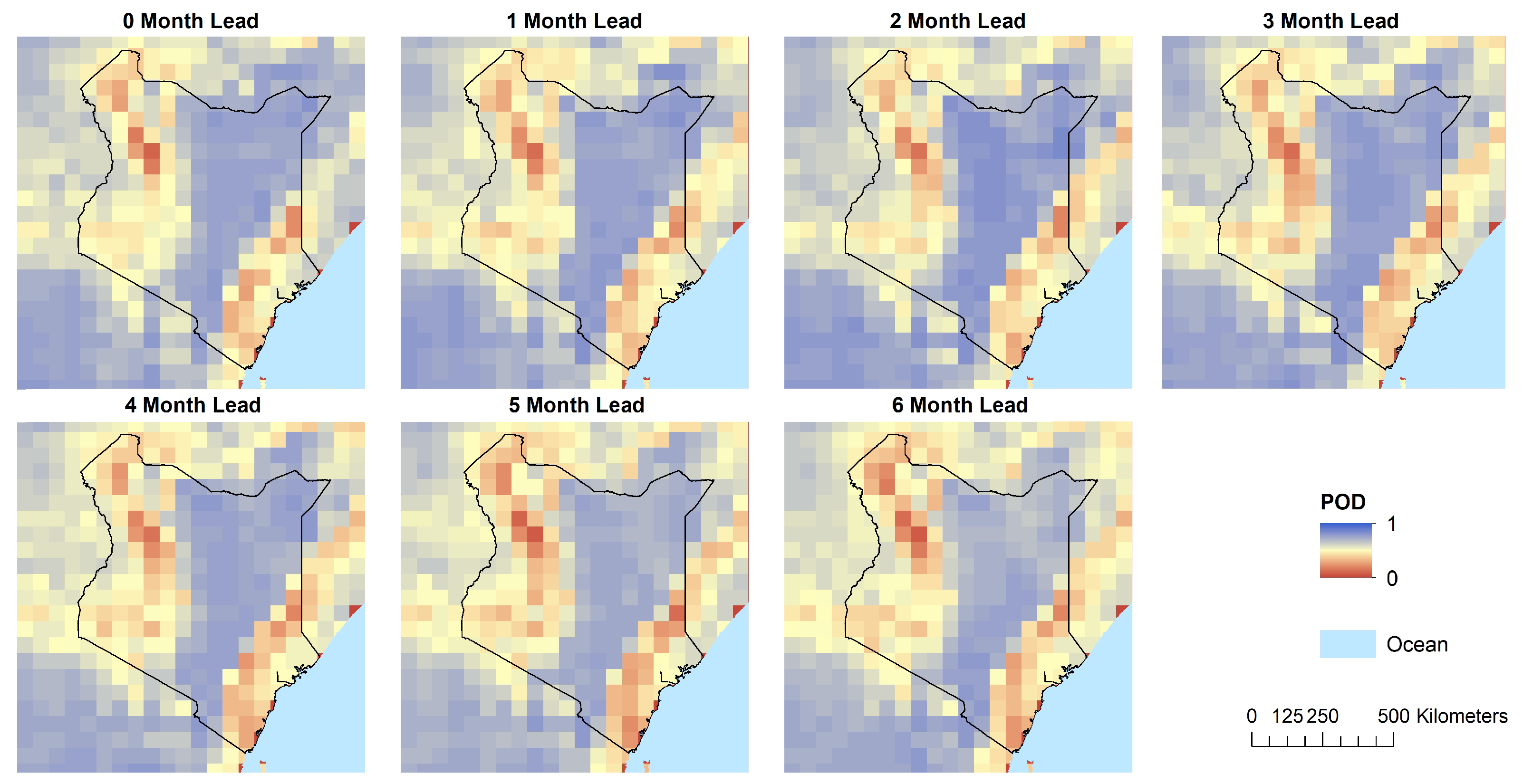
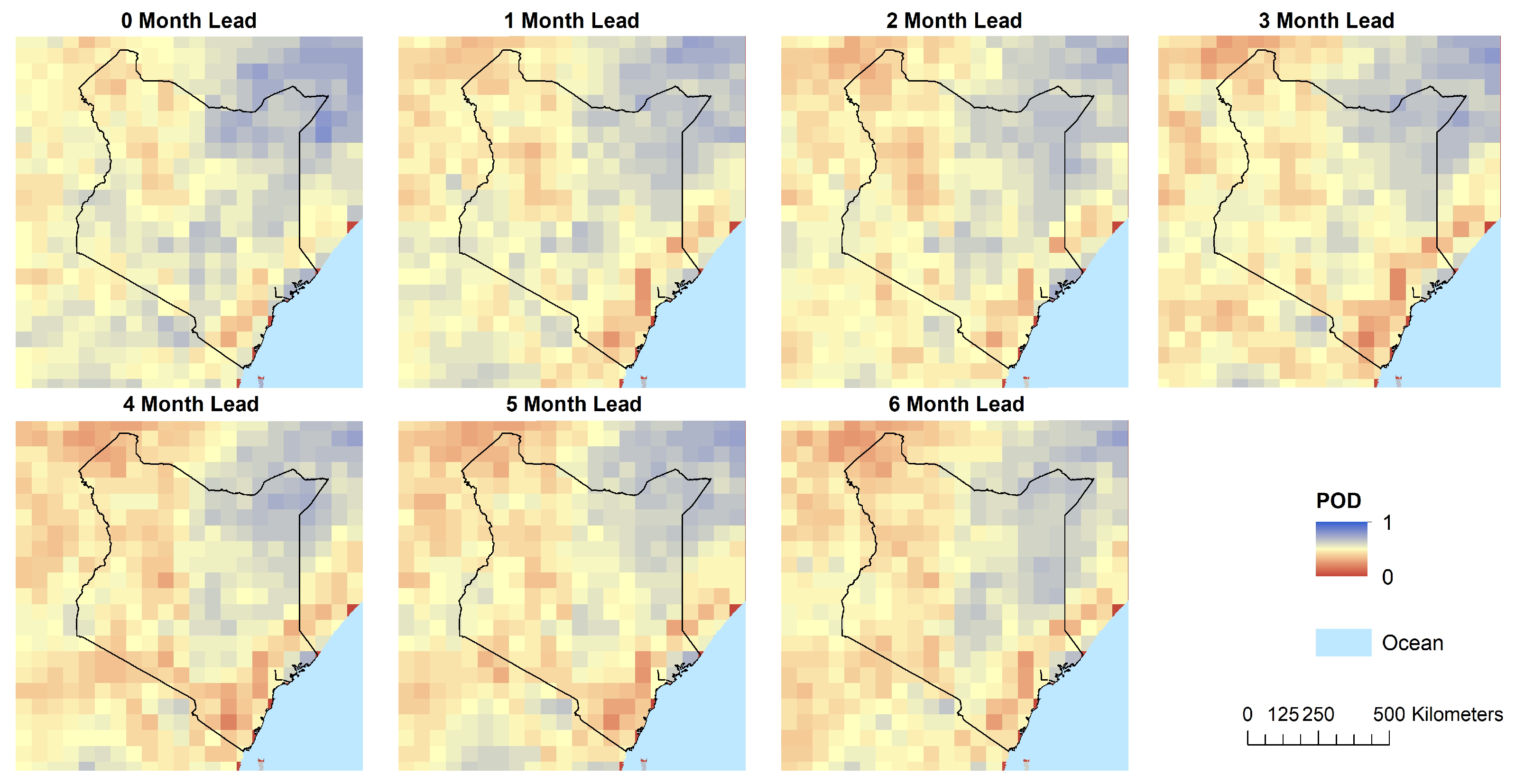
3.2. Seasonal Forecast

Figure 4 and Figure 5 show the spatial patterns of POD over both rainy seasons for dry and wet anomaly events. The spatial distribution of skill did not change much over the different lead times. For the detection of dry events, CFSv2 performed worse in the western half of Kenya and along the coast. Throughout central Kenya, the POD was near perfect. The spatial patterns for the detection of wet events were not as distinct, but they also appeared to perform slightly worse along the coast. POD was best for northeast Kenya, being between 0.25 and 0.5 in the western half of Kenya for wet events. The spatial patterns of FAR and HSS were similar to those of POD. HSS indicated that for wet anomaly events, CFSv2 is more skillful than a random forecast for the whole country, except along the coast. For dry anomaly events, it is more skillful than a random forecast, except along the coast and in a small area of the northwest.
The ROC displayed similar patterns of skill as the other skill scores for dry events (Figure 6), with only a small area in the northwest having lower skill than a random forecast. For wet anomaly events (Figure 7), the pattern of ROC was similar to that of the dry events, but the region of lower skill in the northwest became larger with longer lead times.
The average of each skill score over Kenya during different lead times is summarized in Figure 8. The 0 month lead time appears to be a bit better than the rest, but there is not a consistent decline in skill for most of the indicators.
Table 2 shows the average skill for each ecological zone. For dry anomaly events, forecasts for the sub-humid and semi-arid zones performed well. For wet anomaly events, forecasts for arid and semi-arid zones performed the best, while all other zones performed similarly.
Though there was not much difference in skill between the different lead times when looking at the rainy seasons as a whole, it is obvious that the 0 month lead time performed much better when looking at individual months. The forecasts also performed worse overall when looking at individual months, with HSS being below 0 in many areas, indicating that the forecast is worse than the reference random forecast at those points. Spatial patterns are also different across each month, as shown in Figure 9 and Figure 10. The forecasts for individual months of the rainy seasons performed better than those during the dry seasons.

4. Discussion

4.1. Onset Date

Forecast onset dates from CHIRPS-GEFS are mostly within the standard deviation of each rainy season, and therefore, can be useful to narrow down the onset date prior to the observed onset date availability. The standard deviation of onset date is 15 days for the long rains, and 24 days for the short rains [52]. For applications such as crop forecasting, it can be necessary to have an onset date of the rainy season that is as accurate as possible so that variables, such as planting dates and crop growth phases, match with real life. These variables can greatly impact the forecast yield, as different amounts of water are needed in different growth stages for optimal yield [53]. The onset dates predicted by CHIRPS-GEFS provide a good starting point for such applications before observed precipitation data are available. There are many areas with average differences in predicted onset dates over 15 days during the long rains, particularly in the southwest, where agriculture is concentrated. Onset differences that large could sufficiently affect forecast yields such that any models using CHIRPS-GEFS to estimate onset dates would need to convey the uncertainty associated with it.

4.2. Seasonal Forecast

At a seasonal scale, CFSv2 forecasts performed better than a random forecast over most of Kenya. The main region where CFSv2 had consistently low skill was the coastal region. It was suggested that coastal precipitation is more influenced by the sea surface temperature than other regions [54]. Therefore, a larger scale model may not take the influence of proximity to the ocean into account. General circulation models (GCMs), such as CFSv2, were assessed for applications such as crop forecasting, drought forecasting, and streamflow prediction [22,29,43]. When downscaled to the monthly or daily levels necessary for some applications, precipitation forecasts have lower skill and introduce more uncertainty into models. Sikder et al. [43] demonstrated that for streamflow in the Ganges and Brahmaputra River Basins, GCMs were only useful for management decisions at a seasonal scale or greater.
Our study shows that forecasts at a monthly level had large areas where a random forecast would be more skillful for lead times greater than 0 months. At a monthly scale, forecasts for the long rains had higher skill in the prediction of dry anomaly events, while forecasts for the short rains had higher skill in the prediction of wet anomaly events. This could be due in part to the intensity of these anomaly events; for example, CHIRPS data show much stronger wet anomaly events during the short rains. For dry anomaly events during the dry rains, in certain cases, longer lead times show greater skill. For June forecasts, lead times of 3–5 months show higher skill than shorter lead times. Similarly, lead times of 2–4 months show greater skill than the 1 month lead time for May forecasts. These forecasts have in common that they were initialized between January and March. The decrease in skill for forecasts initialized after March may be due to the Spring predictability barrier (SPB). SPB is a phenomenon of El Niño-Southern Oscillation (ENSO) forecasts, where ENSO predictions from models through the spring tend to be less successful [55,56,57]. Duan and Wei [57] show that prediction errors tended to have the largest growth rate in the April–May–June season, which may provide explanation for the lower skill of forecasts initialized during these months.
For agricultural areas for dry events, CFSv2 performed best over the long rains for forecasts initialized between January and March. Over the short rains, dry event forecast skill was lower in agricultural areas, having lower skill than a random forecast in some parts. The 0 month lead time was the only lead time with consistently skillful forecasts over agricultural areas for the short rains. For crop forecasting efforts in the region, CFSv2 may be of limited use prior to December for the short rains growing season.
For forecasts that provide data at a sub-seasonal level, future forecast validation and correction efforts may want to focus not only on whole seasons, but also on the temporal scale that data are provided, as many months have different spatial patterns of skill. Month-to-month skill was also lower overall than skill calculated over whole rainy seasons. The rains were also influenced by different forcing methods from month to month, and thus, it would make sense for forecasting efforts to tailor forecasting methods to each individual month to derive the best possible forecast [3].
Overall, this work has shown that CHIRPS-GEFS forecasts are useful to narrow down the onset date of the rainy seasons. CFSv2 forecasts were shown to be better than random forecasts for most areas at seasonal scales, but forecast skill for individual months varied. The results will be used to inform stakeholders and organizations using the forecasts for such applications as drought or agriculture forecasting.

5. Conclusions

This study assessed two precipitation forecast products over Kenya for both short-term and seasonal applications. The short-term forecast CHIRPS-GEFS was shown to reasonably predict the onset of rainy seasons over most of the country. However, areas such as the southwest and northeast for the long rains and highlands and coastal areas during the short rains displayed large (> 20 day) differences between predicted and actual onset dates. This would likely have a great impact on models or warning systems relying on the forecast onset date. The seasonal forecast CFSv2 was shown to be more skillful than a random forecast over most areas of Kenya; however, skill varied widely over space, month forecast, and lead times. Given these results, if forecast data are provided at a sub-seasonal scale, future forecast evaluations should assess forecasts at the temporal scale that data are provided, rather than over seasons as a whole.

Author Contributions

Conceptualization, S.M, V.M., W.L.E., E.A., J.R., and A.L.; methodology, S.M, V.M., W.L.E., E.A., J.R., and A.L.; validation, S.M.; formal analysis, S.M.; investigation, S.M.; resources, J.R.; data curation, S.M. and J.R; writing—original draft preparation, S.M; writing—review and editing, S.M, V.M., W.L.E., E.A., J.R., A.L., R.G.; visualization, S.M.; supervision, A.L. and R.G.; project administration, A.L. and R.G.; funding acquisition, R.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the joint U.S. Agency for International Development (USAID) and National Aeronautics and Space Administration (NASA) initiative SERVIR and particularly through the NASA Applied Sciences Capacity Building Program, NASA Cooperative Agreement NNM11AA01A.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

We would like to recognize the University of Alabama in Huntsville (UAH) Earth System Science Center (ESSC) and the RCMRD and SERVIR teams for their support. Individuals affiliated with the ESSC of UAH are funded through the NASA Applied Sciences Capacity Building Program, NASA Cooperative Agreement NNM11AA01A. SERVIR is a joint venture between NASA and USAID that works to bolster the capacity of developing regions to leverage Earth observation data in solving pressing environmental challenges. Lastly, thanks to the reviewers and editors who provided valuable comments and suggestions that improved the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Food and Agriculture Organization of the United Nations. The Agriculture Sector in Kenya. n.d. Available online: http://www.fao.org/kenya/fao-in-kenya/kenya-at-a-glance/en/ (accessed on 1 June 2021).
  2. Food and Agriculture Organization of the United Nations. Kenya. 2018. Available online: http://www.fao.org/faostat/en/#country/114 (accessed on 3 June 2021).
  3. Nicholson, S.E. Climate and climatic variability of rainfall over eastern Africa. Rev. Geophys. 2017, 55, 590–635. [Google Scholar] [CrossRef] [Green Version]
  4. Hastenrath, S.; Polzin, D.; Mutai, C. Circulation mechanisms of Kenya rainfall anomalies. J. Clim. 2011, 24, 404–412. [Google Scholar] [CrossRef]
  5. Hastenrath, S. Circulation mechanisms of climate anomalies in East Africa and the equatorial Indian Ocean. Dyn. Atmos. Ocean. 2007, 43, 25–35. [Google Scholar] [CrossRef]
  6. Hastenrath, S.; Polzin, D.; Camberlin, P. Exploring the predictability of the ‘short rains’ at the coast of East Africa. Int. J. Climatol. J. R. Meteorol. Soc. 2004, 24, 1333–1343. [Google Scholar] [CrossRef]
  7. Funk, C.; Dettinger, M.D.; Michaelsen, J.C.; Verdin, J.P.; Brown, M.E.; Barlow, M.; Hoell, A. Warming of the Indian Ocean threatens eastern and southern African food security but could be mitigated by agricultural development. Proc. Natl. Acad. Sci. USA 2008, 105, 11081–11086. [Google Scholar] [CrossRef] [Green Version]
  8. Williams, A.P.; Funk, C. A westward extension of the warm pool leads to a westward extension of the Walker circulation, drying eastern Africa. Clim. Dyn. 2011, 37, 2417–2435. [Google Scholar] [CrossRef] [Green Version]
  9. Ayugi, B.; Tan, G.; Niu, R.; Dong, Z.; Ojara, M.; Mumo, L.; Babaousmail, H.; Ongoma, V. Evaluation of meteorological drought and flood scenarios over Kenya, East Africa. Atmosphere 2020, 11, 307. [Google Scholar] [CrossRef] [Green Version]
  10. Lyon, B.; DeWitt, D.G. A recent and abrupt decline in the East African long rains. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
  11. Yang, W.; Seager, R.; Cane, M.A.; Lyon, B. The East African long rains in observations and models. J. Clim. 2014, 27, 7185–7202. [Google Scholar] [CrossRef]
  12. Cattani, E.; Merino, A.; Guijarro, J.A.; Levizzani, V. East Africa rainfall trends and variability 1983–2015 using three long-term satellite products. Remote Sens. 2018, 10, 931. [Google Scholar] [CrossRef] [Green Version]
  13. Hillbruner, C.; Moloney, G. When early warning is not enough—Lessons learned from the 2011 Somalia Famine. Glob. Food Secur. 2012, 1, 20–28. [Google Scholar] [CrossRef]
  14. Maxwell, D.; Fitzpatrick, M. The 2011 Somalia famine: Context, causes, and complications. Glob. Food Secur. 2012, 1, 5–12. [Google Scholar] [CrossRef]
  15. Dinku, T.; Ceccato, P.; Connor, S.J. Challenges of satellite rainfall estimation over mountainous and arid parts of east Africa. Int. J. Remote. Sens. 2011, 32, 5965–5979. [Google Scholar] [CrossRef]
  16. Githungo, W.; Otengi, S.; Wakhungu, J.; Masibayi, E. Infilling monthly rain gauge data gaps with satellite estimates for Asal of Kenya. Hydrology 2016, 3, 40. [Google Scholar] [CrossRef] [Green Version]
  17. Schreck III, C.J.; Semazzi, F.H. Variability of the recent climate of eastern Africa. Int. J. Climatol. J. R. Meteorol. Soc. 2004, 24, 681–701. [Google Scholar] [CrossRef]
  18. Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
  19. Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
  20. Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W. A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 2013, 40, 853–858. [Google Scholar] [CrossRef]
  21. Ogutu, G.E.; Franssen, W.H.; Supit, I.; Omondi, P.; Hutjes, R.W. Probabilistic maize yield prediction over East Africa using dynamic ensemble seasonal climate forecasts. Agric. For. Meteorol. 2018, 250, 243–261. [Google Scholar] [CrossRef]
  22. Hansen, J.W.; Mishra, A.; Rao, K.; Indeje, M.; Ngugi, R.K. Potential value of GCM-based seasonal rainfall forecasts for maize management in semi-arid Kenya. Agric. Syst. 2009, 101, 80–90. [Google Scholar] [CrossRef] [Green Version]
  23. Rojas, O. Operational maize yield model development and validation based on remote sensing and agro-meteorological data in Kenya. Int. J. Remote Sens. 2007, 28, 3775–3793. [Google Scholar] [CrossRef] [Green Version]
  24. Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
  25. Shukla, S.; Husak, G.; Turner, W.; Davenport, F.; Funk, C.; Harrison, L.; Krell, N. A slow rainy season onset is a reliable harbinger of drought in most food insecure regions in Sub-Saharan Africa. PLoS ONE 2021, 16, e0242883. [Google Scholar] [CrossRef]
  26. Johnson, S.J.; Stockdale, T.N.; Ferranti, L.; Balmaseda, M.A.; Molteni, F.; Magnusson, L.; Tietsche, S.; Decremer, D.; Weisheimer, A.; Balsamo, G.; et al. SEAS5: The new ECMWF seasonal forecast system. Geosci. Model Dev. 2019, 12, 1087–1117. [Google Scholar] [CrossRef] [Green Version]
  27. Barnston, A.G.; Li, S.; Mason, S.J.; DeWitt, D.G.; Goddard, L.; Gong, X. Verification of the first 11 years of IRI’s seasonal climate forecasts. J. Appl. Meteorol. Climatol. 2010, 49, 493–520. [Google Scholar] [CrossRef]
  28. Borovikov, A.; Cullather, R.; Kovach, R.; Marshak, J.; Vernieres, G.; Vikhliaev, Y.; Zhao, B.; Li, Z. GEOS-5 seasonal forecast system. Clim. Dyn. 2019, 53, 7335–7361. [Google Scholar] [CrossRef]
  29. Kipkogei, O.; Mwanthi, A.; Mwesigwa, J.; Atheru, Z.; Wanzala, M.; Artan, G. Improved seasonal prediction of rainfall over East Africa for application in agriculture: Statistical downscaling of CFSv2 and GFDL-FLOR. J. Appl. Meteorol. Climatol. 2017, 56, 3229–3243. [Google Scholar] [CrossRef]
  30. Shukla, S.; McNally, A.; Husak, G.; Funk, C. A seasonal agricultural drought forecast system for food-insecure regions of East Africa. Hydrol. Earth Syst. Sci. 2014, 18, 3907–3921. [Google Scholar] [CrossRef] [Green Version]
  31. Mo, K.C.; Shukla, S.; Lettenmaier, D.P.; Chen, L.C. Do Climate Forecast System (CFSv2) forecasts improve seasonal soil moisture prediction? Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
  32. Sousa, K.d.; Sparks, A.H.; Ashmall, W.; Etten, J.v.; Solberg, S. Ø. Chirps: API Client for the CHIRPS Precipitation Data in R. J. Open Source Softw. 2020. [Google Scholar] [CrossRef]
  33. SERVIR. About ClimateSERV. Available online: https://climateserv.servirglobal.net/aboutclimateserv.html n.d. (accessed on 20 August 2021).
  34. Oceanic, N.; Administration, A. Global Ensemble Forecast System (GEFS) [1 Deg.]. 2018. Available online: https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ncdc:C00691 (accessed on 31 August 2021).
  35. Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—a new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  36. Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef] [Green Version]
  37. Bosire, E.; Opijah, F.; Gitau, W. Assessing the skill of precipitation forecasts on seasonal time scales over East Africa from a Climate Forecast System model. Glob. Meteorol. 2014, 3. [Google Scholar] [CrossRef] [Green Version]
  38. Shukla, S.; Roberts, J.; Hoell, A.; Funk, C.C.; Robertson, F.; Kirtman, B. Assessing North American multimodel ensemble (NMME) seasonal forecast skill to assist in the early warning of anomalous hydrometeorological events over East Africa. Clim. Dyn. 2019, 53, 7411–7427. [Google Scholar] [CrossRef]
  39. Wang, W.; Chen, M.; Kumar, A. An assessment of the CFS real-time seasonal forecasts. Weather. Forecast. 2010, 25, 950–969. [Google Scholar] [CrossRef]
  40. Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
  41. Teluguntla, P.; Thenkabail, P.S.; Xiong, J.; Gumma, M.K.; Giri, C.; Milesi, C.; Ozdogan, M.; Congalton, R.; Tilton, J.; Sankey, T.T.; et al. Global Cropland Area Database (GCAD) Derived from Remote Sensing in Support of Food Security in the Twenty-First Century: Current Achievements and Future Possibilities. In Land Resources Monitoring, Modeling, and Mapping with Remote Sensing (Remote Sensing Handbook); CRC Press Inc.: Boca Raton, FL, USA, 2015; pp. 1–45. [Google Scholar]
  42. Koo, J.; Cox, C.M.; Bacou, M.; Azzarri, C.; Guo, Z.; Wood-Sichra, U.; Gong, Q.; You, L. CELL5M: A geospatial database of agricultural indicators for Africa South of the Sahara. F1000Research 2016, 5. [Google Scholar] [CrossRef] [Green Version]
  43. Sikder, S.; Chen, X.; Hossain, F.; Roberts, J.B.; Robertson, F.; Shum, C.; Turk, F.J. Are general circulation models ready for operational streamflow forecasting for water management in the Ganges and Brahmaputra river basins? J. Hydrometeorol. 2016, 17, 195–210. [Google Scholar] [CrossRef]
  44. Wood, A.W.; Maurer, E.P.; Kumar, A.; Lettenmaier, D.P. Long-range experimental hydrologic forecasting for the eastern United States. J. Geophys. Res. Atmos. 2002, 107, 6–15. [Google Scholar] [CrossRef]
  45. Sheffield, J.; Goteti, G.; Wood, E.F. Development of a 50-year high-resolution global dataset of meteorological forcings for land surface modeling. J. Clim. 2006, 19, 3088–3111. [Google Scholar] [CrossRef] [Green Version]
  46. UCSB. Data Sets. n.d. Available online: https://www.chc.ucsb.edu/data (accessed on 15 July 2021).
  47. AGRHYMET. Méthodologie de suivi des zones à risque. In AGRHYMET FLASH Bulletin de Suivi de la Campagne Agricole au Sahel 0/96; Centre Regional AGRHYMET, B.P. 11011: Niamey, Niger, 1996; Volume 2. [Google Scholar]
  48. Chantarat, S.; Mude, A.G.; Barrett, C.B.; Carter, M.R. Designing index-based livestock insurance for managing asset risk in northern Kenya. J. Risk Insur. 2013, 80, 205–237. [Google Scholar] [CrossRef] [Green Version]
  49. Miller, S.E.; Adams, E.C.; Markert, K.N.; Ndungu, L.; Ellenburg, W.L.; Anderson, E.R.; Kyuma, R.; Limaye, A.; Griffin, R.; Irwin, D. Assessment of a spatially and temporally consistent MODIS derived NDVI product for application in index-based drought insurance. Remote Sens. 2020, 12, 3031. [Google Scholar] [CrossRef]
  50. Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
  51. International Research Institute for Climate and Society. Descriptions of the IRI Climate Forecast Verification Scores. 2013. Available online: http://iri.columbia.edu/wp-content/uploads/2013/07/scoredescriptions.pdf (accessed on 21 July 2021).
  52. Camberlin, P.; Moron, V.; Okoola, R.; Philippon, N.; Gitau, W. Components of rainy seasons’ variability in Equatorial East Africa: Onset, cessation, rainfall frequency and intensity. Theor. Appl. Climatol. 2009, 98, 237–249. [Google Scholar] [CrossRef] [Green Version]
  53. Domínguez, A.; De Juan, J.; Tarjuelo, J.; Martínez, R.; Martínez-Romero, A. Determination of optimal regulated deficit irrigation strategies for maize in a semi-arid environment. Agric. Water Manag. 2012, 110, 67–77. [Google Scholar] [CrossRef]
  54. Camberlin, P.; Planchon, O. Coastal precipitation regimes in Kenya. Geogr. Ann. Ser. A Phys. Geogr. 1997, 79, 109–119. [Google Scholar] [CrossRef]
  55. Webster, P.J.; Yang, S. Monsoon and ENSO: Selectively interactive systems. Q. J. R. Meteorol. Soc. 1992, 118, 877–926. [Google Scholar] [CrossRef]
  56. Lau, K.M.; Yang, S. The Asian monsoon and predictability of the tropical ocean–atmosphere system. Q. J. R. Meteorol. Soc. 1996, 122, 945–957. [Google Scholar] [CrossRef]
  57. Duan, W.; Wei, C. The ‘spring predictability barrier’for ENSO predictions and its possible mechanism: Results from a fully coupled model. Int. J. Climatol. 2013, 33, 1280–1292. [Google Scholar] [CrossRef]
Atmosphere 12 01371 g001 550
Figure 1. Yearly precipitation in Kenya from CHIRPS (top left) [35], elevation (top right) [40], cropland from Global Food-Support Analysis Data (bottom left) [41], and ecological zone (bottom right) [42].
Figure 1. Yearly precipitation in Kenya from CHIRPS (top left) [35], elevation (top right) [40], cropland from Global Food-Support Analysis Data (bottom left) [41], and ecological zone (bottom right) [42].
Atmosphere 12 01371 g001
Atmosphere 12 01371 g002 550
Figure 2. This figure shows the average difference in onset date between CHIRPS-GEFS and CHIRPS. Negative values mean that CHIRPS-GEFS predicts a later start date than observed; positive values mean that CHIRPS-GEFS predicts an earlier start date.
Figure 2. This figure shows the average difference in onset date between CHIRPS-GEFS and CHIRPS. Negative values mean that CHIRPS-GEFS predicts a later start date than observed; positive values mean that CHIRPS-GEFS predicts an earlier start date.
Atmosphere 12 01371 g002
Atmosphere 12 01371 g003 550
Figure 3. This image shows the average absolute difference in onset date between CHIRPS-GEFS and CHIRPS.
Figure 3. This image shows the average absolute difference in onset date between CHIRPS-GEFS and CHIRPS.
Atmosphere 12 01371 g003
Atmosphere 12 01371 g004 550
Figure 4. Probability of detection for dry anomaly events.
Figure 4. Probability of detection for dry anomaly events.
Atmosphere 12 01371 g004
Atmosphere 12 01371 g005 550
Figure 5. Probability of detection for wet anomaly events.
Figure 5. Probability of detection for wet anomaly events.
Atmosphere 12 01371 g005
Atmosphere 12 01371 g006 550
Figure 6. This image shows the ROC for dry anomaly events.
Figure 6. This image shows the ROC for dry anomaly events.
Atmosphere 12 01371 g006
Atmosphere 12 01371 g007 550
Figure 7. This image shows the ROC for wet anomaly events.
Figure 7. This image shows the ROC for wet anomaly events.
Atmosphere 12 01371 g007
Atmosphere 12 01371 g008 550
Figure 8. This image shows the ROC for wet anomaly events.
Figure 8. This image shows the ROC for wet anomaly events.
Atmosphere 12 01371 g008
Atmosphere 12 01371 g009 550
Figure 9. This image shows the Heidke skill score over individual months for dry anomaly events.
Figure 9. This image shows the Heidke skill score over individual months for dry anomaly events.
Atmosphere 12 01371 g009
Atmosphere 12 01371 g010 550
Figure 10. This image shows the Heidke skill score over individual months for wet anomaly events.
Figure 10. This image shows the Heidke skill score over individual months for wet anomaly events.
Atmosphere 12 01371 g010
Table
Table 1. Contingency table displaying categories of how forecasts compare to observed events.
Table 1. Contingency table displaying categories of how forecasts compare to observed events.
Observed YesObserved No
Forecast Yesab
Forecast Nocd
Table
Table 2. This table shows the average skill over each ecological zone for a 3 month lead time.
Table 2. This table shows the average skill over each ecological zone for a 3 month lead time.
EcologicalWETDRY
ZonePODFARHSSROCPODFARHSSROC
Arid0.5830.5080.4050.8250.5490.5000.4130.849
Semi-Arid0.6310.3890.5230.8310.5240.4920.3910.796
Sub-Humid0.6280.4090.5040.8220.4570.5700.3000.783
Humid0.5750.4720.4310.7860.4670.5720.3030.790
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Miller, S.; Mishra, V.; Ellenburg, W.L.; Adams, E.; Roberts, J.; Limaye, A.; Griffin, R. Analysis of a Short-Term and a Seasonal Precipitation Forecast over Kenya. Atmosphere 2021, 12, 1371. https://doi.org/10.3390/atmos12111371

AMA Style

Miller S, Mishra V, Ellenburg WL, Adams E, Roberts J, Limaye A, Griffin R. Analysis of a Short-Term and a Seasonal Precipitation Forecast over Kenya. Atmosphere. 2021; 12(11):1371. https://doi.org/10.3390/atmos12111371

Chicago/Turabian Style

Miller, Sara, Vikalp Mishra, W. Lee Ellenburg, Emily Adams, Jason Roberts, Ashutosh Limaye, and Robert Griffin. 2021. "Analysis of a Short-Term and a Seasonal Precipitation Forecast over Kenya" Atmosphere 12, no. 11: 1371. https://doi.org/10.3390/atmos12111371

APA Style

Miller, S., Mishra, V., Ellenburg, W. L., Adams, E., Roberts, J., Limaye, A., & Griffin, R. (2021). Analysis of a Short-Term and a Seasonal Precipitation Forecast over Kenya. Atmosphere, 12(11), 1371. https://doi.org/10.3390/atmos12111371

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop