A Theoretical Study of the N2 + H2 Reactive Collisions for High Vibrational and Translational Energies
Abstract
:1. Introduction
2. Methodology
3. Results
3.1. Specific Initial-State Reactive Probability and Cross-Section
3.2. Energetic Features in the Reactive Molecular Ensemble
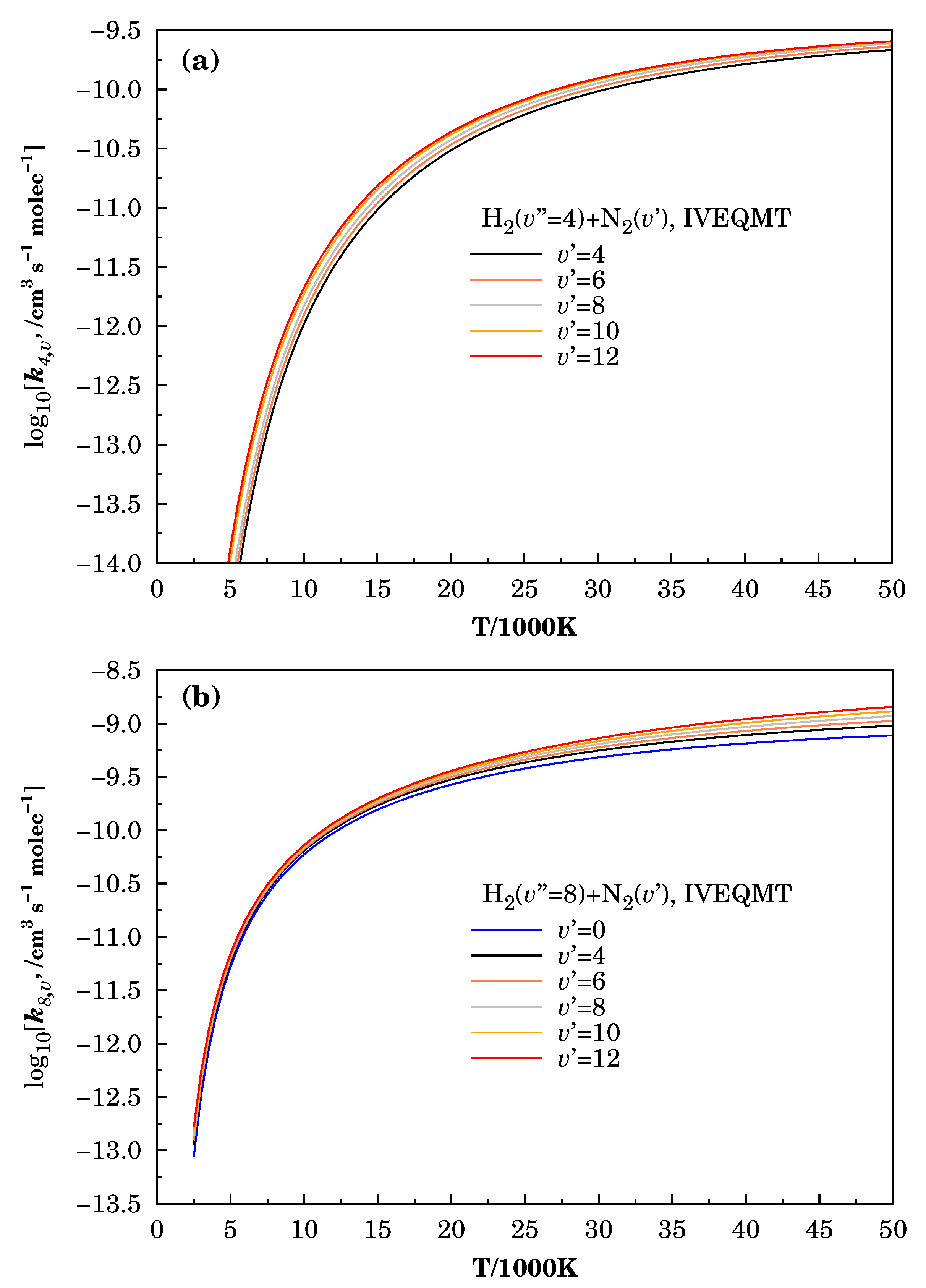
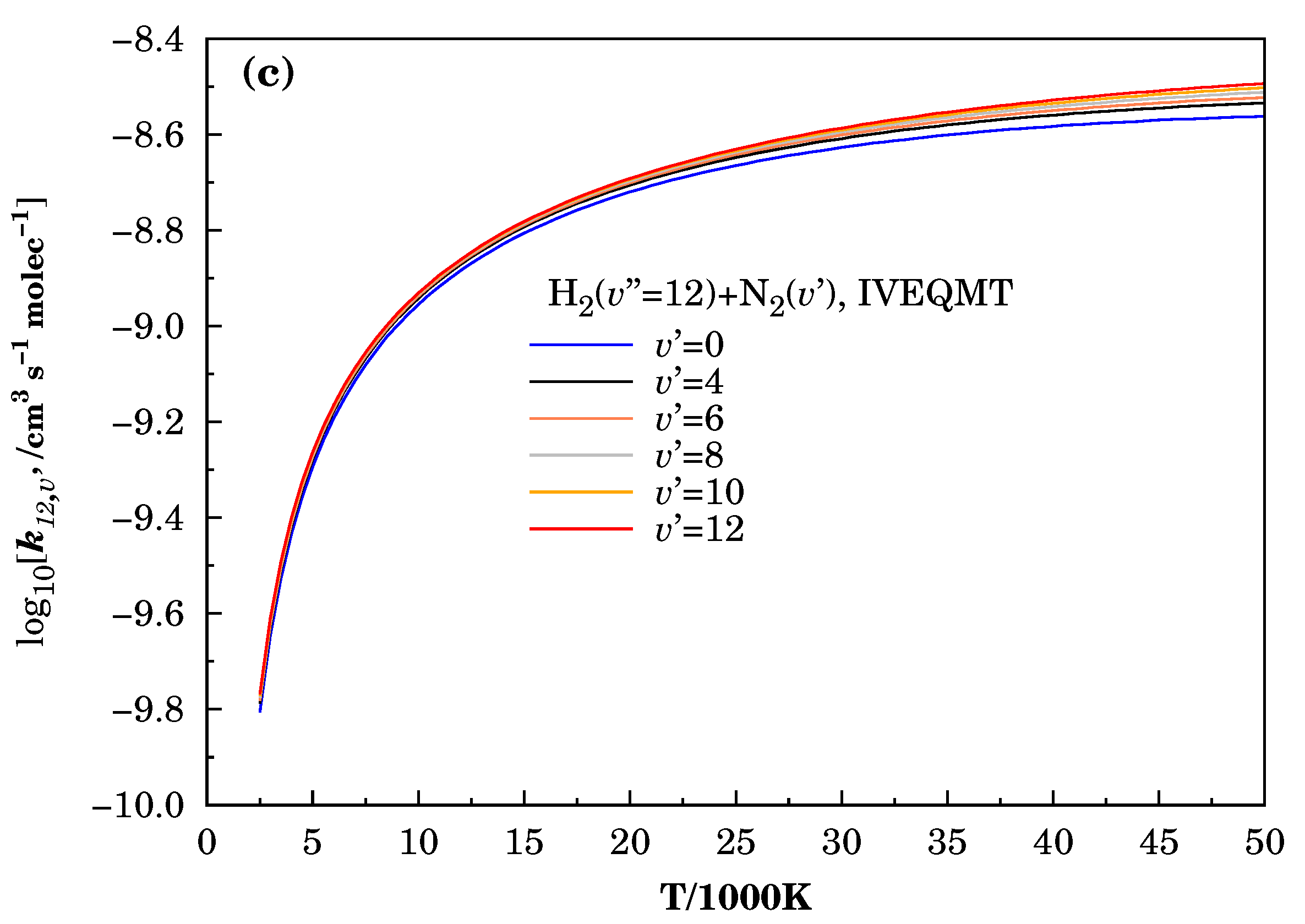
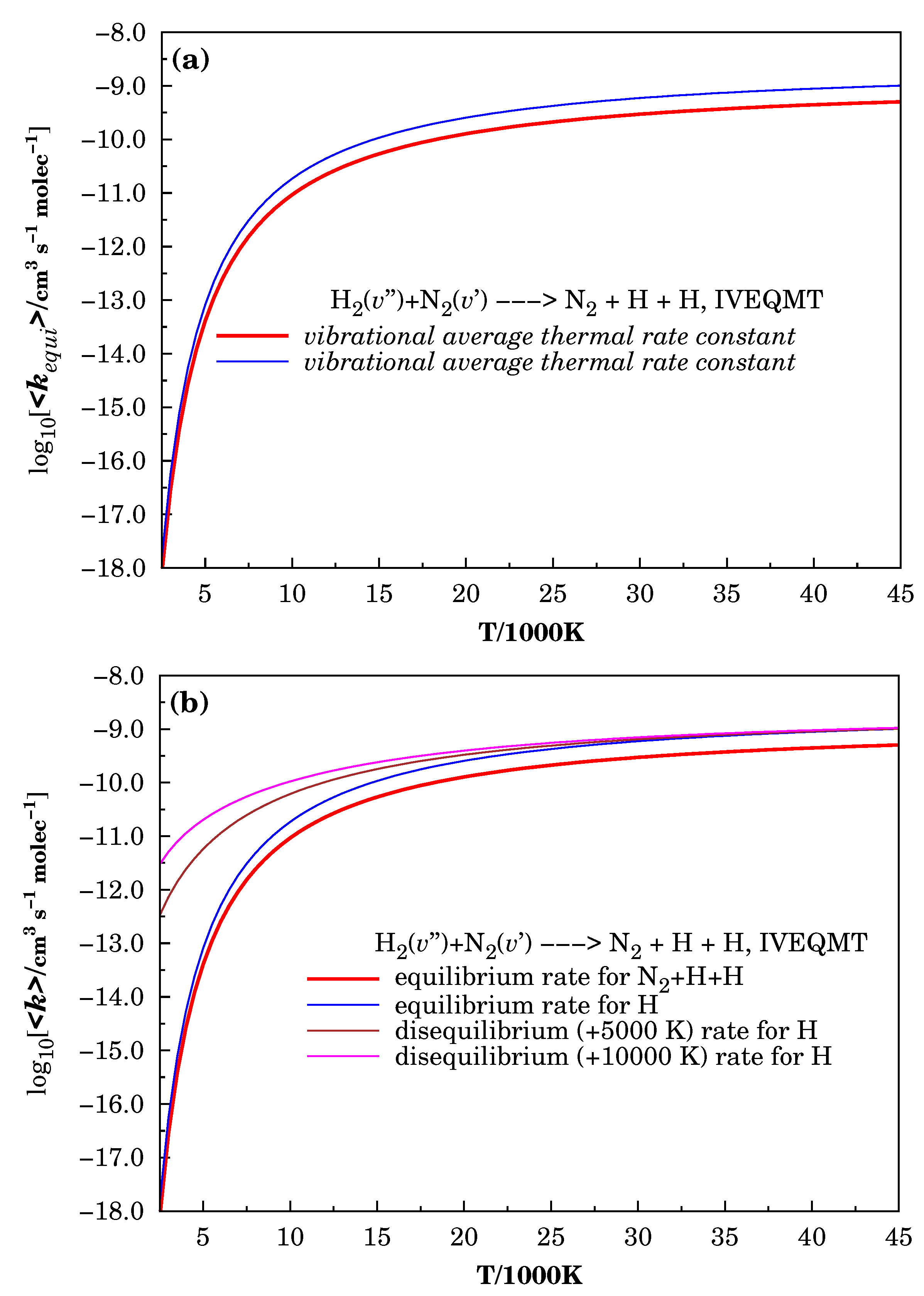
3.3. Specific Initial-State Reactive Thermal Rate Coefficients
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PES | Potential Energy Surface |
| QCT | Quasiclassical Trajectories |
| IVEQMT | Intermediate Vibrational Energy Quantum Mechanical Threshold |
| ZPE | Zero-Point Energy |
| V-T processes | Energy transfer from vibrational to translational degrees of freedom |
| T-R processes | nergy transfer from translational to rotational degrees of freedom |
References
- Keidar, M.; Kim, M.; Boyd, I.D. Electromagnetic Reduction of Plasma Density During Atmospheric Reentry and Hypersonic Flights. J. Spacecr. Rocket. 2008, 45, 445. [Google Scholar] [CrossRef] [Green Version]
- Josyula, E.; Suchyta, C.J.; Vedula, P.; Burt, J.M. Multiquantum Transitions in Oxygen and Nitrogen Molecules in Hypersonic Non-equilibrium Flows. J. Thermophys. Heat Transf. 2019, 33, 378–391. [Google Scholar] [CrossRef]
- Shoev, G.; Oblapenko, G.; Kunova, O.; Mekhonoshina, M.; Kustova, E. Validation of vibration-dissociation coupling models in hypersonic non-equilibrium separated flows. Acta Astronaut. 2018, 144, 147–159. [Google Scholar] [CrossRef]
- Koner, D.; Bemish, R.J.; Meuwly, M. Dynamics on Multiple Potential Energy Surfaces: Quantitative Studies of Elementary Processes Relevant to Hypersonics. J. Phys. Chem. A 2020, 124, 6255–6269. [Google Scholar] [CrossRef] [PubMed]
- Josyula, E. Oxygen Atoms’ Effect on Vibrational Relaxation of Nitrogen in Blunt-Body Flows. J. Thermophys. Heat Trans. 2001, 15, 106–115. [Google Scholar] [CrossRef]
- Kustova, E.V.; Oblapenko, G.P. Reaction and internal energy relaxation rates in viscous thermochemically non-equilibrium gas flows. Phys. Fluids 2015, 27, 016102. [Google Scholar] [CrossRef]
- Kustova, E.V.; Oblapenko, G.P. Mutual effect of vibrational relaxation and chemical reactions in viscous multitemperature flows. Phys. Rev. E 2016, 93, 033127. [Google Scholar] [CrossRef] [PubMed]
- Wayne, R.P. Chemistry of Atmospheres; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Jacob, D.J. Introduction to Atmospheric Chemistry; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Mackenzie, F.; Mackenzie, J.A. Our Changing Planet; Prentice-Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Atkinson, R.; Baulch, D.L.; Cox, R.A.; Hampson, J.R.F.; Troe, J.A. Evaluated kinetic and photochemical data for atmospheric chemistry. Supplement III. J. Phys. Chem. Ref. Data 1989, 18, 881. [Google Scholar] [CrossRef]
- Atkinson, R.; Baulch, D.L.; Cox, R.A.; Hampson, R.F., Jr.; Kerr, J.A.; Rossi, M.J.; Troe, J. Evaluated kinetic, photochemical and heterogeneous data for atmospheric chemistry: Supplement V. IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry. J. Phys. Chem. Ref. Data 1997, 26, 521–1011. [Google Scholar] [CrossRef]
- Gordiets, B.; Ferreira, C.; Pinheiro, M.; Ricard, A. Self-consistent kinetic model of low-pressure N-2-H-2 flowing discharges: I. Volume processes. Plasma Sources Sci. Technol. 1998, 7, 363–378. [Google Scholar] [CrossRef]
- Gordiets, B.; Ferreira, C.M.; Pinheiro, M.J.; Ricard, A. Self-consistent kinetic model of low-pressure N2-H2 flowing discharges: II Surface processes and densities of N, H, NH3 species. Plasma Sources Sci. Technol. 1998, 7, 379–388. [Google Scholar] [CrossRef]
- de Dios Garrido, J.; Ballester, M.Y. Relaxation processes in non-reactive collisions of H2 and N2 at high translational energies. Mol. Phys. 2021, 119, e1831635. [Google Scholar] [CrossRef]
- Poveda, L.A.; Biczysko, M.; Varandas, A.J.C. Accurate ab initio based DMBE potential energy surface for the ground electronic state of N2H2. J. Chem. Phys. 2009, 131, 044309. [Google Scholar] [CrossRef]
- Varandas, A.J.C. Intermolecular and Intramolecular Potentials: Topographical Aspects, Calculation, and Functional Representation via A Double Many-Body Expansion Method. In Advances in Chemical Physics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007; Chapter 2; pp. 255–338. [Google Scholar] [CrossRef]
- Biczysko, M.; Poveda, L.; Varandas, A. Accurate MRCI Study of Ground-State N2H2 Potential Energy Surface. Chem. Phys. Lett. 2006, 424, 46–53. [Google Scholar] [CrossRef] [Green Version]
- de Castro, D.G.; Poveda, L.A.; Crispim, L.W.S.; Ballester, M.Y. Quasi-Classical Trajectory Study of NH(3Σ−) + NH(3Σ−) Reactive Collisions. J. Phys. Chem. A 2019, 123, 9113–9122. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; Porter, R.N.; Sharma, R.D. Exchange Reactions with Activation Energy. I. Simple Barrier Potential for (H, H2). J. Chem. Phys. 1965, 43, 3259–3287. [Google Scholar] [CrossRef]
- Karplus, M.; Porter, R.N.; Sharma, R.D. Dynamics of reactive collisions: The H + H2 exchange reaction. J. Chem. Phys. 1964, 40, 2033–2034. [Google Scholar] [CrossRef]
- Hase, W.L.; Duchovic, R.J.; Hu, X.; Komornik, A.; Lim, K.F.; Lu, D.H.; Peslherbe, G.H.; Swamy, K.N.; van de Linde, S.R.; Varandas, A.J.C.; et al. VENUS 96. Quantum Chem. Program Exch. Bull. 1996, 16, 43. [Google Scholar]
- Levine, R.D. Molecular Reaction Dynamics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Garrido, J.d.D.; Ellakkis, S.; Ballester, M.Y. Relaxation of Vibrationally Excited OH Radical by SO. J. Phys. Chem A. 2019, 123, 8994–9007. [Google Scholar] [CrossRef]
- Truhlar, D.G. Multiple Potential Energy Surfaces for Reactions of Species in Degenerate Electronic States. J. Chem. Phys. 1972, 56, 3189–3190. [Google Scholar] [CrossRef]
- Muckerman, J.T.; Newton, M.D. Comment on “Multiple Potential Energy Surfaces for Reactions of Species in Degenerate Electronic States” by D. G. Truhlar. J. Chem. Phys. 1972, 56, 3191–3192. [Google Scholar] [CrossRef]
- Varandas, A.J.C. Excitation function for H+O2: A study of zero-point energy effects and rotational distributions in trajectory calculations. J. Chem. Phys. 1993, 99, 1076. [Google Scholar] [CrossRef]
- Varandas, A.J.C. A novel nonactive model to account for the leak of zero-point energy in trajectory calculations. Application to H+O2 reaction near threshold. Chem. Phys. Lett. 1994, 225, 18. [Google Scholar] [CrossRef]
- LeRoy, R.L. Relationships between Arrhenius activation energies and excitation functions. J. Phys. Chem. 1969, 73, 4338. [Google Scholar] [CrossRef]
- Veliz, J.C.S.V.; Koner, D.; Schwilk, M.; Bemish, R.J.; Meuwly, M. The N(4S)+O2(X3)→O(3P)+NO(X2Π) reaction: Thermal and vibrational relaxation rates for the 2A′, 4A′ and 2A″ states. Phys. Chem. Chem. Phys. 2020, 22, 3927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
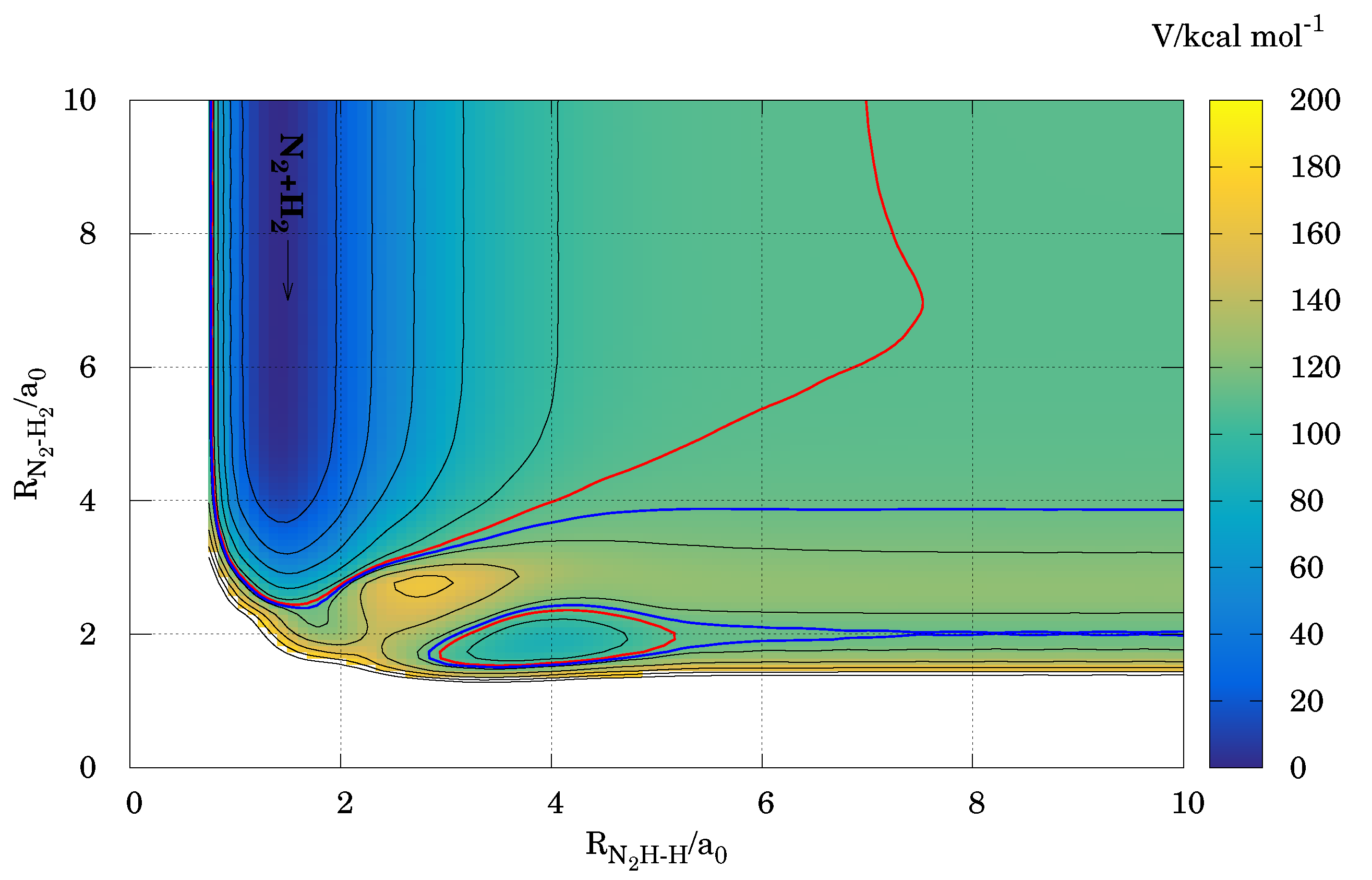
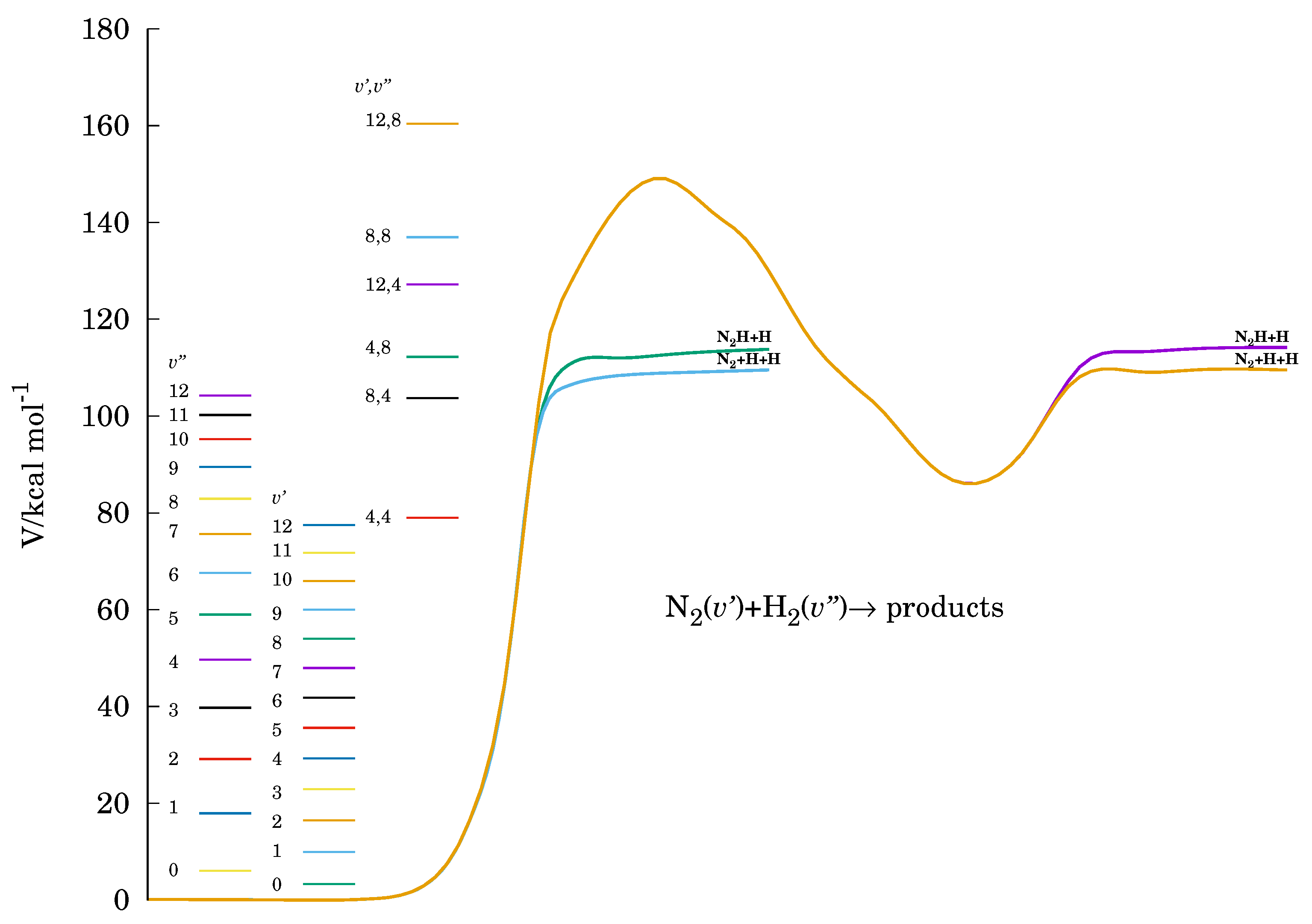
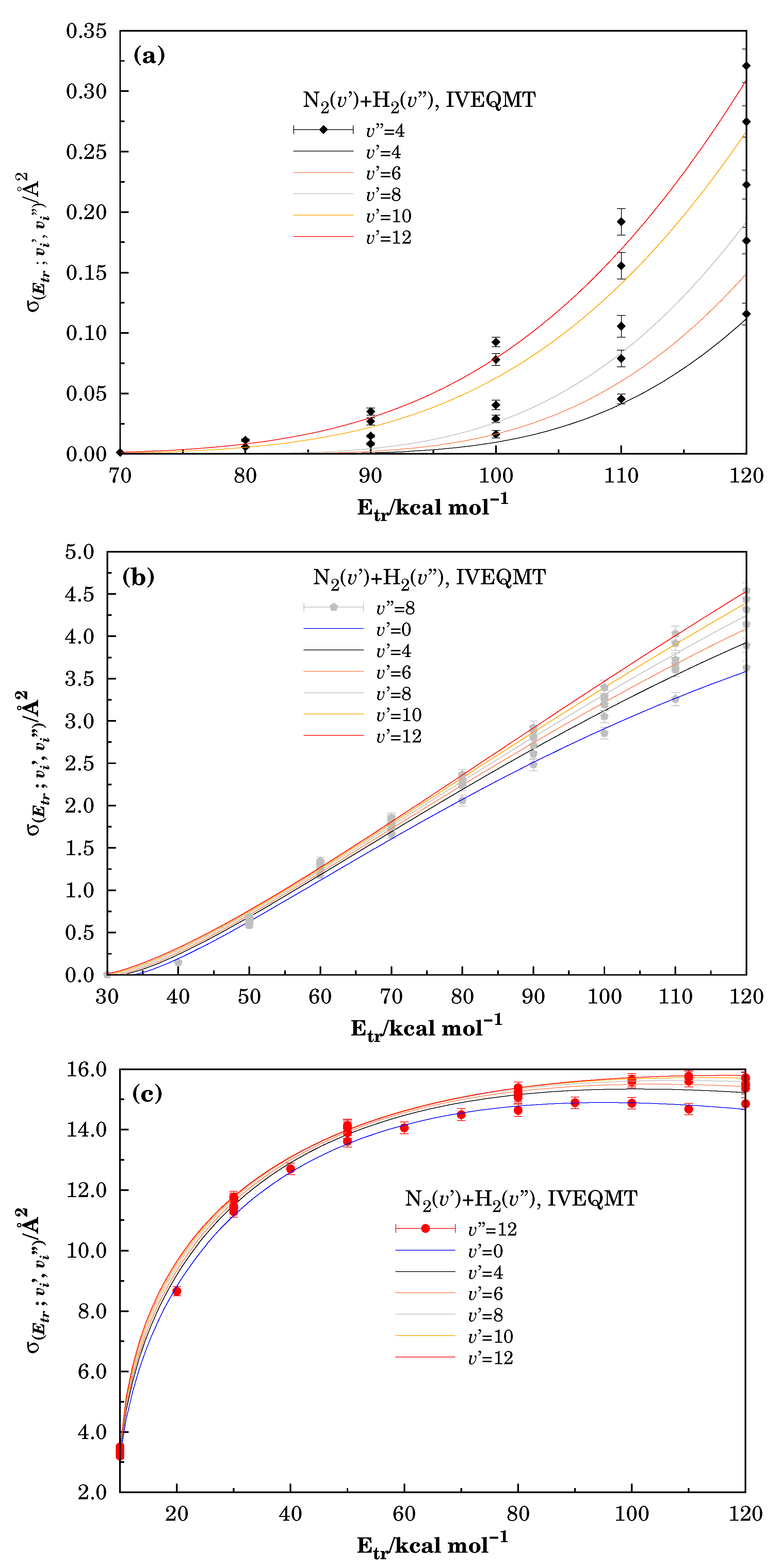
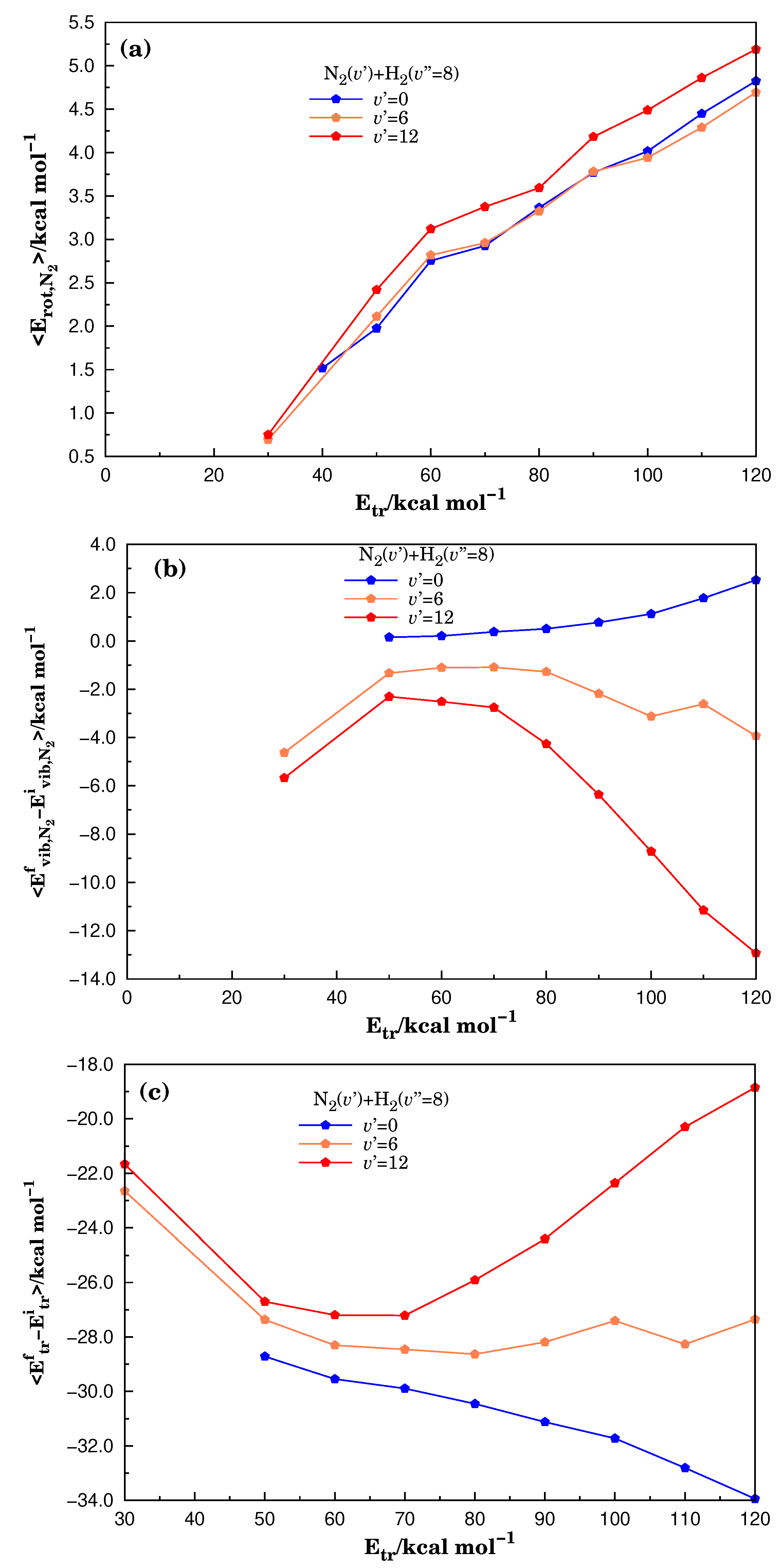
| 70.0 | 4 | 4 | - | - | - | 4 | 6 | - | - | - |
| 80.0 | - | - | - | - | - | - | ||||
| 90.0 | - | - | - | 1.0 | 9996 | 27 | ||||
| 100.0 | 1.1 | 9986 | 43 | 1.1 | 9984 | 76 | ||||
| 110.0 | 1.1 | 9980 | 119 | 1.4 | 9982 | 128 | ||||
| 120.0 | 1.4 | 9970 | 182 | 1.5 | 9980 | 249 | ||||
| 70.0 | 4 | 8 | - | - | - | 4 | 10 | - | - | - |
| 80.0 | - | - | - | 0.5 | 9993 | 73 | ||||
| 90.0 | 0.8 | 9986 | 74 | 1.1 | 9990 | 71 | ||||
| 100.0 | 1.1 | 9985 | 110 | 1.1 | 9982 | 205 | ||||
| 110.0 | 1.6 | 9977 | 131 | 1.6 | 9971 | 193 | ||||
| 120.0 | 1.5 | 9971 | 314 | 1.5 | 9974 | 388 | ||||
| 40.0 | 4 | 12 | - | - | - | 8 | 0 | 1.6 | 9846 | 182 |
| 50.0 | - | - | - | 2.0 | 9786 | 456 | ||||
| 60.0 | - | - | - | 2.3 | 9944 | 710 | ||||
| 70.0 | 0.4 | 9999 | 25 | 2.4 | 9674 | 890 | ||||
| 80.0 | 0.7 | 9997 | 74 | 2.6 | 9664 | 937 | ||||
| 90.0 | 1.1 | 9991 | 92 | 2.7 | 9660 | 1048 | ||||
| 100.0 | 0.9 | 9976 | 363 | 2.5 | 9537 | 1387 | ||||
| 110.0 | 1.4 | 9977 | 311 | 2.6 | 9509 | 1459 | ||||
| 120.0 | 1.5 | 9973 | 453 | 2.6 | 9460 | 1616 | ||||
| 30.0 | 8 | 4 | - | - | - | 8 | 6 | 0.6 | 10,000 | 7 |
| 50.0 | 2.2 | 10,000 | 412 | 2.2 | 10,000 | 405 | ||||
| 60.0 | 2.3 | 9999 | 752 | 2.4 | 10,000 | 723 | ||||
| 70.0 | 2.4 | 9999 | 952 | 2.5 | 9999 | 902 | ||||
| 80.0 | 2.5 | 9998 | 1139 | 2.5 | 10,000 | 1163 | ||||
| 90.0 | 2.5 | 9997 | 1330 | 2.6 | 9995 | 1258 | ||||
| 100.0 | 2.6 | 9989 | 1436 | 2.6 | 9988 | 1469 | ||||
| 110.0 | 2.7 | 9982 | 1572 | 2.6 | 9987 | 1726 | ||||
| 120.0 | 2.6 | 9980 | 1830 | 2.6 | 9977 | 1946 | ||||
| 30.0 | 8 | 8 | 0.6 | 10,000 | 13 | 8 | 10 | 1.1 | 10,000 | 12 |
| 50.0 | 2.2 | 10,000 | 429 | 2.1 | 10,000 | 488 | ||||
| 60.0 | 2.4 | 10,000 | 711 | 2.4 | 10,000 | 716 | ||||
| 70.0 | 2.5 | 10,000 | 929 | 2.5 | 10,000 | 936 | ||||
| 80.0 | 2.5 | 9999 | 1167 | 2.5 | 10,000 | 1173 | ||||
| 90.0 | 2.7 | 9998 | 1224 | 2.7 | 9997 | 1256 | ||||
| 100.0 | 2.6 | 9996 | 1530 | 2.8 | 9998 | 1335 | ||||
| 110.0 | 2.7 | 9988 | 1623 | 2.7 | 9991 | 1709 | ||||
| 120.0 | 2.7 | 9975 | 1880 | 2.7 | 9989 | 1937 | ||||
| 10.0 | 8 | 12 | - | - | - | 12 | 0 | 2.8 | 9996 | 1297 |
| 20.0 | - | - | - | 3.4 | 9988 | 2381 | ||||
| 30.0 | 0.5 | 10,000 | 26 | 3.5 | 9980 | 2925 | ||||
| 40.0 | - | - | - | 3.6 | 9917 | 3093 | ||||
| 50.0 | 2.0 | 10,000 | 540 | 3.5 | 9862 | 3487 | ||||
| 60.0 | 2.5 | 10,000 | 684 | 3.6 | 9812 | 3388 | ||||
| 70.0 | 2.5 | 10,000 | 945 | 3.6 | 9767 | 3477 | ||||
| 80.0 | 2.5 | 10,000 | 1205 | 3.6 | 9712 | 3492 | ||||
| 90.0 | 2.8 | 9998 | 1185 | 3.5 | 9675 | 3743 | ||||
| 100.0 | 2.9 | 9995 | 1285 | 3.5 | 9684 | 3743 | ||||
| 110.0 | 2.7 | 9992 | 1759 | 3.5 | 9640 | 3677 | ||||
| 120.0 | 2.7 | 9997 | 1982 | 3.6 | 9696 | 3538 | ||||
| 10.0 | 12 | 4 | 3.0 | 10,000 | 1164 | 12 | 6 | 3.0 | 9999 | 1169 |
| 30.0 | 3.6 | 9995 | 2798 | 3.6 | 9995 | 2813 | ||||
| 50.0 | 3.6 | 9976 | 3405 | 3.6 | 9986 | 3411 | ||||
| 80.0 | 3.6 | 9943 | 3680 | 3.6 | 9976 | 3706 | ||||
| 100.0 | 3.7 | 9951 | 3607 | 3.7 | 9980 | 3632 | ||||
| 120.0 | 3.6 | 9924 | 3747 | 3.6 | 9955 | 3785 | ||||
| 10.0 | 12 | 8 | 2.9 | 9999 | 1255 | 12 | 10 | 3.0 | 9998 | 1213 |
| 30.0 | 3.6 | 9999 | 2867 | 3.7 | 9999 | 2722 | ||||
| 50.0 | 3.7 | 9995 | 3286 | 3.6 | 9995 | 3467 | ||||
| 80.0 | 3.4 | 9993 | 4184 | 3.5 | 9989 | 3958 | ||||
| 110.0 | 3.5 | 9992 | 4051 | 3.5 | 9989 | 4086 | ||||
| 120.0 | 3.6 | 9968 | 3800 | 3.6 | 9983 | 3854 | ||||
| 10.0 | 12 | 12 | 3.1 | 10,000 | 1161 | |||||
| 30.0 | 3.6 | 10,000 | 2890 | |||||||
| 50.0 | 3.6 | 9996 | 3452 | |||||||
| 80.0 | 3.5 | 9994 | 3996 | |||||||
| 110.0 | 3.6 | 9988 | 3869 | |||||||
| 120.0 | 3.6 | 9993 | 3852 |
| 4 | 4 | 90.0 | - | - | 4 | 6 | 90.0 | 0.0084 | 0.001 |
| 100.0 | 0.0163 | 0.003 | 100.0 | 0.0289 | 0.233 | ||||
| 110.0 | 0.0452 | 0.004 | 110.0 | 0.0789 | 0.233 | ||||
| 120.0 | 0.1120 | 0.009 | 120.0 | 0.1763 | 0.011 | ||||
| 4 | 8 | 80.0 | - | - | 4 | 10 | 80.0 | 0.0057 | 0.0006 |
| 90.0 | 0.0148 | 0.001 | 90.0 | 0.0270 | 0.003 | ||||
| 100.0 | 0.0418 | 0.004 | 100.0 | 0.0780 | 0.005 | ||||
| 110.0 | 0.1056 | 0.009 | 110.0 | 0.1556 | 0.011 | ||||
| 120.0 | 0.2226 | 0.012 | 120.0 | 0.2749 | 0.013 | ||||
| 4 | 12 | 40.0 | - | - | 8 | 0 | 40.0 | 0.1486 | 0.010 |
| 50.0 | - | - | 50.0 | 0.5855 | 0.026 | ||||
| 60.0 | - | - | 60.0 | 1.1866 | 0.043 | ||||
| 70.0 | 0.0012 | 0.0002 | 70.0 | 1.6647 | 0.053 | ||||
| 80.0 | 0.0114 | 0.001 | 80.0 | 2.0591 | 0.063 | ||||
| 90.0 | 0.0350 | 0.003 | 90.0 | 2.4846 | 0.072 | ||||
| 100.0 | 0.0925 | 0.004 | 100.0 | 2.8555 | 0.070 | ||||
| 110.0 | 0.1920 | 0.011 | 110.0 | 3.2584 | 0.078 | ||||
| 120.0 | 0.3210 | 0.014 | 120.0 | 3.6278 | 0.082 | ||||
| 8 | 4 | 50.0 | 0.6264 | 0.030 | 8 | 6 | 50.0 | 0.6158 | 0.029 |
| 60.0 | 1.2500 | 0.044 | 60.0 | 1.3083 | 0.046 | ||||
| 70.0 | 1.7228 | 0.053 | 70.0 | 1.7712 | 0.056 | ||||
| 80.0 | 2.2368 | 0.062 | 80.0 | 2.2835 | 0.062 | ||||
| 90.0 | 2.6123 | 0.067 | 90.0 | 2.6729 | 0.070 | ||||
| 100.0 | 3.0530 | 0.074 | 100.0 | 3.1234 | 0.075 | ||||
| 110.0 | 3.6067 | 0.083 | 110.0 | 3.6703 | 0.080 | ||||
| 120.0 | 3.8935 | 0.083 | 120.0 | 4.1422 | 0.084 | ||||
| 8 | 8 | 30.0 | 0.0014 | 0.0004 | 8 | 10 | 30.0 | 0.0045 | 0.001 |
| 50.0 | 0.6523 | 0.030 | 50.0 | 0.6761 | 0.029 | ||||
| 60.0 | 1.2866 | 0.046 | 60.0 | 1.2956 | 0.046 | ||||
| 70.0 | 1.8240 | 0.057 | 70.0 | 1.8378 | 0.057 | ||||
| 80.0 | 2.2914 | 0.063 | 80.0 | 2.3031 | 0.063 | ||||
| 90.0 | 2.8037 | 0.075 | 90.0 | 2.8773 | 0.075 | ||||
| 100.0 | 3.2505 | 0.076 | 100.0 | 3.2881 | 0.082 | ||||
| 110.0 | 3.7214 | 0.084 | 110.0 | 3.9175 | 0.086 | ||||
| 120.0 | 4.3164 | 0.089 | 120.0 | 4.4410 | 0.090 | ||||
| 8 | 12 | 10.0 | - | - | 12 | 0 | 10.0 | 3.1958 | 0.082 |
| 20.0 | - | - | 20.0 | 8.6574 | 0.154 | ||||
| 30.0 | 0.0020 | 0.0004 | 30.0 | 11.2792 | 0.175 | ||||
| 40.0 | - | - | 40.0 | 12.6985 | 0.189 | ||||
| 50.0 | 0.6785 | 0.028 | 50.0 | 13.6073 | 0.185 | ||||
| 60.0 | 1.3430 | 0.049 | 60.0 | 14.0585 | 0.195 | ||||
| 70.0 | 1.8555 | 0.057 | 70.0 | 14.4943 | 0.197 | ||||
| 80.0 | 2.3660 | 0.064 | 80.0 | 14.6393 | 0.198 | ||||
| 90.0 | 2.9192 | 0.079 | 90.0 | 14.8886 | 0.190 | ||||
| 100.0 | 3.3957 | 0.087 | 100.0 | 14.8748 | 0.190 | ||||
| 110.0 | 4.0317 | 0.087 | 110.0 | 14.6792 | 0.190 | ||||
| 120.0 | 4.5405 | 0.091 | 120.0 | 14.8566 | 0.199 | ||||
| 12 | 4 | 10.0 | 3.2911 | 0.090 | 12 | 6 | 10.0 | 3.3056 | 0.090 |
| 30.0 | 11.3978 | 0.183 | 30.0 | 11.4588 | 0.183 | ||||
| 50.0 | 13.8968 | 0.193 | 50.0 | 13.9073 | 0.193 | ||||
| 80.0 | 15.0690 | 0.197 | 80.0 | 15.1252 | 0.196 | ||||
| 100.0 | 15.5895 | 0.207 | 100.0 | 15.6519 | 0.207 | ||||
| 120.0 | 15.3727 | 0.198 | 120.0 | 15.4803 | 0.198 | ||||
| 12 | 8 | 10.0 | 3.31614 | 0.087 | 12 | 10 | 10.0 | 3.43036 | 0.092 |
| 30.0 | 11.6741 | 0.184 | 30.0 | 11.7080 | 0.191 | ||||
| 50.0 | 14.1396 | 0.202 | 50.0 | 14.1229 | 0.193 | ||||
| 80.0 | 15.2055 | 0.179 | 80.0 | 15.2489 | 0.188 | ||||
| 110.0 | 15.6025 | 0.190 | 110.0 | 15.7420 | 0.189 | ||||
| 120.0 | 15.5214 | 0.198 | 120.0 | 15.7183 | 0.198 | ||||
| 12 | 12 | 10.0 | 3.50514 | 0.096 | |||||
| 30.0 | 11.7666 | 0.184 | |||||||
| 50.0 | 14.0604 | 0.193 | |||||||
| 80.0 | 15.3876 | 0.188 | |||||||
| 110.0 | 15.7715 | 0.198 | |||||||
| 120.0 | 15.6944 | 0.198 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garrido, J.d.D.; Ballester, M.Y. A Theoretical Study of the N2 + H2 Reactive Collisions for High Vibrational and Translational Energies. Atmosphere 2021, 12, 1349. https://doi.org/10.3390/atmos12101349
Garrido JdD, Ballester MY. A Theoretical Study of the N2 + H2 Reactive Collisions for High Vibrational and Translational Energies. Atmosphere. 2021; 12(10):1349. https://doi.org/10.3390/atmos12101349
Chicago/Turabian StyleGarrido, Juan de Dios, and Maikel Yusat Ballester. 2021. "A Theoretical Study of the N2 + H2 Reactive Collisions for High Vibrational and Translational Energies" Atmosphere 12, no. 10: 1349. https://doi.org/10.3390/atmos12101349
APA StyleGarrido, J. d. D., & Ballester, M. Y. (2021). A Theoretical Study of the N2 + H2 Reactive Collisions for High Vibrational and Translational Energies. Atmosphere, 12(10), 1349. https://doi.org/10.3390/atmos12101349






