A Fast-Converging Kernel Density Estimator for Dispersion in Horizontally Homogeneous Meteorological Conditions
Abstract
:1. Introduction
2. Methodology
2.1. Kernel Smoothing
2.2. Path Integral-Based Kernel Density Estimator
2.3. Boundary Condition at the Ground Surface
2.4. Discretization
2.5. Computational Set-Up
3. Results
3.1. Convergence Study
3.2. Demonstration on Project Prairie Grass
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Atmospheric Parameterization
Appendix B. The Wiener Measure Applied to the Langevin Equation
Appendix C. Derivation of the Recursion Formula for D nk,k
References
- Izenman, A.J. Recent developments in nonparametric density estimation. J. Am. Stat. Assoc. 1991, 86, 205–224. [Google Scholar] [CrossRef]
- Rosenblatt, M. Remarks on some nonparametric estimates. Ann. Math. Stat. 1956, 27, 832–837. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Lorimer, G.S. The kernel method for air quality modelling–I. mathematical foundation. Atmos. Environ. 1986, 20, 1447–1452. [Google Scholar] [CrossRef]
- Fasoli, B.; Lin, J.C.; Bowling, D.R.; Mitchell, L.; Mendoza, D. Simulating atmospheric tracer concentrations for spatially distributed receptors: Updates to the Stochastic Time-Inverted Lagrangian Transport model’s R interface (STILT-R version 2). Geosci. Model Dev. 2018, 11, 2813–2824. [Google Scholar] [CrossRef] [Green Version]
- Björnham, O.; Brännström, N.; Grahn, H.; Lindgren, P.; von Schoenberg, P. Post-Processing of Results from a Particle Dispersion Model by Employing Kernel Density Estimation; Technical Report FOI-R–4135–SE; FOI: Stockholm, Sweden, 2015. [Google Scholar]
- Stohl, A.; Forster, C.; Frank, A.; Seibert, P.; Wotawa, G. The Lagrangian particle dispersion model FLEXPART version 6.2. Atmos. Chem. Phys. 2005, 5, 2461–2474. [Google Scholar] [CrossRef] [Green Version]
- Chacón, J.E.; Duong, T. Multivariate Kernel Smoothing and Its Applications, 1st ed.; Number 160 in Monographs on Statistics and Applied Probability; CRC Press: Boca Raton, FL, USA, 2018; p. 248. [Google Scholar]
- Xie, X.R.; Wu, J.J. Some Improvement on Convergence Rates of Kernel Density Estimator. Appl. Math. 2014, 5, 1684–1696. [Google Scholar] [CrossRef] [Green Version]
- Crawford, A. The use of Gaussian mixture models with atmospheric Lagrangian particle dispersion models for density estimation and feature identification. Atmosphere 2020, 11, 1369. [Google Scholar] [CrossRef]
- Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. Kernel density estimation via diffusion. Ann. Stat. 2010, 38, 2916–2957. [Google Scholar] [CrossRef] [Green Version]
- Wiener, N. The average of an analytic functional. Proc. Natl. Acad. Sci. USA 1921, 7, 253–260. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alvarez, A.; Pennel, R.; Garau, B.; Tintore, J. A Fourier-transform path integral formalism to compute dispersion probability distributions in variable ocean environments. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Hurley, P. PARTPUFF—A Lagrangian Particle-Puff Approach for Plume Dispersion Modeling Applications. J. Appl. Meteorol. Climatol. 1994, 33, 285–294. [Google Scholar] [CrossRef] [Green Version]
- Lamb, R.G. Diffusion in the convective boundary layer. In Atmospheric Turbulence and Air Pollution Modelling; Springer: Berlin/Heidelberg, Germany, 1984; Volume 1, pp. 159–229. [Google Scholar]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations, 2nd ed.; Stochastic Modelling and Applied Probability; Springer-Verlag: Berlin/Heidelberg, Germany, 1992; Volume 23. [Google Scholar]
- Thomson, D.J.; Wilson, J.D. Lagrangian Modeling of the Atmosphere; Geophysical Monograph Series; Chapter History of Lagrangian Stochastic Models for Turbulent Dispersion; American Geophysical Union: Washington, DC, USA, 2012; Volume 200, pp. 19–36. [Google Scholar]
- Müller, H.G. Nonparametric Regression Analysis of Longitudinal Data, 1st ed.; Lecture Notes in Statistics; Springer: New York, NY, USA, 1988; Volume 46, pp. XIV, 369. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall/CRC: London, UK, 1986; Monographs on Statistics and Applied Probability. [Google Scholar]
- Paley, R.E.A.C.; Wiener, N.; Zygmund, A. Notes on random functions. Math. Z. 1933, 37, 647–668. [Google Scholar] [CrossRef]
- Nasstrom, J.S.; Ermak, D.L. A homogeneous Langevin equation model, part II: Simulation of dispersion in the convective boundary layer. Bound. Layer Meteorol. 1999, 92, 371–405. [Google Scholar] [CrossRef]
- Legg, B.; Raupach, M. Markov-chain simulation of particle dispersion in inhomogeneous flows: The mean drift velocity induced by a gradient in Eulerian velocity variance. Bound. Layer Meteorol. 1982, 24, 3–13. [Google Scholar] [CrossRef]
- Barad, M.L. Project Prairie Grass, a Field Program in Diffusion; Technical Report 59; Air Force Cambridge Research Center: Bedford, MA, USA, 1958; Volume I & II. [Google Scholar]
- Haugen, D.A. Project Prairie Grass, a Field Program in Diffusion; Technical Report 59; Air Force Cambridge Research Center: Bedford, MA, USA, 1959; Volume III. [Google Scholar]
- Nieuwstadt, F. The computation of the friction velocity u* and the temperature scale T* from temperature and wind velocity profiles by least-square methods. Bound. Layer Meteorol. 1978, 14, 235–246. [Google Scholar] [CrossRef]
- Van Ulden, A.P. Simple estimates for vertical diffusion from sources near the ground. Atmos. Environ. 1978, 12, 2125–2129. [Google Scholar] [CrossRef]
- Andreas, E.L.; Claffey, K.J.; Jordan, R.E.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G.; Grachev, A.A. Evaluations of the von Kármán constant in the atmospheric surface layer. J. Fluid Mech. 2006, 559, 117–149. [Google Scholar] [CrossRef] [Green Version]
- Arya, S.P. Introduction to Micrometeorology, 2nd ed.; International Geophysics Series; Academic Press: Cambridge, MA, USA, 2001; Volume 79. [Google Scholar]
- Briggs, G.A.; McDonald, K.R. Prairie Grass revisited: Optimum indicators of vertical spread. In Proceedings of the 9th NATO-CCMS International Technical Symposium on Air Pollution Modeling and its Application, Toronto, ON, Canada, 28–31 August 1978; pp. 209–220. [Google Scholar]
- Chang, J.C.; Hanna, S.R. Air quality model performance evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Marron, J.S.; Ruppert, D. Transformations to reduce boundary bias in kernel density estimation. J. R. Stat. Soc. B 1994, 56, 653–671. [Google Scholar] [CrossRef]
- Vitali, L.; Monforti, F.; Bellasio, R.; Bianconi, R.; Sachero, V.; Mosca, S.; Zanini, G. Validation of a Lagrangian dispersion model implementing different kernel methods for density reconstruction. Atmos. Environ. 2006, 40, 8020–8033. [Google Scholar] [CrossRef]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Stull, R.B. Chapter 9: Similarity Theory. In An Introduction to Boundary Layer Meteorology (Atmospheric Sciences Library); Kluwer Academics Publishers: Dordrecht, The Netherlands, 1988; Volume 13, pp. 347–404. [Google Scholar]
- Vickers, D.; Mahrt, L. Observations of the cross-wind velocity variance in the stable boundary layer. Environ. Fluid Mech. 2007, 7, 55–71. [Google Scholar] [CrossRef]
- Hanna, S.R. Applications in air pollution modeling. In Atmospheric Turbulence and Air Pollution Modelling; Springer: Berlin/Heidelberg, Germany, 1984; Volume 1, pp. 275–310. [Google Scholar]
- Caughey, S.J. Observed characteristics of the atmospheric boundary layer. In Atmospheric Turbulence and Air Pollution Modelling; Springer: Berlin/Heidelberg, Germany, 1984; pp. 107–158. [Google Scholar]
- Vervecken, L.; Camps, J.; Meyers, J. Accounting for wind-direction fluctuations in Reynolds-averaged simulation of near-range atmospheric dispersion. Atmos. Environ. 2013, 72, 142–150. [Google Scholar] [CrossRef] [Green Version]
- Bijloos, G.; Camps, J.; Tubex, L.; Meyers, J. Parametrization of homogeneous forested areas and effect on simulated dose rates near a nuclear research reactor. J. Environ. Radioact. 2020, 225, 106445. [Google Scholar] [CrossRef] [PubMed]
- Chaichian, M.; Demichev, A. Path Integrals in Physics; Stochastic Processes and Quantum Mechanics; CRC Press: Boca Raton, FL, USA, 2001; Volume 1, p. 336. [Google Scholar]
- Obukhov, A.M. Description of turbulence in terms of Lagrangian variables. Adv. Geophys. 1959, 6, 113–116. [Google Scholar]
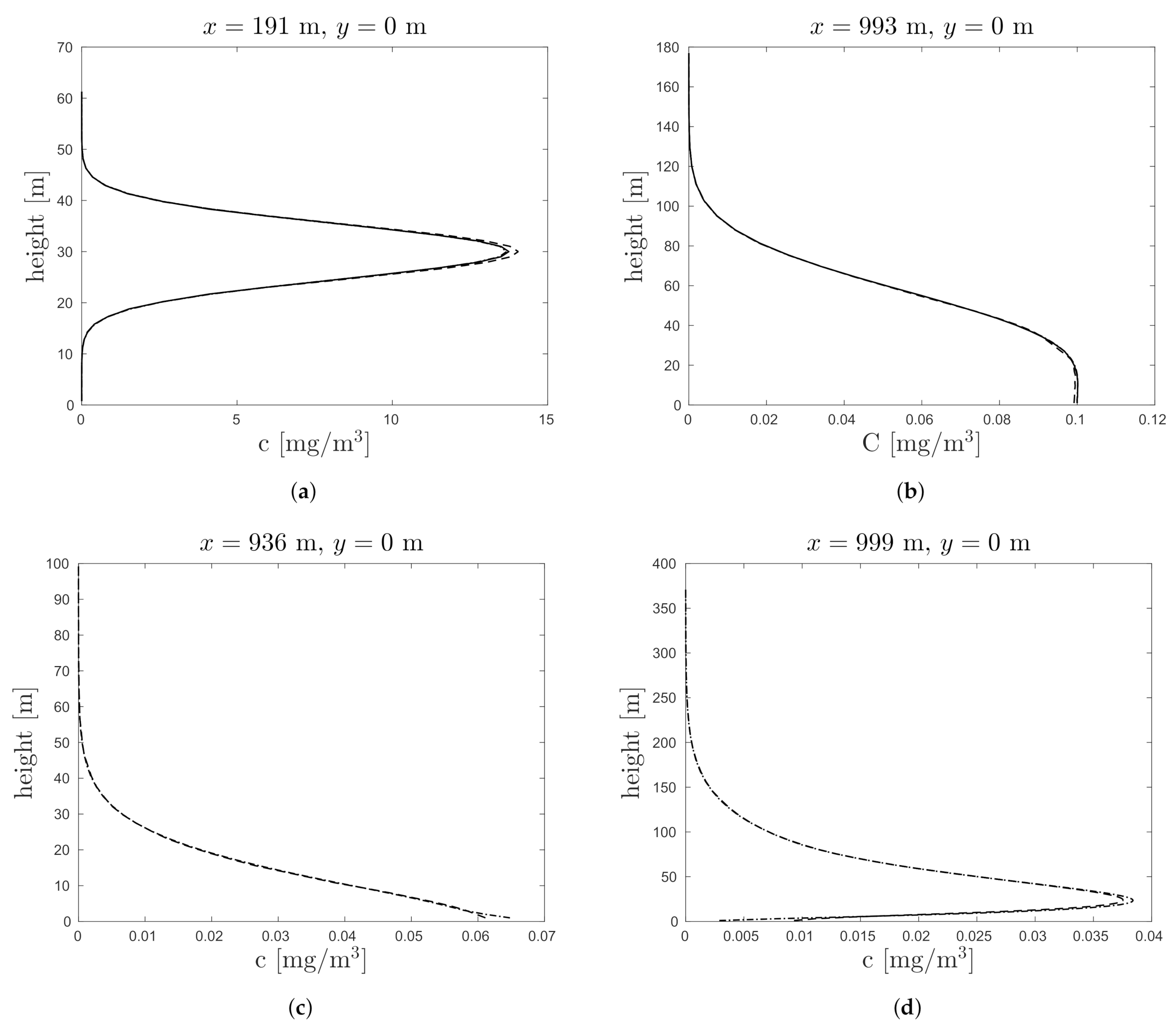
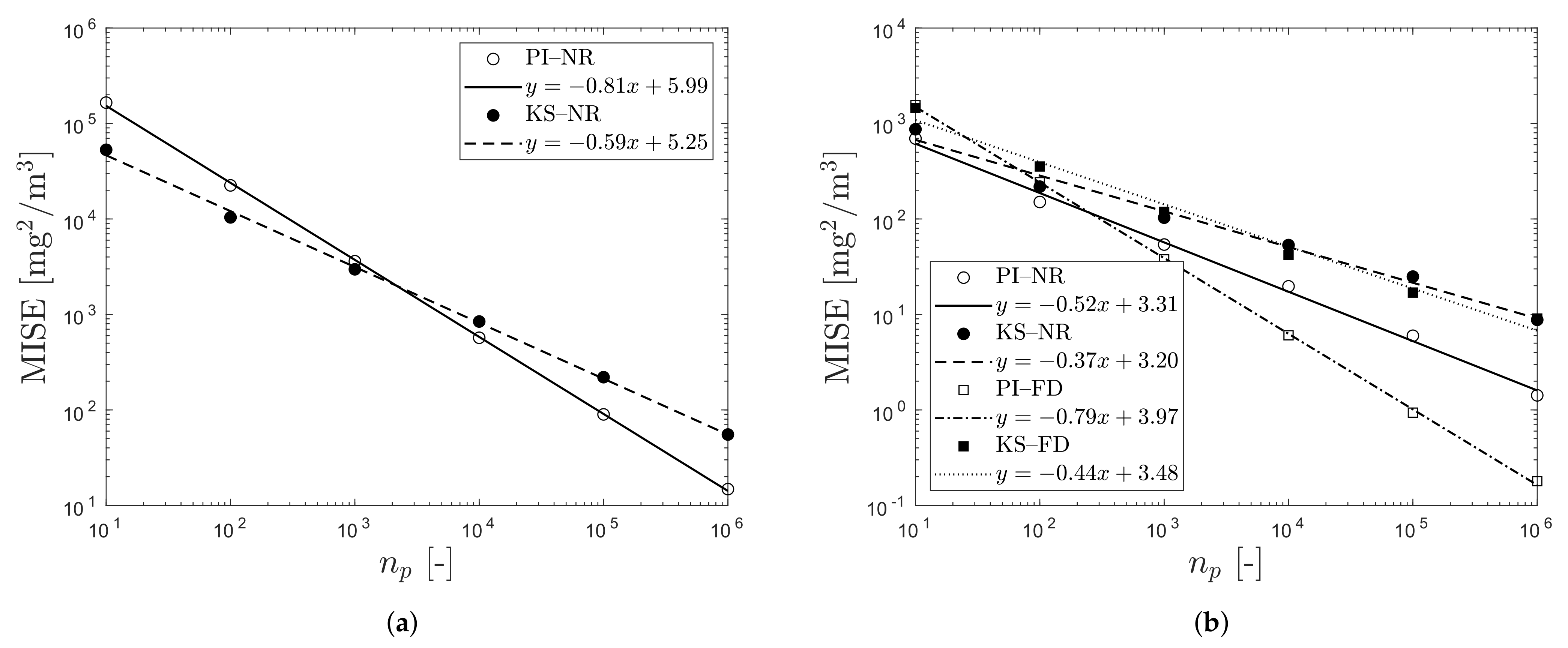

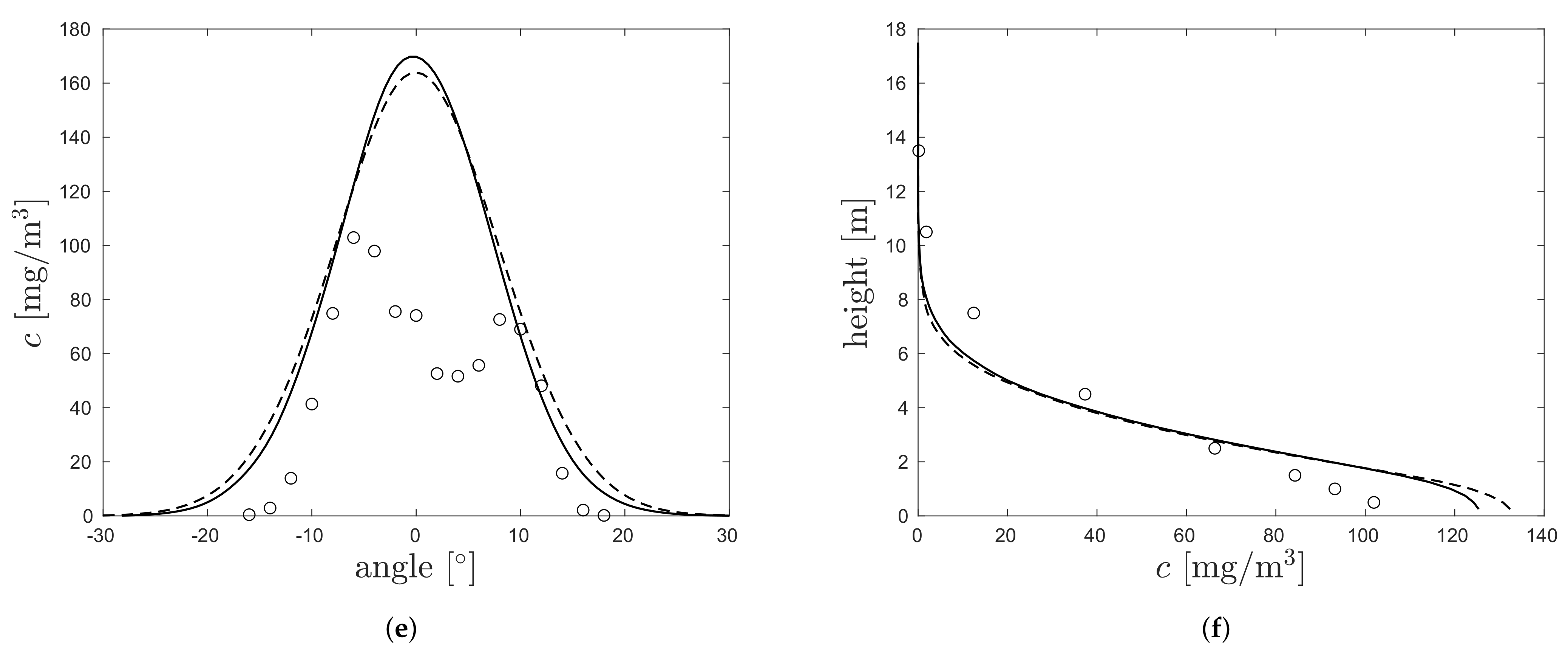
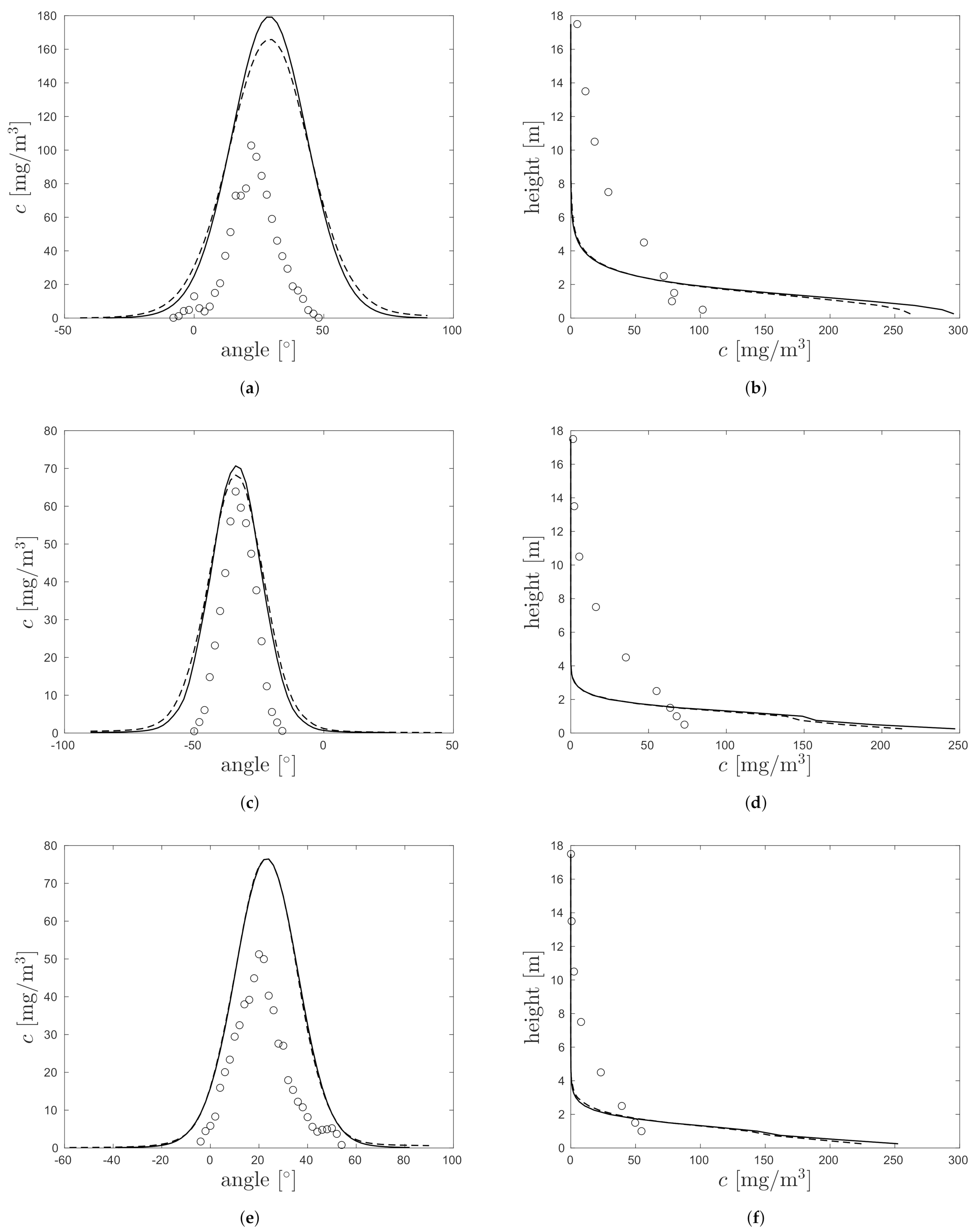
| Case | L (m) | (m s) | (-) | (m s) | (m s) | (m) | (m) | (m) | (kg) |
|---|---|---|---|---|---|---|---|---|---|
| I | 248 | 0.38 | 0.35 | / | / | / | 0.008 | 30 | 0.1 |
| II | 53 | 0.24 | 0.35 | 0.59 | 0.38 | / | 0.008 | 30 | 0.1 |
| III | 0.39 | 0.35 | / | / | 836 | 0.008 | 30 | 0.1 |
| Case | Method | Time (s) | (-) | |||
|---|---|---|---|---|---|---|
| I–HT | PI | NR | 20 | 5.34 | 0.99 | |
| NR | 104 | 3.31 | 1.00 | |||
| KS | NR | 20 | 6.02 | 1.00 | ||
| NR | 104 | 3.95 | 1.00 | |||
| I | PI | NR | 20 | 5.29 | 1.00 | |
| NR | 120 | 3.44 | 1.00 | |||
| FD | 120 | 3.33 | 1.00 | |||
| KS | NR | 20 | 5.22 | 1.00 | ||
| NR | 120 | 3.55 | 1.00 | |||
| FD | 120 | 3.53 | 1.00 | |||
| II | PI | NR | 27 | 5.51 | 1.00 | |
| NR | 156 | 4.20 | 1.00 | |||
| FD | 156 | 4.26 | 1.00 | |||
| KS | NR | 27 | 5.77 | 1.00 | ||
| NR | 156 | 4.17 | 0.99 | |||
| FD | 156 | 4.12 | 1.00 | |||
| III | PI | NR | 24 | 5.99 | 1.00 | |
| NR | 118 | 3.31 | 1.00 | |||
| FD | 118 | 3.97 | 1.00 | |||
| KS | NR | 24 | 5.25 | 1.00 | ||
| NR | 118 | 3.20 | 0.99 | |||
| FD | 118 | 3.48 | 0.99 |
| Case | Time (s) | FD (m) | NR (m) |
|---|---|---|---|
| I–HT | 20 | 4.5 × 10 | 4.8 × 10 |
| I | 120 | 1.05 × 10 | 6.4 × 10 |
| II | 156 | 2.4 × 10 | 5.1 × 10 |
| III | 118 | 1.0 × 10 | 1.3 × 10 |
| Stratification | Method | MARE (%) | FB (%) | FAC1.05 (%) | Number of Data Points (#) |
|---|---|---|---|---|---|
| stable | PI | 12 | 58 | 370 | |
| KS | 61 | 22 | 408 | ||
| unstable | PI | 58 | 11 | 939 | |
| KS | 147 | 5.6 | 1135 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bijloos, G.; Meyers, J. A Fast-Converging Kernel Density Estimator for Dispersion in Horizontally Homogeneous Meteorological Conditions. Atmosphere 2021, 12, 1343. https://doi.org/10.3390/atmos12101343
Bijloos G, Meyers J. A Fast-Converging Kernel Density Estimator for Dispersion in Horizontally Homogeneous Meteorological Conditions. Atmosphere. 2021; 12(10):1343. https://doi.org/10.3390/atmos12101343
Chicago/Turabian StyleBijloos, Gunther, and Johan Meyers. 2021. "A Fast-Converging Kernel Density Estimator for Dispersion in Horizontally Homogeneous Meteorological Conditions" Atmosphere 12, no. 10: 1343. https://doi.org/10.3390/atmos12101343
APA StyleBijloos, G., & Meyers, J. (2021). A Fast-Converging Kernel Density Estimator for Dispersion in Horizontally Homogeneous Meteorological Conditions. Atmosphere, 12(10), 1343. https://doi.org/10.3390/atmos12101343






