Abstract
With the aim of ascertaining the effects of the widths () of valleys on near-surface turbulence, flows over an isolated symmetric three-dimensional valley of constant depth () and slopes are characterized in a large-boundary-layer wind tunnel. Starting at A = 4H, valley widths were systematically varied to A = 12H with constant increments of 2H. High-resolution laser-Doppler velocimetry measurements were made at several equivalent locations above each of the resulting valley geometries and compared with data from undisturbed flows over flat terrain. Flow separation caused by the first ridges generated inner-valley recirculation bubbles with lengths dependent on the valley widths. Secondary recirculation zones were also observed downstream from the crests of the second ridges. Results show that the width modifications exert the strongest effects on turbulence within the valleys and the vicinities of the second ridges. Above these locations, maximal magnitudes of turbulence are generally found for the larger width geometries. Furthermore, lateral turbulence overpowers the longitudinal counterparts nearest to the surface, with maximal gains occurring for the smaller widths. Our data indicate that valley widths are impactful on near-surface flows and should be considered together with other more established geometric parameters of influence.
1. Introduction
Atmospheric boundary layer (ABL) flows are affected by irregular orography, which impacts a wide variety of applications, such as wind engineering, air quality, and agriculture, amongst others. The strongest topographic effects on microscale ABL flows occur nearest to the surfaces, but are not well understood. Early studies of flow disturbances posed by single hills date back to the late 1940s, but were limited to larger-scale effects while assuming laminar flows [1]. The first major contribution to the field of ABL flows over complex terrain came in 1975 with the Jackson and Hunt linear theory of flows over low two-dimensional hills [2]. Their analytical theory applied to attached flows over gentle-sloped hills and motivated a number of extensions and alternative theories proposed throughout the following decade [1,2,3]. The advent of the wind energy industry led to increased efforts to understand near-surface microscale flow characteristics and to improve the accuracy of numerical models [1,3]. Thus, the majority of the literature on flows over single-terrain features aims to quantify gains of wind velocity (or speed-up) over low hills and ridges. Fewer efforts have been made to understand how isolated orography affects near-ground turbulence characteristics, and further investigation is required.
The most accurate flow data result from field campaigns, but complex logistics and high costs are major limitations of such efforts. Furthermore, a scarcity of real-world isolated terrain features with well-defined inflow characteristics constitutes a major challenge for field campaigns dedicated to isolated terrain features. The campaigns at Askervein hill [4], Bolund hill [5], and most recently at a valley in Perdigão [6] correspond to the most documented of the field campaigns dedicated to flows over isolated, non-mountainous terrain. Cost-effective numerical simulations are the primary flow modeling approach applied to flows over complex terrain. Improvements to computational capacities have allowed the integration of higher grid resolutions to numerical simulations. However, increased resolutions make smaller surface heterogeneities more influential on the results. This leads to larger uncertainties of the near-surface numerical predictions, where substantial disagreements with corresponding experimental data are commonly found (e.g., [7,8,9]). The scarcity of validation data from experiments can be partially addressed through physical modeling. Physical modeling is advantageous in allowing full control of the modeled ABL flow characteristics without requirements for additional turbulence modeling. Furthermore, large eddy size distributions are generated directly and are only inhibited by the scales of the modeled flows.
The majority of wind tunnel studies involving complex terrain have been focused on idealized two-dimensional hills of infinite width, i.e., the terrain models extend to the wind tunnel side walls (e.g., [10,11,12]). This can create unrealistic lateral flow phenomena and entrap portions of air with insufficient upwind kinetic energy to overcome the orography in the vertical planes [13]. However, idealized terrain features are useful in providing maximal data transferability between different landforms of equivalent types (e.g., ridge-type landforms) and in ascertaining the effects of individual geometric parameters (e.g., slopes) of the terrain on the flows. Moreover, they have no requirements for modeling site-specific ABL flow characteristics [14]. The simple geometries of idealized landforms and their smaller study domains are also beneficial in providing validation data for numerical models [15]. While wind tunnel studies of flows over idealized hills are abundant, experimental investigations focused on flows over valleys are comparatively scarce [1].
Ref. [16] studied flows and pollutant dispersions over three idealized two-dimensional valleys of constant depth (H) and varying slopes (10°, 16°, and 26°), reporting the occurrence of flow separation at the upstream edge of the steep slope. This originated a steady vertical-plane recirculation zone that extended to a longitudinal distance of almost 75% of H. The longitudinal turbulence intensity was maximal above the center of the steepest valley (≈170% at z/H = 0.5), and the largest magnitudes of the vertical fluxes were found near to the surface above the downstream edge of the valley. Ref. [17] evaluated the flows above a two-dimensional valley (of slope 27°) for two inflow directions. The authors reported flow recirculation above the inner valley, with the corresponding length of the recirculation zones being just under 70% of the valley width. The peaks of shear, longitudinal, and vertical stresses were found above the center of the valley. Ref. [14] investigated near-surface flows over three-dimensional valleys of constant depth (H) and width (A = 12H) and varying slopes (10°, 30°, and 75°). Inner-valley recirculation zones were observed for all geometries and their lengths were found to be independent of the slope inclinations. Maximal magnitudes of near-surface three-dimensional turbulence were generally found above the crests of the downwind ridges and the lateral components of turbulence overpowered the longitudinal and vertical counterparts downstream from the first ridges.
The present study evaluates the effects of the widths of isolated three-dimensional valleys on near-surface ABL flows, with particular emphasis on turbulence characteristics. In the context of how individual geometric parameters of complex terrain affect microscale ABL flows, this study aims to provide insight into a scarcely addressed gap of knowledge in the literature. Characterizations of flows over five idealized valleys are made through physical modeling in a large-boundary-layer wind tunnel. The valleys were built of two symmetric three-dimensional ridges of constant depth and slopes, with fixed lengths and spanwise dimensions. Valley widths (A) were systematically varied from A = 4H to A = 12H with increments of ∆A = 2H. Results of the high-resolution measurements performed above the valleys demonstrate a dependence of the near-surface flow properties on the widths, which is most evident downstream from the first ridges.
2. Methodology
Experiments were performed in the WOTAN wind tunnel of the Environmental Wind Tunnel Laboratory (EWTL) of the University of Hamburg. WOTAN is the largest of the wind tunnels of the EWTL and is a closed-section/open-return-type boundary layer wind tunnel. The test section has a length of 18 m, a width of 4 m, and an adjustable ceiling height that ranges between 2.75 and 3.25 m. WOTAN has no heating capabilities, thus the modeled ABL flows are neutrally stable.
2.1. Experimental Setup
Large turbulence structures of the wind tunnel ABL flow were generated with thirty-one isosceles spires (of base 7 cm and height 27 cm), which were symmetrically placed at the start of the wind tunnel test section. A downstream fetch of 10.5 m built up of roughness elements was used to create smaller near-surface eddies of the flows. Roughness elements consisted of equidistant rows of brass chains with two alternating diameters (4 and 6 mm), as can be perceived from Figure 1a. A flat surface of length 7.5 m was placed in the model section to ensure flow continuity until the wind tunnel outlet and to inhibit the generation of internal boundary layer flows. The homogeneous flat surface was built of three-dimensional pyramids of height 1.2 mm, as displayed in Figure 1b, and painted black to minimize reflective backscatter of laser light used for the flow measurements. This surface also represented a flat terrain reference case to enable comparative assessments of the effects of the valleys on the ABL flows.

Figure 1.
(a) Upstream view of the boundary layer development section built of spires and roughness elements; (b) zoomed view of the surface pyramids placed further downstream in the model section.
Correlated flow velocity measurements were carried out with a Prandtl tube and a laser-Doppler velocimeter (LDV). The in-house manufactured Prandtl tube was positioned centrally above the spires at an intake height of 1.9 m and provided reference longitudinal velocity () data via differential pressure transduction with a Setra PT239 (Setra Systems Inc., Boxborough, MA, USA). The LDV (Dantec Dynamics, Skovlunde, Denmark), equipped with a two-dimensional fiber-optic probe (of diameter 27 cm) and an F80 Burst Spectrum Analyzer (software version 4.50.03), was applied for single-point, high-resolution, three-dimensional velocity measurements (2 × 2D) above the terrain in the model section. All measurements were made using the Cartesian flow coordinate system and applied transit-time weighting due to the highly turbulent nature of the flows over the valleys. Point-specific measurements had a duration of t = 120 s, which was verified through temporal data convergence tests to ensure the statistical representativeness of the time-averaged data. At a model scale of 1:1000, the measurement times correspond to approximately 33 h at full scale. Several repetitive measurements were performed above each location under different environmental conditions and are used as a measure of reproducibility of the measurement data (or data uncertainty). The resulting data uncertainties are represented by error bars in the plots displayed in Section 3.
Flow blockages posed by the flat terrain and valley models were verified through analyses of cross-sectional geometric blockages and longitudinal pressure gradients. All models were below the 5% thresholds established for geometric blockages (≈3%) and pressure gradients (≈4%) [18]. Lateral symmetry of the modeled ABL flows was evaluated for normalized longitudinal velocities and velocity fluctuations at 5 cm above ten equidistant spanwise locations over the flat terrain. Maximum deviations of about ±3% from the average normalized velocities were observed and are attributed to small lateral inhomogeneities inherent to the wind tunnel facility.
2.2. Flow Similarity
The representativeness of scaled ABL flows in boundary-layer wind tunnels depends on the fulfillment of flow similarity criteria. Flow similarity requires that full- and model-scale systems exhibit correspondence when scaled by characteristic values of prescribed boundary conditions and dimensionless flow parameters. Boundary conditions include matching geometries and surface roughness between full and model scales, which were fulfilled for the present experiments. The most relevant dimensionless flow parameters that are independent of thermal effects are the Rossby and Reynolds numbers.
The present microscale study domains imply that effects of Coriolis forces on the modeled ABL flows were negligible. Thus, flow similarity according to the Rossby number was fulfilled. Characteristics of the larger-scale turbulence structures of ABL flows remain unaffected if the Reynolds number is greater than 10,000 and laminar sublayer generation is minimized. Under such conditions, scaled flows are fully turbulent and independent of the Reynolds number [19,20]. Tests to evaluate independence according to the normalized longitudinal velocities and velocity fluctuations were carried out above the flat terrain and valley models. A bandwidth of 2% of the corresponding mean values was applied as a criterion for independence. Reynolds number independence was verified for free-stream velocities starting at 3 m/s, and a reference velocity of ≈5 m/s was selected for the present experiments. The corresponding free-stream turbulence intensity was ≈5%. Under these conditions, a Reynolds number of about 28,500 results from a characteristic length equivalent to the valley depth (H).
2.3. Valley Geometries
Idealized symmetric three-dimensional valleys were created through combinations of two equivalent, symmetric, three-dimensional ridge geometries of constant height (H = 8 cm) and slopes (30°), as schematized in Figure 2a. The half-lengths of each of the curved-peak (R = 5 mm) ridges were 14 cm, and their spanwise lengths were 1.8 m. Side slopes of the ridges were constructed with a width reduction algorithm based on a cosine smoothing function. The models of the ridges were placed centrally in the cross-sectional plane of the wind tunnel, thus occupying the central 1.8 m of the wind tunnel in the spanwise direction. All model surfaces were built of identical three-dimensional pyramids to those used for the flat terrain scenario (as in Figure 1b).
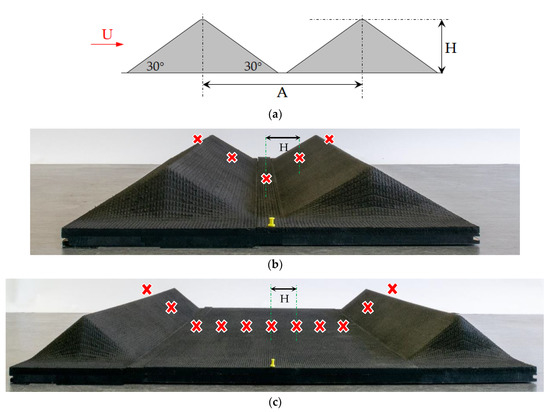
Figure 2.
(a) Schematic of the idealized valleys of the present experiments, where the angles correspond to the inclinations of the ridge slopes, A represents the valley width, H corresponds to the valley depth, and U the longitudinal flow direction; (b) lateral view of the smallest width valley model (A = 4H); (c) lateral view of the largest width valley model (A = 12H). The yellow pin in (b,c) marks the approximate midpoints of the valleys, and the X symbolizes the approximate measurement locations in the horizontal plane.
The valley widths (A) are defined as the longitudinal distances between the crests of each of the ridges. Starting with the smallest geometry, A = 4H (as in Figure 2b), the valley widths were systematically increased to A = 12H (Figure 2c) by constant increments of twice the valley depth (ΔA = 2H). Interchangeable ridge models and combinations of strips of flat terrain were used to obtain each of the five valley widths (4H, 6H, 8H, 10H, and 12H) of the present experiments. In particular, the A = 8H geometry corresponds to a simplified approximation of the geometry of the field campaign site in Perdigão, which has dimensions of H ≈ 200 m, A ≈ 1400 m (A ≈ 7H), and ridge slopes of ≈35° [21].
2.4. Measurement Locations
Flow measurements were carried out at the lateral centerline above equidistant longitudinal locations (ΔX = H) starting upwind from the first ridges and extending far downstream of the second ridges, as shown in Figure 2. Measurements were concentrated on near-surface heights (z), where effects of shear overpower those of buoyancy for real-world neutrally stable ABL flows. Vertical coordinates are terrain following and are normalized with H and are presented in Table 1.

Table 1.
Measurement heights above local ground level in normalized (z/H) and absolute (z) coordinates. Absolute heights are presented for a model scale of 1:1000.
3. Results
The characterization of the undisturbed ABL flow over flat terrain is provided in Section 3.1 and constitutes the reference scenario for this study. This is followed by the analyses of the flows over the valleys of varying width in Section 3.2, which include qualitative flow visualizations and turbulence characterizations above each of the ridges, the inner valley regions, and downstream from the valleys. All presented flow properties are normalized with the reference velocity (), except for the longitudinal integral length scales that are normalized with the valley depth (H).
3.1. Undisturbed Flow Characteristics
Characteristics of the undisturbed flow were verified above fourteen equidistant longitudinal positions (ΔX = 0.5 m) above the homogeneous flat terrain surface. The modeled ABL flow displayed streamwise uniformity throughout the wind tunnel model section for all flow properties, with data being contained within the respective ranges of uncertainty for all positions. All components of the turbulence intensity were contained above the lower limits of a moderately rough class ABL flow, which corresponds to ABL flows over grass or farmlands [18]. As can be ascertained from the profiles of the velocity fluctuations in Figure 3, the largest observed values of longitudinal and lateral turbulence are predictably found nearest to the surface (z/H = 0.15), the maximum of which for the longitudinal component (). At the same height, the ratios of longitudinal to lateral and vertical turbulence are ≈1:0.8:0.5. These are in close agreement with the theoretical values for neutrally stable ABL flows, ≈1:0.75:0.5 [18].
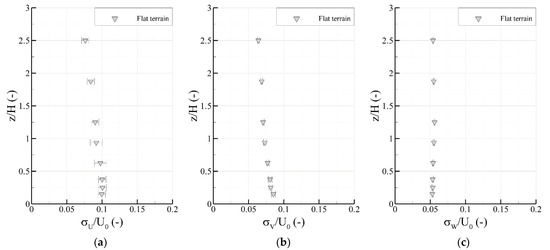
Figure 3.
Vertical profiles of the longitudinal (a), lateral (b), and vertical (c) velocity fluctuations of the undisturbed flow above flat terrain.
The full-scale aerodynamic surface roughness length of the modeled ABL flow is approximately 0.025 ± 0.015 m for a model scale of 1:1000. The corresponding profile exponent is about 0.14 ± 0.01. A moderately rough classed flow also resulted from the semilogarithmic relationship between roughness length and profile exponent. The functional relationship between the normalized longitudinal integral length scales and roughness length yielded a moderately rough ABL flow at z/H ≤ 0.25 [14,22]. At higher altitudes, the length scales shifted to slightly rough class reference values [14]. Taking into account that the integral length scales are the most challenging turbulence parameter to match with the full scale, we consider the data physically consistent with a moderately rough ABL flow. At a model scale of 1:1000, the friction velocity of the undisturbed flow was approximately 0.2 m/s. This results in a Reynolds roughness number of about 0.4, considered permissible for ABL flows over complex terrain [13].
The depth of the modeled atmospheric surface layer (ASL) was verified through the normalized longitudinal velocities and the vertical fluxes. According to the semilogarithmic vertical profiles of the fluxes, the ASL depth is the height where data deviates from the average of the near-surface values [19]. The undisturbed flow data were contained within a ±5% range centered on the near-surface mean values until z/H ≈ 1.25 [14]. Hence, the modeled ASL had a depth of approximately 100 m at a model scale of 1:1000. This roughly corresponds to the lowest 10% of the neutrally stable ABL, meaning that the depth of the ABL is about 1000 m [23].
3.2. Flows over Valleys
Qualitative descriptions of the flows observed with laser light-sheet are followed by characterizations of time-averaged flow properties above the valleys. Results are separated by flow regions that follow the longitudinal flow direction. Flows above the first ridges contemplate the windward slopes and crests of the first ridges of each valley. The inner valley regions correspond to the regions between the crests of the first and second ridges, including the leeside slopes of the first ridges and the windward slopes of the second ridges. The second ridge flow region consists of the crests and leeside slopes of the second ridges, whereas the downwind region begins at the foot of the leeside slopes of the second ridges and extends to the end of the wind tunnel test section.
3.2.1. Laser Light-Sheet Observations
Visualizations of the vertical-plane flow structures above the spanwise centerline were carried out for all valley geometries using a laser light-sheet. This approach is particularly advantageous in providing qualitative observations of the turbulence structures present in the flows. Long-term exposures of the illuminated vertical planes enable the capture of approximate flow streaklines above the terrain. Observations made above the smallest and largest width valleys are presented in Figure 4.
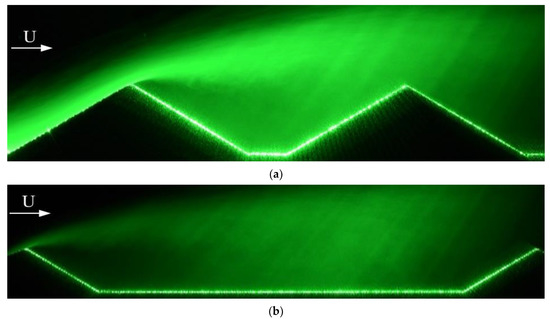
Figure 4.
Lateral views of the approximate streaklines observed in the vertical planes with a laser light-sheet and smoke above the smallest width valley, A = 4H (a), and the largest width valley, A = 12H (b). U represents the longitudinal flow direction.
For all valleys, the disturbances posed by the first ridge caused the flow direction to conform to the underlying windward slope and accelerate towards its crest. Flow separation took place at the crests of the first ridges of all geometries and generated highly turbulent recirculation bubbles above the inner valley regions. These were mainly contained within the vertical planes delimited by the leeside slopes of the first ridges, the windward slopes of the second ridges, the inner valley surfaces, and heights approximately equivalent to the valley depth (H). Longitudinal flow reversal took place at near-surface heights and the bubbles capped by accelerated flow above ridge height (z/H > 1). The lengths of the recirculation bubbles increased with increasing valley widths, which led to width-dependent flow characteristics above the second ridges and their downwind vicinities. The separated flows exhibited highly chaotic behaviors when reaching the crests of the second ridges for the smaller widths (A ≤ 8H). This contrasted with the more stable flows observed above the valleys of larger width. The second ridges generated secondary recirculation bubbles downwind from the crests that extended to the foot of the leeside slopes of the second ridges.
3.2.2. Flows above the First Ridges
The flows above the first ridges are independent of the modifications made to the valley widths. The negligible scatter between data from the different widths above the crests of the first ridges (not shown here) verifies this. Increases in near-surface longitudinal velocities relative to the undisturbed flow occurred above the crests. Maximum increases of approximately 45% were expectedly found at z/H = 0.15, which mirrors the speed-up characteristics of flows over two-dimensional single hills or ridges reported in the literature (e.g., [10,11,12]). Lateral velocity fluctuations displayed the largest increases of the near-surface mean turbulence parameters relative to the undisturbed flow data. Inversely, the longitudinal components presented the closest agreement with the flow over flat terrain. The corresponding ratios of longitudinal to lateral and vertical turbulence at z/H = 0.15 above the crests, approximately 1:1.4:0.8, highlight the gains of lateral and vertical turbulence over the longitudinal counterparts due to the disturbances posed by the first ridges. Vertical fluxes increased by about 55% between z/H = 0.15 and z/H = 0.38 above the crests. Thus, the constant shear properties of the flat terrain ASL were lost above the first ridges.
3.2.3. Inner Valley Flows
Table 2 presents estimates of the lengths of the steady vertical-plane recirculation bubbles that originated at the crests of the first ridges. These correspond to the distances where longitudinal flow reversal () relative to the upstream flows was observed. Recirculating flow characteristics of the smaller width valleys (A ≤ 6H) reached the valley midpoints, but extended beyond for the larger widths. The recirculation bubbles of A ≥ 10H present similar lengths (≈7H), the maximum length relative to the width being that of A = 10H (about 70% of the valley width). The largest observed magnitudes of reversed flow were found at z/H = 0.15 and increased with increasing valley widths.

Table 2.
Approximate lengths of the inner valley vertical-plane recirculation bubbles based on near-surface longitudinal flow reversal observed at z/H ≤ 0.25.
All components of the velocity fluctuations tend to increase with increasing valley widths above the inner valley regions. The vertical profiles of the longitudinal fluctuations above the valley midpoints in Figure 5a exemplify this. The maximum magnitude ( at z/H = 1.25) corresponds to A = 12H and is about 15% larger than the maximum of A = 4H. The lateral and vertical components of the inner valley regions present analogous width dependencies, as observed in Figure 5b,c, respectively. For all valley geometries, the lateral fluctuations overpower the longitudinal components at z/H ≤ 0.38. The ratios of longitudinal to lateral and vertical turbulence at z/H = 0.15 above the valley midpoints are approximately 1:1.3:0.8 and exhibit negligible variations with the valley width modifications.
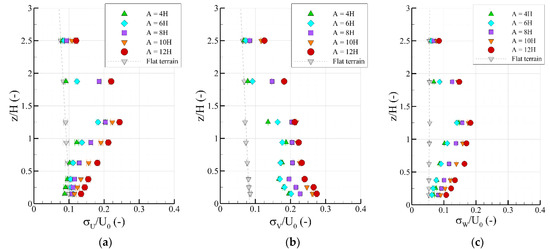
Figure 5.
Vertical profiles of the normalized longitudinal velocity fluctuations above the valley midpoints (a), lateral velocity fluctuations above the windward slopes of the second ridges (b), and vertical velocity fluctuations above the valley midpoints (c).
The horizontal fluxes above the valley midpoints (Figure 6a) present close agreement with the undisturbed flow data and negligible differences between valley widths. Vertical fluxes exhibit similar width dependencies to the corresponding velocity fluctuations, as exemplified above the valley midpoints in Figure 6b. Accordingly, the maximum magnitude ( at z/H = 1.25, A = 12H) constitutes an increase of an order of magnitude when compared with the undisturbed flow. The integral length scales tend to decrease relative to the flat terrain data at z/H ≤ 1.25, with maximal decreases of an order of magnitude observed at z/H = 1.25. Thus, smaller longitudinal energy-intensive eddies result from the flow separation that occurs above the first ridges. As evidenced by the data being contained within the respective ranges of uncertainty in the profiles above the valley midpoints (Figure 6c), the effects of the valley modifications on the integral length scales are negligible above the inner valley regions.
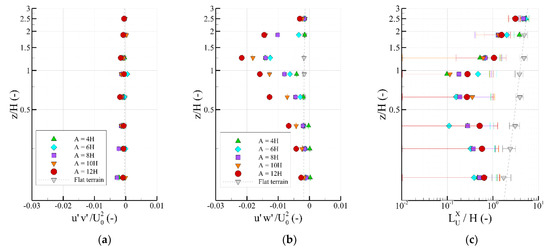
Figure 6.
Semilogarithmic vertical profiles of the normalized horizontal (a) and vertical (b) turbulent fluxes above the valley midpoints; logarithmic vertical profiles of the normalized longitudinal integral length scales above the valley midpoints (c).
3.2.4. Flows above the Second Ridges
Near-surface flows above the second ridges are generally more turbulent than observed above the inner valley regions. This is exemplified by the increases in magnitude of all components of the velocity fluctuations at z/H < 0.63 above the crests of the second ridges, displayed in Figure 7. Maximal magnitudes of the longitudinal components in this height range are found for A = 4H, with the larger valley widths presenting the largest intensities at z/H ≥ 0.94. The maximum magnitude ( at z/H = 0.94) is found for A = 10H and constitutes a threefold increase over the corresponding flat terrain data. Similar width variation effects occur for the vertical components, for which the maximum magnitude ( at z/H = 0.63) is found for A = 12H. Maximal magnitudes of the lateral components are found nearest to the surface (z/H = 0.15) and tend to increase with increasing valley widths. The maximum (, A = 12H) is approximately 35% larger than the maximum of A = 4H. Unlike the turbulence ratios above the inner valley regions, the ratios obtained above the second ridges show valley width dependence. The average ratios of turbulence at z/H ≤ 1.25 above the crests of the second ridges of each valley in Table 3 exemplify this. Accordingly, longitudinal to lateral and longitudinal to vertical ratios increase by approximately 33% and 43%, respectively, between A = 4H and A = 12H.
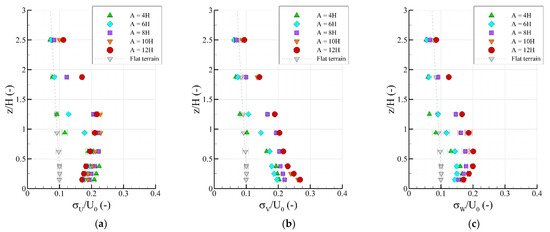
Figure 7.
Vertical profiles of the normalized longitudinal (a), lateral (b), and vertical (c) velocity fluctuations above the crests of the second ridges.

Table 3.
Average ratios of longitudinal to lateral and vertical turbulence from z/H ≤ 1.25 above the crests of the second ridges.
Horizontal fluxes exhibit maximal magnitudes and valley width dependence at z/H = 0.15, as can be observed in Figure 8a, where the largest fluxes are found for the larger valley widths. The vertical components in Figure 8b present similar width dependence as that of the longitudinal velocity fluctuations. The maximum magnitude ( at z/H = 0.94) is found for A = 10H. Nearest to the surface (z/H ≤ 0.38), the largest fluxes correspond to A = 4H and present twice the magnitude of the other widths at z/H = 0.15. The integral length scales exhibit closer agreement with the flat terrain data above the second ridges than observed in the inner valley regions, as exemplified by the logarithmic vertical profiles displayed in Figure 8c. This indicates that larger dominant longitudinal eddies than those of the inner valley regions govern the near-surface flows above the second ridges. However, the modifications made to the valley widths produce negligible effects on the integral length scales above the second ridges. This is ascertained from the data from different geometries contained within the respective ranges of uncertainty.
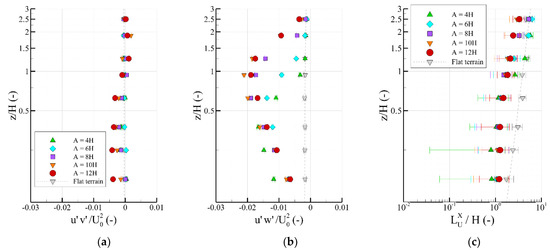
Figure 8.
Semilogarithmic vertical profiles of the normalized horizontal (a) and vertical (b) turbulent fluxes above the crests of the second ridges; Logarithmic vertical profiles of the normalized longitudinal integral length scales above the crests of the second ridges (c).
3.2.5. Flows Downwind from Valleys
Secondary vertical-plane recirculation bubbles originate above the crests and extend to the foot of the leeside slopes of the second ridges for A ≥ 6H, thus have lengths of roughly 2H. The maximal length of recirculation downwind from the crests (approximately 3H) is that of A = 4H, which extends beyond the foot of the second ridge. Turbulence characteristics of the flows tend to decrease with increasing downstream distances from the valleys. This is exemplified by the profiles of the velocity fluctuations at X = 2H from the foot of the second ridges displayed in Figure 9. The turbulence ratios at z/H = 0.15 are approximately 1:1.3:0.9. As evidenced by the close agreement between datasets, the effects of the width modifications are negligible on the velocity fluctuations at z/H ≤ 1.25. The maximal influence of the valley widths on all components of the fluctuations is found at z/H = 2.5, where the largest scatter between data can be observed. At this altitude, fluctuations of A ≥ 8H are in close agreement, whereas those of A = 4H present roughly half the magnitude for all components. The vertical fluxes follow similar width trends to those set by the corresponding profiles of the corresponding velocity fluctuations. Due to the proximity to the recirculation bubble, the longitudinal integral length scales at X = 2H from the valleys (not shown) tend to decrease compared to the data above the second ridges, the largest of which found for the smaller width valleys.
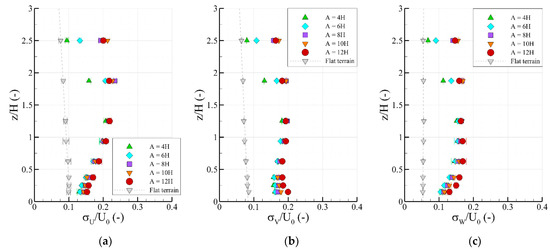
Figure 9.
Vertical profiles of the normalized longitudinal (a), lateral (b), and vertical (c) velocity fluctuations at a longitudinal distance of X = 2H downwind from the valleys.
4. Discussion
Our results show that the constant-amplitude modifications made to the valley widths affect near-surface ABL turbulence characteristics, and these are most evident in the inner valley regions and above the second ridges. These flow characteristics are supported by the vertical-plane flow observations made with the laser light-sheet for each of the valley geometries. The maximal magnitudes of the time-averaged turbulence properties in these regions, which also correspond to the largest increases relative to the reference flat terrain data, are generally those of the valleys of larger width. This is due to the larger extension of the valley floor, for which the strongest effects of the disturbances posed by the first ridge on the flow are contained within the inner valley regions. For the smaller widths, larger portions of turbulent kinetic energy bypass the inner valley regions and this leads to augmented near-surface longitudinal turbulence above the second ridges. The largest magnitudes of the longitudinal velocity fluctuations and the vertical fluxes at z/H ≤ 0.38 above the crests of the second ridges, which are those of the smallest valley width (A = 4H), supports this observation. This also shows agreement with the findings of [16] for flows above idealized 2D valleys of varying widths and slopes, with maximal longitudinal turbulence intensities being found for the smallest valley width (A = 6H) and steepest slopes (26°). Lateral components dominate the turbulence characteristics at the lowest altitudes of the area starting above the crests of the first ridges and extending beyond the second ridges. This can be credited to the occurrence of horizontal-plane flow separation around the sides of the 3D ridges that form the valleys and consequent lateral flow channeling downwind from each of the ridges. The maximum of the gains of lateral over longitudinal turbulence is observed within the primary recirculation bubbles and is unaffected by the width modifications. However, gains of lateral and vertical turbulence relative to the longitudinal counterparts are affected by the width variations above the second ridges, tending to increase with increasing valley widths.
Primary and secondary steady vertical-plane recirculation bubbles originate at the crests of the first and second ridges, respectively, regardless of the valley widths. Thus, the recirculation zones occur due to flow separation caused by the ridges and their characteristics mainly influenced by the slope inclinations [14]. However, our results do show that the valley width modifications do affect the longitudinal lengths of the recirculation bubbles. This is most noticeable for the primary recirculation bubbles of the inner valley regions, their lengths increasing with valley width until a maximum of about 7H for the larger widths (A ≥ 10H). When compared to the recirculation zone observed under neutral atmospheric stability at the Perdigão field campaign site, about 58% of the width (peak-to-peak distance), the recirculation length of the similar geometry of the present study (A = 8H) shows reasonable agreement at about 63% of the width [24]. This is also in agreement with the length of the recirculation zone obtained by [17], about 70% of the width, for a 2D idealized valley of equivalent width (A = 8H) and similar slopes (20° to 25°) through wind tunnel experiments. However, the recirculation bubble of the present A = 6H geometry (about 50% of the valley width) compares less favorably with that observed by [16] for their 2D idealized valley of equivalent width and 26° slopes, at about 67% of the width. This could be due to their idealized 2D valleys corresponding to depressions in otherwise flat terrain, rather than combinations of two ridges. Thus, the effects of the windward slopes of the first ridges or leeside slopes of the second ridges are not included in their wind tunnel flows.
The maximum magnitude of reversed longitudinal velocity within the primary recirculation bubble generated by the present A = 8H valley is about 20% of the magnitude of the inflow (at z/H = 0.15), whereas the maximum observed at Perdigão corresponds to 17% of the inflow [24]. The longitudinal turbulence intensities at z = 100 m above the second ridges of the present experiments and the Perdigão field data also show good agreement, at approximately 26% and 21%, respectively [24]. At the same height above the first ridges, the present data show a deficit of 4% relative to the longitudinal turbulence intensity of the field campaign [24]. Our results show that the secondary recirculation bubbles that originate at the crests of the second ridges exhibit a reverse width dependency when compared with the primary recirculation zones, tending to increase in length with decreasing valley widths. Unlike our observations, no secondary recirculation zones result from the experimental flows over the 2D valleys of [16], whereas in the experiments of [17], the vertical fluxes above the trailing edge of their 2D valley indicate the occurrence of flow separation but the mean longitudinal velocities remain positive. Downwind from the valleys, the turbulence characteristics of the near-surface flows tend to converge with the undisturbed flow data with increasing distances from the second ridges. The downwind effects of the valley width modifications on the flows are negligible at large downstream distances from the valleys, where turbulence characteristics differ from the undisturbed flow data at z/H > 1. With the findings made at the same far downwind locations from valleys of varying slopes (10°, 30°, and 75°) using the setups of [14], this indicates that the flow perturbations caused by the presence of the valleys outlast those resulting exclusively from the variations of the valley widths or the slopes of the ridges.
5. Conclusions
We have studied the effects of varying valley widths on microscale near-surface atmospheric boundary layer (ABL) flows through physical modeling in a large-boundary-layer wind tunnel. Neutrally stable, moderately rough ABL flows were characterized over five idealized three-dimensional valleys of constant depth (H) and slopes. The valley widths (A), defined as the distances between the crests of the ridges, were systematically increased from A = 4H to A = 12H (∆A = 2H), and the resulting flows were evaluated at equivalent relative locations. Our data show that the valley widths can be as impactful on turbulence characteristics within the lowest 100–150 m (above local terrain) as more established individual geometric parameters of isolated landforms, such as ridge slopes or heights.
Unlike the effects of varying slopes, characterized for the same flow setups in [14], the impacts of the width modifications produced negligible effects on the ABL flows in regions upwind from the crests of the first ridges. Within the inner valley regions up to the windward slopes of the second ridges, increases in turbulence due to the varying slopes generally exceed those of the varying valley widths. However, the lengths of the vertical-plane primary recirculation bubbles are impacted by the width modifications. Such differences were not observed for the varying slopes. Above the second ridges, the effects of the width modifications on the turbulence characteristics exceed those resulting from the changes in slope inclinations (by up to 20%).
For the particular case of the intermediate valley width (A = 8H), the longitudinal flow data shows agreement with that of the Perdigão field campaign for neutrally stable ABL flows [24]. Our geometry represents a simplified approximation to the field campaign site, with homogeneous surfaces and constant slopes. The effects of smaller surface heterogeneities that exist at Perdigão, such as slope gradients or vegetation, are neglected. Thus, the agreement between the data shows that the finer surface details are less impactful than the individual geometric parameters of the terrain on near-surface flows. However, at the height above local terrain at which the reported field data were sampled (z = 100 m), the smaller surface obstacles would expectedly be less influential, as exemplified by the substantial disagreements between field data and numerical simulations previously reported at heights closer to the ground [1]. This could be further investigated through the addition of surface heterogeneities to the present ridge models.
Our experiments have provided insights into the exclusive effects of the slopes and the widths of valleys on near-surface microscale ABL flows. The systematic parameter variations used for the valley widths are particularly useful for detailed assessments of the impacts of specific geometric parameters of single-terrain features on flows over complex terrain. Thus, high-resolution characterizations of near-surface ABL flow interactions with orography are feasible through physical modeling.
Author Contributions
Conceptualization, S.F. and B.L.; Formal analysis, S.F.; Funding acquisition, B.L.; Investigation, S.F. and F.H.; Methodology, S.F. and F.H.; Project administration, B.L.; Resources, F.H. and B.L.; Writing—original draft preparation, S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Research Foundation (DFG) under project Grant LE2181/3-1.
Institutional Review Board Statement
Not applicable, no humans or animals involved.
Informed Consent Statement
Not applicable.
Data Availability Statement
The experimental data from this study will be made available upon request. For more information, please contact Bernd Leitl (bernd.leitl@uni-hamburg).
Acknowledgments
No additional acknowledgements required.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Finnigan, J.; Ayotte, K.; Harman, I.; Katul, G.; Oldroyd, H.; Patton, E.; Poggi, D.; Ross, A.; Taylor, P. Boundary-layer flow over complex topography. Bound.-Layer Meteorol. 2021, 177, 247–313. [Google Scholar] [CrossRef]
- Jackson, P.S.; Hunt, J.C.R. Turbulent flow over a low hill. Q. J. R. Meteorol. Soc. 1975, 101, 929–955. [Google Scholar] [CrossRef]
- Wood, N. Wind flow over complex terrain: A historical perspective and the prospect for large-eddy modelling. Bound.-Layer Meteorol. 2000, 96, 11–32. [Google Scholar] [CrossRef]
- Taylor, P.A.; Teunissen, H.W. The Askervein hill project: Overview and background data. Bound.-Layer Meteorol. 1987, 39, 15–39. [Google Scholar] [CrossRef]
- Bechmann, A.; Berg, J.; Courtney, M.; Ejsing Jorgensen, H.; Mann, J.; Sorensen, N.N. The Bolund Experiment: Overview and Background; Danmarks Tekniske Universitet, Riso National Laboratory for Sustainable Energy: Roskilde, Denmark, 2009. [Google Scholar]
- Fernando, H.J.S.; Mann, J.; Palma, J.M.L.M.; Lundquist, J.K.; Barthelmie, R.J.; Belo-Pereira, M.; Brown, W.O.J.; Chow, F.K.; Gerz, T.; Hocut, C.M.; et al. The Perdigão: Peering into microscale details of mountain winds. Bull. Am. Meteorol. Soc. 2019, 100, 799–819. [Google Scholar] [CrossRef]
- Bechmann, A.; Sorensen, N.N.; Berg, J.; Mann, J.; Réthoré, P.E. The Bolund experiment, part II: Blind comparison of microscale flow models. Bound.-Layer Meteorol. 2011, 141, 245–271. [Google Scholar] [CrossRef]
- Abdi, D.S.; Bitsuamlak, G.T. Wind flow simulations on idealized and real complex terrain using various turbulence models. Adv. Eng. Softw. 2014, 75, 30–41. [Google Scholar] [CrossRef]
- Conan, B.; Chaudhari, A.; Aubrun, S.; van Beeck, J.; Hamalainen, J.; Hellsten, A. Experimental and numerical modelling of flow over complex terrain: The Bolund hill. Bound.-Layer Meteorol. 2016, 158, 183–208. [Google Scholar] [CrossRef]
- Ayotte, K.W.; Hughes, D.E. Observations of boundary-layer wind-tunnel flow over isolated ridges of varying steepness and roughness. Bound.-Layer Meteorol. 2004, 112, 525–556. [Google Scholar] [CrossRef]
- Cao, S.; Tamura, T. Effects of roughness blocks on atmospheric boundary layer flow over a two-dimensional low hill with/without sudden roughness change. J. Wind Eng. Ind. Aerodyn. 2007, 95, 679–695. [Google Scholar] [CrossRef]
- Takahashi, T.; Ohtsu, T.; Yassin, M.F.; Kato, S.; Murakami, S. Turbulence characteristics of wind over a hill with a rough surface. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1697–1706. [Google Scholar] [CrossRef]
- Meroney, R.N. Fluid dynamics of flow over hills/mountains—Insights obtained through physical modelling. In Atmospheric Processes over Complex Terrain; Blumen, W., Ed.; Meteorological Monographs; American Meteorological Society: Boston, MA, USA, 1990; pp. 145–171. [Google Scholar]
- Freitas, S.; Harms, F.; Leitl, B. Influence of slopes of isolated three-dimensional valleys on near-surface turbulence. Bound.-Layer Meteorol. 2021. [Google Scholar] [CrossRef]
- Kempf, A.M. LES vlidtion from experiments. Flow Turb. Combust. 2008, 80, 351–373. [Google Scholar] [CrossRef]
- Snyder, W.H.; Khurshudyan, L.H.; Nekrasov, R.E.; Lawson, R.E.; Thompson, R.S. Flow and dispersion of pollutants within two-dimensional valleys. J. Atmos. Environ. 1991, 25, 1347–1375. [Google Scholar] [CrossRef]
- Garvey, B.; Castro, I.P.; Wiggs, G.; Bullard, J. Measurements of flows over isolated valleys. Bound.-Layer Meteorol. 2005, 117, 417–446. [Google Scholar] [CrossRef][Green Version]
- VDI-Verein Deutscher Ingenieure. Environmental Meteorology: Physical Modelling of Flow and Dispersion Processes in the Atmospheric Boundary Layer-Application of Wind Tunnels; VDI-3783-12; Beuth Verlag: Berlin, Germany, 2000. [Google Scholar]
- Snyder, W.H. Guideline for Fluid Modelling of Atmospheric Dispersion; Environmental Protection Agency: Washington, DC, USA, 1981. [Google Scholar]
- Townsend, A.A. The Structure of Turbulent Shear Flow, 2nd ed.; Cambridge University Press: Cambridge, UK, 1976. [Google Scholar]
- Vasiljevic, N.; Palma, J.M.; Angelou, N.; Carlos Matos, J.; Menke, R.; Lea, G.; Mann, J.; Courtney, M.; Frölen Ribeiro, L.; Gomes, V.M.M.G.C. Perdigão 2015: Methodology for atmospheric multi-Doppler lidar experiments. Atmos. Meas. Technol. 2017, 10, 3463–3483. [Google Scholar] [CrossRef]
- Counihan, J. Adiabatic atmospheric boundary layers: A review and analysis of data from the period 1880–1972. Atmos. Environ. 1975, 9, 871–905. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Menke, R.; Vasiljevic, N.; Mann, J.; Lundquist, J.K. Characterization of flow recirculation zones at the Perdigão site using multi-lidar measurements. Atmos. Chem. Phys. 2019, 19, 2713–2723. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).