A Comparison of the Performance of Different Interpolation Methods in Replicating Rainfall Magnitudes under Different Climatic Conditions in Chongqing Province (China)
Abstract
:1. Introduction
2. Study Area and Data Analysis
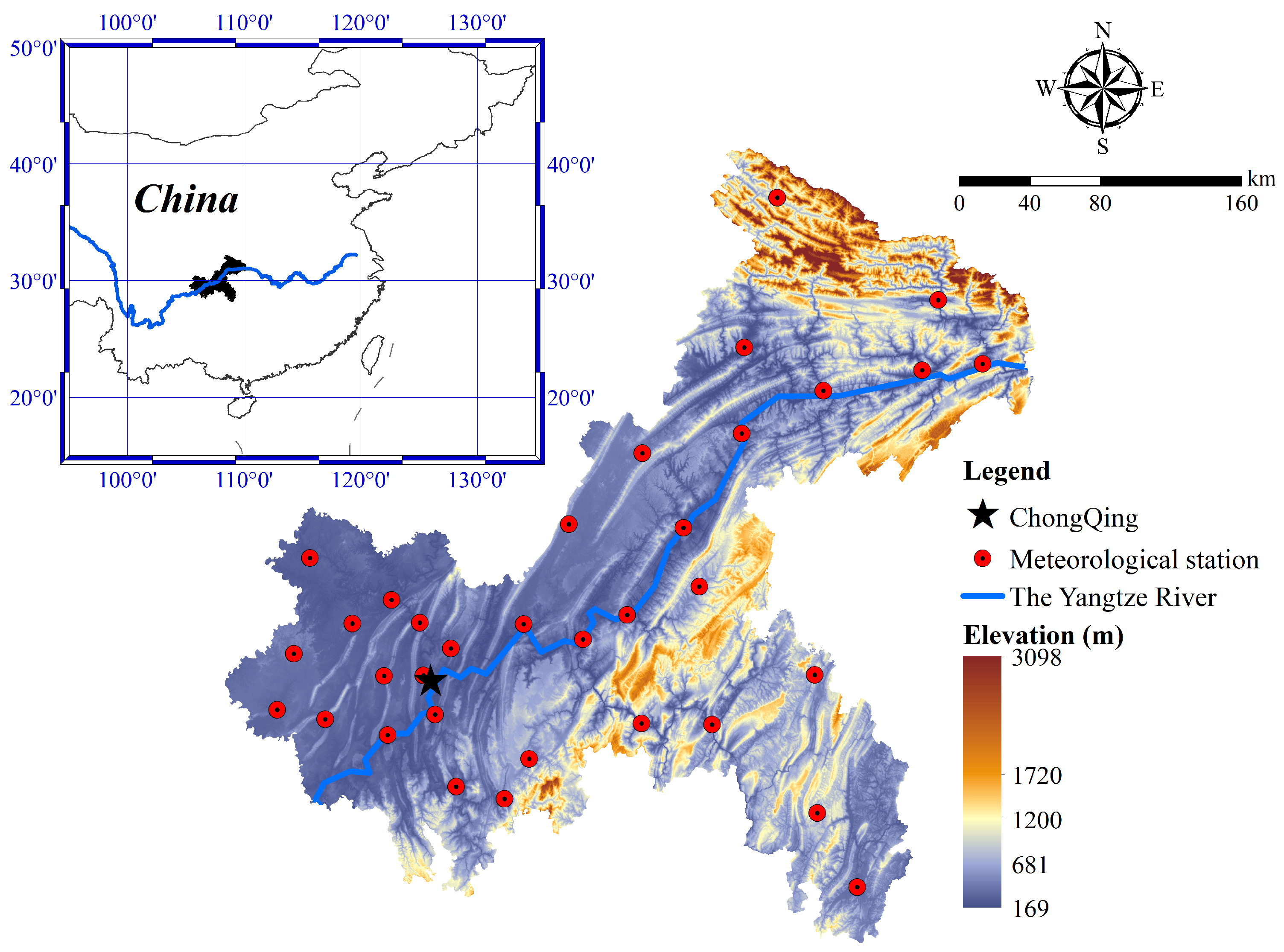
2.1. Study Area
2.2. Data Analysis
3. Methodology
3.1. Spatial Interpolation Methods
3.1.1. Inverse Distance Weighting (IDW)
3.1.2. Radial Basis Function (RBF)
3.1.3. Diffusion Interpolation with Barrier (DIB)
3.1.4. Kernel Interpolation with Barrier (KIB)
3.1.5. Ordinary Kriging (OK)
3.1.6. Empirical Bayesian Kriging (EBK)
3.2. Cross-Validation
3.2.1. Evaluation Criterion
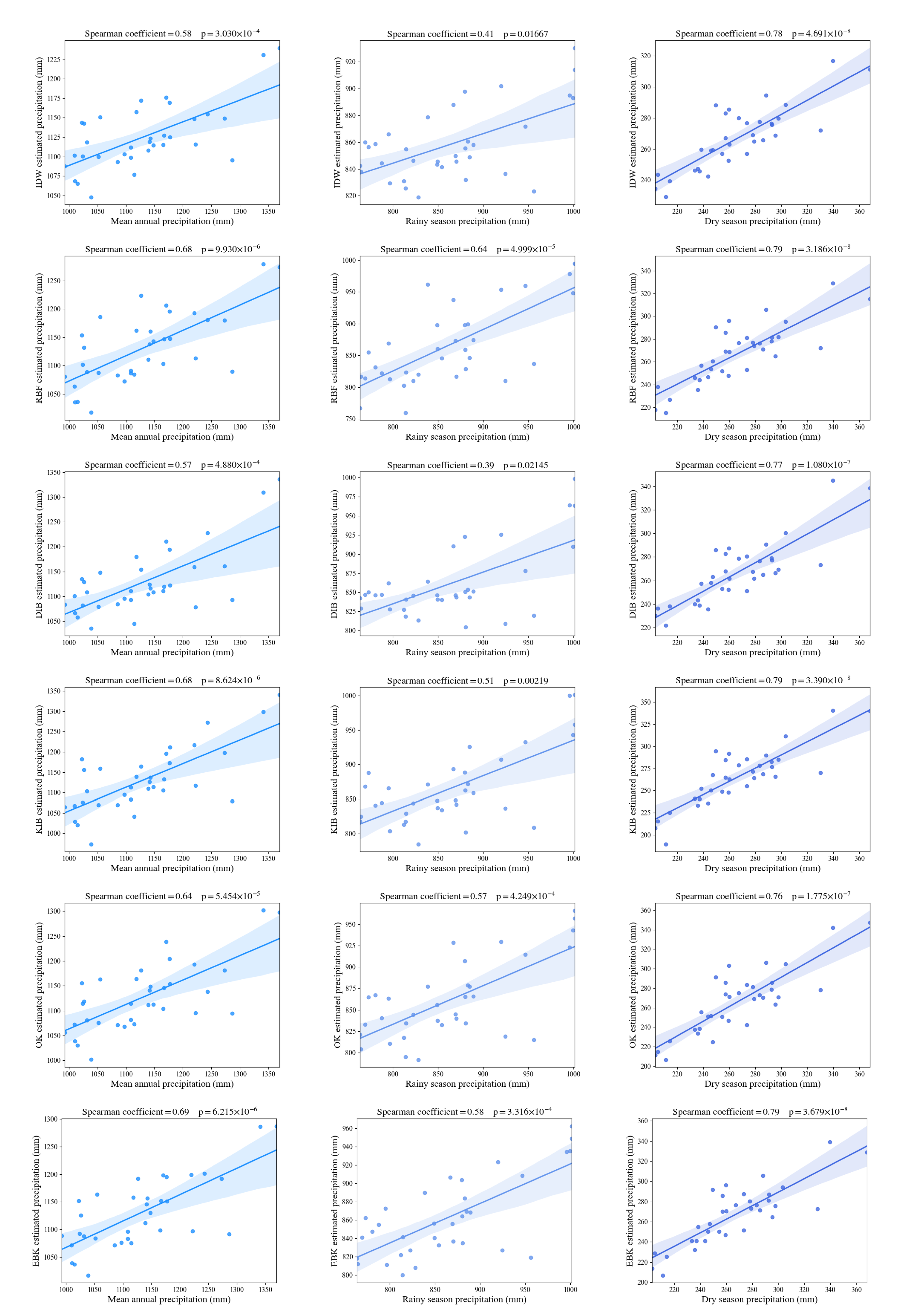
3.2.2. Correlation Analysis
3.3. Entropy-Weighted TOPSIS Method
4. Results
4.1. Spatial Distribution Patterns of Precipitation under Different Climatic Conditions
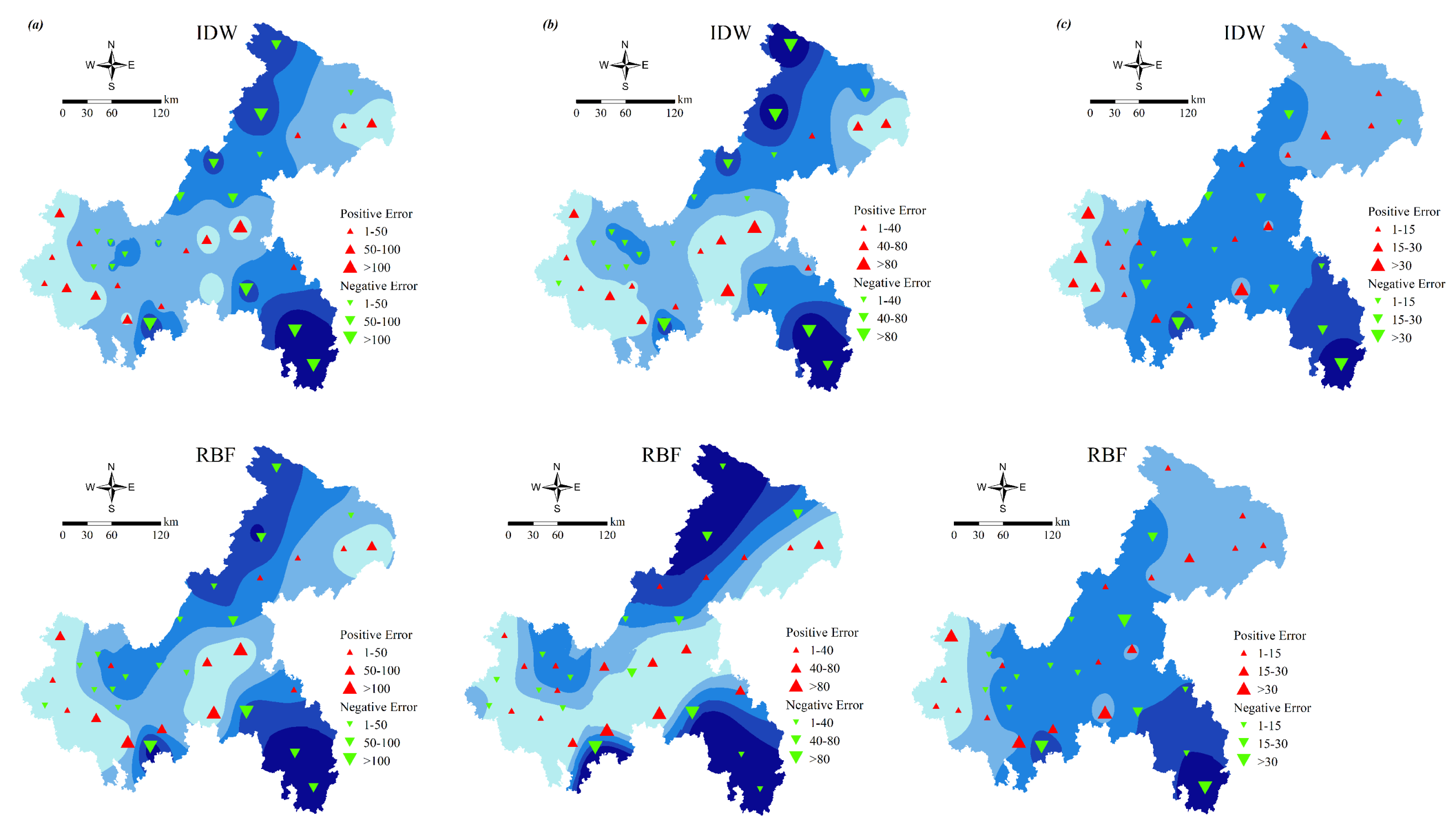
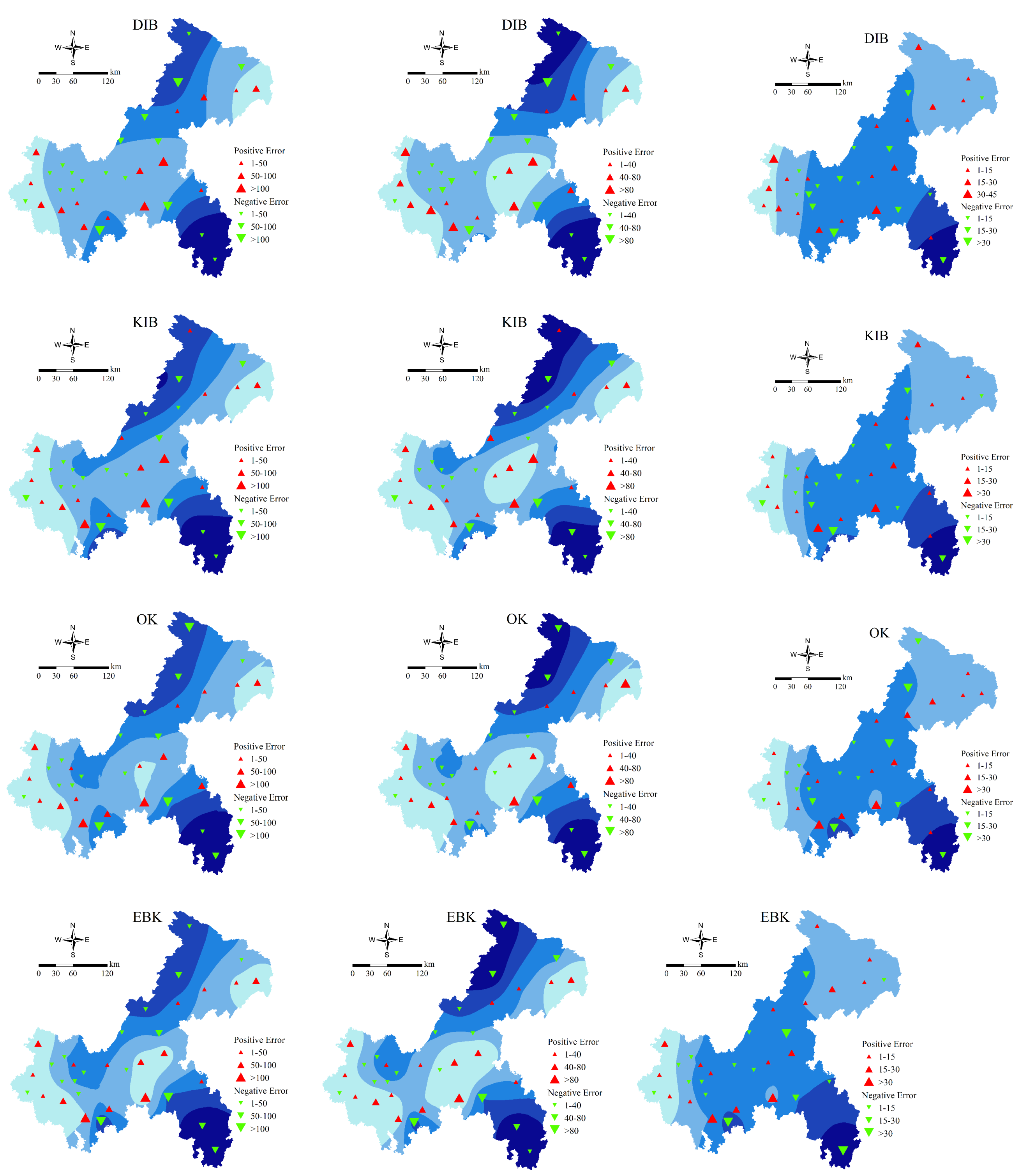
4.2. Performance of Different Spatial Interpolation Methods
Comparison of Interpolation Methods under Different Climatic Conditions
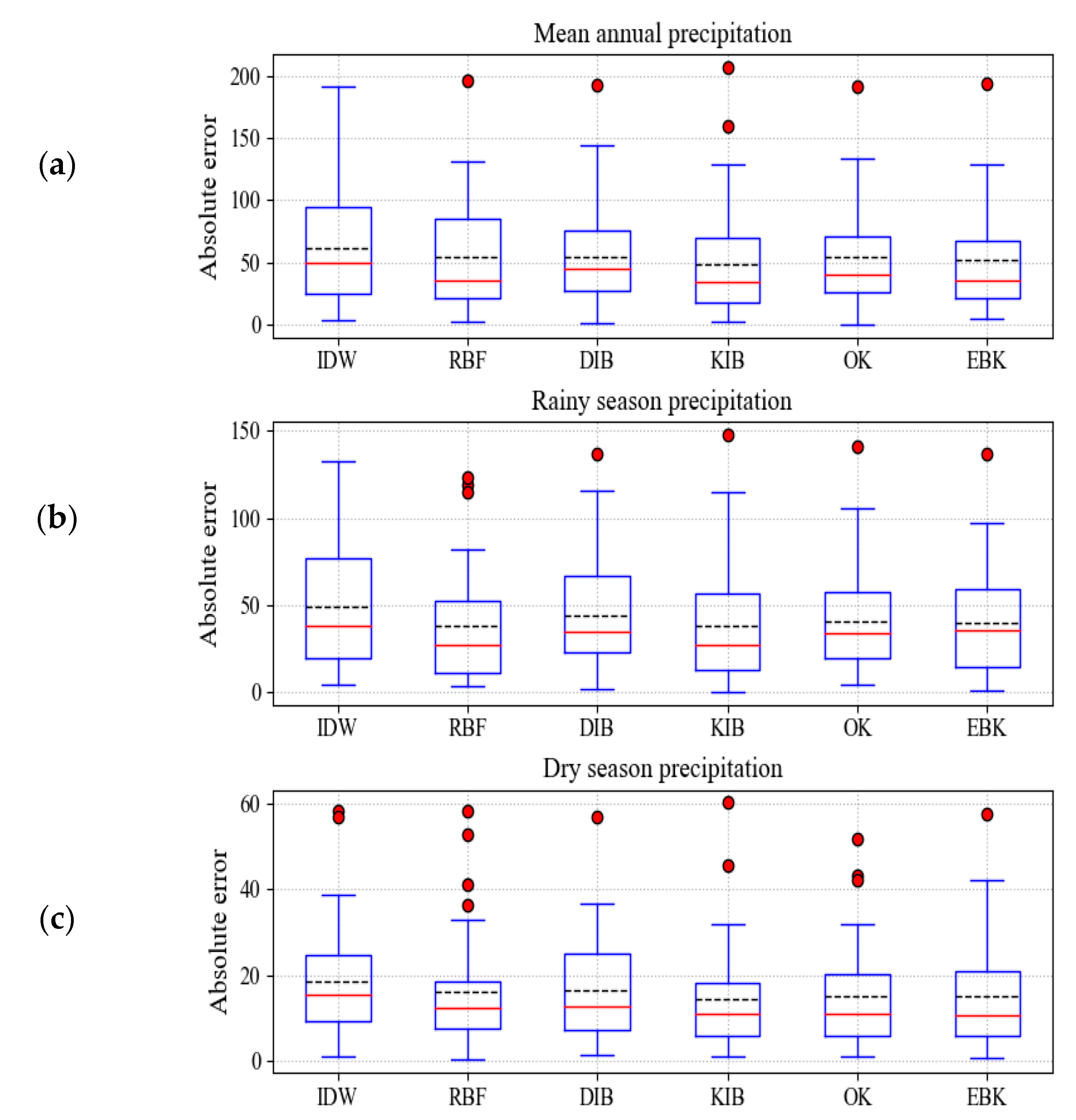
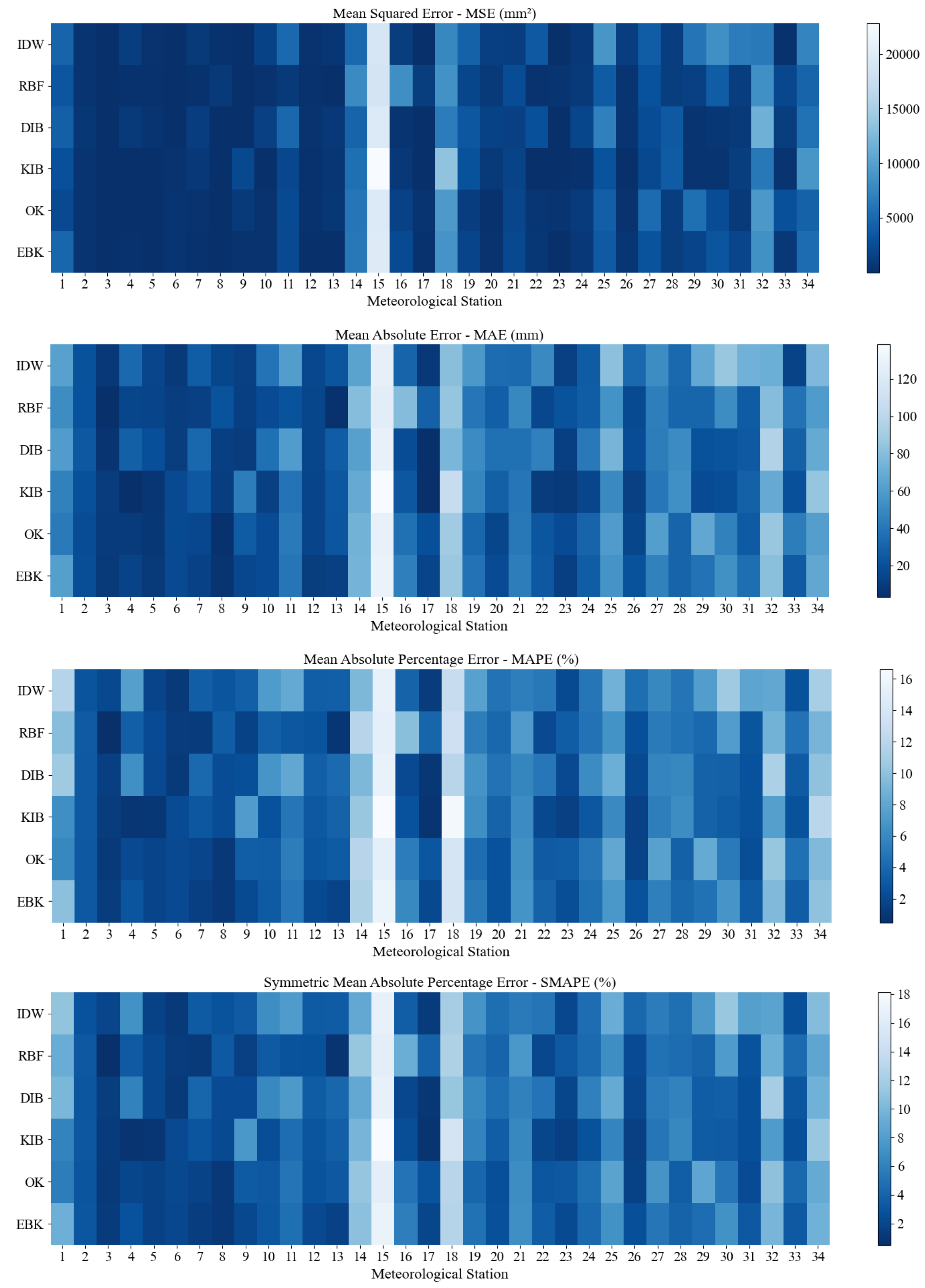
4.3. The Error and Correlation Analysis
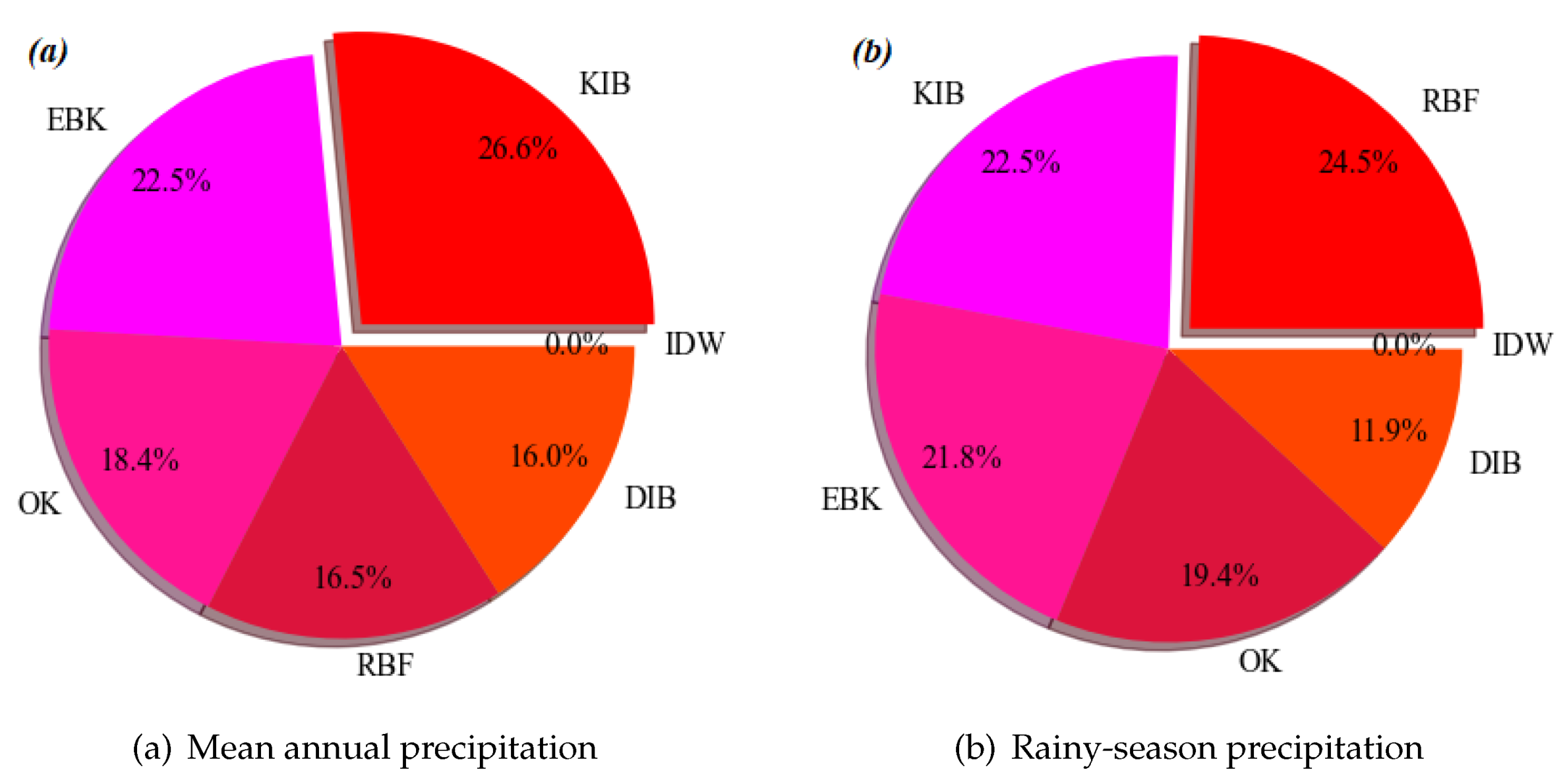
4.4. Comprehensive Ranking by Entropy-Weighted TOPSIS
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hadi, S.J.; Tombul, M. Long-term spatiotemporal trend analysis of precipitation and temperature over Turkey. Meteorol. Appl. 2018, 25, 445–455. [Google Scholar] [CrossRef] [Green Version]
- Hu, D.; Shu, H. Spatiotemporal interpolation of precipitation across Xinjiang, China using space-time CoKriging. J. Cent. South Univ. 2019, 26, 684–694. [Google Scholar] [CrossRef]
- Hadi, S.J.; Tombul, M. Comparison of Spatial Interpolation Methods of Precipitation and Temperature Using Multiple Integration Periods. J. Indian Soc. Remote Sens. 2018, 46, 1187–1199. [Google Scholar] [CrossRef]
- Portalés, C.; Boronat, N.; Pardo-Pascual, J.; Balaguer-Beser, A. Seasonal precipitation interpolation at the Valencia region with multivariate methods using geographic and topographic information. Int. J. Climatol. 2009, 30, 1547–1563. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Zhao, Q.; Fu, D.; Guo, S.; Liu, P.; Zeng, Y. Comparison of spatial interpolation methods for the estimation of precipitation patterns at different time scales to improve the accuracy of discharge simulations. Hydrol. Res. 2020, 51, 583–601. [Google Scholar] [CrossRef]
- Ma, J.; Yan, X.; Hu, S.; Guo, Y. Can monthly precipitation interpolation error be reduced by adding periphery climate stations? A case study in China’s land border areas. J. Water Clim. Chang. 2017, 8, 102–113. [Google Scholar] [CrossRef]
- Li, H.; Wang, D.; Singh, V.; Wang, Y.; Wu, J.; Wu, J. Developing an entropy and copula-based approach for precipitation monitoring network expansion. J. Hydrol. 2021, 598, 126366. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, C.; Wang, Y.; Ma, Z. Spatiotemporal Variations of Precipitation in China Using Surface Gauge Observations from 1961 to 2016. Atmosphere 2020, 11, 303. [Google Scholar] [CrossRef] [Green Version]
- Buttafuoco, G.; Conforti, M. Improving Mean Annual Precipitation Prediction Incorporating Elevation and Taking into Account Support Size. Water 2021, 13, 830. [Google Scholar] [CrossRef]
- Wang, S.; Huang, G.; Lin, Q.; Li, Z.; Zhang, H.; Fan, Y. Comparison of interpolation methods for estimating spatial distribution of precipitation in Ontario, Canada. Int. J. Climatol. 2014, 34, 3745–3751. [Google Scholar] [CrossRef]
- Cheng, M.; Yonggui, W.; Engel, B.; Zhang, W.; Peng, H.; Chen, X.; Xia, H. Performance Assessment of Spatial Interpolation of Precipitation for Hydrological Process Simulation in the Three Gorges Basin. Water 2017, 9, 838. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liu, G.; Wang, H.; Li, X. Application of a Hybrid Interpolation Method Based on Support Vector Machine in the Precipitation Spatial Interpolation of Basins. Water 2017, 9, 760. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, P.K.; Pradhan, R.K.; Petropoulos, G.P.; Pandey, V.; Gupta, M.; Yaduvanshi, A.; Wan Jaafar, W.Z.; Mall, R.K.; Sahai, A.K. Long-Term Trend Analysis of Precipitation and Extreme Events over Kosi River Basin in India. Water 2021, 13, 1695. [Google Scholar] [CrossRef]
- Dumitrescu, A.; Birsan, M.; Manea, A. Spatio-temporal interpolation of sub-daily (6 h) precipitation over Romania for the period 1975–2010. Int. J. Climatol. 2016, 36, 1331–1343. [Google Scholar] [CrossRef] [Green Version]
- Gajbhiye, S.; Meshram, C.; Singh, S.K.; Srivastava, P.; Islam, T. Precipitation trend analysis of Sindh River basin, India, from 102-year record (1901–2002). Atmos. Sci. Lett. 2016, 17, 71–77. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G. Space-time conditional disaggregation of precipitation at high resolution via simulation. Water Resour. Res. 2016, 52, 920–937. [Google Scholar] [CrossRef] [Green Version]
- Teegavarapu, R.S.V.; Meskele, T.; Pathak, C. Geo-spatial grid-based transformations of precipitation estimates using spatial interpolation methods. Comput. Geosci. 2012, 40, 28–39. [Google Scholar] [CrossRef]
- Tobin, C.; Nicotina, L.; Parlange, M.; Berne, A.; Rinaldo, A. Improved interpolation of meteorological forcings for hydrologic applications in a Swiss Alpine region. J. Hydrol. 2011, 401, 77–89. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G. Interpolation of precipitation under topographic influence at different time scales. Water Resour. Res. 2013, 49, 4545–4565. [Google Scholar] [CrossRef]
- da Silva, A.S.A.; Stosic, B.; Menezes, R.; Singh, V. Comparison of Interpolation Methods for Spatial Distribution of Monthly Precipitation in the State of Pernambuco, Brazil. J. Hydrol. Eng. 2019, 24, 04018068. [Google Scholar] [CrossRef]
- Romman, Z.A.; Al-Bakri, J.; Kuisi, M.A. Comparison of methods for filling in gaps in monthly rainfall series in arid regions. Int. J. Climatol. 2021, 1–16. [Google Scholar] [CrossRef]
- Alsafadi, K.; Mohammed, S.; Mokhtar, A.; Sharaf, M.; He, H. Fine-resolution precipitation mapping over Syria using local regression and spatial interpolation. Atmos. Res. 2021, 256, 105524. [Google Scholar] [CrossRef]
- Antal, A.; Guerreiro, P.; Cheval, S. Comparison of spatial interpolation methods for estimating the precipitation distribution in Portugal. Theor. Appl. Climatol. 2021, 145, 1193–1206. [Google Scholar] [CrossRef]
- Tan, J.; Xie, X.; Zuo, J.; Xing, X.; Liu, B.; Xia, Q.; Zhang, Y. Coupling Random Forest and Inverse Distance Weighting to Generate Climate Surfaces of Precipitation and Temperature with Multiple-Covariates. J. Hydrol. 2021, 598, 126270. [Google Scholar] [CrossRef]
- Getis, A. Spatial Pattern Analysis. In Encyclopedia of Social Measurement; k. Kempf-Leonard: New York, NY, USA, 2005; pp. 627–632. ISBN 978-0-123-69398-3. [Google Scholar] [CrossRef]
- Zou, W.; Yin, S.; Wang, W. Spatial interpolation of the extreme hourly precipitation at different return levels in the Haihe River basin. J. Hydrol. 2021, 598, 126273. [Google Scholar] [CrossRef]
- Adhikary, P.P.; Dash, C. Comparison of deterministic and stochastic methods to predict spatial variation of groundwater depth. Appl. Water Sci. 2017, 7, 339–348. [Google Scholar] [CrossRef] [Green Version]
- Fan, C.; Yin, S.; Chen, D. Spatial correlations of daily precipitation over mainland China. Int. J. Climatol. 2021, 1–16. [Google Scholar]
- Sahu, B.; Ghosh, A.K.; Seema. Deterministic and geostatistical models for predicting soil organic carbon in a 60 ha farm on Inceptisol in Varanasi, India. Geoderma Reg. 2021, 26, e00413. [Google Scholar] [CrossRef]
- Das, S.; Islam, A.R.M.T. Assessment of mapping of annual average rainfall in a tropical country like Bangladesh: Remotely sensed output vs. kriging estimate. Theor. Appl. Climatol. 2021, 146, 111–123. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, Y.; Sun, H.; Qi, L.; Liu, H.; Wang, Z. Spatial variation and distribution of soil organic carbon in an urban ecosystem from high-density sampling. Catena 2021, 204, 105364. [Google Scholar] [CrossRef]
- Katipoğlu, O.M.; Acar, R.; Şenocak, S. Spatio-temporal analysis of meteorological and hydrological droughts in the Euphrates Basin, Turkey. Water Supply 2021, 21, 1657–1673. [Google Scholar] [CrossRef]
- Hurtado, S.I.; Zaninelli, P.; Agosta, E.; Ricetti, L. Infilling methods for monthly precipitation records with poor station network density in Subtropical Argentina. Atmos. Res. 2021, 254, 105482. [Google Scholar] [CrossRef]
- Zaghiyan, M.R.; Eslamian, S.; Gohari, A.; Ebrahimi, M.S. Temporal correction of irregular observed intervals of groundwater level series using interpolation techniques. Theor. Appl. Climatol. 2021, 145, 1027–1037. [Google Scholar] [CrossRef]
- Ananias, D.R.S.; Liska, G.R.; Beijo, L.A.; Liska, G.J.R.; de Menezes, F.S. The Assessment of Annual Rainfall Field by Applying Different Interpolation Methods in the State of Rio Grande do Sul, Brazil. SN Appl. Sci. 2021, 3, 687. [Google Scholar] [CrossRef]
- Tang, H.; Wen, T.; Shi, P.; Qu, S.; Zhao, L.; Li, Q. Analysis of Characteristics of Hydrological and Meteorological Drought Evolution in Southwest China. Water 2021, 13, 1846. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, X.; Tang, H.; Li, Y. Prediction and correction of in situ summer precipitation in Southwest China based on a downscaling method with the BCC_CSM. Theor. Appl. Climatol. 2021, 145, 1145–1159. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.; Wang, W.; Li, C. Meteorological Drought Events and Their Evolution from 1960 to 2015 Using the Daily SWAP Index in Chongqing, China. Water 2021, 13, 1887. [Google Scholar] [CrossRef]
- Chen, P. Effects of the entropy weight on TOPSIS. Expert Syst. Appl. 2021, 168, 114186. [Google Scholar] [CrossRef]
- Li, H.; Huang, J.; Hu, Y.; Wang, S.; Liu, J.; Yang, L. A new TMY generation method based on the entropy-based TOPSIS theory for different climatic zones in China. Energy 2021, 231, 120723. [Google Scholar] [CrossRef]
- Jiang, R.; Ci, S.; Liu, D.; Cheng, X.; Pan, Z. A Hybrid Multi-Objective Optimization Method Based on NSGA-II Algorithm and Entropy Weighted TOPSIS for Lightweight Design of Dump Truck Carriage. Machines 2021, 9, 156. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Chen, A. Does high risk mean high loss: Evidence from flood disaster in southern China. Sci. Total Environ. 2021, 785, 147127. [Google Scholar] [CrossRef] [PubMed]
- Xiang, B.; Zhou, J.; Li, Y. Asymmetric relationships between El Niño/La Niña and floods/droughts in the following summer over Chongqing, China. Atmos. Ocean. Sci. Lett. 2020, 13, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Wen, T.; Xing, D.; Zhang, Y. Associations between floods and bacillary dysentery cases in main urban areas of Chongqing, China, 2005–2016: A retrospective study. Environ. Health Prev. Med. 2021, 26, 49. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Fan, J.; Yang, W. Flooding Risk Assessment and Analysis Based on GIS and the TFN-AHP Method: A Case Study of Chongqing, China. Atmosphere 2021, 12, 623. [Google Scholar] [CrossRef]
- Célicourt, P.; Gumière, S.; Lafond, J.; Gumiere, T.; Gallichand, J.; Rousseau, A. Automated Mapping of Water Table for Cranberry Subirrigation Management: Comparison of Three Spatial Interpolation Methods. Water 2020, 12, 3322. [Google Scholar] [CrossRef]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007; pp. 47–76. ISBN 978-0-470-02858-2. [Google Scholar] [CrossRef] [Green Version]
- Schuenemeyer, J.H.; Drew, L.J. Statistics for Earth and Environmental Scientists; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; pp. 193–241. ISBN 978-1-118-10221-3. [Google Scholar] [CrossRef]
- Ferreira, R.G.; da Silva, D.D.; Elesbon, A.A.A.; dos Santos, G.R.; Veloso, G.; Fraga, M.D.S.; Fernandes-Filho, E.I. Geostatistical modeling and traditional approaches for streamflow regionalization in a Brazilian Southeast watershed. J. South Am. Earth Sci. 2021, 108, 103355. [Google Scholar] [CrossRef]
- Krivoruchko, K.; Gribov, A. Pragmatic Bayesian Kriging for Non-Stationary and Moderately Non-Gaussian Data. In Mathematics of Planet Earth; Springer: Berlin/Heidelberg, Germany, 2014; pp. 61–64. ISBN 978-3-642-32408-6. [Google Scholar] [CrossRef]
- Li, M.; Sun, H.; Singh, V.; Zhou, Y.; Ma, M. Agricultural Water Resources Management Using Maximum Entropy and Entropy-Weight-Based TOPSIS Methods. Entropy 2019, 21, 364. [Google Scholar] [CrossRef] [Green Version]
- Liu, E.; Wang, Y.; Chen, W.; Chen, W.; Ning, S. Evaluating the transformation of China’s resource-based cities: An integrated sequential weight and TOPSIS approach. Soc. Econ. Plan. Sci. 2021, 77, 101022. [Google Scholar] [CrossRef]
- Xiang, B.; Zeng, C.; Dong, X.; Wang, J. The Application of a Decision Tree and Stochastic Forest Model in Summer Precipitation Prediction in Chongqing. Atmosphere 2020, 11, 508. [Google Scholar] [CrossRef]




| 2]*Data Set | Estimation | MSE | MAE | MAPE | SMAPE | 2]*NSE |
|---|---|---|---|---|---|---|
| Method | (mm) | (mm) | (%) | (%) | ||
| IDW | 5782.79 | 61.17 | 5.37 | 5.38 | 0.37 | |
| RBF | 4898.53 | 54.44 | 4.81 | 4.78 | 0.47 | |
| Mean | DIB | 4826.71 | 54.70 | 4.86 | 4.87 | 0.48 |
| Annual | KIB | 4545.94 | 49.01 | 4.38 | 4.36 | 0.51 |
| OK | 4698.02 | 54.25 | 4.78 | 4.79 | 0.49 | |
| EBK | 4429.45 | 51.70 | 4.58 | 4.57 | 0.52 | |
| IDW | 3525.09 | 48.69 | 5.60 | 5.62 | 0.29 | |
| RBF | 2562.31 | 38.05 | 4.44 | 4.42 | 0.48 | |
| Rainy | DIB | 2970.41 | 43.92 | 5.12 | 5.12 | 0.40 |
| Season | KIB | 2704.41 | 38.29 | 4.51 | 4.49 | 0.46 |
| OK | 2651.52 | 40.99 | 4.76 | 4.76 | 0.47 | |
| EBK | 2543.79 | 39.85 | 4.63 | 4.62 | 0.49 | |
| IDW | 519.05 | 18.35 | 6.90 | 6.84 | 0.61 | |
| RBF | 454.31 | 16.23 | 6.00 | 5.96 | 0.66 | |
| Dry | DIB | 411.32 | 16.28 | 6.17 | 6.13 | 0.69 |
| Season | KIB | 371.46 | 14.50 | 5.38 | 5.39 | 0.72 |
| OK | 390.93 | 15.15 | 5.61 | 5.60 | 0.71 | |
| EBK | 400.93 | 15.14 | 5.59 | 5.57 | 0.70 |
| Method | Positive Distance (D) | Negative Distance (D-) | Comparatively Proximity (C) | Sort Result | |
|---|---|---|---|---|---|
| KIB | 0.016 | 0.441 | 0.964 | 1 | |
| EBK | 0.083 | 0.374 | 0.818 | 2 | |
| Mean | OK | 0.155 | 0.311 | 0.667 | 3 |
| Annual | RBF | 0.18 | 0.269 | 0.6 | 4 |
| DIB | 0.191 | 0.265 | 0.581 | 5 | |
| IDW | 0.448 | 0 | 0 | 6 | |
| RBF | 0.01 | 0.442 | 0.978 | 1 | |
| KIB | 0.046 | 0.41 | 0.899 | 2 | |
| Rainy | EBK | 0.06 | 0.401 | 0.87 | 3 |
| Season | OK | 0.104 | 0.353 | 0.773 | 4 |
| DIB | 0.238 | 0.214 | 0.474 | 5 | |
| IDW | 0.448 | 0 | 0 | 6 | |
| KIB | 0 | 0.447 | 1 | 1 | |
| OK | 0.063 | 0.386 | 0.86 | 2 | |
| Dry | EBK | 0.073 | 0.375 | 0.836 | 3 |
| Season | DIB | 0.189 | 0.27 | 0.588 | 4 |
| RBF | 0.213 | 0.238 | 0.528 | 5 | |
| IDW | 0.447 | 0 | 0 | 6 | |
| KIB | 0.024 | 0.49 | 0.954 | 1 | |
| EBK | 0.07 | 0.44 | 0.863 | 2 | |
| Integrated | OK | 0.126 | 0.379 | 0.75 | 3 |
| Scenario | RBF | 0.127 | 0.373 | 0.746 | 4 |
| DIB | 0.241 | 0.265 | 0.524 | 5 | |
| IDW | 0.5 | 0 | 0 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Xing, B. A Comparison of the Performance of Different Interpolation Methods in Replicating Rainfall Magnitudes under Different Climatic Conditions in Chongqing Province (China). Atmosphere 2021, 12, 1318. https://doi.org/10.3390/atmos12101318
Yang R, Xing B. A Comparison of the Performance of Different Interpolation Methods in Replicating Rainfall Magnitudes under Different Climatic Conditions in Chongqing Province (China). Atmosphere. 2021; 12(10):1318. https://doi.org/10.3390/atmos12101318
Chicago/Turabian StyleYang, Ruting, and Bing Xing. 2021. "A Comparison of the Performance of Different Interpolation Methods in Replicating Rainfall Magnitudes under Different Climatic Conditions in Chongqing Province (China)" Atmosphere 12, no. 10: 1318. https://doi.org/10.3390/atmos12101318
APA StyleYang, R., & Xing, B. (2021). A Comparison of the Performance of Different Interpolation Methods in Replicating Rainfall Magnitudes under Different Climatic Conditions in Chongqing Province (China). Atmosphere, 12(10), 1318. https://doi.org/10.3390/atmos12101318





