Rapid Update with EnVar Direct Radar Reflectivity Data Assimilation for the NOAA Regional Convection-Allowing NMMB Model over the CONUS: System Description and Initial Experiment Results
Abstract
:1. Introduction
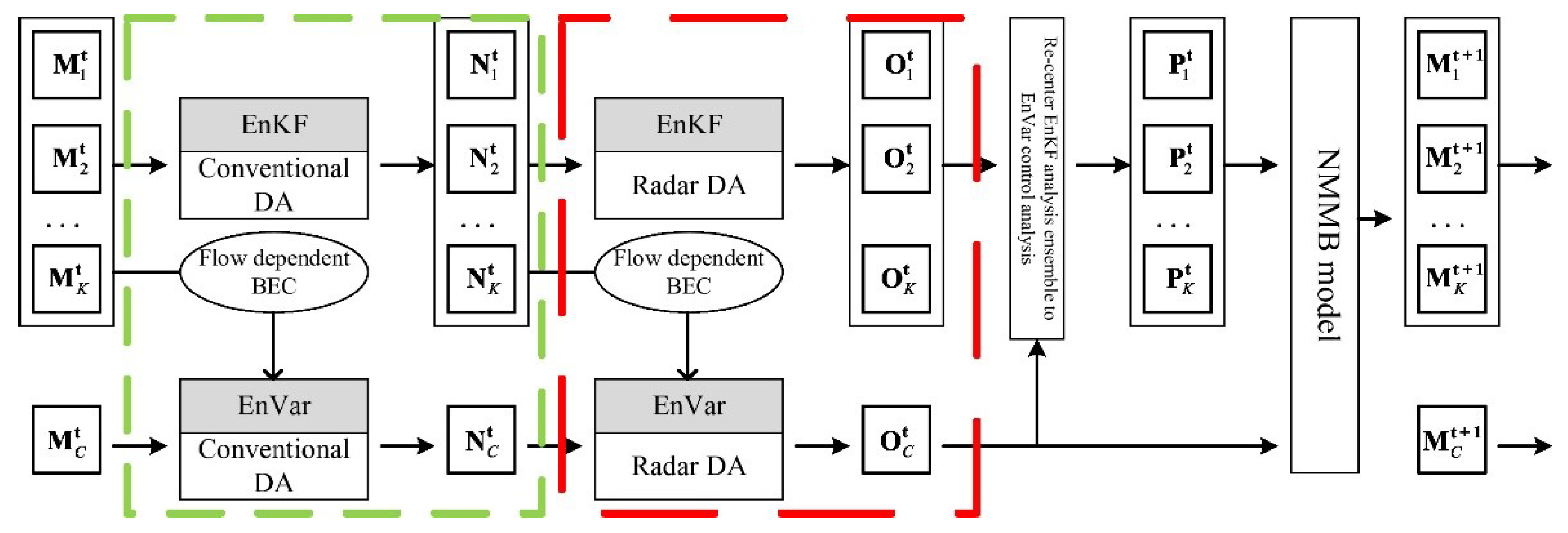
2. System Description
2.1. GSI-Based EnVar Data Assimilation System within NAMRR
2.2. Methodology of GSI-Based EnVar DA System for Direct Assimilation of Reflectivity within NAMRR
2.2.1. GSI-Based EnVar and its Extensions of Direct Reflectivity Assimilation for NMMB
2.2.2. GSI-Based EnKF and its Extensions of Direct Reflectivity Assimilation for NMMB
3. Experimental Setups
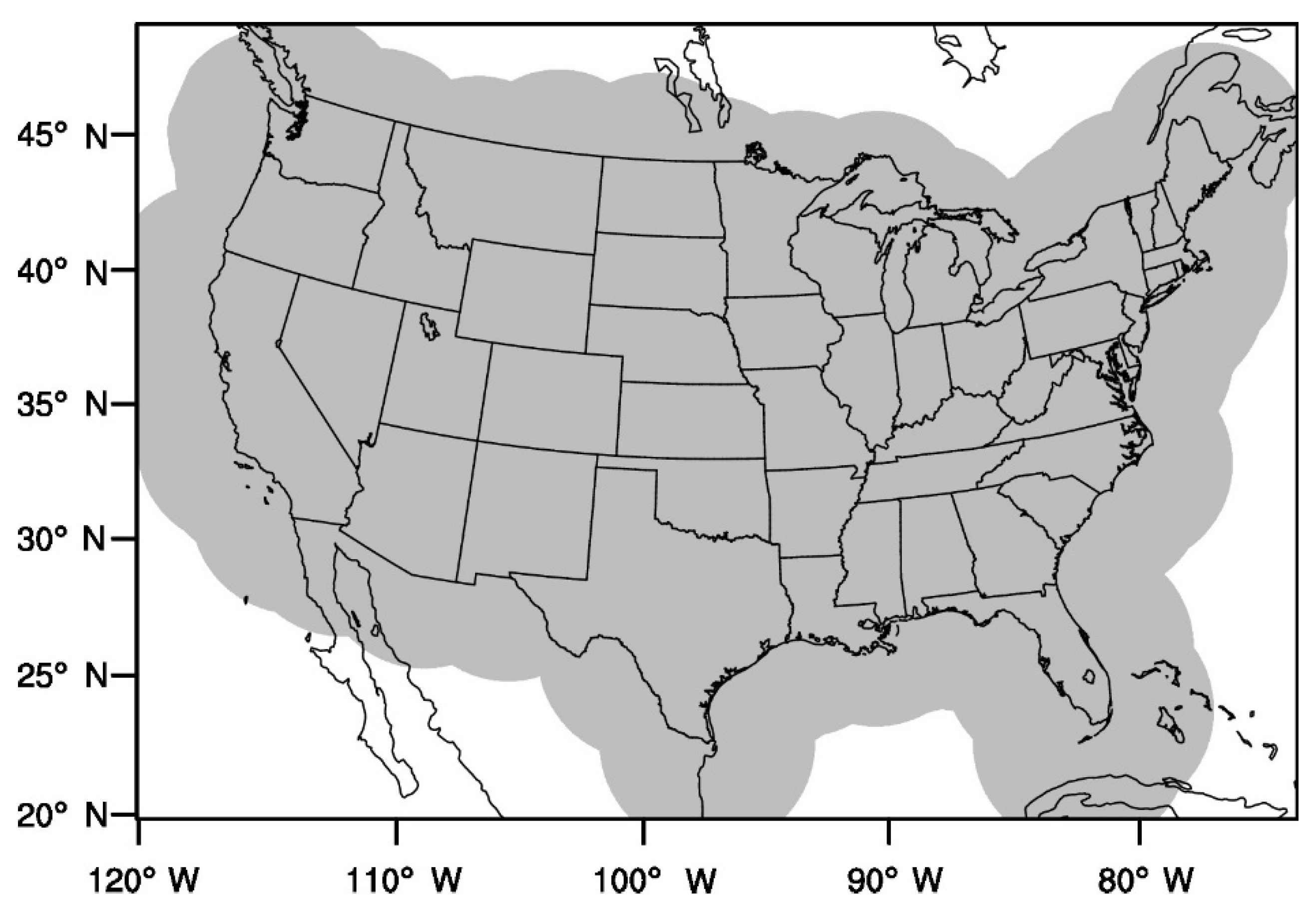
3.1. Model Configuration
3.2. DA Configuration and Experimental Design
3.3. Verification
4. Results
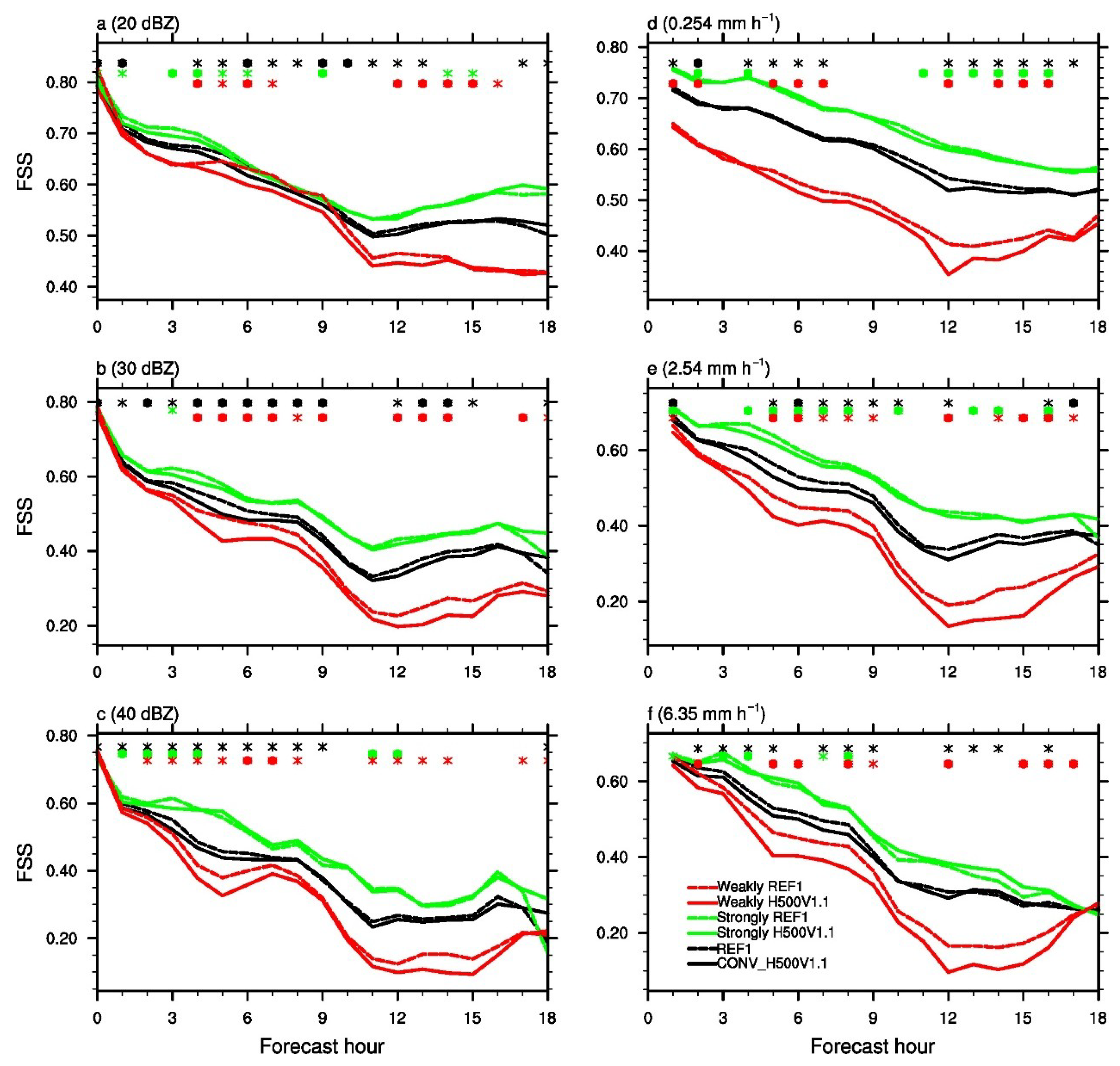
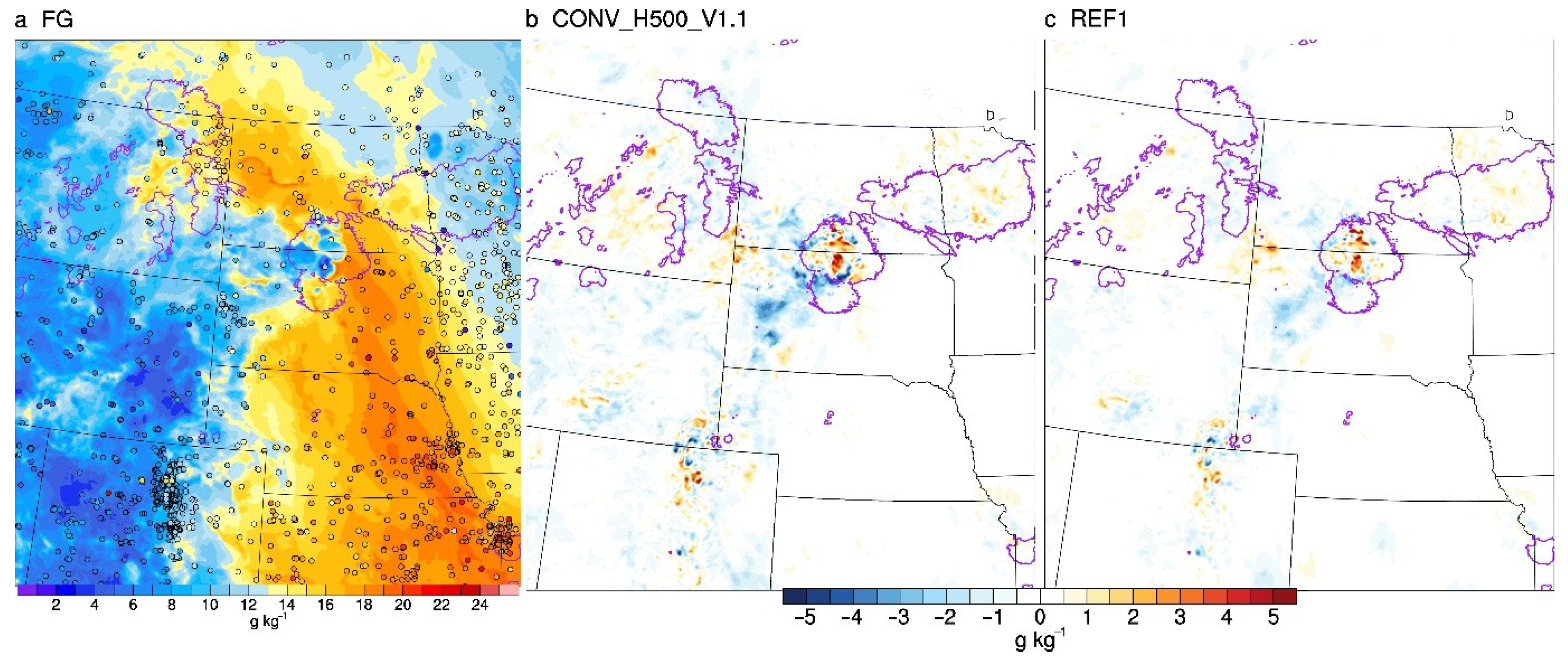
4.1. Impact of Localization Radii for Conventional DA
4.2. Impact of Localization Radii for Radar DA
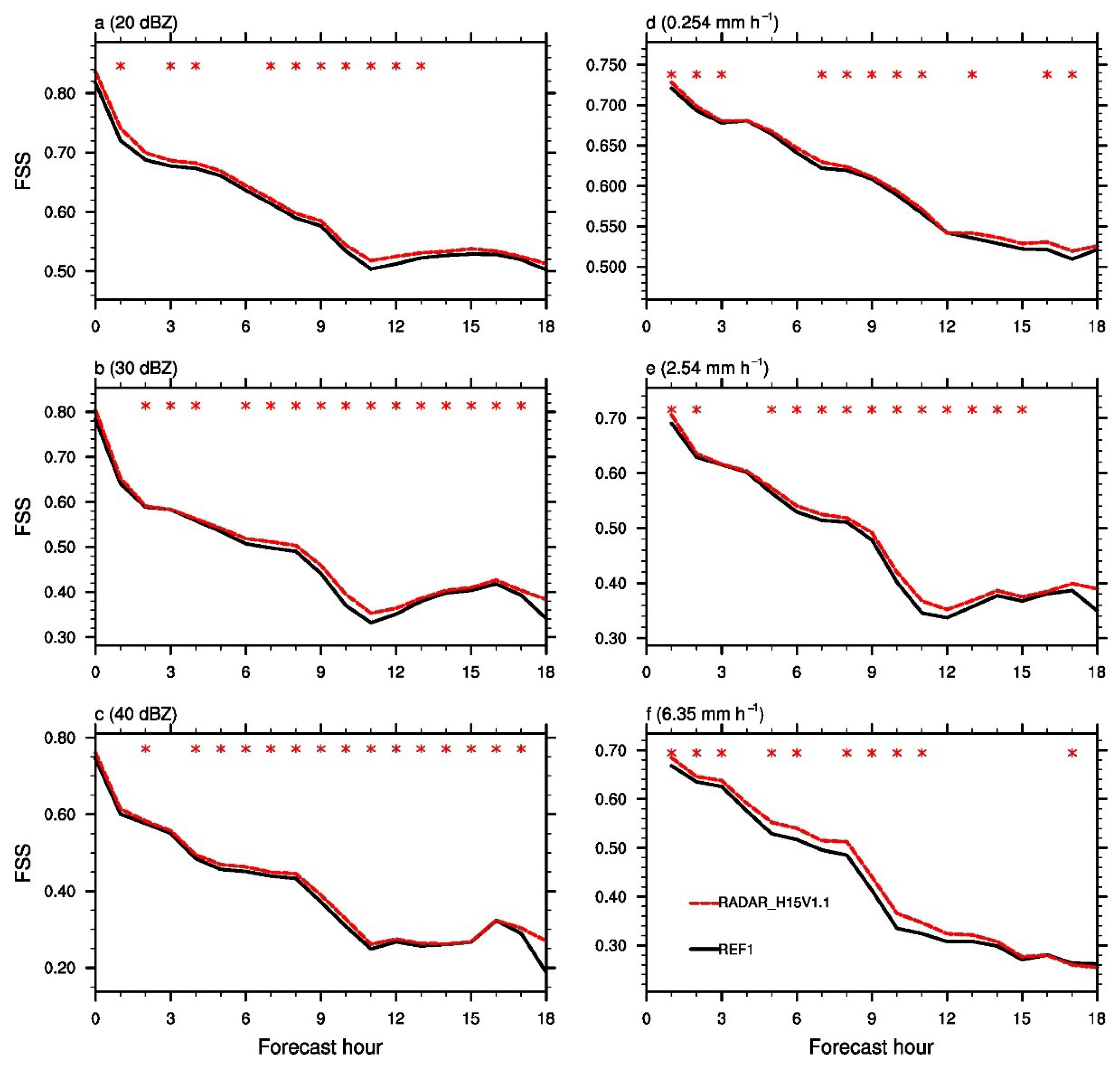
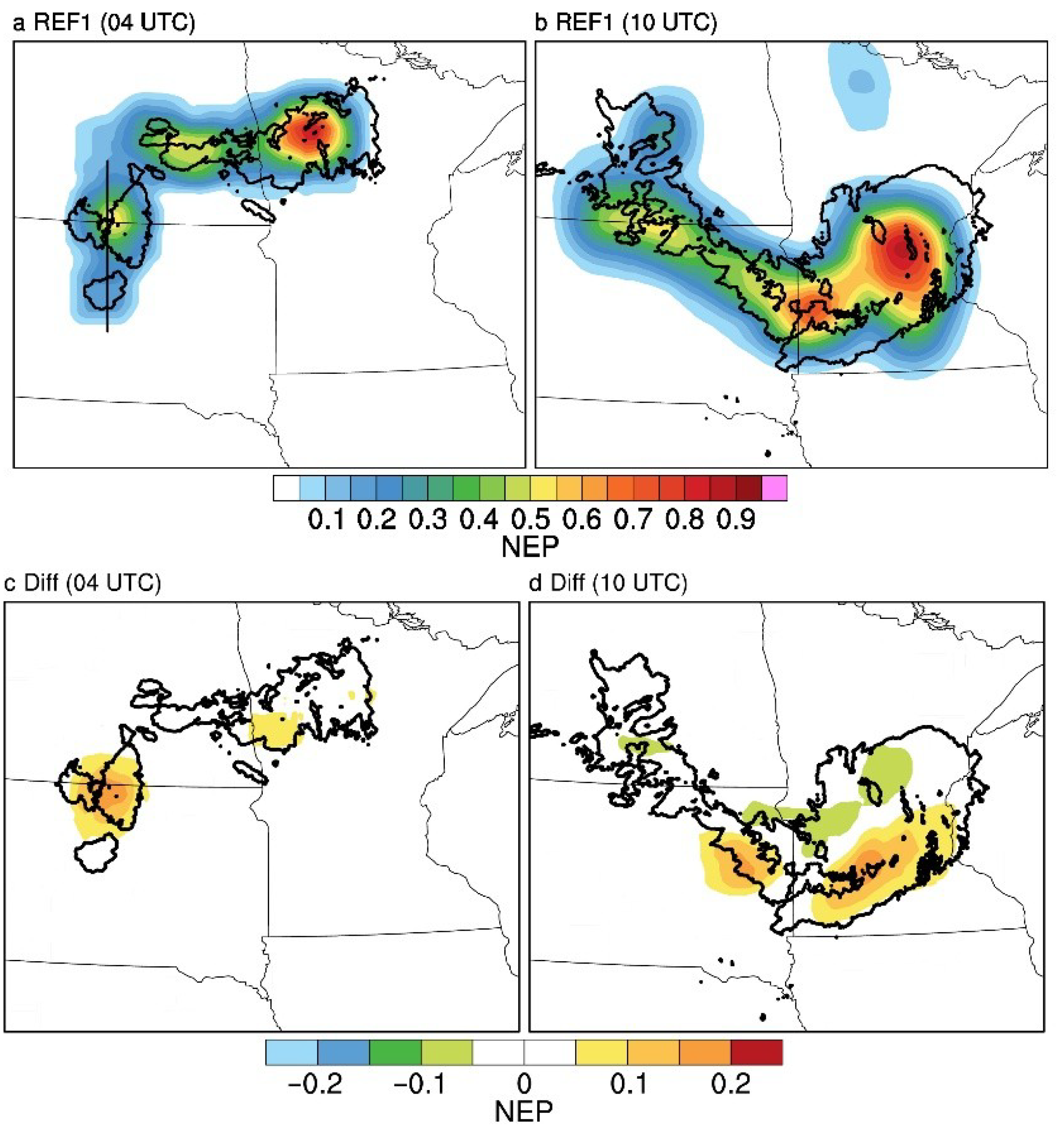
4.3. Impact of Inflating Ensemble Spread through RTPS
5. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamill, T.M.; Snyder, C. A Hybrid Ensemble Kalman Filter–3D Variational Analysis Scheme. Mon. Weather Rev. 2000, 128, 2905–2919. [Google Scholar] [CrossRef]
- Lorenc, A.C. The potential of the ensemble Kalman filter for NWP—A comparison with 4D-Var. Q. J. R. Meteorol. Soc. 2003, 129, 3183–3203. [Google Scholar] [CrossRef]
- Etherton, B.; Bishop, C.H. Resilience of Hybrid Ensemble/3DVAR Analysis Schemes to Model Error and Ensemble Covariance Error. Mon. Weather Rev. 2004, 132, 1065–1080. [Google Scholar] [CrossRef]
- Zupanski, M. Maximum Likelihood Ensemble Filter: Theoretical Aspects. Mon. Weather Rev. 2005, 133, 1710–1726. [Google Scholar] [CrossRef]
- Wang, X.; Hamill, T.M.; Whitaker, J.S.; Bishop, C. A Comparison of Hybrid Ensemble Transform Kalman Filter–Optimum Interpolation and Ensemble Square Root Filter Analysis Schemes. Mon. Weather Rev. 2007, 135, 1055–1076. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Snyder, C.; Hamill, T.M. On the Theoretical Equivalence of Differently Proposed Ensemble–3DVAR Hybrid Analysis Schemes. Mon. Weather Rev. 2007, 135, 222–227. [Google Scholar] [CrossRef]
- Wang, X.; Barker, D.M.; Snyder, C.; Hamill, T.M. A hybrid ETKF–3DVAR data assimilation scheme for the WRF model. Part I: Observation system simulation experiment. Mon. Weather Rev. 2008, 136, 5116–5131. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Barker, D.M.; Snyder, C.; Hamill, T.M. A hybrid ETKF–3DVAR data assimilation scheme for the WRF model. Part II: Real observation experiments. Mon. Weather Rev. 2008, 136, 5132–5147. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Hamill, T.M.; Whitaker, J.S.; Bishop, C. A Comparison of the Hybrid and EnSRF Analysis Schemes in the Presence of Model Errors due to Unresolved Scales. Mon. Weather Rev. 2009, 137, 3219–3232. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Xiao, Q.; Wang, B. An Ensemble-Based Four-Dimensional Variational Data Assimilation Scheme. Part I: Technical Formulation and Preliminary Test. Mon. Weather Rev. 2008, 136, 3363–3373. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Xiao, Q.; Wang, B. An ensemble-based four-dimensional variational data assimilation scheme. Part II: Observing System Simulation Experiments with the Advanced Research WRF (ARW). Mon. Weather Rev. 2009, 137, 1687–1704. [Google Scholar] [CrossRef]
- Wang, X. Incorporating ensemble covariance in the Gridpoint Statistical Interpolation (GSI) variational mini-mization: A mathematical framework. Mon. Weather Rev. 2010, 138, 2990–2995. [Google Scholar] [CrossRef] [Green Version]
- Wang, X. Application of the WRF Hybrid ETKF–3DVAR Data Assimilation System for Hurricane Track Forecasts. Weather Forecast. 2011, 26, 868–884. [Google Scholar] [CrossRef]
- Wang, X.; Parrish, D.; Kleist, D.T.; Whitaker, J.S. GSI 3DVar-Based Ensemble–Variational Hybrid Data Assimilation for NCEP Global Forecast System: Single-Resolution Experiments. Mon. Weather Rev. 2013, 141, 4098–4117. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, F. E4DVar: Coupling an ensemble Kalman filter with four-dimensional variational data assimilation in a limited-area weather prediction model. Mon. Weather Rev. 2012, 140, 587–600. [Google Scholar] [CrossRef] [Green Version]
- Barker, D. Coauthors the Weather Research and Forecasting Model’s community variational/ensemble data assimilation system: WRFDA. Bull. Amer. Meteor. Soc. 2012, 93, 831–843. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, X.; Xue, M. Assimilation of radar radial velocity data with the WRF hybrid ensemble–3DVAR hy-brid system for the prediction of Hurricane Ike (2008). Mon. Weather Rev. 2012, 140, 3507–3524. [Google Scholar] [CrossRef] [Green Version]
- Gustafsson, N.; Bojarova, J. Four-dimensional ensemble variational (4D-En-Var) data assimilation for the HIgh Resolution Limited Area Model (HIRLAM). Nonlinear Process. Geophys. 2014, 21, 745–762. [Google Scholar] [CrossRef] [Green Version]
- Buehner, M. Coauthors Implementation of deterministic weather forecasting systems based on ensemble–variational data assimilation at Environment Canada. Part I: The global system. Mon. Weather Rev. 2015, 143, 2532–2559. [Google Scholar] [CrossRef]
- Caron, J.F.; Milewski, T.; Buehner, M.; Fillion, L.; Reszka, M.; Macpherson, S.; St-James, J. Implementation of de-terministic weather forecasting systems based on ensemble–variational data assimilation at Environment Canada. Part II: The regional system. Mon. Weather Rev. 2015, 143, 2560–2580. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Li, Y.; Tong, M.; Ma, X. GSI-based ensemble-variational hybrid data assimilation for HWRF for hurricane initialization and prediction: Impact of various error covariances for airborne radar observation as-similation. Quart. J. Roy. Meteor. Soc. 2017, 143, 223–239. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X. Direct Assimilation of Radar Reflectivity without Tangent Linear and Adjoint of the Nonlinear Observation Operator in the GSI-Based EnVar System: Methodology and Experiment with the 8 May 2003 Oklahoma City Tornadic Supercell. Mon. Weather Rev. 2017, 145, 1447–1471. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X. Prediction of Tornado-Like Vortex (TLV) Embedded in the 8 May 2003 Oklahoma City Tor-nadic Supercell Initialized from the Subkilometer Grid Spacing Analysis Produced by the Dual-Resolution GSI-Based EnVar Data Assimilation System. Mon. Weather Rev. 2020, 148, 2909–2934. [Google Scholar] [CrossRef]
- Wu, W.S.; Parrish, D.F.; Rogers, E.; Lin, Y. Regional ensemble–variational data assimilation using global ensemble forecasts. Weather Forecast 2017, 32, 83–96. [Google Scholar] [CrossRef]
- Hu, M.; Benjamin, S.G.; Ladwig, T.T.; Dowell, D.C.; Weygandt, S.S.; Alexander, C.R.; Whitaker, J.S. GSI three-dimensional ensemble–variational hybrid data assimilation using a global ensemble for the regional Rap-id Refresh model. Mon. Weather Rev. 2017, 145, 4205–4225. [Google Scholar] [CrossRef]
- Smith, T.L.; Benjamin, S.G.; Brown, J.M.; Weygandt, S.; Smirnova, T.; Schwartz, B. Convection forecasts from the hourly updated, 3-km High Resolution Rapid Refresh (HRRR) model. In Proceedings of the 24th Conference on Severe Local Storms, Savannah, GA, USA, 27–31 October 2018. [Google Scholar]
- Benjamin, S.G.; Weygandt, S.S.; Brown, J.M.; Hu, M.; Alexander, C.R.; Smirnova, T.G.; Olson, J.B.; James, E.P.; Dowell, D.C.; Grell, G.A.; et al. A North American hourly assimilation and model forecast cycle: The Rapid Refresh. Mon. Weather Rev. 2016, 144, 1669–1694. [Google Scholar] [CrossRef]
- Carley, J.; Rogers, E.; Liu, S.; Ferrier, B.; Aligo, E.; Pyle, M.; Zhang, X.; DiMego, G. A Status Update for the NAMRR, an Hourly-Updated Version of NAM Forecast System. In Proceedings of the 19th Conference on Integrated Observing and Assimilation Systems for the Atmosphere, Oceans, and Land Surface (IOAS-AOLS), Phoenix, AZ, USA, 4–8 January 2015. [Google Scholar]
- Montmerle, T.; Michel, Y.; Arbogast, E.; Ménétrier, B.; Brousseau, P. A 3D ensemble variational data assimilation scheme for the limited-area AROME model: Formulation and preliminary results. Q. J. R. Meteorol. Soc. 2018, 144, 2196–2215. [Google Scholar] [CrossRef]
- Duda, J.; Wang, X.; Wang, Y.; Carley, J. Comparing the Assimilation of Radar Reflectivity Using the Direct GSI-Based Ensemble–Variational (EnVar) and Indirect Cloud Analysis Methods in Convection-Allowing Forecasts over the Continental United States. Mon. Weather Rev. 2019, 147, 1655–1678. [Google Scholar] [CrossRef]
- Janjic, Z.I. A nonhydrostatic model based on a new approach. Theor. Appl. Clim. 2003, 82, 271–285. [Google Scholar] [CrossRef]
- Janjić, Z.I. A unified model approach from meso to global scales. In Geophysical Research Abstracts; SRef–ID 1607–7962/gra/EGU05–A–05 582; European Geosciences Union: Vienna, Austria, 2005; Volume 7, pp. 24–29. [Google Scholar]
- Janjić, Z.; Black, T.L. An ESMF unified model for a broad range of spatial and temporal scales. In Geophysical Re-Search Abstracts; SRef–ID 1607–7962/gra/EGU2007–A–05 025; European Geosciences Union: Vienna, Austria, 2007; Volume 9, pp. 5–25. [Google Scholar]
- Janjic, Z.; Gall, R. Scientific Documentation of the NCEP Nonhydrostatic Multiscale Model on the B Grid (NMMB). Part 1 Dynamics; University Corporation for Atmospheric Research: Boulder, CO, USA, 2012. [Google Scholar] [CrossRef]
- Sun, J. Convective-scale assimilation of radar data: Progress and challenges. Q. J. R. Meteorol. Soc. 2005, 131, 3439–3463. [Google Scholar] [CrossRef]
- Dowell, D.C.; Wicker, L.J.; Snyder, C. Ensemble Kalman Filter Assimilation of Radar Observations of the 8 May 2003 Oklahoma City Supercell: Influences of Reflectivity Observations on Storm-Scale Analyses. Mon. Weather Rev. 2011, 139, 272–294. [Google Scholar] [CrossRef] [Green Version]
- Albers, S.C.; McGinley, J.A.; Birkenheuer, D.L.; Smart, J.R. The Local Analysis and Prediction System (LAPS): Analyses of Clouds, Precipitation, and Temperature. Weather Forecast. 1996, 11, 273–287. [Google Scholar] [CrossRef] [Green Version]
- Souto, M.J.; Balseiro, C.F.; Perez-Munuzuri, V.; Xue, M.; Brewster, K. Impact of Cloud Analysis on Numerical Weather Prediction in the Galician Region of Spain. J. Appl. Meteorol. 2003, 42, 129–140. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Stensrud, D.J. Assimilation of Reflectivity Data in a Convective-Scale, Cycled 3DVAR Framework with Hydrometeor Classification. J. Atmospheric Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M.; Wei, X.; Song, Y.; Toth, Z. Ensemble Data Assimilation with the NCEP Global Forecast System. Mon. Weather Rev. 2008, 136, 463–482. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Shen, F.; Min, J. Effect of background error tuning on assimilating radar radial velocity observations for the forecast of hurricane tracks and intensities. Meteorol. Appl. 2020, 27, e1820. [Google Scholar] [CrossRef] [Green Version]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. A sequential ensemble Kalman filter for atmospheric data assimilation. Mon. Weather Rev. 2001, 129, 123–137. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Fiorino, M.; Benjamin, S. Global Ensemble Predictions of 2009’s Tropical Cyclones Initialized with an Ensemble Kalman Filter. Mon. Weather Rev. 2011, 139, 668–688. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.L.; Anderson, S.L. A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts. Mon. Weather Rev. 1999, 127, 2741–2758. [Google Scholar] [CrossRef]
- Whitaker, J.; Hamill, T.M. Ensemble Data Assimilation without Perturbed Observations. Mon. Weather Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. Data assimilation using an ensemble Kalman filter technique. Mon. Weather Rev. 1998, 126, 796–811. [Google Scholar] [CrossRef]
- Sobash, R.A.; Stensrud, D.J. The impact of covariance localization for radar data on EnKF analyses of a devel-oping MCS: Observing system simulation experiments. Mon. Weather Rev. 2013, 141, 3691–3709. [Google Scholar] [CrossRef]
- Yussouf, N.; Mansell, E.R.; Wicker, L.J.; Wheatley, D.M.; Stensrud, D.J. The ensemble Kalman filter analyses and forecasts of the 8 May 2003 Oklahoma City tornadic supercell storm using single- and double-moment micro-physics schemes. Mon. Weather Rev. 2013, 141, 3388–3412. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X.; Carely, J.; Wicker, L.; Karstens, C. A Comparison of Multi-scale GSI-based EnKF and 3DVar Data Assimilation using Radar and Conventional Observations for Mid-latitude Convective-scale Pre-cipitation Forecasts. Mon. Weather Rev. 2015, 143, 3087–3108. [Google Scholar] [CrossRef]
- Supinie, T.A.; Yussouf, N.; Jung, Y.; Xue, M.; Cheng, J.; Wang, S. Comparison of the Analyses and Forecasts of a Tornadic Supercell Storm from Assimilating Phased-Array Radar and WSR-88D Observations. Weather Forecast. 2017, 32, 1379–1401. [Google Scholar] [CrossRef]
- Derber, J.; Rosati, A. A Global Oceanic Data Assimilation System. J. Phys. Oceanogr. 1989, 19, 1333–1347. [Google Scholar] [CrossRef] [Green Version]
- Aligo, E.A.; Ferrier, B.; Carley, J. Modified NAM Microphysics for Forecasts of Deep Convective Storms. Mon. Weather Rev. 2018, 146, 4115–4153. [Google Scholar] [CrossRef]
- Müller, M.D.; Janjic, Z. Verification of the New Nonhydrostatic Multiscale Model on the B Grid (NMMB): A View on Global Predictability of Surface Parameters. Weather Forecast. 2015, 30, 827–840. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef] [Green Version]
- Janjić, Z.I. The Step-Mountain Coordinate: Physical Package. Mon. Weather Rev. 1990, 118, 1429–1443. [Google Scholar] [CrossRef]
- Janjić, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef] [Green Version]
- Janjić, Z.I. Nonsingular Implementation of the Mellor–Yamada Level 2.5 Scheme in the NCEP Meso Model. In NCEP Office Note; NCEP: Boulder, CO, USA, 2002; Volume 437, p. 61. [Google Scholar]
- Chen, F.; Dudhia, J. Coupling an advanced land surface–hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef] [Green Version]
- Iacono, M.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Space Phys. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Peckham, S.E.; Smirnova, T.G.; Benjamin, S.G.; Brown, J.M.; Kenyon, J.S. Implementation of a digital filter ini-tialization in the WRF Model and Its application in the Rapid Refresh. Mon. Weather Rev. 2016, 144, 99–106. [Google Scholar] [CrossRef]
- Dowell, D.C.; Zhang, F.; Wicker, L.J.; Snyder, C.; Crook, N.A. Wind and Temperature Retrievals in the 17 May 1981 Arcadia, Oklahoma, Supercell: Ensemble Kalman Filter Experiments. Mon. Weather Rev. 2004, 132, 1982–2005. [Google Scholar] [CrossRef]
- Aksoy, A.; Dowell, D.C.; Snyder, C. A multicase comparative assessment of the ensemble Kalman filter for as-similation of radar observations. Part I: Storm-scale analyses. Mon. Weather Rev. 2009, 137, 1805–1824. [Google Scholar] [CrossRef] [Green Version]
- Whitaker, J.S.; Hamill, T.M. Evaluating methods to account for system errors in ensemble data assimilation. Mon. Weather Rev. 2012, 140, 3078–3089. [Google Scholar] [CrossRef]
- Gasperoni, N.A.; Wang, X.; Wang, Y. A comparison of methods to sample model errors for convection-allowing ensemble forecasts in the setting of multiscale initial conditions produced by the GSI-based EnVar assimilation system. Mon. Weather Rev. 2020, 148, 1177–1203. [Google Scholar] [CrossRef]
- Davis, C.; Brown, B.; Bullock, R. Object-Based Verification of Precipitation Forecasts. Part I: Methodology and Application to Mesoscale Rain Areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef] [Green Version]
- Wolff, J.K.; Harrold, M.; Fowler, T.; Gotway, J.H.; Nance, L.; Brown, B.G. Beyond the basics: Evaluating model-based precipitation forecasts using traditional, spatial, and object-based methods. Weather Forecasting 2014, 29, 1451–1472. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X. Verification and Calibration of Neighborhood and Object-Based Probabilistic Precipitation Forecasts from a Multimodel Convection-Allowing Ensemble. Mon. Weather Rev. 2012, 140, 3054–3077. [Google Scholar] [CrossRef]
- Zhang, J. Coauthors Multi-Radar Multi-Sensor (MRMS) quantitative precipitation estimation: Initial operating capabilities. Bull. Amer. Meteor. Soc. 2016, 97, 621–638. [Google Scholar] [CrossRef]
- De Pondeca, M.S.F.V.; Manikin, G.S.; DiMego, G.; Benjamin, S.G.; Parrish, D.F.; Purser, R.J.; Wu, W.-S.; Horel, J.D.; Myrick, D.T.; Lin, Y.; et al. The Real-Time Mesoscale Analysis at NOAA’s National Centers for Environmental Prediction: Current Status and Development. Weather Forecast 2011, 26, 593–612. [Google Scholar] [CrossRef]
- Hamill, T.M. Hypothesis Tests for Evaluating Numerical Precipitation Forecasts. Weather Forecast 1999, 14, 155–167. [Google Scholar] [CrossRef]
- LaCorte, J. Improving Convective Forecasts in Weakly Forced Environments. Eastern Region Technical Attachment. Available online: https://www.weather.gov/media/erh/ta99-3.pdf (accessed on 30 September 2021).
- Bishop, C.H.; Hodyss, D. Flow adaptive moderation of spurious ensemble correlations and its use in ensem-ble-based data assimilation. Q. J. R. Meteorol. Soc. 2007, 133, 2029–2044. [Google Scholar] [CrossRef]
- Bishop, C.H.; Hodyss, D. Ensemble covariances adaptively localized with ECO-RAP. Part 2: A strategy for the atmosphere. Tellus A Dyn. Meteorol. Oceanogr. 2009, 61, 97–111. [Google Scholar] [CrossRef]
- Buehner, M.; Shlyaeva, A. Scale-dependent background-error covariance localisation. Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 28027. [Google Scholar] [CrossRef]
- Huang, B.; Wang, X.; Kleist, D.; Lei, T. A simultaneous multiscale data assimilation using scale-dependent local-ization in GSI-based hybrid 4DEnVar for NCEP FV3-based GFS. Mon. Weather Rev. 2021, 149, 479–501. [Google Scholar] [CrossRef]
- Wang, X.; Chipilski, H.G.; Bishop, C.H.; Satterfield, E.; Baker, N.; Whitaker, J.S. A multiscale local gain form en-semble transform Kalman filter (MLGETKF). Mon. Weather Rev. 2021, 3, 605–622. [Google Scholar] [CrossRef]
- Corfidi, S.F. Cold Pools and MCS Propagation: Forecasting the Motion of Downwind-Developing MCSs. Weather Forecast 2003, 18, 997–1017. [Google Scholar] [CrossRef]
- Dowell, D.C.; Wicker, L.J. Additive Noise for Storm-Scale Ensemble Data Assimilation. J. Atmospheric Ocean. Technol. 2009, 26, 911–927. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.J. A “vertically Lagrangian” finite-volume dynamical core for global models. Mon. Weather Rev. 2004, 132, 2293–2307. [Google Scholar] [CrossRef] [Green Version]
- Harris, L.M.; Lin, S.-J. A Two-Way Nested Global-Regional Dynamical Core on the Cubed-Sphere Grid. Mon. Weather Rev. 2013, 141, 283–306. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X. Development of Convective-Scale Static Background Error Covariance within GSI-Based Hybrid EnVar System for Direct Radar Reflectivity Data Assimilation. Mon. Weather Rev. 2021, 149, 2713–2736. [Google Scholar] [CrossRef]







| Exp. | Localization Scales | RTPS | |||
|---|---|---|---|---|---|
| Mesoscale | Storm-Scale | ||||
| H | V | H | V | ||
| REF1 | 300 | 0.55 | 12 | 0.55 | 0.95 |
| CONV_H500_V1.1 | 500 | 1.1 | 12 | 0.55 | 0.95 |
| RADAR_H15_V1.1 (REF2) | 300 | 0.55 | 15 | 1.1 | 0.95 |
| RTPS_065 | 300 | 0.55 | 15 | 1.1 | 0.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, X. Rapid Update with EnVar Direct Radar Reflectivity Data Assimilation for the NOAA Regional Convection-Allowing NMMB Model over the CONUS: System Description and Initial Experiment Results. Atmosphere 2021, 12, 1286. https://doi.org/10.3390/atmos12101286
Wang Y, Wang X. Rapid Update with EnVar Direct Radar Reflectivity Data Assimilation for the NOAA Regional Convection-Allowing NMMB Model over the CONUS: System Description and Initial Experiment Results. Atmosphere. 2021; 12(10):1286. https://doi.org/10.3390/atmos12101286
Chicago/Turabian StyleWang, Yongming, and Xuguang Wang. 2021. "Rapid Update with EnVar Direct Radar Reflectivity Data Assimilation for the NOAA Regional Convection-Allowing NMMB Model over the CONUS: System Description and Initial Experiment Results" Atmosphere 12, no. 10: 1286. https://doi.org/10.3390/atmos12101286
APA StyleWang, Y., & Wang, X. (2021). Rapid Update with EnVar Direct Radar Reflectivity Data Assimilation for the NOAA Regional Convection-Allowing NMMB Model over the CONUS: System Description and Initial Experiment Results. Atmosphere, 12(10), 1286. https://doi.org/10.3390/atmos12101286






