Abstract
Structure–activity (SAR) methods are presented for estimating rate constants at 298 K and approximate temperature dependences for the reactions of organic compounds with OH, NO3, and Cl radicals and O3, and O(3P) in the lower atmosphere. These are needed for detailed mechanisms for the atmospheric reactions of organic compounds. Base rate constants are assigned for the various types of H-abstraction and addition reactions, with correction factors for substituents around the reaction site and in some cases for rings and molecule structure or size. Rate constant estimates are made for hydrocarbons and a wide variety of oxygenates, organic nitrates, amines, and monosubstituted halogen compounds. Rate constants for most hydrocarbons and monofunctional compounds can be estimated to within ±30%, though predictions are not as good for multifunctional compounds, and predictions for ~15% of the rate constants are off by more than a factor of 2. Estimates are more uncertain in the case of NO3 and O3 reactions. The results serve to demonstrate the capabilities and limitations of empirical methods for predicting rate constants for the full variety of organic compounds that may be of interest. Areas where future work is needed are discussed.
1. Introduction
Many hundreds of types of volatile organic compounds (VOCs) are emitted into the atmosphere, from both anthropogenic and biogenic sources (e.g., [,,]). Most of these will react in the atmosphere with OH radicals and (if present) Cl atoms, and many also react with other atmospheric oxidants such as ozone (O3), NO3 radicals, and O(3P) atoms [,]. The atmospheric reaction mechanisms for most of these compounds are complex, larger molecules can react in many ways and form large numbers of oxidized organic products, and most of these will also react in the atmosphere and form additional oxidized organic products [,,]. Predictions of the lifetimes and fates of these compounds, and of their impacts on formation of secondary pollutants such as ozone, secondary organic aerosols, and toxic organic products, require a knowledge of the rate constants for the reactions of emitted organics or their products with atmospheric oxidants. Because of this, rate constants have been measured for many VOCs and atmospheric oxidants, and a number of compilations of these rate constants exist relevant to atmospheric modeling [,,,,,,]. However, the available data do not include rate constants for many of the emitted compounds and for most of the oxidized products that are known or predicted to be formed. In addition, most compounds can react in more than one way, forming different intermediates and ultimately different products, and relatively few have data concerning rate constants or branching ratios for the individual processes. Therefore, it is necessary to estimate rate constants for all the possible reactions of a wide variety of compounds in order to assess atmospheric impacts of VOCs and develop comprehensive mechanisms to represent their reactions in models.
Various structure–reactivity (SAR) methods have been developed to estimate rate constants for the reactions of organics with atmospheric oxidants [], though all are limited in scope in terms of the types of compound or oxidant studied, some are not designed to predict rate constants at different sites of the molecule, and none incorporate all the available kinetic data that have been recently been compiled []. Despite their limitations, various SARs have been used in the development of the current chemically detailed atmospheric reaction mechanisms, including the near-explicit Master Chemical Mechanism (MCM) [,,,,] and the detailed SAPRC mechanisms [,,,,], and also in the GECKO-A [,] and SAPRC [,,] automated atmospheric chemical mechanism generation systems. Because of the complexity of the atmospheric chemistry of organics, mechanism generation systems provide the most practical way to develop and update detailed mechanisms [], and serves as the basis for the continuing development of the SAPRC mechanisms [,,,] and for the ongoing update of the MCM and GECKO-A systems for the MAGNIFY project [,]. In the case of GECKO-A, the current version incorporates the recently published SARs of Jenkin et al. [,] for estimating rate constants for OH reactions, the SARs of Kerdouci et al. [] for NO3 reactions, and those of Jenkin et al. [] for O3 reactions.
In this paper, we describe the independently-developed SARs for estimating rate constants for initial reactions of organic compounds and their atmospheric oxidation products that are incorporated in the current SAPRC mechanism generation system [,,], discuss their scope, predictive capability, and limitations, and compare them with the SARs recently developed for GECKO-A. The scope includes reactions of many organics with OH and NO3 radicals, O3, and Cl and (for a more limited number of compounds) O(3P) atoms. The objective is to utilize existing rate constant data to estimate rate constants for the full variety of organic compounds that might be emitted or formed in the lower atmosphere whose rate constants have not been measured. To be useful for mechanism development, branching ratios for all the non-negligible modes of reaction also need to be estimated. Therefore, the quantities estimated in this work are rate constants for reactions at various positions of the molecule, which are summed up to obtain the total rate constant for the compound that can be compared with experimental data. The approach is entirely empirical, utilizing methods and parameters to predict the available data as closely as possible to make predictions for as wide a variety of compounds as possible. Note that derivation and evaluation of these estimates against theoretically calculated rate constants or using product yield data are beyond the scope of the present study, though this would be useful for future work.
2. Scope and Rate Constant Database
The compounds covered by the estimation methods discussed by this work include the major classes of compounds that are emitted or formed in the atmosphere, and other compounds with similar functional groups. These include alkanes, alkenes, alkynes, alkylbenzenes, naphthalenes, oxygenates with –OH, –O–, and –CO– groups (and combinations thereof), oxidized nitrogen compounds with –NO2, –ONO2, and –ONO groups, amines, amides, and monohalogenated halocarbons (see Table 1). Compounds with atoms other than H, C, O, or N and polycyclic aromatics other than naphthalenes are beyond the scope of this work. The methods employed here did not perform satisfactorily for compounds with more than one halogen and for halogenated oxygenates, where long-range interactions, which are not considered here, appear to be important. Therefore, these compounds are not covered in this work. In addition, the limitations of our rate constant database for O(3P) reactions limit the scope of our estimates for these reactions. However, the methods employed should be applicable for most of the types of compounds that are emitted or formed in the atmosphere.

Table 1.
List of groups contained in organic reactants that are used as a basis of the structure–reactivity estimates in this work.
The estimation methods developed in this work focus on the estimation of rate constants at approximately 298 K, though approximate temperature dependences around this temperature are also estimated. Separate estimates are made for each reaction pathway that may be nonnegligible under atmospheric conditions, but estimates are not made for pathways expected to be too slow to be important at atmospheric temperatures and pressures. Therefore, these estimates are not applicable to combustion or extremely low temperature conditions. Because of limited data, extending the temperature range would require greatly reducing the types of compounds for which estimates could be made, thus reducing the utility of this work for detailed atmospheric chemical mechanism development. In addition, the focus of the estimates is on net rate constants for loss of the reactants at atmospheric pressures and temperatures, which are not always the same as rate constants for elementary reactions if these reactions can be reversed. All estimates are for atmospheric pressure only. However, except for well-studied reactions of smaller molecules where estimates are not really needed, most rate constants estimated in this work are believed to be at or near the high pressure limit.
The derivation of rate constant estimates requires as large and comprehensive a database as possible to derive and evaluate the estimation methods. Recently, McGillen et al. [] compiled a comprehensive database of measured and evaluated rate constants for gas-phase reactions of a wide variety of organic compounds with OH, Cl, NO3, and O3 under atmospheric conditions, and that was utilized in this work. Rate constants for O(3P) reactions were not included in the McGillen et al. [] database, so those used previously when developing the estimates for the SAPRC-07 mechanism [,] were used in this work with a few additions. The numbers of compounds in the database used for estimating the various types of reaction are summarized on Table 2. The database employed is discussed further in Section S1.1 of the Supplementary Information (SI), which also contains a graphic showing the numbers of different types of compounds (Figure S1). Most compounds were used to derive the estimation parameters, but some were used for evaluation only for reasons discussed below.

Table 2.
Summary of numbers of rate constants and estimation parameters used in this work.
Table 2.
Summary of numbers of rate constants and estimation parameters used in this work.
| Reaction With | OH | Cl | NO3 | O3 | O(3P) |
|---|---|---|---|---|---|
| Rate constants in database used | 853 | 421 | 331 | 266 | 40 |
| Rate constants used for parameter derivation | 507 | 276 | 207 | 172 | 40 |
| Rate constants used for evaluation only | 346 | 145 | 124 | 94 | 0 |
| Total parameters used for estimates (Table 3) | 324 | 319 | 312 | 154 | 72 |
| Parameters adjusted to fit data | 95 | 72 | 58 | 56 | 16 |
| Fraction of parameters estimated | 71% | 77% | 81% | 64% | 78% |
| Fitting rate constants per adjusted parameter | 4.3 | 3.8 | 3.6 | 3.1 | 2.5 |
| Estimates from previous work (Section 4.3) | 378 | 152 | 185 |

Table 3.
Summary of parameters used for estimation of rate constants in this work.
Table 3.
Summary of parameters used for estimation of rate constants in this work.
| Parameter | Depends on | Description | Used in Eq. | Tables of Values | |
|---|---|---|---|---|---|
| Name | Count [a] | ||||
| H abstraction from group G1 by OH, Cl, or NO3 | |||||
| kHbase | 9–17 | G1 | Base rate constant for H abstraction from G1 | 1 | S11 |
| FHnbrs | 178–183 | G1 Substs | Correction for a each substituent on G1 | 1–3 | S12–S14 |
| FHstruct | 10–20 | Ring | Ring strain correction if G1 is in a ring | 1 | S15 |
| Addition of OH, Cl, or NO3 to G1=G2, G1≡G2, or G1=C=G2 | |||||
| kAbase | 31–32 | G1, G2 | Base rate constant for addition to G1 | 4, 5 | S16 |
| FA1nbr | 36–43 | G1 Substs | Correction for a each substituent on G1 | 4, 5 | S17 |
| FA2nbr | 36–43 | G2 Substs | Correction for a each substituent on G2 | 4, 5 | S17 |
| FAstruct | 0–1 | nC [b] | Correction based on molecule size | 4, 6 | see text |
| Addition of O3 or O(3P) to G1=G2, G1≡G2, G1=G2-G3=G4, or G1=G2-X [c] | |||||
| kA′ base | 69–89 | Gs, X | Addition to the double-bond system | 7 | S18 |
| FA′ nbr | 0–37 | Substs [d] | Corrections for substituents around the bond | 7 | S19 |
| FA′ struct | 0–29 | Ring [d] | Corrections if the Gs are in a ring | 7 | S19 |
| FA′ struct | 0–1 | Struct [d] | Steric correction | 7, 8 | see text |
| Additions of OH, Cl, or NO3 to aromatic rings at aromatic group G | |||||
| kArobase | 3–6 | G | Base rate constant for addition to G | 9 | S16, S18 |
| FAloc | 36–80 | Substs on ring | Correction factors for groups on the aromatic ring. Separate factors for ortho, meta, para, and ipso | 9 | S20 |
| Additions to amino or iodo group G | |||||
| kA″ base | 3–6 | G | Base rate constant for addition to G | 10 | S16 |
[a] Minimum and maximum number of parameters for the applicable types of reactions. [b] This correction is only used for NO3 reactions. nC is the number of carbons in the molecule. [c] X is a non-alkyl substituent on a double-bond system for which a separate base rate constant is derived. [d] These corrections used only for O3 reactions. The steric correction is based on the number of groups in the β position relative to the double-bond system.
3. Methods
The general approach employed is to separately derive estimation methods for the rate constant at temperatures of approximately 298 K using the relatively large database of measured rate constants around this temperature, and to estimate temperature dependences separately based on the more limited database of temperature dependence measurements in the lower atmospheric temperature range. The 298 K rate constant estimates are made using group-additivity or empirically-based methods similar to those employed by Atkinson and co-workers [,], and applied more recently for developing SARs proposed for updating MCM [,,,,,]. These are based on estimating base rate constants for reactions at various positions in the molecule (determined in some cases by substituents present), multiplied by correction factors applied for certain substituents and also, in some cases, by correction factors based on the structure of the molecule. This approach has the advantage that it gives branching ratios for initial reactions at different positions of the molecule, which are needed for mechanism development, as well as the total rate constants. These base rate constants or correction factors are either adjusted to minimize differences between estimated and measured rate constants, or are estimated from other parameters or based on other considerations when sufficient data are not available, or when independent adjustment is not judged to be appropriate.
Note that the approach used in this work considers only the nature of the reaction site and the substituents or groups of substituents adjacent to it. Other than having different base rate constants for additions to 1,2-disubstitutend double bonds with cis or trans configurations, it does not consider stereo-specificity or steric effects where rates of reactions are may be affected by the geometry of the molecule. While this limitation is not expected to significant for most compounds covered by the scope of this work, it can cause poor predictions in some cases, as indicated in Section 4.2.
The types of individual reactions for which estimates are made include H-abstraction reactions, additions to non-aromatic double or triple bonds, additions to aromatic rings, additions to the N-atom in amines and amides, and additions to iodide atoms. These are believed to be the main modes of reactions for these compounds at approximately 298 K, though the possibility for other types of reactions cannot be ruled out. In the case of additions to double bonds, the method used depended on the oxidant involved. In the case of additions by OH, NO3, and Cl, separate base rate constants are assigned for additions to each side of the double or triple bond(s), which has the advantage of requiring the least number of parameters to cover all cases of interest. However, this was found to be unsatisfactory for predicting O3 rate constants, where the initial reaction is believed to be cycloaddition rather than addition to either side of the bond. Cycloaddition is also expected to be the mechanism for the reactions of O(3P) with double bonds. Therefore, for O3 and O(3P) predictions, the base rate constants are assigned for each possible conjugated multiple-bond structure. This is more appropriate for cycloaddition reactions, though it requires more parameters. Note that the limited database of O(3P) rate constants can be fit about as well by either method, but this would not be expected if the database were more comprehensive.
For the purpose of these structure–reactivity estimates, molecules are broken down into “groups” that are shown in Table 1. Most of the parameters used in estimates refer to these groups, either singly or in combination, being either base rate constants for reactions at these groups, or corrections to the base rate constants due to the presence of these groups next to the reaction site. Other parameters refer to corrections due to reactions at rings or in some cases corrections for the size or the extent of branching in the molecule. The various types of parameters used are summarized on Table 3 and the total numbers of parameters required for each type of reaction are included in Table 2. A large number of parameters are required because of the wide variety of structures of the molecules and the different ways they can react, as discussed for the various cases in the sections below.
Clearly, it is not possible to derive all these parameters by solely by optimizations (especially since there are more parameters than experimental rate constants in some cases), so many need to be estimated. In most cases, the estimates were based on assuming that sets of related parameters have the same values, but in some cases estimates were made using other methods, as discussed below and in the SI. A balance must be struck between having too few or too many fitting parameters. Using the absolute minimum number of parameters may be more satisfying, but may not give the best predictions that could be supported by the data. Using the maximum number of adjustable parameters that give the absolute best fits to the data might magnify the effects of measurement uncertainties and variabilities that could cause chemically unreasonable parameters and resulting in inappropriate extrapolations. There also may not be unique solutions to the optimization procedures, resulting in different sets of “best fit” parameter values giving significantly different predictions for other compounds. While using statistical or other formal means to derive the optimum number of parameters for this purpose is beyond the scope of this work, an attempt was made to strike this balance in this work based on expert or subjective opinions, as well as results of previous studies.
Although estimates or assumed relationships between parameters significantly reduce the numbers of parameters that have to be adjusted to fit the data, there are still large numbers of parameters to derive for each type of reaction. These were derived in a stepwise manner, with those involved in predicting rate constants using the smallest number of parameters being derived first (e.g., H abstractions from acyclic alkanes), followed by those for predictions involving the least number of additional parameters (e.g., additions to double bonds in alkenes, using the alkane-derived parameters for H abstractions from alkyl substituents, or H abstractions from acyclic compounds or additions to double bonds with single non-alkane substituents), and finally those involving additional considerations (e.g., cyclic compounds). For this purpose, rate constants in the database are grouped by the types of compounds used in the sequential optimizations. Note that not all available rate constants were used to derive the parameters because some involve reactions of compounds with multiple functional groups, for which the applicability of the estimation methods used are much more uncertain. Therefore, rate constants for such compounds were not used to derive the parameters, but instead were used to test the applicability of these estimates to these types of compounds. These are indicated on Table 2 and elsewhere as “rate constants used for evaluation only”.
Although the preferred approach from a statistical and uncertainty analysis perspective would be to use a randomly-determined subset of the data for parameter derivation and the rest for evaluation and error analysis, this could not be performed in this work because of the large number of parameters relative to the size of our evaluation dataset. Therefore, only multifunctional and other compounds where the estimates are the most uncertain, and a small number of whose rate constants appeared to be inconsistent with related compounds, were excluded from the dataset. These cases are discussed in Section S1.2 of the SI.
Additional information about the optimization procedure is given in Section S1.2 of the SI. The estimation procedures discussed in this work were implemented and tested using the SAPRC mechanism generation system (MechGen) [,], with an Excel spreadsheet employed to organize and optimize the parameters and organize and analyze the results. Tables S1–S5 in the SI list the parameters that were optimized, giving the order in which they were derived and the groups of compounds used for each. The specific compounds used in the optimizations are included in the listings of experimental and estimated rate constants in the tables in Section S3 of the SI.
The following sections discuss the specific methods used to estimate the rate constants and temperature dependences for the various types of reactions. Examples of applications of these methods are given in Section S4 of the SI.
3.1. H-Abstraction Reactions
OH, NO3, and Cl radicals can react with organic compounds by abstracting H atoms, forming the corresponding organic radical and H2O, HNO3, or HCl, respectively. H-atom abstraction reactions involving O3 or O(3P) are assumed not to be important at atmospheric temperatures, so are not estimated in this work. These abstraction reactions can occur at any group that has H atoms, with the rate constant depending on type of group and also its neighboring groups and sometimes on the structure of the molecule around the reaction site. In most cases, the abstraction rate constants are estimated using
where FHnbrs(nbrs, group) is a function of the set of FHnbr(nbr,group) values as discussed below. Here, “H” is used to indicate that this is an H-abstraction process, and kH is the H-abstraction rate constant at 298 K; “group” is the group in the molecule from which H is abstracted, which in some cases can depend on the neighboring groups; “site” refers to characteristics of the molecule around the group where the reaction occurs, such as the group being in a ring; “nbrs” refers to the neighboring groups or α substituents (each designated “nbr”), which in some cases can depend on their neighbors (β substituents). The adjustable or estimated parameters are: kHbase(group), the rate constant for H abstraction from the group if all the neighbors were methyl groups; FHstruct(site), a correction factor used for reaction at certain sites in the molecule, if applicable; and FHnbrs(nbr, group) is an overall substituent correction factor derived for the set of neighboring groups, which may also depend on the group where the reaction occurs.
kH(group, site, nbrs) = kHbase(group) × FHstruct(site) × FHnbrs(nbrs, group),
Neighboring group correction factors are derived for the various possible substituent groups, which in some cases can also depend on the groups bonded to it as indicated on Tables S12–S14 in the SI. If there is no more than one substituent group containing atoms other than C or H (non-alkyl substituent), then the overall substituent correction factor is given by the product of correction factors assigned for the individual substituent groups, i.e.,
FHnbrs(nbrs, group) = ∏nbrs FHnbr(nbr, group).
However, this may not be the best approach if there is more than one non-alkyl substituent, especially if the corrections are large. Although there are insufficient data to derive overall correction factors for all possible combinations of non-alkyl substituents, there are sufficient data to derive correction factors for some combinations. Table S7 and Figure S2 of the SI compares these with various functions of the individual single group correction factors derived for monofunctional compounds. Based on these results, as discussed in Section S1.3, for estimation purposes, we use the averages for the factors for the individual groups when their product is greater than 1, or the product otherwise, i.e.,
where HCnbrs refers to the set of hydrocarbon substituents, if any, and nHCnbrs refers to the set of other substituents. This is used in all cases with more than one α substituent on an alkyl group, even if a best fit pair factor could be derived.
FHnbrs(nbrs, group) = ∏HCnbrs FHnbr(nbr, group) × ∏nHCnbrs FHnbr(nbr,group)
if ∏nbrs FHnbr(nbr, group) ≤ 1, or
FHnbrs(nbrs, group) = ∏HCnbrs FHnbr(nbr, group) × AveragenHCnbrs [ FHnbr(nbr,group) ]
if ∏nbrs FHnbr(nbr, group) > 1
if ∏nbrs FHnbr(nbr, group) ≤ 1, or
FHnbrs(nbrs, group) = ∏HCnbrs FHnbr(nbr, group) × AveragenHCnbrs [ FHnbr(nbr,group) ]
if ∏nbrs FHnbr(nbr, group) > 1
Note that most previously developed SARs for H abstractions assume that Fnbr depends only on the substituent and not the group where the abstraction occurs, but in some cases much better fits are obtained if this is not assumed. For example, in general, it is necessary to assume different correction factors for abstractions from HC(O)– compared to abstractions from alkyl (–CH3, –CH2– or –CH<) groups. However, in most (but not all) cases, the same factors are used for abstractions from the three types of alkyl groups, with the exceptions being cases where the data are sufficient to unambiguously derive separate values depending on the group, and also where the values so derived are significantly different.
In some cases, better predictions are obtained if base rate constants are defined for certain group and neighbor combinations, with the substituent effect incorporated in the base rate constant rather than using a correction factor. This is used in cases where very high values of Fnbr are required to fit the data, suggesting that the substituent may significantly affect how the reaction proceeds, and which would could give absurd estimates for some multifunctional compounds. This was found to be the case for –O– substituents for abstractions from HC(O)– groups and –O–, –C(O)–, and aromatic substituents on OH groups. In addition, large corrections for α and β –OH and –O– neighbors for abstractions from alkyl groups by NO3 radicals are needed, and better results are obtained if these neighbors are incorporated in the base rate constant. This was not needed for abstractions by OH or Cl, where use of Fsub for α –OH or –O– substituents gave satisfactory results.
If the group where the abstraction is occurring is on a ring, then a ring strain correction factor is also applied as Fstruct, which depends on the size of the ring. No other types of structure-dependent corrections were found to significantly improve estimates for abstractions. However, separate sets of ring strain correction factors were found to be necessary if the ring contains a –CO–, CO–O–, or –O– groups for OH abstractions. In the case of Cl abstractions, there are sufficient data to derive only one set of ring strain correction factors, and in the case of NO3, there are insufficient data to derive any strain factors, and these are estimated based on those derived for OH. There are insufficient data to derive a comprehensive set of ring strain correction factors for multiple ring structures, so if the group where the reaction occurs is in more than one ring, the factor derived for the smallest ring is used.
Although almost 200 parameters were needed to estimate abstraction rate constants (Table 2), only approximately 25% (~10% in the case of NO3) were treated as independent adjusted parameters that were optimized to fit the data. The various assumptions and estimates that were used are indicated in the tables in the SI listing the base rate constants (Table S11) and correction factors (Tables S12–S14). Those that yielded the greatest reduction in parameters were as follows: (1) correction factors for reactions at –CH3, –CH2– and –CH< groups are the same; (2) no correction is used (factor = 1) when the data are insufficient and an estimate cannot be justified (resulting in a highly uncertain estimate); and (3) β substituents have no effect unless the data unambiguously indicate otherwise.
In addition, because of limitations of the available kinetic data relative to H atom abstractions by NO3 and lower sensitivities of total NO3 rate constants to abstraction estimates, it was necessary to estimate some for abstractions by NO3 using correlations with those derived for abstractions by OH or Cl. These estimates are discussed in Section S1.4 of the SI.
3.2. Additions of Radicals to Non-Aromatic Double and Triple Bonds
Atmospheric radicals such as OH, NO3 and Cl can react with some organic compounds by adding to double or triple bonds, forming an adduct on one side of the bond and a carbon-centered radical group on the other. For additions of these radicals to compounds with separated double or triple bonds, the estimates are made based on assigning group rate constants for each type of group about the bond where the addition occurs (which also depends on the type of group on the other side in most cases), plus corrections for substituents or structural characteristics. If G1 and G2 are groups on each side of the bond, the rate constant for addition to G1 is estimated by
where “A” indicates that this is an addition process, kAbase(G1, G2) is the base rate constant for addition to G1 when G2 is on the other side of the bond, nbrs1 and nbrs2 refers to any non-alkyl group bonded to G1 or G2, respectively, FAstruct(site) are structural corrections, where applicable, and FA1nbr(nbr) and FA2nbr(nbr) are correction factors for non-alkyl substituents on G1 or G2. FA1nbr and FA2nbr can in general be different for a given nbr (though they are assumed to be the same if data are inadequate to determine them separately), but are assumed to be independent of G1 and G2. The sum of kA(G1, G2) and kA(G2, G1) is then used to derive the total rate constant for addition to the bond, with their ratios determining the estimated branching ratios for additions to the different sides.
kA(G1, G2, site, nbrs) = kAbase(G1, G2) × FAstruct(site) × ∏nbrs1 FA1nbr(nbr) × ∏nbrs2 FA2nbr(nbr),
Equation (4) is also used to estimate rate constants for reactions at conjugated double bonds. The main difference is that groups that are bonded to a second group with a double bond is treated as a different type of group when defining G1 and G2 when determining base rate constants. For example, for additions to the structure Ga=Gb–Gc=Gd, the base rate constant for addition to Ga is derived using Equation (4) with G1 based on Ga if it were in an isolated bond, and G2 based on Gb in the middle of a conjugated bond system, whose base rate constants generally are different than that based on Gb in an isolated bond. Because of lack of data, estimates for conjugated triple bonds are made in the same way as for isolated bonds.
In the case of cumulated double bonds, defined as G1=C=G2, all the addition is represented as occurring at the central position, because that results in allylic stabilized radicals, while addition to the ends form much less favorable vinylic radicals. The addition rate constant is then estimated using
where “CA” refers to addition to a cumulated bond system, with the base rate constant, kCAbase, depending on the groups at ends of cumulated bonds. No structural corrections are used because of insufficient data to derive them (no compounds with cumulated double bonds in a ring are in the database, and they are unlikely to be important in any case). Because of insufficient data, the FA values are the same as derived for isolated double bonds. The only addition is that that Fnbr factors for =CH or =C< substituents are required for estimates for compounds with adjacent conjugated and cumulated systems, though no corrections are made (FA = 1) for these cases because of insufficient data.
kA(G1, G2, nbrs) = kCAbase(G1, G2) × ∏nbrs1 FA1nbr(nbr) × ∏nbrs2 FA2nbr(nbr)
No structural corrections were used (i.e., FAstruct = 1) when estimating OH or Cl additions because there were found not to be clearly indicated by the available data. However, Kedouchi et al. [] found it necessary to include various ring and molecule size corrections in their estimates for NO3 additions. We found that the available data were insufficient to clearly indicate consistent or reasonable ring corrections, so these were not used in this work. On the other hand, significant improvement to predictions of NO3 addition rate constants were obtained if the addition rate constant was assumed to increase with the size of the molecule, with
where nC is the number of carbons in the molecule and FSNO3 is a parameter adjusted to fit the data, and yields FAstruct = 0.79, 1, 1.19, 1.37, 1.57, and 1.67 for 3 through 8 carbons, respectively. The maximum number of carbons for this correction was set at 12 (FAstruct = 2.11), since there has to be an upper limit and using this for larger carbon numbers did not improve the predictions. Equation (6) was used regardless of the type of double-bond group, since the data were insufficient to clearly derive separate FSNO3 values for different types of groups. Note that structural corrections were also found to be necessary for O3 additions, as discussed in the next section.
FAstruct(nC) = {1 − exp(−min(nC, 12) × FSNO3)/{1 − exp(−4 × FSNO3)}
FSNO3 = 0.101,
FSNO3 = 0.101,
Since the total rate constants for unsubstituted alkenes and alkynes depend only on the total of the two group rate constants but not the ratio, the ratios of group rate constants, or branching ratios for reactions at various types of multiple bonds, cannot be unambiguously derived from a database containing only total rate constants. These branching ratios were estimated as discussed in Section S1.5 of the SI. Briefly, the ratios for OH reactions were derived by assuming the group rate constants depended on the radical formed by the addition rather than the number of hydrogens on the group where the addition occurred, and on the yields of furan products from isoprene and 2,3-butadiene []. 100% addition to the most favorable position was assumed for NO3 additions and equal addition to both positions was assumed for Cl additions, based on considerations of expected selectivity. However, these branching ratio estimates do not affect predictions of total rate constants that are discussed in this work.
The base rate constants and correction factors for these additions, and notes indicating how they were derived, are given in Tables S16 and S17 in the SI.
3.3. Additions of O3 or O(3P) to Non-Aromatic Double and Triple Bonds
Ozone and O(3P) also add to double or triple bonds, with the rate-determining step assumed to be the formation of cyclic intermediates that subsequently react. Although Equation (4), above, could be used to estimate these addition reactions as well, the method developed by Jenkin et al. [] is more appropriate for cycloadditions, and was found to perform significantly better for O3. An important difference between the two methods is that base rate constants are assigned separately for each different type of separated and conjugated double-bond system, with the presence of a non-alkyl α substituent defining additional double-bond systems where separate base rate constants are derived.
This method is not used for the radical addition estimates discussed in the previous section because it requires more parameters to make addition rate constant estimates, and has the additional disadvantage that it requires separate assignments of fractions of reactions at different positions in order to estimate mechanisms, which cannot be derived using rate constant data alone. In addition, it does not provide a means to estimate rate constants for more complex double-bond structures for which rate constant data are inadequate (e.g., more than two conjugated bonds). This is why we use Equation (4) for the radical addition reactions discussed above, since it performs almost as well in these cases. Both methods perform equally well in fitting the limited data for the O(3P) rate constants, but the same method is used as used for O(3P) as used for O3 because their mechanisms are expected to be more similar to each other than to additions by radicals.
The total rate constant for addition of O3 and O(3P) to any position in the bond, kA′(bond), is estimated using
where “bond” refers to each distinct set of groups around the multiple-bond structure, with separate base rate constants (kA′ base) for groups with non-alkyl α substituents if needed, and substituent corrections (FA′ nbr) being the same regardless of the position of the non-alkyl group about the bond. Note that substituent corrections are not used if the presence of the substituent is taken into account in defining kA′ base, so they are only needed if no base rate constant is assigned for this type of α substituent, or for compounds with more than one non-alkyl α substituent around the bond.
kA′(bond, site, nbrs) = kA′ base(bond) × FA′ struct(site) × ∏nbrs FA′ nbr(nbr),
Although the only structural correction found to be necessary in estimating radical addition rate constants concerned a size correction for NO3 additions, Jenkin et al. [] also used ring corrections and corrections for branched structures, as well as size corrections in some cases for estimations of O3 rate constants. We found that the available data did not support using as many structural corrections as used by Jenkin et al. [], but some were still necessary. These included several ring corrections, with different factors derived for separated and conjugated bonds, as discussed in Section S1.6 of the SI, and included in Table S19. Note, however, the available data are not particularly well fit using correction factors that depend only on the ring sizes (see Figure S6), so estimates for rate constants for additions of O3 to double bonds in cyclic compounds are quite uncertain.
Jenkin et al. [] also found that use of steric corrections could improve predictions for compounds with branched structures. This is implemented in this work using a correction based on the numbers of β substituents around the double bond, i.e.,
where nβ is the number of β substituents other than H (either alkyl or otherwise), and FβO3 is a parameter adjusted to fit the data. This parameter value gave correction factors of 0.732 and 0.464 for two and 3 β substituents, respectively (3 being the maximum nβ in the current O3 rate constant database). The available data were insufficient to derive structural corrections for O(3P) reactions, so no such corrections were used for O(3P).
FA′ struct(nβ) = 1 − (FβO3 × {(min [4, max(1, nβ)] − 1})
FβO3 = 0.268
FβO3 = 0.268
The base rate constants for O3 and O(3P) additions and notes documenting their derivations are given in Table S18 in the SI, and Table S19 gives the substituent and structure correction factors derived for O3 additions. There were insufficient data to derive base rate constants for all the conjugated and α-substituted double-bond structures needed for comprehensive estimates, so some had to be estimated based on empirical relationships derived between base rate constants and numbers of substituents around the bonds, as discussed in Section S1.7 of the SI. Because of insufficient data, no correction factors are used for O(3P) additions, so O(3P) rate constant estimates for compounds with non-alkyl substituents, or where structural corrections might be appropriate, are more uncertain.
The equations and parameters discussed above provide a means for estimating total rate constants for reactions at a double-bond structure, but, unlike the methods used to estimate radical additions discussed in Section 3.2, do not provide a means of estimating branching ratios for the purposes of mechanism estimation if more than one reaction is possible. The assumptions made in this regard when implementing these estimates in the SAPRC mechanism generation system [,] are discussed in Section S1.8 of the SI. However, these considerations do not affect predictions of total rate constants that are discussed in this work.
3.4. Additions to Aromatic Rings
Atmospheric radicals can also add to aromatic rings, with this being a major process in the case of reactions of aromatics with OH radicals under atmospheric conditions, and a non-negligible process for the reactions of Cl with some aromatics. NO3 radicals can also add to aromatic rings, though these reactions are relatively slow compared to other loss processes, except for phenols. Reasonably good fits to the rate constant data for aromatic hydrocarbons can be obtained if the rate constant for addition to each aromatic group is estimated using
where kArobase is the base rate constant for addition to an aromatic –aCH= or –sC= group, aSub being the set of substituents on the ring, with aSubi is the substituent at the i’th position about the ring relative to where the addition occurs (1 being ipso), and FAipso, etc., being the aromatic ring substituent factor for a substituent at this position, where FAany(H) (i.e., no substituent) set at 1.
kAro(aGrp, aSubs) = kArobase(aGrp) × FAipso(aSub1) × FAortho(aSub2) × FAmeta(aSub3) × FApara(aSub4) × FAmeta(aSub5) × FAortho(aSub6)
Aromatic hydrocarbons can contain up to three types of aromatic groups, two occurring in single rings with (–aC<) and without (–aCH–) substituents, and the third being in two rings with polycyclic aromatic hydrocarbon (PAH) structures (–pC<, or PAH groups). Note that “substituent” in this case excludes the neighboring aromatic groups next to where the addition occurs. Since aromatic groups can have more than one ortho, meta, and (for PAHs) para substituents, multiple correction factors can be applied for substituent groups. The total rate constant for the addition to the aromatic ring is then the sum of the group rate constants for addition at each position, each multiplied by correction factors for substituents at various positions on the aromatic rings, with the yield of any particular OH-aromatic adduct being the ratio of the rate constant for OH addition at that position, divided by the total rate constant.
It is important to recognize that the rate constants derived using Equation (9) reflect the net effect of OH addition to form adducts that react further, so should not be used in models that include back decomposition of the adduct back to OH and the aromatic compound. That is because the base rate constants and correction factors were derived based on observed total OH + aromatic rate constants, not rate constants for elementary reversible reactions.
Use of Equation (9) does not give satisfactory results in the case of reactions of NO3 with phenols, whose rate constants are many orders of magnitude greater than that for reactions of NO3 with other aromatics. This can be attributed to the possibility that in most cases aromatic-NO3 adducts rapidly back-decompose before they can react further, yielding a low rate constant for the overall reaction, while phenolic aromatic-NO3 adducts in either the ipso or ortho position might undergo a rapid H shift from the -OH to the -ONO2 group, yielding HNO3 and a phenoxy radical []. Assuming this is the case, we use the approach of assigning separate (much higher) base rate constants for aromatic groups with -OH substituent in the ipso or ortho position, and set FAipso(OH) = 1. This results in fits to the data for the various phenolic compounds using Equation (9), though it is also necessary to use relatively high values of FAortho(OH) = 23 and FApara(OH) = 10 (Table S20) to fit the data for catechols.
The base rate constants for the additions of OH, NO3, and Cl radicals to groups in aromatic rings and notes documenting their derivations are included in Table S16 in the SI, and the correction factors for substituents on the aromatic ring, and their documentation, are given in Table S20. The available data are insufficient to derive separate aromatic correction factors for each of the four possible positions around the ring for all the possible substituents of interest, so estimates need to be made as indicated in the footnotes to Table S20. For example, if a substituent is found to deactivate addition (have FA values < 1) or have a relatively small effect, it was assumed that FAortho = FAmeta = FApara = FAipso, so only one parameter had to be adjusted. If the substituent was found to have a positive effect, as was the case for alkyl substituents, the factors for the positions found to be most important for alkyl substituents were adjusted, and the others were held at 1. There were sufficient data to adjust parameters for each position for alkyl substitution, but the optimized values were close to 1 except for ortho positions for OH and Cl or ortho or para positions for NO3, so the other values used in those cases were set at 1 (see Table S20).
3.5. Other Addition Reactions
Certain addition reactions are assumed to consist of addition to an atom in the group, forming an intermediate centered on that group, at a rate constant that is independent of substituents or the structure of the molecule. Their rate constants are estimated using only assigned base rate constants, without corrections.
where G1 is a group where such an addition can occur. The cases where this is used are discussed below.
kAddgroup (G1) = kA″ base(G1),
3.5.1. Reactions of Radicals with Amines
Although atmospheric radicals such as OH can react with amines with abstraction reactions, the predictions of the methods discussed in Section 3.1 are not consistent with the available data, as discussed in Section S1.9 of the SI. Instead, the available data are much better fit by treating these as addition reactions, which is kinetically equivalent to the initial reaction being the formation of a strong complex, as discussed in the review by Nielsen et al. []. This is implemented by assigning base rate constants for additions to –NH2, –NH–, –N<, NH2(CO)–, –NH(CO)–, and –N(CO)< groups. (Separate base rate constants were used for additions to amides because using a substituent correction factor for –CO– did not give satisfactory estimates). No substituent corrections were used, so the estimated rate constants were equal to the base rate constants. There were sufficient data to estimate rate constants for Cl and OH additions but in the case of NO3, data are available only for reactions N-alkyl carbamates and N,N-dimethyl amides, i.e., compounds with –NH(CO)O– groups, and –N(CO)< groups. These data, combined with the base rate constant data derived for the OH and Cl additions, were used to estimate base rate constants for NO3 additions to other amine or amide groups as discussed in Section S1.4 in the SI. The base rate constants derived for the radical + amine addition reactions, and their associated documentation, are included in Table S16.
3.5.2. Reactions of O3 and O(3P) with Amines
Rate constants have also been measured for reactions of O3 and O(3P) with amines, and these are also estimated as addition reactions using base rate constants with no substituent corrections. These reactions are discussed further in Section S1.9 of the SI. These base rate constants and documentation notes are included in Table S18 in the SI. Note that there were insufficient data to include estimates for amides.
3.5.3. Reactions of NO3 with Iodides
Our database includes rate constants for reactions of radicals with methyl and ethyl iodides, and in most cases these can be estimated using the H-abstraction estimation procedures of Section 3.1, with the correction factors indicating effects similar to other halogen substituents. However, their rate constants for reactions with NO3 are orders of magnitude higher than for similar unsubstituted and are poorly predicted using Equation (1). The data are much more consistent with assuming that the reactions of NO3 with iodides is initiated by adding or associating with the I group, then reacting further. Theoretical studies of reactions of iodides with NO3 radicals are discussed by Bai et al. []. Therefore, for estimation purposes we treat reactions of NO3 with iodides as additions, with the base rate constant that fits the data included in Table S16 in the SI. This treatment predicts that reactions of NO3 with methyl and ethyl iodides would have the same rate constant, though the rate constant for iodomethane is approximately 1.7-fold faster than iodoethane, perhaps due to steric effects or measurement uncertainties. However, there are insufficient data to refine these estimates. Possible mechanisms for these reactions are discussed by Bai et al. [].
3.6. Estimating Temperature Dependences
The focus of this work is estimating rate constants at 298 K, though approximate temperature dependence estimates are also made to estimate rate constants for mechanisms applied to lower atmospheric conditions at different temperatures in the approximate range of 270–330 K. Estimates in this work are applicable for atmospheric pressure only, and no attempts are made to estimate rate constants for reactions with complex temperature or pressure dependences, or for large temperature ranges. All temperature dependence estimates in this work are based on the assumption that, at least for temperatures relevant to the lower atmosphere, the temperature dependence can be approximated by the two-parameter Arrhenius expression
where k is the rate constant at temperature T, A is the rate constant at the high temperature limit, and Ea is an overall activation energy in temperature units. Although temperature dependences for many reactions or for large temperature ranges are better described by more complex expressions with more parameters, deriving these additional parameters for estimation purposes is not straightforward and is beyond the scope of this work. Use of the two-parameter expression will limit the range of temperatures for which the estimates are valid in many cases, but this is not the largest source of uncertainty in our temperature-dependence estimates.
k(T) = A × exp(−Ea/T)
The data and methods used to derive the estimated A factors used in this work are discussed in Section S1.10 of the SI. As discussed there, although the rate constant database has 298 K rate constants for a wide variety of compounds, it has usable temperature-dependence information for only a subset of them, and for many types of compounds the A factors do not show consistent patterns usable for estimates. This means that temperature dependences derived for many types are highly uncertain, and should only be applied for temperatures near 298 K. Furthermore, although substituent and structure correction effects are likely to be temperature dependent, temperature dependences were only estimated for base rate constants. Despite the large uncertainties and many approximations made in these temperature dependence estimates, they are considered preferable to ignoring known temperature effects entirely when making rate constant estimates.
4. Results
4.1. Parameters and Rate Constants
The parameters for estimating rate constants and approximate temperature dependences for all types of reactions are given in various tables in Section S2 of the SI, where footnotes summarize how they were derived or estimated. Plots of estimated vs. experimental rate constants and error distribution plots for the estimates for five types of reactions are given in Figure 1, with separate plots for compounds used to derive the parameters and for those used for evaluations only. Distribution plots of factor errors for hydrocarbons, non-hydrocarbons used for parameter derivations, and compounds used for evaluation only are shown in Figure 2. Table 4 lists the compounds with the greatest estimation error, and also gives characteristics of their structures that may affect the reliability of the estimates. Figure 3 and Table 5 show the fractions and numbers of compounds where the estimates differed from the experimental data by various factors. Tables S21–S25 in Section S3 of the SI give the experimental and estimated rate constants and error factors for all compounds in the database, grouped by whether they were used for parameter derivations or not, and also by type of compound. Those tables also give the error factors and the estimated and experimental A factors for those compounds that were used to derive the A factor estimates.
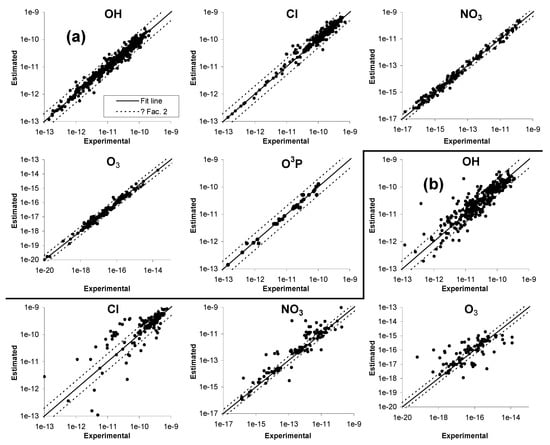
Figure 1.
Plots of estimated vs. experimental 298 K rate constants for (a) compounds used for parameter derivations, and (b) compounds used for evaluation only.
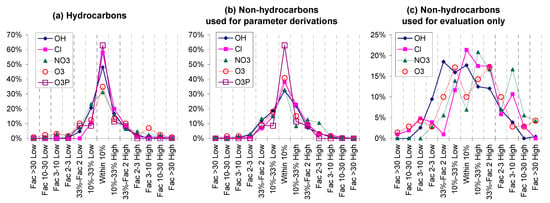
Figure 2.
Distribution plots of factor errors in rate constant in estimates at 298 K. Rate constants for (a) hydrocarbons, (b) non-hydrocarbons used to derive parameters, and (c) non-hydrocarbons used for evaluation only.

Table 4.
Compounds where estimates of the rate constants failed by the largest factors.
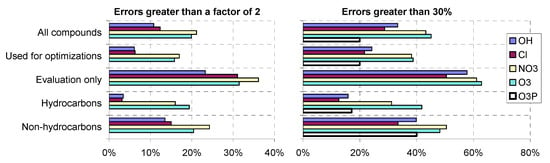
Figure 3.
Fractions of compounds with errors greater than 30% or a factor of 2 for estimations of rate constants for reactions with OH, Cl, NO3, and O3.

Table 5.
Summary of fractions and numbers of compounds with error factors greater than specified amounts.
4.2. Performance of Estimates
The performance of our estimates is the best for O(3P) reactions, where all rate constants fit within a factor of 2 and where 80% are predicted within ±30%. This can be attributed to the relatively limited database used for O(3P) reactions and the fact that it does not include bifunctional or other types of compounds where estimates are more uncertain. The results for the other types of reactions, where the databases are more comprehensive and include larger varieties of compounds, are more comparable and indicative of the overall performance of our estimates. In the case of both OH and Cl, approximately 70% of the rate constants are predicted within ±30% and almost ~90% within a factor of 2. The performance is not quite as good in this respect for NO3 and O3, with approximately 55% being fit to within ±30% and approximately 80% to within a factor of 2. In terms of outliers where estimates are worse than a factor of 5, OH is the best with only 8 of the rate constants being in this group (~1% of the total), and O3 is the worst with 27 (almost 10%).
4.3. Comparison with Other Recent SARs
The SARs developed in this work are comparable to those previously developed by Jenkin et al. [,,] for reactions of organics with OH and O3, and by Kerdouchi et al. [] for reactions with NO3. These were also developed with the objective of predicting rate constants for a wide variety of compounds for use in developing detailed atmospheric mechanisms, and have been or are being in ongoing updates of the GECKO-A mechanism generation system and the next version of the MCM [,]. There development was mostly independent of the work discussed here, though as discussed above some of the methods and results of the previous work were used to inform the work here on SARs for NO3 and O3 reactions.
Figure 4 shows a comparison of the estimated OH, NO3, and O3 rate constants published by Jenkin et al. [,], Kedouchi et al. [], and Jenkin et al. [] against those predicted in this work. Note that there are published estimates for only approximately 50% of the rate constants used in this work (see Table 2), since we used a larger database of experimental data. Figure 4 shows that that this work gives estimates of very similar rate constants than those previously published, with the vast majority agreeing within a factor of 2, though there are several cases where greater differences are observed. The greatest prediction differences were for 3,4-diethyl-2-hexene, n-butyl acrylate, 3-carene, and ethyl methacrylate for O3, allyl acetate for NO3, and nitroethene for OH.
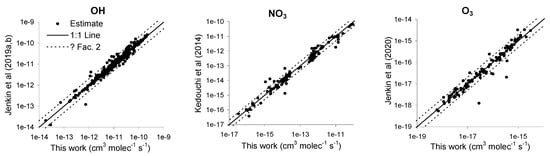
Figure 4.
Comparison of estimates from Jenkin et al. [,,] and Kedouchi et al. [] with those from this work.
Figure 5 shows distribution plots of factor errors comparing the performance of the previous estimates with this work in predicting the experimental data, and show very similar performance for all three types of reactions. These show distributions for all rate constants that were estimated in both this and the previous works, which are subsets of the rate constants estimated in this work. Additional plots are shown in Figure S11 in the SI, which have separate plots for compounds used for parameter derivation in this work and those that were used for evaluation only. The error distributions are almost identitical for the compounds used to derive the parameters, reflecting the fact that estimates for these compounds tend to be somewhat less uncertain and therefore less sensitive to differences in the methods employed. The differences are somewhat greater for the compounds that were not used to derive the parameters in this work, with the published estimates being slightly better, but the differences are still relatively small considering the larger uncertainties.
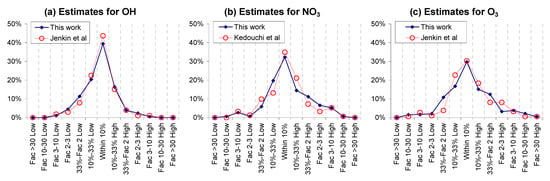
Figure 5.
Comparison of distribution plots of factor errors for estimates from Jenkin et al. [,,] and Kedouchi et al. [] with those from this work.
Since the published estimates are only a subset of the estimates derived in this work, we also compared the distributions of our estimates for compounds also estimated in the previous works with those that are estimated in this work only, which are also shown in Figure S11 in the SI. Although the performance is somewhat better for the compounds where previous estimates are available, reflecting the fact that these estimates may be somewhat less uncertain, the performance for the other compounds is not significantly different. Therefore, it is likely that the previous estimation methods would perform similarly for the additional compounds in our database, at least for compounds that are within the scope of their methods.
5. Discussion
The estimation approach discussed in this work is entirely empirical, with the overall objective being to estimate rate constants and branching ratios for compounds for reactions or organic compounds with major atmospheric oxidants where no data are available. The methods employed are based largely on those SARs originally developed by Atkinson and co-workers and others for predicting rate constants for reactions with OH (e.g., [,]), and more recently by Jenkin et al. [,], Kerdouci et al. [], and Jenkin et al. [] for predicting rate constants for OH, NO3 and O3, and which are being used to update the GECKO-A mechanism generation system and the MCM []. The main contributions of the work discussed here include the ability to make estimates for more of the types of compounds that may be emitted or formed in the atmosphere, the extension of the methods to reactions of Cl and O(3P), and the use of the comprehensive rate constant database for atmospheric reactions recently compiled by McGillen et al. []. This also serves as partial documentation of the estimation methods used in the SAPRC mechanism generation system [,] for initial reactions of VOCs. In addition, the results of this work serve to demonstrate the limitations of the types of empirical methods used in these SARs for predicting rate constants for the full variety of organic compounds that may be of interest.
Estimates can be made for most types of C-, H-, O-, or N-containing organic compounds that are emitted or formed in the atmosphere, including almost all types of compounds whose mechanisms can be generated or predicted to be formed by the current near-explicit mechanisms such as the MCM [,,,] or by current mechanism generation systems [,,,]. This approach works extremely well, making predictions to within ±30% in most cases, for most hydrocarbons and reasonably well for most compounds with no more than one non-alkyl substituent, though there are some exceptions. As expected, this approach does not work as well for compounds with multiple substituents or where multiple corrections are needed, though most are still predicted to within a factor of two or better. This approach is not designed to handle cases where steric considerations are important, since the only structural characteristics taken into account are corrections when the reaction site is in a ring (when sufficient data are available) or an empirical relationship between addition rate constants and molecule size in the case of NO3 addition reactions, or a relationship between the number of β substituents and the rate constants in the case of O3 additions. It is also not designed to handle long-range interactions, which are apparently important for many halogenated compounds.
Overall, approximately 2/3 of the rate constants in our large experimental database are predicted to within ±30% for reactions with OH and Cl, and somewhat over half in the case of reactions with NO3 and O3 (see Table 4). Predictions to within ±30% are probably as good as can be reasonably expected given uncertainties in rate constant measurements and the assumptions behind the predictions. Almost 90% of the rate constants in our experimental database are predicted within a factor of 2 for OH and Cl, and approximately 80% in the case of NO3 and O3. Except for O(3P), where all rate constants are predicted within a factor of 2 because of limitations in the experimental database, there are a number of outliers where estimates are off by more than a factor of 5, with the most being for O3 and NO3 and the least being for OH. These outliers can be attributed to a number of different factors, as discussed in Table 4. The poorer performance in the case of NO3 and O3 relative to OH and Cl might be attributed to increased importance of steric factors for the reactions of these larger oxidant species, and also the nature of the O3 addition reactions, where more parameters are needed for estimates. The performance of our estimates for OH, NO3, and O3 is very close to the estimates developed for GECKO-A and MCM [,,,,], which is expected since very similar methods were used.
One might question the relevance of estimating O(3P) rate constants for atmospheric mechanisms, since such reactions are generally minor sinks for consumptions of organic compounds in the atmosphere. However, reactions of O(3P) with alkenes can be a non-negligible process under higher NOx conditions that might occur in some smog chamber experiments used to evaluate mechanisms (e.g., see []) or in plumes. Our estimates performed well against our database of O(3P) rate constants, but this is because few compounds in this more limited database required multiple correction factors where estimates are more uncertain. Therefore, estimates of O(3P) rate constants for the full variety of compounds in the atmosphere are either uncertain or beyond the scope of the estimates in this work. However, we would expect steric factors to be much less for O(3P) than is the case for O3, so better performance for O(3P) than for O3 might be expected if a more comprehensive database were available for use in its development, as is the case for OH and the other oxidants.
Although we believe that this work, along with recent works of Jenkin et al. [,,] and Kedouchi et al. [], represents an improvement in our ability to estimate the initial reactions of many types of compounds in the atmosphere, it is clear that more work is needed. Empirical methods such as these require the availability of a sufficiently comprehensive rate constant database to derive the full variety of parameters that are needed. Although we believe that the rate constant database used in this work for the OH, Cl, NO3 and O3 reactions is reasonably comprehensive in terms of the available literature and evaluations [], it is not sufficient to derive all the parameters that are needed without making uncertain assumptions that are difficult to test. Rate constant measurements for targeted compounds could reduce the number of instances where estimated parameters that could not be experimentally verified had to be used, or could test the validity of the many assumptions and estimates had to be employed. (The comments in Tables S11–S20 discussing how certain parameters have to be estimated can indicate the types of compounds where more data are needed.) In addition, quantum calculation methods combined with theoretical kinetic analyses have reached the point where they may provide credible estimates for rate constants for individual reactions where no data are available, but such data were not used in this work. They could be particularly useful for multifunctional compounds that are difficult to obtain or study experimentally. This could allow for the development of better estimates for such compounds, and better methods to estimate base rate constants, substituent factors, or effects of multiple interacting factors, when no experimental data are available. Use of high-quality theoretical data clearly represents one way this could be extended to improve and evaluate the estimates.
Halogenated compounds are important classes of organic emissions, so methods are needed to estimate their atmospheric rate constants. Unfortunately, although the current methods include hydrocarbons with single halogen substituents, they do not work for compounds with multiple halogens, nor for many halogenated oxygenated compounds. DeMore et al. [] developed a method that works reasonably well for rate constants of abstractions of OH radicals from halocarbons, based on treating groups with multiple halogen substituents separately, but we found that these methods do not extend well to halogen-substituted ethers and other larger molecules with multiple halogen substituents. This is apparently due to longer range interactions between non-adjacent groups, and use of parameters representing only α or β substitution effects is not sufficient. Methods that take these longer range interactions need to be developed before rate constants for hydrocarbons with multiple halogens or oxygenated halogen compounds substituents can be estimated with sufficient reliability to be useful.
Aromatic oxygenates, nitrates, and nitro compounds are also emitted or formed in the atmosphere, and the methods developed here need to be extended to cover more than one such substituent about the aromatic ring. Although some classes of multisubstituted aromatics can be estimated, most are beyond the scope of the present work either because of limited data or because the current SAPRC mechanism generation system [,] cannot process reactions of such compounds. In principle, these methods could be extended if sufficient data were available, though some revisions in the methods employed may be needed.
Although this work includes approximate methods to estimate temperature dependences, the focus is on estimating rate constants near 298 K, which is relevant to atmospheric modeling. The temperature dependences estimated here are not adequate for reliable extrapolation to higher temperatures more relevant to combustion, or to the lower temperatures relevant to the upper atmosphere. More attention is needed to how to estimate temperature effects if a single method is to be reliably applied to such a wide temperature range. In the meantime, it might be more straightforward to separately develop SARs for specific temperature ranges, utilizing measured (or theoretically calculated or extrapolated) rate constants for the specific conditions of interest. This is the approach used in this work, and a similar approach could be used to develop SARs for combustion modeling.
The procedures developed in this work estimate rates of reactions at the different positions of the molecule, but have been developed and tested using only total rate constant measurements. However, data are also available concerning product yields for many of these reactions, which in many cases can be used to derive branching ratios for reactions at different positions. These could provide a useful test of branching ratio estimates and potentially allow some estimates to be refined. This would be especially useful for estimates for relatively minor routes that do not have large effects on the total rate constants, but may affect predictions of formation of toxic or non-volatile products that may be of interest. Initial work on this by Orlando and co-workers, discussed by Aumont et al. [], compared branching ratios for reactions of ~60 organics with OH derived from product yield data with those predicted by OH SARs being developed for GECKO-A and MCM [,,,,,]. The results showed that the estimated branching ratios were reasonably reliable for alkanes (root mean squares error, RMSE of 2%), but the reliability decreased with increasing numbers of groups (RMSEs of 15% and 19% for monofunctional and bifunctional species, respectively). This appears to be consistent with the performance of the estimates for total rate constants discussed here, though a comprehensive statistical analysis has not been carried out. This work needs to be extended to other compounds and reaction where data may be available, and where possible the results used to improve estimates for minor pathways and a more comprehensive evaluation of the methods.
The empirical methods developed in this work require a relatively large number of parameters to take maximum advantage of the available data to make the estimates as closely as possible, on the assumption that this will improve accuracy for estimates for other compounds. There are more parameters than can be reliably derived from the data, and use of too many adjustable parameters may result in multiple sets of parameters that fit the data, with each potentially giving significantly different predictions when applied to unstudied reactions, or in overfitting where normal variabilities and uncertainties in the measurement data affect parameter values and predictions in chemically unrealistic ways. Ideally, judgments on which parameters to adjust and which parameters to estimate or lump with other parameters should be aided by systematic statistical or mathematical analyses, with the criteria employed being clearly specified. However, in this work, these judgments were primarily based on expert opinion concerning whether there are sufficient data to unambiguously derive a parameter, and whether the parameters so derived are chemically reasonable. (If the optimization gave parameters judged to be unreasonable, they were estimated or lumped instead.) The development of the SARs for GECKO-A/MCM [,,,,,] employed similar expert judgments, and the fact that similar results are obtained tends to support the utility of this approach. However, use of more systematic procedures to decide what to optimize, lump, or estimate would give more scientifically justifiable results, and could aid uncertainty analysis.
A major omission in this work, which is also the case for the previously developed SARs, is a lack of methods developed to derive uncertainty ranges for the estimates. The wide variability in the quality of the predictions, the uncertainties in many of the estimated parameters, and the variable uncertainties in the measurement data used to derive the parameters indicate that uncertainty estimates are important when interpreting the results. This is an important area where further work is needed, and a logical next step in this effort.
Estimation methods such as those developed in this work should undergo thorough peer review to assure that it incorporates all the appropriate data and theoretical considerations and makes reasonable assumptions before its estimates are used in regulatory modeling and research. Because of this, the author is in a SAR evaluation working group to develop, review, and evaluate structure–reactivity estimation methods. The perspective of this group and the current status and outlook of SAR development are discussed elsewhere [].
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/atmos12101250/s1, additional discussion, tables of parameters, tables of rate constants, and calculation examples.
Funding
Partial support for this work was provided by the Coordinating Research Council through Project A-108, and additional support was provided by the California Air Resources Board through contract 11-761 and by the University of California Retirement System.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available in the Supplementary Information are available from the author in Excel spreadsheet format upon request.
Acknowledgments
The author gratefully acknowledges members of the SAR evaluation panel, particularly Max McGillen, John Orlando, Benedicte Picquet-Varrault, Wahid Mellouki, and Tim Wallington for helpful discussions, and particularly Max McGillen for leading the team to develop the rate constant database used in this work. The author also thanks Mike Jenkin for helpful discussions regarding the SARs he developed. The author also thanks one of the reviewers for very helpful comments and thorough editing of this manuscript and the supplement.
Conflicts of Interest
The author declares no conflict of interest.
References
- Guenther, A.B.; Jiang, X.; Heald, C.L.; Sakulyanontvittaya, T.; Duhl, T.; Emmons, L.K.; Wang, X. The Model of Emissions of Gases and Aerosols from Nature version 2.1 (MEGAN2.1): An extended and updated framework for modeling biogenic emissions. Geosci. Model Dev. 2012, 5, 1471–1492. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Brook, R.; Crippa, M.; Janssens-Maenhout, G.; Schieberle, C.; Dore, C.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Friedrich, R. Speciation of anthropogenic emissions of non-methane volatile organic compounds: A global gridded data set for 1970–2012. Atmos. Chem. Phys. Discuss. 2017, 17, 7683–7701. [Google Scholar] [CrossRef] [Green Version]
- Carter, W. Development of a database for chemical mechanism assignments for volatile organic emissions. J. Air Waste Manag. Assoc. 2015, 65, 1171–1184. [Google Scholar] [CrossRef]
- Finlayson-Pitts, B.J.; Pitts, J.N., Jr. Chemistry of the Upper and Lower Atmosphere: Theory, Experiments, and Applications; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Calvert, J.G.; Orlando, J.J.; Stockwell, W.R.; Wallington, T.J. The Mechanisms of Reactions Influencing Atmospheric Ozone; Oxford University Press: New York, NY, USA, 2015. [Google Scholar]
- Aumont, B.; Szopa, S.; Madronich, S. Modelling the evolution of organic carbon during its gas-phase tropospheric oxidation: Development of an explicit model based on a self generating approach. Atmos. Chem. Phys. Discuss. 2005, 5, 2497–2517. [Google Scholar] [CrossRef] [Green Version]
- Jenkin, M.E.; Saunders, S.M.; Wagner, V.; Pilling, M.J. Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part B): Tropospheric degradation of aromatic volatile organic compounds. Atmos. Chem. Phys. Discuss. 2003, 3, 181–193. [Google Scholar] [CrossRef] [Green Version]
- MCM. The Master Chemical Mechanism, Version 3.3.1. 2020. Available online: http://mcm.york.ac.uk/ (accessed on 23 September 2021).
- Calvert, J.G.; Atkinson, R.; Kerr, J.A.; Madronich, S.; Moortgat, G.K.; Wallington, T.J.; Yarwood, G. The Mechanisms of Atmospheric Oxidation of Alkenes; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Calvert, J.G.; Atkinson, R.; Becker, K.H.; Kamens, R.M.; Seinfeld, J.H.; Wallington, T.J.; Yarwood, G. The Mechanisms of Atmospheric Oxidation of Aromatic Hydrocarbons; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Calvert, J.; Mellouki, A.; Orlando, J.; Pilling, M.; Wallington, T. The Mechanisms of the Atmospheric Oxidation of the Oxygenates; Oxford University Press: New York, NY, USA, 2011. [Google Scholar]
- NASA. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies; Evaluation Number 18 JPL Publication 15-10; Jet Propulsion Laboratory: Pasadena, CA, USA, October 2015. Available online: https://jpldataeval.jpl.nasa.gov/ (accessed on 23 September 2021).
- IUPAC. Evaluated Kinetic and Photochemical Data; IUPAC Subcommittee on Gas Kinetic Data Evaluation for Atmospheric Chemistry. Web Version. 2019. Available online: http://iupac.pole-ether.fr (accessed on 23 December 2019).
- McGillen, M.R.; Carter, W.P.L.; Mellouki, A.; Orlando, J.J.; Picquet-Varrault, B.; Wallington, T.J. Database for the kinetics of the gas-phase atmospheric reactions of organic compounds. Earth Syst. Sci. Data 2020, 12, 1203–1216. [Google Scholar] [CrossRef]
- Vereecken, L.; Aumont, B.; Barnes, I.; Bozzelli, J.; Goldman, M.; Green, W.; Madronich, S.; McGillen, M.; Mellouki, A.; Orlando, J.; et al. Perspective on Mechanism Development and Structure-Activity Relationships for Gas-Phase Atmospheric Chemistry. Int. J. Chem. Kinet. 2018, 50, 435–469. [Google Scholar] [CrossRef]
- Jenkin, M.E.; Saunders, S.M.; Pilling, M.J. The tropospheric degradation of volatile organic compounds: A protocol for mechanism development. Atmos. Environ. 1997, 31, 81–104. [Google Scholar] [CrossRef]
- Saunders, S.M.; Jenkin, M.E.; Derwent, R.G.; Pilling, M.J. Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part A): Tropospheric degradation of non-aromatic volatile organic compounds. Atmos. Chem. Phys. Discuss. 2003, 3, 161–180. [Google Scholar] [CrossRef] [Green Version]
- Bloss, C.; Wagner, V.; Jenkin, M.E.; Volkamer, R.; Bloss, W.J.; Lee, J.D.; Heard, D.E.; Wirtz, K.; Martin-Reviejo, M.; Rea, G.; et al. Development of a detailed chemical mechanism (MCMv3.1) for the atmospheric oxidation of aromatic hydrocarbons. Atmos. Chem. Phys. Discuss. 2005, 5, 641–664. [Google Scholar] [CrossRef] [Green Version]
- Carter, W.P. A detailed mechanism for the gas-phase atmospheric reactions of organic compounds. Atmos. Environ. Part A Gen. Top. 1990, 24, 481–518. [Google Scholar] [CrossRef]
- Carter, W.P. Development of the SAPRC-07 chemical mechanism. Atmos. Environ. 2010, 44, 5324–5335. [Google Scholar] [CrossRef]
- Carter, W.P.L. Development of the SAPRC-07 Chemical Mechanism and Updated Ozone Reactivity Scales. Final Report to the California Air Resources Board Contract No. 03-318. Available online: www.cert.ucr.edu/~carter/SAPRC (accessed on 27 January 2010).
- Carter, W.P.L. Documentation of the SAPRC-18 Mechanism, Draft Report to California Air Resources Board Contract No. 11-761. 29 May 2020. Available online: http://www.cert.ucr.edu/~carter/SAPRC/18/ (accessed on 23 September 2021).
- Carter, W.P.; Heo, G. Development of revised SAPRC aromatics mechanisms. Atmos. Environ. 2013, 77, 404–414. [Google Scholar] [CrossRef]
- Aumont, B.R.; Valorso, M.; Camredon, M.; Jenkin, M.; Rickard, A.; Brauer, B.; Newland, M.; Evans, M.; Mouchel-Vallon, C.; Madronich, S.; et al. Structure-Activity Relationships for the Development of MCM/GECKOA Mechanisms. Presented at the International Conference on Atmospheric Chemical Mechanisms, Davis, CA, USA, 5–7 December 2018; Available online: https://acm.aqrc.ucdavis.edu/sites/g/files/dgvnsk3471/files/inline-files/Bernard%20Aumont.pdf (accessed on 23 September 2021).
- Carter, W.P.L. Documentation of the SAPRC-16 Mechanism Generation System. Draft Interim Report to California Air Resources Board Contract 11-761. 25 May 2019. Available online: https://intra.engr.ucr.edu/~carter/SAPRC/18/MechGen.pdf (accessed on 25 September 2021).
- Carter, W.P.L. Gateway to the SAPRC Mechanism Generation System. 2021. Available online: http://mechgen.cert.ucr.edu/ (accessed on 12 August 2021).
- Kaduwela, A.; Luecken, D.; Carter, W.; Derwent, R. New directions: Atmospheric chemical mechanisms for the future. Atmos. Environ. 2015, 122, 609–610. [Google Scholar] [CrossRef]
- MAGNIFY. Mechanisms for Atmospheric Chemistry, Generation, Interpretation and FidelitY. 2021. Available online: https://anr.fr/Project-ANR-14-CE01-0010 (accessed on 9 August 2021).
- Jenkin, M.E.; Valorso, R.; Aumont, B.; Rickard, A.R.; Wallington, T.J. Estimation of rate coefficients and branching ratios for gas-phase reactions of OH with aliphatic organic compounds for use in automated mechanism construction. Atmos. Chem. Phys. Discuss. 2018, 18, 9297–9328. [Google Scholar] [CrossRef] [Green Version]
- Jenkin, M.E.; Valorso, R.; Aumont, B.; Rickard, A.R.; Wallington, T.J. Estimation of rate coefficients and branching ratios for gas-phase reactions of OH with aromatic organic compounds for use in automated mechanism construction. Atmos. Chem. Phys. Discuss. 2018, 18, 9329–9349. [Google Scholar] [CrossRef] [Green Version]
- Kerdouci, J.; Picquet-Varrault, B.; Doussin, J.-F. Structure–activity relationship for the gas-phase reactions of NO3 radical with organic compounds: Update and extension to aldehydes. Atmos. Environ. 2014, 84, 363–372. [Google Scholar] [CrossRef]
- Jenkin, M.E.; Valorso, R.; Aumont, B.; Newland, M.J.; Rickard, A.R. Estimation of rate coefficients for the reactions of O3 with unsaturated organic compounds for use in automated mechanism construction. Atmos. Chem. Phys. Discuss. 2020, 20, 12921–12937. [Google Scholar] [CrossRef]
- Atkinson, R. A structure-activity relationship for the estimation of rate constants for the gas-phase reactions of OH radicals with organic compounds. Int. J. Chem. Kinet. 1987, 19, 799–828. [Google Scholar] [CrossRef]
- Kwok, E.; Atkinson, R. Estimation of hydroxyl radical reaction rate constants for gas-phase organic compounds using a structure-reactivity relationship: An update. Atmos. Environ. 1995, 29, 1685–1695. [Google Scholar] [CrossRef]
- Bolzacchini, E.; Bruschi, M.; Hjorth, J.; Meinardi, S.; Orlandi, M.; Rindone, B.; Rosenbohm, E. Gas-phase reaction of phenol with NO3. Environ. Sci. Technol. 2001, 35, 1791–1797. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, C.J.; Herrmann, H.; Weller, C. Atmospheric chemistry and environmental impact of the use of amines in carbon capture and storage (CCS). Chem. Soc. Rev. 2012, 41, 6684–6704. [Google Scholar] [CrossRef]
- Bai, F.-Y.; Sun, Y.-Q.; Wang, X.; Pan, X.-M. Atmospheric chemistry of alkyl iodides: Theoretical studies on the mechanisms and kinetics of CH 3 I/C 2 H 5 I + NO 3 reactions. RSC Adv. 2015, 5, 88087–88095. [Google Scholar] [CrossRef]
- DeMore, W.B. Experimental and Estimated Rate Constants for the Reactions of Hydroxyl Radicals with Several Halocarbons. J. Phys. Chem. 1996, 100, 5813–5820. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).