Artificial Intelligence-Based Techniques for Rainfall Estimation Integrating Multisource Precipitation Datasets
Abstract
:1. Introduction
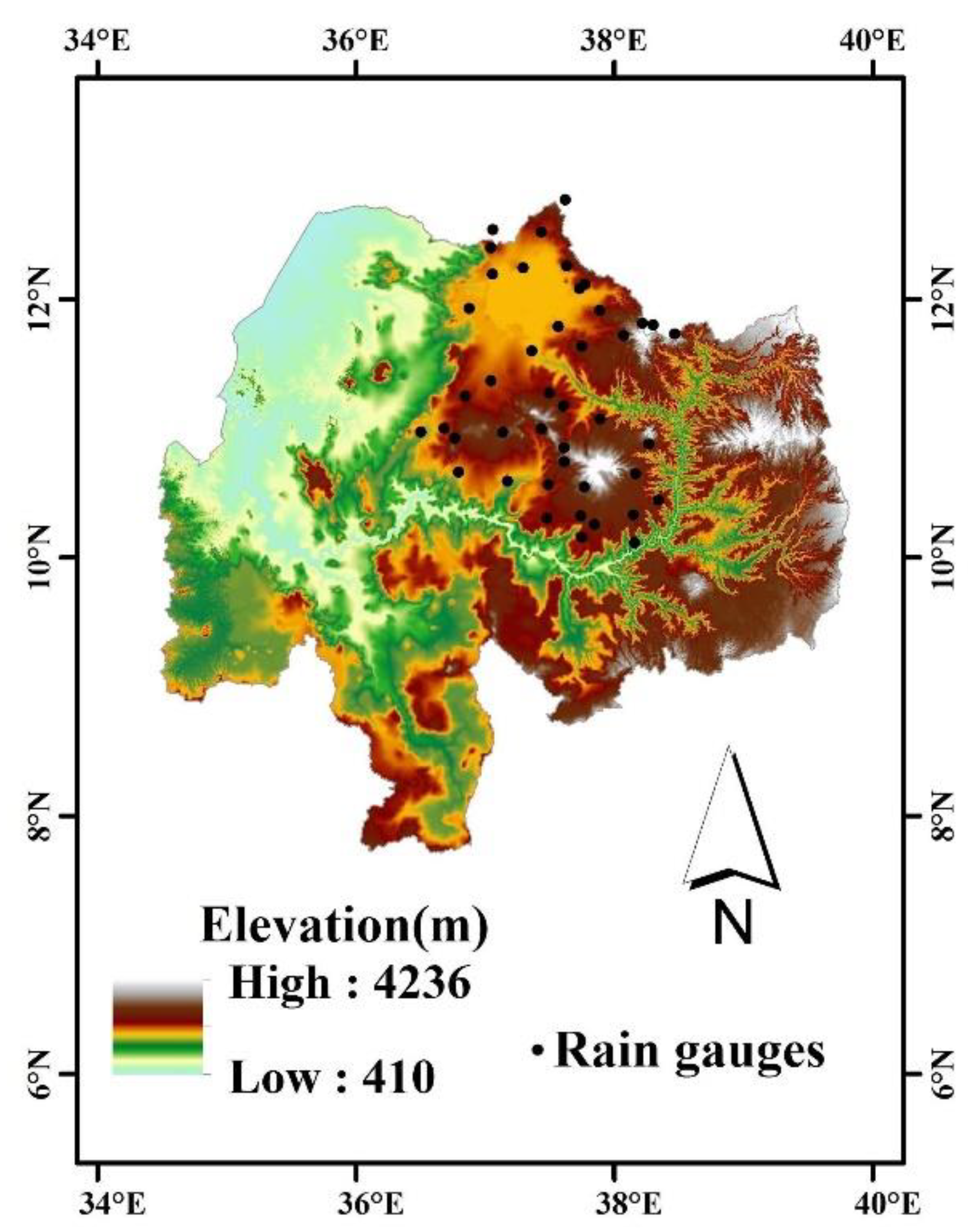
2. Data and Study Area
3. Methodology
3.1. Decision Tree Regressor (DT)
3.2. Random Forest Regressor (RF)
3.3. Gradient Boosting Regressor (GB)
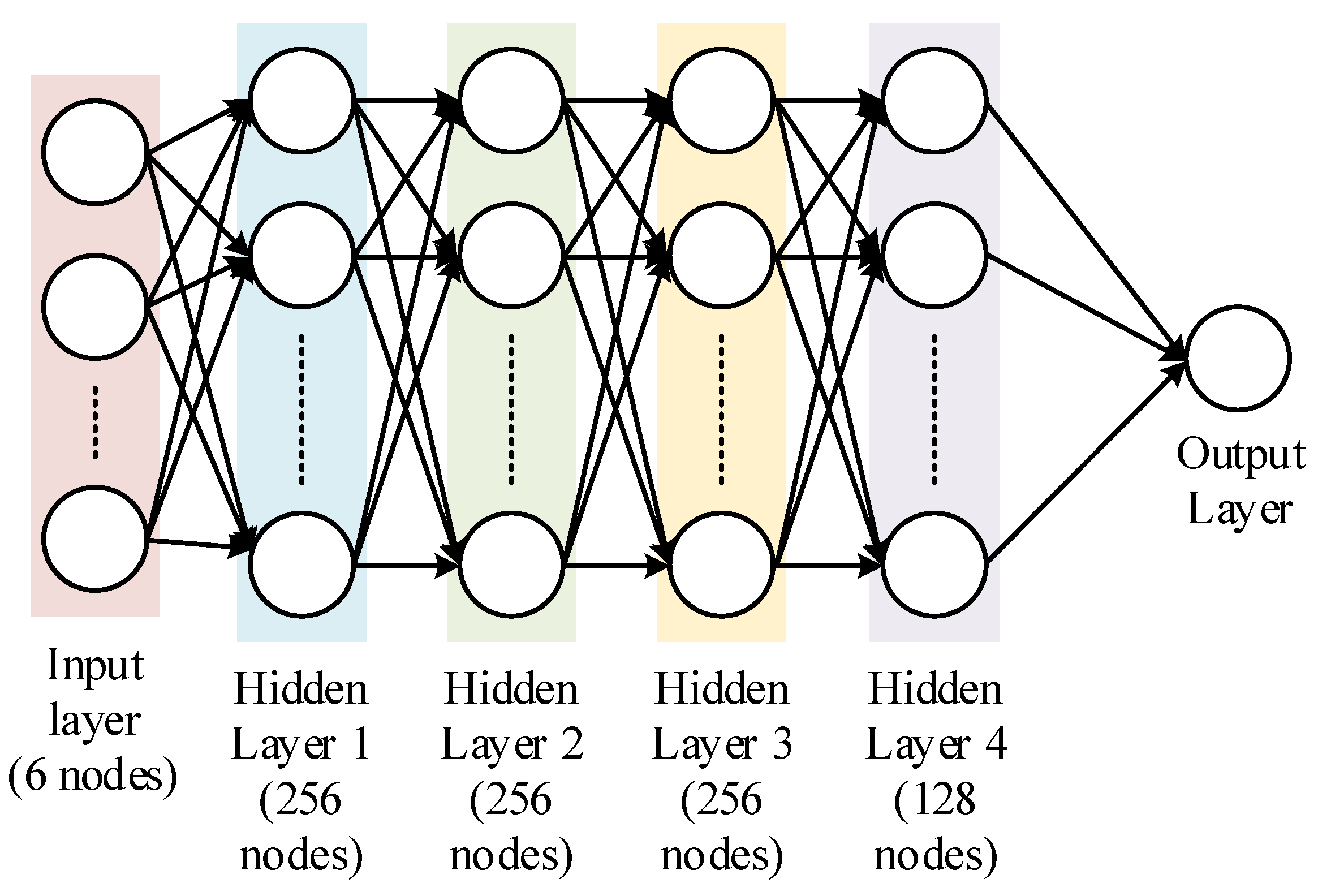
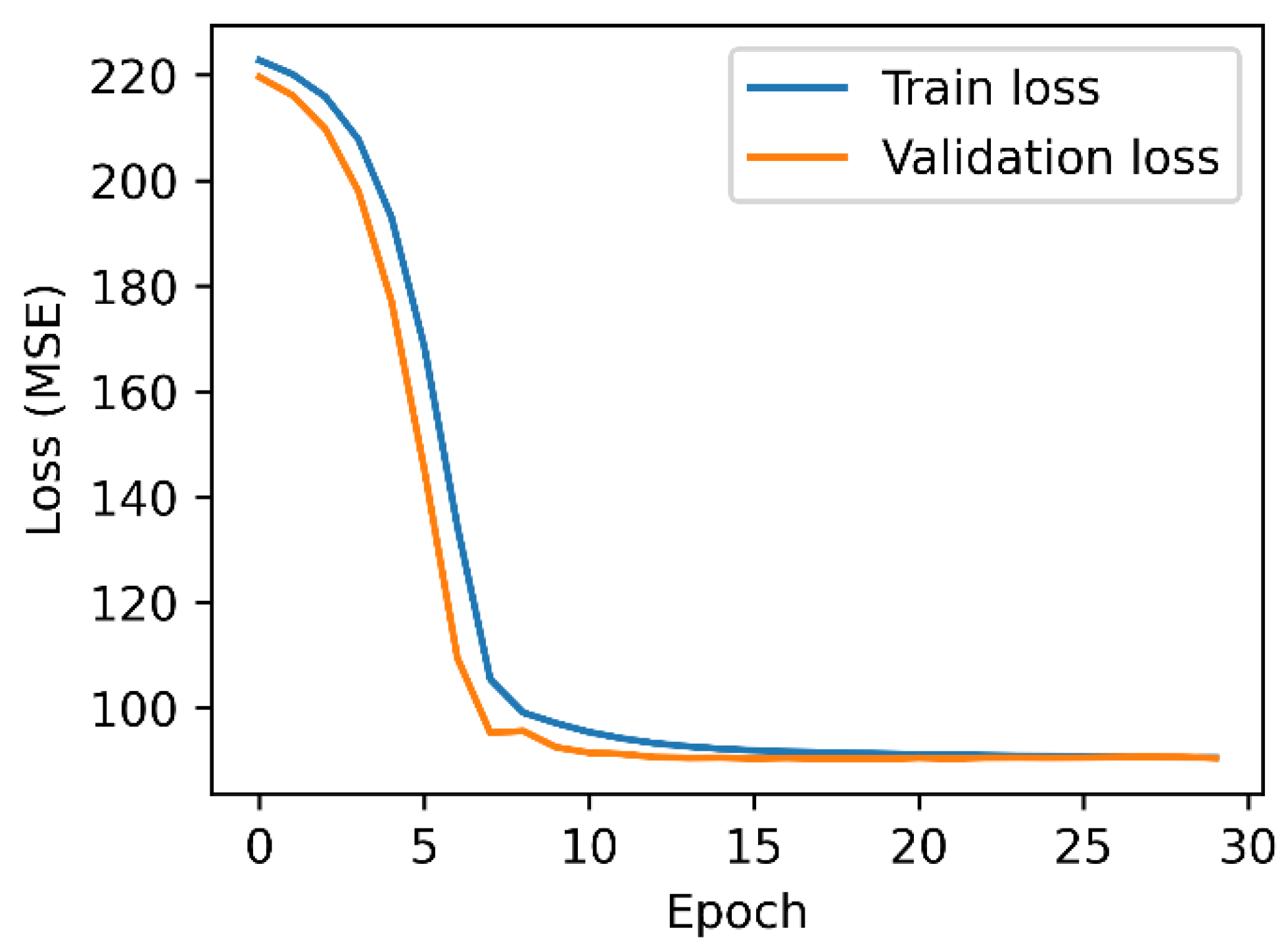
3.4. Neural Network (NN)
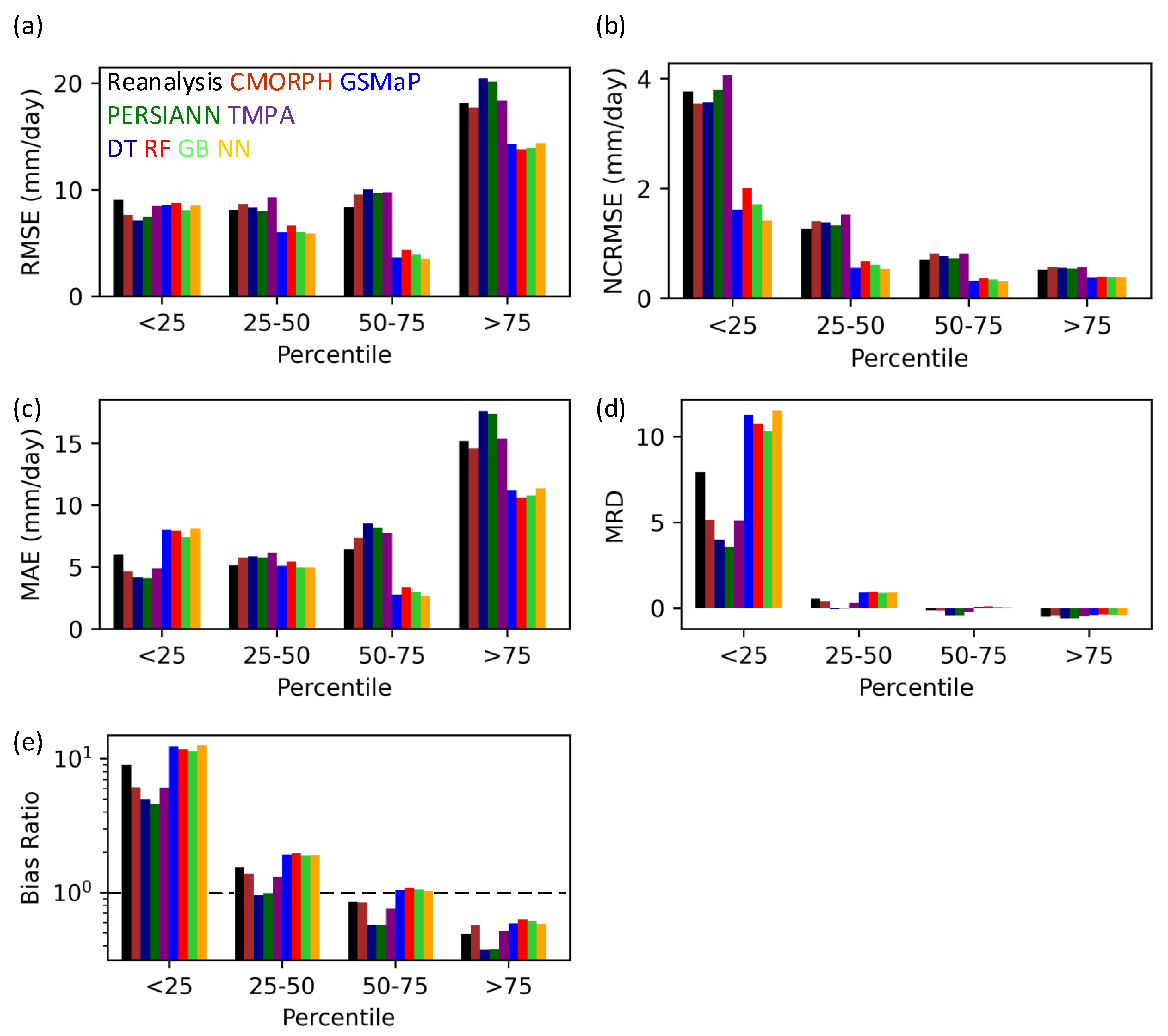
4. Performance Evaluation Error Metrics
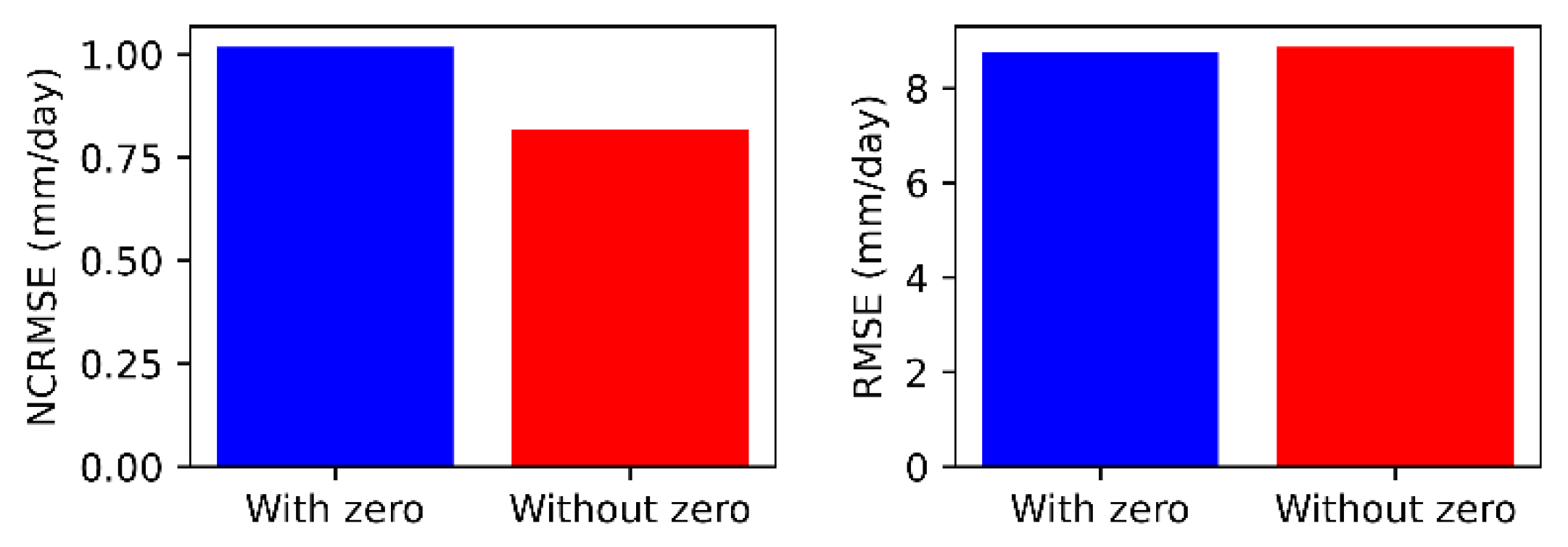
4.1. Root Mean Square Error (RMSE) and Normalized Centered Root Mean Square Error (NCRMSE)
4.2. Mean Absolute Error (MAE)
4.3. Mean Relative Difference (MRD)
4.4. Bias Ratio (BR)
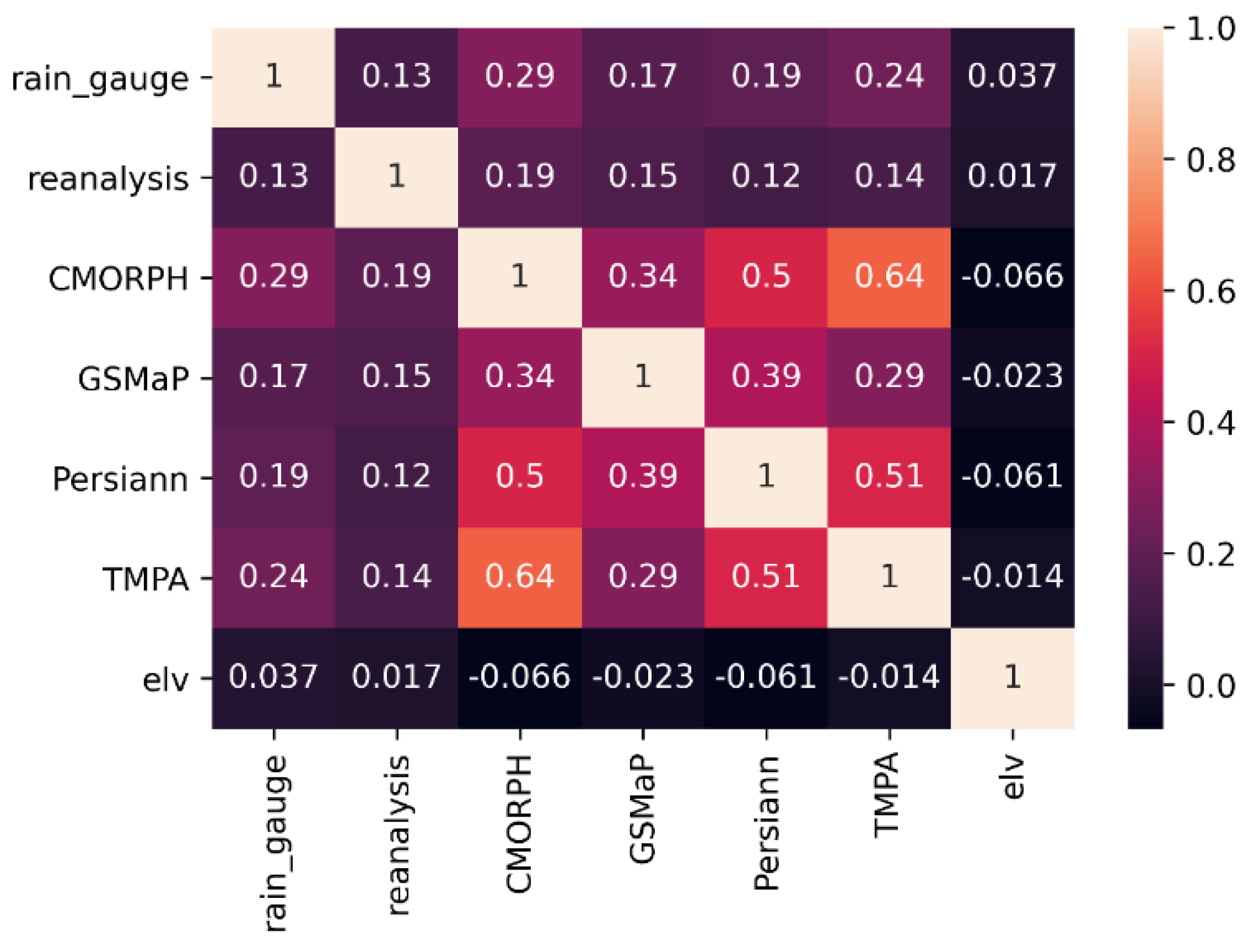
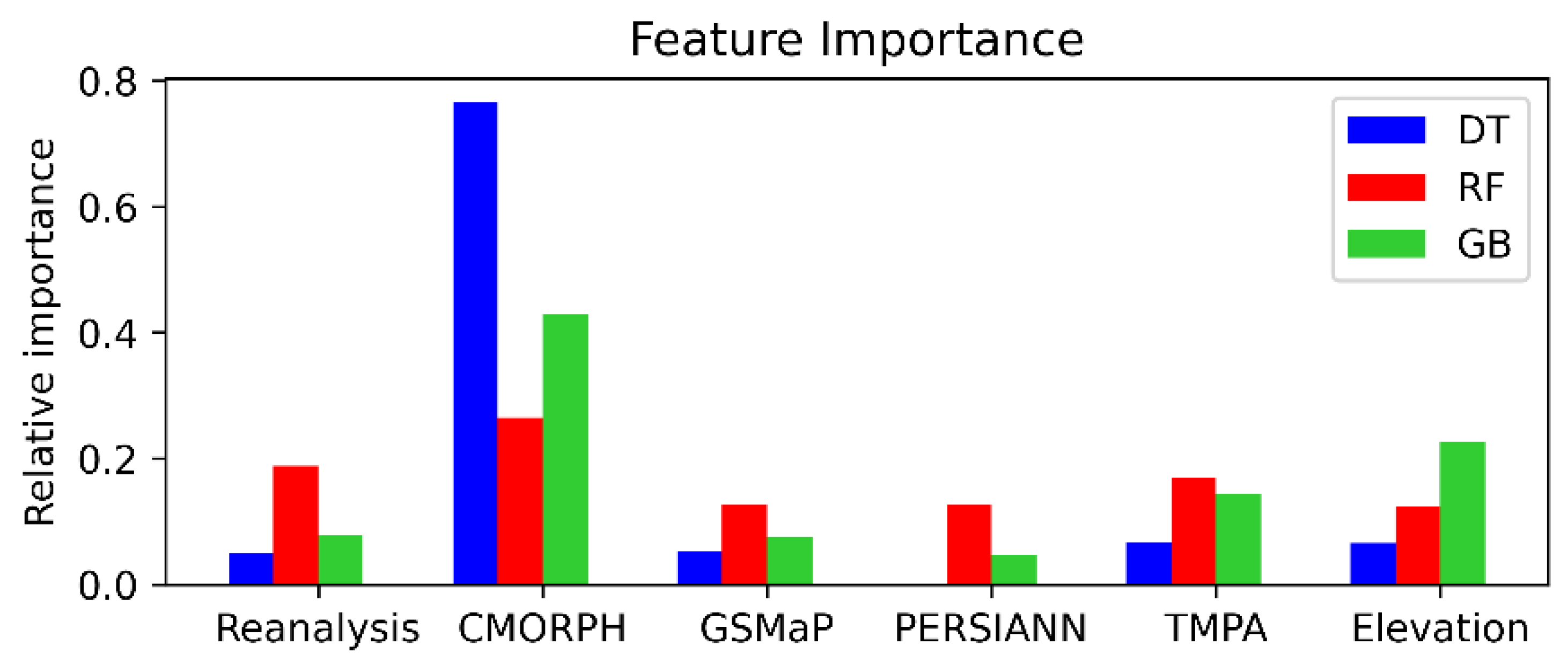
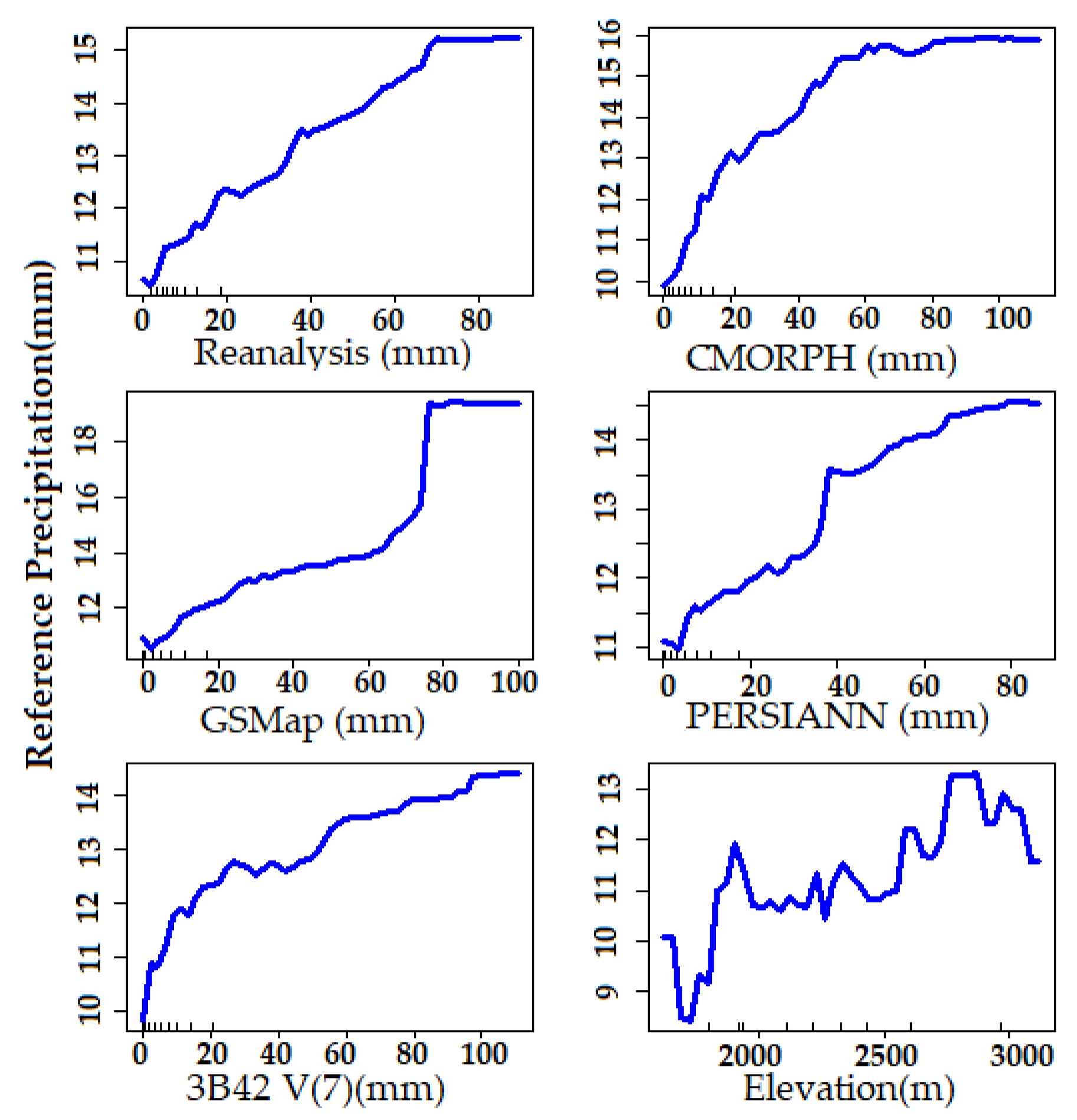
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Z. Comparison of versions 6 and 7 3-hourly TRMM multi-satellite precipitation analysis (TMPA) research products. Atmos. Res. 2015, 163, 91–101. [Google Scholar] [CrossRef] [Green Version]
- Mei, Y.; Anagnostou, E.N.; Nikolopoulos, E.I.; Borga, M. Error analysis of satellite precipitation products in mountainous basins. J. Hydrometeorol. 2014, 15, 1778–1793. [Google Scholar] [CrossRef]
- Ehsan Bhuiyan, M.A.; Nikolopoulos, E.I.; Anagnostou, E.N. Machine learning–based blending of satellite and reanalysis precipitation datasets: A multiregional tropical complex terrain evaluation. J. Hydrometeorol. 2019, 20, 2147–2161. [Google Scholar] [CrossRef]
- Derin, Y.; Anagnostou, E.; Berne, A.; Borgo, M.; Boudevillain, B.; Buytaert, W.; Chang, C.-H.; Delrieu, G.; Hong, Y.; Hsu, Y.C.; et al. Multiregional satellite precipitation products evaluation over complex terrain. J. Hydrometeorol. 2016, 17, 1817–1836. [Google Scholar] [CrossRef]
- Grecu, M.; Tian, L.; Olson, W.S.; Tanelli, S. A robust dual-frequency radar profiling algorithm. J. Appl. Meteorol. Climatol. 2011, 50, 1543–1557. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); Algorithm Theoretical Basis Document Version 06; National Aeronautics and Space Administration: Greenbelt, MD, USA, 2015; Volume 4, p. 26.
- Derin, Y.; Bhuiyan, M.A.E.; Anagnostou, E.; Kalogiros, J.; Anagnostou, M.N. Modeling Level 2 Passive Microwave Precipitation Retrieval Error Over Complex Terrain Using a Nonparametric Statistical Technique. IEEE Trans. Geosci. Remote Sens. 2020, 1–12. [Google Scholar] [CrossRef]
- Weedon, G.P.; Balsamo, G.; Bellouin, N.; Gomes, S.; Best, M.J.; Viterbo, P. The WFDEI meteorological forcing data set: WATCH Forcing Data methodology applied to ERA-Interim reanalysis data. Water Resour. Res. 2014, 50, 7505–7514. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitcchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; McCollum, J. Hydrologic evaluation of satellite and reanalysis precipitation datasets over a mid-latitude basin. Atmos. Res. 2015, 164, 37–48. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Shige, S.; Kida, S.; Ashiwake, H.; Kubota, T.; Aonashi, K. Improvement of TMI rain retrievals in mountainous areas. J. Appl. Meteorol. Climatol. 2013, 52, 242–254. [Google Scholar] [CrossRef] [Green Version]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakumura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Anagnostou, E.N.; Kirstetter, P.E. A nonparametric statistical technique for modeling overland TMI (2A12) rainfall retrieval error. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1898–1902. [Google Scholar] [CrossRef]
- Dinku, T. Challenges with availability and quality of climate data in Africa. In Extreme Hydrology and Climate Variability; Elsevier: Amsterdam, The Netherlands, 2019; pp. 71–80. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, M.K.; Shige, S.; Yu, C.K.; Cheng, L.-W. Further improvement of the heavy orographic rainfall retrievals in the GSMaP algorithm for microwave radiometers. J. Appl. Meteorol. Climatol. 2017, 56, 2607–2619. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Yang, F.; Biswas, N.K.; Rahat, S.H.; Neelam, T.J. Machine learning-based error modeling to improve GPM IMERG precipitation product over the brahmaputra river basin. Forecasting 2020, 2, 248–266. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Quintana-Seguí, P.; Barella-Ortiz, A. A nonparametric statistical technique for combining global precipitation datasets: Development and hydrological evaluation over the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2018, 22, 1371–1389. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Guo, S.; Gu, L.; Zeng, Z.; Liu, D.; Chen, J.; Shen, Y.; Xu, C.-Y. Blending multi-satellite, atmospheric reanalysis and gauge precipitation products to facilitate hydrological modelling. J. Hydrol. 2021, 593, 125878. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Hao, R.; Quan, S.; Xu, Y.; Gu, Z. Precipitation assimilation from gauge and satellite products by a Bayesian method with Gamma distribution. Int. J. Remote Sens. 2021, 42, 1017–1034. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Maathuis, B.; Adem, A.A.; Demissie, S.S.; Langan, S.; Steenhuis, T.S. Comparison of rainfall estimations by TRMM 3B42, MPEG and CFSR with ground-observed data for the Lake Tana basin in Ethiopia. Hydrol. Earth Syst. Sci. 2014, 18, 4871–4881. [Google Scholar] [CrossRef] [Green Version]
- Romilly, T.G.; Gebremichael, M. Evaluation of satellite rainfall estimates over Ethiopian river basins. Hydrol. Earth Syst. Sci. 2011, 15, 1505–1514. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, S.E.; Klotter, D.A. Assessing the Reliability of Satellite and Reanalysis Estimates of Rainfall in Equatorial Africa. Remote Sens. 2021, 13, 3609. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of high-resolution satellite precipitation products over very complex terrain in Ethiopia. J. Appl. Meteorol. Climatol. 2010, 49, 1044–1051. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Barnard, E.; Cole, R.A. A Neural-Net Training Program Based on Conjugate-Gradient Optimization; Oregon Graduate Center: Beaverton, OR, USA, 1989. [Google Scholar]
- Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Polcher, J.; Albergel, C.; Dutra, E.; Fink, G.; la Torre, A.M.; Munier, S. Assessment of precipitation error propagation in multi-model global water resource reanalysis. Hydrol. Earth Syst. Sci. 2019, 23, 1973–1994. [Google Scholar] [CrossRef] [Green Version]

| Precipitation Product | Original Spatiotemporal Resolution |
|---|---|
| TMPA | 0.25 degree, daily |
| CMORPH | |
| PERSIANN | |
| ERA-Interim | |
| GSMap | 0.1 degree daily |
| Reanalysis | CMORPH | GSMaP | PERSIANN | TMPA | Rain Gauge | |
|---|---|---|---|---|---|---|
| Min (0%) | 0 | 0 | 0 | 0 | 0 | 0.02 |
| 25% | 4.09 | 2.25 | 0 | 0 | 1.25 | 3.8 |
| Median (50%) | 6.94 | 6.09 | 2.54 | 2.97 | 5.15 | 8.6 |
| 75% | 11.47 | 12.60 | 9.26 | 9.06 | 11.90 | 15.4 |
| Max (100%) | 89.26 | 112.05 | 100.00 | 86.61 | 110.91 | 166 |
| Standard Deviation | 7.91 | 9.71 | 8.63 | 8.74 | 9.85 | 9.92 |
| Parameter | Description | DT | RF | GB |
|---|---|---|---|---|
| Criterion | Function to measure the quality of a split | Mean Square Error (MSE) | MSE | MSE |
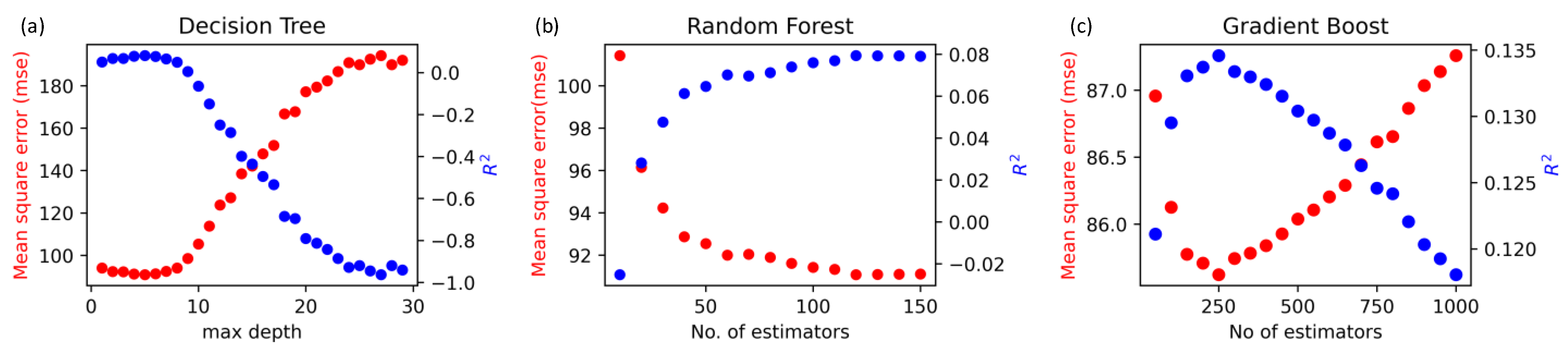
| Number of estimators | Number of trees in the forest | N/A | Figure 3b | Figure 3c |
| Splitter | Strategy to choose the split at each node | Best | N/A | N/A |
| Max Depth | Maximum depth of the tree | Figure 3a | until all leaves contain less than minimum samples for splitting (2) | 3 |
| Min samples at leaf node | Minimum number of samples required to be at a leaf node | 1 | 1 | 1 |
| Bootstrap | Using bootstrap samples to build the tree | N/A | True | N/A |
| Percentile(th) | RMSE | NCRMSE | MAE | MRD | BR | |
|---|---|---|---|---|---|---|
| <25 | Best input | GSMaP | CMORPH | PERSIANN | PERSIANN | PERSIANN |
| Best ML Model | GB | NN | GB | GB | GB | |
| Performance (%) | 13.7 | 60.0 | 80.9 | 187.5 | 146.6 | |
| 25-50 | PERSIANN | Reanalysis | Reanalysis | PERSIANN | PERSIANN | |
| NN | NN | GB | GB | GB | ||
| 26.1 | 57.5 | 3.8 | 11,549.7 | 90.2 | ||
| 50-75 | Reanalysis | Reanalysis | Reanalysis | Reanalysis | Reanalysis | |
| NN | NN | NN | NN | NN | ||
| 57.6 | 56.4 | 58.2 | 119.6 | 21.0 | ||
| >75 | CMORPH | Reanalysis | CMORPH | CMORPH | CMORPH | |
| RF | DT | RF | RF | RF | ||
| 21.9 | 26.3 | 27.2 | 13.9 | 10.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, R.S.; Bhuiyan, M.A.E. Artificial Intelligence-Based Techniques for Rainfall Estimation Integrating Multisource Precipitation Datasets. Atmosphere 2021, 12, 1239. https://doi.org/10.3390/atmos12101239
Khan RS, Bhuiyan MAE. Artificial Intelligence-Based Techniques for Rainfall Estimation Integrating Multisource Precipitation Datasets. Atmosphere. 2021; 12(10):1239. https://doi.org/10.3390/atmos12101239
Chicago/Turabian StyleKhan, Raihan Sayeed, and Md Abul Ehsan Bhuiyan. 2021. "Artificial Intelligence-Based Techniques for Rainfall Estimation Integrating Multisource Precipitation Datasets" Atmosphere 12, no. 10: 1239. https://doi.org/10.3390/atmos12101239
APA StyleKhan, R. S., & Bhuiyan, M. A. E. (2021). Artificial Intelligence-Based Techniques for Rainfall Estimation Integrating Multisource Precipitation Datasets. Atmosphere, 12(10), 1239. https://doi.org/10.3390/atmos12101239







