Temporal Variability of Drought in Nine Agricultural Regions of China and the Influence of Atmospheric Circulation
Abstract
1. Introduction
2. Study Area and Data
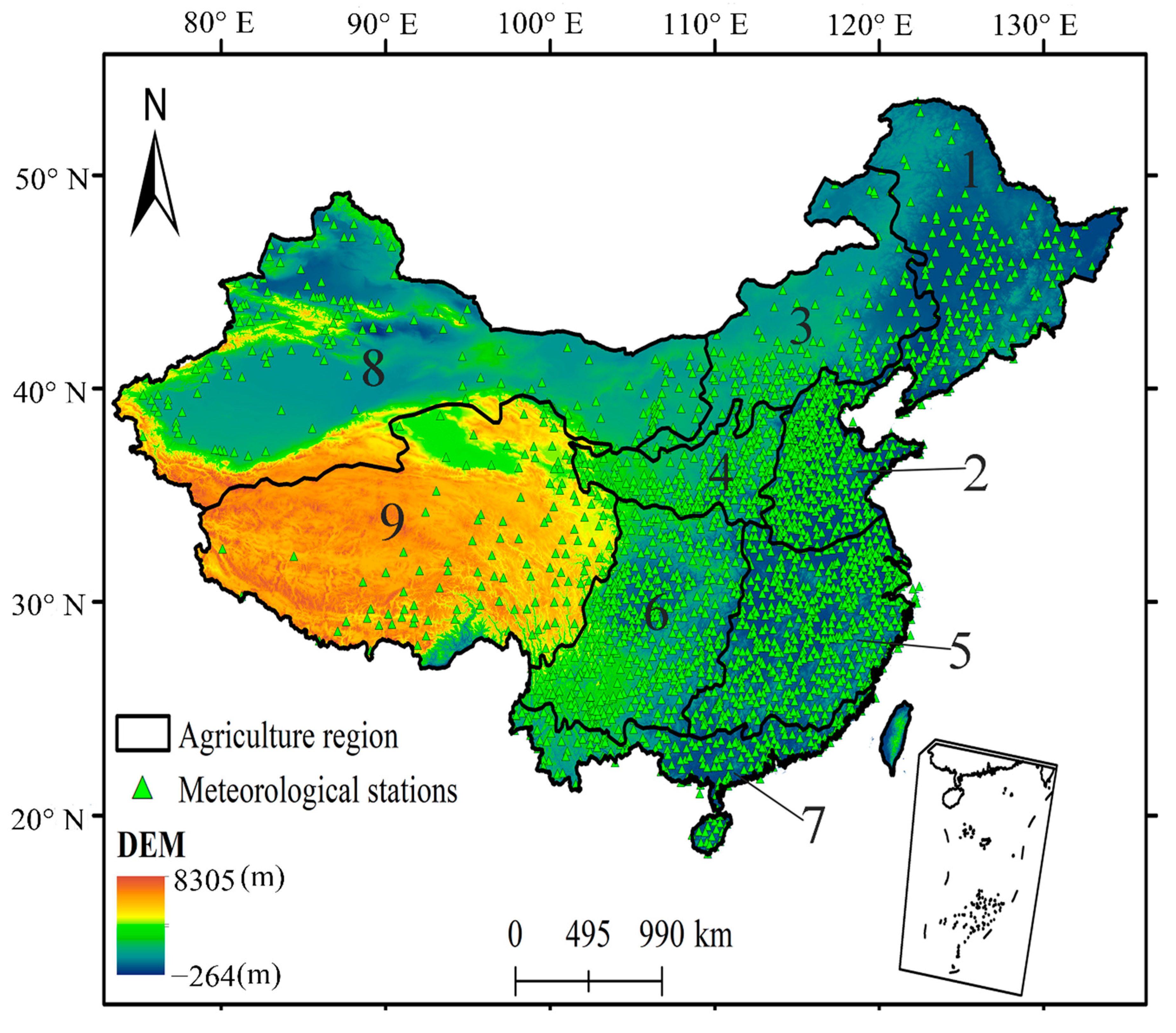
2.1. Study Area
2.2. Data
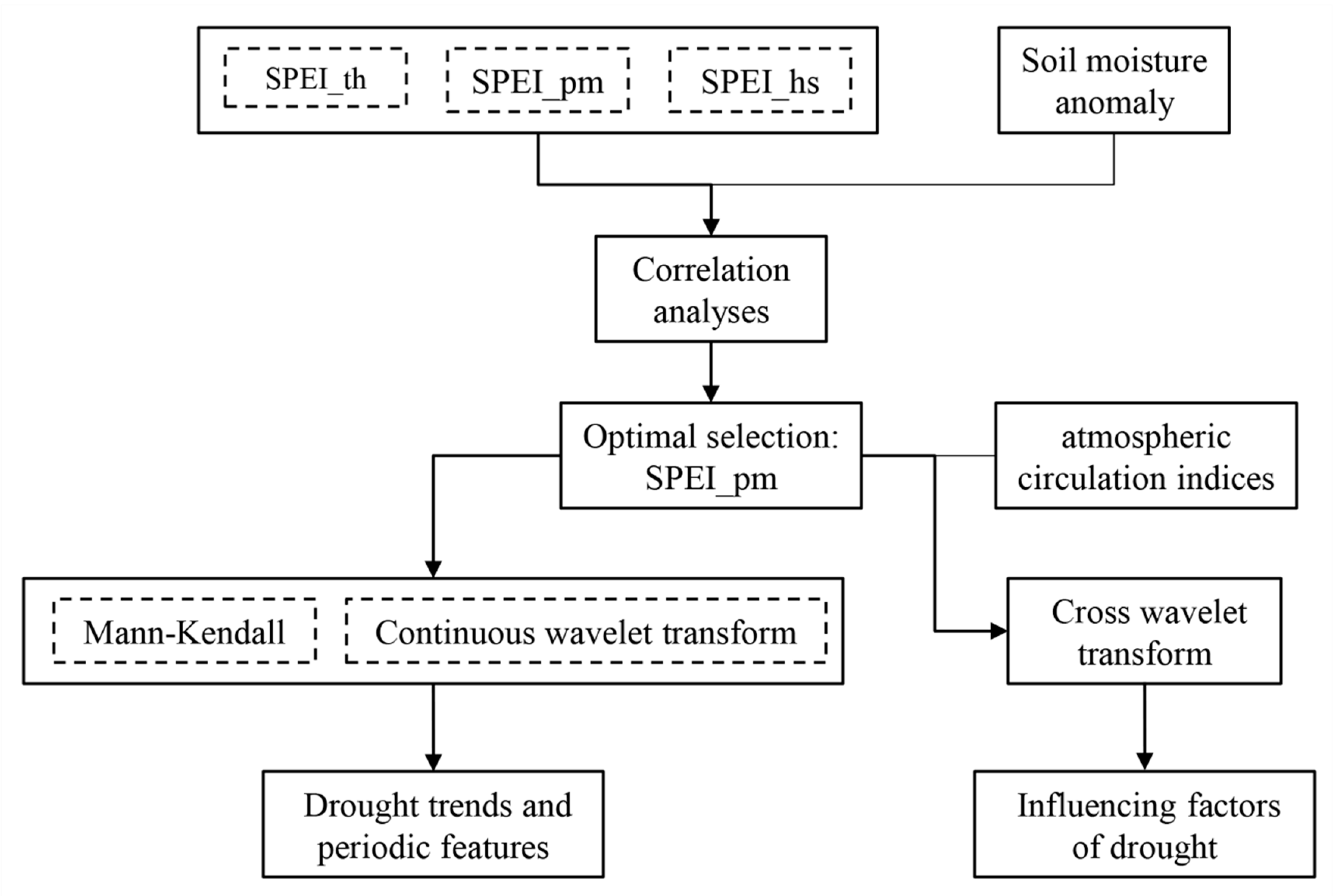
3. Methodology
3.1. PET Calculation Methods
3.1.1. TH Equation
3.1.2. HS Equation
3.1.3. PM Equation
3.2. SPEI
3.3. Continuous Wavelet Transform (CWT)
3.4. Cross-Wavelet Transform (XWT)
3.5. Mann–Kendall (MK) Test
4. Results and Discussion
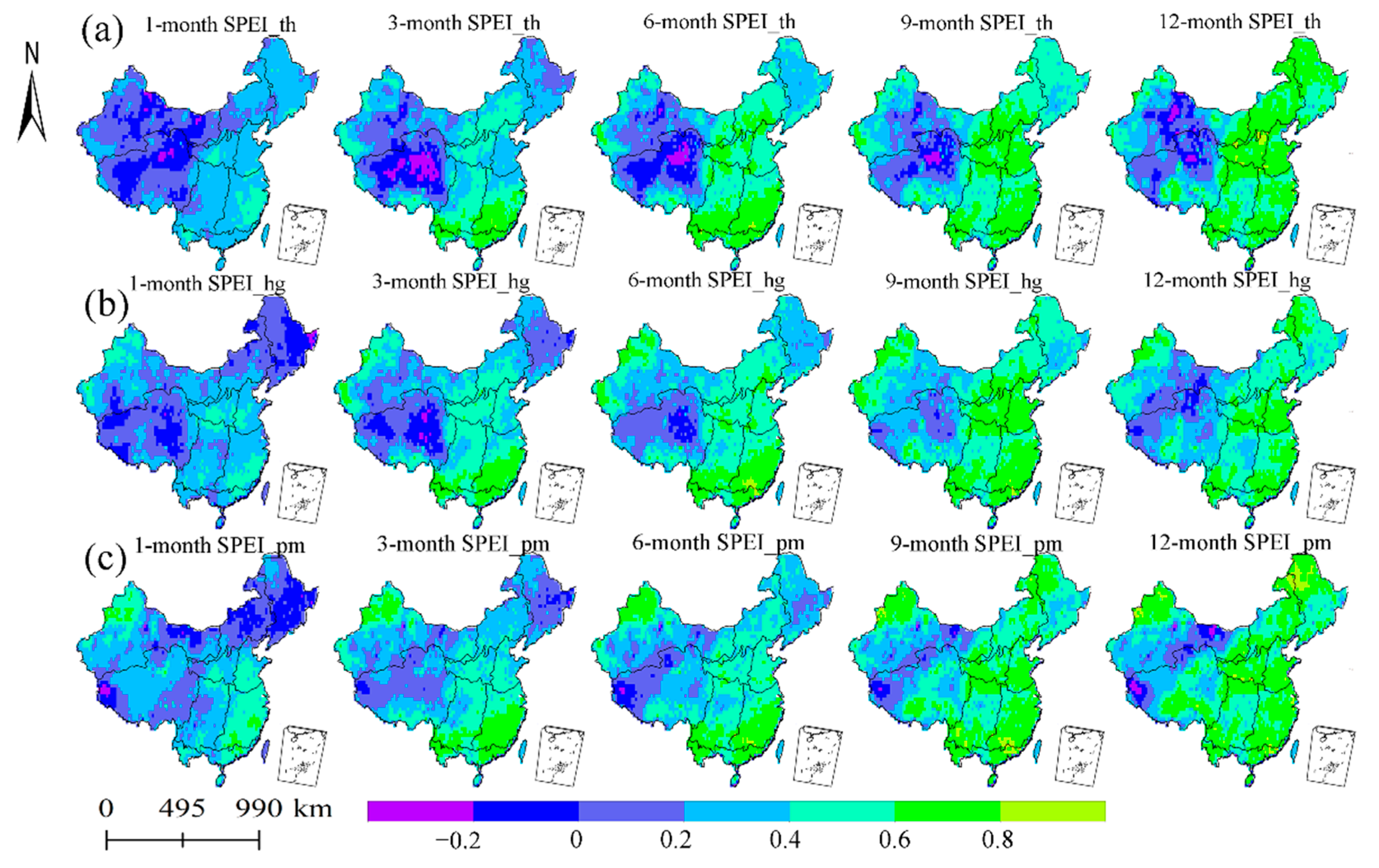
4.1. The Relation between SPEI and Soil Moisture Anomalies
4.2. Drought Trends and Periodic Features
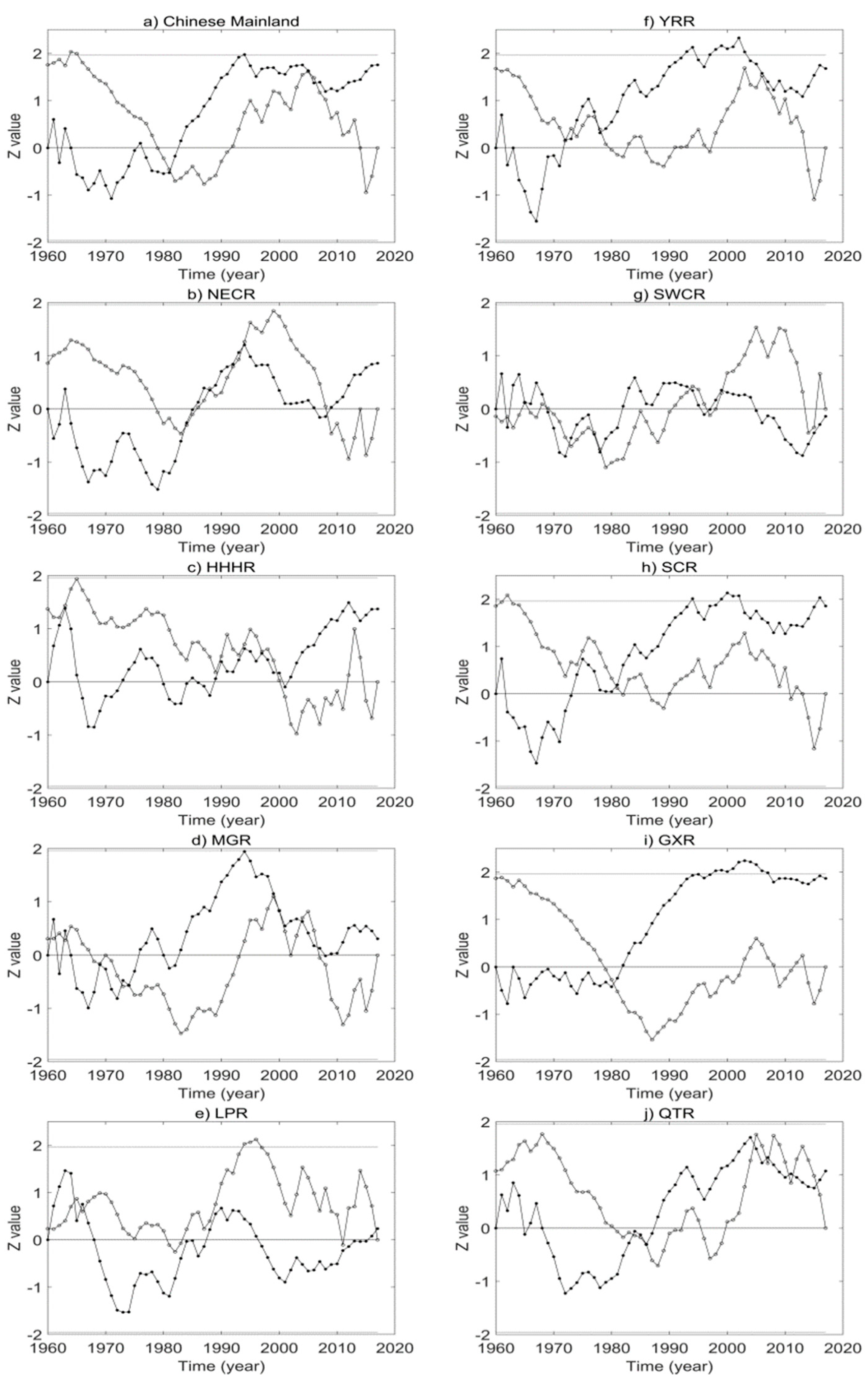
4.2.1. Drought Trends and Abrupt Change Analysis
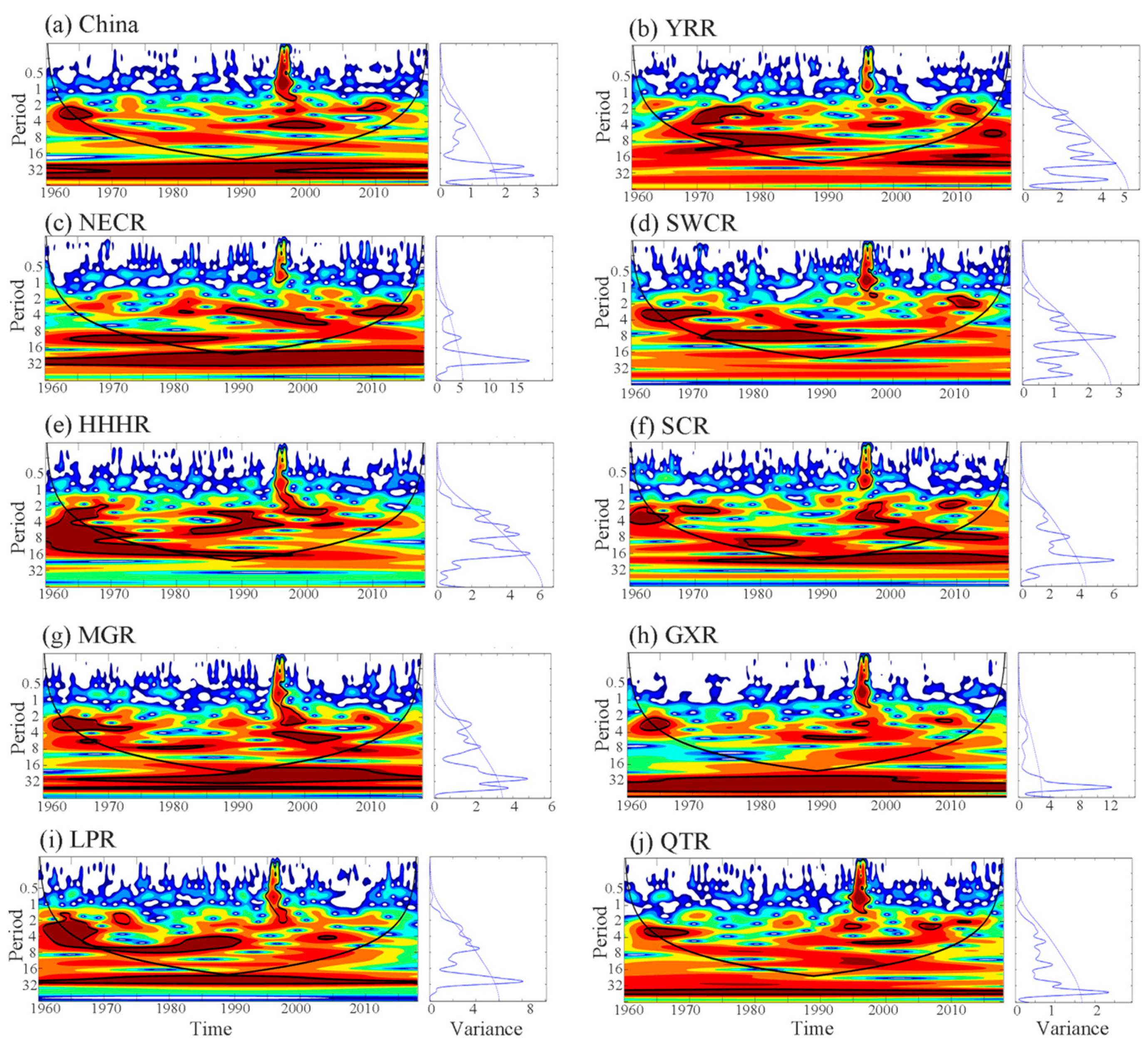
4.2.2. Periodic Oscillation
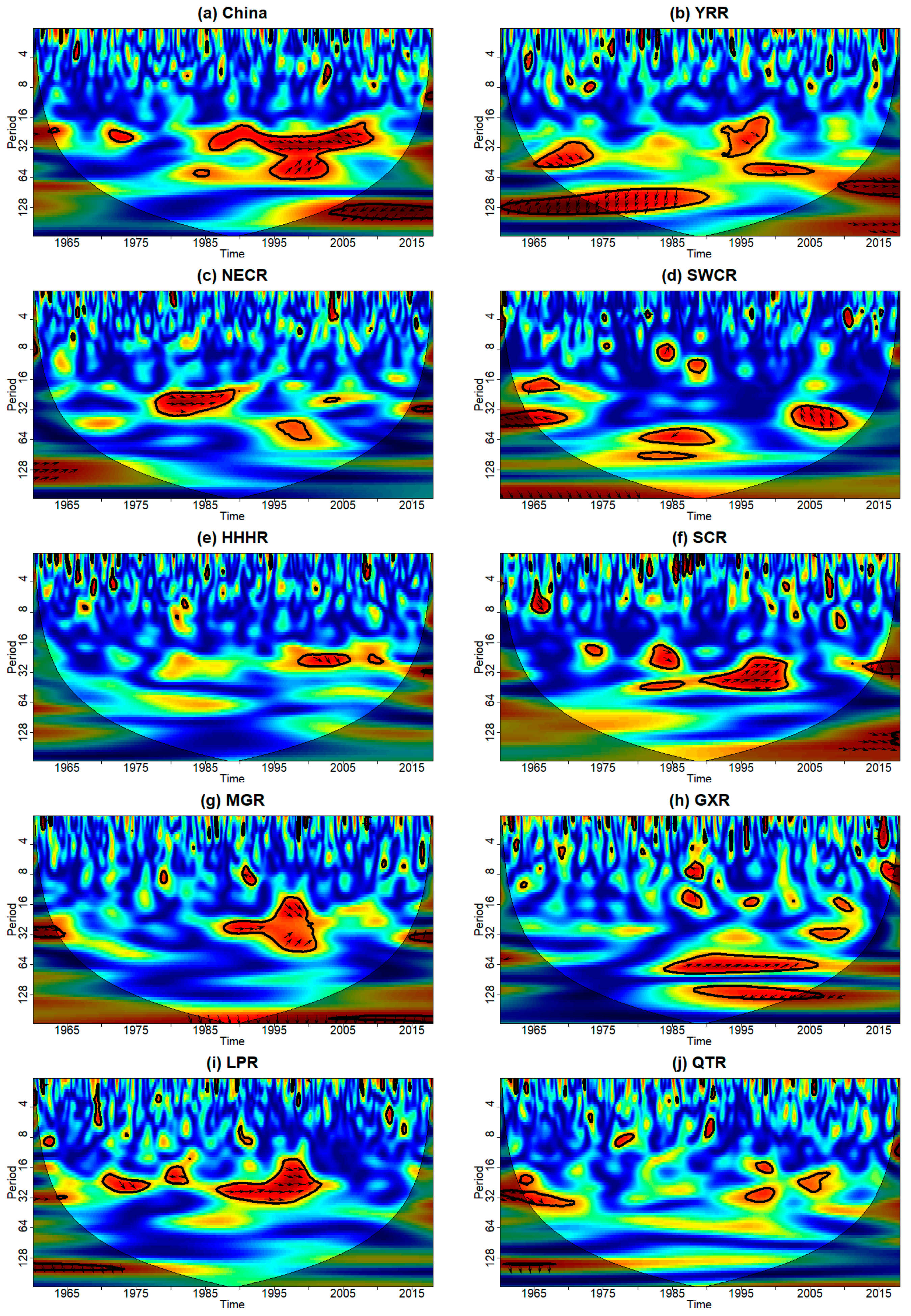
4.3. Correlations with Large-Scale Atmospheric Circulation Indices
5. Conclusions
- Compared with the TH and HS methods, the PM method was most suitable for calculating PET. The correlation between the SPEI calculated using the PM equation and soil moisture anomalies was the strongest and was even stronger when a 12-month time interval was used.
- The NECR, YRR, QTR, HHHR, GXR, and Chinese mainland all showed significant wetting trends. Most of the abrupt changes in wetting occurred in the 1970s and 1980s, while in other agricultural areas, there was an insignificant change in their trends. The primary periods of the Chinese mainland were 2.3, 2.8, and 4.6-year periods and the primary periods of the nine major agricultural areas were 2.8, 3.3, and 7.8-year periods. A significant 2–4-year drought cycle period was detected in the Chinese mainland, while the lengths of the drought cycles in the nine major agricultural areas were generally distributed in the 2–8-year range.
- The AAO, SCA, WPTW, PSH, CPTW, PSHA, and WPSHI had the greatest impact on drought in China. In the NECR and HHHR, the WPTW index had the strongest positive correlation with the SPEI. In the MGR, LPR, and QTR, the CPTW index had the strongest positive correlations with the SPEI. In the YRR and SCR, the WPSHI index had the strongest positive correlation with the SPEI, and in GXR, the AAO index had the strongest positive correlations with the SPEI. Interestingly, the EPSH exhibited the dominant influence over the SPEI in the SWCR but had a negative correlation. In addition, a common period between the SPEI of the mainland of China and WPTW appeared in the 16–64-year scale from 1986 to 2009. For the nine major agricultural areas, however, the most significant common periods between their SPEI and their respective, most influential indices were in the 16–32-year scale.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Huang, S.; Wang, L.; Wang, H.; Huang, Q.; Leng, G.; Fang, W.; Zhang, Y. Spatio-temporal characteristics of drought structure across china using an integrated drought index. Agric. Water Manag. 2019, 218, 182–192. [Google Scholar] [CrossRef]
- Riebsame, W.E. Assessing the Social Implications of Climate Fluctuations: A Guide to Climate Impact Studies; World Climate Impacts Programme, United Nations Environment Programme: Boulder, CO, USA, 1988; pp. 75–82. [Google Scholar]
- Xiao, M.; Zhang, Q.; Singh, V.P.; Liu, L. Transitional properties of droughts and related impacts of climate indices in the pearl river basin, china. J. Hydrol. 2016, 534, 397–406. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Lai, C. Severe drought events inducing large decrease of net primary productivity in mainland china during 1982–2015. Sci. Total Environ. 2020, 703, 135541. [Google Scholar] [CrossRef]
- Papadopoulou, M.P.C.D.; Spanoudaki, K.; Karali, A.; Varotsos, K.V.; Giannakopoulos, C.; Markou, M.; Loizidou, M. Agricultural water vulnerability under climate change in cyprus. Atmosphere 2020, 11, 648. [Google Scholar] [CrossRef]
- Drysdale, R.E.; Bob, U.; Moshabela, M. Socio-economic determinants of increasing household food insecurity during and after a drought in the district of ilembe, south africa. Ecol. Food Nutr. 2020, 1–19. [Google Scholar] [CrossRef]
- Hao, C.; Zhang, J.; Yao, F. Combination of multi-sensor remote sensing data for drought monitoring over southwest china. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 270–283. [Google Scholar] [CrossRef]
- Lai, C.; Zhong, R.; Wang, Z.; Wu, X.; Chen, X.; Wang, P.; Lian, Y. Monitoring hydrological drought using long-term satellite-based precipitation data. Sci. Total Environ. 2019, 649, 1198–1208. [Google Scholar] [CrossRef]
- McKee, T.; Doesken, N.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; p. 17. [Google Scholar]
- Li, J.; Wang, Z.L.; Wu, X.S.; Xu, C.Y.; Guo, S.L.; Chen, X.H. Toward monitoring short-term droughts using a novel daily scale, standardized antecedent precipitation evapotranspiration index. J. Hydrometeorol. 2020, 21, 891–908. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Jiao, W.; Tian, C.; Chang, Q.; Novick, K.A.; Wang, L. A new multi-sensor integrated index for drought monitoring. Agric. For. Meteorol. 2019, 268, 74–85. [Google Scholar] [CrossRef]
- Zhong, R.; Chen, X.; Lai, C.; Wang, Z.; Lian, Y.; Yu, H.; Wu, X. Drought monitoring utility of satellite-based precipitation products across mainland china. J. Hydrol. 2019, 568, 343–359. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Van der Schrier, G.; Beguería, S.; Azorin-Molina, C.; Lopez-Moreno, J.-I. Contribution of precipitation and reference evapotranspiration to drought indices under different climates. J. Hydrol. 2015, 526, 42–54. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate distributions for climatological drought indices (spi and spei). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (spei) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Yu, M.X.; Li, Q.F.; Hayes, M.J.; Svoboda, M.D.; Heim, R.R. Are droughts becoming more frequent or severe in china based on the standardized precipitation evapotranspiration index: 1951–2010? Int. J. Climatol. 2014, 34, 545–558. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Z.; Zhong, R.; Zeng, Z.; Chen, X.; Li, J.; Lai, C. Increasing drought has been observed by spei_pm in southwest china during 1962–2012. Theor. Appl. Climatol. 2018, 133, 23–38. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef]
- Unes, F.; Kaya, Y.Z.; Mamak, M. Daily reference evapotranspiration prediction based on climatic conditions applying different data mining techniques and empirical equations. Theor. Appl. Climatol. 2020, 141, 763–773. [Google Scholar] [CrossRef]
- Yuan, S.; Quiring, S.M. Drought in the us great plains (1980–2012): A sensitivity study using different methods for estimating potential evapotranspiration in the palmer drought severity index. J. Geophys. Res. Atmos. 2014, 119, 10996–11010. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.Z.; Huang, Q.; Huang, G.H.; Meng, E.H.; Luan, J.K. Reference evapotranspiration forecasting based on local meteorological and global climate information screened by partial mutual information. J. Hydrol. 2018, 561, 764–779. [Google Scholar] [CrossRef]
- Van der Schrier, G.; Jones, P.D.; Briffa, K.R. The sensitivity of the pdsi to the thornthwaite and penman-monteith parameterizations for potential evapotranspiration. J. Geophys. Res. Atmos. 2011, 116, 116. [Google Scholar] [CrossRef]
- Dai, A. Characteristics and trends in various forms of the palmer drought severity index during 1900–2008. J. Geophys. Res. Atmos. 2011, 116, 79–83. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Lai, C.; Zhang, Z. Tree-ring-width based streamflow reconstruction based on the random forest algorithm for the source region of the yangtze river, china. Catena 2019, 183, 104216. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, Z.; Chen, G. A sensitivity study of applying a two-source potential evapotranspiration model in the standardized precipitation evapotranspiration index for drought monitoring. Land Degrad. Dev. 2017, 28, 783–793. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; FAO, Irrigation and Drainage: Roma, Italy, 1998; p. 56. [Google Scholar]
- Hargreaves, G.H.; Allen, R.G. History and evaluation of hargreaves evapotranspiration equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Hui-Mean, F.; Yusop, Z.; Yusof, F. Drought analysis and water resource availability using standardised precipitation evapotranspiration index. Atmos. Res. 2018, 201, 102–115. [Google Scholar] [CrossRef]
- Chen, H.P.; Sun, J.Q. Anthropogenic warming has caused hot droughts more frequently in china. J. Hydrol. 2017, 544, 306–318. [Google Scholar] [CrossRef]
- Yang, J.; Gong, D.Y.; Wang, W.S.; Hu, M.; Mao, R. Extreme drought event of 2009/2010 over southwestern China. Meteorol. Atmos. Phys. 2012, 115, 173–184. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Lai, C.; Zeng, Z.; Zhong, R.; Chen, X.; Zhou, X.; Wang, M. Does drought in china show a significant decreasing trend from 1961 to 2009? Sci. Total Environ. 2017, 579, 314–324. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Li, Y.; Song, S.; Yao, N. Spatial comparability of drought characteristics and related return periods in mainland china over 1961–2013. J. Hydrol. 2017, 550, 549–567. [Google Scholar] [CrossRef]
- Ionita, M.; Chelcea, S.; Rimbu, N.; Adler, M.J. Spatial and temporal variability of winter streamflow over romania and its relationship to large-scale atmospheric circulation. J. Hydrol. 2014, 519, 1339–1349. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wu, X.; Chen, J.; Guo, S. A new framework for tracking flash drought events in space and time. Catena 2020, 194, 104763. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Zhang, F.; Liu, X.; Chen, G. Spatiotemporal characteristics of dryness/wetness conditions across qinghai province, northwest china. Agric. For. Meteorol 2013, 182–183, 101–108. [Google Scholar] [CrossRef]
- Rubinetti, S.T.; Alessio, S.; Rubino, A.; Bizzarri, I.; Zanchettin, D. Robust decadal hydroclimate predictions for northern italy based on a twofold statistical approach. Atmosphere 2020, 11, 671. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Li, W. Spatial and temporal variability of drought in the arid region of china and its relationships to teleconnection indices. J. Hydrol. 2015, 523, 283–296. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Z.; Saito, Y.; Liu, J.P.; Sun, X. Interannual and seasonal variation of the huanghe (yellow river) water discharge over the past 50 years: Connections to impacts from enso events and dams. Glob. Planet. Chang. 2006, 50, 212–225. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Jiang, T.; Wu, Y. Possible influence of enso on annual maximum streamflow of the yangtze river, china. J. Hydrol. 2007, 333, 265–274. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Hu, Q.; Lv, H. Spatial variability of the trends in climatic variables across china during 1961–2010. Theor. Appl. Climatol. 2015, 120, 773–783. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Lu, G.H.; Wen, L.; Lin, C.A. Reconstructing and analyzing china’s fifty-nine year (1951–2009) drought history using hydrological model simulation. Hydrol. Earth Syst. Sci. 2011, 15, 2881–2894. [Google Scholar] [CrossRef]
- Zou, X.K.; Zhai, P.M.; Zhang, Q. Variations in droughts over china: 1951–2003. Geophys. Res. Lett. 2005, 32, 32. [Google Scholar] [CrossRef]
- Xu, C.Y.; Gong, L.B.; Jiang, T.; Chen, D.L.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in changjiang (yangtze river) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Xu, X.; Lin, H.; Hou, L.; Yao, X. An assessment for sustainable developing capability of integrated agricultural regionallization in china. Chin. Geogr. Sci. 2002, 12, 1–8. [Google Scholar] [CrossRef]
- China Meteorological Administration. Available online: http://cdc.nmic.cn/home.do (accessed on 31 December 2018).
- Community Land Model (CLM) of the Global Land Data Assimilation System (GLDAS). Available online: https://ldas.gsfc.nasa.gov/gldas) (accessed on 31 December 2018).
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.R.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Wang, W.C.; Wei, J.F. Assessing land-atmosphere coupling using soil moisture from the global land data assimilation system and observational precipitation. J. Geophys. Res. Atmos. 2008, 113, 14. [Google Scholar] [CrossRef]
- Feng, X.; Fu, B.; Piao, S.; Wang, S.; Ciais, P.; Zeng, Z.; Lü, Y.; Zeng, Y.; Li, Y.; Jiang, X.; et al. Revegetation in china’s loess plateau is approaching sustainable water resource limits. Nat. Clim. Chang. 2016, 6, 1019. [Google Scholar] [CrossRef]
- Climate Diagnostics and Prediction Division of the National Climate Center of China. Available online: https://cmdp.ncc-cma.net/cn/ (accessed on 31 December 2018).
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Hargreaves, G.L.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. An r package for modelling actual, potential and reference evapotranspiration. Environ. Model. Softw. 2016, 78, 216–224. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Zhang, Z.; Chen, Y.D.; Liu, C.L. Spatial and temporal variability of precipitation over china, 1951–2005. Theor. Appl. Climatol. 2009, 95, 53–68. [Google Scholar] [CrossRef]
- Charlier, J.-B.; Ladouche, B.; Marechal, J.C. Identifying the impact of climate and anthropic pressures on karst aquifers using wavelet analysis. J. Hydrol. 2015, 523, 610–623. [Google Scholar] [CrossRef]
- Gan, T.Y.; Gobena, A.K.; Wang, Q. Precipitation of southwestern canada: Wavelet, scaling, multifractal analysis, and teleconnection to climate anomalies. J. Geophys. Res. Atmos. 2007, 112, 112. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, J.; Wang, J.; Li, R.; Hao, P.; Zhan, H. How does the anthropogenic activity affect the spring discharge? J. Hydrol. 2016, 540, 1053–1065. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Processes Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Khalil, B.; Biswas, A. Inter-annual to inter-decadal streamflow variability in quebec and ontario in relation to dominant large-scale climate indices. J. Hydrol. 2016, 536, 426–446. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Hamed, K.H.; Ramachandra Rao, A. A modified mann-kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the mann-kendall test. Water Resour. Res. 2002, 38, 1068. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, H.; Chen, X.; Hagan, D.F.T.; Wang, G.; Gao, Z.; Shi, T. Robust drying and wetting trends found in regions over china based on koppen climate classifications. J. Geophys. Res. Atmos. 2017, 122, 4228–4237. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Zeng, Z.; Lian, Y.; Bai, X. Climate change enhances the severity and variability of drought in the pearl river basin in south china in the 21st century. Agric. For. Meteorol. 2018, 249, 149–162. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Suhaila, J.; Yusop, Z. Spatial and temporal variabilities of rainfall data using functional data analysis. Theor. Appl. Climatol. 2017, 129, 229–242. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in china. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, P.; Lai, C.; Chen, X.; Wu, X.; Zeng, Z.; Li, L. Spatiotemporal variability of reference evapotranspiration and contributing climatic factors in china during 1961–2013. J. Hydrol. 2017, 544, 97–108. [Google Scholar] [CrossRef]
- Zhang, K.-X.; Pan, S.-M.; Zhang, W.; Xu, Y.-H.; Cao, L.-G.; Hao, Y.-P.; Wang, Y. Influence of climate change on reference evapotranspiration and aridity index and their temporal-spatial variations in the yellow river basin, china, from 1961 to 2012. Quat. Int. 2015, 380–381, 75–82. [Google Scholar] [CrossRef]
- Sun, J.; Huang, Y.M.; Han, J.; Zhang, X.P. Comparison on relationship between western pacific subtropical high and summer precipitation over dongting lake basin based on different datasets. Asia-Pac. J. Atmos. Sci 2020, 16. [Google Scholar] [CrossRef]
- Ma, L.H.; Han, Y.B.; Yin, Z.Q. Quasi-biennial oscillation signals in outgoing long-wave radiation of the equator. Adv. Space Res. 2010, 46, 1477–1481. [Google Scholar] [CrossRef]
- Fan, K.; Wang, H. Antarctic oscillation and the dust weather frequency in north china. Geophys. Res. Lett. 2004, 31, 31. [Google Scholar] [CrossRef]
- Guo, X.; Wu, Z.-F.; He, H.S.; Du, H.; Wang, L.; Yang, Y.; Zhao, W. Variations in the start, end, and length of extreme precipitation period across china. Int. J. Climatol. 2018, 38, 2423–2434. [Google Scholar] [CrossRef]
- Sun, J.; Ming, J.; Zhang, M.; Yu, S. Circulation features associated with the record-breaking rainfall over south china in June 2017. J. Clim. 2018, 31, 7209–7224. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H.; Yuan, W. A possible mechanism for the co-variability of the boreal spring antarctic oscillation and the yangtze river valley summer rainfall. Int. J. Climatol. 2009, 29, 1276–1284. [Google Scholar] [CrossRef]
| Categories | SPEI Values |
|---|---|
| Extremely dryness | Less than −2 |
| Severe dryness | −1.99 to −1.5 |
| Moderate dryness | −1.49 to −1.0 |
| Near normal | −1.0 to 1.0 |
| Moderate wetness | 1.0 to 1.49 |
| Severe wetness | 1.50 to 1.99 |
| Extremely wetness | More than 2 |
| Original Words | Acronyms |
|---|---|
| Antarctic Oscillation | AAO |
| Scandinavian Model | SCA |
| West Pacific 850 mb Trade Wind Index | WPTW |
| Pacific Subtropical High Intensity Index | PSH |
| Central Pacific 850 mb Trade Wind Index | CPTW |
| Pacific Subtropical High Area Index | PSHA |
| Western Pacific Subtropical High Intensity Index | WPSHI |
| The East Pacific subtropical ridge position index | EPSH |
| The standardized precipitation evapotranspiration index | SPEI |
| Northeast China Region | NECR |
| Huang-Huai-Hai Region | HHHR |
| Inner Mongolia and the Great Wall Region | MGR |
| Loess Plateau Region | LPR |
| Middle and lower regions of the Yangtze River | YRR |
| Southwest China Region | SWCR |
| South China Region | SCR |
| Gan-Xin Region | GXR |
| Qinghai-Tibet Plateau Region | QTR |
| Soil moisture standardized anomaly | SMA |
| NECR | HHHR | MGR | LPR | YRR | SWCR | SCR | GXR | QTR | Mainland |
|---|---|---|---|---|---|---|---|---|---|
| 2.11 | 2.04 | −0.47 | 0.21 | 2.15 | −0.47 | 0.72 | 6.45 | 2.41 | 2.61 |
| Region | Period | Min Period | Inter-Annual Oscillations | Significant Period |
|---|---|---|---|---|
| NECR | 3.3/11 | 3.3 11 | 2–4-year band 8–12-year band | 2008–2016 1965–1988 |
| HHHR | 2.8/4.6/6.6 | 2.8 4.6 6.6 | 0–4-year band 2–8-year band 2–16-year band | 1996–2004 1983–1996 1961–1998 |
| MGR | 2.8/4.6/6.6 | 2.8 6.6 | 2–4-year band 6–8-year band | 1962–1974 1974–1985 |
| LPR | 2.8/4.6/6.6 | 2.8 4.6 6.6 | 1–8-year band 3–4-year band 4–8-year band | 1962–1970 2002–2006 1970–1992 |
| YRR | 2.3/3.9/7.8 | 2.3 | 1–4-year band | 1969–1980 |
| SWCR | 3.3/4.6/7.8 | 3.3 7.8 | 2–4-year band 6–10-year band | 1962–1973 1970–1995 |
| SCR | 3.3/3.9/7.8 | 3.3 7.8 | 1–3-year band 4–8-year band | 2008–2012 1999–2017 |
| GXR | 2.8/4.6 | 2.8 | 2–4-year band | 1963–1968 |
| QTR | 3.3/4.6 | - | - | - |
| Index | SCR | YRR | SWCR | LPR | QTR | HHHR | MGR | GXR | NECR | Mainland |
|---|---|---|---|---|---|---|---|---|---|---|
| WPTW | 0.207 | 0.159 | 0.076 | 0.091 | 0.151 | 0.169 | 0.104 | 0.152 | 0.136 | 0.184 |
| AAO | 0.241 | 0.216 | 0.015 | 0.080 | 0.096 | 0.094 | 0.095 | 0.198 | 0.080 | 0.174 |
| SCA | −0.146 | −0.154 | −0.051 | −0.061 | −0.103 | −0.069 | −0.069 | −0.165 | −0.081 | −0.147 |
| PSH | 0.272 | 0.288 | 0.008 | −0.042 | 0.004 | 0.047 | −0.004 | 0.143 | 0.126 | 0.127 |
| CPTW | 0.010 | −0.026 | 0.087 | 0.229 | 0.152 | 0.154 | 0.125 | 0.036 | 0.078 | 0.111 |
| PSHA | 0.259 | 0.276 | −0.005 | −0.053 | −0.001 | 0.041 | −0.003 | 0.146 | 0.129 | 0.122 |
| WPSHI | 0.292 | 0.310 | −0.001 | −0.081 | −0.011 | 0.032 | −0.014 | 0.138 | 0.120 | 0.119 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Hu, H.; Wang, Z.; Lai, C. Temporal Variability of Drought in Nine Agricultural Regions of China and the Influence of Atmospheric Circulation. Atmosphere 2020, 11, 990. https://doi.org/10.3390/atmos11090990
Sun H, Hu H, Wang Z, Lai C. Temporal Variability of Drought in Nine Agricultural Regions of China and the Influence of Atmospheric Circulation. Atmosphere. 2020; 11(9):990. https://doi.org/10.3390/atmos11090990
Chicago/Turabian StyleSun, Haowei, Haiying Hu, Zhaoli Wang, and Chengguang Lai. 2020. "Temporal Variability of Drought in Nine Agricultural Regions of China and the Influence of Atmospheric Circulation" Atmosphere 11, no. 9: 990. https://doi.org/10.3390/atmos11090990
APA StyleSun, H., Hu, H., Wang, Z., & Lai, C. (2020). Temporal Variability of Drought in Nine Agricultural Regions of China and the Influence of Atmospheric Circulation. Atmosphere, 11(9), 990. https://doi.org/10.3390/atmos11090990





