Abstract
Glacio-hydrological models combine both glacier and catchment hydrology modeling and are used to assess the hydrological response of high-mountain glacierized catchments to climate change. To capture the uncertainties from these model combinations, it is essential to compare the outcomes of several model entities forced with the same climate projections. For the first time, we compare the results of two completely independent glacio-hydrological models: (i) HQsim-GEM and (ii) AMUNDSEN. In contrast to prevailing studies, we use distinct glacier models and glacier initialization times. At first glance, the results achieved for future glacier states and hydrological characteristics in the Rofenache catchment in Ötztal Alps (Austria) appear to be similar and consistent, but a closer look reveals clear differences. What can be learned from this study is that low-complexity models can achieve higher accuracy in the calibration period. This is advantageous especially when data availability is weak, and priority is given to efficient computation time. Furthermore, the time and method of glacier initialization play an important role due to different data requirements. In essence, it is not possible to make conclusions about the model performance outside of the calibration period or more specifically in the future. Hence, similar to climate modeling, we suggest considering different modeling approaches when assessing future catchment discharge or glacier evolution. Especially when transferring the results to stakeholders, it is vital to transparently communicate the bandwidth of future states that come with all model results.
1. Introduction
Future high-mountain hydrology is heavily dependent on glacier evolution (i.e., the changes of glacier characteristics over time, such as volume, elevation or length). The ongoing climate-induced mass loss of mountain glaciers affects the hydrological cycle on multiple scales [1]. In this context, glacio-hydrological modeling, the combined modeling of both glaciers and catchment hydrology, received a lot of attention in the recent past [2,3,4,5,6,7]. Glacio-hydrological models include one main process for each model component: first, glacier mass balance, the accumulation of snow and ice; second, the water balance, the storage and release of water. The “glacio” component allows changing ice-covered areas to be taken into account when modeling runoff from high-alpine glacierized catchments. Indeed, there are various approaches to model glacier retreat. Dealing with the (variable) glacier volume and area is one of the major challenges in modeling glaciers [8]. On the one hand, there are empirical methods using (i) a volume-area-scaling [9] that estimate the glacier volume based on the glacier area, or (ii) a approach [10], relating an integrated mass balance to changes in ice thickness (h) and glaciated area. On the other hand, sophisticated state of the art model frameworks, such as the Open Global Glacier Model OGGM [11], comprise “data downloading tools (glacier outlines, topography, climate, validation data), a preprocessing module, a mass-balance model, a distributed ice thickness estimation model, and an ice-flow model” to simulate changes in glacier geometry. However, by including glacier change data in the model chain of hydrological modeling (empirical or physical-based), the associated contribution of ice melt to the river flow can be estimated.
Various studies have attempted to simulate future runoff with glacio-hydrological models using different climate simulations and/or scenarios for the 21st century, while taking into account that the model-based projections show remarkable uncertainties from different origins [3,7,12,13,14]. Although the projected future hydrological responses to glacier mass loss are globally highly variable in space and time [15], the results of existing studies on hydrological responses of glacierized catchments across the Alps reveal the following key findings: An initial increase of water availability connected to higher temperatures and respective melt rates is expected to turn into a decrease as the glaciers dwindle. Accordingly, future runoff characteristics are assumed to shift from a prior ice melt dominated regime towards a snow melt dominated regime [5,16]. On the one hand, runoff most likely increases in spring and early summer, attributed to an earlier onset of annual snow/ice melt season; on the other hand, it appears that runoff contribution from glacier melt in the summer months decreases significantly, due to the rapid glacier retreat [3,17,18,19,20]. Thus, by the end of this century, the annual peak runoff is expected to shift from late summer to earlier months [7]. From a regional and local perspective, the future evolution of river flow is of great interest, especially the timing, magnitude and variability of the expected changes.
Although modeling the hydrological response to climate change including changing glacier variables is the main focus of several studies (e.g., [3,4,5,12,21,22,23]), only very few studies exist relating to model comparisons. Based on different climate projections, Wijngaard et al. [16] found minor differences comparing the outcome of two independent hydrological models, HBV [24,25] and HQsim [26,27], which use data of glacial extent from the same empirical glacier model by a 10-year interval. When comparing existing glacio-hydrological models, there are considerable differences in the type of complexity, the temporal and spatial resolution and the required data basis, respectively. Some are high-complexity models with long computational time associated with many input variables. Data availability in complex terrain is however a major issue. Conversely, low-complexity models with lower resolution can often manage simulations with only a few input data and are fairly simple and fast. There are broad advantages of using low-complexity models: The wide availability of air temperature data makes interpolation and forecasting possibilities relatively easy; moreover, the model implementation is time-efficient due to its simplicity and the model performance often is satisfying. A comprehensive study comparing discharge projections of various catchments using three different hydrological models to assess uncertainties of the model chain was carried out by Addor et al. [6]. The authors reveal robust regime changes under climate change by the models of different complexity. Similarly, Mackay et al. [28] compared different modeling alternatives in glacierized catchments. However, besides the fact that numerous different model components are compared, both studies [6,28] neglect to address competing hypotheses—a term suggested by Clark et al. [29]—to describe glacier evolution or more specifically changes in glacier characteristics over time. Indeed, there is a wide range of sophisticated glacio-hydrological models available in diverse types of complexity. A detailed comparison of these models is however beyond the scope of this work.
For the first time, we compare the outcome of two glacio-hydrological models, being a representative example for a wide range of existing models in terms of complexity (low vs. high). The novelty of this comparison is that we combine each hydrological model with different glacier models, as opposed to other studies that only concentrate on hydrological models. Besides separate glacier models, we also use different glacier initialization times for both model approaches (i) HQsim-GEM and (ii) AMUNDSEN. Both are forced with the same downscaled and bias-corrected climate projections for the RCPs (Representative Concentration Pathways) 2.6, 4.5, and 8.5. The first glacio-hydrological model HQsim-GEM is a coupled version of two independent models on different timescales: a low-complexity glacier evolution model (GEM) by Marzeion et al. [30] based on a temperature-index approach on a monthly resolution; and a semi-distributed hydrological model (HQsim), originally developed for operational flood forecasting, allowing a daily resolution within this context. It only requires the meteorological variables air temperature and precipitation, two components assumed to be the main drivers of glacier mass balances to simplify matters. The ability of reproducing glacier advances is the key advantage of this model setup compared to other glacio-hydrological models. Our second model, AMUNDSEN [31,32], implemented the method [10] to adjust glacier geometry in a more complex, physical-based approach, with a high temporal and spatial resolution. To estimate uncertainties from the input data, we use multi-model ensemble means based on different emission scenarios.
We apply the two models in the catchment of the Rofenache (Ötztal Alps, Austria), by focusing on the model comparison rather than the results itself. The Rofenache is a well-studied research catchment for which many studies have already been carried out [33]. What we want to learn from this study is how comparable are the results of two completely independent glacio-hydrological models with different resolution in time and space. The central question that motivates this paper is: What can we learn from comparing two fully independent glacio-hydrological models?
The paper is structured as follows: Section 2 introduces the study area and the meteorological, hydrological, glaciological and climatological data used for the study. Section 3 provides a short description of the two employed glacio-hydrological models including their setup for the study area. Subsequently, Section 4 contains the results of the scenario simulations in terms of changes in glacierization and hydrology, followed by a discussion of the results in Section 5 and our conclusions in Section 6.
2. Data and Methods
2.1. Catchment
The study area of the catchment Rofenache (98.1 ; Figure 1; Strasser et al. [33]) is located in the south of the Ötztal Valley. Rofenache is a headwater stream of the Ötztaler Ache, flowing into the Inn and finally contributing to the Danube system. The Ötztal Alps as part of the Alpine main ridge are situated in the Eastern Alps, in the south-west of Tyrol (Austria). This area comprises several headwater catchments within the bordering valleys, all entering the river Inn. The catchment is comprising 19 glaciers in total (year 2006; from 21 in 1969), including some of the world’s most intensively studied glaciers, such as Hintereisferner, Kesselwandferner, and Vernagtferner. The elevation ranges from the catchment’s lowest point at the gauge in Vent (1891 m a.s.l.) to the summit of Wildspitze (3772 m a.s.l.). The glacierization relative to the total area in 2006 was approximately 34% (1969: 43.6% and 1997: 37.7%), see Section 2.3. The runoff regime within this highly glacierized catchment is dominated by the snow and ice melt season during spring and summer, with a significant maximum in July and August [33]. The longest available time series of meteorological data is Vent station, located at 1891 m a.s.l. at the end of the valley, with daily recordings of temperature and precipitation since 1935 [34]. Climatological long-term averages from 1971–2000 calculated from this data reveal a mean monthly air temperature ranging from −5.5 to 10.6 . Mean annual total precipitation within this climate period is 666 mm. Maximum accumulated monthly precipitation occurred in the summer months (79 mm in July), whereas minimum average monthly precipitation appeared in winter (32 mm in February). Yearly sum of areal precipitation is approximately 1200–1500 mm [7,35]. A precipitation gradient of 4–5% per 100 m is found in [36] for this study area.
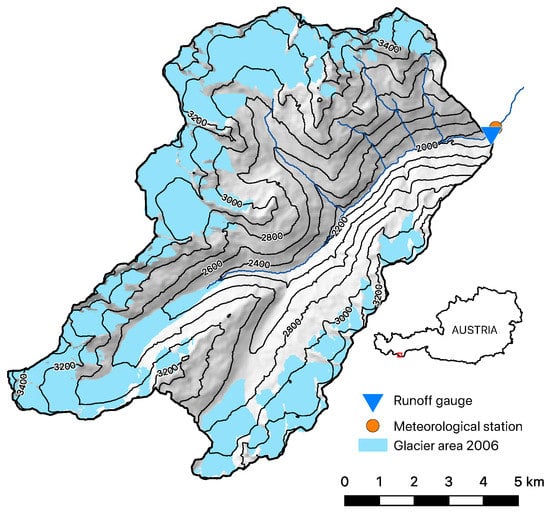
Figure 1.
Map of the Rofenache catchment including glacierized areas and the locations of the runoff gauge and the meteorological station in Vent.
2.2. Meteorological and Hydrological Data
Long-term observations of daily air temperature and precipitation data are available for the station Vent dating back to 1935 by courtesy of the Institute of Atmospheric and Cryospheric Sciences (ACINN) [34]. Although the low-complexity model relies on air temperature and precipitation data, the high-complexity model additionally refers to relative humidity, global radiation and wind speed, see Hanzer et al. [7].
The runoff gauge in Vent is placed in the first order stream of the Rofenache operated by the Hydrographic service Tyrol, HD, see Figure 1. Daily mean values of observed runoff, which have been derived from water level measurements, were used to calibrate and validate the model. These time series have been divided into decades, showing the fluctuation of runoff within the available period. In the decadal average of the 1970s and the 1990s, summer peak discharge occurred in August, whereas this peak shifted to July within the other decades. However, the 30-year mean shows no difference between July and August runoff (not shown here). Lowest decadal average discharge could be found in 1971–1980, which is known as a period of glacier advance, as shown by [37,38].
2.3. Glacier Information Data
Past glacier survey data are available from the Austrian Glacier Inventory (AGI) for the years 1969, 1997, 2006 [39,40,41] and 2015/2016 [42]. The dataset includes glacier outlines.
2.4. Climate Simulations
Future climate simulation data are acquired from EURO-CORDEX [43,44], the European branch of the international CORDEX (Coordinated Downscaling Experiment) initiative. The ensemble members of 14 GCM-RCM combinations are used for the Representative Concentration Pathways RCP4.5, and RCP8.5 (with a high-resolution of 12.5 km-EUR-11). To include a mitigation scenario as well, we include the RCP2.6 scenario, available for three of 14 GCM-RCM combinations. The data has been used to reflect climatic changes within different climate projections and bundled together as a multi-model ensemble of each scenario. The reference climate period (1998–2011) combines data of historical (1998–2005) and projected (2006–2011) simulation runs. For the future projections we define three different climate periods from 2011–2040, 2041–2070 and 2071–2099 and compute the mean monthly runoff. The latter period only consists of 29 years, since some ensemble members simulations ended in 2099. Climate periods of the simulated runoff are compared to the observed/measured runoff data from the past period. A detailed description and analysis of the climate simulations can be found in Hanzer et al. [7].
2.5. Downscaling/Bias Correction of the Climate Simulations
The spatial resolution of the initial EURO-CORDEX data is too coarse for our model application in rugged terrain, therefore a spatial downscaling of the data was applied by using a quantile mapping approach according to Gudmundsson et al. and Thrasher et al. [45,46], respectively. This statistical transformation relates to the distribution function of each parameter (air temperature and precipitation for HQsim-GEM, and additionally relative humidity, global radiation and wind speed for AMUNDSEN) of the RCM, which is adjusted to the distribution function of the station data. In addition, an optimum scale approach was applied to find the most suitable grid points [47]. Within the study area long-term data of the weather station in Vent were available to accomplish the adjustment for HQsim-GEM, as well as several other stations for AMUNDSEN [7]. For simulations that require sub-daily forcing data, temporal disaggregation from daily to hourly resolution was performed using the disaggregation tool MELODIST [48]. A more detailed description of the preprocessing of the meteorological data can be found in Hanzer et al. [7].
3. Glacio-Hydrological Models
3.1. Overview of the Two Independent Glacio-Hydrological Models
In our study, we compare the two independent glacio-hydrological models HQsim-GEM and AMUNDSEN, which were both applied to project future changes in glacier and hydrological characteristics in the Rofenache catchment in the Ötztal Alps (Austria). Although the results achieved using AMUNDSEN are described in detail by Hanzer et al. [7], HQsim-GEM has not yet been addressed in such level of detail before. Therefore, this section includes a description of the model coupling scheme HQsim-GEM (Section 3.2.1), followed by an individual model description for each model: HQsim (Section 3.2.2), GEM (Section 3.2.3), and their combined setup (Section 3.2.4) in more detail, while AMUNDSEN is briefly introduced (Section 3.3).
Table 1 summarizes the key difference of both glacio-hydrological models in terms of different relevant characteristics. This includes spatial and temporal resolution as well as required meteorological input variables. HQsim-GEM operates at daily temporal resolution, including precipitation and temperature, while AMUNDSEN is forced by sub-daily values of precipitation, temperature, relative humidity, wind speed, and solar radiation. Special emphasis in this comparison is put on the representation of glaciers and their temporal evolution. HQsim-GEM is zero-dimensional, neglecting the actual shape of the glacier geometry. Instead, glaciers are modeled using the Volume-Area-Time-scaling approach, which relates these characteristics to each other in a meaningful way [49]. In contrast, AMUNDSEN incorporates an explicit distributed representation of glaciers in terms of their spatial extent through employing the approach [10].

Table 1.
Overview of the two glacio-hydrological models HQsim-GEM and AMUNDSEN.
The different types of glacier representations also affects the initialization of glaciers in both models. The modest Volume-Area-Time scaling approach is more flexible in terms of initialization, since the desired glacier state required for initialization is found through iterations of the scaling approach in order to match the observed glacier area in terms of size. This way, an initialization is even possible for 1969, for which glacier outlines have been made available for all of Austria. The explicit distributed representation of area and volume in the method in AMUNDSEN requires ice thickness estimates for initializing the glaciers, which restricts the initialization of the model to more recent periods, for which detailed information of the glacier volume exist. Moreover, the scaling approach in HQsim-GEM can represent glacier expansion, which is relevant for reconstructing glacier characteristics in the 1980s—a decade which has seen expanding glaciers. The approach instead, is not capable of representing this expansion, which is why its application is limited to periods of glacier shrinkage.
3.2. HQsim-GEM Model Coupling
3.2.1. Model Coupling Strategy
We coupled the two independent models, namely the semi-distributed hydrological model HQsim (Section 3.2.2) and a glacier evolution model [30] referred to as GEM (Section 3.2.3). As depicted in the scheme of working processes in Figure 2. For the two-way coupling of the semi-distributed hydrological model HQsim and the glacier evolution model GEM three main steps are required:
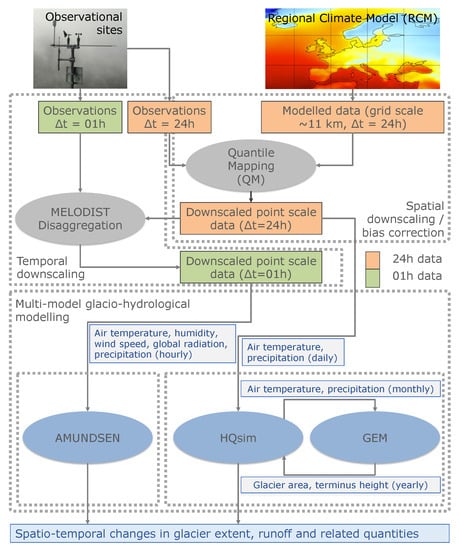
Figure 2.
Flow chart of data and models.
- First (‘static’) model run of HQsim: Input data include daily minimum, maximum and mean air temperature as well as precipitation from either measured meteorological data or downscaled EURO-CORDEX climate data referred to the closest station, and the AGI information data to initialize the model in 1969, for a constant glacier simulation run.
- Air temperature and precipitation data are adjusted to account for altitudinal differences between the station and the locations of the glaciers.
- HQsim converts daily air temperature and precipitation for each glacier to monthly values. These time series are used to force GEM in a subsequent step.
- Coupling with the GEM: Running the GEM with input data delivered from the first HQsim run. Characteristics such as glacier area and terminus height are calculated for each year and transferred back to HQsim to account for glacier changes.
- Second (‘dynamic’) model run of HQsim: In a second HQsim run, dynamical glacier changes data provided by the GEM are updated each glaciological year (in September). Glacierized Hydrological Response Units (Section 3.2.2) are updated in terms of spatial extent and mean elevation (through updated terminus height). This way, updated calculations of hydrological quantities (like total runoff and glacier melt, etc.) are considered in this second iteration, complementing the model coupling scheme.
Both HQsim and GEM are briefly introduced in the following sections.
3.2.2. Model Description of HQsim
HQsim is a deterministic semi-distributed hydrological modeling system for the meso-scale, which has been developed on the basis of the BROOK model [50] for water balance simulations in small mountainous head catchments [26]. At present, the model is applied for flood forecasting of tributaries in the Inn River catchment in the Austrian federal state of Tyrol [51,52] and flood risk related studies [27]. Following the semi-distributed concept, the catchment is subdivided into hydrological response units (HRU), which summarize areas of similar hydrological response, and channel segments. Runoff generation and runoff concentration are calculated for each HRU independently incorporating the most relevant hydrological processes.
Most approaches are conceptual and parsimonious with respect to data demand enabling simulations in data sparse regions. In contrast to the model applications for flood prediction, some modifications tailored to this study have been introduced [14]. The potential evapotranspiration is calculated according to the simplified but physics-based approach after Priestly and Taylor [53,54]. Global radiation is estimated based on minimum and maximum temperature using the Bristow and Campbell method [55], which is also relevant for snowmelt computations. Although the standard version of HQsim employs a simple temperature-index model, a more advanced scheme, adopted from Walter et al. [56] is utilized here. It is a simplified energy balance approach that also benefits from the approximation of shortwave radiation using minimum and maximum temperature. In a model inter-comparison study [57], it demonstrated a similar model skill like the more complex energy balance methods ESCIMO [58,59], which is a point-scale version of AMUNDSEN [31] (see, Section 3.3), and the Utah Energy Balance Model [60]. First, snow is accumulated if the temperature falls below a user-defined temperature threshold. Melt is computed solving the energy balance equation, which consists of simple approximations of the turbulent fluxes [56]. The snow albedo needs to be parameterized, assuming a time-dependent decay similar to ESCIMO. Likewise, albedo values need to be defined for glacierized HRUs to compute firn and ice melt, respectively. In the snowpack, liquid water storage, cold content and variable density are also accounted for in a simplified way.
Leaf Area Index (LAI) dependent interception is simulated according to the method used in the BROOK model [50]. The inter- and intra-annual course of the LAI is dynamically calculated using weather data [61]. This is also relevant to adjust the interception capacity in the vegetation season, whereby snow and rain interception is computed using a bucket approach [62]. Subsequently, the simulation of infiltration and surface runoff is based on a simple contributing area approach, which is dependent on volumetric soil moisture. The soil is divided into two storages including a top layer. HQsim includes a simplified soil water balance approach, which builds upon the work of van Genuchten [63]. Actual evapotranspiration depends on the available soil moisture and the LAI. Water fluxes are derived according to the van Genuchten–Mualem method, which is applied for interflow and seepage calculation. These values depend on hydraulic conductivity, which itself is a function of saturated hydraulic conductivity (a model parameter). The latter flux is the inflow to the groundwater storage, which is simply represented using a linear reservoir approach. For simulating water fluxes in the soil, a numerical scheme is applied, which solves the water balance equation for sub-time steps for reasons of numerical stability.
Runoff concentration is calculated assuming a time-area diagram. A sub-time step method similar to the solution of the soil water balance is used for calculating river reach routing in channel segments, using a non-linear storage approach which is based on velocity calculations [64].
3.2.3. Model Description of GEM
The glacier evolution model (GEM) developed by Marzeion et al. [30] was used to reconstruct and project glacier surface mass-balance data on a global scale in order to assess past and future sea-level rise. The mass-balance model is based on a zero-dimensional, statistical approach, including simple assumptions for reproducing glacier geometry changes, such as glacier area and terminus height. As this model is simple with respect to input data and works with monthly climatological air temperature and precipitation data, it is widely and easily applicable. The GEM extracts monthly anomalies of air temperature and precipitation relative to the 1961–1990 mean from the input series. These anomalies are added to 1961–1990 climatology of the Climate Research Unit CRU dataset (CRU CL 2.0 [65], provided in 10’ latitude/longitude resolution) on which the model was calibrated. Data is always taken from the grid point closest to the glacier.
Annual specific surface mass balances for each individual glacier are calculated using the area-related mean solid precipitation fallen onto the glacier surface and the mean air temperature of the glacier’s terminus. Monthly anomalies of both variables are added to the CRU climatology data. Glacier variables, such as area, volume, length and terminus height can be derived from the modeled mass balances by using the volume-area-time scaling approach [9,49]. Glacier specific parameters such as the temperature sensitivity of the glacier and a bias correction factor are computed for glaciers for which mass-balance observations exist. For glaciers without observations, a regionalization approach to transfer parameters is applied [30]. Glacier initialization is performed through iterative runs minimizing differences in predicted and observed glaciated area. A more detailed description of the model is available in Marzeion et al. [30].
3.2.4. Setup of the Coupled Model for the Rofenache Catchment
First, HRUs are delineated using a script that automatically calls GIS functionalities, taking into consideration the following terrain characteristics, which are grouped in each watershed: (i) Elevation, (ii) aspect, (iii) soil type, and (iv) land-use including maximum glacier extent. The latter is derived from the 1969 glacier outlines using a buffer to account for the increased extent in the 1980s. Each glacier outline is linked via a unique id to the corresponding glacier in GEM. This id is used internally to organize the data exchange between the individual steps described in Section 3. The total number of HRUs obtained by this approach amounts to 70. Finally, according to the terrain characteristics, each HRU is connected to a downstream reach element (17 in total) and from the geometric dimensions of the flow path, the travel time is computed using an empirical, slope-dependent travel time formula.
The coupled hydrological model (i.e., the ‘dynamic’ run from Section 3), forced by meteorological data from the Vent station in the catchment only, was calibrated and validated for the basin Rofenache by comparing runoff observations with the modeled runoff on daily basis, and monthly mean, respectively. Since the ‘dynamic’ run is considered, the modeled runoff takes into account dynamical glacier areas, computed by GEM. The only values adjusted in the calibration step are the albedo values for snow (i.e., the value for fresh snow), firn, and ice. Other parameters, especially those for the other hydrological processes (e.g., soil water) are set to default values, which were found to be suitable in earlier studies [16,66]. GEM is not calibrated at this stage. Instead, the parameterization from the global run [30] is used here without any other adjustment. This also involves the interpolation of parameters to glaciers without mass-balance observations as described by Marzeion et al. [30], making the coupled modeling approach transferable in a way that only requires the calibration of the hydrological model component. Consequently, we split the time series in two parts [67], with each first year being the model warm-up: 1971–1990 for calibration and 1991–2010 for validation. How well the model reproduces observed daily discharge data is assessed by using several skill scores, such as the Nash–Sutcliffe efficiency (NSE) and the Benchmark efficiency (BE) which is less sensitive to model skill inherent in climatology [68], the percent bias (PBIAS) and the root mean square error (RMSE). For example, NSE and BE values range between and 1. The latter would indicate a ‘perfect model’, suggesting a perfect match of simulated and observed data. A value of zero indicates a model performance not better than the use of an average value of the observed data. Values below zero indicate that the model application is questionable, since the observed mean in this case is a better predictor. Low absolute PBIAS and RMSE values are commonly assumed to reveal satisfactory model performance [69]. However, the calculated skill scores show a good performance of the low-complexity HQsim-GEM model, see Table 2. Specific model parameters are shown in Table 3.

Table 2.
Skill scores (Nash–Sutcliffe efficiency NSE, benchmark efficiency BE, percent bias PBIAS and root mean square error RMSE, see Table A1) of the calibration and validation of the Rofenache catchment, based on daily runoff data. Calibration and validation periods for the HQsim-GEM model are 1971–1990 and 1991–2010 (note that the first year of each period is the model warm-up) and for the AMUNDSEN model 1998–2006 and 2007–2013.

Table 3.
Specific model parameters of both glacio-hydrological models HQsim and AMUNDSEN. Calibrated parameters are italic and bold. Model parameters for the glacier model GEM are identical to those in Marzeion et al. [30].
3.3. AMUNDSEN
AMUNDSEN [31,32] is a fully distributed hydroclimatological model specifically designed for the application in high-mountain regions. As it resolves the full snow and ice surface energy and mass balance, time series of air temperature, precipitation, relative humidity, global radiation and wind speed in hourly to three-hourly resolution are required. The meteorological point data are interpolated to the model grid (with a resolution typically in the range of 10–1000 m) using a combined lapse rate–inverse distance weighting approach. Catchment discharge is calculated using a linear reservoir cascade approach with distinct reservoirs for snow on glaciers, firn, bare ice, snow outside of glaciers and soil. For the application in glacierized regions, a glacier geometry update module based on the method [10] has been implemented. With this method, the ice thickness distribution of each glacier is updated annually based on the simulated surface mass balance and previous observed thickness changes. Specific parameters can be found in Table 3. For further details on the AMUNDSEN model and the setup of the model for the study region we refer to Hanzer et al. [7,32].
For the present study, the setup from Hanzer et al. [7] was used, i.e., a spatial and temporal resolution of 100 m and 3 h, respectively. Glaciers were initialized with distributed ice thicknesses calculated using the glacier outlines from 1997 with the approach by Huss and Farinotti [70]. The bias-corrected meteorological time series from the EURO-CORDEX simulations were temporally disaggregated from their original daily resolution to the three-hourly model resolution using the disaggregation tool MELODIST [48].
The linear reservoir cascade model was calibrated using the runoff observations for the period 1998–2006 and validated for the period 2007–2013. Table 2 shows the resulting skill scores based on daily runoff data. For the AMUNDSEN simulations, both results acquired using observed hourly meteorological data (denoted as AMUNDSEN (original) in Table 2) as well as—to be consistent with the subsequent scenario simulations—aggregated-and-disaggregated data (i.e., the hourly data were first aggregated to daily values and subsequently disaggregated again to hourly values using the same methods as applied for the EURO-CORDEX data) are shown. Hence, the rather unsatisfactory performance of the runoff simulations in this case is not due to a model deficiency, but rather due to the necessary temporal disaggregation of the meteorological driving data. When driven with the original hourly meteorological observations, the multilevel validation of the AMUNDSEN simulations yields a very high overall model performance (see Table 2 and [32]).
4. Results
4.1. Downscaling/Bias Correction of Climate Simulations
Both glacio-hydrological models were forced with the spatially and temporally (AMUNDSEN) downscaled (point-scale station Vent in HQsim) and bias-corrected EURO-CORDEX emission scenarios RCP 2.6, RCP 4.5, and RCP 8.5. In Figure 3, the evolution for both (i) the annual mean of air temperature and (ii) the yearly sum of precipitation is depicted, showing a future evolution of the multi-model ensemble mean including a 11-year centered moving average for each scenario and uncertainties covering the total bandwidth of all ensemble members within the 95% confidence interval. Air temperature rise is most pronounced for the worst-case scenario RCP 8.5, whereas RCP 4.5 will very likely suggest an increase in temperature, and RCP 2.6 (which is the closest to the 2015 Paris agreement) is projected to stabilize during the second half of the 21st century. Multi-model projections of annual precipitation sums under the RCP 2.6 scenario have a vast bandwidth, showing a marked divergence between the three ensemble members, making general statements difficult. RCP 4.5 and RCP 8.5 tend to evolve similarly, except for the period between 2040 and 2050. RCP 8.5 is assumed to have a greater amount of precipitation sums, especially for winter precipitation, see Hanzer et al. [7] for a more detailed information on projected seasonal changes for both variables.
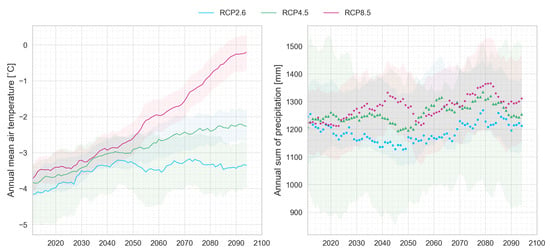
Figure 3.
Future multi-model ensemble mean projections of (i) annual mean air temperature and (ii) annual sum of precipitation by using a centered 11-year moving average (both parameters refer to the entire catchment area of the upper Ötztal). Shadows display the full range of the ensembles within the 95% confidence interval.
4.2. Comparison of Model Results
4.2.1. Glacierization
Figure 4 shows the results for the catchment glacierization from our two glacio-hydrological models, (i) HQsim-GEM (left sub-figures), and (ii) AMUNDSEN (right sub-figures). In the top row only the three GCM-RCM combinations which are available for all three RCPs are shown, in the middle row all GCM-RCM combinations (i.e., three for RCP 2.6 and 14 each for RCP 4.5 and 8.5), and in the bottom row the same but with the uncertainty (95% confidence interval) shown as shaded bands instead of the individual model realizations. The result of each sub-figure is based on EURO-CORDEX data, showing a multi-model ensemble mean (thick lines) and single GCM-RCM combinations (thin lines) for historical climate simulations (before 2006) and climate scenarios (starting in 2006). The model results before 2006 are based on historical climate simulation data from 1969–2005 for all GCM-RCM combinations (black thin lines), and the multi-model ensemble mean (black thick lines). Please note that both models have different starting points depending on the year of glacier initialization (1969 for GEM, 1997 for AMUNDSEN).
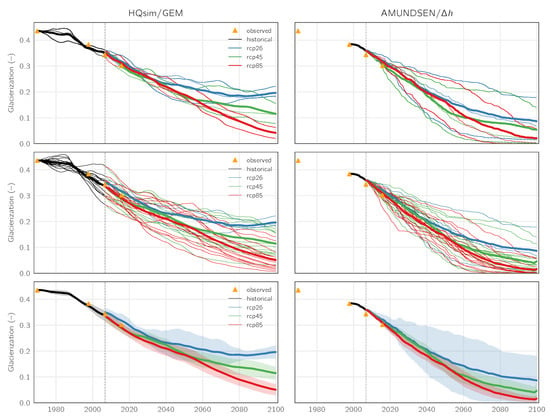
Figure 4.
Results for the catchment glacierization from the two glacio-hydrological models HQsim-GEM (left sub-figures) and AMUNDSEN (right sub-figures). The top row shows only the three GCM-RCM combinations which are available for all three RCPs, the middle row all GCM-RCM combinations (i.e., three for RCP 2.6 and 14 each for RCP 4.5 and 8.5), and the bottom row the same but with the uncertainty (95% confidence interval) shown as shaded bands instead of the individual model realizations.
The ability of the GEM model to reproduce glacier advances is one key advantage compared to the approach implemented in AMUNDSEN. Especially during the 1970s and 1980s advancing glaciers are simulated for some GCM-RCM combinations, which is consistent with observations [37,38]. Measured AGI data (yellow triangles) in 1969 and 1997 were used as initial data for the different glacier models, whereas 1997, 2006 and 2015 serve to evaluate modeled glacier area data. When including all ensemble members for RCP 4.5 and RCP 8.5 the model outputs of GEM fit very well with the observation values. AMUNDSEN model results as well as the RCP 2.6 run of GEM are slightly overestimated. The latter might be attributed to the small number of ensemble members. Beyond that, uncertainties reveal a greater spread with less members.
The overall results of the ensemble mean over the coming decades seem to be more optimistic for the GEM. Following approximate values show the glacierization by the end of this century of GEM vs. AMUNDSEN: 20% vs. 9% for RCP 2.6; 12% vs. 5% for RCP 4.5; and 5% vs. 2% for RCP 8.5. Consequently, a general rapid retreat of all glacier areas within the study area will continue within the next decades, independent of the chosen scenario. In the second half of this century glaciers might start to respond on today’s mitigation against climate change, since they react very slowly to changing climatic conditions [71]. In case of the most extreme scenario RCP 8.5 almost all the glaciers within the Rofenache catchment will have disappeared by the end of this century. Consequently, glaciers in highly ice-covered catchments might very likely sustain only at high altitude, leading to almost completely ice free low glacierized elevation bands [5,15,72,73].
4.2.2. Runoff Regimes
Past and future river discharge estimates for the catchment Rofenache are shown in Figure 5 for both glacio-hydrological model runs HQsim-GEM (left column) and AMUNDSEN (right column) under the different emission scenarios RCP 2.6 (top row), RCP 4.5 (middle row) and RCP 8.5 (bottom row). These results represent monthly multi-model ensemble means for both (i) total runoff (solid lines), and (ii) ice melt (dashed lines) for three different future climate periods (colored lines). Additionally, observed runoff during the period 1998–2011 (grey lines) and the corresponding simulation results based on historical climate data (black lines) are shown.
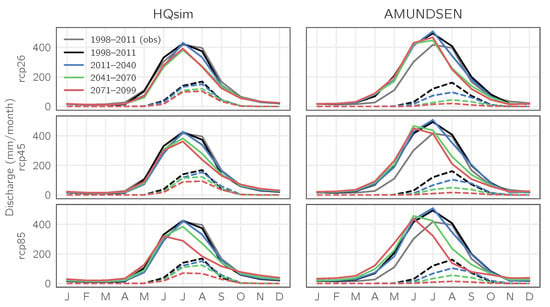
Figure 5.
Simulated runoff for HQsim-GEM (left) and AMUNDSEN (right) under the different emission scenarios RCP 2.6 (top), RCP 4.5 (middle) and RCP 8.5 (bottom). Lines represent monthly multi-model ensemble means for total runoff (solid lines) and ice melt (dashed lines) for three different future climate periods (colored lines). Grey and black lines correspond to observed runoff during the period 1998–2011 (grey) and the corresponding simulation results (black).
At first glance, all model outputs for the past (black and grey) and current/future climate periods show a runoff regime as expected for glacier-fed rivers; low flow during winter and high flow during spring and summer associated with the melt season. Peak flow in the end of summer is a typical characteristic of high-alpine glacierized watersheds, such as the Rofenache catchment [72]. A closer view reveals a shift of runoff characteristics from a glacial/glacio-nival regime (runoff peak in July) towards a nivo-glacial regime (runoff peak in June), and a decreasing contribution of ice melt to the streamflow. The simulation run of the historical data fits very well with the total runoff observation data for the HQsim-GEM model combination, while for the AMUNDSEN model runoff volumes are subject to a certain overestimation especially during spring, which can be attributed to the necessary temporal disaggregation of the meteorological time series (see also Section 3.3 and Table 2). Furthermore, this high-complex model is able to capture more detailed processes (e.g., ice thickness), which is why the uncertainties inherent in disaggregation might lead to significant differences in estimating discharge volumes during the summer season. As a further consequence of this, the regime shift can be found in earlier time periods (RCP 4.5 and RCP 8.5, 2041–2070 and 2071–2099), as well as an earlier onset of the snow and ice melt season (March). In contrast to the low-complexity model, HQsim-GEM, the melt season starts in April, and the regime shift appears only in the last climate period of the ‘worst-case’ scenario. The estimated contribution of ice melt to river streamflow depends on the respective modeled glacier area. By the end of the century, this contribution of ice melt seems almost twice as high for the low-complexity model compared to the physical-based model results, which shows a vanishingly small proportion of glacier meltwater. However, with the ongoing glacier retreat, it is not surprising that both model outputs show a decreasing trend of future annual total runoff in the late summer months (July–September).
Moreover, both model data suggest the moment of peak discharge (tipping point) being in the recent past. This reinforces the assertion of other local studies that peak water in some catchments within the European Alps has already passed [15,74,75].
5. Discussion
Generally, modeling glacio-hydrological processes is always a simplification of reality. Thus, regardless of the model complexity used, future projections of discharge and glacier evolution are rather an approximation than a reliable quantification. To assess uncertainties from modeling processes, it seems essential to analyze the results of several independent model structures. However, the Rofenache catchment is a well-studied area [33], which has led us to focus on the comparison of the model results rather than the results itself. For the first time we compare the results of two independent, completely different glacio-hydrological models that are based on separate glacier models (GEM, [30]; approach, [10]) with different years of initialization (1969 and 1997). Furthermore, the models show considerable differences in the type of complexity (physical-based vs. empirical approach), the temporal and spatial resolution and the associated data requirements. We follow up on the study of Addor et al. [6], who addressed uncertainties from modeling future discharge projections using three different hydrological models while however using glacier data from the same glacier model for all simulations. In contrast to this study, we emphasize that various glacier models very likely might have a distinct influence on changes of hydrological regime changes. By using two different glacier models, we obtain two completely independent glacio-hydrological model results.
Past glacierization is reproduced very well by both modeling approaches. However, the sparser data requirements by the HQsim-GEM approach along with the ability to simulate glacier advances allows the initialization of the simulations already in 1969, while for AMUNDSEN the simulations start in 1997. This model feature of advancing glaciers, along with possibly overestimated spring melt rates in AMUNDSEN due to the employed disaggregation methods, leads to more optimistic future estimations of glacier retreat by the low-complexity glacio-hydrological model combination HQsim-GEM. Consequently, it is not surprising that future discharge volume estimations between both models appear slightly different, since runoff data are dependent from the glacier model input data. Therefore, the contribution of ice melt from the AMUNDSEN model appears vanishingly low as response to the more pronounced glacier retreat by the end of this century. Having two different dates of initialization might also play an important role, since different initializations in the past might lead to the same present glacier state [76]. Despite the varying estimation of future glacierization and total runoff between the two glacio-hydrological models, the overall results are consistent and some main findings, which are more or less pronounced for each emission scenario and which are in accordance with [1,72,77,78], can be summarized: First, runoff characteristics seem to shift from a prior ice melt dominated regime towards a snow melt dominated regime characterized by an earlier onset of the snow and ice melt season and lower ice volume; second, future discharge volumes show a decreasing trend of ice melt contribution, indeed, annual discharge volumes seem not to change considerably until the second half of the century due to stable projections of annual precipitation sums. In summary, high-alpine catchments being extremely sensitive and vulnerable to climate warming. Even without further temperature increases, these projected trends in glacierization and runoff regime changes will persist over the coming decades due to the delayed reaction of glaciers to past climatic changes [79,80].
What can be learned from this study is that low-complexity models can achieve higher accuracy at least in the calibration period. However, it is not clear if this also applies to future periods. Models with lower complexity are advantageous especially when data availability is weak and priority is given to efficient computation time. On the contrary, high-complexity models allow for a much more detailed investigation of the involved processes, including the addition of new parameters to improve the simulation with the consequence of possibly increasing uncertainties.
6. Conclusions
In this study, we focus on what we learn from comparing glacio-hydrological models. To our best knowledge, existing studies are limited to compare different hydrological models processing glacier input data from the same model origin. For this purpose, we compare two model combinations that are fully independent—except for the model input—covering low and high complexity. We use separate glacier models with different initialization times to model the hydrological response to climate change based on different emission scenarios. Overall results show roughly similar outcomes, but in detail major differences. The time and method of glacier initialization might play an important role on the simulation outcome, as well as the type of complexity. Even though the HQsim-GEM showed slightly better model skill in the calibration period, it is not clear if it also better predicts future states.
Hence, it is not possible to make conclusions which model will perform better outside of the calibration period, since this is heavily dependent on the research question and the time resolution desired. As future projections always deliver an approximation rather than an exact value, we propose considering results from different glacio-hydrological model combinations, since most likely each model setup provides a different outcome. More recently, the highly sophisticated model framework OGGM [11], a comprehensive expansion of the GEM model, can simulate glacier geometry. Therefore, coupling this framework with the physical-based hydrological model WaSiM [81,82] is part of ongoing research, which serves as another independent hypothesis to describe glacio-hydrological processes. Even though we only compare two different approaches in the current study, we suggest considering different modelling approaches when assessing future catchment discharge or glacier evolution. Especially when transferring the results to stakeholders, it is vital to transparently communicate the bandwidths of future states that come with all model results.
Author Contributions
Conceptualization, E.S., F.H. and K.F.; methodology, E.S., F.H., J.N. and K.F.; software development, E.S., F.H., F.O., J.N. and K.F.; validation, E.S., F.H., F.O. and K.F.; formal analysis, E.S., F.H., J.N. and K.F.; investigation, E.S., F.H. and K.F.; writing—original draft preparation, E.S., F.H. and K.F.; writing—review and editing, F.O., J.N., J.S. and M.H.; visualization, E.S., F.H. and K.F.; supervision, M.H. and K.F.; project administration, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out as part of the project W01 MUSICALS II-Multiscale Snow/Ice Melt Discharge Simulation for Alpine Reservoirs project at alpS-Centre for Climate Change Adaptation in Innsbruck, Austria. The K1-Centre alpS was funded through the Federal Ministry of Transport, Innovation and Technology (BMVIT), the Federal Ministry of Science, Research and Economy (BMWFW), and the Austrian federal states of Tyrol and Vorarlberg within the scope of COMET-Competence Centers for Excellent Technologies. The COMET programme is managed by the Austrian Research Promotion Agency (FFG). We want to thank Tiroler Wasserkraft AG (TIWAG) for the collaboration and for co-funding the project.
Acknowledgments
For the data support we thank the TIWAG, and the HD-Hydrographic Service of Tyrol, the ACINN-Department of Atmospheric and Cryospheric Sciences of the University Innsbruck. We gratefully acknowledge Ben Marzeion for providing the GEM model. Moritz Zimmermann, Stefan Berlin, and Benjamin Winter helped with GIS. Finally, we thank all reviewers for their helpful comments.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AMUNDSEN | Alpine Multiscale Numerical Distributed Simulation Engine |
| BE | Benchmark efficiency |
| CRU | Climate Research Unit |
| GCM | General Circulation Model |
| GEM | Glacier Evolution Model |
| GIS | Geographic Information System |
| HQsim | HQ (high flow Q) simulation |
| HRU | Hydrological Response Unit |
| LAI | Leaf Area Index |
| MELODIST | MEteoroLOgical observation time series DISaggregation Tool |
| NSE | Nash–Sutcliffe efficiency |
| OGGM | Open Global Glacier Model |
| PBIAS | Percent bias |
| RCM | Regional Climate Model |
| RCP | Representative Concentration Pathway |
| RMSE | Root Mean Square Error |
Appendix A. Definitions and Parameters

Table A1.
Skill measures used throughout the manuscript. Time series of observed and modeled quantities, each consisting of N values, are considered for all time steps t, whereby represents the mean observed values and is a long-term average computed for the day of the year corresponding to time step i, respectively.
Table A1.
Skill measures used throughout the manuscript. Time series of observed and modeled quantities, each consisting of N values, are considered for all time steps t, whereby represents the mean observed values and is a long-term average computed for the day of the year corresponding to time step i, respectively.
| Skill Measure | Formula |
|---|---|
| Nash–Sutcliffe model efficiency | |
| Benchmark Nash–Sutcliffe model efficiency [68] | |
| Percent Bias | |
| Root Mean Square Error |
References
- Radić, V.; Hock, R. Glaciers in the Earth’s hydrological cycle: Assessments of glacier mass and runoff changes on global and regional scales. Surv. Geophys. 2014, 35, 813–837. [Google Scholar] [CrossRef]
- Schaefli, B.; Hingray, B.; Niggli, M.; Musy, A. A conceptual glacio-hydrological model for high mountainous catchments. Hydrol. Earth Syst. Sci. 2005, 9, 95–109. [Google Scholar] [CrossRef]
- Huss, M.; Farinotti, D.; Bauder, A.; Funk, M. Modelling runoff from highly glacierized alpine drainage basins in a changing climate. Hydrol. Process. 2008, 22, 3888–3902. [Google Scholar] [CrossRef]
- Finger, D.; Heinrich, G.; Gobiet, A.; Bauder, A. Projections of future water resources and their uncertainty in a glacierized catchment in the Swiss Alps and the subsequent effects on hydropower production during the 21st century. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Farinotti, D.; Usselmann, S.; Huss, M.; Bauder, A.; Funk, M. Runoff evolution in the Swiss Alps: Projections for selected high-alpine catchments based on ENSEMBLES scenarios. Hydrol. Process. 2012, 26, 1909–1924. [Google Scholar] [CrossRef]
- Addor, N.; Rössler, O.; Köplin, N.; Huss, M.; Weingartner, R.; Seibert, J. Robust changes and sources of uncertainty in the projected hydrological regimes of Swiss catchments. Water Resour. Res. 2014, 50, 7541–7562. [Google Scholar] [CrossRef]
- Hanzer, F.; Förster, K.; Nemec, J.; Strasser, U. Projected cryospheric and hydrological impacts of 21st century climate change in the Ötztal Alps (Austria) simulated using a physically based approach. Hydrol. Earth Syst. Sci. 2018, 22, 1593–1614. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Bauder, A.; Funk, M. An estimate of the glacier ice volume in the Swiss Alps. Glob. Planet. Chang. 2009, 68, 225–231. [Google Scholar] [CrossRef]
- Bahr, D.B. Global distributions of glacier properties: A stochastic scaling paradigm. Water Resour. Res. 1997, 33, 1669–1679. [Google Scholar] [CrossRef]
- Huss, M.; Jouvet, G.; Farinotti, D.; Bauder, A. Future high-mountain hydrology: A new parameterization of glacier retreat. Hydrol. Earth Syst. Sci. 2010, 14, 815. [Google Scholar] [CrossRef]
- Maussion, F.; Butenko, A.; Champollion, N.; Dusch, M.; Eis, J.; Fourteau, K.; Gregor, P.; Jarosch, A.H.; Landmann, J.; Oesterle, F.; et al. The Open Global Glacier Model (OGGM) v1.1. Geosci. Model Dev. 2019, 12, 909–931. [Google Scholar] [CrossRef]
- Huss, M.; Zemp, M.; Joerg, P.C.; Salzmann, N. High uncertainty in 21st century runoff projections from glacierized basins. J. Hydrol. 2014, 510, 35–48. [Google Scholar] [CrossRef]
- Uhlmann, B.; Jordan, F.; Beniston, M. Modelling runoff in a Swiss glacierized catchment-Part II: Daily discharge and glacier evolution in the Findelen basin in a progressively warmer climate. Int. J. Climatol. 2013, 33, 1301–1307. [Google Scholar] [CrossRef]
- Förster, K.; Oesterle, F.; Hanzer, F.; Huttenlau, M.; Strasser, U. Bestimmung der Auswirkungen des Klimawandels auf die Gletscherdynamik und das Abflussregime im Rofental unter Verwendung eines gekoppelten glazio-hydrologischen Modells. In Innsbrucker Jahresberichte 2014–2015; Institut für Geographie der Universität Innsbruck in Zusammenarbeit mit der Innsbrucker Geographischen Gesellschaft: Innsbruck, Austria, 2015; pp. 23–40. [Google Scholar]
- Huss, M.; Hock, R. Global-scale hydrological response to future glacier mass loss. Nat. Clim. Chang. 2018, 8, 135–140. [Google Scholar] [CrossRef]
- Wijngaard, R.R.; Helfricht, K.; Schneeberger, K.; Huttenlau, M.; Schneider, K.; Bierkens, M.F. Hydrological response of the Ötztal glacierized catchments to climate change. Hydrol. Res. 2016, 47, 979–995. [Google Scholar] [CrossRef]
- Takala, M.; Pulliainen, J.; Metsamaki, S.J.; Koskinen, J.T. Detection of snowmelt using spaceborne microwave radiometer data in Eurasia from 1979 to 2007. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2996–3007. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Stone, R.S.; Dutton, E.G.; Harris, J.M.; Longenecker, D. Earlier spring snowmelt in northern Alaska as an indicator of climate change. J. Geophys. Res. Atmos. 2002, 107, ACL 10-1–ACL 10-13. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Horton, P.; Schaefli, B.; Mezghani, A.; Hingray, B.; Musy, A. Assessment of Climate-Change Impacts on Alpine Discharge Regimes with Climate Model Uncertainty. Hydrol. Process. 2006, 20, 2091–2109. [Google Scholar] [CrossRef]
- Fatichi, S.; Rimkus, S.; Burlando, P.; Bordoy, R.; Molnar, P. High-Resolution Distributed Analysis of Climate and Anthropogenic Changes on the Hydrology of an Alpine Catchment. J. Hydrol. 2015, 525, 362–382. [Google Scholar] [CrossRef]
- Kobierska, F.; Jonas, T.; Zappa, M.; Bavay, M.; Magnusson, J.; Bernasconi, S.M. Future Runoff from a Partly Glacierized Watershed in Central Switzerland: A Two-Model Approach. Adv. Water Resour. 2013, 55, 204–214. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model: Its Structure and Applications; Swedish Meteorological and Hydrological Institute: Norrköping, Sweden, 1992. [Google Scholar]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments. Ph.D. Thesis, Swedish Meteorological and Hydrological Institute, Norrköping, Sweden, 1976. [Google Scholar]
- Kleindienst, H. Erweiterung und Erprobung Eines Anwendungsorientierten Hydrologischen Modells zur Gangliniensimulation in Kleinen Wildbacheinzugsgebieten. Unpublished Diploma Thesis, Ludwig Maximilians Universität München, Munich, Germany, 1996. [Google Scholar]
- Winter, B.; Schneeberger, K.; Förster, K.; Vorogushyn, S. Event generation for probabilistic flood risk modelling: Multi-site peak flow dependence model vs. weather generator based approach. Nat. Hazards Earth Syst. Sci. 2020, 20, 1689–1703. [Google Scholar] [CrossRef]
- Mackay, J.D.; Barrand, N.E.; Hannah, D.M.; Krause, S.; Jackson, C.R.; Everest, J.; Aðalgeirsdóttir, G. Glacio-hydrological melt and run-off modelling: Application of a limits of acceptability framework for model comparison and selection. Cryosphere 2018, 12, 2175–2210. [Google Scholar] [CrossRef]
- Clark, M.P.; Kavetski, D.; Fenicia, F. Pursuing the method of multiple working hypotheses for hydrological modeling. Water Resour. Res. 2011, 47, W09301. [Google Scholar] [CrossRef]
- Marzeion, B.; Jarosch, A.H.; Hofer, M. Past and future sea-level change from the surface mass balance of glaciers. Cryosphere 2012, 6, 1295–1322. [Google Scholar] [CrossRef]
- Strasser, U. Die Modellierung der Gebirgsschneedecke im Nationalpark Berchtesgaden; Berchtesgaden National Park Research Report; Nationalparkverwaltung Berchtesgaden: Berchtesgaden, Germany, 2008; Volume 55. [Google Scholar]
- Hanzer, F.; Helfricht, K.; Marke, T.; Strasser, U. Multilevel spatiotemporal validation of snow/ice mass balance and runoff modeling in glacierized catchments. Cryosphere 2016, 10, 1859–1881. [Google Scholar] [CrossRef]
- Strasser, U.; Marke, T.; Braun, L.; Escher-Vetter, H.; Juen, I.; Kuhn, M.; Maussion, F.; Mayer, C.; Nicholson, L.; Niedertscheider, K.; et al. The Rofental: A High Alpine Research Basin (1890–3770 m a.s.l.) in the Ötztal Alps (Austria) with over 150 Years of Hydrometeorological and Glaciological Observations. Earth Syst. Sci. Data 2018, 10, 151–171. [Google Scholar] [CrossRef]
- Institute of Meteorology and Geophysics. Climate Data Vent, Ötztal Alps, 1935–2011; University of Innsbruck: Innsbruck, Austria, 2013. [Google Scholar] [CrossRef]
- Kuhn, M.; Helfricht, K.; Ortner, M.; Landmann, J.; Gurgiser, W. Liquid water storage in snow and ice in 86 Eastern Alpine basins and its changes from 1970–97 to 1998–2006. Ann. Glaciol. 2016, 57, 11–18. [Google Scholar] [CrossRef][Green Version]
- Schöber, J.; Schneider, K.; Helfricht, K.; Schattan, P.; Achleitner, S.; Schöberl, F.; Kirnbauer, R. Snow cover characteristics in a glacierized catchment in the Tyrolean Alps-Improved spatially distributed modelling by usage of Lidar data. J. Hydrol. 2014. [Google Scholar] [CrossRef]
- Fischer, A.; Olefs, M.; Abermann, J. Glaciers, snow and ski tourism in Austria’s changing climate. Ann. Glaciol. 2011, 52, 89–96. [Google Scholar] [CrossRef]
- Zemp, M.; Paul, F.; Hoelze, M.; Haeberli, W. Glacier fluctuations in the European Alps, 1850–2000. Darkening Peaks Glacier Retreat Sci. Soc. 2008. [Google Scholar] [CrossRef]
- Abermann, J.; Lambrecht, A.; Fischer, A.; Kuhn, M. Quantifying changes and trends in glacier area and volume in the Austrian Ötztal Alps (1969-1997-2006). Cryosphere 2009, 3, 205. [Google Scholar] [CrossRef]
- Lambrecht, A.; Kuhn, M. Glacier changes in the Austrian Alps during the last three decades, derived from the new Austrian glacier inventory. Ann. Glaciol. 2007, 46, 177–184. [Google Scholar] [CrossRef]
- Gross, G. Der Flachenverlust der Gletscher in Osterreich 1850-1920-1969. Z. Gletscherkunde Glazialgeol. 1987, 23, 131–141. [Google Scholar]
- Paul, F.; Rastner, P.; Azzoni, R.S.; Diolaiuti, G.; Fugazza, D.; Le Bris, R.; Nemec, J.; Rabatel, A.; Ramusovic, M.; Schwaizer, G.; et al. Glacier shrinkage in the Alps continues unabated as revealed by a new glacier inventory from Sentinel-2. Earth Syst. Sci. Data 2020, 12, 1805–1821. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Giorgi, F.; Jones, C.; Asrar, G.R. Addressing climate information needs at the regional level: The CORDEX framework. World Meteorol. Organ. (WMO) Bull. 2009, 58, 175. [Google Scholar]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Thrasher, B.; Maurer, E.P.; McKellar, C.; Duffy, P. Bias correcting climate model simulated daily temperature extremes with quantile mapping. Hydrol. Earth Syst. Sci. 2012, 16, 3309. [Google Scholar] [CrossRef]
- Hofer, M.; Nemec, J.; Cullen, N.J.; Weber, M. Evaluating predictor strategies for regression-based downscaling with a focus on glacierized mountain environments. J. Appl. Meteorol. Climatol. 2017, 56, 1707–1729. [Google Scholar] [CrossRef]
- Förster, K.; Hanzer, F.; Winter, B.; Marke, T.; Strasser, U. An open-source MEteoroLOgical observation time series DISaggregation Tool (MELODIST v0.1.1). Geosci. Model Dev. 2016, 9, 2315–2333. [Google Scholar] [CrossRef]
- Bahr, D.B.; Meier, M.F.; Peckham, S.D. The physical basis of glacier volume-area scaling. J. Geophys. Res. Solid Earth 1997, 102, 20355–20362. [Google Scholar] [CrossRef]
- Federer, C.A.; Lash, D. BROOK: A Hydrologic Simulation Model for Eastern Forests; Water Resources Center, University of New Hampshire: Durham, NH, USA, 1978. [Google Scholar]
- Achleitner, S.; Rinderer, M.; Kirnbauer, R. Hydrological modeling in alpine catchments: Sensing the critical parameters towards an efficient model calibration. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2009, 60, 1507–1514. [Google Scholar] [CrossRef] [PubMed]
- Achleitner, S.; Schöber, J.; Rinderer, M.; Leonhardt, G.; Schöberl, F.; Kirnbauer, R.; Schönlaub, H. Analyzing the operational performance of the hydrological models in an alpine flood forecasting system. J. Hydrol. 2012, 412, 90–100. [Google Scholar] [CrossRef]
- Priestley, C.H.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Archibald, J.A.; Walter, M.T. Do Energy-Based PET Models Require More Input Data than Temperature-Based Models?—An Evaluation at Four Humid FluxNet Sites. J. Am. Water Resour. Assoc. 2014, 50, 497–508. [Google Scholar] [CrossRef]
- Bristow, K.L.; Campbell, G.S. On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agric. Forest Meteorol. 1984, 31, 159–166. [Google Scholar] [CrossRef]
- Walter, M.T.; Brooks, E.S.; McCool, D.K.; King, L.G.; Molnau, M.; Boll, J. Process-based snowmelt modeling: Does it require more input data than temperature-index modeling? J. Hydrol. 2005, 300, 65–75. [Google Scholar] [CrossRef]
- Förster, K.; Meon, G.; Marke, T.; Strasser, U. Effect of meteorological forcing and snow model complexity on hydrological simulations in the Sieber catchment (Harz Mountains, Germany). Hydrol. Earth Syst. Sci. 2014, 18, 4703–4720. [Google Scholar] [CrossRef]
- Strasser, U.; Marke, T. ESCIMO.spread—A spreadsheet-based point snow surface energy balance model to calculate hourly snow water equivalent and melt rates for historical and changing climate conditions. Geosci. Model Dev. 2010, 3, 643–652. [Google Scholar] [CrossRef]
- Marke, T.; Mair, E.; Förster, K.; Hanzer, F.; Garvelmann, J.; Pohl, S.; Warscher, M.; Strasser, U. ESCIMO.spread (v2): Parameterization of a spreadsheet-based energy balance snow model for inside-canopy conditions. Geosci. Model Dev. 2016, 9, 633–646. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Luce, C. Utah Energy Balance Snow Accumulation and Melt Model (UEB): Computer Model Technical Description and Users Guide; Utah Water Research Laboratory and USDA Forest Service Intermountain Research Station: Ogden, UT, USA, 1996.
- Förster, K.; Gelleszun, M.; Meon, G. A weather dependent approach to estimate the annual course of vegetation parameters for water balance simulations on the meso- and macroscale. Adv. Geosci. 2012, 32, 15–21. [Google Scholar] [CrossRef][Green Version]
- Rutter, A.; Kershaw, K.; Robins, P.; Morton, A. A predictive model of rainfall interception in forests, 1. Derivation of the model from observations in a plantation of Corsican pine. Agric. Meteorol. 1971, 9, 367–384. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Rickenmann, D. Fliessgeschwindigkeit in Wildbächen und Gebirgsflüssen. Wasser Energie Luft 1996, 88, 298–304. [Google Scholar]
- New, M.; Lister, D.; Hulme, M.; Makin, I. A high-resolution data set of surface climate over global land areas. Clim. Res. 2002, 21, 1–25. [Google Scholar] [CrossRef]
- Bellinger, J.; Achleitner, S.; Schöber, J.; Schöberl, F.; Kirnbauer, R.; Schneider, K. The impact of different elevation steps on simulation of snow covered area and the resulting runoff variance. Adv. Geosci. 2012, 32, 69–76. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Schaefli, B.; Gupta, H.V. Do Nash values have value? Hydrol. Process. 2007, 21, 2075–2080. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Huss, M.; Farinotti, D. Distributed ice thickness and volume of all glaciers around the globe. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Marzeion, B.; Cogley, J.G.; Richter, K.; Parkes, D. Attribution of global glacier mass loss to anthropogenic and natural causes. Science 2014, 345, 919–921. [Google Scholar] [CrossRef] [PubMed]
- Braun, L.; Weber, M.; Schulz, M. Consequences of climate change for runoff from Alpine regions. Ann. Glaciol. 2000, 31, 19–25. [Google Scholar] [CrossRef]
- Beniston, M.; Farinotti, D.; Stoffel, M.; Andreassen, L.M.; Coppola, E.; Eckert, N.; Fantini, A.; Giacona, F.; Hauck, C.; Huss, M.; et al. The European mountain cryosphere: A review of its current state, trends, and future challenges. Cryosphere 2018, 12, 759–794. [Google Scholar] [CrossRef]
- Baraer, M.; Mark, B.G.; McKenzie, J.M.; Condom, T.; Bury, J.; Huh, K.I.; Portocarrero, C.; Gómez, J.; Rathay, S. Glacier recession and water resources in Peru’s Cordillera Blanca. J. Glaciol. 2012, 58, 134–150. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R. Influence of watershed glacier coverage on summer streamflow in British Columbia, Canada. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Eis, J.; Maussion, F.; Marzeion, B. Initialization of a global glacier model based on present-day glacier geometry and past climate information: An ensemble approach. Cryosphere 2019, 13, 3317–3335. [Google Scholar] [CrossRef]
- Stahl, K.; Weiler, M.; Kohn, I.; Freudiger, D.; Seibert, J.; Vis, M.; Gerlinger, K.; Bohm, M. The Snow and Glacier Melt Components of Streamflow of the River Rhine and Its Tributaries Considering the Influence of Climate Change; Technical Report; International Commision for the Hydrology of the Rhine Basin: Lelystad, The Netherlands, 2016. [Google Scholar]
- Braun, L.; Escher-Vetter, H. Glacial discharge as affected by climate change. In Proceedings of the Interpraevent 1996: Protection of Habitat against Floods, Debris Flows and Avalanches, Garmisch-Partenkirchen, Germany, 24–28 June 1996. [Google Scholar]
- Marzeion, B.; Jarosch, A.H.; Gregory, J.M. Feedbacks and Mechanisms Affecting the Global Sensitivity of Glaciers to Climate Change. Cryosphere 2014, 8, 59–71. [Google Scholar] [CrossRef]
- Zekollari, H.; Huss, M.; Farinotti, D. Modelling the Future Evolution of Glaciers in the European Alps under the EURO-CORDEX RCM Ensemble. Cryosphere 2019, 13, 1125–1146. [Google Scholar] [CrossRef]
- Schulla, J. Model Description WaSiM (Water Balance Simulation Model)-Completely Revised Version of 2012 with 2013 to 2015 Extensions; Hydrology Software Consulting J. Schulla: Zurich, Switzerland, 2015. [Google Scholar]
- Förster, K.; Garvelmann, J.; Meißl, G.; Strasser, U. Modelling forest snow processes with a new version of WaSiM. Hydrol. Sci. J. 2018, 63, 1540–1557. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).