Climate and the Global Spread and Impact of Bananas’ Black Leaf Sigatoka Disease
Abstract
1. Introduction
2. Black Sigatoka Leaf Disease & Climate
3. Results
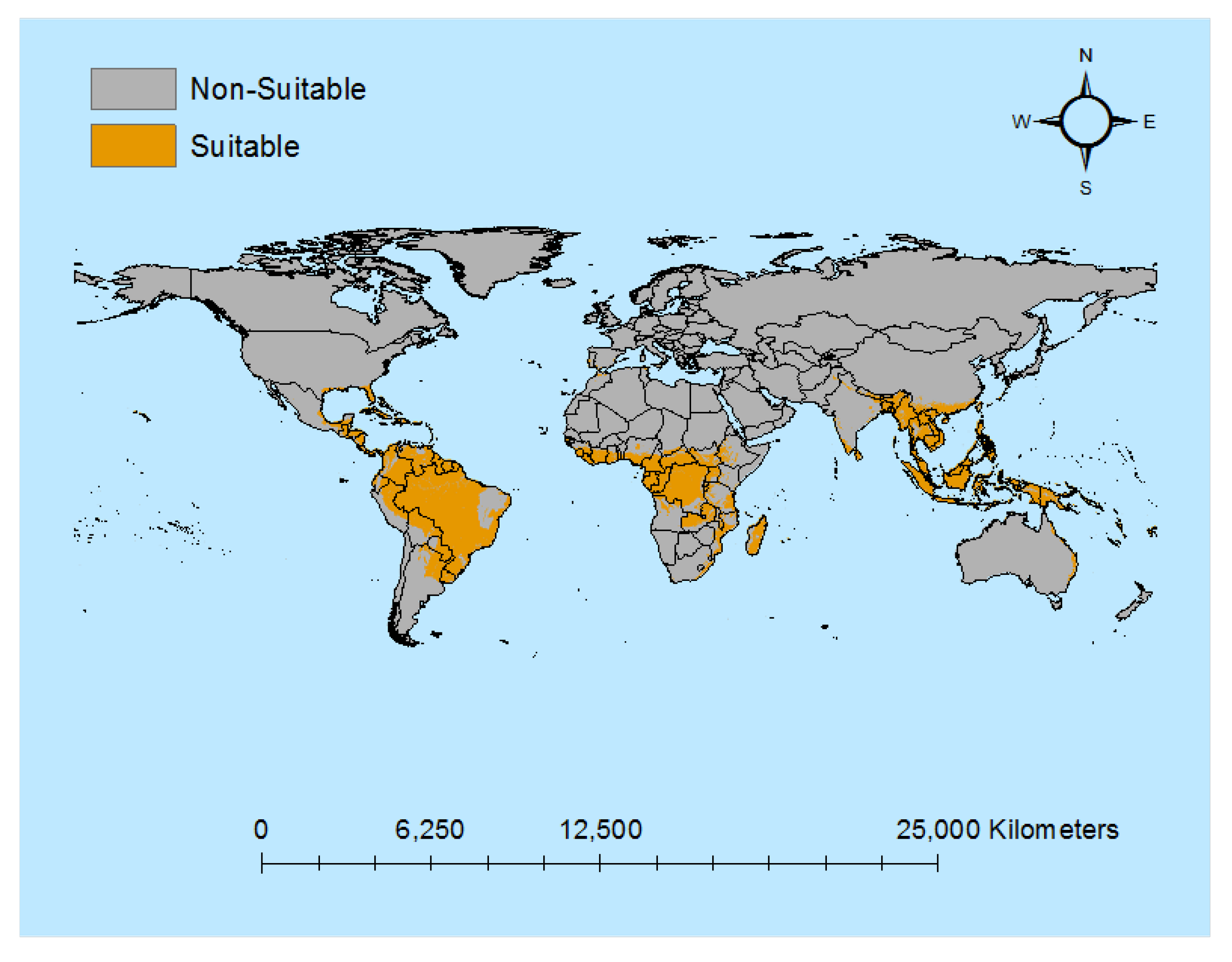
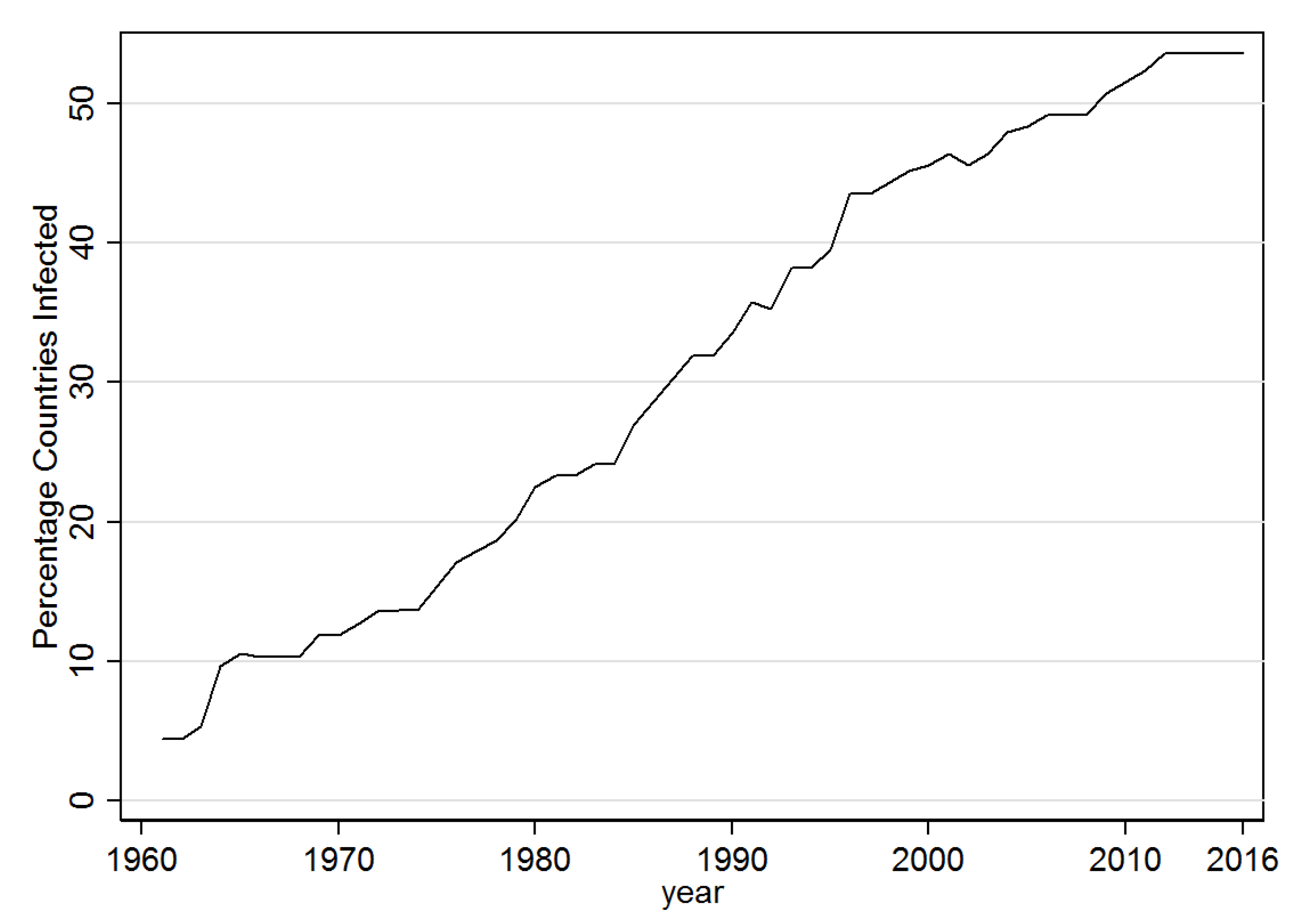
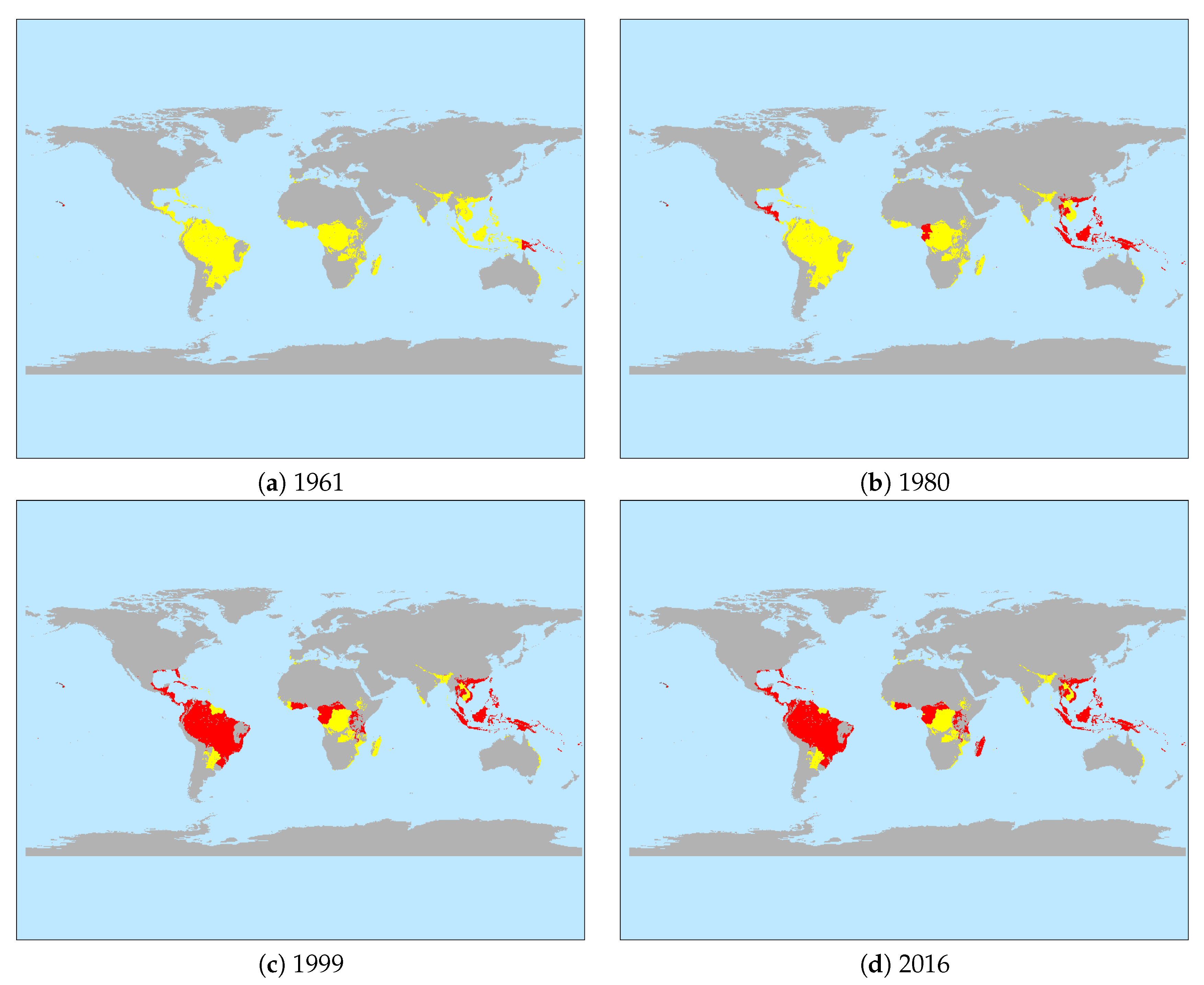
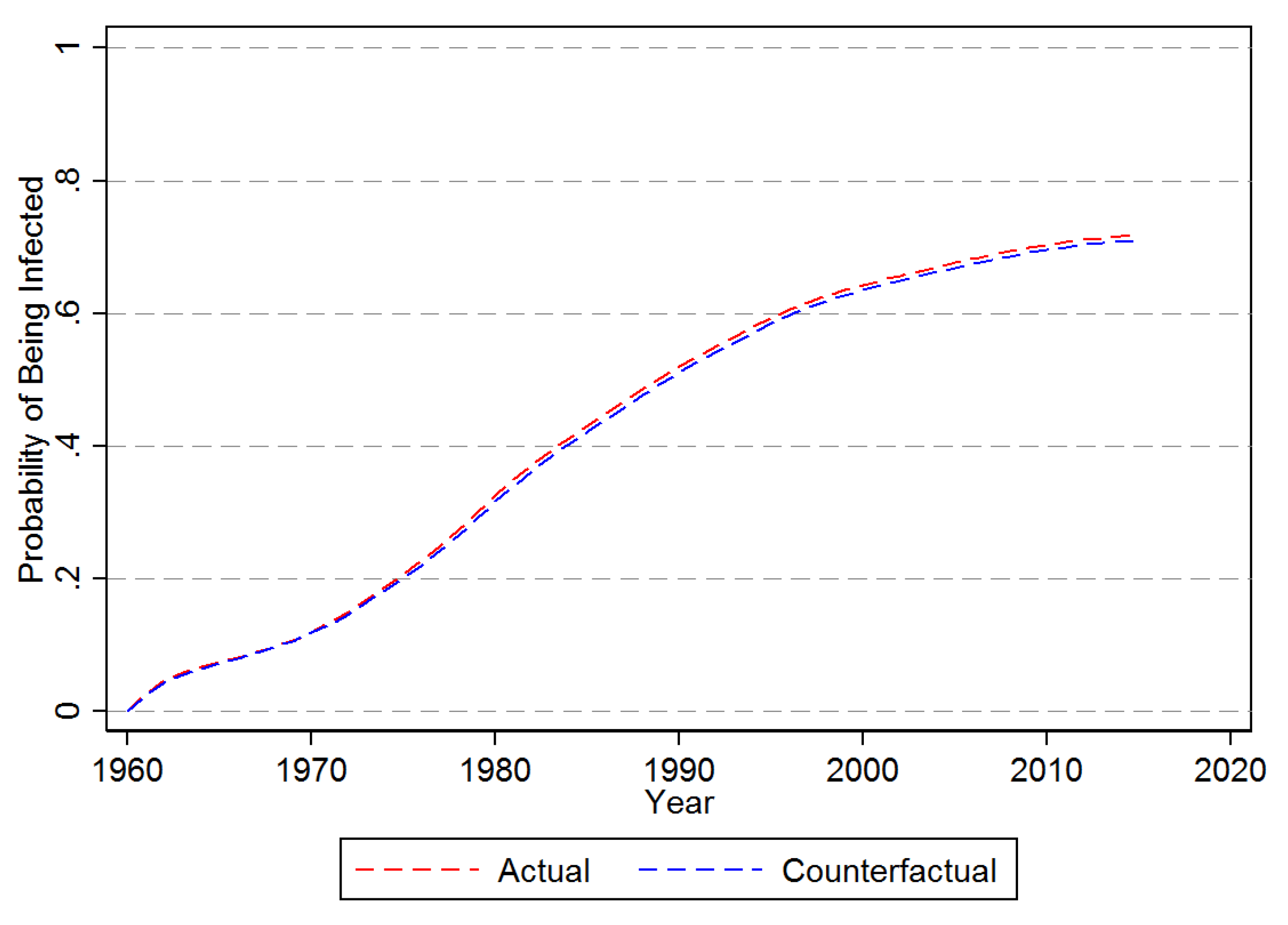
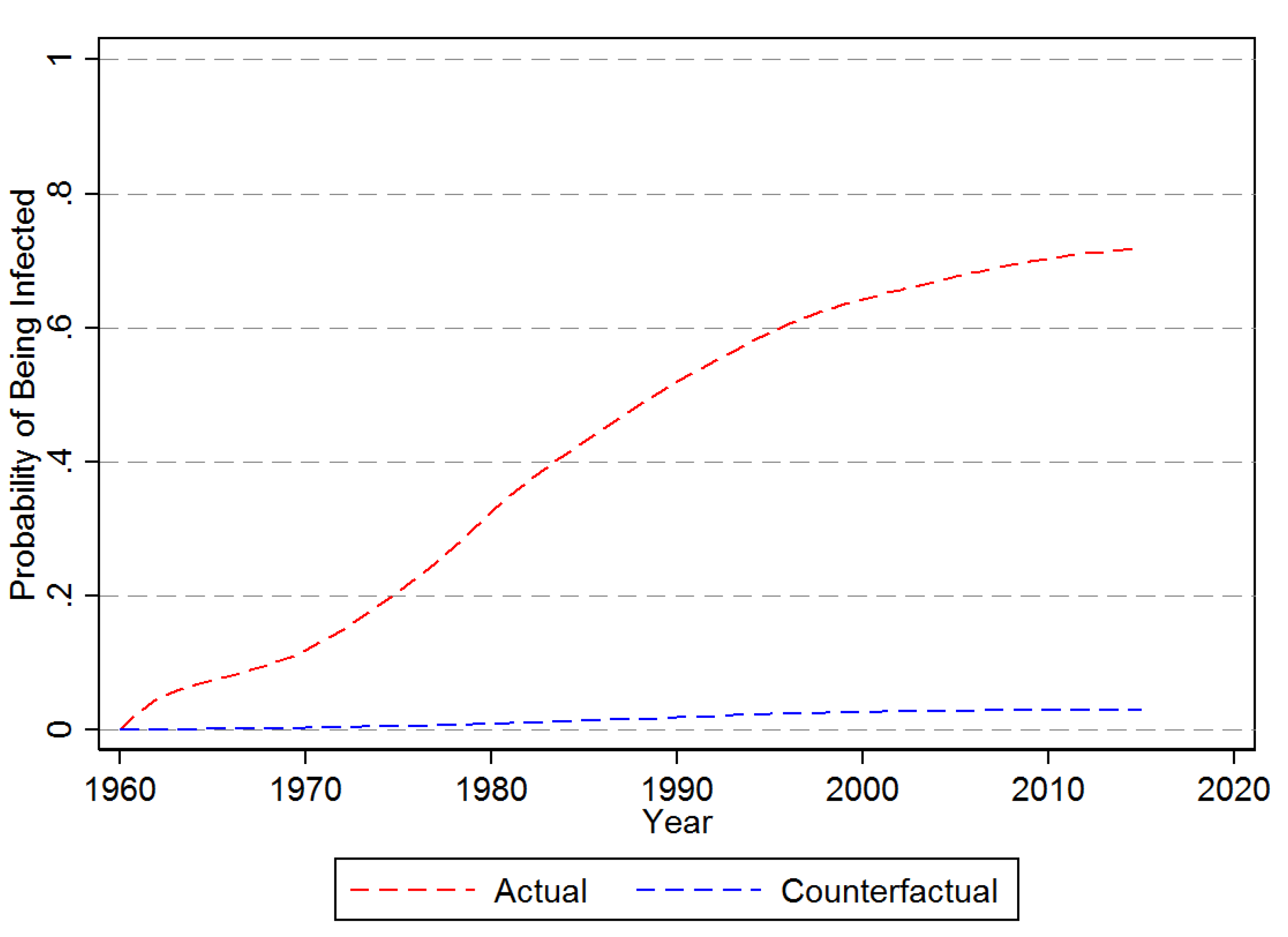
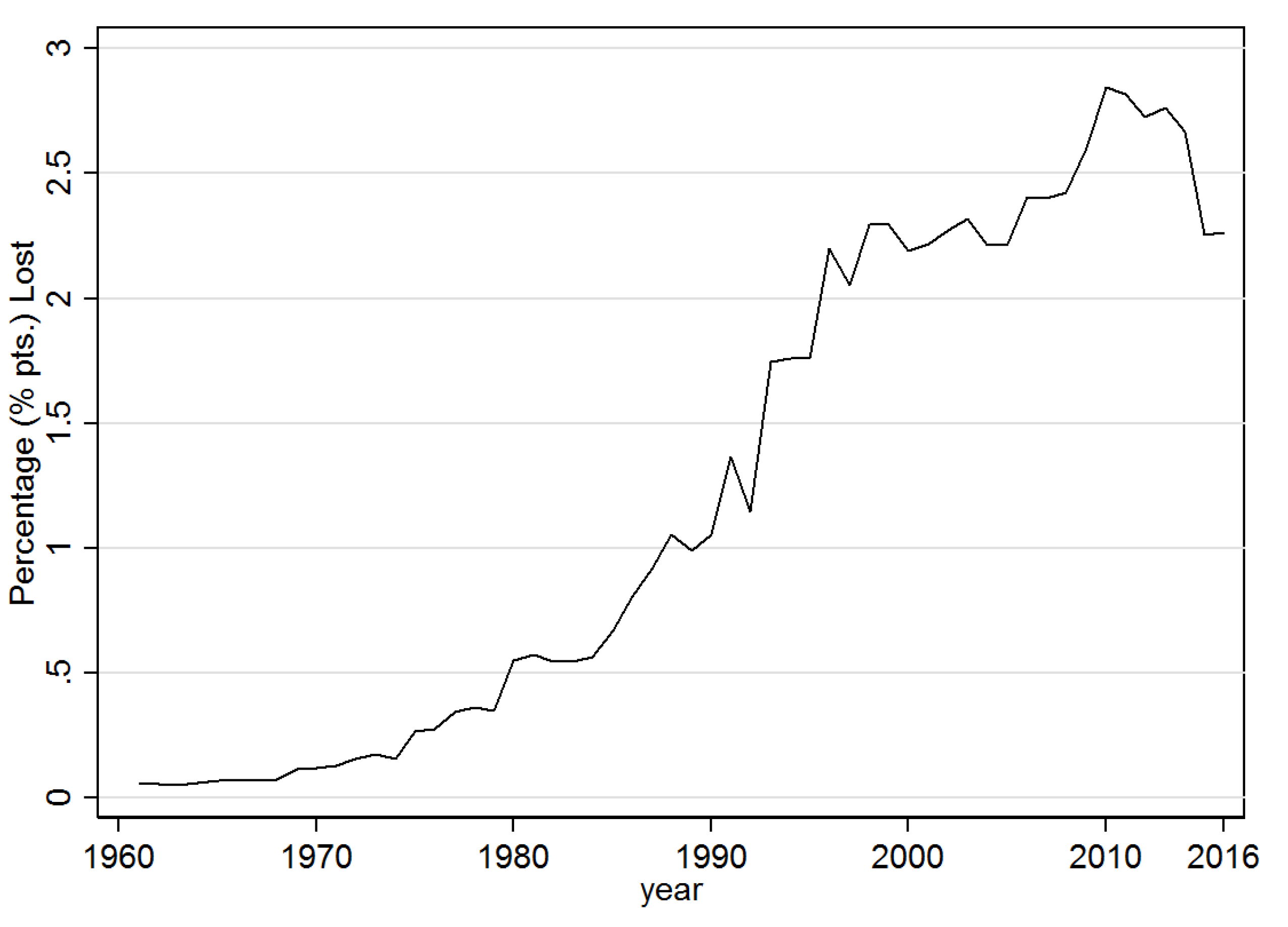
3.1. Descriptive Results
3.2. Regression Results
3.2.1. First Time Infection
3.2.2. Impact of Disease Diffusion on Banana Production
4. Discussion
5. Materials and Methods
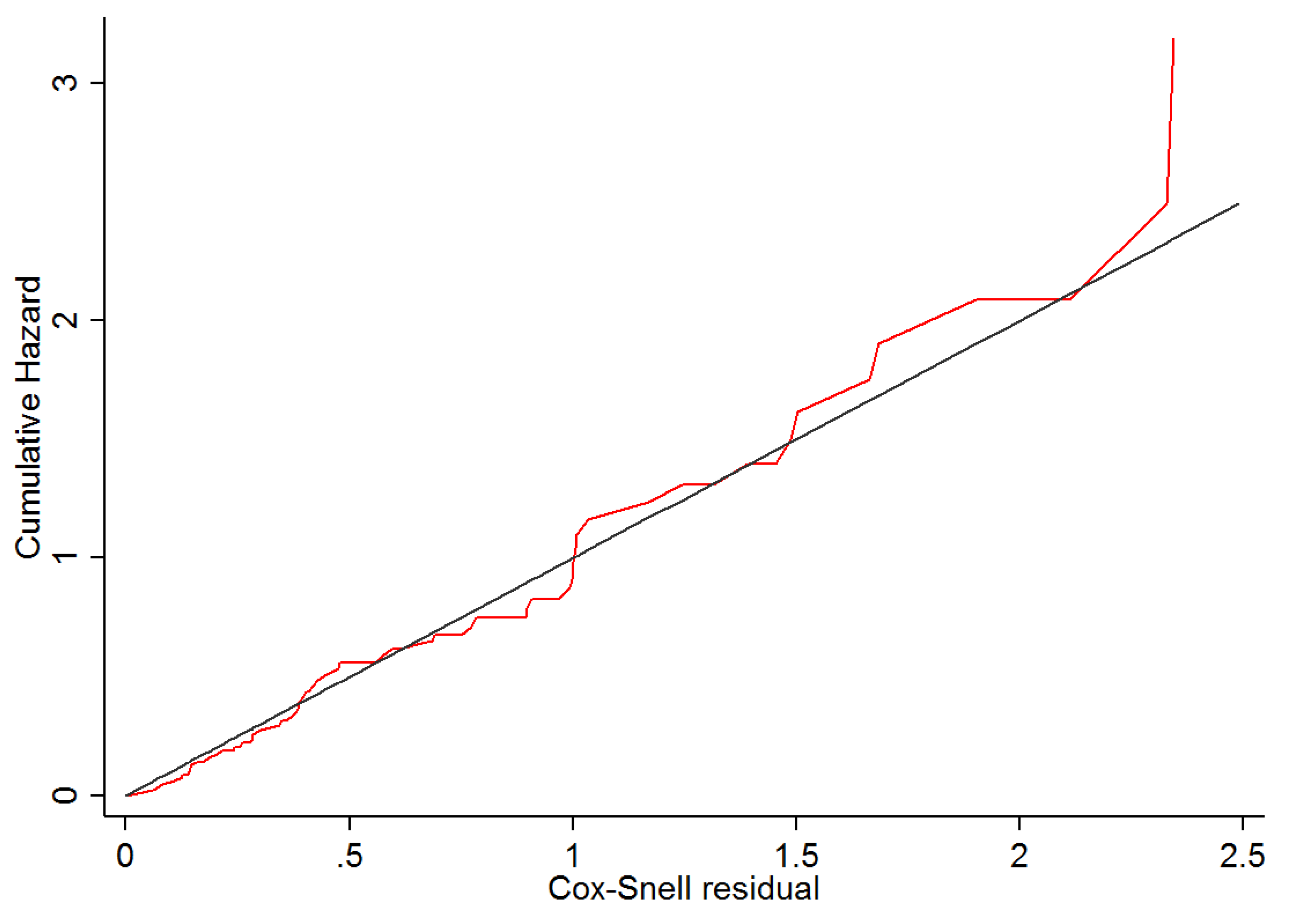
5.1. Methods
Local Disease Spread (LDS)
5.2. Long Distance Dispersal (LDD)
5.3. BSLD Presence
5.4. Empirical Modeling
5.4.1. First Time Infection Model
5.4.2. Impact of Disease Diffusion Model
5.5. Data
5.5.1. BSLD Presence Data
5.5.2. Climatic Data
5.5.3. Banana and Agricultural Products Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Agrios, G.N. Plant Pathology; Academic Press: New York NY, USA, 2005. [Google Scholar]
- Scheffer, R.P. The Nature of Disease in Plants; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Gráda, C.Ó.; O’Rourke, K.H. Migration as disaster relief: Lessons from the Great Irish Famine. Eur. Rev. Econ. Hist. 1997, 1, 3–25. [Google Scholar] [CrossRef]
- Simms, C. The grape depression. New Sci. 2017, 236, 60–62. [Google Scholar] [CrossRef]
- Money, N.P. The Triumph of the Fungi: A Rotten History; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Hunter, D.; Guarino, L.; Spillane, C.; McKeown, P.C. Routledge Handbook of Agricultural Biodiversity; Taylor & Francis: New York, NY, USA, 2017. [Google Scholar]
- Wolfe, M. The current status and prospects of multiline cultivars and variety mixtures for disease resistance. Annu. Rev. Phytopathol. 1985, 23, 251–273. [Google Scholar] [CrossRef]
- Garrett, K.; Mundt, C. Epidemiology in mixed host populations. Phytopathology 1999, 89, 984–990. [Google Scholar] [CrossRef]
- Gergerich, R.C.; Welliver, R.A.; Gettys, S.; Osterbauer, N.K.; Kamenidou, S.; Martin, R.R.; Golino, D.A.; Eastwell, K.; Fuchs, M.; Vidalakis, G.; et al. Safeguarding fruit crops in the age of agricultural globalization. Plant Dis. 2015, 99, 176–187. [Google Scholar] [CrossRef]
- Lucas, J.A.; Hawkins, N.J.; Fraaije, B.A. The Evolution of Fungicide Resistance. In Advances in Applied Microbiology; Elsevier: Amsterdam, The Netherlands, 2015; Volume 90, pp. 29–92. [Google Scholar]
- Oerke, E.C. Crop losses to pests. J. Agric. Sci. 2006, 144, 31–43. [Google Scholar] [CrossRef]
- Perrings, C. Options for managing the infectious animal and plant disease risks of international trade. Food Secur. 2016, 8, 27–35. [Google Scholar] [CrossRef]
- Brown, J.K.; Hovmøller, M.S. Aerial dispersal of pathogens on the global and continental scales and its impact on plant disease. Science 2002, 297, 537–541. [Google Scholar] [CrossRef]
- Fisher, M.C.; Henk, D.A.; Briggs, C.J.; Brownstein, J.S.; Madoff, L.C.; McCraw, S.L.; Gurr, S.J. Emerging fungal threats to animal, plant and ecosystem health. Nature 2012, 484, 186. [Google Scholar] [CrossRef]
- Savary, S.; Willocquet, L.; Pethybridge, S.J.; Esker, P.; McRoberts, N.; Nelson, A. The global burden of pathogens and pests on major food crops. Nat. Ecol. Evol. 2019, 3, 430. [Google Scholar] [CrossRef]
- HE, D.C.; ZHAN, J.S.; XIE, L.H. Problems, challenges and future of plant disease management: From an ecological point of view. J. Integr. Agric. 2016, 15, 705–715. [Google Scholar] [CrossRef]
- Marin, D.H.; Romero, R.A.; Guzmán, M.; Sutton, T.B. Black Sigatoka: An increasing threat to banana cultivation. Plant Dis. 2003, 87, 208–222. [Google Scholar] [CrossRef] [PubMed]
- Abbott, R. A Socio-Economic History of the International Banana Trade, 1870–1930; European Union University: Fiesole, Italy, 2009. [Google Scholar]
- Koeppel, D. Banana: The Fate of the Fruit that Changed the World; Penguin: Harmondsworth, UK, 2007. [Google Scholar]
- Churchill, A.C. Mycosphaerella fijiensis, the black leaf streak pathogen of banana: Progress towards understanding pathogen biology and detection, disease development, and the challenges of control. Mol. Plant Pathol. 2011, 12, 307–328. [Google Scholar] [CrossRef] [PubMed]
- de Bellaire, L.d.L.; Fouré, E.; Abadie, C.; Carlier, J. Black Leaf Streak Disease is challenging the banana industry. Fruits 2010, 65, 327–342. [Google Scholar] [CrossRef][Green Version]
- Alamo, C.; Evans, E.; Brugueras, A.; Nalampang, S. Economic impact and trade implications of the introduction of Black Sigatoka (Mycosphaerella fijiensis) into Puerto Rico. J. Agric. Appl. Econ. 2007, 39, 5–17. [Google Scholar] [CrossRef]
- Jones, D. The distribution and importance of the Mycosphaerella Leaf Spot Diseases of Banana. In Mycosphaerella Leaf spot Diseases of Bananas: Present Status and Outlook; INIBAP: San José, Costa Rica, 2003; pp. 25–41. [Google Scholar]
- Edmeades, S.; Phaneuf, D.J.; Smale, M.; Renkow, M. Modelling the crop variety demand of semi-subsistence households: Bananas in Uganda. J. Agric. Econ. 2008, 59, 329–349. [Google Scholar] [CrossRef]
- Kenneth, A.; Gerald, O.; Edilegnaw, W.; Wilberforce, T. Ex-Ante Adoption of New Cooking Banana (Matooke) Hybrids in Uganda Based on Farmers’ Perceptions; Technical Report; International Association of Agricultural Economists: Foz Do Iguacu, Brazil, 2012. [Google Scholar]
- Cook, D.C.; Liu, S.; Edwards, J.; Villalta, O.N.; Aurambout, J.P.; Kriticos, D.J.; Drenth, A.; De Barro, P.J. Predicted economic impact of black Sigatoka on the Australian banana industry. Crop. Prot. 2013, 51, 48–56. [Google Scholar] [CrossRef]
- Ramsey, M.; Daniells, J.; Anderson, V. Effects of Sigatoka leaf spot (Mycosphaerella musicola Leach) on fruit yields, field ripening and greenlife of bananas in North Queensland. Sci. Hortic. 1990, 41, 305–313. [Google Scholar] [CrossRef]
- Bebber, D.P. Climate change effects on Black Sigatoka disease of banana. Philos. Trans. R. Soc. B 2019, 374, 20180269. [Google Scholar] [CrossRef]
- Norros, V.; Rannik, Ü.; Hussein, T.; Petäjä, T.; Vesala, T.; Ovaskainen, O. Do small spores disperse further than large spores? Ecology 2014, 95, 1612–1621. [Google Scholar] [CrossRef]
- Golan, J.J.; Pringle, A. Long-distance dispersal of fungi. Microbiol. Spectr. 2017, 5. [Google Scholar] [CrossRef]
- Driscoll, J.C.; Kraay, A.C. Consistent covariance matrix estimation with spatially dependent panel data. Rev. Econ. Stat. 1998, 80, 549–560. [Google Scholar] [CrossRef]
- Robert, S.; Ravigné, V.; Zapater, M.F.; Abadie, C.; Carlier, J. Contrasting introduction scenarios among continents in the worldwide invasion of the banana fungal pathogen Mycosphaerella fijiensis. Mol. Ecol. 2012, 21, 1098–1114. [Google Scholar] [CrossRef] [PubMed]
- Rivas, G.G.; Zapater, M.F.; Abadie, C.; Carlier, J. Founder effects and stochastic dispersal at the continental scale of the fungal pathogen of bananas Mycosphaerella fijiensis. Mol. Ecol. 2004, 13, 471–482. [Google Scholar] [CrossRef] [PubMed]
- Burt, P.J.A. Windborne dispersal of Sigatoka leaf spot pathogens. Grana 1994, 33, 108–111. [Google Scholar] [CrossRef]
- Aylor, D.E. Spread of plant disease on a continental scale: Role of aerial dispersal of pathogens. Ecology 2003, 84, 1989–1997. [Google Scholar] [CrossRef]
- Parnell, M.; Burt, P.J.; Wilson, K. The influence of exposure to ultraviolet radiation in simulated sunlight on ascospores causing Black Sigatoka disease of banana and plantain. Int. J. Biometeorol. 1998, 42, 22–27. [Google Scholar] [CrossRef]
- Yonow, T.; Ramirez-Villegas, J.; Abadie, C.; Darnell, R.E.; Ota, N.; Kriticos, D.J. Black Sigatoka in bananas: Ecoclimatic suitability and disease pressure assessments. PLoS ONE 2019, 14, e0220601. [Google Scholar] [CrossRef]
- Júnior, J.; Valadares Júnior, R.; Cecílio, R.A.; Moraes, W.B.; Vale, F.X.R.d.; Alves, F.R.; Paul, P.A. Worldwide geographical distribution of Black Sigatoka for banana: Predictions based on climate change models. Sci. Agric. 2008, 65, 40–53. [Google Scholar] [CrossRef]
- FAO. 2019. Available online: http://www.fao.org/3/y5102e/y5102e04.htm (accessed on 22 March 2020).
- Wooldridge, J.M. Econometric Analysis of Cross Section and Panel Data; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Grambsch, P.M.; Therneau, T.M. Proportional hazards tests and diagnostics based on weighted residuals. Biometrika 1994, 81, 515–526. [Google Scholar] [CrossRef]
- Zheng, Y.; Cai, T. Augmented estimation for t-year survival with censored regression models. Biometrics 2017, 73, 1169–1178. [Google Scholar] [CrossRef] [PubMed]
- Stover, R. Distribution and probable origin of Mycosphaerella fijiensis in southeast Asia. Trop. Agric. Trinidad Tobago 1978, 55, 65–68. [Google Scholar]
- Pasberg-Gauhl, C.; Gauhl, F.; Jones, D. Black leaf streak: Distribution and economic importance. Dis. Banan. Abaca Enset 2000, 37–44. [Google Scholar]
- Jacome, L. Mycosphaerella Leaf Spot Diseases of Bananas: Present Status and Outlook; Bioversity International: Rome, Italy, 2003. [Google Scholar]
- Blomme, G.; Ploetz, R.; Jones, D.; De Langhe, E.; Price, N.; Gold, C.; Geering, A.; Viljoen, A.; Karamura, D.; Pillay, M.; et al. A historical overview of the appearance and spread of Musa pests and pathogens on the African continent: Highlighting the importance of clean Musa planting materials and quarantine measures. Ann. Appl. Biol. 2013, 162, 4–26. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]

| Variable | Definition | Mean | Std. Dev. |
|---|---|---|---|
| PROD | Production (tons) | 464,628 | 1,621,986 |
| HAREA | Area Harvested (Ha) | 3,0087 | 79,202 |
| BSLD | Detection Indicator | 0.3169 | 0.4653 |
| F | Disease Diffusion rate | 0.0259 | 0.0526 |
| F (BSLD = 1) | F once Infected | 0.021 | 0.039 |
| LDD | Long Distance Dispersal Probability | 4.09 × 10 | 0.0003 |
| RAIN | Rainfall (mm/day) | 4.0223 | 2.5112 |
| EVAPO | Evapotranspiration (mm/day) | 2.6141 | 1.1214 |
| HUMID | Relative Humidity (%) | 74.9114 | 11.7134 |
| CMOIST | Moisture Storage on Canopy | 2.2819 | 2.513 |
| CTEMP | Canopy Temperature (C) | 24.0699 | 2.4552 |
| WIND | Wind (m/s) | 2.9039 | 1.7498 |
| WSTRESS | % Days Soil Water Stressed | 0.4804 | 0.3589 |
| CTEMP8 | % Days CTEMP < 8 C | 0.0053 | 0.0188 |
| CTEMP38 | % Days CTEMP > 38 C | 0.0001 | 0.0014 |
| HUMID60 | % Days HUMID > 60% | 0.166 | 0.219 |
| WIND4 | % Days WIND > 4 m/s | 0.403 | 0.3092 |
| BIMPORT | Import of Bananas (tons) | 24,006 | 113,401 |
| AIMPORT | Import of Agr. Products (tons) | 1,720,699 | 4,777,477 |
| BSUIT | Area of Banana Suitability (Ha) | 1691 | 4409 |
| DWBS | Distance Weight. Detection | 0.037 | 0.202 |
| DWAEXP | Distance Weight. logged Agricultural Exports | 0.717 | 2.544 |
| DWBEXP | Distance Weight. logged Bananas Exports | 0.406 | 1.785 |
| (1) | (2) | (3) | |
|---|---|---|---|
| LDD | 0.032 * | 0.0397 ** | 0.0411 ** |
| (0.013) | (0.012) | (0.0116) | |
| log(AIMP) | 0.6039 ** | 0.6735 ** | 0.6328 ** |
| (0.1666) | (0.1684) | (0.1554) | |
| log(BIMP) | −0.0031 | −0.0275 | −0.0356 |
| (0.0928) | (0.0991) | (0.0954) | |
| DWBSLD | −1.4895 * | −1.0984 | |
| (0.6779) | (0.7962) | ||
| FT | −0.2109 | −0.3030 | −01.0721 |
| (2.5275) | (2.5928) | (2.6881) | |
| RAIN | 0.13 | 0.1269 | 0.1619 |
| (0.1384) | (0.1399) | (0.1499) | |
| EVAPO | −0.8477 | −0.8978 | −0.7071 |
| (0.6737) | (0.6778) | (0.7295) | |
| HUMID | 0.0759 | 0.0974 | 0.0327 |
| (0.1153) | (0.1116) | (0.1347) | |
| CMOIST | −0.3582 | −0.4000 | −0.3787 |
| (0.2181) | (0.216) | (0.2319) | |
| CTEMP | 0.1954 | 0.2236 | 0.199 |
| (0.1513) | (0.1467) | (0.1605) | |
| WIND | −0.8690 | −01.1943 | −0.9247 |
| (1.0180) | (1.0125) | (0.9748) | |
| WSTRESS | −4.9328 | −5.2234 | −4.3036 |
| (2.8768) | (2.8953) | (3.1743) | |
| CTEMP8 | 2.5629 | 2.7856 | 2.9621 |
| (13.0638) | (12.6117) | (12.5182) | |
| CTEMP38 | −2968.0320 | −2750.2310 | −5314.0590 |
| (5605.0180) | (5690.3960) | (8580.5970) | |
| HUMID60 | 0.2426 | 1.3038 | −1.8477 |
| (6.6567) | (6.5067) | (8.0296) | |
| WIND4 | 2.9073 | 4.7726 | 3.4434 |
| (5.8018) | (5.8627) | (5.6950) | |
| log(HAREA) | 0.0598 | 0.0494 | 0.0122 |
| (0.1316) | (0.1268) | (0.1534) | |
| log(BAREA) | −0.3020 | −0.3588 | −0.3106 |
| (0.2067) | (0.2156) | (0.2671) | |
| t | 0.2261 ** | ||
| (0.073) | |||
| t | −0.0034 ** | ||
| (0.0011) | |||
| MODEL: | COX | COX | LOGIT |
| Obs. | 4137 | 4137 | 4137 |
| (1) | (2) | |
|---|---|---|
| BS | 0.076 | 0.057 |
| (0.047) | (0.041) | |
| F | −1.315 | −0.732 |
| (1.089) | (0.904) | |
| F × BS | −1.846 ** | −2.717 ** |
| (0.545) | (0.611) | |
| RAIN | −0.025 | −0.012 |
| (0.016) | (0.014) | |
| EVAPO | −0.061 | −0.005 |
| (0.148) | (0.108) | |
| HUMID | 0.011 | 0.01 |
| (0.009) | (0.008) | |
| CMOIST | 0.009 | 0.008 |
| (0.019) | (0.017) | |
| CTEMP | −0.051 | −0.046 |
| (0.027) | (0.025) | |
| WIND | −0.005 | 0.042 |
| (0.043) | (0.042) | |
| WSTRESS | −0.082 | 0.101 |
| (0.244) | (0.214) | |
| CTEMP8 | −4.916 ** | −4.845 ** |
| (1.778) | (1.458) | |
| CTEMP38 | −0.127 | 1.202 |
| (4.859) | (3.754) | |
| HUMID60 | 0.531 | 0.718 |
| (0.431) | (0.37) | |
| WIND4 | −0.471 | −0.488 |
| (0.409) | (0.293) | |
| Dep. Var: | PROD | BAREA |
| Obs. | 6793 | 6793 |
| 0.677 | 0.66 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strobl, E.; Mohan, P. Climate and the Global Spread and Impact of Bananas’ Black Leaf Sigatoka Disease. Atmosphere 2020, 11, 947. https://doi.org/10.3390/atmos11090947
Strobl E, Mohan P. Climate and the Global Spread and Impact of Bananas’ Black Leaf Sigatoka Disease. Atmosphere. 2020; 11(9):947. https://doi.org/10.3390/atmos11090947
Chicago/Turabian StyleStrobl, Eric, and Preeya Mohan. 2020. "Climate and the Global Spread and Impact of Bananas’ Black Leaf Sigatoka Disease" Atmosphere 11, no. 9: 947. https://doi.org/10.3390/atmos11090947
APA StyleStrobl, E., & Mohan, P. (2020). Climate and the Global Spread and Impact of Bananas’ Black Leaf Sigatoka Disease. Atmosphere, 11(9), 947. https://doi.org/10.3390/atmos11090947





