Abstract
To study the influence of complex terrain with different scales on the structure of near-surface turbulence, the turbulence observational data from Semi-Arid Climate and Environment Observatory of Lanzhou University (SACOL) were analyzed. SACOL is located in typical Loess Plateau topography. The terrain around the site varies greatly with the direction. Representative data from the Northeast, Southeast, Southwest, and Northwest were selected to study the structure characteristics of the near surface turbulence. The complex topography within the flux footprint enhances the vertical scale of turbulence σw and thereby increases the vertical–longitudinal ratio of turbulence Ar. While the turbulent horizontal scale σu is also significantly affected by the distant terrain beyond the flux footprint. The upwind terrain undulation increases σu and reduces Ar. Affected by the complex terrain, the ratio of the spectrum of the vertical velocity to that of the longitudinal velocity, Sw(n)/Su(n), is far less than 4/3 in the southwest direction, and the turbulence is significantly anisotropic.
1. Introduction
Boundary layer turbulence connects the surface thermal, hydrology, and biochemical processes with atmospheric motions, thus affecting the global atmospheric circulation and climate system. It is a crucial concern to research regional responses and feedback to climate change, as well as the impact of human activities on the environment and climate [1,2]. Atmospheric turbulence is also an important process that affects extreme weather and climate disasters such as heavy rain, sand, and hail. Near-surface turbulent fluxes are the most important indicators in the study of land–atmosphere interaction, which is one of the core issues for developing atmospheric models and improving the accuracy of the simulation, and they are also key input parameters for studying the carbon cycle of the earth–atmosphere system and estimating crop yields. In addition, to understand the diffusion of atmospheric pollutants [3] and the utilization of wind energy [4], it is necessary to understand the structure and motion characteristics of boundary layer turbulence.
The concepts that relate to the turbulence of the atmospheric boundary layer (ABL), such as the Monin–Obukhov similarity theory (MOST), were usually developed over a horizontally homogeneous surface [5]. However, the turbulence in the ABL is directly affected by the underlying surface [6]. As a result, the laws that describe the average field and turbulent field established under the condition of flat and uniform underlying surface are not completely applicable to the ABL on the inhomogeneous underlying surface. However, since it is affected by factors such as topographic fluctuations, soil types, and surface vegetation differences, the actual underlying surface is ever-changing and often inhomogeneous. Data from TRACT (TRansport of Air pollutants over Complex Terrain) showed that the terrain had a significant impact on the structure of the boundary layer, and the topography-induced secondary circulation affected the surface energy budget and the development of convective boundary [7,8]. The results of wind tunnel experiments and numerical simulations also showed that complex terrain has a significant effect on the near-surface turbulence [9,10]. Martins et al. [11] analyzed the turbulence data on a 400 m cliff in Brazil and found that the dimensionless standard deviations of vertical velocity and temperature met MOST for all stability regimes, while the dimensionless standard deviations of horizontal components of the turbulent velocity appeared to be independent of the stability when ζ > 0.5 (where ζ = z/L with z as the height and L as the Obukhov length), and the same turbulence behavior was also observed at the bottom of a river valley [12]. Mainly with a small-scale, the turbulence in the vertical direction can adapt to the terrain quickly, and thus it is insensitive to mesoscale terrain fluctuations, which has been confirmed by multiple observation experiments under unstable conditions [13,14]. However, in a stable situation, the dimensionless standard deviations increase rapidly with ζ [13]. Observations on complex terrain also showed that, even under neutral stratification, dimensionless standard deviation of vertical velocity was larger than that on the homogeneous surface [15]. The influence of the complex terrain increases the difficulty of parameterization of the boundary layer turbulence [16], challenging the accuracy of weather and climate models.
The complex underlying surface makes the structure of the ABL turbulence extremely complicated. Local circulation adjustment [17], low-level jets [18], terrain-induced gravity waves, solitary and quasi-wave events [19,20], and many other complex motion forms will have an important impact on turbulence, which increases the uncertainty in the land–atmosphere interaction. These studies, while accumulating knowledge of turbulence on complex underlying surfaces, have also raised questions about turbulence structures and transport characteristics on complex underlying surfaces. It is the lack of understanding of the turbulent characteristics that conduce to numerical models, such as the Mellor and Yamada model, which produce unsatisfactory results for the turbulence when applied to complex underlying surfaces [10].
The Loess Plateau is located in the North of central China, going to the Great Wall in the North, Qinling Mountains in the South, Taihang Mountains in the East, and Riyue Mountain in the West, with an elevation of 800–3000 m and an area of 620,000 square kilometers. As an important component of China’s arid and semi-arid regions, the Loess Plateau is also the transition zone between China’s semi-arid and semi-humid climate and ecological environment. Owing to low soil moisture, high potential evapotranspiration, sparse vegetation, and soil erosion, the ecosystem in this region is extremely fragile and is very sensitive to climate change [21,22]. However, the scarcity of observation sites and observation data limits our understanding of the land–atmosphere interaction in this area, which has hindered the land surface parameterization scheme of the regional climate model. Therefore, understanding the characteristics of surface turbulence on the Loess Plateau is of great significance for studying the parameterization of climate models in this region, and then for studying global climate change. Our previous research found that in the Loess Plateau, non-stationary motions affected by complex terrain occur frequently, which disrupt the flux-gradient profile, and challenge the application of MOST to complex terrain [16]. As an important source of local turbulence, non-stationary motions seriously affect the structure of local turbulence, resulting in weakened heat mixing in the vertical direction and stronger unclosure of energy [23,24]. However, there is little knowledge about the influence of the terrain scale on the turbulence scale, and further research is needed.
Focusing on the effect of terrain on the turbulence scale, we analyzed the turbulence observation data from the Semi-Arid Climate and Environment Observatory of Lanzhou University (SACOL) in the year 2008. Representative data from different directions were selected to study the characteristics of the near-surface turbulence and the influence of terrain on the turbulence scale.
2. Observations and Methods
2.1. Site Description
The Semi-Arid Climate and Environment Observatory of Lanzhou University (SACOL) is located on the top of Cuiying Mountain (35.946° N, 104.137° E) at Yuzhong Campus of Lanzhou University. SACOL was established in 2005 to fill in the gaps in long-term observations of land–atmosphere interaction on the Loess Plateau, to study the effects of atmospheric aerosols on the surface water cycle and climate change and to understand the impact of human activities on climate change in this semi-arid region.
From a mesoscale perspective, SACOL is located on a loess mesa, Cuiying Mountain, which is roughly north–south trending with a 1965.8 m elevation (Figure 1, right bottom), surrounded by typical landforms of the Loess Plateau, such as intricate gullies, beams, and ridges. The relative height of Cueiying Mountain is about 200 m, at the foot of which on the east side lies the Yuzhong Campus of Lanzhou University. On the west side is Phoenix Mountain with an elevation of 1994 m. The valley between the two mountains is about 1 km wide. On a large scale, Cueiying Mountain is located in a southeast–northwest valley (Figure 1, left), with an average elevation of about 1800 m. The with an elevation of of Xinglong Mountain in the Southeast of Cueiying Mountain is more than 3000 m. In the Northwest, peaks and valleys criss-cross, with an average elevation above 2000 m. In the Southeast, the terrain is flat, with the Jiejiazui Mountain more than 10 km away. The airflow runs along the valley, causing the prevailing winds of SACOL to be northwesterly and southeasterly winds, with an average annual wind speed of about 1.6 m s−1. The terrain varies greatly in different wind directions.
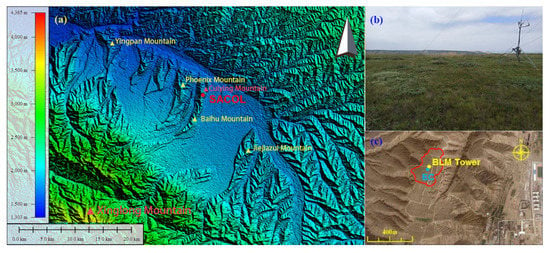
Figure 1.
(a) The topographic map of the Semi-Arid Climate and Environment Observatory of Lanzhou University (SACOL), (b) the area surrounding the observation field obtained from Google Earth, and (c) the vegetation of the flux observation field in summer. The area surrounded by the yellow line is the observation field, and circles filled with yellow and blue represent the locations of the boundary layer meteorological tower (BLM tower) and the eddy covariance system (EC). The topographic map in Figure 1 (a) is drawn using ASTER GDEM v2 data [25].
The flux observation field is basically flat, about 200 m in the east–west direction, and about 400 m in the north–south direction, evenly covered with Stipa bungeana, Artemisia frigida, and Leymus secalinus. The height of the vegetation is about 0.24 m in summer and 0.10 m in winter. Except for a long and narrow area west to the south of the observation field, the periphery of the observation field in other directions is a hillside, and the terrain height decreases rapidly. The vegetation is basically in its native state, with a height of about 0.10 m in winter and 0.24 m in summer. For more information about SACOL, please refer to Huang et al. [26].
2.2. Instruments
SACOL has accumulated a large amount of data for long-term continuous observation in the semi-arid region of the Loess Plateau, which has provided a basis for studying the characteristics of land–atmosphere interactions on the complex terrain in the semi-arid region of the Loess Plateau. The observations used in this study include the boundary layer meteorological observing tower (BLM tower) and the eddy covariance system (EC). The BLM tower is 32.5 m high, with wind speed, temperature, and humidity sensors installed at the heights of 1, 2, 4, 8, 12, 16, and 32 m, respectively, and a wind direction sensor at 8 m. Moreover, a CS105 barometric pressure sensor and a TE525MM-L rain gauge are used to detect and record the atmospheric pressure and snow. The BLM tower data are automatically collected and recorded every half hour. The EC consists of a three-axis sonic anemometer (CSAT3) and an open-path infrared CO2 and H2O analyzer with a sampling frequency of 10 Hz, which are placed 3.0 m above the surface and are calibrated in May every year. The orientation of the CSAT3 is 15° east by north. The main observation instruments, observation items, and installation locations are presented in Table 1. The time involved in this study is in Beijing time (BJT) unless otherwise specified. BJT is 8 h earlier than universal time and 1 h earlier than the local time of SACOL.

Table 1.
Main observation items and observation instruments.
2.3. Data and Methods
Observation data of the EC and BLM tower of SACOL in 2008 were selected to analyze the characteristics of near-surface turbulence on complex terrain. Figure 2 shows the wind direction and velocity distribution of SACOL in 2008. Located in a southeast–northwest valley, the dominant wind directions of SACOL are southeast and northwest winds. Blocked by the mountains on both sides, the northeast and southwest winds are rare and weak. To compare the turbulence characteristics over different terrains, the turbulence data of the EC were filtered according to the wind direction: observations with wind directions of 0°–60°, 90°–150°, 180°–240°, and 270°–330° and the standard deviation of the wind direction within 30 min being less than 30° were selected, and then, they were run through the following quality controls:
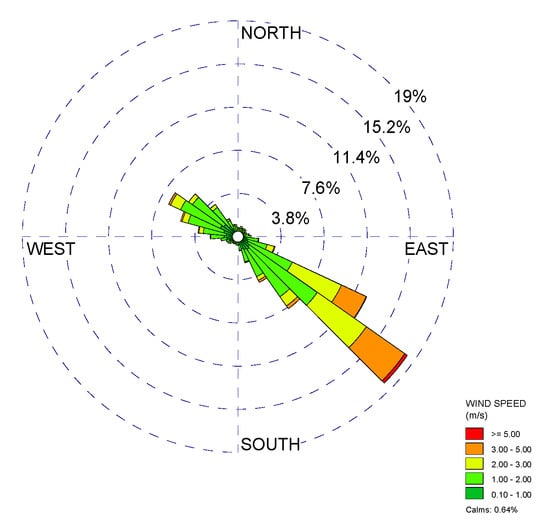
Figure 2.
Wind direction and wind speed distribution of SACOL in 2008.
- (1)
- Runs when the instrument’s warning signals arose or when precipitation occurred were rejected.
- (2)
- Runs with more than 10 consecutive observed values that did not meet the physical threshold of the instrument were rejected.
- (3)
- Spikes were removed following the algorithm from Vickers and Mahrt [27].
Then, we obtained 400, 6546, 422, and 3112 records (here and after, a 30-min time series of the EC is called a record), respectively, as the representative data of the northeast (NE), southeast (SE), southwest (SW) and northwest (NW) direction.
To eliminate the influence caused by the slope of the terrain or the installation tilt of the instrument, double coordinate rotation was performed for each record, in such a way that the x-axis is along the average airflow direction, and the z-axis is perpendicular to the ground. After the double rotation, the wind speeds in the x, y, and z directions are, respectively, denoted as u, v, w, which in turn represent the longitudinal wind, lateral wind and vertical velocity. Then, the turbulence statistics in the four directions of NE, SE, SW, and NW were calculated, and the characteristics of the turbulence in different directions were compared, subsequently the influence of the terrain on the turbulence structure was analyzed.
The gradient Richardson Number Ri was used as a stability parameter instead of ζ to avoid the self-correlation caused by the shared use of the same turbulent fluctuation in both the independent and dependent variables.
where U and θ are the average of wind speed and potential temperature, respectively, and g is the gravitational acceleration. Ri was evaluated based on local scaling from the BLM tower data measured at 2 m and 4 m.
The flux footprints of the representative data in each direction were calculated by Kljun’s model [28] (Figure 3), which is suitable for application to long time series and has been used and confirmed in many studies [29,30]. In the NE and SW directions, 80% of the turbulence came from the flat surface of the flux observation field, while in the NW and SE directions, a larger part of the turbulence observed by the EC came from the surrounding undulating surface outside the observation field. It should be noted that although the observed turbulence comes from the observation field, it is still very different from that recorded over a uniform surface, because of the airflow distortion caused by the complex terrain outside the flux footprint.
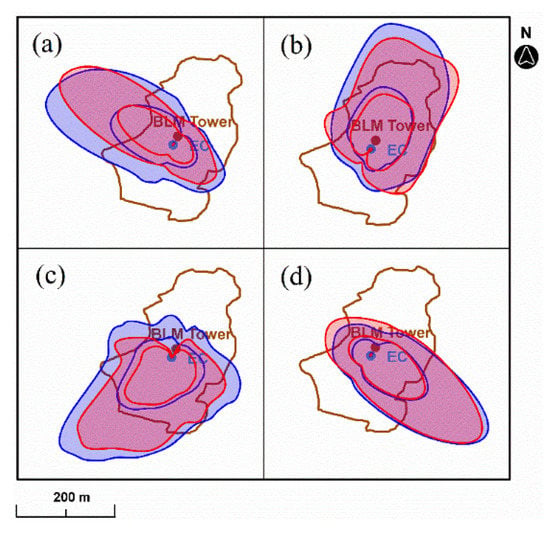
Figure 3.
Flux footprint of each direction, estimated by the Flux Footprint Prediction model of Kljun et al. [28]. The red and blue coverage areas are flux footprints for unstable and stable conditions, respectively, and the two contours of each footprint indicate 80% and 90% flux of the contributing source area. (a) NW direction; (b) NE direction; (c) SW direction; (d) SE direction.
3. Statistical Characteristics of the Turbulence
3.1. The Mean Flow
In the direction of NW, NE, SE and SW, the strong stratification with |Ri| > 1 accounted for 14.3%, 4.8%, 5.1% and 6.8%, respectively (Figure 4). Complex terrain, on the one hand, changes the structure of airflow to inhibit the development of stratification [7], and on the other hand, it generates turbulence through surface friction, which increases the momentum and heat exchange between the upper and lower layers and weakens the stability of the stratification.
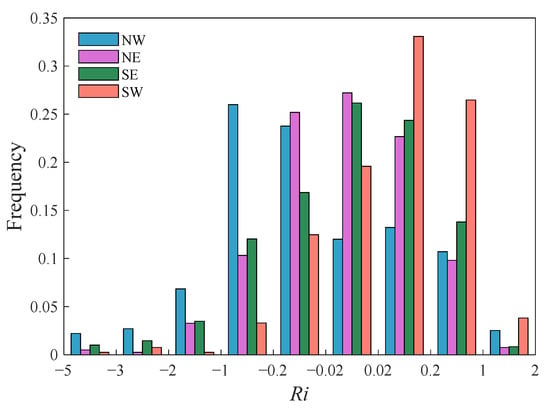
Figure 4.
Distribution of the stratification stability Ri in each direction.
According to the distribution of Ri, we divided the stratification stability into several categories: strongly unstable (Ri < −1), moderately unstable (−1 ≤ Ri < −0.5), weakly unstable (−0.5 ≤ Ri < −0.02), neutral/near-neutral (−0.01 ≤ Ri < 0.01), weakly stable (0.02 ≤ Ri < 0.25), moderately stable (0.25 ≤ Ri < 1), and strongly stable (Ri ≥ 1). It was dominated by unstable stratification in the direction of NW, which was mainly of weak and moderate instability, while it was dominated by stable stratification in the SW direction.
Figure 5 is the average value of the longitudinal wind speed, u, in different stable ranges. To reduce the random error of the data, samples with less than 15 records were not counted. Except for the neutral/near-neutral condition in the SE direction, the mean value of the u component of the wind speed was less than 3.0 m/s in the NW, NE, and SW directions. Because the valley SACOL location is northwest–southeast, and at the same time is affected by the weather-scale movements in the region, the airflow mainly runs along the valley. Due to the blocking and fragmentation of the western mesa, the northwest wind is weak. The distant terrain in the southeast direction is flat, having a small blocking effect on the airflow in such a way that winds with a u component greater than 3 m/s are mainly concentrated in this direction, and they are usually accompanied by weak stratification of −0.5 ≤ Ri < 0.25 (conditions of weakly unstable, neutral/near-neutral, and weakly stable). The southeast wind decreased with the increase in the stratification. Under strong stratification (strongly stable, strongly unstable), u decreased to less than 2.0 m/s, which was not significantly different from the wind speed during the stratification in the northwest direction.
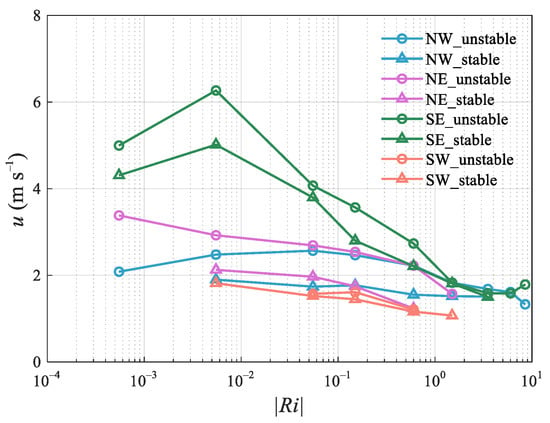
Figure 5.
The dependence of the longitudinal wind speed, u, on the stratification stability Ri. Each point in the figure represents the average value of u in the corresponding Ri interval. The hollow circles and the hollow triangles represent unstable and stable conditions respectively. Only data with a sample size greater than 15 in the corresponding Ri range are shown.
3.2. Turbulence Scale
To analyze the turbulence scale, we chose the standard deviations of the longitudinal and vertical wind σu and σw as the research objects, without using the friction velocity u* to normalize them. The purpose of this choice was to pay attention to the absolute mean scale of the turbulence directly and to avoid the false instability caused by a small denominator during stable stratification.
Figure 6 shows the distribution of σu in different wind directions with Ri. For the specific direction, σu was the largest at the neutral/near-neutral condition and decreased while the stratification increased. In a stable stratification, σu was smaller than in an unstable condition and decreases faster with stability. It was basically consistent with the change of u with Ri in the corresponding direction. Comparing σu in the NW and SE directions, at neutral/near neutral, the much stronger wind in the SE direction resulted in σu being greater than in the NW direction, while under moderately strong stratification, it was greater than the latter, although the wind speed in the SE direction was stronger or comparable to the NW direction. This finding reflects the “memory” of horizontal turbulence to distant terrain, in other words, affected by the undulating terrain; the scale of horizontal turbulence blowing from the northwest is larger. Compared with running along the valley, excluding the significant difference in the wind speed, σu in the NE was greater under the same stability. Under weak stratification, σu in the NE was between that in the NW and SE, but it was somewhat smaller under the strong stratification. The wind in the NE is related to the local circulation of the mountain-valley breezes, and the special landform makes the valley wind circulation extremely complicated by many factors, which results in larger horizontal scales of turbulence. For the same reason, although the winds in the SW are much weaker than those in the NW and SE in the stable boundary layer, σu was similar to these two directions.
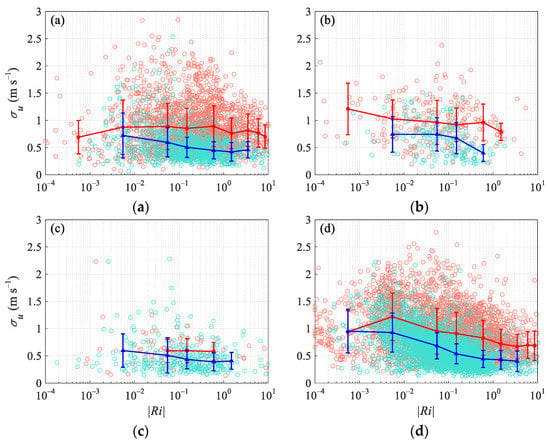
Figure 6.
The dependence of the horizontal longitudinal wind standard deviation, σu, on the stratification stability Ri (a) northwest, (b) northeast, (c) southwest, (d) southeast. The scattered points represent the average value of each record. The curves represent the average value of different Ri intervals, and the error bars represent the standard deviation of each interval. The unstable and stable conditions are indicated in red and blue colors, respectively.
Figure 7 is the variation of σw in different wind directions with Ri. For the near-neutral stratification, due to the high wind speed and strong shear in the SE, σw was the largest, at 0.53 m s−1. From weakly stable/unstable to strongly stable/unstable stratification, although there were significant differences in the wind speeds in the NW, NE, and SE, there was no significant difference in σw under the same stability conditions, and the vertical scale of the turbulence was approximately the same. Turbulence in the vertical direction was mainly small-scale and can quickly adapt to surface changes, that is, σw was mainly affected by the surface of the flux footprint area. The surface features in the flux footprint area in the NW and SE were similar, and thus the vertical scale of the turbulence was close. In the NE, σu was larger, and the shear of the horizontal airflow in the vertical direction was stronger. However, the turbulence was more from the flat surface near the observation field and the surface friction was small, which weakened the shear generation of the airflow. As a result, σw was almost the same as the directions along the valley. In the SW, most of the fluxes came from the flat surface, and the wind speed itself was small, which caused the σw to be significantly smaller than in other directions.
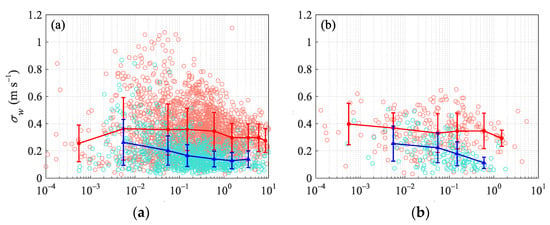
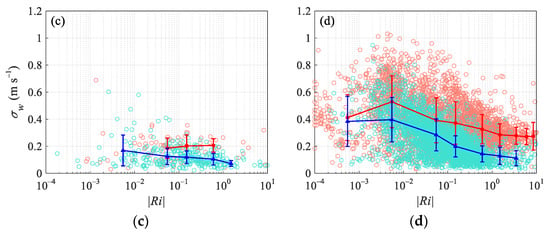
Figure 7.
The dependence of the horizontal longitudinal wind standard deviation, σw, on the stratification stability Ri (a) northwest, (b) northeast, (c) southwest, (d) southeast. The scattered points represent the average value of each record. The curves represent the average value of different Ri intervals, and the error bars represent the standard deviation of each interval. The unstable and stable conditions are indicated in red and blue colors, respectively.
It can be concluded from this section that the vertical scale of the turbulence is related to the surface characteristics in the flux footprint area, while the turbulent horizontal scale is also significantly affected by the distant terrain at the same time, because of the influence of the upstream terrain on the airflow. The more the terrain undulates in the flux footprint area, the larger the vertical scale of the turbulence is, and the greater the upwind terrain undulation, the larger the turbulent horizontal scale is. In addition, we noticed that under strongly unstable stratification, where the thermal convection develops to the strongest, σw decreases significantly. The reason for this phenomenon is not well explained by the current data, and further research is needed.
3.3. Vertical–Longitudinal Ratio of the Turbulence
Our previous study on the stable boundary layer turbulence at SACOL showed that topography-induced nonstationary motions, on the time scales of minutes or tens of minutes leading to abrupt variability in the wind direction or wind speed, are important for the condition of u < 3.0 m/s. The nonstationary motions are anisotropic with strong horizontal fluctuations and weak vertical fluctuations, and they affect the structure of the local turbulence generated by the local shear, resulting in a weakened σw/σu. To describe the spatial structure of turbulence, we defined the vertical–longitudinal ratio of the turbulence, which is the ratio of the vertical scale to the horizontal scale of the turbulence, that is, Ar = σw/σu. Ar can reflect the combined influence of undulating terrain at different scales on the turbulence scale (Figure 8). From a comparison of the different directions, under the same stratification conditions, Ar in the four directions was SE > NW > NE > SW in turn, which is consistent with the terrain in the corresponding direction. In the NW and SE, the turbulent footprint covered more undulating surfaces, with Ar being the largest; in the SW, the turbulence mainly came from a flat surface, with Ar being the smallest, even less than 0.3 under stable stratification; and the NE was in the middle. In the NW and SE, the topographic features in the turbulent flux footprint were similar, while the upwind topography was much more undulating in the NW, causing Ar in the NW to be smaller than SE under any stability conditions. The complex topography within the flux footprint increased Ar, and the distant topographic relief reduced Ar.
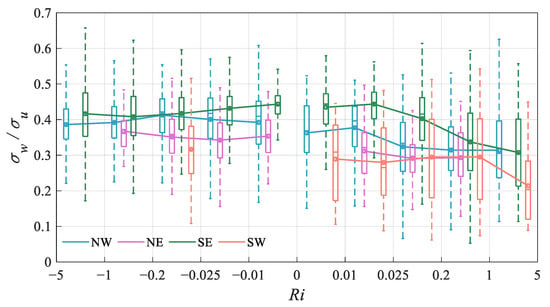
Figure 8.
The dependence of the turbulent aspect ratio Ar on stability Ri in different wind directions. The box plots represent the statistic of Ar in different Ri intervals. For a certain box, the bottom is the lower quartile Q1, the top is the upper quartile Q3, the horizontal line in the middle of the box is the median Q2 and the open circle is the average; the top of the whisker is O3 + 1.5IQR, and the bottom is Q1 − 1.5IQR, where IQR is the interquartile range IQR = Q3 − Q1.
In the same direction, the SE, Ar varied with the stability. In the neutral condition, Ar was approximately 0.45, which is close to the observation results of Martins et al. [14] on a 400 m hillside, and lower than the ideal surface (σw/u* = 1.25, σu/u* = 2.39, Ar = 0.52). The rapid decrease in Ar in the stable boundary layer indicates that the friction of the surface on the turbulence is mainly in the horizontal direction, and the turbulence is quasi-two-dimensional. Under unstable conditions, the addition of thermal turbulence did not change the spatial structure of the turbulence, and Ar was equal to or even slightly reduced from the neutral layer structure. It shows that the terrain has a large influence on the turbulence, even in the strongly unstable boundary layer. The friction of the complex terrain produces strong dynamic turbulence, which increases the vertical mixing and weakens the thermal stratification.
4. Turbulence Spectra
To compare the effect of the terrain scale on the turbulent structure, the power spectral densities of the longitudinal Su(n) and vertical velocity Sw(n) in the NW and SE were analyzed, with n being the frequency. The power spectra densities were multiplied by the frequency n, and thus the area under the spectral function curve can represent the total variance. At the same time, to visually reflect the turbulence variance at different degrees of stability in each direction, we have not normalized the spectra. The longitudinal/vertical velocity spectra classified by the stability are shown in Figure 9. Note that the protrusions at the high-frequency ends of the spectra are mainly caused by white noise and aliasing, having no significant effect on the turbulent fluxes [31], so we calculated the turbulence statistics without filtering.
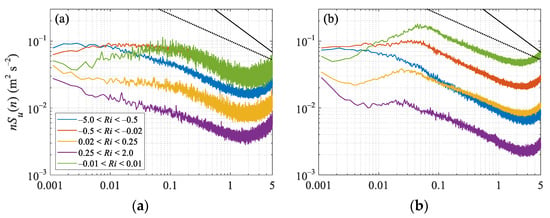
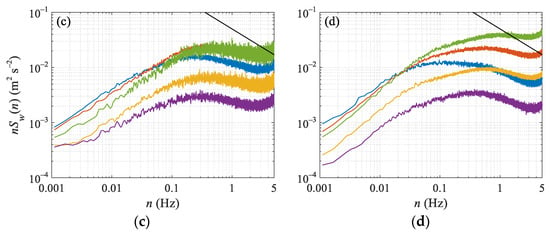
Figure 9.
The spectra of longitudinal wind (a,b) and vertical velocity (c,d) in the directions of northwest (a,c) and southeast (b,d). The color curves in the figure indicate different stability intervals. The solid and dotted black lines are the −2/3 and −2/5 law curves, respectively.
4.1. Turbulence Spectra
The longitudinal velocity u spectra do not comply with the −2/3 law in the high-frequency range, and the spectral curves are smoother, following a −2/5 law (Figure 9a,b). The friction of the complex terrain causes small-scale turbulence to increase and contribute to the flux. In the SE, there were sharp peaks in the spectra from neutral to stable stratification, which was approximately 0.05 Hz under neutral conditions and decreased with increasing stability. There were no clear spectral peaks in the unstable boundary layer, and the spectra did not change much at the low-frequency end. In the NW, the spectral peak at neutral stratification was around 0.1 Hz, but the shape is rather flat, and there is no peak in the u spectra in stable and unstable stabilities. The more complicated surface friction in the NW made the turbulence horizontal scale larger, that is, low-frequency turbulence contributed a large amount to the total variance, especially in stable boundary layers.
In the SE, from stable to neutral stratification, the low-frequency bands of the u spectra are upturned. The more stable the boundary layer is, the steeper the spectral curve is, and the inflection points decrease with decreased stability. Moreover, this phenomenon disappears in the unstable boundary layer. The observation data in Antarctica also found that the u spectra were upturned at the low-frequency end, and this was attributed to the disturbance caused by the terrain [32]. Högström et al. [33] also found the same phenomenon and thought it was the result of mesoscale atmospheric waves. However, in the NW, no buoyancy subrange appears in the stable stratification. The possible reasons for this difference are:
- (1)
- There is a series of hills with different scales along with the airflow in the NW. The complicated terrain has a severe crushing effect on the airflow and, as a result, it is difficult to form stable mesoscale atmospheric waves.
- (2)
- The scale of the atmospheric wave in the NW is large and cannot be observed within an average time of 30 min.
In the NW and SE, the shapes of the vertical velocity w spectra were almost the same under various stability conditions (Figure 9c,d), that is, under the same stability conditions, the vertical turbulent scale components in the two directions were the same. This further confirms the point in Section 3.2. From weakly stable/unstable to strongly stable/unstable conditions, the vertical scale of the turbulence is about the same under the same stability conditions. Additionally, the turbulence in the vertical direction is mainly affected by the surface of the flux footprint, while the distant complex terrain has little effect on it.
4.2. Local Anisotropy of the Turbulence
According to Kolmogorov’s turbulence theory, if the spectral densities of longitudinal velocity Su(n), the lateral velocity Sv(n), and the vertical velocity Sw(n) in the inertial subrange satisfy the relationship of Sv(n)/Su(n) = Sw(n)/Su(n) = 4/3, then the turbulence is isotropic. In the NW of SACOL, the w spectra were smaller than the corresponding u spectra under all the stability stratifications (Figure 10). The phenomenon that Sw(n)/Su(n) is less than 4/3 has been found in many previous studies [34,35,36,37]. Chamecki and Dias [38] tested the applicability of the local isotropy hypothesis to surface-layer turbulent flow. They concluded that sonic anemometry, at the currently available measurement frequencies and sensor path lengths, was unable to resolve the full inertial range of the velocity spectra. Even in some cases, whether the turbulence can reach isotropy outside the resolution limit of the sensor remains an unidentifiable question.
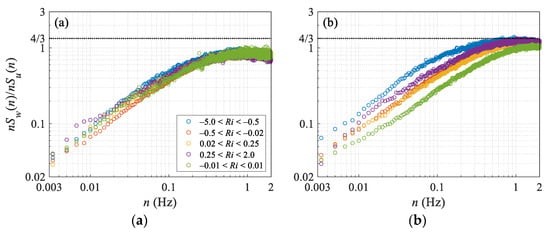
Figure 10.
Ratio of vertical velocity spectral density Sw(n) to longitudinal velocity spectral density Su(n) for different stability ranges the directions of northwest (a) and southeast (b).
In the SE, however, when the stratification was relatively strong (Ri < −0.5 or Ri > 0.25), the vertical-to-longitudinal velocity component spectra tended to converge towards a 4/3 value at the high-frequency range, which is an indicator of local isotropy. In the SE, the ratio Sw(n)/Su(n) changed significantly with Ri, while it was almost not related to the stability in the NW. The upwind terrain undulation caused the turbulence, which was more anisotropic with a strong horizontal fluctuation and a weak vertical fluctuation. On a sufficiently complex surface, the dynamic effects of topography have greater influence on the turbulence anisotropic than thermal stratification.
5. Summary
The Semi-Arid Climate and Environment Observatory of Lanzhou University (SACOL) is in a very complex terrain environment, and the terrain in each direction is different, which provides valuable data for studying the impact of the terrain scale on the turbulence scale. Using the observational data of SACOL in the year 2008, the characteristics of the near-surface turbulence on the complex terrain of the Loess Plateau were analyzed, and the influence of the terrain scale on the turbulence scale was discussed. The data with wind directions of 0–60°, 90–150°, 180–240°, and 270–330°, and the standard deviations of the wind directions within 30 min less than 30°, were taken as representative data for the directions of northeast, southeast, southwest, and northwest respectively. The main results are as follows:
- (1)
- The undulations of the terrain in the flux footprint were in the order of Southeast ≈ Northwest > Northeast >Southwest. Except for the flat terrain in the southeast direction, the distant terrain outside the footprint area was very complicated. The complex terrain resulted in weak stratification stability. Ri was mainly distributed between −1 and 1, and it was even more concentrated in the range of −0.2–0.2 in the directions of the northeast and southeast. Except for the northwest direction, the records with strong stratification, where Ri was greater than 1 or smaller than −1, accounted for fewer than 10% of the total records.
- (2)
- The vertical scale of the turbulence is related to the surface characteristics in the flux footprint area, while the turbulent horizontal scale is also significantly affected by the distant terrain. The more the terrain undulates in the flux footprint area, the larger the vertical scale of the turbulence is; the greater the upwind terrain undulation, the larger the turbulent horizontal scale is.
- (3)
- The vertical–longitudinal ratio, Ar = σw/σu, is used to indicate the influence of the topographic scale on the turbulent structure in different directions. Under the same stratification conditions, Ar was in the order of Southeast > Northwest > Northeast > Southwest. The complex topography within the flux footprint increased Ar, and the distant topographic fluctuations reduced Ar. In the southeast direction, Ar was about 0.45 in the neutral/near-neutral stratification, and it decreased in the unstable stratification with an average value of above 0.4. In the northwest, northeast, and southwest directions, from unstable to neutral/near-neutral stratification, Ar changed slightly, fluctuating around 0.4, 0.35, and 0.3, respectively. In the stable boundary layer, Ar decreased rapidly with increasing stability, and the turbulence was quasi-two-dimensional.
- (4)
- In the southeast direction, there was a buoyancy subrange in the u spectrum of the stable boundary layer, and the inflection point was of the order of 10−3 Hz, which increased with increasing stability; in the northwest direction, affected by the distant complex terrain, there was no buoyant subzone observed in the records of 30 min. Affected by the complex terrain in the Northwest, Sw(n)/Su(n) was far less than 4/3, and the turbulence was significantly anisotropic.
Author Contributions
Conceptualization, methodology, and writing—original draft preparation, J.L.; validation, J.L., Q.G., and Z.Z.; writing—review and editing, M.Z., P.T., and L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 41605005, 41475008.
Acknowledgments
The authors would like to thank the Semi-Arid Climate and Environment Observatory of Lanzhou University (SACOL) for providing the observational data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zeng, N.; Neelin, J.D.; Lau, K.M.; Tucker, C.J. Enhancement of interdecadal climate variability in the Sahel by vegetation interaction. Science 1999, 286, 1537–1540. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Udina, M.; Soler, M.R.; Olid, M.; Jimenez-Esteve, B.; Bech, J. Pollutant vertical mixing in the nocturnal boundary layer enhanced by density currents and low-level jets: Two representative case studies. ADS 2020, 174, 203–230. [Google Scholar] [CrossRef]
- Zhang, M.Q.; Stevens, R.J.A.M. Characterizing the coherent structures within and above large wind farms. Bound.-Layer Meteorol. 2020, 174, 61–80. [Google Scholar] [CrossRef]
- Foken, T. 50 years of the Monin-Obukhov similarity theory. Bound.-Layer Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Sun, J.L.; Lenschow, D.H.; Mahrt, L.; Nappo, C. The relationships among wind, horizontal pressure gradient, and turbulent momentum transport during CASES-99. J. Atmos. Sci. 2013, 70, 3397–3414. [Google Scholar] [CrossRef]
- Kossmann, M.; Vogtlin, R.; Corsmeier, U.; Vogel, B.; Fiedler, F.; Binder, H.J.; Kalthoff, N.; Beyrich, F. Aspects of the convective boundary layer structure over complex terrain. Atmos. Environ. 1998, 32, 1323–1348. [Google Scholar] [CrossRef]
- Kalthoff, N.; Binder, H.J.; Kossmann, M.; Vogtlin, R.; Corsmeier, U.; Fiedler, F.; Schlager, H. Temporal evolution and spatial variation of the boundary layer over complex terrain. Atmos. Environ. 1998, 32, 1179–1194. [Google Scholar] [CrossRef]
- Carvalho, J.C.; Anfossi, D.; Castelli, S.T.; Degrazia, G.A. Application of a model system for the study of transport and diffusion in complex terrain to the TRACT experiment. Atmos. Environ. 2002, 36, 1147–1161. [Google Scholar] [CrossRef]
- Castelli, S.T.; Ferrero, E.; Anfossi, D. Turbulence closures in neutral boundary layer over complex terrain. Bound.-Layer Meteorol. 2001, 100, 405–419. [Google Scholar] [CrossRef]
- Martins, C.A.; Moraes, O.L.L.; Acevedo, O.C.; Degrazia, G.A. Turbulence intensity parameters over a very complex terrain. Bound.-Layer Meteorol. 2009, 133, 35–45. [Google Scholar] [CrossRef]
- Acevedo, O.C.; Moraes, O.L.L.; Da Silva, R.; Anabor, V.; Bittencourt, D.P.; Zimmermann, H.R.; Magnago, R.O.; Degrazia, G.A. Surface-to-atmosphere exchange in a river valley environment. J. Appl. Meteorol. Climatol. 2007, 46, 1169–1181. [Google Scholar] [CrossRef]
- Al-Jiboori, M.H.; Yumao, X.; Yongfu, Q. Turbulence characteristics over complex terrain in west china. Bound.-Layer Meteorol. 2001, 101, 109–126. [Google Scholar] [CrossRef]
- Moraes, O.L.L.; Acevedo, O.C.; Degrazia, G.A.; Anfossi, D.; da Silva, R.; Anabor, V. Surface layer turbulence parameters over a complex terrain. Atmos. Environ. 2005, 39, 3103–3112. [Google Scholar] [CrossRef]
- Founda, D.; Tombrou, M.; Lalas, D.P.; Asimakopoulos, D.N. Some measurements of turbulence characteristics over complex terrain. Bound.-Layer Meteorol. 1997, 83, 221–245. [Google Scholar] [CrossRef]
- Liang, J.N.; Zhang, L.; Wang, Y.; Cao, X.J.; Zhang, Q.; Wang, H.B.; Zhang, B.D. Turbulence regimes and the validity of similarity theory in the stable boundary layer over complex terrain of the Loess Plateau, China. J. Geophys. Res.-Atmos. 2014, 119, 6009–6021. [Google Scholar] [CrossRef]
- Vincent, C.L.; Larsen, X.G.; Larsen, S.E.; Sorensen, P. Cross-Spectra over the sea from observations and mesoscale modelling. Bound.-Layer Meteorol. 2013, 146, 297–318. [Google Scholar] [CrossRef]
- Karipot, A.; Leclerc, M.Y.; Zhang, G.S.; Lewin, K.F.; Nagy, J.; Hendrey, G.R.; Starr, G. Influence of nocturnal low-level jet on turbulence structure and CO2 flux measurements over a forest canopy. J. Geophys. Res.-Atmos. 2008, 113, D10102. [Google Scholar] [CrossRef]
- Smith, S.; Baumgardner, J.; Mendillo, M. Evidence of mesospheric gravity-waves generated by orographic forcing in the troposphere. Geophys. Res. Lett. 2009, 36, L08807. [Google Scholar] [CrossRef]
- Valkonen, T.; Vihma, T.; Kirkwood, S.; Johansson, M.M. Fine-scale model simulation of gravity waves generated by Basen nunatak in Antarctica. Tellus A 2010, 62, 319–332. [Google Scholar] [CrossRef]
- Huang, J.P.; Yu, H.P.; Guan, X.D.; Wang, G.Y.; Guo, R.X. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
- Ji, F.; Wu, Z.H.; Huang, J.P.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Liang, J.N.; Zhang, L.; Cao, X.J.; Wen, J.; Wang, J.M.; Wang, G.Y. Energy balance in the semiarid area of the Loess Plateau, China. J. Geophys. Res.-Atmos. 2017, 122, 2155–2168. [Google Scholar] [CrossRef]
- Yuan, G.H.; Zhang, L.; Liang, J.N.; Cao, X.J.; Liu, H.; Yang, Z.H. Understanding the partitioning of the available energy over the semi-arid areas of the Loess Plateau, China. Atmosphere 2017, 8, 87. [Google Scholar] [CrossRef]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Huang, J.P.; Zhang, W.; Zuo, J.Q.; Bi, J.R.; Shi, J.S.; Wang, X.; Chang, Z.L.; Huang, Z.W.; Yang, S.; Zhang, B.D.; et al. An overview of the semi-arid climate and environment research observatory over the Loess Plateau. Adv. Atmos. Sci. 2008, 25, 906–921. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Babić, K.; Rotach, M.W. Turbulence kinetic energy budget in the stable boundary layer over a heterogeneous surface. Q. J. R. Meteorol. Soc. 2018, 144, 1045–1062. [Google Scholar] [CrossRef]
- Helbig, M.; Chasmer, L.E.; Desai, A.R.; Kljun, N.; Quinton, W.L.; Sonnentag, O. Direct and indirect climate change effects on carbon dioxide fluxes in a thawing boreal forest-wetland landscape. Glob. Chang. Biol. 2017, 23, 3231–3248. [Google Scholar] [CrossRef]
- Wen, X.F.; Yu, G.R.; Sun, X.M.; Liu, Y.F. Turbulence flux measurement above the overstory of a subtropical Pinus plantation over the hilly region in southeastern China. Sci. China Ser. D 2005, 48, 63–73. [Google Scholar] [CrossRef]
- Cava, D.; Giostra, U.; Tagliazucca, M. Spectral maxima in a perturbed stable boundary layer. Bound.-Layer Meteorol. 2001, 100, 421–437. [Google Scholar] [CrossRef]
- Högström, U.; Hunt, J.C.R.; Smedman, A.S. Theory and measurements for turbulence spectra and variances in the atmospheric neutral surface layer. Bound.-Layer Meteorol. 2002, 103, 101–124. [Google Scholar] [CrossRef]
- Liu, S.H.; Liu, H.P.; Xu, M.; Leclerc, M.Y.; Zhu, T.Y.; Jin, C.J.; Hong, Z.X.; Li, J.; Liu, H.Z. Turbulence spectra and dissipation rates above and within a forest canopy. Bound.-Layer Meteorol. 2001, 98, 83–102. [Google Scholar] [CrossRef]
- Roth, M.; Salmond, J.A.; Satyanarayana, A.N.V. Methodological considerations regarding the measurement of turbulent fluxes in the urban roughness sublayer: The role of scintillometery. Bound.-Layer Meteorol. 2006, 121, 351–375. [Google Scholar] [CrossRef]
- Christen, A.; Rotach, M.W.; Vogt, R. The budget of turbulent kinetic energy in the urban roughness sublayer. Bound.-Layer Meteorol. 2009, 131, 193–222. [Google Scholar] [CrossRef]
- Vecenaj, Z.; De Wekker, S.F.J.; Grubisic, V. Near-surface characteristics of the turbulence structure during a mountain-wave event. J. Appl. Meteorol. Climatol. 2011, 50, 1088–1106. [Google Scholar] [CrossRef]
- Chamecki, M.; Dias, N.L. The local isotropy hypothesis and the turbulent kinetic energy dissipation rate in the atmospheric surface layer. Q. J. R. Meteorol. Soc. 2004, 130, 2733–2752. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).