A Chemical Transport Model Emulator for the Interactive Evaluation of Mercury Emission Reduction Scenarios
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation of the Hganthr Atmospheric Cycle
2.2. Building the HERMES Emulator
3. Results
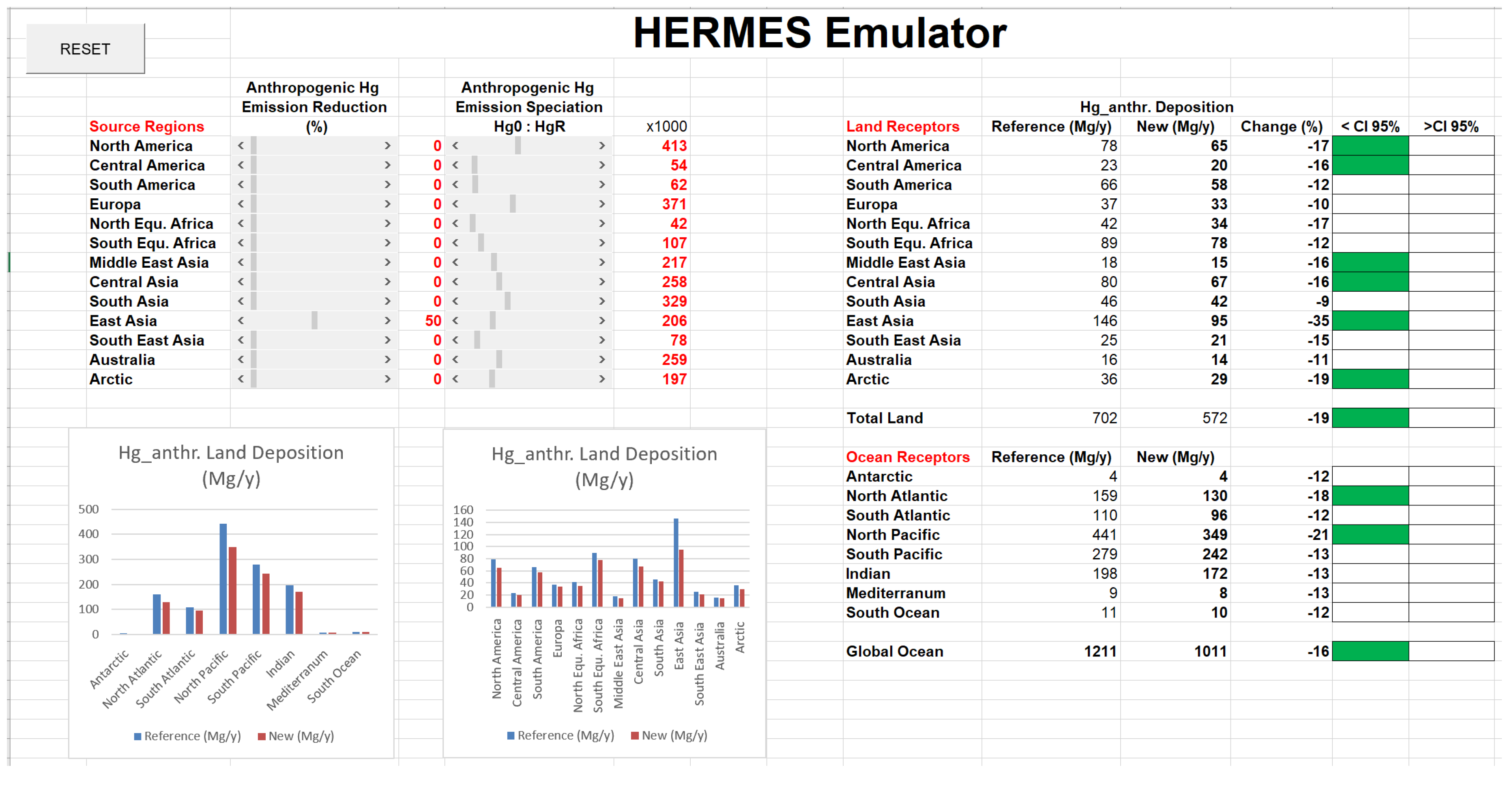
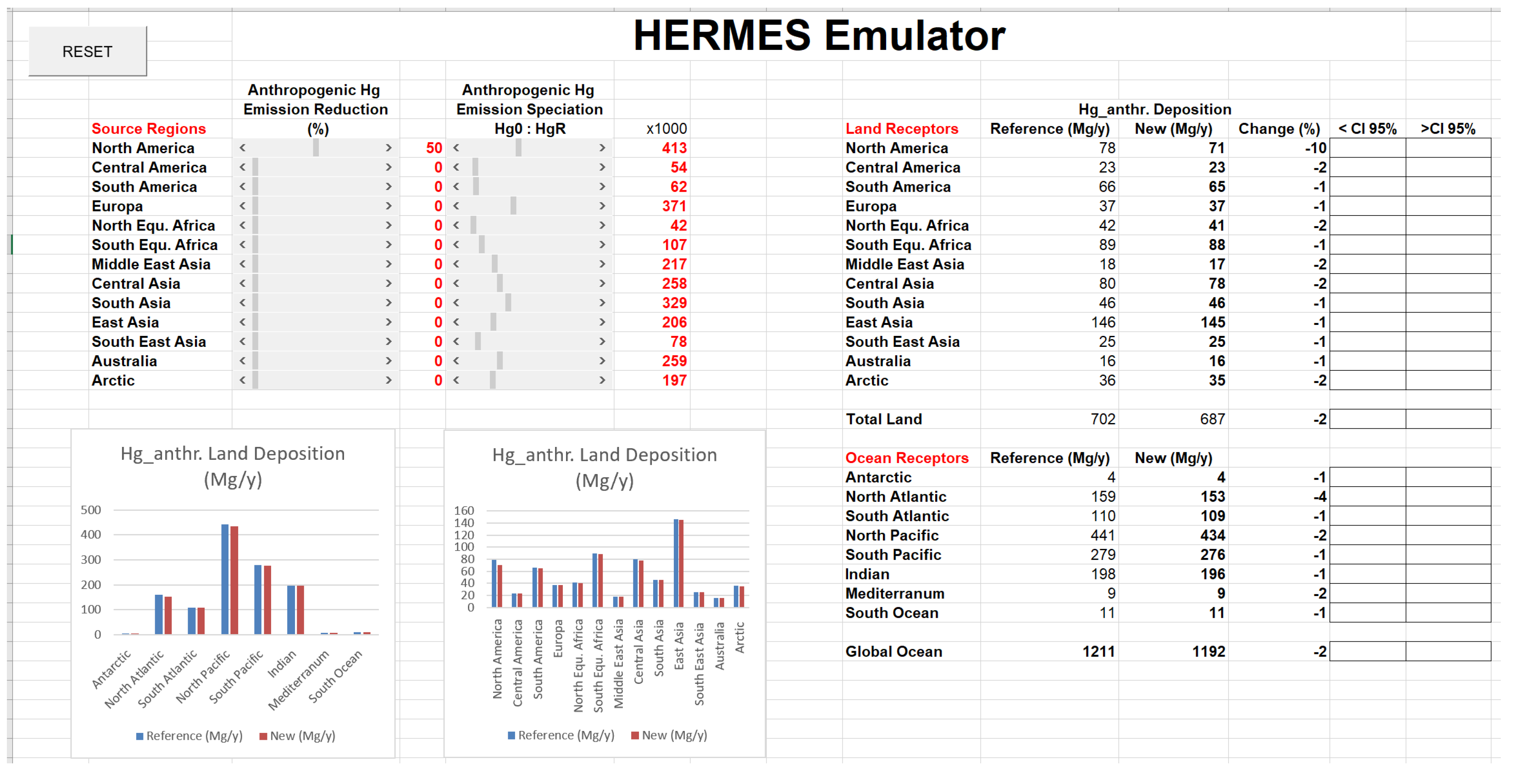
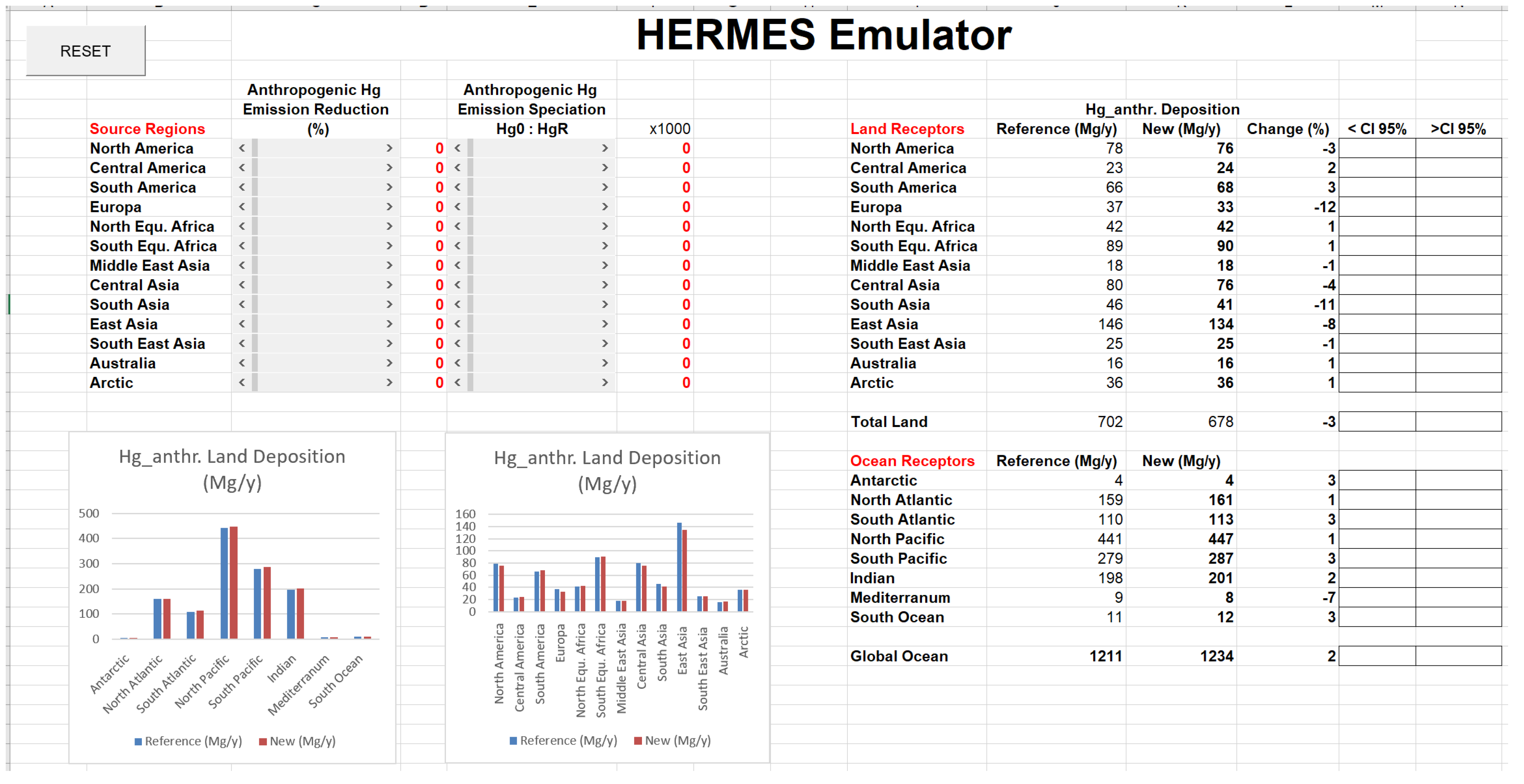
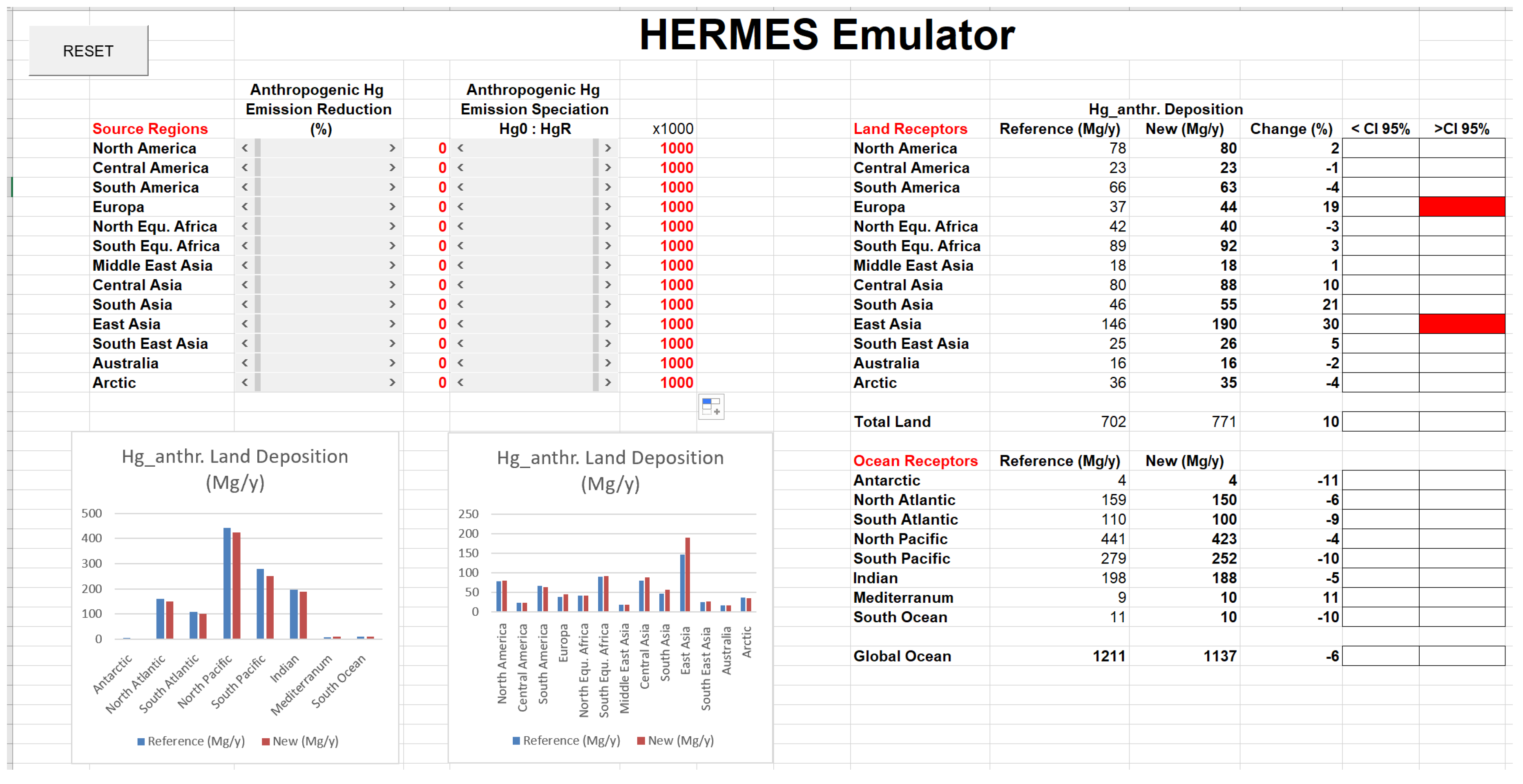
3.1. HERMES Case Studies
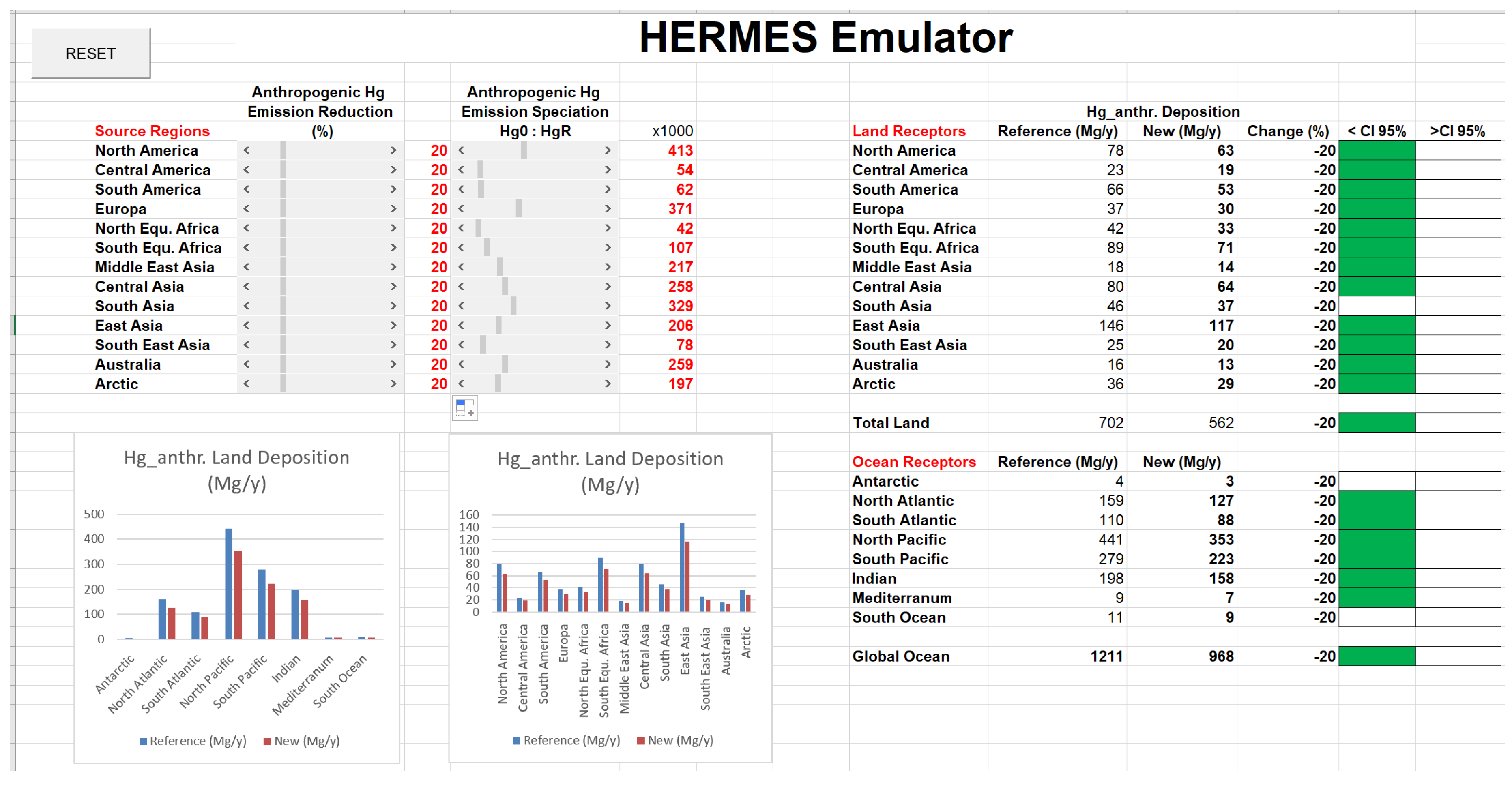
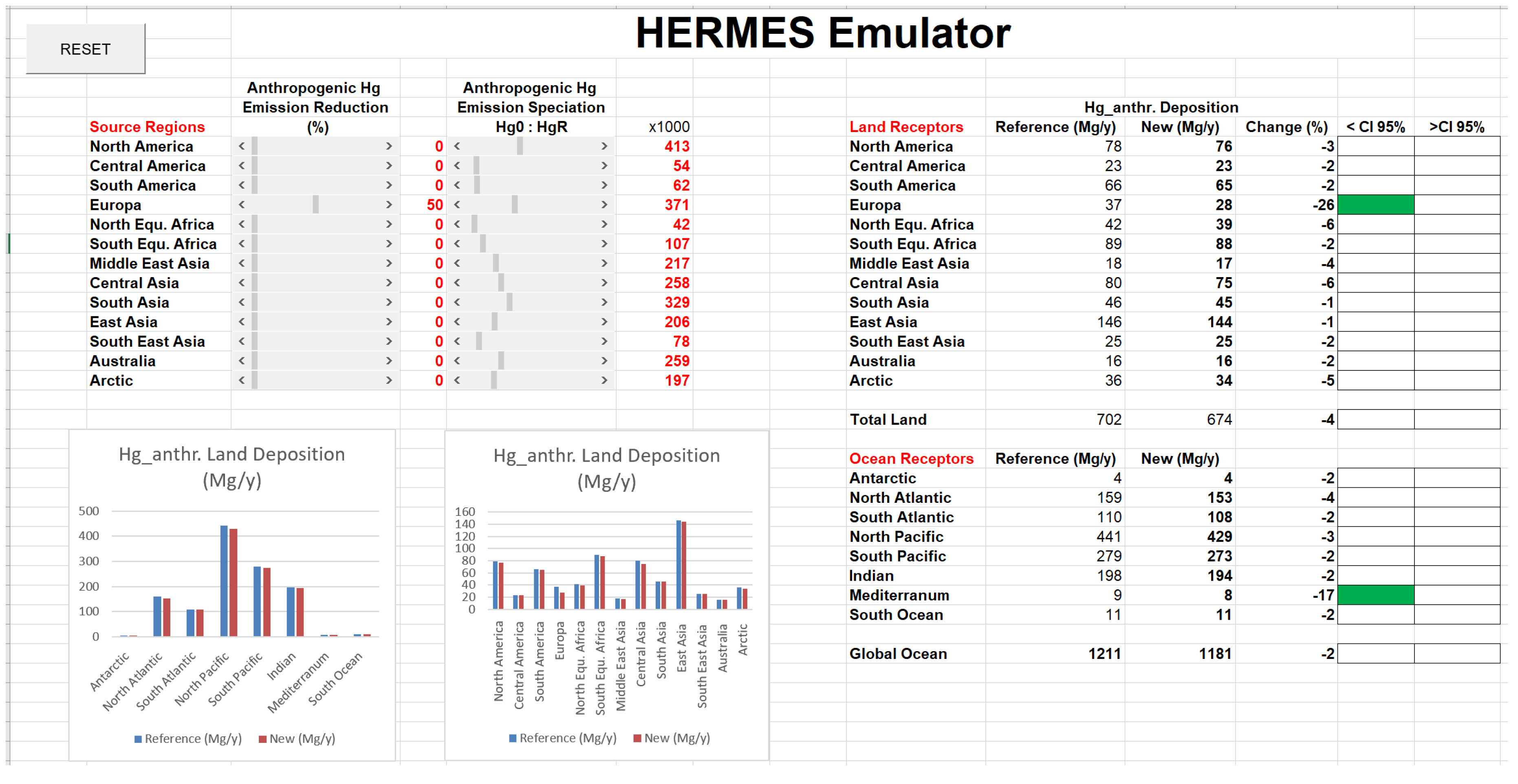
3.2. Hg Emission Reduction
3.2.1. Emissions—20% in all Source Regions
3.2.2. Emissions—50% in Key Regions: Europe, East Asia, and North America
3.3. Hg Speciation Perturbation
4. Discussion and Further Development
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Hganthr | Hg emitted from anthropogenic activities |
| Hg | Hg circulating within the Earth System; Hg includes Hganthr |
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
References
- Fitzgerald, W.F.; Engstrom, D.R.; Mason, R.P.; Nater, E.A. The case for atmospheric mercury contamination in remote areas. Environ. Sci. Technol. 1998, 32, 1–7. [Google Scholar] [CrossRef]
- Selin, H.; Keane, S.E.; Wang, S.; Selin, N.E.; Davis, K.; Bally, D. Linking science and policy to support the implementation of the Minamata Convention on Mercury. Ambio 2018, 47, 198–215. [Google Scholar] [CrossRef] [PubMed]
- Selin, N.E. A proposed global metric to aid mercury pollution policy. Science 2018, 360, 607–609. [Google Scholar] [CrossRef] [PubMed]
- De Simone, F.; Hedgecock, I.M.; Carbone, F.; Cinnirella, S.; Sprovieri, F.; Pirrone, N. Estimating Uncertainty in Global Mercury Emission Source and Deposition Receptor Relationships. Atmosphere 2017, 8, 236. [Google Scholar] [CrossRef]
- Kwon, S.Y.; Selin, N.E. Uncertainties in atmospheric mercury modeling for policy evaluation. Curr. Pollut. Rep. 2016, 2, 103–114. [Google Scholar] [CrossRef]
- Gustin, M.S.; Evers, D.C.; Bank, M.S.; Hammerschmidt, C.R.; Pierce, A.; Basu, N.; Blum, J.; Bustamante, P.; Chen, C.; Driscoll, C.T.; et al. Importance of Integration and Implementation of Emerging and Future Mercury Research into the Minamata Convention. Environ. Sci. Technol. 2016, 50, 2767–2770. [Google Scholar] [CrossRef]
- Daniel, J.S.; Solomon, S.; Albritton, D.L. On the evaluation of halocarbon radiative forcing and global warming potentials. J. Geophys. Res. Atmos. 1995, 100, 1271–1285. [Google Scholar] [CrossRef]
- Giang, A.; Stokes, L.C.; Streets, D.G.; Corbitt, E.S.; Selin, N.E. Impacts of the minamata convention on mercury emissions and global deposition from coal-fired power generation in Asia. Environ. Sci. Technol. 2015, 49, 5326–5335. [Google Scholar] [CrossRef]
- De Simone, F.; Cinnirella, S.; Gencarelli, C.N.; Yang, X.; Hedgecock, I.M.; Pirrone, N. Model study of global mercury deposition from biomass burning. Environ. Sci. Technol. 2015, 49, 6712–6721. [Google Scholar] [CrossRef]
- De Simone, F.; Gencarelli, C.N.; Hedgecock, I.M.; Pirrone, N. A modeling comparison of mercury deposition from current anthropogenic mercury emission inventories. Environ. Sci. Technol. 2016, 50, 5154–5162. [Google Scholar] [CrossRef]
- De Simone, F.; Artaxo, P.; Bencardino, M.; Cinnirella, S.; Carbone, F.; D’Amore, F.; Dommergue, A.; Feng, X.B.; Gencarelli, C.N.; Hedgecock, I.M.; et al. Particulate-phase mercury emissions from biomass burning and impact on resulting deposition: A modelling assessment. Atmos. Chem. Phys. 2017, 17, 1881–1899. [Google Scholar] [CrossRef] [PubMed]
- Lindberg, S.; Bullock, R.; Ebinghaus, R.; Engstrom, D.; Feng, X.; Fitzgerald, W.; Pirrone, N.; Prestbo, E.; Seigneur, C. A synthesis of progress and uncertainties in attributing the sources of mercury in deposition. Ambio 2007, 36, 19–32. [Google Scholar] [CrossRef]
- Jung, G.; Hedgecock, I.M.; Pirrone, N. ECHMERIT v1.0—A new global fully coupled mercury-chemistry and transport model. Geosci. Model Dev. 2009, 2, 175–195. [Google Scholar] [CrossRef]
- De Simone, F.; Gencarelli, C.; Hedgecock, I.; Pirrone, N. Global atmospheric cycle of mercury: A model study on the impact of oxidation mechanisms. Environ. Sci. Pollut. Res. 2014, 21, 4110–4123. [Google Scholar] [CrossRef] [PubMed]
- Holden, P.B.; Edwards, N.R.; Garthwaite, P.H.; Fraedrich, K.; Lunkeit, F.; Kirk, E.; Labriet, M.; Kanudia, A.; Babonneau, F. PLASIM-ENTSem v1.0: A spatio-temporal emulator of future climate change for impacts assessment. Geosci. Model Dev. 2014, 7, 433–451. [Google Scholar] [CrossRef]
- Castruccio, S.; McInerney, D.J.; Stein, M.L.; Liu Crouch, F.; Jacob, R.L.; Moyer, E.J. Statistical emulation of climate model projections based on precomputed GCM runs. J. Clim. 2014, 27, 1829–1844. [Google Scholar] [CrossRef]
- Xing, J.; Ding, D.; Wang, S.; Zhao, B.; Jang, C.; Wu, W.; Zhang, F.; Zhu, Y.; Hao, J. Quantification of the enhanced effectiveness of NO x control from simultaneous reductions of VOC and NH 3 for reducing air pollution in the Beijing–Tianjin–Hebei region, China. Atmos. Chem. Phys. 2018, 18, 7799–7814. [Google Scholar] [CrossRef]
- Xing, J.; Zheng, S.; Ding, D.; Kelly, J.T.; Wang, S.; Li, S.; Qin, T.; Ma, M.; Dong, Z.; Jang, C.J.; et al. Deep learning for prediction of the air quality response to emission changes. Environ. Sci. Technol. 2020, 54, 8589–8600. [Google Scholar] [CrossRef]
- Beddows, A.V.; Kitwiroon, N.; Williams, M.L.; Beevers, S.D. Emulation and sensitivity analysis of the community multiscale air quality model for a UK Ozone pollution episode. Environ. Sci. Technol. 2017, 51, 6229–6236. [Google Scholar] [CrossRef]
- Gustin, M.S.; Bank, M.S.; Bishop, K.; Bowman, K.; Branfireun, B.; Chételat, J.; Eckley, C.S.; Hammerschmidt, C.R.; Lamborg, C.; Lyman, S.; et al. Mercury biogeochemical cycling: A synthesis of recent scientific advances. Sci. Total. Environ. 2020, 737, 139619. [Google Scholar] [CrossRef]
- AMAP/UNEP. Technical Background Report for the Global Mercury Assessment 2013; Technical Report; Arctic Monitoring and Assessment Programme: Oslo, Norway; UNEP ChemicalsBranch: Geneva, Switzerland, 2013. [Google Scholar]
- Muntean, M.; Janssens-Maenhout, G.; Song, S.; Selin, N.E.; Olivier, J.G.; Guizzardi, D.; Maas, R.; Dentener, F. Trend analysis from 1970 to 2008 and model evaluation of {EDGARv4} global gridded anthropogenic mercury emissions. Sci. Total. Environ. 2014, 494–495, 337–350. [Google Scholar] [CrossRef]
- Streets, D.G.; Zhang, Q.; Wu, Y. Projections of Global Mercury Emissions in 2050. Environ. Sci. Technol. 2009, 43, 2983–2988. [Google Scholar] [CrossRef] [PubMed]
- Corbitt, E.S.; Jacob, D.J.; Holmes, C.D.; Streets, D.G.; Sunderland, E.M. Global source–receptor relationships for mercury deposition under present-day and 2050 emissions scenarios. Environ. Sci. Technol. 2011, 45, 10477–10484. [Google Scholar] [CrossRef] [PubMed]
- Climate Data Operators. Max-Plank Institute fur Meteorologie, 2014. Available online: https://code.zmaw.de/projects/cdo (accessed on 23 February 2015).
- Simpson, D.; Benedictow, A.; Berge, H.; Bergström, R.; Emberson, L.D.; Fagerli, H.; Flechard, C.R.; Hayman, G.D.; Gauss, M.; Jonson, J.E.; et al. The EMEP MSC-W Chemical Transport Model-Technical Description; Copernicus: Göttingen, Germany, 2012. [Google Scholar]
- Emmons, L.K.; Walters, S.; Hess, P.G.; Lamarque, J.F.; Pfister, G.G.; Fillmore, D.; Granier, C.; Guenther, A.; Kinnison, D.; Laepple, T.; et al. Description and evaluation of the Model for Ozone and Related chemical Tracers, version 4 (MOZART-4). Geosci. Model Dev. 2010, 3, 43–67. [Google Scholar] [CrossRef]
- Hurrell, J.; National Center for Atmospheric Research Staff (Eds.) The Climate Data Guide: Hurrell North Atlantic Oscillation (NAO) Index (Station-Based). 2020. Available online: https://climatedataguide.ucar.edu/climate-data/hurrell-north-atlantic-oscillation-nao-index-station-based (accessed on 24 April 2020).
- National Center for Atmospheric Research Staff (Ed.) The Climate Data Guide: Multivariate ENSO Index. 2019. Available online: https://climatedataguide.ucar.edu/climate-data/multivariate-enso-index (accessed on 15 July 2019).
- Hynes, A.J.; Donohoue, D.L.; Goodsite, M.E.; Hedgecock, I.M. Our current understanding of major chemical and physical processes affecting mercury dynamics in the atmosphere and at the air-water/terrestrial interfaces. In Mercury Fate and Transport in the Global Atmosphere: Emissions, Measurements and Models; Pirrone, N., Mason, R.P., Eds.; Springer: New York, NY, USA, 2009; Chapter 14; pp. 427–457. [Google Scholar]
- Subir, M.; Ariya, P.A.; Dastoor, A.P. A review of uncertainties in atmospheric modeling of mercury chemistry I. Uncertainties in existing kinetic parameters—Fundamental limitations and the importance of heterogeneous chemistry. Atmos. Environ. 2011, 45, 5664–5676. [Google Scholar] [CrossRef]
- Subir, M.; Ariya, P.A.; Dastoor, A.P. A review of the sources of uncertainties in atmospheric mercury modeling II. Mercury surface and heterogeneous chemistry—A missing link. Atmos. Environ. 2012, 46, 1–10. [Google Scholar] [CrossRef]
- Yang, X.; Cox, R.A.; Warwick, N.J.; Pyle, J.A.; Carver, G.D.; O’Connor, F.M.; Savage, N.H. Tropospheric bromine chemistry and its impacts on ozone: A model study. J. Geophys. Res. Atmos. 2005, 110, 1984–2012. [Google Scholar] [CrossRef]
- Yang, X.; Pyle, J.A.; Cox, R.A.; Theys, N.; Van Roozendael, M. Snow-sourced bromine and its implications for polar tropospheric ozone. Atmos. Chem. Phys. 2010, 10, 7763–7773. [Google Scholar] [CrossRef]
- Mudelsee, M. Climate Time Series Analysis: Classical Statistical and Bootstrap Methods; Springer International Publishing: Geneva, Switzerland, 2014. [Google Scholar]
- Selin, N.E. Global change and mercury cycling: Challenges for implementing a global mercury treaty. Environ. Toxicol. Chem. 2014, 33, 1202–1210. [Google Scholar] [CrossRef]
Sample Availability: The HERMES CTM emulator is provided as a spreadsheet within the Supplementary Information. |
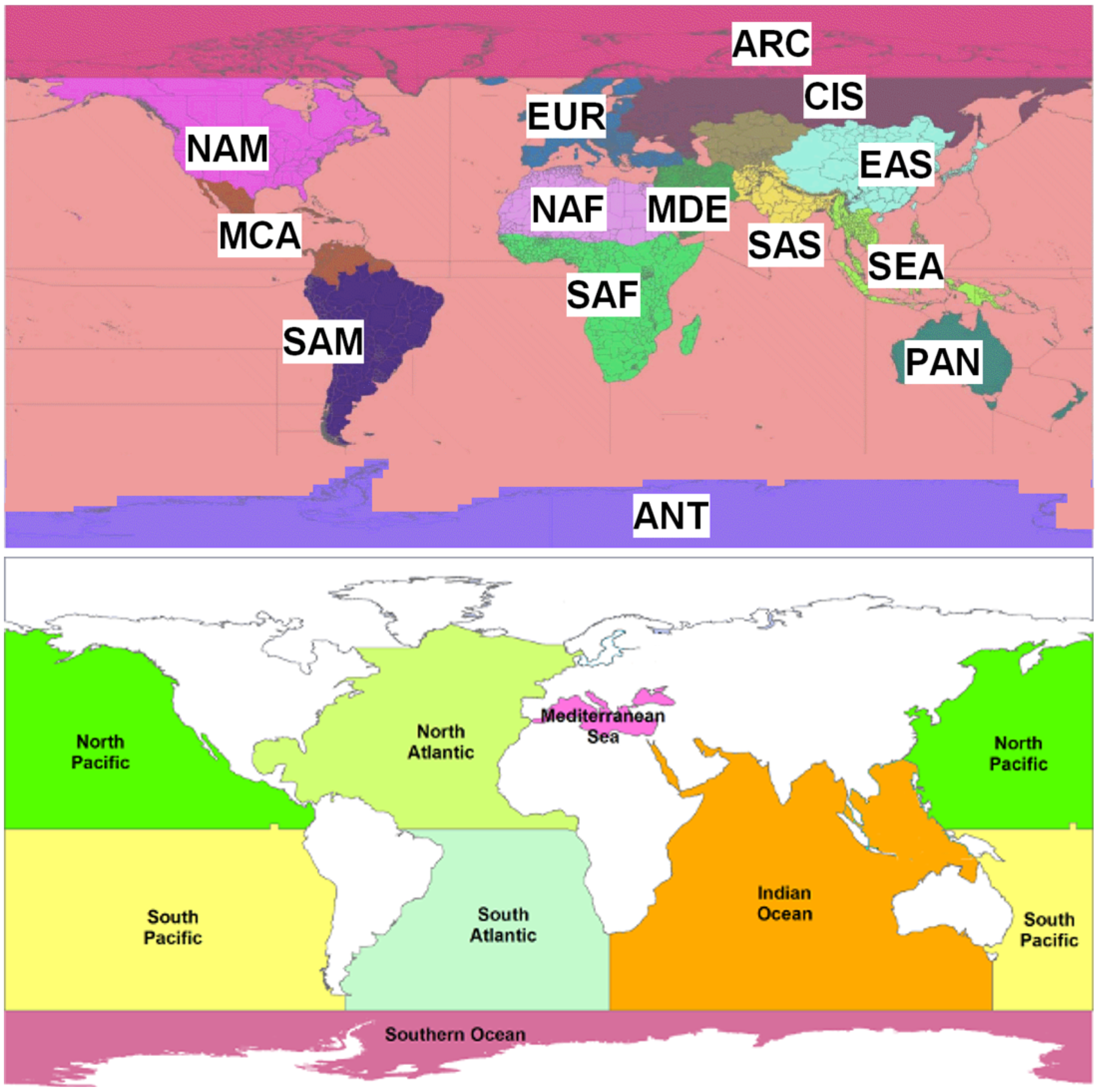
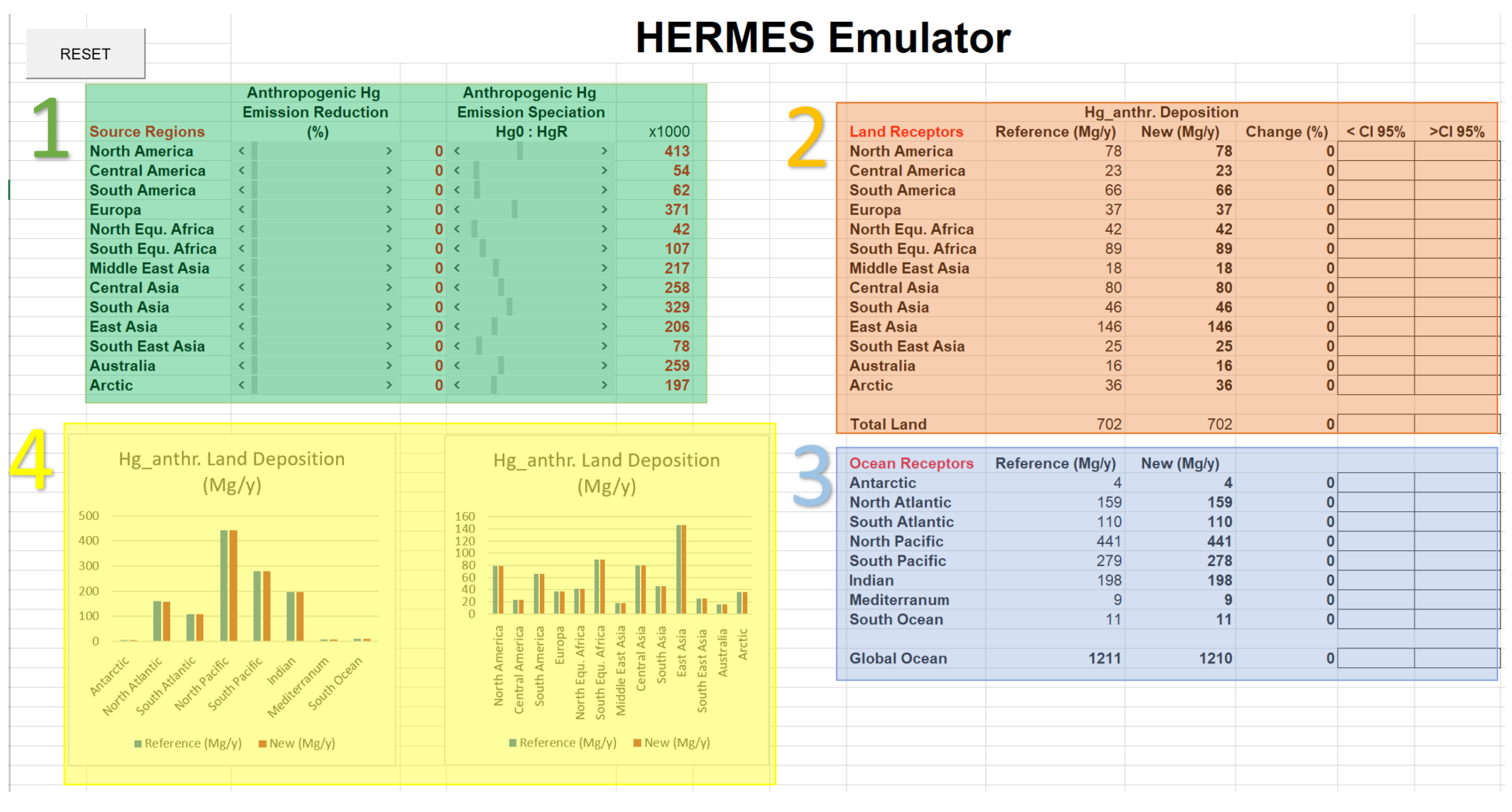
| Run | Inventory | Ref. Year | Meteor. Year | Speciation | Vertical Profile | Oxidation |
|---|---|---|---|---|---|---|
| BASE | AMAP-2010 | 2010 | 2010 | Native | Native | O3+OH |
| BASE-2005 | AMAP-2010 | 2010 | 2005 | Native | Native | O3+OH |
| BASE-1998 | AMAP-2010 | 2010 | 1998 | Native | Native | O3+OH |
| APBL | AMAP-2010 | 2010 | 2010 | Native | Uniform PBL | O3+OH |
| NSP0 | AMAP-2010 | 2010 | 2010 | as | Native | O3+OH |
| NSP50 | AMAP-2010 | 2010 | 2010 | :HgII(g) = 50:50 | Native | O3+OH |
| BRTO | AMAP-2010 | 2010 | 2010 | Native | Native | Bromine |
| STREETS | STREETS | 2010 | 2010 | Native | Uniform PBL | O3+OH |
| EDGAR | EDGAR | 2010 | 2010 | Native | Native-SNAP | O3+OH |
| Run | Emissions | HgR:Hg0 | Reduction |
|---|---|---|---|
| BASE | AMAP | Original | None |
| BaseR20 | AMAP | Original | 20% |
| BaseR40 | AMAP | Original | 40% |
| BaseR60 | AMAP | Original | 60% |
| BaseR80 | AMAP | Original | 80% |
| BaseS00 | AMAP | 0:100 | None |
| BaseS20 | AMAP | 20:80 | None |
| BaseS40 | AMAP | 40:60 | None |
| BaseS60 | AMAP | 60:40 | None |
| BaseS80 | AMAP | 80:60 | None |
| BaseS100 | AMAP | 100:0 | None |
| Region | Lower Bound | Reference | Upper Bound |
|---|---|---|---|
| North America | 66.87 | 78.41 | 87.96 |
| Australia | 12.86 | 16.08 | 18.97 |
| South East Asia | 117.68 | 146.08 | 182.35 |
| Europe | 30.60 | 37.11 | 43.21 |
| Indonesia | 21.21 | 25.15 | 28.39 |
| Arctic | 32.46 | 35.95 | 38.85 |
| Central America | 20.12 | 23.44 | 26.31 |
| Middle East Asia | 15.42 | 17.65 | 19.35 |
| North Equatorial Africa | 33.61 | 41.56 | 59.13 |
| Central Asia | 69.35 | 79.56 | 89.37 |
| South Equatorial Africa | 74.47 | 89.35 | 101.95 |
| South America | 55.27 | 65.89 | 74.82 |
| South Asia | 34.50 | 45.87 | 57.75 |
| Antarctic | 2.60 | 4.34 | 7.26 |
| Ocean Basins | Lower Bound | Reference | Upper Bound |
| North Atlantic | 143.15 | 159.07 | 168.66 |
| South Atlantic | 90.73 | 109.85 | 125.38 |
| North Pacific | 392.65 | 440.93 | 471.62 |
| South Pacific | 230.59 | 278.56 | 316.00 |
| Indian | 163.22 | 197.70 | 223.76 |
| Mediterranean | 7.87 | 9.05 | 10.33 |
| South Ocean | 8.35 | 11.17 | 15.25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Simone, F.; D’Amore, F.; Marasco, F.; Carbone, F.; Bencardino, M.; Hedgecock, I.M.; Cinnirella, S.; Sprovieri, F.; Pirrone, N. A Chemical Transport Model Emulator for the Interactive Evaluation of Mercury Emission Reduction Scenarios. Atmosphere 2020, 11, 878. https://doi.org/10.3390/atmos11080878
De Simone F, D’Amore F, Marasco F, Carbone F, Bencardino M, Hedgecock IM, Cinnirella S, Sprovieri F, Pirrone N. A Chemical Transport Model Emulator for the Interactive Evaluation of Mercury Emission Reduction Scenarios. Atmosphere. 2020; 11(8):878. https://doi.org/10.3390/atmos11080878
Chicago/Turabian StyleDe Simone, Francesco, Francesco D’Amore, Francesco Marasco, Francesco Carbone, Mariantonia Bencardino, Ian M. Hedgecock, Sergio Cinnirella, Francesca Sprovieri, and Nicola Pirrone. 2020. "A Chemical Transport Model Emulator for the Interactive Evaluation of Mercury Emission Reduction Scenarios" Atmosphere 11, no. 8: 878. https://doi.org/10.3390/atmos11080878
APA StyleDe Simone, F., D’Amore, F., Marasco, F., Carbone, F., Bencardino, M., Hedgecock, I. M., Cinnirella, S., Sprovieri, F., & Pirrone, N. (2020). A Chemical Transport Model Emulator for the Interactive Evaluation of Mercury Emission Reduction Scenarios. Atmosphere, 11(8), 878. https://doi.org/10.3390/atmos11080878








