Why Does Fog Deepen? An Analytical Perspective
Abstract
1. Introduction
2. An Analytical Description for the Interface of a Saturated Layer
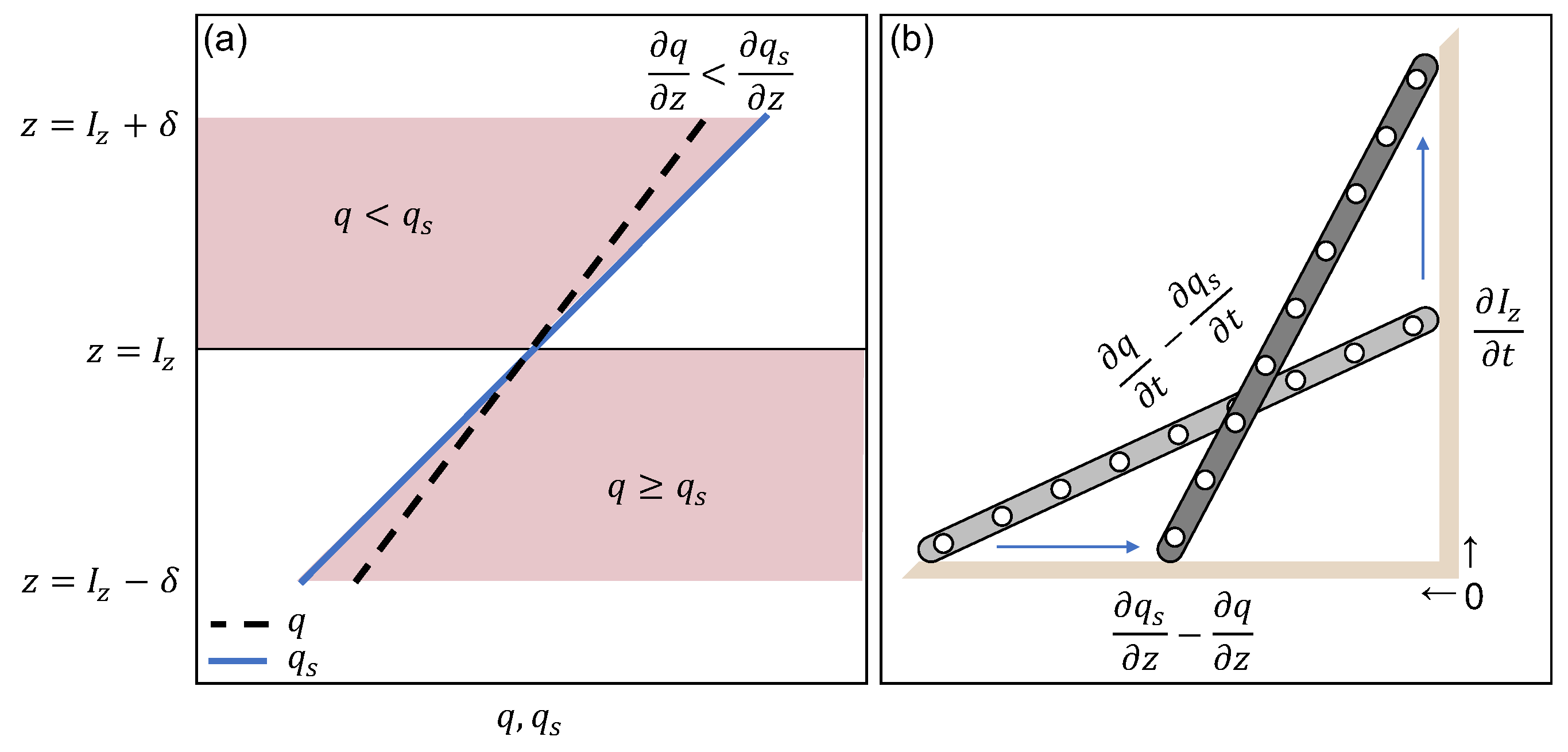
2.1. Derivation of Interfacial Evolution
2.1.1. Equation (7) in the Case of Constant Moisture
2.1.2. Equation (7) in a Stable Boundary Layer
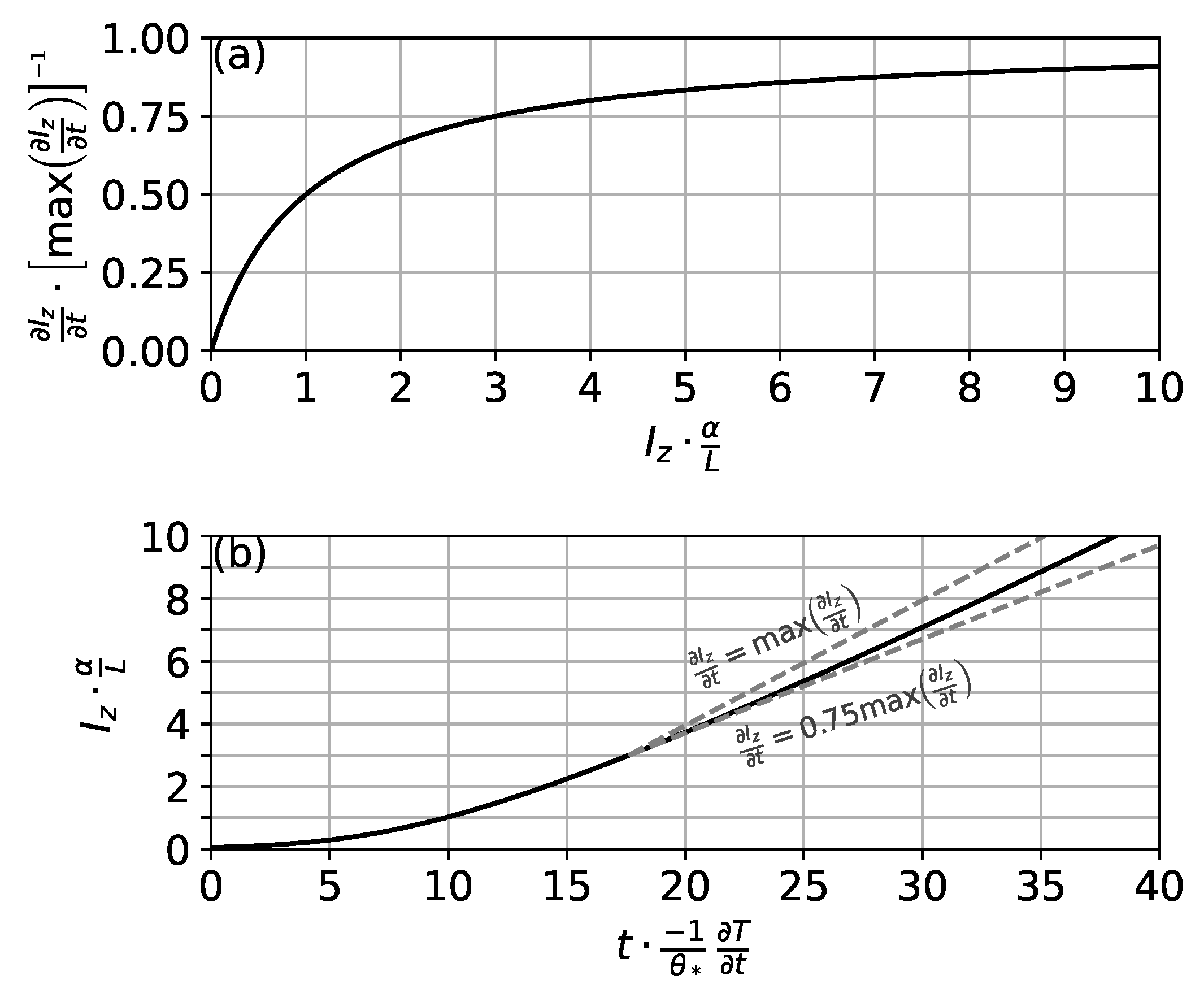
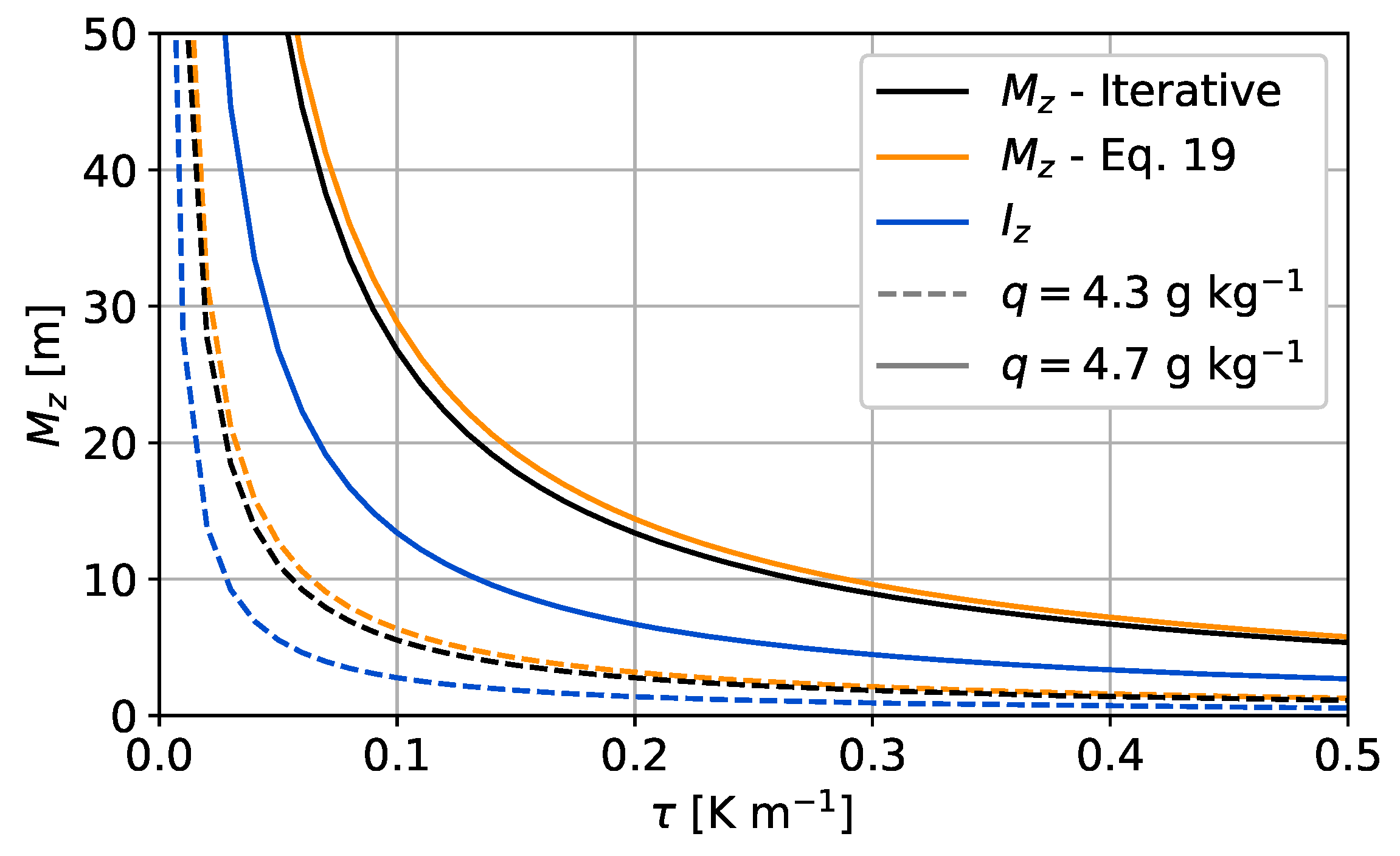
2.2. The Maximum Attainable Mixed Depth
2.2.1. in an Idealized Atmosphere with Linear Temperature Profile
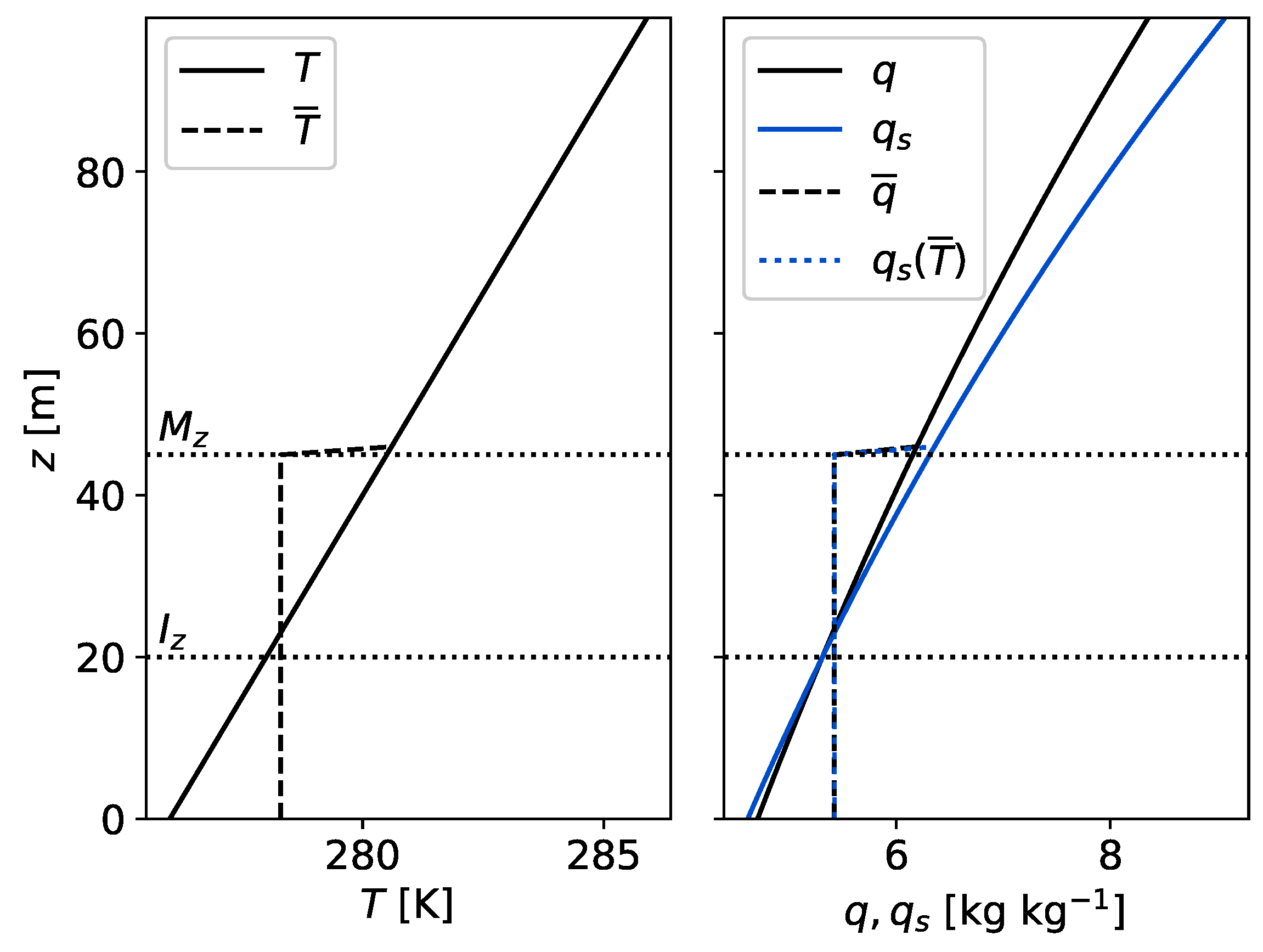
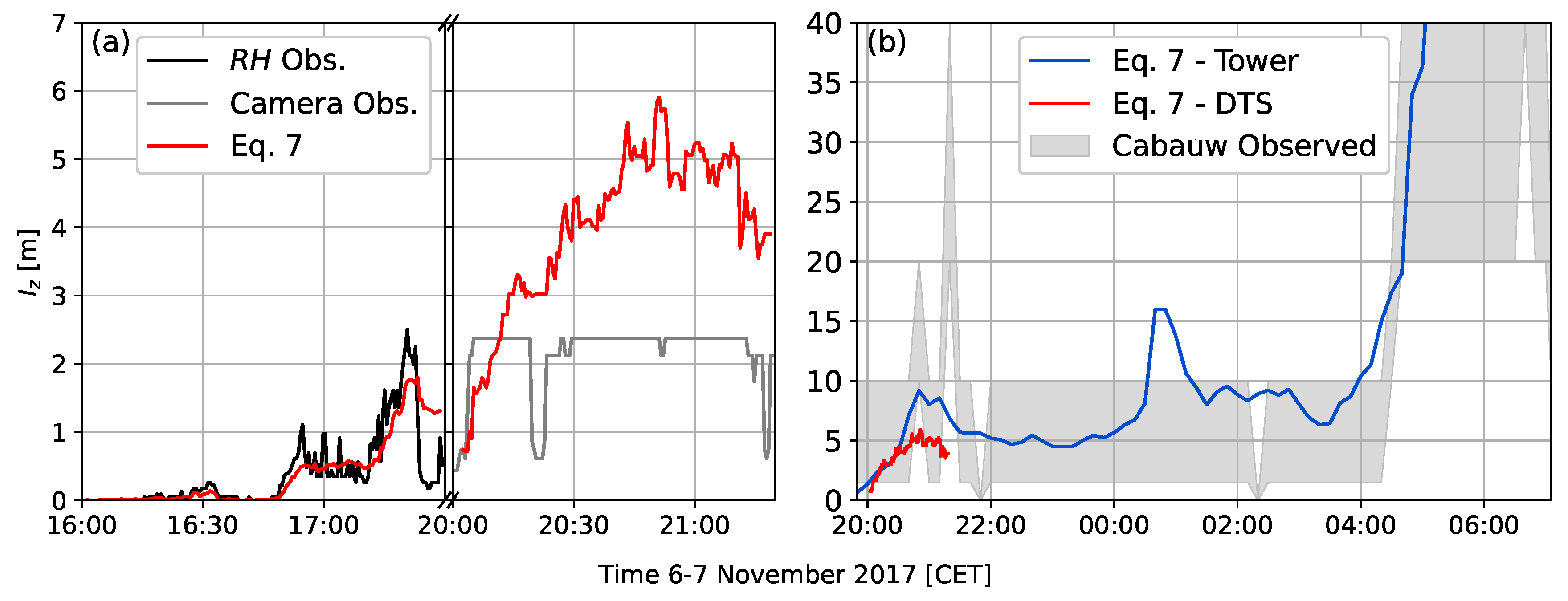
3. Comparison with Observational Data
3.1. Description of the Observational Data and Methods
3.2. Comparison with High-Resolution Observations
3.3. Comparison with Tower Observations
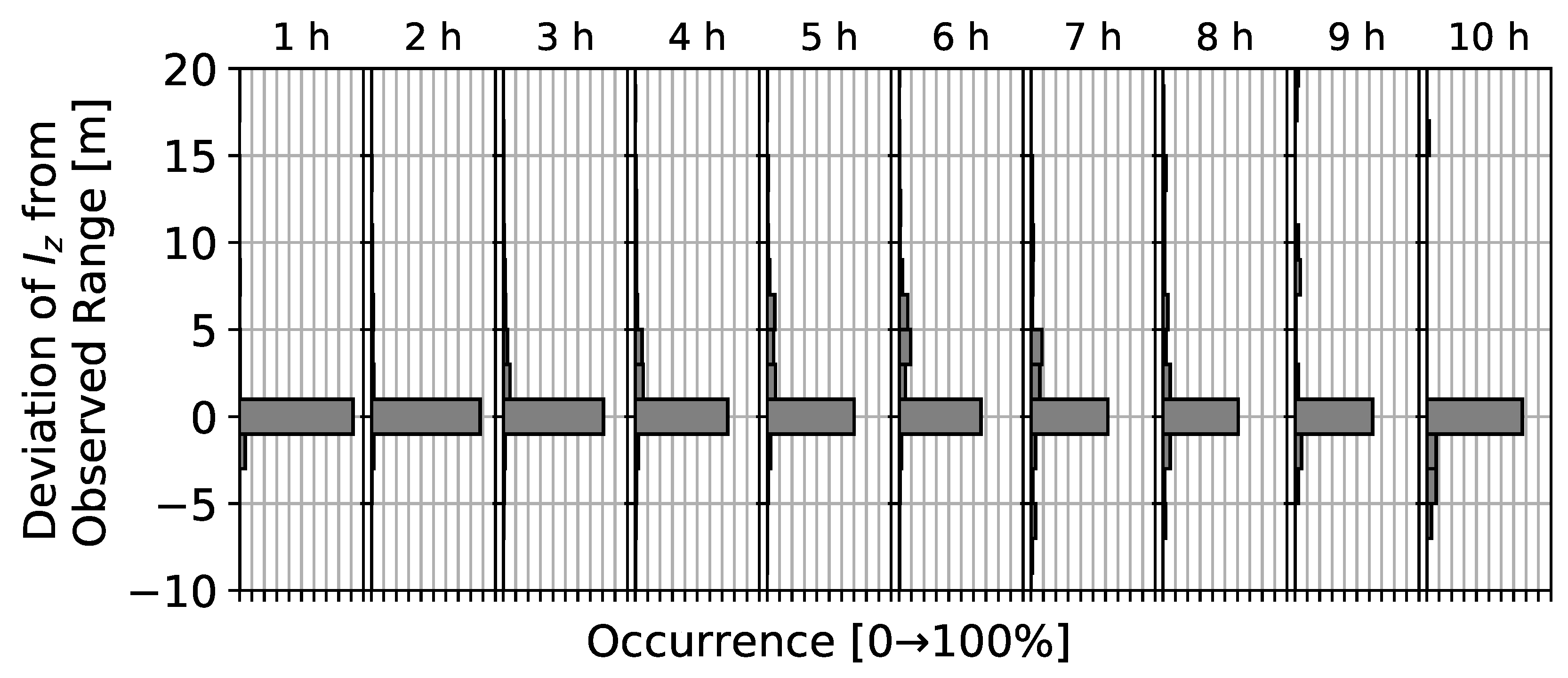
3.4. Errors and Uncertainty
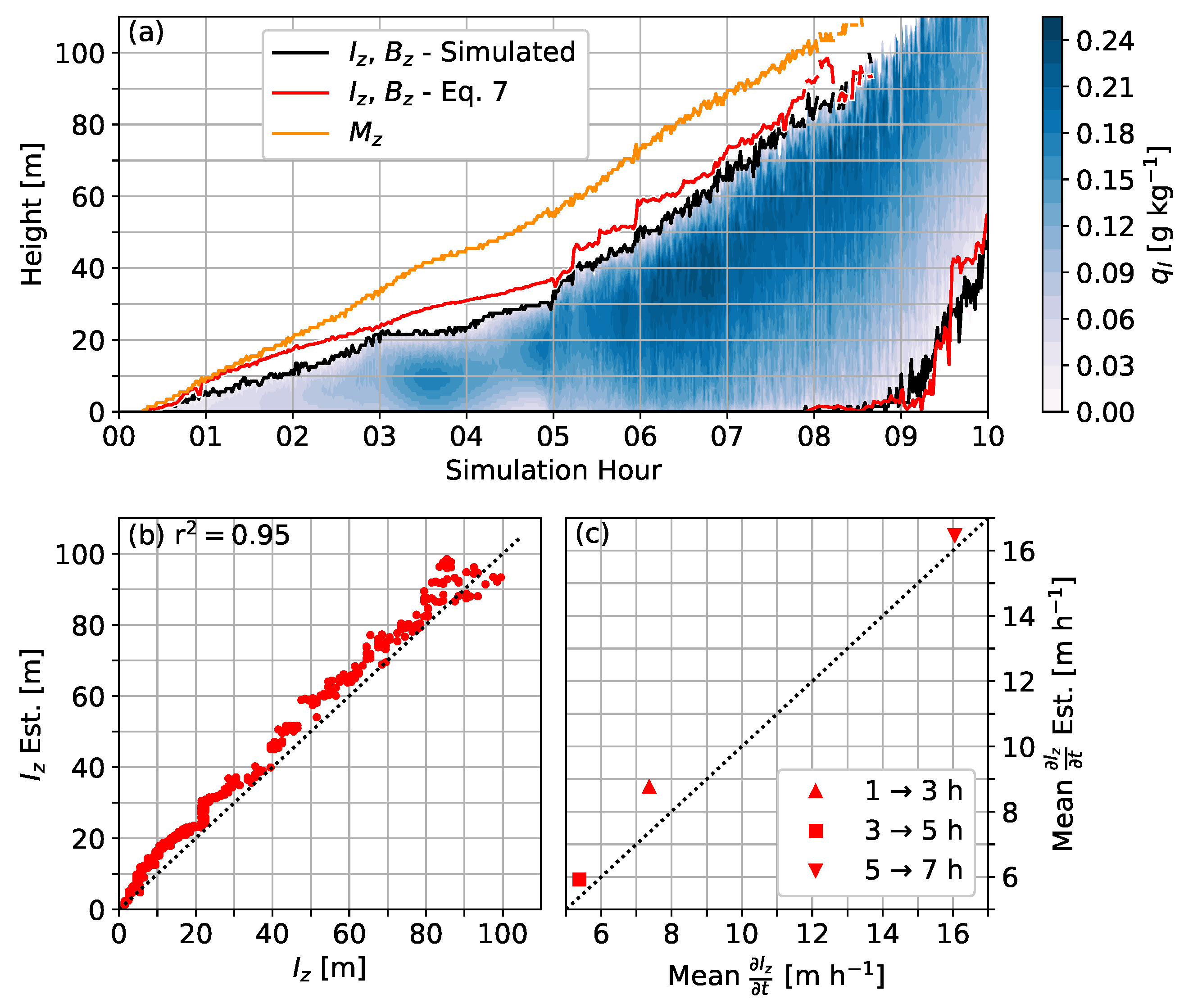
4. Comparison with Large-Eddy Simulation Output
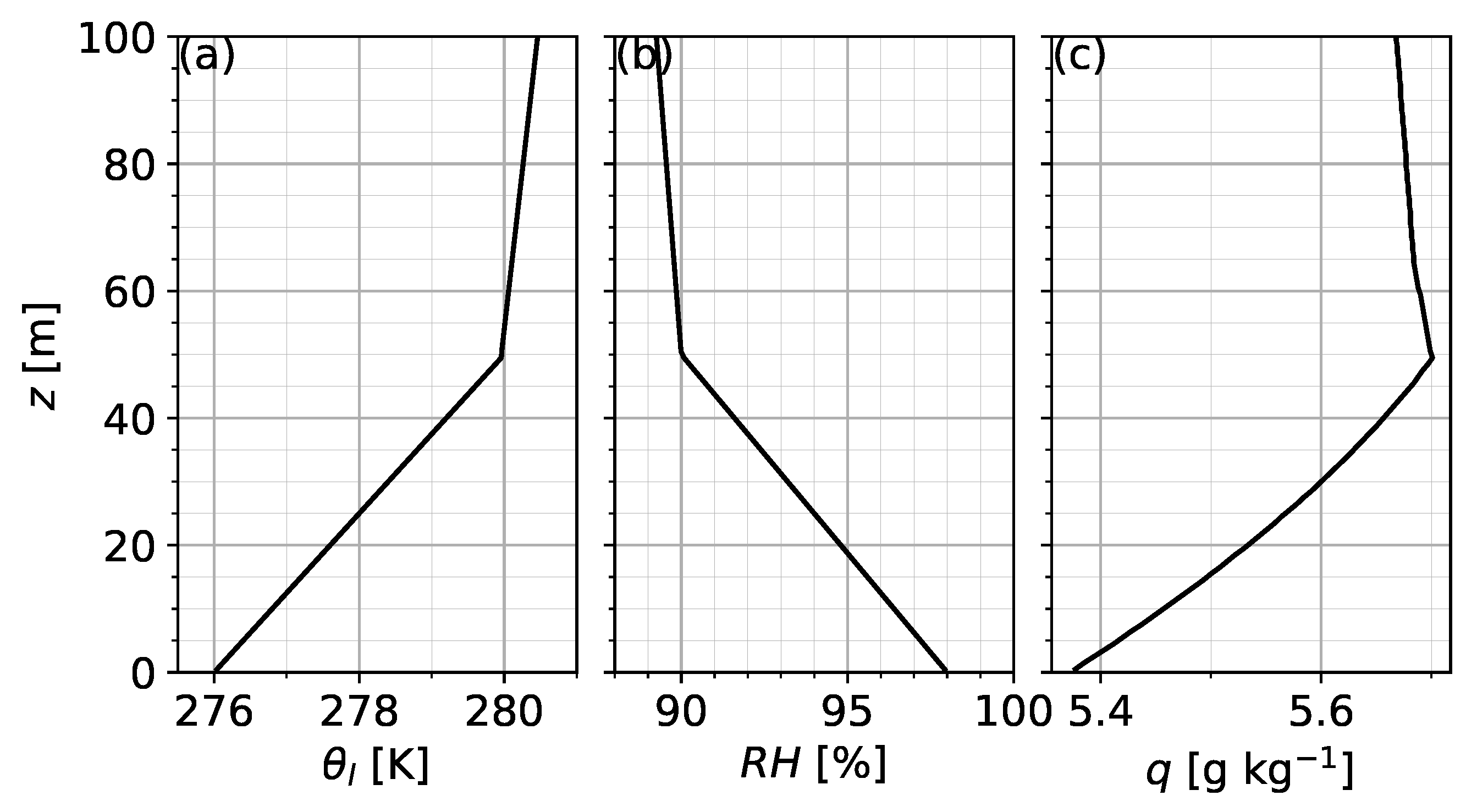
4.1. Case Setup
4.2. Simulation Results
5. Summary and Discussion
5.1. Equation (7) to Interpret the Evolution of Typical Fog Layer
5.2. Equation (7) as a Diagnostic Tool
5.3. Specific Processes at the Interface
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Estimating Errors and Uncertainties
Appendix A.1. Propagation of Uncertainties
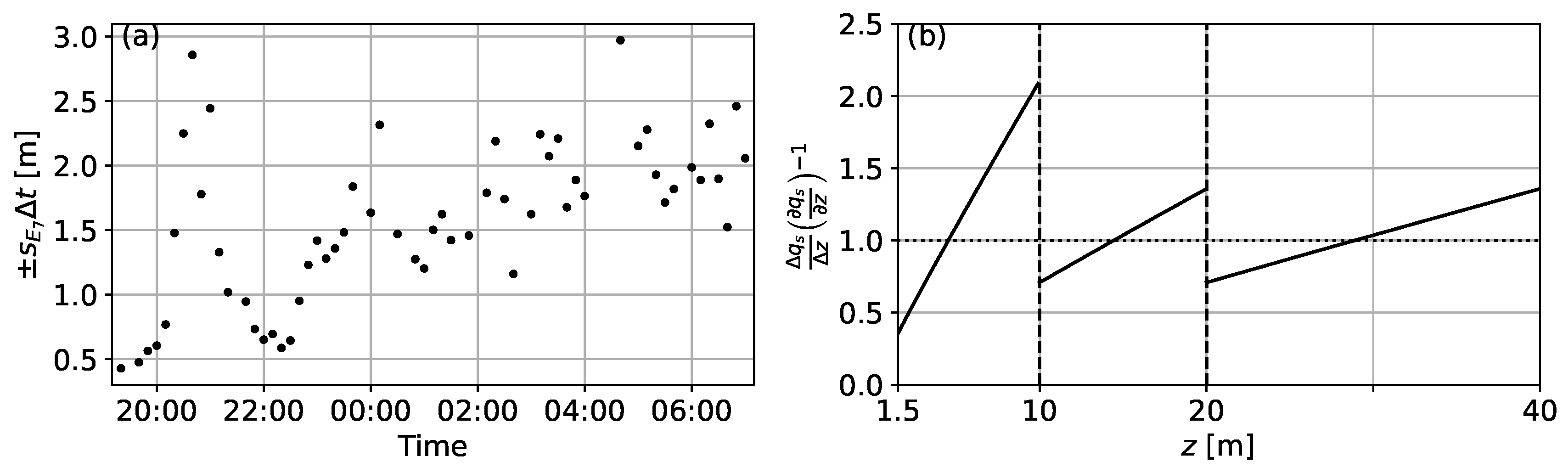
Appendix A.2. Error Due to Discrete Vertical Gradients
Appendix B. Additional Information Regarding the Large-Eddy Simulations
| Symbol | Parameter | Value |
|---|---|---|
| Surface conductivity | 4 W K m | |
| Droplet number concentration | 150 cm | |
| Slope of temperature in the BL | 0.08 K m | |
| Slope of temperature in the RL | 0.01 K m | |
| RH | Surface relative humidity | 98% |
| RH | Relative humidity at BL top | 90% |
| RH | Relative humidity at top of domain | 85% |
| Surface temperature | 276 K | |
| Soil temperature | 279 K | |
| Geostrophic wind speed | 4 m s | |
| Maximum height of domain | 384 m | |
| Depth of the initial boundary layer | 50 m | |
| Roughness length for momentum | 0.15 m | |
| Roughness length for heat | 0.235 × 10 m |
| Simulation | Changed Parameters | |
|---|---|---|
| AEI | Aerosols increased | cm |
| EMI | Enhanced mixing | m, m |
| RWI | Reduced geostrophic wind speed | m s |
| IWI | Increased geostrophic wind speed | m s |
| IRS | Increased residual slope | K m |
| IBL | BL-depth increased | K m, m |
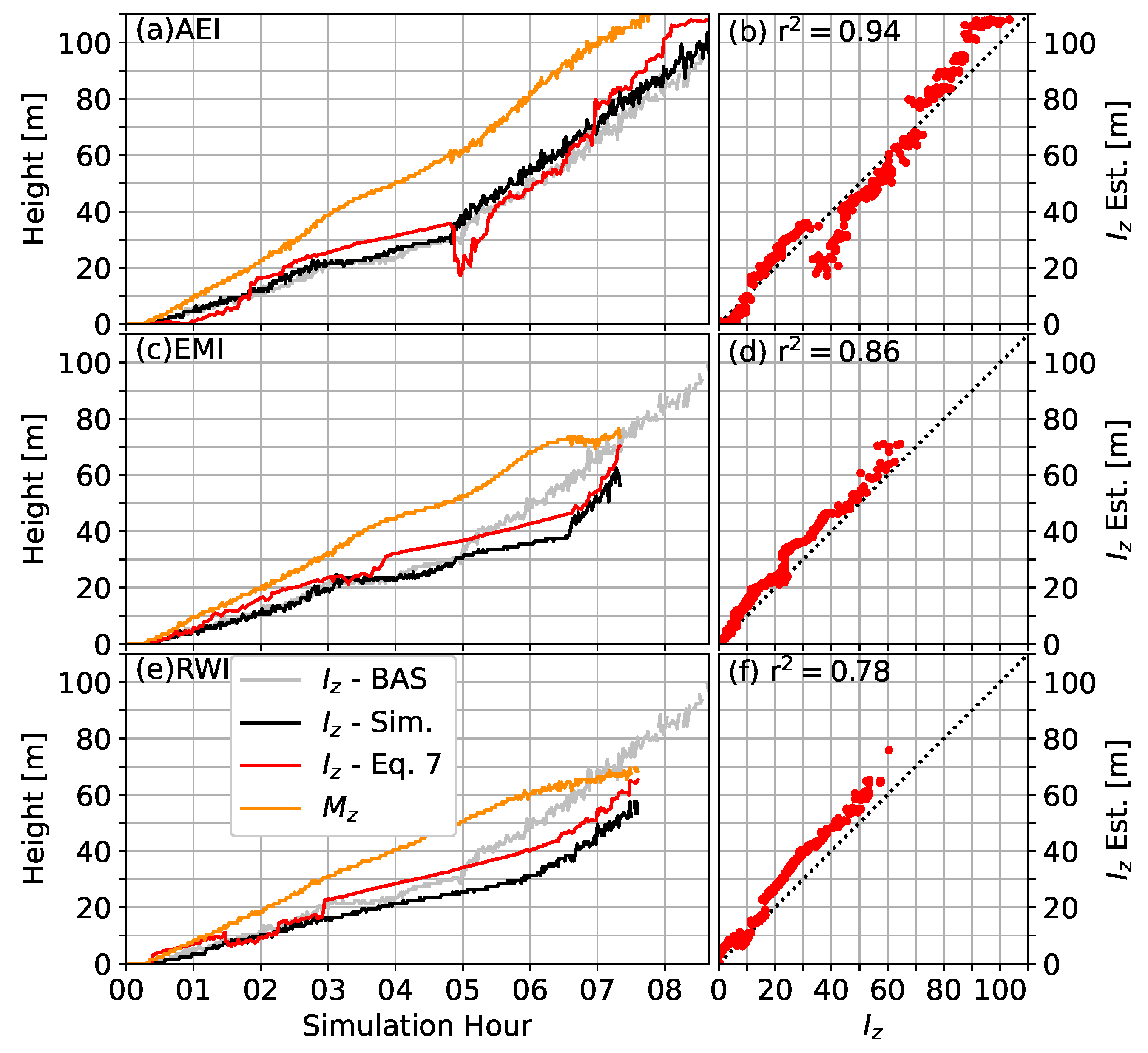
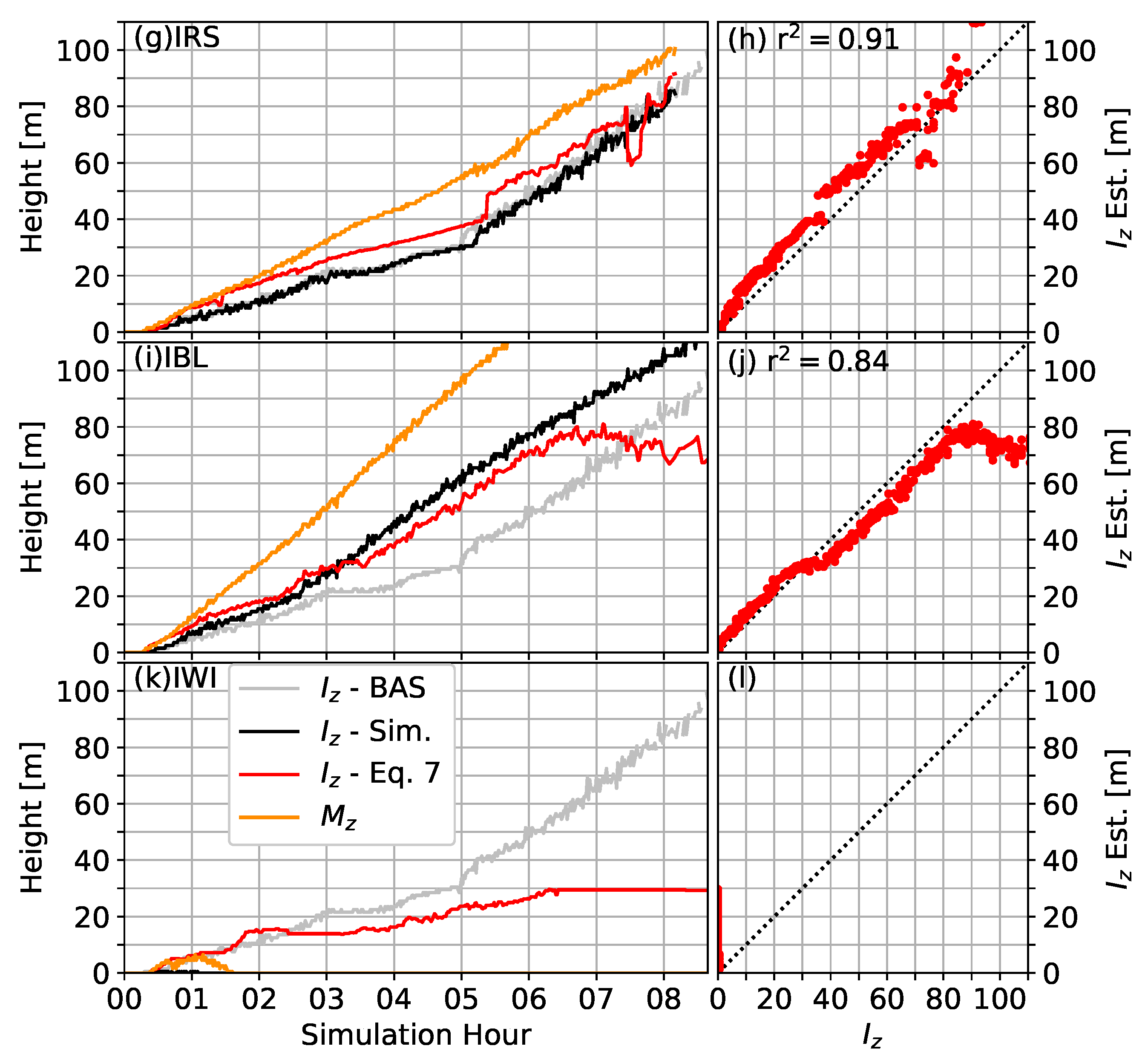
References
- Smith, D.K.E.; Renfrew, I.A.; Price, J.D.; Dorling, S.R. Numerical Modelling of the Evolution of the Boundary Layer during a Radiation Fog Event. Weather 2018, 73, 310–316. [Google Scholar] [CrossRef]
- Izett, J.G.; Schilperoort, B.; Coenders-Gerrits, M.; Baas, P.; Bosveld, F.C.; van de Wiel, B.J.H. Missed Fog? On the Potential of Obtaining Observations at Increased Resolution during Shallow Fog Events. Bound. Layer Meteorol. 2019. [Google Scholar] [CrossRef] [PubMed]
- Román-Cascón, C.; Yagüe, C.; Steeneveld, G.J.; Sastre, M.; Arrillaga, J.A.; Maqueda, G. Estimating Fog-Top Height through near-Surface Micrometeorological Measurements. Atmos. Res. 2016, 170, 76–86. [Google Scholar] [CrossRef][Green Version]
- Ju, T.; Wu, B.; Zhang, H.; Liu, J. Parameterization of Radiation Fog-Top Height and Methods Evaluation in Tianjin. Atmosphere 2020, 11, 480. [Google Scholar] [CrossRef]
- Maronga, B.; Bosveld, F.C. Key Parameters for the Life Cycle of Nocturnal Radiation Fog: A Comprehensive Large-Eddy Simulation Study. Q. J. R. Meteorol. Soc. 2017, 143, 2463–2480. [Google Scholar] [CrossRef]
- Price, J.D. On the Formation and Development of Radiation Fog: An Observational Study. Bound.-Layer Meteorol. 2019, 172, 167–197. [Google Scholar] [CrossRef]
- Moene, A.F.; van Dam, J.C. Transport in the Atmosphere-Vegetation-Soil Continuum; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Dyer, A.J. A Review of Flux-Profile Relationships. Bound.-Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Monna, W.; Bosveld, F. In Higher Spheres: 40 Years of Observations at the Cabauw Site; Koninklijk Nederlands Meteorologisch Instituut: De Bilt, The Netherlands, 2013; Volume 232. [Google Scholar]
- Selker, J.S.; Thévanez, L.; Huwald, H.; Mallet, A.; Luxemburg, W.; de Giesen, N.V.; Stejskal, M.; Zeman, J.; Westhoff, M.; Parlange, M.B. Distributed Fiber-Optic Temperature Sensing for Hydrologic Systems. Water Resour. Res. 2006, 42, W12202. [Google Scholar] [CrossRef]
- Izett, J.G.; Schilperoort, B.; Coenders-Gerrits, M.; van de Wiel, B.J.H. High-Resolution DTS Temperature Measurements during Fog at Cabauw. Dataset 2018. [Google Scholar] [CrossRef]
- Heus, T.; van Heerwaarden, C.C.; Jonker, H.J.J.; Siebesma, A.P.; Axelsen, S.; van den Dries, K.; Geoffroy, O.; Moene, A.F.; Pino, D.; de Roode, S.R.; et al. Formulation of the Dutch Atmospheric Large-Eddy Simulation (DALES) and Overview of Its Applications. Geosci. Model Dev. 2010, 3, 415–444. [Google Scholar] [CrossRef]
- Wærsted, E.G.; Haeffelin, M.; Steeneveld, G.J.; Dupont, J.C. Understanding the Dissipation of Continental Fog by Analysing the LWP Budget Using Idealized LES and in Situ Observations. Q. J. R. Meteorol. Soc. 2019, 145, 784–804. [Google Scholar] [CrossRef]
- Boers, R.; Klein Baltink, H.; Hemmink, H.J.; Bosveld, F.C.; Moerman, M. Ground-Based Observations and Modeling of the Visibility and Radar Reflectivity in a Radiation Fog Layer. J. Atmos. Ocean. Technol. 2013, 30, 288–300. [Google Scholar] [CrossRef]
- Pilie, R.; Eadie, W.; Mack, E.; Rogers, C.; Kochmond, W. Project Fog Drops Part I: Investigations of Warm Fog Properties; Contractor Report CR-2078; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1972.
- Izett, J.G.; van de Wiel, B.J.H.; Baas, P.; Bosveld, F.C. Understanding and Reducing False Alarms in Observational Fog Prediction. Bound. Layer Meteorol. 2018, 169, 347–372. [Google Scholar] [CrossRef]
- Price, J.; Stokkereit, K. The Use of Thermal Infra-Red Imagery to Elucidate the Dynamics and Processes Occurring in Fog. Atmosphere 2020, 11, 240. [Google Scholar] [CrossRef]
- Taylor, G.I. The Formation of Fog and Mist. Q. J. R. Meteorol. Soc. 1917, 43, 241–268. [Google Scholar] [CrossRef]
- Roach, W.T.; Brown, R.; Caughey, S.J.; Garland, J.A.; Readings, C.J. The Physics of Radiation Fog: I-a Field Study. Q. J. R. Meteorol. Soc. 1976, 102, 313–333. [Google Scholar] [CrossRef]
- Duynkerke, P.G. Turbulence, Radiation, and Fog in Dutch Stable Boundary Layers. Bound.-Layer Meteorol. 1999, 90, 447–477. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences, 3rd ed.; McGraw-Hill: Boston, MA, USA, 2003. [Google Scholar]
- Bosveld, F.C. Cabauw In-Situ Observational Program 2000–Now: Instruments, Calibrations and Set-Up. 2019. Available online: http://projects.knmi.nl/cabauw/insitu/observations/documentation (accessed on 14 August 2020).
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative Transfer for Inhomogeneous Atmospheres: RRTM, a Validated Correlated-k Model for the Longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Seifert, A.; Beheng, K.D. A Double-Moment Parameterization for Simulating Autoconversion, Accretion and Selfcollection. Atmos. Res. 2001, 59–60, 265–281. [Google Scholar] [CrossRef]
- Seifert, A.; Beheng, K.D. A Two-Moment Cloud Microphysics Parameterization for Mixed-Phase Clouds. Part 1: Model Description. Meteorol. Atmos. Phys. 2006, 92, 45–66. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izett, J.G.; van de Wiel, B.J.H. Why Does Fog Deepen? An Analytical Perspective. Atmosphere 2020, 11, 865. https://doi.org/10.3390/atmos11080865
Izett JG, van de Wiel BJH. Why Does Fog Deepen? An Analytical Perspective. Atmosphere. 2020; 11(8):865. https://doi.org/10.3390/atmos11080865
Chicago/Turabian StyleIzett, Jonathan G., and Bas J. H. van de Wiel. 2020. "Why Does Fog Deepen? An Analytical Perspective" Atmosphere 11, no. 8: 865. https://doi.org/10.3390/atmos11080865
APA StyleIzett, J. G., & van de Wiel, B. J. H. (2020). Why Does Fog Deepen? An Analytical Perspective. Atmosphere, 11(8), 865. https://doi.org/10.3390/atmos11080865






