A High Spatiotemporal Resolution Global Gridded Dataset of Historical Human Discomfort Indices
Abstract
1. Introduction
2. Data and Methods
2.1. Source of Meteorological Variables
2.2. Data Acquisition and Processing
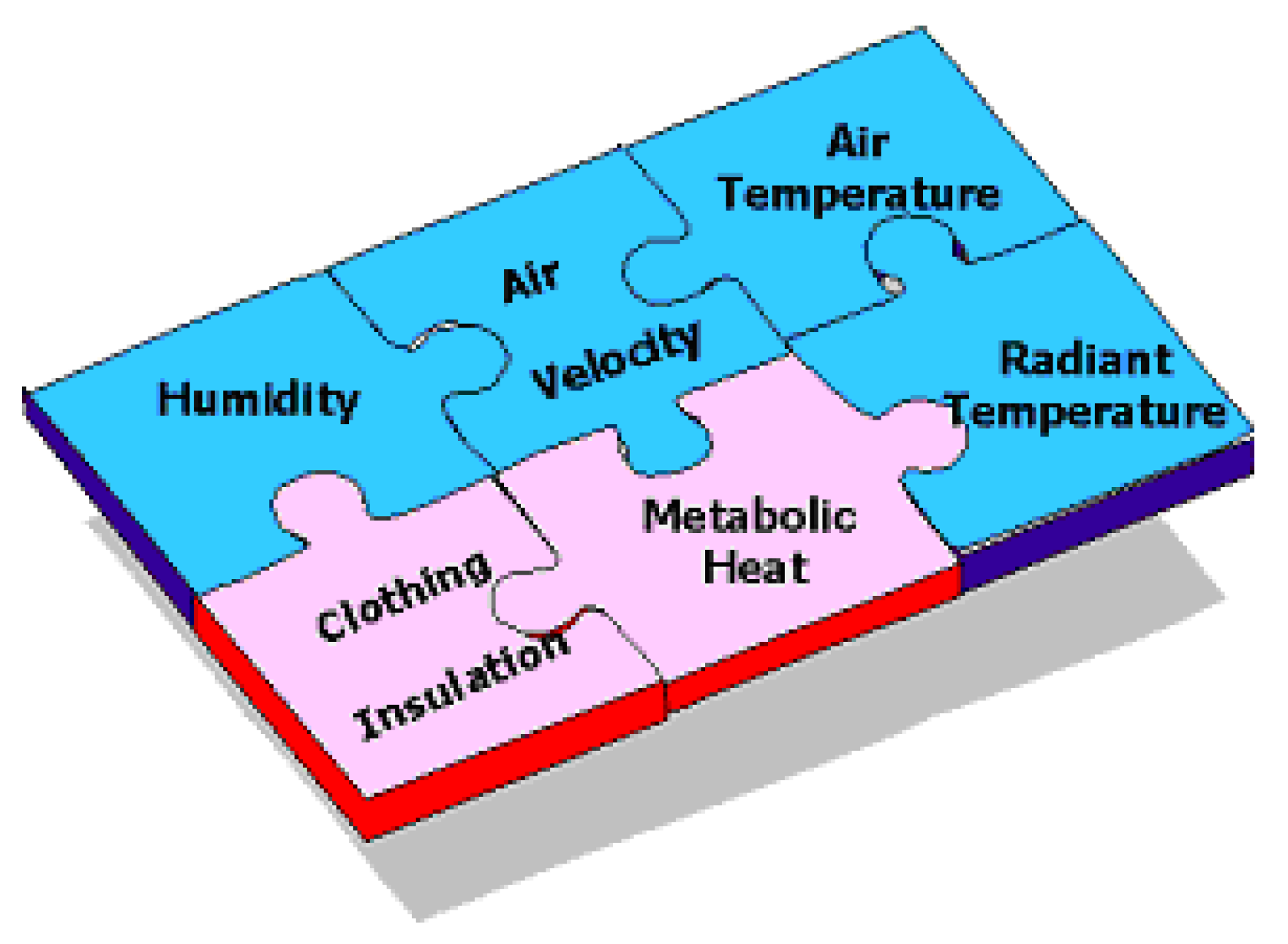
2.3. Compilation of HDIs, Historical Origins, and Operational Limits of Usage
2.3.1. Apparent Temperature (AT), Units: °C
2.3.2. Heat Index (HI) as defined by the U.S. National Oceanic and Atmospheric Administration (NOAA)—National Weather Service (NWS), Units: °C
RH2 + 1.23 × 10−3 × T2a × RH + 8.5 × 10−4 × Ta × RH2 − 1.99 × 10−6 × T2a × RH2
2.3.3. Humidex (HDEX) or Humidity Index, as defined by Environment and Climate Change Canada, Units: °C
2.3.4. Wet-Bulb Temperature (WBT), Units: °C
1.676331) + 0.00391838 × (RH)1.5 × atan(0.023101 × RH) − 4.686035
2.3.5. Simplified Wet Bulb Globe Temperature (WBGT), Units: °C
2.3.6. Thom Discomfort Index (DI), also referred to as Thermal-Heat Index, Thermohygrometric Index or Temperature-Humidity Index, Units: °C
2.3.7. Windchill Temperature (WCT), or Windchill Equivalent Temperature, Units: °C
3. Data Records
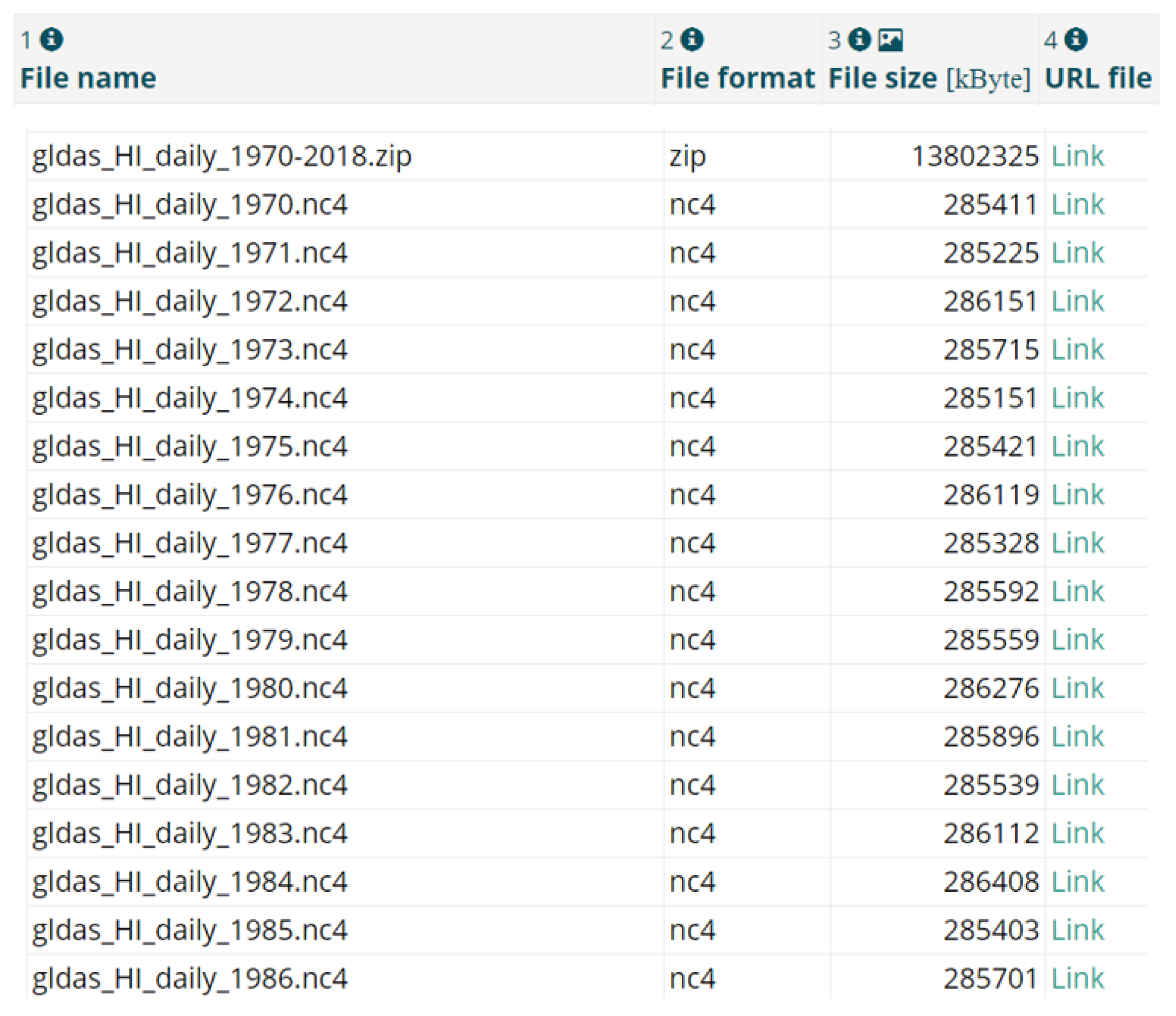
3.1. Data Repository and File Format
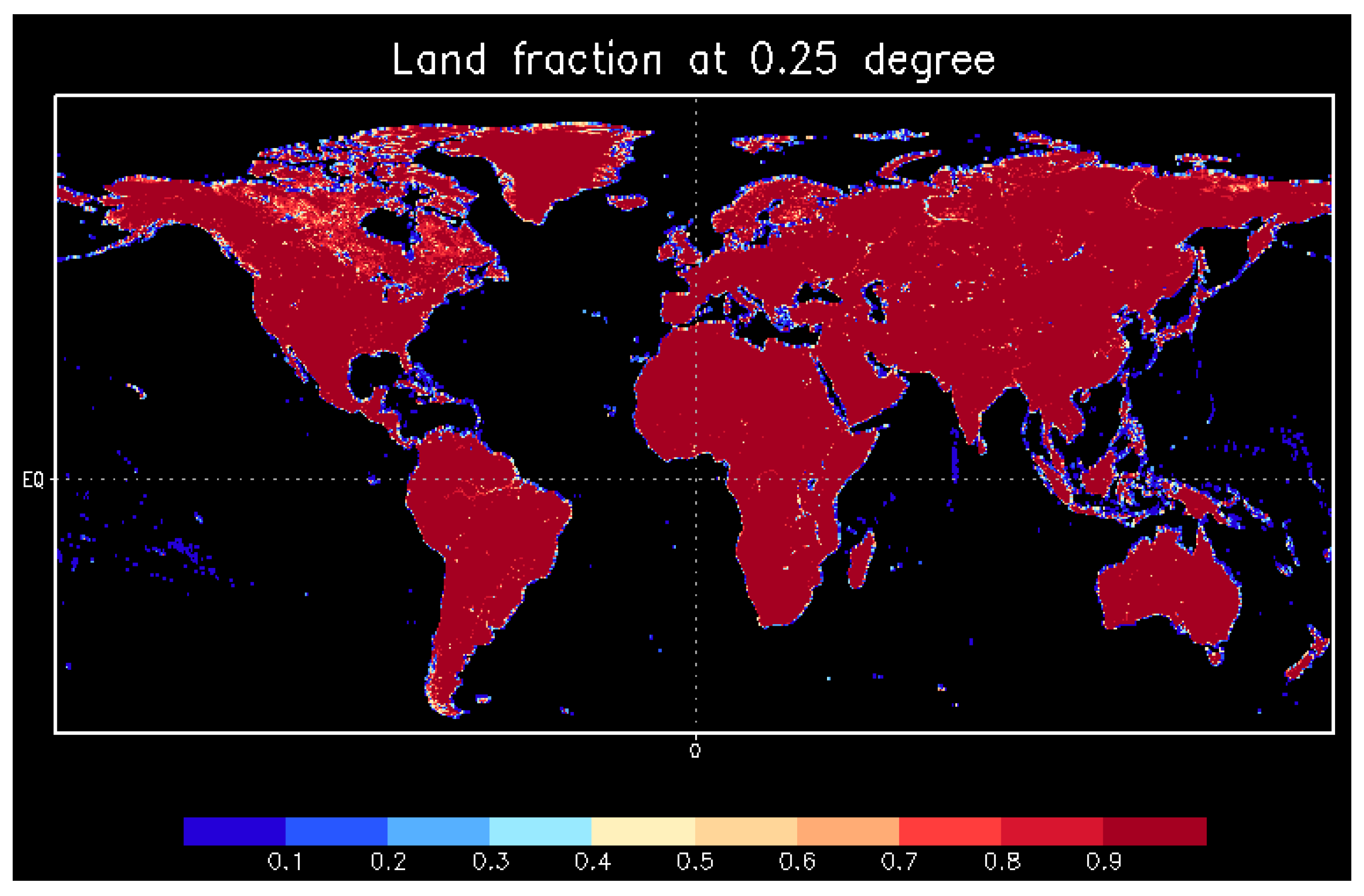
3.2. Data Grid, Spatial Coverage, Resolution, and Projection
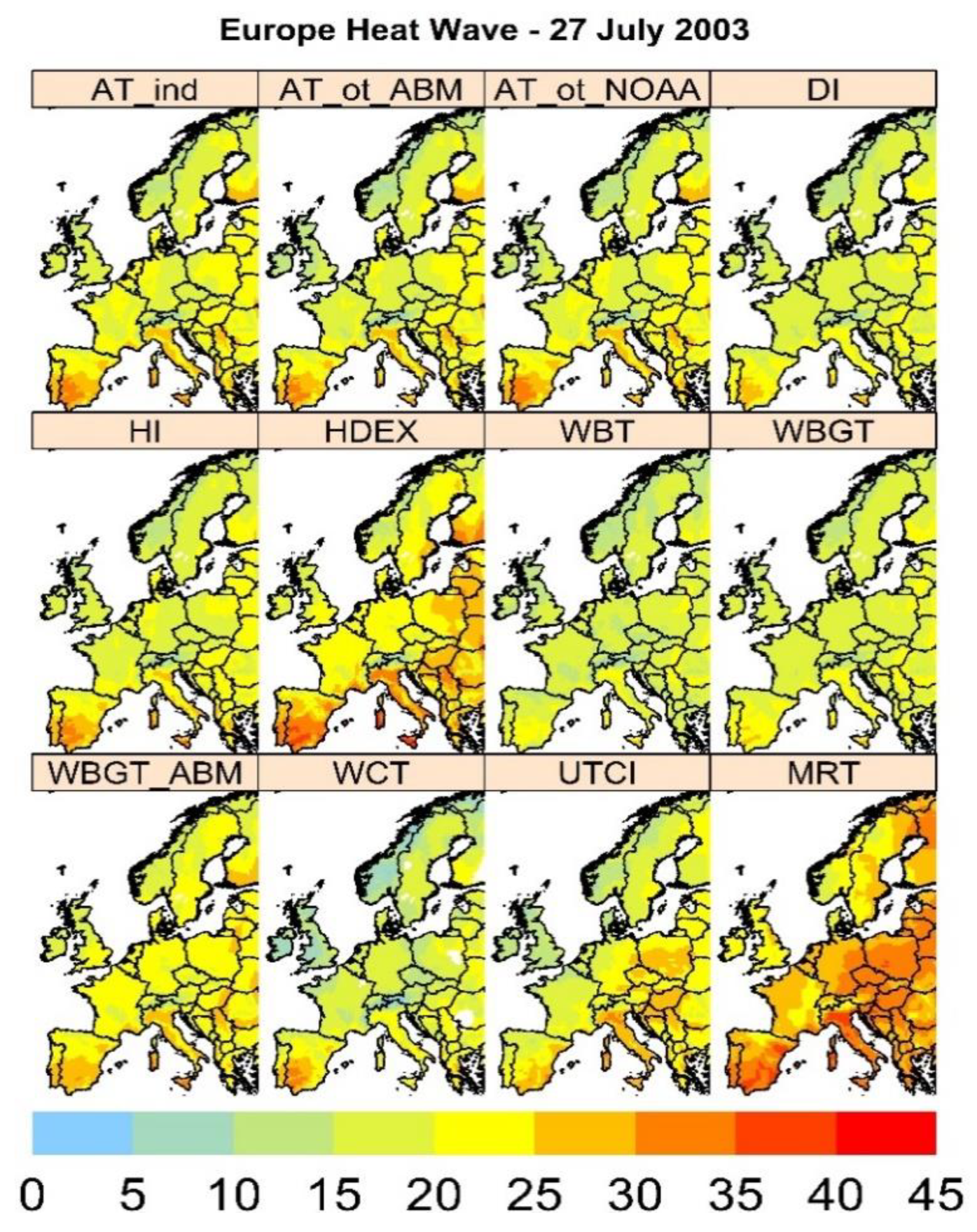
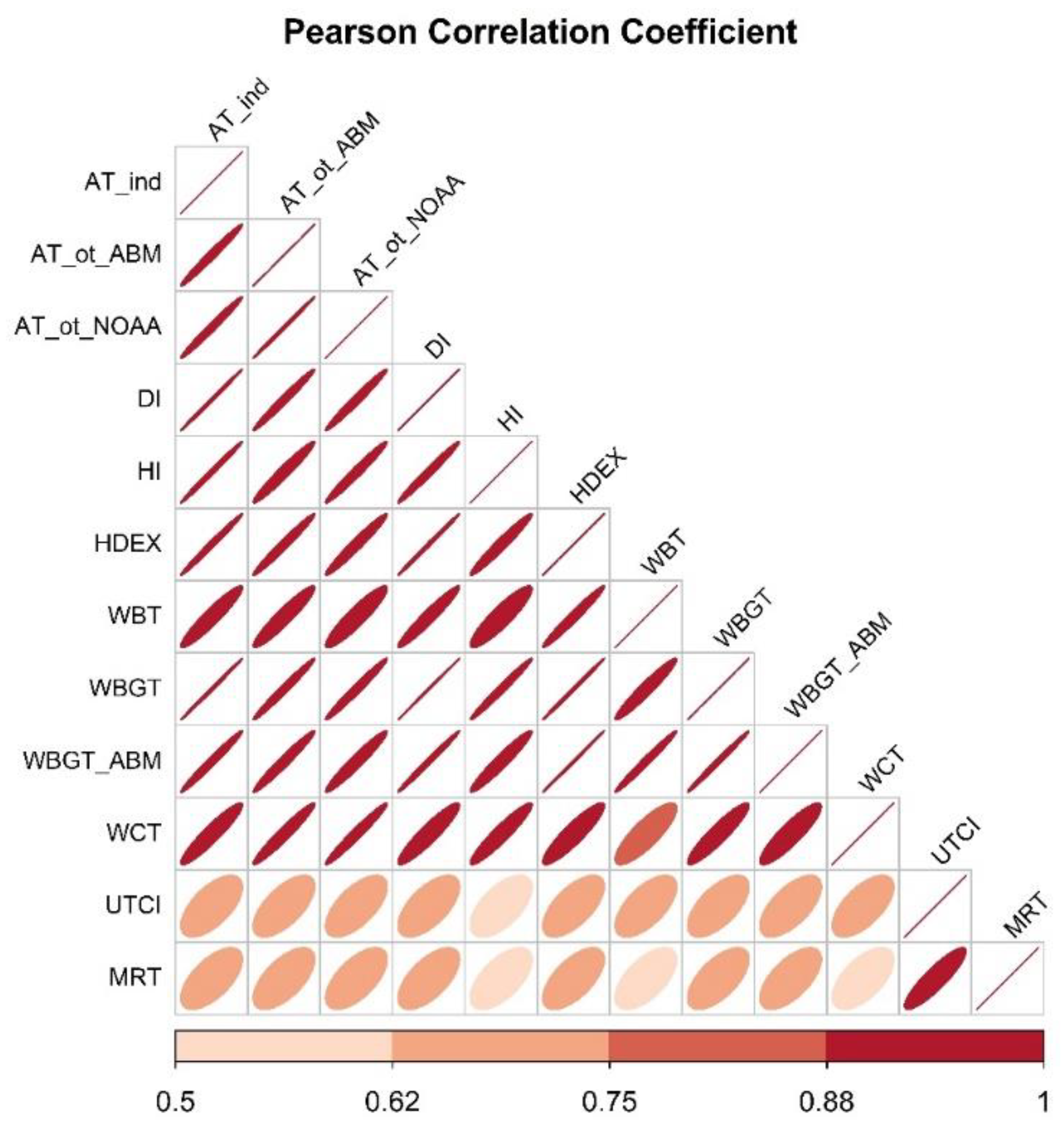
3.3. Technical Validation
4. Discussion
4.1. Data Limitations
4.1.1. Data Limitations in HDI_0p25_1970_2018 Emanating from GLDAS
4.1.2. Limitations in the Current Set of HDIs Presented in This Article
4.2. Key Features of the Dataset
4.3. Scope of Application
4.4. Tools and Recommended Ways to Use the Dataset
- (i)
- Downloads “gldas_DI_daily_2003.nc4” from the PANGAEA repository within R environment (a direct download from the repository is another alternative);
- (ii)
- Using the downloaded global gridded daily data, annual and monthly averages of DI for year 2003 are computed at each grid-cell for the full global domain (although this is for illustration purpose only as temporal aggregation is not recommended, discussed above);
- (iii)
- Utilizing a country shape file for Italy (Admin 1 level, regional boundaries), the grid-cell level monthly averages computed in step (ii) are cropped to the national boundary of Italy;
- (iv)
- The monthly grid-cells extracted in step (iii) are aggregated over the Italian regional boundaries, to produce regional level monthly values of DI for 2003;
- (v)
- Sample plot (map) of the aggregated index obtained from step (iv) is saved as a “.png” file;
- (vi)
- The aggregated data index from steps (iii) and (iv) are saved as output in three different file formats (a) Ascii, “.csv”, (b) Netcdf, “.nc”, and (c) GeoTiff “.tiff”.
5. Work Planned for Future
6. Code Availability
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tomczyk, A.M.; Bednorz, E. Heat waves in Central Europe and tropospheric anomalies of temperature and geopotential heights. Int. J. Climatol. 2019, 39, 4189–4205. [Google Scholar] [CrossRef]
- Tomczyk, A.M.; Bednorz, E.; Matzarakis, A. Human-biometeorological conditions during heat waves in Poland. Int. J. Climatol. 2020, 1–13. [Google Scholar] [CrossRef]
- Satyanarayana, G.C.; Rao, D.V.B. Phenology of heat waves over India. Atmos. Res. 2020, 245, 105078. [Google Scholar] [CrossRef]
- Krzyżewska, A.; Wereski, S.; Demczuk, P. Biometeorological conditions during an extreme heatwave event in Poland in August 2015. Weather 2020, 75, 183–189. [Google Scholar] [CrossRef]
- Hoy, A.; Hänsel, S.; Maugeri, M. An endless summer: 2018 heat episodes in Europe in the context of secular temperature variability and change. Int. J. Climatol. 2020, 1–22. [Google Scholar] [CrossRef]
- Loughran, T.F.; Perkins-Kirkpatrick, S.E.; Alexander, L. V Understanding the spatio-temporal influence of climate variability on Australian heatwaves. Int. J. Climatol. 2017, 37, 3963–3975. [Google Scholar] [CrossRef]
- Kjellstrom, T. Climate change, heat exposure and labour productivity. Epidemiology 2000, 11, S144. [Google Scholar]
- Kjellstrom, T.; Holmer, I.; Lemke, B. Workplace heat stress, health and productivity—An increasing challenge for low and middle-income countries during climate change. Glob. Health Action 2009, 2. [Google Scholar] [CrossRef]
- Kjellstrom, T.; Briggs, D.; Freyberg, C.; Lemke, B.; Otto, M.; Hyatt, O. Heat, Human Performance, and Occupational Health: A Key Issue for the Assessment of Global Climate Change Impacts. Annu. Rev. Public Health 2016, 37, 97–112. [Google Scholar] [CrossRef]
- Opitz-Stapleton, S.; Sabbag, L.; Hawley, K.; Tran, P.; Hoang, L.; Nguyen, P.H. Heat index trends and climate change implications for occupational heat exposure in Da Nang, Vietnam. Clim. Serv. 2016, 2–3, 41–51. [Google Scholar] [CrossRef]
- Orlov, A.; Sillmann, J.; Aaheim, A.; Aunan, K.; de Bruin, K. Economic Losses of Heat-Induced Reductions in Outdoor Worker Productivity: A Case Study of Europe. Econ. Disasters Clim. Chang. 2019, 3, 191–201. [Google Scholar] [CrossRef]
- Mora, C.; Dousset, B.; Caldwell, I.R.; Powell, F.E.; Geronimo, R.C.; Bielecki, C.R.; Counsell, C.W.W.; Dietrich, B.S.; Johnston, E.T.; Louis, L.V.; et al. Global risk of deadly heat. Nat. Clim. Chang. 2017, 7, 501–506. [Google Scholar] [CrossRef]
- Matthews, T. Humid heat and climate change. Prog. Phys. Geogr. 2018, 42, 391–405. [Google Scholar] [CrossRef]
- De Cian, E.; Pavanello, F.; Randazzo, T.; Mistry, M.; Davide, M. Households’ adaptation in a warming climate. Air conditioning and thermal insulation choices. Environ. Sci. Policy 2019, 100, 136–157. [Google Scholar] [CrossRef]
- De Cian, E.; Sue Wing, I. Global Energy Consumption in a Warming Climate. Environ. Resour. Econ. 2019, 72, 365–410. [Google Scholar] [CrossRef]
- Van Ruijven, B.J.; De Cian, E.; Sue Wing, I. Amplification of future energy demand growth due to climate change. Nat. Commun. 2019, 10, 1–12. [Google Scholar] [CrossRef]
- Wong, H.T.; Lai, P.C. Weather inference and daily demand for emergency ambulance services. Emerg. Med. J. 2012, 29, 60–64. [Google Scholar] [CrossRef]
- Turner, L.; Connell, D.; Tong, S. The Effect of Heat Waves on Ambulance Attendances in Brisbane, Australia. Prehosp. Disaster Med. 2013, 28, 1–6. [Google Scholar] [CrossRef]
- Gao, C.; Kuklane, K.; Östergren, P.-O.; Kjellstrom, T. Occupational heat stress assessment and protective strategies in the context of climate change. Int. J. Biometeorol. 2018, 62, 359–371. [Google Scholar] [CrossRef]
- Kjellstrom, T.; Freyberg, C.; Lemke, B.; Otto, M.; Briggs, D. Estimating population heat exposure and impacts on working people in conjunction with climate change. Int. J. Biometeorol. 2018, 62, 291–306. [Google Scholar] [CrossRef]
- Epstein, Y.; Moran, D.S. Thermal Comfort and the Heat Stress Indices. Ind. Health 2006, 44, 388–398. [Google Scholar] [CrossRef] [PubMed]
- Parsons, K. Human Thermal Environments: The Effects of Hot, Moderate, and Cold Environments on Human Health, Comfort, and Performance, 3rd ed.; CRC Press, Inc.: Boca Raton, FL, USA, 2014; ISBN 146659599X, 9781466595996. [Google Scholar]
- Health and Safety Executive (HSE) Six Factors of Thermal Discomfort. Available online: https://www.hse.gov.uk/temperature/thermal/factors.htm (accessed on 10 May 2020).
- Rothfusz, L. The Heat Index “Equation” (or, More Than You Ever Wanted to Know About Heat Index). Available online: https://www.weather.gov/media/ffc/ta_htindx.pdf (accessed on 20 March 2020).
- Jendritzky, G.; Staiger, H.; Bucher, K.; Graetz, A.; Laschewski, G. The Perceived Temperature: The Method of the Deutscher Wetterdienst for the Assessment of Cold Stress and Heat Load for the Human Body. Int. J. Biometeorol. 2012, 56, 165–176. [Google Scholar]
- Stull, R. Wet-Bulb Temperature from Relative Humidity and Air Temperature. J. Appl. Meteorol. Climatol. 2011, 50, 2267–2269. [Google Scholar] [CrossRef]
- Tetens, O. Uber cinige meteorologische Begriffe. Z. Geophys. 1930, 6, 297–309. [Google Scholar]
- Thom, E.C. The Discomfort Index. Weatherwise 1959, 12, 57–61. [Google Scholar] [CrossRef]
- Masterton, J.M.; Richardson, F.A. Humidex: A Method of Quantifying Human Discomfort Due to Excessive Heat and Humidity; CLI 1-79; Environment Canada, Atmospheric Environment: Downsview, ON, USA, 1979; p. 45.
- Buzan, J.R.; Oleson, K.; Huber, M. Implementation and comparison of a suite of heat stress metrics within the Community Land Model version 4.5. Geosci. Model Dev. 2015, 8, 151–170. [Google Scholar] [CrossRef]
- De Lima, C.Z.; Buzan, J.R.; Hertel, T.W.; Moore, F.C.; Baldos, U.L.C. Consequences of heat stress on agricultural workers dominates crop impacts of climate change. In Proceedings of the 22th Annual Conference on Global Economic Analysis GTAP, Warsaw, Poland, 19–21 June 2019. [Google Scholar]
- Havenith, G.; Fiala, D. Thermal indices and thermophysiological modeling for heat stress. Compr. Physiol. 2016, 6, 255–302. [Google Scholar]
- Streinu-Cercel, A.; Costoiu, S.M.M.; Streinu-Cercel, A.; Mârza, M. Models for the indices of thermal comfort. J. Med. Life 2008, 1, 148–156. [Google Scholar]
- Davis, R.E.; Knight, D.; Hondula, D.; Knappenberger, P.C. A comparison of biometeorological comfort indices and human mortality during heat waves in the United States. In Proceedings of the 17th Symposium on Boundary Layers and Turbulence, 27th Conference on Agricultural and Forest Meteorology, 17th Conference on Biometeorology and Aerobiology, San Diego, CA, USA, 21–25 May 2006. [Google Scholar]
- Quayle, R.; Doehring, F. Heat Stress. Weatherwise 1981, 34, 120–124. [Google Scholar] [CrossRef]
- Di Napoli, C.; Barnard, C.; Prudhomme, C.; Cloke, H.L.; Pappenberger, F. ERA5-HEAT: A global gridded historical dataset of human thermal comfort indices from climate reanalysis. Geosci. Data J. 2020, 1–9. [Google Scholar] [CrossRef]
- Copernicus Climate Data Store. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/derived-utci-historical?tab=overview (accessed on 27 July 2020).
- Steadman, R.G. The Assessment of Sultriness. Part I: A Temperature-Humidity Index Based on Human Physiology and Clothing Science. Appl. Meteorol. 1979, 18, 861–873. [Google Scholar] [CrossRef]
- Steadman, R.G. A Universal Scale of Apparent Temperature. Clim. Appl. Meteorol. 1984, 23, 1674–1687. [Google Scholar] [CrossRef]
- Steadman, R.G. Norms of apparent temperature in Australia. Aust. Meteorol. Oceanogr. 1994, 43, 1–16. [Google Scholar]
- Krstić, G. Apparent temperature and air pollution vs. elderly population mortality in Metro Vancouver. PLoS ONE 2011, 6, e25101. [Google Scholar] [CrossRef]
- Mohan, M.; Gupta, A.; Bhati, S. A Modified Approach to Analyze Thermal Comfort Classification. Atmos. Clim. Sci. 2013, 4, 7–19. [Google Scholar] [CrossRef][Green Version]
- Schoen, C. A New Empirical Model of the Temperature–Humidity Index. J. Appl. Meteorol. 2005, 44, 1413–1420. [Google Scholar] [CrossRef]
- Dahl, K.; Licker, R.; Abatzoglou, J.T.; Declet-Barreto, J. Increased frequency of and population exposure to extreme heat index days in the United States during the 21st century. Environ. Res. Commun. 2019, 1, 075002. [Google Scholar] [CrossRef]
- Russo, S.; Sillmann, J.; Sterl, A. Humid heat waves at different warming levels. Sci. Rep. 2017, 7, 7477. [Google Scholar] [CrossRef]
- Atalla, T.; Gualdi, S.; Lanza, A. A global degree days database for energy-related applications. Energy 2018, 143, 1048–1055. [Google Scholar] [CrossRef]
- Haldane, J.S. The Influence of High Air Temperatures: No. 1. J. Hyg. (Lond.) 1905, 5, 494–513. [Google Scholar] [CrossRef] [PubMed]
- Pal, J.S.; Eltahir, E.A.B. Future temperature in southwest Asia projected to exceed a threshold for human adaptability. Nat. Clim. Chang. 2016, 6, 197–200. [Google Scholar] [CrossRef]
- Gagge, A.P.; Nishi, Y. Physical indices of the thermal environment. ASHRAE J. 1976, 18, 1. [Google Scholar]
- Lemke, B.; Kjellstrom, T. Calculating workplace WBGT from meteorological data: A tool for climate change assessment. Ind. Health 2012, 50, 267–278. [Google Scholar] [CrossRef]
- ABM Wet Bulb Globe Temperature as defined by Australian Bureau of Meteorology. Available online: http://www.bom.gov.au/info/thermal_stress/ (accessed on 2 June 2019).
- Siple, P.A.; Passel, C.F. Measurements of Dry Atmospheric Cooling in Subfreezing Temperatures. Proc. Am. Philos. Soc. 1945, 89, 177–199. [Google Scholar] [CrossRef]
- Groen, G. Wind Chill Equivalent Temperature (WCET) Climatology and Scenarios for Schiphol Airport; KNMI Tech. Report; Koninklijk Nederlands Meteorologisch Instituut: De-Bilt, The Netherlands, 2009; p. 18. [Google Scholar]
- Quayle, R.G.; Steadman, R.G. The Steadman Wind Chill: An Improvement over Present Scales. Weather Forecast. 1998, 13, 1187–1193. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Kumar, S.V.; Peters-Lidard, C.D.; Tian, Y.; Houser, P.R.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.L.; Doty, B.; Dirmeyer, P.; et al. Land information system: An interoperable framework for high resolution land surface modeling. Environ. Model. Softw. 2006, 21, 1402–1415. [Google Scholar] [CrossRef]
- Peters-Lidard, C.D.; Houser, P.R.; Tian, Y.; Kumar, S.V.; Geiger, J.; Olden, S.; Lighty, L.; Doty, B.; Dirmeyer, P.; Adams, J.; et al. High-performance Earth system modeling with NASA/GSFC’s Land Information System. Innov. Syst. Softw. Eng. 2007, 3, 157–165. [Google Scholar] [CrossRef]
- Colston, J.M.; Ahmed, T.; Mahopo, C.; Kang, G.; Kosek, M.; de Sousa, F., Jr.; Shrestha, P.S.; Svensen, E.; Turab, A.; Zaitchik, B. Evaluating meteorological data from weather stations, and from satellites and global models for a multi-site epidemiological study. Environ. Res. 2018, 165, 91–109. [Google Scholar] [CrossRef]
- NASA-GSFC GLDAS Data. Available online: https://disc.gsfc.nasa.gov/datasets/GLDAS_NOAH025_3H_V2.1/summary (accessed on 12 November 2019).
- NASA-GSFC-DISC GLDAS Data Access. Available online: https://disc.gsfc.nasa.gov/datasets?page=1&project=GLDAS&temporalResolution=3hours&spatialResolution=0.25°x0.25° (accessed on 15 November 2019).
- Zender, C.S. Analysis of self-describing gridded geoscience data with netCDF Operators (NCO). Environ. Model. Softw. 2008, 23, 1338–1342. [Google Scholar] [CrossRef]
- Uwe SCHULZWEIDA of Max Planck Institute for Meteorology. Climate Data Operators (CDO) User Guide, Version 1.9.0; Uwe SCHULZWEIDA: Hamburg, Germany, 2018. [Google Scholar]
- Webb, A. Principles of environmental physics. By J. L. Monteith & M. H. Unsworth. Edward Arnold, Sevenoaks. 2nd edition, 1990. pp. xii + 291. Q. J. R. Meteorol. Soc. 1994, 120, 1700. [Google Scholar]
- Stull, R.B. Meteorology for Scientists and Engineers, 3rd ed. 2011. Available online: https://www.eoas.ubc.ca/books/Practical_Meteorology/mse3.html (accessed on 12 November 2019).
- Steadman, R.G. The Assessment of Sultriness. Part II: Effects of Wind, Extra Radiation and Barometric Pressure on Apparent Temperature. J. Appl. Meteorol. 1979, 18, 874–885. [Google Scholar] [CrossRef]
- Gonzalez, R.R.; Nishi, Y.; Gagge, A.P. Experimental evaluation of standard effective temperature a new biometeorological index of man’s thermal discomfort. Int. J. Biometeorol. 1974, 18, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Almeida, S.P.; Casimiro, E.; Calheiros, J. Effects of apparent temperature on daily mortality in Lisbon and Oporto, Portugal. Environ. Heal. 2010, 9, 12. [Google Scholar] [CrossRef]
- Wichmann, J.; Ketzel, M.; Ellermann, T.; Loft, S. Apparent temperature and acute myocardial infarction hospital admissions in Copenhagen, Denmark: A case-crossover study. Environ. Health 2012, 11, 19. [Google Scholar] [CrossRef]
- Kalkstein, L.S.; Valimont, K.M. An evaluation of summer discomfort in the United States using a relative climatological index. Bull.—Am. Meteorol. Soc. 1986, 67, 842–848. [Google Scholar] [CrossRef]
- Yaglou, C.P.; Minaed, D. Control of Heat Casualties at Military Training Centers. Arch. Indust. Heal. 1957, 16, 302–316. [Google Scholar]
- Moran, D.; Pandolf, K.B.; Shapiro, Y.; Heled, Y.; Shani, Y.; Mathew, W.T.; Gonzalez, R. An environmental stress index (ESI) as a substitute for the wet bulb globe temperature (WBGT). J. Therm. Biol. 2001, 26, 427–431. [Google Scholar] [CrossRef]
- Budd, G.M. Wet-bulb globe temperature (WBGT)-its history and its limitations. J. Sci. Med. Sport 2008, 11, 20–32. [Google Scholar] [CrossRef]
- Zare, S.; Hasheminejad, N.; Shirvan, H.E.; Hemmatjo, R.; Sarebanzadeh, K.; Ahmadi, S. Comparing Universal Thermal Climate Index (UTCI) with selected thermal indices/environmental parameters during 12 months of the year. Weather Clim. Extrem. 2018, 19, 49–57. [Google Scholar] [CrossRef]
- Goldie, J.; Alexander, L.; Lewis, S.C.; Sherwood, S. Comparative evaluation of human heat stress indices on selected hospital admissions in Sydney, Australia. Aust. N. Z. J. Public Health 2017, 41, 381–387. [Google Scholar] [CrossRef] [PubMed]
- Dear, K. Modelling productivity loss from heat stress. Atmosphere 2018, 9, 286. [Google Scholar] [CrossRef]
- Sohar, E.; Adar, R.; Kaly, J. Comparison of the environmental heat load in various parts of Israel. Bull. Res. Counc. Isr. E 1963, 10, 111–115. [Google Scholar]
- Sohar, E.; Birenfeld, C.; Shoenfeld, Y.; Shapiro, Y. Description and forecast of summer climate in physiologically significant terms. Int. J. Biometeorol. 1978, 22, 75–81. [Google Scholar] [CrossRef]
- Almendra, R.; Santana, P.; Vasconcelos, J.; Silva, G.; Gonçalves, F.; Ambrizzi, T. The influence of the winter North Atlantic Oscillation index on hospital admissions through diseases of the circulatory system in Lisbon, Portugal. Int. J. Biometeorol. 2017, 61, 325–333. [Google Scholar] [CrossRef]
- Osczevski, R.J. The Basis of Wind Chill. Arctic 1995, 48, 372–382. [Google Scholar] [CrossRef]
- Steadman, R.G. Indices of windchill of clothed persons. J. Appl. Meteorol. 1971, 10, 674–683. [Google Scholar] [CrossRef]
- LeBlanc, J.; Blais, B.; Barabe, B.; Cote, J. Effects of temperature and wind on facial temperature, heart rate, and sensation. J. Appl. Physiol. 1976, 40, 127–131. [Google Scholar] [CrossRef]
- Virokannas, H.; Anttonen, H. Thermal responses in the body during snowmobile driving. Arctic Med. Res. 1994, 53 (Suppl. 3), 12–18. [Google Scholar]
- Mistry, M.N. A High Spatiotemporal Resolution Global Gridded Dataset of Historical (1970–2018) Human Discomfort Indices Based on GLDAS Data. Available online: https://doi.org/10.1594/PANGAEA.904282 (accessed on 14 May 2020).
- Ji, L.; Senay, G.B.; Verdin, J.P. Evaluation of the Global Land Data Assimilation System (GLDAS) Air Temperature Data Products. J. Hydrometeorol. 2015, 16, 2463–2480. [Google Scholar] [CrossRef]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An Overview of the Global Historical Climatology Network-Daily Database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Mistry, M.N. A High-Resolution Global Gridded Historical Dataset of Climate Extreme Indices. Data 2019, 4, 41. [Google Scholar] [CrossRef]
- Mistry, M.N. Historical global gridded degree-days: A high-spatial resolution database of CDD and HDD. Geosci. Data J. 2019, 6, 214–221. [Google Scholar] [CrossRef]
- GLDAS Previous Studies. Available online: https://ldas.gsfc.nasa.gov/gldas/publications (accessed on 29 May 2020).
- Hijmans, R.J.; van Etten, J. Raster: Geographic Data Analysis and Modeling. Available online: https://cran.r-project.org/package=raster (accessed on 15 December 2019).
- Pebesma, E.J.; Bivand, R.S. Classes and methods for spatial data in {R}. R News 2005, 5, 9–13. [Google Scholar]
- Bivand, R.S.; Pebesma, E.; Gomez-Rubio, V. Applied spatial data analysis with {R}, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Wei, T.; Simko, V. R package “corrplot”: Visualization of a Correlation Matrix. Available online: https://github.com/taiyun/corrplot (accessed on 26 July 2020).
- Havenith, G. Individualized model of human thermoregulation for the simulation of heat stress response. J. Appl. Physiol. 2001, 90, 1943–1954. [Google Scholar] [CrossRef]
- Pappenberger, F.; Jendritzky, G.; Staiger, H.; Dutra, E.; Di Giuseppe, F.; Richardson, D.S.; Cloke, H.L. Global forecasting of thermal health hazards: The skill of probabilistic predictions of the Universal Thermal Climate Index (UTCI). Int. J. Biometeorol. 2015, 59, 311–323. [Google Scholar] [CrossRef]
- Fiala, D.; Havenith, G.; Bröde, P.; Kampmann, B.; Jendritzky, G. UTCI-Fiala multi-node model of human heat transfer and temperature regulation. Int. J. Biometeorol. 2012, 56, 429–441. [Google Scholar] [CrossRef]
- Bröde, P.; Fiala, D.; Błażejczyk, K.; Holmér, I.; Jendritzky, G.; Kampmann, B.; Tinz, B.; Havenith, G. Deriving the operational procedure for the Universal Thermal Climate Index (UTCI). Int. J. Biometeorol. 2012, 56, 481–494. [Google Scholar] [CrossRef]
- Alexander, L.; Herold, N. ClimPACT2 Indices and Software (R Software Package). Available online: https://htmlpreview.github.io/?https://raw.githubusercontent.com/ARCCSS-extremes/climpact2/master/user_guide/ClimPACT2_user_guide.htm (accessed on 11 December 2019).
- Perkins, S.E.; Alexander, L. V On the Measurement of Heat Waves. J. Clim. 2013, 26, 4500–4517. [Google Scholar] [CrossRef]
- Dobrinescu, A.; Busuioc, A.; Birsan, M.-V.; Dumitrescu, A.; Orzan, A. Changes in thermal discomfort indices in Romania and their connections with large-scale mechanisms. Clim. Res. 2015, 64, 213–226. [Google Scholar] [CrossRef]
- Talukdar, M.S.; Hossen, M.; Baten, A. Trends of Outdoor Thermal Discomfort in Mymensingh: An Application of Thoms’ Discomfort index. J. Environ. Sci. Nat. Resour. 2018, 10, 151–156. [Google Scholar] [CrossRef][Green Version]
- Day, E.; Fankhauser, S.; Kingsmill, N.; Costa, H.; Mavrogianni, A. Upholding labour productivity under climate change: An assessment of adaptation options. Clim. Policy 2019, 19, 367–385. [Google Scholar] [CrossRef]
- Klok, E.J.; Klein Tank, A.M.G. Updated and extended European dataset of daily climate observations. Int. J. Climatol. 2009, 29, 1182–1191. [Google Scholar] [CrossRef]
- Xavier, A.C.; King, C.W.; Scanlon, B.R. Daily gridded meteorological variables in Brazil (1980–2013). Int. J. Climatol. 2016, 36, 2644–2659. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Rajeevan, M.; Kshirsagar, S.R. Development of a high resolution daily gridded temperature data set (1969–2005) for the Indian region. Atmos. Sci. Lett. 2009, 10, 249–254. [Google Scholar] [CrossRef]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Wang, T.; Hamann, A.; Spittlehouse, D.; Carroll, C. Locally downscaled and spatially customizable climate data for historical and future periods for North America. PLoS ONE 2016, 11, e0156720. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Tung, K.-K. Global-mean surface temperature variability: Space–time perspective from rotated EOFs. Clim. Dyn. 2018, 51, 1719–1732. [Google Scholar] [CrossRef]
- ILO Working On a Warmer Planet: The Impact of Heat Stress on Labour Productivity and Decent Work. Available online: https://www.ilo.org/wcmsp5/groups/public/---dgreports/---dcomm/---publ/documents/publication/wcms_711919.pdf (accessed on 27 April 2020).
- NASA GISS Panoply Software. Available online: https://www.giss.nasa.gov/tools/panoply/ (accessed on 12 January 2020).
- Pierce, D.W. Ncview Software Scripps Institution of Oceanography. Available online: http://meteora.ucsd.edu/~pierce/ncview_home_page.html (accessed on 11 January 2020).
- R Core Team R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 21 October 2019).
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009; ISBN 1441412697. [Google Scholar]
- QGIS.org QGIS Geographic Information System. Open Source Geospatial Foundation Project. Available online: http://qgis.org (accessed on 18 January 2020).
- GRASS Development Team Geographic Resources Analysis Support System (GRASS GIS) Software, Version 7.2. Available online: http://grass.osgeo.org (accessed on 14 May 2020).
- Land-Water Pixels in GLDAS (https://lpdaac.usgs.gov/). Available online: https://ldas.gsfc.nasa.gov/gldas/publications (accessed on 10 May 2020).
| HDI (Full Description) | Abbreviation | Units | Reference Equation(s) in this Article | Discussion Paper(s) | Selective Studies Implementing the HDI |
|---|---|---|---|---|---|
| Apparent Temperature indoors | ATind | °C | Equation (1) | [38] | [10,13] |
| Apparent Temperature outdoors in shade as defined by National Oceanic and Atmospheric Administration (NOAA) | ATot_NOAA | °C | Equation (2) | [38,39] | [10,30] |
| Apparent Temperature outdoors in shade as defined by Australian Bureau of Meteorology (ABM) | ATot_ABM | °C | Equation (3) | [40] | [10,30,41] |
| Heat Index as defined by the U.S. National Weather Service (NWS) | HI | °C | Equations (4)–(7) | [24] | [10,30,42,43,44,45] |
| Humidex as defined by the Environment and Climate Change Canada | HDEX | °C | Equation (8) | [29] | [13,30,31,46] |
| Wet Bulb Temperature | WBT | °C | Equation (9) | [26,47] | [13,21,30,48] |
| Simplified Wet Bulb Globe Temperature | WBGT | °C | Equations (10)–(13) | [49] | [20,21,30,50] |
| Simplified Wet Bulb Globe Temperature outdoors in shade as defined by ABM | WBGT_ABM | °C | [51] | [21,30] | |
| Thom Discomfort Index (also known as Thermal-Heat Index or Temperature-Humidity Index) | DI | °C | Equations (14)–(16) | [28] | [10,19,21,30,42,43] |
| Windchill Temperature | WCT | °C | Equation (17) | [52] | [53,54] |
| GLDAS Variable | Equation for Derived Variables where Relevant (See Section 3.1 for Further Details) | Units | HDIs where Variable Utilized |
|---|---|---|---|
| Ta | -- | °C | ATind, ATot_ABM, ATot_NOAA, HI, HDEX, DI, WBT, WBGT, WBGT_ABM, WCT |
| P | -- | Hecto-Pascal (hPa) # | -- |
| Q | -- | kg kg−1 | -- |
| VP | Equation (18) | hPa | ATind, ATot_ABM, ATot_NOAA, HDEX, WBGT, WBGT_ABM |
| SVP | Equation (19) ## | hPa | -- |
| RH | Equation (20) | % | HI, WBT |
| VPD | Equation (21) | hPa | -- |
| W | -- | meter-sec−1 (m/s) | ATot_ABM, ATot_NOAA, WCT |
| Thermal Perception (Category of Heat Stress) | HDIs (°C) |  | |||
| AT, HI | HDEX | WBGT | DI | ||
| Comfortable (No Thermal Stress) | <27 | <35 | <28 | <21 | |
| Slightly Warm (Caution) | 27–32 | 35–40 | 28–32 | 21–25 | |
| Moderately Warm (Extreme Caution) | 32–41 | 40–45 | 32–35 | 25–28 | |
| Hot (Danger) | 41–54 | 45–54 | 35–38 | 28–31 | |
| Sweltering (Extreme Danger) | >54 | >55 | >38 | >31 | |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mistry, M.N. A High Spatiotemporal Resolution Global Gridded Dataset of Historical Human Discomfort Indices. Atmosphere 2020, 11, 835. https://doi.org/10.3390/atmos11080835
Mistry MN. A High Spatiotemporal Resolution Global Gridded Dataset of Historical Human Discomfort Indices. Atmosphere. 2020; 11(8):835. https://doi.org/10.3390/atmos11080835
Chicago/Turabian StyleMistry, Malcolm N. 2020. "A High Spatiotemporal Resolution Global Gridded Dataset of Historical Human Discomfort Indices" Atmosphere 11, no. 8: 835. https://doi.org/10.3390/atmos11080835
APA StyleMistry, M. N. (2020). A High Spatiotemporal Resolution Global Gridded Dataset of Historical Human Discomfort Indices. Atmosphere, 11(8), 835. https://doi.org/10.3390/atmos11080835





