1. Introduction
On 23 June 2016, the Netherlands was hit by a severe storm, with a storm track particularly over the southern province of Noord-Brabant. The storm comprehended lightning, heavy precipitation, downbursts, and hail with a diameter of ≈10 cm [
1] The storm damage has been estimated at 675 million euros. The extreme weather was a result of a Mesoscale Convective System (MCS) formed by a Spanish plume over Europe. The relatively hot dry air was advected from the Iberian Peninsula over the Pyrenees to the north, acting as a lid to the less warm but moist air underneath. In the upper air, the cold dry air was drawn from the Atlantic Ocean. As a result, radio sounding observations indicated that a potentially highly unstable atmosphere was therefore present over northern France, Belgium and the Netherlands. Surface heating during the day increased the Convective Available Potential Energy (CAPE) to values of ≈3.10
3 J kg
−1. However, due to the capping of the middle atmosphere, deep convection could only occur when the Convective Inhibition (CIN) was overcome, by frontogenesis and surface heating, which broke the inversion and the CAPE was released.
Understanding and forecasting of critical weather phenomenon are crucial for many sectors in society, for example, transportation, agriculture, hydrology, and urban areas. In the past four decades, mesoscale numerical weather prediction (NWP)models have evolved from using coarse grid spacings (≈100 km) with few vertical levels and simplistic physical processes to high resolution (1 km) models with a sophisticated representation of physical processes today [
2]. Consequently, it is not a priori clear whether grid-scale parameterisations are needed and whether convection is resolved well enough to be explicitly handled by the dynamics of the fully non-hydrostatic equations [
2]. Lilly [
3] already noted that increased resolution forecasts may have a higher quality since high resolution allows for removing potentially inaccurate parameterisations. Mesoscale models with grid spacing exceeding 10 km must use cumulus parameterisation schemes (CPS) to represent sub-grid convective column processes associated with updrafts, downdrafts and environmental subsidence. They assume these processes to occur within the grid column. Grid spacings smaller than 10 km appear in the so-called ‘grey-zone’. In that case, the assumptions of the CPS might be invalid, but in particular the grid is too coarse to resolve the updrafts explicitly [
2]. Particularly, subsidence may occur on a scale broader than the column. The CPS might be still active, their tendencies drive the vertical motions and subsidence, but it is unclear whether the results are realistic [
2]. Thereto also several so-called scale-aware CPS approaches at an “intermediate position” between fully parameterised and fully resolved convection have been developed. Herein, the activity of the scheme depends on the model grid spacing and allows for a smooth transition from coarse to fine grid spacing [
4]. In this study we hypothesize that high-resolution mesoscale simulations contribute to a more accurate representation of convective processes, but also that a direct representation of the convective processes provides preferential results compared to parameterised convection. Moreover, we discuss the impact of scale-aware properties of some CPS and compare their behaviour with results from fully explicit simulations and from fully parameterised convection simulations.
In addition, the pre-convective environment has a large influence on the timing and location of convection for 18–30-h forecasts. It is unclear how the environmental forecasts at high resolution compare to the forecasts at relatively coarse resolution. Understanding the nature of the forecast errors is important for the development of high resolution modelling at research and operational forecasting centres [
5].
The development of new forecasting techniques for extreme weather remains an ongoing challenge. To contribute to these innovations for The Netherlands, we investigate this grey-zone issue for this particular MCS, since this study will apply a grid spacing of 4 km to the storm case in Noord-Brabant. The study utilises the Weather Research and Forecasting (WRF) model [
6,
7]. To investigate whether the model can resolve the storm case or that the convection needs parameterisation, five experiments are performed. The model is first run without a CPS (at 2 and 4 km grid spacing), and subsequently with three CPS (only at 4 km resolution). The CPS runs are to investigate the differences in the storm forecasts. The following CPS schemes are used: the Betts–Miller–Janjic scheme (BMJ), the scale-aware Grell–Freitas ensemble scheme (GF) and the Kain–Fritsch scheme (KF). These schemes are often used and together represent models of contrasting complexity (see
Section 3 and
Appendix A).
Also, model forecasts are in general sensitive to uncertainties in the models initial and boundary conditions. Convection is a key process that is efficiently able to transfer these initially small uncertainties into larger differences in terms of storm onset and precipitation. So far, little is known whether resolved convection and parameterised convection deals with this uncertainty differently. This will be studied in this paper as a second novel aspect by varying the spatial distribution of the initial soil moisture field in 10 ensemble members (see
Section 2).
To gain further insights in forecasting of the described event, the main research questions are:
How does the WRF model perform for the storm on 23 June 2016 in Noord-Brabant, The Netherlands, for explicit and parameterised convection?
Do spatial perturbations in soil moisture result in different representation of deep convection for parameterised convection and resolved convection?
Section 2 reports on the synoptic situation, the experimental set-up and available observations for model validation.
Section 3 discusses the formulations of the different convections schemes. The results of the experiments are presented in
Section 4 and discussed in
Section 5. Finally, conclusions are drawn in
Section 6.
4. Results
This section presents the model results. First, spatial results of the five experiments and of radar observations are presented (daily accumulated rainfall, maximum reflectivity). Subsequently, the time evolution of the modelled CAPE, CIN, Lifting Condensation Level (LCL), Level of Free Convection (LFC), accumulated rainfall and wind speed are discussed.
4.1. Daily Accumulated Precipitation
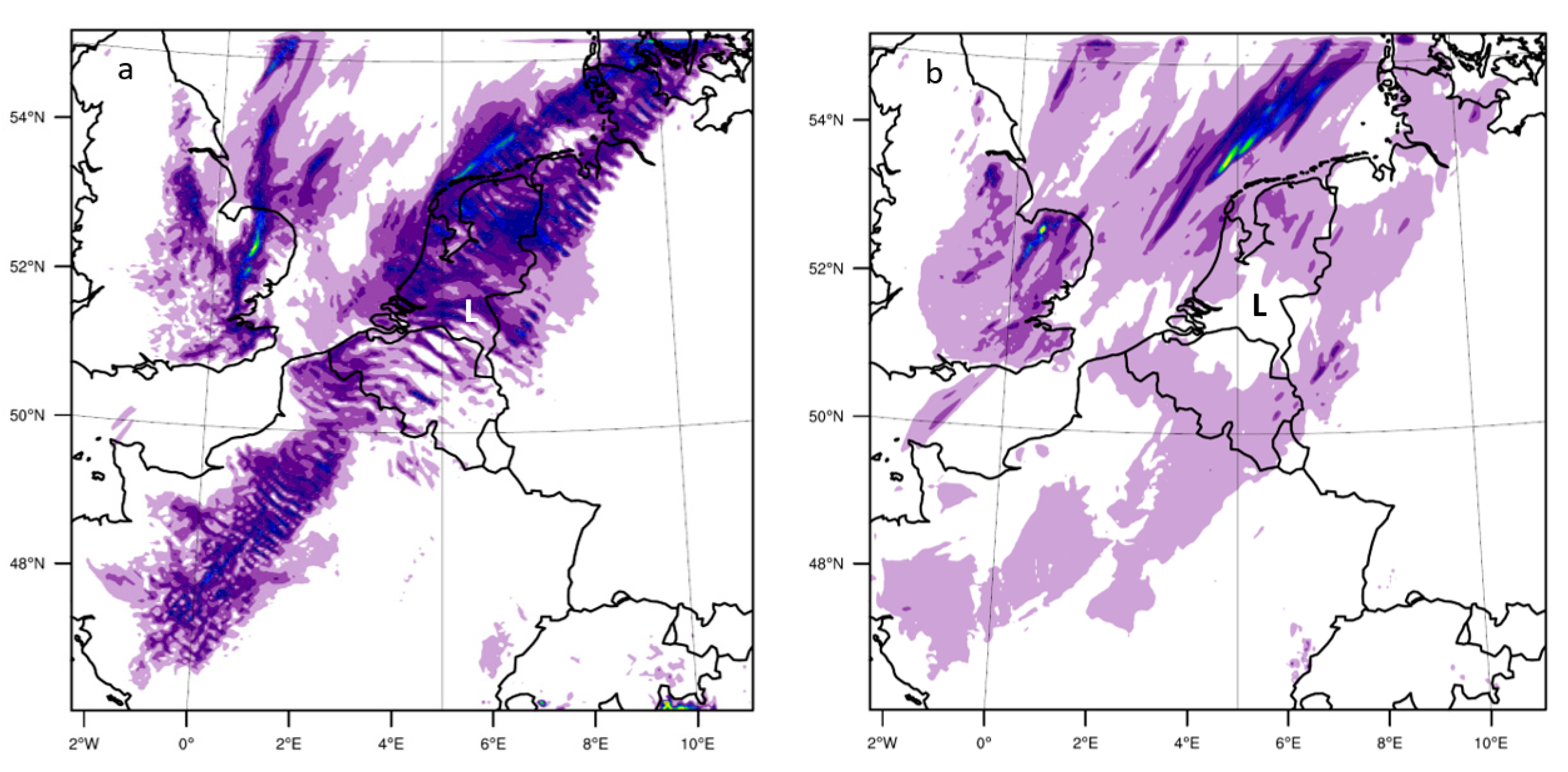
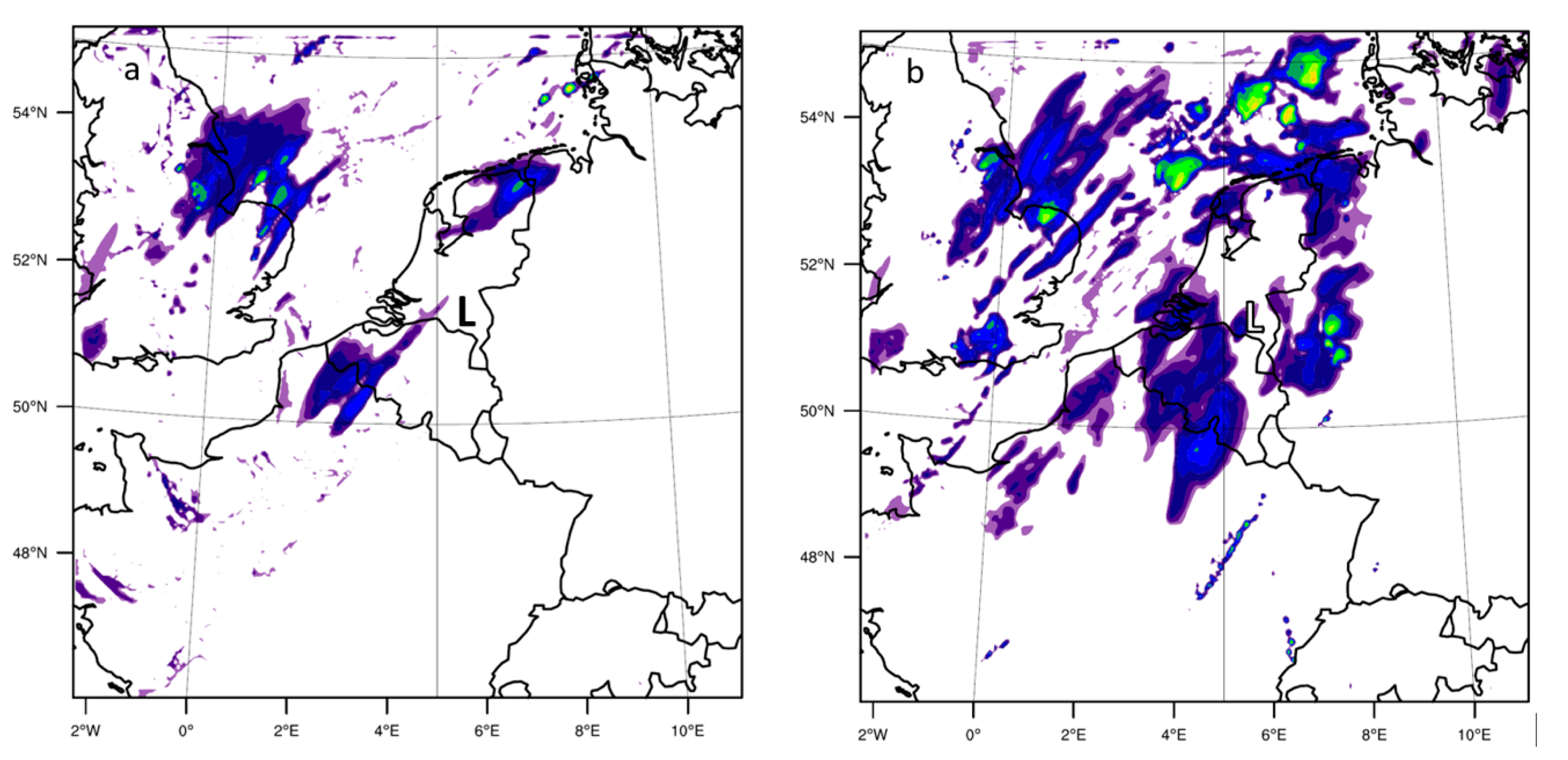
Figure 3 shows the modelled accumulated rainfall over the Netherlands between 23 June 2016 14:00 UTC and 24 June 2016 0:00 UTC of the explicit experiments (
Figure 3d,e) and of the three experiments with CPS (
Figure 3a–c).
Figure 3f depicts the accumulated rainfall from over the same period as observed by the Dutch weather radar product. The zone of intense precipitation under study developed over the northwest of France and the English Channel. Around 16:00 UTC, the convection was strengthened and the system crossed at 17:30 UTC the southern Dutch border. The following 9.5 h precipitation continued over Noord-Brabant. The peak of the storm was at around 18:45 UTC.
The BMJ scheme (
Figure 3b) simulates only maximum precipitation of around 5 mm over Noord-Brabant. The GF scheme (
Figure 3c) forecasts slightly higher maximum accumulated rainfall (≈15 mm), and the KF (
Figure 3a) forecasts even slightly higher amounts of about 25 mm. However, this is still in prominent contrast with the observed precipitation by the radar over southeast Noord-Brabant (65 mm). The explicit run at 4 km resolution has more realistic results (maximum of ≈45 mm), but this is still 20 mm less precipitation than observed (
Figure 3f). The model run with 2 km resolution using the explicit convection improves the forecasts further with a more pronounced line structure in the system from northwest Germany to Noord-Brabant, while at 4 km more isolated showers are found in the simulations (
Figure 3d). Moreover, the 2 km resolution run (
Figure 3e) shows less precipitation over the middle of the Netherlands, which corresponds better to the observations. Comparing the three CPS results we find GF is closest to the results with explicit convection representation, which might be due to the scale-aware properties of the scheme. For all CPS, the parameterised precipitation tendency is higher (1–10 mm h
−1) than the explicit precipitation tendency over the Netherlands. The difference is largest for the KF scheme. The simulations with explicit convection appears to have simulated the strong convection over northwest Germany quite good. The storm over Noord-Brabant is compared to that less well simulated, but still substantially better compared to the three CPS runs.
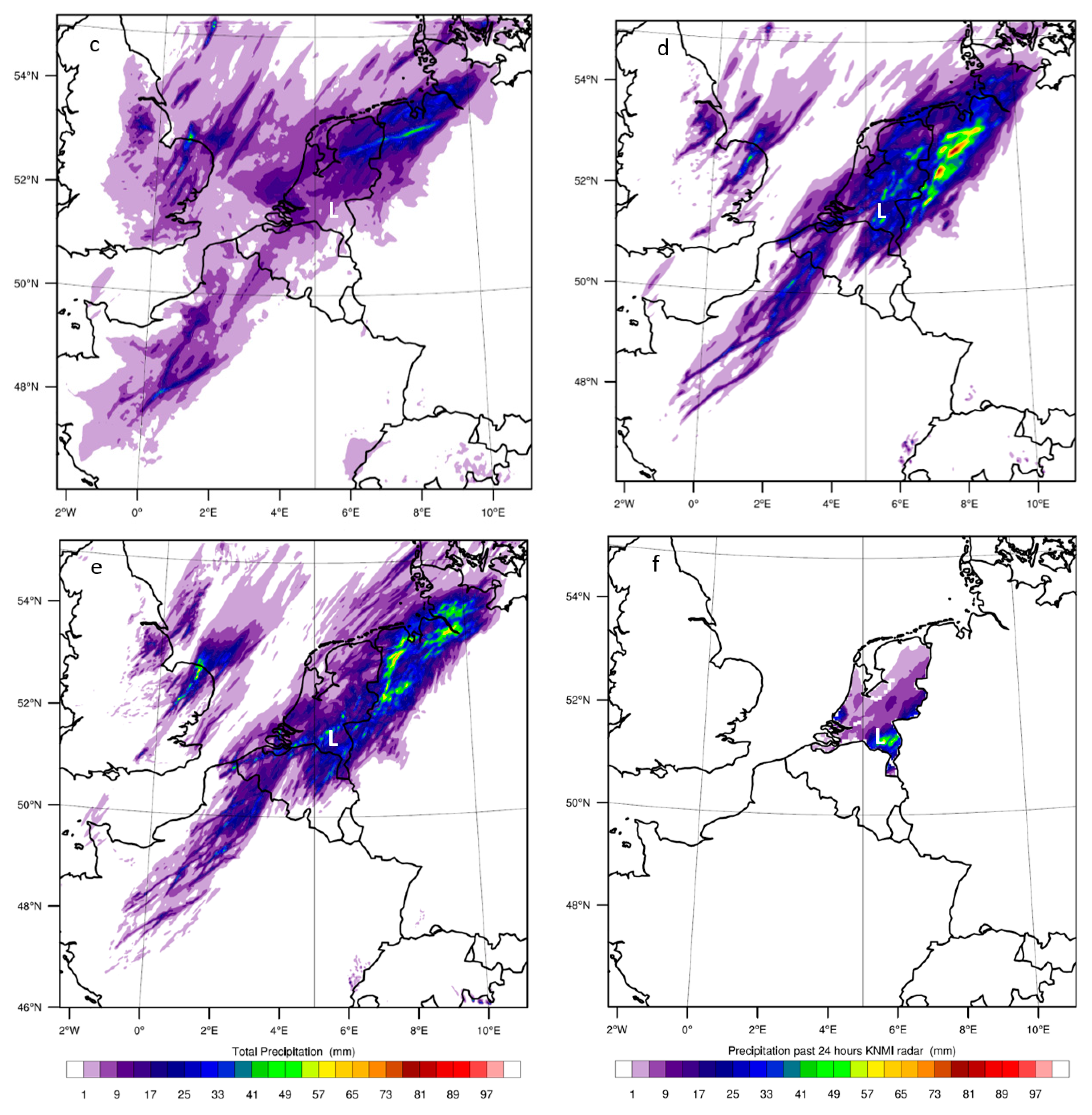
4.2. Maximum Reflectivity
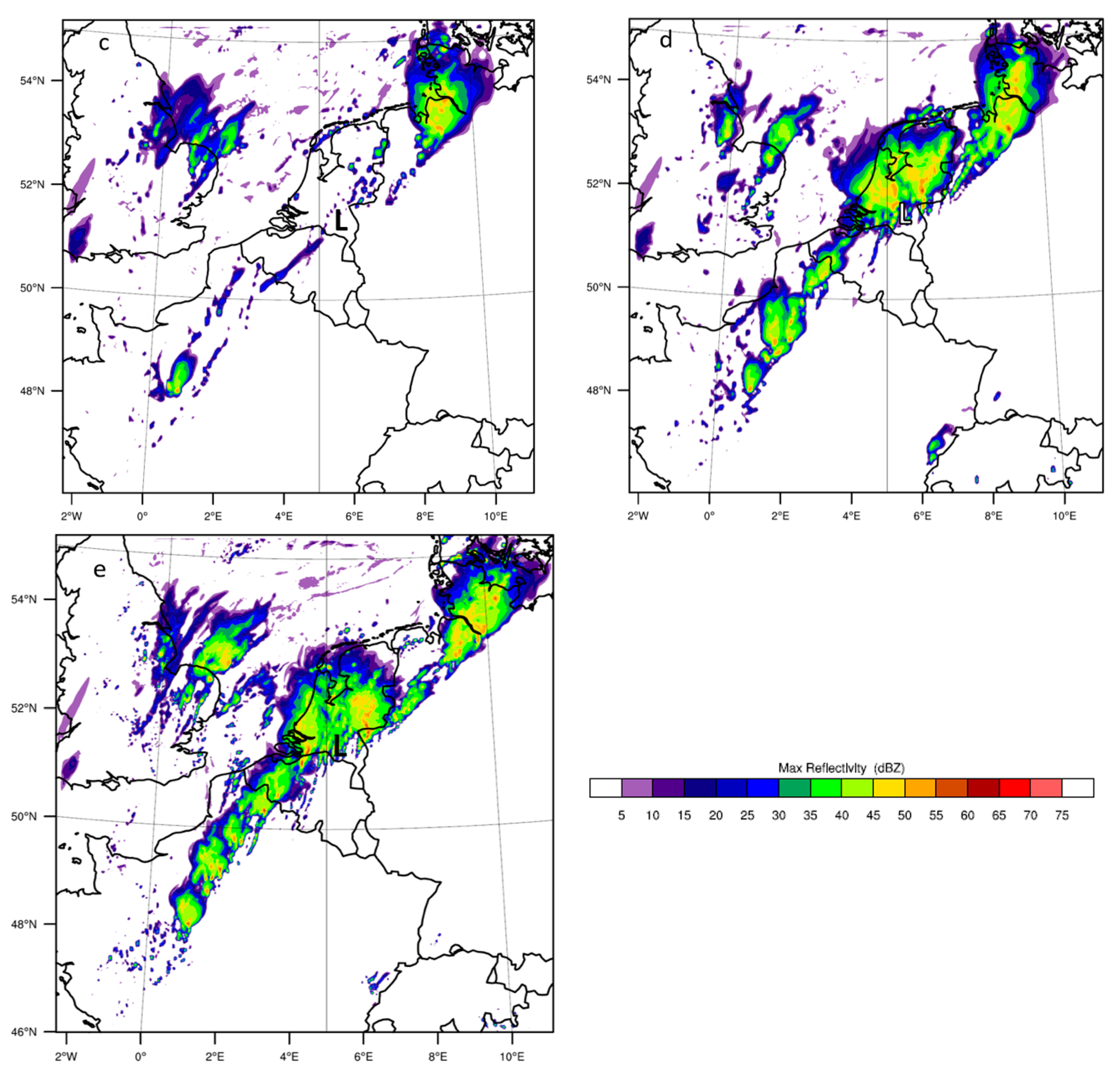
Figure 4 shows the maximum reflectivity (based on the microphysics) on 23 June 2016 at 18:00 UTC as simulated by the model for the four experiments. This quantity is a meaningful indicator for the instantaneous precipitation field. The BMJ (
Figure 4b) fails in simulating any similar structure, spatial distribution and deep convection as observed. The two areas of a max reflectivity of ≈20 dBZ simulated by KF (
Figure 4a) are linked to the two most convective showers in the neighbourhood of the Netherlands. The KF scheme, however, fails to simulate intense convection and any other spatial distribution. The GF scheme simulates some of the north–south structure that has a southwest–northeast direction (
Figure 4c). Above northwest Germany, WRF simulates a system with high maximum reflectivity (≈45 dBZ) that corresponds to the observed shower over northwest Germany. The showers associated with deep clouds over the Netherlands and Belgium are however not visible in the results. The explicit run (
Figure 4d) has the same southwest–northeast orientation as in the GF scheme, but simulates high maximum reflectivity over the whole structure (≈45 dBZ), which indicates strong convective motions. Both the 2 and 4 km run with explicit convection simulates deeper and stronger convection over the southwest–northeast structure than the runs with parameterised convection. In general, the difference between the 2 and 4 km run with explicit convection is rather small. We only find slightly higher reflectivity values with the 2 km run over the North Sea, just northeast of East Anglia. The experiments with explicit convection are the only ones simulating large showers and deep clouds over the Netherlands and Noord-Brabant. All results coincide with the expectations derived from the daily accumulated precipitation results.
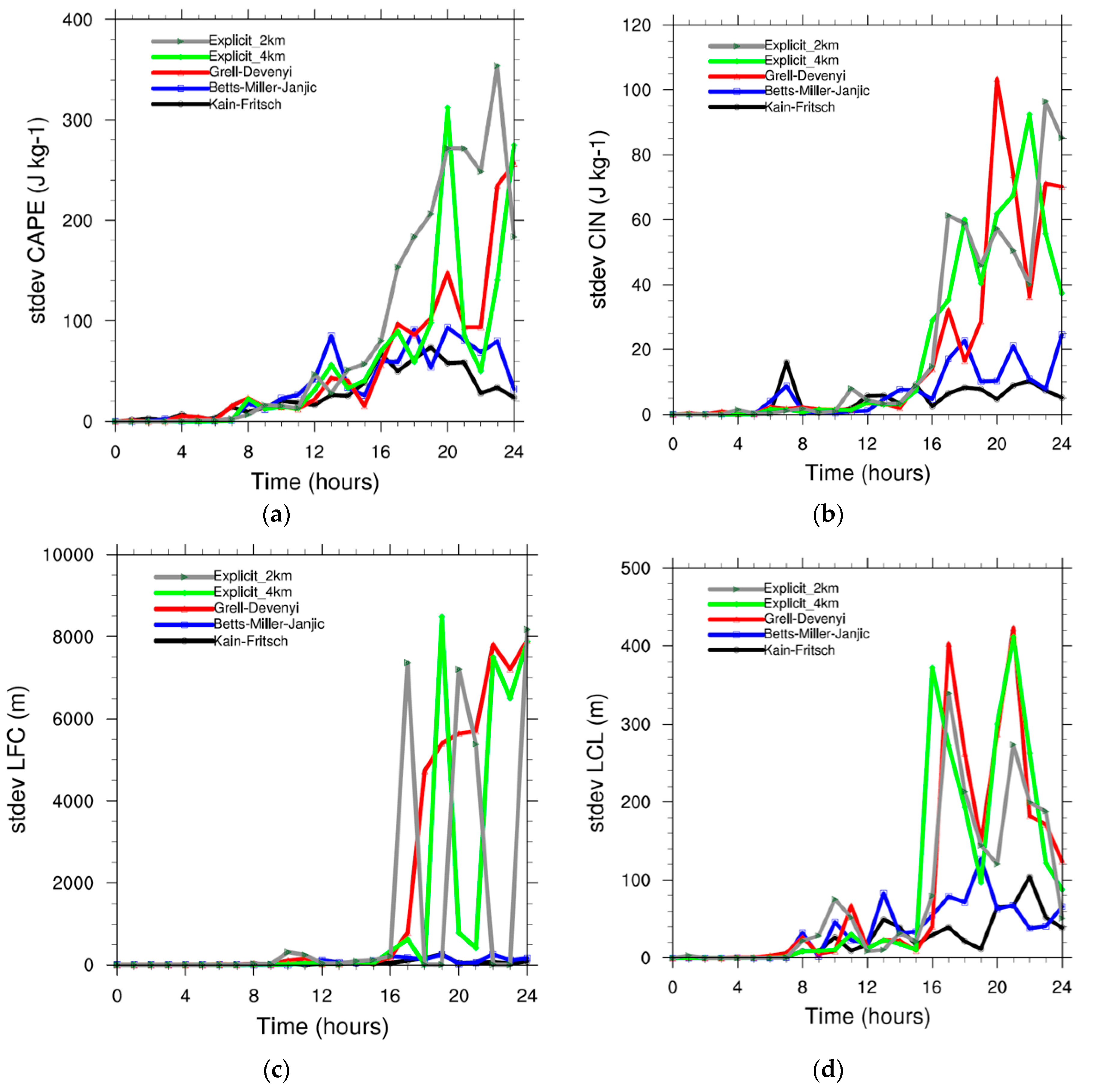
4.3. Evolution of Convection Indicators over Southwest Noord-Brabant
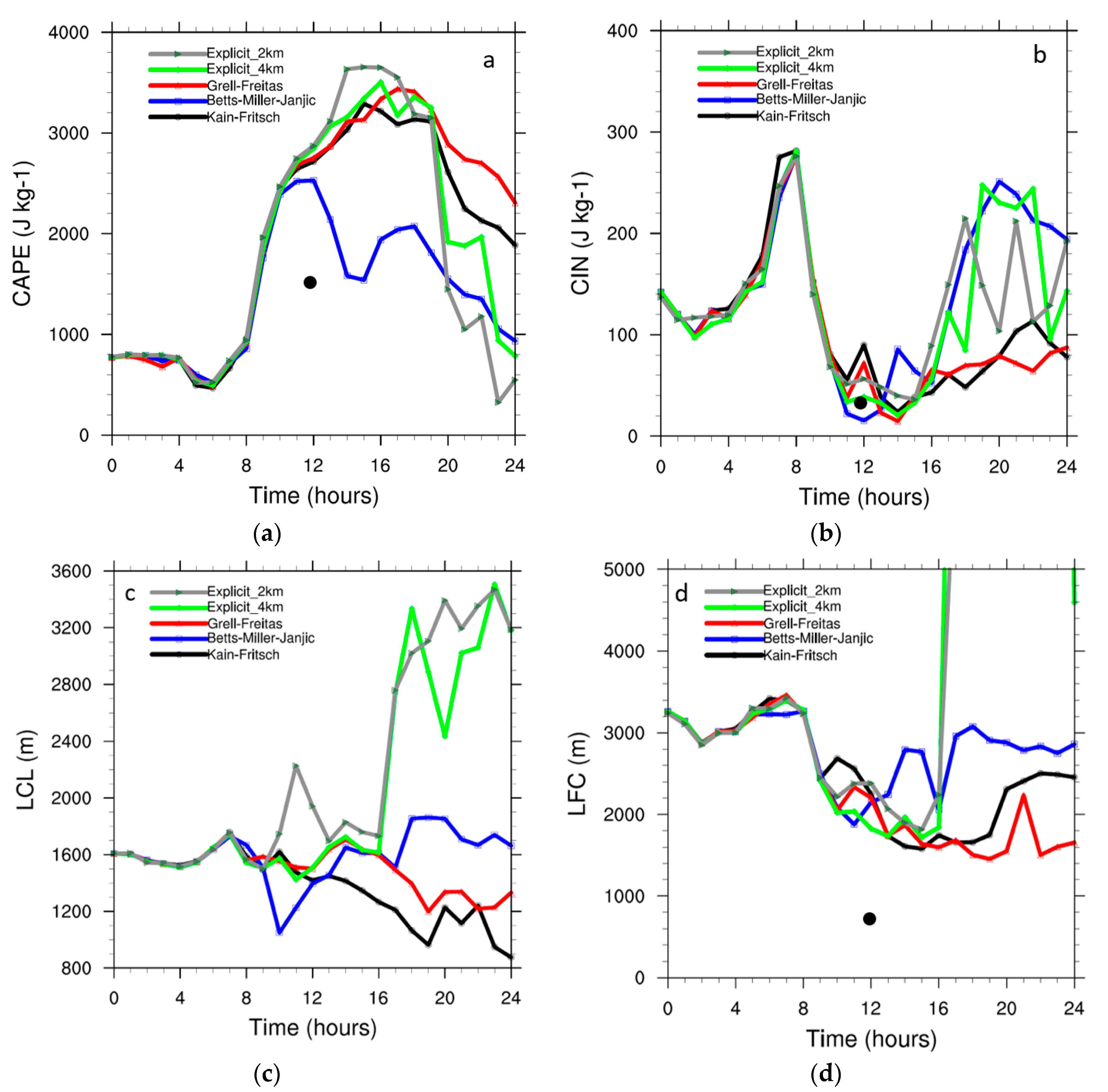
To explain the model results we assess CAPE, CIN and LFC and LCL. When a CPS is activated it will consume instability and therefore CAPE. The modelled CAPE evolution is therefore an indicator of the CPS effectiveness. The maximum CAPE in southeast Noord-Brabant for each experiment is plotted against time (
Figure 5a).
Figure 4b shows the location of southeast Noord-Brabant (L). CAPE values of regular thunderstorms are about 1.10
3 J kg
−1 in the Netherlands. Typical CAPE values for mesoscale convective systems and Spanish Plumes in western Europe are about 2.5.10
3 J kg
−1 [
28]. The maximum CAPE observed for this case was ~3.10
3 J kg
−1 (based on the sounding taken in Essen (Germany) and adjusting the surface temperature and dew point to the observed values in Eindhoven), so this case was (potentially) more unstable than average.
The BMJ is activated very early (around noon) and therefore never reaches CAPE value of 2.5
.10
3 J kg
−1. The results of the daily accumulated rainfall and the maximum reflectivity also show that the scheme fails in simulating strong convection and high precipitation. The BMJ scheme needs relatively high amounts of moisture in low and mid levels [
29]. Also, the scheme does not account for the CIN [
27]. The CIN was relatively high in this situation, so this explains the early triggering compared to the other experiments. Apparently enough moisture was available to activate the scheme, despite the dry air in mid and high levels, or the high CAPE availability triggered the scheme even despite the absence of a relatively deep moisture depth. According to [
27], the BMJ often produces too much precipitation when the reference profile is too dry or the transition to the reference profile is too rapid. The results do not show a relatively high amount of precipitation, thus the scheme did not find the reference profile too dry. A rapid transition to the reference profile can, however, be an additional reason for the lack of deep convection. A final possible explanation considers that reference profiles in the BMJ scheme are fixed based on climatological observations, therefore the unique situation of a system is not fully taken into account. As a result, important vertical structures may be eliminated [
27].
The other two CPSs start to reduce CAPE at the same time as CAPE reduction occurs in the explicit convection runs (18:00 UTC). The CAPE decreases afterwards the slowest with the GF scheme, while KF simulates a steeper decrease, and the runs with explicit convection show the fastest CAPE consumption. The temporal evolution of the consumed CAPE is in agreement with the results of the daily accumulated rainfall and maximum reflectivity over southeast Noord-Brabant as seen before.
The KF scheme is suggested to consume CAPE at a relatively high rate [
27]. High CAPE consumption results in high mass fluxes and therefore high precipitation, which in turn can result in higher downdraft mass fluxes. Higher downdraft mass fluxes can also trigger more convection, which in turn creates more convection [
30]. KF parameterises entrainment and detrainment over the whole vertical profile of a cloud instead of only at the top and the bottom of a cloud as by the GF scheme. This enhances the rate of CAPE consumption in KF compared to GF.
Figure 5 also shows that the two runs with explicitly resolved convection reach higher CAPE values than the runs of this parameterised convection. At the same time, the decrease of the CAPE after the stabilisation of the atmosphere occurs more rapidly than with parameterised convection (particularly compared to GF and KF). As such, the slow stabilisation is a deficiency in the GF and KF schemes, at least for this case study. Note that GF is a scale-aware scheme which means its activity is adjusted with the grid spacing. Later on, we will also evaluate the performance of a recently developed scale-aware version of KF.
Previous results show that the explicit run is best in predicting the storm in location and intensity. [
2] found that when a grid scale is too coarse to properly represent convective development explicitly, often delayed development is seen, though followed by intense convection. The large CAPE consumption could suggest that this statement is true for this case, which we will investigate in
Section 4.4.
Figure 5b indicates that the CIN develops roughly similarly for all experiments, which is expected since the boundary-layer scheme and land-surface scheme will be mostly responsible for governing the atmospheric structure near the surface. After 8:00 UTC, the CIN drops rapidly and reaches values around 40 J kg
−1 around noon, and slowly increases again after 16:00 UTC. Obviously the two runs with explicit convection and the BMJ scheme recover the CIN more substantially than KF and GF. Considering the modelled LCL, we find a clear distinction between the runs with parameterised convection and resolved convection. All runs show an LCL of about 1600 m before the onset of the convective precipitation, while after 18.00 UTC the LCL amounts to 3200 m in the runs with resolved convection while the CPS-based runs all generate an LCL between 800–1600 m. As such, the resolved convection runs reduce the instability more rigorously, which is consistent with the high CIN and LFC values in the resolved convection run after the event.
4.4. Accumulated Precipitation over Time over Southeast Noord-Brabant
To validate the explicit results and research the possible delay mentioned by [
2],
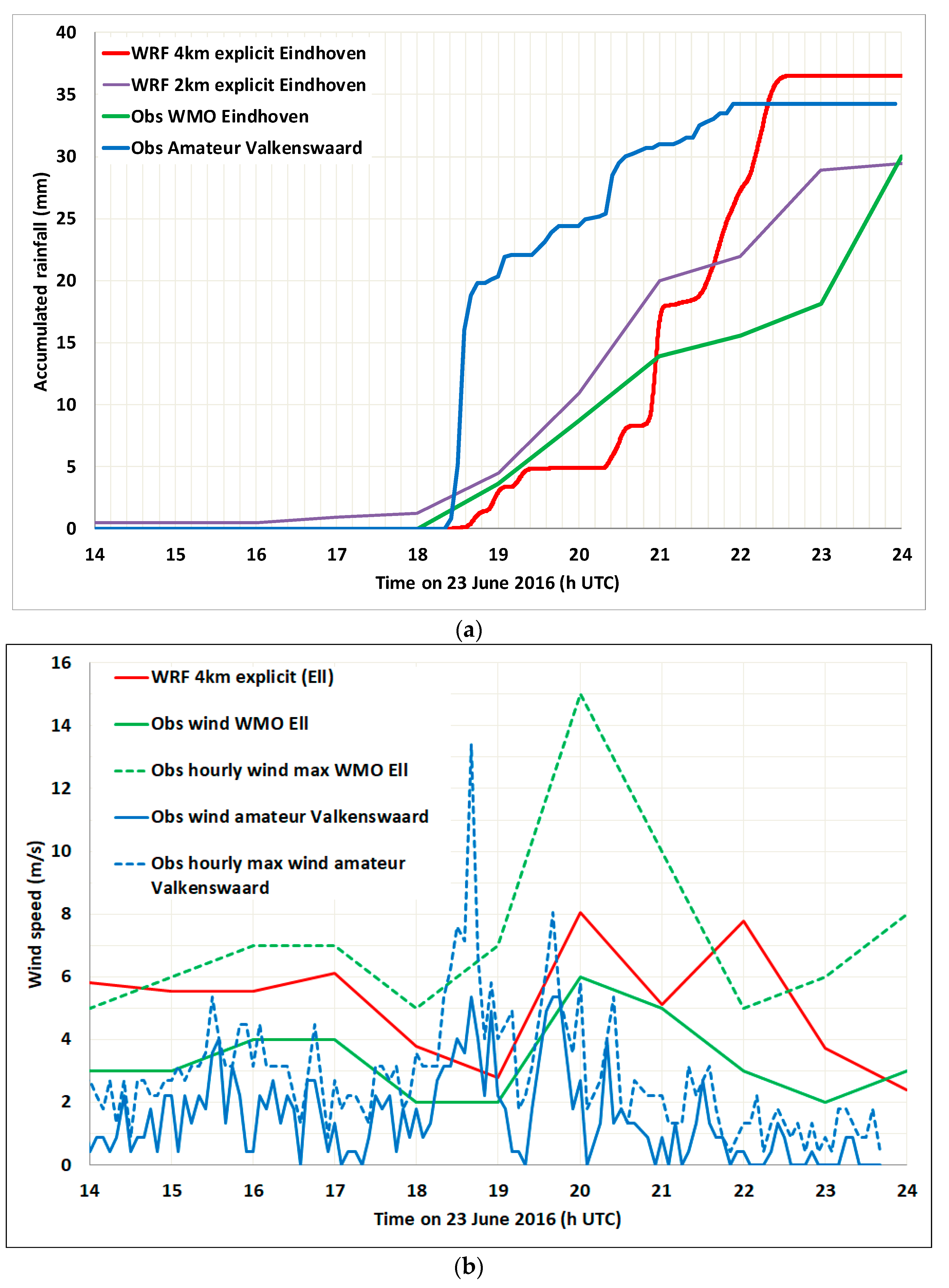
Figure 6 shows the explicit accumulated rainfall with weather observations from 12:00 UTC till 00:00 UTC over a location in southeast Noord-Brabant. The observations from weather station Eindhoven is hourly averaged, the data from WU amateur weather station in Valkenswaard have a 5-min interval.
Compared with the observations, the 4-km explicit run has a delay of about an hour. It first simulates less precipitation and then (at 21:00 UTC) a steeper increase in precipitation till accumulated precipitation values of 37 mm more. The onset of the simulated rainfall compared to the WU observations is nearly the same (18:30 UTC). The observations show a very intense precipitation in only a few minutes with afterwards a trend of about 5 mmh−1 till it stays constant at 22:00 UTC. The 4-km explicit experiment simulates first low amounts of precipitation and only a steep increase at 21:00 UTC, which continues till 22:30 UTC. Final accumulated rainfall amounts are 2 mm more than observed. There is thus a delay in precipitation for the 4-km explicit run with high precipitation rate from 21:00–22:30 UTC. This may suggest that the current grid scale is too coarse to properly represent convective development explicitly. The 2-km explicit run starts with a very low-intensity precipitation at 16:00 UTC, but increases intensity at Eindhoven station from 18:00 UTC and throughout the evening follows reasonably well the observations. The 2-km run gives a slightly (8 mm) less accumulated precipitation than the 4-km explicit convection run.
4.5. Wind Speed Evolution over Southwest Noord-Brabant
Additionally, we evaluate the model results for wind speed.
Figure 6b shows the wind speed over the southeast area of Noord-Brabant. The wind speed observations station in Ell are hourly and rounded off to whole values. The WU observations have a 5 min interval. In dotted lines, the maximum wind speed observations are given.
Comparing the KNMI and WU observations, the trend of the wind speed over time is very similar. However, the WU wind speed observations are slightly lower (on average ≈2 m s−1). The difference between maximum wind speed is much higher (on average ≈5 m s−1). The results for wind speed using the explicit convection show a very similar trend. However, on average they simulate higher wind speeds over time (0–7.5 m s−1). The peak intensity of the storm was at 18:45 UTC. The storm also included downbursts and wind gusts. Both observations and the WRF model results indicate a rapid increase in wind speed with high maximum values (KNMI 15 m s−1; Amateur 13.7 m s−1; WRF_4km 9.6 m s−1; WRF_2km = 8.4 m s−1) just before 19:00 UTC. The peak in wind speed intensity is associated with the storm. The 4-km explicit experiment simulated a steep increase of precipitation between 21:00–22.30 UTC, but no obvious increase in wind speed is found. At that time the wind speed stays almost constant whereas the observations show a decrease. The explicitly calculated wind speed does not show a distinct delay or relatively higher wind speed intensity compared to the observations.
4.6. Impact Soil Moisture Variability
Figure 7 shows the model results addressing the spatial variability of soil moisture in order to study whether the different convection schemes scale this variability in soil moisture up to variability in convective activity in a different manner. Here, the variability is expressed as the standard deviation over the 10 members in an area of 76 × 112 km around Luyksgestel (
Figure 1). Note that for each of the convection schemes, the 10 members are generated with the same soil moisture fields, which are simply generated by redistributing the existing soil moisture values over land through the model domain. We find clearly an increase in variability in time, but substantial differences in variability occurs between schemes. Concerning CAPE and CIN we find that the KF and BMJ schemes generate a rather small standard deviation compared to the other schemes (
Figure 7a,b). The explicit schemes generate the highest variability, which is reasonably well followed by the GF scheme. As such, we may say that GF behaves in best agreement with the results of resolved convection, which might be explained by the scale-awareness of the scheme. Considering the LFC and the LCL, we find a similar grouping of schemes, where explicit convection and GF create high LFC and LCL variability, while LFC and LCL are more smooth in BMJ and KF, and therefore appear not to be effective in upscaling uncertainties in soil moisture. However, the signal is more noisy from time step to time step. In general, we conclude that the soil-moisture induced model uncertainty provides the widest variability using the resolved convection approach.
5. Discussion
In this section we discuss the modelling results and put them in perspective of the results by earlier studies. We find the convection schemes have their peculiarities concerning the representation of this convective event. Here we explore the role of the convection scheme in a grid spacing around the grey zone. In general, grid spacings between 1–4 km might be “convection-permitting” though still requires a convection parameterisation to remove instability or to produce the correct rainfall amount [
31]. On the other hand, practical modelling has shown for 1–4 km turning off the convection parameterisation, though theoretically problematic, usually performs better than a parameterised model at various scales (e.g. [
32,
33]). This actually illustrates that most convection schemes cannot behave reasonably under the grey-zone resolution (1–10 km). Hence, turning the convection scheme off is a practical choice.
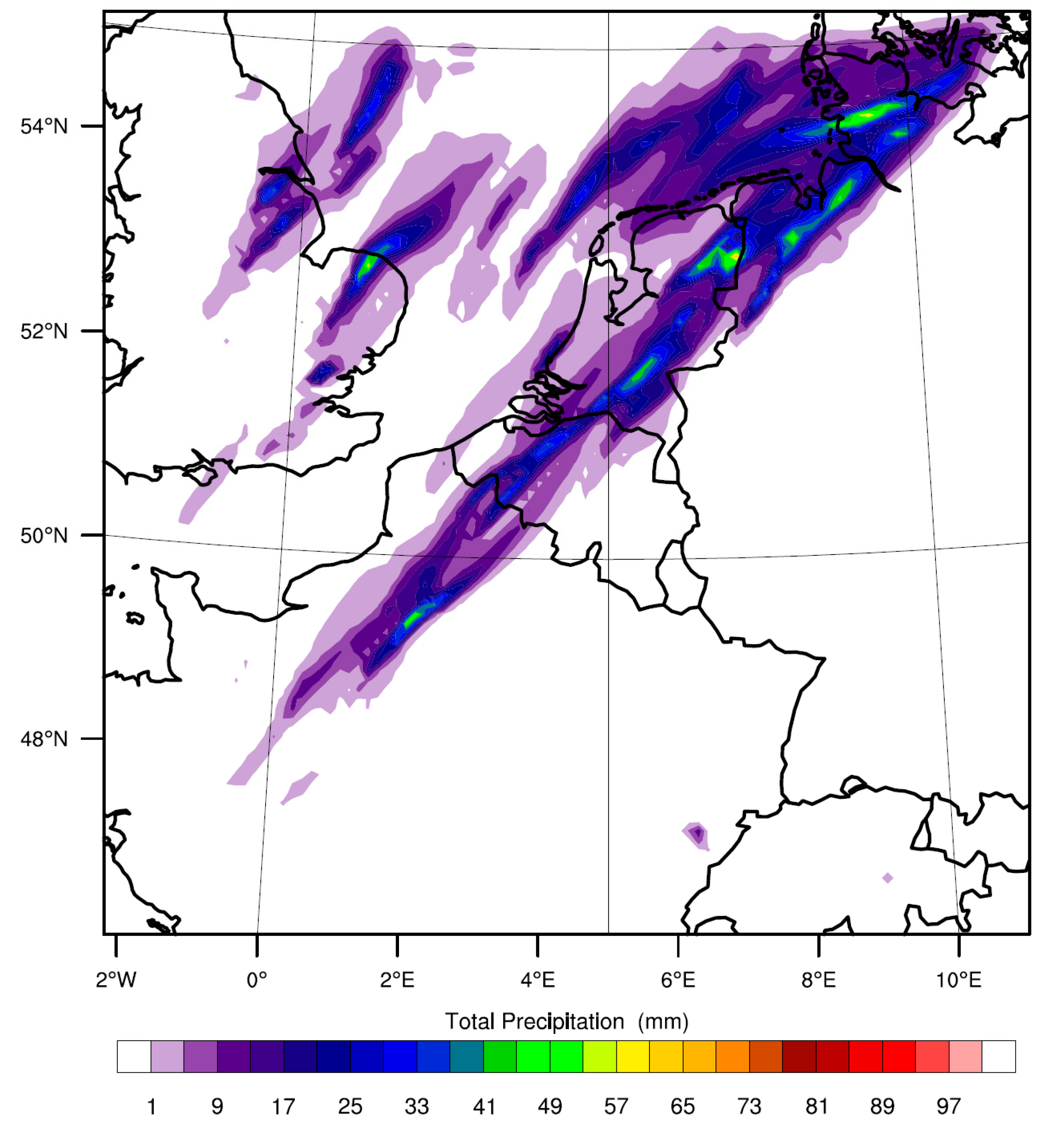
To further illustrate the impact of spatial model grid spacing on the degree whether the model simulation is convection-permitting, we performed a model run at 10 km resolution without a convection scheme (
Figure 8). Although the modelled precipitation is well aligned from southwest–northeast, with a maximum in the province of North Brabant and in northwest Germany, we find, as expected, a rather limited amount of accumulated precipitation (≈40 mm). This finding supports the need of a CPS at such coarse resolution.
We find the resolved convection better represents the evolution of the life cycle of the thunderstorm under study, in terms of more sharply timed CAPE growth and decay compares to CPS application. The study by [
15] finds corresponding results that BMJ develops the least intense storm. Also, in their case, the 2-km and 4-km simulations without CPS produces the most intense storms. It appears that the convection in their 2-km run is slightly weaker than in the 4-km runs. This also occurs in our simulation where the radar reflectivity and the accumulated precipitation over northwest Germany is smaller in the 2-km run than in the 4-km run. Moreover, the superior performance of the GF scheme over BMJ and KF is confirmed for a case study in Northern Thailand [
34]. Moreover, [
17] also found that GF outperforms the other CPS in their case over Cuba. They also state that no added value of the GF scheme is seen for a resolution of 1 km. In our study we find GF results are closest to the explicit convection, likely due to the scale-aware nature of the scheme, though the explicit results are still substantially different from GF, and as such GF is not a perfect replacement for resolved convection. For a case study of an extreme precipitation event, [
35] confirm deficiencies using the KF scheme, i.e., a relatively small heavy rainfall area, smaller maximum precipitation rate, wider area of weak precipitation. They report that simulations without CPS have some negative effects in their case such as the overprediction of area-averaged precipitation rate. [
36] compared the performance of the KF parameterisation, with a simulation using explicitly resolved deep convection. They find that the model is capable of reproducing the number of observed precipitation episodes, but the performance decreases with the forecast range and rainfall intensity. The KF scheme significantly overestimates the surface area with rainfall when compared to the simulations with deep convection explicitly resolved. This is confirmed by the current study (
Figure 3a,d). [
36] also report that none of their test model settings were able to resolve a highly local episode of an intensive rainfall event.
In addition, [
37] compared the WRF skill for three different spatial resolutions, with and without CPS. In their case, finer grid spacing and no CPS improved the spatial distribution and improved the monthly precipitation compared to coarse resolution. They also found that runs with CPS tends to predict more continuous weak precipitation due to the excessive CAPE release and thus relatively weak precipitation intensity compared to experiments with resolved convection. Furthermore, [
38] evaluated the WRF model performance for parameterised and explicitly resolved convection at 4 km, in their case for the Ural. They found that runs with explicitly resolved convection outperformed runs with any parameterisation scheme. On the other hand, they also report that even with explicit convection, 9 of their 23 cases are not satisfactorily forecast, mainly due to errors in timing and position of the mesoscale convective system. Their findings are thus in agreement with our findings for the current case.
We wish to remark that the current study utilises 6-h update intervals for the boundary conditions. A rather more short time step is preferable when boundary conditions are available at that frequency. Here we preferred to take advantage of the relatively high quality of the European Centre for Medium-Range Weather Forecasts (ECMWF) operational analysis instead of fields from a free forecast available at a relatively high output frequency.
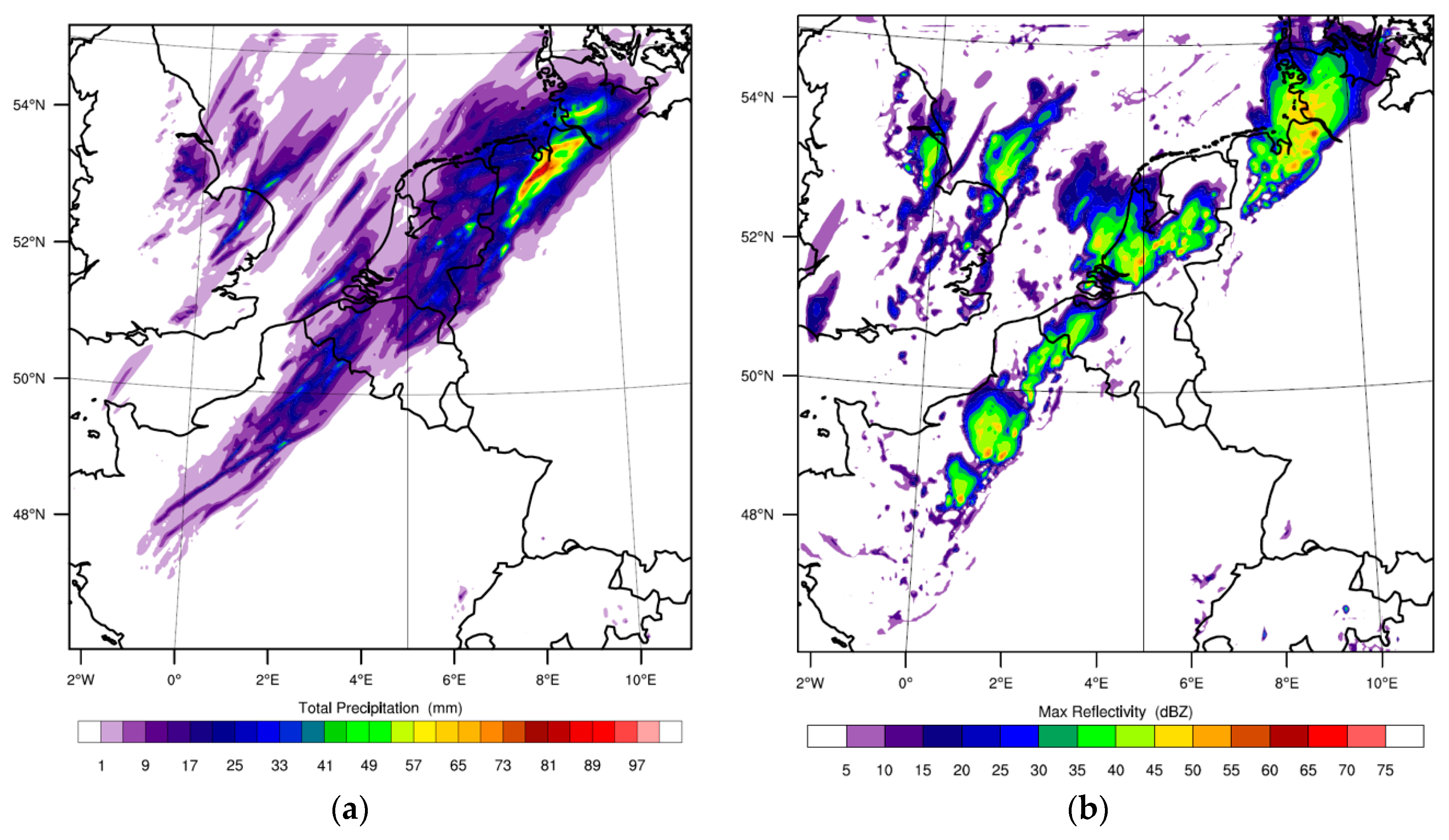
Finally, in this study we discussed purely the difference in model behaviour between convection schemes. In the recent years, also a scale-aware approach of the KF scheme has been developed. For the case under study,
Figure 9 shows the model results for the scale-aware version of the Kain–Fritsch scheme as an illustration [
39] We find that the results of this experiment are substantially different from the reference KF scheme shown in
Figure 3a. The scale-aware KF version shows an accumulated precipitation that is more closely organised and especially the accumulated precipitation in northwest Germany reflects similarities with the 2-km and 4-km explicit runs (
Figure 9a) with values around 80 mm, while the reference KF scheme hardly produces intense precipitation in that region (
Figure 3a). Also, the modelled pseudo radar reflectivity with the scale-aware KF version compares well with the explicit simulations despite that the latter have a more intense signal in the middle of the Netherlands compared to the scale-ware KF scheme. Interestingly the accumulated precipitation with the scale-aware KF scheme (
Figure 9) is substantially higher than with the scale-aware GF scheme (
Figure 3c). This contradicts with findings by [
40] where both schemes showed comparable performance (their
Figure 5). Possibly the GF scheme performs better with more sophisticated microphysics than utilised here. On the other hand, [
40] reported limited sensitivity to the selected microphysics scheme. An additional simulation with the more sophisticated WSM6 microphysics scheme for the current case revealed limited difference with the original simulation using WSM3 (not shown). Overall, we conclude that at least for KF, utilising the scale-aware version is a suitable alternative. Also, [
41] performed 4-km simulations for the Colorado Front Range using six different CPSs and found large sensitivity with respect to the amount of precipitation. For their case study they found the multiscale KF is more scale aware and less prone to overactivity. They conclude that model skill may be acutely lost when employing a CPS that has not been adapted to be scale-aware. Our results confirm that the scale aware KF scheme outperforms the simulations with traditional CPS and the spatial structure of the results come very close to the convection permitting simulations (WRF_2km).
6. Conclusions
This study analyses an extreme weather event in the southern province Noord-Brabant in the Netherlands on 23 June 2016, when a hail storm was responsible for severe damage to buildings and crops. The representation of deep convection in NWP models is challenging, and it is difficult to know the role convection schemes play when NWP models run at resolutions in the grey zone (1–4 km). For this case we compare the WRF model performance for simulations applying explicit convection and parameterised convection at 4 km grid spacing. Also, we discuss the role of scale-aware convection parameterisations. Five experiments with the following cumulus parameterisation schemes (CPS) were conducted with WRF at a grid spacing of 4 km: 1. Betts–Miller–Janjic scheme; 2. Grell–Freitas ensemble (scale-aware) scheme; 3. Kain–Fritsch scheme; 4. No CPS (explicit) at both 2 km and 4 km grid spacing.
We conclude that the explicit runs were reproducing a similar extreme weather event over Noord-Brabant as was observed, and generates active convection over northwest Germany as well. The Betts–Miller–Janjic scheme failed in reproducing a strong convective system because the scheme was activated too early, resulting in a too early consumption of the instability. The Grell–Freitas scheme and Kain–Fritsch scheme were activated at the correct moment, but they were not able to produce similar deep convection at the correct location. However, the scale-aware Grell–Freitas scheme was able to reproduce showers over northwest Germany and as such the GF results are closest to the explicit convection experiment. The Kain–Fritsch scheme predicted a convective system over Noord-Brabant, though with a much lower intensity than was observed. Interestingly, additional simulations with a scale-aware version of the Kain–Fritsch scheme reflected the results of the explicit runs rather well, with high precipitation amounts in northwest Germany, and even more than the scale-aware GF scheme. We conclude that utilising scale-aware parameterisation schemes are to some extent beneficial for the representation of deep convection in the grey zone.
In addition, we studied whether uncertainty in spatial distribution of the soil moisture is scaled up differently by the convection schemes and the explicit convection schemes. For this case, the Betts–Miller–Janjic and Kain–Fritsch schemes show a much smaller variability in CAPE, CIN, LCL and LFC than the other modelling approaches. Interestingly we find that the variability generated by the scale-aware GF scheme behaves most closely to the explicit convection experiments.