Trends of UV Radiation in Antarctica
Abstract
1. Introduction
2. Materials and Methods
2.1. Network Sites
2.2. Instrumentation
2.3. Calibration of the SUV-100 Spectroradiometer
2.4. Calibration Traceability and History
2.5. Review of Calibrations
- At the South Pole, the SoSI of two traveling standards (lamps 200WN004 and 200WN014) used at this site and the two long-term standards (lamps 200WN005 and 200WN006) kept on station disagreed by 0.5% to 1.9%, between 2014 and 2018. This discrepancy was long not understood, because all four lamps were calibrated against the primary lamp F-616 at around the same time. Solar data were published based on the assumption that the SoSI of the traveling standards is correct. Review of all available information suggests that this assumption is questionable and that the SoSI of the long-term standards was more likely correct. Therefore, solar data should be scaled upward between 0.5% and 1.9%. In addition, discrepancies between the SoSI of traveling and working standards between 2007 and 2011 ranged between 0.7% and 0.8%, and the solar data should be corrected accordingly.
- For the 2009/2010 period at Arrival Heights, the SoSI of the traveling standard 200W017 and the long-term standard 200W011 disagreed by 1.9%. Solar data were published based on the assumption that the SoSI of the traveling standards is correct, while in hindsight, the SoSI of the long-term standard appears to be more accurate. Solar data should be scaled upward by 1.9%.
- The documentation associated with data recorded before 2000 is incomplete and hampered our ability to assess the accuracy of calibrations performed between 1996 and 1999.
2.6. Detection of Drifts in Calibration using Radiative Transfer Modeling
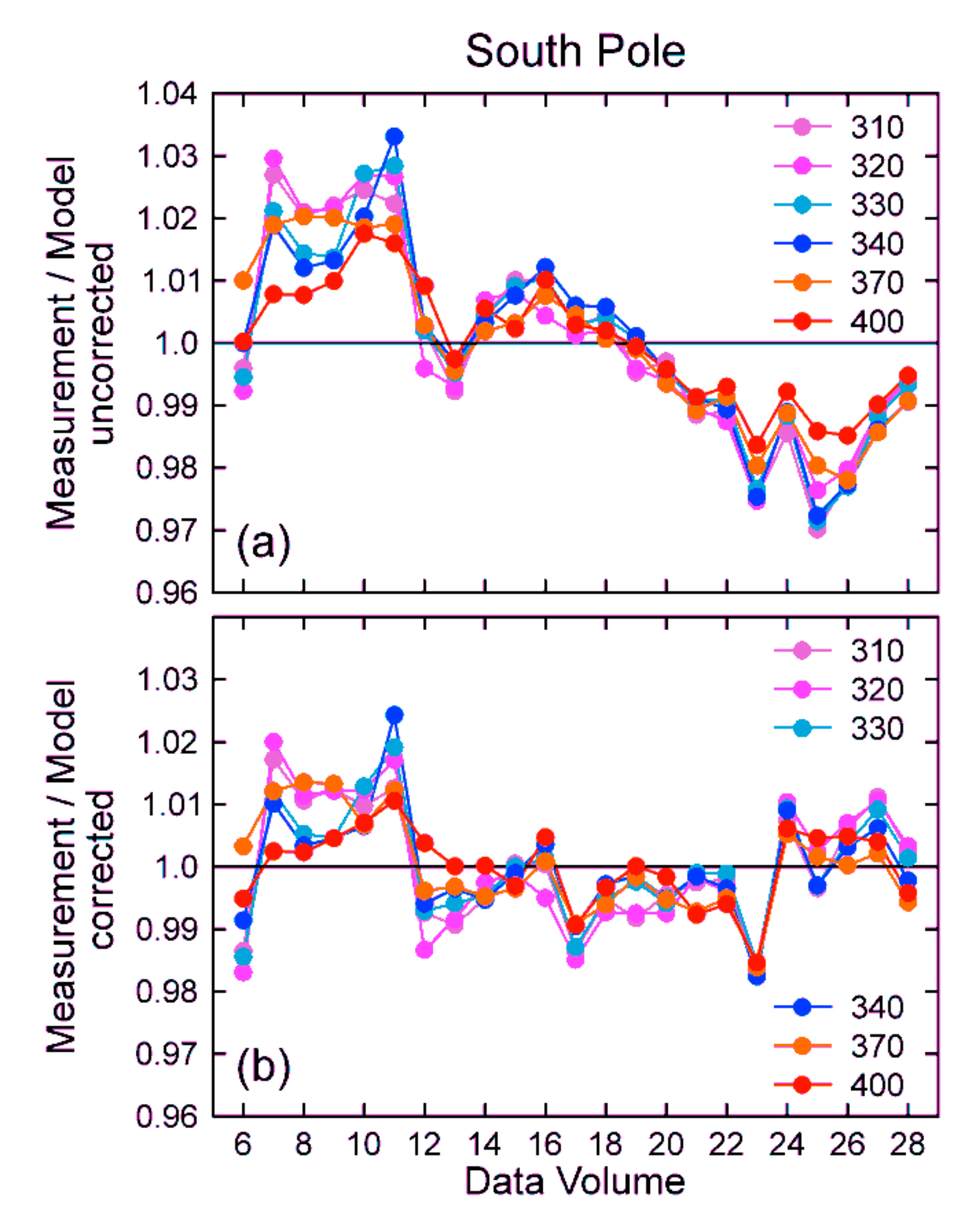
2.6.1. South Pole
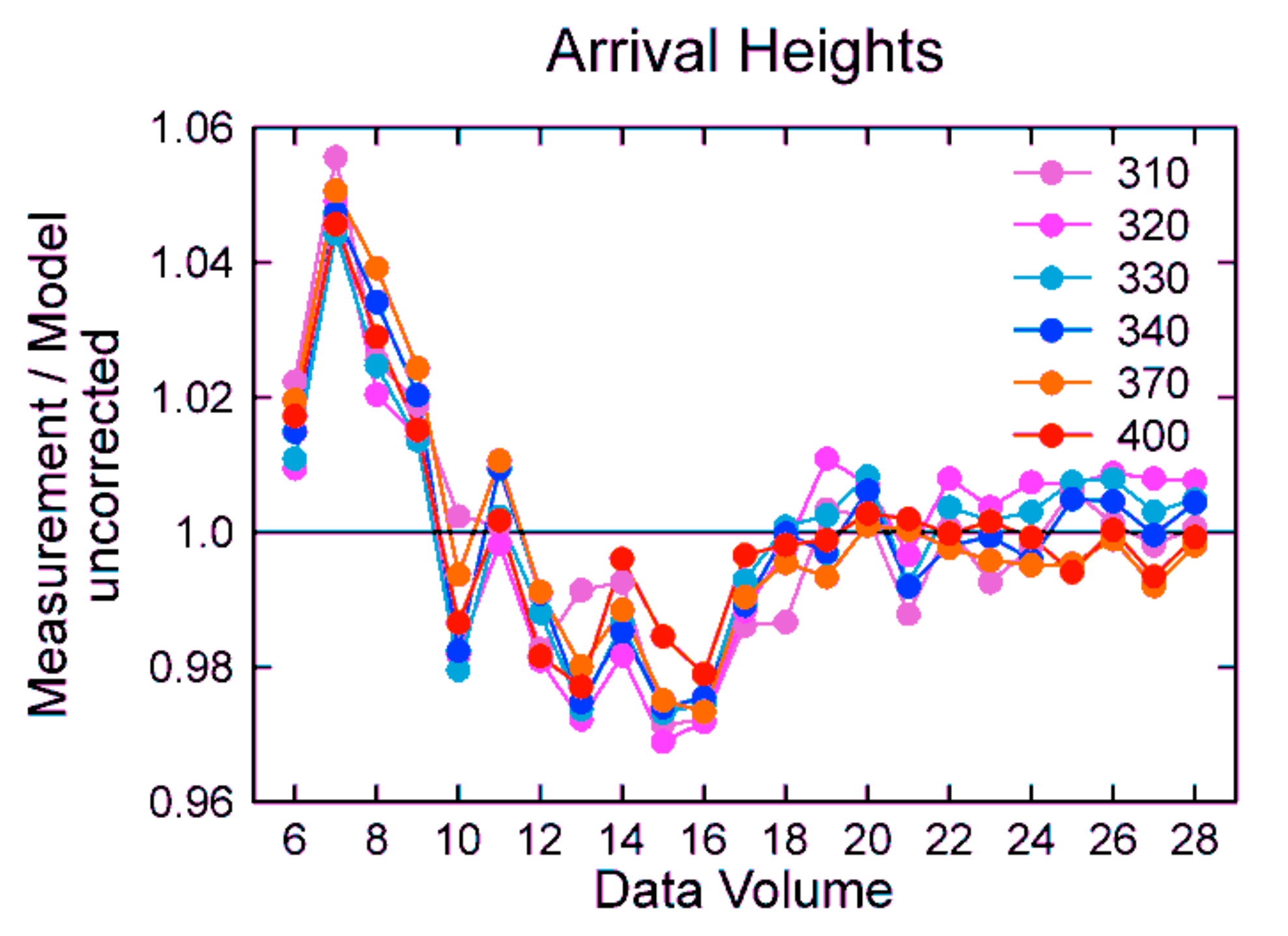
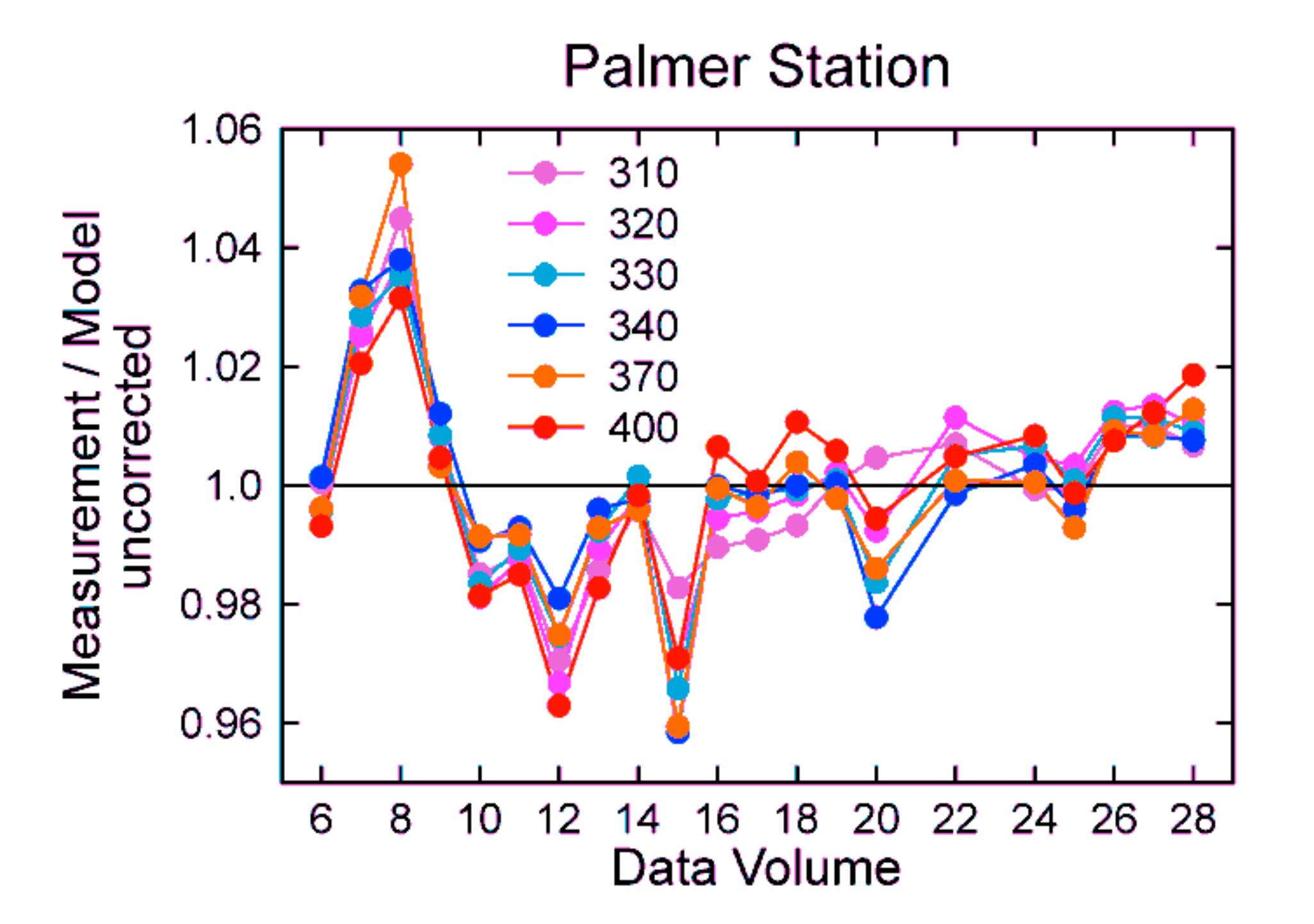
- Normalized median ratios vary by ±2.0% between Volumes 6 and 16 with no obvious trend. Between Volumes 16 and 26, the ratios decrease systematically by about 3%.
- Median ratios for wavelengths that are either affected by ozone (310, 320, 330 nm) or not affected by ozone (340, 370, 400 nm) generally agree to within ±0.5%. This suggests that TOCs were consistently calculated from the measurements over the period under consideration.
2.6.2. Arrival Heights
2.6.3. Palmer Station
2.6.4. Effect of Diffuser Upgrade
2.7. Method of Trend Analysis
3. Results of Trend Analysis
3.1. Trends at the South Pole
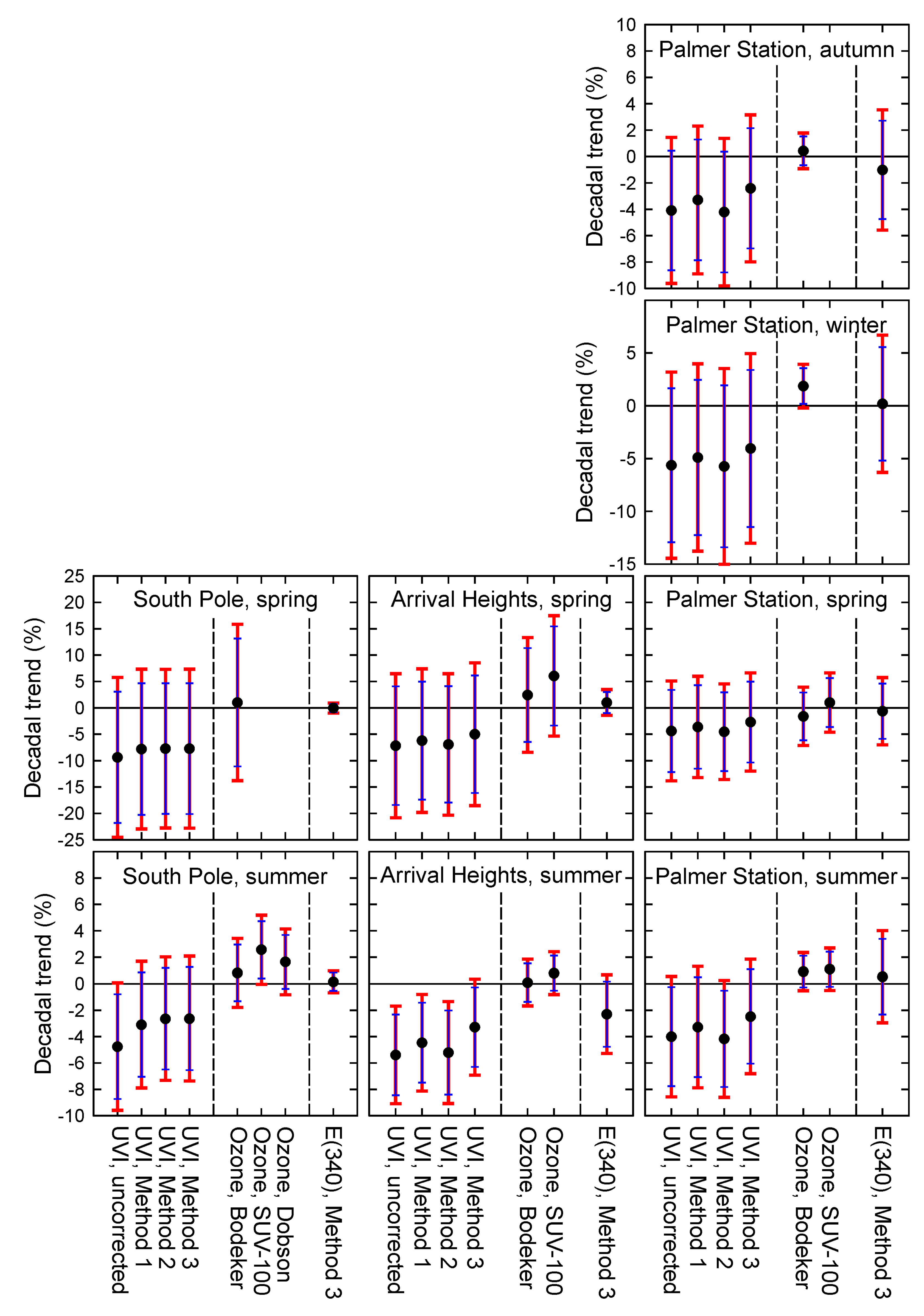
- Significant trends in UVI exist in January and February. For January, decadal trends in UVI calculated from the datasets and corrected with Method 1, 2, and 3 are −4.1%, −3.9%, and −3.9%, respectively, and are significant at 95%. Trends in UVI for February are slightly smaller than those for January but also significant at 95%.
- Trends in TOC calculated from the SUV-100 and Dobson datasets are 3.1% and 2.8% per decade for January, respectively, and are significant at 95%. In contrast, ozone trends calculated from the Bodeker dataset are considerably smaller and significant only at 90%.
- Trends in E(340) range between −1.1% and 0.8% per decade (trends for spring and summer are 0.0% and 0.2%, respectively), and they are not significant. This confirms that there is no evidence for a change in albedo or cloud cover at the South Pole.
- Trends in TOC and UVI for January and February are opposite in sign and of similar magnitude, while there is no trend at 340 nm. This suggests that these negative UVI trends are predominantly caused by positive trends in ozone.
- Trends in UVI calculated with the three correction methods are very consistent; the maximum difference is 0.5% per decade for summer. The difference between UVI trends calculated with the uncorrected and corrected (Method 3) ranges between −1.6% and −2.1% per decade, with an average of −1.7%.
- Uncertainties of trends in ozone for the three datasets are almost identical, suggesting that these uncertainties are caused by actual year-to-year variability in ozone.
3.2. Trends at Arrival Heights
- Estimates of UVI trends are negative for all months and seasons. The trend in UVI for summer calculated from data corrected with Method 3 is −3.3% per decade and significant at 90%.
- The decadal trend in TOC calculated from SUV-100 data is 1.5% for January and significant at 90%. Trends calculated from the Bodeker dataset are generally not significant and are generally smaller than those calculated from SUV-100 data.
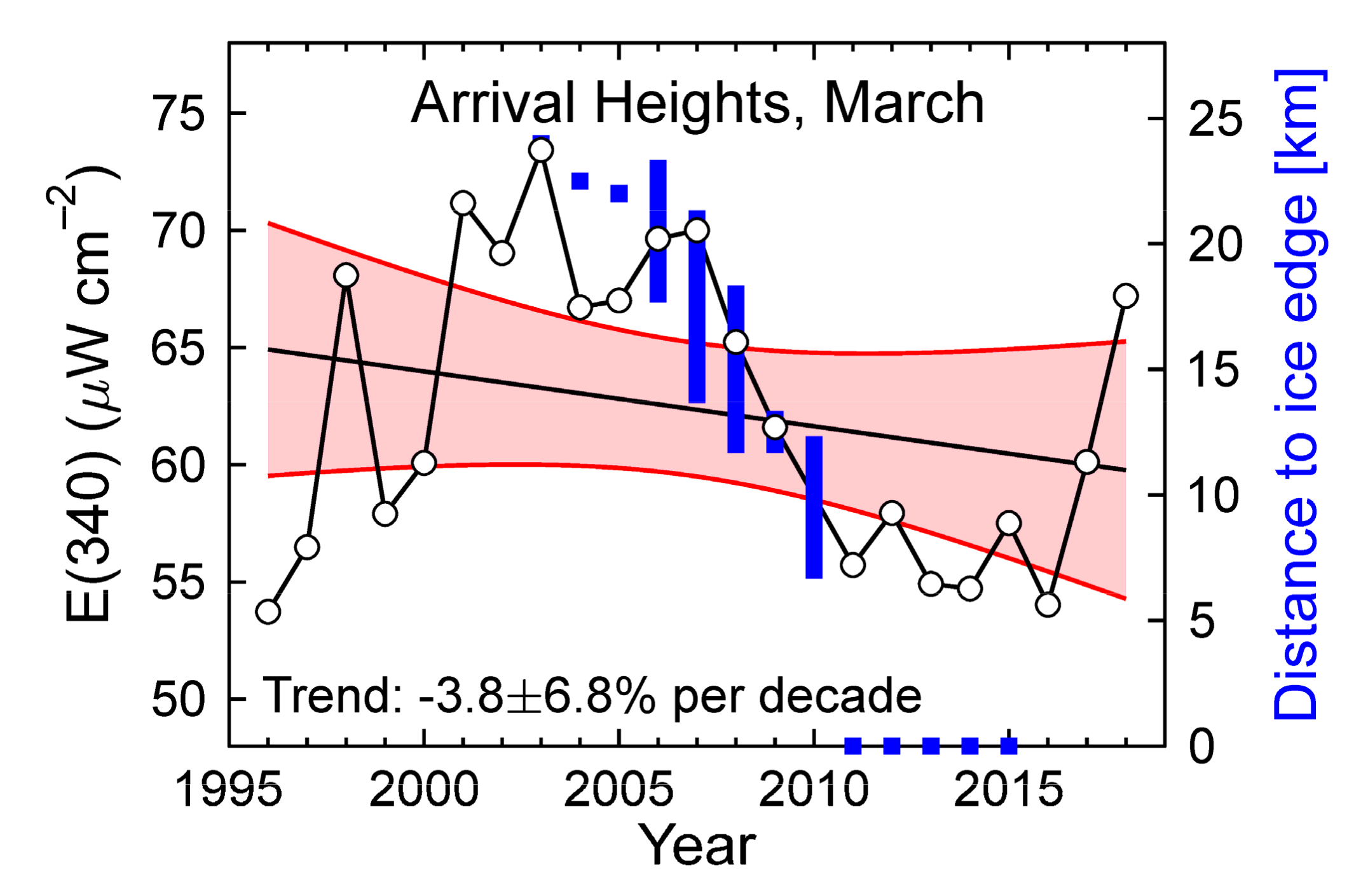
- The irradiance at 340 nm, E(340), changes by −4.7% per decade in February and −2.3% in summer. The trend for February is almost significant at the 90% level. These changes are likely caused by variations in sea ice conditions (Section 4).
- The difference between UVI trends calculated with the uncorrected and corrected (Method 3) datasets ranges between −1.8% and −2.3% per decade, with an average of −2.1%.
3.3. Trends at Palmer Station
- UVI trends calculated from the corrected datasets are generally not significant, with the exception of June, where significant trends in UVI, TOC, and E(340) are observed. These trends have little importance, as the Sun is barely (<3°) above the horizon in this month.
- There is a good agreement between Bodeker and SUV-100 ozone trends and their uncertainty.
- The difference between UVI trends calculated with the uncorrected and corrected (Method 3) datasets ranges between –1.5% and –1.9% per decade, with an average of −1.6%
4. Discussion
- Since the TOC was unusually large in the spring of 2019, trends in TOC calculated for the longer period are generally larger than for the period considered by McKenzie et al. [14]. At the South Pole, the largest difference is observed for October: according to ozone data from the SUV-100, best estimates of decadal TOC trends increased from 4.4% to 8.8% when October 2019 was included. At Arrival Heights, the largest increase (from 4.2% to 9.5%) occurred in September. Despite these large changes, trends in ozone did not become significant for any month between September and December.
- As expected from the increasing trends in ozone, trends in UVI at the South Pole generally become more negative when including data from the 2019/2020 season. The largest change (from −3.2% to −6.7%) was calculated for October. At Arrival Heights, trends became more negative for September, October, November, March, and April; the largest change (from −6.3% to −9.6%) was observed for September. Trends for months between September and December did not become significant, confirming that one year with a small ozone hole is not sufficient to overcome the large year-to-year variability in ozone.
- At Arrival Heights, trends in UVI for December and January become more positive when data from the 2018/2019 and 2019/2020 seasons are included, despite trends in ozone becoming more positive also for these months. Positive changes in UVI trends coincide with similar positive changes in E(340). This may suggest that the surface albedo in the two seasons was above average. However, a test of this hypothesis would require sea ice data and other ancillary information, which is not yet available.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Traceability of Calibration Standards
Appendix A.1. Scale of Spectral Irradiance Used up to 2007
Appendix A.2. Scale of Spectral Irradiance Used between 2008 and 2012
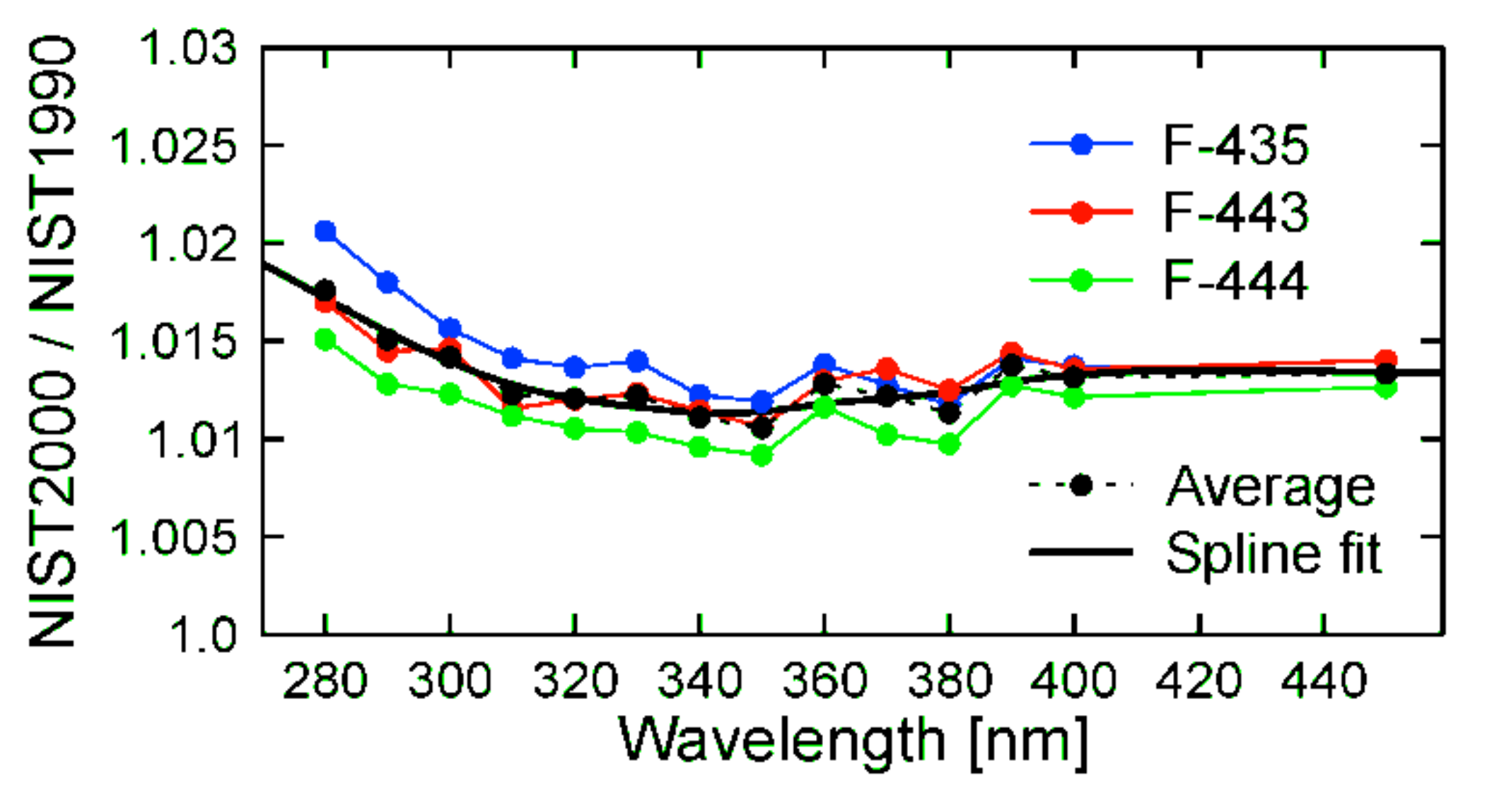
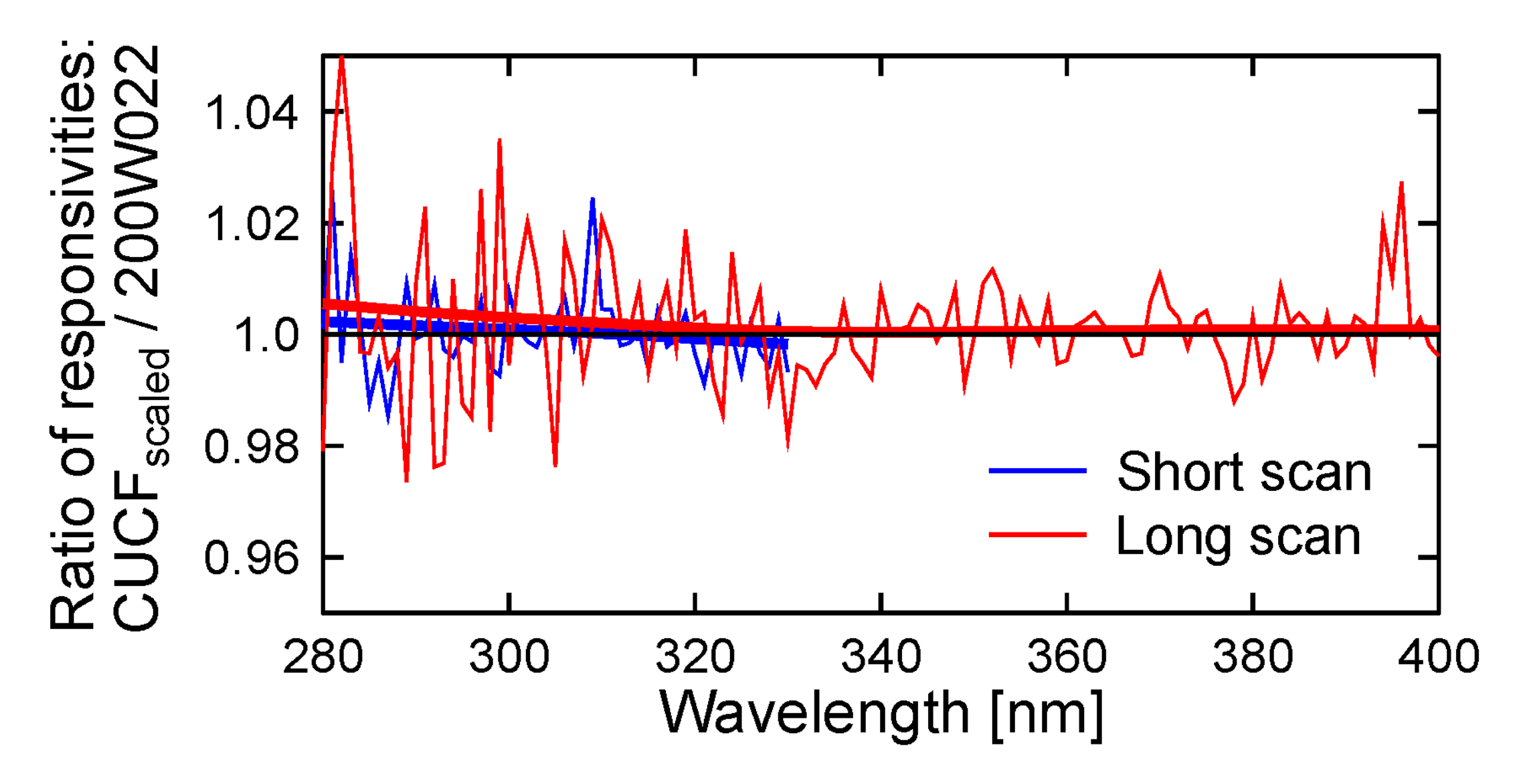
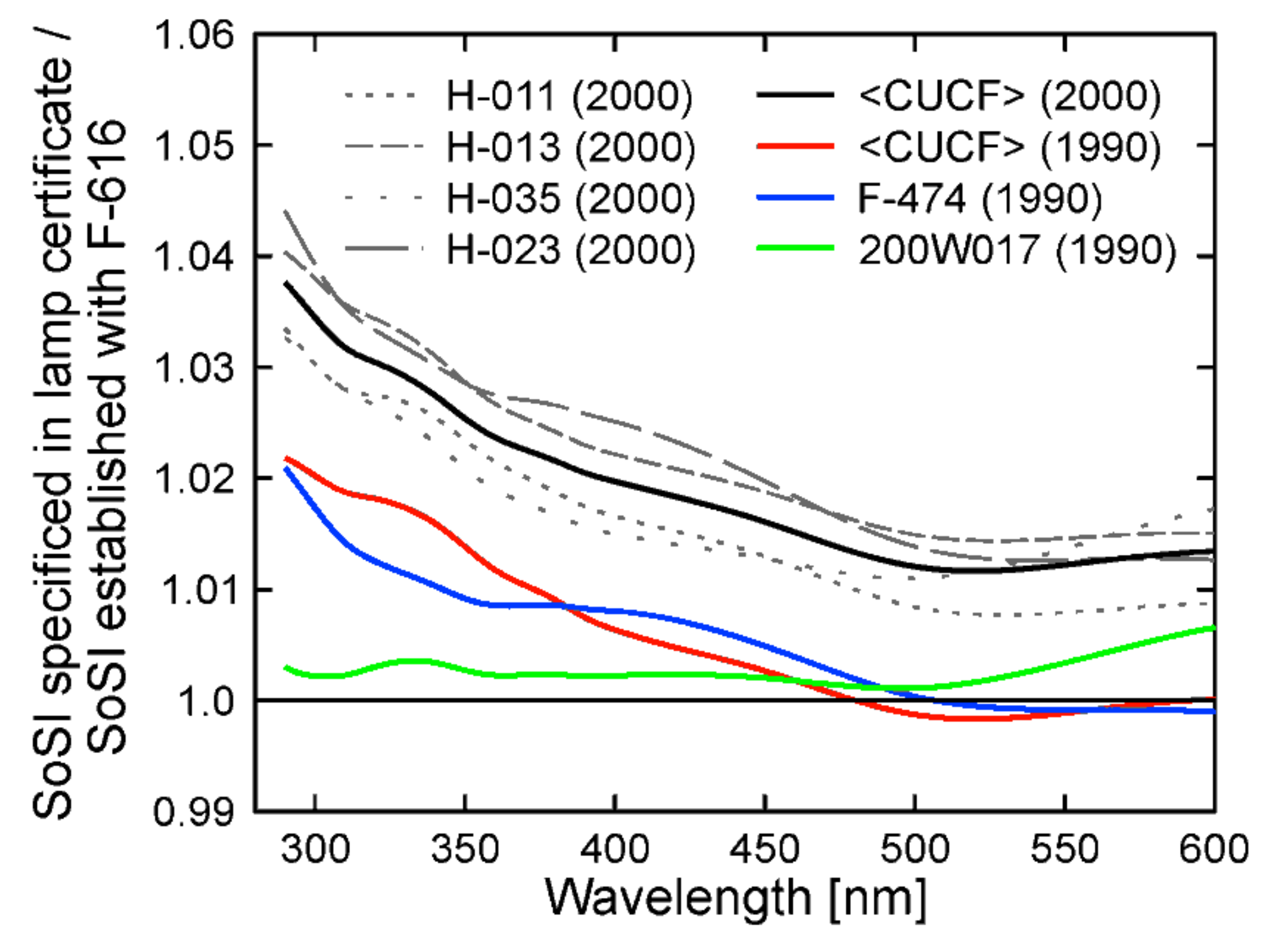
Appendix A.3. Scale of Spectral Irradiance Used between 2013 and 2019
- The SoSI of the CUCF lamps referenced to the NIST2000 scale (gray lines in Figure A3) is biased high relative to the SoSI of lamp F-616 by 2.7% to 4.4% in the UV-B, 1.5% to 3.5% in the UV-A, and 0.9% to 2.5% in the visible range. These large differences were surprising, as both the CUCF lamps and lamp F-616 are traceable to the NIST2000 scale. The relative expanded (k = 2) uncertainties of standard F-616 are 1.74% at 250 nm, 1.27% at 350 nm, 0.91% at 450 nm, and 0.77% at 555 nm [36], and the observed differences are inconsistent with these specifications.
- The average SoSI of the CUCF lamps referenced to the NIST1990 scale (red line in Figure A3) agrees within ±0.5% with the SoSI of lamp F-474 with no obvious bias. This good agreement gives credence to the SoSI of the CUCF lamps and their scaling to the NIST1990 scale. The good agreement also confirms the method of comparing lamps with horizontal and vertical filament using the XGUV.
- The SoSI of traveling standard 200W017 is biased high by about 0.3% relative to the SoSI of lamp F-616 for wavelengths below 500 nm (green lines in Figure A3). This good agreement was surprising, as 200W017 had been calibrated against the NIST1990 scale realized by the CUCF lamps. Hence, the ratio was expected to be similar to the red line in Figure A3.
References
- Molina, M.J.; Rowland, F.S. Stratospheric sink for chlorofluoromethanes: Chlorine atom-catalysed destruction of ozone. Nature 1974, 249, 810–812. [Google Scholar] [CrossRef]
- Synthesis of the 2014 Reports of the Scientific, Environmental Effects, and Technology & Economic Assessment Panels of the Montreal Protocol. 2015. Available online: https://www.ozone.unep.org/sites/default/files/2019-05/SynthesisReport2014_0.pdf. (accessed on 26 July 2020).
- Bais, A.F.; Bernhard, G.; McKenzie, R.L.; Aucamp, P.J.; Young, P.J.; Ilyas, M.; Jockel, P.; Deushi, M. Ozone-climate interactions and effects on solar ultraviolet radiation. Photochem. Photobiol. Sci. 2019, 18, 602–640. [Google Scholar] [CrossRef] [PubMed]
- Lucas, R.M.; Yazar, S.; Young, A.R.; Norval, M.; de Gruijl, F.R.; Takizawa, Y.; Rhodes, L.E.; Sinclair, C.A.; Neale, R.E. Human health in relation to exposure to solar ultraviolet radiation under changing stratospheric ozone and climate. Photochem. Photobiol. Sci. 2019, 18, 641–680. [Google Scholar] [CrossRef] [PubMed]
- Bornman, J.F.; Barnes, P.W.; Robson, T.M.; Robinson, S.A.; Jansen, M.A.K.; Ballare, C.L.; Flint, S.D. Linkages between stratospheric ozone, UV radiation and climate change and their implications for terrestrial ecosystems. Photochem. Photobiol. Sci. 2019, 18, 681–716. [Google Scholar] [CrossRef] [PubMed]
- Williamson, C.E.; Neale, P.J.; Hylander, S.; Rose, K.C.; Figueroa, F.L.; Robinson, S.A.; Hader, D.P.; Wangberg, S.A.; Worrest, R.C. The interactive effects of stratospheric ozone depletion, UV radiation, and climate change on aquatic ecosystems. Photochem. Photobiol. Sci. 2019, 18, 717–746. [Google Scholar] [CrossRef]
- Sulzberger, B.; Austin, A.T.; Cory, R.M.; Zepp, R.G.; Paul, N.D. Solar UV radiation in a changing world: Roles of cryosphere-land-water-atmosphere interfaces in global biogeochemical cycles. Photochem. Photobiol. Sci. 2019, 18, 747–774. [Google Scholar] [CrossRef]
- Wilson, S.R.; Madronich, S.; Longstreth, J.D.; Solomon, K.R. Interactive effects of changing stratospheric ozone and climate on composition of the troposphere, air quality, and consequences for human and ecosystem health. Photochem. Photobiol. Sci. 2019, 18, 775–803. [Google Scholar] [CrossRef]
- Andrady, A.L.; Pandey, K.K.; Heikkila, A.M. Interactive effects of solar UV radiation and climate change on material damage. Photochem. Photobiol. Sci. 2019, 18, 804–825. [Google Scholar] [CrossRef]
- Farman, J.C.; Gardiner, B.G.; Shanklin, J.D. Large losses of total ozone in Antarctica reveal seasonal ClOx/NOx interaction. Nature 1985, 315, 207–210. [Google Scholar] [CrossRef]
- United Nations. Montreal Protocol on Substances that Deplete the Ozone Layer; United Nations Treaty Series: Montreal, Canada, 1987; p. 1522. Available online: https://treaties.un.org/Pages/showDetails.aspx?objid=080000028003f7f7 (accessed on 26 July 2020).
- Newman, P.A.; Oman, L.D.; Douglass, A.R.; Fleming, E.L.; Frith, S.M.; Hurwitz, M.M.; Kawa, S.R.; Jackman, C.H.; Krotkov, N.A.; Nash, E.R.; et al. What would have happened to the ozone layer if chlorofluorocarbons (CFCs) had not been regulated? Atmos. Chem. Phys. 2009, 9, 2113–2128. [Google Scholar] [CrossRef]
- Newman, P.; McKenzie, R. UV impacts avoided by the Montreal Protocol. Photochem. Photobiol. Sci. 2011, 10, 1152–1160. [Google Scholar] [CrossRef] [PubMed]
- McKenzie, R.; Bernhard, G.; Liley, B.; Disterhoft, P.; Rhodes, S.; Bais, A.; Morgenstern, O.; Newman, P.; Oman, L.; Brogniez, C.; et al. Success of Montreal Protocol Demonstrated by Comparing High-Quality UV Measurements with “World Avoided” Calculations from Two Chemistry-Climate Models. Sci. Rep. 2019, 9, 12332. [Google Scholar] [CrossRef] [PubMed]
- Booth, C.R.; Lucas, T.B.; Morrow, J.H.; Weiler, C.S.; Penhale, P.A. The United States National Science Foundation’s polar network for monitoring ultraviolet radiation. In Ultraviolet Radiation in Antarctica: Measurements and Biological Effects; American Geophysical Union: Washington, DC, USA, 1994; Volume 62, pp. 17–37. [Google Scholar]
- WMO. Scientific Assessment of Ozone Depletion: 2018; World Meteorological Organization: Geneva, Switzerland, 2018; p. 588. [Google Scholar]
- Solomon, S.; Ivy, D.J.; Kinnison, D.; Mills, M.J.; Neely, R.R., III; Schmidt, A. Emergence of healing in the Antarctic ozone layer. Science 2016, 353, 269–274. [Google Scholar] [CrossRef] [PubMed]
- Kuttippurath, J.; Nair, P.J. The signs of Antarctic ozone hole recovery. Sci. Rep. 2017, 7, 585. [Google Scholar] [CrossRef] [PubMed]
- Nash, E.R.; Newman, P.A.; Rosenfield, J.E.; Schoeberl, M.R. An objective determination of the polar vortex using Ertel’s potential vorticity. J. Geophys. Res.: Atmos. 1996, 101, 9471–9478. [Google Scholar] [CrossRef]
- NOAA Antarctic UV Monitoring Network. Available online: https://www.esrl.noaa.gov/gmd/grad/antuv/ (accessed on 26 July 2020).
- Bernhard, G.; Booth, C.R.; Ehramjian, J.C. Climatology of ultraviolet radiation at high latitudes derived from measurements of the National Science Foundation’s spectral irradiance monitoring network. In UV Radiation in Global Change: Measurements, Modeling and Effects on Ecosystems; Gao, W., Schmoldt, D.L., Slusser, J.R., Eds.; Tsinghua University Press: Beijing, China; Springer: New York, NY, USA, 2010; p. 544. [Google Scholar]
- Grenfell, T.C.; Warren, S.G.; Mullen, P.C. Reflection of solar radiation by the Antarctic snow surface at ultraviolet, visible, and near-infrared wavelengths. J. Geophys. Res. 1994, 99, 18669–18684. [Google Scholar] [CrossRef]
- Nichol, S.E.; Pfister, G.; Bodeker, G.E.; McKenzie, R.L.; Wood, S.W.; Bernhard, G. Moderation of cloud reduction of UV in the Antarctic due to high surface albedo. J. Appl. Meteorol. 2003, 42, 1174–1183. [Google Scholar] [CrossRef]
- Bernhard, G.; Booth, C.R.; Ehramjian, J.C. Version 2 data of the National Science Foundation’s Ultraviolet Radiation Monitoring Network: South Pole. J. Geophys. Res.: Atmos. 2004, 109, D21207. [Google Scholar] [CrossRef]
- Kim, S.; Saenz, B.; Scanniello, J.; Daly, K.; Ainley, D. Local climatology of fast ice in McMurdo Sound, Antarctica. Antarct. Sci. 2018, 30, 125–142. [Google Scholar] [CrossRef]
- Lenoble, J.; Kylling, A.; Smolskaia, I. Impact of snow cover and topography on ultraviolet irradiance at the Alpine Station of Briançon. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Shaw, G.E. Atmospheric turbidity in the polar regions. J. Appl. Meteorol. 1982, 21, 1080–1088. [Google Scholar] [CrossRef]
- Bernhard, G.; Booth, C.R.; Ehramjian, J.C. UV climatology at Palmer Station, Antarctica, based on version 2 NSF network data. Proc. SPIE 2005, 5886, 588607. [Google Scholar]
- Bernhard, G.; Booth, C.R.; Ehramjian, J.C.; Quang, V.V. NSF Polar Programs UV Spectroradiometer Network 2006–2007 Operations Report, vol. 16.0; Biospherical Instruments Inc.: San Diego, CA, USA, 2008. [Google Scholar]
- Bernhard, G.; Booth, C.R.; Ehramjian, J.C.; Nichol, S.E. UV climatology at McMurdo Station, Antarctica, based on version 2 data of the National Science Foundation’s Ultraviolet Radiation Monitoring Network. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- McKinlay, A.F.; Diffey, B.L. A reference action spectrum for ultra-violet induced erythema in human skin. In Human Exposure to Ultraviolet Radiation: Risks and Regulations; Passchier, W.F., Bosnajakovic, B.F.M., Eds.; Elsevier: Amsterdam, The Netherlands, 1987; pp. 83–87. [Google Scholar]
- De Mazière, M.; Thompson, A.M.; Kurylo, M.J.; Wild, J.D.; Bernhard, G.; Blumenstock, T.; Braathen, G.O.; Hannigan, J.W.; Lambert, J.-C.; Leblanc, T.; et al. The Network for the Detection of Atmospheric Composition Change (NDACC): History, status and perspectives. Atmos. Chem. Phys. 2018, 18, 4935–4964. [Google Scholar] [CrossRef]
- McKenzie, R.L.; Johnston, P.V. UV spectro-radiometry in the network for the detection of stratospheric change (NDSC). In Solar Ultraviolet Radiation. Modelling, Measurements and Effects; Seckmeyer, G., Zerefos, C.S., Bais, A.F., Eds.; Springer: Berlin, Germany, 1997; Volume 1.52, pp. 279–287. [Google Scholar]
- Bernhard, G.; Booth, C.R.; Ehramjian, J.C. Real-time ultraviolet and column ozone from multichannel ultraviolet radiometers deployed in the National Science Foundation’s ultraviolet monitoring network. Opt. Eng. 2005, 44, 1–12. [Google Scholar] [CrossRef]
- Walker, J.H.; Saunders, R.D.; Jackson, J.K.; McSparron, D.A. Spectral Irradiance Calibrations; National Bureau of Standards, US Dept. of Commerce: Gaithersburg, MD, USA, 1987.
- Yoon, H.W.; Gibson, C.E.; Barnes, P.Y. Realization of the National Institute of Standards and Technology detector-based spectral irradiance scale. Appl. Opt. 2002, 41, 5879–5890. [Google Scholar] [CrossRef]
- Central UV Calibration Facility. Central UV Calibration Facility. Available online: https://www.esrl.noaa.gov/gmd/grad/calfacil/cucfhome.html (accessed on 26 July 2020).
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations-description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Tomasi, C.; Lupi, A.; Mazzola, M.; Stone, R.S.; Dutton, E.G.; Herber, A.; Radionov, V.F.; Holben, B.N.; Sorokin, M.G.; Sakerin, S.M.; et al. An update on polar aerosol optical properties using POLAR-AOD and other measurements performed during the International Polar Year. Atmos. Environ. 2012, 52, 29–47. [Google Scholar] [CrossRef]
- Sakai, T.; Uchino, O.; Nagai, T.; Liley, B.; Morino, I.; Fujimoto, T. Long-term variation of stratospheric aerosols observed with lidars over Tsukuba, Japan from 1982 and Lauder, New Zealand from 1992 to 2015. J. Geophys. Res. Atmos. 2016, 121, 10283–10293. [Google Scholar] [CrossRef]
- Jaross, G.; Warner, J. Use of Antarctica for validating reflected solar radiation measured by satellite sensors. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Bernhard, G.; Booth, C.R.; McPeters, R.D. Calculation of total column ozone from global UV spectra at high latitudes. J. Geophys. Res. 2003, 108, 4510–4532. [Google Scholar] [CrossRef]
- Bernhard, G.; Booth, C.R.; Ehramjian, J.C. Comparison of UV irradiance measurements at Summit, Greenland; Barrow, Alaska; and South Pole, Antarctica. Atmos. Chem. Phys. 2008, 8, 4799–4810. [Google Scholar] [CrossRef]
- Bernhard, G. Trends of solar ultraviolet irradiance at Barrow, Alaska, and the effect of measurement uncertainties on trend detection. Atmos. Chem. Phys. 2011, 11, 13029–13045. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; John Wiley & Sons Inc.: New York, NY, USA, 1998. [Google Scholar]
- Bodeker, G.E.; Scott, J.C.; Kreher, K.; McKenzie, R.L. Global ozone trends in potential vorticity coordinates using TOMS and GOME intercompared against the Dobson network: 1978–1998. J. Geophys. Res. Atmos. 2001, 106, 23029–23042. [Google Scholar] [CrossRef]
- Booth, C.R.; Madronich, S. Radiation amplification factors: Improved formulation accounts for large increases in ultraviolet radiation associated with Antarctic ozone depletion. In AGU Antarctic Research Series; Weiler, C.S., Penhale, P.A., Eds.; AGU: Washington, DC, USA, 1994; Volume 62, pp. 39–42. [Google Scholar]
- Seckmeyer, G.; Bais, A.; Bernhard, G.; Blumthaler, M.; Booth, C.R.; Lantz, K.; McKenzie, R.L.; Disterhoft, P.; Webb, A. Instruments to Measure Solar Ultraviolet Radiation. Part 2: Broadband Instruments Measuring Erythemally Weighted Solar Irradiance; World Meteorological Institution: Geneva, Switzerland, 2005; p. 50. [Google Scholar]
- Brunt, K.M.; Sergienko, O.; MacAyeal, D.R. Observations of unusual fast-ice conditions in the southwest Ross Sea, Antarctica: Preliminary analysis of iceberg and storminess effects. Ann. Glaciol. 2017, 44, 183–187. [Google Scholar] [CrossRef][Green Version]
- Ricchiazzi, P.; Gautier, C. Cloud scattering optical depth and local surface albedo in the Antarctic: Simultaneous retrieval using ground-based radiometry. J. Geophys. Res. Atmos. 1995, 100, 21091–21104. [Google Scholar] [CrossRef]
- Stein, T. Ozone Hole Smallest on Record. 2019. Available online: https://research.noaa.gov/article/ArtMID/587/ArticleID/2566/2019-ozone-hole-smallest-on-record (accessed on 30 June 2020).
- Hooker, S.B.; Bernhard, G.; Morrow, J.H.; Booth, C.R.; Comer, T.; Lind, R.N.; Quang, V. Optical Sensors for Planetary Radiant Energy (OSPREy): Calibration and Validation of Current and Next-Generation NASA Missions; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2012.
| Volume | South Pole | Arrival Heights | Palmer Station | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Period | Traceability | Method | Period | Traceability | Method | Period | Traceability | Method | |||||||
| SoSI | 1 | 2 | 3 | SoSI | 1 | 2 | 3 | SoSI | 1 | 2 | 3 | ||||
| 6 | 1/96–1/97 | OL | 1 | 1.008 | 1.016 | 1/96–1/97 | OL | 1 | 0.991 | 0.986 | 1/96–4/97 | OL | 1 | 1.004 | 1.000 |
| 7 | 1/97–1/98 | OL | 1 | 0.971 | 0.979 | 1/97–1/98 | OL | 1 | 0.953 | 0.949 | 4/97–3/98 | OL | 1 | 0.975 | 0.972 |
| 8 | 1/98–1/99 | OL | 1 | 0.979 | 0.987 | 1/98–1/99 | OL | 1 | 0.980 | 0.975 | 4/98–5/99 | OL | 1 | 0.964 | 0.960 |
| 9 | 1/99–1/00 | OL | 1 | 0.979 | 0.987 | 1/99–1/00 | OL | 1 | 0.986 | 0.981 | 5/99–3/00 | OL | 1 | 0.992 | 0.988 |
| 10 | 1/00–1/01 | OL | 0.995 | 0.974 | 0.995 | 2/00–1/01 | OL | 1 | 1.018 | 1 | 3/00–5/01 | OL | 1 | 1.019 | 1 |
| 11 | 1/01–1/02 | OL | 1 | 0.974 | 1 | 1/01–1/02 | OL | 1 | 1.002 | 1 | 7/01–7/02 | OL | 1 | 1.013 | 1 |
| 12 | 1/02–1/03 | OL | 1 | 1.004 | 1 | 1/02–1/03 | OL | 1 | 1.019 | 1 | 7/02–3/03 | OL | 1 | 1.034 | 1 |
| 13 | 1/03–1/04 | OL | 1.008 | 1.007 | 1.008 | 1/03–2/04 | OL | 1 | 1.029 | 1 | 3/03–5/04 | OL | 1 | 1.011 | 1 |
| 14 | 1/04–1/05 | OL | 1 | 0.993 | 1 | 2/04–1/05 | OL | 1 | 1.019 | 1 | 6/04–6/05 | OL | 1 | 1.002 | 1 |
| 15 | 1/05–1/06 | OL | 1 | 0.992 | 1 | 1/05–1/06 | OL | 1 | 1.032 | 1 | 6/05–4/06 | OL | 1 | 1.030 | 1 |
| 16 | 1/06–1/07 | OL | 1 | 0.996 | 1 | 1/06–1/07 | OL | 1 | 1.029 | 1 | 4/06–7/07 | OL | 1 | 1.006 | 1 |
| 17 | 1/07–1/08 | OL/CUCF | 0.993 | 0.999 | 0.993 | 1/07–1/08 | CUCF | 1 | 1.012 | 1 | 7/07–5/08 | OL/CUCF | 1 | 1.004 | 1 |
| 18 | 1/08–3/09 | CUCF | 1 | 0.998 | 1 | 2/08–3/09 | CUCF | 1.008 | 1.002 | 1.008 | 5/08–2/09 | OL/CUCF | 1 | 1.002 | 1 |
| 19 | 9/09–3/10 | CUCF | 1.006 | 1.004 | 1.006 | 4/09–2/10 | CUCF | 1.019 | 0.989 | 1.019 | 3/09–9/10 | CUCF | 1 | 0.998 | 1 |
| 20 | 9/10–3/11 | CUCF | 1.008 | 1.006 | 1.008 | 8/10–4/11 | CUCF | 1 | 0.993 | 1 | 10/10–12/11 | CUCF | 1 | 1.008 | 1 |
| 21 | 9/11–3/12 | CUCF/F-616 | 1.017 | 1.011 | 1.017 | 8/11–4/12 | CUCF | 1 | 1.003 | 1 | – | – | – | – | – |
| 22 | 9/12–3/13 | CUCF/F-616 | 1.017 | 1.013 | 1.017 | 8/12–4/13 | F-616 | 1.0175 | 0.992 | 1.0175 | 1/12–12/13 | CUCF | 1 | 0.989 | 1 |
| 23 | 9/13–3/14 | CUCF/F-616 | 1.017 | 1.026 | 1.017 | 8/13–4/14 | F-616 | 1.0175 | 0.996 | 1.0175 | – | – | – | – | – |
| 24 | 9/14–3/15 | F-616 | 1.030 | 1.011 | 1.030 | 8/14–4/15 | F-616 | 1.0175 | 0.993 | 1.0175 | 1/14–3/15 | F-616 | 1.018 | 0.995 | 1.018 |
| 25 | 9/15–3/16 | F-616 | 1.035 | 1.024 | 1.035 | 8/15–4/16 | F-616 | 1.0175 | 0.993 | 1.0175 | 3/15–7/16 | F-616 | 1.018 | 0.997 | 1.018 |
| 26 | 9/16–3/17 | F-616 | 1.036 | 1.021 | 1.036 | 8/16–4/17 | F-616 | 1.0175 | 0.991 | 1.0175 | 8/16–5/17 | F-616 | 1.018 | 0.988 | 1.018 |
| 27 | 9/17–3/18 | F-616 | 1.030 | 1.011 | 1.030 | 8/17–4/18 | F-616 | 1.0175 | 0.992 | 1.0175 | 6/17–6/18 | F-616 | 1.018 | 0.987 | 1.018 |
| 28 | 9/18–3/19 | F-616 | 1.017 | 1.005 | 1.017 | 8/18–4/19 | F-616 | 1.0175 | 0.992 | 1.0175 | 7/18–3/19 | F-616 | 1.018 | 0.990 | 1.018 |
| Period | Trend (% per Decade) | |||||||
|---|---|---|---|---|---|---|---|---|
| Uvi | Total Ozone Column | E (340) | ||||||
| Uncorrected | Corrected with | Bodeker | SUV-100 | Dobson | Corrected with | |||
| Method 1 | Method 2 | Method 3 | Method 3 | |||||
| South Pole | ||||||||
| Jan | −5.5 ± 2.0 (±1.6) | −4.1 ± 2.0 (±1.7) | −3.9 ± 1.7 (±1.4) | −3.9 ± 1.9 (±1.5) | 1.8 ± 1.9 (±1.6) | 3.1 ± 1.5 (±1.2) | 2.8 ± 1.6 (±1.3) | −0.3 ± 0.9 (±0.7) |
| Feb | −4.7 ± 2.9 (±2.4) | −3.2 ± 3.0 (±2.5) | −3.1 ± 2.8 (±2.3) | −3.1 ± 3.0 (±2.5) | 1.1 ± 3.1 (±2.6) | 2.4 ± 2.8 (±2.3) | 1.2 ± 3.0 (±2.5) | −0.3 ± 0.8 (±0.6) |
| Mar | −2.5 ± 3.6 (±2.9) | −0.9 ± 3.6 (±3.0) | −0.6 ± 3.6 (±2.9) | −0.6 ± 3.7 (±3.0) | −1.8 ± 2.5 (±2.0) | −1.1 ± 1.4 (±1.2) | ||
| Oct | −5.0 ± 12.2 (±10.1) | −3.3 ± 12.3 (±10.2) | −3.3 ± 12.1 (±10.0) | −3.2 ± 12.3 (±10.1) | −1.5 ± 12.6 (±10.3) | 4.4 ± 11.6 (±9.5) | 0.3 ± 1.3 (±1.1) | |
| Nov | −9.7 ± 16.0 (±13.1) | −8.2 ± 15.9 (±13.0) | −7.9 ± 15.9 (±13.0) | −8.0 ± 15.9 (±13.0) | 4.4 ± 16.8 (±13.7) | 6.5 ± 16.4 (±13.4) | 7.4 ± 16.4 (±13.4) | −0.1 ± 0.8 (±0.7) |
| Dec | −2.5 ± 8.0 (±6.6) | −1.0 ± 8.0 (±6.5) | −0.7 ± 7.9 (±6.4) | −0.7 ± 7.9 (±6.5) | −0.6 ± 5.5 (±4.5) | 1.2 ± 5.6 (±4.6) | 1.0 ± 5.5 (±4.5) | 0.8 ± 1.1 (±0.9) |
| Dec–Feb | −4.8 ± 4.8 (±4.0) | −3.1 ± 4.8 (±3.9) | −2.6 ± 4.7 (±3.8) | −2.6 ± 4.7 (±3.9) | 0.8 ± 2.6 (±2.1) | 2.6 ± 2.6 (±2.2) | 1.7 ± 2.5 (±2.0) | 0.2 ± 0.8 (±0.7) |
| Sep–Nov | −9.4 ± 15.1 (±12.5) | −7.8 ± 15.1 (±12.5) | −7.7 ± 15.0 (±12.4) | −7.7 ± 15.1 (±12.4) | 1.0 ± 14.8 (±12.1) | 0.0 ± 0.9 (±0.8) | ||
| Arrival Heights | ||||||||
| Jan | −4.7 ± 3.7 (±3.1) | −3.8 ± 3.7 (±3.0) | −4.6 ± 3.7 (±3.1) | −2.6 ± 3.5 (±2.9) | 0.7 ± 1.5 (±1.2) | 1.5 ± 1.6 (±1.3) | −0.7 ± 3.6 (±3.0) | |
| Feb | −7.1 ± 6.8 (±5.6) | −6.3 ± 6.7 (±5.6) | −7.2 ± 7.5 (±6.2) | −5.3 ± 7.1 (±5.8) | −0.1 ± 2.4 (±2.0) | −0.1 ± 2.2 (±1.9) | −4.7 ± 5.8 (±4.8) | |
| Mar | −6.4 ± 7.3 (±6.0) | −5.5 ± 7.2 (±5.9) | −6.5 ± 8.1 (±6.7) | −4.6 ± 7.5 (±6.2) | 0.3 ± 2.5 (±2.0) | 1.0 ± 2.2 (±1.8) | −3.8 ± 6.8 (±5.6) | |
| Apr | −3.2 ± 7.6 (±6.2) | −2.2 ± 7.5 (±6.2) | −3.3 ± 8.0 (±6.6) | −1.2 ± 7.6 (±6.3) | −0.1 ± 2.1 (±1.7) | −0.7 ± 6.1 (±5.0) | ||
| Sep | −8.5 ± 11.4 (±9.4) | −7.5 ± 11.5 (±9.5) | −8.3 ± 11.3 (±9.3) | −6.3 ± 11.5 (±9.5) | 2.1 ± 10.0 (±8.2) | 4.2 ± 11.4 (±9.4) | 0.2 ± 3.5 (±2.9) | |
| Oct | −10.6 ± 15.8 (±13.0) | −9.7 ± 15.7 (±12.9) | −10.3 ± 15.4 (±12.7) | −8.4 ± 15.5 (±12.8) | 2.9 ± 14.4 (±11.8) | 9.3 ± 13.9 (±11.4) | 0.1 ± 2.8 (±2.3) | |
| Nov | −5.1 ± 15.3 (±12.6) | −4.2 ± 15.3 (±12.6) | −4.9 ± 15.2 (±12.5) | −3.0 ± 15.3 (±12.6) | 2.3 ± 12.4 (±10.1) | 4.6 ± 12.7 (±10.5) | 1.8 ± 2.7 (±2.2) | |
| Dec | −5.5 ± 5.5 (±4.5) | −4.5 ± 5.4 (±4.5) | −5.3 ± 5.6 (±4.6) | −3.4 ± 5.4 (±4.4) | −0.2 ± 3.9 (±3.2) | 1.3 ± 4.1 (±3.4) | −1.5 ± 2.9 (±2.4) | |
| Dec–Feb | −5.4 ± 3.7 (±3.1) | −4.5 ± 3.7 (±3.0) | −5.2 ± 3.9 (±3.2) | −3.3 ± 3.6 (±3.0) | 0.1 ± 1.8 (±1.5) | 0.8 ± 1.6 (±1.3) | −2.3 ± 3.0 (±2.5) | |
| Sep–Nov | −7.2 ± 13.7 (±11.2) | −6.2 ± 13.6 (±11.2) | −6.9 ± 13.4 (±11.0) | −5.0 ± 13.5 (±11.1) | 2.4 ± 10.9 (±8.9) | 6.1 ± 11.4 (±9.4) | 1.0 ± 2.4 (±2.0) | |
| Period | Trend (% per Decade) | ||||||
|---|---|---|---|---|---|---|---|
| UVI | Total Ozone Column | E (340) | |||||
| Uncorrected | Corrected with | Bodeker | SUV–100 | Corrected with | |||
| Method 1 | Method 2 | Method 3 | Method 3 | ||||
| Palmer Station | |||||||
| Jan | –4.0 ± 4.4 (±3.6) | –3.3 ± 4.4 (±3.6) | –4.4 ± 4.7 (±3.8) | –2.6 ± 4.3 (±3.5) | –0.2 ± 2.1 (±1.7) | 0.0 ± 2.4 (±1.9) | –1.9 ± 4.1 (±3.3) |
| Feb | –0.3 ± 6.1 (±5.0) | 0.5 ± 6.0 (±4.9) | –0.6 ± 5.9 (±4.8) | 1.2 ± 5.9 (±4.8) | 0.5 ± 2.2 (±1.8) | 0.6 ± 2.4 (±2.0) | 3.4 ± 5.5 (±4.5) |
| Mar | –5.4 ± 6.7 (±5.5) | –4.6 ± 6.7 (±5.5) | –5.7 ± 6.5 (±5.3) | –3.9 ± 6.6 (±5.4) | 0.5 ± 1.9 (±1.6) | 0.7 ± 2.0 (±1.6) | –2.6 ± 5.7 (±4.7) |
| Apr | –0.4 ± 4.8 (±4.0) | 0.4 ± 4.9 (±4.1) | –0.5 ± 5.0 (±4.1) | 1.3 ± 5.0 (±4.1) | 0.6 ± 2.0 (±1.6) | –0.9 ± 2.3 (±1.9) | 2.3 ± 3.9 (±3.2) |
| May | –3.1 ± 4.4 (±3.6) | –2.3 ± 4.4 (±3.7) | –2.9 ± 4.6 (±3.8) | –1.2 ± 4.5 (±3.7) | 0.1 ± 2.2 (±1.8) | –1.9 ± 3.6 (±3.0) | |
| Jun | –8.9 ± 4.7 (±3.9) | –8.1 ± 4.8 (±3.9) | –8.9 ± 4.9 (±4.1) | –7.3 ± 4.8 (±4.0) | 1.9 ± 1.8 (±1.5) | –4.6 ± 4.0 (±3.3) | |
| Jul | 1.2 ± 8.9 (±7.3) | 1.9 ± 9.0 (±7.5) | 1.0 ± 9.2 (±7.7) | 2.8 ± 9.0 (±7.4) | 0.9 ± 2.8 (±2.3) | 3.8 ± 7.7 (±6.4) | |
| Aug | –6.7 ± 9.5 (±7.9) | –6.0 ± 9.6 (±7.9) | –7.0 ± 10.1 (±8.3) | –5.2 ± 9.7 (±8.0) | 3.0 ± 3.5 (±2.8) | 5.0 ± 4.0 (±3.3) | –0.3 ± 7.0 (±5.8) |
| Sep | –7.1 ± 13.4 (±11.0) | –6.4 ± 13.4 (±11.1) | –7.4 ± 13.6 (±11.2) | –5.5 ± 13.4 (±11.0) | 0.6 ± 7.6 (±6.2) | 4.7 ± 7.9 (±6.5) | –1.2 ± 8.7 (±7.2) |
| Oct | –5.7 ± 12.5 (±10.3) | –5.0 ± 12.5 (±10.3) | –5.9 ± 12.3 (±10.1) | –4.0 ± 12.3 (±10.1) | –2.0 ± 9.0 (±7.3) | 1.5 ± 8.2 (±6.8) | 0.7 ± 7.4 (±6.1) |
| Nov | –2.3 ± 15.0 (±12.4) | –1.6 ± 15.1 (±12.5) | –2.4 ± 14.6 (±12.0) | –0.6 ± 14.9 (±12.3) | –2.9 ± 9.8 (±8.0) | –2.1 ± 10.8 (±8.8) | –1.4 ± 7.2 (±5.9) |
| Dec | –4.8 ± 7.9 (±6.5) | –4.1 ± 8.0 (±6.5) | –5.0 ± 7.4 (±6.1) | –3.2 ± 7.6 (±6.3) | 2.2 ± 2.5 (±2.1) | 1.8 ± 2.7 (±2.3) | 1.9 ± 6.2 (±5.1) |
| Dec–Feb | –4.0 ± 4.6 (±3.8) | –3.3 ± 4.6 (±3.8) | –4.2 ± 4.4 (±3.6) | –2.5 ± 4.3 (±3.6) | 0.9 ± 1.4 (±1.2) | 1.1 ± 1.6 (±1.3) | 0.5 ± 3.5 (±2.9) |
| Mar–May | –4.1 ± 5.5 (±4.5) | –3.3 ± 5.6 (±4.6) | –4.2 ± 5.6 (±4.6) | –2.4 ± 5.6 (±4.6) | 0.4 ± 1.3 (±1.1) | –1.0 ± 4.6 (±3.7) | |
| Jun–Aug | –5.6 ± 8.8 (±7.3) | –4.9 ± 8.9 (±7.4) | –5.7 ± 9.3 (±7.7) | –4.0 ± 9.0 (±7.4) | 1.9 ± 2.1 (±1.7) | 0.2 ± 6.5 (±5.4) | |
| Sep–Nov | –4.4 ± 9.5 (±7.8) | –3.6 ± 9.6 (±7.9) | –4.5 ± 9.1 (±7.5) | –2.7 ± 9.3 (±7.7) | –1.6 ± 5.5 (±4.5) | 1.0 ± 5.6 (±4.6) | –0.6 ± 6.4 (±5.2) |
| Period | Trend at South Pole (% per Decade) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| UVI | Total Ozone Column | E (340) | ||||||||
| SUV-100 | Dobson | |||||||||
| Mar 2019 | Mar 2020 | Mar 2019 | Mar 2020 | Mar 2019 | Mar 2020 | Mar 2019 | Mar 2020 | |||
| Jan | −3.9 ± 1.9 | −4.2 ± 1.7 | 3.1 ± 1.5 | 3.4 ± 1.4 | 2.8 ± 1.6 | 3.0 ± 1.5 | −0.3 ± 0.9 | −0.3 ± 0.8 | ||
| Feb | −3.1 ± 3.0 | −3.2 ± 2.8 | 2.4 ± 2.8 | 2.6 ± 2.6 | 1.2 ± 3.0 | 1.7 ± 2.8 | −0.3 ± 0.8 | −0.5 ± 0.7 | ||
| Mar | −0.6 ± 3.7 | −1.3 ± 3.5 | −1.1 ± 1.4 | −1.5 ± 1.4 | ||||||
| Oct | −3.2 ± 12.3 | −6.7 ± 12.1 | 4.4 ± 11.6 | 8.8 ± 11.7 | 8.0 ± 14.5 | 13.0 ± 14.6 | 0.3 ± 1.3 | 0.1 ± 1.2 | ||
| Nov | −8.0 ± 15.9 | −10.9 ± 15.1 | 6.5 ± 16.4 | 10.3 ± 15.5 | 7.4 ± 16.4 | 10.8 ± 15.4 | −0.1 ± 0.8 | −0.2 ± 0.8 | ||
| Dec | −0.7 ± 7.9 | −2.1 ± 7.4 | 1.2 ± 5.6 | 2.2 ± 5.3 | 1.0 ± 5.5 | 2.0 ± 5.2 | 0.8 ± 1.1 | 0.7 ± 1.0 | ||
| Dec−Feb | −2.6 ± 4.7 | −3.1 ± 4.0 | 2.6 ± 2.6 | 2.8 ± 2.3 | 1.7 ± 2.5 | 2.0 ± 2.2 | 0.2 ± 0.8 | −0.1 ± 0.7 | ||
| Sep−Nov | −7.7 ± 15.1 | −10.8 ± 14.4 | 0.0 ± 0.9 | −0.2 ± 0.9 | ||||||
| Period | Trend at Arrival Heights (% per Decade) | |||||
|---|---|---|---|---|---|---|
| UVI | Total Ozone Column SUV-100 | E (340) | ||||
| April 2018 | April 2020 | April 2018 | April 2020 | April 2018 | April 2020 | |
| Jan | −2.6 ± 3.5 | −2.3 ± 3.0 | 1.5 ± 1.6 | 2.1 ± 1.4 | −0.7 ± 3.6 | 0.0 ± 3.1 |
| Feb | −5.3 ± 7.1 | −7.3 ± 6.2 | −0.1 ± 2.2 | 0.7 ± 2.0 | −4.7 ± 5.8 | −6.3 ± 5.0 |
| Mar | −4.6 ± 7.5 | −6.4 ± 6.5 | 1.0 ± 2.2 | 1.2 ± 1.9 | −3.8 ± 6.8 | −5.2 ± 5.9 |
| Apr | −1.2 ± 7.6 | −2.5 ± 6.6 | −0.7 ± 6.1 | −1.8 ± 5.4 | ||
| Sep | −6.3 ± 11.5 | −9.6 ± 10.9 | 4.2 ± 11.4 | 9.5 ± 13.2 | 0.2 ± 3.5 | −0.6 ± 3.0 |
| Oct | −8.4 ± 15.5 | −8.7 ± 14.1 | 9.3 ± 13.9 | 10.1 ± 13.3 | 0.1 ± 2.8 | −0.6 ± 2.5 |
| Nov | −3.0 ± 15.3 | −5.4 ± 13.3 | 4.6 ± 12.7 | 6.1 ± 11.0 | 1.8 ± 2.7 | 1.1 ± 2.4 |
| Dec | −3.4 ± 5.4 | −3.1 ± 4.5 | 1.3 ± 4.1 | 1.6 ± 3.5 | −1.5 ± 2.9 | −1.0 ± 2.4 |
| Dec−Feb | −3.3 ± 3.6 | −3.0 ± 2.8 | 0.8 ± 1.6 | 1.2 ± 1.4 | −2.3 ± 3.0 | −1.8 ± 2.3 |
| Sep−Nov | −5.0 ± 13.5 | −6.8 ± 12.1 | 6.1 ± 11.4 | 8.2 ± 11.0 | 1.0 ± 2.4 | −0.3 ± 2.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernhard, G.; Stierle, S. Trends of UV Radiation in Antarctica. Atmosphere 2020, 11, 795. https://doi.org/10.3390/atmos11080795
Bernhard G, Stierle S. Trends of UV Radiation in Antarctica. Atmosphere. 2020; 11(8):795. https://doi.org/10.3390/atmos11080795
Chicago/Turabian StyleBernhard, Germar, and Scott Stierle. 2020. "Trends of UV Radiation in Antarctica" Atmosphere 11, no. 8: 795. https://doi.org/10.3390/atmos11080795
APA StyleBernhard, G., & Stierle, S. (2020). Trends of UV Radiation in Antarctica. Atmosphere, 11(8), 795. https://doi.org/10.3390/atmos11080795





