1. Introduction
Wildfires occur across the globe, with varied degrees of impact on nature and society. Low intensity wildfires can be beneficial from a landscape ecology perspective, while high-intensity fires, especially at the wildland-urban interface can be catastrophic in terms of threat to infrastructure, economic losses as well as loss of lives. The fundamental physics governing wildland fires are immensely complex. However, because landscape-scale fires often impact human and ecological well-being, an improved understanding of fire physics and accurate wildfire models are necessary to anticipate and mitigate catastrophic scenarios, as well as designing prescribed burns. Prescribed burns are usually low intensity fires that are aimed at reducing heavy fuel loads in order to reduce future fire intensity. Therefore a detailed understanding of the energetics, regulating factors and scales responsible for fire propagation are important from a management perspective [
1]. This work applies a coupled fire/atmosphere model (FIRETEC) to elucidate our understanding of phenomena that have recently been found to be key to the spread of wildland fires [
2]. More specifically, turbulent coherent structures in the form of counter-rotational vortices or “towers and troughs” are computationally explored here, and their key physical characteristics are investigated. Flaming wildfires have been observed to spread predominantly via convective heat transfer to surrounding unburnt fuels, and in both laboratory and large-scale fires, a series of towers and troughs have been observed to arise naturally and play a major role in convective heat transfer [
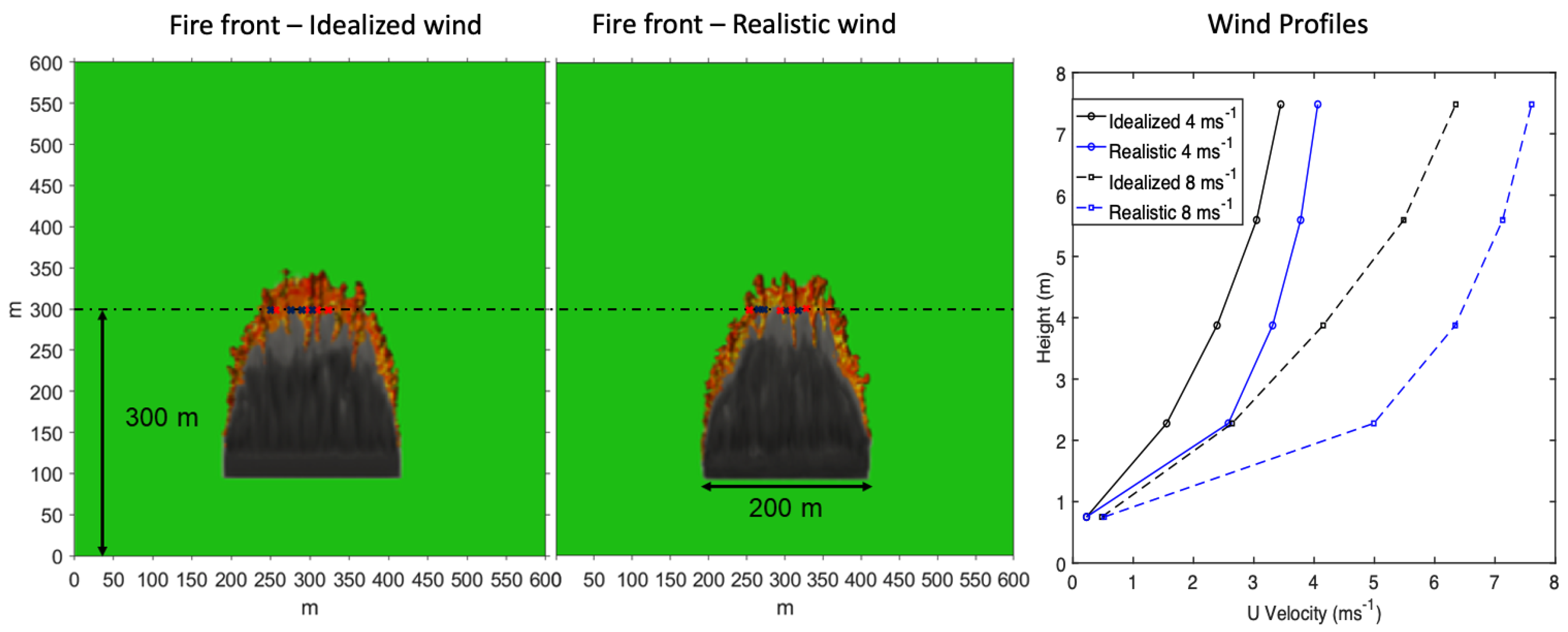
2]. These towers and troughs are the visible manifestations of the interaction between ambient wind and heated gases rising from the burning fuel (towers), and corresponding down drafts of air drawn towards the base of the tower along a pressure gradient (troughs), as shown in
Figure 1. The origin of the streamwise vorticity and tower trough structures in spreading fires is not trivial due to the number of complex feedbacks that develop in the vicinity of the fire front.
The observation of towers and trough-like structures associated with strong buoyancy driven environments can be traced back to several studies involving heated plates [
4,
5,
6,
7]. Stationary diffusion flames have also been used in efforts to study the interactions between forward momentum and buoyancy without the additional complexities of combustion [
8,
9,
10]. Boundary layer instabilities could develop into counter-rotating streamwise vortices which were associated with the visible tower and trough pattern in wind-driven fire scenarios. These structures were observed in several experiments on isothermal, flat plates, indicating that the towers and troughs can exist without the presence of inhomogeneity in temperature or fuel. The authors [
4,
5,
6,
7] concluded that the counter-rotational vortices must be accounted for to accurately describe or model the three-dimensional boundary layer in combustion scenarios. A viscous wall length was defined, and the authors confirmed that the tower and trough pattern had approximately the expected wavelength of 100 viscous wall units (in the streamwise direction), as has been in observed in other boundary layers [
11,
12]. Moreover, the growth of the tower and trough amplitude was found to approximately agree with Rayleigh-Taylor scaling laws in existing literature, but the authors postulate that tendencies of pre-existing vorticity in the flow may also be a contributing factor to tower and trough behavior. In addition, the heat flux to the surface immediately after the flame was considerably higher under and ahead of the troughs (as opposed to the towers). In the wind tunnel experiments involving flat, isothermally heated plates and no subsequent diffusion flame, it was demonstrated that the spacing and width of the counter-rotational vortices both have a lognormal distribution. Interestingly, the spacing and width grow as streamwise distance increases along the heated plate, and the spacing and width of vortices decrease considerably as plate temperature increases and (to lesser degree) as wind speed increases [
8,
13,
14].
Building on the observations from the heated plate experiments and diffusion flame studies, several authors have reported the tower and trough pattern as observed in lab experiments, wildfires, and physics-based landscape- scale simulations [
2,
15,
16,
17,
18,
19,
20,
21]. Canfield et al. [
21] pointed out the presence of the streamwise vorticity patterns and their connection to the fire front structure, which was further supported by Cunningham and Linn [
19]. These studies suggest that vortices could be more heavily accentuated in fires (as opposed to heated plates) because the towers and troughs produce self-reinforcing patterns of “fingers” of burned fuel. Moreover, intense burning in upwash zones, where the buoyant plume and local turbulence result in towers that are
poor and fuel rich, allows for residual burning after the flame-front passes. In these simulations no significant dependence of vortex spacing on initial fireline length was noted, but longer fire lines and faster ambient winds caused vortices to merge more often.
Experiments conducted at the Missoula Fire Sciences Laboratory in (US Forest Service Rocky Mountain Research Station) Montana recently noted the tower and trough behavior as an important flame-spread mechanism. The mechanism is clearly shown to be a principal method of convective heat transfer, and convective heat transfer is in turn experimentally determined to dominate fire spread in wildland fires. Finney et al. [
2] suggest that the convective heat transfer may be due to flame “bursts” as the fire intermittently heats the fuel downwind. These bursts were observed in a series of experiments to range between 1.4 and 4.9 Hz [
15], but this likely varies for other experiments. In general, flame bursts are poorly understood [
22,
23], but they are presumably related to the observed instabilities in the tower and trough structures [
2], and consistent with the observation that heat flux is higher ahead of and below a flame trough.
Moreover, the tower trough structures are persistently present even in well-developed fires, not only in transition flows. Other authors have found similar results on inclined plates [
13,
24], and some researchers have noted that the counter-rotational vortices have some similarities to Görtler vortices [
2,
8,
9,
10,
19,
20,
21]. It is important to note that the tower and trough pattern is similar but not identical to Görtler vortices, which arise as a result of fluid impinging upon a curved surface (i.e., Görtler vortices are a combination of forward momentum and centrifugal force, while the heated plate towers and troughs arise from forward momentum and the force due to buoyancy) [
25,
26,
27].
Therefore, it is evident that although lab scale experiments have investigated tower trough structures with relatively more accuracy, the characterization of such coherent structures have been qualitative at best in the landscape scales. The current work is an attempt to address this gap and we quantitatively answer the following questions:
What is the nature of fire—atmosphere interactions in the tower-trough structures?
What is the impact of controlling factors such as fuel loading, fuel height and wind in modulating the tower trough structures?
The nature of these quantified results can help target measurement schemes in future experiments for testing hypotheses and validating physics-based fire models. Moreover, the results will create a baseline of tower and trough characteristics in more complex scenarios.
3. Results and Discussions
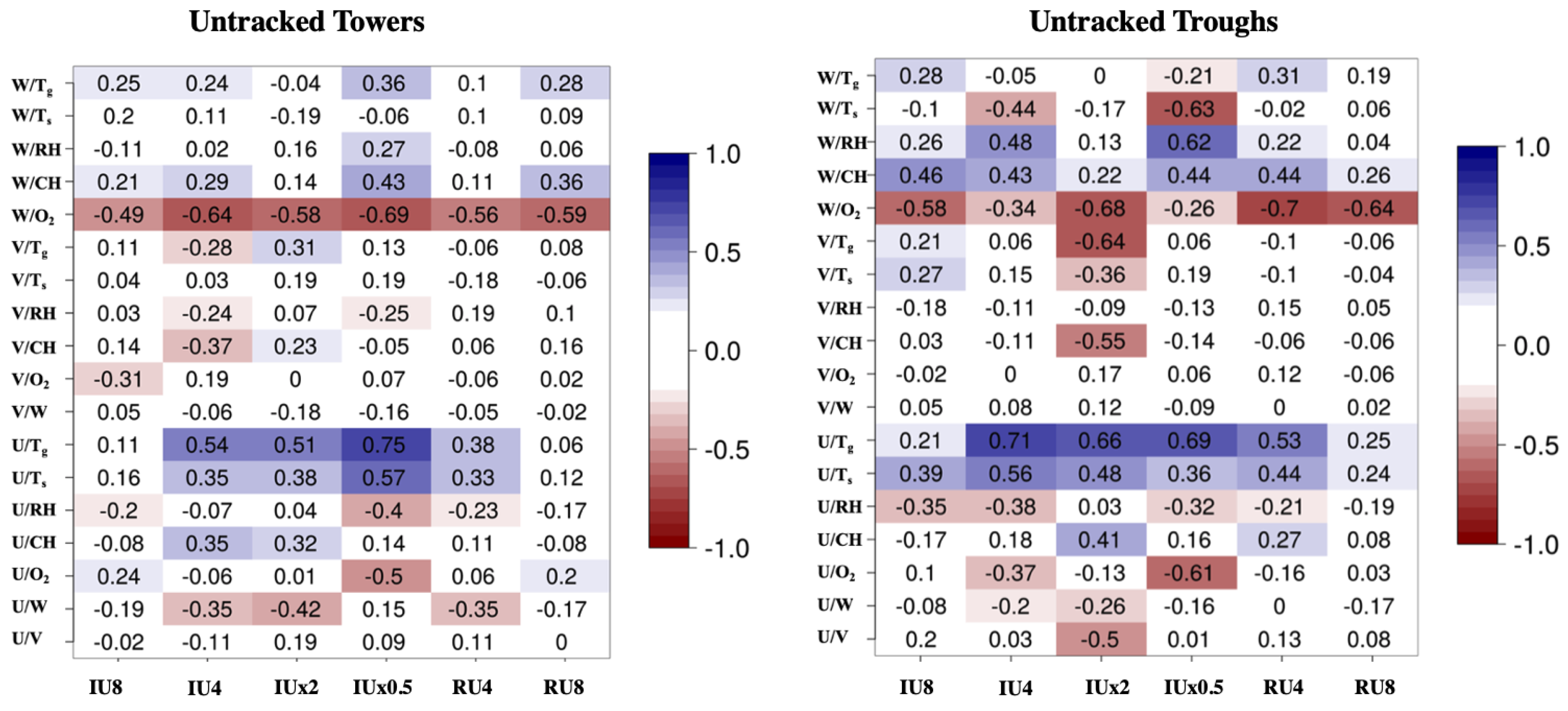
To quantify the trends in towers and trough type structures, Pearson correlation coefficients were computed between the individual components of the wind vector and other quantities of interest, shown in
Figure 3 and
Figure 4. From a micrometeorological perspective, correlation coefficient of the fluctuations (from mean) of a scalar quantity such as heat of a gas with the fluctuations (from mean) of a velocity component represents the efficiency of advective flux transport of the scalar by the moving gas in a specified direction. Hence in the context of wildfires, the correlations of the oxygen concentration, gas temperature or heating are quantities that can provide additional insights into the net influence of the highly turbulent environment on the movement of these scalars. Noting that the coherent structures are a direct result of heat transfer coupling the fuel combustion to the gas phase, the tower and trough structures are naturally only observed during active heating and combustion. Therefore, the data at each location were divided into pre-combustion, combustion, and post-combustion phases as determined by the time step when the fuel first rose above 500 K (or subsequently fell below 500 K as the flaming front moved on). Therefore, a fixed averaging time was not selected apriori for computing correlation coefficients. This calculation was done at the post-processing stage. However, as an approximation, each tower or trough was tracked for about 120 s. The actual time was different from case to case and was determined by the combustion threshold described earlier.
3.1. Stationary Tower and Trough Characteristics
The correlation coefficients shown in
Figure 3 for the spatially static quantities of interest show a general lack of correlation. In the left panel the correlation coefficients are computed for towers, where
w is a positive value, and thus a positive correlation indicates that the correlated quantity is also positive (while anti-correlation indicates that the correlated quantity is negative). For example,
in towers is generally depleted, making the correlation negative. The converse is true for the right panel, where
w is negative for troughs and thus a positive correlation coefficient indicates a negative quantity (such as
w and the convective heating (CH) where CH is consistently negative as the trough is characterized by convective cooling). However, the meandering movement due to streamwise vorticity (pairs of vortices either have dominant upward or downward motion), which is related to the turbulent nature of the atmosphere surrounding the fire, weakens correlations as expected. In light of this chaotic environment, correlation coefficients are considered noteworthy in a range of 0.2 to 0.4, and strong in a range of 0.4 to 0.6 in the following discussion. Correlations that are not considered noteworthy (correlation coefficients that are below a magnitude of 0.2) are not discussed. Numerical values of the correlation coefficients are available in
Figure 3.
There is a strong correlation between local streamwise velocities, u (the wind component in the x direction), and both (gas temperature) and (solid temperature). This correlation is likely associated with the fact that intense burning induces strong updrafts and thus strong horizontal indrafts. The temperature correlation is considerably stronger between u values and because strong winds enhance both heating and cooling of the solids at different times, weakening the correlation between wind and solid temperature . The correlation of the u and v (the wind component in the y direction) with (the concentration of oxygen normalized to 1.0 at background atmospheric concentration) are noteworthy but far from consistent across the six simulation cases. In general, the tables indicate anti-correlation, or that high values of wind correlate with low values of oxygen. This is to be expected, given that the high winds are correlated with more intense combustion and thus more depleted oxygen, while low velocity winds tend to do the opposite. Conversely, high winds also bring about a stronger flux of oxygen from ambient to combusting regions.
The high-speed winds and the turbulent wind simulations (IU8, RU8, and RU4) show lower levels of correlation in general compared to the low wind speed idealized cases, likely because the turbulence and high wind speed distort the coherent structures and cause the towers and troughs to shift locations to a greater degree. By contrast, the idealized wind experiments have the cleanest delineation between towers and troughs (as indicated by the highest average correlation coefficient magnitude). This is especially true at the 4
base wind speed, and further implies that turbulence and high wind speed distort coherent structures. In other studies, this sort of distortion process has been shown to frequently be achieved as a result of dynamic pressure fluctuations. Because of its isotropization tendency (turbulent fluctuations in one direction stir up and move energy to fluctuations in other directions over time), pressure tends to decorrelate covariances, distorting finite coherent structures [
31]. A strong dynamic pressure perturbation had been observed between the upstream and downstream sides of the fire front during previous simulations involving FIRETEC [
21].
The correlation between w and both net convective and radiative heating (CH and RH, respectively) is generally strong in troughs but barely noteworthy in towers, with considerable variation between different simulations. This is a more complex interaction that is clarified later by more carefully tracking the towers and troughs as they change location. The strongest correlation is between w and depletion, which generally shows that areas of depleted are towers, and regions of minimal depletion are troughs. This is interpreted as towers being regions of intense burning and relatively little mixing. When relatively little fresh air is mixed in, it comes in from above the fire where ambient air is carried down. Conversely air in the towers is being drafted up from the surface where there is significant combustion and thus the is not renewed.
Though the burn scars (
Figure 2) show fairly linear features parallel to the mean flow, the towers and troughs do meander dynamically on spatial scales up to several meters perpendicular to bulk wind flow (i.e., the towers and troughs often wander across several cells in the cross-stream direction, both in real fires and in the simulation). The tendency for flame structures to wiggle in the lateral is physically realistic given the turbulent nature of the flame front, but it partially reduces the value of the results in this section where simulated data are taken at stationary points that were held stationary in the cross-stream direction. Unfortunately, while the signatures of towers and troughs can be clearly visualized in burn patterns in the fuel and vorticity patterns in the gas, the pattern is still not as stationary and the meandering of these patterns in time or downwind direction requires care to be taken in the analysis. This can most clearly be seen in contrast between
Figure 3 vs.
Figure 4. These results are still included here as they illustrate some characteristics of the towers and troughs as well as the meandering nature of these features, but they also illustrate the care that should be taken when analyzing point field measurements.
3.2. Non-Stationary Tower and Trough Characteristics
Coherent structures surrounding a stationary point were found to transition between being a tower and trough at different time steps, which contaminated the results of
Section 3.1. In some cases, the transient behavior was so erratic that a given location might even be an approximately equal blend of tower or trough behavior over the duration of the simulation. The results were therefore somewhat ambiguous, with both towers and troughs appearing at the same location at different time steps. Similar difficulties are likely to be encountered in physical experiments, where detectors might be entirely fixed or at least unable to keep pace with the rapid flickering of the flame. However, in simulations, because we have such a larger richness of virtual data, it is possible to attempt to de-convolute the characteristics of towers from troughs as much as possible.
In order it improve our ability to use the simulation data to provide useful analysis of this fireline structure and make inferences relevant to laboratory data where the positions of towers and troughs might be more static, we attempted to track to positions of rising and falling seams of the streamwise vorticity patterns in the test plane.
Figure 4 supports the following trends seen when the updrafts and downdrafts are tracked as they shift spatially in the test plane.
The correlation coefficient of
w and
is, again, the strongest of all the quantities of interest in the left panel of
Figure 4. It is a consistent, strong anti-correlation, indicating that generally positive values of
w (towers or updrafts in the streamwise pattern behind the fire front) coincide with heavily depleted oxygen, while the opposite is generally true for troughs or downdraft locations. This is likely the clearest differentiation between a tower or trough. The
w component of the wind is relatively small compared to the
u component (ambient) because the statistics are being recorded close to the ground and even in the towers, the air is still accelerating as it moves upward. When the updraft is fire-induced (rather than a result of ambient turbulence) it is due to relatively intense local combustion and oxygen consumption. Interestingly, the anticorrelations can be seen in the untracked towers as well. The troughs also show this anticorrelation but with opposite signs on both the oxygen and velocity fluctuations. In these locations, downward motions carry oxygen rich air from above. By spatially tracking the updrafts and downdrafts, it becomes apparent that an even stronger anticorrelation exists between
w and
concentration in the updrafts, and its magnitude is weaker in the troughs. This can be thought of as similar to the circulations in an unstable mixing environment where there is large but diffuse downdraft regions and more concentrated updrafts. Here it is similar for the flux of oxygen.
In general, IUx0.5 has relatively strong correlations (or anticorrelations) between related quantities, while IUx2 correlation coefficients are far lower. From plots of their respective quantities of interest over time, IUx0.5 (half as much fuel as base case) is a rapidly propagating, short duration flame with strong characteristics of a wind driven fire and winds easily penetrate through the fire’s plume. The larger quantity of fuel in IUx2 (twice as much fuel as base case) leads to a deeper flame front with more characteristics of a plume dominated fire and highly chaotic behavior inside the fire perimeter as mean wind is less effective at blowing through the plume, thus degrading correlation coefficient magnitude. Similar to the untracked cases (
Section 3.1), high streamwise winds (wind in the
u direction) are correlated with high solid and gas temperatures (
and
). Also as seen in the untracked towers and troughs analyses, the correlation between gas temperature and
u is stronger than the
correlation because high winds also contribute to convective cooling.
As with u, there is a strong correlation between w and both and in the spatially tracked experiments. This is in striking contrast to the much lower low correlation in the untracked experiments (the flickering nature of the tower-trough structures weakens the correlations), and must be interpreted differently than the correlations. In the case of vertical air flow, both positive and negative values are critical for interpretation. In the case of towers, the vertical airflow is positive, and the correlation with is slightly weaker than the correlation between positive w and , which implies a strong coupling between a high w value due to a large amount of energy released into the gas and a strong buoyant force with a slightly weaker coupling to the solid temperature. In the case of negative w values, the gas temperature is relatively weakly correlated with the value of w as compared to the correlation in towers. The correlation implies that strong downdrafts are associated with cooler air, which is intuitive, and the weaker value can be thought of again as an analogy to the circulations present in the atmosphere where there are small strong concentrated updraft locations, but larger areas of weaker downward motions. More interestingly, the coupling between negative values of w and is strong relative to both the trough correlation and the tower correlation. This is caused by the negative w values carrying cool ambient air and convectively cooling fuels, leading to low , resulting in warming of the air which is advected away.
On the other hand, there is very low correlation between v velocity and the variables of interest. This is due to the fact that the pairs of streamwise vortices and thus the towers and troughs have converging and diverging lateral flows associated with them. There is no preferential difference between a positive and negative v since they are occurring in somewhat symmetric pairs.
3.3. Temporal Evolution of Towers and Trough Structures
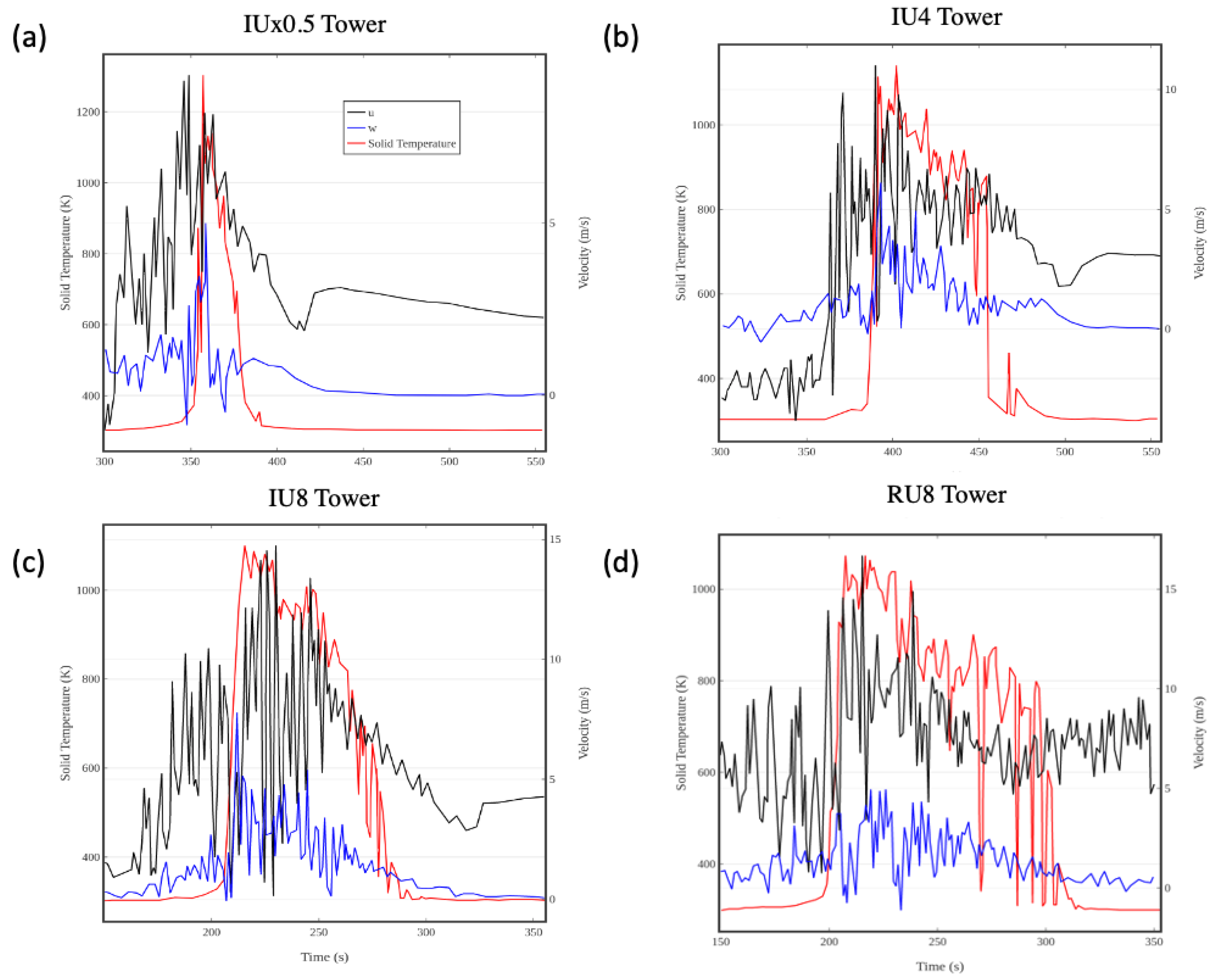
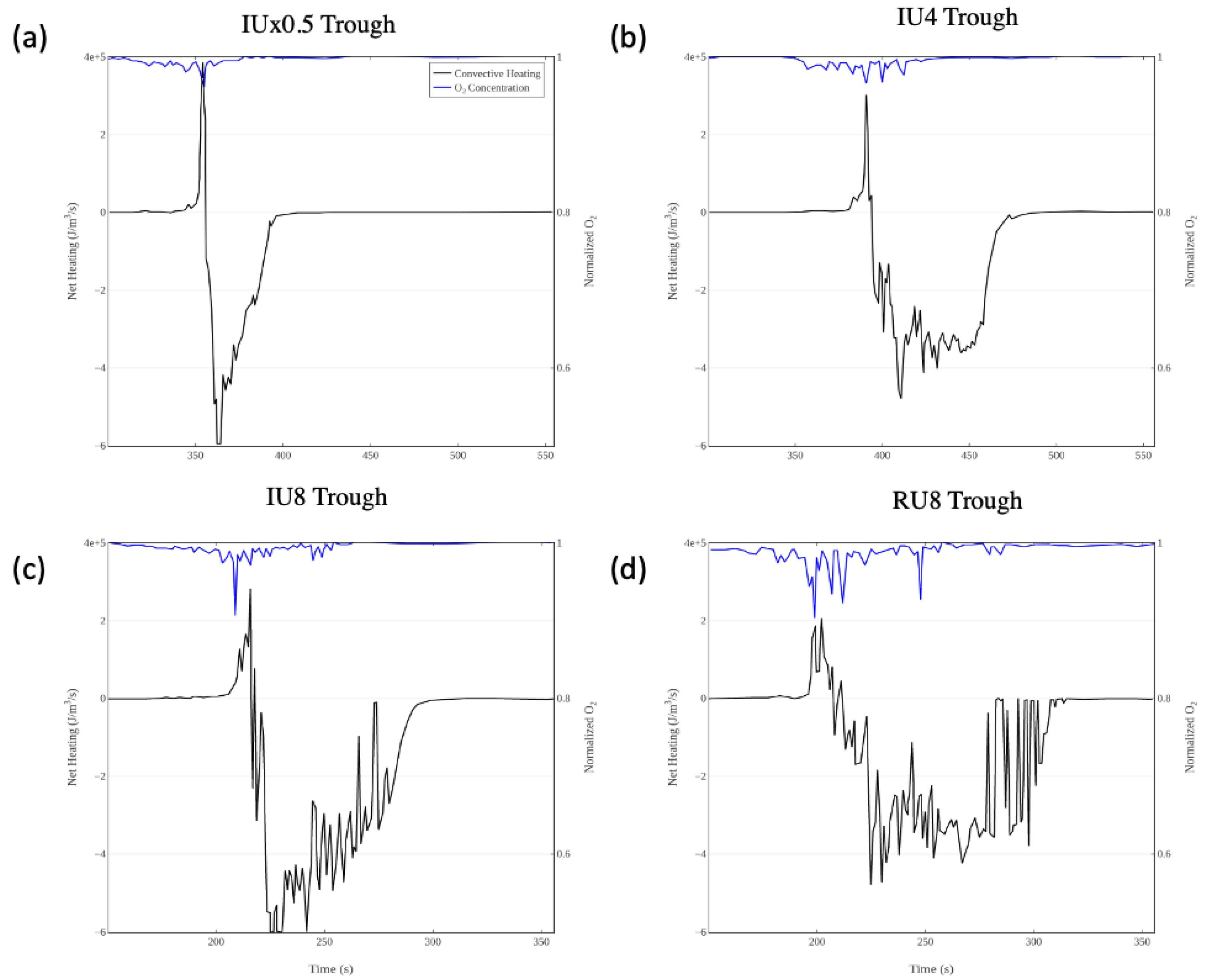
The various simulation scenarios produced dozens of towers and troughs. It is unnecessary and impractical to plot results from every flame structure, but temporal signatures from representative towers and troughs (from the non-stationary analysis) are shown below (
Figure 5,
Figure 6,
Figure 7 and
Figure 8).
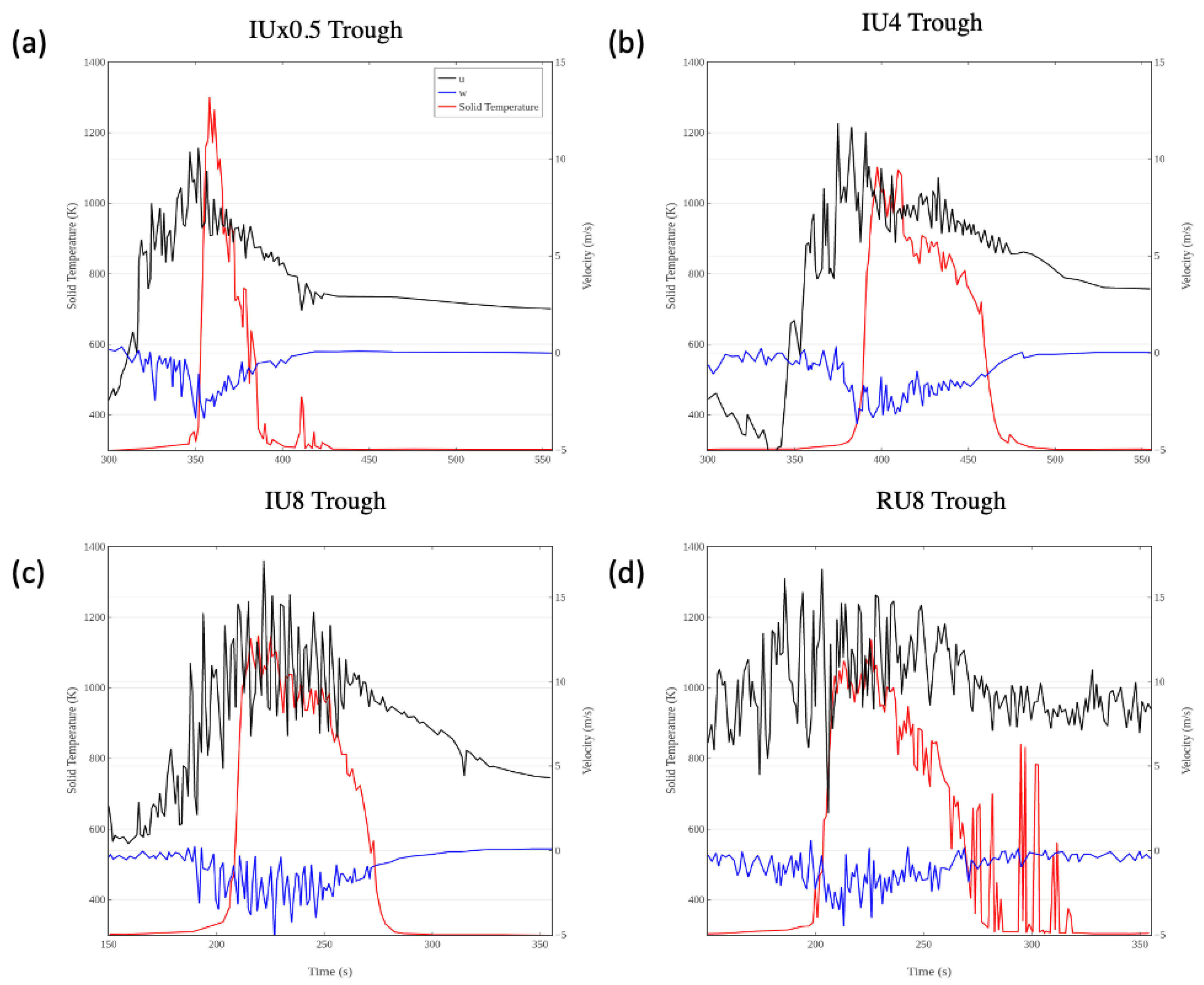
Figure 5, which illustrates the convective heating to the fuel and oxygen depletion, shows that for all of the simulations there is a rapid convective heating period followed by a longer convective cooling period, which occurs once the fuel temperatures gets sufficiently elevated. In all of the simulations, oxygen depletion at the tower locations begins during the heating phase (near the fire front) and in most cases oxygen continues into the time period where the fuel is hot and starts being convectively cooled. During this period when there is significant oxygen depletion there are intermittent partial recovery of the oxygen concentration levels associated with turbulent wind gusts. The duration of the oxygen depletion as well as the period of convective cooling is dependent on the amount of fuel that is present to burn as illustrated by the much shorter timescales for these values in the IUx0.5 simulation.
Figure 6 confirms that the transition from convective heating to convective cooling is consistent with time when the temperature of the fuel has grown significantly. The temperature spike has associated elevated velocity periods as well. This figure also illustrates the fact that in the realistic wind case the mixing is more effective at bringing faster moving air down to the surface as the streamwise velocity is higher in this case (RU) at the surface before and after the fire. Behind the fire, the streamwise winds settle back to a value higher than the wind speed before the effects of the fire were felt due to reduced drag (but to a lesser degree in RU case, where mixing plays a bigger role in bringing high speed winds to the surface). Another interesting observation is that in most of the cases, the streamwise winds increase in magnitude before the fuel temperature starts to rise. This is probably due to the convective pre-heating of fuel elements before the flame front reaches a particular location. It is also important to note that high wind-speeds and turbulence degrade the correlations, and a higher temporal and spatial resolution are needed to study the effects on coherent structure at higher wind speeds.
Figure 7 shows that the rapid convective heating followed by convective cooling for a longer duration exists in the troughs as well, but there is minimal oxygen depletion in these regions. The most noteworthy difference between the towers and troughs is shown in
Figure 8 where the vertical velocity actually becomes negative during most of the period when the temperatures are elevated.
Figure 8 also shows that in the troughs the streamwise winds are consistently elevated before the fire reaches the test plane as winds push through the toughs. The fluctuations in the streamwise wind are less in the case of half as much fuel, IUx0.5, and the velocity and temperature signatures in this case are much shorter than in the cases with more fuel.
Both
Figure 6 and
Figure 8 illustrate the rapid growth of solid temperatures upon ignition and the decrease of the same nearly as sharply upon burnout. Please note that these simulations consider only fine fuels that cool quickly. The duration of the elevated temperature period is tied to the fuel load and is thus shorter when there is less fuel. The frequency and amplitude of wind fluctuations are often dampened in the combustion region. This is especially true of troughs and lower wind speeds, presumably because the pressure gradient caused by the tower induces a substantial portion of the trough winds, especially at low ambient wind speeds.
4. Conclusions
The current work investigated the characteristic features of tower and trough type structures using numerical simulations, which has been recently identified as the dominant coherent structures associated with fire front propagation. We attempted to address two major aspects: (1) the nature of fire—atmosphere interaction specific to the tower and trough type structures; and (2) the sensitivity of such structures to fuel loading, fuel height and wind speeds. To address these issues, a physics-based wildland fire behavior model called FIRETEC was used to simulate grass fires starting from a linear ignition and moving through a homogeneous fuel bed for a range of wind speeds. Some simulations tested the effects of altering the amount of fuel as well. Macro-scale structures that emerged from simulations and were common to all simulations were investigated to extract tower and trough type features. Towers were designated as zones that are burning and associated with updrafts of the vertical wind velocity. Troughs were classified as zones with downdrafts of the vertical wind velocity. Combined, they result in a ‘finger like’ organizations in the flame front. These structures were found to be move laterally in space, which means they can meander around the location from where they originate, yet maintaining their coherence. Studying the structure of the towers and troughs therefore required tracking them in neighboring locations perpendicular to the wind direction in order to study their features in time. Using this approach, highly coherent features were detected in both towers and troughs. Apart from the obvious defining features of positive vertical velocity in towers and negative vertical velocity in troughs, oxygen concentration is the most important parameters defining their characteristics. Towers are associated with depleted oxygen, where troughs are oxygen rich. They are also associated with different rates of radiative and convective heating and cooling. The structures are also sensitive to fuel height and wind speeds. Shorter fuel heights result in thinner and rapidly progressing fire fronts compared to a thicker flame front for larger fuel depths, which makes it more difficult to observe tower-trough dynamics. Higher wind speeds also mean more rapid downdrafts leading to faster replacement of warm air with cold air in the flame front, which changes the characteristic time and spatial scales of the towers and troughs. One major outcome of this study is delineating the differences between the tower and trough structures, as they relate to coupled fuel-fire-atmosphere interaction in different ways, yet organize together in the flame structure. Another important conclusion from this study is the fact that physics-based simulations can consistently demonstrate and reproduce tower trough type structures under a range of environmental conditions as an emergent feature, without any applied artificial numerical forcing. Earlier these structures were observed in lab experiments and some limited simulation studies. This lends confidence in the practice of using physics-based models in fire and fuel management. Future works will be targeted to compare physics-based models and lab/field experiments in accurately predicting the locations and distributions of towers and troughs as well as elucidating their intermittent turbulent features. Nonetheless, it can be concluded that this work has defined some quantified baseline cases against which future experimental studies can be benchmarked for simple homogeneous fuel loadings.