Abstract
An algorithm has been developed to isolate the gravity waves (GWs) of different scales from airglow images. Based on the discrete wavelet transform, the images are decomposed and then reconstructed in a series of mutually orthogonal spaces, each of which takes a Daubechies (db) wavelet of a certain scale as a basis vector. The GWs in the original airglow image are stripped to the peeled image reconstructed in each space, and the scale of wave patterns in a peeled image corresponds to the scale of the db wavelet as a basis vector. In each reconstructed image, the extracted GW is quasi-monochromatic. An adaptive band-pass filter is applied to enhance the GW structures. From an ensembled airglow image with a coverage of 2100 km × 1200 km using an all-sky airglow imager (ASAI) network, the quasi-monochromatic wave patterns are extracted using this algorithm. GWs range from ripples with short wavelength of 20 km to medium-scale GWs with a wavelength of 590 km. The images are denoised, and the propagating characteristics of GWs with different wavelengths are derived separately.
1. Introduction
Gravity waves (GWs) have gained research interest for decades, because of their important role in energy and momentum transport throughout the atmosphere [1,2,3,4]. GWs can be excited by various sources in the lower atmosphere, namely, orography [5], jet [6], deep convection such as thunderstorms [7,8], and typhoons [9]. GWs of various scales often exist simultaneously in the atmosphere [10,11].
Since Peterson and Adams [12] utilized the all-sky airglow imagers (ASAIs) to observe GWs from induced perturbations of airglow, ASAIs have been widely used to observe GWs. Based on the temporal and spatial information provided by ASAIs, quasi-monochromatic GWs can be studied to reveal the relationship between the wave scale and the propagation characteristics. Due to the limited field of view of ASAIs, most previous studies have focused on the GWs of wavelengths shorter than 100 km [13]. On the other hand, some studies have focused on small-scale ripples from broken GWs, revealing the instability of the local atmosphere [14]. Airglow sensors onboard low-earth orbit satellites can capture large-scale GWs, but without temporal information [15,16]. To overcome these limitations, Xu et al. established a no gap ASAI observation network in Northern China, making the continuous measurement of medium-scale GWs from the ground possible [17]. Both airglow sensors and ASAI provide horizontal information of GWs, while metal-fluorescence lidar can capture the temperature and wind vertical profiles for the study of vertical variations of GWs [18,19]. The combinations of airglow images and lidar data are utilized to analyze 3-D model [20] of GWs and ripples caused by GW breaking [21].
In some of the previous studies [22,23,24], most of the observed GWs were considered quasi-monochromatic wave bands and the other spatial patterns in the images were ignored. With the installation of an ASAI network, it is possible to capture GWs of various scales, ranging from tens of kilometers to hundreds of kilometers [25]. Isolating these waves is helpful to give a wider spectral coverage of the GWs observed by ASAI. Another advantage of extracting the GWs of different wavelengths is that the extracted wave patterns in one peeled image are quasi-monochromatic waves, which enable denoising by band-pass filtering. Our previous study [25] has succeeded in extracting large-scale GWs from the airglow images by two-dimensional fast Fourier transform (2D FFT). 2D FFT focuses on frequency information only, so that it works effectively for extracting the large-scale waves existing in most areas of the airglow images, while it is less effective at isolating the GWs at small scales in some regions and in the local ripples. In the present work, we took both the frequency and spatial location into consideration, and made an advancement in isolating the GWs of multiple scales, regardless of the scale and existing area.
In this work, we developed an algorithm based on discrete wavelet transform (DWT), and applied it to peel off sub images containing wave patterns of different scales from a large-area airglow image captured by an ASAI network. After denoising the peeled images with an adaptive scan band-pass filter, we measured the propagating characteristics of the GWs of different scales. In addition, we obtained a final image of the clear wave patterns by adding all of the denoised peeled images together.
This paper is arranged as follows: Section 2 introduces the ASAI network and the data used in this work. The algorithms of extraction and denoise with an adaptive filter are presented in Section 3. A case study is presented in Section 4 for the reliability and capacity of our algorithm. Discussions on the algorithm and measurements are given in Section 5. Finally, the conclusion is presented in Section 6.
2. Observation
An ASAI network containing six stations (Table 1) was established in Northern China since 2012 [17]. A single ASAI at a station consists of a fisheye lens, a near-infrared filter, a CCD (Charge-coupled Device) detector and an optical imaging system. The imager at the Xinglong station uses a Mamiya 24 mm/f4.0 fisheye lens and the imagers of the other five stations use a Nikkor 16 mm f/2.8D fisheye lens. The near-infrared filter allows OH emission (715–930 nm) to pass through and filters O2 emission (865.5 nm) so that the ASAI can focus on the OH layer. The captured airglow image information is stored in CCD in the form of hexadecimal files and will be transformed to grayscale image before image processing. The viewing angle of ASAI is 180°, including a complete sky view. The resolution at the zenith is the highest, up to 0.27 km. The resolution decreases as the angle increases so that considering the sharply decreasing resolution and strong distortion, the effective zenith angle is assumed to be 160° [17]. For the focused OH layer (87 ± 5 km) [25], this angle is equivalent to an effective radius of 420 km [17].

Table 1.
Position of stations in the airglow observation network.
An ASAI takes photos at every 64 s, 60 s for exposure and 4 s for data saving. The hexadecimal data is transformed to airglow images in the following four steps: reorientation, removing stars, enhancing by subtracting a 40-min-averaged starless image, and geographic projection [26]. The processed images captured simultaneously by different stations are assembled together according to their geographic coordinates, in order to obtain an assembled wide-area airglow image [25]. Images from different stations that make up one mosaic image are normalized to the same mean value.
3. Image Processing
3.1. GW Events
Two GW events (shown in Figure 1) can be spotted easily at the same time on the night of 21 December 2014 (UTC): one propagated from northeast to southwest, lasting from 15:20 p.m. to 18:46 p.m. (UTC), and another wave propagated from north to south, lasting from 17:36 p.m. to 18:37 p.m. (UTC). An assembled image of 2100 pixels × 1200 pixels (one pixel denotes one kilometer) is shown in Figure 1, exhibiting an area of 2100 km × 1200 km. The blank area at the right lower corner is due to the breakdown of an ASAI at Rongcheng Station. No convective weather can be found around the center derived from the waveform. As thunderstorms are very rare in winter in Northern China, this GW event was possibly triggered by a frontal system or jet [6].
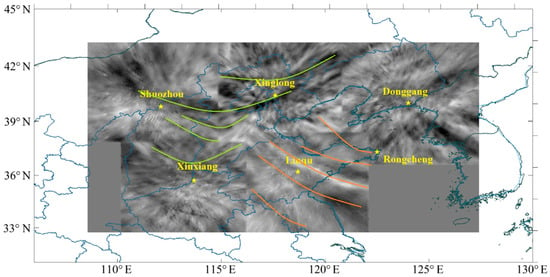
Figure 1.
Airglow gravity waves captured at 18:00:07 p.m. (UTC) on 21 December 2014. The airglow image matrix is 2100 km × 1200 km. The all-sky airglow imager (ASAI) stations are marked with yellow stars. The two GW events are marked by orange and green, respectively. The blank area at the right lower corner is due to the breakdown of the ASAI at Rongcheng Station. The left lower corner is out of the effective radius of Xinxiang and Shuozhou station, so that the area is blank.
3.2. Discrete Wavelet Transform (DWT)
DWT is an ideal algorithm to separate waves of different scales from the raw GWs with wide spectrum by peeling the wave patterns from a large to small scale. DWT divides the function space of object function F(x) into a series of mutually orthogonal subspaces. Information of different scales in F(x) are reconstructed and expressed separately in these subspaces with corresponding basis vectors. The function space L2(R) of F(x) is a square integrable [27] and can be decomposed as follows:
where the direct sum symbol means the union of spaces. V indicates the scale space, used to construct an approximation to F(x). W is the wavelet space, used to construct waves representing the difference between the approximation and actual function. j is the scale factor. According to Equation (1), F(x) is divided into an approximation with lower frequency and wave of higher frequency. Subsequently, in the same way, the approximation with a lower frequency in scale space Vj can be further decomposed into a new approximation of a lower frequency in spaces Vj−1 and a new wave of higher frequency in Wj−1 [27]:
Equation (1) can then be expanded as follows:
where all of the subspaces of V0 and Wj are orthogonal to each other. Wj0 is the wavelet subspace with the smallest scale s0 and the finest resolution. The scale of a basis vector of Wj is . In order of scale from small to large, information is peeled from F(x) and reconstructed in the wavelet subspace Wj of the corresponding scale.
The component fj(x) of F(x) in the scale space Vj can be denoted by a linear combination:
where a is the scale coefficient. The scale function is the basis vector of Vj:
where k is the translation factor.
Wj is the wavelet subspace, with wavelet function as its basis vector. Component gj(x) of F(x) in the wavelet space Wj can be also decomposed into a linear combination:
where b is the wavelet coefficient and
In our work, Daubechies 45 (db 45) wavelet [28] was adopted in DWT; 45 indicates the maximum vanishing moment allowed in the MATLAB function library. A large vanishing moment leads to a smooth fitting, but at the cost of poor compact support in the frequency domain and more computing cost. In the db 45 wavelet, neither in Equation (5) nor in Equation (7) had an analytic expression (shown in Figure 2).
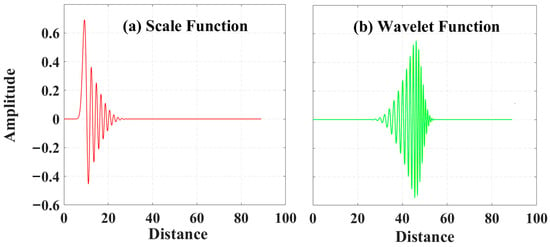
Figure 2.
(a) Scale function and (b) wavelet function of db 45. The horizontal axis is the distance in pixels and the vertical axis is the amplitude (grayscale in this paper), for both images (a) and (b).
Through DWT, F(x) is expanded as the sum of the linear combinations in the scale subspace and a number of wavelet subspaces:
where
In short, Equation (8) is rewritten as follows:
where f0 is the approximation to F(x) by scale function with basis vector at scale , and gj is the DWT expansion with basis vector at scale .
In the image processing, the two-dimensional image matrix is decomposed by DWT along three directions—vertical, horizontal, and diagonal. Then, the two-dimensional DWT expansion of different scales is reconstructed based on the DWT expansions along three directions [27]. The reconstructed two-dimensional DWT expansions are a series of images peeled from the original image, with both vertical and horizontal basis vector scales at pixels. In the following image processing, s0 is 2 pixels. We used n (n = j0 – j + 1) to define a peeled layer. The wave patterns reconstructed in the peeled image at the nth layer with a basis vector at the scale of 2n pixels is a quasi-monochromatic wave with a wavelength between the 2n and 2n+1 pixels. However, considering that the wavelet function (shown in Figure 2b) with a large vanishing moment is not a pulse, the wavelength in the nth layer may slightly exceed the range of 2n to 2n+1, especially when n is small.
3.3. Enhancing the Wave Pattern
The wave patterns in a peeled image are limited in a narrow spectrum, so that they can be enhanced by a scan kernel with band-pass filtering. The kernel is a square with a side length of triple the basis vector of the layered image, going through the image with a stride of the basis vector. For example, a window of 48 pixels × 48 pixels slides on the image of the fourth layer (n = 4) with the stride of 16 pixels. In each step, the region covered by the filter (Figure 3a) was transferred to the frequency domain by two-dimensional fast Fourier transform, so that two symmetric frequency peaks could be revealed. Then, the spectrum of the covered region (Figure 3c) was filtered by multiplying the following filtering function (shown in Figure 4):
where u and v are the zonal and meridional frequency, respectively. umax and vmax are the frequencies of the maximum intensity. Due to the symmetry of spectrum, two peak points can be spotted at (umax, vmax) and (−umax, −vmax), respectively.
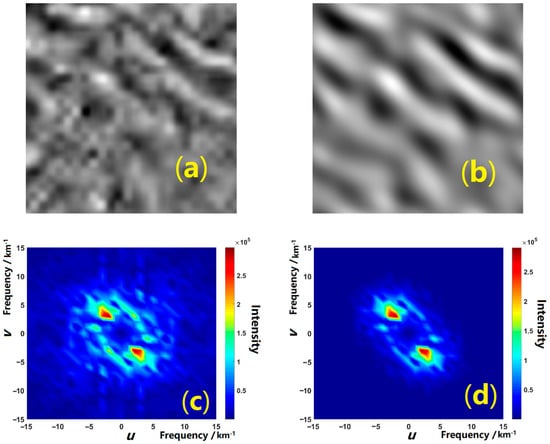
Figure 3.
(a) Covered region before filtering. (b) Covered region after filtering. (c) Spectrum before filtering. (d) Spectrum after filtering. In (c) and (d), u and v are the zonal and meridional frequencies, respectively. The color bar indicates the intensity, which is proportional to the grayscale. After filtering, the wave pattern in the image becomes more visible, and the spectrum becomes clearer.
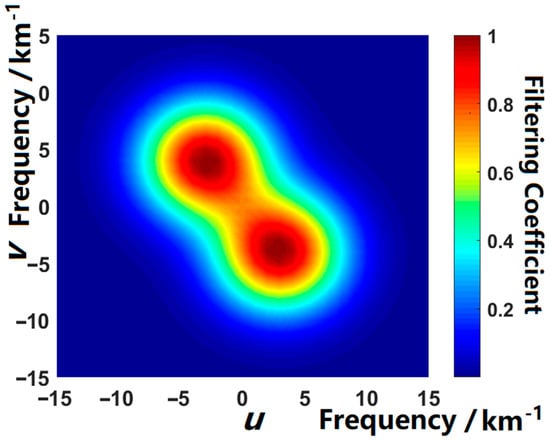
Figure 4.
Filtering function. u and v are the zonal and meridional frequency, respectively. The color bar indicates the filtering coefficient.
After frequency filtering, the noise was removed in the frequency domain. Then, the product (Figure 3d) of the original spectrum and H was transferred back to the image domain by two-dimensional inverse fast Fourier transform. Figure 3b shows the wave patterns became more visible after the wave enhancement.
4. Multiple Scale Analysis of GW Events
The OH airglow image (Figure 1) captured by the ASAI network contained GWs with a broad spectrum, which could be isolated separately through DWT. Considering that the assembled airglow image is 2100 pixels × 1200 pixels, the max n was set to 9. In other words, the largest scale of the basis vector was 29. Figure 5 shows a series of layered images reconstructed with a basis vector at the scale of 2n (n = 1, 2, …, 9) pixels, with one pixel representing one kilometer.
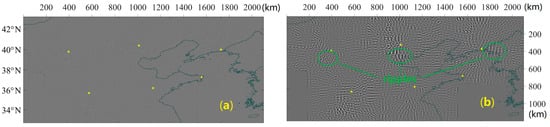
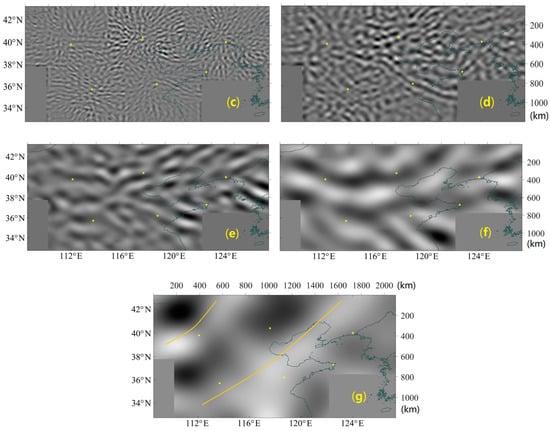
Figure 5.
The peeled layers from the original image. The axes above and to the right represent the position. The lower and left axes indicate the longitude and latitude, respectively. The ASAI stations are marked with yellow points. Every peeled layer is denoised by a band filter to enhance the wave pattern. (a) Sum of the first three layers (n = 1, 2, 3), mainly noise; (b) 4th layer, ripples are marked in the image; (c–f) 5–8th layers, waves reconstructed by basis vector with the scale of 5–8 power of 2 pixels (kilometers in reality); and (g) 9th layer, medium-scale gravity wave (GW) propagating to the southeast, marked by orange curves. The one-hour evolutions of GWs at different layer can be seen in the videos in Supplementary Materials.
In each peeled image, the dominant wave pattern was much stronger than the noise caused by the background, clouds, or GWs of other scales, so that denoising could be performed by enhancing the strongest spectrum. For better visibility, all of the peeled images in Figure 5 were processed by the filtering kernel mentioned in Section 3.3 in order to reduce the noise and thus enhanced the wave patterns. Considering the spectrum peak of the various GWs in different regions of the peeled image, a local spectrum peak centered band-pass filter is required. An adaptive filtering kernel was applied for denoising, scanning through the peeled image region by region and making band-pass filtering with the peak of each local spectrum.
Waves with horizontal wavelengths of less than 12 km ere too weak to be observed by ASAI [29], so the first three layers (n = 1, 2, 3) were superposed together (Figure 5a), containing noises and a few vague ripples. Ripples with wavelengths of 25 ± 2 km, possibly from breaking GWs, were marked in Figure 5b. These ripples were perpendicular to the local GWs shown in the following sub-figures (Figure 5c–f), indicating dynamical instability [14].
The peeled images of the fifth to ninth layers are represented in Figure 5c–g, respectively. The GWs at different scales are illustrated in the corresponding images and their wavelengths are listed in Table 2. The medium-scale GW of the 591 ± 75 km wavelength (Figure 5g) was rarely found on ground observation [18], because its wavelength was beyond the field of view of a single ASAI and can be only captured by the ASAI network. By extracting the medium-scale GW from various GW spectrums, DWT offers a new way to measure the parameters of medium-scale GW, especially the temporal information absent in low-earth orbit satellite observations.

Table 2.
Wavelength, horizontal speed, and relative fluctuation of quasi-monochromatic GWs with different scales. The values listed are the average and variance of multiple measurements.
A new assembled image (Figure 6) with clearer wave patterns than the original one (Figure 1) could be obtained by superposing all of the peeled and denoised images together. To derive the wave parameters, we selected the data along the green arrow in Figure 6, along which the waveforms were very clear in each peeled image. Except in layer 9 (Figure 5g), all of the measurements were made along this line in the corresponding images (shown in Table 2). The relative fluctuation Ir is defined as follows:
where Imax denotes the grayscale of the pixels at the wave peak. Iavg and I0avg are the mean value of the corresponding peeled image (shown in Figure 5) and the original image (Figure 1), respectively. As discussed in Section 3.2, the data extracted from the original image were the wave pattern only and the background was still left in the original image, so that I0avg was used as the denominator to compare the relative fluctuation between the different scales. Then, the horizontal propagation speeds were measured by tracking the movement of the wave peaks (Figure 7). The periods ere represented by the time interval between the peaks of relative fluctuation, shown in Figure 8.
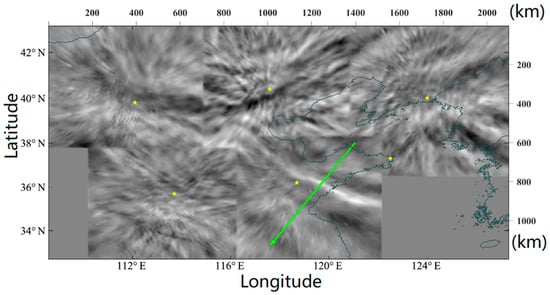
Figure 6.
Assembled airglow image after denoising. The axes above and to the right represent the position. The lower and left axes indicate the longitude and latitude, respectively. The ASAI stations are marked with yellow points. This image is obtained by superposing all of the images in Figure 5, showing wave patterns with more visibility than Figure 1. The green arrow indicates the propagating direction of the local GWs, which is perpendicular to most wave surfaces it crosses.
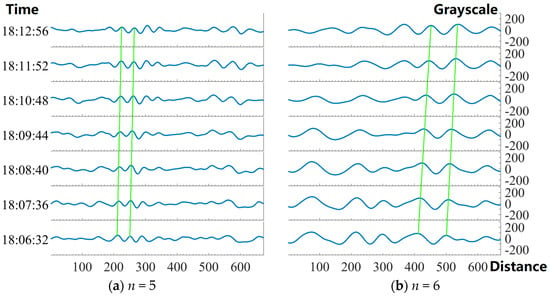
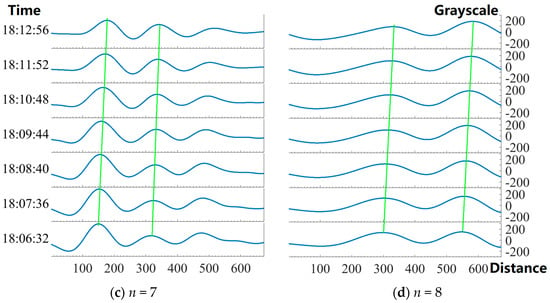
Figure 7.
Waveforms along the measuring line. Subfigures (a–d) represent the evolutions of wave forms in 5–8th layers, individually. The horizontal axes indicate the distance (in km) from the starting point of the green arrow. The left axes are the time (UTC) and the right axes are the grayscale. The green lines mark out the movement of wave peaks along the time.
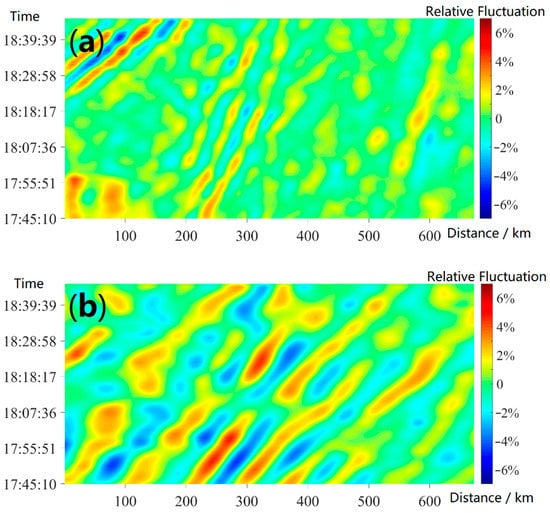
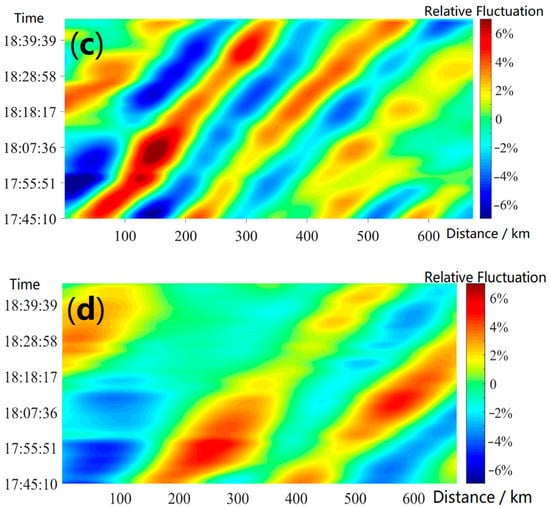
Figure 8.
Relative intensity change within one hour. (a–d) Measured along the measuring line in the layer of n = 5, 6, 7, 8, respectively. The horizontal axes denote the distance (in kilometer) from the starting point of the measuring line. The left vertical axes are the time (UTC). The right color bar indicates the relative fluctuation defined by Equation (12).
5. Discussion
Based on DWT, we extracted the wave patterns of different scales form the airglow image, ranging from ripples with wavelengths of 25 ± 2 km to medium-scale GWs with wavelengths of 591 ± 75 km. To our knowledge, the medium-scale GW in Figure 5g is the first report of continuous observation on the GWs with wavelengths of hundreds of kilometers. With the temporal information from ground-based observations, we could fill the gap of satellite observations of medium-scale GWs.
The waves are displayed in the corresponding peeled images separately, so that the propagation characteristics of the GW at different scales can be measured accurately without mutual interference. Table 2 shows that both the period and horizontal speed had positive correlations with the horizontal wavelength, except those for the horizontal speed of the 7th layer, which had a decreasing value. We need more statistical analysis in order to determine whether the obvious large amplitude of the GW in the 7th layer causes this exception.
The extraction based on DWT also provides a new method of noise reduction. The quasi-monochromatic GW was dominant in the frequency domain, so that the noise and other interferences could be effectively removed from the scan of the adaptive band-pass filtering kernel. An airglow image with more visible GWs could be obtained by superposing the peeled images together after denoising. A comparison of spectra and waveforms along the measuring line before (in Figure 1) and after (in Figure 6) denoising are shown in Figure 9. All of the grayscales of the pixels measured in the original image (Figure 1) were subtracted by their average to simply remove the mean background noise, leading to the missing peak at the zero point in the spectrum before denoising (Figure 9a). In the spectrum after denoising (Figure 9b), the noise of the high frequency and the frequency between the marked peaks were removed, besides the mean background noise. The marked peaks in Figure 9b corresponded to the frequency of the quasi-monochromatic GWs in layers 5, 6, 7, and 8, respectively. The peaks around 20 Hz indicate the mixed waves in layer 5 (Figure 5c). Due to the 1/f noise, whose power spectral density was inversely proportional to frequency, the peak values of the low frequency were higher than that of the high frequency. Figure 9c,d represents the waveform before and after denoise, from which we could see the waveform becomes smoother after denoise.
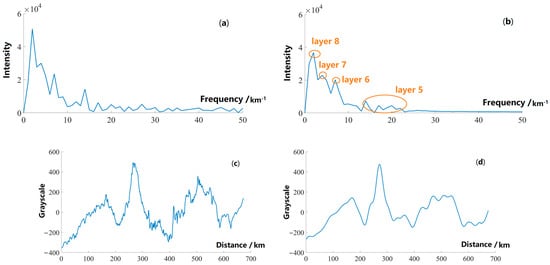
Figure 9.
Comparison before and after denoising. (a,b) The spectra before and after denoising, respectively. The horizontal axis is the frequency, and the vertical axis is the intensity. The intensity indicates the unnormalized proportion of the wave in the corresponding frequency band. (c,d) The waveforms before and after denoising, respectively. The horizontal axis is the distance from the starting point of the measuring line and the vertical axis denotes grayscale.
6. Conclusions
The algorithm based on DWT worked effectively for isolating the GWs of different scales in airglow images. The original airglow image was peeled into a series of image layers, taking the db wavelets of the different scales as their basis vectors, respectively. According to the order of the basis vector from small to large, the GWs were reconstructed in the image layer with the corresponding scale. In each peeled image, the reconstructed GW was a quasi-monochromatic wave.
The algorithm isolates the quasi-monochromatic GWs of different scales according to their wavelengths, expanding the research object from the strongest quasi-monochromatic GW to GWs of multiple scales in the airglow images. In addition, an airglow image with clearer wave patterns could be obtained via reconstructing the peeled images denoised by an adaptive band-pass filter kernel. Based on the observation of the ASAI network, the extraction algorithm can represent the temporal and spatial information of GWs of various scales, ranging from small-scale GWs of tens of kilometers, to medium-scale GWs of hundreds of kilometers. The denoise algorithm makes the wave patterns more visible in the image, which will be helpful in the auto detection of GW by machine learning [30]. We will also extend this method to satellite images (visible infrared imaging radiometer suit day night band). Compared with the wave patterns, the ground artificial light, which causes a serious disturbance in the satellite image, has the characteristics of a small scale and high spatial frequency. The denoise algorithm based on DWT provides a potential way to remove the disturbances in the satellite image, and makes the GWs in the image more visible for auto detection by machine learning.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/11/6/615/s1, Video S1: wave_4.DivX.avi. One-hour evolution of the GW isolated in layer 4 (shown in Figure 5b). Video S2: wave_5.DivX.avi. One-hour evolution of the GW isolated in layer 5 (shown in Figure 5c). Video S3: wave_6.DivX.avi. One-hour evolution of the GW isolated in layer 6 (shown in Figure 5d). Video S4: wave_7.DivX.avi. One-hour evolution of the GW isolated in layer 7 (shown in Figure 5e). Video S5: wave_8.DivX.avi. One-hour evolution of the GW isolated in layer 8 (shown in Figure 5f). Video S6: wave_9.DivX.avi. One-hour evolution of the GW isolated in layer 9 (shown in Figure 5g).
Author Contributions
Conceptualization, C.L.; methodology, C.L. and W.L.; software, W.L.; validation, C.L.; formal analysis, C.L.; investigation, W.L.; resources, W.Y.; data curation, Q.L.; writing—original draft preparation, C.L.; writing—review and editing, J.Y. and X.L.; visualization, W.L.; supervision, C.L.; project administration, J.X.; funding acquisition, J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (41831073 and 41874182), the Open Research Project of Large Research Infrastructures of CAS, “Study on the interaction between low-/mid-latitude atmosphere and ionosphere based on the Chinese Meridian Project”, and the Specialized Research Fund for State Key Laboratories.
Acknowledgments
We acknowledge the use of data from the Chinese Meridian Project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fritts, D.C. Gravity wave saturation in the middle atmosphere: A review of theory and observation. Rev. Geophys. 1984, 22, 275–308. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Hoffmann, L.; Xue, X.; Alexander, M.J. A global view of stratospheric gravity wave hostspots located with Atmospheric Infrared Sounder observations. J. Geophys. Res. Atmos. 2013, 118, 416–434. [Google Scholar] [CrossRef]
- Qian, L.; Burns, A.; Yue, J. Evidence of the lower thermospheric winter-to-summer circulation from SABER CO2 observation. Geophys. Res. Lett. 2017, 44, 10100–10107. [Google Scholar] [CrossRef]
- Smith, S.; Baumgardner, J.; Mendillo, M. Evidence of mesospheric gravity-waves generated by orographic forcing in the troposphere. Geophys. Res. Lett. 2009, 36, 8. [Google Scholar] [CrossRef]
- Plougonven, R.; Zhang, F.Q. Internal gravity waves from atmospheric jets and fronts. Rev. Geophys. 2014, 52, 33–76. [Google Scholar] [CrossRef]
- Yue, J.; Vadas, S.L.; She, C.Y.; Nakamura, T.; Reising, S.C.; Liu, H.-L.; Stamus, P.; Krueger, D.A.; Lyons, W.; Li, T. Concentric gravity waves in the mesosphere generated by deep convective plumes in the lower atmosphere near Fort Collins, Colorado. J. Geophys. Res. 2009, 114, D06104. [Google Scholar] [CrossRef]
- Vadas, S.; Yue, J.; Nakamura, T. Mesospheric concentric gravity waves generated by multiple convection storms over the North America Great Plain. J. Geophys. Res. Atmos. 2012, 117, D07113. [Google Scholar] [CrossRef]
- Suzuki, S.; Vadas, S.L.; Shiokawa, K.; Otsuka, Y.; Kawamura, S.; Murayama, Y. Typhoon-induced concentric airglow structures in the mesopause region. Geophys. Res. Lett. 2013, 40, 5983–5987. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, F. Mesoscale Gravity Waves in Moist Baroclinic Jet-Front Systems. J. Atmos. Sci. 2014, 71, 929–952. [Google Scholar] [CrossRef]
- Zhang, F.; Wei, J.; Zhang, M.; Bowman, K.B.; Pan, L.L.; Atlas, E.; Wofsy, S.C. Aircraft measurements of gravity waves in the upper troposphere and lower stratosphere during the START08 field experiment. Atmos. Chem. Phys. 2015, 15, 7667–7684. [Google Scholar] [CrossRef]
- Peterson, A.W.; Adams, G.W. OH airglow phenomena during the 5–6 July 1982 total lunar eclipse. Appl. Opt. 1983, 22, 2682–2685. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.H.; Dou, X.K.; Li, T.; Nakamura, T.; Xue, X.; Huang, C.; Manson, A.; Meek, C.; Thorsen, D.; Avery, S. Gravity wave characteristics in the mesopause region revealed from OH airglow imager observations over Northern Colorado. J. Geophys. Res. Space. 2016, 121, 9204–9221. [Google Scholar] [CrossRef]
- Hecht, J.H. Instability layers and airglow imaging. Rev. Geophys. 2004, 42, RG1001. [Google Scholar] [CrossRef]
- Gong, J.; Wu, D.L.; Eckermann, S.D. Gravity wave variances and propagation derived from AIRS radiances. Atmos. Chem. Phys. 2012, 12, 1701–1720. [Google Scholar]
- Miller, S.D.; Straka, W.C., III; Yue, J.; Smith, S.M.; Alexander, M.J.; Hoffmann, L.; Setvak, M.; Partain, P.T. Upper atmospheric gravity wave details revealed in nightglow satellite imagery. Proc. Natl. Acad. Sci. USA 2015, 112, E6728–E6735. [Google Scholar] [CrossRef]
- Xu, J.Y.; Li, Q.Z.; Yue, J.; Hoffmann, L.; Straka, W.C.; Wang, C.; Liu, M.; Yuan, W.; Han, S.; Miller, S.D.; et al. Concentric gravity waves over northern China observed by an airglow imager network and satellites. J. Geophys. Res. Atmos. 2015, 120, 11058–11078. [Google Scholar] [CrossRef]
- Cai, X.; Yuan, T.; Zhao, Y.; Pautet, P.D.; Taylor, M.J.; Pendleton, W.R. A coordinated investigation of the gravity wave breaking and the associated dynamical instability by a Na lidar and an Advanced Mesosphere Temperature Mapper over Logan, UT (41.7° N, 111.8° W). J. Geophys. Res. Space Physics. 2014, 119, 6852–6864. [Google Scholar] [CrossRef]
- Li, T.; She, C.Y.; Liu, H.L.; Montgomery, M.T. Evidence of a gravity wave breaking event and the estimation of wave characteristics from sodium lidar observation over Fort Collins, CO (41° N, 105° W). Geophys. Res. Lett. 2007, 34, L05815. [Google Scholar] [CrossRef]
- Fritts, D.C.; Isler, J.R.; Hecht, J.H.; Walterscheid, R.L.; Andreassen, O. Wave breaking signatures in sodium densities and OH nightglow: 2. Simulation of wave and instability structures. J. Geophys. Res. 1997, 102, 6669–6684. [Google Scholar] [CrossRef]
- Li, T.; She, C.Y.; Williams, B.P.; Yuan, T.; Collins, R.L.; Kieffaber, L.M.; Peterson, A.W. Concurrent OH imager and sodium temperature/wind lidar observation of localized ripples over northern Colorado. J. Geophys. Res. 2005, 110, D13110. [Google Scholar] [CrossRef]
- Swenson, G.R.; Mende, S.B. OH emission and gravity waves (including a breaking wave) in all-sky imagery from Bear Lake, UT. Geophys. Res. Lett. 1994, 21, 2239–2242. [Google Scholar] [CrossRef]
- Swenson, G.R.; Haque, R.; Yang, W.; Gardner, C.S. Momentum and energy fluxes of monochromatic gravity waves observed by an OH imager at Starfire Optical Range, New Mexico. J. Geophys. Res. Atmo. 1999, 104, 6067–6080. [Google Scholar] [CrossRef]
- Tang, J.; Kamalabadi, F.; Franke, S.J.; Liu, A.Z.; Swenon, G.R. Estimation of gravity wave momentum flux with spectroscopic. IEEE Trans. Geosci. Remote Sens. 2005, 43, 103. [Google Scholar] [CrossRef]
- Lai, C.; Yue, J.; Xu, J.Y.; Yuan, W.; Li, Q.Z.; Liu, X. Detection of large-scale concentric gravity waves from a Chinese airglow imager network. J. Atmos. Sol. Terr. Phy. 2018, 171, 269–276. [Google Scholar] [CrossRef]
- Li, Q.Z.; Xu, J.Y.; Yue, J.; Yuan, W.; Liu, X. Statistical characteristics of gravity wave activities observed by an OH airglow imager at Xinglong, in northern China. Ann. Geophys. 2011, 29, 1401–1410. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets. 1992, pp. 129–133. Available online: https://epubs.siam.org/doi/abs/10.1137/1.9781611970104?mobileUi=0& (accessed on 16 April 2020).
- Daubechies, I. Orthonormal bases of compactly supported wavelets. Commun. Pur. Appl. Math. 1988, 41, 909–996. [Google Scholar] [CrossRef]
- Swenson, G.; Alexander, M.; Haque, R. Dispersion imposed limits on atmospheric gravity waves in the mesosphere: Observations from OH airglow. Geopys. Res. Lett. 2000, 27, 875–878. [Google Scholar] [CrossRef]
- Lai, C.; Xu, J.; Yue, J.; Yuan, W.; Liu, X.; Li, W.; Li, Q. Automatic Extraction of Gravity Waves from All-Sky Airglow Image Based on Machine Learning. Remote Sens. 2019, 11, 1516. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).