SARIMA Approach to Generating Synthetic Monthly Rainfall in the Sinú River Watershed in Colombia
Abstract
1. Introduction
2. Materials and Methods
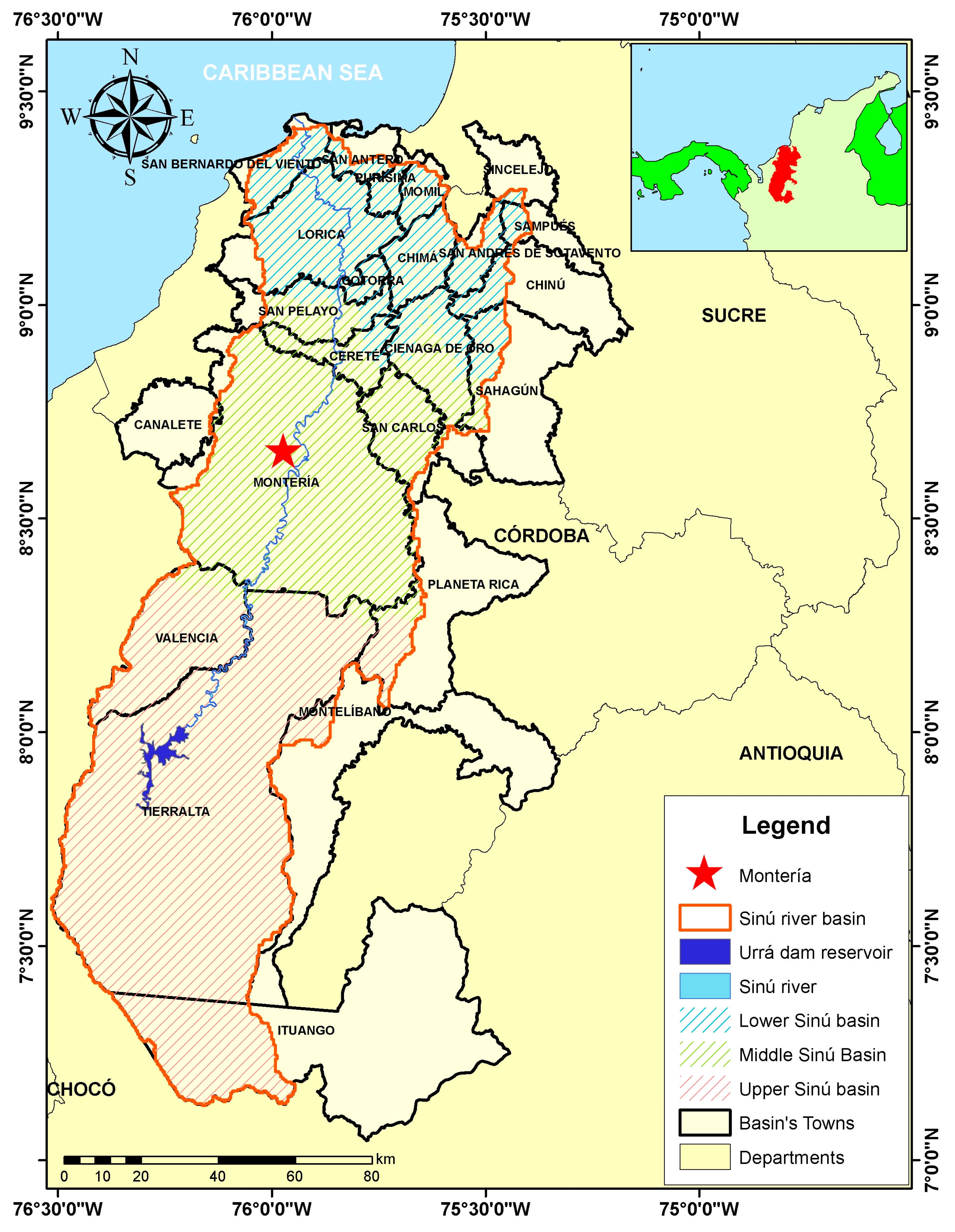
2.1. Study Area
2.2. SARIMA Models
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dastorani, M.; Mirzavand, M.; Dastorani, M.T.; Sadatinejad, S.J. Comparative study among different time series models applied to monthly rainfall forecasting in semi-arid climate condition. Nat. Hazards 2016, 81, 1811–1827. [Google Scholar] [CrossRef]
- Venkata, R.R.; Krishna, B.; Kumar, S.R.; Pandey, N.G. Monthly rainfall prediction using wavelet neural network analysis. Water Resour. Manag. 2013, 27, 3697–3711. [Google Scholar] [CrossRef]
- Li, Y.P.; Nie, S.; Huang, C.Z.; McBean, E.A.; Fan, Y.R.; Huang, G.H. An integrated risk analysis method for planning water resource systems to support sustainable development of an arid region. J. Environ. Inform. 2017, 29, 1–15. [Google Scholar] [CrossRef]
- Radhakrishnan, P.; Dinesh, S. An alternative approach to characterize time series data: Case study on Malaysian rainfall data. Chaos Solitons Fractals 2006, 27, 511–518. [Google Scholar] [CrossRef]
- Wang, S.; Feng, J.; Liu, G. Application of seasonal time series model in the precipitation forecast. Math. Comput. Model. 2013, 58, 677–683. [Google Scholar] [CrossRef]
- Chang, T.J.; Kavvas, M.L.; Delleur, J.W. Daily precipitation modelling by discrete autoregressive moving average processes. Water Resour. Res. 1984, 20, 565–580. [Google Scholar] [CrossRef]
- Ben, A.M.A.; Chebana, F.; Ouarda, T.B.M.J. Probabilistic multisite statistical downscaling for daily precipitation using a Bernoulli-generalized pareto multivariate autoregressive model. J. Clim. 2015, 28, 2349–2364. [Google Scholar] [CrossRef]
- Kim, J.W.; Kim, K.Y.; Kim, M.K.; Cho, C.H.; Lee, Y.; Lee, J. Statistical multisite simulations of summertime precipitation over South Korea and its future change based on observational data. Asia-Pac. J. Atmos. Sci. 2013, 49, 687–702. [Google Scholar] [CrossRef]
- Chatfield, C.; Xing, H. The Analysis of Time Series an Introduction with R, 7th ed.; Chapman and Hall/CRC: London, UK, 2019; ISBN 978-1-4987-9563-0. [Google Scholar]
- Yule, G.U. Why do we sometimes get nonsense-correlations between time-series?—A study in sampling and the nature of time-series. J. R. Stat. Soc. 1926, 89, 1. [Google Scholar] [CrossRef]
- Yule, G.U. On a method of investigating periodicities in disturbed series, with special reference to Wolfer’s sunspot numbers. J. R. Stat. Soc. 1927, 226, 267–298. [Google Scholar]
- Slutzky, E. the summation of random causes as the source of cyclic processes. Econometrica 1937, 5, 105–146. [Google Scholar] [CrossRef]
- Wold, H.O. The Analysis of Stationary Time Series, 1st ed.; Almqvist & Wiksells boktrycheri ab: Estocolmo, Sweden, 1954; ISBN B00086YNV8. [Google Scholar]
- Cox, D.R.; Miller, H.D. The Theory of Stochastic Processes, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 1977; ISBN 0-412-15170-7. [Google Scholar]
- Sanvicente-Sánchez, H.; Solís-Alvarado, Y. Generator of synthetic rainfall time series through markov hidden states. In Computational Science and Its Applications—ICCSA 2008; Springer: Berlin, Germany, 2008; Volume 5073, pp. 959–969. ISBN 3-540-69840-X. [Google Scholar]
- Lee, T. Stochastic simulation of precipitation data for preserving key statistics in their original domain and application to climate change analysis. Theor. Appl. Climatol. 2015, 124, 91–102. [Google Scholar] [CrossRef]
- Papalaskaris, T.; Panagiotidis, T.; Pantrakis, A. Stochastic monthly rainfall time series analysis, modeling and forecasting in Kavala City, Greece, North-Eastern Mediterranean Basin. Procedia Eng. 2016, 162, 254–263. [Google Scholar] [CrossRef]
- Cantet, P.; Arnaud, P. Gains from modelling dependence of rainfall variables into a stochastic model: Application of the copula approach at several sites. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 11227–11266. [Google Scholar] [CrossRef]
- Bang, S.; Bishnoi, R.; Chauhan, A.S.; Dixit, A.K.; Chawla, I. Fuzzy logic based crop yield prediction using temperature and rainfall parameters predicted through ARMA, SARIMA, and ARMAX models. In Proceedings of the 2019 Twelfth International Conference on Contemporary Computing (IC3), Noida, India, 8–10 August 2019; pp. 1–6. [Google Scholar]
- NOAA (National Centers for Environmental Information). Equatorial Pacific Sea Surface Temperatures; NOAA: Silver Spring, MD, USA, 2017.
- Sun, H.; Furbish, D.J. Annual precipitation and river discharges in Florida in response to El Niño- and La Niña-sea surface temperature anomalies. J. Hydrol. 1997, 199, 74–87. [Google Scholar] [CrossRef]
- Ubilava, D.; Helmers, C.G. Forecasting ENSO with a smooth transition autoregressive model. Environ. Model. Softw. 2013, 40, 181–190. [Google Scholar] [CrossRef]
- Arganis, J.M.L.; Dominguez, M.R.; Fuentes, M.G.; Gutierrez-Lopez, A. Synthetic generation of monthly sea surface temperatures in “El Niño” regions by means of the Fiering-Svanidze method. Atmósfera 2010, 23, 367–386. [Google Scholar]
- Gershenfeld, N.A.; Weigend, A.S. The Future of Time Series; Xerox Corporation, Palo Alto Research Center: Palo Alto, CA, USA, 1993. [Google Scholar]
- Babovic, V. Data mining in hydrology. Hydrol. Process. 2005, 19, 1511–1515. [Google Scholar] [CrossRef]
- Babovic, V.; Keijzer, M. Forecasting of river discharges in the presence of chaos and noise. Flood Issues Contemp. Water Manag. 2000, 405–419. [Google Scholar] [CrossRef]
- Sun, Y.; Babovic, V.; Chan, E.S. Multi-step-ahead model error prediction using time-delay neural networks combined with chaos theory. J. Hydrol. 2010, 395, 109–116. [Google Scholar] [CrossRef]
- Yu, X.; Liong, S.Y.; Babovic, V. EC-SVM approach for real-time hydrologic forecasting. J. Hydroinformat. 2004, 6, 209–223. [Google Scholar] [CrossRef]
- Keller, D.E.; Fischer, A.M.; Frei, C.; Liniger, M.A.; Appenzeller, C.; Knutti, R. Stochastic modelling of spatially and temporally consistent daily precipitation time-series over complex topography. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 8737–8777. [Google Scholar] [CrossRef]
- Breinl, K.; Turkington, T.; Stowasser, M. Simulating daily precipitation and temperature: A weather generation framework for assessing hydrometeorological hazards. Meteorol. Appl. 2015, 22, 334–347. [Google Scholar] [CrossRef]
- Chapman, T.G. Stochastic models for daily rainfall in the Western Pacific. Math. Comput. Simul. 1997, 43, 351–358. [Google Scholar] [CrossRef]
- Sharma, A.; Lall, U. A nonparametric approach for daily rainfall simulation. Math. Comput. Simul. 1999, 48, 361–371. [Google Scholar] [CrossRef]
- Carvajal, E.Y.; Segura, J.B.M. Modelos multivariados de predicción de caudal mensual utilizando variables macroclimáticas. Caso de estudio Río Cauca, Colombia. Rev. Ing. Y Compet. 2005, 7, 18–32. [Google Scholar]
- Mohammadi, K.; Eslami, H.R.; Kahawita, R. Parameter estimation of an ARMA model for river flow forecasting using goal programming. J. Hydrol. 2006, 331, 293–299. [Google Scholar] [CrossRef]
- Chao, Z.; Hua-sheng, H.; Wei-min, B.; Luo-ping, Z. Robust recursive estimation of auto-regressive updating model parameters for real-time flood forecasting. J. Hydrol. 2008, 349, 376–382. [Google Scholar] [CrossRef]
- Akpanta, A.C.; Okorie, I.E.; Okoye, N.N. SARIMA modelling of the frequency of monthly rainfall in Umuahia, Abia State of Nigeria. Am. J. Math. Stat. 2015, 5, 82–87. [Google Scholar] [CrossRef]
- Mahmud, I.; Bari, S.H.; Ur Rahman, M.T. Monthly rainfall forecast of Bangladesh using autoregressive integrated moving average method. Environ. Eng. Res. 2017, 22, 162–168. [Google Scholar] [CrossRef]
- Etuk, E.H.; Moffat, I.U.; Chims, B.E. Modelling monthly rainfall data of Port Harcourt, Nigeria by Seasonal Box-jenkins methods. Int. J. Sci. 2013, 2, 1–8. [Google Scholar]
- Lata, K.; Misra, A.K. The influence of forestry resources on rainfall: A deterministic and stochastic model. Appl. Math. Model. 2020, 81, 673–689. [Google Scholar] [CrossRef]
- Berhane, T.; Shibabaw, N.; Awgichew, G.; Kebede, T. Option pricing of weather derivatives based on a stochastic daily rainfall model with Analogue Year component. Heliyon 2020, 6, e03212. [Google Scholar] [CrossRef] [PubMed]
- Cujia, A.; Agudelo-Castañeda, D.; Pacheco-Bustos, C.; Teixeira, E.C. Forecast of PM10 time-series data: A study case in Caribbean cities. Atmos. Pollut. Res. 2019, 10, 2053–2062. [Google Scholar] [CrossRef]
- Jing, Z.; An, W.; Zhang, S.; Xia, Z. Flood control ability of river-type reservoirs using stochastic flood simulation and dynamic capacity flood regulation. J. Clean. Prod. 2020, 257, 120809. [Google Scholar] [CrossRef]
- Corporación Autónoma Regional de los Valles del Sinú y San Jorge (CVS). Fases de Prospección y Formulación Del Plan de Ordenamiento y Manejo Integral de la Cuenca Hidrográfica del RÍO SINÚ (POMCA-RS); CVS: Montería, Colombia, 2006. [Google Scholar]
- Valbuena, D.L. Geomorfología y Condiciones Hidráulicas del Sistema Fluvial del RÍO SINÚ. Integración Multiescalar. 1945–1999–2016. Ph.D. Thesis, Universidad Nacional de Colombia, Bogotá, Colombia, 2017. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; Hill, M.G., Ed.; Tata McGraw-Hill Education: New York, NY, USA, 1988; ISBN 0-07-010810-2. [Google Scholar]
- Esquivel, G.; Cerano, J.; Sánchez, I.; López, A.; Gutiérrez, O.G. Validación del modelo ClimGen en la estimación de variables de clima ante escenarios de datos faltantes con fines de modelación de procesos. Tecnol. Cienc. Agua 2015, VI, 117–130. [Google Scholar]
- Mckague, K.; Rudra, R.; Ogilvie, J. ClimGen—A convenient weather generation tool for Canadian Climate Stations. In Proceedings of the Meeting of the CSAE/SCGR Canadian Society for Engineering in Agricultural Food and Biological Systems, Montreal, QC, Canada, 6–9 July 2003; pp. 1–26. [Google Scholar]
- Dabral, P.P.; Murry, M.Z. Modelling and forecasting of rainfall time series using SARIMA. Environ. Process. 2017, 4, 399–419. [Google Scholar] [CrossRef]
- Nury, A.H.; Hasan, K.; Alam, M.J.B. Comparative study of wavelet-ARIMA and wavelet-ANN models for temperature time series data in northeastern Bangladesh. J. King Saud Univ. Sci. 2017, 29, 47–61. [Google Scholar] [CrossRef]
- Chatfield, C. Time-Series Forecasting, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2000; ISBN 978-1-4200-3620-6. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Ahaneku, I.E.; Otache, Y.M. Stochastic characteristics and modelling of monthly rainfall time series of Ilorin, Nigeria. Open J. Mod. Hydrol. 2014, 4, 67–79. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis Forecasting and Control; Prentice-Hall: Upper Saddle River, NJ, USA, 1994; ISBN 0253-9624. [Google Scholar]
- Salas, J.D.; Obeysekera, J.T.B. ARMA model identification of hydrologic time series. Water Resour. Res. 1982, 18, 1011–1021. [Google Scholar] [CrossRef]
- Burlando, P.; Rosso, R.; Cadavid, L.G.; Salas, J.D. Forecasting of short-term rainfall using ARMA models. J. Hydrol. 1993, 144, 193–211. [Google Scholar] [CrossRef]
- Ljung, G.M.; Box, G.E.P. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the Second Inernational Symposium on Information Theory, Tsahkadsor, Armenia, 2–8 September 1973; pp. 267–281. [Google Scholar]
- Said, S.E.; Dickey, D.A. Testing for unit roots in autoregressive-moving average models of unknown order. Biometrika 1984, 71, 599–607. [Google Scholar] [CrossRef]
- Mendenhall, W.; Beaver, R.J.; Beaver, B.M. Introduction to Probability and Statistics, 14th ed.; Cengage Learning: Boston, MA, USA, 2012; ISBN 978-1-133-10375-2. [Google Scholar]
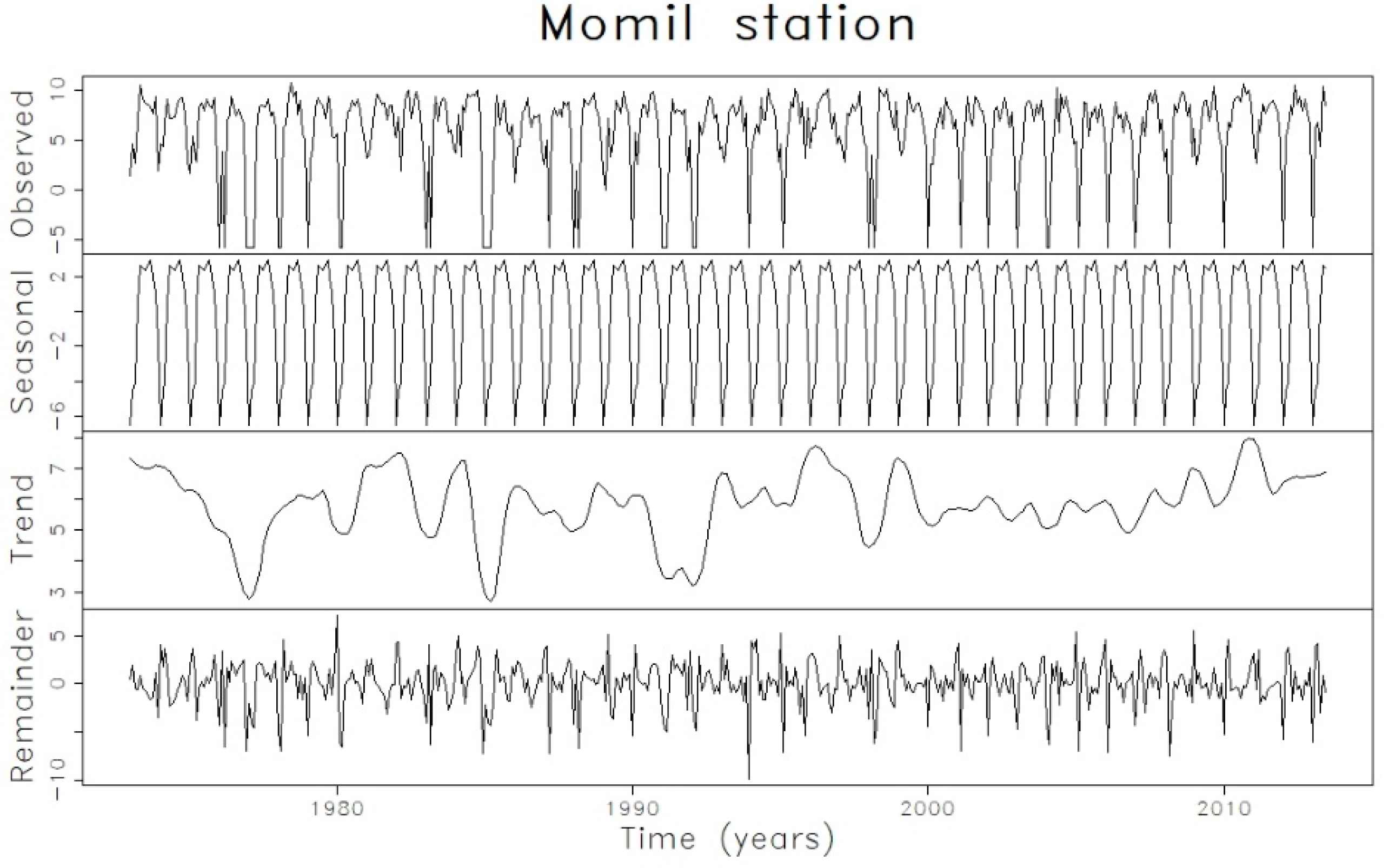
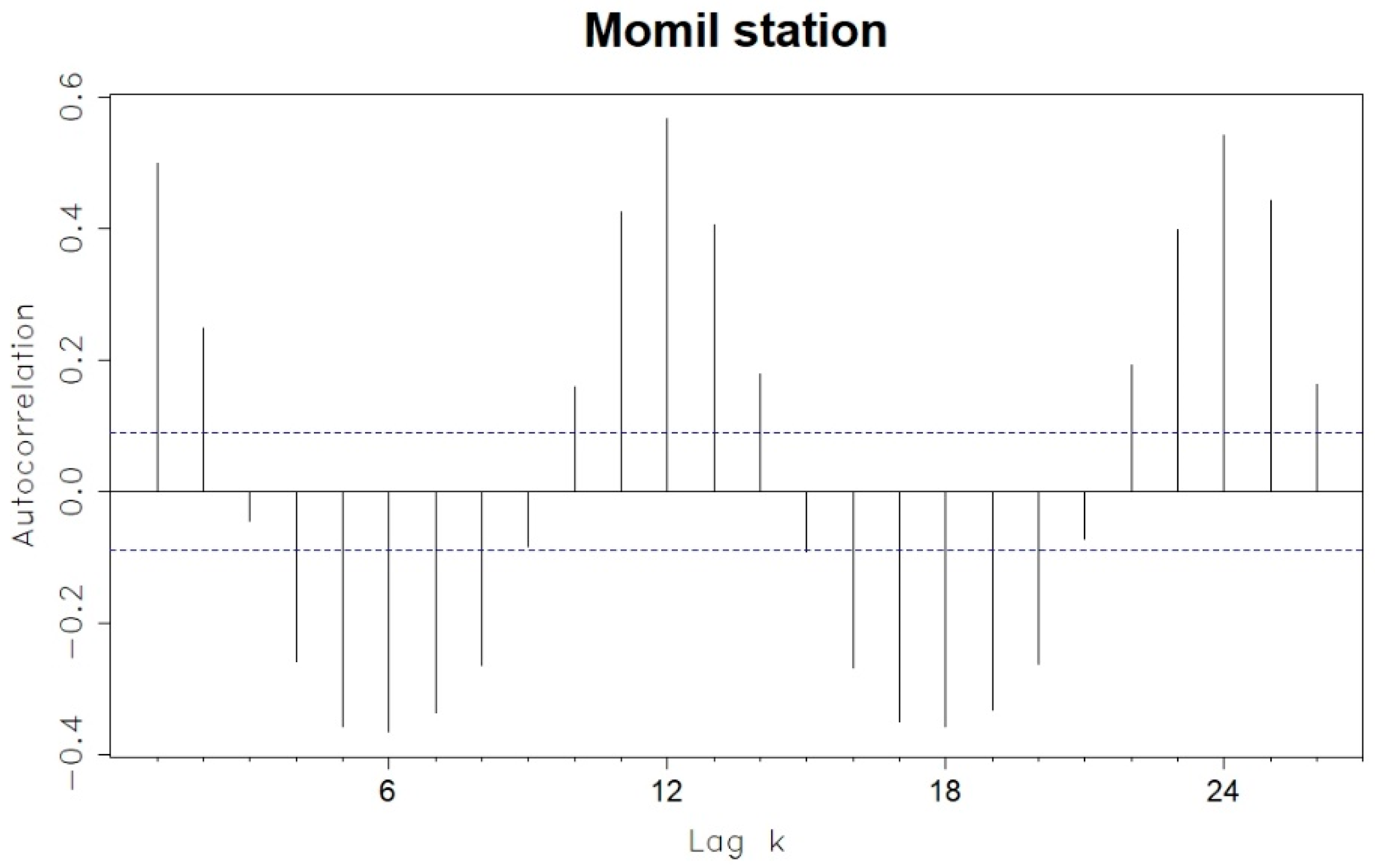
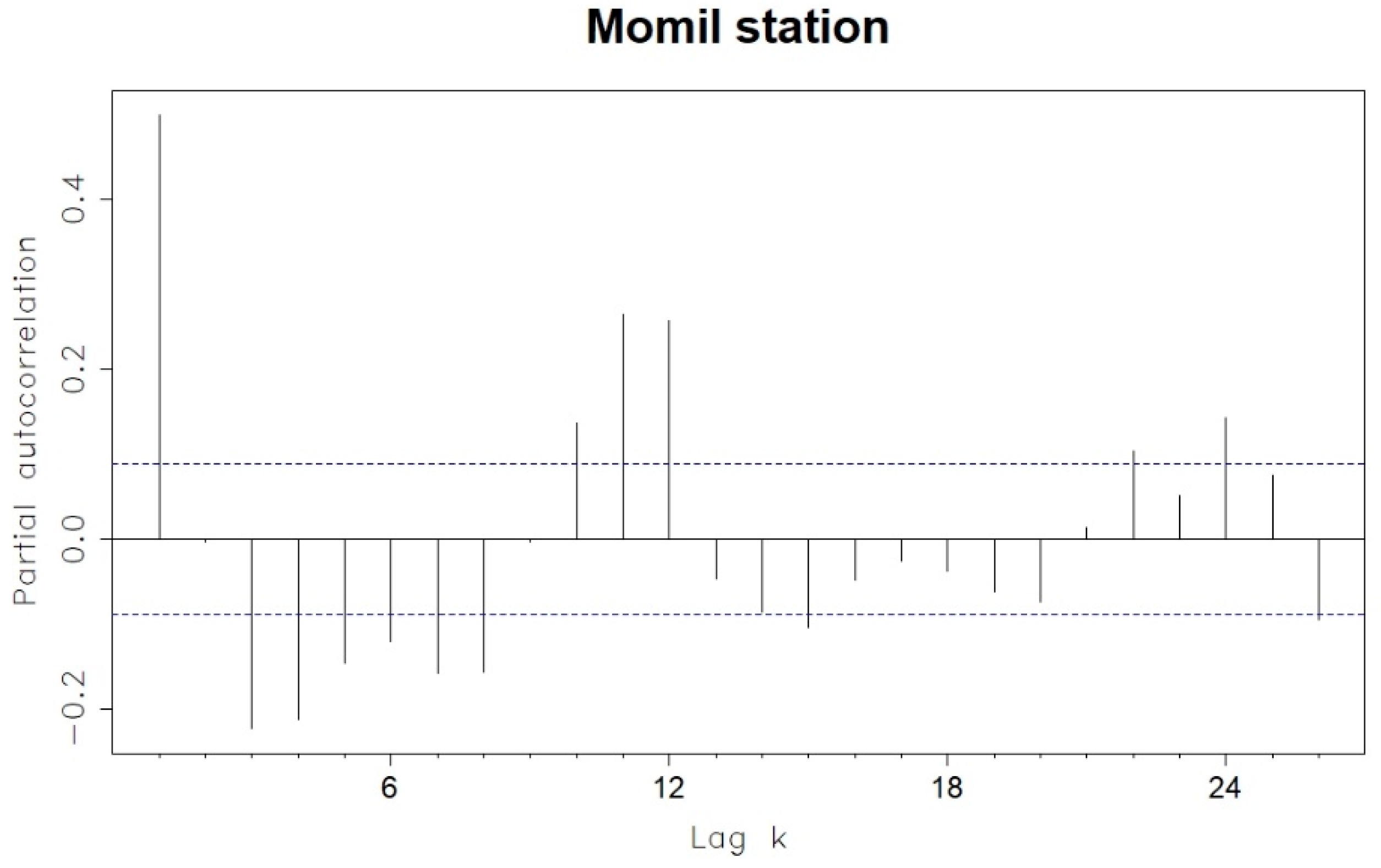
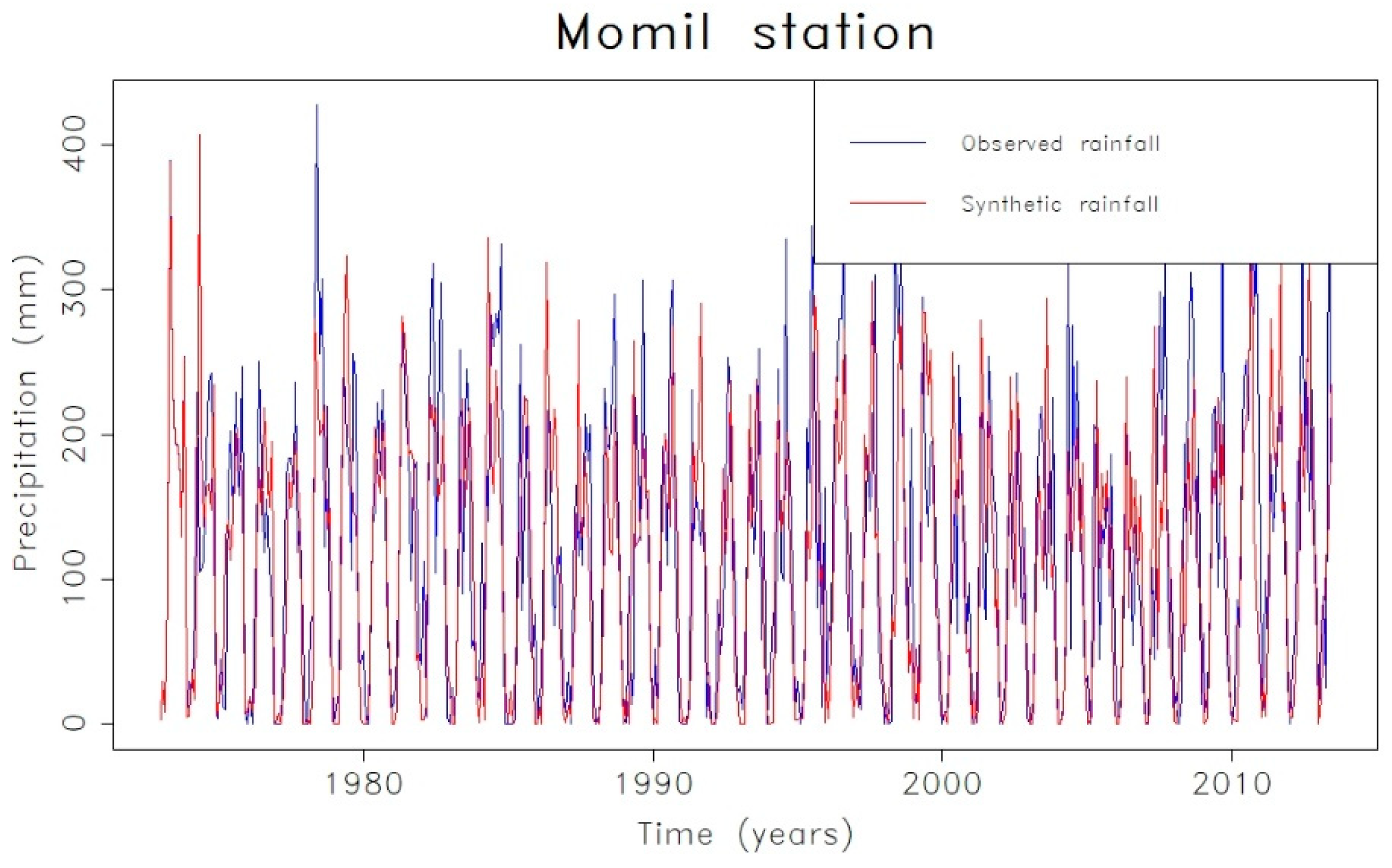
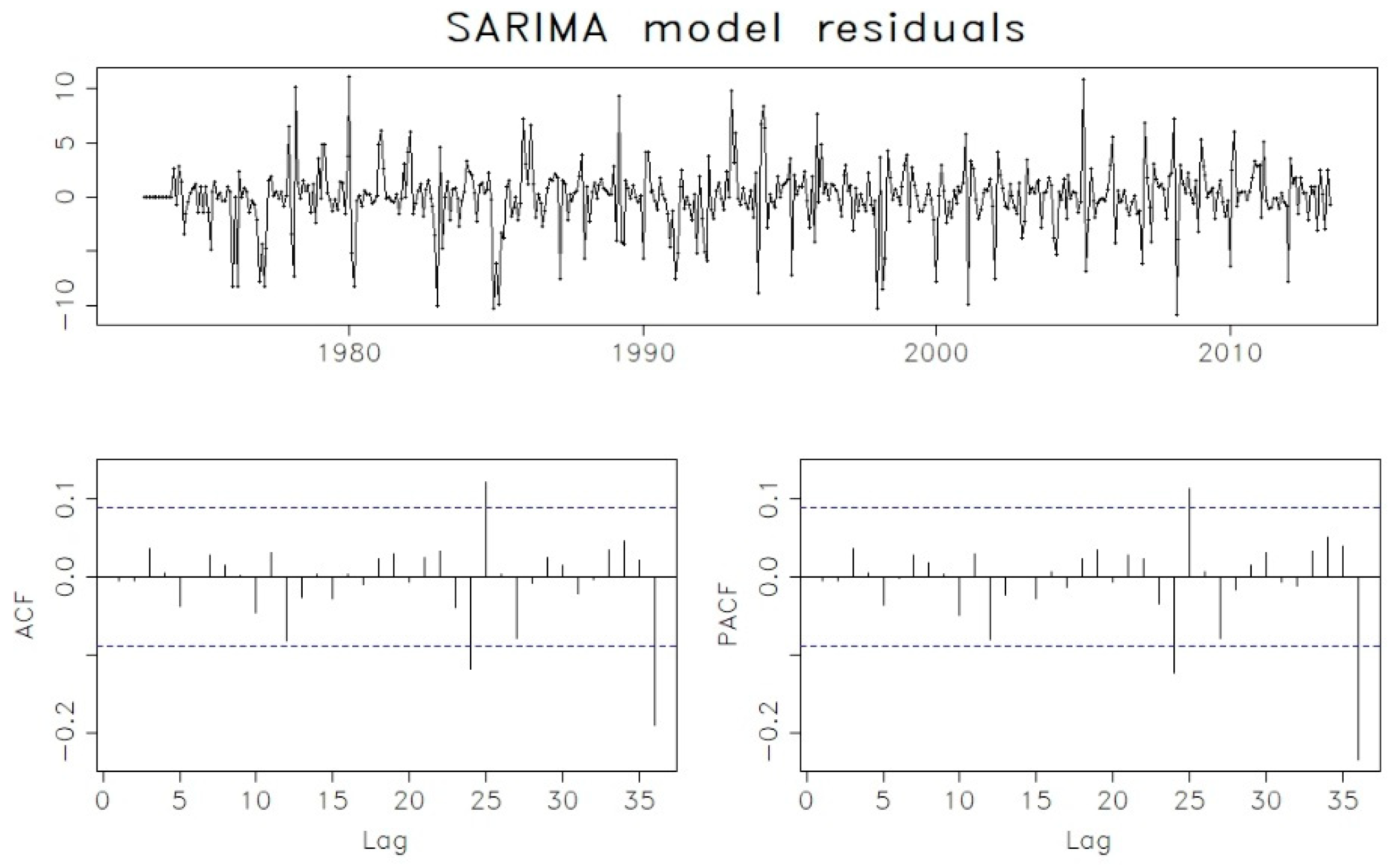
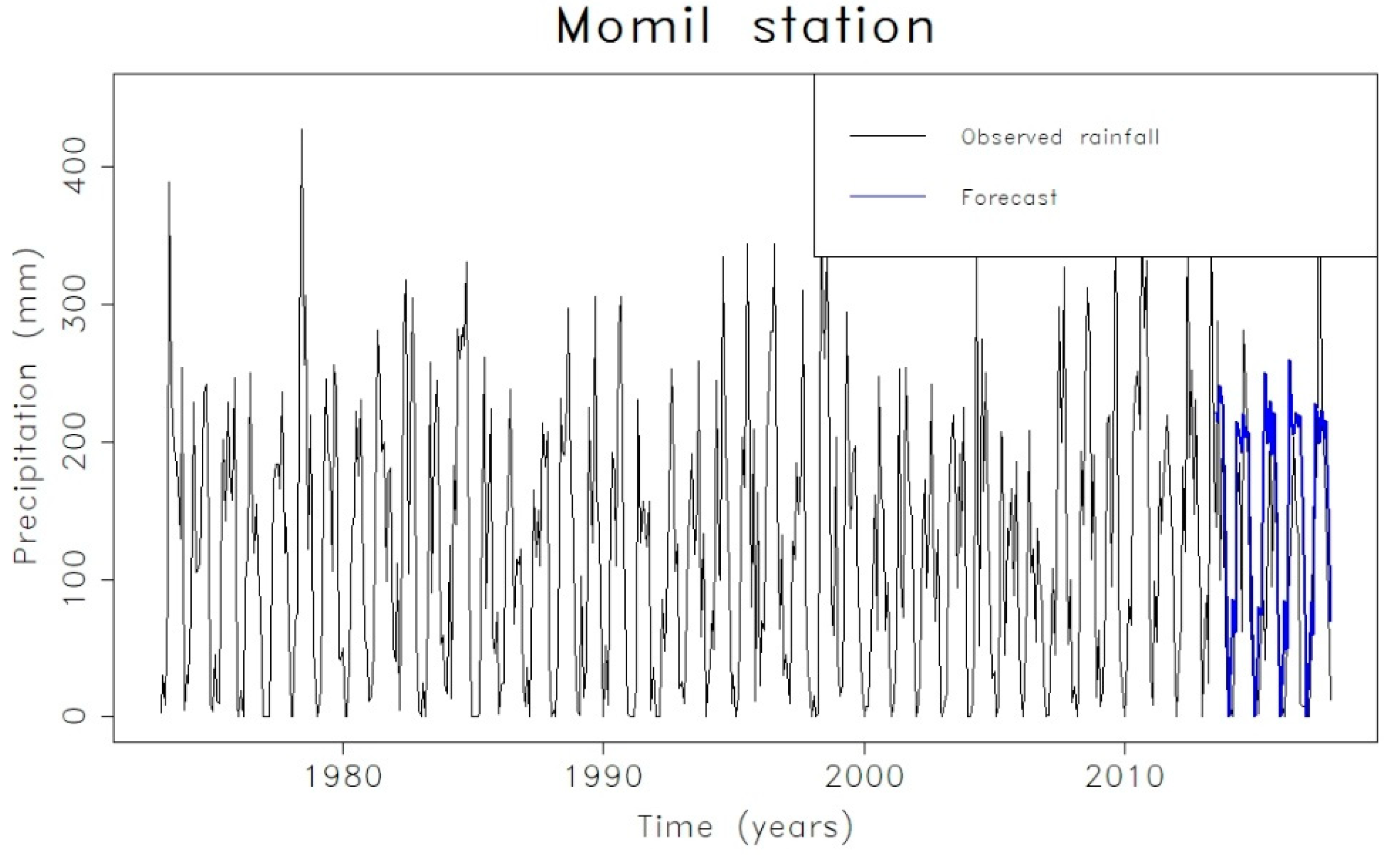
| Model | AIC |
|---|---|
| SARIMA(2,0,0) × (2,1,0)12 | 2433.599 |
| SARIMA(1,0,2) × (2,1,0)12 | 2435.017 |
| SARIMA(3,0,0) × (2,1,0)12 | 2435.188 |
| SARIMA(2,0,1) × (2,1,0)12 | 2435.246 |
| Sample | Mean | Significance Level | Confidence Interval Lower Limit | Confidence Interval Upper Limit | p-Value |
|---|---|---|---|---|---|
| Calibration vector | 120.4084 | 5% | −3.146883 | 20.391518 | 0.1508 |
| Synthetic series | 111.7861 | ||||
| Validation vector | 107.9265 | 2% | −0.8160514 | 79.6505786 | 0.02259 |
| Forecast | 147.3437 |
| Climatogical Station | SARIMA Model | ϕ1 | ϕ2 | ϕ3 | θ1 | θ2 | θ3 | Φ1 | Φ2 | Θ1 | Θ2 | µD |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Loma Verde | (0,0,0)(0,1,1)12 | −0.8834 | ||||||||||
| El Siglo | (0,0,0)(0,1,2)12 | −1.0793 | 0.2068 | |||||||||
| California | (0,0,0)(2,1,0)12 | −0.6461 | −0.3850 | |||||||||
| Colomboy | (0,0,0)(2,1,0)12 | −0.6755 | −0.2983 | |||||||||
| Planeta Rica | (0,0,0)(2,1,0)12 | −0.6189 | −0.3164 | |||||||||
| Sahagún | (0,0,0)(2,1,0)12 | −0.682 | −0.349 | |||||||||
| Mocarí | (0,0,0)(2,1,0)12 | −0.6398 | −0.3180 | |||||||||
| Cotorra | (0,0,0)(2,1,1)12 | −0.0295 | −0.0545 | −0.8652 | ||||||||
| San Francisco del Rayo | (0,0,0)(2,1,2)12 | 0.4976 | −0.1149 | −1.4319 | 0.4998 | |||||||
| Lorica (13080020) | (0,0,1)(0,1,1)12 | 0.2257 | −0.7728 | |||||||||
| Aguas Mohosas | (0,0,1)(2,1,0)12 | 0.1256 | −0.7689 | −0.3523 | ||||||||
| Ciénaga de Oro | (0,0,1)(2,1,0)12 | 0.2233 | −0.7156 | −0.3461 | ||||||||
| Rabolargo | (0,0,1)(2,1,0)12 | 0.1902 | −0.5654 | −0.2140 | ||||||||
| Sta Lucia | (0,0,1)(2,1,0)12 | 0.2207 | −0.7197 | −0.3296 | ||||||||
| Sta Rosa | (0,0,1)(2,1,0)12 | 0.2514 | −0.6611 | −0.3805 | ||||||||
| Cerro Bahía | (0,0,1)(2,1,2)12 | 0.2661 | −0.8306 | −0.2828 | −0.1806 | −0.5501 | 0.0012 | |||||
| Villa Marcela | (0,0,2)(0,1,1)12 | 0.2154 | 0.269 | −0.7186 | ||||||||
| Cristo Rey | (0,0,2)(2,1,0)12 | 0.2167 | 0.1387 | −0.7206 | −0.3576 | |||||||
| Lorica_(13085020) | (0,0,2)(2,1,0)12 | 0.1615 | 0.1828 | −0.6843 | −0.3757 | |||||||
| Galan | (0,0,2)(2,1,0)12 | 0.1478 | 0.1158 | −0.6043 | −0.2768 | |||||||
| Berastegui | (0,0,3)(0,1,2)12 | −0.0146 | 0.106 | 0.1564 | −0.9694 | 0.0969 | ||||||
| La Doctrina | (0,0,3)(2,1,0)12 | 0.2198 | 0.1056 | 0.1546 | −0.6658 | −0.3496 | ||||||
| Apto Los Garzones | (0,0,3)(2,1,0)12 | 0.0402 | 0.0749 | 0.1227 | −0.5984 | −0.3440 | ||||||
| Turipaná | (0,0,3)(2,1,0)12 | 0.0707 | 0.0833 | 0.0861 | −0.6659 | −0.3591 | ||||||
| Centro Alegre | (1,0,0)(0,1,1)12 | 0.1299 | −0.8857 | |||||||||
| San Antonio | (1,0,0)(0,1,1)12 | 0.1667 | −0.8655 | |||||||||
| Caramelo | (1,0,0)(2,1,0)12 | 0.0657 | −0.6017 | −0.3545 | ||||||||
| Buenos Aires | (1,0,0)(2,1,0)12 | 0.0999 | −0.6416 | −0.3361 | ||||||||
| Carrillo | (1,0,0)(2,1,0)12 | 0.2737 | −0.6719 | −0.3577 | ||||||||
| Chimá | (1,0,0)(2,1,0)12 | 0.1147 | −0.6356 | −0.294 | ||||||||
| Chinú | (1,0,0)(2,1,0)12 | 0.1063 | −0.7288 | −0.3523 | ||||||||
| La Esmeralda | (1,0,0)(2,1,0)12 | 0.1934 | −0.7593 | −0.4226 | ||||||||
| Jobo El Tablón | (1,0,0)(2,1,0)12 | 0.1458 | −0.6508 | −0.3557 | ||||||||
| Lamas 3 | (1,0,0)(2,1,0)12 | 0.1994 | −0.6914 | −0.4064 | ||||||||
| Montería | (1,0,0)(2,1,0)12 | 0.1859 | −0.6725 | −0.3422 | ||||||||
| Sabana Nueva | (1,0,0)(2,1,0)12 | 0.2379 | −0.6474 | −0.346 | ||||||||
| Sincelejo | (1,0,0)(2,1,0)12 | 0.2976 | −0.6623 | −0.3649 | ||||||||
| Tierralta | (1,0,0)(2,1,0)12 | 0.193 | −0.6672 | −0.2934 | ||||||||
| Venecia | (1,0,0)(2,1,0)12 | 0.2314 | −0.6749 | −0.3314 | ||||||||
| Coroza 1 | (1,0,0)(2,1,0)12 | 0.1853 | −0.5819 | −0.3239 | ||||||||
| Maracayo | (1,0,0)(2,1,0)12 | 0.0946 | −0.6326 | −0.3116 | ||||||||
| San Carlos | (1,0,0)(2,1,0)12 | 0.2240 | −0.7045 | −0.3688 | ||||||||
| Sta Cruz Hda | (1,0,0)(2,1,0)12 | 0.1214 | −0.6337 | −0.2864 | ||||||||
| La Despensa | (1,0,0)(2,1,1)12 | 0.2429 | −0.0524 | −0.0393 | −0.876 | |||||||
| Univ de Córdoba | (1,0,0)(2,1,1)12 | 0.1578 | −0.0136 | −0.0165 | −0.8869 | |||||||
| Palma de Vino | (1,0,0)(2,1,2)12 | 0.2719 | 0.4669 | −0.2038 | −1.3881 | 0.5083 | ||||||
| Sabanal | (1,0,0)(2,1,2)12 | 0.1481 | 0.4505 | −0.1412 | −1.3249 | 0.408 | ||||||
| Pica Pica | (1,0,1)(0,1,2)12 | 0.8508 | −0.7203 | −1.0251 | 0.1244 | |||||||
| El Cielo | (1,0,1)(1,1,2)12 | 0.8734 | −0.4547 | 0.5283 | −1.6284 | 0.6619 | 0.0057 | |||||
| Boca de la Ceiba | (1,0,1)(2,1,0)12 | 0.6920 | −0.5635 | −0.6869 | −0.3355 | |||||||
| Carrizal | (1,0,1)(2,1,0)12 | 0.8387 | −0.7691 | −0.7033 | −0.2817 | |||||||
| Coroza 2 | (1,0,1)(2,1,0)12 | 0.6065 | −0.4798 | −0.6835 | −0.3534 | |||||||
| Horizonte | (1,0,1)(2,1,0)12 | 0.7063 | −0.557 | −0.6029 | −0.2798 | |||||||
| Jaraguay | (1,0,1)(2,1,0)12 | 0.9261 | −0.7508 | −0.6285 | −0.3626 | |||||||
| El Limón | (1,0,1)(2,1,0)12 | 0.6210 | −0.5041 | −0.6884 | −0.3463 | |||||||
| San Anterito | (1,0,1)(2,1,0)12 | 0.8305 | −0.6224 | −0.6904 | −0.3417 | |||||||
| Tampa | (1,0,1)(2,1,0)12 | 0.8516 | −0.7476 | −0.652 | −0.3254 | |||||||
| El Trapiche | (1,0,1)(2,1,0)12 | 0.8098 | −0.6725 | −0.5771 | −0.3797 | |||||||
| Villa Arteaga | (1,0,1)(2,1,0)12 | 0.804 | −0.6505 | −0.6582 | −0.2823 | |||||||
| La Pastora | (1,0,2)(0,1,1)12 | 0.9727 | −0.8175 | −0.0911 | −0.8712 | |||||||
| Sajonia Hda | (1,0,2)(0,1,1)12 | 0.9534 | −0.7198 | −0.1231 | −0.8531 | |||||||
| Trementino | (1,0,2)(0,1,2)12 | −0.9449 | 1.1363 | 0.2131 | −0.9278 | 0.0373 | ||||||
| Callemar | (1,0,3)(0,1,1)12 | 0.9875 | −0.7092 | −0.0832 | −0.1580 | −0.8647 | ||||||
| Apto Berastegui | (2,0,0)(2,1,0)12 | 0.1331 | 0.1471 | −0.5945 | −0.3333 | |||||||
| Flor del Sinú | (2,0,0)(2,1,0)12 | 0.0941 | 0.1483 | −0.6181 | −0.3056 | |||||||
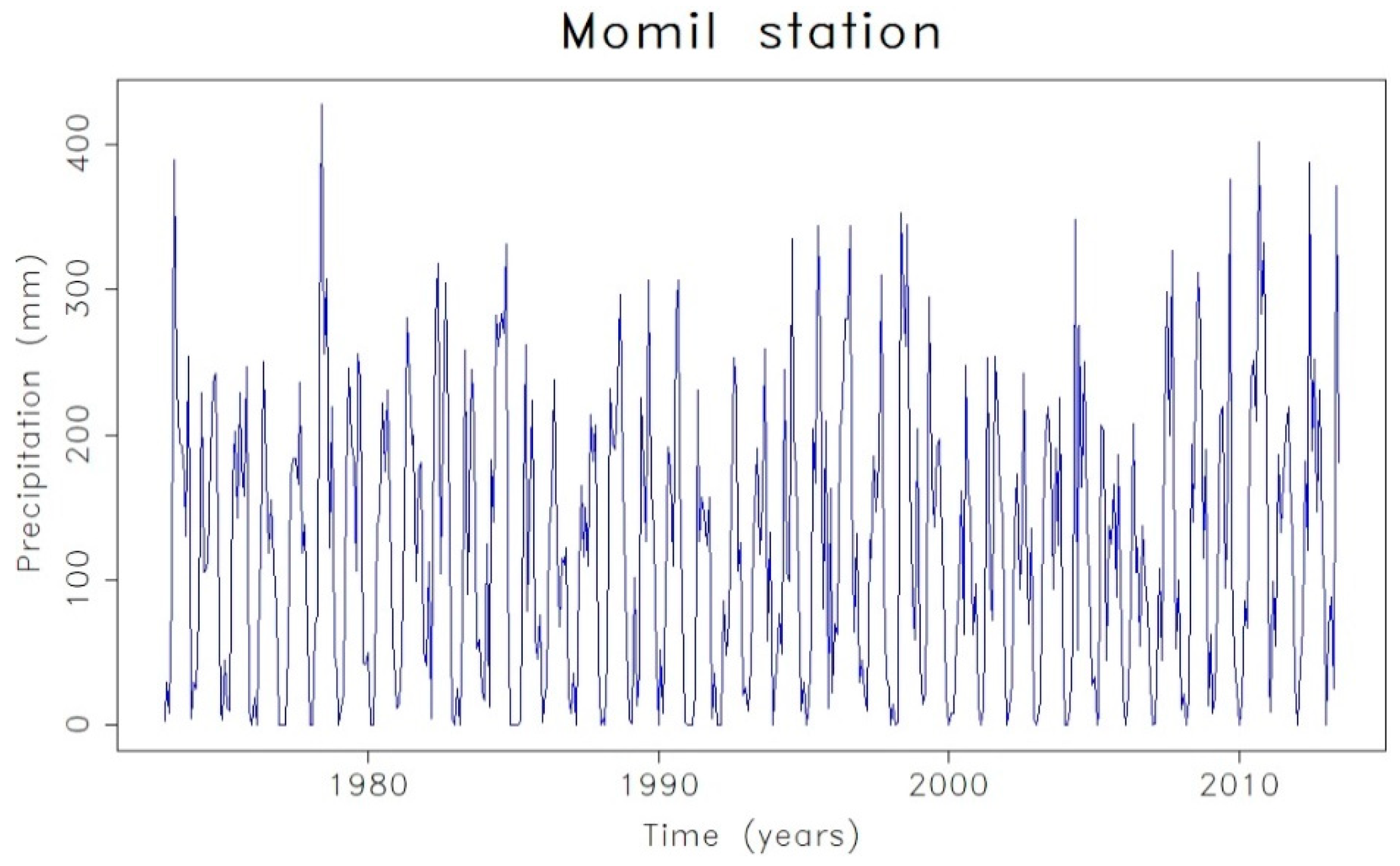
| Momil | (2,0,0)(2,1,0)12 | 0.1294 | 0.1494 | −0.6378 | −0.3567 | |||||||
| San Bernardo | (2,0,0)(2,1,0)12 | 0.092 | 0.1452 | −0.7489 | −0.3671 | |||||||
| Salado El | (2,0,0)(2,1,0)12 | 0.1046 | 0.1261 | −0.7196 | −0.3762 | |||||||
| Pezval | (2,0,0)(2,1,1)12 | 0.1296 | 0.0843 | −0.0191 | −0.1493 | −0.8849 | ||||||
| Puerto Nuevo | (2,0,0)(2,1,1)12 | 0.207 | 0.0079 | −0.1806 | −0.254 | −0.7325 | 0.001 | |||||
| La Granja | (2,0,1)(2,1,0)12 | −0.4645 | 0.2069 | 0.6187 | −0.634 | −0.3466 | ||||||
| Buenos Aires 1 | (2,0,1)(2,1,0)12 | −0.6891 | 0.1377 | 0.7795 | −0.5973 | −0.2836 | ||||||
| Corocito | (3,0,0)(2,1,0)12 | 0.322 | −0.0043 | 0.1264 | −0.6021 | −0.2633 | ||||||
| Quimarí | (3,0,0)(2,1,0)12 | 0.0831 | 0.031 | −0.1579 | −0.7179 | −0.3972 | ||||||
| Cereté | (3,0,0)(2,1,0)12 | 0.2795 | 0.0277 | 0.1427 | −0.7331 | −0.3709 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Acosta, L.; Medrano-Barboza, J.P.; López-Ramos, Á.; Remolina López, J.F.; López-Lambraño, Á.A. SARIMA Approach to Generating Synthetic Monthly Rainfall in the Sinú River Watershed in Colombia. Atmosphere 2020, 11, 602. https://doi.org/10.3390/atmos11060602
Martínez-Acosta L, Medrano-Barboza JP, López-Ramos Á, Remolina López JF, López-Lambraño ÁA. SARIMA Approach to Generating Synthetic Monthly Rainfall in the Sinú River Watershed in Colombia. Atmosphere. 2020; 11(6):602. https://doi.org/10.3390/atmos11060602
Chicago/Turabian StyleMartínez-Acosta, Luisa, Juan Pablo Medrano-Barboza, Álvaro López-Ramos, John Freddy Remolina López, and Álvaro Alberto López-Lambraño. 2020. "SARIMA Approach to Generating Synthetic Monthly Rainfall in the Sinú River Watershed in Colombia" Atmosphere 11, no. 6: 602. https://doi.org/10.3390/atmos11060602
APA StyleMartínez-Acosta, L., Medrano-Barboza, J. P., López-Ramos, Á., Remolina López, J. F., & López-Lambraño, Á. A. (2020). SARIMA Approach to Generating Synthetic Monthly Rainfall in the Sinú River Watershed in Colombia. Atmosphere, 11(6), 602. https://doi.org/10.3390/atmos11060602








