Abstract
The widespread increase in global temperature is driving more frequent and more severe local heatwaves within the contiguous United States (CONUS). General circulation models (GCMs) show increasing, but spatially uneven trends in heatwave properties. However, the wide range of model outputs raises the question of the suitability of this method for indicating the future impacts of heatwaves on human health and well-being. This work examines the fitness of 32 models from CMIP5 and their ensemble median to predict a set of heatwave descriptors across the CONUS, by analyzing their capabilities in the simulation of historical heatwaves during 1950–2005. Then, we use a multi-criteria decision-making tool and rank the overall performance of each model for 10 locations with different climates. We found GCMs have different capabilities in the simulation of historical heatwave characteristics. In addition, we observed similar performances for GCMs over the areas with a partially similar climate. The ensemble model showed better performance in simulation of historical heatwave intensity in some locations, while other individual GCMs represented heatwave time-related components more similar to observations. These results are a step towards the use of contemporary weather models to guide heatwave impact predictions.
1. Introduction
Observations of global warming from increased greenhouse gases (GHGs) are widespread and the recent four decades are among the warmest in the recorded history [1]. From the 1950s to 2000s, the global annual average minimum and maximum land surface air temperatures show decadal increases of 0.20 °C and 0.14 °C, respectively [2]. For the northern hemisphere, the intergovernmental panel on climate change (IPCC) found that the warmest consecutive 30 years of the last 1400 years were from 1983 to 2012 [3]. Kunkel et al. [4] reported that the average temperature increase across the contiguous United States (CONUS) from 1895 to 2011 was 0.11, 0.07, 0.05 and 0.05 °C per decade for winter, spring, summer and fall, respectively. Additionally, that study found a significant difference in the regional average temperature increase over the same period equivalent to 0.08, 0.07, 0.08, 0.1, 0.05, 0.05, 0.09 °C per decade for northeast, southeast, midwest, Great Plains north and south, northwest and southwest of the CONUS, respectively. General circulation models (GCMs) project various increases in average regional temperature, based on differences in the Representative Concentration Pathways (RCPs) for the CONUS. These projections indicate more frequent hot days, with significant spatial variability [5,6]. In the northeast, GCMs project warming of 3 to 10 °F (1.7 to 5.6 °C) by the 2080s with an increase in the number of days per year above 90 °F (32 °C) [7]. In the southeast region, the average temperature increase is projected to range between 4 and 8 °F (2.2 to 4.4 °C) by the year 2100, while the interior states of the southeast USA can expect temperature increases of 1 to 2 °F (0.55 to 1.1 °C), with more hot days and fewer freezing events [8]. These models project the midwest region may warm by 5 °F (2.8 °C) and experience at least 25 more days above 95 °F (35 °C) by the end of this century, compared to the 1971–2000 period. Similar to the southeast, the midwest will experience longer frost-free seasons [9]. According to Third National Climate Assessment report in the United States, the Great Plains region will experience extreme temperatures by end of this century with increased frequency of days above 95 °F toward the north and 100 °F toward the south (35 and 37.7 °C) and more nights above 80 °F (26.6 °C) across this region [10]. The temperature increase in the northwest and northeast USA is similar, with the projected average annual temperature expected to rise between 3.3 and 9.7 °F (1.8 to 5.4 °C) by 2070 to 2099, compared to the 1970 to 1999 period. Even larger changes are expected during the summer months [11]. In the southwest, some GCMs indicate increases of 2.5 to 5.5 °F (1.4 to 3.1 °C) by 2041–2070 and a cumulative increase of 5.5 to 9.5 °F (3.1 to 5.3 °C) by 2070–2099. These projections are based on scenarios with continued growth in global emissions followed by inevitable more frequent summer heat waves and less wintertime cold days [12].
A warmer future climate is expected to be attended by greater frequency of occurrence and intensity of Extreme Heat Events (EHE) across the CONUS. These events will likely be followed by more frequent and severe heat waves [13,14]. The rise in the future heat waves is expected to be attended by other meteorological extremes such as droughts, causing more frequent and intense concurrent extreme events for the CONUS [5,15,16,17]. Even a significant reduction in GHG emissions will not stop this warming pattern in the near future, and it would be prudent to prepare for warmer future weather [18]. An important question is how to make an appropriate quantitative representation of the spatial distribution of temperature indices across the CONUS. Russo & Sterl [19] used the ECHAM5/MPI-OM climate model to calculate extreme weather indices proposed by Expert Team on Climate Change Detection, Monitoring and Indices (ETCCDMI) and described by Alexander et al. [20] in a global scale. They found that the number of warm days (defined as days with daytime temperature above the 90th percentile of the reference period (TX90p) in this study 1951–1975) by 2100 will be up to 100 days more than 1951–1975. Sillmann et al. [21] analyzed 19 CMIP5 models to calculate ETCCDMI based on three RCP scenarios (RCP2.6, 4.5 and 8.5) globally in which the CONUS is divided into three regions including East north America (ENA), Central north America (CNA) and West north America (WNA). They found that over the period 2081–2100, the annual maximum of daily maximum temperature (TXx, see Alexander et al. [20] for details) in WNA, CNA and ENA will be between 0.5 and 10.5 °C further compared to reference period 1981–2000. In addition, this study revealed that days with frost will decrease significantly in WNA by the end of this century. Diffenbaugh & Ashfaq [22] studied 22 GCMs across the CONUS and found that by 2039 intense heat events will be more frequent than ever.
Regional studies also found that by the end of this century, heat wave intensity will be 3 to 8 °C greater, and the number of heat wave days may increase by up 30 to 60 days compared to historical observations over much of the western and southern CONUS [23]. Similarly, Zubler et al. [24] found that in 2070–2100 the summertime temperature and average heat wave intensity in the great plains will be 20% greater and 0.6 °C more than during the period of 1980–2010. Gershunov & Guirguis [25] used a 12 × 12 km2 resolution observed dataset and four downscaled GCMs to study future heat waves in the state of California and found that urban heat island effect will be more frequent and intense by the end of this century. Targeted studies in New York City suggest that the number of days with a maximum temperature greater than 32.2 °C will more than double from the 1990s to the 2050s [26].
Proper climate change information is a prerequisite for analyses that project the range of future climatological extremes at an acceptable scale. Pierce et al. [27] proposed that a spatial scale on the order of 10 km is required to assess the numerous impacts of climate change on societies. However, most GCMs have a spatial resolution of 100 km. Downscaling methods address this issue by providing smaller spatial scale data for different purposes. However, the question of the reliability of future weather projections remains due to uncertainties in climate models and limits the availability of robust, actionable and reliable projections of the future climate [28,29]. These uncertainties in climate projections originate from three main sources, including internal variability of the climate system, model uncertainties and future scenarios uncertainties [30] and in most cases, it is not possible to remove these uncertainties [31].
Different methods are available to decrease the uncertainties identified above, particularly on a regional scale. Regional climate models reduce prediction biases by developing higher spatial resolution analyses and better represent the local physical processes [23]. However, national and global scale studies lack sufficient resolution for spatial comparison. One common approach to overcome this problem is to calculate an arithmetic multimodel mean of downscaled data, assuming the same weight for each model [21,23,32,33,34]. This popular method is controversial because there are many arguments that due to different structures of the GCMs, ensemble modeling physically may be implausible [35]. In addition, there are known issues and uncertainties in a few of these models and accordingly, the use of an even large number of subsets could result in very poor representation of the range of projections [36,37]. At the same time, we know some models work better than others, particularly for some regions and purposes [38]. For example, there are many values in focusing on the “seamless models” which have both weather forecasting and climate change projection components [39]. On the other hand, if the impact of human interaction with the atmosphere is of interest, those models that incorporate human processes with earth’s physical properties and climate projections have higher priorities to be used [40]. Accordingly, we can focus on the most reliable and accurate GCMs when we know the aim and scope of a specific study [41,42], while acknowledging the pitfalls of model averaging [35]. Furthermore, many studies that have used and compared different approaches, such as Multi-Model Mean (MMM), weighted approaches, probabilistic methods, random and ranked ensembling methods, mentioned the different performance of GCMs [43,44,45,46].
A practical reality for many impact studies is the selection of appropriate ancillary deterministic outputs from other methods to inform decision makers and prepare response plans. For example, in preparing Intensity–Duration–Frequency (IDF) curves for flood modeling, it is important to select particular downscaled GCMs based on regional characteristics. For example, four different GCMs (i.e., HadGEM2-ES, CNRM-CM5, CanESM2, and MICROC5) were selected for the state of California in the United States to provide IDF curves for preparing the state for increasing floods risk [47].
In this regard, several methods have been introduced which consider the performance of each individual GCM or downscaled GCM. Abramowitz & Bishop [38] used a “perfect model” approach to testing whether an ensemble dependence transformation can improve CMIP projections. Similarly, Herger et al. [48] analyzed a different subset of ensembles from complete 81 CMIP5 simulations and compared them with a simple multi-model mean (MMM) of all 81 simulations. There are many other sophisticated and complicated approaches that aim to provide a robust prediction of future temperature or precipitation [49,50,51]. However, these models are often complex and there is no general agreement on methods of assessment [31]. In this regard, many scholars have tried to prepare a simpler method to select a GCM for a particular purpose. Geil et al. [52] analyzed 21 downscaled GCMs and compared the result with observations over North America for 1979–2005, then ranked these models based on the correlation between models and observations. Knutti et al. [53] suggested using a weighted average over the GCMs. Following this method, Lorenz et al. [31] applied a weighting approach to investigate projections of summer maximum temperature across north America. Most of these methods rely on sophisticated approaches and require enormous computational effort, yet there is no universal agreement on the robustness of their outcomes. Furthermore, it is challenging to integrate a local setting in selecting the process of these models for impact studies.
In this study, we introduce a novel method to rank downscaled GCMs based on detection sensitivity for a series of heat wave properties. We analyze eight “time” and “intensity” related heat wave properties from 1950 to 2005 in 10 different locations across the CONUS (as described in Section 2.2.). Then, we use 32 downscaled GCMs and the ensemble median GCM (hereafter Median_GCM) for each observation station and analyze them for the same eight heat wave properties. In every location, we compare the observation and model results for each heat wave property using Nash–Sutcliffe efficiency (NSE) coefficient [54]. Then we use a multi-criteria decision-making (MCDM) tool to rank the models by location. The findings of this research introduce a simple ranking method for GCMs based on the agreement between analyses of local historical heat wave components. This approach is directed to help policymakers and managers to best prepare for future extreme events in their jurisdictions by focusing on more reliable projections of future heatwaves.
2. Method
2.1. Study Area and Data
This study focuses on ten cities in the CONUS with different climates; Baltimore, MD, Bismarck, ND, Colorado Springs, CO, Dallas, TX, Des Moines, IA, Miami, FL, New York City, NY, Phoenix, AZ, Portland, OR and Syracuse, NY (Figure 1; city names are followed by the abbreviation of State names in the USA). We obtain historical daily weather data (minimum and maximum temperatures) for each location from the U.S. National Centers for Environmental Information (NCEI) for 1950–2005. Then, we obtain downscaled historical simulations from 32 GCMs, for grid cells (hereafter pixel) corresponding to these ten weather stations which were conducted using the Localized Constructed Analogs (LOCA) method [27]. The LOCA downscaled products are available for historical (i.e., retrospective analysis for 1950–2005) and future (2006–2100) periods for intermediate (RCP4.5) and high (RCP8.5) radiative scenarios at a 1/16 degree resolution (~6 km × 6 km). LOCA method downscales GCMs using the Livneh data set and the latter data set is model-derived from observed data developed for the Variable Infiltration Capacity (VIC) simulations over north America [27]. Livneh dataset is constructed based on more than 20,000 National Oceanic and Atmospheric Administration (NOAA) Cooperative Observer Network (COOP) stations across the CONUS [55]. LOCA method downscales the daily GCMs maximum and minimum temperature outputs (i.e., retrospective analysis for 1950–2005) point-by-point from a single best match analog day, based on the observed data for the same date during 1950–2005 [27]. Accordingly, this downscaled dataset with a temporal correspondence between daily retrospective analysis and observations (1950–2005) is a suitable source for the study of extreme events [56]. For example, LOCA dataset was used widely in different climate extreme events’ studies, such as heatwaves [57], droughts [58], extreme precipitation events [59] and hydrologic modeling [60]. In addition, we calculate the median daily maximum and minimum temperature values of 32 models in each location, Median_GCM, to compare the performance of that with the GCMs. Furthermore, we examine the capability of LOCA dataset and Median_GCM to reproduce historical (1950–2005) mean climate variables in each location:
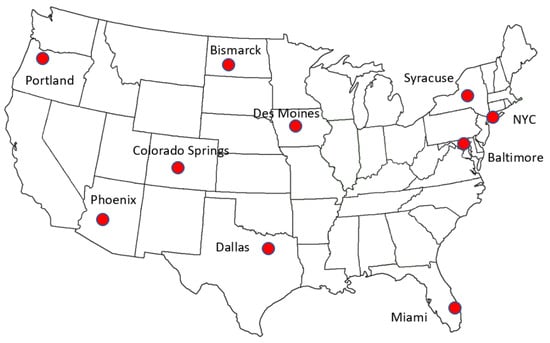
Figure 1.
Location of the selected cities for this study across the contiguous United States (CONUS).
- We compare the average long-term maximum and minimum daily temperatures obtained from the observation and models.
- We investigate differences between the observation and models for maximum and minimum daily temperatures with NSE coefficients.
The results show the LOCA dataset is capable of reproducing daily maximum and minimum temperature accurately (details are shown in Appendix A, Table A1, Table A2, Table A3 and Table A4). In addition, Table 1 shows these 32 GCMs’ general information.

Table 1.
Examined GCMs general information and atmospheric model grid resolution (number of longitudinal grids × number of latitudinal grids) [42,52,61].
2.2. Heat Wave Definition and Components
There is no universal heat wave definition, and many debates exist on the parameters that should be included in the heat wave definition [62,63]. In this study, we define a heat wave as an event that has at least two consecutive days with minimum and maximum daily temperatures greater than 90th percentiles of the minimum and maximum daily temperatures in that location during 1950–2005 (thresholds), respectively. This definition has been widely used before in heat wave studies [64,65,66]. Following traditional heat wave components, including frequency, intensity, duration and timing [62] and in accordance with our previous research, we have defined the succeeding eight heat wave components that are computable in each pixel based on the available climatological data [66]. In addition, we use a developed R code to calculate these heat wave properties for each location for 1950–2005 [67].
- Number of hot days (Days): A hot day has both maximum and minimum temperatures higher than defined thresholds;
- Frequency of heat wave (waves): Number of independent heat waves in each calendar year;
- total length of heat waves (total): The cumulative duration of all heat waves in each calendar year;
- longest heat wave event (longest): The longest heat wave event occurrence in each calendar year;
- Daytime heat wave intensity (Intensity): The cumulative value of daytime temperatures above the maximum temperature threshold during a heat wave;
- Nighttime heat wave intensity (Night): The cumulative value of nighttime temperatures above the minimum temperature threshold during a heat wave;
- First heat wave event (First): The number of the first day of the first heat wave in a calendar year;
- Last heat wave event (Last): The number of the last day of the last heat wave in a calendar year.
Two examples: 1. A heat wave of two consecutive days with the minimum and maximum daily temperatures of 30 °C, 35 °C, 35 °C and 42 °C at one station with defined thresholds of 28 °C and 33 °C, respectively, has the daytime heat wave intensity and nighttime heat wave intensity of 11 °C and 9 °C, respectively. 2. If in a given year, there are three consecutive hot days in a month, 2 consecutive hot days two months thereafter, followed by 1 hot day four months later, then Days is 6 (i.e., 3 + 2 + 1 = 6), the waves is 2 (i.e., only first two events are heat waves), the total is 5 (i.e., only length of heatwaves, 3 + 2 = 5), and the longest is 3 (i.e., length of the first event).
We analyze the historical observed and 32 downscaled simulated GCM and Median_GCM data in each location during 1950–2005 to compare the capability of these models in the simulation of the heat wave components based on the NSE coefficient. For this purpose, we first calculate eight heatwave components time series based on observations in each location. Then, we repeat the same analysis with each downscaled GCM and the Median_GCM daily data for the same heatwave components in each location. Then, we use NSE coefficient to compare the results from observations and each of the models’ outputs for eight different heatwave components and in ten different locations. The models show different coefficients for each of the eight heatwave components in each of 10 locations (Appendix A, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12). Accordingly, it is not possible to rank the performance of the downscaled GCMs based on simulations of eight different heatwave components in these locations. Therefore, we apply a multi-criteria decision-making (MCDM) approach to rank the downscaled GCMs based on their performance in each location, simultaneously and considering all eight heat wave properties.
2.3. Multi Criteria Decision Making
Multi-criteria decision-making (MCDM) methods solve complex problems with multiple competing criteria and no optimal solution, in order to meet the user preferences or a procedural goal [68]. MCDM problems have five main components, including goal, decision-maker priorities, available alternatives, decision criteria and outcomes or ranks [69,70]. The most popular MCDM methods include weighted sum model, weighted product model, ELECTRE, TOPSIS, MAUT, PROMETHEE, VIKOR and AHP [69]. Each model has strengths and limitations and one should carefully select a method based on the characteristics of the model and available data [71]. For this study, we select the TOPSIS method for the simple method of computation and no restrictions on the number of alternatives or criteria [72]. Similarly, the criteria can be weighted independently with no limitation of the range of values [73]. Therefore, the heat wave property information (i.e., heat wave properties) could be correlated without impacting the process of making a decision [74]. This method has been widely used in different scientific fields including, natural hazards, atmospheric sciences and environmental engineering [68,75,76]. We describe the TOPSIS method below and use it to find the five best and five least fit downscaled GCMs based on the NSE coefficient between heat wave properties obtained from each model and observed data [68,77,78]:
- Calculate of the decision matrix, D, including alternatives (for i = 1 to m, which is the number of models) and Criteria, , which is NSE between each downscaled GCM and observation for that particular heat wave property (for j = 1 to n, which is the number of heat wave properties):
- Normalize of the elements in the decision matrix for each criterion:
- Calculate of the weighted normalized decision matrix values:where is the weight of each criterion that highlights the importance of that criteria (i.e., each of heat wave components) and . In this study, we assume the same values of for the heat wave components importance in the selection of a GCM.
- Find the best and least fit (or ideal and negative-ideal) solutions for each criterion:where J is associated with benefit criteria and J′ is associated with negative criteria. In this study, a higher NSE coefficient is associated with benefit (or better choice).
- Calculate the distance from best and least fit ideal solutions for each alternative using Euclidean distance method:
- Compute the relative closeness to the ideal solution, which can be the best or least fit outcome, based on the goal:
- Rank each alternative () based on the calculated relative closeness to the ideal solution ().
This method sorts downscaled GCMs (i.e., alternatives) based on the NSE coefficient by assuming an equal weight of importance for heat wave components. However, the previously described method to distribute weights among eight heat wave components [66] may vary in future studies addressing the sensitivity of this method to weights of selected criteria.
3. Results
First, we analyze the NSE coefficient for eight heatwave components based on observational data and output from 32 downscaled GCMs and Median_GCM to identify the best-fit models (Appendix A, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11 and Table A12). Table 2 shows the best and least fit models for each heatwave property across the 10 study sites. EC-EARTH is the best model for Days in Baltimore, Portland and Syracuse. Interestingly, eight different downscaled GCMs are identified as the best models for waves and EC-EARTH is among them for the city of Syracuse. Then, EC-EARTH is the best-fit for total in Baltimore, Bismarck and Syracuse. Similar to waves, eight different downscaled GCMs are selected as the best models for the longest heat wave events across the 10 study sites. EC-EARTH is also the best model for Intensity for Baltimore, NYC and Syracuse, while it remains the best for Night only for Baltimore and NYC. This model also is the best for the timing component of heatwaves (First and Last) in Miami, Phoenix, Syracuse and NYC. An interesting result of this study is that in Syracuse, EC-EARTH is the best model for six heatwave components and in Colorado Springs, we observe CMCC-CM remains the best for three heatwave components. In addition, we found Median_GCM as the best model for the temperature based components of heatwaves, Intensity and/or Night, in Bismarck, Colorado Springs, Dallas and Des Moines.

Table 2.
Best and Least fit downscaled general circulation models (GCMs) for simulating individual historical heat wave properties in each location.
A similar analysis for least fit downscaled GCMs identifies ACCESS1-0, BCC-CSM1-1, HADGEM2-CC, MIROC5, FGOALS-G2 and MICRO-ESM-CHEM among the poorest GCMs across the study sites in the simulation of historical heatwave components. Contrary to the results above, EC-EARTH is least fit for simulation of historical Days and First for Phoenix and Portland, respectively. Surprisingly, EC-EARTH acts as the best fit model for First and least fit for Days in Phoenix and as the best for Days and least fit for First in Portland. Although this analysis shows which downscaled GCM is preferred for any heatwave component across the study sites, we expand the analysis with the MCDM to rank the downscaled GCMs based on overall accuracy in simulations of historical heatwave events.
We apply the TOPSIS method to sort the models based on their overall accuracy in the simulation of historical heatwave properties, as discussed in Section 2.3 ( see Appendix A, Table A13). Accordingly, the EC-EARTH model was selected as the best model (ranked 1 among 33 models) for Baltimore, Bismarck, NYC and Syracuse weather stations. Considering the rank of this model for individual heatwave components across these cities, this result was predictable for Baltimore, NYC and Syracuse. In Colorado Springs, Dallas, Des Moines, Miami, Phoenix and Portland, we found the CMCC-CM, ACCESS1-0, GFDL-ESM2M M, GISS-E2-R, CCSM4 and MPI-ESM-LR as the best downscaled GCMs, respectively. Interestingly, Median_GCM is selected as the 5th best model for Colorado Springs based on its performances in simulation of daytime and nighttime heatwave intensity in this location. In addition, this model is among the top 10 preferred models for Bismarck, Dallas and Des Moines. Considering the overall downscaled GCMs rank, being among the top 5 models—and avoiding being among five least fit models—we suggest the EC-EARTH, MPI-ESM-LR, CANESM2, CMCC-CM and GFDL-ESM2M M as the five best downscaled GCMs for heat wave studies in the CONUS.
In contrast, we find the FGOALS-G2, HADGEM2-CC, ACCESS1-0, MIROC-ESM-CHEM, ACCESS1-3, CESM1-CAM5, MIROC5, GFDL-ESM2M M, HADGEM2-CC and CMCC-CM as the least fit GCMs (ranked 33 among 33 models) for heat wave studies in Baltimore, Bismarck, Colorado Springs, Dallas, Des Moines, Miami, NYC, Phoenix, Portland and Syracuse, respectively. Median_GCM, which was selected among the top 10 models for Bismarck, Colorado Springs, Dallas and Des Moines, is also among the models with rank 12 to 25 for the other locations. We observe a few models have disparate performance across sites. For example, ACCESS1-0 is selected as the best for Dallas and least fit for Colorado Springs. Similarly, we find the FGOALS-G2, GFDL-ESM2G, HADGEM2-CC, ACCESS1-0 and INMCM4 GCMs as the five models with the poorest performance in the simulation of historical heat wave properties of ten study sites. Table 3 summarizes the rank of each downscaled GCM for the study sites considering the model performances in simulation of historical heat wave properties and a multi-criteria decision-making approach. Hereafter we use the abbreviated names for the cities within the tables including BAL for Baltimore, BIS for Bismarck, COL for Colorado Springs, DAL for Dallas, DES for Des Moines, MIA for Miami, NYC for New York City, PHO for Phoenix, POR for Portland, and SYR for Syracuse.

Table 3.
Downscaled GCMs performance rank in the simulation of historical heat wave properties for the period 1950–2005 according to a multi-criteria decision-making (MCDM) approach on Nash–Sutcliffe efficiency (NSE) coefficients. (The five best and least fit downscaled GCMs for each city are shown in bold text).
4. Discussion
We demonstrate a wide range of coherence between GCM and key heat wave features across space and through time. Geil et al. [52] prioritized six models based on one criterion, GCM capability to represent the daily precipitation of the north American Monsoon, including CNRM-CM5, CSIRO Mk3.6.0, HADGEM2-CC, HADGEM2-ES, IPSL-CM5A-LR and IPSL-CM5A-MR. We expand that approach, with several criteria to prioritize downscaled GCMs in this study. Whereas, this new approach did not select the abovementioned GCMs as the best models for heat wave studies across the CONUS, they remain among the selected models for individual study sites. Navarro-Estupiñan et al. [79] used the same six models suggested by Geil et al. [52] for the projection of extreme heat events in Sonora, Mexico. Although we argue that their selection for heatwave study should be based on GCMs suitable for simulation of historical heat waves rather than precipitation, we support their approach, which is more robust than GCM averaging. A strength of these six models is the ability to simulate precipitation, which is an important climate variable in the region. Phoenix is the closest site to Sonora and interestingly, we proposed two common models for heat wave studies, including HADGEM2-CC and CSIRO-MK3-6–0. Accordingly, it seems local climate settings are important components for performance of GCMs.
We find that the performance of the EC-EARTH model is the best fit for historical heat wave properties across the four locations, including Syracuse, NYC, Baltimore and Bismarck. These sites have similar Köppen climate classifications. NYC and Baltimore share Cfa (humid subtropical climate) and Syracuse and Baltimore share a similar Dfb (humid continental mild summer, wet all year) climate type [80]. Although the investigation of the structure and data analysis of these 32 downscaled GCMs is not in the scope of this study, we briefly describe the EC-EARTH model. This model is an Earth System Model (ESM) built based on European Center for medium-range weather forecasts [81]. This model benefits both weather forecasting and climate change projection components simultaneously and is among “seamless prediction” models [39]. In addition, these models incorporate biogeochemical and human processes with the earth’s physical properties and climate projections [40]. The performance of this model has been tested in different settings and for various purposes with satisfying results for temperature prediction [82], tropical upper tropospheric water concentration [40], Arctic energy budget [83] and Arctic climate change [84]. Although the reliability of a climate model depends on the selection of model components, EC-EARTH benefits a robust ocean modeling component and it is a strong choice for extreme climate studies [82,84,85,86,87].
Our analysis indicates that model assembly changes output characteristics relative to a single model, as suggested by Knutti et al. [35], challenging the plausibility of ensemble modeling for climate projections. Median_GCM is ranked under 10 of 33 models for the sites with a continental climate, including Bismarck, Colorado Springs, Dallas and Des Moines. This ensemble shows less reliability for coastal cities, where other individual downscaled GCMs provide more accurate simulations. This observation highlights the importance of selecting those models with a better performance in their ocean modeling components for the study of extreme events in coastal areas [84,85,88].
There are several limitations to the current research that arise from heat wave definition method and the validity of downscaled climate data. The MCDM tool ranks 32 downscaled GCMs and one ensemble median GCM based on the heat wave properties, all connected to heat wave definition. As mentioned before, there are many definitions for heat waves and accordingly, repeating this ranking process using another definition (e.g., a longer period of consecutive days or higher thresholds) could potentially change the rank of downscaled GCMs for any of the locations. Examining the sensitivity of this method to different heat wave definitions is not in the scope of this research. A caveat to the use of downscaled climate data are awareness of uncertainty propagation during downscaling. The use of dynamical downscaling methods (i.e., Regional climate models) could address this problem; however, limited availability of RCMs or dynamically downscaled data across many regions challenges the substitution of LOCA data set with them. Despite this limitation, the comparison of downscaled retrospective LOCA data sets with various land-based observation data are a common method for evaluating the performance of GCMs for many purposes [57,58,59,60,89].
Although we base this research on the downscaled GCMs instead of GCMs, we highlight the following benefits of this work for future improvements in GCMs:
- We demonstrated how downscaled GCMs represent a better or least fit performance across the cities with similar climates. We observe that this variation in the performance of models has a direct link to the structure of the model(s).
- We demonstrated a few models with previously known robust ocean modeling components simulated historical heatwaves in coastal cities better than other downscaled GCMs. This observation encourages their approach and also sheds light on the possible improvement opportunities for the other models.
Eventually, this ranking is a function of allocated weights for heatwave components, for which we assume equal values.
5. Conclusions
We examine 32 CMIP5 coupled general circulation models to determine how well these models represent the heat wave properties at 10 measurement stations across CONUS for 1950–2005. In this analysis, we compare the observed data and downscaled historical LOCA meteorological products that cover the same weather stations. The results show that the performance of each model varies significantly across the CONUS. We then use a Multi-criteria decision-making approach to conclude the performance of each downscaled GCM, considering eight predefined heat wave components to show the five best and least fit models for each location. We also select the five best and five least fit models based on their overall performance across the CONUS. Similar to Parker [90], we conclude that the findings of this study simply show “adequacy-for-purpose” of “predicting those farther-further values of” temperature data and heat wave occurrences. Nevertheless, the active discussion still remains on the topics of parameter selection, metrics and assessment methods [53].
If we assume that the best model predictions presented here are robust, reliable and locally available, they may inform the assessment of actions to ameliorate the impact of future heat waves [28,29]. The method developed here provides a pathway to define other approaches for prioritizing global climate models based on the local needs, with the goal of providing more accurate and on-time local adaption and mitigation plans.
Author Contributions
Conceptualization, J.S.S. and D.G.C.; methodology, J.S.S.; software, J.S.S.; validation, J.S.S. and D.G.C.; formal analysis, J.S.S.; investigation, J.S.S. and D.G.C.; resources, J.S.S. and D.G.C.; data curation, J.S.S.; writing—original draft preparation, J.S.S.; writing—review and editing, J.S.S. and D.G.C.; visualization, J.S.S.; supervision, D.G.C.; project administration, D.G.C.; funding acquisition, D.G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Urban Resilience to Extremes Sustainability Research Network under National Science Foundation Grant Number AGS-1444755. Any opinions, findings, and conclusions or recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Acknowledgments
The authors would like to thank three anonymous reviewers and the editor for their comprehensive review and productive comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Average observed and simulated daily maximum temperature (°C) for 1950–2005.
Table A1.
Average observed and simulated daily maximum temperature (°C) for 1950–2005.
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Observed | 18.49 | 12.29 | 17.16 | 24.47 | 15.44 | 28.47 | 15.95 | 29.97 | 16.97 | 14.07 |
| 2 | ACCESS1-0 | 18.646 | 12.273 | 17.182 | 24.620 | 15.581 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 3 | ACCESS1-3 | 18.647 | 12.273 | 17.183 | 24.620 | 15.579 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 4 | BCC-CSM1-1 | 18.646 | 12.272 | 17.182 | 24.621 | 15.578 | 28.504 | 16.334 | 29.952 | 16.841 | 13.863 |
| 5 | BCC-CSM1-1-M | 18.647 | 12.272 | 17.180 | 24.619 | 15.579 | 28.505 | 16.335 | 29.951 | 16.840 | 13.865 |
| 6 | CANESM2 | 18.646 | 12.272 | 17.182 | 24.621 | 15.579 | 28.505 | 16.335 | 29.951 | 16.840 | 13.864 |
| 7 | CCSM4 | 18.645 | 12.273 | 17.182 | 24.621 | 15.580 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 8 | CESM1-BGC | 18.646 | 12.272 | 17.183 | 24.620 | 15.578 | 28.505 | 16.333 | 29.952 | 16.841 | 13.863 |
| 9 | CESM1-CAM5 | 18.645 | 12.272 | 17.182 | 24.620 | 15.579 | 28.505 | 16.333 | 29.953 | 16.841 | 13.864 |
| 10 | CMCC-CM | 18.647 | 12.272 | 17.183 | 24.620 | 15.580 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 11 | CMCC-CMS | 18.646 | 12.272 | 17.182 | 24.621 | 15.579 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 12 | CNRM-CM5 | 18.646 | 12.272 | 17.182 | 24.619 | 15.579 | 28.505 | 16.334 | 29.951 | 16.841 | 13.864 |
| 13 | CSIRO-MK3-6–0 | 18.646 | 12.273 | 17.182 | 24.621 | 15.579 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 14 | EC-EARTH | 18.645 | 12.271 | 17.181 | 24.620 | 15.579 | 28.505 | 16.334 | 29.951 | 16.841 | 13.863 |
| 15 | FGOALS-G2 | 18.646 | 12.272 | 17.183 | 24.621 | 15.579 | 28.505 | 16.334 | 29.953 | 16.841 | 13.863 |
| 16 | GFDL-CM3 | 18.646 | 12.272 | 17.183 | 24.621 | 15.580 | 28.505 | 16.334 | 29.952 | 16.842 | 13.863 |
| 17 | GFDL-ESM2G | 18.647 | 12.273 | 17.182 | 24.621 | 15.580 | 28.505 | 16.334 | 29.952 | 16.841 | 13.863 |
| 18 | GFDL-ESM2M M | 18.647 | 12.273 | 17.183 | 24.623 | 15.580 | 28.505 | 16.335 | 29.952 | 16.840 | 13.865 |
| 19 | GISS-E2-H | 18.644 | 12.271 | 17.182 | 24.620 | 15.578 | 28.505 | 16.333 | 29.951 | 16.840 | 13.862 |
| 20 | GISS-E2-R | 18.646 | 12.272 | 17.182 | 24.622 | 15.580 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 21 | HADGEM2-AO | 18.646 | 12.272 | 17.182 | 24.621 | 15.580 | 28.505 | 16.334 | 29.951 | 16.840 | 13.864 |
| 22 | HADGEM2-CC | 18.646 | 12.272 | 17.182 | 24.620 | 15.578 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 23 | HADGEM2-ES | 18.646 | 12.273 | 17.183 | 24.620 | 15.580 | 28.505 | 16.334 | 29.953 | 16.841 | 13.864 |
| 24 | INMCM4 | 18.647 | 12.272 | 17.181 | 24.619 | 15.579 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |
| 25 | IPSL-CM5A-LR | 18.646 | 12.273 | 17.183 | 24.621 | 15.580 | 28.505 | 16.334 | 29.952 | 16.840 | 13.863 |
| 26 | IPSL-CM5A-MR | 18.647 | 12.274 | 17.184 | 24.622 | 15.581 | 28.505 | 16.334 | 29.952 | 16.840 | 13.864 |
| 27 | MIROC-ESM | 18.646 | 12.270 | 17.182 | 24.620 | 15.579 | 28.505 | 16.334 | 29.952 | 16.841 | 13.863 |
| 28 | MIROC-ESM-CHEM | 18.645 | 12.273 | 17.182 | 24.619 | 15.579 | 28.505 | 16.333 | 29.952 | 16.841 | 13.863 |
| 29 | MIROC5 | 18.647 | 12.273 | 17.182 | 24.621 | 15.579 | 28.505 | 16.335 | 29.951 | 16.841 | 13.864 |
| 30 | MPI-ESM-LR | 18.646 | 12.273 | 17.184 | 24.621 | 15.580 | 28.505 | 16.334 | 29.952 | 16.841 | 13.863 |
| 31 | MPI-ESM-MR | 18.645 | 12.272 | 17.183 | 24.620 | 15.579 | 28.505 | 16.333 | 29.952 | 16.841 | 13.863 |
| 32 | MRI-CGCM3 | 18.646 | 12.270 | 17.181 | 24.621 | 15.579 | 28.505 | 16.333 | 29.951 | 16.840 | 13.863 |
| 33 | NORESM1-M | 18.645 | 12.272 | 17.182 | 24.620 | 15.578 | 28.505 | 16.334 | 29.951 | 16.841 | 13.863 |
| 34 | Median_GCM | 18.646 | 12.272 | 17.182 | 24.621 | 15.579 | 28.505 | 16.334 | 29.952 | 16.841 | 13.864 |

Table A2.
Average observed and simulated daily minimum temperature (°C) for 1950–2005.
Table A2.
Average observed and simulated daily minimum temperature (°C) for 1950–2005.
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Observed | 7.48 | 1.18 | 2.59 | 12.02 | 4.61 | 20.64 | 8.46 | 15.54 | 7.09 | 3.66 |
| 2 | ACCESS1-0 | 7.618 | 1.111 | 2.298 | 12.205 | 4.743 | 20.442 | 8.193 | 14.883 | 6.942 | 3.355 |
| 3 | ACCESS1-3 | 7.618 | 1.112 | 2.298 | 12.204 | 4.742 | 20.442 | 8.193 | 14.883 | 6.943 | 3.354 |
| 4 | BCC-CSM1-1 | 7.617 | 1.112 | 2.298 | 12.204 | 4.742 | 20.442 | 8.192 | 14.883 | 6.942 | 3.353 |
| 5 | BCC-CSM1-1-M | 7.618 | 1.112 | 2.297 | 12.204 | 4.741 | 20.442 | 8.194 | 14.883 | 6.943 | 3.355 |
| 6 | CANESM2 | 7.618 | 1.113 | 2.298 | 12.205 | 4.742 | 20.442 | 8.193 | 14.883 | 6.941 | 3.354 |
| 7 | CCSM4 | 7.617 | 1.112 | 2.299 | 12.206 | 4.744 | 20.441 | 8.193 | 14.883 | 6.943 | 3.354 |
| 8 | CESM1-BGC | 7.617 | 1.112 | 2.299 | 12.205 | 4.741 | 20.442 | 8.193 | 14.883 | 6.942 | 3.354 |
| 9 | CESM1-CAM5 | 7.617 | 1.111 | 2.298 | 12.204 | 4.742 | 20.441 | 8.193 | 14.884 | 6.944 | 3.355 |
| 10 | CMCC-CM | 7.617 | 1.112 | 2.297 | 12.204 | 4.743 | 20.442 | 8.193 | 14.882 | 6.942 | 3.355 |
| 11 | CMCC-CMS | 7.618 | 1.111 | 2.299 | 12.205 | 4.743 | 20.442 | 8.193 | 14.884 | 6.944 | 3.354 |
| 12 | CNRM-CM5 | 7.616 | 1.111 | 2.298 | 12.204 | 4.742 | 20.442 | 8.193 | 14.884 | 6.943 | 3.354 |
| 13 | CSIRO-MK3-6-0 | 7.617 | 1.111 | 2.298 | 12.205 | 4.743 | 20.441 | 8.194 | 14.883 | 6.942 | 3.355 |
| 14 | EC-EARTH | 7.616 | 1.113 | 2.298 | 12.203 | 4.741 | 20.441 | 8.193 | 14.882 | 6.942 | 3.354 |
| 15 | FGOALS-G2 | 7.617 | 1.112 | 2.299 | 12.205 | 4.742 | 20.441 | 8.192 | 14.884 | 6.942 | 3.353 |
| 16 | GFDL-CM3 | 7.617 | 1.112 | 2.299 | 12.205 | 4.744 | 20.442 | 8.193 | 14.882 | 6.943 | 3.354 |
| 17 | GFDL-ESM2G | 7.618 | 1.111 | 2.298 | 12.205 | 4.742 | 20.441 | 8.193 | 14.883 | 6.943 | 3.354 |
| 18 | GFDL-ESM2M | 7.619 | 1.110 | 2.300 | 12.207 | 4.744 | 20.442 | 8.195 | 14.884 | 6.942 | 3.356 |
| 19 | GISS-E2-H | 7.616 | 1.113 | 2.299 | 12.205 | 4.741 | 20.441 | 8.192 | 14.883 | 6.942 | 3.353 |
| 20 | GISS-E2-R | 7.617 | 1.112 | 2.298 | 12.205 | 4.742 | 20.442 | 8.194 | 14.884 | 6.943 | 3.355 |
| 21 | HADGEM2-AO | 7.617 | 1.112 | 2.299 | 12.205 | 4.743 | 20.441 | 8.194 | 14.883 | 6.942 | 3.354 |
| 22 | HADGEM2-CC | 7.617 | 1.112 | 2.299 | 12.204 | 4.742 | 20.442 | 8.193 | 14.883 | 6.942 | 3.354 |
| 23 | HADGEM2-ES | 7.617 | 1.111 | 2.299 | 12.204 | 4.743 | 20.442 | 8.193 | 14.884 | 6.942 | 3.354 |
| 24 | INMCM4 | 7.618 | 1.111 | 2.298 | 12.204 | 4.743 | 20.441 | 8.194 | 14.883 | 6.943 | 3.355 |
| 25 | IPSL-CM5A-LR | 7.617 | 1.111 | 2.299 | 12.205 | 4.743 | 20.441 | 8.193 | 14.884 | 6.942 | 3.355 |
| 26 | IPSL-CM5A-MR | 7.618 | 1.111 | 2.301 | 12.205 | 4.745 | 20.442 | 8.193 | 14.883 | 6.942 | 3.355 |
| 27 | MIROC-ESM | 7.618 | 1.114 | 2.298 | 12.205 | 4.742 | 20.442 | 8.193 | 14.884 | 6.943 | 3.354 |
| 28 | MIROC-ESM-CHEM | 7.616 | 1.111 | 2.298 | 12.204 | 4.741 | 20.441 | 8.192 | 14.883 | 6.943 | 3.353 |
| 29 | MIROC5 | 7.618 | 1.111 | 2.299 | 12.205 | 4.743 | 20.442 | 8.194 | 14.883 | 6.943 | 3.354 |
| 30 | MPI-ESM-LR | 7.617 | 1.111 | 2.300 | 12.205 | 4.743 | 20.441 | 8.193 | 14.884 | 6.944 | 3.353 |
| 31 | MPI-ESM-MR | 7.617 | 1.111 | 2.299 | 12.205 | 4.742 | 20.442 | 8.193 | 14.883 | 6.942 | 3.353 |
| 32 | MRI-CGCM3 | 7.617 | 1.113 | 2.298 | 12.205 | 4.742 | 20.441 | 8.192 | 14.883 | 6.942 | 3.353 |
| 33 | NORESM1-M | 7.477 | 1.176 | 2.599 | 12.022 | 4.608 | 20.640 | 8.475 | 15.539 | 7.090 | 3.661 |
| 34 | Median_GCM | 7.617 | 1.112 | 2.2985 | 12.205 | 4.742 | 20.442 | 8.193 | 14.883 | 6.942 | 3.354 |

Table A3.
NSE coefficient of maximum temperature between observed and simulated data (1950–2005).
Table A3.
NSE coefficient of maximum temperature between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | 0.534 | 0.542 | 0.305 | 0.441 | 0.558 | 0.258 | 0.629 | 0.640 | 0.479 | 0.571 |
| 2 | ACCESS1-3 | 0.543 | 0.547 | 0.295 | 0.451 | 0.562 | 0.247 | 0.636 | 0.635 | 0.472 | 0.589 |
| 3 | BCC-CSM1-1 | 0.549 | 0.558 | 0.293 | 0.434 | 0.567 | 0.246 | 0.634 | 0.621 | 0.471 | 0.585 |
| 4 | BCC-CSM1-1-M | 0.539 | 0.556 | 0.303 | 0.434 | 0.561 | 0.235 | 0.628 | 0.640 | 0.466 | 0.581 |
| 5 | CANESM2 | 0.536 | 0.558 | 0.304 | 0.445 | 0.555 | 0.247 | 0.624 | 0.637 | 0.471 | 0.571 |
| 6 | CCSM4 | 0.538 | 0.544 | 0.290 | 0.449 | 0.565 | 0.246 | 0.633 | 0.645 | 0.477 | 0.581 |
| 7 | CESM1-BGC | 0.545 | 0.559 | 0.295 | 0.445 | 0.566 | 0.236 | 0.639 | 0.627 | 0.469 | 0.589 |
| 8 | CESM1-CAM5 | 0.557 | 0.542 | 0.295 | 0.451 | 0.559 | 0.235 | 0.643 | 0.633 | 0.460 | 0.591 |
| 9 | CMCC-CM | 0.542 | 0.564 | 0.296 | 0.437 | 0.566 | 0.238 | 0.640 | 0.630 | 0.473 | 0.579 |
| 10 | CMCC-CMS | 0.536 | 0.562 | 0.303 | 0.445 | 0.575 | 0.241 | 0.630 | 0.636 | 0.464 | 0.582 |
| 11 | CNRM-CM5 | 0.538 | 0.544 | 0.278 | 0.435 | 0.551 | 0.244 | 0.627 | 0.637 | 0.474 | 0.588 |
| 12 | CSIRO-MK3-6-0 | 0.550 | 0.552 | 0.288 | 0.442 | 0.560 | 0.233 | 0.637 | 0.634 | 0.467 | 0.588 |
| 13 | EC-EARTH | 0.546 | 0.565 | 0.297 | 0.448 | 0.565 | 0.238 | 0.633 | 0.635 | 0.467 | 0.590 |
| 14 | FGOALS-G2 | 0.539 | 0.564 | 0.298 | 0.462 | 0.560 | 0.223 | 0.631 | 0.634 | 0.463 | 0.577 |
| 15 | GFDL-CM3 | 0.545 | 0.540 | 0.292 | 0.445 | 0.553 | 0.235 | 0.642 | 0.639 | 0.462 | 0.590 |
| 16 | GFDL-ESM2G | 0.543 | 0.551 | 0.296 | 0.442 | 0.566 | 0.241 | 0.630 | 0.625 | 0.462 | 0.577 |
| 17 | GFDL-ESM2M | 0.541 | 0.555 | 0.288 | 0.439 | 0.568 | 0.233 | 0.630 | 0.631 | 0.476 | 0.582 |
| 18 | GISS-E2-H | 0.541 | 0.552 | 0.298 | 0.458 | 0.565 | 0.246 | 0.632 | 0.625 | 0.469 | 0.586 |
| 19 | GISS-E2-R | 0.536 | 0.553 | 0.306 | 0.446 | 0.558 | 0.263 | 0.627 | 0.632 | 0.471 | 0.581 |
| 20 | HADGEM2-AO | 0.546 | 0.549 | 0.289 | 0.446 | 0.556 | 0.250 | 0.639 | 0.626 | 0.478 | 0.589 |
| 21 | HADGEM2-CC | 0.548 | 0.547 | 0.291 | 0.448 | 0.558 | 0.239 | 0.634 | 0.644 | 0.472 | 0.582 |
| 22 | HADGEM2-ES | 0.533 | 0.553 | 0.290 | 0.439 | 0.551 | 0.256 | 0.625 | 0.635 | 0.467 | 0.573 |
| 23 | INMCM4 | 0.541 | 0.560 | 0.307 | 0.436 | 0.569 | 0.254 | 0.637 | 0.649 | 0.471 | 0.586 |
| 24 | IPSL-CM5A-LR | 0.546 | 0.555 | 0.300 | 0.440 | 0.559 | 0.255 | 0.641 | 0.635 | 0.465 | 0.586 |
| 25 | IPSL-CM5A-MR | 0.540 | 0.549 | 0.295 | 0.450 | 0.554 | 0.219 | 0.633 | 0.628 | 0.463 | 0.579 |
| 26 | MIROC-ESM | 0.534 | 0.556 | 0.298 | 0.440 | 0.559 | 0.236 | 0.632 | 0.637 | 0.458 | 0.581 |
| 27 | MIROC-ESM-CHEM | 0.541 | 0.545 | 0.298 | 0.440 | 0.554 | 0.238 | 0.636 | 0.637 | 0.465 | 0.582 |
| 28 | MIROC5 | 0.538 | 0.550 | 0.293 | 0.434 | 0.564 | 0.230 | 0.630 | 0.631 | 0.481 | 0.585 |
| 29 | MPI-ESM-LR | 0.544 | 0.559 | 0.310 | 0.445 | 0.564 | 0.237 | 0.626 | 0.632 | 0.477 | 0.580 |
| 30 | MPI-ESM-MR | 0.546 | 0.561 | 0.300 | 0.453 | 0.570 | 0.256 | 0.640 | 0.632 | 0.482 | 0.589 |
| 31 | MRI-CGCM3 | 0.543 | 0.566 | 0.302 | 0.447 | 0.570 | 0.215 | 0.633 | 0.633 | 0.470 | 0.582 |
| 32 | NORESM1-M | 0.537 | 0.557 | 0.297 | 0.429 | 0.557 | 0.223 | 0.624 | 0.639 | 0.482 | 0.584 |
| 33 | Median_GCM | 0.561 | 0.544 | 0.307 | 0.435 | 0.551 | 0.229 | 0.643 | 0.645 | 0.481 | 0.592 |

Table A4.
NSE coefficient of minimum temperature between observed and simulated data (1950–2005).
Table A4.
NSE coefficient of minimum temperature between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | 0.564 | 0.539 | 0.555 | 0.495 | 0.565 | 0.122 | 0.638 | 0.659 | 0.376 | 0.518 |
| 2 | ACCESS1-3 | 0.580 | 0.549 | 0.570 | 0.526 | 0.586 | 0.112 | 0.649 | 0.691 | 0.376 | 0.531 |
| 3 | BCC-CSM1-1 | 0.570 | 0.543 | 0.512 | 0.503 | 0.581 | 0.097 | 0.675 | 0.658 | 0.374 | 0.539 |
| 4 | BCC-CSM1-1-M | 0.567 | 0.527 | 0.487 | 0.512 | 0.565 | 0.086 | 0.660 | 0.663 | 0.387 | 0.524 |
| 5 | CANESM2 | 0.567 | 0.538 | 0.519 | 0.495 | 0.579 | 0.085 | 0.687 | 0.637 | 0.378 | 0.517 |
| 6 | CCSM4 | 0.573 | 0.547 | 0.525 | 0.504 | 0.583 | 0.086 | 0.648 | 0.687 | 0.373 | 0.533 |
| 7 | CESM1-BGC | 0.577 | 0.549 | 0.530 | 0.510 | 0.593 | 0.100 | 0.646 | 0.680 | 0.371 | 0.523 |
| 8 | CESM1-CAM5 | 0.583 | 0.543 | 0.531 | 0.518 | 0.585 | 0.085 | 0.655 | 0.683 | 0.376 | 0.526 |
| 9 | CMCC-CM | 0.568 | 0.581 | 0.557 | 0.496 | 0.584 | 0.086 | 0.652 | 0.662 | 0.370 | 0.519 |
| 10 | CMCC-CMS | 0.590 | 0.566 | 0.567 | 0.527 | 0.611 | 0.073 | 0.661 | 0.686 | 0.372 | 0.541 |
| 11 | CNRM-CM5 | 0.575 | 0.535 | 0.539 | 0.514 | 0.565 | 0.094 | 0.650 | 0.665 | 0.393 | 0.516 |
| 12 | CSIRO-MK3-6–0 | 0.594 | 0.574 | 0.532 | 0.496 | 0.585 | 0.084 | 0.659 | 0.677 | 0.376 | 0.535 |
| 13 | EC-EARTH | 0.567 | 0.532 | 0.488 | 0.512 | 0.559 | 0.071 | 0.667 | 0.668 | 0.373 | 0.522 |
| 14 | FGOALS-G2 | 0.575 | 0.579 | 0.548 | 0.513 | 0.588 | 0.054 | 0.658 | 0.677 | 0.368 | 0.520 |
| 15 | GFDL-CM3 | 0.577 | 0.572 | 0.547 | 0.528 | 0.594 | 0.086 | 0.672 | 0.663 | 0.353 | 0.550 |
| 16 | GFDL-ESM2G | 0.584 | 0.579 | 0.549 | 0.529 | 0.604 | 0.087 | 0.672 | 0.657 | 0.365 | 0.536 |
| 17 | GFDL-ESM2M | 0.537 | 0.526 | 0.510 | 0.485 | 0.564 | 0.079 | 0.632 | 0.684 | 0.335 | 0.500 |
| 18 | GISS-E2-H | 0.566 | 0.568 | 0.560 | 0.507 | 0.574 | 0.082 | 0.640 | 0.678 | 0.335 | 0.528 |
| 19 | GISS-E2-R | 0.560 | 0.566 | 0.571 | 0.505 | 0.570 | 0.094 | 0.639 | 0.678 | 0.367 | 0.522 |
| 20 | HADGEM2-AO | 0.566 | 0.557 | 0.561 | 0.496 | 0.573 | 0.091 | 0.648 | 0.675 | 0.367 | 0.536 |
| 21 | HADGEM2-CC | 0.532 | 0.546 | 0.546 | 0.502 | 0.579 | 0.074 | 0.632 | 0.679 | 0.355 | 0.515 |
| 22 | HADGEM2-ES | 0.558 | 0.541 | 0.508 | 0.490 | 0.570 | 0.088 | 0.654 | 0.649 | 0.348 | 0.513 |
| 23 | INMCM4 | 0.576 | 0.544 | 0.539 | 0.495 | 0.575 | 0.116 | 0.668 | 0.647 | 0.334 | 0.530 |
| 24 | IPSL-CM5A-LR | 0.583 | 0.564 | 0.561 | 0.527 | 0.616 | 0.106 | 0.666 | 0.695 | 0.381 | 0.553 |
| 25 | IPSL-CM5A-MR | 0.587 | 0.561 | 0.557 | 0.534 | 0.614 | 0.082 | 0.667 | 0.686 | 0.365 | 0.548 |
| 26 | MIROC-ESM | 0.602 | 0.565 | 0.542 | 0.518 | 0.607 | 0.071 | 0.684 | 0.672 | 0.384 | 0.538 |
| 27 | MIROC-ESM-CHEM | 0.569 | 0.560 | 0.556 | 0.483 | 0.579 | 0.087 | 0.648 | 0.681 | 0.360 | 0.519 |
| 28 | MIROC5 | 0.567 | 0.565 | 0.544 | 0.496 | 0.601 | 0.073 | 0.645 | 0.675 | 0.385 | 0.529 |
| 29 | MPI-ESM-LR | 0.550 | 0.532 | 0.504 | 0.484 | 0.558 | 0.099 | 0.648 | 0.671 | 0.360 | 0.508 |
| 30 | MPI-ESM-MR | 0.553 | 0.559 | 0.519 | 0.511 | 0.586 | 0.104 | 0.648 | 0.661 | 0.369 | 0.519 |
| 31 | MRI-CGCM3 | 0.575 | 0.575 | 0.547 | 0.500 | 0.593 | 0.073 | 0.649 | 0.672 | 0.373 | 0.518 |
| 32 | NORESM1-M | 0.543 | 0.527 | 0.520 | 0.472 | 0.566 | 0.089 | 0.636 | 0.690 | 0.330 | 0.500 |
| 33 | Median_GCM | 0.580 | 0.543 | 0.553 | 0.495 | 0.572 | 0.076 | 0.661 | 0.685 | 0.381 | 0.534 |

Table A5.
NSE coefficient of Days between observed and simulated data (1950–2005).
Table A5.
NSE coefficient of Days between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | −2.00 | −1.35 | −1.58 | −0.19 | −1.66 | −0.10 | −1.62 | −0.80 | −0.39 | −1.43 |
| 2 | ACCESS1-3 | −0.80 | −0.96 | −0.83 | −0.88 | −1.32 | −0.01 | −0.73 | −1.26 | −1.10 | −0.80 |
| 3 | BCC-CSM1-1 | −0.91 | −1.13 | −1.76 | −0.86 | −1.56 | 0.11 | −0.99 | −0.40 | −0.70 | −1.26 |
| 4 | BCC-CSM1-1-M | −0.94 | −0.75 | −1.30 | −0.43 | −1.18 | 0.00 | −0.97 | −0.69 | −0.51 | −0.91 |
| 5 | CANESM2 | −1.35 | −0.77 | −0.63 | −0.35 | −1.13 | 0.09 | −0.51 | −0.66 | −0.47 | −1.06 |
| 6 | CCSM4 | −1.57 | −1.62 | −1.04 | −0.39 | −0.84 | −0.08 | −0.90 | −0.21 | −0.69 | −1.16 |
| 7 | CESM1-BGC | −1.18 | −0.72 | −1.00 | −0.56 | −1.41 | −0.05 | −1.58 | −0.46 | −0.49 | −1.57 |
| 8 | CESM1-CAM5 | −1.13 | −1.44 | −1.08 | −0.79 | −1.30 | −0.74 | −0.91 | −0.63 | −0.41 | −0.80 |
| 9 | CMCC-CM | −1.49 | −0.82 | −0.10 | −0.78 | −0.94 | 0.04 | −1.16 | −0.60 | −0.61 | −1.60 |
| 10 | CMCC-CMS | −0.78 | −1.29 | −1.48 | −0.83 | −1.33 | −0.17 | −0.74 | −0.34 | −1.04 | −1.27 |
| 11 | CNRM-CM5 | −1.38 | −2.20 | −0.91 | −0.24 | −1.68 | −0.32 | −1.66 | −0.57 | −0.57 | −1.35 |
| 12 | CSIRO-MK3-6–0 | −1.11 | −1.85 | −0.92 | −0.82 | −1.37 | −0.26 | −1.75 | −0.23 | −0.68 | −1.43 |
| 13 | EC-EARTH | −0.19 | −0.52 | −0.91 | −0.50 | −0.92 | −0.05 | −0.10 | −0.60 | −1.37 | −0.36 |
| 14 | FGOALS-G2 | −2.01 | −1.53 | −1.06 | −0.86 | −0.89 | −0.30 | −0.99 | −1.27 | −1.31 | −1.28 |
| 15 | GFDL-CM3 | −0.97 | −1.79 | −0.91 | −0.72 | −1.64 | −0.09 | −1.21 | −0.60 | −1.00 | −0.72 |
| 16 | GFDL-ESM2G | −1.49 | −2.17 | −1.65 | −0.71 | −1.14 | −0.04 | −1.52 | −1.13 | −1.10 | −1.66 |
| 17 | GFDL-ESM2M | −1.21 | −0.99 | −0.65 | −1.11 | −0.52 | −0.03 | −0.94 | −1.07 | −0.51 | −0.54 |
| 18 | GISS-E2-H | −1.74 | −1.36 | −0.72 | −0.42 | −1.99 | 0.00 | −1.30 | −0.66 | −0.72 | −1.57 |
| 19 | GISS-E2-R | −1.34 | −1.06 | −0.69 | −0.53 | −0.91 | 0.13 | −1.47 | −0.94 | −0.57 | −1.22 |
| 20 | HADGEM2-AO | −1.60 | −0.81 | −1.15 | −1.22 | −2.07 | −0.21 | −0.81 | −0.60 | −0.42 | −0.92 |
| 21 | HADGEM2-CC | −0.85 | −1.82 | −1.61 | −0.55 | −1.81 | −0.32 | −1.20 | −0.38 | −1.19 | −1.08 |
| 22 | HADGEM2-ES | −1.04 | −1.90 | −0.95 | −1.37 | −1.77 | 0.11 | −0.82 | −0.53 | −1.03 | −1.03 |
| 23 | INMCM4 | −1.09 | −1.13 | −1.66 | −0.92 | −1.49 | −0.15 | −0.62 | −0.90 | −0.43 | −0.86 |
| 24 | IPSL-CM5A-LR | −0.83 | −1.01 | −0.66 | −0.78 | −1.13 | 0.00 | −1.45 | −0.65 | −1.04 | −0.70 |
| 25 | IPSL-CM5A-MR | −1.41 | −1.42 | −0.80 | −0.24 | −1.00 | −0.17 | −1.33 | −1.05 | −1.31 | −0.94 |
| 26 | MIROC-ESM | −1.18 | −0.83 | −0.52 | −0.64 | −1.00 | 0.04 | −1.27 | −0.45 | −0.35 | −1.42 |
| 27 | MIROC-ESM-CHEM | −1.28 | −0.77 | −1.39 | −1.51 | −1.47 | 0.10 | −1.18 | −0.46 | −1.04 | −0.99 |
| 28 | MIROC5 | −1.18 | −0.76 | −1.39 | −1.46 | −0.87 | −0.13 | −2.27 | −0.35 | −0.41 | −1.86 |
| 29 | MPI-ESM-LR | −0.80 | −1.58 | −1.26 | −0.20 | −0.57 | −0.17 | −1.06 | −0.62 | −0.23 | −0.75 |
| 30 | MPI-ESM-MR | −1.04 | −1.24 | −0.38 | −1.08 | −0.99 | −0.10 | −0.60 | −0.49 | −0.28 | −0.76 |
| 31 | MRI-CGCM3 | −1.18 | −1.23 | −0.93 | −1.02 | −0.87 | −0.28 | −1.48 | −0.92 | −0.71 | −1.66 |
| 32 | NORESM1-M | −1.52 | −0.51 | −1.10 | −1.38 | −0.79 | 0.02 | −1.17 | −0.78 | −0.86 | −0.94 |
| 33 | Median_GCM | −1.08 | −0.77 | −0.71 | −0.48 | −1.00 | −0.04 | −0.93 | −0.39 | −0.66 | −0.94 |

Table A6.
NSE coefficient of waves between observed and simulated data (1950–2005).
Table A6.
NSE coefficient of waves between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | −1.20 | −0.75 | −1.07 | −0.74 | −1.26 | −0.21 | −1.04 | −1.27 | −0.40 | −1.35 |
| 2 | ACCESS1-3 | −0.70 | −0.74 | −0.72 | −0.73 | −1.48 | 0.11 | −0.88 | −1.13 | −0.85 | −0.88 |
| 3 | BCC-CSM1-1 | −1.05 | −1.02 | −1.38 | −0.41 | −1.44 | 0.05 | −1.32 | −1.24 | −0.91 | −1.12 |
| 4 | BCC-CSM1-1-M | −0.48 | −0.90 | −0.80 | −0.58 | −1.02 | −0.06 | −0.80 | −0.85 | −0.57 | −0.72 |
| 5 | CANESM2 | −1.28 | −0.81 | −0.43 | −0.55 | −0.89 | −0.18 | −0.95 | −0.69 | −0.15 | −1.39 |
| 6 | CCSM4 | −0.70 | −1.18 | −0.82 | −0.73 | −0.89 | −0.20 | −0.69 | −0.47 | −0.54 | −1.26 |
| 7 | CESM1-BGC | −0.69 | −1.20 | −1.00 | −0.49 | −1.07 | −0.33 | −1.40 | −0.87 | −0.63 | −1.94 |
| 8 | CESM1-CAM5 | −1.29 | −1.22 | −0.55 | −0.73 | −1.12 | −0.79 | −1.63 | −0.66 | −0.57 | −1.04 |
| 9 | CMCC-CM | −1.06 | −0.54 | −0.23 | −0.80 | −0.67 | −0.27 | −1.08 | −1.24 | −0.18 | −0.97 |
| 10 | CMCC-CMS | −0.73 | −0.86 | −1.10 | −0.99 | −1.09 | −0.37 | −1.31 | −0.81 | −0.78 | −1.54 |
| 11 | CNRM-CM5 | −1.33 | −1.37 | −0.22 | −0.94 | −1.00 | −0.20 | −1.31 | −1.06 | −0.86 | −1.42 |
| 12 | CSIRO-MK3-6-0 | −0.93 | −1.05 | −0.52 | −0.56 | −1.15 | −0.27 | −1.66 | −0.63 | −0.37 | −1.06 |
| 13 | EC-EARTH | −0.71 | −0.49 | −0.77 | −0.93 | −0.69 | −0.20 | −0.62 | −0.82 | −0.81 | −0.56 |
| 14 | FGOALS-G2 | −1.48 | −1.16 | −0.96 | −1.78 | −0.73 | −0.13 | −1.07 | −1.31 | −1.24 | −0.95 |
| 15 | GFDL-CM3 | −1.02 | −0.98 | −1.17 | −0.68 | −0.92 | −0.19 | −1.06 | −0.92 | −0.60 | −0.99 |
| 16 | GFDL-ESM2G | −1.12 | −1.41 | −1.13 | −0.50 | −1.31 | −0.15 | −1.59 | −1.17 | −0.46 | −1.58 |
| 17 | GFDL-ESM2M | −1.19 | −0.95 | −0.53 | −0.95 | −0.51 | −0.13 | −0.84 | −1.64 | −0.52 | −1.23 |
| 18 | GISS-E2-H | −1.14 | −1.02 | −0.67 | −1.06 | −1.16 | −0.09 | −1.29 | −0.84 | −1.09 | −1.30 |
| 19 | GISS-E2-R | −0.50 | −1.05 | −0.94 | −1.08 | −1.13 | −0.13 | −0.38 | −1.13 | −0.46 | −1.16 |
| 20 | HADGEM2-AO | −1.00 | −0.47 | −0.78 | −1.04 | −1.12 | −0.24 | −0.73 | −0.65 | −0.50 | −1.10 |
| 21 | HADGEM2-CC | −0.62 | −1.36 | −0.88 | −0.47 | −1.01 | −0.53 | −1.26 | −1.00 | −1.02 | −1.32 |
| 22 | HADGEM2-ES | −0.99 | −1.30 | −1.36 | −1.46 | −1.56 | −0.13 | −0.88 | −1.31 | −1.23 | −1.11 |
| 23 | INMCM4 | −1.23 | −0.68 | −0.98 | −1.52 | −1.38 | −0.33 | −0.81 | −1.33 | −0.21 | −0.83 |
| 24 | IPSL-CM5A-LR | −1.07 | −0.92 | −0.63 | −1.71 | −1.39 | −0.25 | −0.90 | −0.41 | −0.81 | −0.76 |
| 25 | IPSL-CM5A-MR | −1.10 | −1.28 | −0.39 | −0.55 | −0.98 | −0.35 | −1.12 | −0.66 | −0.59 | −0.94 |
| 26 | MIROC-ESM | −1.11 | −0.82 | −0.45 | −1.00 | −0.97 | −0.02 | −1.22 | −0.91 | −0.32 | −1.37 |
| 27 | MIROC-ESM-CHEM | −1.59 | −0.85 | −1.11 | −1.55 | −0.88 | −0.14 | −1.06 | −1.03 | −0.91 | −0.80 |
| 28 | MIROC5 | −0.73 | −0.39 | −1.35 | −1.60 | −1.08 | −0.07 | −0.94 | −0.91 | −0.13 | −1.58 |
| 29 | MPI-ESM-LR | −0.52 | −1.36 | −0.87 | −0.69 | −0.76 | −0.25 | −1.40 | −0.79 | −0.25 | −0.98 |
| 30 | MPI-ESM-MR | −1.05 | −0.78 | −0.45 | −0.81 | −0.54 | −0.39 | −0.98 | −0.54 | −0.12 | −0.72 |
| 31 | MRI-CGCM3 | −1.17 | −1.16 | −0.78 | −1.06 | −1.12 | −0.24 | −1.57 | −1.02 | −0.53 | −1.32 |
| 32 | NORESM1-M | −1.28 | −0.72 | −1.26 | −1.08 | −0.57 | −0.07 | −1.02 | −1.48 | −0.74 | −0.93 |
| 33 | Median_GCM | −1.07 | −0.77 | −0.61 | −0.73 | −0.96 | −0.20 | −1.19 | −0.66 | −0.56 | −1.03 |

Table A7.
NSE coefficient of total between observed and simulated data (1950–2005).
Table A7.
NSE coefficient of total between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | −2.13 | −1.33 | −1.54 | −0.13 | −1.55 | −0.16 | −1.36 | −0.78 | −0.51 | −1.24 |
| 2 | ACCESS1-3 | −0.80 | −0.93 | −0.95 | −0.81 | −1.07 | −0.06 | −0.77 | −1.31 | −1.23 | −0.54 |
| 3 | BCC-CSM1-1 | −1.14 | −1.23 | −1.75 | −0.78 | −1.44 | 0.03 | −1.15 | −0.36 | −0.80 | −0.93 |
| 4 | BCC-CSM1-1-M | −0.96 | −0.85 | −1.26 | −0.36 | −1.16 | −0.06 | −1.13 | −0.68 | −0.48 | −0.78 |
| 5 | CANESM2 | −1.45 | −0.80 | −0.56 | −0.36 | −1.02 | 0.02 | −0.43 | −0.69 | −0.52 | −0.97 |
| 6 | CCSM4 | −1.68 | −1.59 | −0.98 | −0.34 | −0.90 | −0.07 | −0.95 | −0.20 | −0.79 | −0.96 |
| 7 | CESM1-BGC | −1.39 | −0.62 | −1.00 | −0.50 | −1.19 | −0.09 | −1.66 | −0.47 | −0.43 | −1.38 |
| 8 | CESM1-CAM5 | −1.14 | −1.50 | −1.03 | −0.69 | −1.26 | −0.88 | −1.00 | −0.60 | −0.40 | −0.72 |
| 9 | CMCC-CM | −1.64 | −0.86 | −0.13 | −0.71 | −0.79 | −0.05 | −1.29 | −0.59 | −0.70 | −1.35 |
| 10 | CMCC-CMS | −0.92 | −1.20 | −1.56 | −0.82 | −1.11 | −0.25 | −0.85 | −0.34 | −1.11 | −1.02 |
| 11 | CNRM-CM5 | −1.38 | −2.19 | −0.76 | −0.22 | −1.43 | −0.44 | −1.31 | −0.58 | −0.57 | −0.97 |
| 12 | CSIRO-MK3-6-0 | −1.10 | −1.59 | −0.90 | −0.78 | −1.40 | −0.33 | −1.61 | −0.25 | −0.69 | −1.29 |
| 13 | EC-EARTH | −0.34 | −0.53 | −0.91 | −0.45 | −0.98 | −0.17 | −0.22 | −0.64 | −1.34 | −0.20 |
| 14 | FGOALS-G2 | −2.01 | −1.49 | −1.05 | −0.78 | −0.78 | −0.37 | −0.81 | −1.15 | −1.45 | −1.09 |
| 15 | GFDL-CM3 | −0.92 | −1.82 | −0.94 | −0.68 | −1.61 | −0.13 | −1.11 | −0.55 | −1.00 | −0.47 |
| 16 | GFDL-ESM2G | −1.61 | −2.06 | −1.56 | −0.71 | −1.04 | −0.07 | −1.47 | −1.16 | −1.18 | −1.34 |
| 17 | GFDL-ESM2M | −1.07 | −1.08 | −0.57 | −1.05 | −0.39 | −0.06 | −0.72 | −1.02 | −0.52 | −0.33 |
| 18 | GISS-E2-H | −1.80 | −1.44 | −0.66 | −0.35 | −1.65 | −0.13 | −1.34 | −0.58 | −0.85 | −1.23 |
| 19 | GISS-E2-R | −1.41 | −1.13 | −0.71 | −0.41 | −0.85 | 0.10 | −1.27 | −0.83 | −0.62 | −1.15 |
| 20 | HADGEM2-AO | −1.73 | −0.97 | −1.16 | −1.13 | −1.94 | −0.31 | −0.84 | −0.52 | −0.47 | −0.61 |
| 21 | HADGEM2-CC | −1.00 | −1.84 | −1.51 | −0.48 | −1.75 | −0.35 | −1.22 | −0.35 | −1.27 | −0.78 |
| 22 | HADGEM2-ES | −0.96 | −1.80 | −0.87 | −1.22 | −1.58 | 0.13 | −0.70 | −0.47 | −1.15 | −0.80 |
| 23 | INMCM4 | −1.17 | −1.33 | −1.71 | −0.87 | −1.20 | −0.13 | −0.66 | −0.94 | −0.37 | −0.74 |
| 24 | IPSL-CM5A-LR | −0.88 | −0.95 | −0.64 | −0.75 | −0.96 | −0.06 | −1.16 | −0.67 | −0.99 | −0.54 |
| 25 | IPSL-CM5A-MR | −1.51 | −1.45 | −0.87 | −0.25 | −0.99 | −0.20 | −1.17 | −1.10 | −1.30 | −0.86 |
| 26 | MIROC-ESM | −1.16 | −0.86 | −0.48 | −0.57 | −0.95 | −0.01 | −1.20 | −0.39 | −0.36 | −1.06 |
| 27 | MIROC-ESM-CHEM | −1.35 | −0.87 | −1.53 | −1.35 | −1.22 | 0.06 | −1.30 | −0.47 | −1.20 | −0.74 |
| 28 | MIROC5 | −1.03 | −0.69 | −1.32 | −1.40 | −0.71 | −0.15 | −2.14 | −0.29 | −0.46 | −1.46 |
| 29 | MPI-ESM-LR | −0.79 | −1.61 | −1.32 | −0.12 | −0.49 | −0.22 | −1.21 | −0.58 | −0.41 | −0.72 |
| 30 | MPI-ESM-MR | −1.09 | −1.14 | −0.51 | −1.07 | −0.78 | −0.18 | −0.53 | −0.47 | −0.31 | −0.50 |
| 31 | MRI-CGCM3 | −1.01 | −1.30 | −0.93 | −1.00 | −0.63 | −0.35 | −1.42 | −0.86 | −0.79 | −1.14 |
| 32 | NORESM1-M | −1.56 | −0.58 | −1.19 | −1.23 | −0.73 | 0.01 | −0.97 | −0.70 | −0.88 | −0.65 |
| 33 | Median_GCM | −1.63 | −0.91 | −0.75 | −0.65 | −1.06 | −0.34 | −1.46 | −0.47 | −1.22 | −1.13 |

Table A8.
NSE coefficient of longest between observed and simulated data (1950–2005).
Table A8.
NSE coefficient of longest between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | −2.21 | −1.94 | −2.41 | −0.18 | −3.04 | −0.92 | −0.77 | −0.59 | −1.18 | −2.73 |
| 2 | ACCESS1-3 | −0.81 | −1.75 | −0.95 | −0.63 | −2.11 | −0.82 | −0.80 | −0.70 | −2.03 | −1.10 |
| 3 | BCC-CSM1-1 | −1.34 | −2.44 | −1.83 | −0.57 | −1.64 | −1.45 | −1.66 | −0.14 | −1.18 | −0.85 |
| 4 | BCC-CSM1-1-M | −1.04 | −0.89 | −1.16 | −0.36 | −1.15 | −1.13 | −0.93 | −0.58 | −0.77 | −0.81 |
| 5 | CANESM2 | −0.91 | −1.99 | −1.33 | −0.54 | −0.53 | −0.57 | −0.64 | −0.62 | −1.32 | −0.86 |
| 6 | CCSM4 | −0.96 | −1.79 | −0.95 | −0.39 | −1.54 | −0.40 | −0.91 | −0.46 | −1.01 | −1.68 |
| 7 | CESM1-BGC | −1.07 | −1.68 | −0.55 | −0.76 | −0.90 | −0.49 | −1.01 | −0.37 | −0.34 | −1.09 |
| 8 | CESM1-CAM5 | −0.28 | −6.57 | −0.75 | −0.51 | −1.89 | −2.31 | −0.51 | −0.80 | −0.81 | −0.13 |
| 9 | CMCC-CM | −0.45 | −1.65 | −0.50 | −0.55 | −0.68 | −0.74 | −1.65 | −0.57 | −0.85 | −3.02 |
| 10 | CMCC-CMS | −1.27 | −1.97 | −2.97 | −0.64 | −1.20 | −0.45 | −1.43 | −0.37 | −1.57 | −1.29 |
| 11 | CNRM-CM5 | −0.75 | −2.66 | −1.72 | −0.24 | −1.58 | −1.94 | −1.41 | −0.46 | −0.56 | −1.84 |
| 12 | CSIRO-MK3-6-0 | −0.42 | −2.89 | −1.33 | −0.80 | −0.87 | −0.78 | −0.87 | −0.46 | −1.00 | −1.46 |
| 13 | EC-EARTH | −0.39 | −1.40 | −0.80 | −0.52 | −1.48 | −0.74 | −0.70 | −0.78 | −2.51 | −0.08 |
| 14 | FGOALS-G2 | −2.17 | −2.00 | −1.82 | −0.73 | −1.33 | −1.36 | −1.01 | −1.55 | −1.74 | −1.21 |
| 15 | GFDL-CM3 | −1.47 | −2.54 | −2.56 | −0.41 | −3.87 | −0.58 | −1.30 | −0.50 | −0.51 | −1.51 |
| 16 | GFDL-ESM2G | −1.35 | −5.14 | −2.41 | −0.76 | −0.83 | −0.71 | −1.20 | −0.97 | −2.24 | −1.24 |
| 17 | GFDL-ESM2M | −0.75 | −2.81 | −0.95 | −1.92 | −0.95 | −1.21 | −1.46 | −1.89 | −1.68 | −0.87 |
| 18 | GISS-E2-H | −0.73 | −3.45 | −1.07 | −0.20 | −1.36 | −3.04 | −1.18 | −0.36 | −1.61 | −1.62 |
| 19 | GISS-E2-R | −2.09 | −1.43 | −1.22 | −0.68 | −1.02 | −0.21 | −1.38 | −0.80 | −0.99 | −1.51 |
| 20 | HADGEM2-AO | −1.19 | −1.93 | −1.63 | −0.55 | −2.08 | −0.32 | −0.68 | −0.41 | −1.05 | −0.66 |
| 21 | HADGEM2-CC | −1.15 | −2.85 | −2.52 | −0.55 | −3.93 | −0.68 | −0.94 | −0.56 | −1.17 | −0.84 |
| 22 | HADGEM2-ES | −1.02 | −5.96 | −1.55 | −0.96 | −1.18 | 0.03 | −1.23 | −0.83 | −2.53 | −0.93 |
| 23 | INMCM4 | −0.44 | −2.49 | −2.37 | −0.60 | −0.47 | −0.80 | −0.83 | −1.02 | −1.42 | −1.00 |
| 24 | IPSL-CM5A-LR | −0.53 | −5.82 | −0.55 | −0.32 | −1.50 | −1.02 | −0.51 | −0.59 | −1.74 | −0.58 |
| 25 | IPSL-CM5A-MR | −1.05 | −2.84 | −1.26 | −0.16 | −1.23 | −0.86 | −1.10 | −1.11 | −2.64 | −0.72 |
| 26 | MIROC-ESM | −0.80 | −1.00 | −0.97 | −0.33 | −1.20 | −0.27 | −0.75 | −0.21 | −0.59 | −1.02 |
| 27 | MIROC-ESM-CHEM | −0.40 | −1.45 | −1.14 | −1.29 | −1.49 | −0.12 | −1.10 | −0.21 | −1.24 | −0.79 |
| 28 | MIROC5 | −1.09 | −1.45 | −0.90 | −1.07 | −0.55 | −0.44 | −3.51 | −0.38 | −0.40 | −1.18 |
| 29 | MPI-ESM-LR | −1.08 | −3.67 | −1.37 | −0.41 | −0.89 | −0.47 | −1.09 | −0.45 | −0.56 | −0.77 |
| 30 | MPI-ESM-MR | −0.64 | −4.87 | −1.58 | −1.04 | −1.55 | −0.70 | −1.27 | −0.51 | −0.50 | −1.09 |
| 31 | MRI-CGCM3 | −0.30 | −1.50 | −0.70 | −0.91 | −0.72 | −0.85 | −1.12 | −0.58 | −1.29 | −0.94 |
| 32 | NORESM1-M | −1.51 | −1.94 | −2.63 | −1.12 | −0.51 | −0.87 | −0.70 | −1.82 | −2.31 | −0.72 |
| 33 | Median_GCM | −1.05 | −1.73 | −0.96 | −0.55 | −1.11 | −0.74 | −1.10 | −0.46 | −1.53 | −1.28 |

Table A9.
NSE coefficient of Intensity between observed and simulated data (1950–2005).
Table A9.
NSE coefficient of Intensity between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | −2.09 | −1.24 | −1.76 | −0.22 | −1.53 | −0.16 | −1.81 | −0.75 | −0.55 | −1.22 |
| 2 | ACCESS1-3 | −0.72 | −0.84 | −1.12 | −1.00 | −1.01 | −0.10 | −0.93 | −1.26 | −1.24 | −0.50 |
| 3 | BCC-CSM1-1 | −1.08 | −1.18 | −1.95 | −0.97 | −1.34 | 0.01 | −1.59 | −0.29 | −0.79 | −0.90 |
| 4 | BCC-CSM1-1-M | −0.96 | −0.77 | −1.41 | −0.42 | −1.13 | −0.07 | −1.65 | −0.64 | −0.47 | −0.75 |
| 5 | CANESM2 | −1.29 | −0.73 | −0.71 | −0.46 | −0.95 | 0.00 | −0.72 | −0.71 | −0.49 | −0.90 |
| 6 | CCSM4 | −1.62 | −1.51 | −1.12 | −0.42 | −0.78 | −0.09 | −1.36 | −0.12 | −0.78 | −0.93 |
| 7 | CESM1-BGC | −1.38 | −0.59 | −1.15 | −0.60 | −1.16 | −0.11 | −2.13 | −0.36 | −0.47 | −1.31 |
| 8 | CESM1-CAM5 | −1.06 | −1.53 | −1.23 | −0.95 | −1.20 | −0.94 | −1.34 | −0.58 | −0.39 | −0.61 |
| 9 | CMCC-CM | −1.53 | −0.87 | −0.16 | −0.96 | −0.72 | −0.08 | −1.78 | −0.53 | −0.70 | −1.29 |
| 10 | CMCC-CMS | −0.89 | −1.06 | −1.77 | −0.98 | −0.99 | −0.28 | −1.22 | −0.24 | −1.09 | −0.96 |
| 11 | CNRM-CM5 | −1.33 | −2.13 | −0.90 | −0.26 | −1.44 | −0.46 | −1.63 | −0.52 | −0.56 | −0.89 |
| 12 | CSIRO-MK3-6-0 | −1.00 | −1.48 | −1.03 | −0.99 | −1.30 | −0.38 | −2.08 | −0.20 | −0.73 | −1.24 |
| 13 | EC-EARTH | −0.31 | −0.54 | −1.11 | −0.59 | −0.95 | −0.18 | −0.45 | −0.58 | −1.41 | −0.19 |
| 14 | FGOALS-G2 | −1.88 | −1.40 | −1.20 | −1.04 | −0.79 | −0.44 | −1.14 | −1.08 | −1.49 | −1.07 |
| 15 | GFDL-CM3 | −0.80 | −1.76 | −1.14 | −0.92 | −1.67 | −0.14 | −1.44 | −0.49 | −0.95 | −0.43 |
| 16 | GFDL-ESM2G | −1.54 | −2.07 | −1.82 | −0.96 | −1.03 | −0.09 | −1.93 | −1.18 | −1.24 | −1.32 |
| 17 | GFDL-ESM2M | −0.96 | −0.94 | −0.67 | −1.38 | −0.38 | −0.08 | −1.00 | −0.97 | −0.49 | −0.27 |
| 18 | GISS-E2-H | −1.75 | −1.37 | −0.84 | −0.41 | −1.56 | −0.18 | −1.72 | −0.49 | −0.80 | −1.30 |
| 19 | GISS-E2-R | −1.43 | −1.05 | −0.84 | −0.57 | −0.75 | 0.10 | −1.81 | −0.78 | −0.62 | −1.13 |
| 20 | HADGEM2-AO | −1.72 | −0.92 | −1.38 | −1.39 | −1.95 | −0.35 | −1.18 | −0.47 | −0.52 | −0.63 |
| 21 | HADGEM2-CC | −0.95 | −1.65 | −1.78 | −0.62 | −1.68 | −0.35 | −1.66 | −0.28 | −1.26 | −0.71 |
| 22 | HADGEM2-ES | −0.92 | −1.65 | −0.91 | −1.46 | −1.49 | 0.14 | −1.13 | −0.44 | −1.15 | −0.69 |
| 23 | INMCM4 | −1.04 | −1.19 | −1.91 | −1.00 | −1.12 | −0.14 | −0.92 | −0.94 | −0.35 | −0.67 |
| 24 | IPSL-CM5A-LR | −0.82 | −0.90 | −0.75 | −0.89 | −0.97 | −0.07 | −1.63 | −0.61 | −1.08 | −0.47 |
| 25 | IPSL-CM5A-MR | −1.49 | −1.38 | −1.03 | −0.33 | −0.97 | −0.23 | −1.64 | −1.05 | −1.36 | −0.77 |
| 26 | MIROC-ESM | −1.08 | −0.83 | −0.61 | −0.79 | −0.94 | −0.03 | −1.57 | −0.32 | −0.37 | −1.00 |
| 27 | MIROC-ESM-CHEM | −1.26 | −0.80 | −1.71 | −1.76 | −1.21 | 0.05 | −1.79 | −0.38 | −1.16 | −0.69 |
| 28 | MIROC5 | −0.94 | −0.71 | −1.48 | −1.68 | −0.63 | −0.16 | −2.77 | −0.26 | −0.47 | −1.38 |
| 29 | MPI-ESM-LR | −0.70 | −1.53 | −1.44 | −0.21 | −0.43 | −0.25 | −1.64 | −0.51 | −0.42 | −0.63 |
| 30 | MPI-ESM-MR | −0.94 | −1.13 | −0.69 | −1.28 | −0.78 | −0.21 | −0.89 | −0.42 | −0.33 | −0.49 |
| 31 | MRI-CGCM3 | −0.92 | −1.22 | −1.03 | −1.19 | −0.55 | −0.40 | −1.82 | −0.82 | −0.77 | −1.03 |
| 32 | NORESM1-M | −1.50 | −0.51 | −1.35 | −1.52 | −0.77 | −0.03 | −1.38 | −0.64 | −0.89 | −0.59 |
| 33 | Median_GCM | −1.08 | −0.50 | −0.14 | −0.74 | −0.35 | −0.80 | −1.82 | −0.46 | −1.16 | −1.06 |

Table A10.
NSE coefficient of Night between observed and simulated data (1950–2005).
Table A10.
NSE coefficient of Night between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | −2.07 | −1.25 | −2.23 | −0.21 | −1.46 | −0.33 | −2.12 | −0.78 | −0.93 | −1.13 |
| 2 | ACCESS1-3 | −0.59 | −0.61 | −1.29 | −0.60 | −0.88 | −0.67 | −0.71 | −0.95 | −1.51 | −0.35 |
| 3 | BCC-CSM1-1 | −1.12 | −1.11 | −2.13 | −0.95 | −1.14 | −0.33 | −1.41 | −0.17 | −1.04 | −0.74 |
| 4 | BCC-CSM1-1-M | −1.01 | −0.54 | −1.65 | −0.32 | −0.95 | −0.31 | −1.60 | −0.61 | −0.58 | −0.58 |
| 5 | CANESM2 | −0.90 | −0.66 | −1.21 | −0.47 | −0.72 | −0.37 | −0.51 | −0.88 | −0.59 | −0.66 |
| 6 | CCSM4 | −1.63 | −1.25 | −1.14 | −0.15 | −0.42 | −0.38 | −1.47 | −0.20 | −0.86 | −0.80 |
| 7 | CESM1-BGC | −1.54 | −0.49 | −1.42 | −0.37 | −1.04 | −0.37 | −1.98 | −0.23 | −0.89 | −1.07 |
| 8 | CESM1-CAM5 | −1.05 | −1.89 | −1.75 | −0.70 | −1.12 | −1.51 | −1.34 | −0.81 | −0.52 | −0.35 |
| 9 | CMCC-CM | −1.54 | −1.04 | −0.29 | −1.11 | −0.56 | −0.51 | −1.82 | −0.50 | −0.84 | −1.01 |
| 10 | CMCC-CMS | −1.08 | −0.79 | −2.16 | −0.86 | −0.71 | −0.74 | −1.44 | −0.18 | −1.35 | −0.76 |
| 11 | CNRM-CM5 | −1.31 | −2.01 | −1.37 | −0.16 | −1.36 | −0.81 | −1.32 | −0.54 | −0.75 | −0.63 |
| 12 | CSIRO-MK3-6-0 | −0.70 | −1.25 | −1.23 | −0.66 | −1.06 | −1.02 | −2.07 | −0.30 | −1.13 | −0.99 |
| 13 | EC-EARTH | −0.32 | −0.69 | −1.41 | −0.51 | −0.83 | −0.43 | −0.31 | −0.50 | −1.86 | −0.24 |
| 14 | FGOALS-G2 | −2.03 | −1.40 | −1.65 | −0.84 | −0.82 | −1.11 | −1.22 | −0.62 | −1.90 | −0.95 |
| 15 | GFDL-CM3 | −0.69 | −1.77 | −1.90 | −0.73 | −1.79 | −0.51 | −1.18 | −0.47 | −0.97 | −0.29 |
| 16 | GFDL-ESM2G | −1.65 | −2.19 | −2.68 | −0.95 | −0.96 | −0.53 | −1.71 | −1.22 | −1.79 | −1.21 |
| 17 | GFDL-ESM2M | −1.06 | −0.82 | −0.85 | −1.19 | −0.39 | −0.40 | −1.27 | −0.74 | −0.90 | −0.12 |
| 18 | GISS-E2-H | −1.81 | −1.26 | −1.31 | −0.10 | −1.34 | −0.86 | −1.61 | −0.40 | −0.77 | −1.54 |
| 19 | GISS-E2-R | −1.80 | −0.97 | −0.94 | −0.39 | −0.67 | −0.16 | −2.14 | −0.74 | −0.84 | −1.00 |
| 20 | HADGEM2-AO | −2.06 | −1.03 | −1.91 | −0.97 | −2.03 | −0.67 | −1.26 | −0.64 | −0.92 | −0.68 |
| 21 | HADGEM2-CC | −1.29 | −1.20 | −2.80 | −0.66 | −1.49 | −0.54 | −1.94 | −0.42 | −1.88 | −0.56 |
| 22 | HADGEM2-ES | −0.95 | −1.65 | −0.90 | −1.01 | −1.30 | 0.02 | −1.09 | −0.63 | −1.66 | −0.32 |
| 23 | INMCM4 | −0.72 | −1.13 | −2.50 | −0.80 | −0.99 | −0.42 | −0.73 | −0.96 | −0.49 | −0.50 |
| 24 | IPSL-CM5A-LR | −0.64 | −0.72 | −0.95 | −0.63 | −0.99 | −0.34 | −1.52 | −0.60 | −1.49 | −0.35 |
| 25 | IPSL-CM5A-MR | −1.29 | −1.08 | −1.39 | −0.22 | −0.84 | −0.57 | −1.38 | −0.98 | −1.82 | −0.47 |
| 26 | MIROC-ESM | −0.90 | −0.85 | −1.04 | −0.73 | −0.90 | −0.35 | −1.42 | −0.28 | −0.55 | −0.76 |
| 27 | MIROC-ESM-CHEM | −1.30 | −0.61 | −1.93 | −1.66 | −1.15 | −0.18 | −1.70 | −0.30 | −1.28 | −0.49 |
| 28 | MIROC5 | −0.83 | −0.88 | −1.92 | −1.25 | −0.42 | −0.39 | −2.63 | −0.43 | −0.71 | −0.92 |
| 29 | MPI-ESM-LR | −0.63 | −1.62 | −1.54 | −0.37 | −0.32 | −0.60 | −1.53 | −0.51 | −0.65 | −0.38 |
| 30 | MPI-ESM-MR | −0.63 | −1.20 | −1.41 | −0.87 | −0.81 | −0.65 | −1.01 | −0.60 | −0.70 | −0.45 |
| 31 | MRI-CGCM3 | −0.83 | −1.04 | −1.23 | −0.85 | −0.41 | −0.95 | −1.56 | −0.71 | −0.90 | −0.53 |
| 32 | NORESM1-M | −1.90 | −0.48 | −1.72 | −1.17 | −0.89 | −0.52 | −1.77 | −0.66 | −1.36 | −0.48 |
| 33 | Median_GCM | −1.11 | −0.77 | −0.15 | −0.05 | −0.72 | −0.59 | −1.71 | −0.41 | −1.50 | −0.72 |

Table A11.
NSE coefficient of First between observed and simulated data (1950–2005).
Table A11.
NSE coefficient of First between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | −0.86 | −1.43 | −1.14 | −0.66 | −1.75 | −0.11 | −0.78 | −1.36 | −0.22 | −0.91 |
| 2 | ACCESS1-3 | −0.71 | −0.74 | −1.01 | −3.45 | −2.68 | −0.30 | −0.36 | −0.78 | −0.48 | −1.67 |
| 3 | BCC-CSM1-1 | −0.92 | −1.61 | −1.74 | −0.90 | −1.24 | −0.57 | −1.08 | −0.78 | −0.92 | −1.27 |
| 4 | BCC-CSM1-1-M | −0.82 | −0.87 | −1.18 | −1.09 | −1.79 | −0.25 | −0.44 | −1.49 | −0.67 | −1.29 |
| 5 | CANESM2 | −1.64 | −1.38 | −0.49 | −0.77 | −1.20 | −0.32 | −0.93 | −0.85 | −0.76 | −0.95 |
| 6 | CCSM4 | −1.14 | −0.98 | −1.18 | −0.63 | −1.07 | −0.29 | −1.12 | −1.11 | −0.85 | −1.43 |
| 7 | CESM1-BGC | −0.68 | −0.91 | −1.03 | −1.06 | −1.47 | −0.48 | −1.17 | −0.97 | −0.81 | −1.46 |
| 8 | CESM1-CAM5 | −1.09 | −1.05 | −0.79 | −4.37 | −0.90 | −0.71 | −1.13 | −0.95 | −0.35 | −1.40 |
| 9 | CMCC-CM | −1.54 | −0.56 | −0.62 | −1.48 | −0.98 | −0.34 | −1.08 | −1.43 | −0.89 | −1.38 |
| 10 | CMCC-CMS | −1.61 | −1.03 | −1.35 | −2.04 | −2.33 | −0.56 | −0.99 | −0.85 | −1.02 | −1.60 |
| 11 | CNRM-CM5 | −0.94 | −1.04 | −1.45 | −0.31 | −2.31 | −0.41 | −1.25 | −1.17 | −0.98 | −1.16 |
| 12 | CSIRO-MK3-6-0 | −0.63 | −1.74 | −0.37 | −0.94 | −0.93 | −0.28 | −1.33 | −1.22 | −0.67 | −1.36 |
| 13 | EC-EARTH | −0.68 | −0.86 | −0.79 | −0.64 | −1.67 | −0.11 | −0.87 | −0.52 | −1.54 | −0.60 |
| 14 | FGOALS-G2 | −1.47 | −1.73 | −0.69 | −5.79 | −2.06 | −0.57 | −1.14 | −0.68 | −0.86 | −0.87 |
| 15 | GFDL-CM3 | −1.09 | −1.07 | −1.32 | −3.46 | −1.68 | −0.68 | −0.69 | −1.02 | −0.86 | −1.40 |
| 16 | GFDL-ESM2G | −1.11 | −1.15 | −0.78 | −5.75 | −1.38 | −0.58 | −1.54 | −2.07 | −0.63 | −1.43 |
| 17 | GFDL-ESM2M | −0.91 | −1.04 | −1.18 | −2.56 | −1.22 | −0.38 | −0.85 | −1.41 | −0.79 | −0.84 |
| 18 | GISS-E2-H | −0.29 | −1.08 | −1.21 | −1.14 | −1.88 | −0.56 | −0.62 | −1.10 | −0.71 | −0.61 |
| 19 | GISS-E2-R | −0.36 | −1.12 | −1.24 | −1.01 | −1.61 | −0.34 | −1.25 | −1.67 | −0.73 | −1.23 |
| 20 | HADGEM2-AO | −0.90 | −0.61 | −0.62 | −1.31 | −2.27 | −0.63 | −0.51 | −0.91 | −0.57 | −1.18 |
| 21 | HADGEM2-CC | −0.45 | −2.31 | −0.65 | −0.74 | −1.46 | −0.15 | −1.06 | −1.13 | −1.39 | −1.46 |
| 22 | HADGEM2-ES | −0.89 | −1.38 | −1.56 | −2.61 | −1.33 | −0.45 | −0.79 | −2.34 | −0.90 | −1.60 |
| 23 | INMCM4 | −0.98 | −1.88 | −1.24 | −3.34 | −3.23 | −0.25 | −0.92 | −0.70 | −1.11 | −1.46 |
| 24 | IPSL-CM5A-LR | −1.20 | −0.90 | −1.15 | −1.28 | −1.37 | −0.57 | −0.69 | −1.00 | −0.78 | −1.55 |
| 25 | IPSL-CM5A-MR | −0.78 | −1.50 | −0.79 | −1.76 | −1.23 | −0.46 | −1.03 | −0.92 | −0.39 | −1.86 |
| 26 | MIROC-ESM | −0.78 | −0.51 | −0.37 | −0.72 | −0.99 | −0.49 | −1.02 | −0.58 | −0.42 | −1.87 |
| 27 | MIROC-ESM-CHEM | −1.72 | −0.91 | −0.91 | −8.19 | −1.44 | −0.47 | −0.88 | −0.99 | −0.93 | −1.58 |
| 28 | MIROC5 | −0.66 | −1.08 | −1.19 | −3.86 | −0.74 | −0.85 | −0.57 | −1.20 | −0.83 | −0.77 |
| 29 | MPI-ESM-LR | −0.70 | −1.04 | −0.89 | −0.36 | −0.77 | −0.51 | −1.29 | −2.40 | −0.56 | −1.46 |
| 30 | MPI-ESM-MR | −1.17 | −0.87 | −1.54 | −2.85 | −1.79 | −0.60 | −0.70 | −1.47 | −0.60 | −1.24 |
| 31 | MRI-CGCM3 | −0.84 | −1.06 | −0.51 | −0.66 | −1.61 | −0.40 | −1.12 | −1.14 | −1.05 | −1.77 |
| 32 | NORESM1-M | −0.24 | −1.14 | −1.20 | −9.57 | −1.23 | −0.57 | −0.20 | −1.21 | −0.76 | −0.87 |
| 33 | Median_GCM | −1.39 | −0.91 | −0.62 | −0.66 | −1.57 | −0.59 | −1.13 | −0.78 | −0.93 | −1.46 |

Table A12.
NSE coefficient of Last between observed and simulated data (1950–2005).
Table A12.
NSE coefficient of Last between observed and simulated data (1950–2005).
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | −1.23 | −0.95 | −2.51 | −1.04 | −0.94 | 0.05 | −1.23 | −1.02 | −0.15 | −0.91 |
| 2 | ACCESS1-3 | −0.46 | −0.98 | −1.09 | −8.99 | −5.11 | −0.16 | −0.71 | −1.64 | −0.21 | −0.73 |
| 3 | BCC-CSM1-1 | −0.70 | −0.44 | −1.72 | −0.46 | −1.97 | −0.21 | −1.65 | −0.82 | −0.15 | −0.93 |
| 4 | BCC-CSM1-1-M | −0.66 | −0.88 | −0.56 | −0.18 | −0.83 | −0.09 | −1.31 | −0.43 | −0.21 | −1.11 |
| 5 | CANESM2 | −1.12 | −1.07 | −0.15 | −0.26 | −0.84 | −0.10 | −1.16 | −0.47 | −0.05 | −1.75 |
| 6 | CCSM4 | −0.60 | −0.68 | −0.91 | −1.29 | −1.07 | −0.05 | −0.89 | −0.31 | −0.13 | −0.48 |
| 7 | CESM1-BGC | −0.73 | −1.10 | −1.20 | −0.43 | −1.29 | −0.14 | −1.52 | −0.91 | −0.23 | −1.50 |
| 8 | CESM1-CAM5 | −0.54 | −1.19 | −1.09 | −8.63 | −2.07 | −0.48 | −0.57 | −1.32 | −0.18 | −0.93 |
| 9 | CMCC-CM | −1.02 | −0.46 | −0.44 | −0.91 | −0.44 | −0.03 | −0.60 | −0.51 | 0.04 | −1.05 |
| 10 | CMCC-CMS | −2.64 | −0.38 | −1.30 | −4.08 | −1.44 | −0.02 | −0.70 | −0.90 | −0.20 | −0.60 |
| 11 | CNRM-CM5 | −0.76 | −1.41 | −0.34 | −1.20 | −1.23 | −0.07 | −1.36 | −0.63 | −0.25 | −1.45 |
| 12 | CSIRO-MK3-6-0 | −0.94 | −0.89 | −1.24 | −0.97 | −1.26 | −0.12 | −1.29 | −0.09 | −0.12 | −0.81 |
| 13 | EC-EARTH | −0.57 | −0.81 | −1.66 | −1.46 | −1.66 | −0.08 | −0.27 | −1.15 | −0.02 | −1.14 |
| 14 | FGOALS-G2 | −1.60 | −5.86 | −1.43 | 11.91 | −1.21 | −0.28 | −0.67 | −1.08 | −0.17 | −1.89 |
| 15 | GFDL-CM3 | −1.05 | −1.81 | −1.91 | −4.58 | −1.12 | −0.22 | −1.41 | −0.60 | −0.24 | −1.49 |
| 16 | GFDL-ESM2G | −1.30 | −1.74 | −1.46 | 10.41 | −1.27 | −0.07 | −1.78 | −1.01 | −0.01 | −2.27 |
| 17 | GFDL-ESM2M | −0.83 | −1.08 | −1.39 | −5.46 | −0.44 | −0.05 | −0.64 | −1.27 | −0.29 | −0.95 |
| 18 | GISS-E2-H | −1.12 | −0.97 | −2.20 | −0.95 | −1.01 | −0.01 | −1.22 | −0.85 | −0.18 | −1.65 |
| 19 | GISS-E2-R | −0.45 | −0.54 | −1.17 | −0.86 | −1.68 | 0.09 | −0.47 | −1.04 | −0.16 | −0.83 |
| 20 | HADGEM2-AO | −1.40 | −0.83 | −2.31 | −1.34 | −0.90 | −0.03 | −0.43 | −1.10 | −0.07 | −0.69 |
| 21 | HADGEM2-CC | −1.12 | −5.84 | −1.13 | −0.51 | −0.82 | −0.18 | −1.06 | −0.31 | −1.01 | −1.10 |
| 22 | HADGEM2-ES | −0.47 | −0.83 | −1.70 | −4.94 | −1.12 | −0.04 | −1.35 | −0.54 | −0.07 | −1.22 |
| 23 | INMCM4 | −0.62 | −4.12 | −1.42 | −7.61 | −5.03 | −0.14 | −0.80 | −1.36 | −0.18 | −0.52 |
| 24 | IPSL-CM5A-LR | −0.83 | −0.59 | −1.26 | −1.54 | −1.53 | −0.15 | −0.56 | −0.58 | −0.38 | −0.32 |
| 25 | IPSL-CM5A-MR | −1.28 | −1.45 | −0.93 | −4.03 | −0.80 | −0.08 | −0.83 | −1.12 | −0.12 | −1.01 |
| 26 | MIROC-ESM | −0.73 | −1.20 | −0.60 | −0.97 | −1.02 | 0.05 | −1.65 | −1.08 | −0.24 | −1.57 |
| 27 | MIROC-ESM-CHEM | −1.10 | −0.38 | −1.50 | 14.08 | −0.97 | −0.19 | −0.91 | −0.93 | −0.29 | −0.89 |
| 28 | MIROC5 | −1.10 | −0.86 | −1.41 | −8.38 | −1.51 | −0.26 | −1.03 | −0.78 | −0.04 | −2.12 |
| 29 | MPI-ESM-LR | −0.37 | −0.96 | −1.29 | −1.03 | −0.88 | −0.13 | −0.97 | −0.76 | −0.05 | −1.21 |
| 30 | MPI-ESM-MR | −0.35 | −0.71 | −0.51 | −4.47 | −1.17 | −0.19 | −1.34 | −1.17 | −0.06 | −0.48 |
| 31 | MRI-CGCM3 | −0.69 | −0.59 | −1.90 | −0.97 | −0.98 | −0.06 | −1.61 | −1.44 | −0.29 | −1.02 |
| 32 | NORESM1-M | −1.26 | −1.21 | −1.49 | 18.23 | −0.79 | −0.21 | −1.41 | −1.60 | −0.13 | −1.78 |
| 33 | Median_GCM | −1.11 | −0.85 | −0.59 | −0.24 | −0.83 | −0.07 | −1.58 | −0.92 | −0.24 | −1.55 |

Table A13.
Relative Closeness to the Ideal Solution for each GCM.
Table A13.
Relative Closeness to the Ideal Solution for each GCM.
| Model No | GCM Name | BAL | BIS | COL | DAL | DES | MIA | NYC | PHO | POR | SYR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS1-0 | 0.32 | 0.689 | 0.204 | 0.934 | 0.525 | 0.737 | 0.523 | 0.501 | 0.794 | 0.335 |
| 2 | ACCESS1-3 | 0.778 | 0.833 | 0.584 | 0.602 | 0.422 | 0.75 | 0.78 | 0.349 | 0.556 | 0.695 |
| 3 | BCC-CSM1-1 | 0.607 | 0.693 | 0.217 | 0.721 | 0.582 | 0.745 | 0.49 | 0.746 | 0.658 | 0.579 |
| 4 | BCC-CSM1-1-M | 0.692 | 0.846 | 0.496 | 0.89 | 0.715 | 0.775 | 0.619 | 0.601 | 0.753 | 0.654 |
| 5 | CANESM2 | 0.492 | 0.786 | 0.746 | 0.862 | 0.806 | 0.798 | 0.739 | 0.591 | 0.815 | 0.541 |
| 6 | CCSM4 | 0.523 | 0.658 | 0.564 | 0.891 | 0.807 | 0.761 | 0.639 | 0.844 | 0.72 | 0.51 |
| 7 | CESM1-BGC | 0.587 | 0.8 | 0.544 | 0.809 | 0.698 | 0.706 | 0.44 | 0.729 | 0.73 | 0.37 |
| 8 | CESM1-CAM5 | 0.649 | 0.505 | 0.565 | 0.601 | 0.616 | 0.073 | 0.628 | 0.541 | 0.795 | 0.736 |
| 9 | CMCC-CM | 0.494 | 0.853 | 0.929 | 0.7 | 0.89 | 0.765 | 0.512 | 0.622 | 0.803 | 0.312 |
| 10 | CMCC-CMS | 0.427 | 0.766 | 0.253 | 0.662 | 0.678 | 0.631 | 0.615 | 0.766 | 0.572 | 0.514 |
| 11 | CNRM-CM5 | 0.563 | 0.499 | 0.607 | 0.905 | 0.58 | 0.509 | 0.466 | 0.652 | 0.675 | 0.453 |
| 12 | CSIRO-MK3-6-0 | 0.694 | 0.592 | 0.615 | 0.724 | 0.69 | 0.561 | 0.437 | 0.823 | 0.749 | 0.446 |
| 13 | EC-EARTH | 0.883 | 0.905 | 0.554 | 0.816 | 0.722 | 0.723 | 0.855 | 0.604 | 0.528 | 0.858 |
| 14 | FGOALS-G2 | 0.222 | 0.36 | 0.47 | 0.447 | 0.754 | 0.49 | 0.649 | 0.335 | 0.501 | 0.458 |
| 15 | GFDL-CM3 | 0.595 | 0.545 | 0.353 | 0.684 | 0.473 | 0.666 | 0.572 | 0.679 | 0.636 | 0.632 |
| 16 | GFDL-ESM2G | 0.416 | 0.429 | 0.278 | 0.515 | 0.729 | 0.742 | 0.42 | 0.269 | 0.62 | 0.32 |
| 17 | GFDL-ESM2M | 0.628 | 0.743 | 0.654 | 0.473 | 0.937 | 0.756 | 0.663 | 0.246 | 0.662 | 0.778 |
| 18 | GISS-E2-H | 0.499 | 0.642 | 0.536 | 0.87 | 0.584 | 0.64 | 0.533 | 0.675 | 0.63 | 0.34 |
| 19 | GISS-E2-R | 0.535 | 0.76 | 0.593 | 0.8 | 0.751 | 0.892 | 0.524 | 0.436 | 0.751 | 0.464 |
| 20 | HADGEM2-AO | 0.403 | 0.829 | 0.409 | 0.627 | 0.488 | 0.623 | 0.744 | 0.649 | 0.808 | 0.688 |
| 21 | HADGEM2-CC | 0.643 | 0.288 | 0.333 | 0.813 | 0.495 | 0.528 | 0.539 | 0.756 | 0.184 | 0.611 |
| 22 | HADGEM2-ES | 0.675 | 0.501 | 0.458 | 0.517 | 0.609 | 0.862 | 0.652 | 0.539 | 0.552 | 0.63 |
| 23 | INMCM4 | 0.667 | 0.481 | 0.248 | 0.596 | 0.446 | 0.676 | 0.741 | 0.387 | 0.736 | 0.68 |
| 24 | IPSL-CM5A-LR | 0.683 | 0.665 | 0.658 | 0.704 | 0.684 | 0.715 | 0.63 | 0.646 | 0.506 | 0.773 |
| 25 | IPSL-CM5A-MR | 0.497 | 0.605 | 0.629 | 0.865 | 0.779 | 0.641 | 0.565 | 0.376 | 0.559 | 0.633 |
| 26 | MIROC-ESM | 0.647 | 0.832 | 0.786 | 0.778 | 0.777 | 0.844 | 0.548 | 0.734 | 0.79 | 0.465 |
| 27 | MIROC-ESM-CHEM | 0.502 | 0.852 | 0.382 | 0.187 | 0.682 | 0.788 | 0.557 | 0.713 | 0.539 | 0.666 |
| 28 | MIROC5 | 0.638 | 0.85 | 0.394 | 0.407 | 0.833 | 0.654 | 0.247 | 0.737 | 0.849 | 0.376 |
| 29 | MPI-ESM-LR | 0.761 | 0.579 | 0.455 | 0.932 | 0.929 | 0.645 | 0.54 | 0.576 | 0.89 | 0.677 |
| 30 | MPI-ESM-MR | 0.685 | 0.662 | 0.643 | 0.595 | 0.762 | 0.624 | 0.682 | 0.629 | 0.888 | 0.735 |
| 31 | MRI-CGCM3 | 0.688 | 0.722 | 0.566 | 0.653 | 0.835 | 0.569 | 0.464 | 0.467 | 0.625 | 0.517 |
| 32 | NORESM1-M | 0.46 | 0.831 | 0.339 | 0.222 | 0.855 | 0.734 | 0.624 | 0.353 | 0.618 | 0.646 |
| 33 | Median_GCM | 0.495 | 0.83 | 0.655 | 0.815 | 0.834 | 0.634 | 0.538 | 0.657 | 0.633 | 0.524 |
References
- Lyon, B.; Barnston, A.G. Diverse characteristics of U.S. summer heat waves. J. Clim. 2017, 30, 7827–7845. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Jones, P.D.; Ambenje, P.; Bojariu, R.; Easterling, D.; Klein Tank, A.; Parker, D.; Rahimzadeh, F.; Renwick, J.A.; Rusticucci, M.; et al. Observations: Surface and Atmospheric Climate Change. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Qin, D., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Intergovernmental Panel on Climate Change. Climate Change 2014 Synthesis Report Summary for Policymakers; Stocker, T.F., Qin, D., Plattner, G., Tigno, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Kunkel, K.E.; Stevens, L.E.; Stevens, S.E.; Sun, L.; Janssen, E.; Wuebbles, D.; Dobson, J.G. Regional Climate Trends and Scenarios for the U.S. National Climate Assessment Part 9. Climate of the Contiguous United States; NOAA: Washington, DC, USA, 2013. [Google Scholar]
- Melillo, J.M.; Terese, T.C.; Yohe, G.W. (Eds.) Climate Change Impacts in the United States: The Third National Climate Assessment; U.S. Global Change Research Program: Washington, DC, USA, 2014; ISBN 9780160924026. [Google Scholar]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Wehner, M. Changes in temperature and precipitation extremes in the CMIP5 ensemble. Clim. Chang. 2013, 119, 345–357. [Google Scholar] [CrossRef]
- Horton, R.; Yohe, G.; Easterling, W.; Kates, R.; Ruth, M.; Sussman, E.; Whelchel, A.; Wolfe, D.; Lipschultz, F. Ch. 16: Northeast. In Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Terese, T.C., Yohe, G.W., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2014; pp. 371–395. [Google Scholar]
- Carter, L.M.; Jones, J.W.; Berry, L.; Burkett, V.; Murley, J.F.; Obeysekera, J.; Schramm, P.J.; Wear, D. Ch. 17: Southeast and the Caribbean. In Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Terese, T.C., Yohe, G.W., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2014; pp. 396–417. [Google Scholar]
- Pryor, S.; Scavia, D.; Downer, C.; Gaden, M.; Iverson, L.; Nordstrom, R.; Patz, J.; Roberson, G. Ch. 18: Mid- west. In Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Terese, T.C., Yohe, G.W., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2014; pp. 418–440. [Google Scholar]
- Shafer, M.; Ojima, D.; Antle, J.M.; Kluck, D.; McPherson, R.A.; Petersen, S.; Scanlon, B.; Shermand, K. Ch. 19: Great Plains. In Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Terese, T.C., Yohe, G.W., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2014; pp. 441–461. [Google Scholar]
- Mote, P.; Snover, A.K.; Capalbo, S.; Eigenbrode, S.D.; Glick, P.; Littell, J.; Raymondi, R.; Reeder, S. Ch. 21: North- west. In Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Terese, T.C., Yohe, G.W., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2014; pp. 487–513. [Google Scholar]
- Garfin, G.; Franco, G.; Blanco, H.; Comrie, P.; Gonzalez, T.; Piechota, T.; Smyth, R.; Waskom, R. Ch. 20: Southwest. In Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Terese, T.C., Yohe, G.W., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2014; pp. 462–486. [Google Scholar]
- Meehl, G.A.; Tebaldi, C. More Intense, More Frequent, and Longer Lasting Heat Waves in the 21st Century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Russo, S.; Dosio, A.; Graversen, R.G.; Sillmann, J.; Carrao, H.; Dunbar, M.B.; Singleton, A.; Montagna, P.; Barbola, P.; Vogt, J.V. Magnitude of extreme heat waves in present climate and their projection in a warming world. J. Geophys. Res. Atmos. 2014, 119, 12500–12512. [Google Scholar] [CrossRef]
- Hansen, C.; McDonald, S.; Nabors, A.; Shafiei Shiva, J. Using the National Water Model Forecasts to Plan for and Manage Ecological Flow and Low-Flow during Drought. In National Water Center Innovators Program Summer Institute Report 2017; Johnson, J.M., Coll, J.M., Maidment, D.R., Cohen, S., Nelson, J., Ogden, F., Praskievicz, S., Clark, E.P., Eds.; CUAHSI: Cambridge, MA, USA, 2017; pp. 66–74. [Google Scholar]
- Hansen, C.; Shafiei Shiva, J.; McDonald, S.; Nabros, A. Assessing Retrospective National Water Model Streamflow with Respect to Droughts and Low Flows in the Colorado River Basin. J. Am. Water Resour. Assoc. 2019, 55, 964–975. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef]
- Cox, R.A.; Drews, M.; Rode, C.; Nielsen, S.B. Simple future weather files for estimating heating and cooling demand. Build. Environ. 2015, 83, 104–114. [Google Scholar] [CrossRef]
- Russo, S.; Sterl, A. Global changes in indices describing moderate temperature extremes from the daily output of a climate model. J. Geophys. Res. Atmos. 2011, 116, 1–12. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 2006, 111, 1–22. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J. Geophys. Res. Atmos. 2013, 118, 2473–2493. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Ashfaq, M. Intensification of hot extremes in the United States. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Liang, X.Z.; Zhu, J. Regional climate model projections and uncertainties of U.S. summer heat waves. J. Clim. 2010, 23, 4447–4458. [Google Scholar] [CrossRef]
- Zubler, E.M.; Fischer, A.M.; Liniger, M.A.; Croci-Maspoli, M.; Scherrer, S.C.; Appenzeller, C. Localized climate change scenarios of mean temperature and precipitation over Switzerland. Clim. Chang. 2014, 125, 237–252. [Google Scholar] [CrossRef]
- Gershunov, A.; Guirguis, K. California heat waves in the present and future. Geophys. Res. Lett. 2012, 39, 1–7. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Solecki, W.D.; Parshall, L.; Chopping, M.; Pope, G.; Goldberg, R. Characterizing the urban heat island in current and future climates in New Jersey. Environ. Hazards 2005, 6, 51–62. [Google Scholar] [CrossRef]
- Pierce, D.W.; Cayan, D.R.; Thrasher, B.L. Statistical Downscaling Using Localized Constructed Analogs (LOCA). J. Hydrometeorol. 2014, 15, 2558–2585. [Google Scholar] [CrossRef]
- Hazeleger, W.; Van Den Hurk, B.J.J.M.; Min, E.; Van Oldenborgh, G.J.; Petersen, A.C.; Stainforth, D.A.; Vasileiadou, E.; Smith, L.A. Tales of future weather. Nat. Clim. Chang. 2015, 5, 107–113. [Google Scholar] [CrossRef]
- Smith, L.A. What might we learn from climate forecasts? Proc. Natl. Acad. Sci. USA 2002, 99, 2487–2492. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The Potential to Narrow Uncertainty in Regional Climate Predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1108. [Google Scholar] [CrossRef]
- Lorenz, R.; Herger, N.; Sedláček, J.; Eyring, V.; Fischer, E.M.; Knutti, R. Prospects and Caveats of Weighting Climate Models for Summer Maximum Temperature Projections Over North America. J. Geophys. Res. Atmos. 2018, 123, 4509–4526. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, X.; Zwiers, F.W.; Song, L.; Wan, H.; Hu, T.; Yin, H.; Ren, G. Rapid increase in the risk of extreme summer heat in Eastern China. Nat. Clim. Chang. 2014, 4, 1082–1085. [Google Scholar] [CrossRef]
- Teng, H.; Branstator, G.; Meehl, G.A.; Washington, W.M. Projected intensification of subseasonal temperature variability and heat waves in the Great Plains. Geophys. Res. Lett. 2016, 43, 1–9. [Google Scholar] [CrossRef]
- Cowan, T.; Purich, A.; Perkins, S.; Pezza, A.; Boschat, G.; Sadler, K. More frequent, longer, and hotter heat waves for Australia in the Twenty-First Century. J. Clim. 2014, 27, 5851–5871. [Google Scholar] [CrossRef]
- Knutti, R.; Furrer, R.; Tebaldi, C.; Cermak, J.; Meehl, G.A. Challenges in combining projections from multiple climate models. J. Clim. 2010, 23, 2739–2758. [Google Scholar] [CrossRef]
- McSweeney, C.F.; Jones, R.G. How representative is the spread of climate projections from the 5 CMIP5 GCMs used in ISI-MIP? Clim. Serv. 2016, 1, 24–29. [Google Scholar] [CrossRef]
- Annan, J.D.; Hargreaves, J.C. Reliability of the CMIP3 ensemble. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Abramowitz, G.; Bishop, C.H. Climate model dependence and the ensemble dependence transformation of CMIP projections. J. Clim. 2015, 28, 2332–2348. [Google Scholar] [CrossRef]
- Hazeleger, W.; Severijns, C.; Tido, S.; Stefanescu, S.; Yang, S.; Wang, X.; Wyser, K.; Dutra, E.; Baldasano, J.M.; Bintanja, R.; et al. EC-Earth V2.2: Description and validation of a new seamless earth system prediction model. Am. Meteorol. Soc. 2010, 39, 1357–1363. [Google Scholar] [CrossRef]
- Johnston, M.S.; Eriksson, P.; Eliasson, S.; Jones, C.G.; Forbes, R.M.; Murtagh, D.P. The representation of tropical upper tropospheric water in EC Earth V2. Clim. Dyn. 2012, 39, 2713–2731. [Google Scholar] [CrossRef]
- Annan, J.D.; Hargreaves, J.C. Understanding the CMIP3 multimodel ensemble. J. Clim. 2011, 24, 4529–4538. [Google Scholar] [CrossRef]
- Knutti, R.; Masson, D.; Gettelman, A. Climate model genealogy: Generation CMIP5 and how we got there. Geophys. Res. Lett. 2013, 40, 1194–1199. [Google Scholar] [CrossRef]
- Mahlstein, I.; Knutti, R. September Arctic sea ice predicted to disappear near 2°C global warming above present. J. Geophys. Res. Atmos. 2012, 117, 1–11. [Google Scholar] [CrossRef]
- Huber, M.; Mahlstein, I.; Wild, M.; Fasullo, J.; Knutti, R. Constraints on climate sensitivity from radiation patterns in climate models. J. Clim. 2011, 24, 1034–1052. [Google Scholar] [CrossRef]
- Boé, J.; Hall, A.; Qu, X. Deep ocean heat uptake as a major source of spread in transient climate change simulations. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Cox, P.M.; Pearson, D.; Booth, B.B.; Friedlingstein, P.; Huntingford, C.; Jones, C.D.; Luke, C.M. Sensitivity of tropical carbon to climate change constrained by carbon dioxide variability. Nature 2013, 494, 341–344. [Google Scholar] [CrossRef] [PubMed]
- Aghakouchak, A.; Ragno, E.; Love, C.; Moftakhari, H.R. Projected Changes in California’s Precipitation Intensity-Duration-Frequency Curves; Energy Commision of Satet of California: Sacramento, CA, USA, 2018.
- Herger, N.; Abramowitz, G.; Knutti, R.; Angélil, O.; Lehmann, K.; Sanderson, B.M. Selecting a climate model subset to optimise key ensemble properties. Earth Syst. Dyn. 2018, 9, 135–151. [Google Scholar] [CrossRef]
- Karpechko, A.Y.; Maraun, D.; Eyring, V. Improving Antarctic Total Ozone Projections by a Process-Oriented Multiple Diagnostic Ensemble Regression. J. Atmos. Sci. 2013, 70, 3959–3976. [Google Scholar] [CrossRef]
- Eyring, V.; Arblaster, J.M.; Cionni, I.; Sedláček, J.; Perlwitz, J.; Young, P.J.; Bekki, S.; Bergmann, D.; Cameron-Smith, P.; Collins, W.J.; et al. Long-term ozone changes and associated climate impacts in CMIP5 simulations. J. Geophys. Res. Atmos. 2013, 118, 5029–5060. [Google Scholar] [CrossRef]
- Sanderson, B.M.; Knutti, R.; Caldwell, P. A representative democracy to reduce interdependency in a multimodel ensemble. J. Clim. 2015, 28, 5171–5194. [Google Scholar] [CrossRef]
- Geil, K.L.; Serra, Y.L.; Zeng, X. Assessment of CMIP5 model simulations of the North American monsoon system. J. Clim. 2013, 26, 8787–8801. [Google Scholar] [CrossRef]
- Knutti, R.; Sedláček, J.; Sanderson, B.M.; Lorenz, R.; Fischer, E.M.; Eyring, V. A climate model projection weighting scheme accounting for performance and interdependence. Geophys. Res. Lett. 2017, 44, 1909–1918. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Livneh, B.; Bohn, T.J.; Pierce, D.W.; Munoz-Arriola, F.; Nijssen, B.; Vose, R.; Cayan, D.R.; Brekke, L. A spatially comprehensive, hydrometeorological data set for Mexico, the U.S., and Southern Canada 1950–2013. Sci. Data 2015, 2, 150042. [Google Scholar] [CrossRef] [PubMed]
- Pierce, D.; Cayan, D. High-Resolution LOCA Downscaled Climate Projections Aim to Better Represent Extreme Weather Events; Scripps Institution of Oceanography (SIO): La Jolla, CA, USA, 2017. [Google Scholar]
- Guirguis, K.; Gershunov, A.; Cayan, D.R.; Pierce, D.W. Heat wave probability in the changing climate of the Southwest US. Clim. Dyn. 2018, 50, 3853–3864. [Google Scholar] [CrossRef]
- Engström, J.; Keellings, D. Drought in the Southeastern USA: An assessment of downscaled CMIP5 models. Clim. Res. 2018, 74, 251–262. [Google Scholar] [CrossRef]
- Hu, H.; Ayyub, B.M. Validating and Enhancing Extreme Precipitation Projections by Downscaled Global Climate Model Results and Copula Methods. J. Hydrol. Eng. 2019, 24, 1–14. [Google Scholar] [CrossRef]
- Praskievicz, S. Downscaling climate-model output in mountainous terrain using local topographic lapse rates for hydrologic modeling of climate-change impacts. Phys. Geogr. 2018, 39, 99–117. [Google Scholar] [CrossRef]
- Bi, D.; Dix, M.; Marsland, S.J.; O’Farrell, S.; Rashid, H.A.; Uotila, P.; Hirst, A.C.; Kowalczyk, E.; Golebiewski, M.; Sullivan, A.; et al. The ACCESS coupled model: Description, control climate and evaluation. Aust. Meteorol. Oceanogr. J. 2013, 63, 41–64. [Google Scholar] [CrossRef]
- Robinson, P.J. On the definition of a heat wave. J. Appl. Meteorol. 2001, 40, 762–775. [Google Scholar] [CrossRef]
- McPhillips, L.E.; Chang, H.; Chester, M.V.; Depietri, Y.; Friedman, E.; Grimm, N.B.; Kominoski, J.S.; Mcphearson, T.; Méndez-lázaro, P.; Rosi, E.J.; et al. Defining Extreme Events: A Cross-Disciplinary Review. Earth’s Future 2018, 6, 441–455. [Google Scholar] [CrossRef]
- Smith, T.T.; Zaitchik, B.F.; Gohlke, J.M. Heat waves in the United States: Definitions, patterns and trends. Clim. Chang. 2013, 118, 811–825. [Google Scholar] [CrossRef] [PubMed]
- Keellings, D.; Waylen, P. Increased risk of heat waves in Florida: Characterizing changes in bivariate heat wave risk using extreme value analysis. Appl. Geogr. 2014, 46, 90–97. [Google Scholar] [CrossRef]
- Shafiei Shiva, J.; Chandler, D.G.; Kunkel, K.E. Localized Changes in Heat Wave Properties Across the United States. Earth’s Future 2019, 7, 300–319. [Google Scholar] [CrossRef]
- Shafiei Shiva, J. R Code for Calculating Heatwave Properties Using Ambient Temperature (v1.0). Available online: https://zenodo.org/record/1314762 (accessed on 20 December 2019).
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Nor, K.M.D.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications—A review of the literature from 2000 to 2014. Econ. Res. Istraz. 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Boran, F.E.; Genç, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Sun, C.C. A performance evaluation model by integrating fuzzy AHP and fuzzy TOPSIS methods. Expert Syst. Appl. 2010, 37, 7745–7754. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, Y.W.; Tang, D.W.; Chen, Y.W. TOPSIS with Belief Structure for Group Belief Multiple Criteria Decision Making. Int. J. Autom. Comput. 2010, 7, 359–364. [Google Scholar] [CrossRef]
- Behzadian, M.; Khanmohammadi Otaghsara, S.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Cheng, C.T.; Zhao, M.Y.; Chau, K.W.; Wu, X.Y. Using genetic algorithm and TOPSIS for Xinanjiang model calibration with a single procedure. J. Hydrol. 2006, 316, 129–140. [Google Scholar] [CrossRef]
- Rao, R.V. Decision Making in the Manufacturing Environment: Using Graph Theory and Fuzzy Multiple Attribute Decision Making Methods; Springer: London, UK, 2007; ISBN 9781846288180. [Google Scholar]
- Nyimbili, P.H.; Erden, T.; Karaman, H. Integration of GIS, AHP and TOPSIS for earthquake hazard analysis. Nat. Hazards 2018, 92, 1523–1546. [Google Scholar] [CrossRef]
- Navarro-Estupiñan, J.; Robles-Morua, A.; Vivoni, E.R.; Zepeda, J.E.; Montoya, J.A.; Verduzco, V.S. Observed trends and future projections of extreme heat events in Sonora, Mexico. Int. J. Climatol. 2018, 38, 5168–5181. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Hazeleger, W.; Bintanja, R. EC-Earth: A seamless Earth-system prediction approach in action. Clim. Dyn. 2012, 39, 2609–2661. [Google Scholar] [CrossRef][Green Version]
- Weiss, M.; van den Hurk, B.; Haarsma, R.; Hazeleger, W. Impact of vegetation variability on potential predictability and skill of EC-Earth simulations. Clim. Dyn. 2012, 39, 2733–2746. [Google Scholar] [CrossRef]
- Semmler, T.; McGrath, R.; Wang, S. The impact of Arctic sea ice on the Arctic energy budget and on the climate of the Northern mid-latitudes. Clim. Dyn. 2012, 39, 2675–2694. [Google Scholar] [CrossRef][Green Version]
- Sterl, A.; Bintanja, R.; Brodeau, L.; Gleeson, E.; Koenigk, T.; Schmith, T.; Semmler, T.; Severijns, C.; Wyser, K.; Yang, S. A look at the ocean in the EC-Earth climate model. Clim. Dyn. 2012, 39, 2631–2657. [Google Scholar] [CrossRef]
- Herring, S.C.; Hoell, A.; Hoerling, M.P.; Kossin, J.P.; Schreck, C.J.; Stott, P.A. Introduction to explaining extreme events of 2015 from a climate perspective. Bull. Am. Meteorol. Soc. 2016, 97, S1–S3. [Google Scholar] [CrossRef][Green Version]
- Prodhomme, C.; Batté, L.; Massonnet, F.; Davini, P.; Bellprat, O.; Guemas, V.; Doblas-Reyes, F.J. Benefits of increasing the model resolution for the seasonal forecast quality in EC-earth. J. Clim. 2016, 29, 9141–9162. [Google Scholar] [CrossRef]
- Shafiei Shiva, J.; Chandler, D.G. Projection of Future Heat Waves in the United States Based on Locally Selected GCMs; AGU: San Francisco, CA, USA, 2019. [Google Scholar]
- Fayaz, N.; Condon, L.E.; Chandler, D.G. Evaluating the Sensitivity of Projected Reservoir Reliability to the Choice of Climate Projection: A Case Study of Bull Run Watershed, Portland, Oregon. Water Resour. Manag. 2020, 34, 1991–2009. [Google Scholar] [CrossRef]
- Gyawali, R.; Garbrecht, J.; Zhang, J.X. Suitability of global circulation model downscaled BCCA daily precipitation for local hydrologic applications. J. Hydrol. Eng. 2016, 21, 1–8. [Google Scholar] [CrossRef]
- Parker, W.S. II - Confirmation and adequacy-for-purpose in climate modelling. Proc. Aristot. Soc. Suppl. Vol. 2009, 83, 233–249. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).