Pan Evaporation Estimation in Uttarakhand and Uttar Pradesh States, India: Validity of an Integrative Data Intelligence Model
Abstract
1. Introduction
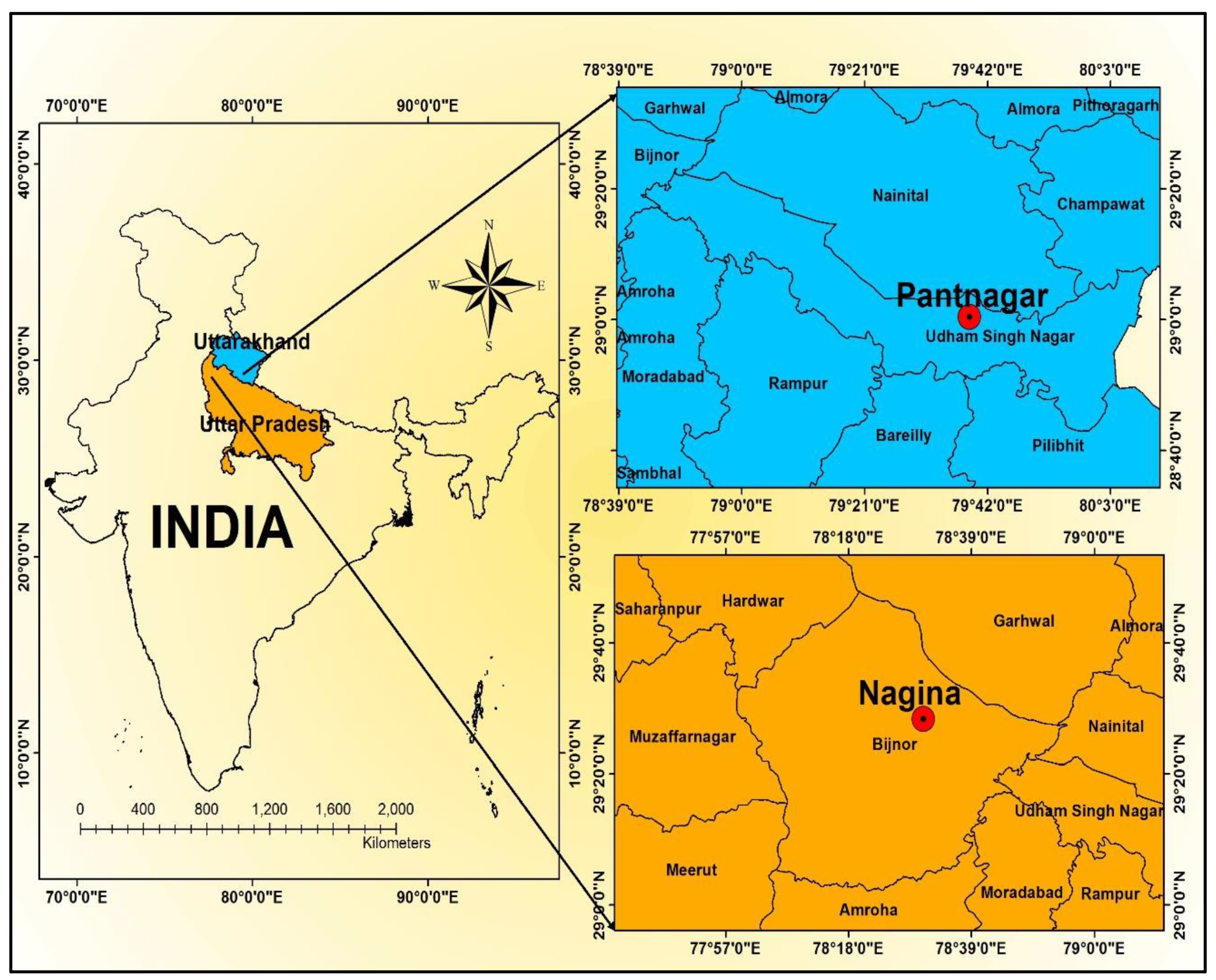
2. Case Study and Data Description
3. Methodology
3.1. Gamma Test (GT)
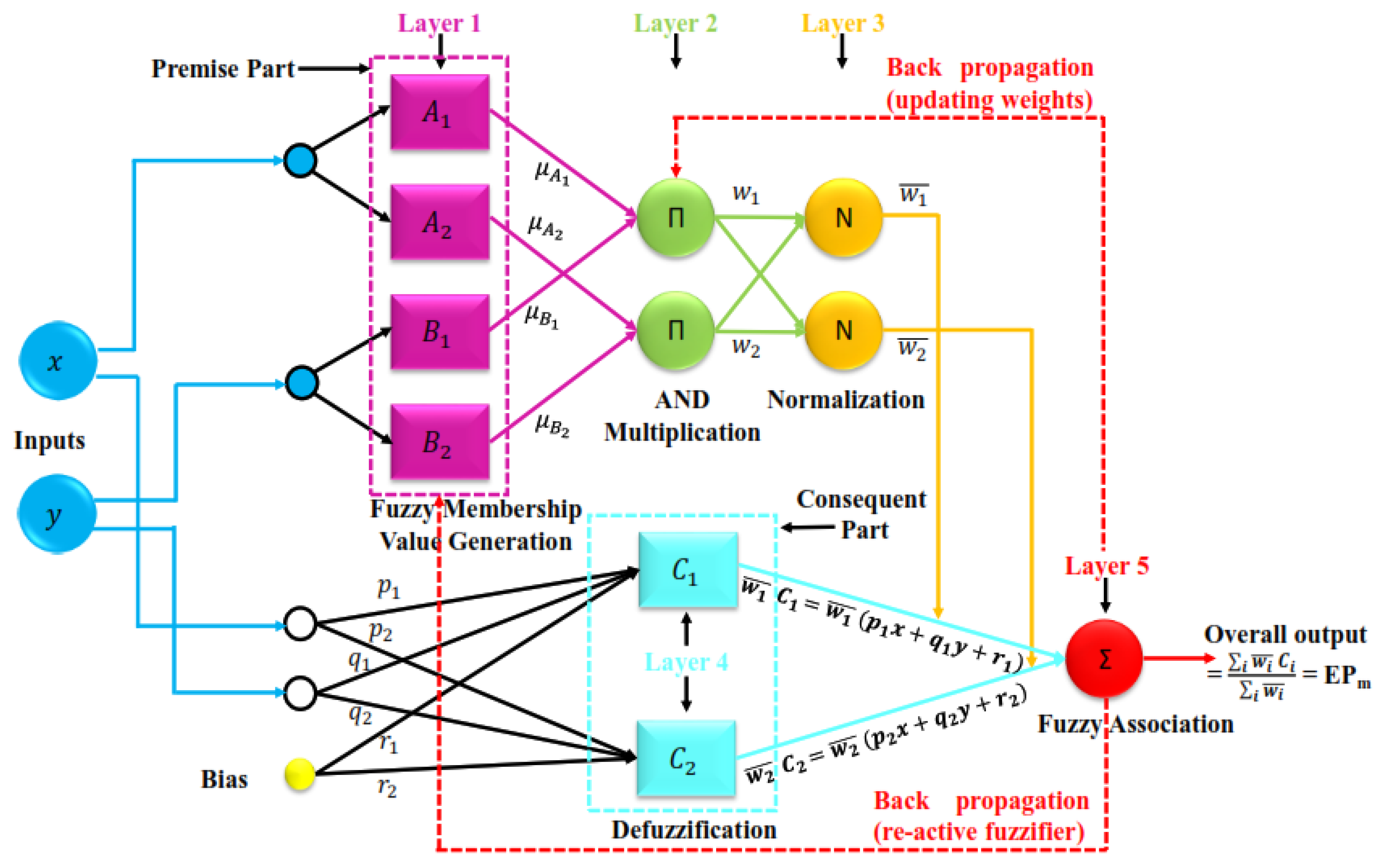
3.2. Co-Active Neuro-Fuzzy Inference System (CANFIS) Model
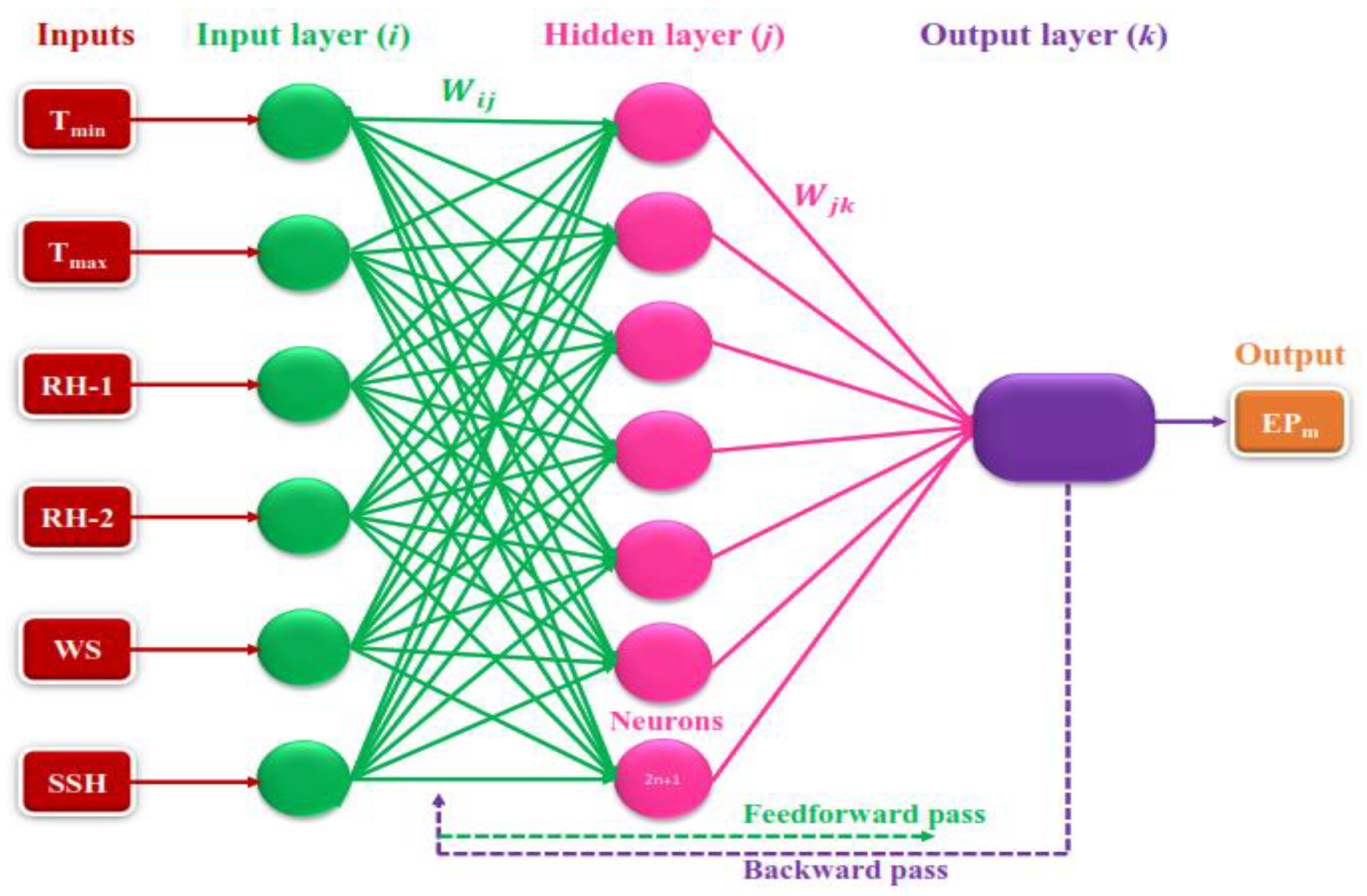
3.3. Multilayer Perceptron Neural Network (MLPNN) Model
3.4. Multiple Linear Regression (MLR) Model
3.5. Penman Model (PM)
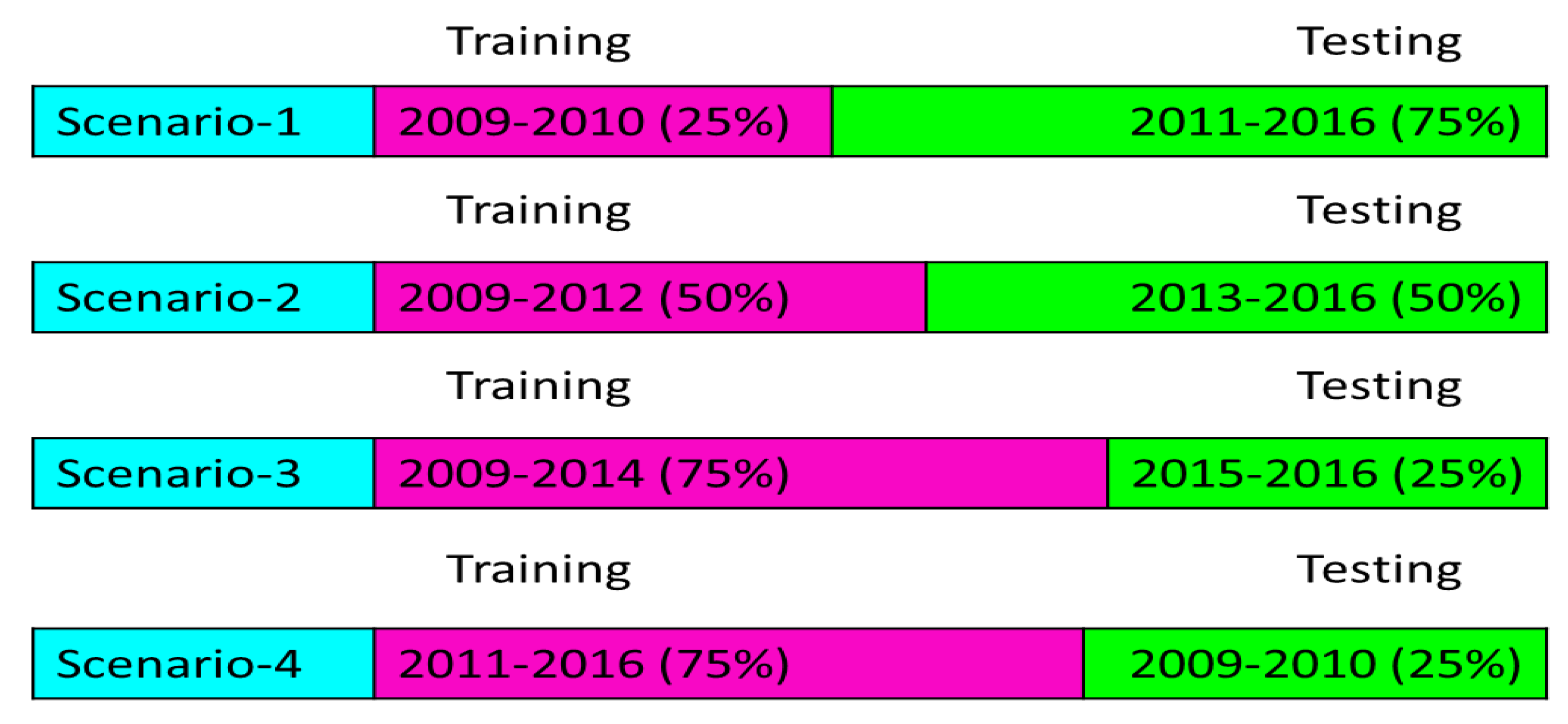
3.6. Modeling Scenarios
- Scenario-1 contains 25% data for training (January 2009 to December 2010) and 75% data for testing (January 2011 to December 2016).
- Scenario-2 contains 50% data for training (January 2009 to December 2012) and 50% data for testing (January 2013 to December 2016).
- Scenario-3 contains 75% data for training (January 2009 to December 2014) and 25% data for testing (January 2015 to December 2016).
- Scenario-4 contains 75% data for training (January 2011 to December 2016) and 25% data for testing (January 2009 to December 2010).
3.7. Performance Appraisal Indicators
4. Application Results and Analysis
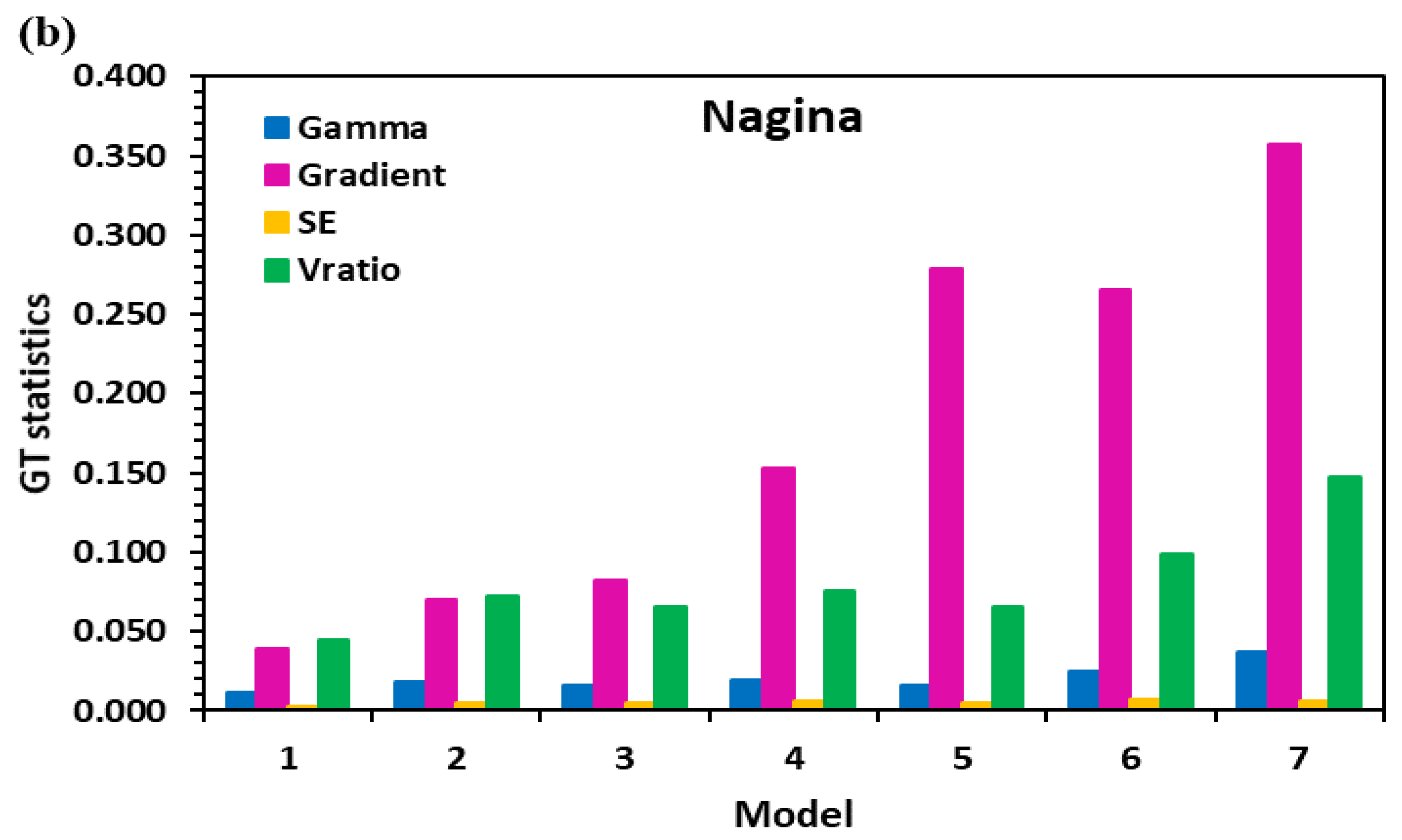
4.1. Optimal Input Variable Selection Using GT
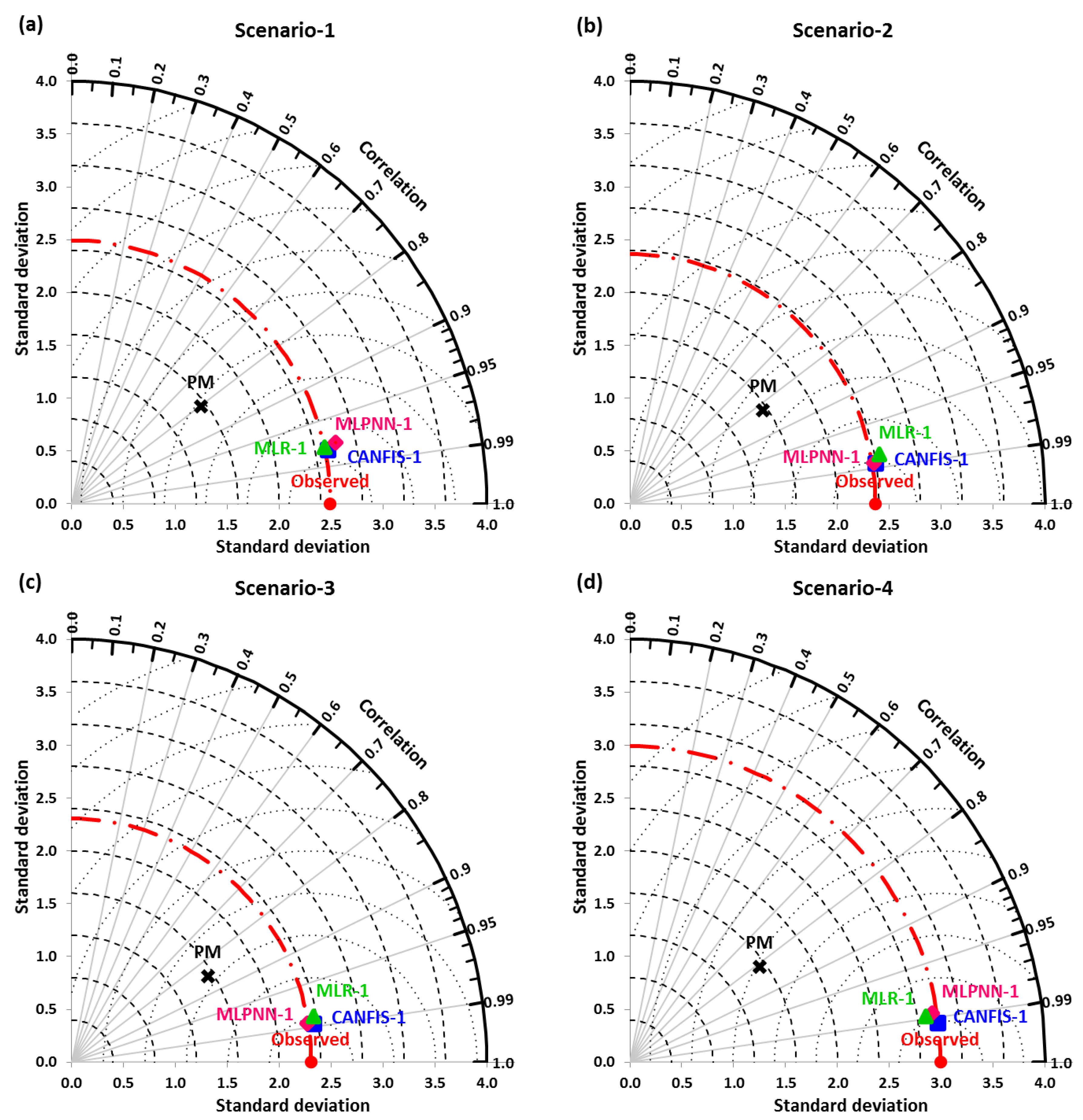
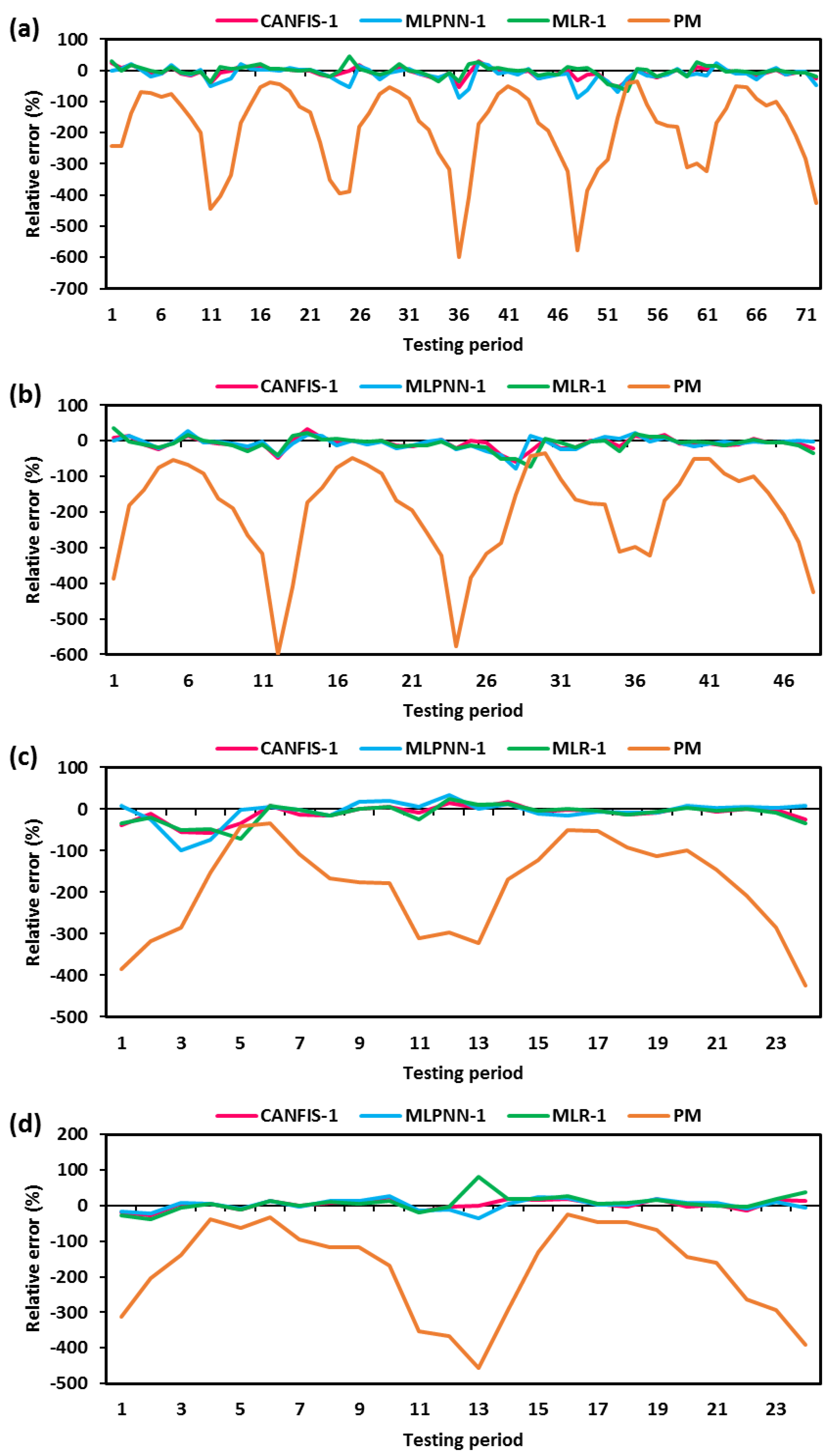
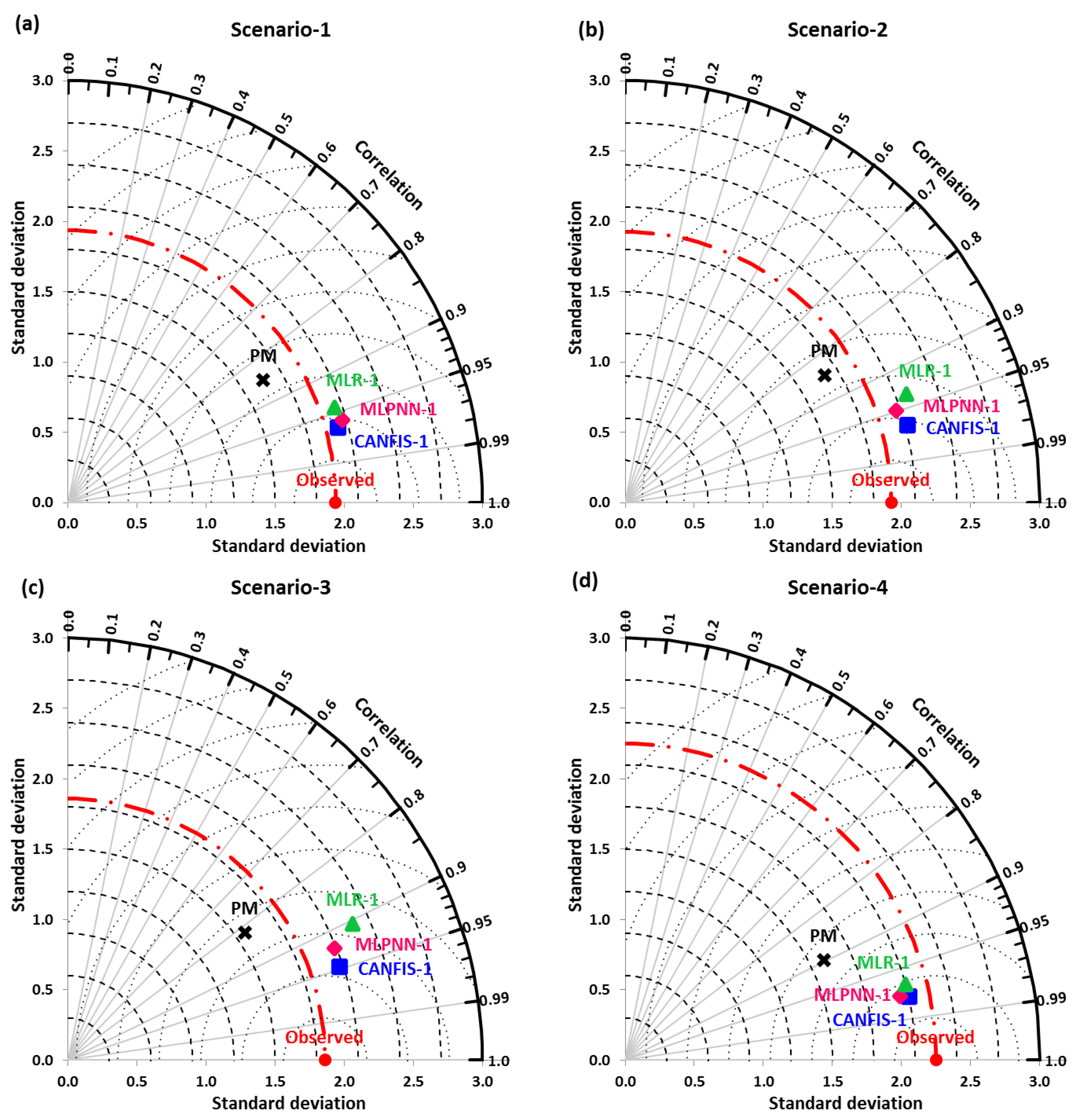
4.2. Estimation of EPm under Different Scenarios at Pantnagar Station
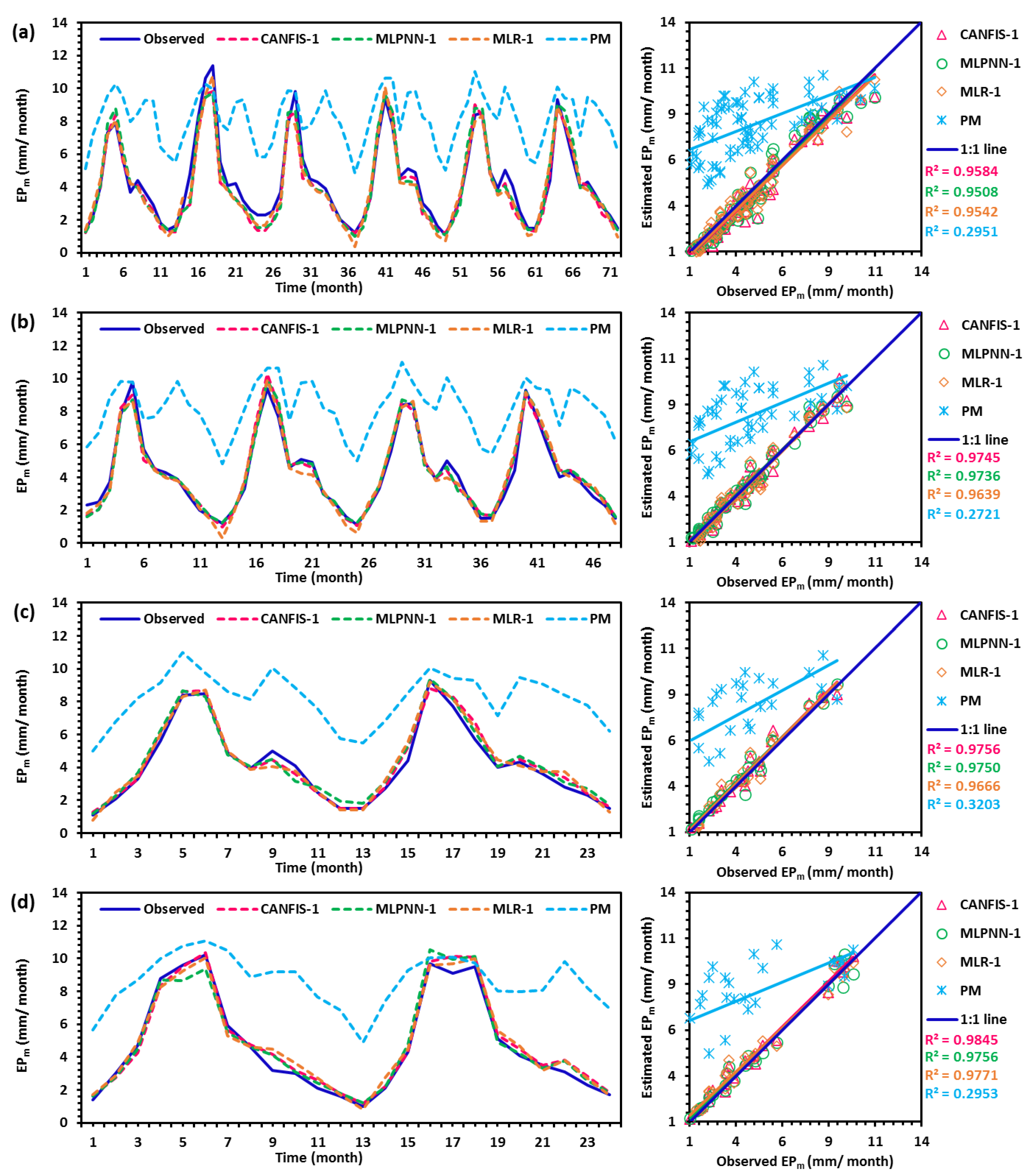
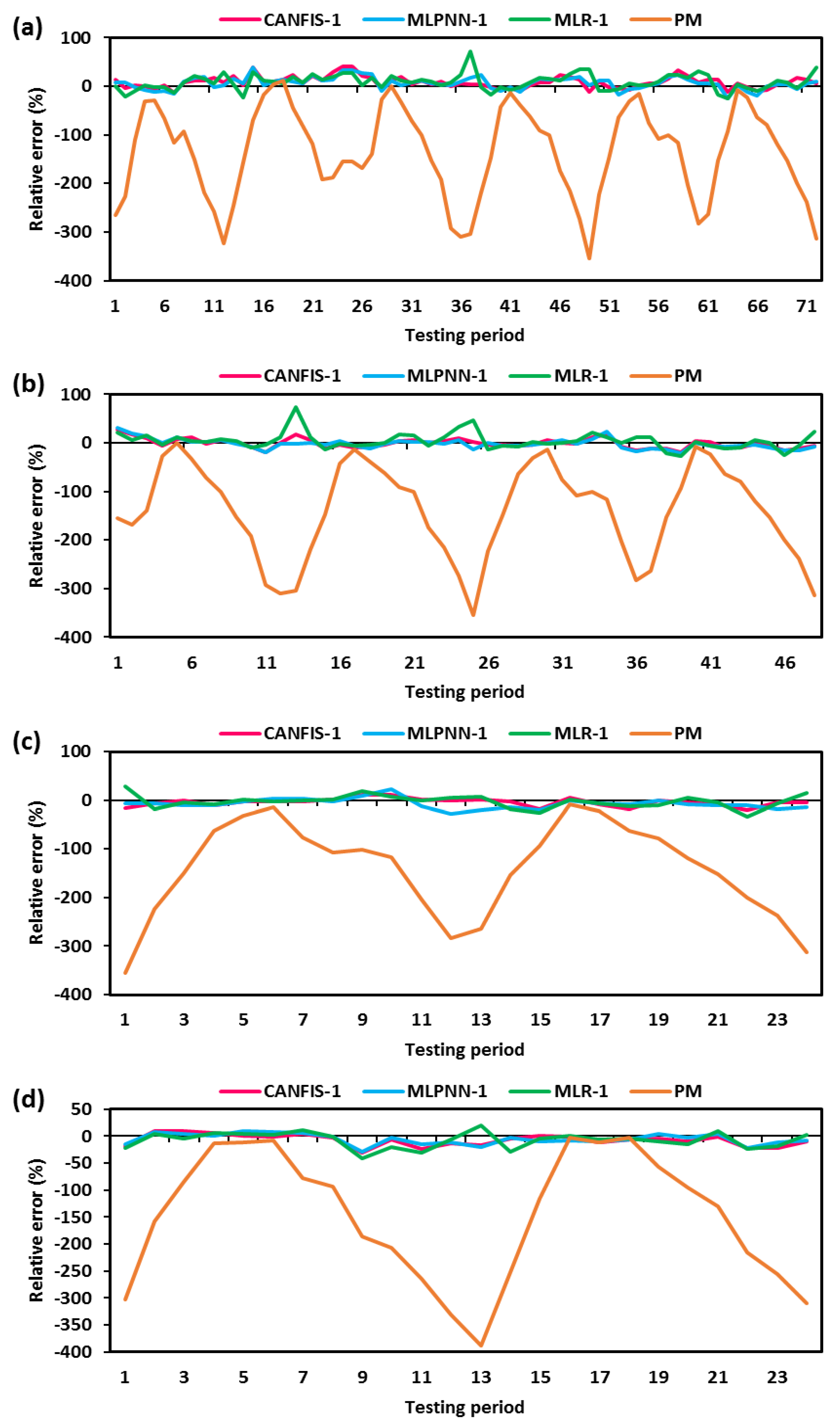
4.3. Estimation of EPm under Different Scenarios at Nagina Station
4.4. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mbangiwa, N.C.; Savage, M.J.; Mabhaudhi, T. Modelling and measurement of water productivity and total evaporation in a dryland soybean crop. Agric. For. Meteorol. 2019, 266–267, 65–72. [Google Scholar] [CrossRef]
- Sayl, K.N.; Muhammad, N.S.; Yaseen, Z.M.; El-shafie, A. Estimation the Physical Variables of Rainwater Harvesting System Using Integrated GIS-Based Remote Sensing Approach. Water Resour. Manag. 2016, 30, 3299–3313. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O.; Maroufpoor, E.; Yaseen, Z.M. Temperature-based modeling of reference evapotranspiration using several artificial intelligence models: Application of different modeling scenarios. Theor. Appl. Climatol. 2019, 135, 449–462. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, H. Estimating reservoir evaporation losses for the United States: Fusing remote sensing and modeling approaches. Remote Sens. Environ. 2019, 226, 109–124. [Google Scholar] [CrossRef]
- Deo, R.C.; Samui, P. Forecasting Evaporative Loss by Least-Square Support-Vector Regression and Evaluation with Genetic Programming, Gaussian Process, and Minimax Probability Machine Regression: Case Study of Brisbane City. J. Hydrol. Eng. 2017, 22, 05017003. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Wang, X.-J. Selection of climate models for projection of spatiotemporal changes in temperature of Iraq with uncertainties. Atmos. Res. 2018, 213, 509–522. [Google Scholar] [CrossRef]
- Wang, K.; Liu, X.; Tian, W.; Li, Y.; Liang, K.; Liu, C.; Li, Y.; Yang, X. Pan coefficient sensitivity to environment variables across China. J. Hydrol. 2019, 572, 582–591. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H.; Abghari, H. Utility of coactive neuro-fuzzy inference system for pan evaporation modeling in comparison with multilayer perceptron. Meteorol. Atmos. Phys. 2012, 116, 147–154. [Google Scholar] [CrossRef]
- Friedrich, K.; Grossman, R.L.; Huntington, J.; Blanken, P.D.; Lenters, J.; Holman, K.D.; Gochis, D.; Livneh, B.; Prairie, J.; Skeie, E.; et al. Reservoir Evaporation in the Western United States: Current Science, Challenges, and Future Needs. Bull. Am. Meteorol. Soc. 2017, 99, 167–187. [Google Scholar] [CrossRef]
- Ali Ghorbani, M.; Kazempour, R.; Chau, K.-W.; Shamshirband, S.; Taherei Ghazvinei, P. Forecasting pan evaporation with an integrated artificial neural network quantum-behaved particle swarm optimization model: A case study in Talesh, Northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 724–737. [Google Scholar] [CrossRef]
- Jing, W.; Yaseen, Z.M.; Shahid, S.; Saggi, M.K.; Tao, H.; Kisi, O.; Salih, S.Q.; Al-Ansari, N.; Chau, K.-W. Implementation of evolutionary computing models for reference evapotranspiration modeling: Short review, assessment and possible future research directions. Eng. Appl. Comput. Fluid Mech. 2019, 13, 811–823. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Danandeh Mehr, A.; Nourani, V.; Kahya, E.; Hrnjica, B.; Sattar, A.M.A.; Yaseen, Z.M. Genetic programming in water resources engineering: A state-of-the-art review. J. Hydrol. 2018, 566, 643–667. [Google Scholar] [CrossRef]
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Fahimi, F.; Yaseen, Z.M.; El-shafie, A. Application of soft computing based hybrid models in hydrological variables modeling: A comprehensive review. Theor. Appl. Climatol. 2016, 128, 875–903. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2018, 569, 387–408. [Google Scholar] [CrossRef]
- Fotovatikhah, F.; Herrera, M.; Shamshirband, S.; Ardabili, S.F.; Piran, J. Mechanics Survey of computational intelligence as basis to big flood management: Challenges, research directions and future work. Eng. Appl. Comput. Fluid Mech. 2018, 2060, 411–437. [Google Scholar]
- Salih, S.Q.; Sharafati, A.; Ebtehaj, I.; Sanikhani, H.; Siddique, R.; Deo, R.C.; Bonakdari, H.; Shahid, S.; Yaseen, Z.M. Integrative stochastic model standardization with genetic algorithm for rainfall pattern forecasting in tropical and semi-arid environments. Hydrol. Sci. J. 2020, 65, 1145–1157. [Google Scholar] [CrossRef]
- Hai, T.; Sharafati, A.; Mohammed, A.; Salih, S.Q.; Deo, R.C.; Al-Ansari, N.; Yaseen, Z.M. Global Solar Radiation Estimation and Climatic Variability Analysis Using Extreme Learning Machine Based Predictive Model. IEEE Access 2020, 8, 12026–12042. [Google Scholar] [CrossRef]
- Qasem, S.N.; Samadianfard, S.; Kheshtgar, S.; Jarhan, S.; Kisi, O.; Shamshirband, S.; Chau, K.-W. Modeling monthly pan evaporation using wavelet support vector regression and wavelet artificial neural networks in arid and humid climates. Eng. Appl. Comput. Fluid Mech. 2019, 13, 177–187. [Google Scholar] [CrossRef]
- Sebbar, A.; Heddam, S.; Djemili, L. Predicting Daily Pan Evaporation (Epan) from Dam Reservoirs in the Mediterranean Regions of Algeria: OPELM vs OSELM. Environ. Process. 2019, 6, 309–319. [Google Scholar] [CrossRef]
- Majhi, B.; Naidu, D.; Mishra, A.P.; Satapathy, S.C. Improved prediction of daily pan evaporation using Deep-LSTM model. Neural Comput. Appl. 2019, 31, 1–15. [Google Scholar] [CrossRef]
- Lu, X.; Ju, Y.; Wu, L.; Fan, J.; Zhang, F.; Li, Z. Daily pan evaporation modeling from local and cross-station data using three tree-based machine learning models. J. Hydrol. 2018, 566, 668–684. [Google Scholar] [CrossRef]
- Eray, O.; Mert, C.; Kisi, O. Comparison of multi-gene genetic programming and dynamic evolving neural-fuzzy inference system in modeling pan evaporation. Hydrol. Res. 2017, 49, 1221–1233. [Google Scholar] [CrossRef]
- Adnan, R.M.; Malik, A.; Kumar, A.; Parmar, K.S.; Kisi, O. Pan evaporation modeling by three different neuro-fuzzy intelligent systems using climatic inputs. Arab. J. Geosci. 2019, 12, 606. [Google Scholar] [CrossRef]
- Moazenzadeh, R.; Mohammadi, B.; Shamshirband, S.; Chau, K. Coupling a firefly algorithm with support vector regression to predict evaporation in northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 584–597. [Google Scholar] [CrossRef]
- Salih, S.Q.; Sharafati, A.; Khosravi, K.; Faris, H.; Kisi, O.; Tao, H.; Ali, M.; Yaseen, Z.M. River suspended sediment load prediction based on river discharge information: Application of newly developed data mining models. Hydrol. Sci. J. 2019, 65, 624–637. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Deo, R.C.; Yaseen, Z.M.; HKashani, M.; Mohammadi, B. Pan evaporation prediction using a hybrid multilayer perceptron-firefly algorithm (MLP-FFA) model: Case study in North Iran. Theor. Appl. Climatol. 2018, 133, 1119–1131. [Google Scholar] [CrossRef]
- Feng, Y.; Jia, Y.; Zhang, Q.; Gong, D.; Cui, N. National-scale assessment of pan evaporation models across different climatic zones of China. J. Hydrol. 2018, 564, 314–328. [Google Scholar] [CrossRef]
- Sharafati, A.; Tafarojnoruz, A.; Shourian, M.; Yaseen, Z.M. Simulation of the depth scouring downstream sluice gate: The validation of newly developed data-intelligent models. J. Hydro Environ. Res. 2020, 29, 20–30. [Google Scholar] [CrossRef]
- Mohammed, M.; Sharafati, A.; Al-Ansari, N.; Yaseen, Z.M. Shallow Foundation Settlement Quantification: Application of Hybridized Adaptive Neuro-Fuzzy Inference System Model. Adv. Civ. Eng. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Kisi, O.; Heddam, S. Evaporation modelling by heuristic regression approaches using only temperature data. Hydrol. Sci. J. 2019, 64, 653–672. [Google Scholar] [CrossRef]
- Shiri, J. Evaluation of a neuro-fuzzy technique in estimating pan evaporation values in low-altitude locations. Meteorol. Appl. 2019, 26, 204–212. [Google Scholar] [CrossRef]
- Deo, R.C.; Ghorbani, M.A.; Samadianfard, S.; Maraseni, T.; Bilgili, M.; Biazar, M. Multi-layer perceptron hybrid model integrated with the firefly optimizer algorithm for windspeed prediction of target site using a limited set of neighboring reference station data. Renew. Energy 2018, 116, 309–323. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O. Monthly pan-evaporation estimation in Indian central Himalayas using different heuristic approaches and climate based models. Comput. Electron. Agric. 2017, 143, 302–313. [Google Scholar] [CrossRef]
- Rezaie-Balf, M.; Kisi, O.; Chua, L.H.C. Application of ensemble empirical mode decomposition based on machine learning methodologies in forecasting monthly pan evaporation. Hydrol. Res. 2019, 50, 498–516. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O. Daily Pan Evaporation Estimation Using Heuristic Methods with Gamma Test. J. Irrig. Drain. Eng. 2018, 144, 04018023. [Google Scholar] [CrossRef]
- Salih, S.Q.; Allawi, M.F.; Yousif, A.A.; Armanuos, A.M.; Saggi, M.K.; Ali, M.; Shahid, S.; Al-Ansari, N.; Yaseen, Z.M.; Chau, K.-W. Viability of the advanced adaptive neuro-fuzzy inference system model on reservoir evaporation process simulation: Case study of Nasser Lake in Egypt. Eng. Appl. Comput. Fluid Mech. 2019, 13, 878–891. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Gan, Y. Comparison of six different soft computing methods in modeling evaporation in different climates. Hydrol. Earth Syst. Sci. Discuss. 2016, 20, 1–51. [Google Scholar] [CrossRef]
- Wang, L.; Niu, Z.; Kisi, O.; Li, C.; Yu, D. Pan evaporation modeling using four different heuristic approaches. Comput. Electron. Agric. 2017, 140, 203–213. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Li, H. Pan evaporation modeling using six different heuristic computing methods in different climates of China. J. Hydrol. 2017, 544, 407–427. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Hu, B.; Bilal, M.; Zounemat-Kermani, M.; Li, H. Evaporation modelling using different machine learning techniques. Int. J. Climatol. 2017, 37, 1076–1092. [Google Scholar] [CrossRef]
- Aytek, A. Co-active neurofuzzy inference system for evapotranspiration modeling. Soft Comput. 2009, 13, 691–700. [Google Scholar] [CrossRef]
- Stefánsson, A.; Končar, N.; Jones, A.J. A note on the gamma test. Neural Comput. Appl. 1997, 5, 131–133. [Google Scholar] [CrossRef]
- Moghaddamnia, A.; Ghafari Gousheh, M.; Piri, J.; Amin, S.; Han, D. Evaporation estimation using artificial neural networks and adaptive neuro-fuzzy inference system techniques. Adv. Water Resour. 2009, 32, 88–97. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A. Comparison of soft-computing and statistical techniques in simulating daily river flow: A case study in India. J. Soil Water Conserv. 2018, 17, 192–199. [Google Scholar] [CrossRef]
- Ashrafzadeh, A.; Malik, A.; Jothiprakash, V.; Ghorbani, M.A.; Biazar, S.M. Estimation of daily pan evaporation using neural networks and meta-heuristic approaches. ISH J. Hydraul. Eng. 2018, 24, 1–9. [Google Scholar] [CrossRef]
- Kakaei Lafdani, E.; Moghaddam Nia, A.; Ahmadi, A. Daily suspended sediment load prediction using artificial neural networks and support vector machines. J. Hydrol. 2013, 478, 50–62. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O.; Shiri, J. Evaluating the performance of four different heuristic approaches with Gamma test for daily suspended sediment concentration modeling. Environ. Sci. Pollut. Res. 2019, 26, 22670–22687. [Google Scholar] [CrossRef]
- Remesan, R.; Shamim, M.A.; Han, D.; Mathew, J. Runoff prediction using an integrated hybrid modelling scheme. J. Hydrol. 2009, 372, 48–60. [Google Scholar] [CrossRef]
- Goyal, M.K. Modeling of Sediment Yield Prediction Using M5 Model Tree Algorithm and Wavelet Regression. Water Resour. Manag. 2014, 28, 1991–2003. [Google Scholar] [CrossRef]
- Rashidi, S.; Vafakhah, M.; Lafdani, E.K.; Javadi, M.R. Evaluating the support vector machine for suspended sediment load forecasting based on gamma test. Arab. J. Geosci. 2016, 9, 583. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Piri, J. Daily suspended sediment concentration simulation using hydrological data of Pranhita River Basin, India. Comput. Electron. Agric. 2017, 138, 20–28. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A. Pan Evaporation Simulation Based on Daily Meteorological Data Using Soft Computing Techniques and Multiple Linear Regression. Water Resour. Manag. 2015, 29, 1859–1872. [Google Scholar] [CrossRef]
- Piri, J.; Amin, S.; Moghaddamnia, A.; Keshavarz, A.; Han, D.; Remesan, R. Daily pan evaporation modeling in a hot and dry climate. J. Hydrol. Eng. 2009, 14, 803–811. [Google Scholar] [CrossRef]
- Singh, A.; Malik, A.; Kumar, A.; Kisi, O. Rainfall-runoff modeling in hilly watershed using heuristic approaches with gamma test. Arab. J. Geosci. 2018, 11, 261. [Google Scholar] [CrossRef]
- Jang, J.-S.R.; Sun, C.-T.; Mizutani, E. Neuro-Fuzzy and Soft Computing A Computational Approach to Learning and Machine Intelligence; Prentice-Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Haykin, S. Neural Networks—A Comprehensive Foundation, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1999; pp. 26–32. [Google Scholar]
- Yaseen, Z.M.; El-Shafie, A.; Afan, H.A.; Hameed, M.; Mohtar, W.H.M.W.; Hussain, A. RBFNN versus FFNN for daily river flow forecasting at Johor River, Malaysia. Neural Comput. Appl. 2015, 27, 1533–1542. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Asadi, H.; Makarynskyy, O.; Makarynska, D.; Yaseen, Z.M. Augmented chaos-multiple linear regression approach for prediction of wave parameters. Eng. Sci. Technol. Int. J. 2017, 20, 1180–1191. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. A 1948, 193, 120–145. [Google Scholar]
- Penman, H.L. Evaporation: An introductory survey. J. Agric. Sci. 1956, 9, 9–29. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop requirements. FAO Irrig. Drain. Pap. 1998, 56, 300. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Shiri, J. Improving the performance of the mass transfer-based reference evapotranspiration estimation approaches through a coupled wavelet-random forest methodology. J. Hydrol. 2018, 561, 737–750. [Google Scholar] [CrossRef]
- Tao, H.; Diop, L.; Bodian, A.; Djaman, K.; Ndiaye, P.M.; Yaseen, Z.M. Reference evapotranspiration prediction using hybridized fuzzy model with firefly algorithm: Regional case study in Burkina Faso. Agric. Water Manag. 2018, 208, 140–151. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Ghorbani, M.A.; Kashani, M.H.; Kisi, O.; Kim, S. The viability of co-active fuzzy inference system model for monthly reference evapotranspiration estimation: Case study of Uttarakhand State. Hydrol. Res. 2019, 50, 1623–1644. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Khosravi, K.; Mao, L.; Kisi, O.; Yaseen, Z.M.; Shahid, S. Quantifying Hourly Suspended Sediment Load Using Data Mining Models: Case Study of a Glacierized Andean Catchment in Chile. J. Hydrol. 2018, 65, 624–637. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Singh, R.P. Application of Heuristic Approaches for Prediction of Hydrological Drought Using Multi-scalar Streamflow Drought Index. Water Resour. Manag. 2019, 33, 3985–4006. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A. Meteorological drought prediction using heuristic approaches based on effective drought index: A case study in Uttarakhand. Arab. J. Geosci. 2020, 13, 276. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Awadh, S.M.; Sharafati, A.; Shahid, S. Complementary data-intelligence model for river flow simulation. J. Hydrol. 2018, 567, 180–190. [Google Scholar] [CrossRef]
- Keskin, M.E.; Terzi, Ö.; Taylan, D. Estimating daily pan evaporation using adaptive neural-based fuzzy inference system. Theor. Appl. Climatol. 2009, 98, 79–87. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O.; Nikpour, M.R.; Dinpashoh, Y. Estimation of Daily Pan Evaporation Using Two Different Adaptive Neuro-Fuzzy Computing Techniques. Water Resour. Manag. 2012, 26, 4347–4365. [Google Scholar] [CrossRef]
- Keskin, M.E.; Terzi, Ö. Artificial Neural Network Models of Daily Pan Evaporation. J. Hydrol. Eng. 2006, 11, 65–70. [Google Scholar] [CrossRef]
- Shirsath, P.B.; Singh, A.K. A Comparative Study of Daily Pan Evaporation Estimation Using ANN, Regression and Climate Based Models. Water Resour. Manag. 2010, 24, 1571–1581. [Google Scholar] [CrossRef]
- Goyal, M.K.; Bharti, B.; Quilty, J.; Adamowski, J.; Pandey, A. Modeling of daily pan evaporation in sub tropical climates using ANN, LS-SVR, Fuzzy Logic, and ANFIS. Expert Syst. Appl. 2014, 41, 5267–5276. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kim, S.; Kashani, M.H.; Karimi, V.; Sharafati, A.; Ghorbani, M.A.; Al-Ansari, N.; Salih, S.Q.; Yaseen, Z.M. Modeling monthly pan evaporation process over the Indian central Himalayas: Application of multiple learning artificial intelligence model. Eng. Appl. Comput. Fluid Mech. 2020, 14, 323–338. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]


| Station/Climatic Variable | Statistical Parameters | ||||||
|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | Std | Skewness | Kurtosis | ||
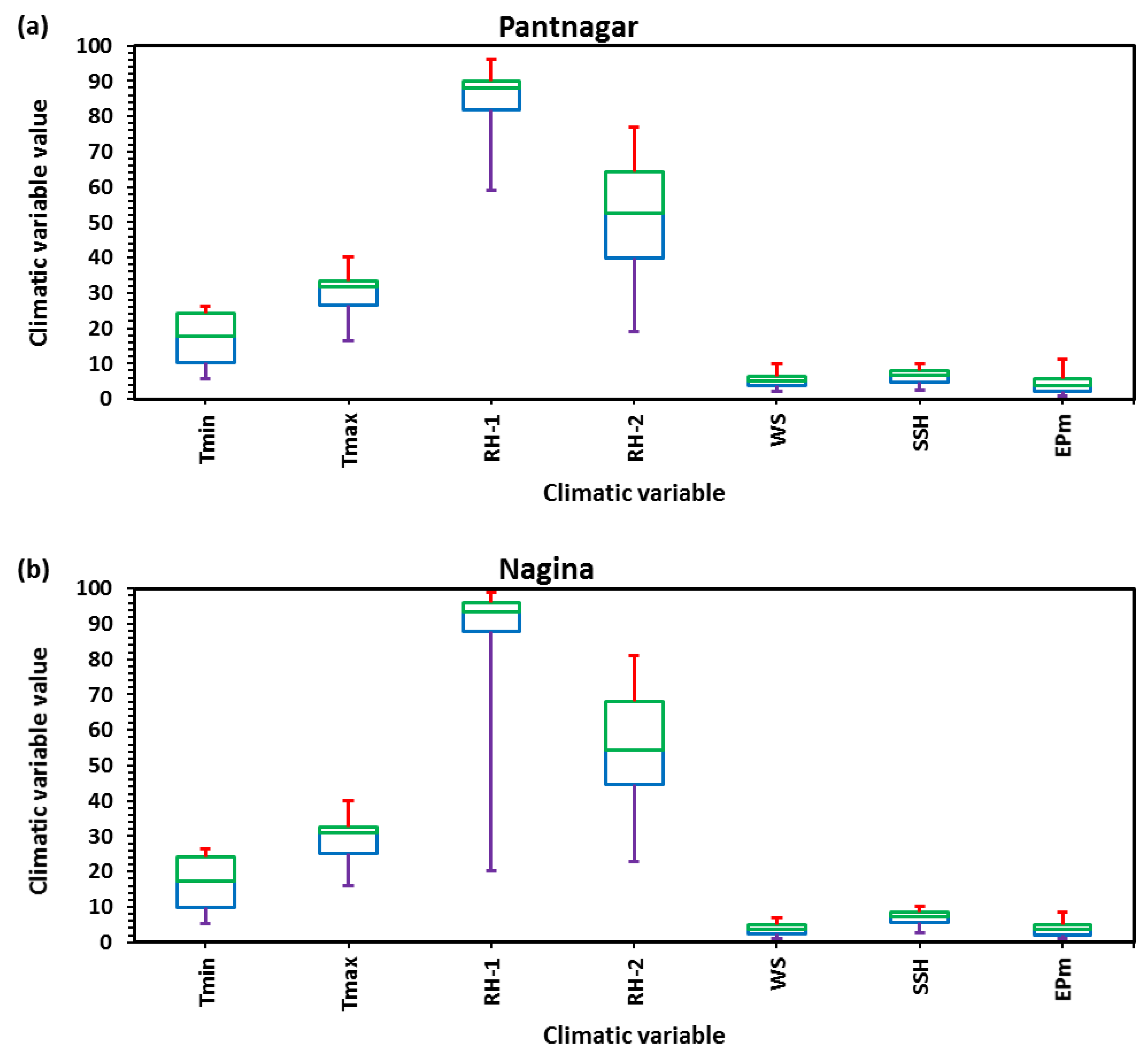
| Pantnagar | Tmin (oC) | 5.80 | 26.30 | 17.27 | 7.07 | −0.15 | −1.55 |
| Tmax (oC) | 16.50 | 40.10 | 29.94 | 5.88 | −0.48 | −0.54 | |
| RH-1 (%) | 59.00 | 96.00 | 84.30 | 9.72 | −1.23 | 0.21 | |
| RH-2 (%) | 19.00 | 77.00 | 51.38 | 15.04 | −0.16 | −0.99 | |
| WS (km/h) | 2.10 | 9.90 | 5.09 | 1.90 | 0.37 | −0.43 | |
| SSH (h) | 2.60 | 9.90 | 6.58 | 1.92 | −0.21 | −0.90 | |
| EPm (mm) | 1.00 | 11.40 | 4.43 | 2.65 | 0.91 | −0.16 | |
| Nagina | Tmin (oC) | 5.40 | 26.50 | 16.84 | 7.40 | −0.14 | −1.55 |
| Tmax (oC) | 16.10 | 40.10 | 29.14 | 5.94 | −0.47 | −0.54 | |
| RH-1 (%) | 20.20 | 99.00 | 88.90 | 12.34 | −2.44 | 9.08 | |
| RH-2 (%) | 23.00 | 81.00 | 55.03 | 14.63 | −0.04 | −0.89 | |
| WS (km/h) | 1.00 | 7.00 | 3.77 | 1.52 | 0.21 | −0.92 | |
| SSH (h) | 2.80 | 10.10 | 6.98 | 1.86 | −0.28 | −0.79 | |
| EPm (mm) | 0.90 | 8.40 | 3.71 | 2.03 | 0.52 | −0.76 | |
| Station/Climatic Variable | Tmin | Tmax | RH-1 | RH-2 | WS | SSH | EPm | |
|---|---|---|---|---|---|---|---|---|
| Pantnagar | Tmin | 1.00 | ||||||
| Tmax | 0.84 * | 1.00 | ||||||
| RH-1 | −0.47 * | −0.79 * | 1.00 | |||||
| RH-2 | 0.21 * | −0.35 * | 0.65 * | 1.00 | ||||
| WS | 0.57 * | 0.62 * | −0.75 * | −0.23 * | 1.00 | |||
| SSH | 0.12 | 0.58 * | −0.64 * | −0.80 * | 0.28 * | 1.00 | ||
| EPm | 0.63 * | 0.88 * | −0.95 * | −0.52 * | 0.82 * | 0.59 * | 1.00 | |
| Nagina | Tmin | 1.00 | ||||||
| Tmax | 0.85 * | 1.00 | ||||||
| RH-1 | −0.48 * | −0.70 * | 1.00 | |||||
| RH-2 | 0.23 * | −0.26 * | 0.55 * | 1.00 | ||||
| WS | 0.50 * | 0.54 * | −0.61 * | −0.18 | 1.00 | |||
| SSH | 0.21 * | 0.61 * | −0.60 * | −0.74 * | 0.38 * | 1.00 | ||
| EPm | 0.73 * | 0.88 * | −0.82 * | −0.37 * | 0.77 * | 0.64 * | 1.00 | |
| Climatic Variables | CANFIS/MLPNN/MLR | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Tmin | √ | ||||||
| Tmax | √ | √ | √ | √ | √ | √ | √ |
| RH-1 | √ | ||||||
| RH-2 | √ | √ | √ | ||||
| WS | √ | √ | √ | √ | |||
| SSH | √ | √ | √ | √ | |||
| Various Input Combinations | GT Statistic | |||||
|---|---|---|---|---|---|---|
| Γ | A | SE | Vratio | Mask | ||
| Pantnagar | Tmin, Tmax, RH-1, RH-2, WS, SSH | 0.0017 | 0.0665 | 0.0013 | 0.0070 | 111111 |
| Tmax, WS, SSH | 0.0109 | 0.0905 | 0.0023 | 0.0436 | 010011 | |
| Tmax, RH-2, WS | 0.0050 | 0.1375 | 0.0031 | 0.0199 | 010110 | |
| Tmax, RH-2, SSH | 0.0105 | 0.1548 | 0.0071 | 0.0419 | 010101 | |
| Tmax, WS | 0.0119 | 0.1934 | 0.0031 | 0.0476 | 010010 | |
| Tmax, SSH | 0.0118 | 0.3441 | 0.0042 | 0.0474 | 010001 | |
| Tmax | 0.0156 | 0.3202 | 0.0024 | 0.0623 | 010000 | |
| Nagina | Tmin, Tmax, RH-1, RH-2, WS, SSH | 0.0112 | 0.0395 | 0.0024 | 0.0448 | 111111 |
| Tmax, WS, SSH | 0.0179 | 0.0704 | 0.0048 | 0.0718 | 010011 | |
| Tmax, RH-2, WS | 0.0163 | 0.0821 | 0.0047 | 0.0652 | 010110 | |
| Tmax, RH-2, SSH | 0.0189 | 0.1528 | 0.0058 | 0.0756 | 010101 | |
| Tmax, WS | 0.0163 | 0.2786 | 0.0047 | 0.0653 | 010010 | |
| Tmax, SSH | 0.0247 | 0.2652 | 0.0071 | 0.0989 | 010001 | |
| Tmax | 0.0370 | 0.3576 | 0.0055 | 0.1479 | 010000 | |
| Model | Structure | Testing Period | ||||
|---|---|---|---|---|---|---|
| NRMSE (mm/month) | NSE | PCC | WI | |||
| Scenario-1 | CANFIS-1 | Bell-3 | 0.1364 | 0.9439 | 0.9790 | 0.9860 |
| MLPNN-1 | 6-9-1 | 0.1404 | 0.9406 | 0.9751 | 0.9857 | |
| MLR-1 | - | 0.1402 | 0.9408 | 0.9768 | 0.9851 | |
| PM | - | 0.9585 | −1.7672 | 0.8047 | 0.5590 | |
| Scenario-2 | CANFIS-1 | Gauss-2 | 0.0904 | 0.9736 | 0.9872 | 0.9934 |
| MLPNN-1 | 6-11-1 | 0.0920 | 0.9726 | 0.9867 | 0.9932 | |
| MLR-1 | - | 0.1110 | 0.9602 | 0.9818 | 0.9903 | |
| PM | - | 0.9871 | −2.1474 | 0.8224 | 0.5486 | |
| Scenario-3 | CANFIS-1 | Gauss-3 | 0.0947 | 0.9703 | 0.9877 | 0.9927 |
| MLPNN-1 | 6-10-1 | 0.0993 | 0.9674 | 0.9874 | 0.9918 | |
| MLR-1 | - | 0.1085 | 0.9611 | 0.9831 | 0.9905 | |
| PM | - | 0.9994 | −2.3051 | 0.8511 | 0.5416 | |
| Scenario-4 | CANFIS-1 | Gauss-2 | 0.0898 | 0.9799 | 0.9922 | 0.9949 |
| MLPNN-1 | 6-9-1 | 0.1021 | 0.9740 | 0.9877 | 0.9934 | |
| MLR-1 | - | 0.1056 | 0.9721 | 0.9885 | 0.9927 | |
| PM | - | 0.9168 | −1.1016 | 0.8103 | 0.5957 | |
| Model | Structure | Testing Period | ||||
|---|---|---|---|---|---|---|
| NRMSE (mm/month) | NSE | PCC | WI | |||
| Scenario-1 | CANFIS-1 | Gauss-3 | 0.1543 | 0.9150 | 0.9643 | 0.9794 |
| MLPNN-1 | 6-10-1 | 0.1813 | 0.8827 | 0.9592 | 0.9723 | |
| MLR-1 | - | 0.1866 | 0.8758 | 0.9437 | 0.9698 | |
| PM | 1.3464 | −5.4677 | 0.8507 | 0.4585 | ||
| Scenario-2 | CANFIS-1 | Gauss-2 | 0.1719 | 0.8962 | 0.9649 | 0.9761 |
| MLPNN-1 | 6-10-1 | 0.1899 | 0.8734 | 0.9486 | 0.9699 | |
| MLR-1 | - | 0.2299 | 0.8144 | 0.9346 | 0.9579 | |
| PM | 1.3989 | −5.8728 | 0.8470 | 0.4493 | ||
| Scenario-3 | CANFIS-1 | Gauss-2 | 0.2067 | 0.8382 | 0.9473 | 0.9632 |
| MLPNN-1 | 6-10-1 | 0.2281 | 0.8031 | 0.9247 | 0.9552 | |
| MLR-1 | - | 0.2939 | 0.6729 | 0.9049 | 0.9313 | |
| PM | 1.3907 | −6.3213 | 0.8158 | 0.4291 | ||
| Scenario-4 | CANFIS-1 | Gauss-2 | 0.1356 | 0.9453 | 0.9762 | 0.9853 |
| MLPNN-1 | 6-10-1 | 0.1477 | 0.9351 | 0.9746 | 0.9820 | |
| MLR-1 | - | 0.1621 | 0.9219 | 0.9666 | 0.9789 | |
| PM | 1.1789 | −3.1294 | 0.8961 | 0.5362 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, A.; Rai, P.; Heddam, S.; Kisi, O.; Sharafati, A.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Pan Evaporation Estimation in Uttarakhand and Uttar Pradesh States, India: Validity of an Integrative Data Intelligence Model. Atmosphere 2020, 11, 553. https://doi.org/10.3390/atmos11060553
Malik A, Rai P, Heddam S, Kisi O, Sharafati A, Salih SQ, Al-Ansari N, Yaseen ZM. Pan Evaporation Estimation in Uttarakhand and Uttar Pradesh States, India: Validity of an Integrative Data Intelligence Model. Atmosphere. 2020; 11(6):553. https://doi.org/10.3390/atmos11060553
Chicago/Turabian StyleMalik, Anurag, Priya Rai, Salim Heddam, Ozgur Kisi, Ahmad Sharafati, Sinan Q. Salih, Nadhir Al-Ansari, and Zaher Mundher Yaseen. 2020. "Pan Evaporation Estimation in Uttarakhand and Uttar Pradesh States, India: Validity of an Integrative Data Intelligence Model" Atmosphere 11, no. 6: 553. https://doi.org/10.3390/atmos11060553
APA StyleMalik, A., Rai, P., Heddam, S., Kisi, O., Sharafati, A., Salih, S. Q., Al-Ansari, N., & Yaseen, Z. M. (2020). Pan Evaporation Estimation in Uttarakhand and Uttar Pradesh States, India: Validity of an Integrative Data Intelligence Model. Atmosphere, 11(6), 553. https://doi.org/10.3390/atmos11060553










