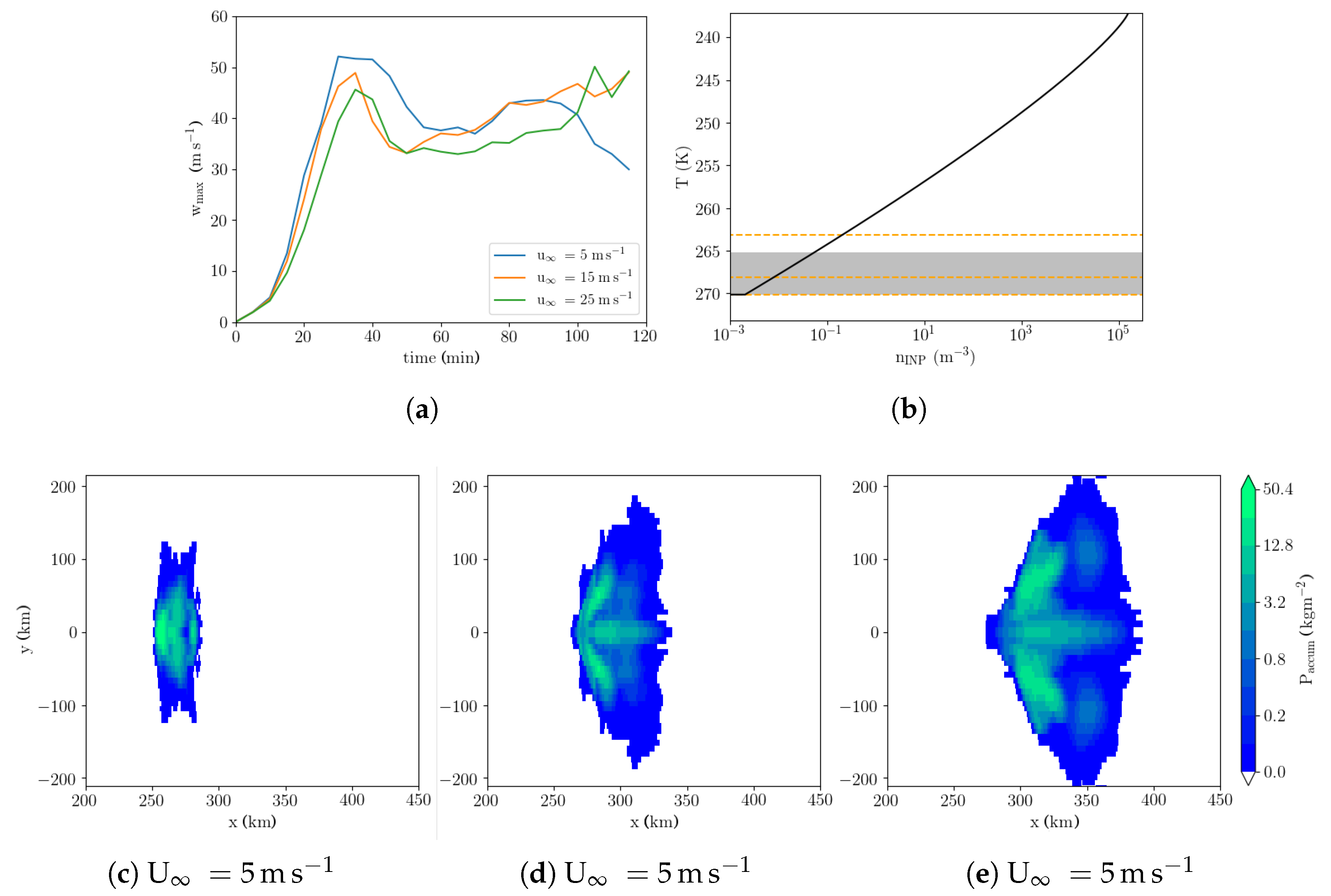
1. Introduction
In many clouds ice and liquid particles co-exist (e.g., reference [
1], and reference therein). Ice particles in the atmosphere are formed by homogeneous nucleation or homogeneous freezing of cloud droplets in the upper troposphere at temperatures colder than −38 °C and by heterogeneous freezing of cloud droplets triggered by aerosol particles at all temperatures below 0 °C. Aerosol particles that initiate the freezing of liquid hydrometeors are known as ice-nucleating particles (INP) and their abundance varies with temperature as well as geographical location and time (e.g., reference [
2], and references therein). The observed number of ice crystals in clouds often exceeds the number of particles expected from the abundance of INP at the same location and temperature. To explain the discrepancy it has been suggested that ice crystals may be formed through what is known as secondary ice production processes. For example, the collision of two or more ice crystals or snow flakes can release a number of additional ice particles (e.g., references [
3,
4,
5]). Other suggested mechanisms are the formation of new ice crystals during the riming of graupel particles (Hallett-Mossop process) (e.g., references [
6,
7]) or the ejection of ice crystals during the freezing of large rain drops (e.g., reference [
8]). Field et al. [
9] provides a comprehensive overview of the current knowledge on secondary ice production. Since the overview by Field et al. [
9], several observational studies provided further evidence for the importance of secondary ice production for explaining cloud glaciation (e.g., references [
10,
11,
12,
13]). In numerical weather prediction models most often only the rime-splintering mechanism is represented although recently formulations for other processes have become available (e.g., references [
14,
15,
16]). However, in the present study we only consider rime-splintering. It is important to note that the parameterisation of secondary ice production (SIP) in models involves considerable uncertainties as they are based on a fairly scant database. Nevertheless, considering how SIP behaves in models and how it affects the cloud evolution can provide interesting insight and serves to develop hypothesis that can be tested with dedicated field or laboratory measurements.
Important issues for understanding SIP and its role for cloud evolution are (i) the initiation of secondary ice production, which necessarily relies on some ice being formed through heterogeneous and/or homogeneous freezing, and (ii) the impact of secondary ice on the further evolution of the cloud (reference [
9], and references therein). Rime-splintering occurs at relatively warm temperatures (about −3 °C to −8 °C, which is referred to as the Hallett-Mossop zone or temperature region. However, at these warm temperatures only very few INPs are typically active (e.g., reference [
2], and reference therein). Hence, specific attention has been placed on the few INP types that are active at temperatures just below 0 °C, which are mainly biological materials, as well as the number concentration of primary ice crystals necessary to initiate secondary ice production (e.g., references [
17,
18]). Based on conceptual considerations Beard [
17] suggests primary ice crystal number concentration in the order of 0.01 L
−1 may suffice to initiate SIP via rime-splintering, which is supported by the idealised 2D simulations by Huang et al. [
18]. In parcel model simulations by Sullivan et al. [
19] even lower INP concentrations are sufficient to trigger SIP as long as moderate updraft regimes and warm cloud base temperatures are assumed. Beard [
17] and Huang et al. [
18] highlight the importance of rain or large drizzle drops for the onset of rime-splintering. By heterogeneous freezing or by collision with ice crystals rain drops can fairly quickly provide the graupel particles necessary for riming. The role of drizzle and/or rain drops is further supported by observational evidence (e.g., references [
20,
21,
22]), which is, however, also compatible with other SIP mechanisms such as drop shattering. Once secondary ice production started ice crystals rapidly multiply [
23]. The sensitivity studies of Huang et al. [
18] and Sullivan et al. [
19] provide some insight into the required concentration of INPs. However, the parcel model approach by Sullivan et al. [
19] does not allow for particles formed at higher levels within the cloud to impact the processes occurring in the Hallett-Mossop temperature zone. The 2D sensitivity simulations by Huang et al. [
18] allow for such interactions, but they do not provide detailed insight into the impact of primary ice nucleation at different temperatures for the initiation of SIP. However, this question is vital for assessing the impact of high-temperature INP (e.g., reference [
24]).
The importance of SIP for the cloud microphysical structure, precipitation formation, and cloud evolution is an active research topic. Several sensitivity studies with numerical weather prediction models assessed the impact of SIP on the evolution of more or less idealised clouds (e.g., references [
16,
25,
26,
27,
28,
29,
30]). While the results for precipitation formation and cloud macroscopic appearance are inconclusive so far, all studies find a clear impact on the cloud microphysical structure in the form of ice crystal number concentration and glaciation around the freezing level. However, the transport of secondary ice from locations, at which rime-splintering occurs, and the spread of secondary ice through the cloud have so far not been investigated in detail.
The question of SIP initiation and the spread of secondary ice through the cloud are challenging to address with the classical Eulerian perspective on the problem. A Lagrangian perspective, that is, following the evolution of individual air parcels, can provide valuable insight into the importance of primary ice nucleation, “in-situ” formation of graupel, rain freezing, as well as the importance of graupel sedimenting from higher cloud altitudes. Due to the recent development of high-resolution trajectory simulation tools [
31], it is now feasible to analyse the evolution of complex three-dimensional cloud simulations from a Lagrangian perspective. In the present study we use this new approach to address the following research questions for idealised three-dimensional simulations of deep convective clouds:
How is secondary ice production via rime-splintering initiated in the modelled deep convective clouds?
Are high-temperature ice nucleating particles (INP) and/or rain freezing crucial for the initiation of rime-splintering?
How does secondary ice spread through the simulated deep convective clouds?
3. Cloud-Microphysical and Thermodynamic History of Air Parcels with Secondary Ice Formation
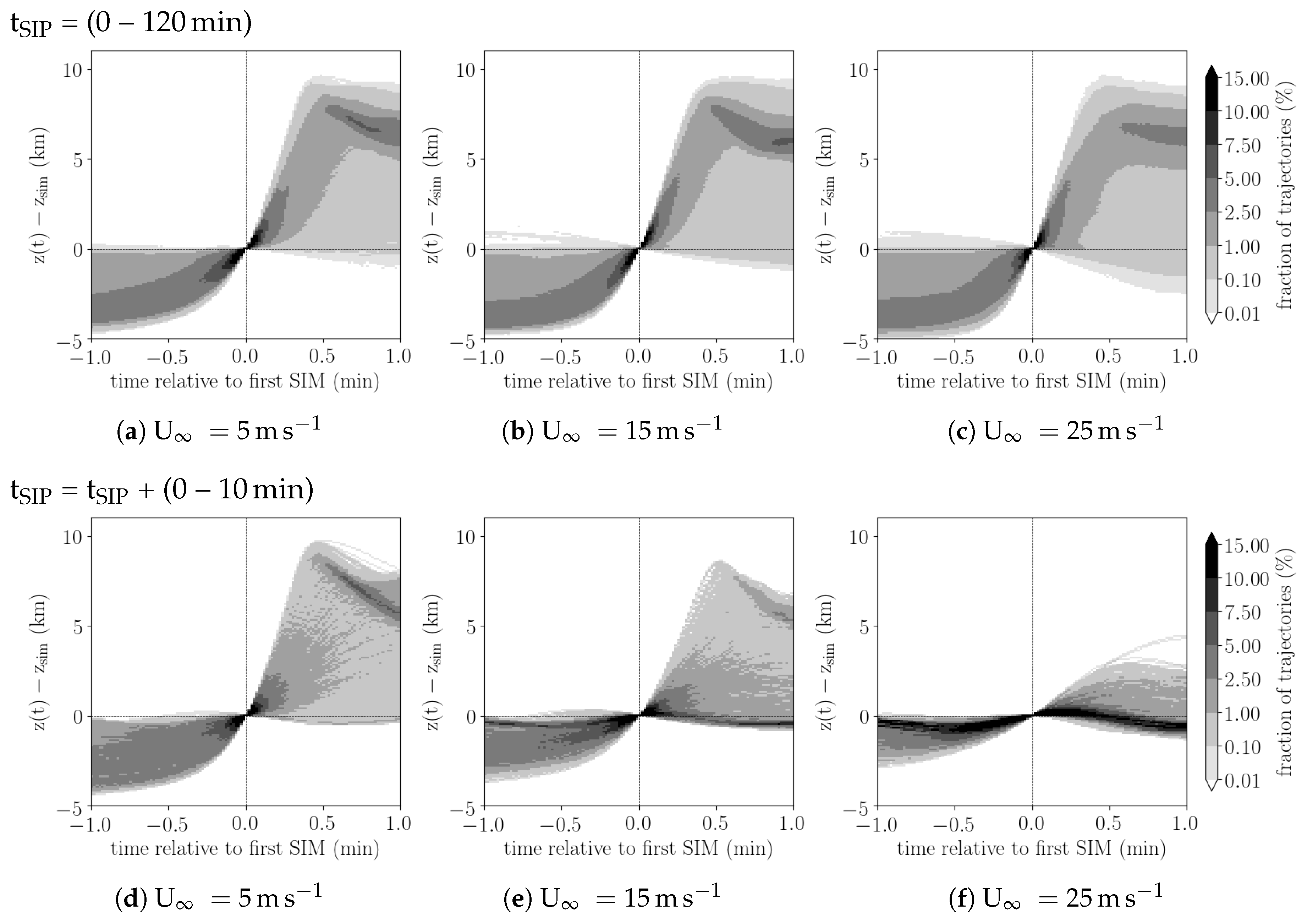
The Lagrangian data allow for an investigation of the thermodynamic and cloud-microphysical history of air parcels before SIP events. The evolution of the air parcel altitude relative to the time of the SIP event is summarised in
Figure 3. In all simulations the majority of air parcels, in which SIP occurs, originate in the boundary layer and typically ascent before the SIP event (
Figure 3a–c). In simulations with U
∞ = 15 m s
−1 and U
∞ = 25 m s
−1 a small number of trajectories originates at altitudes of up to 1 km above the altitude of the SIP event (
Figure 3b,c). If only SIP events in the 10 min after the initial SIP event in each simulation are considered, this picture does change only slightly (
Figure 3d–f). While trajectories still predominately originate in the boundary layer and most ascent before the SIP event, the ascent is less pronounced. This is particularly evident in simulations with larger vertical wind shear (U
∞ = (15, 25) m s
−1). The air parcel altitude after the SIP event is further discussed in
Section 5.
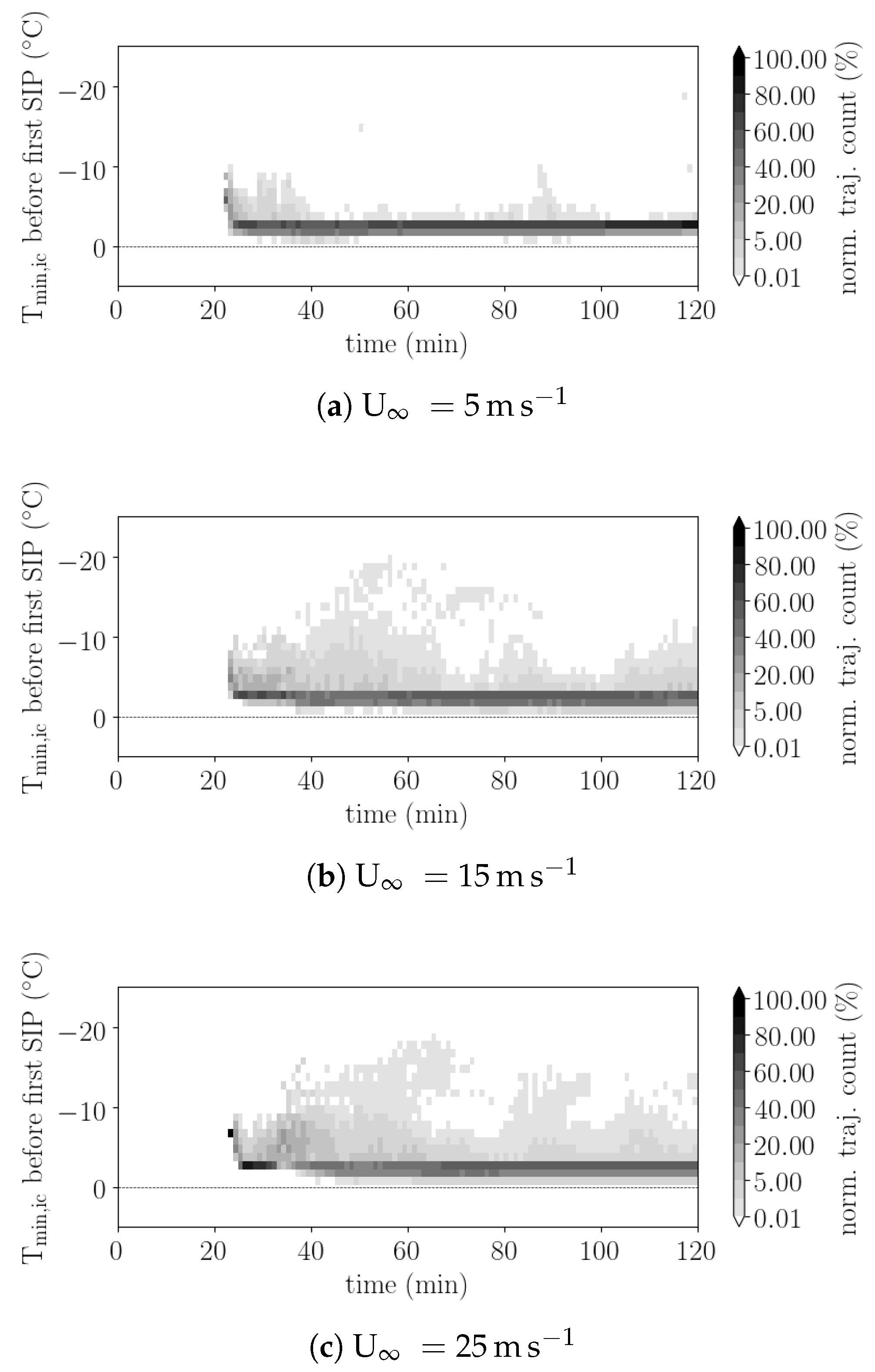
The picture emerging from the analysis of trajectory altitudes is reflected in the distribution of the minimum in-cloud air temperature in the 10 min before SIP events (T
min,ic). T
min,ic is determined by considering the temperature evolution along trajectories, but only where the condensate mass mixing ratio exceeds 1 × 10
−10 kg kg
−1.
Figure 4 shows the distribution of T
min,ic throughout the simulation, where the time (ordinate) corresponds to the simulation time, at which the SIP event occurs. Only a small fraction of trajectories have T
min,ic colder than the coldest temperature of the Hallett-Mossop zone (i.e., −8 °C). Secondary ice production occurs about 20 min into the simulation. T
min,ic for these first events is between −5 °C to −10 °C, that is, well within the Hallett-Mossop range, and cold enough for heterogeneous freezing to occur. After about 2 min to 5 min warmer T
min,ic are recorded, which are a consistent with the upper temperature bound of the Hallett-Mossop zone (i.e., −3 °C). There will be no primary ice formation in these trajectories prior to the SIP event. In simulations with larger wind shear, trajectories with colder T
min,ic remain important throughout the simulation, although minimum temperatures warmer than −3 °C are still most common (
Figure 4b,c). The warm minimum temperatures suggest that primary ice formation in parcels encountering SIP is not important. The few parcels that experience temperatures cold enough for heterogeneous freezing only do so a few minutes (<5 min) before the SIP event, which is probably too short for “in-situ” formation of large rimer particles (graupel). SIP from riming ice crystals is not important for the majority of trajectories (
SI Figure S2).
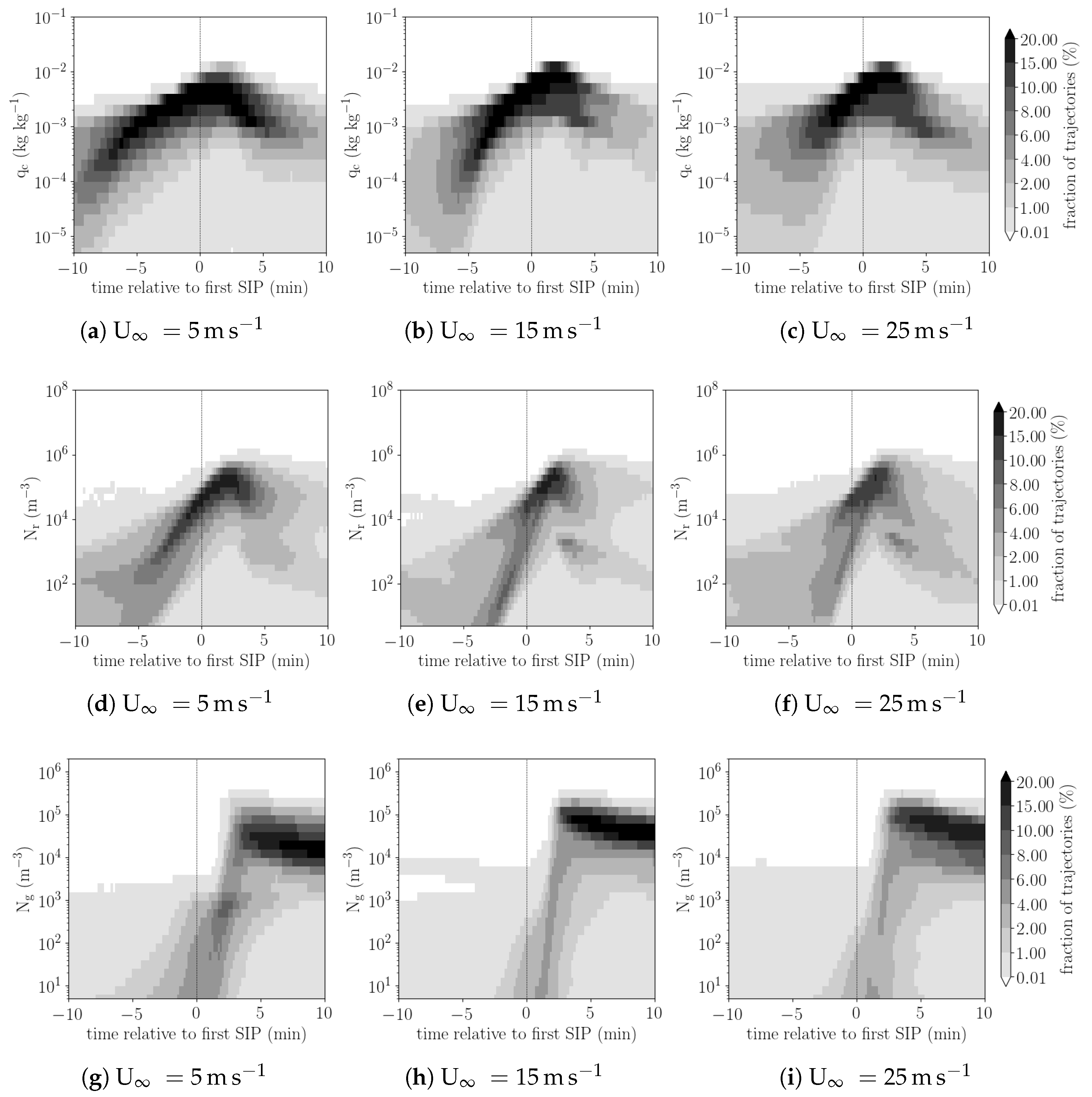
To gain a more detailed insight into the cloud microphysical history of air parcels, the composite evolution of cloud droplet mass mixing ratio as well as of the rain and graupel number density is shown in
Figure 5. The composite evolution of other hydrometeor types mass mixing ratios and number densities is shown in
SI Figures S3 and S4. Consistent with the ascending air parcel motion before the SIP event, the cloud droplet mass mixing ratio increases in the 10 min prior to the event. The rain number density also increase strongly in the 10 min prior to SIP events (
Figure 5d–f) as expected. In the simulations with larger vertical wind shear, two different “branches” are visible in the composite evolution of rain drop number density (
Figure 5d,e): In a number of trajectories rain drop number density steadily increase over the entire 10 min interval considered akin to the evolution in the simulation with U
∞ = 5 m s
−1. Additionally there is a even larger number of trajectories, in which rain drop number density steeply increase in the 4 min prior to the SIP event. The increase of rain drops in the first set of trajectories is likely due to sedimentation of rain drops from higher levels, which is less important in higher vertical wind shear conditions. In the other set of trajectories, conversion of cloud droplets to rain drops via collision-coalescence is likely dominant. Efficient conversion of cloud to rain water in updrafts of around 10 m s
−1 only starts at cloud droplet mass mixing ratios of about 2 g kg
−1 and displays a rapid increase in rain water over the course of a few minutes (e.g., reference [
45]). For the median trajectory, this critical value is only reached about 3 min prior to the SIP event. The composite evolution of graupel number density, that is, the number of rimers available for rime splintering, is shown in
Figure 5g–i. In the majority of trajectories graupel number concentrations only increase in the last about 4 min prior to the SIP event. The increase occurs closer to the SIP event in higher vertical wind shear conditions. This is not surprising as rime-splintering in the model is tied to the riming rate of graupel. Riming rates are likely high as soon as graupel appears in the trajectories, which in general have high liquid water content (
Figure 5a–c).
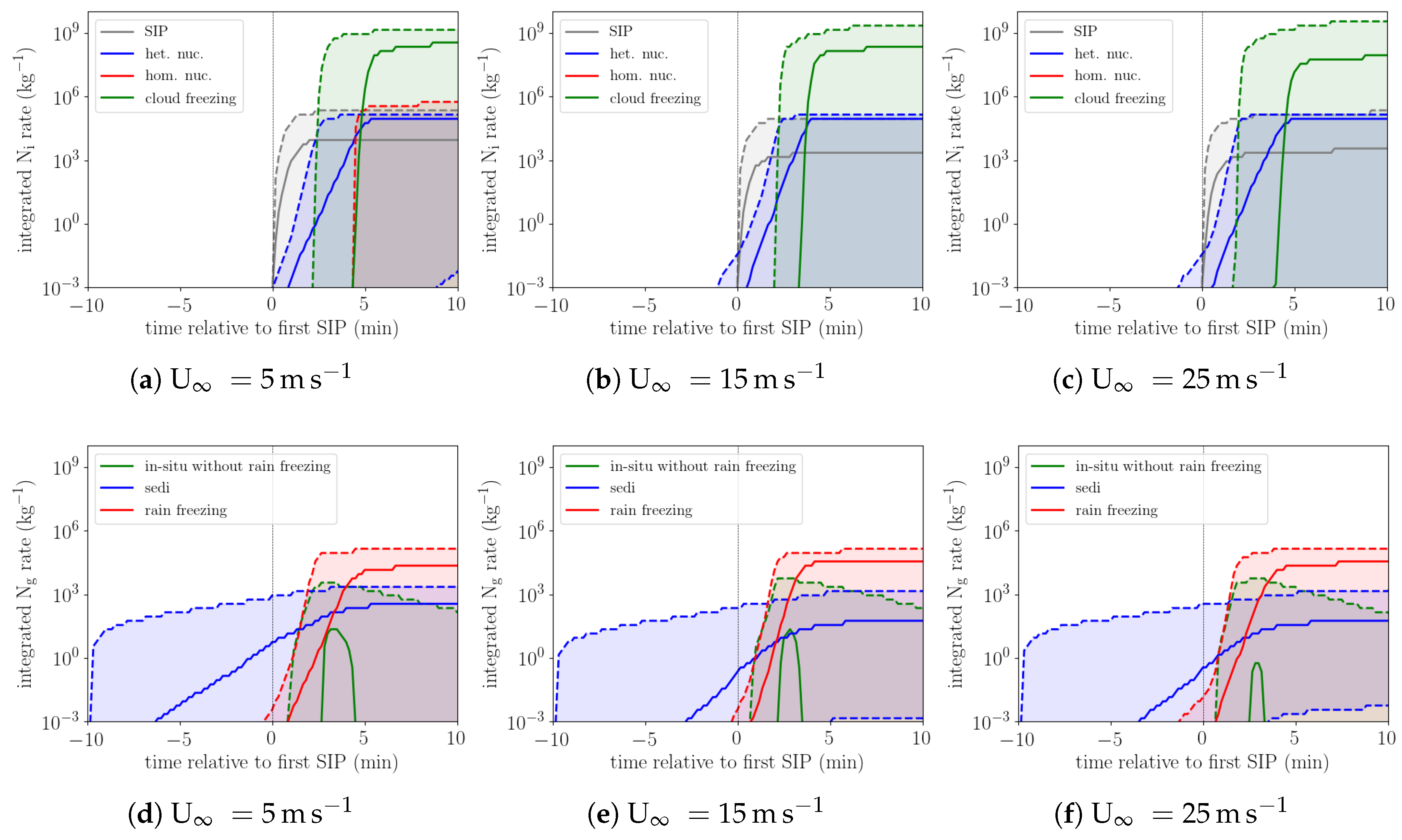
To gain further insight into the origin of graupel in SIP trajectories, the composite evolution of the integrated ice and graupel production rates from different processes is shown in
Figure 6. In most trajectories, secondary ice production is the dominant source of ice crystal at and immediately after the first SIP event (
Figure 6a–c). Only in the simulations with larger vertical wind shear the 99th percentile of heterogeneous freezing rates exceeds 1 × 10
−3 kg
−1 prior to the first SIP event. For graupel, sedimentational influx is the largest source of graupel prior to the first SIP events (
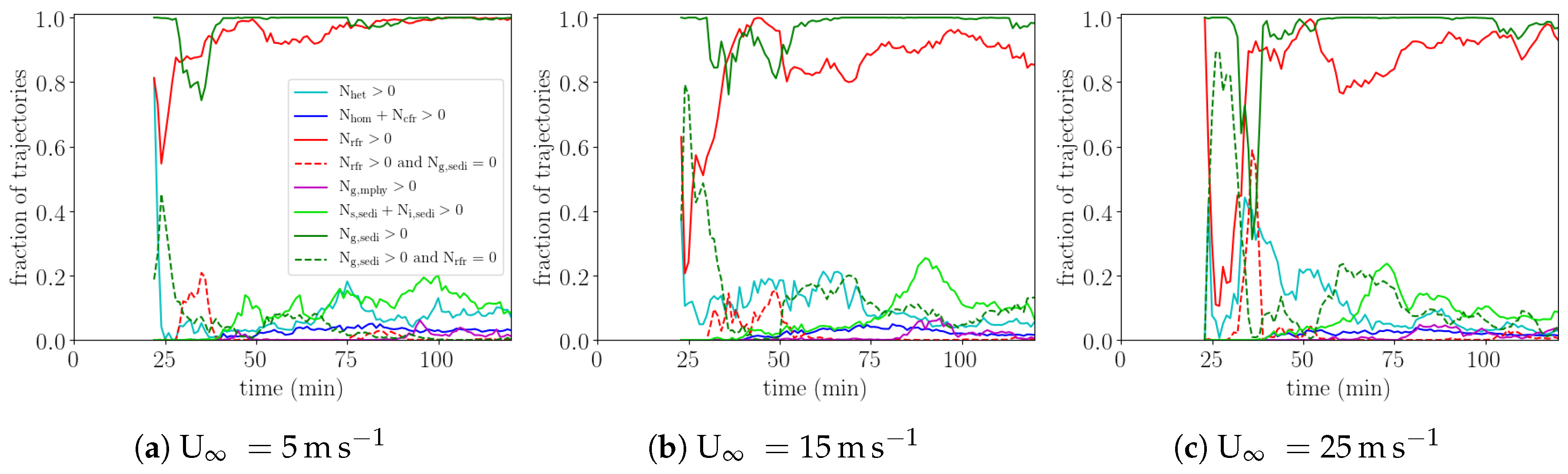
Figure 6d–f). In some trajectories rain freezing occurs prior to the first SIP event, again predominantly in the simulations with larger wind shear. “In-situ” graupel formation from riming or depositional growth is becoming important only after the first SIP event. For investigating the importance of different processes throughout the cloud lifecycle, we consider the fraction of trajectories, in which heterogeneous (cyan) or homogeneous freezing rates (blue) of cloud droplets, influx through sedimentation from higher altitudes (light green: snow and ice, dark green: graupel), or rain freezing rates (red) are larger than 1 × 10
−12 kg s
−1 (
Figure 7). All of the named processes except graupel sedimentation and rain freezing only affect a small fraction of trajectories (<20%). Heterogeneous freezing occurs in less than 20% of the SIP trajectories except for the initial SIP event and for simulations with U
∞ = 25 m s
−1. In the latter in up to 40% of trajectories there is some heterogeneous freezing. Nevertheless SIP from riming ice crystals (
SI Figure S2) and “in-situ” graupel formation through depositional or riming growth (magneta line in
Figure 7) occurs only in less than 1% of trajectories in the first hour of the simulation. “In-situ” graupel formation from deposition and riming occurs in up to 10% of trajectories in the last 40 min of the simulation. Almost all trajectories are affected by sedimentation of graupel particles from higher altitudes. The trajectory fraction with a significant influx of graupel from sedimentation is larger than 80% in the first 10 min after the initial SIP event and increases to almost 100% after roughly the first hour of the simulation. The simulation time, at which graupel sedimentation affects all SIP trajectories increases with the vertical wind shear. Somewhat less frequent, but still relatively common, is the formation of rimers by freezing of rain drops (red line). The fraction of parcels with rain freezing varies between 20% and almost 100% and increases with simulation time. In many parcels both rain freezing and graupel sedimentation occur. The fraction of air parcels, in which only rain freezing or graupel sedimentation play a role are shown by the red and green dashed lines in
Figure 7, respectively. Graupel sedimentation seems to be particularly important in the first 10 min to 20 min after the initial SIP event, while rain freezing is particular important at about 40 min into the simulation. Later in more than 80% of all SIP trajectories both processes occur making it impossible to disentangle from the trajectory data, which is responsible for triggering SIP.
The location of SIP events relative to the position of the updraft cores varies throughout the simulation time and with the vertical wind shear (
Figure 8). Shortly after the initial SIP event, SIP mainly occurs downstream of the updraft core. The distance increases with the vertical wind shear (
Figure 8). This is consistent with the hypothesis that graupel is formed in the high updraft regions and subsequently sediments downstream of the updraft core, where it eventually triggers SIP. The increasing distance between updraft core and SIP region with larger wind shear is expected, and likely is also the reason for the larger importance of rain freezing in simulations with U
∞ of (15, 25) m s
−1. Later in the simulation, the regions with most intense SIP events coincide with strong updrafts, although SIP events continue to occur at the fringes and at greater distance from the updraft cores. At these later stages, graupel is more abundant, but likely is still predominantly formed in the high updraft regions. In the Lagrangian analysis graupel sedimentation dominates even in the high updraft regions, where graupel fall velocities are smaller than the vertical velocity of air. However, in an airstream relative framework, that is, a Lagrangian framework, graupel of course still sediments. As discussed previously, as almost all particles with SIP originate in the boundary layer there is too little time before they reach the Hallett-Mossop temperature zone for “in-situ” graupel formation.
In summary, the Lagrangian analysis of air parcels, in which SIP events occur, suggests that the “in-situ” formation of rimers from primary ice particle formation is negligible but that rain freezing can be an important source of rimers in particular for high wind shear conditions. However, in all considered simulations the sedimentation of graupel from higher levels is the dominant source of rimers. Hence the Lagrangian analysis highlights the importance of considering the three-dimensional cloud evolution over time in order to understand the initiation and occurrence of rime splintering in deep convective clouds. The results from the Lagrangian analysis are consistent with previous more idealised studies and some observational studies of SIP in convective clouds, which suggest that either multiple thermals or the penetration of pre-existing cloud layers are important for the occurrence of rime-splintering (e.g., references [
11,
18,
46]). To corroborate this hypothesis as well as to better understand the role of rain freezing and primary ice formation, it would be interesting to investigate the source of graupel particles. However due to their significant fall speed this is not possible in the current modelling framework. For this purpose, simulations with Lagrangian microphysics would be ideally suited, but such simulations are currently not feasible for the three-dimensional cloud evolution considered here. Instead we resort to conducting sensitivity experiments, in which we either delay the onset of heterogeneous freezing to colder temperature (−10 °C instead of −5 °C) or turn off the parameterisation for rain freezing. While not full addressing the above questions, they at least provide some insight into the role of high-temperature INP and rain freezing for graupel formation and the subsequent triggering of SIP. These simulations are discussed in the following section.
4. Impact of Rain Freezing, INP Concentration, and Heterogeneous Freezing at Warm Temperatures
High-temperature INPs have been hypothesised to be important for the triggering of rime-splintering in convective clouds (e.g., references [
9,
17,
18,
19,
41]). In particular, the freezing of drizzle or rain drops has been suggested to be important as a means to instantly produce graupel-sized frozen particles and thereby rimers for the rime-splintering process (e.g., references [
18,
39,
42]). The Lagrangian analysis in
Section 3 indicates that the “in-situ” formation of graupel is less important than the sedimentation of graupel, although rain freezing plays a certain role in the early stages of the cloud evolution. In order to test the importance of high-temperature INP and rain freezing, we have conducted sensitivity experiments in all three wind shear conditions, in which either heterogeneous freezing occurs only at temperatures colder than −10 °C (T
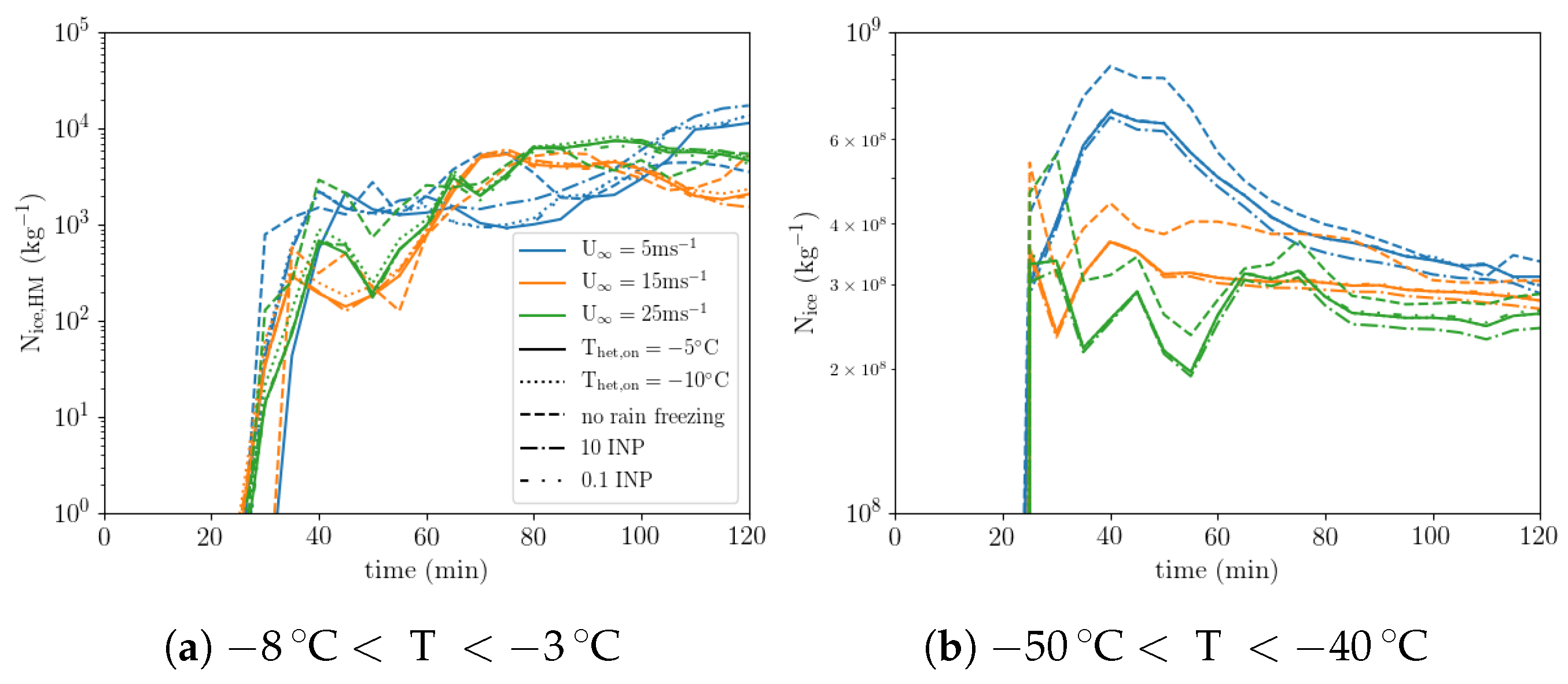
het,on = −10 °C experiment) or there is no freezing of rain drops (“noRF” experiment). Additional sensitivity experiments are conducted with an increased and decreased INP concentration over the entire temperature range (“10 · INP” and “0.1 · INP” experiments, respectively). The time evolution of the mean ice crystal number concentrations (ICNC) from the various sensitivity experiments are shown in
Figure 9. In the Hallett-Mossop temperature zone differences, ICNC is dominated by ice crystals formed by secondary ice production throughout the simulation (not shown) and differences between the sensitivity experiments are generally small (
Figure 9a). The largest deviation from the baseline simualtion is occuring in the simulations without a rain freezing parameterisation in the first simulation hour (up to a factor 2). In the upper troposphere, secondary ice crystals constitute only a tiny fraction of the total ICNC (not shown) and are not directly account for the differences in total ICNC. Using no rain freezing parameterisation has again the largest impact, but this this smaller than the impact of the windshear (
Figure 9b). INP number concentration has also a small impact, as ice crystal concentrations at temperatures below −40 °C are dominated by homogeneously formed ice crystals. ICNC over the full temperature range is shown in
SI Figure S5. Here we focus on the thermodynamic and microphysical history of air parcels, in which SIP occurs, in the different sensitivity experiments. The impact of the altered parameterisation on the intensity of SIP events and the spread of secondary ice crystals through the cloud are discussed in
Section 5.
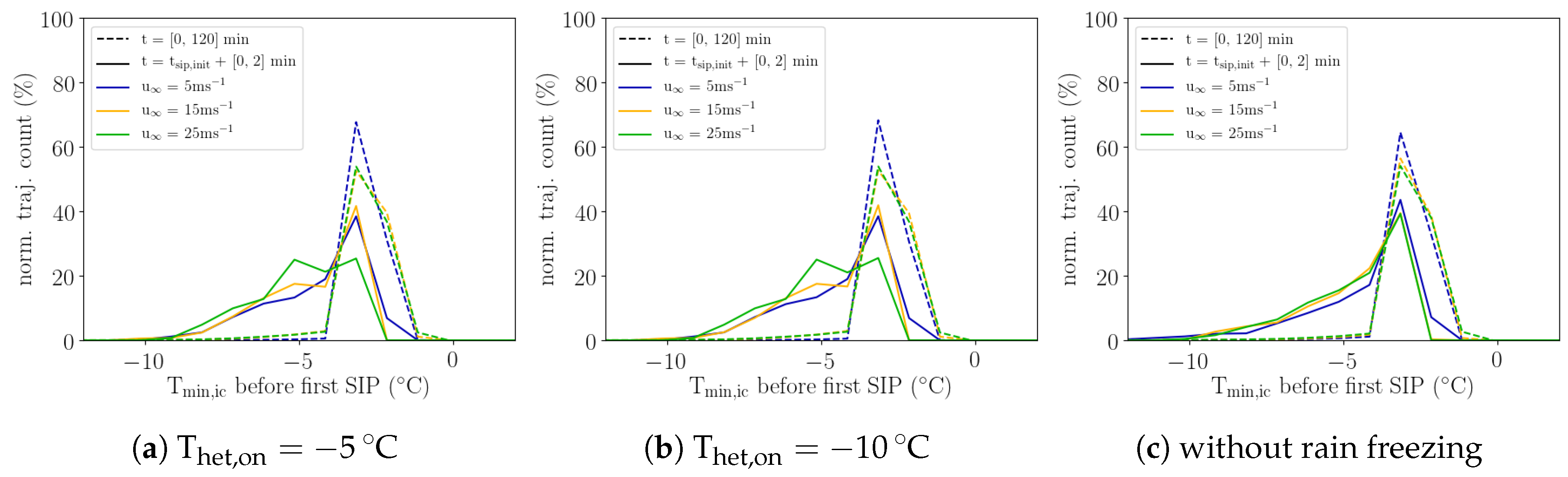
4.1. Impact of High-Temperature INP and INP Concentration
The presence of INP inducing freezing of cloud droplets at temperatures warmer than −10 °C does not have any significant impact on the air parcels, in which SIP occurs. The number of SIP trajectories as well as their thermodynamic and cloud microphysical history is very similar to that of air parcels with SIP in the simulation with T
het,on = −5 °C. For example, the distribution of the minimum temperature T
min,ic in the two simulations is almost identical (
Figure 10a,b). Importantly this does hold not only if the entire simulation is considered but also if only SIP events close to the initial event are considered (solid lines). The timing of the initial SIP event and the altitude evolution of air parcels also do not display major differences (
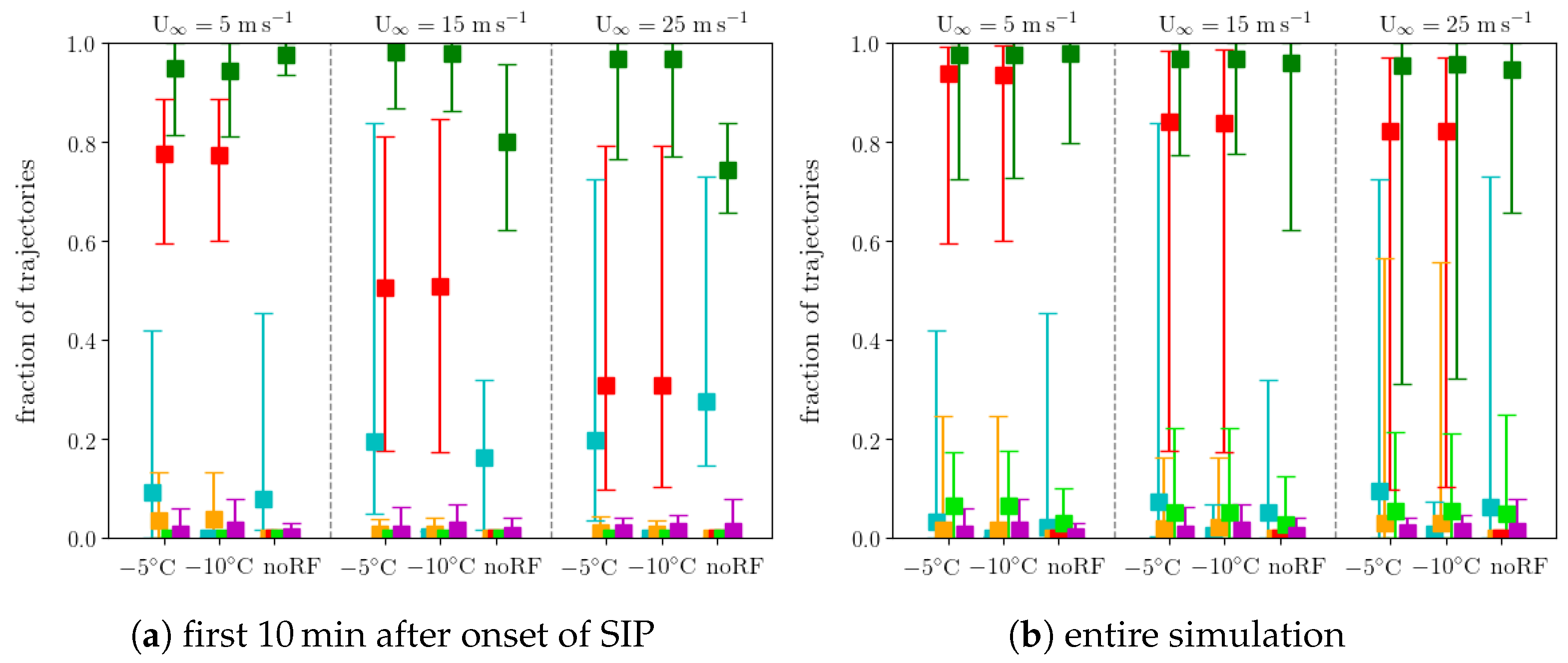
SI Figure S6). Regarding the cloud microphysical history, the fraction of trajectories, for which graupel sedimentation and rime freezing occurs is almost unaltered between the simulation with T
het,on = −5 °C and T
het,on = −10 °C (
Figure 11a,b) again irrespective of the considered time period (not shown). The difference in the fraction of trajectories with heterogeneous freezing is large, but the change in the fraction of trajectories with “in-situ” graupel formation from riming or deposition is almost identical. This is confirmed by the similar composite evolution of cloud microphysical rates (
SI Figures S11 and S12).
Altering the INP concentration by an order of magnitude has only a small impact on the number of SIP trajectories, their thermodynamic or cloud microphysical history prior to the first SIP event (
SI Figures S8–S12). In the 10 · INP scenario, primary ice crystal numbers are somewhat larger at first SIP events in the small number of trajectories, in which heterogeneous freezing occurs before the first SIP event. However, there is no “in-situ” formation of graupel until after the onset of SIP and the difference in rain freezing rates is negligible.
The results further confirm the previous conclusion that “in-situ” growth of primary ice to graupel is irrelevant for the triggering of rime-splintering. This is mostly due to the origin of most SIP trajectories in the warm, below cloud layer and the rapid lifting they undergo between the freezing level and the HM temperature zone. Furthermore, the results suggest that in the model enough graupel forms to efficiently trigger SIP even in the absence of high-temperature INP.
4.2. Impact of Rain Freezing
Not considering rain freezing has a stronger impact on the occurrence of SIP and the air parcels, in which SIP occurs. The number of SIP trajectories decreases by 30% (3%, 7%) in the simulations with U
∞ = 5 m s
−1 (15 m s
−1, 25 m s
−1). However, the initial SIP event in the simulations is only delayed by 1 min to 3 min depending on the vertical wind shear (
SI Figure S7). There are some differences in the thermodynamic and cloud microphysical history of air parcels. These changes are most evident in the 10 min after the initial SIP event. In this time interval, minimum in-cloud temperatures of around −5 °C are less frequent, while minimum temperatures around −10 °C are slightly more frequent (
Figure 10c). Consistently, also larger fraction of trajectories descending from above into the Hallett-Mossop temperature zone compared to the other simulations (
SI Figure S7). By design rain freezing does not occur along any of the trajectories (
Figure 11). Heterogeneous freezing is more abundant in trajectories in particular in the first minutes after the initial SIP event and in higher vertical wind shear. This is consistent with the colder T
min,ic. Interestingly the fraction of trajectories, which are influenced by graupel sedimentation is reduced to a median of around 70% in the first 10 min after the initial SIP event. This suggests that “in-situ” graupel formation due to riming growth and vapour deposition occurs at least in some trajectories. For later stages of the cloud development, the impact of rain freezing on the air parcels, in which SIP occurs, is much smaller and not evident in either the distribution of T
min,ic or the cloud microphysical processes (
Figure 10c and
Figure 11b).
In the “noRF” experiments the SIP regions shift closer to the updraft cores (compare
Figure 8 and
SI Figure S13). Particular in the early stages of the simulation, high SIP rates primarily occur immediately downstream of the updraft core. This is consistent with graupel being formed in the updraft core through riming and falling into lower updraft regions below or downstream.
5. Propagation of Secondary Ice in the Cloud
Once secondary ice crystals have been formed their impact on the cloud system depends on how quickly and how widely they spread. With the extended cloud microphysics scheme (
Section 2.2) and the online trajectories (
Section 2.3) we can explore these questions.
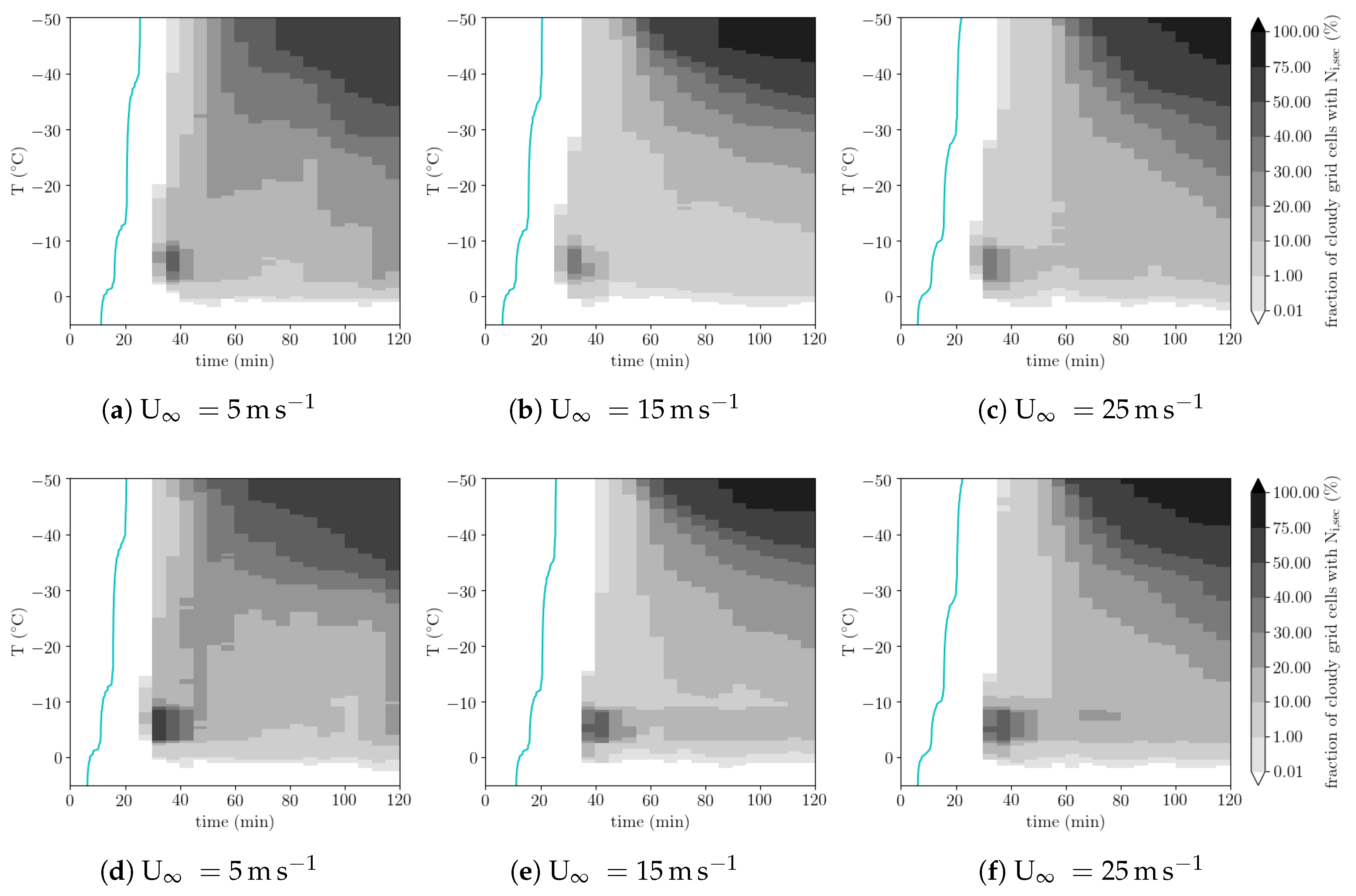
Figure 12a–c shows the fraction of cloudy grid-points, in which the secondary ice crystal number concentration N
i,sec exceeds 0.1 L
−1, as a function of air temperature and simulation time. In all simulations secondary ice appears between 20 min and 30 min after the start of the simulation in the Hallett-Mossop temperature zone, that is between −3 °C and −8 °C. In this temperature region rapidly more than 50% of the cloudy grid points contain secondary ice crystals. After about 15–20 min the fraction of grid boxes in the Hallett-Mossop zone containing secondary ice crystals decreases to below 20%. In the Hallett-Mossop temperature zone secondary ice dominates the total ice crystal number concentrations throughout the simulation (
SI Figure S14). About 45 min into the simulation, secondary ice crystals appear in an increasing number of grid-boxes with very cold temperatures (< −40 °C). After about 70 min more than 50% of the grid-boxes at the coldest temperatures contain secondary ice crystals. However, the average number concentration of secondary ice crystals in cold temperature regions is several orders of magnitude smaller than that of primary ice crystals (
SI Figure S14). Heterogeneous and homogeneous freezing generate enough ice crystals at cold temperatures to dwarf the high ice crystal number concentrations produced in the Hallett-Mossop temperature zone, which is confirmed by the composite evolution of the cloud microphysical rates (
Figure 6a–c). According to these composites already a few minutes after the first SIP event first heterogeneous freezing and then homogenous cloud droplet freezing exceeds the SIP along the majority of trajectories. This is consistent with simulations of realistic deep convective cloud fields by reference [
29] with a different model. At temperatures warmer than −20 °C the average number densities of secondary ice are several orders of magnitudes larger than that of ice crystals formed by other process throughout the simulations (
SI Figure S14).
The overall picture is very similar for simulations with a colder onset temperature of heterogeneous freezing (not shown). In the simulations without rain freezing the overall spatio-temporal spread of secondary ice is also similar. However, the first secondary ice crystals appear slightly later and secondary ice appears slightly earlier in the cold temperature regions of the cloud (
Figure 12d–f). At temperatures colder than −15 °C the total ice crystal number is lower than in the reference simulation, except around 40 min into the simulation where it is larger (
SI Figure S5d–f). The secondary ice crystals are less important in the first 5 min to 15 min after the initial SIP event (several orders of magnitude). But at later times ice enhancement factors from SIP are overall larger (up to an order of magnitude) than in the reference simulation (
SI Figure S14d–f). The sensitivity experiments, in which INP number concentrations have been altered, show a clear impact on total ice number concentration up to 30 min after the start of the simulation (
SI Figure S5g–l). At later times there are mostly only small changes (less than a factor 2). However, in the 10 · INP experiments, there the ice crystal number concentration clearly decreases at around −25 °C for U
∞ = 5 m s
−1. The ratio of secondary to primary ice is reduced for the 10 · INP experiment at temperatures warmer than about −25 °C (up to a factor 10, which is consistent with the expected increase in primary ice crystal numbers). At colder temperatures there is a increase in the ice enhancement factor of up to a factor 2 (
SI Figure S14g–i). Reducing the INP number concentration has only a small impact on the ratio of secondary to primary ice (generally below factor 1.5,
SI Figure S14j–l). Despite the changes in the total number of ice crystals altering the INP number concentration has only a small impact on the number of grid points, in which secondary ice is found (not shown).
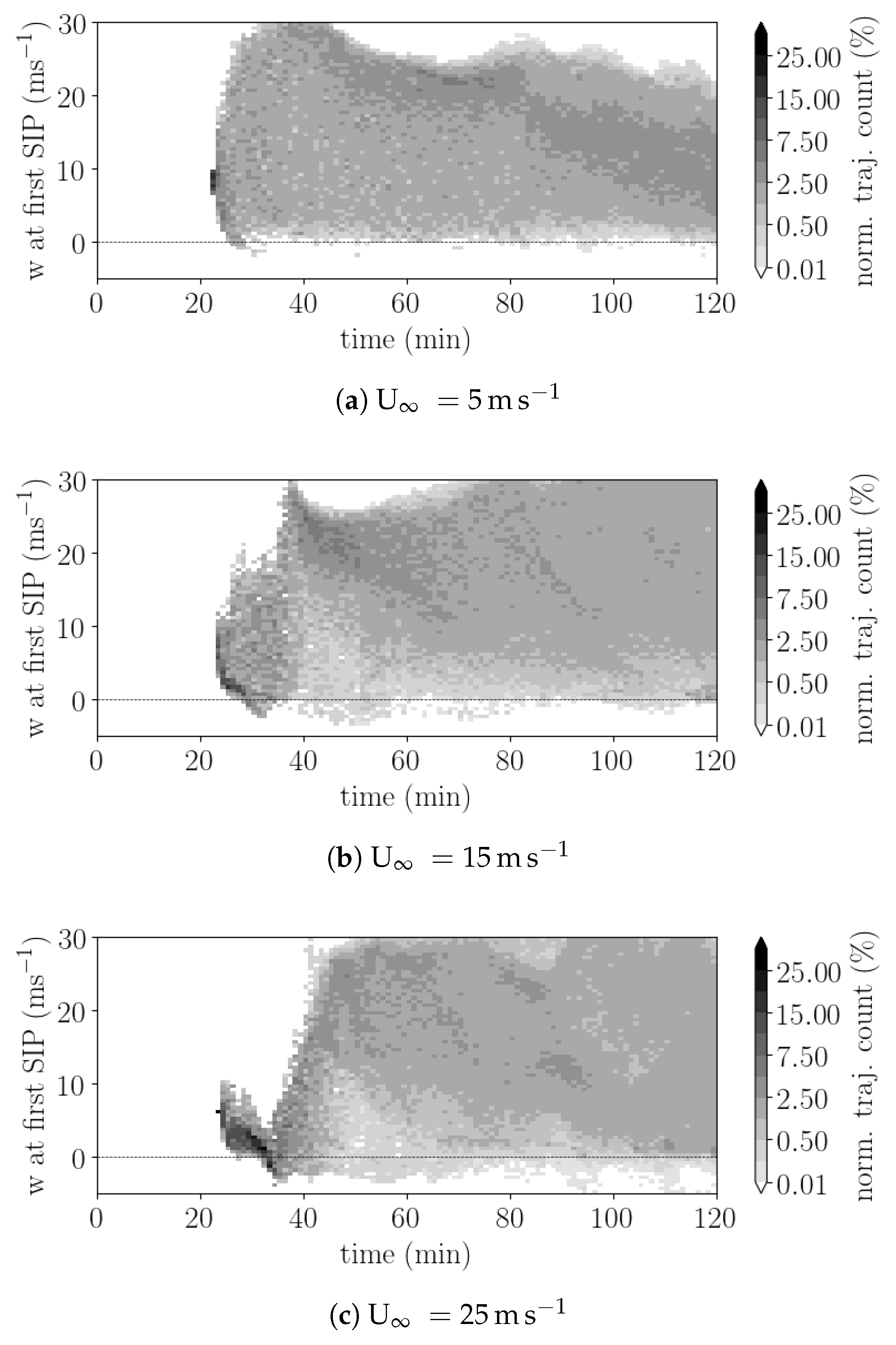
The vertical velocities at the location of SIP events together with the location of SIP events relative to the updraft core is vital to understand the spread of secondary ice through the cloud. The distribution of vertical velocities is shown in
Figure 13. Almost all SIP events occur in regions with positive vertical velocities of up to 30 m s
−1 consistent with the placement of SIP events in or around updraft cores (
Figure 8). In the simulation with the largest vertical wind shear (U
∞ = 25 m s
−1) SIP events occur only at comparatively low updraft speeds (up to 10 m s
−1) until 40 min into the simulation. This is consistent with the relative large distance between SIP events and the updraft core (
Figure 8) and is likely a consequence of the tilt of the updraft core together with significant downstream advection of graupel before sedimenting into the Hallett-Mossop zone. Between 40 min and 50 min there is a rapid shift of SIP events to updraft velocities between 20 m s
−1 and 30 m s
−1, that is, the updraft cores. Around 40 min a large number of trajectories record rain freezing events, which coincides with and may be instrumental for the shift of SIP events to the updraft cores (
Figure 7c). The large vertical velocities, at which SIP events occur, ensure an efficient transport pathways to the cloud top. The transport to the upper tropopause takes less than 7 min for the majority of trajectories (
Figure 3a–c). Accordingly, secondary ice is abundant at outflow levels, while only a much smaller fraction of the cloud contains secondary ice in the mixed-phase region (
Figure 12).
The sensitivity experiments with a lower temperature for the onset of heterogeneous freezing, an altered INP number concentration or without a parameterisation of rain freezing show a very similar general behaviour in terms of the vertical velocity during SIP events (not shown). The only major change in the vertical velocity distributions during SIP events is the occurrence of high updraft velocities up to 30 m s
−1 from the onset of SIP event in the “noRF” experiment with U
∞ = 25 m s
−1. Again this is consistent with the shift of the SIP events closer to the updraft core in this simulation (
SI Figure S13).
6. Conclusions
Idealised simulations based on the Weisman and Klemp [
33] case are used to investigate the initiation of secondary ice production (SIP) via rime-splintering and the spread of secondary ice crystals through the cloud system. The thermodynamic and cloud microphysical evolution of air parcels prior to rime-splintering events is considered by using trajectory data at very high time resolution. It is demonstrated that the online-trajectories, which are computed at the physical time step of the ICON model simulation, successfully capture the rapid vertical motions in intense deep convective clouds and provide sufficient data-points to allow for a meaningful analysis of cloud microphysical processes.
The Lagrangian analysis shows that almost all air parcels, in which SIP occurs, originate in the below cloud layer and ascend prior to SIP events. Accordingly, the air parcel temperatures remain close to 0 °C before air parcels enter the Hallett-Mossop temperature zone, in which rime-splintering occurs. Consistent with the thermodynamic history, heterogeneous freezing of cloud droplets occurs only in less than 1% of air parcels prior to SIP events. The dominant source of graupel, which acts as rimer, is from sedimentation from higher levels and some contribution from freezing of rain drops. As both processes often occur simultaneously it is impossible to disentangle the relative importance of the two processes from the trajectory data alone. Sensitivity experiments, in which the rain freezing parameterisation is not used, suggest, however, the general spatio-temporal distribution of SIP events and the spread of secondary ice through the cloud is not strongly impacted by rain freezing. Nevertheless, rain freezing is more important than the presence of high-temperature INPs for the exact location and timing of SIP events. Previous studies have already suggested that rain freezing is a potentially important source of rimer particles (e.g., references [
18,
39,
42]). While our simulations also suggest rain freezing to be relevant, graupel formation through riming in the updraft core and subsequent sedimentation is clearly more important and seems to be able to produce rimers within about 25 min after the initiation of the cloud. The very efficient formation of graupel is likely dependent on the cloud top temperature and large vertical velocity in the deep convective clouds here. Graupel formation in more shallow cumulus clouds, for which most observational evidence of rime-splintering is available, may be less important and hence in those clouds heterogeneous freezing or rain freezing may be important. Based on our results the importance of warm temperature INP and “in-situ” graupel formation will dependent critically on the air parcel history. If this is found to be similar to what is found in the deep convective clouds investigated here, limits the contribution of “in-situ” graupel formation. It would be very interesting to further explore the formation conditions and the pathway of graupel to the Hallett-Mossop temperature zone. Unfortunately, this is not possible with the current modelling system and available trajectory data due to the significant fall velocities of graupel. However, other Lagrangian frameworks (Lagrangian microphysics schemes) currently in development will allow for an analysis of the graupel pathways in future (e.g., reference [
47]). A recent study has demonstrated the feasibility of such a framework for investigating deep convective cloud microphysics [
48]. Here, we use instead sensitivity experiments without rain freezing and a colder onset temperature for heterogeneous freezing to shed some light on the sensitivity of graupel formation and sedimentation to high-temperature INP and rain freezing. As mentioned previously high-temperature INP seem to have no impact on the supply of graupel to the Hallett-Mossop temperature zone, while rain freezing results in graupel being present slightly earlier (1 to 3 min) and in regions more distant from the updraft cores. While improved parameterisation of heterogeneous freezing of cloud droplets have become available in the last decade and are used in numerical weather prediction models, better constrained rain freezing parameterisations, in particular also including INP information, would be highly desirable.
The Lagrangian data together with an extended ice microphysics scheme, that separately treats populations of ice crystals formed by different cloud microphysical processes, provides information of the spread of secondary ice through the cloud system. The trajectory data shows that secondary ice is rapidly transported from the Hallett-Mossop temperature zone to the cloud top region with transport typically taking around 5 min. In the roughly 15 min after the initial SIP events (of the entire simulation), this transport is less efficient and hence secondary ice is mainly present within the Hallett-Mossop temperature zone itself. In this stage SIP events occur mainly downstream of updraft cores, where graupel formed in the updraft core is likely sedimenting. Later SIP events increasingly shift closer to the updraft cores as riming growth gets more efficient. This coincides with the onset of efficient vertical transport of secondary ice crystals. While this shift in SIP locations is evident for all investigated vertical wind shear conditions, it is most pronounced in the highest wind shear case (U
∞ = 25 m s
−1. After roughly 1 h secondary ice crystals are present in more than 50% of cloudy grid-points close to cloud top (temperatures colder than −40 °C) with an further increasing tendency for longer simulation times. In the mixed phase region, only about 10% to 20% of cloudy grid points contain secondary ice crystals. Except for the early phases of the cloud development (20–45 min into the simulation) this also hold for the Hallett-Mossop temperature zone. Despite the widespread presence of secondary ice in the upper parts of the clouds, the average number concentration (over grid boxes containing secondary ice) is several orders of magnitude smaller than that of primary ice crystals for temperatures colder than about −20 °C. This is consistent with other studies investigating the impact of rime-splintering on the cloud microphysical structure of clouds in more realistic cases (e.g., reference [
29]). However, at warmer temperatures secondary ice crystal number concentration exceeds that of primary ice crystals by up to 4 orders of magnitude, albeit only in a relatively small area of the cloud.
It is important to note that the representation of ice- and mixed-phase cloud processes in numerical weather prediction models is subject to large uncertainties in the parameterisation formulation. The importance of different ice formation pathways depends of course also on the chosen parameterisations. For example, Hawker et al. [
29] show that the impact of secondary ice on the glaciation behaviour and the cloud microphysical properties of the anvil depends on the temperature dependence in the heterogeneous freezing parameterisation. While exploring the sensitivity to various parameterisation schemes is beyond the scope of this study, a systematic investigation of parametric and systematic uncertainty in the model formulation would be very worthwhile. However, there is also substantial uncertainty in representing rime-splintering: The number and size of secondary ice crystals generated per event is highly uncertain and not all observed characteristic of rime-splintering for example regarding necessary properties of the cloud droplet size distribution (e.g., references [
49,
50,
51]) or the surface temperature of graupel (e.g., reference [
52]) can be mirrored in bulk microphyscis schemes (as used here). Previous studies have shown that these details in the formulation of the parameterisation have a non-negligible impact on the modelled cloud properties (e.g., references [
10,
39,
53]). Further a number of other SIP mechanisms have been proposed for which there is some evidence from observational studies (e.g., reference [
13]) but which have not been considered in the present study. Testing the full parameteric and systematic uncertainty of ice formation in numerical weather prediction models and its impact on cloud glaciation as well as macroscopic cloud properties is beyond the scope of the present study, but should be investigated in future studies. In light of these large uncertainties, there is an evident need to test the conclusions of our study with observational data. Most observational evidence for SIP to date comes from marine cumulus convection or convection embedded in frontal cloud systems (e.g., reference [
9], and reference therein). In contrast, here deep convective systems have been considered. As vertical velocities and condensed water content in deep convective systems are much larger than in more shallow convection, differences in the importance of graupel are very likely. Also, the observational evidence mostly comes from clouds with fairly warm cloud top temperatures (>−15 °C), which implies much smaller ice production by heterogeneous and homogeneous freezing of cloud droplets. It is therefore anticipated, that high temperature INP and the rain freezing are more important in these clouds compared to the deep convective system with very cold cloud top temperature considered here. The Lagrangian analysis has clearly illustrated that it is important to consider the three-dimensional transport and sedimentation of hydrometeors for understanding SIP. The transport and sedimentation patterns will be significantly different in less vigourous cloud systems, but may not be less important. Another aspect, which has not been investigated here, is the impact of the aerosol environment. Previous studies have shown that the impact of secondary ice production on the cloud proproperties depends on the abundance of cloud condensation nuclei and ice nucleating particles (e.g., references [
27,
39,
54,
55]). Our sensitivity experiments on the number of INP did shown no significant impact on the initiation of SIP or the distribution of secondary ice throughout the cloud, although in the scenarios the ice enhancement factor through SIP is smaller at temperature larger than required for homogeneous freezing. In addition, the interaction between different clouds can impact the SIP in realistic cloud fields (e.g., reference [
11]). Future studies, ideally combined with field observations, should systematically investigate these issues and thereby contribute to a more complete picture of the importance of SIP for cloud properties and evolution.
However, despite the constraints of the present study, the Lagrangian analysis provides interesting insight into the processes controlling SIP in the model and provides a link to previous parcel model studies. Our analysis clearly highlighted the importance of considering the complex vertical coupling of cloud microphysical processes in deep convective clouds, which has implications for interpreting observational and modelling data and for the anticipated sensitivity of SIP to high-temperature INPs.