Parameterization of Radiation Fog-Top Height and Methods Evaluation in Tianjin
Abstract
1. Introduction
2. Data and Methods
2.1. Experiment Site and Data
2.2. Calculation Methods
3. Results and Discussions
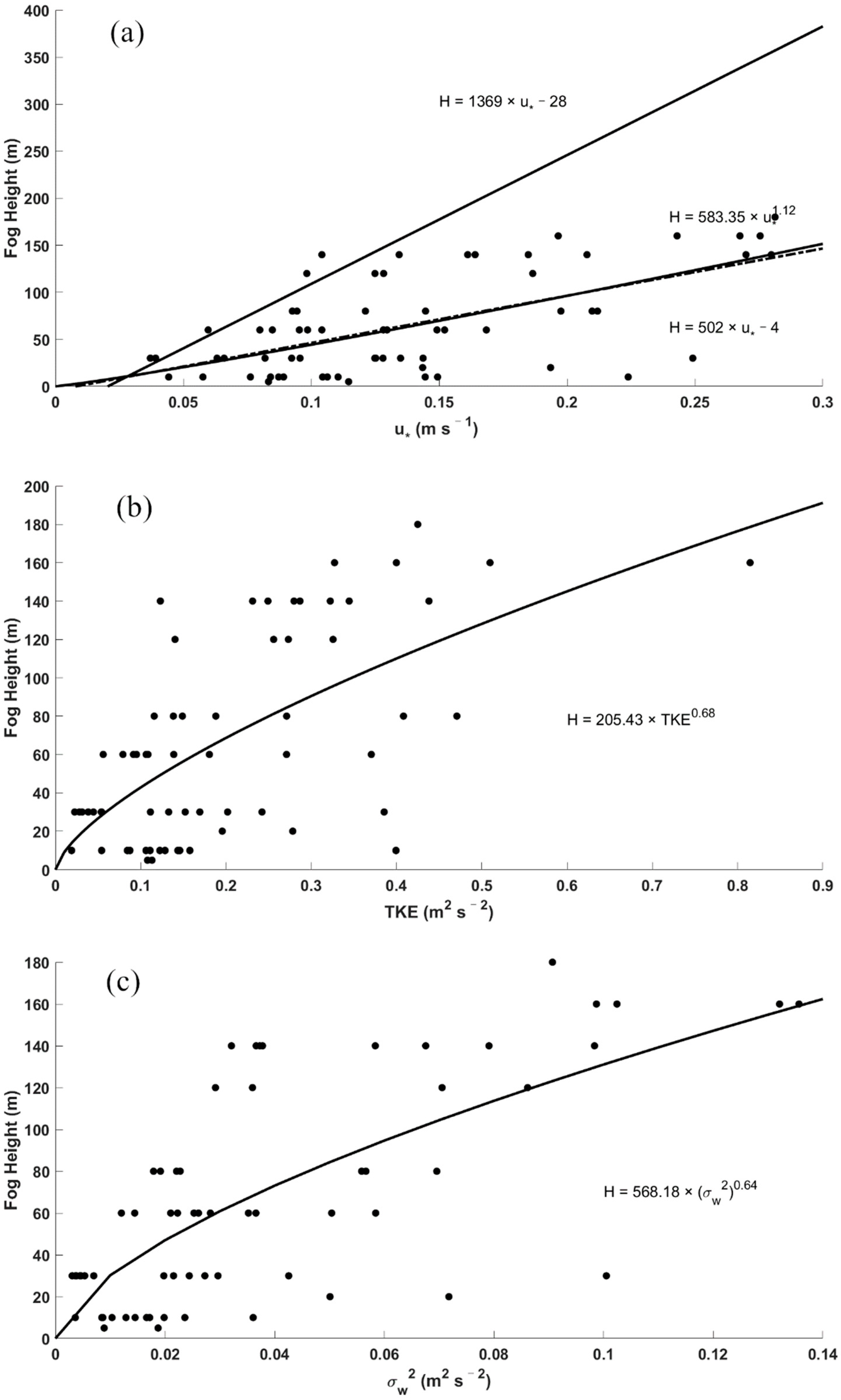
3.1. Fog-Top Height Estimations Using Turbulence Intensity
3.2. Fog-Top Height Estimations using Radiative Cooling
3.3. Fog-Top Height Estimations Using Turbulence and Radiative Cooling
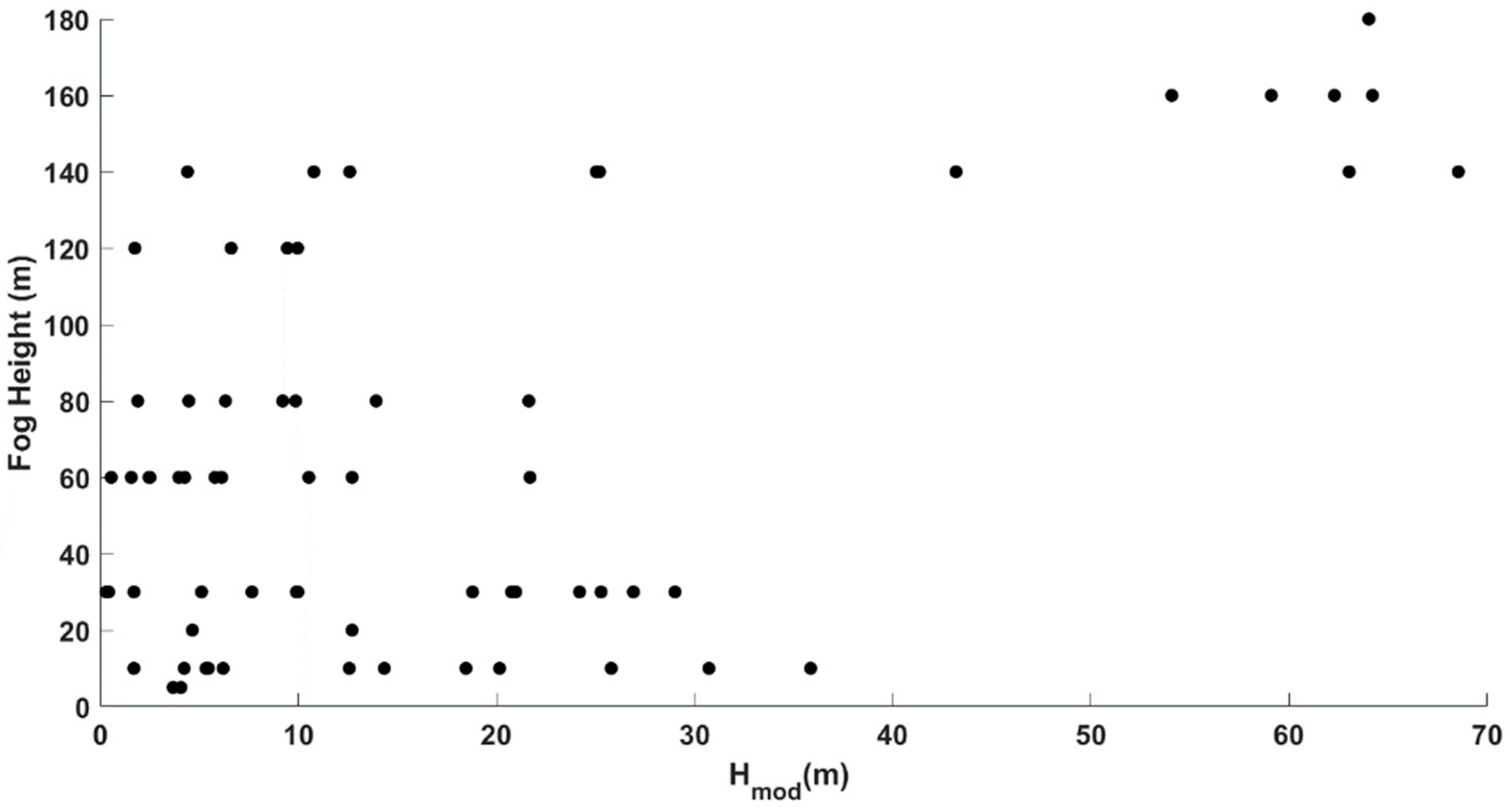
3.4. Fog-Top Height Estimation through Temperature Convergence (TC Method)
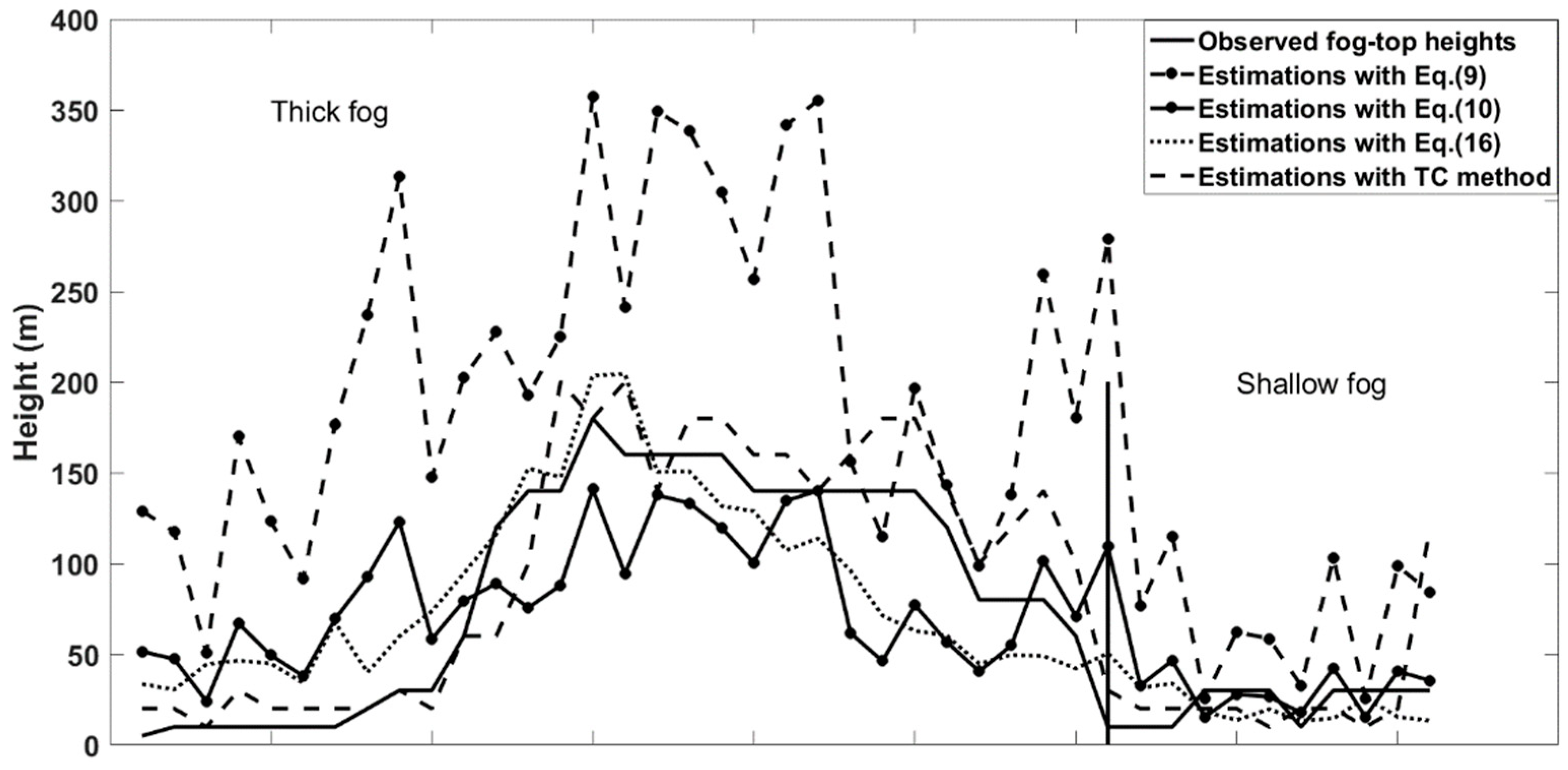
3.5. Comparisons of Fog-Top Height Estimations with Different Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- WMO. International Meteorological Vocabulary; WMO: Geneva, Switzerland, 1992; pp. 1–276. [Google Scholar]
- Bartok, J.; Bott, A.; Gera, M. Fog prediction for road traffic safety in a coastal desert region. Bound. Layer Meteorol. 2012, 145, 485–506. [Google Scholar] [CrossRef]
- Huang, H.B.; Chen, C.Y. Climatological aspects of dense fog at Urumqi Diwopu International Airport and its impacts on flight on-time performance. Nat. Hazards 2016, 81, 1091–1106. [Google Scholar] [CrossRef]
- Gautam, R.; Singh, M.K. Urban heat island over Delhi punches holes in widespread fog in the Indo-Gangetic Plains. Geophys. Res. Lett. 2018, 45, 1114–1121. [Google Scholar] [CrossRef]
- Kim, H.J.; Collier, S.; Ge, X.L.; Xu, J.Z.; Sun, Y.L.; Jiang, W.Q.; Wang, Y.L.; Herckes, P.; Zhang, Q. Chemical processing of water-soluble species and formation of secondary organic aerosol in fogs. Atmos. Environ. 2019, 200, 158–166. [Google Scholar] [CrossRef]
- Fabbian, D.; de Dear, R.; Lellyett, S. Application of artificial neural network forecasts to predict fog at Canberra International Airport. Weather Forecast. 2007, 22, 372–381. [Google Scholar] [CrossRef]
- Stolaki, S.; Pytharoulis, I.; Karacostas, T. A study of fog characteristics using a coupled WRF–COBEL model over Thessaloniki airport, Greece. Pure Appl. Geophys. 2012, 169, 961–981. [Google Scholar] [CrossRef]
- Jia, X.C.; Quan, J.N.; Zheng, Z.Y.; Liu, X.G.; Liu, Q.; He, H.; Liu, Y.G. Impacts of anthropogenic aerosols on fog in North China Plain. J Geophys. Res. Atmos. 2019, 124, 252–265. [Google Scholar] [CrossRef]
- Liu, C.W.; Gao, Z.Q.; Li, Y.B.; Gao, C.Y.; Su, Z.B.; Zhang, X.Y. Surface Energy Budget Observed for Winter Wheat in the North China Plain During a Fog—Haze Event. Bound. Layer Meteorol. 2019, 170, 489–505. [Google Scholar] [CrossRef]
- Rémy, S.; Bergot, T. Assessing the impact of observations on a local numerical fog prediction system. Q. J. R. Meteorol. Soc. 2009, 135, 1248–1265. [Google Scholar] [CrossRef]
- Cuxart, J.; Jiménez, M.A. Deep radiation fog in a wide closed valley: Study by numerical modeling and remote sensing. Pure Appl. Geophys. 2012, 169, 911–926. [Google Scholar] [CrossRef]
- Bergot, T. Large-eddy simulation study of the dissipation of radiation fog. Q. J. R. Meteorol. Soc. 2016, 142, 1029–1040. [Google Scholar] [CrossRef]
- Maalick, Z.; Kühn, T.; Korhonen, H.; Kokkola, H.; Laaksonen, A.; Romakkaniemi, S. Effect of aerosol concentration and absorbing aerosol on the radiation fog life cycle. Atmos. Environ. 2016, 133, 26–33. [Google Scholar] [CrossRef]
- Zhou, B.B.; Du, J.; Gultepe, I.; Dimego, G. Forecast of low visibility and fog from NCEP: Status and efforts. Pure Appl. Geophys. 2012, 169, 895–909. [Google Scholar] [CrossRef]
- Stolaki, S.; Haeffelin, M.; Lac, C.; Dupont, J.C.; Elias, T.; Masson, V. Influence of aerosols on the life cycle of a radiation fog event. A numerical and observational study. Atmos. Res. 2015, 151, 146–161. [Google Scholar] [CrossRef]
- Heo, K.Y.; Ha, K.J.; Mahrt, L.; Shim, J.S. Comparison of advection and steam fogs: From direct observation over the sea. Atmos. Res. 2010, 98, 426–437. [Google Scholar] [CrossRef]
- Boers, R.; Baltink, H.K.; Hemink, H.J.; Bosveld, F.C.; Moerman, M. Ground-based observations and modeling of the visibility and radar reflectivity in a radiation fog layer. J. Atmos. Ocean. Tech. 2013, 30, 288–300. [Google Scholar] [CrossRef]
- Liu, D.Y.; Yang, J.; Niu, S.J.; Li, Z.H. On the evolution and structure of a radiation fog event in Nanjing. Adv. Atmos. Sci. 2011, 28, 223–237. [Google Scholar] [CrossRef]
- Bergot, T. Small-scale structure of radiation fog: A large-eddy simulation study. Q. J. R. Meteorol. Soc. 2013, 193, 1099–1112. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Han, S.Q.; Wu, B.G.; Huang, H.; Yao, Q. Analysis on Characteristics of Atmospheric Boundary Layer During a Fog Process in Tianjin. Meteorol. Mon. 2012, 38, 1103–1109, (In Chinese with English Abstract). [Google Scholar]
- Sorli, B.; Pascal-Delannoy, F.; Giani, A.; Foucaran, A.; Boyer, A. Fast humidity sensor for high range 80–95% RH. Sensor. Actuat. A: Phys. 2002, 100, 24–31. [Google Scholar] [CrossRef]
- Huang, H.J.; Liu, H.N.; Huang, J.; Mao, W.K.; Bi, X.Y. Atmospheric boundary layer structure and turbulence during sea fog on the southern China coast. Mon. Weather Rev. 2015, 143, 1907–1923. [Google Scholar] [CrossRef]
- Guo, J.T.; Li, P.Y.; Fu, G.; Zhang, W.; Gao, S.H.; Zhang, S.P. The structure and formation mechanism of a sea fog event over the Yellow Sea. J. Ocean Univ. China 2015, 14, 27–37. [Google Scholar] [CrossRef]
- Li, Z.H.; Liu, D.Y.; Yan, W.L.; Wang, H.B.; Zhu, C.Y.; Zhu, Y.Y.; Zu, F. Dense fog burst reinforcement over Eastern China: A review. Atmos. Res. 2019, 230, 104639. [Google Scholar] [CrossRef]
- Dabas, A.; Remy, S.; Bergot, T. Use of a sodar to improve the forecast of fogs and low clouds on airports. Pure Appl. Geophys. 2012, 169, 769–781. [Google Scholar] [CrossRef]
- Wu, D.; Lu, B.; Zhang, T.C.; Yan, F.Q. A method of detecting sea fogs using CALIOP data and its application to improve MODIS-based sea fog detection. J. Quant. Spectrosc. Ra. 2015, 153, 88–94. [Google Scholar] [CrossRef]
- Van der Velde, I.R.; Steeneveld, G.J.; Wichers Schreur, B.G.J.; Holtslag, A.A.M. Modeling and forecasting the onset and duration of severe radiation fog under frost conditions. Mon. Weather Rev. 2010, 138, 4237–4253. [Google Scholar] [CrossRef]
- Marchand, R.; Ackerman, T.; Smyth, M.; Rossow, W.B. A review of cloud top height and optical depth histograms from MISR, ISCCP, and MODIS. J. Geophys. Res. Atmos. 2010, 115, D16206. [Google Scholar] [CrossRef]
- Yi, L.; Zhang, S.P.; Thies, B.; Shi, X.M.; Trachte, K.; Bendix, J. Spatio-temporal detection of fog and low stratus top heights over the Yellow Sea with geostationary satellite data as a precondition for ground fog detection—A feasibility study. Atmos. Res. 2015, 151, 212–223. [Google Scholar] [CrossRef]
- Liu, Y.H.; Key, J.R. Detection and analysis of clear-sky, low-level atmospheric temperature inversions with MODIS. J. Atmos. Ocean. Tech. 2003, 20, 1727–1737. [Google Scholar] [CrossRef]
- Cermak, J.; Bendix, J. Detecting ground fog from space—A microphysics—Based approach. Int. J. Remote Sens. 2011, 32, 3345–3371. [Google Scholar] [CrossRef]
- Cermak, J.; Bendix, J. A novel approach to fog/low stratus detection using Meteosat 8 data. Atmos. Res. 2008, 87, 279–292. [Google Scholar] [CrossRef]
- Román-Cascón, C.; Yagüe, C.; Steeneveld, G.J.; Sastre, M.; Arrillaga, J.A.; Maqueda, G. Estimating fog-top height through near-surface micrometeorological measurements. Atmos. Res. 2016, 170, 76–86. [Google Scholar] [CrossRef][Green Version]
- Quan, J.N.; Zhang, Q.; He, H.; Liu, J.; Huang, M.Y.; Jin, H. Analysis of the formation of fog and haze in North China Plain (NCP). Atmos. Chem. Phys. 2011, 11, 8205–8214. [Google Scholar] [CrossRef]
- Han, S.Q.; Cai, Z.Y.; Zhang, Y.F.; Wang, J.; Yao, Q.; Li, P.Y.; Li, X.J. Long-term trends in fog and boundary layer characteristics in Tianjin, China. Particuology 2015, 20, 61–68. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local climate zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Tech. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Oncley, S.P.; Stage, S.A. Sonic anemometer tilt correction algorithms. Bound. Layer Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Clement, R.; Malhi, Y.; Leuning, R.; Cleugh, H.A. A re-evaluation of long-term flux measurement techniques part I: Averaging and coordinate rotation. Bound. Layer Meteorol. 2003, 107, 1–48. [Google Scholar] [CrossRef]
- Ye, X.X.; Wu, B.G.; Zhang, H.S. The turbulent structure and transport in fog layers observed over the Tianjin area. Atmos. Res. 2015, 153, 217–234. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.S.; Wei, W.; Wu, B.G.; Liu, J.L.; Cai, X.H.; Song, Y. Comparison of the turbulence structure during light and heavy haze pollution episodes. Atmos. Res. 2019, 230, 104645. [Google Scholar] [CrossRef]
- Duynkerke, P.G. Radiation fog: A comparison of model simulation with detailed observations. Mon. Weather Rev. 1991, 119, 324–341. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 1971, 28, 181–189. [Google Scholar] [CrossRef]
- Dyer, A.J. A review of flux-profile relationships. Bound. Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Brown, R.; Roach, W.T. The physics of radiation fog: II—A numerical study. Q. J. R. Meteorol. Soc. 1976, 102, 335–354. [Google Scholar] [CrossRef]
- Zhou, B.B.; Ferrier, B.S. Asymptotic Analysis of Equilibrium in Radiation Fog. J. Appl. Meteorol. Clim. 2008, 47, 1704–1722. [Google Scholar] [CrossRef]
- Ding, Y.H.; Liu, Y.J. Analysis of long-term variations of fog and haze in China in recent 50 years and their relations with atmospheric humidity. Sci. China Earth Sci. 2014, 57, 36–46. [Google Scholar] [CrossRef]
- Doyle, M.; Dorling, S. Visibility trends in the UK 1950–1997. Atmos. Environ. 2002, 36, 3161–3172. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Van Oldenborgh, G.J. Decline of fog, mist, and haze in Europe over the past 30 years. Nat. Geosci. 2009, 2, 115. [Google Scholar] [CrossRef]
- Liu, D.Y.; Niu, S.J.; Yang, J.; Zhao, L.J.; Lü, J.J.; Lu, C.S. Summary of a 4-year fog field study in northern Nanjing, Part 1: Fog boundary layer. Pure Appl. Geophys. 2012, 169, 809–819. [Google Scholar] [CrossRef]
- Price, J.D. On the Formation and Development of Radiation Fog: An Observational Study. Bound. Layer Meteorol. 2019, 1–31. [Google Scholar] [CrossRef]
- Price, J. Radiation fog. Part I: Observations of stability and drop size distributions. Bound. Layer Meteorol. 2011, 139, 167–191. [Google Scholar] [CrossRef]
- Bari, D.; Bergot, T.; El Khlifi, M. Numerical study of a coastal fog event over Casablanca, Morocco. Q. J. R. Meteorol. Soc. 2015, 141, 1894–1905. [Google Scholar] [CrossRef]




| Instrument | Mounting Height | Measurements | Sampling Interval | Accuracy |
|---|---|---|---|---|
| Cup and vane anemometer (Changchun, China) | 15 levels a | Wind speed Wind direction | 20 s | 0.1 m s−1 |
| Temperature and relative humidity probe (HMP45C, CAMPBELL, USA) | 15 levels a | Temperature Relative humidity | 20 s | T: ±0.2 °C RH: ±2% (0–90%) ±5% (90–100%) |
| Sonic anemometer-thermometer (CSAT3, CAMPBELL, USA) | 40, 120, 20 m | Three-dimensional (3D) wind components Sonic virtual temperature | 0.1 s | u, v: < ± 0.04 m s−1 w: < ± 0.02 m s−1 Tθ: 0.01 °C |
| CO2/H2O Analyzer (LI-7500, LI-COR, USA) | 40, 120, 220 m | Water vapor density CO2 concentration | 0.1 s | H2O: 0.0047 mmol/mol CO2: 0.11 ppm |
| Visibility sensor (Model 6000, Belfort, USA) | 2 m | Visibility | 1 min | ± 10% (5 m–10 km) ± 20% (10 m–20 km) |
| Net radiometer (CNR4, Kipp & Zonen, Netherlands) | 40, 120, 220 m | Downward/upward short-wave and long-wave radiation | <18 s | Short-wave: ± 5% long-wave: ± 10% |
| Physical Mechanism | Parameterization Scheme | Coefficient of Determination (R2) |
|---|---|---|
| Turbulent mixing | 0.41 | |
| H = 205.43 | 0.44 | |
| H = 420.10 | 0.53 | |
| Radiative cooling | 0.40 | |
| 0.44 | ||
| Turbulent mixing and radiative cooling | H = 1.45+ 35 | 0.26 |
| H = 396.26(σw + 0.1 w*) − 16 | 0.55 | |
| Temperature convergence | < 1 | 0.61 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, T.; Wu, B.; Zhang, H.; Liu, J. Parameterization of Radiation Fog-Top Height and Methods Evaluation in Tianjin. Atmosphere 2020, 11, 480. https://doi.org/10.3390/atmos11050480
Ju T, Wu B, Zhang H, Liu J. Parameterization of Radiation Fog-Top Height and Methods Evaluation in Tianjin. Atmosphere. 2020; 11(5):480. https://doi.org/10.3390/atmos11050480
Chicago/Turabian StyleJu, Tingting, Bingui Wu, Hongsheng Zhang, and Jingle Liu. 2020. "Parameterization of Radiation Fog-Top Height and Methods Evaluation in Tianjin" Atmosphere 11, no. 5: 480. https://doi.org/10.3390/atmos11050480
APA StyleJu, T., Wu, B., Zhang, H., & Liu, J. (2020). Parameterization of Radiation Fog-Top Height and Methods Evaluation in Tianjin. Atmosphere, 11(5), 480. https://doi.org/10.3390/atmos11050480




