Measurement and Prediction of Wind Fields at an Offshore Site by Scanning Doppler LiDAR and WRF
Abstract
1. Introduction
2. Measurement and Prediction Methods
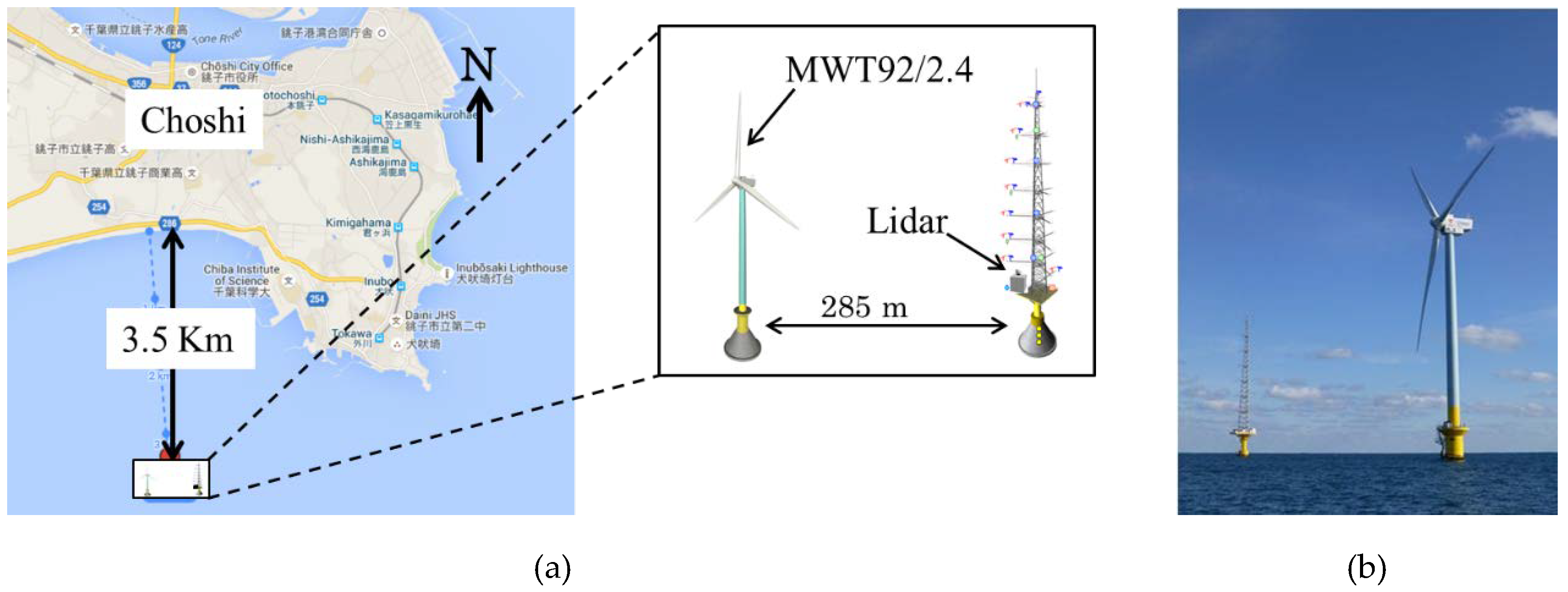
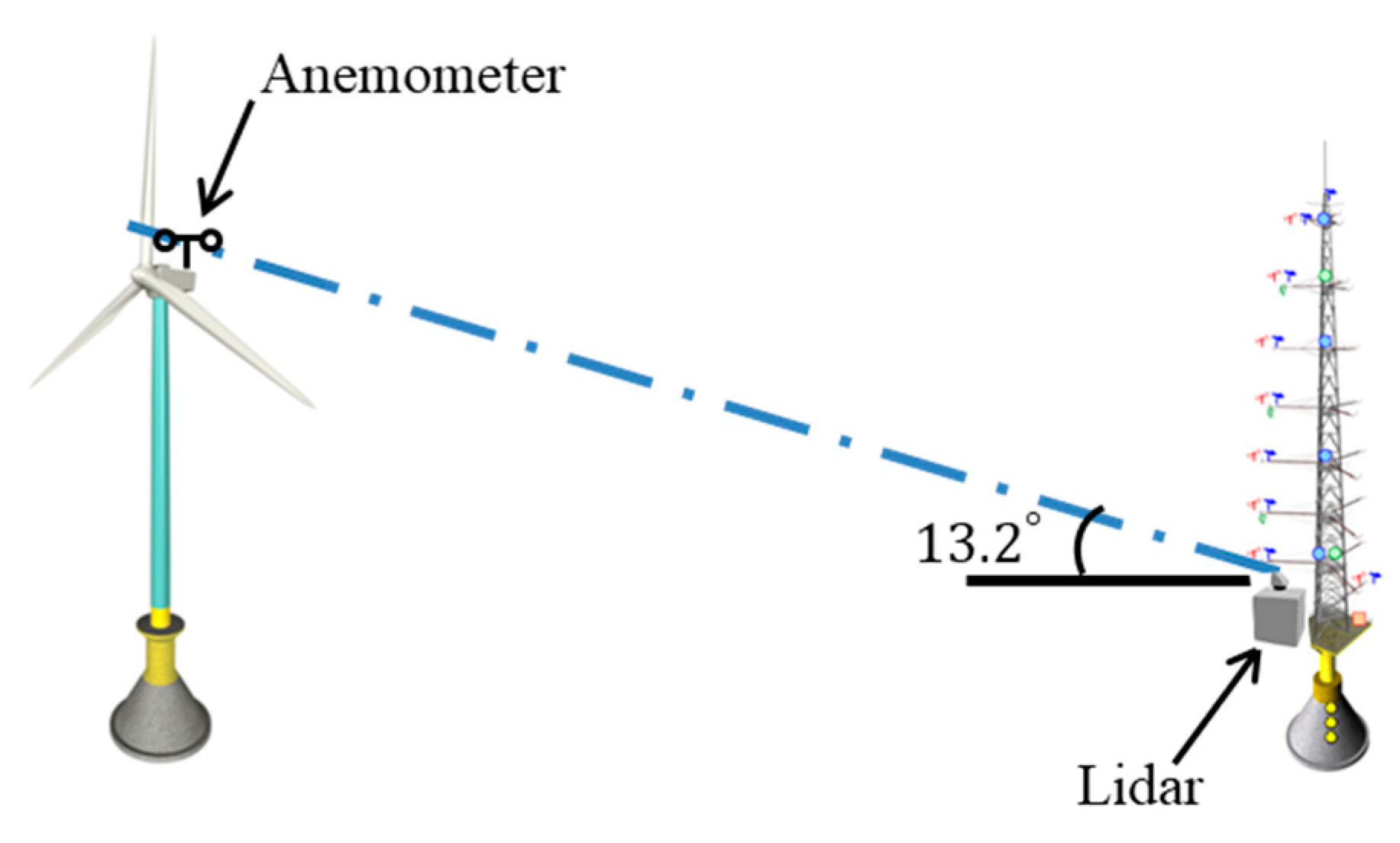
2.1. Test Site for Wind Field Measurement and Prediction
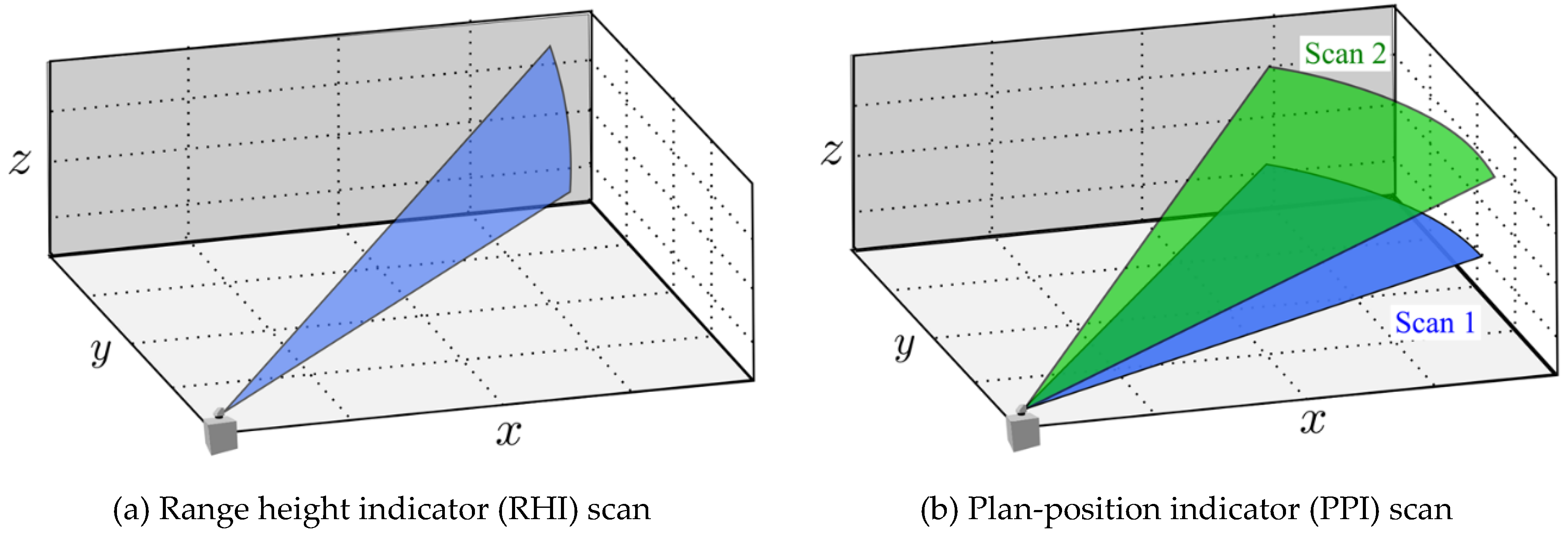
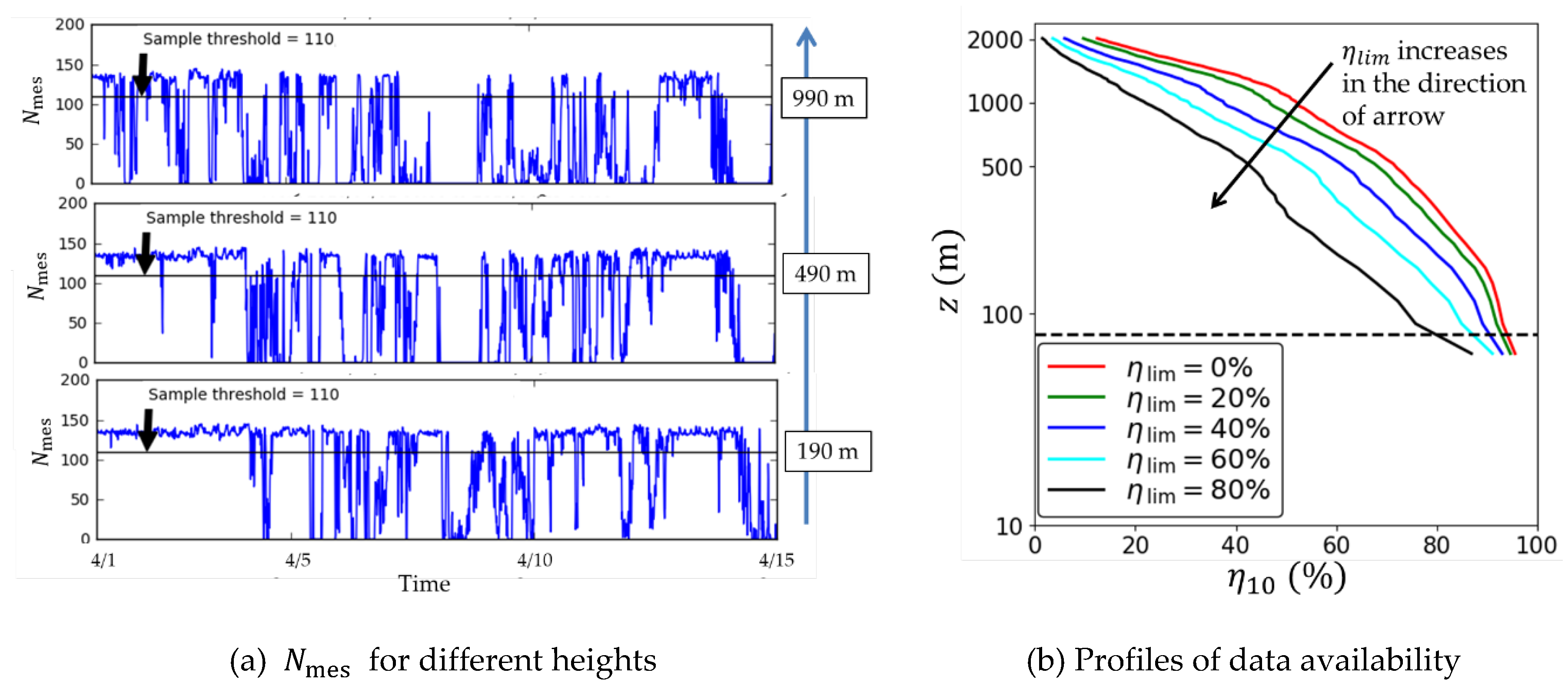
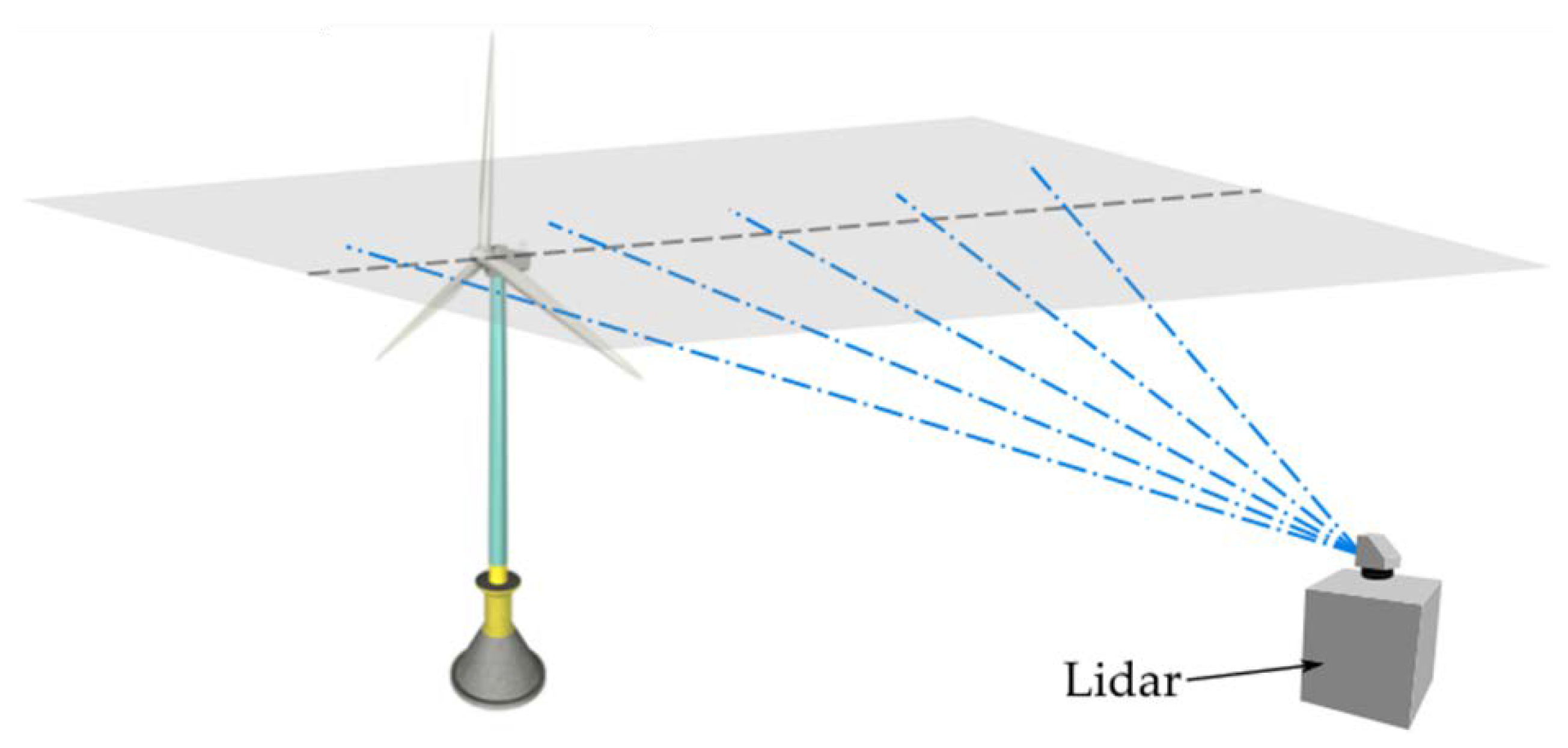
2.2. Wind Field Measurement by Scanning Doppler LiDAR
2.3. Wind Field Prediction by WRF
3. Results and Discussion
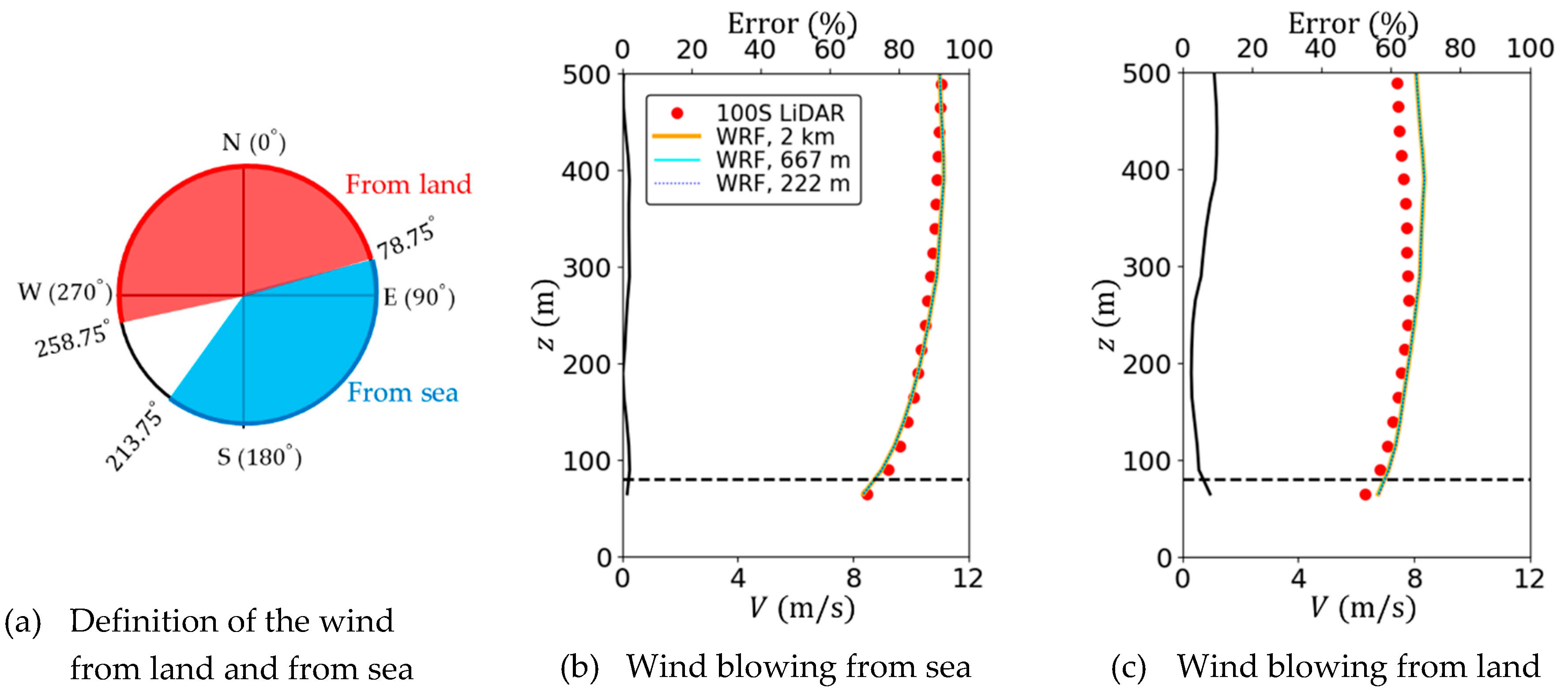
3.1. Measurement and Prediction of Vertical Wind Profiles
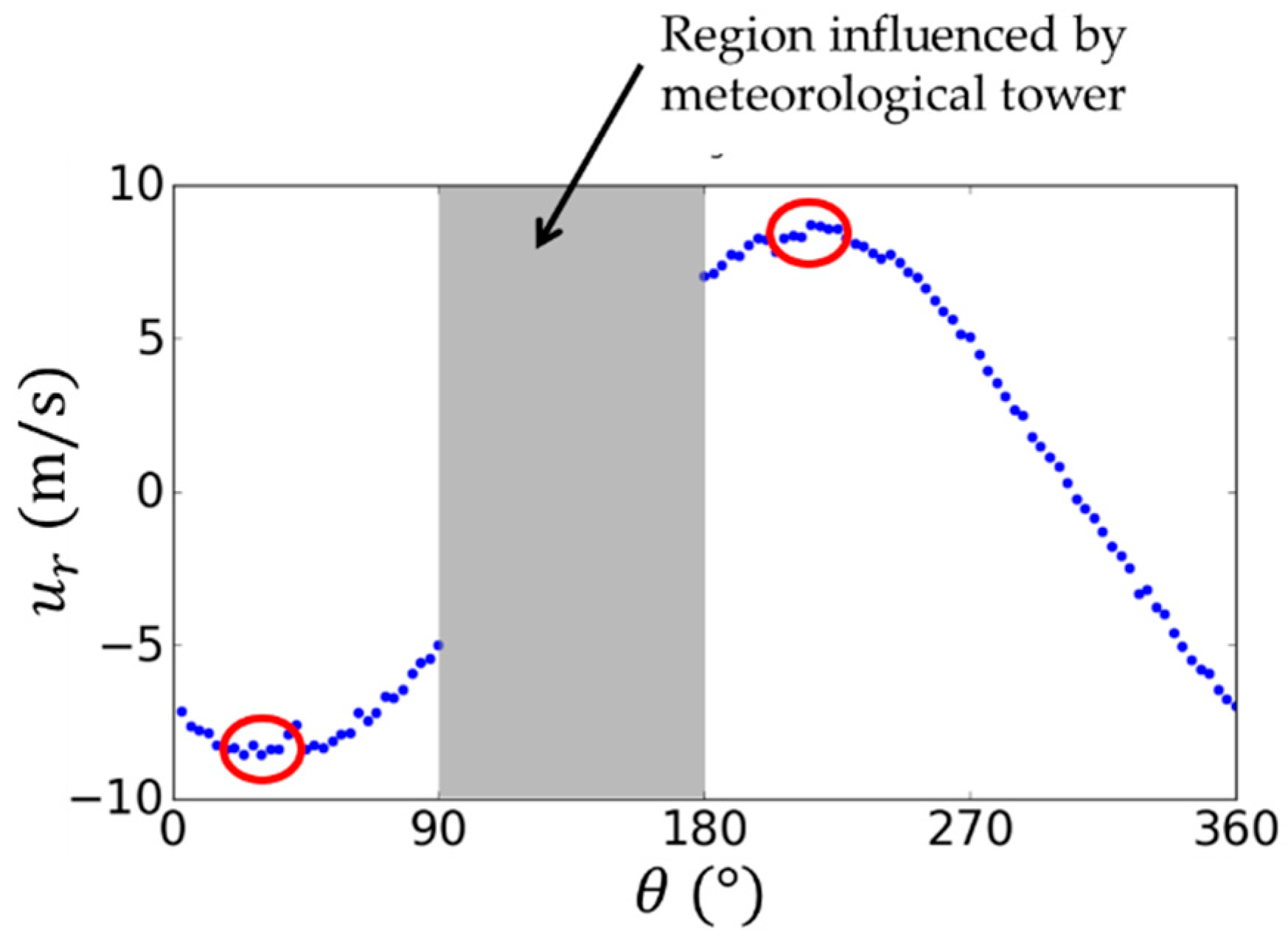
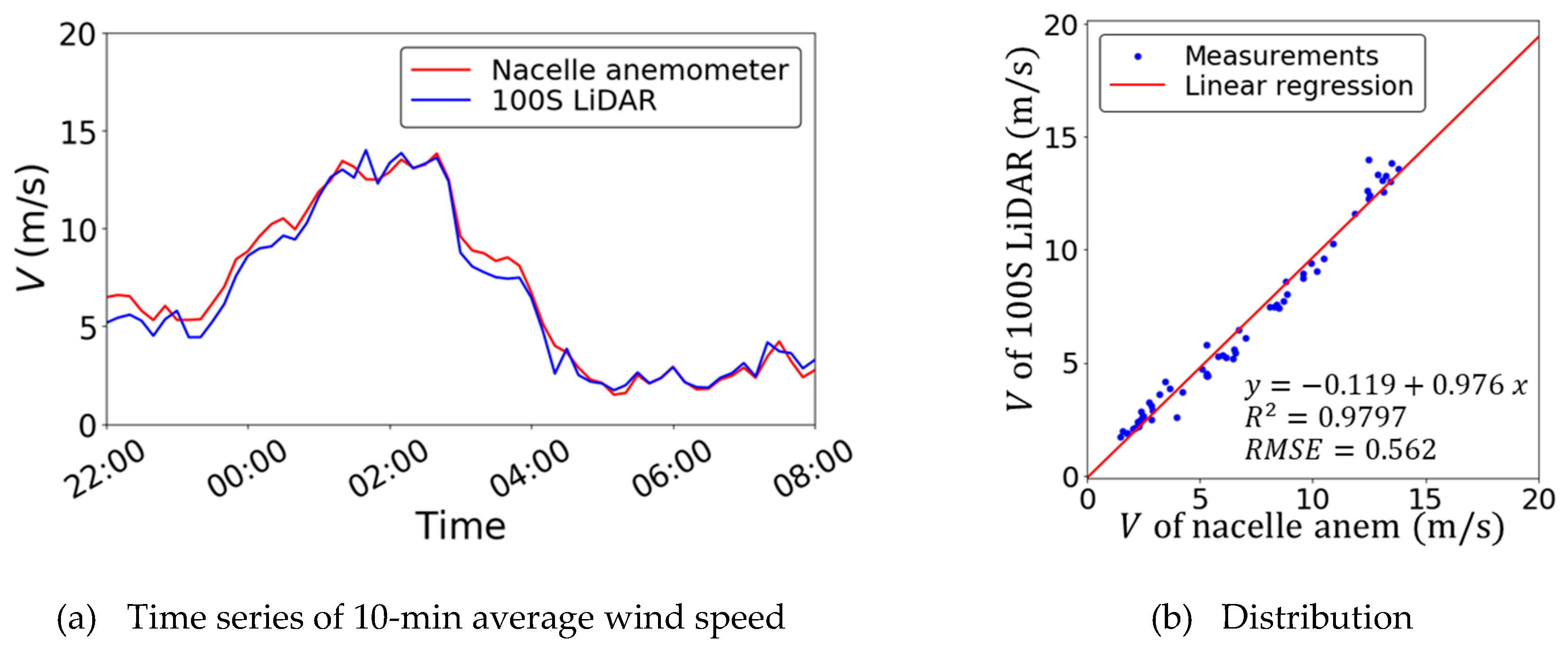
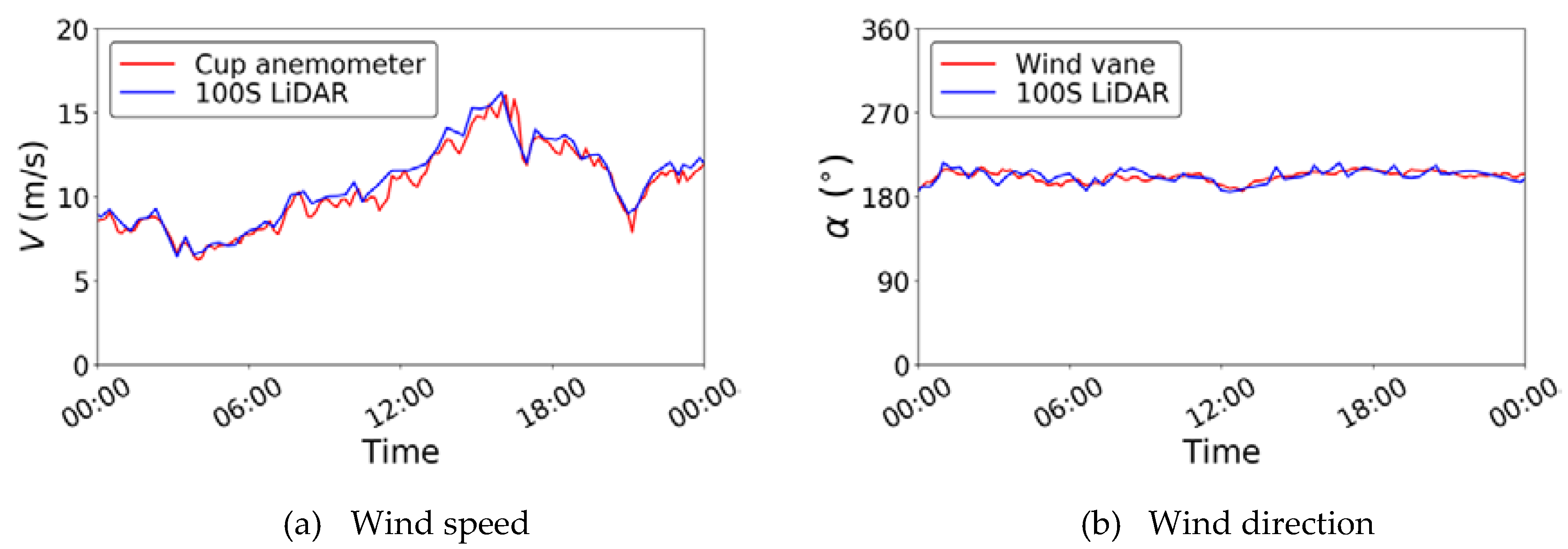
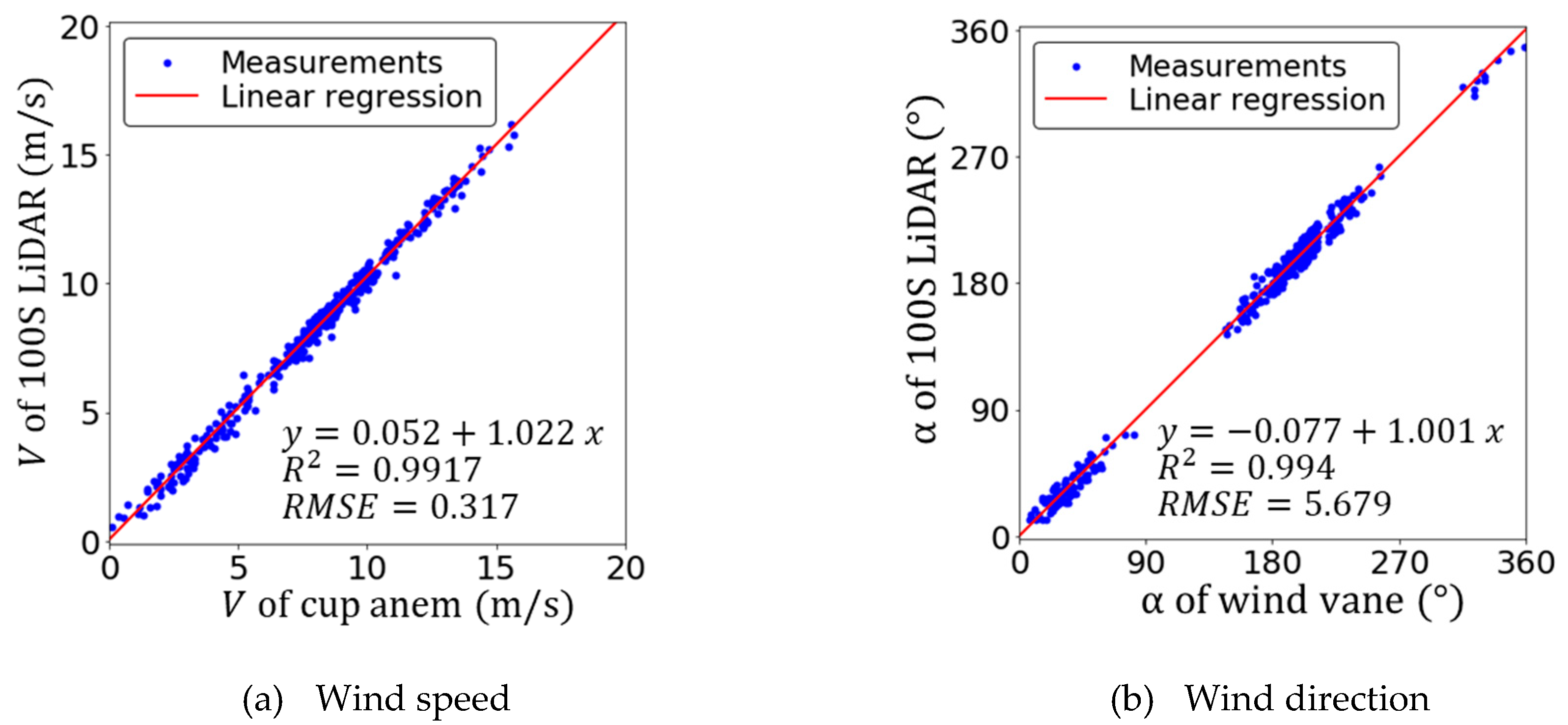
3.2. Validation of Velocity Vector Retrieved from PPI and RHI Scan Data
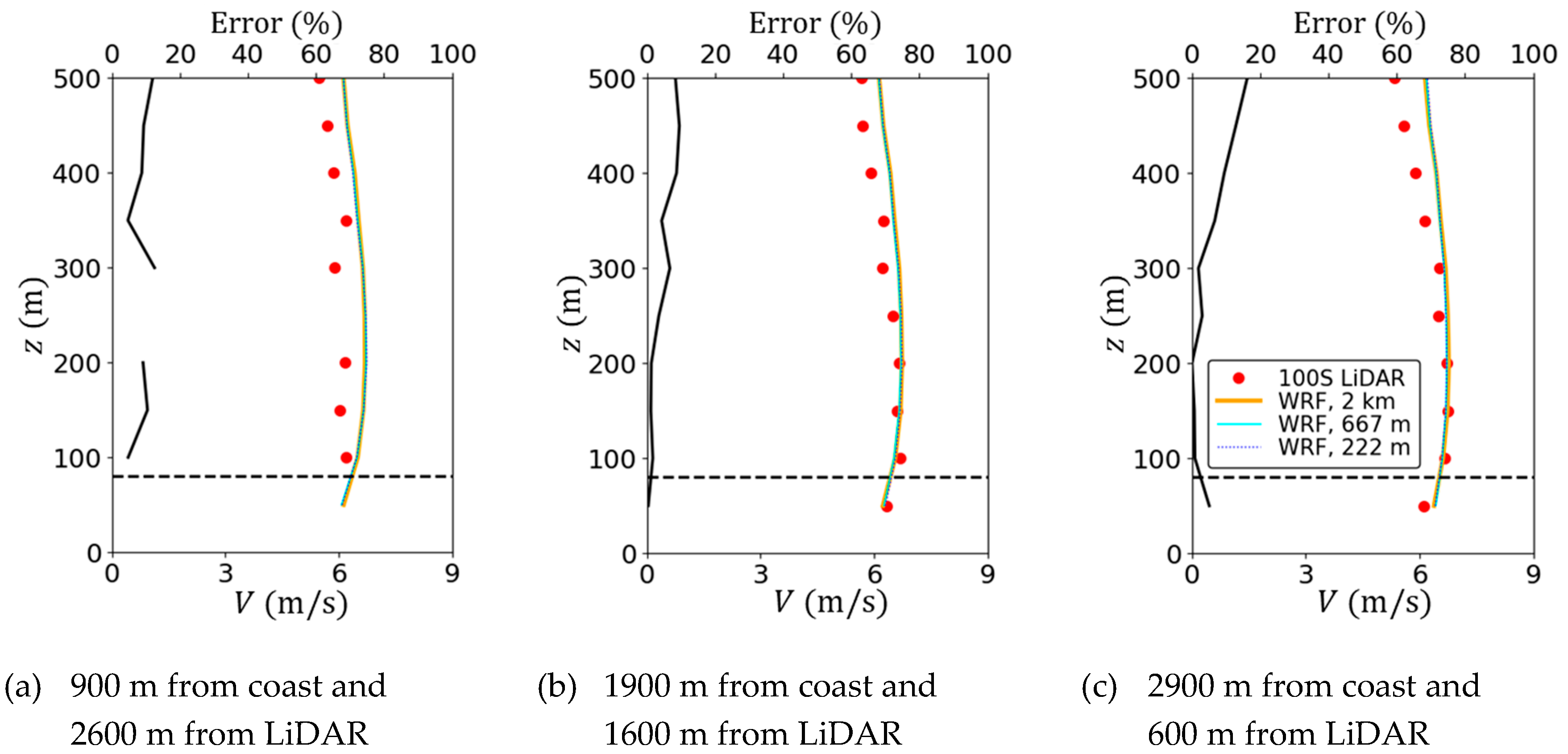
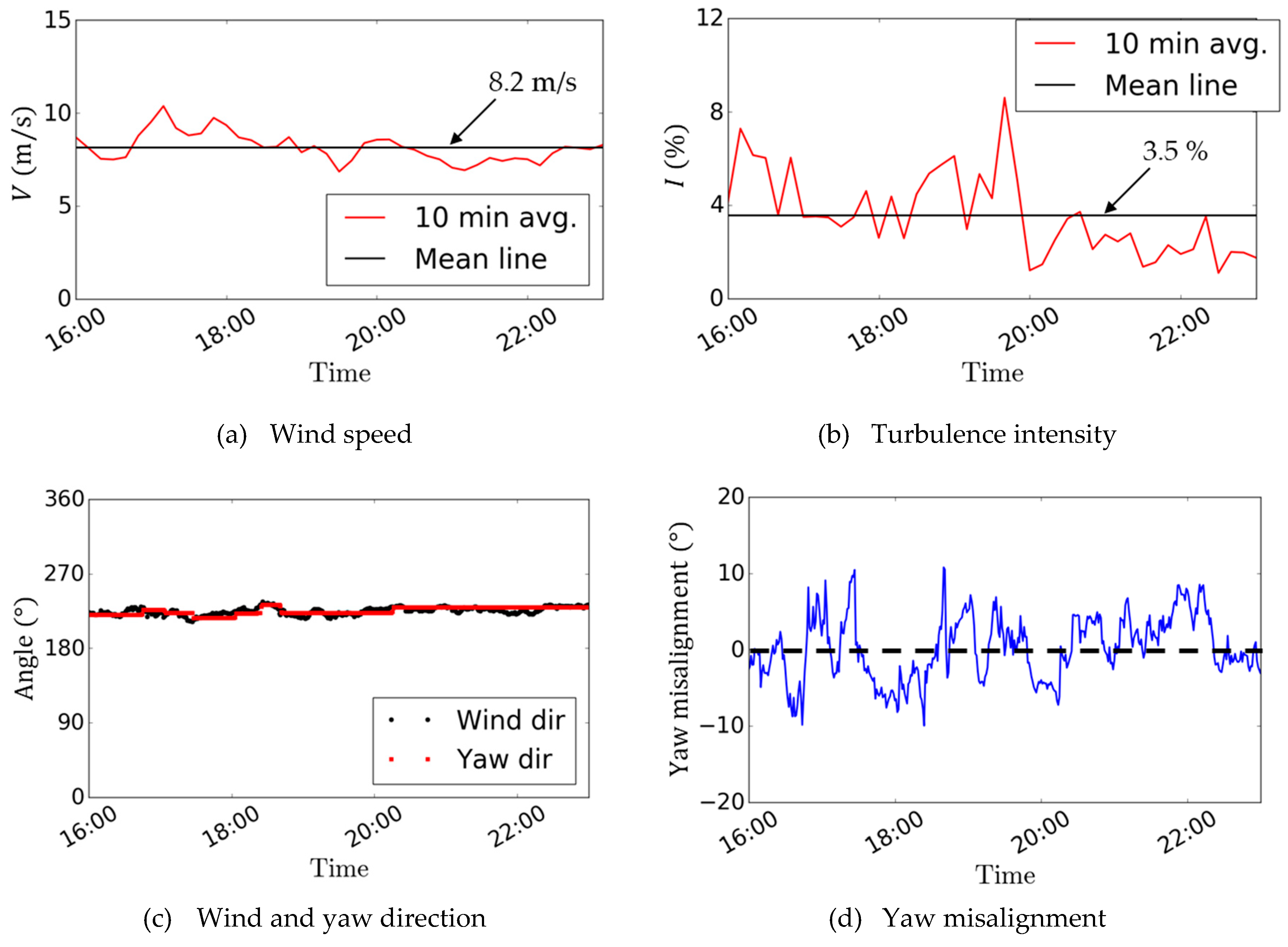
3.3. Measurement and Prediction of Wind Field in Near-Shore Boundary Layer
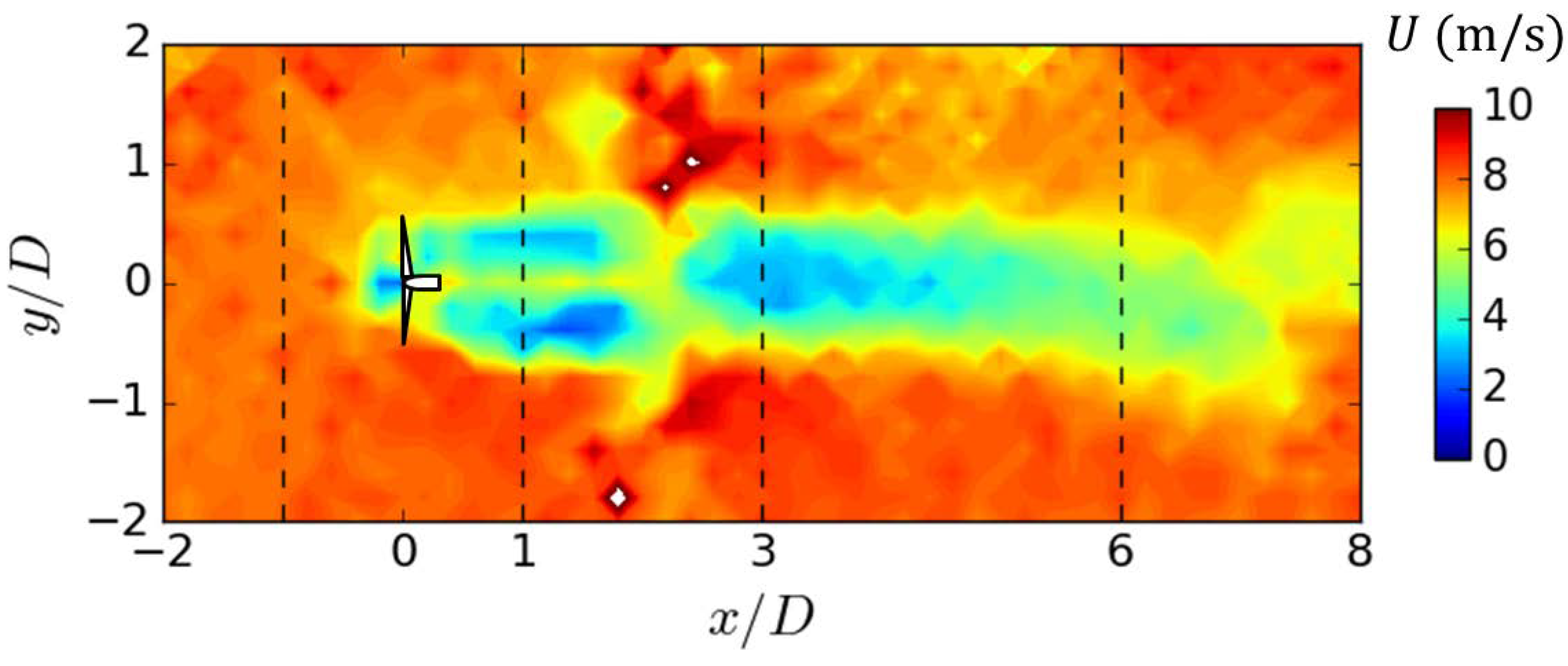
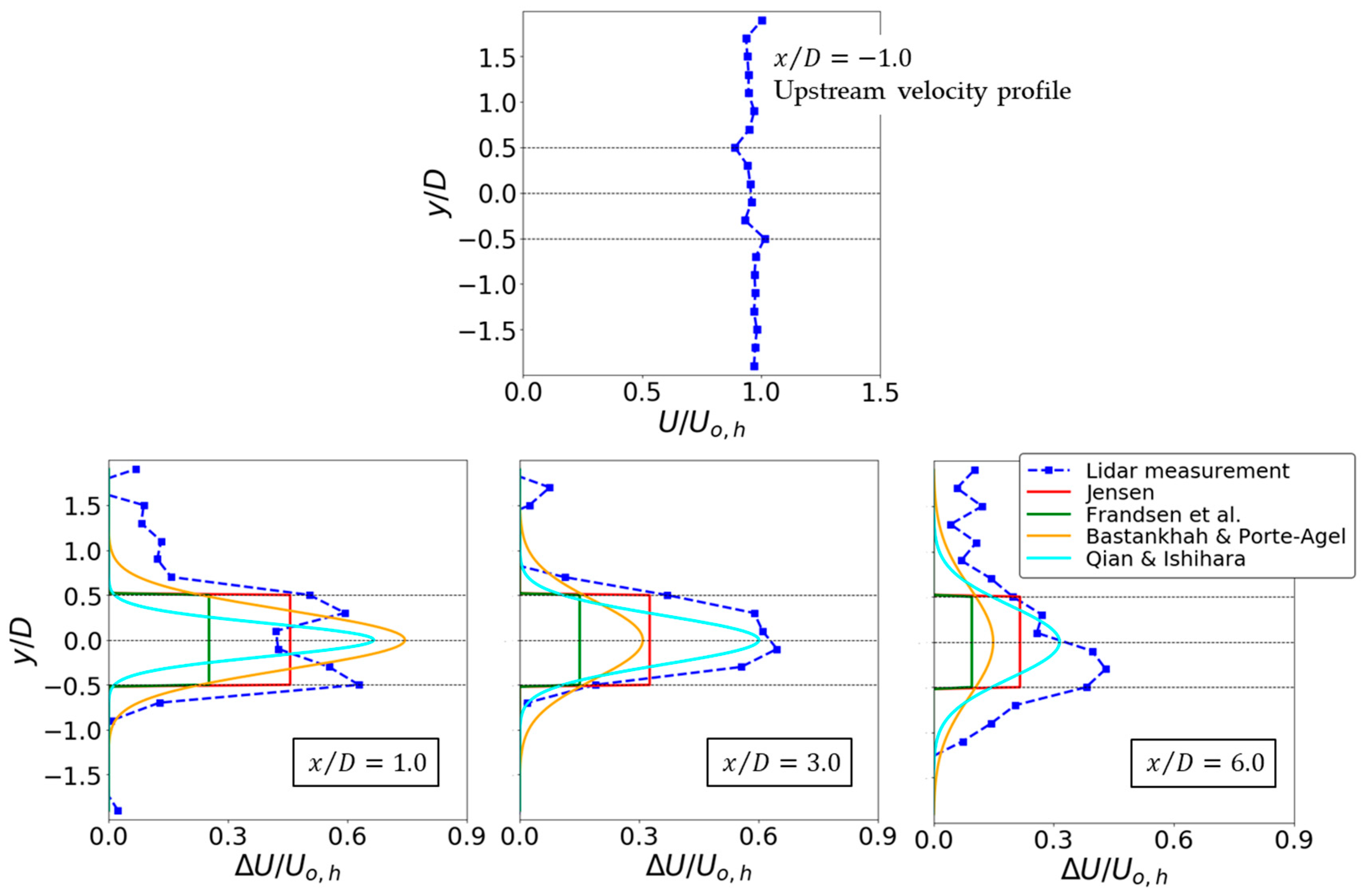
3.4. Measurement and Prediction of Wind Turbine Wake
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holleman, I. Quality control and verification of weather radar wind profiles. J. Atmos. Ocean. Technol. 2005, 22, 1541–1550. [Google Scholar] [CrossRef]
- Browning, K.A.; Wexler, R. The determination of kinematic properties of a wind field using Doppler radar. J. Appl. Meteorol. Climatol. 1968, 7, 105–113. [Google Scholar] [CrossRef]
- Holleman, I. Doppler Radar Wind Profiles; Roya Netherlands Meteorological Institute (KNMI): De Bilt, The Netherlands, 2003. [Google Scholar]
- Smith, D.A.; Harris, M.; Coffey, A.S.; Mikkelsen, T.; Jørgensen, H.E.; Mann, J.; Danielian, R. Wind lidar evaluation at the danish wind test site in Høvsøre. Wind Energy 2006, 9, 87–93. [Google Scholar] [CrossRef]
- Lang, S.; McKeogh, E. LIDAR and SODAR measurements of wind speed and direction in upland terrain for wind energy purposes. Remote Sens. 2011, 3, 1871–1901. [Google Scholar] [CrossRef]
- Goit, J.P.; Shimada, S.; Kogaki, T. Can LiDARs replace meteorological masts in wind energy? Energies 2019, 12, 3680. [Google Scholar] [CrossRef]
- Kelley, N.D.; Jonkman, B.J.; Scott, G.N. Comparing Pulse Doppler LIDAR with SODAR and Direct Measurements for Wind Assessment. In Proceedings of the American Wind Energy Association WindPower 2007 Conference and Exhibition, Los-Angeles, CA, USA, 3–7 June 2007; p. 20. [Google Scholar]
- Pichugina, Y.L.; Banta, R.M.; Brewer, W.A.; Sandberg, S.P.; Hardesty, R.M. Doppler Lidar-based wind-profile measurement system for offshore wind-energy and other marine boundary layer applications. J. Appl. Meteorol. Climatol. 2012, 51, 327–349. [Google Scholar] [CrossRef]
- Gottschall, J.; Courtney, M. Verification Test for Three WindCube WLS7 LiDARs at the Høvsøre Test Site; Tech. Rep. Risø-R-1732; Technical University of Denmark: Roskilde, Denmark, 2010. [Google Scholar]
- Easterbrook, C.C. Estimating horizontal wind fields by two-dimensional curve fitting of single doppler radar measurements. In Proceedings of the Radar Meteorology Conference, Huston, TX, USA, 22–24 April 1975. [Google Scholar]
- Waldteufel, P.; Corbin, H. On the analysis of single-doppler radar data. J. Appl. Meteorol. 1978, 18, 532–542. [Google Scholar] [CrossRef]
- Koscielny, A.J.; Doviak, R.J.; Rabin, R. Statistical considerations in the estimation of divergence from single-Doppler radar and application to prestorm boundary-layer observations. J. Appl. Meteorol. 1982, 21, 197–210. [Google Scholar] [CrossRef][Green Version]
- Banta, R.M.; Newsom, R.K.; Lundquist, J.K.; Pichugina, Y.L.; Coulter, R.L.; Mahrt, L. Nocturnal low-level jet characteristics over Kansas during cases-99. Bound. Layer Meteorol. 2002, 105, 221–252. [Google Scholar] [CrossRef]
- Iungo, G.V.; Porte-Agel, F. Volumetric lidar scanning of wind turbine wakes under convective and neutral atmospheric stability regimes. J. Atmos. Ocean. Technol. 2014, 31, 2035–2048. [Google Scholar] [CrossRef]
- Mann, J.; Cariou, J.P.; Courtney, M.S.; Parmentier, R.; Mikkelsen, T.; Wagner, R.; Lindelöw, P.; Sjöholm, M.; Enevoldsen, K. Comparison of 3D turbulence measurements using three staring wind lidars and a sonic anemometer. Meteorol. Z. 2009, 18, 135–140. [Google Scholar] [CrossRef]
- Fuertes, F.C.; Iungo, G.V.; Porte-Agel, F. 3D turbulence measurements using three synchronous wind lidars: Validation against sonic anemometry. J. Atmos. Ocean. Technol. 2014, 31, 1549–1556. [Google Scholar] [CrossRef]
- Windcube Windcube 100s/200s/400s—3D Wind Doppler LIDAR. Available online: http://www.leosphere.com/wp-content/uploads/2016/12/WINDCUBE-Scannant-Brochure-4p-20151116-HD.pdf (accessed on 23 August 2019).
- Kikuchi, Y.; Fukushima, M.; Ishihara, T. Assessment of a coastal offshore wind climate by means of mesoscale model simulations considering high-resolution land use and sea surface temperature data sets. Atmosphere 2020, 11, 379. [Google Scholar] [CrossRef]
- Goit, J.P.; Yamaguchi, A.; Ishihara, T. Performance Evaluation of Scanning Doppler Lidar and its Application to Wind Field Measurement. Tech. Rep. Japan Wind Energy Assoc. 2018, 42, 7–16. (In Japanese) [Google Scholar]
- Clifton, A. Remote Sensing of Complex Flows by Doppler Wind Lidar: Issues and Preliminary Recommendations; Tech. Rep. NREL/TP-5000-64634; National Renewable Energy Laboratory: Golden, CO, USA, December 2015.
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A description of the advanced research WRF version 3. Tech. Rep. NCAR 2008, NCAR/TN–47, 1–113. [Google Scholar]
- Iizuka, S. Future environmental assessment and urban planning by downscaling simulations. J. Wind Eng. Ind. Aerodyn. 2018, 181, 69–78. [Google Scholar] [CrossRef]
- Yoshie, R.; Miura, S.; Mochizuki, M. Validation of WRF for preparation of standard wind data validation of WRF for preparation of standard wind data for assessment of pedestrian wind environment. J. Wind Eng. JAWE 2015, 40, 113–122, [In Japanese]. [Google Scholar] [CrossRef]
- NOAA Earth System Research Laboratory. NCEP Reanalysis Data Provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA. 2017.5. Available online: https://www.esrl.noaa.gov/psd/ (accessed on 10 August 2019).
- Stark, J.D.; Donlon, C.J.; Martin, M.J.; McCulloch, M.E. OSTIA: An operational, high resolution, real time, global sea surface temperature analysis system. In Proceedings of the OCEANS 2007—Europe, Aberdeen, UK, 18–21 June 2007; pp. 1–4. [Google Scholar]
- Aitken, M.L.; Banta, R.M.; Pichugina, Y.L.; Lundquist, J.K. Quantifying wind turbine wake characteristics from scanning remote sensor data. J. Atmos. Ocean. Technol. 2014, 31, 765–787. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A.; Pichugina, Y.L.; Brewer, W.A.; Banta, R.M.; Lundquist, J.K.; Kelley, N.D. Lidar investigation of atmosphere effect on a wind turbine wake. J. Atmos. Ocean. Technol. 2013, 30, 2554–2570. [Google Scholar] [CrossRef]
- Banta, R.M.; Pichugina, Y.L.; Brewer, W.A.; Lundquist, J.K.; Kelley, N.D.; Sandberg, S.P.; Alvarez, R.J.; Hardesty, R.M.; Weickmann, A.M. 3D volumetric analysis of wind turbine wake properties in the atmosphere using high-resolution Doppler lidar. J. Atmos. Ocean. Technol. 2015, 32, 904–914. [Google Scholar] [CrossRef]
- Iungo, G.V.; Porté-Agel, F. Measurement procedures for characterization of wind turbine wakes with scanning Doppler wind LiDARs. Adv. Sci. Res. 2013, 10, 71. [Google Scholar] [CrossRef]
- Newsom, R.K.; Berg, L.K.; Shaw, W.J.; Fischer, M.L. Turbine-scale wind field measurements using dual-Doppler lidar. Wind Energy 2015, 18, 219–235. [Google Scholar] [CrossRef]
- Jensen, N.O. A Note on Wind Generator Interaction; Tech. Rep. Riso-M-2411; Riso National Laboratory: Roskilde, Denmark, November 1983. [Google Scholar]
- Frandsen, S.; Barthelmie, R.J.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- Qian, G.-W.; Ishihara, T. A new analytical wake model for yawed wind turbines. Energies 2018, 11, 665. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Widyasih, S.P.; Ishihara, T. Load Estimation of a Wind Turbine Support Structure during Operation and Validation by Measurement. In Proceedings of the 23rd Wind Engineering Symposium, Tokyo, Japan, 3–5 December 2014; pp. 133–138. [Google Scholar]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-turbine and wind-farm flows: A Review. Bound. Layer Meteorol. 2019, 174, 1–59. [Google Scholar] [CrossRef]
- Ishihara, T.; Qian, G. A new Gaussian—Based analytical wake model for wind turbines considering ambient turbulence intensities and thrust coefficient effects. J. Wind Eng. Ind. Aerodyn. 2018, 177, 275–292. [Google Scholar] [CrossRef]
- Stevens, R.J.A.M.; Gayme, D.F.; Meneveau, C. Effects of turbine spacing on the power output of extended wind-farms. Wind Energy 2016, 19, 359–370. [Google Scholar] [CrossRef]






| CNR Min (dB) | Minimum Number of Data | Offset | Slope | RMSE (m/s) | ||
|---|---|---|---|---|---|---|
| −20 | 20 | 28 | 0.173 | 0.99 | 0.948 | 1.113 |
| −20 | 80 | 112 | 0.215 | 0.99 | 0.942 | 1.275 |
| −23 | 20 | 28 | 0.126 | 1.0 | 0.957 | 0.929 |
| −23 | 80 | 112 | 0.127 | 1.0 | 0.967 | 0.838 |
| −25 | 20 | 28 | 0.13 | 0.996 | 0.961 | 0.868 |
| −25 | 80 | 112 | 0.122 | 0.996 | 0.969 | 0.784 |
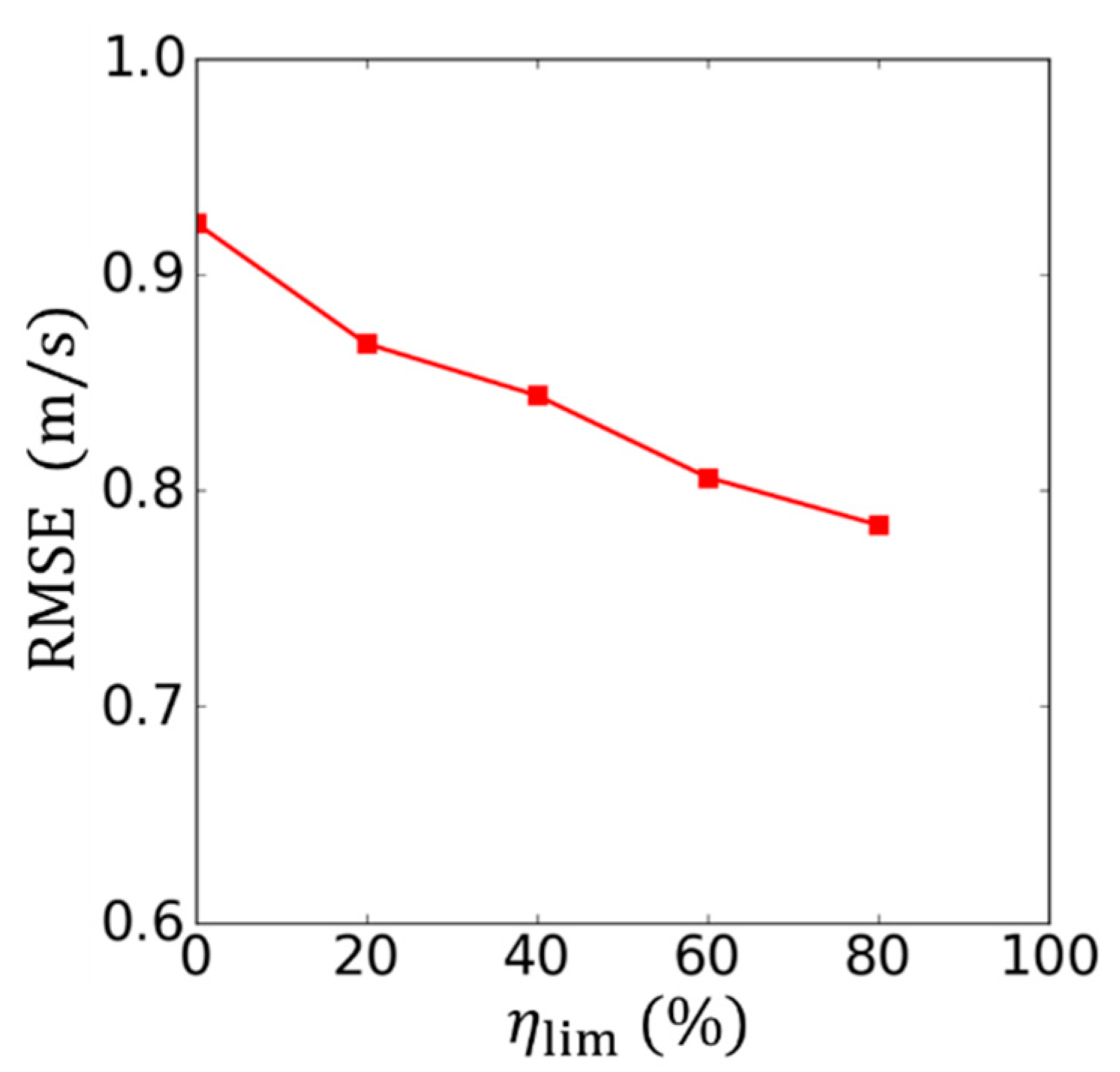
| Minimum Number of Data | Offset | Slope | RMSE (m/s) | ||
|---|---|---|---|---|---|
| 0 | 1 | 0.14 | 0.996 | 0.9549 | 0.924 |
| 20 | 28 | 0.13 | 0.996 | 0.9607 | 0.868 |
| 40 | 56 | 0.126 | 0.99 | 0.9612 | 0.844 |
| 60 | 82 | 0.124 | 0.996 | 0.9672 | 0.806 |
| 80 | 112 | 0.122 | 0.996 | 0.9694 | 0.784 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goit, J.P.; Yamaguchi, A.; Ishihara, T. Measurement and Prediction of Wind Fields at an Offshore Site by Scanning Doppler LiDAR and WRF. Atmosphere 2020, 11, 442. https://doi.org/10.3390/atmos11050442
Goit JP, Yamaguchi A, Ishihara T. Measurement and Prediction of Wind Fields at an Offshore Site by Scanning Doppler LiDAR and WRF. Atmosphere. 2020; 11(5):442. https://doi.org/10.3390/atmos11050442
Chicago/Turabian StyleGoit, Jay Prakash, Atsushi Yamaguchi, and Takeshi Ishihara. 2020. "Measurement and Prediction of Wind Fields at an Offshore Site by Scanning Doppler LiDAR and WRF" Atmosphere 11, no. 5: 442. https://doi.org/10.3390/atmos11050442
APA StyleGoit, J. P., Yamaguchi, A., & Ishihara, T. (2020). Measurement and Prediction of Wind Fields at an Offshore Site by Scanning Doppler LiDAR and WRF. Atmosphere, 11(5), 442. https://doi.org/10.3390/atmos11050442





