Influence of Internal Structure and Composition on Head’s Local Thermal Sensation and Temperature Distribution
Abstract
1. Introduction
2. Materials and Methods
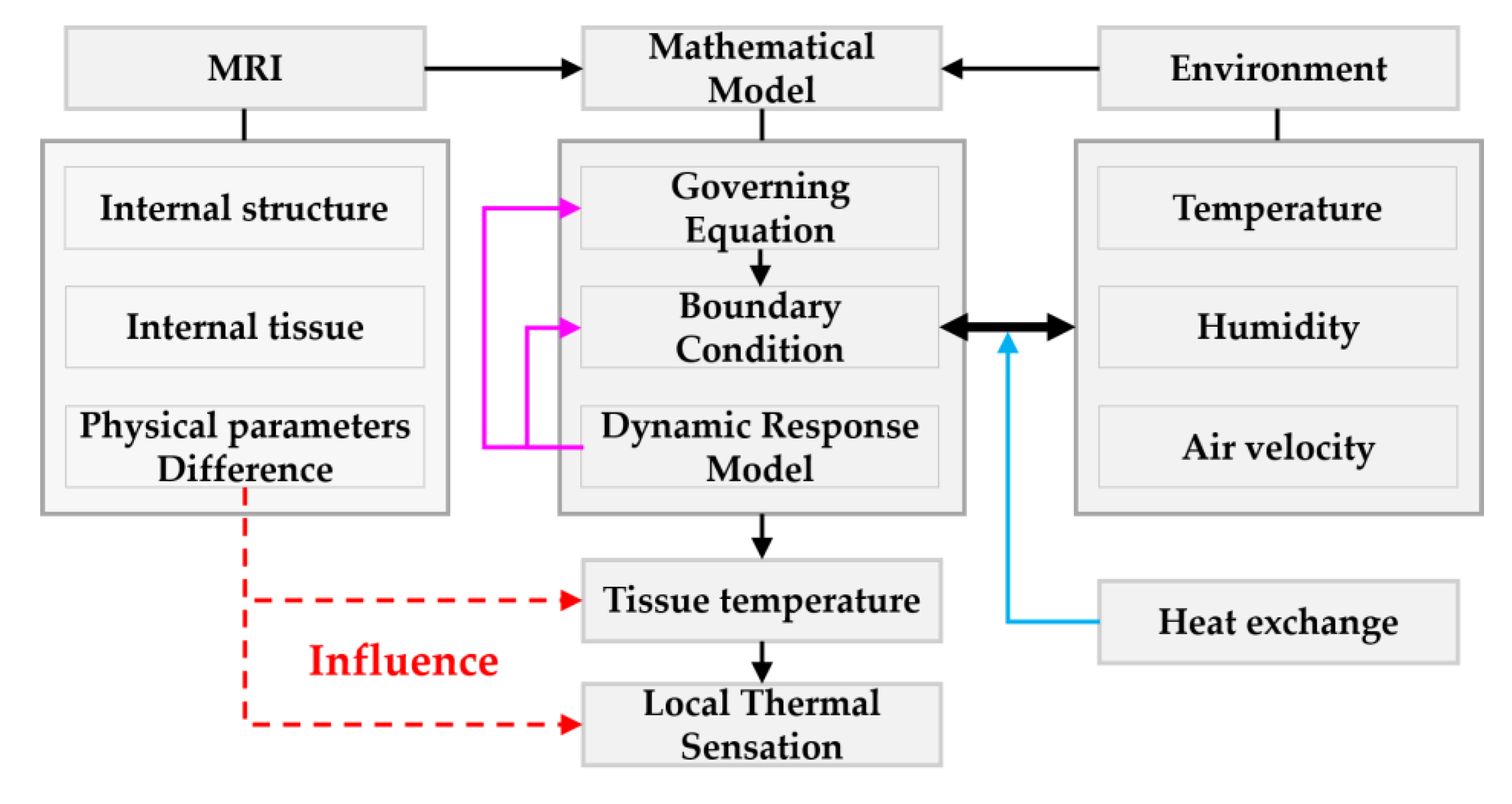
2.1. Mathematical Model
2.1.1. Governing Equation and Boundary Conditions
2.1.2. Dynamic Response of the Model
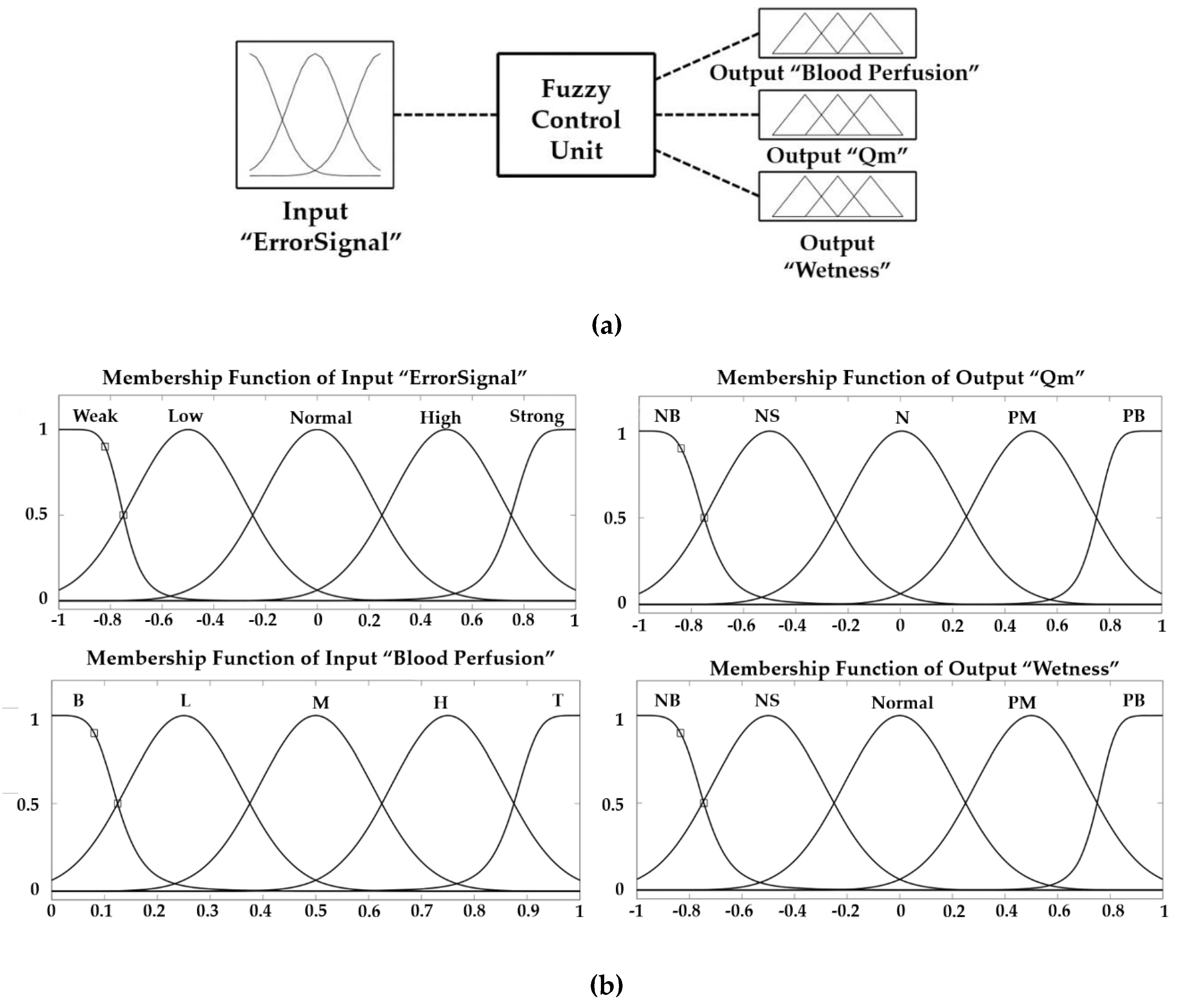
2.1.3. Thermal Sensation Index
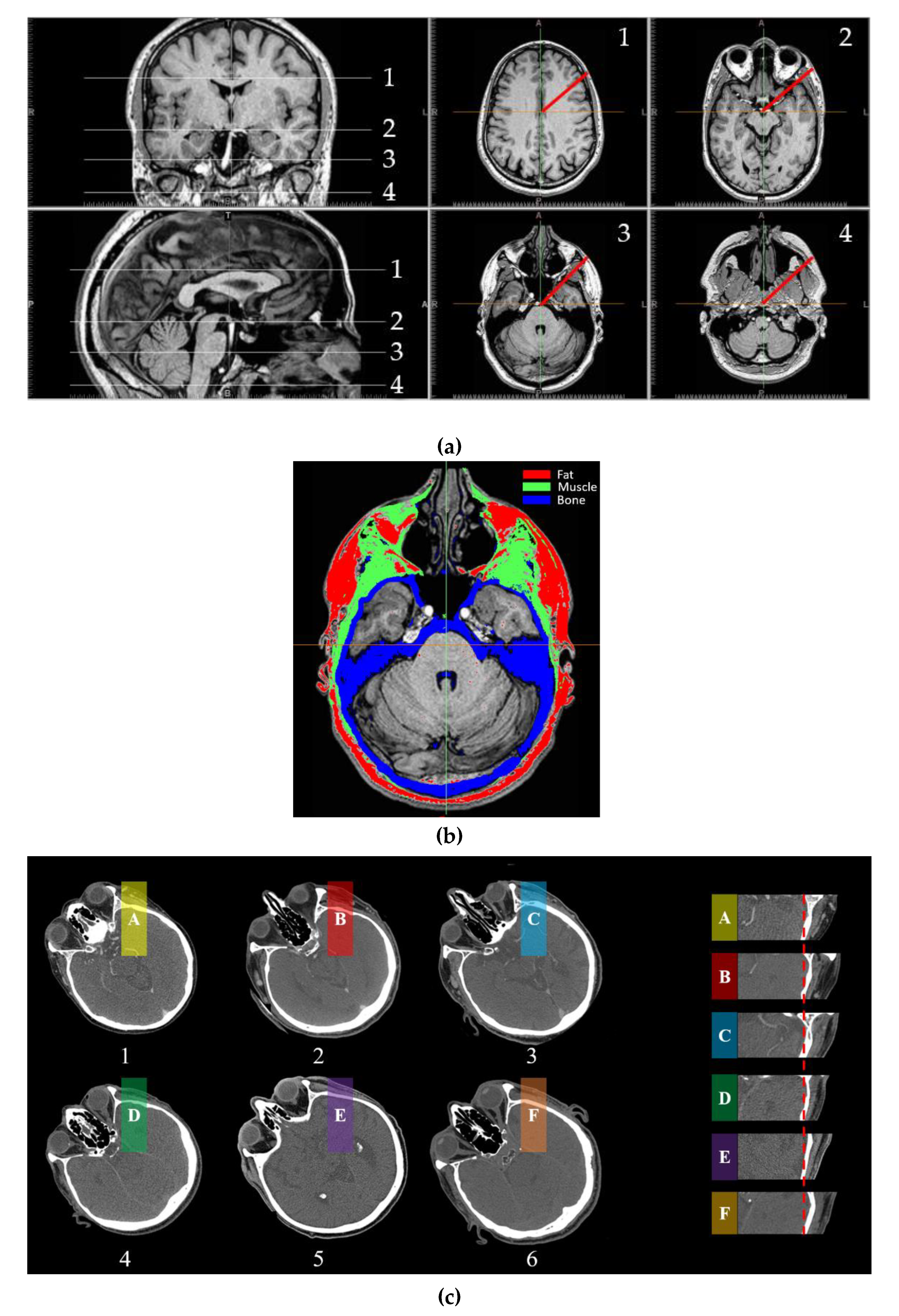
2.2. MRI Analysis of Head Composition and Structure
2.3. Methodology Framework
3. Results and Discussion
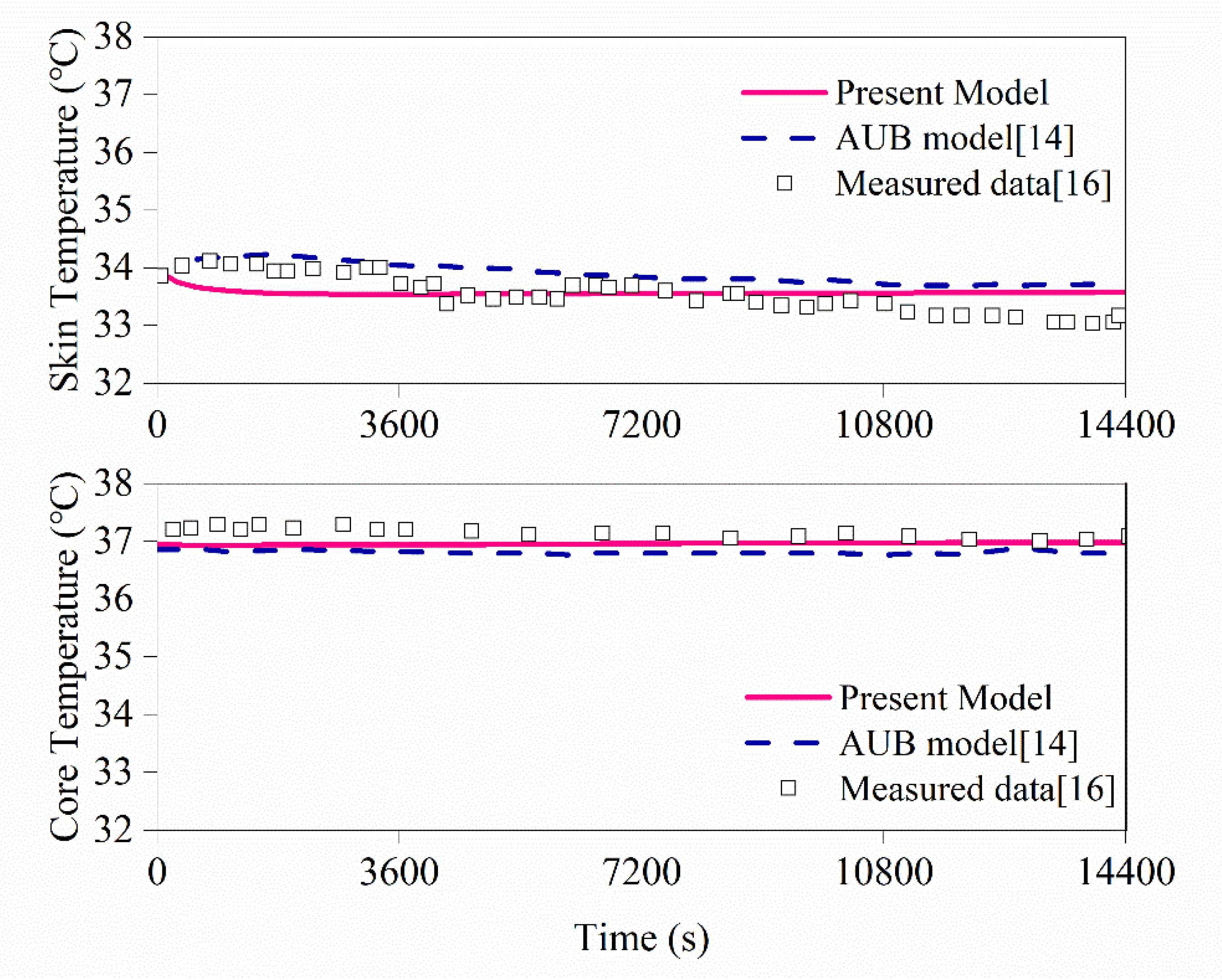
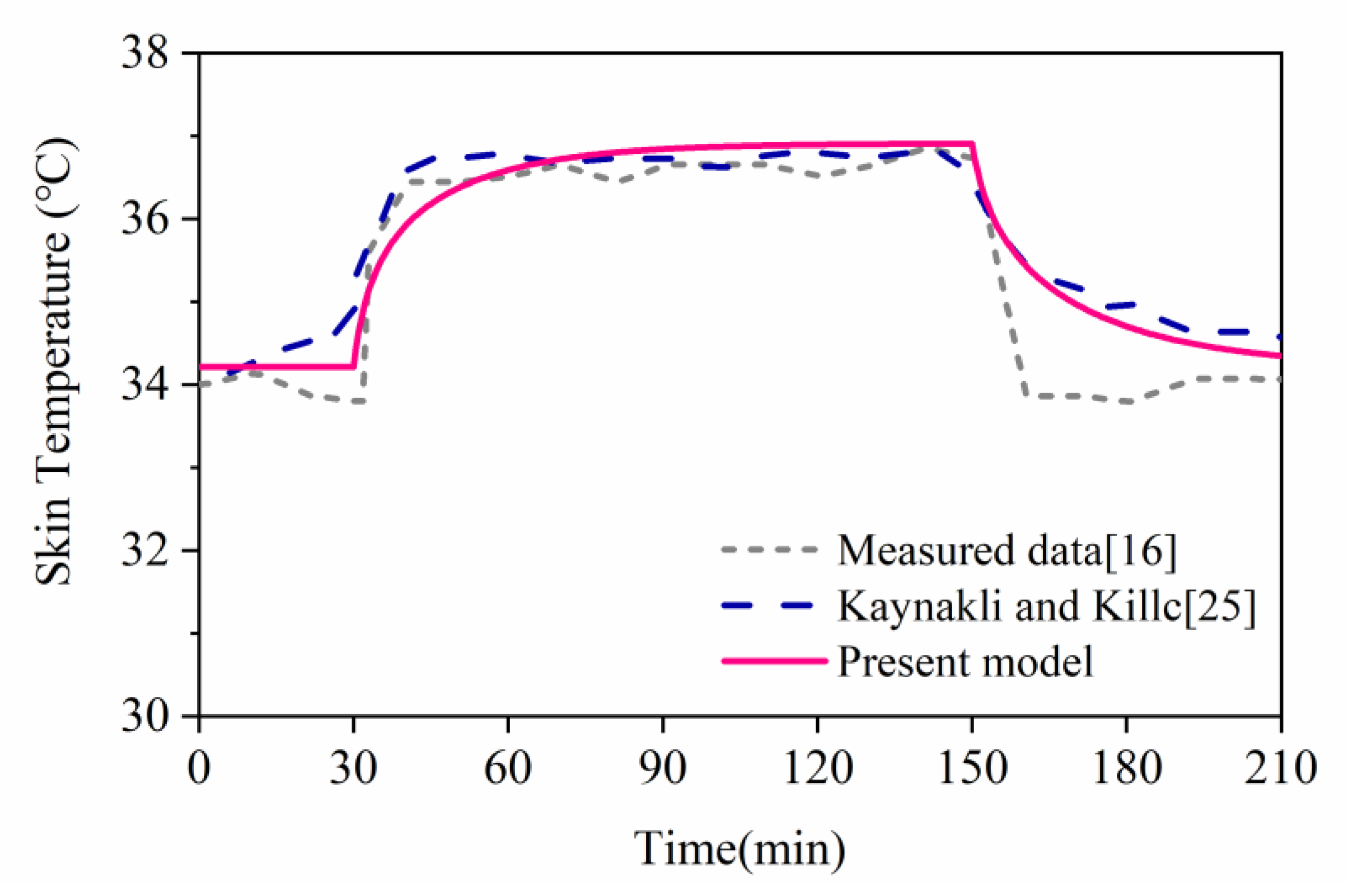
3.1. Model Validation
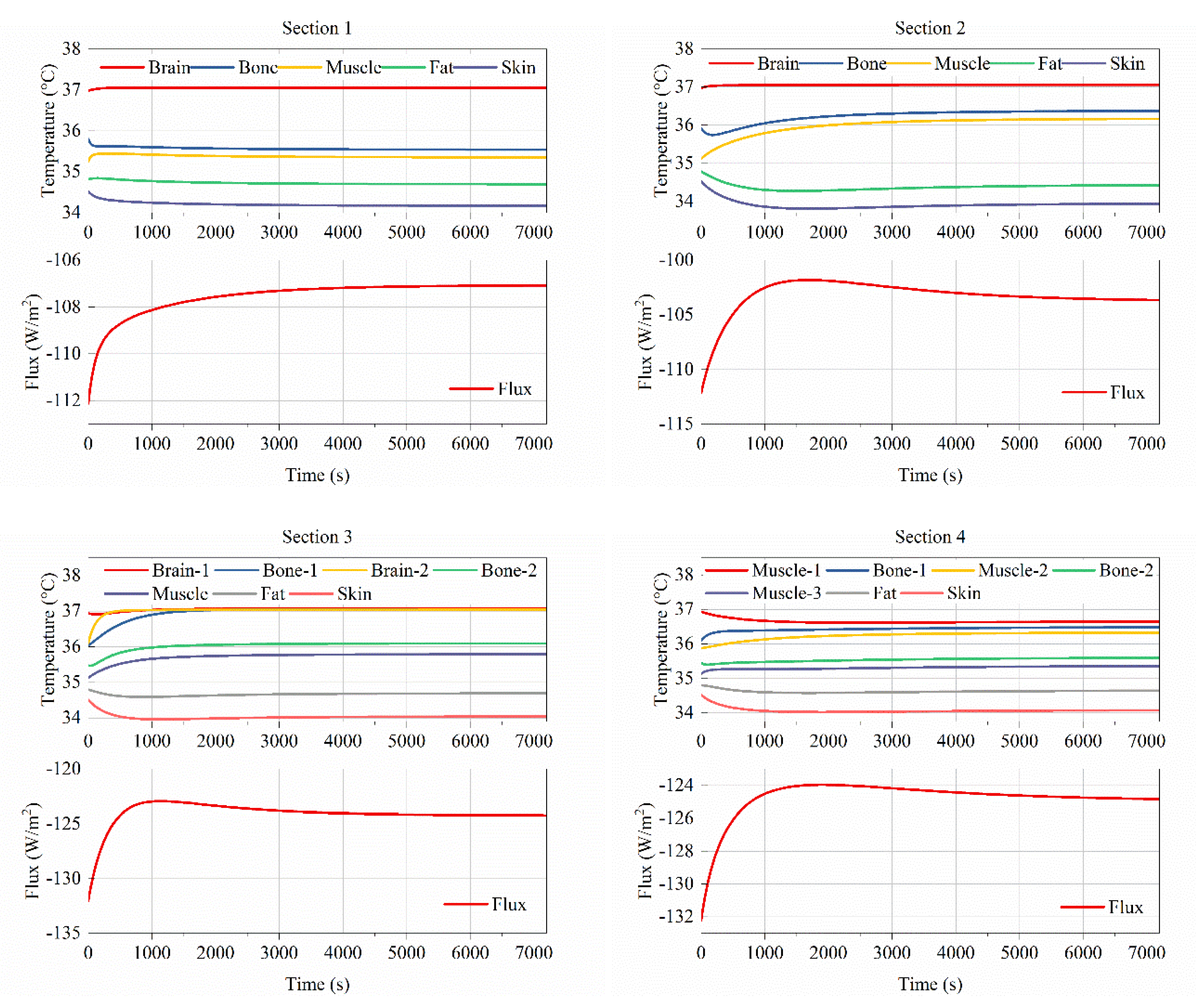
3.2. Influence of Different Structures on Tissue’s Temperature Distribution
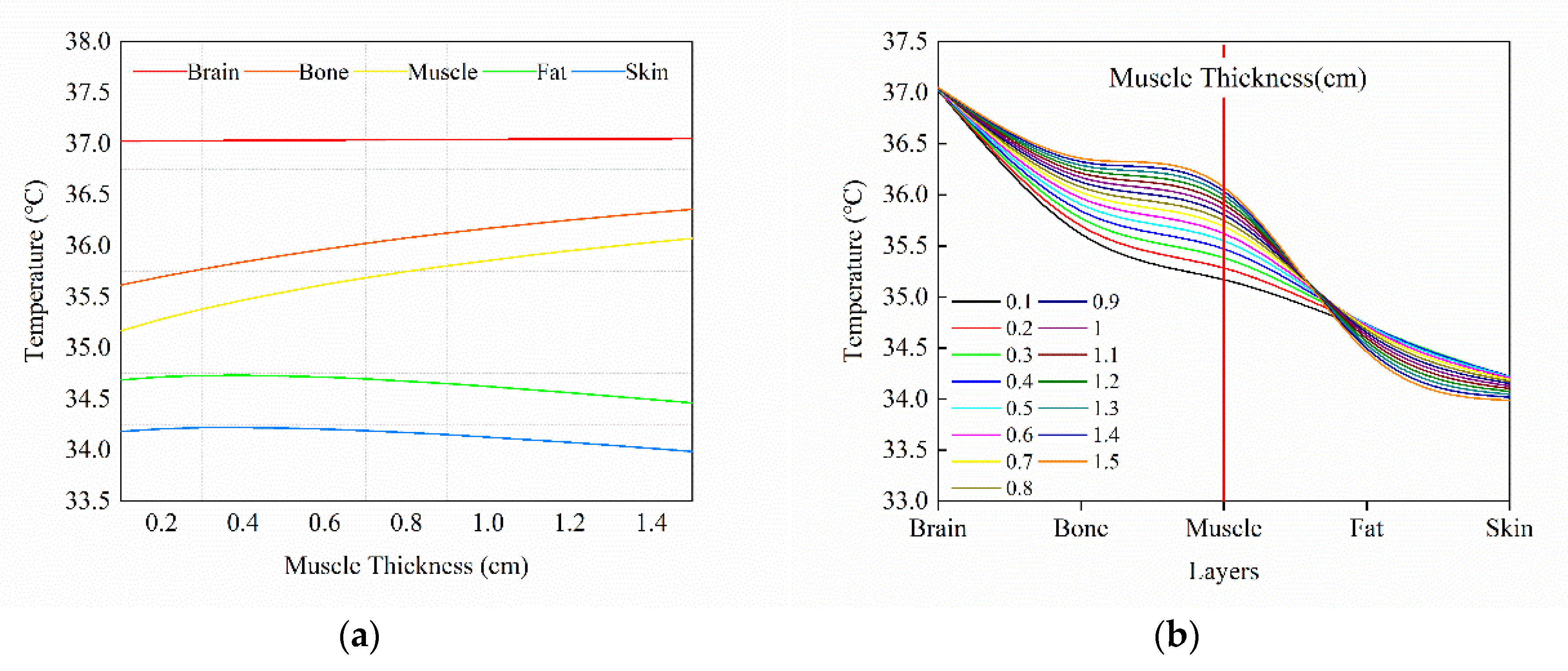
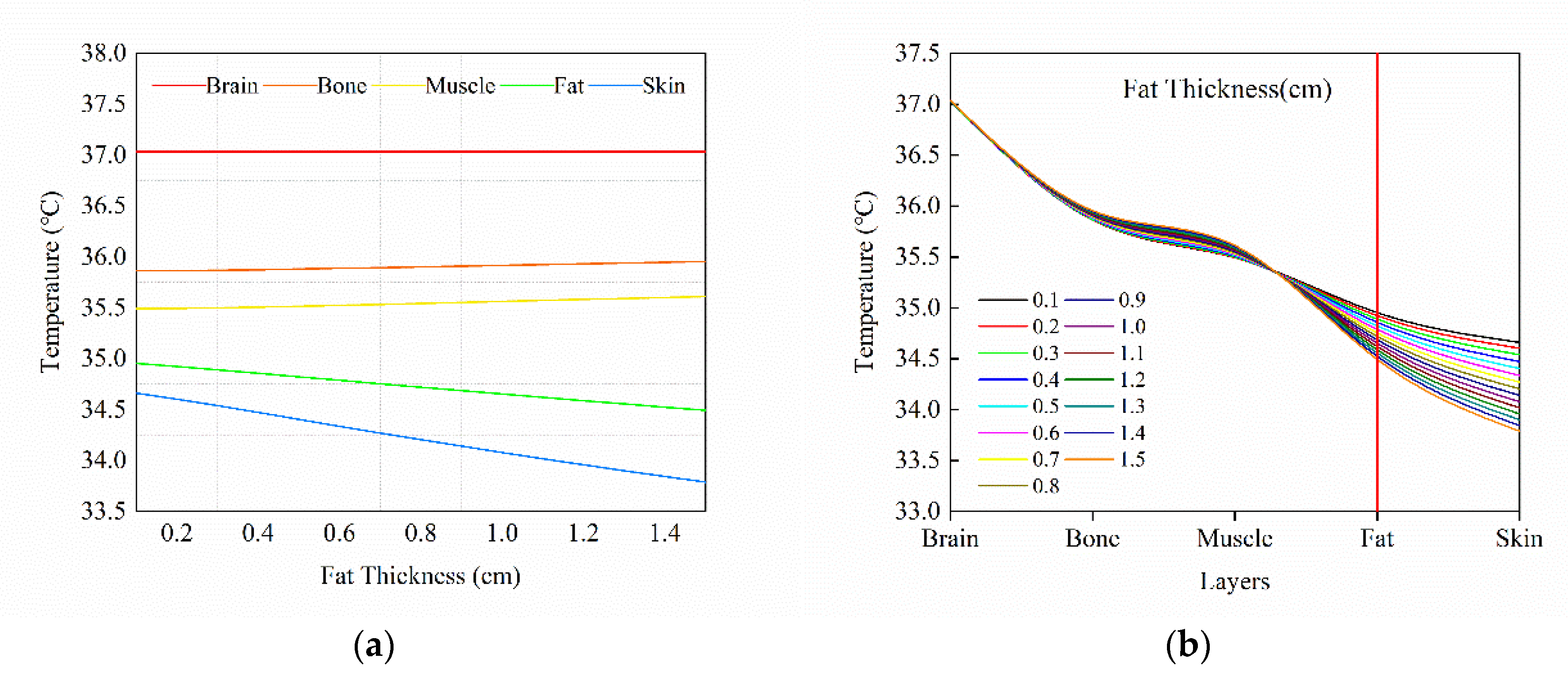
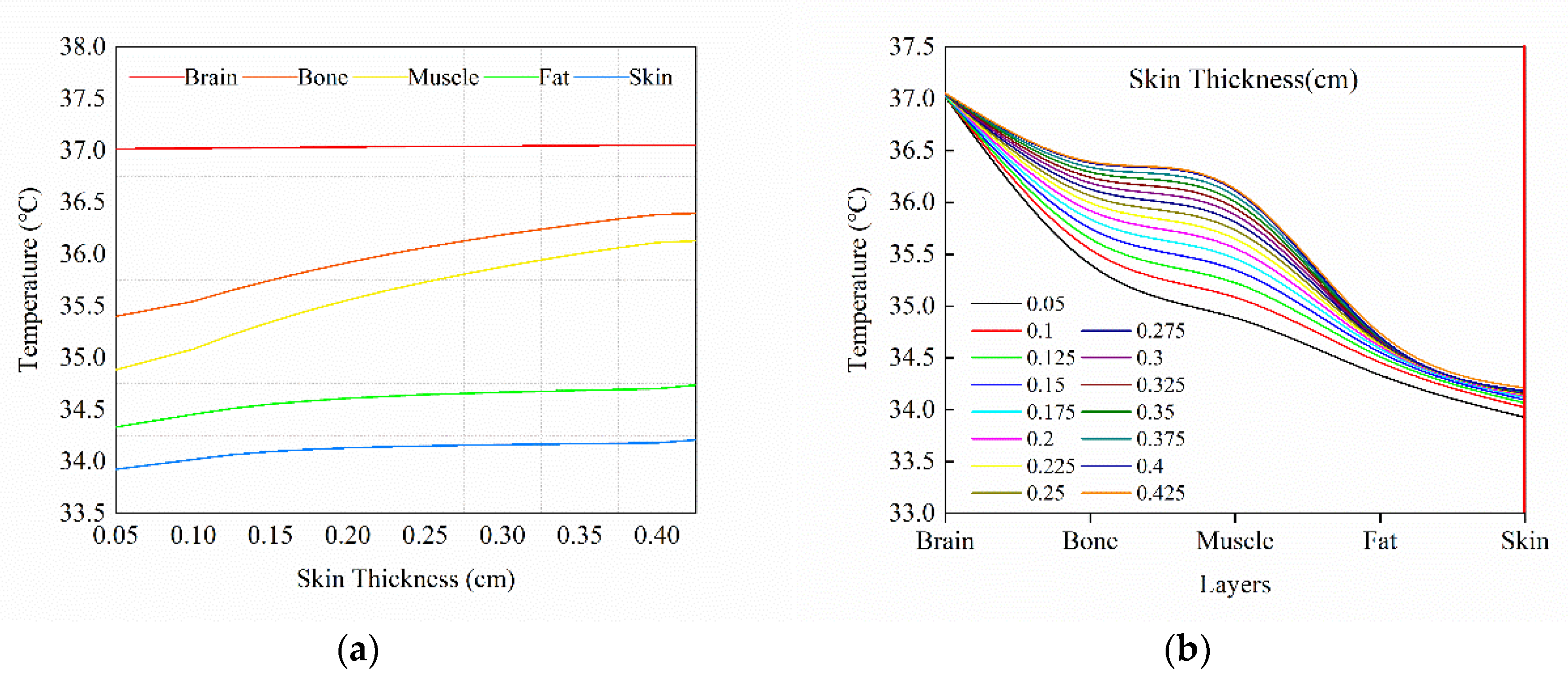
3.3. Effect of Tissue Thickness Step Change on Temperature Distribution
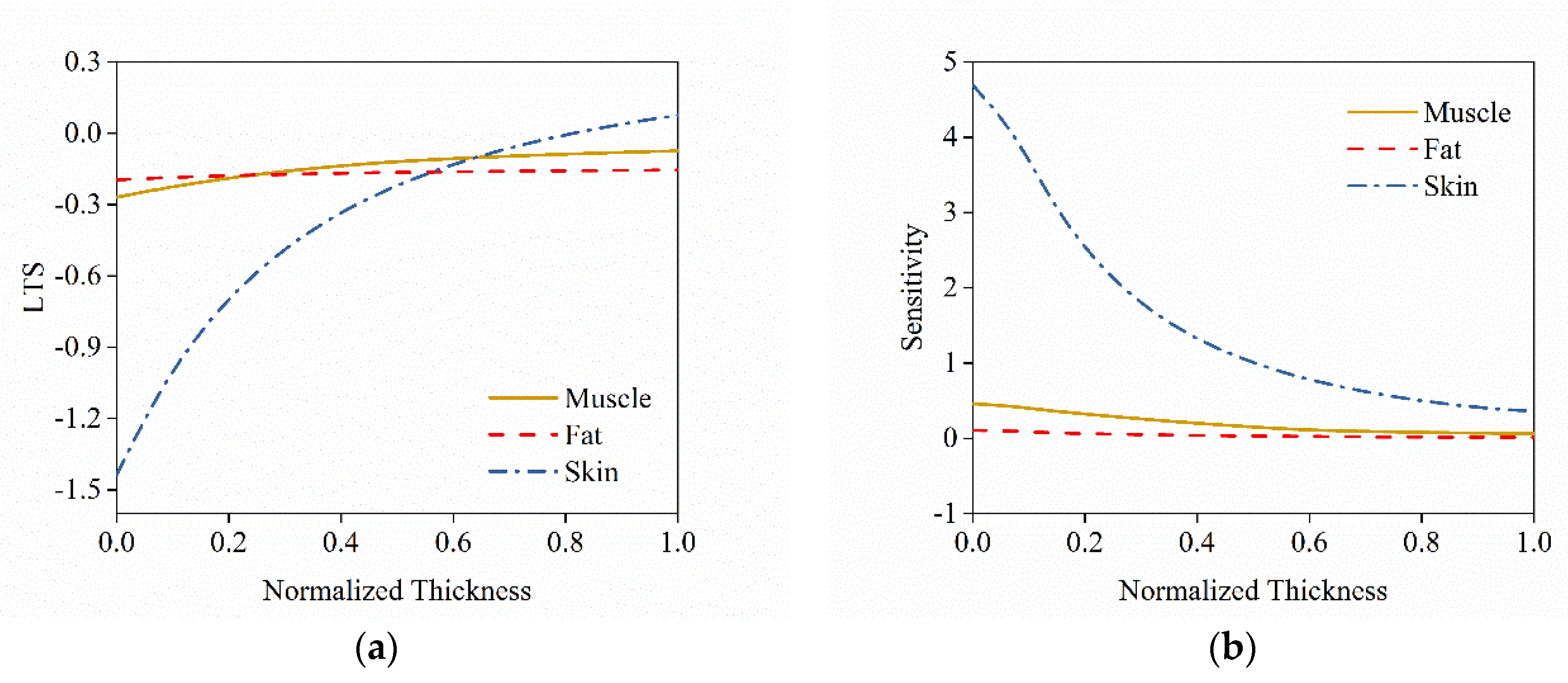
3.4. Thermal Sensation and Its Sensitivity to Tissue Thickness Vriation
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Yao, R.; Li, B.; Liu, H.; Jiang, L. Parameterization of Temperature Perception of Ventilation Changes in Full-Face Motorcycle. Build. Environ. 2015, 87, 1–9. [Google Scholar] [CrossRef]
- Johnson, A.T. Respirator masks protect health but impact performance: A review. J. Biol. Eng. 2016, 10, 4. [Google Scholar] [CrossRef] [PubMed]
- Bogerd, C.P.; Aerts, J.M.; Annaheim, S.; Bröde, P.; de Bruyne, G.; Flouris, A.D.; Kuklane, K.; Sotto Mayor, T.; Rossi, R.M. A review on ergonomics of headgear: Thermal effects. Int. J. Ind. Ergon. 2015, 45, 1–12. [Google Scholar] [CrossRef]
- Yang, Y.; Yao, R.; Li, B.; Liu, H.; Jiang, L. Modelling of the microclimate saturation inside a safety helmet. Build. Environ. 2015, 87, 1–9. [Google Scholar] [CrossRef]
- Halimi, M.T.; Dhahri, H.; Khedher, N.B.; Hassen, M.B.; Sakli, F. Thermal Properties of Industrial Safety Helmets. Build. Environ. 2009, 5, 833–844. [Google Scholar]
- Underwood, L.; Vircondelet, C.; Jermy, M. Thermal comfort and drag of a streamlined cycling helmet as a function of ventilation hole placement. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2018, 232, 15–21. [Google Scholar] [CrossRef]
- Ghani, S.; ElBialy, E.M.A.A.; Bakochristou, F.; Gamaledin, S.M.A.; Rashwan, M.M. The effect of forced convection and PCM on helmets’ thermal performance in hot and arid environments. Appl. Therm. Eng. 2017, 111, 624–637. [Google Scholar] [CrossRef]
- Bogerd, C.P.; Walker, I.; Brühwiler, P.A.; Rossi, R.M. The effect of a helmet on cognitive performance is, at worst, marginal: A controlled laboratory study. Appl. Ergon. 2014, 45, 671–676. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Tanabe, S.I. Development of JOS-2 human thermoregulation model with detailed vascular system. Build. Environ. 2013, 66, 1–10. [Google Scholar] [CrossRef]
- Lv, Y.G.; Liu, J. Effect of transient temperature on thermoreceptor response and thermal sensation. Build. Environ. 2007, 42, 656–664. [Google Scholar] [CrossRef]
- Foda, E.; Almesri, I.; Awbi, H.B.; Sirén, K. Models of human thermoregulation and the prediction of local and overall thermal sensations. Build. Environ. 2011, 46, 2023–2032. [Google Scholar] [CrossRef]
- Zhou, X.; Xiong, J.; Lian, Z. Predication of skin temperature and thermal comfort under two-way transient environments. J. Therm. Biol. 2017, 70, 15–20. [Google Scholar] [CrossRef] [PubMed]
- Lan, L.; Tsuzuki, K.; Liu, Y.F.; Lian, Z.W. Thermal environment and sleep quality: A review. Energy Build. 2017, 149, 101–113. [Google Scholar] [CrossRef]
- Salloum, M.; Ghaddar, N.; Ghali, K. A new transient bioheat model of the human body and its integration to clothing models. Int. J. Therm. Sci. 2007, 46, 371–384. [Google Scholar] [CrossRef]
- Irzmańska, E. Case study of the impact of toecap type on the microclimate in protective footwear. Int. J. Ind. Ergon. 2014, 44, 706–714. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Maerefat, M. A new simplified thermoregulatory bioheat model for evaluating thermal response of the human body to transient environments. Build. Environ. 2010, 45, 2068–2076. [Google Scholar] [CrossRef]
- Ludwig, N.; Trecroci, A.; Caumo, A.; Alberti, G.; Michielon, G.; Formenti, D.; Gargano, M. Dynamics of thermographic skin temperature response during squat exercise at two different speeds. J. Therm. Biol. 2016, 59, 58–63. [Google Scholar]
- Neves, E.B.; Salamunes, A.C.C.; de Oliveira, R.M.; Stadnik, A.M.W. Effect of body fat and gender on body temperature distribution. J. Therm. Biol. 2017, 70, 1–8. [Google Scholar] [CrossRef]
- Lakhssassi, A.; Kengne, E.; Semmaoui, H. Modifed pennes’ equation modelling bio-heat transfer in living tissues: Analytical and numerical analysis. Nat. Sci. 2010, 2, 1375–1385. [Google Scholar] [CrossRef]
- Dixit, A.; Gade, U. A case study on human bio-heat transfer and thermal comfort within CFD. Build. Environ. 2015, 94, 122–130. [Google Scholar] [CrossRef]
- Tuzikiewicz, W.; Duda, M. Bioheat transfer equation. The problem of FDM explicit scheme stability. J. Appl. Math. Comput. Mech. 2015, 14, 139–144. [Google Scholar] [CrossRef][Green Version]
- Lakhssassi, A.; Kengne, E.; Semmaoui, H. Investigation of nonlinear temperature distribution in biological tissues by using bioheat transfer equation of Pennes’ type. Nat. Sci. 2010, 2, 131–138. [Google Scholar] [CrossRef]
- Yang, J.-H.; Kato, S.; Seo, J. Evaluation of the Convective Heat Transfer Coefficient of the Human Body Using the Wind Tunnel and Thermal Manikin. J. Asian Archit. Build. Eng. 2009, 8, 563–569. [Google Scholar] [CrossRef]
- Cano, S.P.; Sillero-Quintana, M.; Brito, C.J.; de Andrade Fernandes, A.; Bouzas Marins, J.C.; Costa, C.M.A.; de Azambuja Pussieldi, G.; Moreira, D.G. Daily rhythm of skin temperature of women evaluated by infrared thermal imaging. J. Therm. Biol. 2017, 72, 1–9. [Google Scholar]
- Kaynakli, O.; Kilic, M. Investigation of indoor thermal comfort under transient conditions. Build. Environ. 2005, 40, 165–174. [Google Scholar] [CrossRef]
- Pang, T.Y.; Subic, A.; Takla, M. Thermal comfort of cricket helmets: An experimental study of heat distribution. Procedia Eng. 2011, 13, 252–257. [Google Scholar] [CrossRef][Green Version]
- Bogerd, C.P.; Rossi, R.M.; Brühwiler, P.A. Thermal perception of ventilation changes in full-face motorcycle helmets: Subject and manikin study. Ann. Occup. Hyg. 2011, 55, 192–201. [Google Scholar]
- Mehnert, P.; Malchaire, J.; Kampmann, B.; Piette, A.; Griefahn, B.; Gebhardt, H. Prediction of the average skin temperature in warm and hot environments. Eur. J. Appl. Physiol. 2000, 82, 52–60. [Google Scholar] [CrossRef]
- Zhou, X.; Lian, Z.; Lan, L. An individualized human thermoregulation model for Chinese adults. Build. Environ. 2013, 70, 257–265. [Google Scholar] [CrossRef]
- Kubota, H.; Kuwabara, K.; Hamada, Y. Prediction of mean skin temperature for use as a heat strain scale by introducing an equation for sweating efficiency. Int. J. Biometeorol. 2014, 58, 1593–1603. [Google Scholar] [CrossRef]
- Mairiaux, P.; Malchaire, J.; Candas, V. Prediction of mean skin temperature in warm environments. Eur. J. Appl. Physiol. Occup. Physiol. 1987, 56, 686–692. [Google Scholar] [CrossRef] [PubMed]
- Katić, K.; Li, R.; Kingma, B.; Zeiler, W. Modelling hand skin temperature in relation to body composition. J. Therm. Biol. 2017, 69, 139–148. [Google Scholar] [CrossRef]
- Abu Bakar, R.; Jusoh, N.; Rasdan Ismail, A.; Zanariah Shamshir Ali, T. Effect on human metabolic rate of skin temperature in an office occupant. MATEC Web Conf. 2017, 90, 01070. [Google Scholar] [CrossRef]
- Laird, I.S.; Goldsmith, R.; Pack, R.J.; Vitalis, A. The effect on heart rate and facial skin temperature of wearing respiratory protection at work. Ann. Occup. Hyg. 2002, 46, 143–148. [Google Scholar] [PubMed]
- Fiala, D.; Lomas, K.J.; Stohrer, M. A computer model of human thermoregulation for a wide range of environmental conditions: The passive system. J. Appl. Physiol. 2017, 87, 1957–1972. [Google Scholar] [CrossRef] [PubMed]
- Dongmei, P.; Mingyin, C.; Shiming, D.; Minglu, Q. A four-node thermoregulation model for predicting the thermal physiological responses of a sleeping person. Build. Environ. 2012, 52, 88–97. [Google Scholar] [CrossRef]
- Katić, K.; Li, R.; Zeiler, W. Thermophysiological models and their applications: A review. Build. Environ. 2016, 106, 286–300. [Google Scholar] [CrossRef]
- Havenith, G.; Fiala, D. Thermal indices and thermophysiological modeling for heat stress. Compr. Physiol. 2016, 6, 255–302. [Google Scholar]
- Zhu He, Z.; Xue, X.; Liu, J. An Effective Finite Difference Method for Simulation of Bioheat Transfer in Irregular Tissues. J. Heat Transf. 2013, 135, 071003. [Google Scholar] [CrossRef]
- Lai, D.; Zhou, X.; Chen, Q. Modelling dynamic thermal sensation of human subjects in outdoor environments. Energy Build. 2017, 149, 16–25. [Google Scholar] [CrossRef]
- Lai, D.; Chen, Q. A two-dimensional model for calculating heat transfer in the human body in a transient and non-uniform thermal environment. Energy Build. 2016, 118, 114–122. [Google Scholar] [CrossRef]
- Weigert, M.; Nitzsche, N.; Kunert, F.; Lösch, C.; Schulz, H. The influence of body composition on exercise-associated skin temperature changes after resistance training. J. Therm. Biol. 2018, 75, 112–119. [Google Scholar] [CrossRef] [PubMed]
- Salamunes, A.C.C.; Stadnik, A.M.W.; Neves, E.B. The effect of body fat percentage and body fat distribution on skin surface temperature with infrared thermography. J. Therm. Biol. 2017, 66, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Davoodi, F.; Hassanzadeh, H.; Zolfaghari, S.A.; Havenith, G.; Maerefat, M. A new individualized thermoregulatory bio-heat model for evaluating the effects of personal characteristics on human body thermal response. Build. Environ. 2018, 136, 62–76. [Google Scholar] [CrossRef]
- Ziade, G.; Semaan, S.; Ghulmiyyah, J.; Kasti, M.; Hamdan, A.L.H. Structural and Anatomic Laryngeal Measurements in Geriatric Population Using MRI. J. Voice 2017, 31, 359–362. [Google Scholar] [CrossRef]
- Chia, C.W.; Ferrucci, L.; Spencer, R.G.; Fishbein, K.W.; Makrogiannis, S.K.; Lukas, V.A.; Okine, M.; Egan, J.M.; Ramachandran, R. Measurement of fat fraction in the human thymus by localized NMR and three-point Dixon MRI techniques. Magn. Reson. Imaging 2018, 50, 110–118. [Google Scholar]
- Lack, C.M.; Lesser, G.J.; Umesi, U.N.; Bowns, J.; Chen, M.Y.; Case, D.; Hightower, R.C.; Johnson, A.J. Making the most of the imaging we have: Using head MRI to estimate body composition. Clin. Radiol. 2016, 71, e1–e402. [Google Scholar] [CrossRef]
- Brooks, T.; Choi, J.E.; Garnich, M.; Hammer, N.; Waddell, J.N.; Duncan, W.; Jermy, M. Finite element models and material data for analysis of infant head impacts. Heliyon 2018, 4, e01010. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal sensation and comfort models for non-uniform and transient environments: Part I: Local sensation of individual body parts. Build. Environ. 2010, 45, 380–388. [Google Scholar] [CrossRef]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal sensation and comfort models for non-uniform and transient environments, part II: Local comfort of individual body parts. Build. Environ. 2010, 45, 389–398. [Google Scholar] [CrossRef]
- Tanabe, S.I.; Kobayashi, K.; Nakano, J.; Ozeki, Y.; Konishi, M. Evaluation of thermal comfort using combined multi-node thermoregulation (65 MN) and radiation models and computational fluid dynamics (CFD). Energy Build. 2002, 34, 637–646. [Google Scholar] [CrossRef]
| Tissue | |||||
|---|---|---|---|---|---|
| W/m·K | kg/m3 | J/kg·K | m3/m3·s | kg/m3 | |
| Brain | 0.49 | 1080 | 3850 | 10.132 | 13,400 |
| Bone | 1.16 | 1500 | 1591 | 0 | 0 |
| Muscle | 0.42 | 1085 | 3768 | 0.538 | 684 |
| Fat | 0.16 | 850 | 2300 | 0.0036 | 58 |
| Skin | 0.47 | 1085 | 3680 | 5.48 | 368 |
| 1 | 2 | 3 | 4 | ||||
|---|---|---|---|---|---|---|---|
| Tissue | Thickness (cm) | Tissue | Thickness (cm) | Tissue | Thickness (cm) | Tissue | Thickness (cm) |
| Brain | 8.81 | Brain | 7.37 | Brain | 1.37 | Muscle | 3.18 |
| Bone | 0.46 | Bone | 0.57 | Bone | 1.46 | Bone | 0.48 |
| Muscle | 0.31 | Muscle | 1.71 | Brain | 4.5 | Muscle | 3.56 |
| Fat | 0.78 | Fat | 0.75 | Bone | 0.66 | Bone | 0.58 |
| Skin | 0.27 | Skin | 0.31 | Muscle | 0.69 | Muscle | 0.46 |
| - | - | - | - | Fat | 0.76 | Fat | 0.52 |
| - | - | - | - | Skin | 0.36 | Skin | 0.4 |
| RMSE | |||
| Present Model | AUB model | ||
| Case1 | Core | 0.2127 | 0.3517 |
| Skin | 0.3080 | 0.3415 | |
| RMSE | |||
| Present Model | Kaynakli and Killc | ||
| Case2 | Skin | 0.5501 | 0.6153 |
| Curve | Muscle (Figure 7) | Fat (Figure 8) | Skin (Figure 9) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Intercept | Slope | r | Intercept | Slope | r | Intercept | Slope | r | |
| Brain | 0.9993 | 0.00074 | 0.99104 | 0.9999 | 0.00009 | 0.9962 | 0.999 | 0.0011 | 0.9885 |
| Bone | 0.9798 | 0.02151 | 0.99104 | 0.9971 | 0.0029 | 0.9962 | 0.9709 | 0.0318 | 0.9885 |
| Muscle | 0.9758 | 0.02597 | 0.98721 | 0.9961 | 0.0038 | 0.9962 | 0.9639 | 0.0394 | 0.9862 |
| Fat | 1.0016 | −0.0081 | −0.91704 | 1.001 | −0.0143 | −0.9999 | 0.99 | 0.0107 | 0.9288 |
| Skin | 1.0014 | −0.0071 | −0.91478 | 1.0017 | −0.0274 | −0.9995 | 0.9934 | 0.0071 | 0.8969 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Zhang, Y.; Huang, Z.; Zhang, G.; Gao, Y. Influence of Internal Structure and Composition on Head’s Local Thermal Sensation and Temperature Distribution. Atmosphere 2020, 11, 218. https://doi.org/10.3390/atmos11020218
He S, Zhang Y, Huang Z, Zhang G, Gao Y. Influence of Internal Structure and Composition on Head’s Local Thermal Sensation and Temperature Distribution. Atmosphere. 2020; 11(2):218. https://doi.org/10.3390/atmos11020218
Chicago/Turabian StyleHe, Shuai, Yinghua Zhang, Zhian Huang, Ge Zhang, and Yukun Gao. 2020. "Influence of Internal Structure and Composition on Head’s Local Thermal Sensation and Temperature Distribution" Atmosphere 11, no. 2: 218. https://doi.org/10.3390/atmos11020218
APA StyleHe, S., Zhang, Y., Huang, Z., Zhang, G., & Gao, Y. (2020). Influence of Internal Structure and Composition on Head’s Local Thermal Sensation and Temperature Distribution. Atmosphere, 11(2), 218. https://doi.org/10.3390/atmos11020218





