Abstract
The correct estimation of Sensible Heat Flux (H) and Latent Heat Flux (LE) (i.e., turbulent fluxes) is vital in the understanding of exchange of energy and mass among hydrosphere, atmosphere, and biosphere in an ecosystem. One of the most popular methods to measure these fluxes is the Eddy Covariance (EC) technique; however, there are a number of setbacks to its application, especially in remote and topographically complex terrain such as the higher altitudes of the Andes. Efforts have been made by the scientific community to parameterise these fluxes based on other more commonly measured variables. One of the most widespread methods is the so-called bulk method, which relates average temperature, humidity, and wind vertical profiles to the turbulent fluxes. Another approach to estimate LE is the Penman-Monteith (PM) equation which uses meteorological measurements at a single level. The objective of this study was to validate these methods for the first time in the Tropical Andes in Southern Ecuador (in the páramo ecosystem at 3780 m a.s.l.) using EC and meteorological measurements. It was determined that the bulk method was the best to estimate H, although some adjustments had to be made to the typical assumptions used to estimate surface meteorological values. On the other hand, the PM equation yielded the best LE estimations. For both fluxes, the error in the estimations was within the uncertainty range of the EC measurements. It can be concluded that it is possible to accurately estimate H and LE using the methods described in this paper in this ecosystem when no direct measurements are available.
1. Introduction
The turbulent fluxes (e.g., the Latent Heat Flux (LE) and Sensible Heat Flux (H)) are crucial elements of an ecosystem’s energy balance. The estimation of these atmospheric processes at the land surface has long been recognized as vital in the understanding of exchange of energy and mass among hydrosphere, atmosphere, and biosphere [1]. One of the most popular methods to measure turbulent fluxes is the eddy covariance technique, which consists of measuring the 3D field of the wind, the air temperature, pressure, humidity, and its water vapour content at high frequencies (typically 10–50 Hz). Once these variables are known, the latent heat flux and the sensible heat flux can be derived [2,3].
One of the major advantages is that this method provides continuous measurements that are spatially averaged [4]. However, the eddy covariance method has some restrictions that limit its applicability: (i) it requires constant supervision and maintenance, (ii) measurements in complex terrain are challenging because of the theoretical assumptions to transform the high-frequency measurements to turbulent fluxes [5], and (iii) because of extensive data quality requisites, gaps are inevitable, particularly under low turbulence mixing conditions [6,7]. Because of these difficulties, efforts have been made to parameterise them based on more commonly measured variables [8,9,10,11,12,13] and to compare among different methods to estimate and measure these fluxes [14,15,16,17,18]. One of the most frequently used approaches is to follow the work of [19] and [20], which relates the average temperature, humidity, and wind speed profiles in the boundary layer to the turbulent fluxes. In this way, the sensible and latent heat flux can be estimated from routine meteorological measurements. Another approach to compute the latent heat flux is to calculate the reference evapotranspiration (ETo), which can be transformed to actual evapotranspiration (ETa) by multiplying it by the crop coefficient (kc). Finally, ETa can be transformed to LE by multiplying it with the latent heat of vaporization of water. However, these methods are not directly applicable and have to be calibrated depending on the specific conditions of the surface such as the vegetation [21], and they might even have seasonal variation [7]. Therefore, observations of H and LE are required.
Because of the complexity and remoteness of the terrain and the fact that high-quality meteorological measurements are scarce in developing countries [22], there is a lack of knowledge about turbulent fluxes in the Tropical Andes. The alternative methods to estimate H and LE have not been tested or calibrated in this region. In this study, we used data from the first eddy covariance tower in the páramo ecosystem, located in the Andean highlands in Ecuador, to evaluate the feasibility of the methods to calculate H and LE based on routine meteorological data.
2. Materials and Methods
2.1. Study Area
The study area is located in the Zhurucay Ecohydrological Observatory at 3870 m a.s.l. in Southern Ecuador, on the divide of waters draining into the Pacific Ocean and through the Amazon River to the Atlantic Ocean on the Andean Cordillera (03°03’45.12” S, 79°14’04.96” W). Annual rainfall is 1345 mm and displays low seasonality, with a relatively dry period from June to August [23]. Maximum seasonal rainfall values are related to the Inter Tropical Convergence Zone [24]. The mean annual temperature is 6 °C (max. = 14.2 °C, min. = 0.4 °C), mean wind speed is 2 m s−1 [25], the relative air humidity is 93.6%, and the prevalent wind direction is from the northeast.
The vegetation within the catchment is typical of páramo grasslands: composed of tussock grass (mainly Calamagrostis sp.), which covers more than 70% of the surface with heights of between 30 and 80 cm [24], and cushion plants (such as Plantago rigida, Xenophyllum humile, and Azorella spp.), which cover around 25% of the surface [26]. The sensors are located in an area where the tussock grass is predominant. More information about the study site can be found in the cited studies in this subsection and several others [27,28,29]. Figure 1 shows the study location and a landscape view of the observatory.
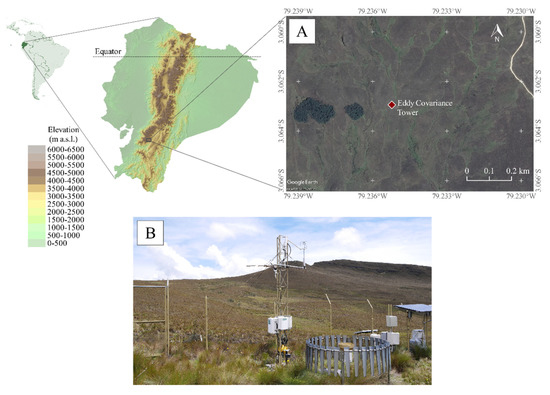
Figure 1.
Study area. (A) Aerial view of the surroundings of the Eddy covariance tower in the Zhurucay Ecohydrological Observatory. It is observed that the main vegetation cover is tussock grass. (B) Eddy covariance tower installed at 3780 m a.s.l.
2.2. Instrumentation
The turbulent fluxes were measured by means of an enclosed path LI-COR Eddy Covariance system (LI-7200) and a Gill WindMaster 3D sonic anemometer. These sensors are installed at 3.6 m above the surface. At a short distance, a separate automatic weather station was installed to measure the basic meteorological variables. Air temperature and relative humidity were measured by means of a Campbell Scientific CS-215 combined probe with radiation shield. A Met-One 034B Windset anemometer was used to measure wind speed and direction and the atmospheric pressure was measured with a Vaisala PTB110 sensor. The measurement height of all sensors was 1.8 m above the surface.
The four radiation components were measured with a Kipp & Zonen CNR4 radiometer installed at 0.5 m above the surface, which is associated with a 3 m radius footprint. This height was chosen in order to cover vegetation only within the sensor footprint. Therefore, both the fence surrounding the site and the small creek down-slope did not disturb the measurements. Another CNR4 installed also at 0.5 m a few meters away was used to double check the measurements, and they were comparable (data not shown).
2.3. Data
The turbulence data were collected at a sampling rate of 20 Hz and averages, variances, and fluxes were calculated every 30 minutes using the EddyPro software (version 6.2.0, LI-COR, Lincoln, NE, USA). This also provides a quality control of the data using quality flags given by the sensors, plausibility limits, and spike removal. Specific corrections were also applied, such as planar fit adjustment, co-spectra filtering, time-lag compensation, and humidity dependent spectrum correction. More information about these corrections can be found in [24].
Measurements from the weather station were sampled every 15 seconds and averages were recorded every 5 minutes, and these data were used to calculate the 30-min averages after quality control was performed. Both data sets were one-year long (March 2017–Feb 2018), with a total of 17,502 half-hourly observations.
Before performing any calculations, we filtered the data to obtain a high-quality data set. From the eddy covariance data-set, missing, low-quality (based on the flag given by the EddyPro software for H and LE, values with a flag value higher than 1 were not considered), or implausible values (LE > 600 W m−2, T < −50 °C, T > 50 °C) were filtered out. The same was done for the weather station data set. After filtering, we selected only measurements for which data was available for both datasets, leaving 11,492 observations (66%), which is an acceptable value for eddy-covariance measurements when compared to other flux sites [30].
2.4. Methods
The sensible and latent heat flux (H and LE, respectively) are defined as:
where ρ is the near-surface air density, cp is the specific heat capacity of air, (ω’θ’)s is the vertical kinematic turbulent heat flux, (ω’q’)s is the vertical kinematic turbulent moisture flux, and Lv is the latent heat of vaporization of water. The subscript s stands for surface values. The fluxes are defined positive towards the surface.
2.4.1. Bulk Method
The bulk method is based on the assumption that the turbulent fluxes (H and LE) can be related to the vertical gradients of temperature, specific humidity, and wind speed between the surface and one level in the atmosphere. The advantage of using the surface as one of the levels is that the gradients become relatively large. Large gradients reduce the sensitivity and measurement errors when compared to calculating the gradient from measurements made at two levels in the atmosphere. The turbulent fluxes for this method are expressed as follows:
where u* is the friction velocity, θ* friction temperature, and q* friction specific humidity, and are defined as:
where V is wind speed, z is the height of the measurements (i.e., 1.8 m), θ is potential temperature, κ the dimensionless Von Karman constant (0.41), zom is the momentum or aerodynamic roughness length, which is defined as the height above the surface where wind speed theoretically becomes zero, and zoh is the roughness length for heat.
We assumed that the roughness lengths for heat and moisture are the same, which is commonly done [31]. We excluded the displacement height from the calculations (Equations (6) and (7)) as we assumed it to be zero. To calculate density, we used the calculations of saturated vapour pressure and water vapour pressure, which are discussed below.
Ψm and Ψh, in Equation (5) to (7), are the vertically integrated stability functions for momentum and heat. The turbulence flux values can then be found via iteration assuming for the first iteration neutral conditions so that z/L = 0. For the definition of the stability functions and the method of iteration we followed [32].
The surface temperature was estimated from the outgoing long-wave radiation data using Equation (8):
where OLR is outgoing long-wave radiation, σ is the Stefan-Boltzmann constant, ε is the emissivity of the surface, and Ts is the surface temperature in Kelvin.
We calculated specific humidity (q) based on temperature, relative humidity, and pressure as follows:
where, psat is saturation vapour pressure, T is air temperature, RH is relative humidity, pv is actual vapour pressure, pd is the pressure of dry air, p is pressure, Rd is the gas constant for dry air, Rv is the gas constant for water vapour, ps0 is the saturation vapour pressure at T0 = 273.16 K, and w is the mass mixing ratio of water vapour to total air. This method was used to calculate specific humidity at 1.8 m and at the surface.
For surface humidity estimations we considered two options. First, we assumed that the surface is always saturated, hence relative humidity RHs = 100% at all times. The second assumption was to limit the relative humidity gradient to a maximum value during daytime. For this second approach, the assumption that RHs = 100% was retained during the night, because the air is more humid as there is no incoming shortwave radiation, and during most nights the RH measured at 1.8 m is also close to saturation (mean RH at night during the study period was about 97%).
To calculate the surface specific humidity a second method was applied as well, following the study from [33]. In this relation, the surface specific humidity can be calculated from the surface temperature:
where rc is the stomatal resistance of the vegetation.
We calculated the roughness length for momentum (zo) using only data with near neutral conditions so that the wind speed profiles are theoretically logarithmic. Neutrally stable conditions were assumed to occur when the temperature difference between T and Ts was smaller than or equal to +/− 0.2 °C. The momentum roughness length was then calculated assuming a logarithmic wind profile:
which yielded an average value of zom = 0.077 m.
To calculate zoh we used two different approaches. First, we assumed it to be constant throughout the entire study period. In this case, it was defined as zoh = zom/7.4 (following the equations from [34]). When z0h is calculated in this manner, it is assumed that the roughness length for heat only depends on the land surface characteristics, as is the case for the momentum roughness length.
In the second approach, the dependence of the value of zoh on u* (and thus on the conditions of the flow) is considered, following the recent work by [35] and [36]. The calculation was performed as follows:
with kB−1 defined as:
where the roughness Reynolds number is Re* = zom u* v−1, in which v is the kinematic viscosity.
2.4.2. The Penman-Monteith Equation
The latent heat flux can also be calculated by means of the Penman-Monteith equation. This approach does not use the vertical profiles as input but combines the energy balance closure and aerodynamic characteristics. As formulated in Equation (17), the method includes all the parameters that govern energy exchange and the corresponding latent heat flux from a uniform extension of the so-called reference crop. The reference crop resembles 0.12 m, well-watered, actively growing grass. We calculated reference evapotranspiration (ETo) following the procedure described by [37]:
where Rn is net radiation, G is soil heat flux (estimated to be 10% of Rn during daytime and 50% during night-time [37]), and V is wind speed. Details about the calculation of γ, Δ, e0(T) and ea can be found in [37]. This method therefore only necessitates routine meteorological measurements as an input (temperature, solar radiation, relative humidity, wind speed, and atmospheric) and avoids the need for assumptions about the values of the variables at the surface.
After this, we calculated actual evapotranspiration (ETa) by multiplying ET0 by the value of kc, which serves to transform ET0 to ETa. The value of kc is first taken as a constant (0.9) according to [24]. However, in the same paper it is reported to vary between 0.87 in the drier period and 0.92 in the wetter period for this study site. Finally, we multiplied this value by Lv to obtain the latent heat flux.
3. Results and Discussion
3.1. The Bulk Method
In this section, the first results shown correspond to H and LE calculated by means of the bulk method using the parameters ε = 1, qs = qsat(Ts), and zom = 0.077 m from the logarithmic wind profile assumption) and constant zoh equal to zom/7.4. Note that the iterations did not converge for wind speed values smaller than 1.5 m s−1. Therefore, we only made the calculations for the time steps with measured wind speed higher than 1.5 m s−1. These results are shown in the scatter plots in Figure 2, where we compare the bulk flux results to those from the turbulence measurements (correlations were found to be significant with p < 0.01).
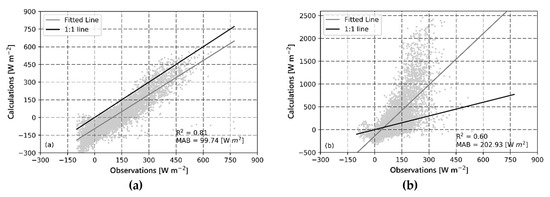
Figure 2.
Turbulent fluxes estimated by the bulk method compared to observations: (a) Sensible Heat Flux (H) and (b) Latent Heat Flux (LE). The correlation for both H and LE was significant (p-value < 0.01).
In the case of H (Figure 2a), even though the calculated values are well correlated to the measurements (R2 = 0.81), there is a systematic underestimation in the results of the bulk method, as indicated by the location of most of the points in the scatter plot below the 1:1 line, and the Mean Absolute Bias (MAB) is close to 100 W m−2. These errors might be related to the assumptions made for the calculation of surface temperature leading to an underestimation of the temperature gradient during daytime and an overestimation of the gradient during night-time. This combination would result in the observed systematic underestimation in sensible heat flux calculations.
In contrast, LE estimations (Figure 2b) are less strongly (R2 = 0.60 compared to R2 = 0.81 for H) correlated to the observations. There is heavy overestimation of the higher values of LE as reflected in the slope of the regression line being much higher than 1. The poor quality of the calculations is also reflected in the value of MAB close to 200 W m−2. These large overestimation for higher values of LE could be related to the assumptions made for the calculation of surface humidity, leading to either an overestimation of the temperature gradient or of the specific humidity gradient. The implications of the assumptions for the estimation of H and LE are addressed in the next subsection.
3.2. Alternative Assumptions in the Application of the Bulk Method
As found in the previous subsection, the bulk method results deviate considerably from those of the Eddy Covariance (EC) method. Most likely this is related to the assumptions that we initially made to estimate the values of Ts and qs at the surface. Therefore, we study a variety of different approaches for the estimation of different parameters in this subsection.
3.2.1. Emissivity (ε)
With ε = 1, as was assumed in the previous subsection, the surface is a black body. Values in the range 0.95–0.975 have been found to be reasonable in the past for natural surfaces [38,39,40]. In this study we found that the optimum value for the páramo is 0.95, as the surface temperature shows the most realistic values (higher values led to freezing temperatures during most nights, which is not the case in the area). Taking a lower ε value will result in higher values of estimated Ts. Therefore, ΔT will be smaller during the night, when negative H is observed, and this will result in less negative H estimations at night. On the other hand, ΔT will be higher during the day and thus H will also be higher. This solves the systematic underestimation problem.
The second row of Table 1 shows the result of applying the bulk method for ε = 0.95. It is observed that H estimations improved significantly, MAB decreased from 99.74 W m−2 to 32.05 W m−2 (this is below the uncertainty range of the H measurements in the study site, as reported by [24]), and R2 increased from 0.81 to 0.90. However, the quality of LE estimations decreased (MAB increased and R2 slightly increased). This was expected as higher temperatures lead to higher specific humidity values in an exponential relationship. Hereafter, we used ε = 0.95 for our calculations, i.e., every next row in Table 1 also show the results using ε = 0.95.

Table 1.
Summary of the results for the different alternatives of the assumptions made for the application of the bulk method. MAB (Mean Absolute Bias) is in W m−2.
3.2.2. Surface Humidity
We used two alternatives to calculate the surface specific humidity estimations, and thus Δq. First, we used the approach presented in Equation (13) [33]. This method was applied only during daytime (06H00–18H00), as the assumption of saturation at the surface seems realistic during night-time. The major drawback of this approach is that it requires a value for the stomatal resistance of the vegetation cover (rc) as input, which is not known for the páramo tussock grasslands. However, we used two values found in the literature to test the potential impact that this refinement in the calculations could have in the estimation of LE.
First, we used 10 s m−1, as representative of green well-watered grasslands [37]. As observed in Table 1, the values for H did not change because this only impacts the humidity gradient, whereas the MAB for LE decreased by a factor of more than 2; however, R2 decreased. Secondly, we used the value estimated by [41] for tussock grasslands in New Zealand (200 s m−1). Even though the vegetation is similar, those estimations were based on measurements of only two days during daytime under dry conditions, which are not representative of our humid study site. The results of this estimation were very poor, LE was largely overestimated, and the correlation was almost zero. Even though these estimations did not yield accurate results, it is important to note that LE appears to be quite sensible to rc, and hence, it shows potential for when the stomatal resistance for this landscape is known.
The second approach we used is based on the idea that the assumption of a permanently saturated surface is unrealistic, especially during daytime (06H00–18H00). This is supported by the observations, which show that RH values as low as 20% (data not shown) are possible and that the soil can get so dry that even soil moisture measurements below the wilting point have been recorded, as is shown later in this section. Thus, we hypothesize that during the daytime the assumption of a saturated surface might not be realistic, causing unrealistically high values of Δq and hence overestimation of LE. In order to mimic this, we limited the daytime relative humidity gradient (ΔRH) to a maximum of 5% and 10% (Table 1) and kept the assumption of saturation at the surface during night-time. In both cases, the value of MAB was considerably reduced and R2 also improved. The best results were obtained when ΔRHmax was set to 5%.
3.2.3. Thermal Roughness Length
Alternatively, we followed [35], who found a relation between the values of z0h and u*. The only unknown value to apply this method is the constant C1 (Equation (16)), which depends on the emissivity of the surface and on the vegetation cover. We calculated the turbulent fluxes using values for C1 in a range between grass and shrub lands, which is representative of our study site. The results in Table 1 show that both H and LE calculations improved via this method. The MAB for H decreased substantially and did not vary too much for the chosen values. It also vastly improved the LE estimations, and the respective MAB values showed a wider range for this flux; R2 was not affected by changes in C1.
3.2.4. The Best Possible Estimation
Based on the results from this section, optimising for best possible results for H and LE was achieved by applying the bulk method using ε = 0.95, ΔRHmax = 5%, and C1 = 0.7. The results of these calculations are summarized in Table 1 and shown in Figure 3. The results for H are quite good for both positive and negative values, with the only exception being a few positive observations that were estimated to be close to zero (Figure 3). In the case of LE, although it was still systematically overestimated, the MAB was for the first time below 100 W m−2. In addition, the correlation was the best among all the methods used (all correlations are found to be significant with p < 0.01).
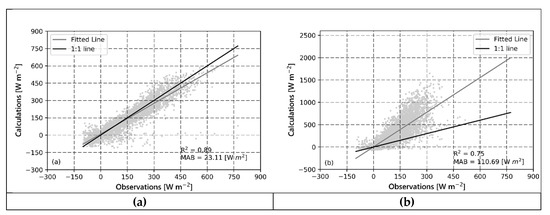
Figure 3.
Turbulent fluxes estimated using the best possible estimation with the bulk method compared to observations (ε = 0.95, ΔRHmax = 5%, and C1 = 0.7): (a) Sensible Heat Flux, (b) Latent Heat Flux (p < 0.01 for both correlations).
3.3. The Penman-Monteith (PM) Equation
As shown in Figure 3, the estimation of LE (Figure 3b) was not as good as the one for H (Figure 3a) using the bulk method even when the alternatives to the assumptions were implemented. The main issue when calculating LE via the bulk method seems to be the estimation of the q gradient. In contrast to this, the PM equation requires only measurements from a weather station and thus has the strength that no assumptions are needed to estimate the equation inputs. This approach outperformed the previously shown estimations of LE: MAB is significantly lower (30.52 W m−2) and R2 is higher than in the previous cases (Figure 4).
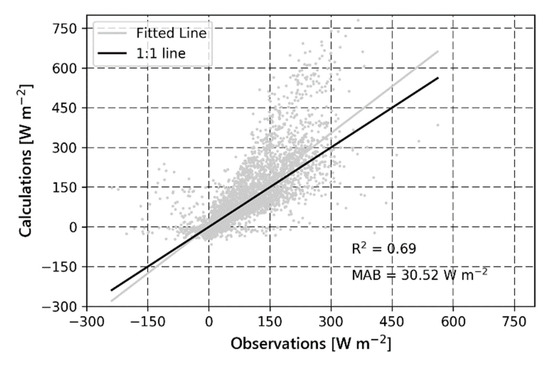
Figure 4.
Latent Heat Flux estimated via the Penman-Monteith equation compared to observations (correlation is found to be significant with p < 0.01).
3.4. Monthly Analysis
In order to gain more insight into our results and to determine which variables control and lead to the best estimation of H and LE, we analysed the calculations on a monthly time scale. The summary is shown in Table 2, in which a seasonal pattern can be recognised. When compared to precipitation and soil moisture during the study period (Figure 5), estimations seem to be better (i.e., the best combinations of high R2 and low MAB) in general for the wet months and worse during the dry months. In particular, the MAB is lower for wet months compared to dry months. When we focus on the turbulent fluxes as estimated by means of the bulk method, March is the month when both estimations have a low MAB, while the correlation is high. In contrast, the estimations are especially erroneous for LE in November (highest MAB of all estimations), when soil moisture reaches its minimum value (Figure 5). Interestingly, for LE estimations based on the Penman-Monteith equation, the estimations were also the poorest (Table 2) during the months of November and December when the soil is drier (Figure 5). It should be noted that soil moisture from June to October is nearly constant, whereas precipitation decreases compared to the March–April and January–February periods. This could be explained by the fact that precipitation in the form of drizzle (a common precipitation type in the páramo [23]) and fog are not measured by the tipping bucket rain gauge. This “occult” precipitation could contribute to maintain the soil moisture at the levels observed in Figure 5b, as hypothesised by [42]. Furthermore, the period when fog occurs more frequently is from June through August (while almost no fog is observed during November and December). Additionally, the highest values of solar radiation were observed in November and December (Figure 5c). The combination of these factors could explain the patterns observed in Figure 5a,b.

Table 2.
Monthly values for the mean absolute bias (MAB is in W m−2) and R2 when applying the best possible estimation and the Penman-Monteith method.
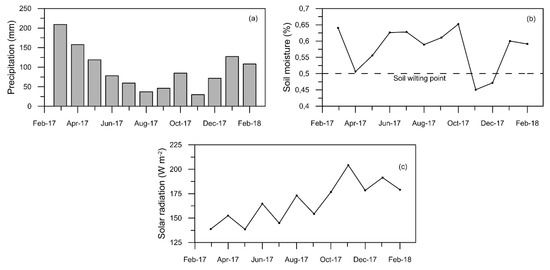
Figure 5.
(a) Total monthly precipitation, (b) monthly average soil moisture, and (c) monthly average solar radiation for the study period. Figure 6 shows the time series for the first 12 days of March and November. In the case of H (Figure 6a,b), it was observed that the fluxes are larger in November, primarily as a result of the increased solar radiation in the study area during this month [43]. The main errors in the H calculations are made when large negative values occur (i.e., when H < 0), as observed in Figure 6a,b. This causes the MAB to be higher in November than in March (Table 2). LE is shown in Figure 6c,d for March and November respectively. In Figure 6c,d, we observe the characteristic overestimation of LE calculations; nonetheless, this overestimation is more pronounced during November (Figure 6d), and this is why MAB is so much higher in this month compared to the March value.
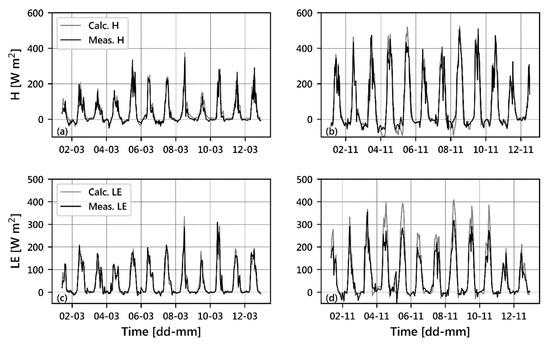
Figure 6.
Time series of observed and estimated Sensible and Latent Heat Flux for a period for when estimations are the best (a and c) and for a period when estimations are worst (b and d). A t-test was performed for the four pairs of time series shown in the figure; the p-values were smaller than 0.05 for all of them. Therefore, it can be concluded that the measurements are significantly different from the calculations for all the figures.
We found that the differences in LE might be explained best by precipitation (Figure 5a) and soil moisture (Figure 5b). March was the wettest month, as can be seen from the precipitation and soil moisture data. The opposite was the case for November, which was the driest month in our study period. The systematic overestimation of the bulk method LE throughout the year stands out in November. Based on precipitation and soil moisture, we can hypothesize that these variables are related to this larger error during this month. As observed in Figure 5b, November is the month where the soil is the driest and below the wilting point (which was found to be 0.5 [44] for the páramo grasslands). The wilting point is the humidity at which the roots of the plants cannot uptake water from the soil pores anymore. Therefore, the larger errors in this month could be explained by the fact that there is no water available to evaporate. Therefore, the bulk method overestimated the latent heat flux, as it does not consider water availability. The systematic overestimation of Δq was also more pronounced during this month because it was the warmest one (data not shown), and the error in the specific humidity estimations is larger for higher temperatures.
However, during the drier months a higher bias was also observed using the Penman-Monteith method. To discriminate between the wet and dry period, Figure 7 shows a scatter plot with the same data shown in Figure 4 but now for separate datasets for the dry and wet period. The brown points and fitted line correspond to data from the dry conditions (November, December, and January). It is observed that they are clustered above the 1:1 line and that the overestimation of LE is higher for this period (MAB = 60.66 W m−2). The data for the wet period is shown using green points and a green fitted line; the line overlaps the 1:1 line. This indicates that the systematic overestimation is restricted to the dry period, and hence, LE is more accurately estimated using this method under wet conditions (MAB decreased to 21.52 W m−2).
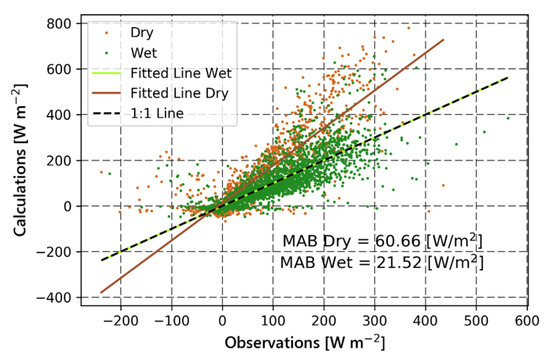
Figure 7.
Latent Heat Flux estimated via the Penman-Monteith equation compared to observations. Brown points correspond to dry conditions and green points to wet conditions.
The reason for this overestimation under dry conditions may be related to the fact that we used a constant value for kc. By keeping the value constant, we assume that the proportion of reference evapotranspiration that is actually realized is also constant throughout the year. This might not be the case in drier periods, when water may not be available for different reasons (i.e., dry soil, limited plant transpiration, plant stress). To test this hypothesis, we used the two different values of kc proposed by [24] for the wet and the dry seasons in the same study site. However, this did not improve our estimations significantly (data not shown). This might be due to the fact that the distinction between the wet and dry seasons in the aforementioned publication was based on monthly precipitation, whereas the differences for LE seem to be more related to soil moisture conditions.
4. Conclusions
The main goal of this project was to determine if Sensible Heat Flux (H) and Latent Heat Flux (LE) can be accurately estimated in the páramo ecosystem located in the high Tropical Andes using data from an automatic weather station. The results were evaluated by comparing them to the measurements from an eddy covariance tower located a few meters away.
The best estimations for H were obtained via the bulk method and a combination of our modifications, i.e., emissivity equal to 0.95 instead of 1, considering zoh as dependent on the conditions of the flow, and limiting the relative humidity gradient to 5%, to reduce the error on dry days. The results of these calculations were significantly and strongly correlated (R2 = 0.9) with the eddy covariance observations and the mean absolute bias (MAB) below the uncertainty range of the H measurements in the study site [24].
The best estimations of LE were obtained via the Penman-Monteith equation. This method is only dependent on variables which are directly available from the weather station measurements. Hence, assumptions for surface temperature and relative humidity are avoided. The results of these calculations were significantly and highly correlated (R2 = 0.69) with the eddy covariance observations and the Mean Absolute Bias (MAB) was close to the uncertainty range of the LE measurements in the study site [24]. However, LE was still overestimated, especially under dry conditions. The best results were obtained in March (the wettest month).
All in all, the evidence from this study suggests that the modified bulk method and the Penman -Monteith equation are suitable to estimate the turbulent fluxes in this ecosystem. Future studies are encouraged to focus on dry periods, when the largest errors were found. Furthermore, one method that could improve the results is to consider the stomatal resistance (rc) dependency on the weather conditions. L was found to be very sensitive to different values of rc, which was assumed to be a constant within this study. Research (e.g., its value, its seasonality, and its dependence on the weather and soil conditions) on this parameter is encouraged as this could lead to better quality estimations of qs, and hence LE.
Author Contributions
Conceptualization, M.C.; methodology, M.C., L.B. and P.S.; software, L.B. and G.C.-R.; formal analysis, M.C. and L.B.; investigation, M.C. and L.B.; resources, G.C.-R.; data curation, G.C.-R.; writing—original draft preparation, M.C. and L.B.; writing—review and editing, all authors; visualization, M.C. and L.B.; supervision, P.S.; project administration, G.C.-R.; funding acquisition, G.C.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Research Office of Universidad de Cuenca (DIUC) through the Project XIII–Conc: “Estudio Comparativo de Métodos de Estimación de Evapotranspiración Actual en Suelos Húmedos de una Micro cuenca de Páramo Andino,” and by the Ecuadorian Secretary of Higher Education, Science, Technology and Innovation (SENESCYT) through “Programa de Fortalecimiento de las Capacidades en Ciencia, Tecnología, Investigación e Innovación de las Instituciones de Educación Superior Públicas (2013–2014)”.
Acknowledgments
M.C. is thankful to Secretaría Nacional de Ciencia y Tecnología (SENESCYT) and Instituto de Fomento al Talento Humano (IFTH). These institutions funded his master’s studies at Utrecht University, where this research was carried out, via the scholarship programme Convocatoria Abierta 2016, scholarship ARSEQ-BEC-002500-2016. The authors thank Elena Popa for her valuable comments and suggestions during early stages of this research. The authors would like to thank the comments received by two anonymous reviewers, which we believe greatly improved the quality and clarity of the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Burba, G.; Anderson, D. A Brief Practical Guide to Eddy Covariance Flux Measurements, 1.0.1th ed.; LI-COR Biosciences Inc.: Lincoln, NE, USA, 2010. [Google Scholar]
- Aubinet, M.; Vesala, T.; Papale, D. Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 9789400723504. [Google Scholar]
- Wang, K.; Liu, C.; Zheng, X.; Pihlatie, M.; Li, B.; Haapanala, S.; Vesala, T.; Liu, H.; Wang, Y.; Liu, G.; et al. Comparison between eddy covariance and automatic chamber techniques for measuring net ecosystem exchange of carbon dioxide in cotton and wheat fields. Biogeosciences 2013, 10, 6865–6877. [Google Scholar] [CrossRef]
- Lee, X.; Massman, W.; Law, B. Handbook of Micrometeorology; Lee, X., Massman, W., Law, B., Eds.; Atmospheric and Oceanographic Sciences Library; Springer: Dordrecht, The Netherlands, 2005; Volume 29, ISBN 978-1-4020-2264-7. [Google Scholar]
- Foken, T.; Wichura, B. Tools for quality assessment of surface-based flux measurements. Agric. For. Meteorol. 1996, 78, 83–105. [Google Scholar] [CrossRef]
- Berkowicz, R.; Prahm, L.P. Evaluation of the profile method for estimation of surface fluxes of momentum and heat. Atmos. Environ. 1982, 16, 2809–2819. [Google Scholar] [CrossRef]
- Tajfar, E.; Bateni, S.M.; Margulis, S.A.; Gentine, P.; Auligne, T.; Tajfar, E.; Bateni, S.M.; Margulis, S.A.; Gentine, P.; Auligne, T. Estimation of Turbulent Heat Fluxes via Assimilation of Air Temperature and Specific Humidity into an Atmospheric Boundary Layer Model. J. Hydrometeorol. 2019. [Google Scholar] [CrossRef]
- Xu, T.; Liang, S.; Liu, S. Estimating turbulent fluxes through assimilation of geostationary operational environmental satellites data using ensemble Kalman filter. J. Geophys. Res. 2011, 116, D09109. [Google Scholar] [CrossRef]
- He, X.; Xu, T.; Bateni, S.; Neale, C.; Auligne, T.; Liu, S.; Wang, K.; Mao, K.; Yao, Y. Evaluation of the Weak Constraint Data Assimilation Approach for Estimating Turbulent Heat Fluxes at Six Sites. Remote Sens. 2018, 10, 1994. [Google Scholar] [CrossRef]
- Radić, V.; Menounos, B.; Shea, J.; Fitzpatrick, N.; Tessema, M.A.; Déry, S.J. Evaluation of different methods to model near-surface turbulent fluxes for a mountain glacier in the Cariboo Mountains, BC, Canada. Cryosphere 2017, 11, 2897–2918. [Google Scholar] [CrossRef]
- Basu, S. Hybrid Profile—Gradient Approaches for the Estimation of Surface Fluxes. Bound. Layer Meteorol. 2019, 170, 29–44. [Google Scholar] [CrossRef]
- Li, Y.; Kustas, W.P.; Huang, C.; Kool, D.; Haghighi, E. Evaluation of soil resistance formulations for estimates of sensible heat flux in a desert vineyard. Agric. For. Meteorol. 2018, 260–261, 255–261. [Google Scholar] [CrossRef]
- Perez-Priego, O.; El-Madany, T.S.; Migliavacca, M.; Kowalski, A.S.; Jung, M.; Carrara, A.; Kolle, O.; Martín, M.P.; Pacheco-Labrador, J.; Moreno, G.; et al. Evaluation of eddy covariance latent heat fluxes with independent lysimeter and sapflow estimates in a Mediterranean savannah ecosystem. Agric. For. Meteorol. 2017, 236, 87–99. [Google Scholar] [CrossRef]
- Mauder, M.; Genzel, S.; Fu, J.; Kiese, R.; Soltani, M.; Steinbrecher, R.; Zeeman, M.; Banerjee, T.; De Roo, F.; Kunstmann, H. Evaluation of energy balance closure adjustment methods by independent evapotranspiration estimates from lysimeters and hydrological simulations. Hydrol. Process. 2018, 32, 39–50. [Google Scholar] [CrossRef]
- Schaller, C.; Foken, T. Flux calculation of short turbulent events—Comparison of three methods. Atmos. Meas. Tech. 2017, 10, 869–880. [Google Scholar] [CrossRef]
- Pozníková, G.; Fischer, M.; van Kesteren, B.; Orság, M.; Hlavinka, P.; Žalud, Z.; Trnka, M. Quantifying turbulent energy fluxes and evapotranspiration in agricultural field conditions: A comparison of micrometeorological methods. Agric. Water Manag. 2018, 209, 249–263. [Google Scholar] [CrossRef]
- Donateo, A.; Cava, D.; Contini, D. A Case Study of the Performance of Different Detrending Methods in Turbulent-Flux Estimation. Bound. Layer Meteorol. 2017, 164, 19–37. [Google Scholar] [CrossRef]
- Dyer, A.J.; Hicks, B.B. Flux-gradient relationships in the constant flux layer. Q. J. R. Meteorol. Soc. 1970, 96, 715–721. [Google Scholar] [CrossRef]
- Businger, J.A.; Wyngaard, J.C.; Izumi, Y.; Bradley, E.F. Flux-Profile Relationships in the Atmospheric Surface Layer. J. Atmos. Sci. 1971, 181–189. [Google Scholar] [CrossRef]
- Abdolghafoorian, A.; Farhadi, L.; Bateni, S.M.; Margulis, S.; Xu, T.; Abdolghafoorian, A.; Farhadi, L.; Bateni, S.M.; Margulis, S.; Xu, T. Characterizing the Effect of Vegetation Dynamics on the Bulk Heat Transfer Coefficient to Improve Variational Estimation of Surface Turbulent Fluxes. J. Hydrometeorol. 2017, 18, 321–333. [Google Scholar] [CrossRef]
- Tabari, H. Evaluation of reference crop evapotranspiration equations in various climates. Water Resour. Manag. 2010, 24, 2311–2337. [Google Scholar] [CrossRef]
- Padrón, R.S.; Wilcox, B.P.; Crespo, P.; Célleri, R. Rainfall in the Andean Páramo: New Insights from High-Resolution Monitoring in Southern Ecuador. J. Hydrometeorol. 2015, 16, 985–996. [Google Scholar] [CrossRef]
- Carrillo-Rojas, G.; Silva, B.; Rollenbeck, R.; Célleri, R.; Bendix, J. The breathing of the Andean highlands: Net ecosystem exchange and evapotranspiration over the páramo of southern Ecuador. Agric. For. Meteorol. 2019, 265, 30–47. [Google Scholar] [CrossRef]
- Córdova, M.; Carrillo-Rojas, G.; Crespo, P.; Wilcox, B.; Célleri, R. Evaluation of the Penman-Monteith (FAO 56 PM) Method for Calculating Reference Evapotranspiration Using Limited Data. Application to the Wet Páramo of Southern Ecuador. Mt. Res. Dev. 2015, 35, 230–239. [Google Scholar] [CrossRef]
- Mosquera, G.M.; Lazo, P.X.; Célleri, R.; Wilcox, B.P.; Crespo, P. Runoff from tropical alpine grasslands increases with areal extent of wetlands. Catena 2015, 125, 120–128. [Google Scholar] [CrossRef]
- Ochoa-Sánchez, A.; Crespo, P.; Célleri, R. Quantification of rainfall interception in the high Andean tussock grasslands. Ecohydrology 2018. [Google Scholar] [CrossRef]
- Sucozhañay, A.; Célleri, R. Impact of Rain Gauges Distribution on the Runoff Simulation of a Small Mountain Catchment in Southern Ecuador. Water 2018, 10, 1169. [Google Scholar] [CrossRef]
- Correa, A.; Breuer, L.; Crespo, P.; Célleri, R.; Feyen, J.; Birkel, C.; Silva, C.; Windhorst, D. Spatially distributed hydro-chemical data with temporally high-resolution is needed to adequately assess the hydrological functioning of headwater catchments. Sci. Total Environ. 2018, 651, 1613–1626. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H.; et al. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agric. For. Meteorol. 2001, 107, 43–69. [Google Scholar] [CrossRef]
- Duynkerke, P.G. The roughness length for heat and other vegetation parameters for a surface of short grass. J. Appl. Meteorol. 1992, 31, 579–586. [Google Scholar] [CrossRef]
- Dyer, A.J. A Review of Flux-Profile Relationships. Bound. Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
- Beljaars, A.C.M.; Holtslag, A.A.M. Flux Parametrization over Land Surfaces for Atmospheric Models. J. Appl. Meteorol. 1990, 30, 327–341. [Google Scholar] [CrossRef]
- Berkowicz, R.; Prahm, L.P. Sensible Heat Flux Estimated from Routine Meteorological Data by the Resistance Method. J. Appl. Meteorol. 1982, 21, 1845–1864. [Google Scholar] [CrossRef][Green Version]
- Rigden, A.; Li, D.; Salvucci, G. Dependence of thermal roughness length on friction velocity across land cover types: A synthesis analysis using AmeriFlux data. Agric. For. Meteorol. 2018, 249, 512–519. [Google Scholar] [CrossRef]
- Park, S.J.; Park, S.U.; Ho, C.H. Roughness length of water vapor over land surfaces and its influence on latent heat flux. Terr. Atmos. Ocean. Sci. 2010, 21, 855–867. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Wang, K.; Wan, Z.; Wang, P.; Sparrow, M.; Liu, J.; Zhou, X.; Haginoya, S. Estimation of surface long wave radiation and broadband emissivity using moderate resolution imaging spectroradiometer (MODIS) land surface temperature/emissivity products. J. Geophys. Res. D Atmos. 2005, 110, 1–12. [Google Scholar] [CrossRef]
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Rubio, E.; Caselles, V.; Coll, C.; Valour, E.; Sospedra, F. Thermal-infrared emissivites of natural surfaces: Improvements on the experimental set-up and new measurements. Int. J. Remote Sens. 2003, 24, 5379–5390. [Google Scholar] [CrossRef]
- Campbell, D.I. Energy Balance and Transpiration from Tussock Grassland in New Zealand. Bound. Layer Meteorol. 1989, 46, 133–152. [Google Scholar] [CrossRef]
- Ochoa-Sánchez, A.; Crespo, P.; Carrillo-Rojas, G.; Sucozhañay, A.; Célleri, R. Actual Evapotranspiration in the High Andean Grasslands: A Comparison of Measurement and Estimation Methods. Front. Earth Sci. 2019, 7, 1–16. [Google Scholar] [CrossRef]
- Carrillo-Rojas, G.; Silva, B.; Córdova, M.; Célleri, R.; Bendix, J. Dynamic Mapping of Evapotranspiration Using an Energy Balance-Based Model over an Andean Páramo Catchment of Southern Ecuador. Remote Sens. 2016, 8, 160. [Google Scholar] [CrossRef]
- Buytaert, W.; Wyseure, G.; De Bievre, B.; Deckers, J. The effect of land-use changes on the hydrological behaviour of Histic Andosols in south Ecuador. Hydrol. Processes 2004, 19, 3985–3997. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).