Abstract
We analyse uncertainties associated with the main features of the annual cycle of West African rainfall (amplitude, timing, duration) in 15 CMIP5 simulations over the Sahelian and Guinean regions with satellite daily precipitation estimates. The annual cycle of indices based on daily rainfall such as the frequency and the intensity of wet days, the consecutive dry (CDD) and wet (CWD) days, the 95th percentile of daily rainfall (R95), have been assessed. Over both regions, satellite datasets provide more consistent results on the annual cycle of monthly precipitation than on higher-frequency rainfall indices, especially over the Guinean region. By contrast, CMIP5 simulations display much higher uncertainties in both the mean precipitation climatology and higher-frequency indices. Over both regions, most of them overestimate the frequency of wet days. Over the Guinean region, the difficulty of models to represent the bimodality of the annual cycle of precipitation involves systematic biases in the frequency of wet days. Likewise, we found strong uncertainties in the simulation of the CWD and the CDD over both areas. Finally, models generally provide too early (late) onset dates over the Sahel (the Guinean region) and overestimate rainfall during the early and late monsoon phases. These errors are strongly coupled with errors in the latitudinal position of the ITCZ and do not compensate at the annual scale or when considering West Africa as a whole.
Keywords:
West Africa; rainfall; annual cycle; CMIP5 models; onset; cessation; extremes; uncertainties 1. Introduction
The annual cycle of monsoon precipitation is a primary feature of West African Climate (e.g., [1,2,3]). In this region, rainfall mainly falls from April to October, with major differences between the wetter Guinean region where precipitation displays two annual peaks (in June and in September) and the more arid Sahelian region, where it displays a single peak centered on August. At longer time scales, observations emphasises alternating periods of extreme rainfall events and dry conditions which have led to a succession of flood/drought years in the last several decades [4,5,6,7]. In this region, observations underline the importance of mesoscale convective events [8] which account for a large amount of annual cumulative rainfall [9,10]. At the same time, dry spell events are also relatively frequent in West Africa during the monsoon [11,12] and were particularly severe during the drought decades of the 70’s and 80’s [13]. Changes in the annual cycle of monsoon precipitation have also been identified, with a notable trend toward more rainfall during the second part of the monsoon in the last 30 years [14,15,16,17]. These important traits of precipitation (frequent heavy-rain events combined with dry spells) have wide implications for social and economic sectors which are strongly linked to agricultural and water resources in West Africa [18]. Furthermore, given the high vulnerability of this region, any climatic changes in monsoon precipitation (either its amount, annual cycle, intensity or intra-seasonal distribution) is likely to affect many socio-economic developments [19,20,21,22,23]. According to the Intergovernmental Panel on Climate Change report [24], climate change induced by increasing anthropogenic greenhouse gas (GHG) concentrations is expected to delay the onset of Sahelian precipitation [25], to intensify the hydrological cycle, and to increase the occurrence of extreme precipitation events [6,7,26,27,28,29,30]. This implies that West African countries will be affected by global warming in many ways and will face important adaptation challenges.
However, studies based on the Coupled Model Inter-comparison Project (CMIP) phase 3 and 5 show that the representation of the West African Monsoon (WAM) mean state, as well as its response to global warming, are both highly model-dependent [31]. As a consequence, model-based projections of the WAM and of the Sahelian climate are highly uncertain [32]. It is therefore important and valuable to more precisely characterize these uncertainties in climate models. Several studies have investigated the CMIP5 representation of West African precipitation trends and climatology. For instance, Vizy [33] found large biases in simulation of the onset and demise of the monsoon and the monsoon-mean temperature and precipitation amount in five CMIP5 models. A more recent study by Zebaze [34] examined the simulations of seasonal mean precipitation and temperature and their historical trends for a multi-model mean (MMM) of 28 CMIP5 models. They found that the CMIP5 MMM fails to capture the sign or magnitude of observed precipitation trends, which was partially due to their strong spatial heterogeneity. These studies mainly focus on seasonal signals and do not investigate the ability of CMIP5 simulations to show sub-seasonal variability in precipitation nor its annual cycle.
In this paper, we address the representation of daily precipitation, as well as wet and dry spells across West Africa in an ensemble of CMIP5 models by comparing them with three observational data sets. Our aim with this evaluation of the uncertainties in these key features of the annual cycle of West African precipitation is to provide a better understanding of biases in climate models and to create benchmarks for comparison with the new generation of CMIP models (CMIP6, [35]). The paper is organized as follows: in Section 2 we present the CMIP5 models, the satellite data used for model evaluation as well as the methodology. Results and discussions are presented in Section 3 and finally, conclusions are given in Section 4.
2. Data and Methods
In this study, all analyses are carried out on daily precipitation retrieved from 15 CMIP5 historical simulations provided by 11 institutions (Table 1, those simulations were chosen so as to cover as much as possible the spread obtained when using more simulations, e.g., [36])) and different satellite-based estimates. In order to partially account for uncertainties in existing observations dataset [37], three widely-used observationally-based estimates are used. These are (i) the Climate Hazards Group Infrared Precipitation with Station data (CHIRPS), which is a blend of Climate Hazards Group Precipitation climatology, satellite infrared measurements and direct rain gauge measurements (which are sparse over West Africa) and is available from 1981 to present at a 0.5 × 0.5 resolution [38], (ii) the Global Precipitation Climatology Project 1 Degree Daily (GPCP 1DD), available from 1996 to present with a 1 × 1 resolution [39] and (iii) the Tropical Rainfall Measuring Mission (TRMM) Multi-satellite Precipitation Analysis (TMPA) 3B42v7 research derived daily product, available from 1998 to present at a 0.25 × 0.25 resolution [40].

Table 1.
Basic information for the 15 Coupled Model Inter-comparison Project Phase 5 (CMIP5) models used in this study (resolution refers to the grid size of the atmospheric component of the model (resolution refers to the grid size of the atmospheric component of the model).
The different simulations as well as the three satellite estimates are all provided on different grids, whose sizes vary from less than 1 to more than 3 (see Table 1). Therefore, for the comparison presented below, all the datasets have been regridded to a spatial resolution of 2.5 × 2.5 using conservative (bilinear) interpolation technique for satellite data (models’ outputs). This relatively coarse resolution roughly matches the grid of the lower-resolution simulations. Some results are quite sensitive to the grid size, and this will be illustrated for a 0.5 × 0.5 resolution grid.
Due to the datasets availability (CHIRPS starts from 1981 and most of CMIP5 historical simulations end in 2004), analyses are focused over the period from 1985 to 2004. The Sahelian and the Guinean regions (boxes on Figure 1) are analysed separately and annual cycles of spatial averaged of total daily rainfall metrics over these two regions have been computed.
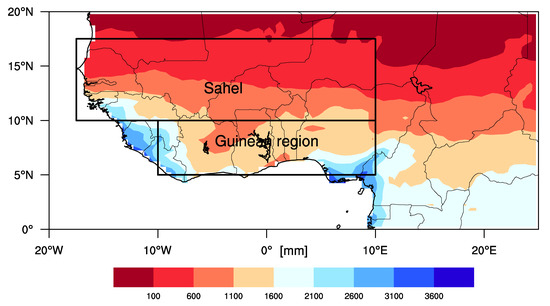
Figure 1.
Climatological annual-mean rainfall (mm/year) averaged over 1985–2004 over West Africa (using CHIRPS data). The black boxes highlight the two-considered subregions (Sahel and Guinean region).
As in Sylla [41], rainfall indices defined by the Expert Team on Climate Change Detection and Indices (ETCCDI [42]), are used to document the variability of daily precipitation, including highly precipitating events:
- The frequency of daily precipitation events is the number of days with precipitation higher than 1 mm;
- The Simple daily intensity index is the mean intensity of daily precipitation events;
- The Consecutive Dry Days (CDD) index is the number of consecutive dry sequences of more than 5 days (dry spells). A dry day is defined as a day with precipitation less than 1 mm;
- The Consecutive Wet Days (CWD) index is the number of consecutive wet sequences (or wet spells) lasting more than 5 days. A wet day is defined as a day with precipitation higher than 1 mm;
- The 95th percentile of daily precipitation events (R95) is the value above which 5% of the daily precipitation events (days with precipitation higher than 1 mm) are found;
- Total precipitation with respect to the R95p (R95ptot) is the fraction of precipitation accounted for by the very wet days (daily rainfall above R95).
These indices are calculated for each grid point, using the full length of each dataset, and then averaged over each month and each domain.
As recalled in the introduction, the Sahelian and Guinean regions display quite distinct rainfall regimes [41,43,44]. The Sahel is characterized by a single rainy season occurring from June to September, while the rainfall regime over the Gulf of Guinea presents a bimodal structure with one peak in June during the northward migration of the Inter-Tropical Convergence Zone (ITCZ) and another one in September during the southward retreat of the ITCZ. Here, the ITCZ position and width are determined over a West African domain extending from 0 to 20 N and 20 W to 25 E following the method of d’Orgeval [45]. The method can be summarized as follows:
First, grid points where precipitation exceeds = 2 mm/day are retained (we did not find any noticeable change with = 1, 3 and 4 mm/day). This threshold value allows to capture a fairly large monsoon band for all the simulations. The threshold is subtracted to the precipitation exceeding it. This provides a mapping of the ITCZ. Then if n is the number of grid points above 2 mm/day; i, the index of one point; , the precipitation at the grid point i; and and the coordinates (longitude and latitude, respectively) of i; the latitudinal position of the center of the ITCZ is computed as follows:
The width of the ITCZ is considered as the standard deviation of the distribution in latitude:
In order to characterize the timing of the monsoon season and its length, the method of Liebmann [3] is used to determine its onset and cessation dates over the Sahel and the Guinean region. The method can be summarized as follows:
First, we determine the start of the climatological water season. At each grid point this is found by first calculating two quantities: (i) the long-term annual-mean and daily average is computed for each day of the year. Starting from 1st January, the sum of the difference between the climatological daily average () and the climatological annual-mean () gives the climatological accumulated anomaly (C). The day when the minimum of C is reached is defined as the start of the climatological water season (noted ) and day of the maximum marks the end ().
The onset for each year and each grid point is then determined and compared to their climatological values. For each year of record, beginning 50 days prior to the start of the climatological water season and ending at its end, daily precipitation () minus the long-term annual-mean daily average () is summed. This sum is called the anomalous accumulation (A). The day after which the value of A reaches its absolute minimum is the onset date since, from that day onward for this particular year, accumulated precipitation exceeds what would be expected from climatology. Conversely, the day on which A reaches the maximum is the cessation date of the wet season.
3. Results
3.1. The Annual Cycle of Mean Precipitation, Intensity and Frequency of Wet Days
This section focuses on the annual cycle of precipitation amount, frequency and intensity of wet days. Figure 2 provides an inter-comparison of CMIP5 results with observational datasets (CHIRPS, TRMM and GPCP). First the annual cycle of monthly-mean precipitation is analysed. Figure 2a indicates that CHIRPS, TRMM and GPCP provide a very close depiction of this cycle over the Sahel, while models capture reasonably well the broad temporal structure of the annual cycle though with a very large spread of the amplitude from less than 2 to more than 8 mm/day in August.
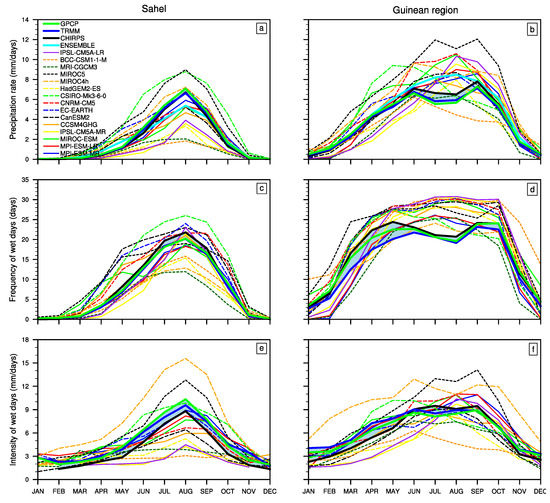
Figure 2.
Annual cycle of rainfall (a,b), frequency (c,d) and intensity of wet days (e,f) over the Sahel (left) and Guinean region (right) from CHIRPS (black), TRMM (blue), GPCP (green) and 15 CMIP5 models and their ensemble mean (cyan). The shaded area indicate the spread between the three satellite estimates.
During the core of the monsoon (July–September), over the Sahel, only two models (CSIRO-Mk3 and MIROC5) present a substantial positive biases compared to satellite datasets (2 mm/day), while most of the other models underestimate the magnitude of rainfall with peaks as low as 2 mm/day (consistently with Roehrig [36]). In August, MPI-ESM-MR, MPI-ESM-LR, EC-EARTH, MIROC4h and MIROC-ESM perform relatively well compared to observations with peaks between 6 and 7 mm/day. The Multi-Models Mean (MMM) performs better than several models but still underestimates the core monsoon rainfall.
Over the Guinean region, the observational datasets also agree quite well even though the “little dry season” [46] is slightly more marked in TRMM and GPCP than in CHIRPS. In contrast, the annual cycles in CMIP5 models display a variety of shapes (Figure 2b). A large spread among models is present and most models overestimate the magnitude of precipitation during the monsoon. The MMM fails to reproduce the bimodal character of precipitation. Only CNRM-CM5, MIROC5 and MIROC4h capture the bimodal structure of this cycle but with bias in the timing. For instance, the CNRM-CM5 first peak (9 mm/day) occurs in June as observed, while the second one (10 mm/day) is observed in August instead of September. MIROC4h similarly displays its first peak in June (9 mm/day) and the second one in October (5.5 mm/day). The second peak in MIROC5 (12.5 mm/day) is observed at the right time (September) but the first one (12 mm/day) occurs one month later, in July.
In general, models which underestimate/overestimate precipitation during the core monsoon do so throughout the monsoon season. However, outside of the monsoon period, when there is hardly any rain observed, almost all models simulate precipitation, i.e., they systematically overestimate precipitation, even those models which underestimate it during the monsoon (e.g., in March in the Sahel).
Focussing now on the annual cycle of the frequency of wet days, satellite datasets agree reasonably well over the Sahel. The maximum frequency occurs during the core monsoon season in August, and it is lower in TRMM and GPCP than in CHIRPS (by 10%). A higher frequency is observed in CHIRPS over the Guinean region too, but there satellite datasets display a large spread in Spring (April–May), reaching about 20%. Interestingly, the annual cycle of the frequency of wet days displays a well-defined bimodal structure in GPCP and CHIRPS, while this characteristic is much less pronounced in TRMM. CMIP5 simulations capture roughly the structure of these annual cycles (Figure 2c,d). In August, over the Sahel, CSIRO-Mk3 and EC-EARTH display the largest biases, of respectively +5 and +3 days compared to observed data.
Over the Guinean region, the bimodal structure associated with the frequency of wet days is lacking in CMIP5 models, most of them simulate a relatively constant or slightly increasing frequency from May to October. Indeed, it is raining almost every day in several models, with biases then reaching about 50% compared to the mean wet day frequency from observational dataset.
Finally, over both regions, models largely overestimate the frequency of wet days prior to and following the monsoon season (up to 50% in May over the Sahel), which means that it rain more frequently in simulations throughout the annual cycle. CMIP5 models are known to precipitate globally too frequently with too little precipitation (e.g., [47]) and ref. [36] showed this was also true in JAS for the West African region. This overestimation may be related to well known issues with the representation of the diurnal cycle of convective precipitation in models (e.g., [36,48]) when convective inhibition is not preventing the onset of convection [48].
Shifting now to the annual cycle of the intensity of wet days, observational datasets are again very close to each other over the Sahel. Models generally simulate a peak in August over the Sahel (Figure 2e), but with strong uncertainties in the amplitude. MIROC4h and MIROC5 are the only two models displaying a higher intensity than satellite datasets. BCC-CSM1, CCSM4GHG, CNRM-CM5, IPSL-CM5A-LR, IPSL-CM5A-MR and MRI-CGCM3 show a significant underestimation with peaks ranging from 2 to 4 mm/day (i.e., an underestimation between 200 and 500% compared to observational datasets).
The situation is quite similar over the Guinean region, where satellite datasets display slight spread. Slight uncertainties are noted in observational datasets especially from January to May (with a difference reaching 40% between CHIRPS and TRMM in April). Furthermore, they display slight distinct structures of the annual cycle of wet days intensity. Observational datasets show a less marked bimodal structure which is much better represented in GPCP and TRMM in June and September. CHIRPS shows its first peak in July and the second one in September whereas TRMM displays peaks in April and June. Note that, in these two datasets, the intensity does not fluctuate much from June to September. There is also a wide spread among models on the representation of the intensity of wet days, but with a dominantly positive bias on the amplitude of the signal (Figure 2f). In terms of temporal evolution, most models display a unimodal structure of the intensity of wet days except for models whose displayed a bimodal structure of the mean precipitation. Given the uncertainties in observational datasets, it is not possible to conclude as to which models perform better over this region.
Finally, it is noticeable that over both regions and in observational datasets as well as in models, the annual cycles of the intensity and of the frequency of wet days are both very strongly correlated with the annual cycle of the mean precipitation (see Table A2), which implies in particular that model biases in the annual cycles of these variables are linked.
In summary, one can retain that the annual cycle of wet days intensity is in general poorly represented in models over the two areas, with particularly large uncertainties regarding the magnitude. Over the Sahel models’ uncertainties in the annual cycle of precipitation are related to both the uncertainties in the frequency and intensity of wet days. On the other hand, biases in the representation of the bimodal structure over the Guinean region appears to be more closely related to the representation of the intensity than the frequency of wet days in models.
It is important to note that with a finer grid resolution (0.5 × 0.5; see Figure A1), the frequency (resp. intensity) of wet days decreases (increases) in observational datasets while the associated uncertainties increase with more differences in the frequency and intensity of wet days among those datasets (e.g., the spread in intensity roughly doubles). By contrast there are no considerable changes noted in CMIP5 models, which leads to a subtantial increase in model biases (e.g., it reaches about 100% of the frequency of wet days).
Quantitative diagnostics within Taylor diagrams confirm these findings (Figure 3, where CHIRPS is the “reference” in that it is the dataset to which other satellite and model datasets are compared). For the annual cycle of precipitation and frequency of wet days over the Sahel, TRMM and GPCP are very strongly correlated (>0.99) with CHIRPS and have a normalized standard deviation close to 1 (slightly lower than 1 for the precipitation and slightly higher than 1 for the frequency), consistently with the fact that TRMM and GPCP indicate a lower frequency of wet days over that area. For the annual cycle of the intensity of wet days, TRMM and GPCP display strong correlation (between 0.95 and 0.99) and have a normalized standard deviation close to 1 (slightly > 1 for GPCP and = 1 for TRMM), again consistent with the slightly higher values of that index in GPCP and TRMM noted in Figure 2e.
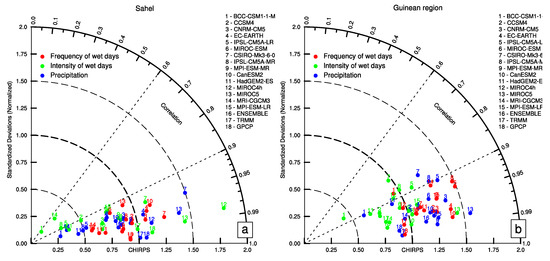
Figure 3.
Taylor diagrams of the annual cycle of daily mean rainfall (mm/day), intensity and frequency of wet days from 1985 to 2004 over the Sahel (a) and the Guinean region (b) for TRMM, GPCP and 15 CMIP5 models compared to CHIRPS. The values have been computed using the monthly-mean of each index averaged over the period 1985–2004.
In line with the results presented in Figure 2b,d,f, over the Guinean region, the correlation of TRMM and GPCP with CHIRPS is stronger on the annual cycle of the mean precipitation and the frequency the intensity. The normalized standard deviation is slightly less than 1 on the annual cycle of precipitation and frequency of wet days, as TRMM and GPCP indicate a lower frequency of wet days than CHIRPS (Figure 2d).
In models, except BCC-CSM1 and MRI-CGCM3, the annual cycles of the mean precipitation, of the frequency and intensity of wet days correlate well with CHIRPS over the Sahel, confirming the fact that in this area, models are in general able to qualitatively capture the unimodal structure of the annual evolution of precipitation (Figure 3a). However, the distribution of values is scattered along the standard deviation axis, which indicate how the uncertainties in the amplitude of precipitation are important in CMIP5 models over the Sahel. For some models (MPI-ESM-MR, MIROC-ESM, CNRM-CM5, MPI-ESM-LR, EC-EARTH, MIROC4h, CanESM2), and for the MMM, the normalized standard deviation is close to 1 but some others models display very strong (1.55 for CSIRO-Mk3) or weak values (<0.50 for BCC-CSM1 and MRI-CGCM3). Figure 3a also reveals that over the Sahel, uncertainties in total precipitation come from both uncertainties on the intensity and the frequency of wet days. Over the Guinean region, Figure 3b shows much weaker correlations compared to the Sahel. This is partly due to the poor representation of the bimodal structure of precipitation in the CMIP5 models over this region. Regarding the normalized standard deviations values, the distribution appears less scattered compared to the Sahel region in agreement with previous conclusions from Figure 3a,b. In contrast with the Sahel region, Figure 3b also indicates that over the Guinean region, the uncertainties in daily total precipitation dominantly involve those in the frequency of wet days. Most models fail to reproduce the frequency of wet days, which also contributes to the poor representation of the bimodal structure of precipitation in that area.
In summary, over both the Sahel and Guinean regions, TRMM, GPCP and CHIRPS datasets provide very consistent results on the annual cycle of precipitation but less so on the frequency of wet days. Conversely, uncertainties are noted on the intensity of wet days over both areas, but especially over the Guinean region. On the other hand, CMIP5 models present very high uncertainties in the seasonal cycle of precipitation. Separate analysis of the frequency and intensity of the wet days reveal that over the Sahel, the uncertainties are important on both the amplitude of frequency and intensity of wet days. It also reveals that over the Guinean region, the difficulty of models to represent the bimodal structure of the mean precipitation is dominated by biases in the representation of the annual cycle of the frequency of wet days. Finally, it is difficult to conclude regarding the simulation of the temporal structure of the annual cycle of the intensity of wet days over the Guinean region, because of uncertainties in observational datasets.
3.2. The Annual Cycle of Extreme Precipitation Indices
In this section, we focus on the annual cycle of extreme precipitation indices (presented in Section 2) provided by satellite datasets and CMIP5 models (Figure 4).
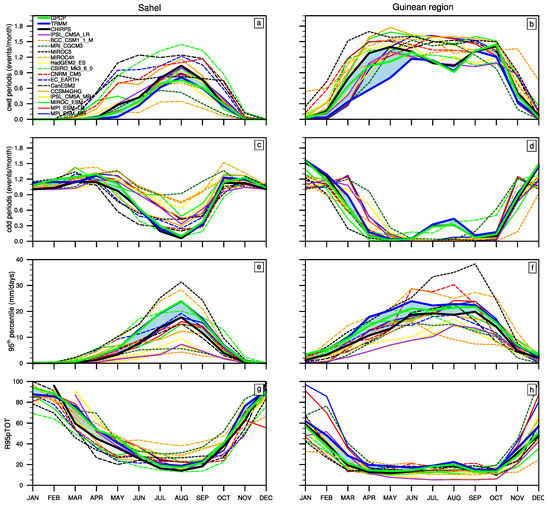
Figure 4.
Annual cycle of wet spells (a,b), dry spells (c,d), 95th percentile (e,f) and the fraction of precipitation accounted for by the very wet days (g,h) over the Sahel (Left) and the Guinean region (right) from 1985 to 2004 in CHIRPS (black), Tropical Rainfall Measuring Mission (TRMM) (blue), GPCP (green) and 15 models CMIP5 and their ensemble mean (cyan).
First, Figure 4a shows that over the Sahel, the structure of the annual cycle of CWD is very similar in the three satellite datasets, but TRMM and GPCP provide less wet spells than CHIRPS. Over the Guinean region, more important differences are noted in observational datasets (Figure 4b) with again less CWD in TRMM and GPCP and a large spread in April-May. Here, satellite datasets display a bimodal structure (although less pronounced in TRMM) but with different dates of maxima: the first maximum occurs in June according to GPCP and TRMM, one month later than with CHIRPS while the second maximum occurs in October according to GPCP and CHIRPS, once month later than with TRMM.
Over the Sahel, most models (MIROC-ESM, MPI-ESM-MR, MPI-ESM-LR, IPSL-CM5A-MR, IPSL-CM5A-LR, HadGEM2, EC-EARTH, CCSM4GHG and CSIRO-Mk3) simulate a CWD peak in August as observed but with strong uncertainties in the amplitude. Several models fail to represent the observed unimodal structure. For instance in EC-EARTH, CanESM2, CNRM-CM5, CCSM4GHG and MIROC5 present a multi-peak structure of the annual cycle of CWD. A few models performs relatively well for CDD in the Sahel (Figure 4c). However, it is important to note that when a model overestimates CDD, it often underestimates CWD and vice versa (this is even more pronounced with the finer 0.5 × 0.5 grid: e.g., MRI-CGCM3 model, which performs the best on wet spells and the worst on dry spells; note also the IPSL simulations which provide a reasonable representation of CDD, but largely underestimate the mean precipitation Figure A2a,c).
Over the Guinea region, very high uncertainties are also noted in models (Figure 4b). Most of the models represent multi peaks structure for CWD and, even more than in the Sahel, they all largely overestimate the magnitude of the CWD (by more than 100% in April-May). For satellite datases, mirroring previously noted differences in CWD, CDD are more numerous in TRMM and GPCP than in CHIRPS while their annual structure are relativity close. In particular, the three datasets indicate an increase of CDD during the little dry season over the Guinean region (Figure 4d). Models are unable to capture this peak of CDD observed from July to August (Figure 4d). Finally, the model biases noted on CDD are relatively lower than those obtained on CWD over both regions, and appear to be relatively less important over the Guinea region than over the Sahel. Therefore, beyond uncertainties in observational datasets, CWD appear to be too much numerous in almost all models over the two regions.
For the 95th percentile of daily precipitation, uncertainties are overall stronger than for the previous indices in observational datasets as well as in CMIP5 models. It takes values around 16 mm/day for CHIRPS and 22 mm/day for GPCP and TRMM in August over the Sahel. Only a few models (MIROC5, MIROC4h and MPI simulations) perform quite well during the monsoon though they performance decrease when considering a finer resolution (Figure A2e).
Over the Guinean region, as noted for the intensity (Figure 2b), differences between datasets are larger prior to the little dry season. Despite these large differences among datasets, it appears that over both regions, numerous models underestimate the 95th percentile, i.e., they simulate more wet days and CWD, but the intensity and extrema of precipitation are much less than observed.
Finally, the annual cycle of of the fraction of precipitation accounted by the very wet days R95ptot is shown in Figure 4g,h. Its structure, with a minimum during the monsoon season (around 30%), is relatively well captured by most models compared to the previous indices (this is not unexpected as this index does not involve model biases in the simulation of precipitation). The main differences are underestimations of this index in April–May over the Sahel, and during “the little dry” season in the Guinean region. Overall, this fraction is relatively small, which suggests that model errors in the highest precipitation values cannot explain a large part of the errors in the mean precipitation.
It is important to note that with a finer grid resolution (0.5 × 0.5; Figure A2) a considerable decrease (increase) is observed on CWD (CDD, 95th percentile and R95pTOT) in observational datasets accompanied with strong uncertainties over the two regions. By contrast in CMIP5 models no noticeable change is observed so that model biases considerably increase (even when taking uncertainties in observational datasets).
Using the Taylor diagrams, these findings have been further quantified (Figure 5). TRMM and GPCP are very strongly correlated (r > 0.95) with CHIRPS and have standard deviations close to or equal 1 on the annual cycle of CDD over the two regions. As expected from Figure 4a,b for CWD, the correlations between either TRMM or GPCP with CHIRPS and the normalized standard deviation are weaker. For CDD, CMIP5 models are weakly correlated with CHIRPS over the Guinean region where the normalized standard deviation is closer to 1, meaning that uncertainties in the annual structure of that index is less important than over the Sahel. On the other hand, for the CWD, distributions along both correlation and standard deviation axes appear highly scattered, pointing to the strong uncertainties qualitatively noted over both regions and on both the temporal evolution and the occurrence of CWD (Figure 4a,b). Regarding now the 95th percentile and R95PTOT indices, their correlations with CHIRPS are higher (r > 0.90) over both regions, which points to a reasonable simulation of the temporal evolution of these indices and contrast with their poor skill in terms of standard deviation.
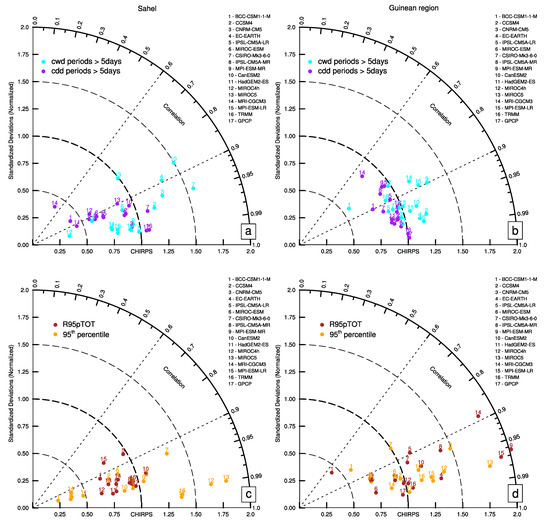
Figure 5.
Taylor diagrams of wet spells (cyan), dry spells (purple), 95th percentile (orange) and the fraction of precipitation accounted for by the very wet days (brown) from 1985 to 2004 in the Sahel (a,c) and the Guinean region (b,d) on TRMM, GPCP and 15 CMIP5 models compared to CHIRPS. The values have been computed using the monthly-mean of each index averaged over the period 1985–2004.
3.3. Timing and Length of the Monsoon Season
As emphasized above, the models do not provide a proper depiction of the annual cycle of precipitation and it is important to characterize these differences in more detail. To do so, the start and end dates of the wet season are determined using the Liebmann method [3].
Figure 6 shows the daily accumulated precipitation anomalies, the onset, the cessation and half of the cumulative precipitation dates from observations and CMIP5 simulations and their MMM over the Sahel and the Guinean region. The evaluation is performed with CHIRPS and CMIP5 models for the period 1985–2004, and over 2000–2010 for TRMM and GPCP reference datasets.
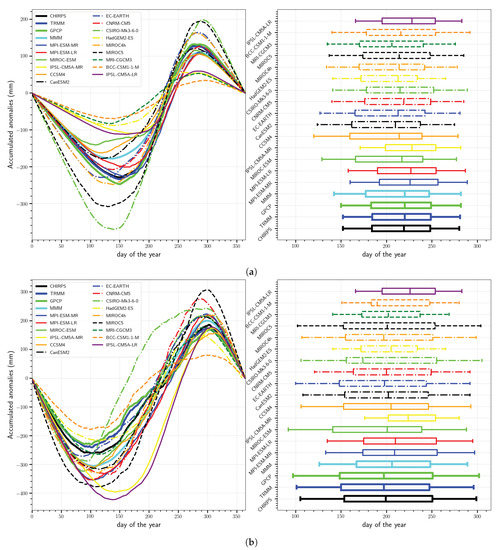
Figure 6.
Daily accumulated-anomalies of precipitation (left panel) from observations (bold lines) and CMIP5 models simulations and their multi-model mean (MMM) over the Sahel (a) and the Guinean region (b); averaged over 1985–2004 for CHIRPS and models and over 2000–2010 for TRMM and GPCP. The box plots (right panel) show the onset (minimum), the cessation (maximum), the date at which half of the total cumulative precipitation is recorded (median), as well as the first and third quartiles.
Over the Sahel, the mean onset and cessation dates are close in the observational datasets (around 1 June for the onset and 9 October for the cessation), with differences of less than three days. The standard deviation of both dates is on average 7 days for these observational datasets.
In CMIP5 models, except for MPI and IPSL simulations, the onset occur earlier than in observational datasets, by up to several weeks (from 1 May for CCSM4 to 21 May for HadGEM-ES) while cessation dates are closer to observed, even though sometimes a bit late in a few models (e.g., 20 October for BCC-CSM1). Conversely in MPI and IPSL models, the monsoon onset occurs later (from 8 to 20 June) and the cessation is also slightly later in the year for MPI. Likewise, the onset is too early in the MMM while the cessation is closed to observed. Finally, rainfall is not distributed uniformly during the monsoon: it rains more during the second half of the monsoon according to CHIRPS and TRMM. This characteristic is at least partly captured by most models (Figure 6b).
Over the Guinean region, there is relatively less agreement in the onset and cessation dates obtained from observational datasets (differences reach 10 days); they respectively occur around the first half of April and in late October. These dates correspond to the start of the first season and the end of the second season, which are both separated by the little dry season. In our case this dry phase is not very pronounced, this is why we can use this method (keeping in mind that it can’t provide the intermediate onset and cessation dates over this region). Half of the annual cumulative rainfall is recorded around 20 July, which is close to the middle of the monsoon season and indicates that there is about as much rainfall during the first and second half of the monsoon season.
For CMIP5 models, the onset occurs either later (60% of models), from 15 April to 24 June or close to observed (40%), while, as previously found over the Sahel, cessation dates are relatively closer to observed. In most models, half of the annual cumulative rainfall is recorded during the first half of the wet season, a date which varies from 15 July (CSIRO-Mk3) to 11 August (IPSL-CM5A-MR). The exact values of these dates can be found in Table A1. Finally, there is a slight length asymmetry between the second (shorter) and third (longer) quartile in most models, in qualitative agreement with observations.
More spatial details are provided by maps of onset and cessation dates over West Africa (Figure 7, Figure A5 and Figure A6). Observational datasets highlight the northward migration of the monsoon. The earlier onset dates occur in the southern part of the domain around late March/early April, consistently with the results of Dunning [2] and Thorncroft [49] over the Guinean coast. Further north, from 10 to 15 N and 10 W to 10 E, the onset dates increase from 4 May to 15 June. In Senegal, close to the coast, onset dates also display a South-West/East-North gradient and the later onset dates occur in north-west Senegal by up to end of June. These results are fully consistent with Liebmann [3] and Dunning [2]. Various methods can be used to determine onset dates (e.g., Fitztpatrick [50], Bombardi [51]) and they lead to different results. For instance, our onset dates are typically earlier than in Marteau [52], by up to a month in some areas (this difference is in the same range as found by Bombardi [51], their Figure 5).
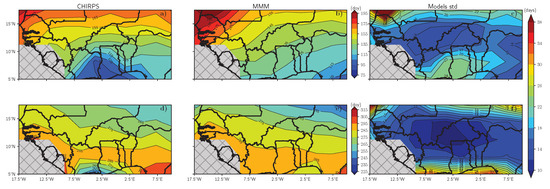
Figure 7.
Mean onset and cessation dates in CHIRPS (a,b) and MMM (d,e) as well as the associated standard deviation in models (c,f).
The southward progression from 17 to 7 N of the cessation dates with a slight West-North East-South tilt, is well defined in observational datasets. Consistently with Liebmann [3], the earlier dates found close to the southernmost coast of West Africa correspond to the end of the first wet season. In this area, the method becomes of limited value as it does not inform on the cessation date of the second wet season (cf. Liebmann [3], their Figure 7b).
The MMM is able to well reproduce the northward shift of the onset dates and the southward progression of cessation dates, including their distinct tilts (Figure 7). By contrast, only a few models (MPI simulations, EC-EARTH and MIROC-ESM) are able to capture these spatial structures (Figure A5). These models display a reasonable pattern over Western Sahel, with in particular later onset dates. Consistently with Figure 6, the MMM display too late onset dates (by up to one month over north-west Senegal) and an eastward shift of its earlier dates compared to CHIRPS. The standard deviation is minimum over Central Sahel where it however still amount to more than 10 days. By contrast, most models are able to capture the southward of the cessation dates over West Africa with typical differences around seven days. The MMM is relatively close to observations, except South of 7 N. More generally, models compare much better to observations over West Africa with weaker standard deviation (Figure 7f).
In summary, observational datasets show a good agreement in their determination of the onset and cessation dates of the rainy season over the two regions. These results are very consistent with the results of Liebmann [3] as well as those of Dunning [2] who found good correlations (around 0.88 to 0.91) of the onset and cessation dates provided by satellite datasets over Africa using this method. CMIP5 models often provide too early/late onset and/or too late cessation dates over the two regions meaning that most models overestimate the precipitation during the early and late monsoon, a result which is also consistent with Seth [53]. The MMM provide a reasonable pattern of onset and cessation dates over the Sahel and an eastward shift of onset dates over the Guinean region.
3.4. Annual-Mean Precipitation over the Sahelian and Guinean Regions
Over West Africa, errors in the simulation of the latitudinal position of the ITCZ is a primary source of precipitation biases (e.g., [54]), and can be associated with compensating errors between the Sahel and Guinean regions. For instance, if the ITCZ is located too much to the South, it can lead to an underestimation of precipitation amounts over the Sahel and potentially to an overestimation over the Guinean zone. This issue is investigated in more details here, via an analysis of the ITCZ latitude and width using a 0.5 × 0.5 grid resolution.
Figure 8a illustrates the monthly-mean latitude centre of the ITCZ band over west Africa and Figure 8b its June to September (JAS) mean latitude and the width for observational datasets and CMIP5 outputs. During the full monsoon (JAS), CHIRPS and TRMM indicate a similar position around 9 N, while it is shifted southward (by about 1) with GPCP. This difference is also obvious for the JAS-mean of that metric, while the width is about 5 in all observations. In most CMIP5 simulations, the ITCZ position is too far to the south (6–8 N) during the core of monsoon and too far to the north during January–March. Only two models, MIROC5 and MIROC4h, display a position of the ITCZ close to observed datasets during the core of the monsoon and only one, CSIRO-Mk3 shows a northward biais of the ITCZ latitude from January to December (More details can be found in Figure A3 showing time-latitude Hovmöller diagram of precipitation).
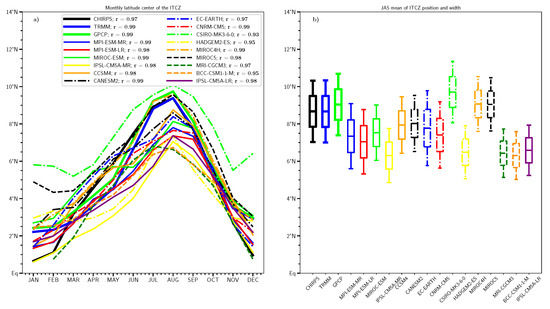
Figure 8.
Monthly mean of the latitude of the centre of the Inter-Tropical Convergence Zone (ITCZ) band over West Africa (a) and the JAS mean of the latitude of the centre and the width of the ITCZ (b). r in legend indicate the correlation between the monthly mean precipitation and latitude of the centre of the ITCZ. For each box plot, the distance from minimum to maximum represent the width and the median is the ITCZ position.
The differences between the observed and simulated width of the ITCZ band are relatively weak. Thus, biases in the latitude and width of the ITCZ may appear relatively small in most models (given their grid size). However, we find that monthly-mean precipitation over the Sahel, the Guinean region and the west Africa are all very strongly correlated to the monthly-mean ITCZ latitude in both models and observations. Thus, models who display a southernmost shift of the ITCZ underestimate precipitation amount over the Sahel.
Most models underestimate rainfall amounts over the Sahel. The strong correlation between JAS biases in the ITCZ location and Sahel precipitation (R = 0.92 see Figure A7) shows that this negative precipitation bias is associated with models that place the ITCZ too far to the south. Previous studies have shown that CMIP5 models also have a southward bias in the Saharan heat low (SHL) which is associated with less precipitation across the Sahel [55], and that changes in global energy transport can alter Sahel precipitation and shift both the ITCZ and SHL [56]. This result is also consistent with results from Roehrig [36] where a southward bias in the ITCZ in CMIP5 historical simulations (compared to AMIP simulations) was associated with a positive SST bias in the Guinean Gulf. Our results are close to those of Monerie [57] who find that most CMIP3 models place the ITCZ too far to the south compared to the observational dataset CRU (Climatic Research Unit). With this dataset, the ITCZ position in August is around 9 N, i.e., it is also similar to our estimations
We can also separate the impact of latitudinal ITCZ biases from biases in its amplitude by comparing the precipitation bias in both the Sahelian and Guinean regions and seeing if there is a corresponding shift in bias between the regions. Table 2 compares the annual mean precipitation and the biases (differences are computed with respect to CHIRPS) over both regions and over “West Africa” (defined here as the ensemble of the two regions).

Table 2.
Annual cumulative precipitation (mm/year) and precipitation difference (in mm/year and percentage) between CHIRPS and GPCP, TRMM, CMIP5 model’s simulations and their multi-model mean over the Sahel, Guinean region and West Africa averaged over the period 1985–2004 for CHIRPS and models and over the period 2000–2010 for GPCP and TRMM.
In agreement with previous results, the differences between the observational datasets are weak. TRMM and GPCP indicate slightly more precipitation over the Sahel (+33 mm and +75 mm respectively) and slightly less over the Guinean region ( mm and mm respectively), leading to slightly more precipitation over West Africa (+9 mm and +48 mm respectively). The differences remain below 10% except between CHIRPS and GPCP over the Sahel (+11%), but they indicate compensations between the Sahel and the Guinean region which narrow the range of differences when considering West Africa as a whole. Table 2 also indicates that, it rains about twice more in the Guinean region compared to the Sahel. Differences are more important in CMIP5 models, and vary from mm (BCC-CSM1-1-M) to +590 mm (CSIRO-Mk3) over the Sahel. Despite this additional unrealistic source of precipitation, on an annual-mean basis, more models display a negative bias over the Sahel (which represents to % of CHIRPS annual rainfall). Conversely over the Guinean region, models’ biases are dominantly positive and represent +5 to +63% (+76 mm to +943 mm) of CHIRPS annual rainfall excepted for MRI-CGCM3 ( mm), HadGEM2-ES ( mm), BCC-CSM1-1-M ( mm) and IPSL-CM5A-MR ( mm). However, on a model-by-model basis, we do not find many cases of underestimation over the Sahel combined with an overestimation over the Guinean region (see also Figure A4 and Figure A7). Rather, in 66% of the models, it rains either too much or not enough over both regions, which points to a primary bias in the simulation of the West African rainfall (rather than biases in its latitudinal distribution), where about half of the models overestimates precipitation and the other half underestimates it.
4. Conclusions and Perspectives
This study highlights how CMIP5 models represent the annual cycle of rainfall characteristics over West Africa, focusing on the timing of the monsoon season (onset, cessation), the frequency and intensity of daily rainfall, and indices for extreme precipitation such as the 95th percentile of precipitation and consecutive wet and dry days, in addition to monthly-mean rainfall. These analyses have been conducted for both the Sahel and the Guinean regions which display distinct annual cycles and precipitation climatologies. A subset of 15 historical CMIP5 simulations has been evaluated using three observational datasets (CHIRPS, TRMM and GPCP) over a 24-year period for CHIRPS and 11-year period for TRMM and GPCP).
Over both regions, CHIRPS, TRMM, and GPCP are found to agree in their depiction of the annual cycle of the mean precipitation and, to a lesser extent, of the frequency of wet days. However, they provide quite distinct structures of the annual cycle of the intensity of wet days, especially over the Guinean region. This lack of agreement in satellite datasets also concerns the 95th percentile of precipitation or the CWD. This result suggests that further analyses of in-situ precipitation data are needed so as to provide more advanced and valuable observational diagnostics for future model evaluation. Indeed, the magnitude of extreme daily precipitation provided by these satellite datasets can fluctuate by up to 100% during the core monsoon in the Sahel, and distinct structures of the annual cycle of this index are found over the Guinean region with these datasets. Despite their limitations, these datasets were nevertheless quite useful for evaluating several aspects of the annual cycle of precipitation and precipitation indices in CMIP5 models, mainly because numerous biases in models were much larger than the spread obtained with satellite datasets.
The performances of the models in simulating the structure of the annual cycle are better over the Sahel than the Guinean region. They are generally able to reproduce the August peak, whereas for the Guinean region only three models display a bimodal structure but with offset dates of their maxima. In terms of amplitude, strong uncertainties in both areas (relatively more pronounced in the Sahel) have been found in the mean precipitation annual cycle, and for most models, these biases generally do not compensate each other when considering precipitation over West Africa, with 66% of the models raining either too much or not enough over both regions. The analysis of intensity and frequency of wet days reveals that over the Guinean area, the uncertainty on total daily precipitation strongly involves the uncertainty associated with the frequency of wet days, whereas in the Sahel, both uncertainties in intensity and frequency are equally important. It must be noted however that models tend to always reproduce higher frequencies than observed, even when they underestimate the mean precipitation amount (indeed, it rains 40–50% more in models than in satellite datasets over the Guinean region and this bias obtained for a 2.5 × 2.5 grid substantially increases at finer resolution).
We found strong uncertainties in the representation of the wet and dry spells (CWD and CDD) over both study areas. Conversely for R95 and R95PTOT, the uncertainties in the annual structure of theses indices in CMIP5 models appear somewhat weaker in Taylor diagrams, but the magnitude of the R95 is largely underestimated in most models. However, as the contribution of extreme rainfall to the total precipitation is relatively limited (less than 30% during the core monsoon season according to satellite data), the strong uncertainties found on the annual cycle of the intensity and frequency of wet days seem to be associated with errors on either the intensity and frequency of the low and/or moderate daily rainfall events rather than the extreme daily events. We also found that the annual cycles of precipitation and several precipitation indices are generally very highly correlated (e.g., R95) in both satellite datasets and models. This results points to the importance of a good simulation of the climatological annual cycle of precipitation, and also suggests that its improvement requires advances in the representation of both the intensity and frequency of daily rainfall in models.
Finally, biases in the latitude of the ITCZ were shown to be connected to biases in precipitation across West African in the annual mean. In JAS, these ITCZ biases are strongly connected to precipitation biases in the Sahel, but not for the Guinean area. This suggests that better representing regional and global controls on the ITCZ can help reproduce biases in Sahel precipitation characteristics.
This study has highlighted the complexity of the representation of daily rainfall characteristics in climate models and how it translates into large biases at regional scale, which are likely to feedback on the monsoon dynamics [58]. From a smaller scale perspective, we found that, from one precipitation index to another, and according to the area, the uncertainties change dramatically. The magnitude of the uncertainties also varies with the considered spatial scale for some indices. Typically, it further increases at smaller scales. It is therefore important for each metric to identify the nature of these uncertainties for impacts studies. Finally, we argue that further studies are necessary in order to understand whether and how these precipitation biases are translated into future projections with climate models over West Africa, in particular shifts in the monsoon season, and changes in mean and extreme precipitation amounts. The methodology and results presented here will prove useful for upcoming CMIP6 analyses.
Author Contributions
Conceptualization, M.S., M.D., R.D.D., F.G. and D.D.; methodology, M.S., M.D., R.D.D., F.G. and D.D.; software, M.S.; validation, M.D., R.D.D. and F.G.; formal analysis, M.S.; investigation, R.D.; resources, A.T.G.; writing–original draft preparation, M.S.; writing–review and editing, M.S., M.D., R.D.D., F.G. and D.D.; visualization, M.S.; supervision, A.T.G.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
Magatte Sow thanks the Prince Albert II of Monaco Foundation for the financial support via the IPCC scholarship program.
Acknowledgments
This document was produced with the financial support of the Prince Albert II of Monaco Foundation. The contents of this document are solely the liability of Magatte Sow and under no circumstances may be considered as a reflection of the Prince Albert II of Monaco Foundation and/or the IPCC. Thanks to the Government of Senegal, the NERC/DFID Future Climate For Africa Programme under the AMMA-2050 project (grant number NE/M020428/1), the LMI ECLAIRS2 Program for the additional financial support. Magatte Sow is grateful to the University Cheikh Anta Diop of Dakar where the LPAO-SF (the host lab) is located and the CNRM’s TROPICS research staff at Météo-France where the last part of this work has been conducted with various supports. We thank the reviewers for their constructive comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WAM | West African Monsoon |
| AEJ | African Easterly Jet |
| AEWs | African easterly waves |
| ITCZ | Inter-tropical Convergence Zone |
| MJO | Madden Julian Oscillation |
| IPCC | Intergovernmental Panel on Climate Change |
| RCP | Representative Concentration Pathways |
| CMIP5 | Coupled Model Intercomparison Project phase 5 |
| GHG | Greenhouse Gas |
| ETCCDI | Expert Team on Climate Change Detection and Indices |
| SDII | Simple daily intensity index |
| CDD | Consecutive Dry Days |
| CWD | Consecutive Wet Days |
| CHIRPS | Climate Hazards Group Infrared Precipitation with Station |
Appendix A
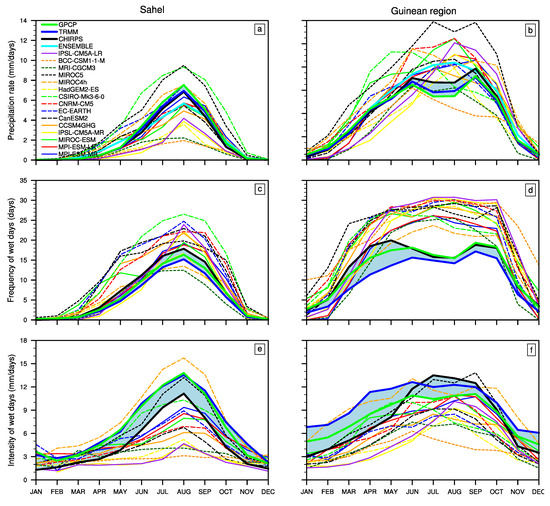
Figure A1.
Same as Figure 2 but with a finer grid resolution: 0.5 × 0.5.
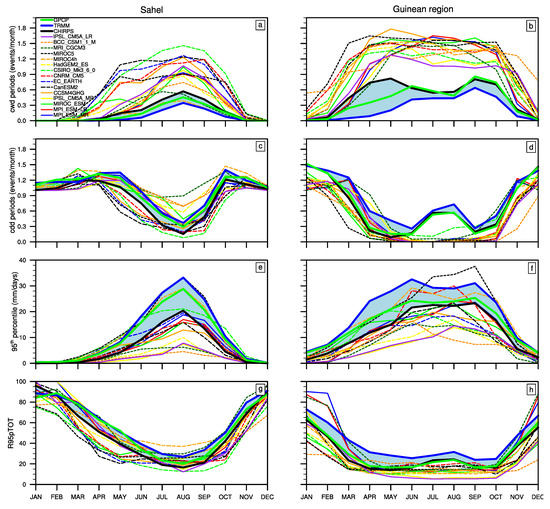
Figure A2.
Same as Figure 4 but with a finer grid resolution: 0.5 × 0.5.
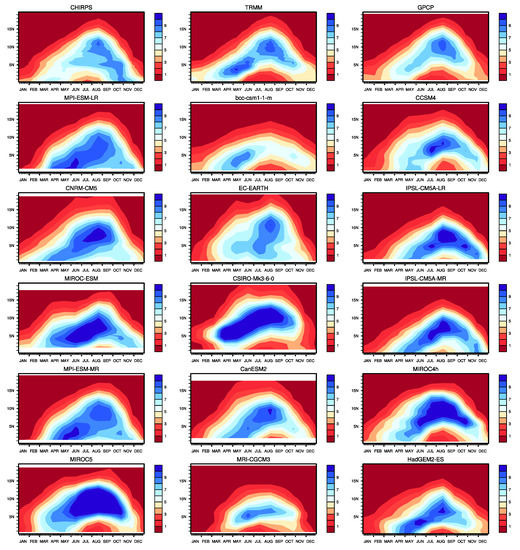
Figure A3.
Hovmuller diagrams of monthly precipitation averaged over 20W-25E for CHIRPS, TRMM and GPCP (first line) and 15 CMIP5 outputs.
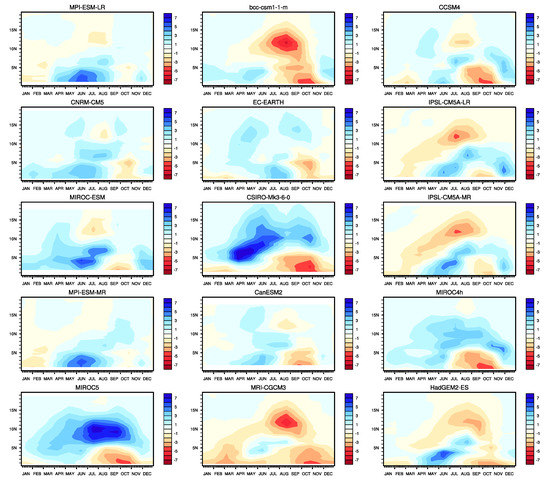
Figure A4.
CMIP5 models bias with CHIRPS on Hovmuller diagrams.
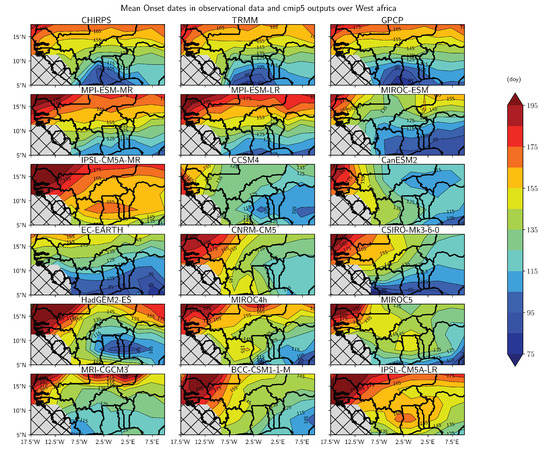
Figure A5.
Mean onset dates over West Africa in CHIRPS, TRMM, GPCP and CMIP5 models outputs. The grey shaded area represent ignored domain.
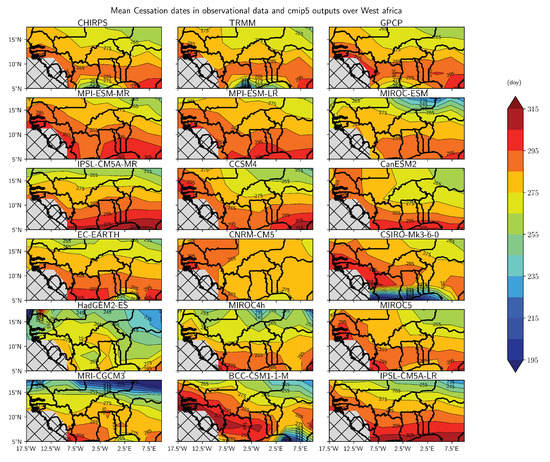
Figure A6.
Mean cessation dates over West Africa in CHIRPS, TRMM, GPCP and CMIP5 models outputs. The grey shaded area represent ignored domain.
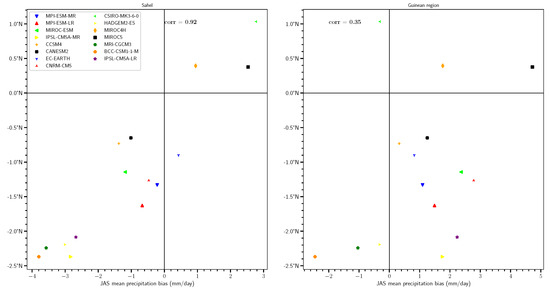
Figure A7.
Relation between the bias of July-September-mean precipitation and the bias of July-September-mean ITCZ position.

Table A1.
Mean onset and cessation dates (in day of the year) in CHIRPS, GPCP, TRMM and CMIP5 model’s simulations and their MMM over the Sahel and Guinean region averaged over 1985–2004 for CHIRPS and models and over 2000–2010 for GPCP and TRMM.
Table A1.
Mean onset and cessation dates (in day of the year) in CHIRPS, GPCP, TRMM and CMIP5 model’s simulations and their MMM over the Sahel and Guinean region averaged over 1985–2004 for CHIRPS and models and over 2000–2010 for GPCP and TRMM.
| Sahel | Guinean Region | |||
|---|---|---|---|---|
| Datasets | Onset | Cessation | Onset | Cessation |
| CHIRPS | 152 | 280 | 105 | 299 |
| GPCP | 150 | 283 | 97 | 303 |
| TRMM | 152 | 283 | 101 | 297 |
| MMM | 142 | 283 | 125 | 277 |
| BCC-CSM1-1-M | 140 | 294 | 153 | 282 |
| CanESM2 | 125 | 276 | 108 | 293 |
| CCSM4 | 121 | 281 | 107 | 294 |
| CNRM-CM5 | 140 | 286 | 121 | 293 |
| CSIRO-Mk3-6-0 | 141 | 291 | 105 | 306 |
| EC-EARTH | 128 | 282 | 99 | 293 |
| HadGEM2-ES | 141 | 265 | 141 | 265 |
| IPSL-CM5A-LR | 165 | 285 | 165 | 285 |
| IPSL-CM5A-MR | 171 | 284 | 174 | 282 |
| MIROC-ESM | 131 | 278 | 93 | 288 |
| MIROC4h | 134 | 280 | 107 | 301 |
| MIROC5 | 140 | 286 | 97 | 305 |
| MPI-ESM-LR | 158 | 288 | 134 | 296 |
| MPI-ESM-MR | 160 | 290 | 134 | 298 |
| MRI-CGCM3 | 135 | 277 | 141 | 272 |

Table A2.
Correlations between the annual cycle of mean precipitation and the frequency of daily precipitation events (), the mean intensity of daily precipitation events (), the cumulative dry () and wet () days, the 95th percentile of daily precipitation events () and the contribution of very wet days (above R95) to total precipitation () for the Sahel (left) and Guinean region (right) in observations and models. For p-values higher than 0.01, the correlation is written in italic. All correlation higher than 0.95 are in bold.
Table A2.
Correlations between the annual cycle of mean precipitation and the frequency of daily precipitation events (), the mean intensity of daily precipitation events (), the cumulative dry () and wet () days, the 95th percentile of daily precipitation events () and the contribution of very wet days (above R95) to total precipitation () for the Sahel (left) and Guinean region (right) in observations and models. For p-values higher than 0.01, the correlation is written in italic. All correlation higher than 0.95 are in bold.
| Sahel | Guinean Region | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Datasets | FREQ | SDII | CDD | CWD | R95 | R95PTOT | FREQ | SDII | CDD | CWD | R95 | R95PTOT |
| CHIRPS | 0.97 | 0.99 | 0.99 | 1.00 | 0.88 | 0.96 | 0.87 | 0.99 | ||||
| GPCP | 0.98 | 0.98 | 0.98 | 1.00 | 0.97 | 0.98 | 0.96 | 0.99 | ||||
| TRMM | 0.99 | 0.97 | 0.97 | 1.00 | 0.98 | 0.95 | 0.90 | 0.99 | ||||
| BCC-CSM1-1-M | 1.00 | 0.87 | 0.98 | 1.00 | 0.91 | 0.98 | 0.81 | 0.95 | ||||
| CanESM2 | 0.96 | 0.99 | 0.90 | 1.00 | 0.28 | 0.91 | 0.99 | 0.88 | 0.97 | |||
| CCSM4 | 0.98 | 0.96 | 0.98 | 1.00 | 0.98 | 0.99 | 0.93 | 1.00 | ||||
| CNRM-CM5 | 0.98 | 0.99 | 0.98 | 1.00 | 0.92 | 0.99 | 0.81 | 0.98 | ||||
| CSIRO-Mk3-6-0 | 0.99 | 0.99 | 0.99 | 0.99 | 0.96 | 1.00 | 0.91 | 0.99 | ||||
| EC-EARTH | 0.98 | 0.99 | 0.98 | 1.00 | 0.98 | 1.00 | 0.92 | 1.00 | ||||
| HadGEM2-ES | 0.97 | 0.97 | 0.96 | 1.00 | 0.91 | 0.99 | 0.82 | 1.00 | ||||
| IPSL-CM5A-LR | 0.97 | 0.98 | 0.96 | 0.99 | 0.33 | 0.90 | 0.99 | 0.73 | 0.99 | |||
| IPSL-CM5A-MR | 0.98 | 0.32 | 0.97 | 1.00 | 0.32 | 0.93 | 0.99 | 0.77 | 0.98 | |||
| MIROC4h | 0.97 | 0.99 | 0.98 | 1.00 | 0.99 | 0.97 | 0.97 | 0.99 | ||||
| MIROC5 | 0.92 | 1.00 | 0.89 | 1.00 | 0.89 | 0.99 | 0.83 | 0.98 | ||||
| MIROC-ESM | 0.97 | 0.98 | 0.93 | 0.99 | 0.98 | 1.00 | 0.94 | 0.99 | ||||
| MPI-ESM-LR | 0.99 | 0.97 | 0.99 | 1.00 | 0.97 | 0.99 | 0.98 | 0.99 | 0.38 | |||
| MPI-ESM-MR | 0.98 | 0.96 | 0.99 | 1.00 | 0.25 | 0.98 | 0.99 | 0.99 | 0.99 | |||
| MRI-CGCM3 | 1.00 | 0.88 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 1.00 | ||||
References
- Fink, A.H.; Engel, T.; Ermert, V.; van der Linden, R.; Schneidewind, M.; Redl, R.; Afiesimama, E.; Thiaw, W.M.; Yorke, C.; Evans, M.; et al. Mean Climate and Seasonal Cycle. In Meteorology of Tropical West Africa; Parker, D.J., Diop-Kane, M., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2017; pp. 1–39. [Google Scholar] [CrossRef]
- Dunning, C.M.; Black, E.C.L.; Allan, R.P. The onset and cessation of seasonal rainfall over Africa: Onset and cessation of african rainfall. J. Geophys. Res. Atmos. 2016, 121, 11405–11424. [Google Scholar] [CrossRef]
- Liebmann, B.; Bladé, I.; Kiladis, G.N.; Carvalho, L.M.V.; Senay, G.B.; Allured, D.; Leroux, S.; Funk, C. Seasonality of African Precipitation from 1996 to 2009. J. Clim. 2012, 25, 4304–4322. [Google Scholar] [CrossRef]
- Hulme, M. Rainfall changes in Africa: 1931–1960 to 1961–1990. Int. J. Clim. 1992, 12, 685–699. [Google Scholar] [CrossRef]
- Rowell, D.P. Reply to comments by Y. C. Sud and W. K.-M. Lau on ‘Variability of summer rainfall over tropical north Africa (1906–92): Observations and modelling’ by D. P. Rowell, C. K. Folland, K. Maskell and M. N. Ward (April A, 1995, 121, 669–704) Further analysis of simulated interdecadal and interannual variability of summer rainfall over tropical north Africa. Q. J. R. Meteorol. Soc. 1996, 122, 1007–1013. [Google Scholar] [CrossRef]
- Panthou, G.; Vischel, T.; Lebel, T. Recent trends in the regime of extreme rainfall in the Central Sahel. Int. J. Clim. 2014, 34, 3998–4006. [Google Scholar] [CrossRef]
- Mouhamed, L.; Traore, S.B.; Alhassane, A.; Sarr, B. Evolution of some observed climate extremes in the West African Sahel. Weather Clim. Extremes 2013, 1, 19–25. [Google Scholar] [CrossRef]
- Zipser, E.J.; Cecil, D.J.; Liu, C.; Nesbitt, S.W.; Yorty, D.P. Where are the most intense thunderstorms on earth? Bull. Am. Meteorol. Soc. 2006, 87, 1057–1072. [Google Scholar] [CrossRef]
- Lebel, T.; Ali, A. Recent trends in the Central and Western Sahel rainfall regime (1990–2007). J. Hydrol. 2009, 375, 52–64. [Google Scholar] [CrossRef]
- Mathon, V.; Laurent, H.; Lebel, T. Mesoscale Convective System Rainfall in the Sahel. J. Appl. Meteorol. 2002, 41, 1081–1092. [Google Scholar] [CrossRef]
- Frappart, F.; Hiernaux, P.; Guichard, F.; Mougin, E.; Kergoat, L.; Arjounin, M.; Lavenu, F.; Koité, M.; Paturel, J.E.; Lebel, T. Rainfall regime across the Sahel band in the Gourma region, Mali. J. Hydrol. 2009, 375, 128–142. [Google Scholar] [CrossRef]
- Salack, S.; Muller, B.; Gaye, A.T.; Hourdin, F.; Cisse, N. Multi-scale analyses of dry spells across Niger and Senegal. Sécheresse 2012, 23, 3–13. [Google Scholar] [CrossRef]
- Sivakumar, M.V.K. Empirical Analysis of Dry Spells for Agricultural Applications in West Africa. J. Clim. 1992, 5, 532–539. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, T.; Zou, L.; Zhang, L.; Chen, X. Reduced exposure to extreme precipitation from 0.5 °C less warming in global land monsoon regions. Nat. Commun. 2018, 9, 3153. [Google Scholar] [CrossRef] [PubMed]
- Sanogo, S.; Fink, A.H.; Omotosho, J.A.; Ba, A.; Redl, R.; Ermert, V. Spatio-temporal characteristics of the recent rainfall recovery in West Africa. Int. J. Clim. 2015, 35, 4589–4605. [Google Scholar] [CrossRef]
- Taylor, C.M.; Belušić, D.; Guichard, F.; Parker, D.J.; Vischel, T.; Bock, O.; Harris, P.P.; Janicot, S.; Klein, C.; Panthou, G. Frequency of extreme Sahelian storms tripled since 1982 in satellite observations. Nature 2017, 544, 475–478. [Google Scholar] [CrossRef]
- Descroix, L.; Guichard, F.; Grippa, M.; Lambert, L.A.; Panthou, G.; Mahé, G.; Gal, L.; Dardel, C.; Quantin, G.; Kergoat, L.; et al. Evolution of Surface Hydrology in the Sahelo-Sudanian Strip: An Updated Review. Water 2018, 10, 748. [Google Scholar] [CrossRef]
- Molua, E.L. Turning up the heat on African agriculture: The impact of climate change on Cameroon’s agriculture. Afr. J. Agric. Resour. Econ. 2008, 2, 45–64. [Google Scholar]
- New, M.; Hewitson, B.; Stephenson, D.B.; Tsiga, A.; Kruger, A.; Manhique, A.; Gomez, B.; Coelho, C.A.S.; Masisi, D.N.; Kululanga, E.; et al. Evidence of trends in daily climate extremes over southern and west Africa. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Lobell, D.B.; Schlenker, W.; Costa-Roberts, J. Climate Trends and Global Crop Production Since 1980. Science 2011, 333, 616–620. [Google Scholar] [CrossRef]
- Anyamba, A.; Small, J.L.; Britch, S.C.; Tucker, C.J.; Pak, E.W.; Reynolds, C.A.; Crutchfield, J.; Linthicum, K.J. Recent Weather Extremes and Impacts on Agricultural Production and Vector-Borne Disease Outbreak Patterns. PLoS ONE 2014, 9, e92538. [Google Scholar] [CrossRef]
- Sané, O.D.; Gaye, A.T.; Diakhaté, M.; Aziadekey, M. Social Vulnerability Assessment to Flood in Medina Gounass Dakar. J. Geogr. Inf. Syst. 2015, 07, 415. [Google Scholar] [CrossRef]
- Sané, O.D.; Gaye, A.T.; Diakhaté, M.; Aziadekey, M. Critical Factors of Vulnerability That Enable Medina Gounass (Dakar/Senegal) to Adapt against Seasonal Flood Events. J. Geogr. Inf. Syst. 2016, 8, 457–469. [Google Scholar] [CrossRef]
- Groupe d’experts intergouvernemental sur l’évolution du climat.; Pachauri, R.K.; Meyer, L.A. Changements climatiques 2014: rapport de synthèse: Contribution des Groupes de travail I, II et III au cinquième Rapport d’évaluation du Groupe d’experts intergouvernemental sur l’évolution du climat; GIEC: Genève, Switzerland, 2015; OCLC: 948289514. [Google Scholar]
- Biasutti, M.; Sobel, A.H. Delayed Sahel rainfall and global seasonal cycle in a warmer climate. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Allan, R.P.; Soden, B.J. Atmospheric Warming and the Amplification of Precipitation Extremes. Science 2008, 321, 1481–1484. [Google Scholar] [CrossRef]
- Giorgi, F.; Coppola, E.; Solmon, F.; Mariotti, L.; Sylla, M.B.; Bi, X.; Elguindi, N.; Diro, G.T.; Nair, V.; Giuliani, G.; et al. RegCM4: Model description and preliminary tests over multiple CORDEX domains. Clim. Res. 2012, 52, 7–29. [Google Scholar] [CrossRef]
- Giorgi, F.; Coppola, E.; Raffaele, F.; Diro, G.T.; Fuentes-Franco, R.; Giuliani, G.; Mamgain, A.; Llopart, M.P.; Mariotti, L.; Torma, C. Changes in extremes and hydroclimatic regimes in the CREMA ensemble projections. Clim. Chang. 2014, 125, 39–51. [Google Scholar] [CrossRef]
- Asrar, G.R.; Hurrell, J.W. (Eds.) Climate Science for Serving Society; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Roehrig, R. Intraseasonal Variability of the West African Monsoon: Characterization and Modelling. Ph.D. Thesis, Université Paris-Est, Champs-sur-Marne, France, 2010. [Google Scholar]
- Monerie, P.A.; Sanchez-Gomez, E.; Boé, J. On the range of future Sahel precipitation projections and the selection of a sub-sample of CMIP5 models for impact studies. Clim. Dyn. 2017, 48, 2751–2770. [Google Scholar] [CrossRef]
- Vizy, E.K.; Cook, K.H.; Crétat, J.; Neupane, N. Projections of a Wetter Sahel in the Twenty-First Century from Global and Regional Models. J. Clim. 2013, 26, 4664–4687. [Google Scholar] [CrossRef]
- Zebaze, S.; Jain, S.; Salunke, P.; Shafiq, S.; Mishra, S.K. Assessment of CMIP5 multimodel mean for the historical climate of Africa. Atmos. Sci. Lett. 2019, 20, e926. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Roehrig, R.; Bouniol, D.; Guichard, F.; Hourdin, F.; Redelsperger, J.L. The Present and Future of the West African Monsoon: A Process-Oriented Assessment of CMIP5 Simulations along the AMMA Transect. J. Clim. 2013, 26, 6471–6505. [Google Scholar] [CrossRef]
- Maidment, R.I.; Grimes, D.; Allan, R.P.; Tarnavsky, E.; Stringer, M.; Hewison, T.; Roebeling, R.; Black, E. The 30 year TAMSAT African Rainfall Climatology And Time series (TARCAT) data set. J. Geophys. Res. Atmos. 2014, 119, 10619–10644. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Huffman, G.J.; Adler, R.F.; Morrissey, M.M.; Bolvin, D.T.; Curtis, S.; Joyce, R.; McGavock, B.; Susskind, J. Global Precipitation at One-Degree Daily Resolution from Multisatellite Observations. J. Hydrometeorol. 2001, 2, 36–50. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Sylla, M.B.; Giorgi, F.; Pal, J.S.; Gibba, P.; Kebe, I.; Nikiema, M. Projected Changes in the Annual Cycle of High-Intensity Precipitation Events over West Africa for the Late Twenty-First Century. J. Clim. 2015, 28, 6475–6488. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Giannini, A.; Saravanan, R.; Chang, P. Oceanic Forcing of Sahel Rainfall on Interannual to Interdecadal Time Scales. Science 2003, 302, 1027–1030. [Google Scholar] [CrossRef]
- Janicot, S.; Caniaux, G.; Chauvin, F.; Coëtlogon, G.d.; Fontaine, B.; Hall, N.; Kiladis, G.; Lafore, J.P.; Lavaysse, C.; Lavender, S.L.; et al. Intraseasonal variability of the West African monsoon. Atmos. Sci. Lett. 2011, 12, 58–66. [Google Scholar] [CrossRef]
- d’Orgeval, T.; Polcher, J.; Li, L. Uncertainties in modelling future hydrological change over West Africa. Clim. Dyn. 2006, 26, 93–108. [Google Scholar] [CrossRef]
- Adejuwon, J.O.; Odekunle, T.O. Variability and the Severity of the “Little Dry Season” in Southwestern Nigeria. J. Clim. 2006, 19, 483–493. [Google Scholar] [CrossRef]
- Stephens, G.L.; L’Ecuyer, T.; Forbes, R.; Gettelmen, A.; Golaz, J.C.; Bodas-Salcedo, A.; Suzuki, K.; Gabriel, P.; Haynes, J. Dreary state of precipitation in global models. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Guichard, F.; Petch, J.; Redelsperger, J.L.; Bechtold, P.; Chaboureau, J.P.; Cheinet, S.; Grabowski, W.; Grenier, H.; Jones, C.; Köhler, M.; et al. Modelling the diurnal cycle of deep precipitating convection over land with cloud-resolving models and single-column models. Q. J. R. Meteorol. Soc. 2004, 130, 3139–3172. [Google Scholar] [CrossRef]
- Thorncroft, C.D.; Nguyen, H.; Zhang, C.; Peyrillé, P. Annual cycle of the West African monsoon: Regional circulations and associated water vapour transport. Q. J. R. Meteorol. Soc. 2011, 137, 129–147. [Google Scholar] [CrossRef]
- Fitzpatrick, R.G.J.; Bain, C.L.; Knippertz, P.; Marsham, J.H.; Parker, D.J. The West African Monsoon Onset: A Concise Comparison of Definitions. J. Clim. 2015, 28, 8673–8694. [Google Scholar] [CrossRef]
- Bombardi, R.J.; Moron, V.; Goodnight, J.S. Detection, variability, and predictability of monsoon onset and withdrawal dates: A review. Int. J. Clim. 2019. [Google Scholar] [CrossRef]
- Marteau, R.; Moron, V.; Philippon, N. Spatial Coherence of Monsoon Onset over Western and Central Sahel (1950–2000). J. Clim. 2009, 22, 1313–1324. [Google Scholar] [CrossRef]
- Seth, A.; Rauscher, S.A.; Biasutti, M.; Giannini, A.; Camargo, S.J.; Rojas, M. CMIP5 Projected Changes in the Annual Cycle of Precipitation in Monsoon Regions. J. Clim. 2013, 26, 7328–7351. [Google Scholar] [CrossRef]
- Diallo, F.B.; Hourdin, F.; Rio, C.; Traore, A.K.; Mellul, L.; Guichard, F.; Kergoat, L. The Surface Energy Budget Computed at the Grid-Scale of a Climate Model Challenged by Station Data in West Africa. J. Adv. Model. Earth Syst. 2017, 9, 2710–2738. [Google Scholar] [CrossRef]
- Dixon, R.D.; Daloz, A.S.; Vimont, D.J.; Biasutti, M. Saharan Heat Low Biases in CMIP5 Models. J. Clim. 2016, 30, 2867–2884. [Google Scholar] [CrossRef]
- Dixon, R.D.; Vimont, D.J.; Daloz, A.S. The relationship between tropical precipitation biases and the Saharan heat low bias in CMIP5 models. Clim. Dyn. 2018, 50, 3729–3744. [Google Scholar] [CrossRef]
- Monerie, P.A.; Roucou, P.; Fontaine, B. Mid-century effects of Climate Change on African monsoon dynamics using the A1B emission scenario. Int. J. Clim. 2013, 33, 881–896. [Google Scholar] [CrossRef]
- Biasutti, M.; Voigt, A.; Boos, W.R.; Braconnot, P.; Hargreaves, J.C.; Harrison, S.P.; Kang, S.M.; Mapes, B.E.; Scheff, J.; Schumacher, C.; et al. Global energetics and local physics as drivers of past, present and future monsoons. Nat. Geosci. 2018, 11, 392–400. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).