Abstract
Using a set of near space high-resolution balloon data released in Hami, Xinjiang, we explored the spectral characteristics of temperature fluctuations and three-dimensional wind field fluctuations. As different from previous studies, which were based on radiosondes, we have increased the height range of spectral analysis to the stratosphere (38 km), which can explore the variation of spectral features with altitude, and can analyze higher wavenumber regions. The results show that horizontal wind field disturbances are isotropic, meridional and zonal winds have relatively consistent spectral structures, while vertical wind fluctuations have completely different spectral structures, which cannot be explained by the existing “universal spectrum” theory. The observed spectrum of horizontal wind field can be explained well by the “wind-shifting” theory. The ratio of spectral kinetic energy to potential energy is approximately constant only in the high wavenumber region but it varies at different height intervals. This study is a necessary extension of the observation for the characteristics of the vertical wavenumber spectrum in northwestern China, and it is also an experimental observation of spectral characteristics using radiosonde data at higher altitudes.
1. Introduction
A gravity wave is an important form of atmospheric motion. It is a wave whose restoring force is gravity generated in the atmosphere with stable stratification. A gravity wave occurring in the atmosphere is called an internal gravity wave, while one occurring near the free surface and lower boundary of the atmosphere is called an external gravity wave. In the process of generation, propagation, saturation and breaking of gravity wave, energy is always transported. Previous studies have shown that the gravity waves in the middle and upper atmosphere are mainly generated in the troposphere and the lower stratosphere [1], which can cause significant temperature and wind field disturbances. Therefore, it is very useful to study the gravity waves by extracting the fluctuation information in the data of atmospheric wind field and temperature field. Gravity waves generated in the lower atmosphere increase in amplitude as the height increases, and when the amplitude reaches a certain level, they break up due to convective instability or dynamic instability, and are considered to have reached saturation. In this case, the airflow changes from layer to turbulence, which is also recognized as the generation mechanism of CAT (clear-air turbulence). The concept of “universal” spectrum was proposed in 1982 [2], showing that the vertical wavenumber spectrum in the troposphere and the lower stratosphere generally has similar shape and power spectrum density regardless of seasonal- and meteorological-conditions, or geographical location. Based on this, linear instability [3,4], nonlinear wave-wave interaction [5], Doppler extension [6,7], saturation cascade similarity theory [8], and other gravity wave saturation models were proposed.
The means to obtain the information about the vertical wavenumber spectrum of gravity waves is limited. Although space-based devices such as satellites cover a wide range, the resolution is too low to reflect small-scale disturbances. At present it is mainly measured by mesosphere-stratosphere-troposphere (MST) radar and middle-upper atmosphere (MU) radar [9,10], rocket detection [11,12], lidar measurements, and balloon observations [13,14,15,16] to obtain mesoscale fluctuations in different regions.
Radiosonde data, due to its high resolution, relatively low release cost, and many years of continuous complete data, has become an important means to obtain the spectral information of gravity wave [13,14,15,16,17,18,19,20]. However, many results show that the values of spectral amplitudes and slopes have a wide range in the high wavenumber region, and some results even show that the observed spectrum amplitudes and slopes do not follow the gravity wave saturation model [3,4,9,10,14,17,19,20]. The above researches show that with the improvement of balloon resolution, after obtaining the vertical wavenumber spectrum with higher resolution, it will be found that the current gravity wave saturation model cannot explain some phenomena. In order to improve and perfect the existing spectrum theory, the research of high-precision vertical wavenumber spectrum is very necessary. In this study, we analysis the vertical wavenumber spectrum characteristics of gravity waves in Hami, Xinjiang using near space high-resolution balloon data and extract the spectrum characteristics of gravity waves from temperature field and three-dimensional wind field. The research on spectrum characteristics is extended to a higher altitude. Our work is a necessary extension to obtain the characteristics of the gravitational wavenumber spectrum in northwest China by radiosonde data.
2. Data and Data Processing Methods
2.1. Data
The data used in this paper is from the CW-Beidou upper-air meteorological detection system, which consists of a GTS3 digital radiosonde, GTC3 telemetry receiving system, GRZ2012 electronic sonde detection box, computer processing terminal, and special software. The system adopts a new TPU (temperature-pressure-humidity) sensor to measure atmospheric temperature, humidity and pressure, and adopts Beidou positioning technology to measure atmospheric wind direction and speed. The detection accuracy of this system is obviously improved compared with the existing detection systems in China, and its anti-interference ability, cost of ground receiving system, automation degree and requirements of application conditions are all greatly superior to other high-altitude detection systems. From 21 September to 26 September 2019, a total of eight near space high-resolution balloon sounding data were released in Hami region of Xinjiang, and meteorological data from the ground to over 40 km were obtained. The sampling frequency of the sensor is 1 HZ, and the ascent rate of the balloon is from 4 m/s at low altitude to 13 m/s at high altitude, with an average vertical resolution of 7 m. The data of temperature and wind speed were interpolated with cubic splines at an interval of 7 m. Compared with previous studies, the advantage of this experiment is that the radiosonde data used in this experiment has higher detection height and higher vertical resolution, which can explore the vertical wavenumber spectrum of most regions in the stratosphere and obtain the corresponding spectrum features of higher wavenumber regions.
Wind shear is an important factor that excites gravity waves and can be obtained by the following formula:
when calculating wind shear, a sliding average of 1 km is taken at the vertical height to filter out small scale fluctuations and jitter points caused by noise. As can be seen from Figure 1, under 10 km, wind shear is generally small, less than 0.015 s−1, and above 20 km, there is a maximum area of wind shear, which can reach 0.02 s−1, especially in the night of 22nd and the day of 23rd. However, the diurnal variation of upper-air wind shear is very obvious, which indicates that the upper-level wind in this region has a great variation.
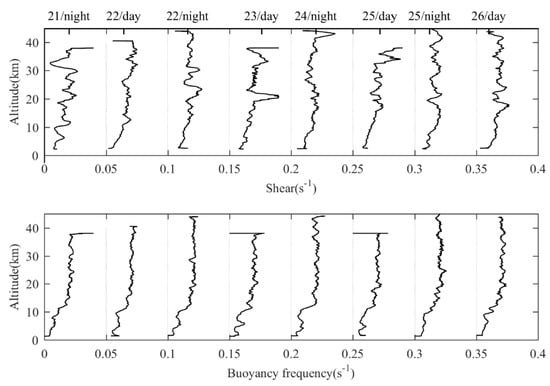
Figure 1.
Vertical wind shear (s−1) (top panel), buoyancy frequency (s−1) (bottom panel) from eight soundings. Successive profiles are displaced by 0.05 s−1 for wind shear and buoyancy frequency.
2.2. Calculation of Vertical Wavenumber Spectrum.
Considering that the use of simple quadratic fitting method to generate the background profile will generate large errors, we use sliding polynomial fitting to extract the gravity wave, which can achieve a better effect [21]. The Savitzky-Gola filter is selected, the filter coefficient is calculated by unweighted linear least squares regression and cubic polynomial, and the selected window width is 10 km. After fitting the whole profile of the temperature field and wind field data, the corresponding background field profile is obtained. The five interval segments mentioned above are selected, and the residual is obtained by subtracting the background profile from the original data. Referring to the method proposed by Dewan and Grossbard [22], taking the vertical wavenumber spectrum of temperature profile as an example, the complete process of wavenumber spectrum extraction is described as follows:
The perturbation profile of temperature is obtained by subtracting the fitting value from the original data (), where is the ith data point. The normalized perturbation of temperature can be obtained form , in order to reduce the spectrum leakage, the perturbation value is pre-whitened here:
where , . The discrete Fourier transform of is:
where , = 1, …, . is the vertical wavenumber, is the vertical step length. Unilateral power spectrum density (PSD) is:
Then use the Hanning window to smooth the power spectrum:
where .The smoothed power spectrum needs to be recovered from the pre-whitening process to compensate for the effects of the difference and cosine taper windows [22]:
Considering the higher range of data coverage, the effect of sensor lag on the temperature spectrum needs to be considered [14]. In particular, the high-wavenumber region of the temperature spectrum attenuates too much in the region above the altitude of 20 km, which needs to be corrected. So the PSD () obtained from the actual atmosphere is:
where, is the ascent rate of the temperature sensor carried by the balloon, and is the response time of the sensor. It is assumed that the ascent rate of the balloon is constant, = 7 m/s, and the response time of the temperature sensor is 3 s.
The saturated gravity wave model adopted here is [4,13]:
where is the gravitational acceleration, is the Brunt -vaisala frequency, and the vertical wavenumber is in cycles per meter.
For wind speed disturbance, the vertical wavenumber spectrum is calculated following the same process. Since the wind speed is measured by Beidou positioning system, lag error correction is not considered. In radiosonde, the wind velocity directly obtained only contains meridional and zonal winds, so the horizontal wind velocity disturbance can be obtained by subtracting the fitted data from the original data. For vertical winds, we consider the disturbance component of the balloon’s ascent rate as a vertical wind velocity disturbance [23]. In the process of extracting the fluctuation of vertical wind speed, in order to eliminate the error caused by turbulence and balloon oscillation [20], the disturbance profile takes a 31-point sliding average (210 m) before the Fourier transform of the vertical disturbance component.
3. Results and Discussion
3.1. Spectrum Analysis of Temperature Field
We take the sounding data of night 24 as an example to illustrate the specific analysis process. Figure 2a shows the temperature and buoyancy frequency profile. Between 10.5–13 km, the buoyancy frequency significantly increases. The average buoyancy frequency below 10 km is 0.0076 rad/s, while the average buoyancy frequency above 14 km is 0.021 rad/s. Figure 2b shows the distribution of wind speed component with height. It can be seen that the zonal component is significantly larger than the meridional wind component, and there is an obvious jet zone near the tropopause. The wind speed within the range of 20–30 km is significantly lower than other heights. Figure 2c is the normalized temperature fluctuation profile, and it can be seen that there is a large disturbance in the temperature profile between 11 km and 13 km, indicating that the convective instability in this region is strong and not suitable for spectrum analysis. Figure 2d shows the normalized temperature fluctuation after pre-whitening, which solves the problem of spectrum leakage. Meanwhile, the fluctuations become more centralized, so the vertical wavenumber spectrum extracted from pre-whitened data can get a better effect.
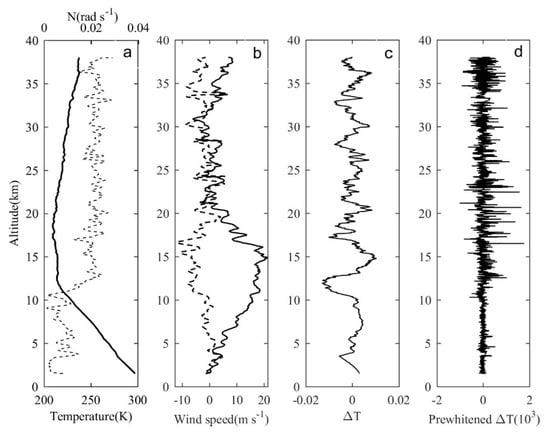
Figure 2.
(a) An example of temperature (solid line) and buoyancy frequency (dashed line), (b) horizontal wind speed component (solid line: zonal wind speed component; dashed line: meridional wind velocity component), (c) normalized temperature disturbance component, and (d) pre-whitened normalized temperature disturbance profiles (from left to right) observed on the night of 21 September, 2019 during the balloon ascent.
The Fourier transform is applied to the pre-whitened data, and the characteristics of the wavenumber spectrum are characterized by the slope and spectral amplitude. In the wavenumber range of 9.97 × 10−4 7.5 × 10−2 cycle/m, we obtained the slope by first-order linear fitting according to the log-log power spectrum, where 7.5 × 10−2 cycle/m corresponds to half the Nyquist wavenumber (with a resolution of 7 m). In this wavenumber range, the aliasing effect can be ignored. When calculating the corresponding amplitude of the power spectrum, in order to avoid the amplitude swing caused by the change of the actual spectrum slope, the power spectrum density corresponding to the “center of mass “wavenumber [22] is used as the spectrum amplitude:
Among them, and respectively correspond to the minimum wavenumber and the maximum wavenumber of the fitting interval, and represents the total number of points in the fitting interval. The “center of mass“ wavenumber can be written as:
Here we use three criteria to determine the feasibility of spectrum estimation in the selected intervals: (1) The height ranges in which the Brunt-Vaisala frequency is approximately constant should be used. (2) Since that the ascent velocity is ∼7 m/s or larger and the horizontal wind speed is not more than about 10 times the balloon ascent rate [24]. (3) A shear criterion (shear > 0.035 s−1) is employed to reject velocity estimates that are clearly not consistent with adjacent points in the spatial series [9]. For the first two criteria, all the height ranges in the eight profiles are satisfied, and for the third criterion, only a small part between 20–26 km on 23 September during the day and a small part between 32–38 km on 25 September during the day cannot meet the criterion. When calculating the average wavenumber spectrum, we excluded the two intervals, and when discussing the changes in spectral characteristics with height, we referred to the results after excluding the two intervals.
The “center of mass” wavenumber of the vertical wavenumber spectrum is 2.8 × 10−2 cycle/m. Figure 3 shows the temperature spectrum calculated at 20–23 km, 20–26 km, and 20–29 km on the night of 24 September. The dash line represents the saturation spectrum predicted by Equation (8). The dotted line represents the spectrum amplitude of optimal linear fitting. With the increase of atmospheric thickness, the minimum wavenumbers that can be achieved decrease to 3.33 × 10−4 cycle/m, 1.67 × 10−4 cycle/m and 1.11 × 10−4 cycle/m, respectively. The corresponding spectrum amplitude are 1.54 × 10−4 (cycle/m)−1, 1.04 × 10−4 (cycle/m)−1 and 1.05 × 10−5 (cycle/m)−1, respectively. We use m to represent the slope of the amplitude of the fitted spectrum. It can be seen that the slope of the observed temperature spectrum is much lower than the “–3” theoretical spectrum, and the slope has a weak downward shift as the atmospheric thickness increases. While the limited thickness of the atmosphere will filter out the longer wavelength and may underestimate the energy and spectrum density of the wave, this offset of slop is much small compared to the value of –3. In order to avoid filtering out excessively long wavelengths in the lower atmospheric thickness, and at the same time, there can be enough intervals to reflect the changes in spectrum characteristics with altitude, 6 km is selected as the atmospheric thickness to extract the vertical wavenumber spectrum.
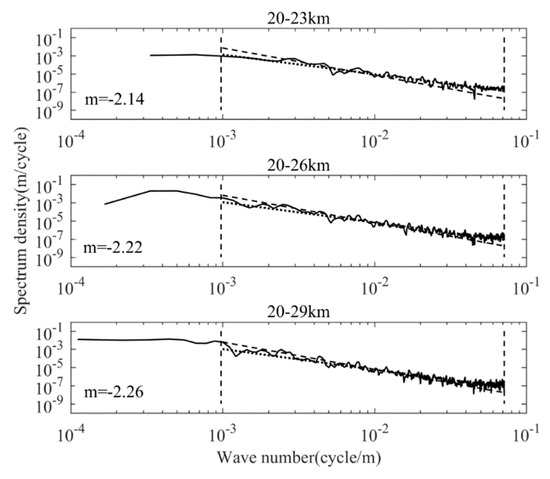
Figure 3.
Vertical wavenumber spectra of normalized temperature fluctuations observed at intervals of 20–26 km (top panel), 20–32 km (mid panel), and 20–38 km (bottom panel). The dashed line indicates the saturated spectrum amplitude predicted by Equation (8); the dotted line indicates the spectrum amplitude of the best linear fit, and the corresponding slope is marked on the graph.
The normalized vertical wavenumber spectrum of temperature fluctuations obtained from eight sounding balloons is shown in Table 1. Each profile is divided into five segments, and the wavenumber spectrum of a total of 40 segments with a thickness of 6 km is calculated. Table 1 shows the spectral slop of fitted amplitude spectrum in the wavenumber range of 9.97 × 10−4 – 7.5 × 10−2 cycle/m, the corresponding spectrum amplitude and theoretical spectrum amplitude at the “center of mass” wavenumber = 2.8 × 10−2 cycle/m. Since the buoyancy frequency in the stratosphere is obviously larger than that in the troposphere, it is closely related to the predicted saturation spectrum. Therefore, it can be seen from Table 1 that the predicted saturation spectrum amplitude in the stratosphere is much larger than that in the troposphere. In the troposphere, the fitted spectrum slope varies between −1.82 and −2.23, while in the stratosphere, the maximum spectrum slope can reach −2.63, and the minimum is only −1.46 (It should be noted that when discussing the magnitude of the slope, we ignore the negative sign). The observed spectrum amplitudes in the troposphere varies between 5.17 × 10−6 – 2.84 × 10−5 (cycle/m)−1, which is significantly higher than the corresponding predicted saturation spectrum amplitudes, with an average value of 3 × 10−6 (cycle/m)−1. In the stratosphere, the observed spectral amplitude is obviously larger than that in the troposphere. A general trend is that the theoretical spectrum amplitude in the low wavenumber region is larger than the observed spectrum, while the theoretical spectrum amplitude in the high wavenumber region is smaller than the observed spectrum.

Table 1.
Spectrum slope and amplitude of normalized temperature fluctuation.
Considering the differences in the slope and amplitude of the wavenumber spectrum at different times, we calculate the average spectrum according to the following formula:
where is the total number of profiles, . The vertical wavenumber spectrum of the normalized temperature fluctuation after averaging is shown in Figure 4. The averaged spectrum is smoother and the fluctuation is smaller in the large wavenumber region, so the fitted amplitude spectrum is more suitable. It can be seen from Figure 4 that the slope of the observed spectrum in the troposphere (2–8 km) is −2.43. As the height increases, the slope of the observed spectrum increases first and then decreases. The maximum value of the spectrum slope is –2.61 between 20–26 km, and the minimum is –2.41 between 32–38 km. Nastrom et al. [15] found that the average spectrum slope in the troposphere and stratosphere is –2.6 and –3 respectively. Our results (troposphere and lower stratosphere) are close to them but slightly lower than their calculated values. In the fitting interval, the entire observed spectrum is above the predicted saturation spectrum amplitude. The observed spectrum amplitude is 2.1 × 10−5 (cycle/m)−1, and the predicted saturation spectrum amplitude is 2.96 × 10−6 (cycle/m)−1, the ratio of the two is 7. In the four height ranges of 14–20 km, 20–26 km, 26–32 km and 32–38 km, the rations are 1.35, 0.90, 0.72, and 0.74, respectively. This result indicates that the obtained tropospheric spectrum amplitude is inconsistent with Smith et al. [4]. The observed spectrum amplitude is six times larger than the model spectral amplitude. However, in the stratosphere, we find that the amplitude ratio of the observed spectrum to the saturation spectrum decreases gradually with the increase of altitude, but both are around 1. This shows that the observed spectral amplitude in the stratosphere can be in good agreement with the saturation spectrum model of Smith et al. It should be noted that the spectrum amplitude is significantly reduced at the lowest wavenumber, which is due to the filtering effect of removing the linear background; while the enhancement of the spectrum amplitude at high wavenumbers is caused by the aliasing effect of noise and spectrum. Additionally, it should be noted that the theoretical models of internal wave spectra [6] predict the onset of wave-induced shear and convective instabilities at high vertical wave numbers. The possible transition in the slope caused by the turbulence spectrum will also result in the deviation from “–3” theoretical spectrum, especially at m >10−2 cycle/m (corresponding to turbulence with vertical scales less than 100 m). And as a comparison, we fit the spectrum between 9.97 × 10−4 – 1 × 10−2 cycle/m and get the spectral slopes at the height ranges of 2–8 km, 14–20 km, 20–26 km, 26–32 km, and 32–38 km are −2.98, −2.69, −2.47, −2.40, and −2.24, respectively. In this case we obtain the spectral slope excluding the effect of the turbulence spectrum.
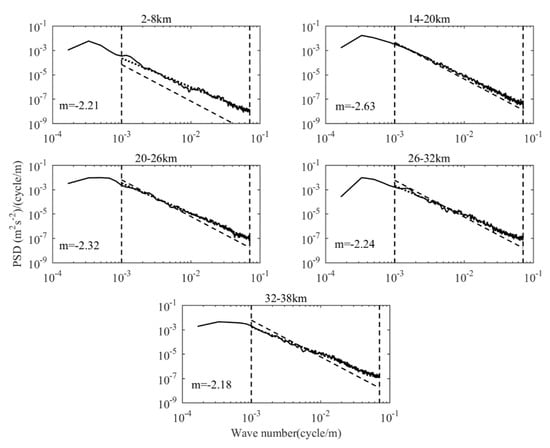
Figure 4.
Mean vertical wavenumbers spectrum of normalized temperature fluctuation observed at intervals of 2–8 km, 14–20 km, 20–26 km, 26–32 km and 32–38 km. The dash line represents the saturated spectrum amplitude predicted by Equation (8), the dotted line represents the spectrum amplitude of the best linear fit, and the corresponding slope m is marked on the graph.
3.2. Spectrum Analysis of 3D Wind Field
We adopt the method used in Section 2 to perform a spectrum analysis on the wind field detected by the balloon. Figure 5 shows the original profile and extracted wind field fluctuations at night on 24 September. The dashed lines represent the original data. From the vertical distribution of the horizontal wind field, it can be seen that there is an area of jet stream around 15 km, and the wind speed exceeds 23 m/s. From 1.5 km to 15 km, the wind speed continued to increase. From 15 km to 20 km, the wind speed decreased rapidly. From 20 km to 28 km, the wind speed remained at a relatively low level. Above 28 km, the wind speed increased again. When extracting the vertical wind fluctuation, the same method as the horizontal wind is applied. The difference is that a moving average of 210 m window area is used for the vertical wind fluctuation to eliminate the deviation caused by turbulence and the pendulum motion of the balloon during the ascent. The ascent rate in the lower troposphere is about 5 m/s. As the height increases, the ascent rate generally increases, and it will exceed 10 m/s above 35 km. Due to the pendulum effect and the self-inductive movement of the balloon, the vertical ascent rate is not as stable as the variation of the horizontal wind speed.
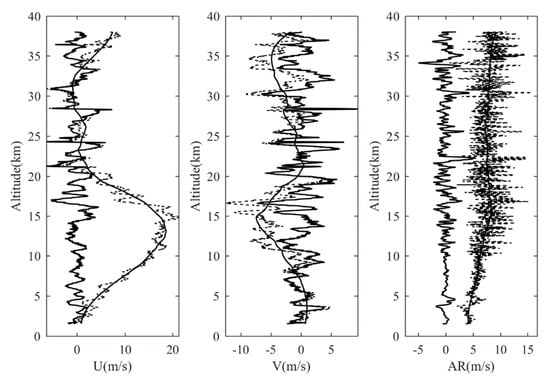
Figure 5.
Original profile and extracted fluctuations of the wind speed component at night on 24 September. From left to right: zonal wind, meridional wind, and ascent rate profiles. The dashed lines represent the original horizontal wind field and ascent rate, the smooth curve represents the extracted background components, and the fluctuation curve near zero represents the extracted wind speed fluctuation (The vertical wind fluctuation curve takes a 31-point moving average.).
For three-dimensional wind fluctuations, the average vertical wavenumber spectrum is calculated according to Equation 11. For the meridional and zonal wind fluctuations, the amplitude spectrum is still fitted in the wavenumber range of 9.97 × 10−4 – 7.5 ×10−2 cycle/ m, and the “center of mass” wavenumber = 2.8 × 10−2 cycle/m. For vertical wind fluctuations, when smoothing and filtering are performed to eliminate the effects of noise and turbulence, the difference of smooth points has great influence on the spectrum structure at large wavenumbers. In order to obtain a more accurate spectrum slope, the wavenumber range for linear fitting is 9.97 × 10−4 – 4.8 × 10−3 cycle/m, 4.8 × 10−3 cycle/m corresponds to a vertical scale of 210 m, which is also a smooth window for vertical wind fluctuations. The corresponding “center of mass” wavenumber is 1.9 × 10−3 cycle/m. The calculated results of the average vertical wavenumber spectrum for zonal, meridional, and vertical wind fluctuations at each height interval are shown in Figure 6. The power spectrum density corresponding to the “center of mass” wavenumber is defined as the spectrum amplitude of the entire vertical wavenumber spectrum. The calculation results of the spectrum slope and spectrum amplitude corresponding to the normalized temperature field and three-dimensional wind field fluctuations at 2–8 km, 14–20 km, 20–26 km, 26–32 km, 32–38 km are shown in Table 2, here the fitting interval of normalized temperature spectrum is 9.97 × 10−4 – 1 × 10−2 cycle/m, and the “center of mass” wavenumber is 4.7 × 10−3 cycle/m, excluding the interference of the turbulence spectrum.
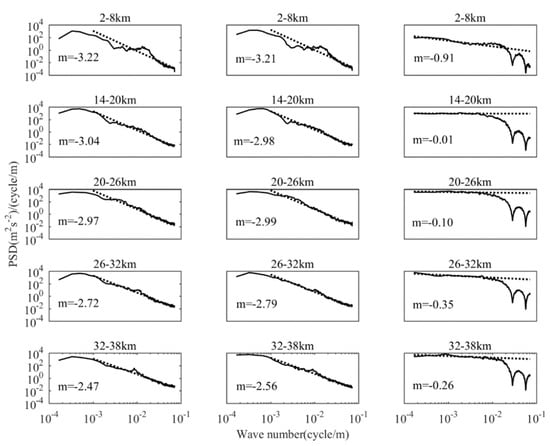
Figure 6.
Average vertical wavenumber spectrum of zonal wind (left panel), meridional wind (middle panel), vertical wind (right panel), the dashed line represents the linear fitting result, and the corresponding slope m is marked on the figure.

Table 2.
Spectrum slope and amplitude of normalized temperature fluctuation.
In general, the characteristics of vertical wavenumber spectrum for zonal and meridional wind fluctuations are very consistent, and the slope in each height range is almost the same. In the troposphere, the spectrum slopes of zonal and meridional wind fluctuations are deeper than the slope of “–3” of the saturation spectrum, but we find that the curve of the observed power spectrum has obvious fluctuations, and the power spectrum is deeper in the high and low wavenumber regions, while it is shallower in the middle wavenumber regions. There is an obvious “spectrum gap” between 2.2 × 10−3 cycle/m – 7.2 × 10−3 cycle/m, and an obvious “spectrum peak” between 1.0 × 10−2 cycle/m – 2.2 × 10−2 cycle/m. This phenomenon occurs in the interval of 2–8 km in each balloon sounding profile, and the wavenumber interval corresponding to “spectrum gap” and “spectrum peak” is basically unchanged. This indicates that the spectrum structure of the horizontal wind field in the troposphere may be affected by other geophysical processes besides gravity waves. This indicates that the vertical wavenumber spectrum of the horizontal wind fluctuations is complex, and it is at least controlled by the non-gravity wave process whose saturation process is not yet clear. In the middle and lower stratosphere (14–26 km), the spectrum slopes of the zonal and meridional winds are well in line with the “–3” slopes of the saturation spectrum, then the spectrum slope decreases with the increases of altitude. As for spectrum amplitude, zonal and meridional wind fluctuations are basically in the same order within the same height range, although the spectrum amplitude of the meridional wind is slightly larger than that of the zonal wind. In the troposphere, the mean spectrum amplitudes of zonal and meridional wind disturbances are 3.97 × 10−3 (cycle/m)−1 and 5.96 × 10−3 (cycle/m)−1, respectively, which are significantly lower than those in the stratosphere. In the stratosphere, as height increases, the spectrum amplitudes increase first and then decrease, reaching the maximum at 20–26 km, which are 2.53 × 10−2 (cycle/m)−1 and 2.73 × 10−2 (cycle/m)−1, respectively. From the above discussion, it can be seen that the spectrum amplitude and spectrum slope of zonal wind fluctuations are very close to that of meridional wind, indicating the universality of vertical wavenumber spectrum of horizontal wind field and the isotropy of horizontal wind fluctuation.
For the normalized temperature spectrum, after excluding the slope transition caused by the turbulence spectrum, we found that the trend of spectral slope and spectral amplitude with height is consistent with the horizontal wind field. When the slope transition of the turbulence spectrum is considered, the most obvious decrease in the spectral slope is at the height interval of 2–8 km, which decreases from –2.98 to –2.21, while the changes in other height intervals are not obvious. The above phenomenon shows that the turbulence activity is significantly stronger in the troposphere than that in the stratosphere.
The spectrum characteristics of vertical wind fluctuation are obviously different from the horizontal wind field, and it has a significantly shallower spectrum structure, showing a much smaller spectrum slope than the horizontal wind field. The largest spectrum slope is –0.91 in the troposphere, and the corresponding spectrum amplitude is 17.44 (cycle/m)−1. As the height continues to increase, the spectrum slope decreases. The spectrum amplitude in the stratosphere is much smaller than that in the troposphere. For a single profile, in the troposphere, the spectrum slope changes from –0.27 to –1.48, in the stratosphere, the spectrum slope significantly decreases, and can even be positive. Considering that the daily variation of the wavenumber spectrum for the vertical wind fluctuation is significantly larger, and especially in the low stratosphere, it is reasonable to obtain such a small slope. The above spectrum slope results from vertical wind fluctuation are basically consistent with [19,20], and the results are significantly larger than [9,25,26]. What needs to be explained here is that the height we compare with their research is limited to the troposphere and lower stratosphere, and the spectrum slope and spectrum amplitude obtained from radiosonde data at higher altitudes have almost no reference. Regardless of the vertical distribution of spectrum slope, spectrum amplitude, or the overall structure of the frequency spectrum, the vertical wavenumber spectrum of vertical wind disturbance is significantly different from the horizontal wind field, which indicates that the vertical wind field obviously follows a different spectrum law, which cannot be explained by the current “universal spectrum” theory.
Due to the low frequency of the horizontal wind field [2,27], if gravity waves in the troposphere propagate upwards, when low-frequency horizontal wind waves pass through jet stream, they are easier to be absorbed by the “critical layer” caused by the jet stream near the tropopause. However, it can be seen from the results of this paper that the amplitude of the horizontal wind field in the troposphere (2–8 km) is significantly smaller than that in the lower stratosphere (14–20 km), indicating that the gravity waves in the stratosphere that cause large horizontal wind field disturbance are not just from the troposphere. Therefore, we speculate that there are at least two sources of gravity wave activity during 21–26 September.
In order to explain the variation of the amplitude and slope of the vertical wavenumber spectrum with height, we explore the effect of the background wind field on the wavenumber spectrum according to the “wind shifting” theory proposed by Echermann [12]. Since the change of the background zonal wind will simultaneously produce the system change of speed variance and wavenumber, they will affect the shape of the vertical wavenumber power spectrum. The effect is represented by the sign parameter as follows:
is the background wind field, and is the horizontal phase velocity relative to the ground. Given the vertical profile of the background wind field and horizontal phase velocity, can be obtained. When = −1, the refraction effect caused by “shifting” of the background wind field will increase the intrinsic frequency, resulting in a reduction in the wavenumber, and the variance of the zonal wind speed decreases with height. The “downshifting” effect of the wavenumber spectrum in the large wavenumber region will be generated, resulting in a deeper spectrum slope. On the contrary, when = +1, vertical wavenumber spectrum in large wavenumber region will produce an “upshifting” effect, the spectrum slope decreases, and the zonal wind speed oscillation increases with altitude. The specific effect can refer to Figure 3 in [12].
Figure 7 shows the mean zonal winds observed over Hami from 21 September to 26 September. Using the mean zonal wind as the background wind field , and the dashed arrows represent the gravity waves propagating upward. The triangle arrow represents the gravity wave with and the V shape arrow represents the gravity wave with . The five height ranges used to calculate the wavenumber spectrum are represented by shaded regions. The Hami area is dominated by hilly terrain and affected by the Tianshan Mountains, so mountain wave activities are very active. Regarding the ground as a wave source, the phase velocity of the topographic wave is close to 0. According to “wind shifting” theory, in the troposphere (2–8 km), = −1, the change of the average zonal wind speed will produce a “downshifting” wavenumber spectrum and lead to a deeper slope. For the gravity wave with , when <18 m/s, considering there is a jet stream near 15 km, when the mountain waves propagating upward from the troposphere encounters this “critical layer”, it cannot enter the stratosphere, which means mountain waves will primarily deposit the wave momentum in the troposphere and affect the tropospheric circulation rather than the general circulation in the middle atmosphere [28,29]. Combined with the background wind field, by comparing the observed spectrum slope of zonal wind with the “–3” theoretical spectrum, the source characteristics of gravity waves can be explored. In the 2–8 km interval, the zonal wind spectrum slope is larger than –3, so the “downshifting” of the wavenumber spectrum is generated with = −1, indicating that the gravity waves with in the troposphere are mainly affected by mountain waves. At a height range of 14–26 km, the observed spectrum slope meets the “−3” theoretical spectrum. For the mountain wave, after entering the stratosphere, since and decreases with altitude, so = +1, the mountain wave will cause the “upshifting” of the wavenumber spectrum and the spectrum slope will decrease. Considering that the observed spectrum slope is basically equal to “–3”, it is assumed that a stratospheric gravity wave will be generated near the jet stream, and the “downshifting” of the wavenumber spectrum will be generated to offset the effect of the topographic wave. It can be seen from Figure 7 that, for the gravity wave propagating upward generated above jet stream area, = –1 and decreases with altitude, resulting in a decrease in the observed spectrum slope, which is consistent with the above hypothesis. For the height range of 26–32 km, the observed spectrum slope is smaller than “–3” and the wavenumber spectrum is “upshifting”. This can be explained that the horizontal phase velocity of gravity wave near 27 km is near 0, and the gravity wave is removed after encountering this “critical layer”. Only the gravity wave existing in the 27–32 km interval produces an “upshifting”. For the height range of 32–38 km, the whole range satisfies = +1, so it has a smaller spectrum slope.
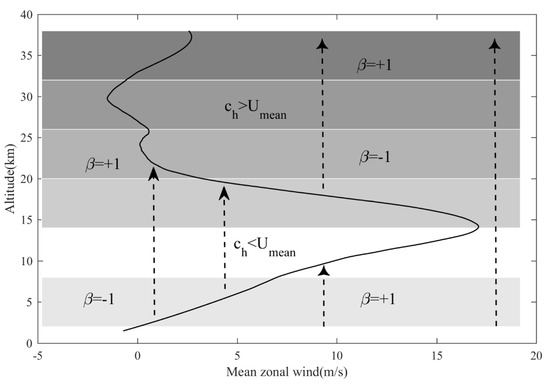
Figure 7.
The mean zonal wind (solid line) observed from 21 September to 26 September over Hami. Dotted arrows represent gravity waves propagating upwards. The triangle arrow represents the waves for which , and the V-shaped arrow represents the waves for which .
3.3. Ratio of Spectrum Kinetic Energy to Potential Energy
We use R to represent the ratio of spectrum kinetic energy to spectrum potential energy, which can be written as:
and are the vertical wavenumber spectrum of normalized temperature and the total horizontal wind field respectively, where , , , and are the buoyancy frequency, the acceleration of gravity, and the vertical wavenumber. When R is a constant, which means that and have a good correlation. To further discuss the distribution of R, we refer to the gravity spectrum mode proposed by [30]. The premise of this mode is , where is intrinsic frequency. This model assumes that the gravity wave spectrum is separable in and , and it follows a linear polarization relationship. Figure 8 (on the left) shows the actual R value of the observed spectrum after averaging as a function of wavenumber . From the top to the bottom, it shows the height interval of 2–8 km, 14–20 km, 20–26 km, 26–32 km, and 32–38 km respectively. In order to highlight the variation characteristics of wavenumber, here the ordinate is and the abscissa is . It can be seen that the distribution of in the low wavenumber region is relatively sparse and has large fluctuations, which indicates that and does not have a good correlation in the low wavenumber region and does not meet the linear polarization relationship of the “theoretical spectrum” described above. Only when the wavenumber is greater than a certain value, shows a more concentrated distribution. The distribution of in the stratosphere is more stable and has smaller fluctuations near a constant value in the high wavenumber region than in the troposphere. It is shown that the observed spectra of and only show correlation when the wavenumber is greater than a certain value. In order to exclude the influence of the pendulum-like self-induced motions on the balloon-gondola response in the low wavenumber region during the ascent of the balloon, here refer to the processing method of Torre [31], we take the interval on the right of as the region where is approximately constant, and m, representing the distance from the balloon to the gondola. The dotted line in the figures of left panel represent . The data points that located on the right of is 249. Auto-correlation analysis is performed on and , and the maximum lag order with auto-correlation are both 5. In order to reduce the dispersion of R and avoid the interference of turbulence and noise, we take a five-point average of the value on the right of (the last four consecutive points are averaged), and the results are shown on the right panel of Figure 8. The dashed line is the average value of all the values in the region. values in height ranges of 2–8 km, 14–20 km, 20–26 km, 26–32 km, and 32–38 km are 0.2 ( = −0.68), 1.4 ( = 0.15), 3.1 ( = 0.49), 3.2 ( = 0.51), and 3.7 ( = 0.56) respectively. It can be seen that although the values at high wavenumbers satisfy the polarization relationship, the observed spectrum at different heights has different values of .
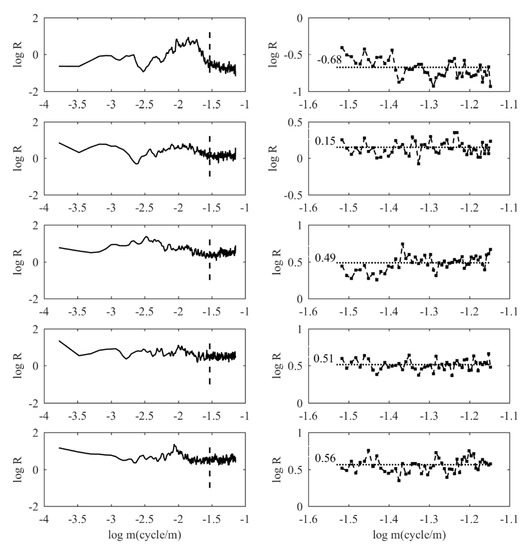
Figure 8.
Distribution of R with wavenumber (left panel), averaged R value after filtering out noise and turbulence in the interval to the right of m (right panel). From top to bottom are height ranges of 2–8 km, 14–20 km, 20–26 km, 26–32 km, and 32–38 km.
4. Results and Discussion
By analyzing the data from eight near space balloons released in Hami from 21 September to 26 September in 2019, we obtained the vertical wavenumber spectrum characteristics of the normalized temperature and three-dimensional wind fluctuations in the troposphere and the middle-lower stratosphere. Different from conventional sounding data, this is the first analysis of the spectrum characteristics in northwestern China based on near space high-resolution balloon, and the observed spectrum results can reach the middle stratosphere. Higher resolution allows us to analyze the spectrum structure at higher wavenumbers. Temperature field data is from GTS3 digital radiosonde and the wind field data is from Beidou positioning system. The fluctuation of vertical wind field is calculated from the ascent rate. Interestingly, exacting profiles of gravity waves may also be helpful to the problem of earthquake forecast [32], which also provides new ideas for future research on gravity spectrum information, and the use of radiosonde data for the spectral analysis of gravity waves to a higher altitude will help to improve the understanding of the characteristics of the atmospheric temperature and dynamic structure in the near space [33].
For the vertical wavenumber spectrum of normalized temperature fluctuations, the spectrum slope is significantly lower than the “–3” slope of the theoretical spectrum over the entire detection height. In the lower stratosphere, the spectrum slope reached maximum, and then decreases with altitude. As the thickness of the atmosphere increases, the spectral slope has a weak downward shift. The limited thickness will filter out longer wavelengths, which may underestimate the energy and spectrum density of the wave. However, this change is much small compared to the value of –3. For three-dimensional wind field fluctuations, the vertical wavenumber spectra of the meridional wind and the zonal wind are relatively consistent, indicating that the horizontal wind speed fluctuation is isotropic. With the increase of the height, the spectrum slope of the horizontal wind field has been decreasing. The observed spectrum slope is in good agreement with the theoretical spectrum in the interval of 20–32 km. The vertical wind fluctuations have a spectrum structure that is significantly different from the horizontal wind fluctuations. The slope is much lower than the horizontal wind field. The largest spectrum slope occurs in the troposphere, and the smallest spectrum slope is only −0.01 at 20–26 km. Then the spectrum slope begins to increase. The spectrum amplitude of normalized temperature fluctuations and the three-dimensional wind fluctuations in the stratosphere are significantly larger than those in the troposphere. This shows that observed spectrums do not meet the theoretical spectrum model well. In particular, the vertical wavenumber spectrum of the wind field fluctuations has completely different structural characteristics, indicating that it follows different spectral law which cannot be explained by the current “universal spectrum” theory. Considering the possible existence of turbulent activity in high wavenumber region (vertical scale less than 100 m), the deviation of spectral slope in the region of high wavenumber can be clearly seen in the vertical wavenumber spectrum of normalized temperature fluctuations, while the effect on the horizontal wind field is not obvious since this article only discusses turbulence in the vertical direction.
Considering the existence of the “critical layer” produced by the jet stream, the horizontal wind fluctuations with relatively low frequency will pass through the critical layer, which will significantly reduce the spectral amplitude, while the vertical wind disturbance with relatively high frequency will not be easily absorbed by the “critical layer” near the tropopause [2,27]. However, we obtained higher spectral amplitudes of the horizontal wind field in the stratosphere, so it is speculated that in addition to the wave source generated by mountain waves in the lower troposphere due to terrain, there is also at least a second wave source in the stratosphere. At the same time, the observed spectral slopes of the horizontal wind field in all height ranges are consistent with those predicted by the “wind shifting” model, which also verifies the existence of stratospheric wave sources. By calculating R, the ratio of the spectral kinetic energy to potential energy, we find that R has an approximately constant value between , the result in this paper suggests the separability of the and m is reasonable for relatively high-wavenumber region, but less well justified at lower wavenumber, which means in the region with low wavenumber other nonlinear models of “theoretical spectrum” is more suitable. Moreover, the observed spectrum results show that the R values in the region with high wavenumber are variable at different height intervals, and the R values increase with height.
It can be seen from the results that the observed spectral cannot match the predicted spectrum model well, and the observation results at different heights are also different. The slope predicted by the theoretical spectral model is closer to the observed spectrum in the lower stratosphere, but there are systematic differences in the troposphere and middle stratosphere. There are two unstable zones where the waves can be excited [34] (below 20 km and higher 40 km, in reality such altitude ranges can be changed), perhaps the effects of wave excitation can result in the violation of the “universal spectrum” theory in the corresponding height range. But further exploration is needed, which is also our next step. Since saturation spectrum model is widely used in the global model of gravity wave parameterization, the difference between the observation results and the theoretical spectrum also shows that the spectral characteristics in the atmosphere cannot be explained well with the existing spectral theory. More work is needed to be done on observation data with high spatio-temporal resolution and large spatio-temporal coverage to improve and correct the existing spectral theory.
Author Contributions
Y.H. and Z.S. designed the experiments; Y.H., Z.S., and M.H. performed the experiments; M.H. and Z.S. analyzed the data; Y.H. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant no. 41875045, 41576171, 41775039).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alexander, P.A.; Tsuda, T.; Kawatani, Y.; Takahashi, M. Global distribution of atmospheric waves in the equatorial upper troposphere and lower stratosphere: COSMIC observations of wave mean flow interactions. J. Geophys. Res. 2008, 113, D24115. [Google Scholar] [CrossRef]
- VanZandt, T.E. A universal spectrum of buoyancy waves in the atmosphere. Geophys. Res. Lett. 1982, 9, 575–578. [Google Scholar] [CrossRef]
- Dewan, E.M.; Good, R.E. Saturation and the ‘‘universal’’ spectrum for vertical profiles of horizontal scalar winds in the atmosphere. J. Geophys. Res. 1986, 91, 2742–2748. [Google Scholar] [CrossRef]
- Smith, S.E.; Fritts, D.C.; VanZandt, T.E. Evidence of saturated spectrum of atmospheric gravity waves. J. Atmos. Sci. 1987, 44, 1404–1410. [Google Scholar] [CrossRef]
- Weinstock, J. Saturated and unsaturated spectra of gravity waves and scale-dependent diffusion. J. Atmos. Sci. 1990, 47, 2211–2225. [Google Scholar] [CrossRef]
- Hines, C.O. The saturation of gravity waves in the middle atmosphere. Part II: Development of Doppler-spread theory. J. Atmos. Sci. 1991, 48, 1360–1379. [Google Scholar] [CrossRef]
- Gardner, C.S. Diffusive filtering theory of gravity wave spectra in the atmosphere. J. Geophys. Res. 1994, 99, 601–620. [Google Scholar] [CrossRef]
- Dewan, E.M. Saturated-cascade similitude theory of gravity wave spectra. J. Geophys. Res. 1997, 102, 29799–29817. [Google Scholar] [CrossRef]
- Fritts, D.C.; Chou, H.G. An investigation of the vertical wavenumber and frequency spectra of gravity wave motions in the lower stratosphere. J. Atmos. Sci. 1987, 44, 3610–3624. [Google Scholar] [CrossRef][Green Version]
- Tsuda, T.; Inoue, T.; Kato, S.; Fukao, S. MST radar observations of a saturated gravity wave spectrum. J. Atmos. Sci. 1989, 46, 2440–2447. [Google Scholar] [CrossRef][Green Version]
- Dewan, E.M.; Grossbard, N.; Quesada, A.F.; Good, R.E. Spectral analysis of 10m resolution scalar velocity profiles in the stratosphere. Geophys. Res. Lett. 1984, 11, 80–83. [Google Scholar] [CrossRef]
- Eckermann, S.D.; Hirota, I.; Hocking, W.K. Gravity wave and equatorial wave morphology of the stratosphere derived from long-term rocket soundings. Q. J. R. Meteorol. Soc. 1995, 121, 149–186. [Google Scholar] [CrossRef]
- Tsuda, T.; VanZandt, T.E.; Mizumoto, M.; Kato, S.; Fukao, S. Spectral analysis of temperature and Brunt-V¨ais¨ al¨a frequency fluctuations observed by Radiosondes. J. Geophys. Res. 1991, 96, 17265–17278. [Google Scholar] [CrossRef]
- Allen, S.J.; Vincent, R.A. Gravity wave activity in the lower atmosphere: Seasonal and latitudinal variations. J. Geophys. Res. 1995, 100, 1327–1350. [Google Scholar] [CrossRef]
- Nastrom, G.D.; VanZandt, T.E.; Warnock, J.M. Vertical wavenumber spectra of wind and temperature from highresolution balloon soundings over Illinois. J. Geophys. Res. 1997, 102, 6685–6701. [Google Scholar] [CrossRef]
- Nastrom, G.D.; VanZandt, T.E. Seasonal variability of the observed vertical wave number spectra of wind and temperature and the effects of prewhitening. J. Geophys. Res. 2001, 106, 14369–14375. [Google Scholar] [CrossRef]
- Fritts, D.C.; Tsuda, T.; Sato, T.; Fukao, S.; Kato, S. Observational evidence of a saturated gravity wave spectrum in the tropo- sphere and lower stratosphere. J. Atmos. Sci. 1988, 45, 1741–1759. [Google Scholar] [CrossRef][Green Version]
- Pfenninger, M.; Liu, A.Z.; Papen, G.C.; Gardner, C.S. Gravity wave characteristics in the lower atmosphere at south pole. J. Geophys. Res. 1999, 104, 5963–5984. [Google Scholar] [CrossRef]
- Zhang, S.D.; Huang, C.M.; Huang, K.M.; Zhang, Y.H.; Gong, Y.; Gan, Q. Vertical wavenumber spectra of three dimensional winds revealed by radiosonde observations at midlatitude. Ann. Geophys. 2017, 35, 107–116. [Google Scholar] [CrossRef]
- Zhang, S.D.; Huang, C.M.; Huang, K.M.; Gong, Y.; Chen, G.; Gan, Q.; Zhang, Y.H. Latitudinal and seasonal variations of vertical wave number spectra of three-dimensional winds revealed by radiosonde observations. J. Geophys. Res. Atmos. 2017, 122, 13–174. [Google Scholar] [CrossRef]
- Alexander, P.; de la Torre, A.; Llamedo, P.; Hierro, R.; Schmidt, T.; Haser, A.; Wickert, J. A method to improve the determination of wave perturbations close to the tropopause by using a digital filter. Atmos. Meas. Tech. 2011, 4, 1777–1784. [Google Scholar] [CrossRef]
- Dewan, E.; Grossbard, N. Power spectral artifacts in published balloon data and implications regarding saturated gravity wave theories. J. Geophys. Res. Atmos. 2000, 105, 4667–4683. [Google Scholar] [CrossRef]
- Lane, T.P.; Reeder, M.J.; Morton, B.R.; Clark, T.L. Observations and numerical modeling of mountain waves over the Southern Alps of New Zealand. Q. J. Roy Meteor. Soc. 1999, 126, 765–2788. [Google Scholar] [CrossRef]
- Gardner, C.S.; Gardner, N.F. Measurements distortion in aircraft, space shuttle, and balloon observations of atmospheric density and temperature perturbation spectra. J. Geophys. Res. 1993, 98, 1023–1033. [Google Scholar] [CrossRef]
- Larsen, M.F.; Woodman, R.F.; Sato, T.; Davis, M.K. Power spectra of oblique velocities in the troposphere and lower stratosphere observed at Arecibo, Puerto Rico. J. Atmos. Sci. 1986, 43, 2230–2240. [Google Scholar] [CrossRef][Green Version]
- Larsen, M.F.; Röttger, J.; Holden, D.N. Direct Measurements of Vertical-Velocity Power Spectra with Sousy-VHF-Radar Wind Profiler System. J. Atmos. Sci. 1987, 43, 3442–3448. [Google Scholar] [CrossRef]
- Geller, M.A.; Gong, J. Gravity wave kinetic, potential, and vertical fluctuation energies as indicators of different frequency gravity waves. J. Geophys. Res. 2010, 115, D11111. [Google Scholar] [CrossRef]
- Zhang, S.D.; Yi, F.; Huang, C.M.; Huang, K.M. High vertical resolution analyses of gravity waves and turbulence at a mid-latitude station. J. Geophys. Res. 2012, 117, D02103. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Xue, M.; Zhu, K. Impacts of horizontal propagation of orographic gravity waves on the wave drag in the stratosphere and lower mesosphere. J. Geophys. Res. 2017, 122, 11301–11312. [Google Scholar] [CrossRef]
- Fritts, D.C.; Van Zandt, T.E. Spectral estimates of gravity wave energy and momentum fluxes. Part I: Energy dissipation, acceleration, and constraints. J. Atmos. Sci. 1993, 50, 3685–3694. [Google Scholar] [CrossRef]
- de la Torre, A.; Alexander, P.; Giraldez, A. The kinetic to potential energy ratio and spectral separability from high-resolution balloon soundings near the Andes mountains. Res. Lett. 1999, 26, 1413–1416. [Google Scholar] [CrossRef]
- Adushkin, V.V.; Nifadiev, V.I.; Chen, B.B.; Popel, S.I.; Kogai, G.A.; Dubinskii, A.Y.; Weidler, P.G. Variations of the parameters of internal gravity waves in the atmosphere of Central Asia before earthquakes. Doklady Earth Sci. 2019, 487, 841–845. [Google Scholar] [CrossRef]
- Zhao, X.R.; Sheng, Z.; Li, J.W.; Yu, H.; Wei, K.J. Determination of the “wave turbopause” using a numerical differentiation method. J. Geophy. Res. Atmos. 2019, 124, 10592–10607. [Google Scholar] [CrossRef]
- Yu, N.; Izvekova Popel, S.I.; Chen, B.B. Nonlinear acoustic-gravity waves and dust particle redistribution in earth’s atmosphere. J. Atmos. Sol.-Terr. Phys. 2015, 134C, 41–46. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).