Advanced Rainfall Trend Analysis of 117 Years over West Coast Plain and Hill Agro-Climatic Region of India
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
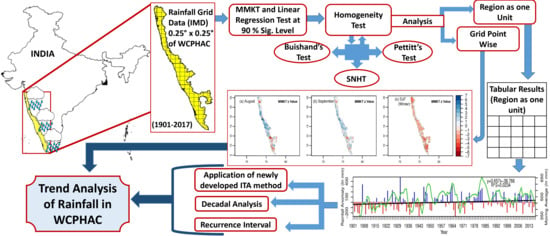
2.3. Method
- Descriptive statistics of monthly and seasonal rainfall for WCHAC region are calculated and used for the period 1901–2017.
- MMKT and linear regression techniques were used to extract the months and seasons showing a significant trend at a 90% level. Only those periods, which commonly fall into the 90% level of significance block of MMKT and linear regression test were extracted and used in the analysis. The significant period obtained using the linear regression was used to obtain MMKT trend results and therefore the extracted data obtained using linear regression and MMKT in this study were not supplementary but complementary to each other.
- The obtained trend results in step 2 are verified with the results of the recently developed ITA statistical technique.
2.3.1. Modified Mann–Kendall’s Test
2.3.2. Linear Regression
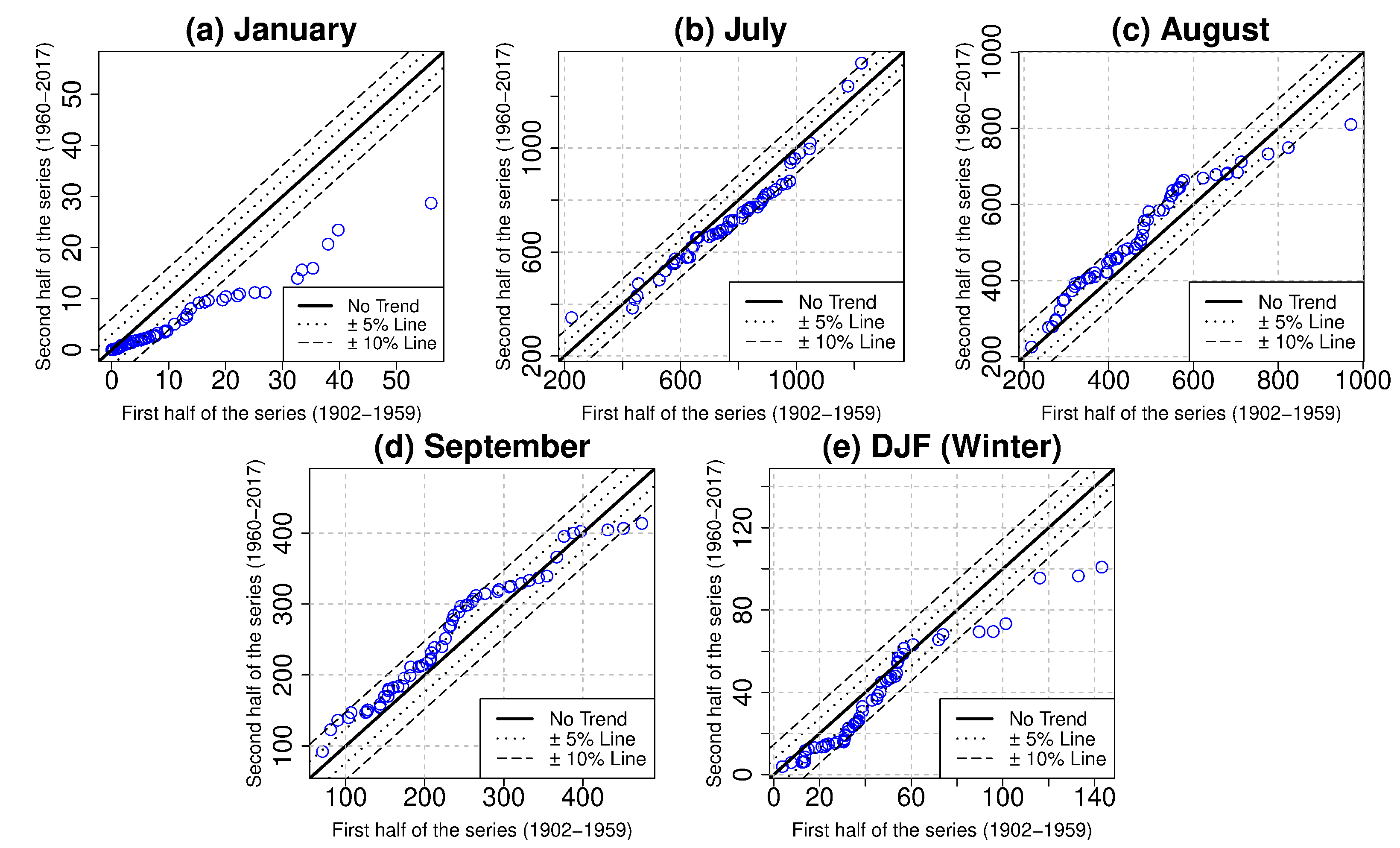
2.3.3. Innovative Trend Analysis (ITA)
2.3.4. Sen’s Slope
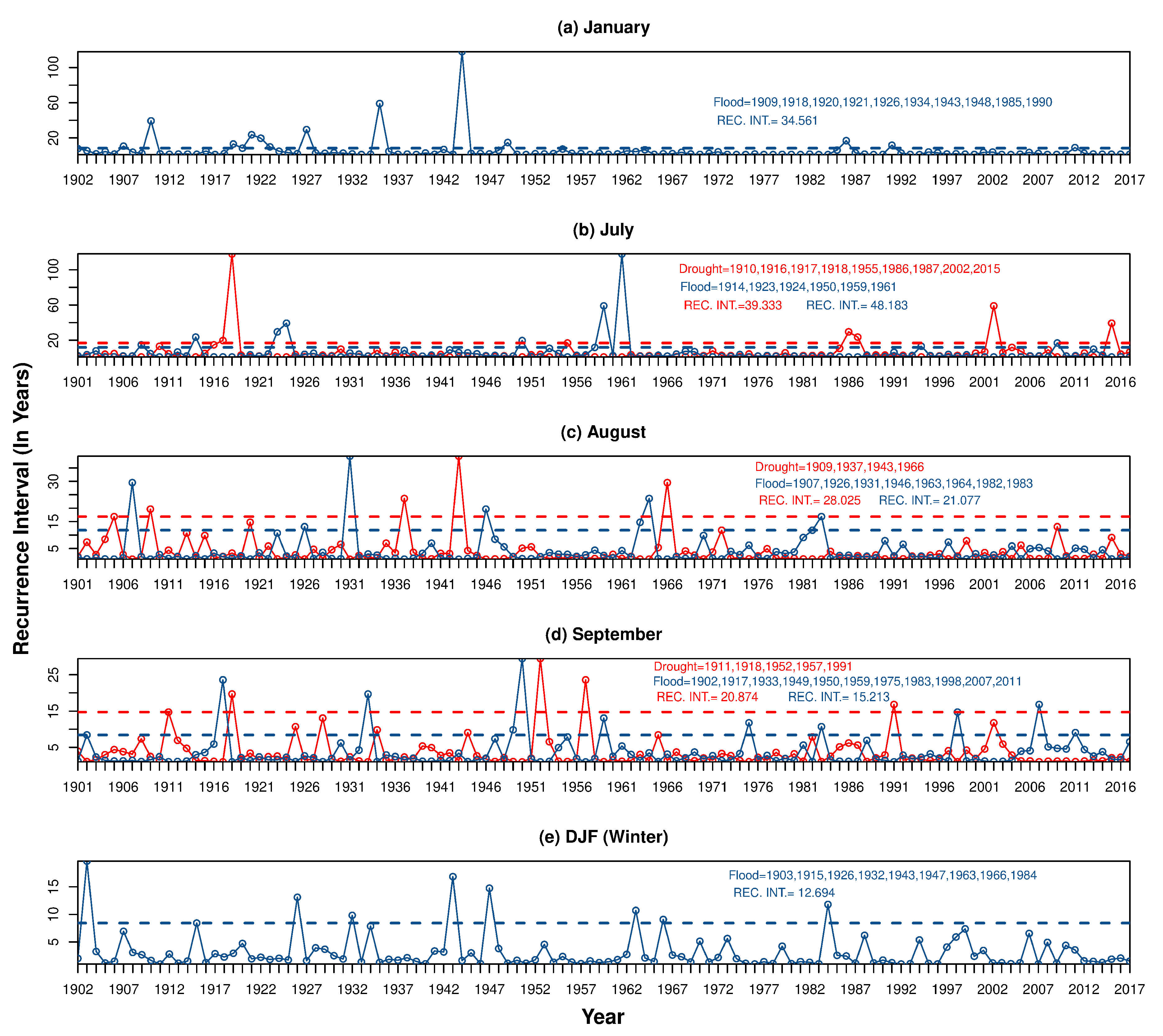
2.3.5. Weibull’s Recurrence Interval or Return Period (T)
- Ranking the rainfall event based on rainfall amount, ranking highest to lowest (lowest to highest) in case of exceedance (decadence). Here, in the case of exceedance (decadence), the lowest rank 1 (highest rank 117) is assigned to the rainfall event with the largest amount (Equation (10)).
- Cumulative probability calculation. Here, n is the total number of observations i.e., 117 in the present study.
- Ranking cumulative probability with highest to lowest value scheme resulting in m (exceedance/decadence probability rank) and to obtain the exceedance/decadence probability calculation, step 4 is followed.
- Calculation of exceedance/decadence probability (Equation (11)).
- Recurrence interval is obtained using the exceedance/decadence probability . T is the average interval of occurrence of more than or equal to the certain magnitude of the rainfall event. It is calculated as given in Equation (12):
3. Results
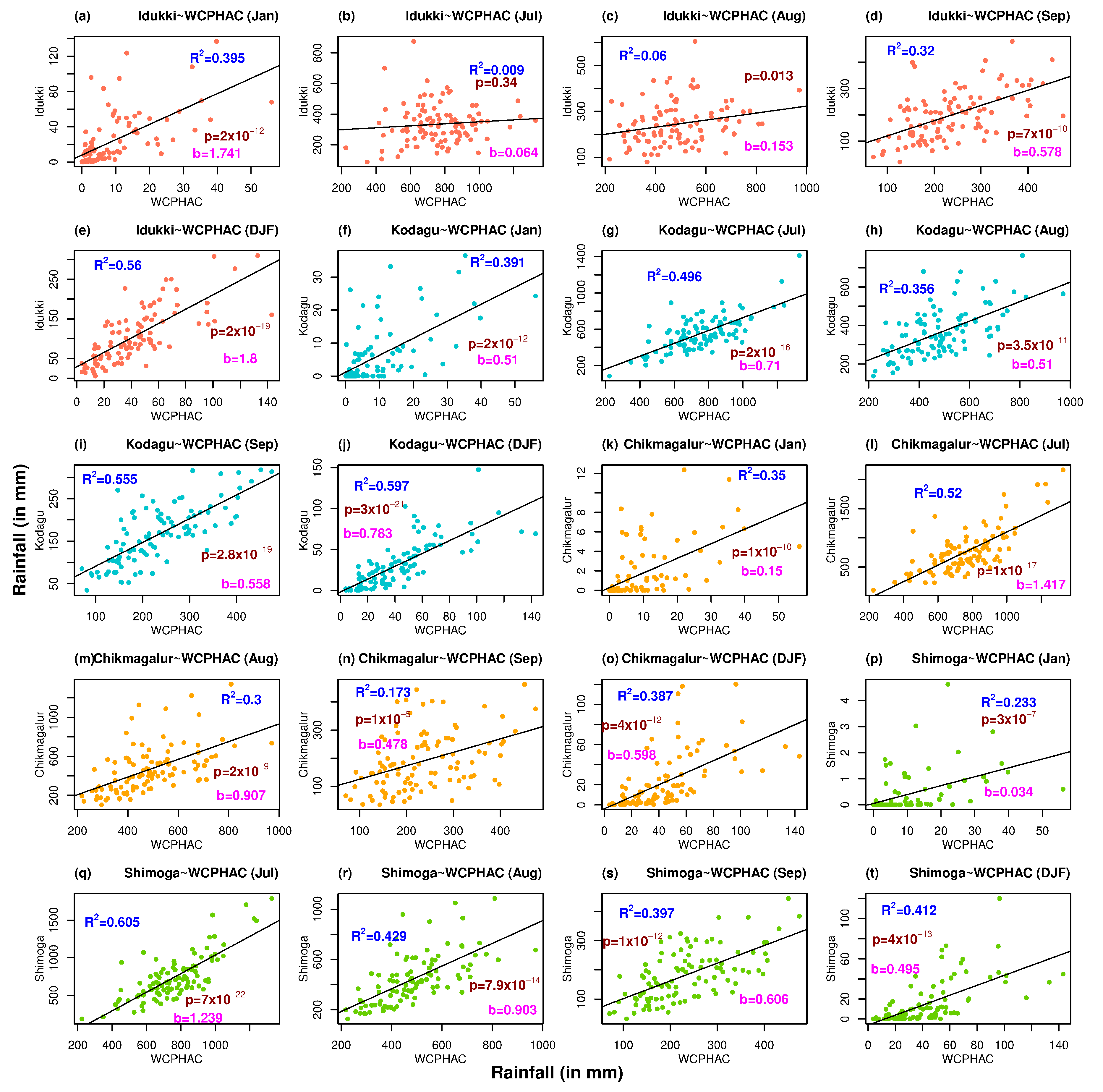
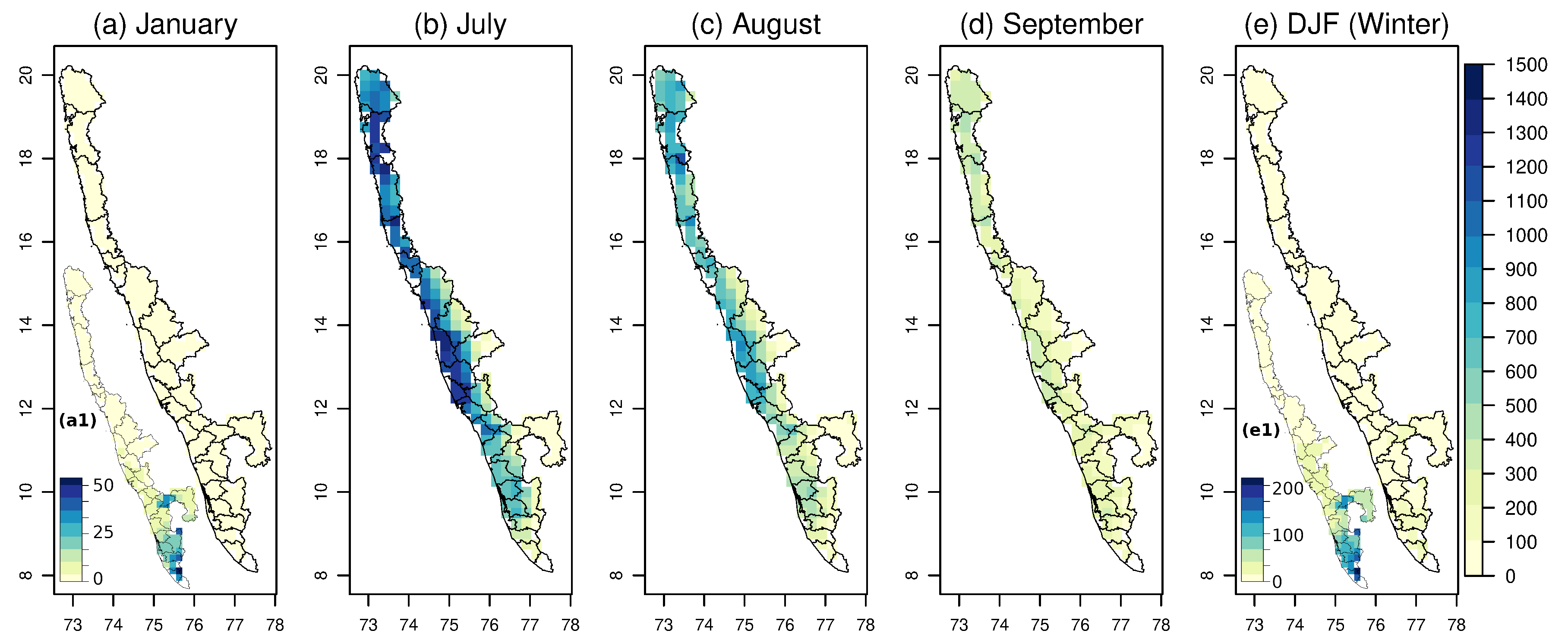
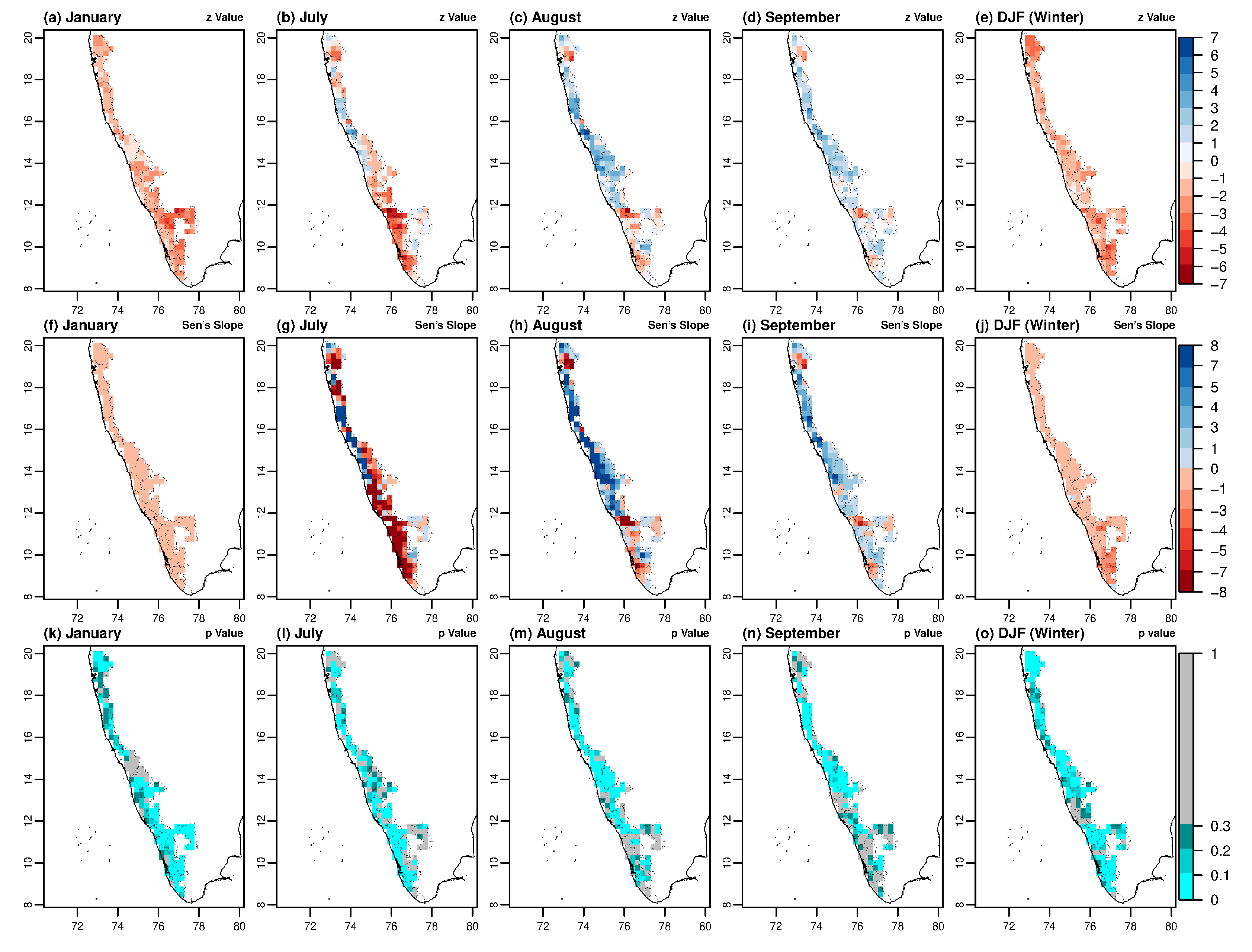
3.1. Monthly and Seasonal Analysis
3.1.1. January and July (Monthly Negative Trend)
3.1.2. August and September (Monthly Positive Trend)
3.1.3. Winter Rainfall Trend
3.2. Decadal Analysis
3.3. Recurrence Interval
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WCPHAC | West Coast Plain and Hill Agro-Climatic |
| MMKT | Modified Mann–Kendall’s Test |
| ITA | Innovative Trend Analysis |
| DJF | December–January–February |
| MAM | March–April–May |
| JJAS | June–July–August–September |
| ON | October–November |
| SD | Standard Deviation |
References
- Foster, G.L.; Royer, D.L.; Lunt, D.J. Future climate forcing potentially without precedent in the last 420 million years. Nat. Commun. 2017, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Barnosky, A.D.; Kraatz, B.P. The Role of Climatic Change in the Evolution of Mammals. BioScience 2007, 57, 523–532. [Google Scholar] [CrossRef] [Green Version]
- Sörlin, S.; Lane, M. Historicizing climate change-engaging new approaches to climate and history. Clim. Chang. 2018, 151, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Steffen, W.; Rockström, J.; Richardson, K.; Lenton, T.; Folke, C.; Liverman, D.; Summerhayes, C.; Barnosky, A.; Cornell, S.; Crucifix, M.; et al. Trajectories of the Earth System in the Anthropocene. Proc. Natl. Acad. Sci. USA 2018, 115, 8252–8259. [Google Scholar] [CrossRef] [Green Version]
- Boyce, C.K.; Lee, J.E. Plant Evolution and Climate Over Geological Timescales. Annu. Rev. Earth Planet. Sci. 2017, 45, 61–87. [Google Scholar] [CrossRef]
- Kabanda, T. Long-term rainfall trends over the Tanzania coast. Atmosphere 2018, 9, 155. [Google Scholar] [CrossRef] [Green Version]
- Rao, V.B.; Franchito, S.H.; Santo, C.M.E.; Gan, M. An update on the rainfall characteristics of Brazil: Seasonal variations and trends in 1979–2011. Int. J. Climatol. 2016, 36, 291–302. [Google Scholar] [CrossRef]
- Frazier, A.G.; Giambelluca, T.W. Spatial trend analysis of Hawaiian rainfall from 1920 to 2012. Int. J. Climatol. 2017, 37, 2522–2531. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Kidson, J.W.; Newell, R.E. African rainfall and its relation to the upper air circulation. Q. J. R. Meteorol. Soc. 1977, 103, 441–456. [Google Scholar] [CrossRef]
- Sahu, N.; Behera, S.K.; Ratnam, J.V.; Silva, R.V.D.; Parhi, P.; Duan, W.; Takara, K.; Singh, R.B.; Yamagata, T. El Niño Modoki connection to extremely-low streamflow of the Paranaíba River in Brazil. Clim. Dyn. 2014, 42, 1509–1516. [Google Scholar] [CrossRef]
- Sahu, N.; Singh, R.B.; Kumar, P.; Silva, R.V.D.; Behera, S.K. La Niña Impacts on Austral Summer Extremely HighStreamflow Events of the Paranaíba River in Brazil. Adv. Meteorol. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Sahu, N.; Behera, S.K.; Yamashiki, Y.; Takara, K.; Yamagata, T. IOD and ENSO impacts on the extreme stream-flows of Citarum river in Indonesia. Clim. Dyn. 2012, 39, 1673–1680. [Google Scholar] [CrossRef]
- Rajeevan, M.; Sridhar, L. Inter-annual relationship between Atlantic sea surface temperature anomalies and Indian summer monsoon. Geophys. Res. Lett. 2008, 35, 21. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Roy, I. Indian Summer Monsoon and El Niño Southern Oscillation in CMIP5 models: A few areas of agreement and disagreement. Atmosphere 2017, 8, 154. [Google Scholar] [CrossRef] [Green Version]
- Doranalu Chandrashekar, V.; Shetty, A.; Patel G C, M. Estimation of Monsoon Seasonal Precipitation Teleconnection with El Niño-Southern Oscillation Sea Surface Temperature Indices over the Western Ghats of Karnataka. Asia-Pac. J. Atmos. Sci. 2019, 1–15. [Google Scholar] [CrossRef]
- Manjunatha, B.; Balakrishna, K.; Krishnakumar, K.; Manjunatha, H.; Avinash, K.; Mulemane, A.; Krishna, K. Increasing Trend of Rainfall Over Agumbe, Western Ghats, India in the Scenario of Global Warming. Open Oceanogr. J. 2015, 8, 39–44. [Google Scholar] [CrossRef]
- Varikoden, H.; Revadekar, J.V.; Kuttippurath, J.; Babu, C.A. Contrasting trends in southwest monsoon rainfall over the Western Ghats region of India. Clim. Dyn. 2019, 52, 4557–4566. [Google Scholar] [CrossRef]
- Raj, P.P.N.; Azeez, P.A. Trend analysis of rainfall in Bharathapuzha River basin, Kerala, India. Int. J. Climatol. 2012, 32, 533–539. [Google Scholar] [CrossRef]
- Mudbhatkal, A.; Amai, M. Regional climate trends and topographic influence over the Western Ghats catchments of India. Int. J. Climatol. 2018, 38, 2265–2279. [Google Scholar] [CrossRef]
- Prakash, S.; Sathiyamoorthy, V.; Mahesh, C.; Gairola, R. Is summer monsoon rainfall over the west coast of India decreasing? Atmos. Sci. Lett. 2013, 14, 160–163. [Google Scholar] [CrossRef]
- Paul, S.; Ghosh, S.; Rajendran, K.; Murtugudde, R. Moisture Supply From the Western Ghats Forests to Water Deficit East Coast of India. Geophys. Res. Lett. 2018, 45, 4337–4344. [Google Scholar] [CrossRef]
- Zhang, G.; Smith, R.B. Numerical Study of Physical Processes Controlling Summer Precipitation over the Western Ghats Region. J. Clim. 2018, 31, 3099–3115. [Google Scholar] [CrossRef]
- Sreelash, K.; Sharma, R.K.; Gayathri, J.A.; Upendra, B.; Maya, K.; Padmalal, D. Impact of Rainfall Variability on River Hydrology: A Case Study of Southern Western Ghats, India. J. Geol. Soc. India 2018, 92, 548–554. [Google Scholar] [CrossRef]
- Alvi, S.M.A.; Koteshwaram, P. Time Series Analysis of Rainfall over India. MAUSAM 1985, 36, 479–490. [Google Scholar]
- Naidu, C.V.; Durgalakshmi, K.; Krishna, K.M.; Rao, S.R.; Satyanarayana, G.C.; Lakshminarayana, P.; Rao, L.M. Is summer monsoon rainfall decreasing over India in the global warming era? J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Koteswaram, P.; Alvi, S.M.A. Trends and Periodicities in Rainfall at West Coast Stations in India. Curr. Sci. 1969, 38, 229–231. [Google Scholar]
- Daniel, B.; Darwall, W.; Molur, S.; Smith, K.C. (Eds.) The Status and Distribution of Freshwater Biodiversity in the Western Ghats, India; IUCN: Cambridge, UK; Gland, Switzerland, 2011. [Google Scholar]
- Shrestha, D.; Deshar, R.; Nakamura, K. Characteristics of Summer Precipitation around the Western Ghats and the Myanmar West Coast. Int. J. Atmos. Sci. 2015, 2015, 1–10. [Google Scholar] [CrossRef]
- Verma, R.R.; Manjunath, B.L.; Singh, N.P.; Kumar, A.; Asolkar, T.; Chavan, V.; Srivastava, T.K.; Singh, P. Soil mapping and delineation of management zones in the Western Ghats of coastal India. Land Degrad. Dev. 2018, 29, 4313–4322. [Google Scholar] [CrossRef]
- Manigandan, P.K.; Chandar Shekar, B. Risk assessment of radioactivity in soils of forest and grassland ecosystems of the Western Ghats, India. Radioprotection 2015, 50, 259–264. [Google Scholar] [CrossRef]
- Thomas, J.; Joseph, S.; Thrivikramji, K.P. Assessment of soil erosion in a tropical mountain river basin of the southern Western Ghats, India using RUSLE and GIS. Geosci. Front. 2018, 9, 893–906. [Google Scholar] [CrossRef]
- Pandit, P.; Mangala, P.; Saini, A.; Bangotra, P.; Kumar, V.; Mehra, R.; Ghosh, D. Radiological and pollution risk assessments of terrestrial radionuclides and heavy metals in a mineralized zone of the siwalik region (India). Chemosphere 2020, 254. [Google Scholar] [CrossRef]
- Jha, C.; Dutt, C.; Bawa, S. Deforestation and land use changes in Western Ghats, India. Curr. Sci. 2000, 79, 231–238. [Google Scholar]
- Davidar, P.; Arjunan, M.; Mammen, P.C.; Garrigues, J.; Puyravaud, J.P.; Roessingh, K. Forest degradation in the Western Ghats biodiversity hotspot: Resource collection, livelihood concerns and sustainability. Curr. Sci. 2007, 93, 1573–1578. [Google Scholar]
- Panda, A.; Sahu, N. Trend analysis of seasonal rainfall and temperature pattern in Kalahandi, Bolangir and Koraput districts of Odisha, India. Atmos. Sci. Lett. 2019, 20, e932. [Google Scholar] [CrossRef] [Green Version]
- Sahu, N.; Saini, A.; Behera, S.; Sayama, T.; Nayak, S.; Sahu, L.; Duan, W.; Avtar, R.; Yamada, M.; Singh, R.B.; et al. Impact of indo-pacific climate variability on rice productivity in Bihar, India. Sustainability 2020, 12, 7023. [Google Scholar] [CrossRef]
- Sahu, N.; Saini, A.; Behera, S.K.; Sayama, T.; Sahu, L.; Nguyen, V.T.V.; Takara, K. Why apple orchards are shifting to the higher altitudes of the Himalayas? PLoS ONE 2020, 15, e0235041. [Google Scholar] [CrossRef]
- Duan, W.; He, B.; Sahu, N.; Luo, P.; Nover, D.; Hu, M.; Takara, K. Spatiotemporal variability of Hokkaido’s seasonal precipitation in recent decades and connection to water vapour flux. Int. J. Climatol. 2017, 37, 3660–3673. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Bayley, A.G.V.; Hammersley, J.M.; Supplement, S.; Society, S. The “Effective” Number of Independent Observations in an Autocorrelated Time Series. Suppl. J. R. Stat. Soc. 1946, 8, 184–197. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Gachon, P.; Sushama, L.; St-Hilaire, A. Identification of hydrological trends in the presence of serial and cross correlations: A review of selected methods and their application to annual flow regimes of Canadian rivers. J. Hydrol. 2009, 368, 117–130. [Google Scholar] [CrossRef]
- Storch, H.V. Misuses of Statistical Analysis in Climate. In Analysis of Climate Variability; Springer: Berlin/Heidelberg, Germany, 1999; pp. 11–26. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Lohani, A.K.; Tiwari, H.L. Statistical Analysis for Change Detection and Trend Assessment in Climatological Parameters. Environ. Process. 2015, 2, 729–749. [Google Scholar] [CrossRef] [Green Version]
- Chattopadhyay, S.; Edwards, D. Long-Term Trend Analysis of Precipitation and Air Temperature for Kentucky, United States. Climate 2016, 4, 10. [Google Scholar] [CrossRef]
- Huth, R.; Pokorn, L. Parametric versus non-parametric estimates of climatic trends. Theor. Appl. Climatol. 2004, 77, 107–112. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Kisi, O. Trend Analysis of Maximum Hydrologic Drought Variables Using Mann-Kendall and Sens Innovative Trend Method. River Research and Applications. River Res. Appl. 2016, 33, 597–610. [Google Scholar] [CrossRef]
- Caloiero, T. Evaluation of rainfall trends in the South Island of New Zealand through the innovative trend analysis (ITA). Theor. Appl. Climatol. 2019, 139, 493–504. [Google Scholar] [CrossRef]
- Alifujiang, Y.; Abuduwaili, J.; Maihemuti, B.; Emin, B.; Groll, M. Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan. Atmosphere 2020, 11, 332. [Google Scholar] [CrossRef] [Green Version]
- Gedefaw, M.; Yan, D.; Wang, H.; Qin, T.; Girma, A.; Abiyu, A.; Batsuren, D. Innovative Trend Analysis of Annual and Seasonal Rainfall Variability in Amhara Regional State, Ethiopia. Atmosphere 2018, 9, 326. [Google Scholar] [CrossRef] [Green Version]
- Meena, H.M.; Machiwal, D.; Santra, P.; Moharana, P.C.; Singh, D.V. Trends and homogeneity of monthly, seasonal, and annual rainfall over arid region of Rajasthan, India. Theor. Appl. Climatol. 2018, 136, 795–811. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Application of the Innovative Trend Analysis Method for the Trend Analysis of Rainfall Anomalies in Southern Italy. Water Resour. Manag. 2018, 32, 4971–4983. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Tabari, H.; Wang, J.; Wang, Q.; Song, S.; Hu, Z. Innovative trend analysis of annual and seasonal rainfall in the Yangtze River Delta, eastern China. Atmos. Res. 2020, 231. [Google Scholar] [CrossRef]
- Khanna. Agro-Climatic Regional Planning: An Overview; Planning Commission, Government of India: New Delhi, India, 1989.
- ICAR. Agriculture Research Databook 2019; Technical report; ICAR-Indian Agricultural Statistics Research Institute: New Delhi, India, 2019. [Google Scholar]
- Mannan, A.; Chaudhary, S.; Dhanya, C.T.; Swamy, A.K. Regionalization of rainfall characteristics in India incorporating climatic variables and using self-organizing maps. ISH J. Hydraul. Eng. 2017, 24, 147–156. [Google Scholar] [CrossRef]
- Dash, S.K.; Mamgain, A. Changes in the Frequency of Different Categories of Temperature Extremes in India. J. Appl. Meteorol. Climatol. 2011, 50, 1842–1858. [Google Scholar] [CrossRef]
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. Development of a new high spatial resolution (0.25° × 0.25°) Long Period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. MAUSAM 2014, 65, 1–18. [Google Scholar]
- Rajeevan, M.; Bhate, J.; Kale, J.; Lal, B. A High Resolution Daily Gridded Rainfall Data for the Indian Region: Analysis of break and active monsoon spells. Curr. Sci. 2006, 91, 296–306. [Google Scholar]
- Shepard, D.S. Computer Mapping: The SYMAP Interpolation Algorithm. In Spatial Statistics and Models; Springer: Dordrecht, The Netherlands, 1984; pp. 133–145. [Google Scholar] [CrossRef]
- Kothawale, D.R.; Rajeevan, M. Monthly, Seasonal and Annual Rainfall Time Series for All-India, Homogeneous Regions and Meteorological Subdivisions: 1871–2016; Technical Report RR-138; Indian Institute of Tropical Meteorology: Pune, India, 2017. [Google Scholar]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 163–171. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Rao, A.R.; Hamed, K.H.; Chen, H.L. Nonstationarities in Hydrologic and Environmental Time Series; Springer: Dordrecht, The Netherlands, 2003. [Google Scholar] [CrossRef]
- Sen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Wu, H.; Qian, H. Innovative trend analysis of annual and seasonal rainfall and extreme values in Shaanxi, China, since the 1950s. Int. J. Climatol. 2016, 37, 2582–2592. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Proc. R. Neth. Acad. Arts Sci. 1950, 53, 386–392. [Google Scholar]
- Weibull, W. A statistical study of the strength of material. Ing. Vetenskaps Akad. Handl. (Stockh.) 1939, 151, 15. [Google Scholar]
- Fernández-Martínez, M.; Vicca, S.; Janssens, I.A.; Carnicer, J.; Martín-Vide, J.; Peñuelas, J. The consecutive disparity index, D: A measure of temporal variability in ecological studies. Ecosphere 2018, 9, 12. [Google Scholar] [CrossRef] [Green Version]
- Meseguer-Ruiz, O.; Cantos, J.O.; Sarricolea, P.; Martín-Vide, J. The temporal fractality of precipitation in mainland Spain and the Balearic Islands and its relation to other precipitation variability indices. Int. J. Climatol. 2016, 37, 849–860. [Google Scholar] [CrossRef]
- Meseguer-Ruiz, V.; Vide, M.; Cantos, J.O.; Espinoza, P.S. La distribución espacial de la fractalidad temporal de la precipitación en la Espańa peninsular y su relación con el Índice de Concentración. Investig. Geogr. 2014, 48, 73–84. [Google Scholar] [CrossRef] [Green Version]
- Lana, X.; Martínez, M.; Serra, C.; Burgueño, A. Spatial and temporal variability of the daily rainfall regime in Catalonia(northeastern Spain), 1950–2000. Int. J. Climatol. 2004, 24, 613–641. [Google Scholar] [CrossRef]
- Martín-Vide, J. Notes per a la definició d’un índex de «desordre» en pluviometria. Soc. Catalana Geogr. 1986, 7, 89–96. [Google Scholar]
- MartínVide, J. El Temps i el Clima; Departament de Medi Ambient i Rubes: Barcelona, Spain, 2002. [Google Scholar]
- Gaston, K.J.; McArdle, B.H. The temporal variability of animal abundances: Measures, methods and patterns. Philos. Trans. R. Soc. B Biol. 1994, 345, 335–358. [Google Scholar] [CrossRef]
- Nkrumah, F.; Vischel, T.; Panthou, G.; Klutse, N.A.B.; Adukpo, D.C.; Diedhiou, A. Recent Trends in the Daily Rainfall Regime in Southern West Africa. Atmosphere 2019, 10, 741. [Google Scholar] [CrossRef] [Green Version]
- Saeed, F.; Haensler, A.; Weber, T.; Hagemann, S.; Jacob, D. Representation of Extreme Precipitation Events Leading to Opposite Climate Change Signals over the Congo Basin. Atmosphere 2013, 4, 254–271. [Google Scholar] [CrossRef] [Green Version]
- Gozzo, L.; Palma, D.; Custodio, M.; Machado, J. Climatology and Trend of Severe Drought Events in the State of Sao Paulo, Brazil, during the 20th Century. Atmosphere 2019, 10, 190. [Google Scholar] [CrossRef] [Green Version]
- Sahu, N.; Yamashiki, Y.; Behera, S.; Takara, K.; Yamagata, T. Large Impacts of Indo-Pacific Climate Modes on the Extreme Streamflows of Citarum River in Indonesia. J. Glob. Environ. Eng. 2012, 17, 1–8. [Google Scholar]
- Revadekar, J.; Varikoden, H.; Murumkar, P.; Ahmed, S. Latitudinal variation in summer monsoon rainfall over Western Ghat of India and its association with global sea surface temperatures. Sci. Total Environ. 2018, 613–614, 88–97. [Google Scholar] [CrossRef]
- Krishnakumar, K.; Prasada Rao, G.; Gopakumar, C. Rainfall trends in twentieth century over Kerala, India. Atmos. Environ. 2009, 43, 1940–1944. [Google Scholar] [CrossRef]
- Nayak, S.; Mandal, M. Impact of land use and land cover changes on temperature trends over India. Land Use Policy 2019, 89, 104–238. [Google Scholar] [CrossRef]


| Month/Season | Minimum | Maximum | Mean | D (%) | 75% Probability | Contribution to Annual (%) |
|---|---|---|---|---|---|---|
| Jan | 0 | 56.1 | 7.95 | 197.14 | 1.34 | 0.3 |
| Feb | 0.06 | 43.8 | 7.79 | 161.04 | 1.88 | 0.3 |
| Mar | 0.05 | 140.4 | 18.49 | 97.45 | 7.75 | 0.8 |
| Apr | 4.96 | 132.65 | 55.3 | 52.66 | 36.86 | 2.2 |
| May | 27.78 | 358.48 | 110.7 | 58.63 | 64.76 | 4.5 |
| Jun | 134.93 | 718.8 | 487.14 | 31.34 | 400.65 | 19.7 |
| Jul | 224.06 | 1327.19 | 747.44 | 25.68 | 625.68 | 30.2 |
| Aug | 217.98 | 971.38 | 487.89 | 35.36 | 392.83 | 19.7 |
| Sep | 70.59 | 474.86 | 242.59 | 43.6 | 170.06 | 9.8 |
| Oct | 71.1 | 360.3 | 189.55 | 30.56 | 151.56 | 7.7 |
| Nov | 12.39 | 243.49 | 93.79 | 65.83 | 49.54 | 3.8 |
| Dec | 0.01 | 133.27 | 25.51 | 142.8 | 7.43 | 1 |
| Annual Mean | 150.93 | 300.65 | 206.18 | 11.79 | 189.95 | 100 |
| Annual Total | 1811.12 | 3607.84 | 2474.14 | 11.79 | 2279.4 | 100 |
| MAM (Pre-monsoon) | 66.29 | 410.36 | 184.48 | 37.32 | 136.66 | 7.5 |
| JJAS (Monsoon) | 1007.39 | 2912.82 | 1965.05 | 15.65 | 1794.76 | 79.4 |
| Oct-Nov | 98.90 | 496.16 | 283.34 | 29.89 | 225.08 | 11.5 |
| (Post-monsoon) | ||||||
| DJF (Winter) | 3.78 | 143.16 | 40.92 | 85.72 | 112.4 | 1.7 |
| Month/Season | MMKT | ITA | Kurtosis | Skewness | ||
|---|---|---|---|---|---|---|
| z-Stat | Sen’s Slope | Value | Slope | |||
| Jan | −2.44 | −0.04 | −5.24 | −0.1 | 5.32 | 1.27 |
| Feb | −1.1 | −0.01 | −1.58 | −0.02 | 3.48 | 1.31 |
| Mar | −0.66 | −0.02 | −0.66 | −0.02 | 19.79 | 0.79 |
| Apr | −0.45 | −0.03 | −1.07 | −0.11 | 0.04 | 0.13 |
| May | −0.54 | −0.07 | −1.02 | −0.2 | 2.11 | 1.02 |
| Jun | 0.59 | 0.23 | −0.06 | −0.05 | −0.37 | −0.21 |
| Jul | −1.63 | −1.01 | −0.57 | −0.75 | 0.56 | 0.03 |
| Aug | 1.84 | 0.81 | 0.83 | 0.67 | 0.04 | 0.26 |
| Sep | 1.77 | 0.45 | 0.88 | 0.35 | −0.59 | 0.38 |
| Oct | −0.74 | −0.13 | −0.96 | −0.33 | 0.14 | 0.42 |
| Nov | −1.05 | −0.19 | −0.92 | −0.15 | −0.27 | 0.55 |
| Dec | −0.72 | −0.03 | −0.47 | −0.02 | 3.31 | 0.84 |
| Annual Mean | −0.11 | −0.12 | −0.18 | −0.06 | 1.13 | 0.04 |
| MAM (Pre-monsoon) | −0.64 | −0.10 | −1 | −0.33 | 0.72 | 0.67 |
| JJAS (Monsoon) | 0.61 | 0.45 | 0.06 | 0.21 | 2.18 | 0.27 |
| Oct-Nov (Post-monsoon) | −1.97 | −0.31 | −0.95 | −0.48 | −0.36 | 0.53 |
| DJF (Winter) | −2.38 | −0.14 | −1.87 | −0.14 | 2.62 | 0.46 |
| Month/Season | Linear Regression Equation | t-Stat | p-Value |
|---|---|---|---|
| January | y = −0.0832x + 4.9059 | −3.14584 | 0.0021 |
| July | y = −0.8568x + 50.554 | −1.67144 | 0.09735 |
| August | y = 0.657x − 38.766 | 1.6604702 | 0.0995 |
| September | y = 0.4132x + 24.379 | 1.67022155 | 0.097 |
| DJF (Winter) | y =−0.1588x + 50.207 | −2.14917 | 0.0337 |
| Decade | January | July | August | September | DJF (Winter) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Anomaly (%) | Contribution (%) | Anomaly (%) | Contribution (%) | Anomaly (%) | Contribution (%) | Anomaly (%) | Contribution (%) | Anomaly (%) | Contribution (%) | |
| 1901–1910 | 60.71 | 0.54 | 2.54 | 32.66 | −12.29 | 18.24 | −13.66 | 8.93 | 31.60 | 2.29 |
| 1911–1920 | 26.95 | 0.43 | −12.67 | 27.92 | −15.77 | 17.58 | −4.82 | 9.88 | 1.09 | 1.77 |
| 1921–1930 | 86.64 | 0.59 | 11.00 | 33.25 | −1.05 | 19.35 | −7.04 | 9.04 | 17.97 | 1.93 |
| 1931–1940 | −12.57 | 0.27 | 0.96 | 29.15 | 4.41 | 19.68 | −1.31 | 9.25 | −2.72 | 1.54 |
| 1941–1950 | 63.17 | 0.50 | 12.83 | 32.29 | −2.42 | 18.23 | 10.58 | 10.27 | 36.15 | 2.13 |
| 1951–1960 | −35.73 | 0.19 | 10.55 | 30.69 | 2.88 | 18.65 | −2.88 | 8.75 | −29.68 | 1.07 |
| 1961–1970 | −10.59 | 0.28 | 13.14 | 33.63 | 5.69 | 20.51 | 2.89 | 9.93 | 28.03 | 2.08 |
| 1971–1980 | −76.28 | 0.08 | −6.14 | 29.05 | 2.16 | 20.64 | 0.38 | 10.08 | −27.05 | 1.24 |
| 1981–1990 | 4.44 | 0.36 | −16.14 | 27.15 | 13.97 | 24.08 | −5.67 | 9.91 | −6.88 | 1.65 |
| 1991–2000 | −40.60 | 0.19 | 5.51 | 31.20 | 0.70 | 19.44 | −3.76 | 9.24 | −11.84 | 1.43 |
| 2001–2010 | −30.58 | 0.23 | −15.20 | 26.41 | 0.58 | 20.45 | 9.13 | 11.03 | −21.72 | 1.33 |
| 2011–2017 | −50.81 | 0.16 | −9.09 | 27.98 | 1.64 | 20.41 | 23.09 | 12.29 | −16.84 | 1.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saini, A.; Sahu, N.; Kumar, P.; Nayak, S.; Duan, W.; Avtar, R.; Behera, S. Advanced Rainfall Trend Analysis of 117 Years over West Coast Plain and Hill Agro-Climatic Region of India. Atmosphere 2020, 11, 1225. https://doi.org/10.3390/atmos11111225
Saini A, Sahu N, Kumar P, Nayak S, Duan W, Avtar R, Behera S. Advanced Rainfall Trend Analysis of 117 Years over West Coast Plain and Hill Agro-Climatic Region of India. Atmosphere. 2020; 11(11):1225. https://doi.org/10.3390/atmos11111225
Chicago/Turabian StyleSaini, Atul, Netrananda Sahu, Pankaj Kumar, Sridhara Nayak, Weili Duan, Ram Avtar, and Swadhin Behera. 2020. "Advanced Rainfall Trend Analysis of 117 Years over West Coast Plain and Hill Agro-Climatic Region of India" Atmosphere 11, no. 11: 1225. https://doi.org/10.3390/atmos11111225
APA StyleSaini, A., Sahu, N., Kumar, P., Nayak, S., Duan, W., Avtar, R., & Behera, S. (2020). Advanced Rainfall Trend Analysis of 117 Years over West Coast Plain and Hill Agro-Climatic Region of India. Atmosphere, 11(11), 1225. https://doi.org/10.3390/atmos11111225