Insight into Construction of Tikhonov-Type Regularization for Atmospheric Retrievals
Abstract
1. Introduction
2. Theory
2.1. Forward Problem
2.1.1. Radiative Transfer in the UV–VIS–NIR
2.1.2. Radiative Transfer in the IR/Microwave
2.1.3. Modeling of Instrumental Effect
2.2. Inverse Problem
2.2.1. Nonlinear Optimization
- the estimated change in the quadratic model and
- the actual change in the objective function .
2.2.2. Regularization Matrix
3. Results and Discussion
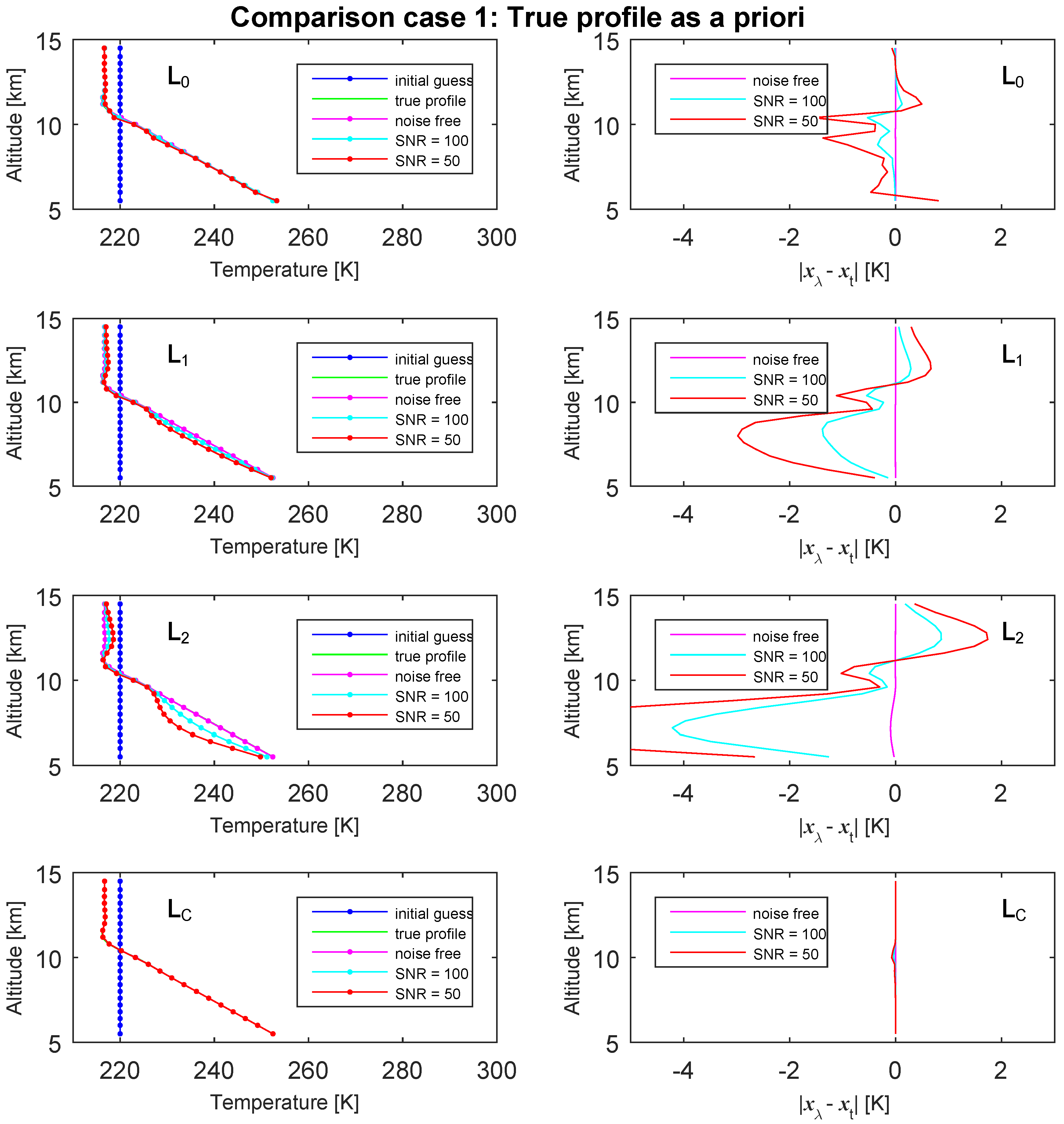
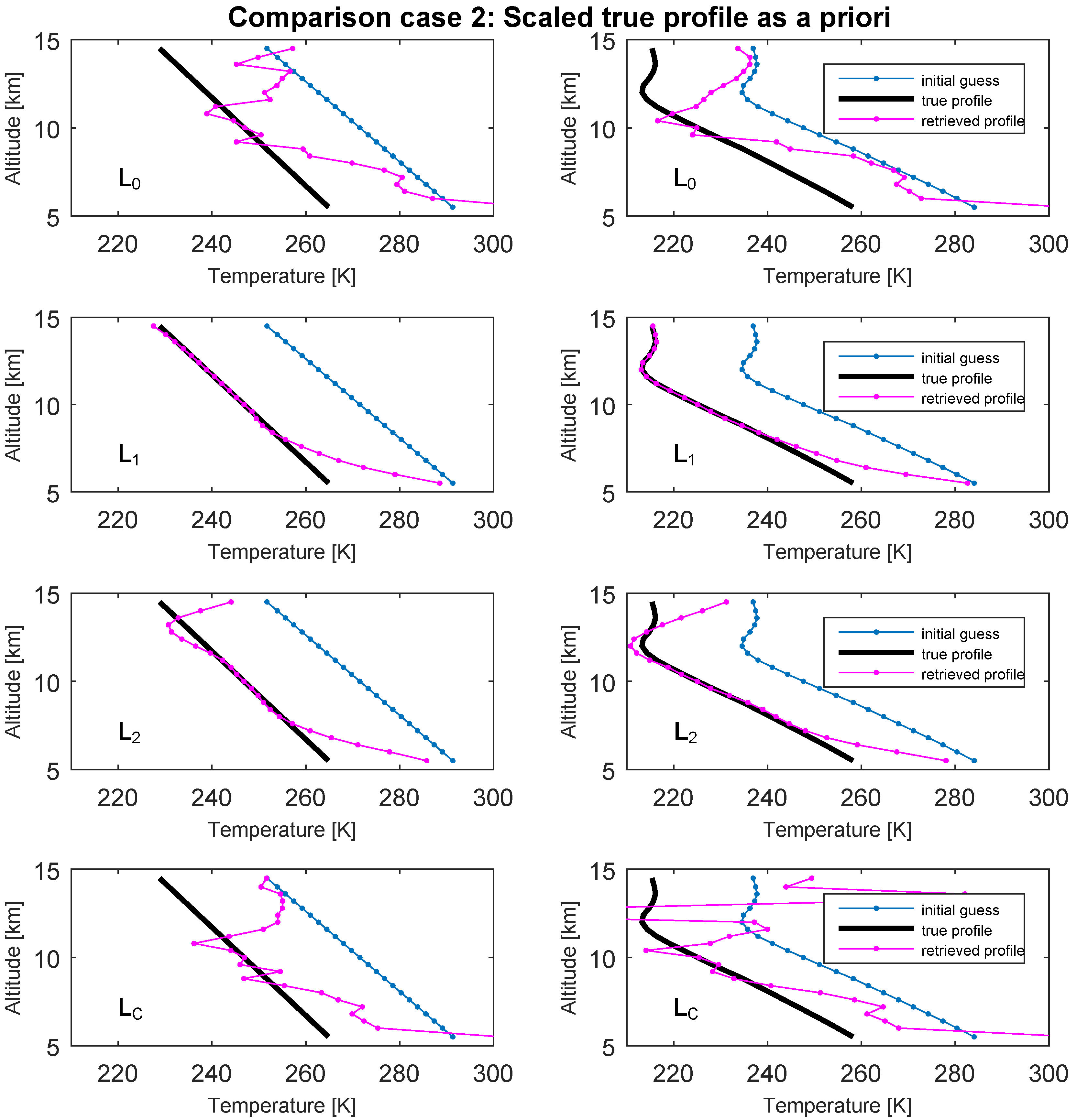
3.1. Temperature Profile Retrieval
- ase 1
- the true profile used as the a priori profile;
- Case 2
- the scaled true profile used as the a priori profile.
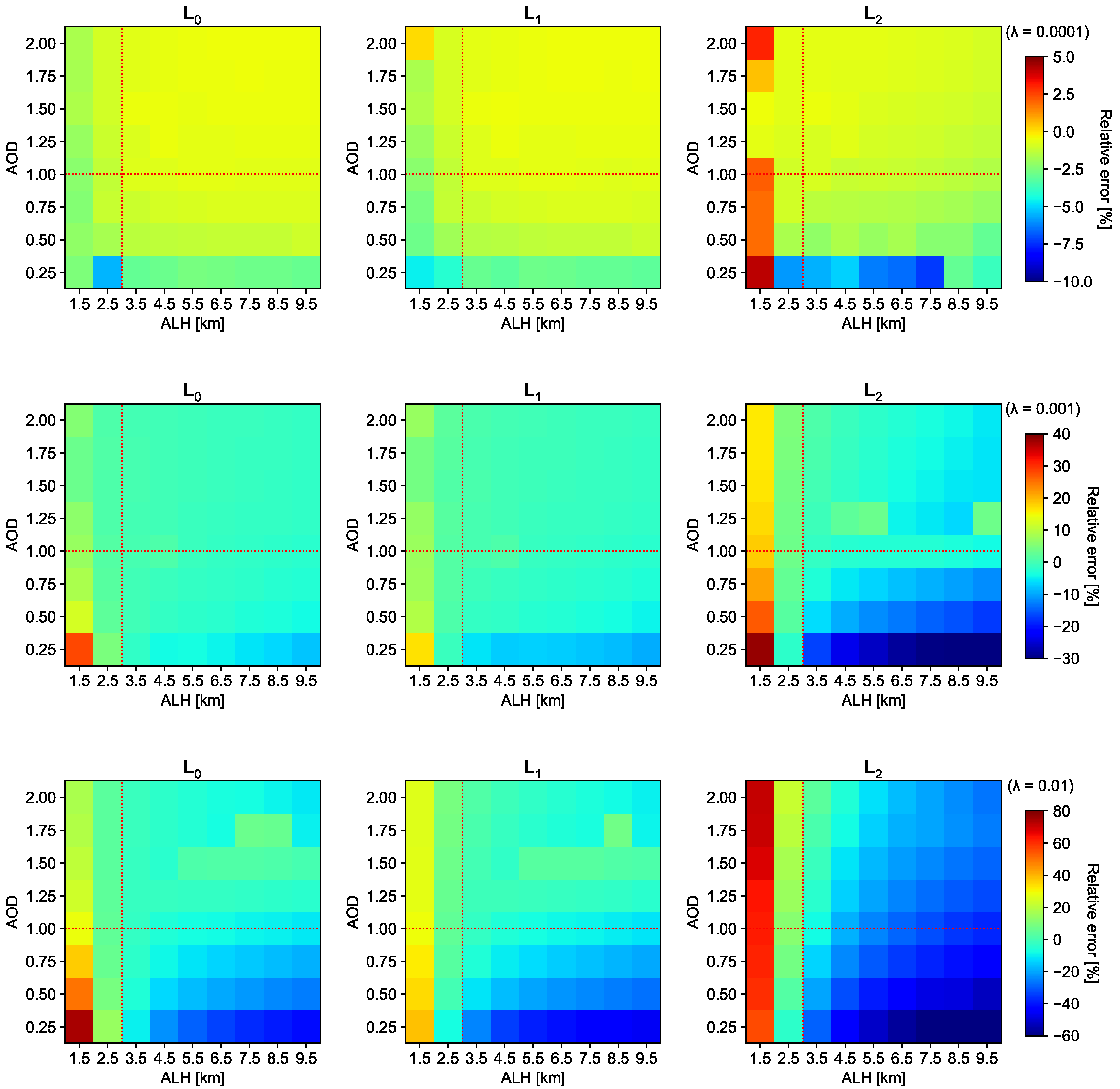
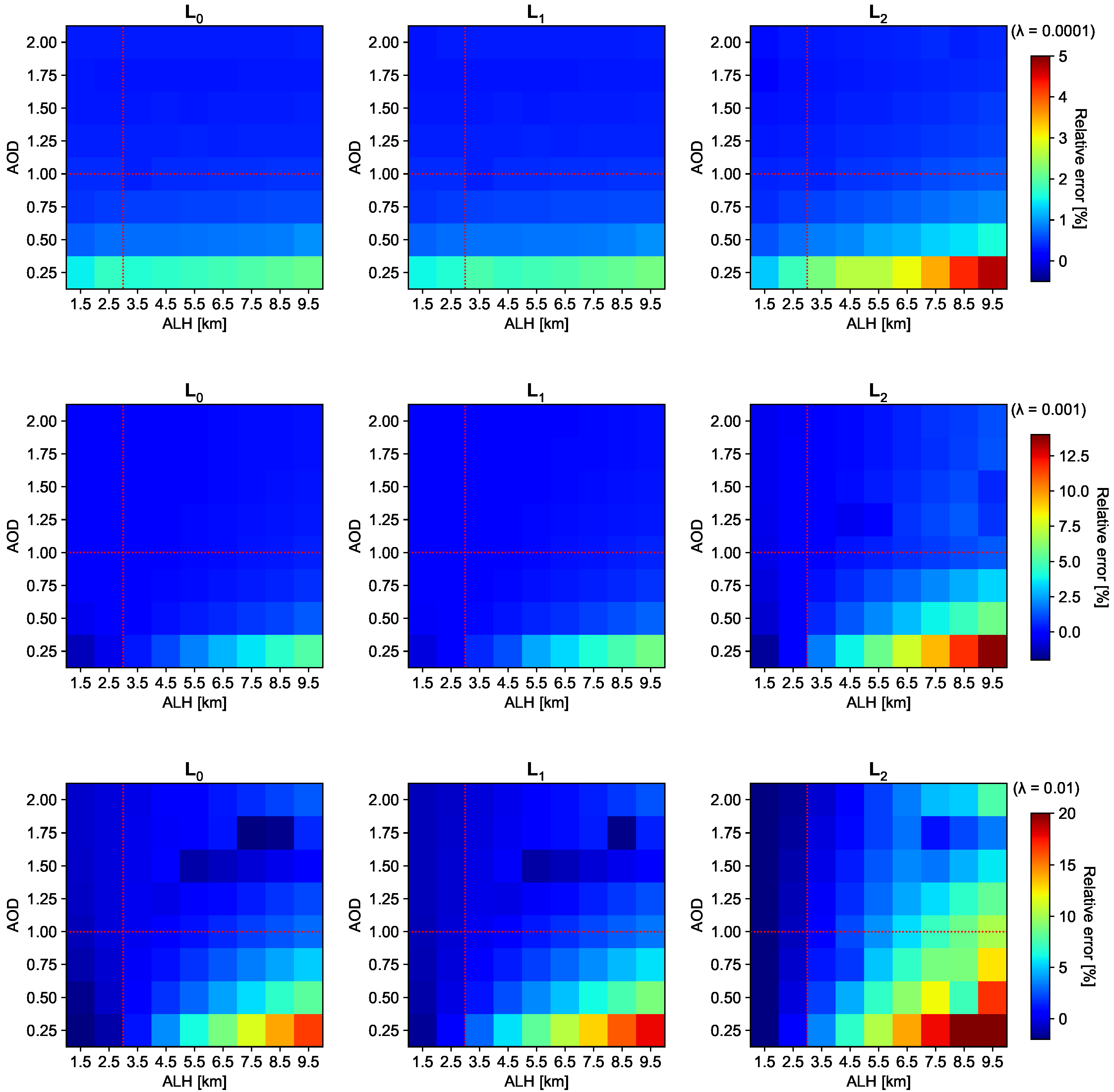
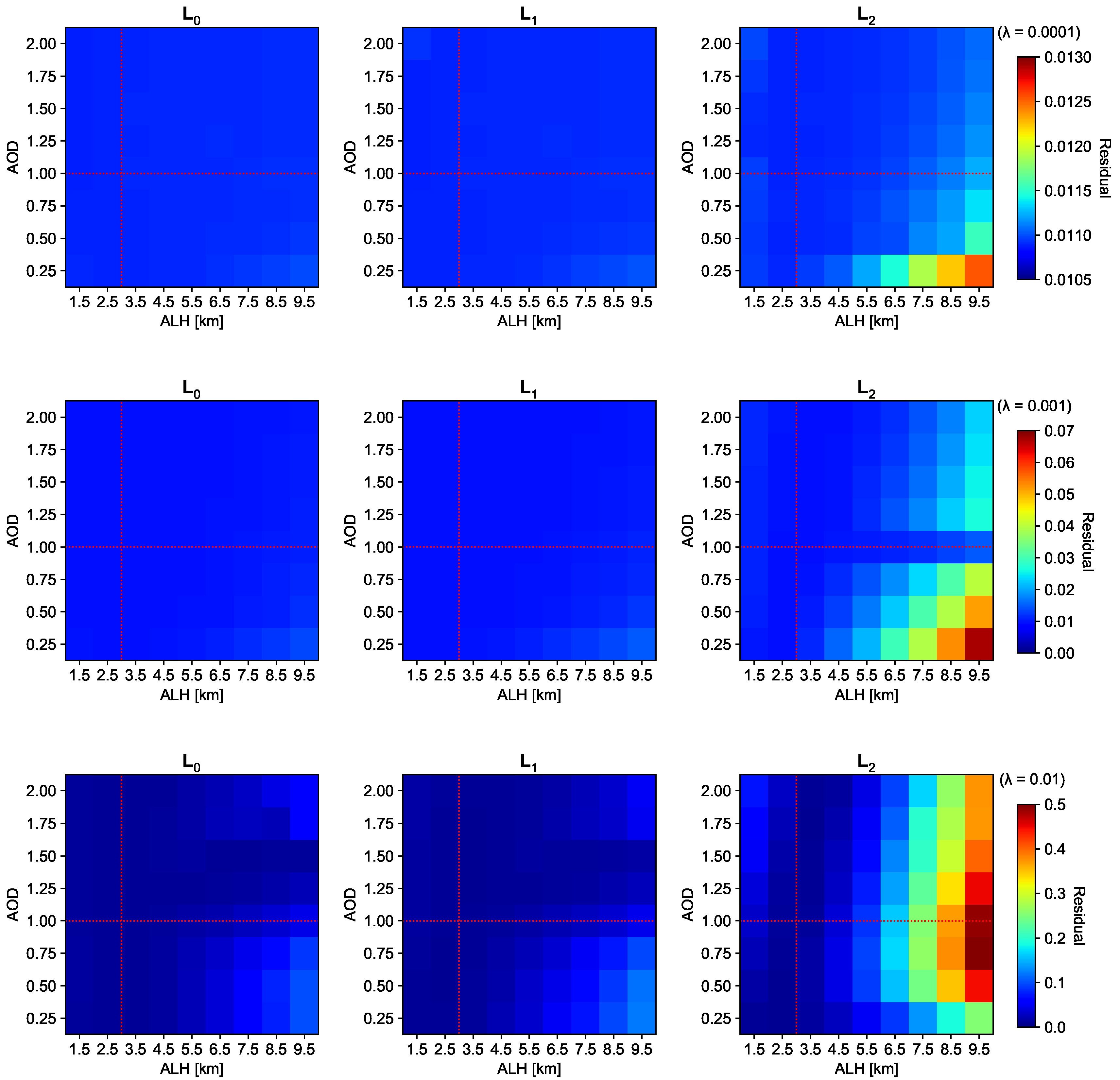
3.2. Aerosol Retrieval
4. Conclusions
- has a good control on the magnitude of the solution;
- imposes the smoothness of the solution with satisfactory retrieval accuracy even when the a priori information is not reliable;
- also tends to produce a smoothed solution, but the retrieval accuracy can be degraded when the a priori information is not reliable;
- associates with the a priori information.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Engl, H.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Kress, R. Linear Integral Equations, 3rd ed.; Applied Mathematical Sciences; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Twomey, S. Introduction to the Mathematics of Inversion in Remote Sensing and Indirect Measurements; Elsevier Science: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Stephens, G. Remote Sensing of the Lower Atmosphere; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Rodgers, C. Inverse Methods for Atmospheric Sounding: Theory and Practise; World Scientific: Singapore, 2000. [Google Scholar]
- Efremenko, D.; Doicu, A.; Loyola, D.; Trautmann, T. Acceleration techniques for the discrete ordinate method. J. Quant. Spectrosc. Radiat. Transf. 2013, 114, 73–81. [Google Scholar] [CrossRef]
- del Águila, A.; Efremenko, D.S.; Molina García, V.; Xu, J. Analysis of two dimensionality reduction techniques for fast simulation of the spectral radiances in the Hartley-Huggins band. Atmosphere 2019, 10, 142. [Google Scholar] [CrossRef]
- del Águila, A.; Efremenko, D.S.; Thomas, T. A review of dimensionality reduction techniques for processing hyper-spectral optical signal. Light Eng. 2019, 27, 85–98. [Google Scholar] [CrossRef]
- Hansen, P. Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Vogel, C. Computational Methods for Inverse Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Doicu, A.; Trautmann, T.; Schreier, F. Numerical Regularization for Atmospheric Inverse Problems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Hansen, P. Discrete Inverse Problems: Insight and Algorithms; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar] [CrossRef]
- Tikhonov, A. On the Solution of Incorrectly Stated Problems and a Method of Regularization. Dokl. Acad. Nauk SSSR 1963, 151, 501–504. [Google Scholar]
- Tikhonov, A.; Arsenin, V. Solutions of Ill-Posed Problems; Wiley: Hoboken, NJ, USA, 1977. [Google Scholar]
- Allmaras, M.; Bangerth, W.; Linhart, J.; Polanco, J.; Wang, F.; Wang, K.; Webster, J.; Zedler, S. Estimating Parameters in Physical Models through Bayesian Inversion: A Complete Example. SIAM Rev. 2013, 55, 149–167. [Google Scholar] [CrossRef]
- Eriksson, P. Analysis and comparison of two linear regularization methods for passive atmospheric observation. J. Geophys. Res. 2000, 105, 18157–18167. [Google Scholar] [CrossRef]
- Brezinski, C.; Rodriguez, G.; Seatzu, S. Error estimates for linear systems with applications to regularization. Numer. Algorithms 2008, 49, 85–104. [Google Scholar] [CrossRef]
- Xu, J.; Schreier, F.; Doicu, A.; Trautmann, T. Assessment of Tikhonov-type regularization methods for solving atmospheric inverse problems. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 274–286. [Google Scholar] [CrossRef]
- Ceccherini, S. Analytical determination of the regularization parameter in the retrieval of atmospheric vertical profiles. Opt. Lett. 2005, 30, 2554–2556. [Google Scholar] [CrossRef]
- Ridolfi, M.; Sgheri, L. A self-adapting and altitude-dependent regularization method for atmospheric profile retrievals. Atmos. Chem. Phys. 2009, 9, 1883–1897. [Google Scholar] [CrossRef]
- Koner, P.K.; Drummond, J.R. A comparison of regularization techniques for atmospheric trace gases retrievals. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 514–526. [Google Scholar] [CrossRef]
- Thomas, G.; Stamnes, K. Radiative Transfer in the Atmosphere and Ocean; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Liou, K.N. An Introduction to Atmospheric Radiation, 2nd ed.; Academic Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Bohren, C.F.; Clothiaux, E.E. Fundamentals of Atmospheric Radiation; Wiley-VCH Verlag: Weinheim, Germany, 2006. [Google Scholar]
- Petty, G.W. A First Course in Atmospheric Radiation, 2nd ed.; Sundog Publishing: Madison, WI, USA, 2006. [Google Scholar]
- Zdunkowski, W.; Trautmann, T.; Bott, A. Radiation in the Atmosphere — A Course in Theoretical Meteorology; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Dahlback, A.; Stamnes, K. A new spherical model for computing the radiation field available for photolysis and heating at twilight. Planet. Space Sci. 1991, 39, 671–683. [Google Scholar] [CrossRef]
- Wick, G. über ebene Diffusionsprobleme. Z. Phys. 1943, 121, 702–718. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover Publications Inc.: New York, NY, USA, 1960. [Google Scholar]
- Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically Stable Algorithm for Discrete–Ordinate– Method Radiative Transfer in Multiple Scattering and Emitting Layered Media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef] [PubMed]
- Efremenko, D.S.; Molina García, V.; Gimeno García, S.; Doicu, A. A review of the matrix-exponential formalism in radiative transfer. J. Quant. Spectrosc. Radiat. Transf. 2017, 196, 17–45. [Google Scholar] [CrossRef]
- Schreier, F.; Gimeno García, S.; Hedelt, P.; Hess, M.; Mendrok, J.; Vasquez, M.; Xu, J. GARLIC—A general purpose atmospheric radiative transfer line-by-line infrared-microwave code: Implementation and evaluation. J. Quant. Spectrosc. Radiat. Transf. 2014, 137, 29–50. [Google Scholar] [CrossRef]
- Schreier, F.; Gimeno García, S.; Hochstaffl, P.; Städt, S. Py4CAtS—PYthon for Computational ATmospheric Spectroscopy. Atmosphere 2019, 10, 262. [Google Scholar] [CrossRef]
- Dennis, J., Jr.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar] [CrossRef]
- Eriksson, P.; Jiménez, C.; Buehler, S.A. Qpack, a general tool for instrument simulation and retrieval work. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 47–64. [Google Scholar] [CrossRef]
- Wehr, T.; Bühler, S.; von Engeln, A.; Künzi, K.; Langen, J. Retrieval of stratospheric temperatures from spaceborne microwave limb sounding measurement. J. Geophys. Res. Atmos. 1998, 103, 25997–26006. [Google Scholar] [CrossRef]
- von Engeln, A.; Bühler, S. Temperature profile determination from microwave oxygen emissions in limb sounding geometry. J. Geophys. Res. Atmos. 2002, 107, ACL-12. [Google Scholar] [CrossRef]
- Stähli, O.; Murk, A.; Kämpfer, N.; Mätzler, C.; Eriksson, P. Microwave radiometer to retrieve temperature profiles from the surface to the stratopause. Atmos. Meas. Tech. 2013, 6, 2477–2494. [Google Scholar] [CrossRef]
- Massaro, G.; Stiperski, I.; Pospichal, B.; Rotach, M.W. Accuracy of retrieving temperature and humidity profiles by ground-based microwave radiometry in truly complex terrain. Atmos. Meas. Tech. 2015, 8, 3355–3367. [Google Scholar] [CrossRef]
- Denning, R.F.; Guidero, S.L.; Parks, G.S.; Gary, B.L. Instrument description of the airborne microwave temperature profiler. J. Geophys. Res. Atmos. 1989, 94, 16757–16765. [Google Scholar] [CrossRef]
- Mahoney, M.; Denning, R. A State-of-the-Art Airborne Microwave Temperature Profiler (MTP). In Proceedings of the 33rd International Symposium on the Remote Sensing of the Environment, Stresa, Italy, 4–8 May 2009. [Google Scholar]
- Gary, B.L. Mesoscale temperature fluctuations in the stratosphere. Atmos. Chem. Phys. 2006, 6, 4577–4589. [Google Scholar] [CrossRef]
- Nielsen-Gammon, J.W.; Powell, C.L.; Mahoney, M.; Angevine, W.M.; Senff, C.; White, A.; Berkowitz, C.; Doran, C.; Knupp, K. Multisensor estimation of mixing heights over a coastal city. J. Appl. Meteorol. Climatol. 2008, 47, 27–43. [Google Scholar] [CrossRef]
- Davis, C.A.; Ahijevych, D.A.; Haggerty, J.A.; Mahoney, M.J. Observations of Temperature in the Upper Troposphere and Lower Stratosphere of Tropical Weather Disturbances. J. Atmos. Sci. 2014, 71, 1593–1608. [Google Scholar] [CrossRef]
- Voigt, C.; Schumann, U.; Minikin, A.; Abdelmonem, A.; Afchine, A.; Borrmann, S.; Boettcher, M.; Buchholz, B.; Bugliaro, L.; Costa, A.; et al. ML-CIRRUS: The airborne experiment on natural Cirrus and contrail cirrus with the High-Altitude Long-Range Research Aircraft HALO. Bull. Am. Met. Soc. 2017, 98, 271–288. [Google Scholar] [CrossRef]
- Kenntner, M.; Fix, A.; Jirousek, M.; Schreier, F.; Xu, J.; Rapp, M. Measurement Characteristics of an airborne Microwave Temperature Profiler (MTP). Atmos. Meas. Tech. Discuss. 2020, 2020, 1–55. [Google Scholar] [CrossRef]
- Gordon, I.; Rothman, L.; Hill, C.; Kochanov, R.; Tan, Y.; Bernath, P.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Anderson, G.; Clough, S.; Kneizys, F.; Chetwynd, J.; Shettle, E. AFGL Atmospheric Constituent Profiles (0–120 km); Technical Report TR-86-0110; AFGL: Hanscom, MA, USA, 1986. [Google Scholar]
- Levy, R.C.; Remer, L.A.; Mattoo, S.; Vermote, E.F.; Kaufman, Y.J. Second-generation operational algorithm: Retrieval of aerosol properties over land from inversion of Moderate Resolution Imaging Spectroradiometer spectral reflectance. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Levy, R.C.; Remer, L.A.; Dubovik, O. Global aerosol optical properties and application to Moderate Resolution Imaging Spectroradiometer aerosol retrieval over land. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
| Parameter | Description |
|---|---|
| LO frequency | 56.363 GHz, 57.612 GHz, 58.363 GHz |
| Bandwidth | 200 MHz |
| Viewing angle | +80, +55, +42, +25, +12, ±0, −12, −25, −42, −80 |
| Signal-to-noise ratio (SNR) | 50, 100 |
| Field-of-view | Gaussian |
| Observer altitude | 10 km |
| Regularization Matrix | DOFS | ||
|---|---|---|---|
| Noise-Free | |||
| 16.35 | 13.49 | 11.11 | |
| 16.10 | 13.95 | 11.54 | |
| 15.77 | 14.01 | 11.67 | |
| 14.96 | 13.20 | 10.28 | |
| Regularization Matrix | RMSE | DOFS | ||
|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 1 | Scenario 2 | |
| 9.32 | 9.59 | 14.40 | 14.29 | |
| 4.19 | 3.99 | 15.34 | 15.62 | |
| 4.62 | 4.78 | 14.83 | 14.72 | |
| 9.11 | 12.46 | 14.09 | 15.35 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Rao, L.; Schreier, F.; Efremenko, D.S.; Doicu, A.; Trautmann, T. Insight into Construction of Tikhonov-Type Regularization for Atmospheric Retrievals. Atmosphere 2020, 11, 1052. https://doi.org/10.3390/atmos11101052
Xu J, Rao L, Schreier F, Efremenko DS, Doicu A, Trautmann T. Insight into Construction of Tikhonov-Type Regularization for Atmospheric Retrievals. Atmosphere. 2020; 11(10):1052. https://doi.org/10.3390/atmos11101052
Chicago/Turabian StyleXu, Jian, Lanlan Rao, Franz Schreier, Dmitry S. Efremenko, Adrian Doicu, and Thomas Trautmann. 2020. "Insight into Construction of Tikhonov-Type Regularization for Atmospheric Retrievals" Atmosphere 11, no. 10: 1052. https://doi.org/10.3390/atmos11101052
APA StyleXu, J., Rao, L., Schreier, F., Efremenko, D. S., Doicu, A., & Trautmann, T. (2020). Insight into Construction of Tikhonov-Type Regularization for Atmospheric Retrievals. Atmosphere, 11(10), 1052. https://doi.org/10.3390/atmos11101052







