Regional Characteristics of Long-Term Variability of Summer Precipitation in the Poyang Lake Basin and Possible Links with Large-Scale Circulations
Abstract
1. Introduction
2. Study Area and Data
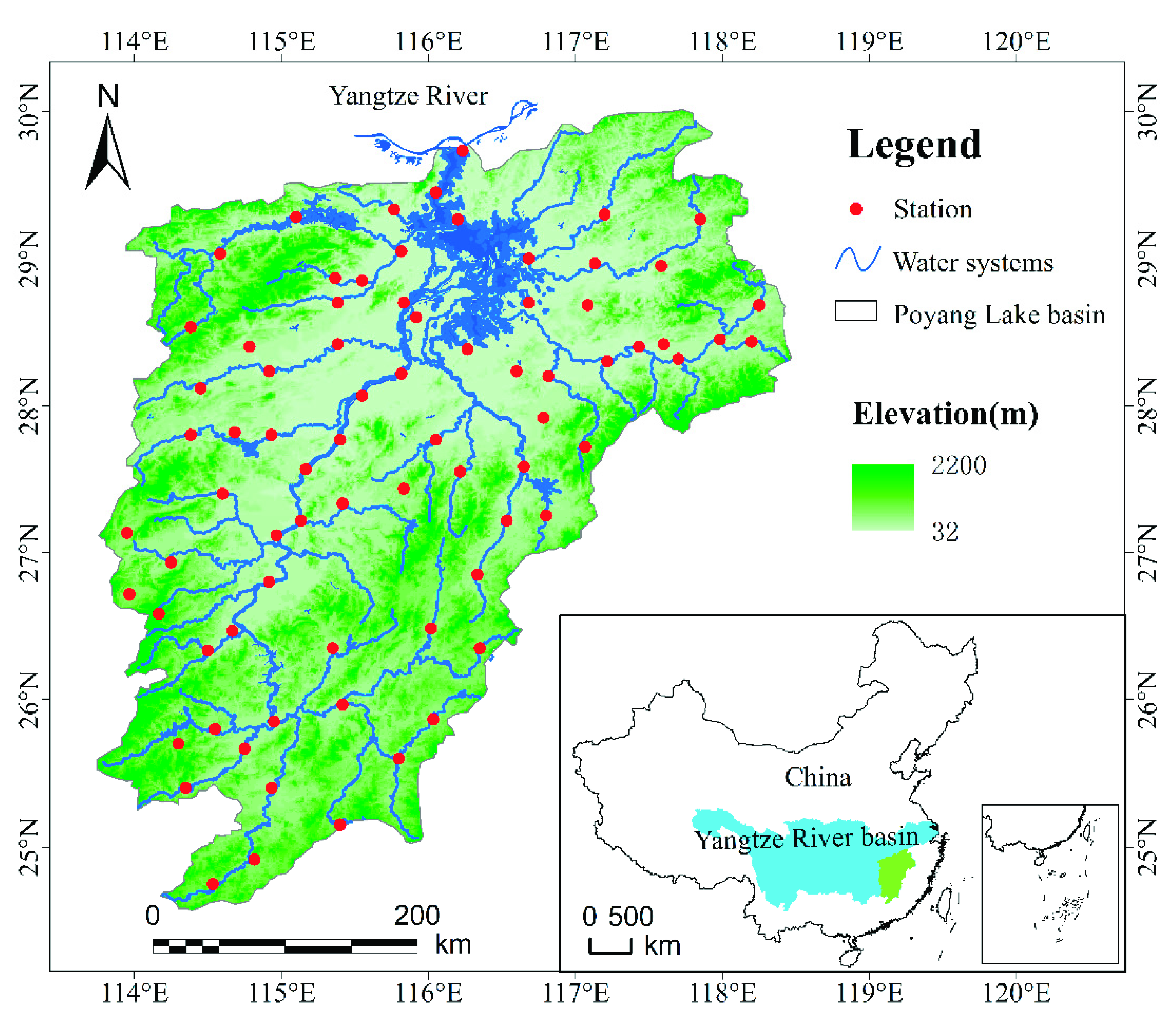
2.1. Description of Study Area
2.2. Data Source and Processing
3. Methods
3.1. EOF/REOF
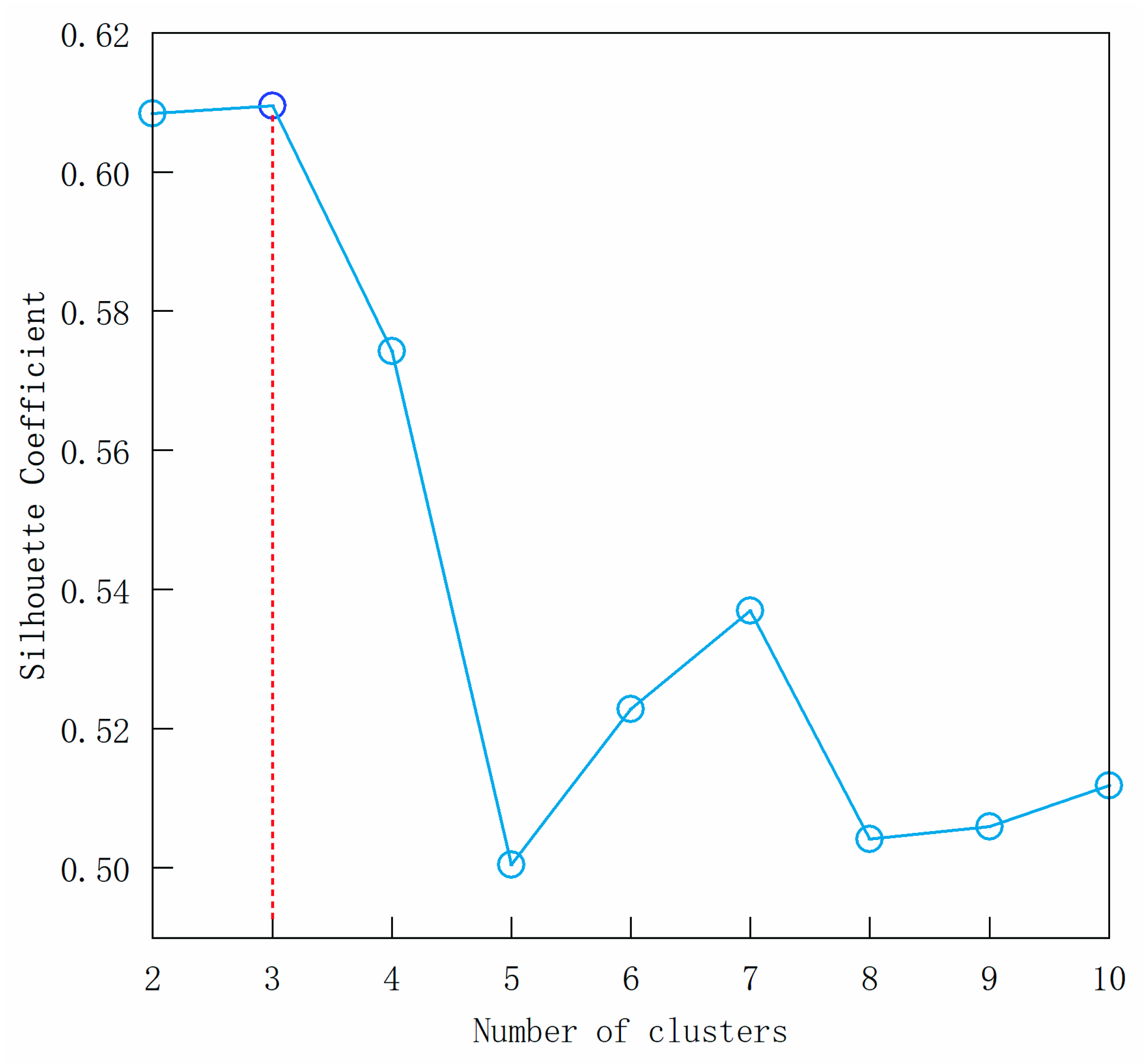
3.2. Hierarchical Clustering Algorithm
3.3. Multiple Trend Analyses
3.4. Wavelet Analysis
4. Results
4.1. Spatial Patterns of Summer Precipitation in the PYLB
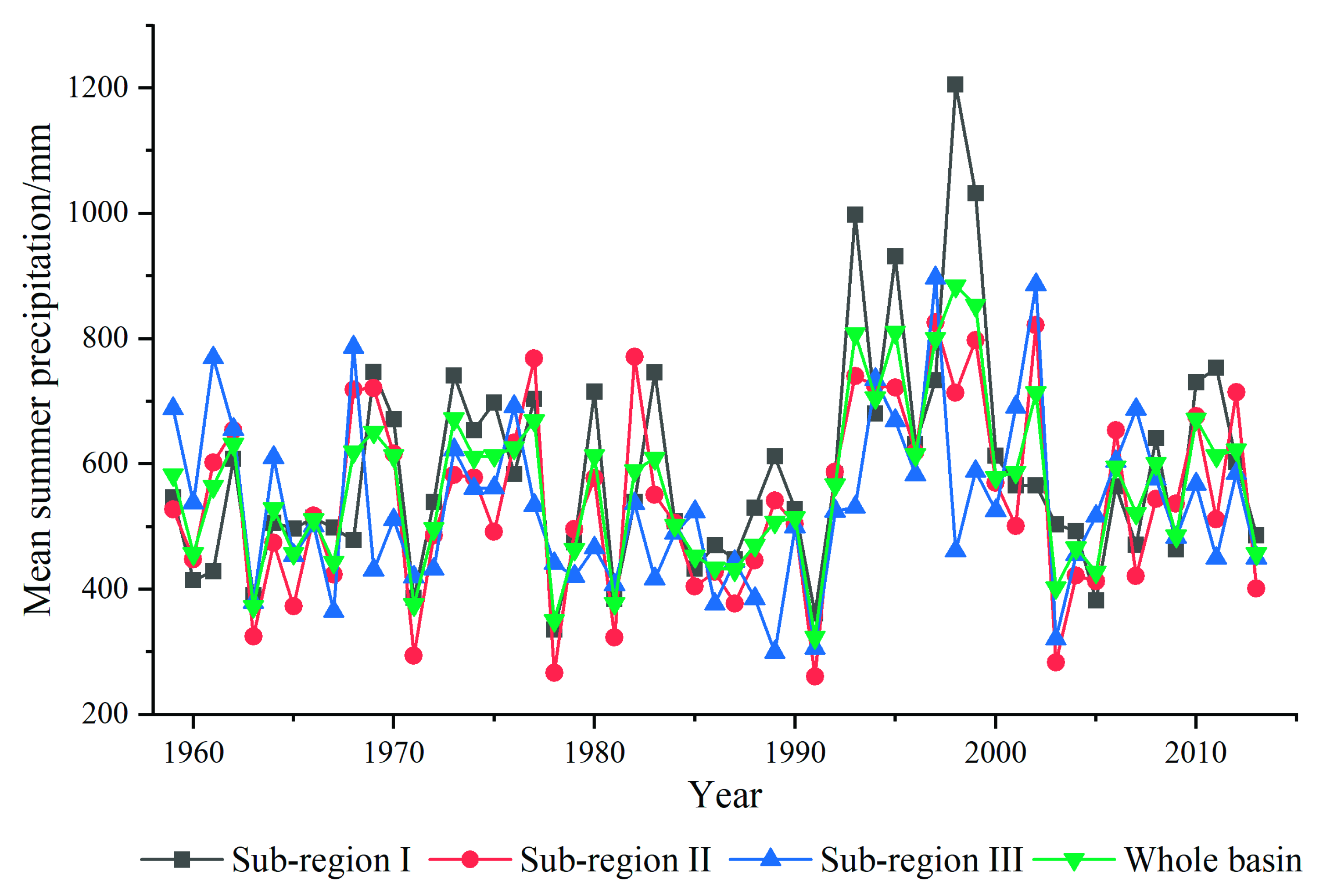
4.2. Multi-Time Scale Characteristic of Summer Precipitation of Sub-Regions
4.3. The Relationship between Summer Precipitation and Large-Scale Circulations
5. Discussion
6. Conclusions
- (1)
- Two key precipitation areas in the PYLB were identified by REOF. These key areas were optimally divided into three sub-regions on the basis of the HCA method, which were northern PYLB (sub-region I), central PYLB (sub-region II), and southern PYLB (sub-region III), respectively. The area of sub-region I was lightly less than that of sum of sub-region II and sub-region III. This will help us understand the spatial distribution of water resources in the PYLB, which will also be conducive to make better use of water resources.
- (2)
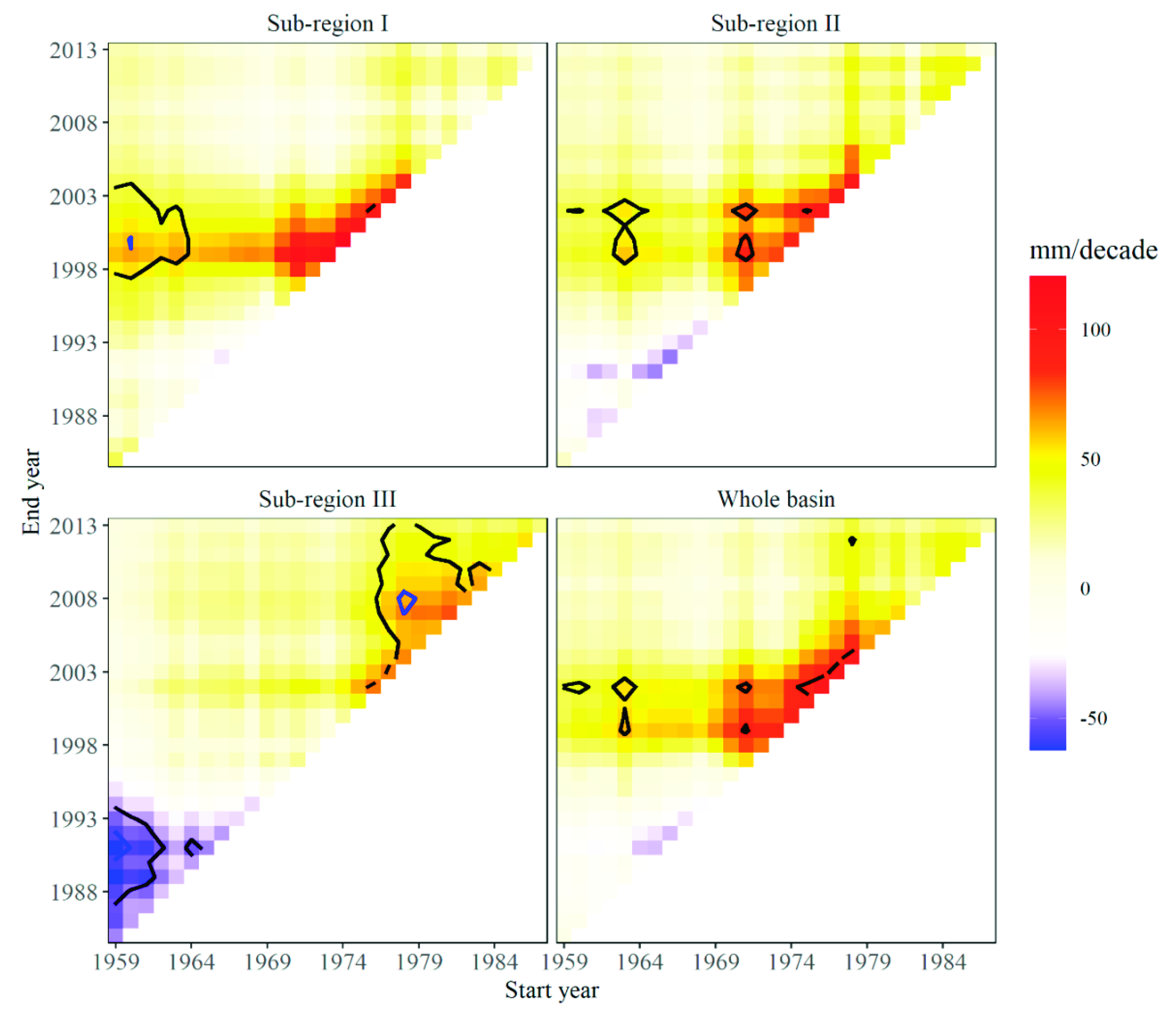
- The same trends per decade in annual summer precipitation were found in sub-region I and sub-region II, which was distinctly increasing from 1974 to 2000. Sub-region III, meanwhile, showed summer precipitation apparently in a decreasing trend in the period from 1959 to late 1970s and apparently in an increasing trend from late 1970s to 2000. Summer rainfall in the three sub-regions of the PYLB exhibited distinct periodicities, to be specific, 2–3 and 4–6 years periods in sub-region I and sub-region III, and 16 years and 2–3 years periods in sub-region II. Such results reveal the variation trend and periodic characteristics of summer precipitation in the PYLB and will help to predict drought and flood disasters.
- (3)
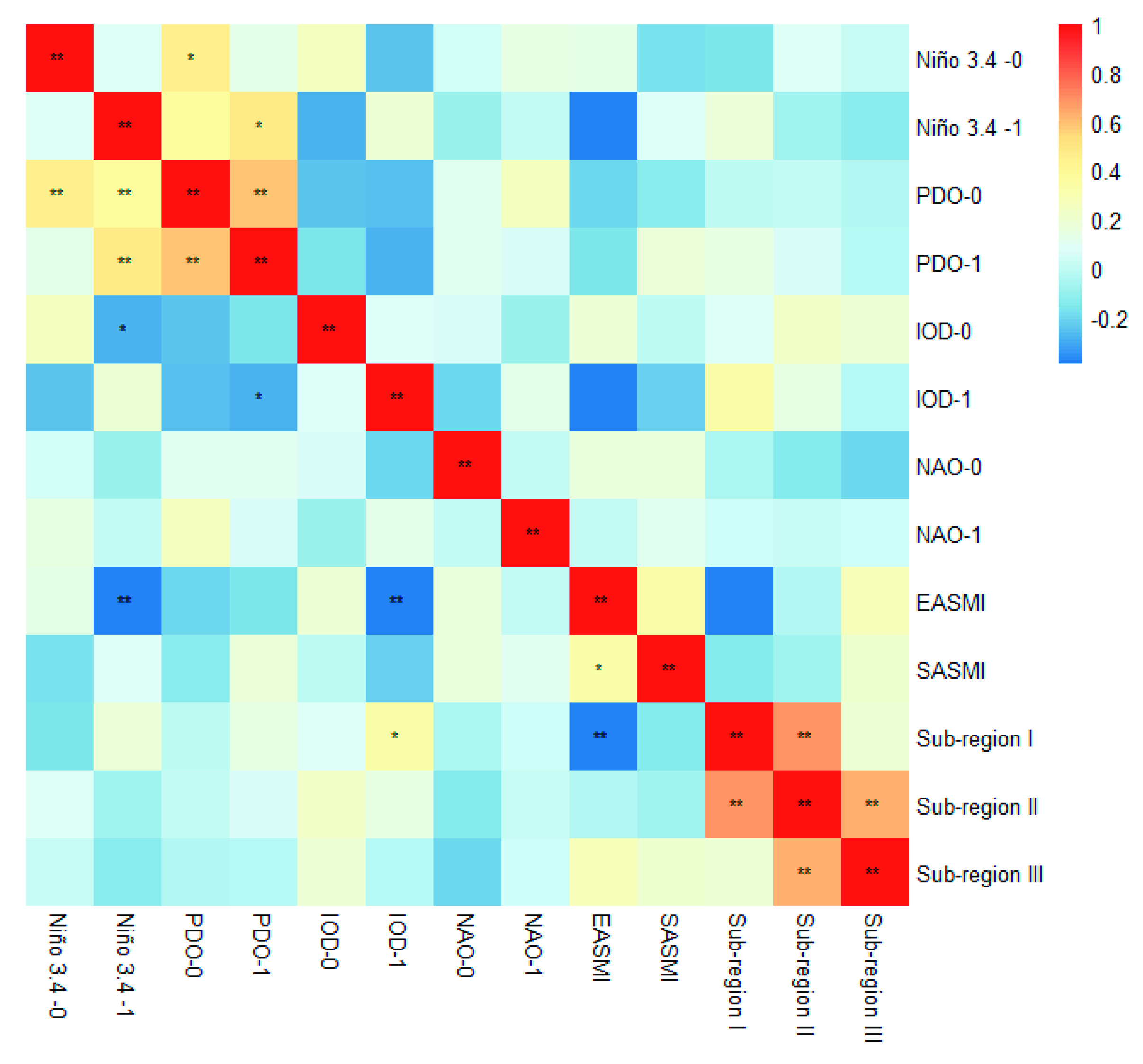
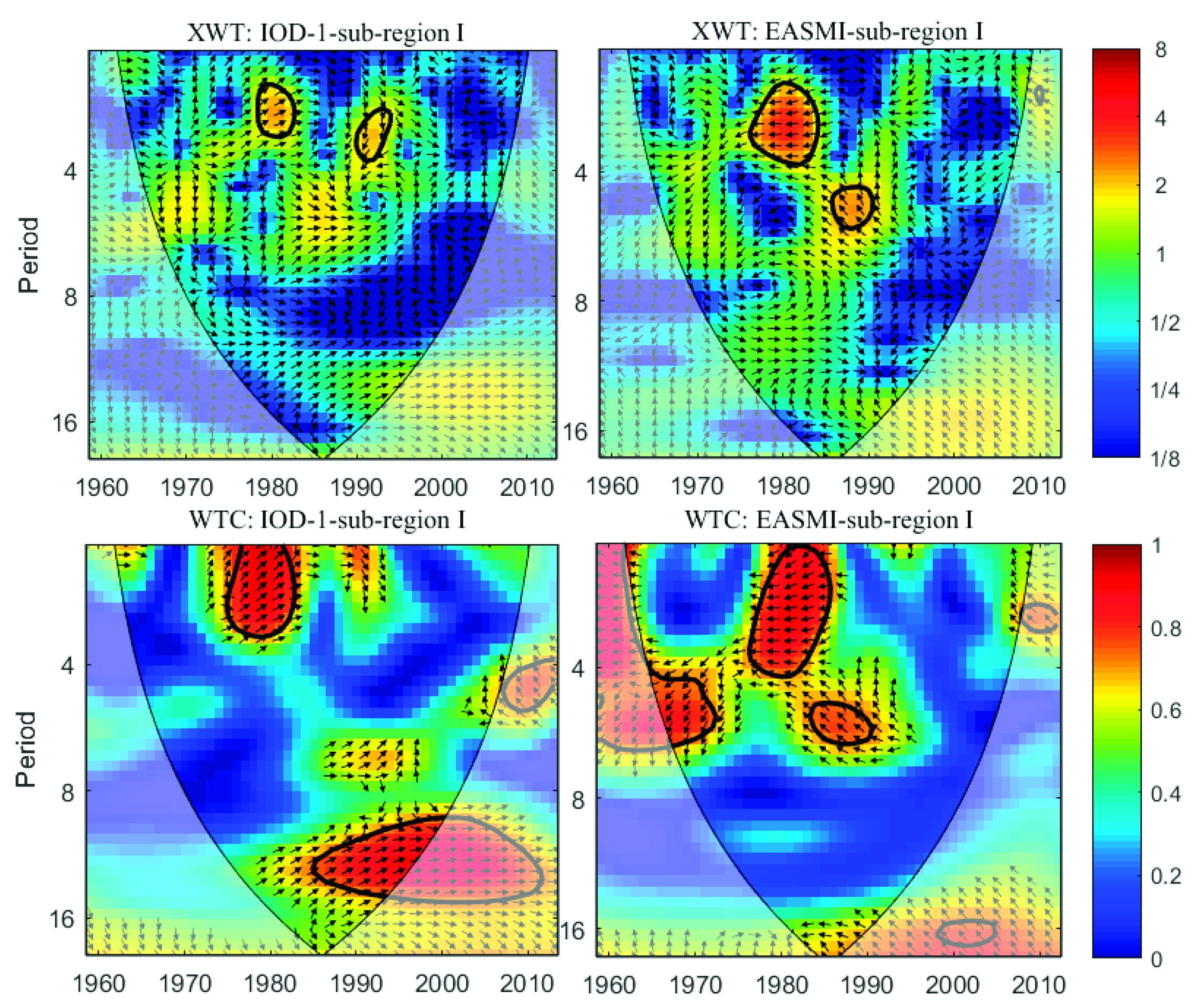
- Summer precipitation in sub-region I was positively correlated with previous IOD events (at 95% significant confidence level) and the common 2–4 years resonance period was found between them. Wavelet coherence spectra showed IOD–1 was one–quarter phase earlier than the summer precipitation of sub-region I. Summer precipitation in sub-region I was negatively correlated with EASM (at 99% significant confidence level) and they exhibited common 2–4 years and 4–6 years resonance periods. Wavelet coherence spectra demonstrates EASM was prior to summer precipitation in sub-region I. Summer precipitation in sub-region II and sub-region III showed weak correlations with multiple indices. The findings of these results may help to better understand the possible influence of circulations on the spatial patterns of summer precipitation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2014: Mitigation of Climate Change. Available online: https://www.ipcc.ch/report/ar5/wg3/ (accessed on 16 September 2014).
- Lu, D.H.; Tighe, S.L.; Xie, W.C. Pavement Risk Assessment for Future Extreme Precipitation Events under Climate Change. Transp. Res. Rec. 2018, 2672, 122–131. [Google Scholar] [CrossRef]
- Yu, R.; Zhai, P.M.; Chen, Y. Facing Climate Change–Related Extreme Events in Megacities of China in the Context of 1.5 Degrees C Global Warming. Curr. Opin. Environ. Sustain. 2018, 30, 75–81. [Google Scholar] [CrossRef]
- Menzel, L.; Burger, G. Climate Change Scenarios and Runoff Response in the Mulde Catchment (Southern Elbe, Germany). J. Hydrol. 2002, 267, 53–64. [Google Scholar] [CrossRef]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Analysis of Spatial and Temporal Rainfall Trends in Sicily During the 1921–2012 Period. Appl. Clim. 2016, 126, 113–129. [Google Scholar] [CrossRef]
- Bragazza, L.; Buttler, A.; Robroek, B.J.M.; Albrecht, R.; Zaccone, C.; Jassey, V.E.J.; Signarbieux, C. Persistent High Temperature and Low Precipitation Reduce Peat Carbon Accumulation. Glob. Chang. Biol. 2016, 22, 4114–4123. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Karl, T.R.; Easterling, D.R.; Redmond, K.; Young, J.; Yin, X.; Hennon, P. Probable Maximum Precipitation and Climate Change. Geophys. Res. Lett. 2013, 40. [Google Scholar] [CrossRef]
- Coulibaly, P. Spatial and Temporal Variability of Canadian Seasonal Precipitation (1900–2000). Adv. Water Resour. 2006, 29, 1846–1865. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Y.; Huang, R. The Interannual Variability of Summer Rainfall in the Arid and Semiarid Regions of Northern China and Its Association with the Northern Hemisphere Circumglobal Teleconnection. Adv. Atmos. Sci. 2011, 28, 257–268. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, J.Q.; Guo, E.L.; Zhao, C.L.; Cao, T.H. Spatial and Temporal Variations of Precipitation Concentration and Their Relationships with Large–Scale Atmospheric Circulations across Northeast China. Atmos. Res. 2019, 222, 62–73. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, H.; He, D.; Chen, J. Integrating Precipitation Zoning with Random Forest Regression for the Spatial Downscaling of Satellite–Based Precipitation: A Case Study of the Lancang–Mekong River Basin. Int. J. Climatol. 2019, 39, 3947–3961. [Google Scholar] [CrossRef]
- Liu, H.-L.; Zhang, Q.; Guo, J.-Q.; Zhang, J.-G.; Wang, S. Spatiotemporal Variability and Change of the South China Spring Precipitation During 1961–2012. Adv. Meteorol. 2015. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.M.; Chen, X.L.; Cai, X.B.; Tian, L.Q.; Gan, W.X. Assessment of Inundation Changes of Poyang Lake Using Modis Observations between 2000 and 2010. Remote Sens. Environ. 2012, 121, 80–92. [Google Scholar] [CrossRef]
- Wan, R.; Yang, G.; Dai, X.; Zhang, Y.; Li, B. Water Security–Based Hydrological Regime Assessment Method for Lakes with Extreme Seasonal Water Level Fluctuations: A Case Study of Poyang Lake, China. Chin. Geogr. Sci. 2018, 28, 456–469. [Google Scholar] [CrossRef]
- Li, X.H.; Zhang, Q. Variation of Floods Characteristics and Their Responses to Climate and Human Activities in Poyang Lake, China. Chin. Geogr. Sci. 2015, 25, 13–25. [Google Scholar] [CrossRef]
- Li, X.H.; Ye, X.C. Spatiotemporal Characteristics of Dry-Wet Abrupt Transition Based on Precipitation in Poyang Lake Basin, China. Water 2015, 7, 1943–1958. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.Z.; Li, J.F.; Singh, V.P.; Wang, Z.Z. Topography-Based Spatial Patterns of Precipitation Extremes in the Poyang Lake Basin, China: Changing Properties and Causes. J. Hydrol. 2014, 512, 229–239. [Google Scholar] [CrossRef]
- Li, X.H.; Hu, Q. Spatiotemporal Changes in Extreme Precipitation and Its Dependence on Topography over the Poyang Lake Basin, China. Adv. Meteorol. 2019, 2019, 1253932. [Google Scholar] [CrossRef]
- Zhang, Q.A.; Liu, Y.; Yang, G.D.; Zhang, Z.X. Precipitation and Hydrological Variations and Related Associations with Large–Scale Circulation in the Poyang Lake Basin, China. Hydrol. Process 2011, 25, 740–751. [Google Scholar] [CrossRef]
- Guo, R.; Zhu, Y.; Liu, Y. A Comparison Study of Precipitation in the Poyang and the Dongting Lake Basins from 1960–2015. Sci. Rep. 2020, 10, 3381. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, Y.; Tang, C.; Zhang, C.; Zhang, C. Temporal and Spatial Variations of Extreme Precipitation Events in Flood Season of Jiangxi in Recent 52 years. Resour. Environ. Yangtze Basin 2013, 22, 1348–1355. [Google Scholar]
- Ding, Y.H.; Wang, Z.Y.; Sun, Y. Inter-Decadal Variation of the Summer Precipitation in East China and Its Association with Decreasing Asian Summer Monsoon. Part I: Observed Evidences. Int. J. Climatol. 2008, 28, 1139–1161. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Zhang, Z.X.; Chen, Y.Q.D.; Liu, C.L.; Lin, H. Spatial and Temporal Variability of Precipitation Maxima During 1960–2005 in the Yangtze River Basin and Possible Association with Large–Scale Circulation. J. Hydrol. 2008, 353, 215–227. [Google Scholar] [CrossRef]
- Xiao, M.Z.; Zhang, Q.; Singh, V.P. Influences of Enso, Nao, Iod and Pdo on Seasonal Precipitation Regimes in the Yangtze River Basin, China. Int. J. Climatol. 2015, 35, 3556–3567. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.L.; Lu, J.Z.; Fu, X.K.; Zhang, Y.F.; Liang, D.; Xu, Q.Q. Precipitation Projections Using a Spatiotemporally Distributed Method: A Case Study in the Poyang Lake Watershed Based on the Mri–Cgcm3. Hydrol. Earth Syst. Sci. 2019, 23, 1649–1666. [Google Scholar] [CrossRef]
- Xiao, M.Z. Quantifying Spatiotemporal Influences of Climate Index on Seasonal Extreme Precipitation Based on Hierarchical Bayesian Method. Int. J. Climatol. 2019, 40, 3087–3098. [Google Scholar] [CrossRef]
- Wei, J.; Knoche, H.R.; Kunstmann, H. Atmospheric Residence Times from Transpiration and Evaporation to Precipitation: An Age-Weighted Regional Evaporation Tagging Approach. J. Geophys. Res.-Atmos. 2016, 121, 6841–6862. [Google Scholar] [CrossRef]
- Dong, N.; Yu, Z.; Gu, H.; Yang, C.; Yang, M.; Wei, J.; Wang, H.; Arnault, J.; Laux, P.; Kunstmann, H. Climate-Induced Hydrological Impact Mitigated by a High-Density Reservoir Network in the Poyang Lake Basin. J. Hydrol. 2019, 579, 124148. [Google Scholar] [CrossRef]
- Li, J.P.; Zeng, Q.C. A Unified Monsoon Index. Geophys. Res. Lett. 2002, 29, 115-1–115-4. [Google Scholar] [CrossRef]
- Li, J.P.; Zheng, Q.C. A New Monsoon Index and the Geographical Distribution of the Global Monsoons. Adv. Atmos. Sci. 2003, 20, 299–302. [Google Scholar] [CrossRef]
- Lorenz, E.N. Section of Planetary Sciences: The Predictability of Hydrodynamic Flow. Trans. N. Y. Acad. Sci. 2012, 25, 409–432. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling Errors in the Estimation of Empirical Orthogonal Functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Richman, M.B. Obliquely Rotated Principal Components—An Improved Meteorological Map Typing Technique. J. Appl. Meteorol. 1981, 20, 1145–1159. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Rotation of Principal Components—Some Comments. J. Climatol. 1987, 7, 507–510. [Google Scholar] [CrossRef]
- Horel, J.D. A Rotated Principal Component Analysis of the Interannual Variability of the Northern Hemisphere 500 Mb Height Field. Mon. Weather Rev. 1981, 109, 2080–2092. [Google Scholar] [CrossRef]
- Govender, P.; Sivakumar, V. Application of K-Means and Hierarchical Clustering Techniques for Analysis of Air Pollution: A Review (1980–2019). Atmos. Pollut. Res. 2020, 11, 40–56. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes—A Graphical Aid to the Interpretation and Validation of Cluster–Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Lovmar, L.; Ahlford, A.; Jonsson, M.; Syvanen, A.C. Silhouette Scores for Assessment of Snp Genotype Clusters. Bmc Genom. 2005, 6, 35. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Unal, Y.S.; Deniz, A.; Toros, H.; Incecik, S. Temporal and Spatial Patterns of Precipitation Variability for Annual, Wet, and Dry Seasons in Turkey. Int. J. Climatol. 2012, 32, 392–405. [Google Scholar] [CrossRef]
- Ding, Y.H.; Sun, Y.; Wang, Z.Y.; Zhu, Y.X.; Song, Y.F. Inter-Decadal Variation of the Summer Precipitation in China and Its Association with Decreasing Asian Summer Monsoon Part Ii: Possible Causes. Int. J. Climatol. 2009, 29, 1926–1944. [Google Scholar] [CrossRef]
- Wei, F.Y.; Zhang, T. Oscillation Characteristics of Summer Precipitation in the Huaihe River Valley and Relevant Climate Background. Sci. China–Earth Sci. 2010, 53, 301–316. [Google Scholar] [CrossRef]
- Jiaxing, X.; Qiong, W.; Fengmin, M. Analysis on Precipitation Patterns During the Flood Season in Jiangxi Province from 1961 to 2017. Meteorol. Disaster Reduct. Res. 2018, 41, 161–167. [Google Scholar]
- Suqin, S.; Aihua, X.; Jing, Z.; Xiangxiang, C.; Fengmin, M. The Regionalization and Spatial–Temporal Characteristics of the Torrential–Rain in Jiangxi Province During the Flood Season. Meteorol. Disaster Reduct. Res. 2016, 39, 90–97. [Google Scholar]
- Gao, H.; Jiang, W.; Li, W.J. Changed Relationships between the East Asian Summer Monsoon Circulations and the Summer Rainfall in Eastern China. J. Meteorol. Res. 2014, 28, 1075–1084. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.Z.; Singh, V.P.; Wang, Y.Q. Spatiotemporal Variations of Temperature and Precipitation Extremes in the Poyang Lake Basin, China. Appl Clim. 2016, 124, 855–864. [Google Scholar] [CrossRef]
- Shao, J.; Wang, J.; Lv, S.Y.; Bing, J.P. Spatial and Temporal Variability of Seasonal Precipitation in Poyang Lake Basin and Possible Links with Climate Indices. Hydrol. Res. 2016, 47, 51–68. [Google Scholar] [CrossRef]
- Yang, H.; Sun, S.Q. Longitudinal Displacement of the Subtropical High in the Western Pacific in Summer and Its Influence. Adv. Atmos. Sci. 2003, 20, 921–933. [Google Scholar]
- Yuan, Y.; Yang, H.; Zhou, W.; Li, C.Y. Influences of the Indian Ocean Dipole on the Asian Summer Monsoon in the Following Year. Int. J. Climatol. 2008, 28, 1849–1859. [Google Scholar] [CrossRef]
- Liu, X.-f.; Yuan, H.-z.; Guan, Z.-y. Effects of Enso on the Relationship between Iod and Summer Rainfall in China. J. Trop. Meteorol. 2009, 15, 59–62. [Google Scholar] [CrossRef]
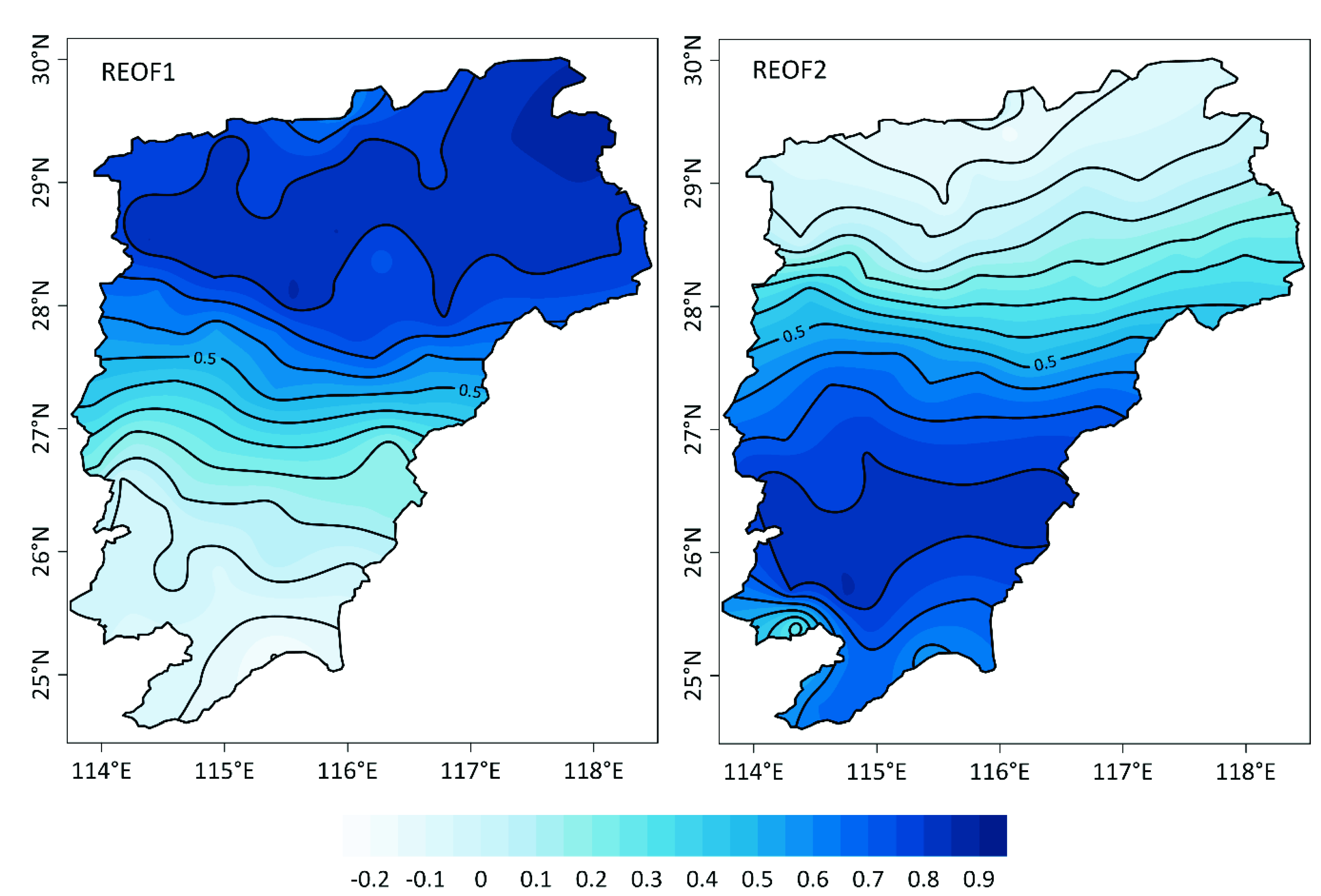


| Mode | EOF | REOF | ||
|---|---|---|---|---|
| Variance (%) | Cumulative Variance (%) | Variance (%) | Cumulative Variance (%) | |
| 1 | 45.4 | 45.4 | 38.8 | 38.8 |
| 2 | 19.1 | 64.5 | 25.7 | 64.5 |
| Name of Sub-Region | Number of Stations | Area of Sub-Regions/km2 | Percentage of Sub-Regions/% | Mean Summer Precipitation/mm |
|---|---|---|---|---|
| sub-region I | 38 | 75,157.5 | 47.3 | 587.8 |
| sub-region II | 17 | 33,331.1 | 21.0 | 543.5 |
| sub-region III | 22 | 50,461.7 | 31.7 | 533.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; He, H.; Fan, H.; Xu, L.; Jiang, J.; Jiang, M.; Xu, Y. Regional Characteristics of Long-Term Variability of Summer Precipitation in the Poyang Lake Basin and Possible Links with Large-Scale Circulations. Atmosphere 2020, 11, 1033. https://doi.org/10.3390/atmos11101033
Zhu H, He H, Fan H, Xu L, Jiang J, Jiang M, Xu Y. Regional Characteristics of Long-Term Variability of Summer Precipitation in the Poyang Lake Basin and Possible Links with Large-Scale Circulations. Atmosphere. 2020; 11(10):1033. https://doi.org/10.3390/atmos11101033
Chicago/Turabian StyleZhu, Hua, Handan He, Hongxiang Fan, Ligang Xu, Jiahu Jiang, Mingliang Jiang, and Yanxue Xu. 2020. "Regional Characteristics of Long-Term Variability of Summer Precipitation in the Poyang Lake Basin and Possible Links with Large-Scale Circulations" Atmosphere 11, no. 10: 1033. https://doi.org/10.3390/atmos11101033
APA StyleZhu, H., He, H., Fan, H., Xu, L., Jiang, J., Jiang, M., & Xu, Y. (2020). Regional Characteristics of Long-Term Variability of Summer Precipitation in the Poyang Lake Basin and Possible Links with Large-Scale Circulations. Atmosphere, 11(10), 1033. https://doi.org/10.3390/atmos11101033






