Monitoring and Modeling Roof-Level Wind Speed in a Changing City
Abstract
1. Introduction
- (a)
- In urban districts with low element height and density it may be possible to use a site where the ‘open country’ standard exposure guidelines can be met. To use the 10 m height the closest obstacles should be at least 10 times their height distant from the anemometer and not be more than about 6 m tall on average;
- (b)
- In more densely built-up districts, with relatively uniform element height and density (buildings and trees), wind speed and direction measurements should be made with the anemometer mounted on a mast of open construction at 10 m or 1.5 times the mean height of the elements, whichever is the greater;
- (c)
- In urban districts with scattered tall buildings the recommendations are as in (b) but with special concern to avoid the wake zone of the tall structures;
- (d)
- It is not recommended to measure wind speed or direction in densely built areas with multiple high-rise structures unless a very tall tower is used.
2. Experiments
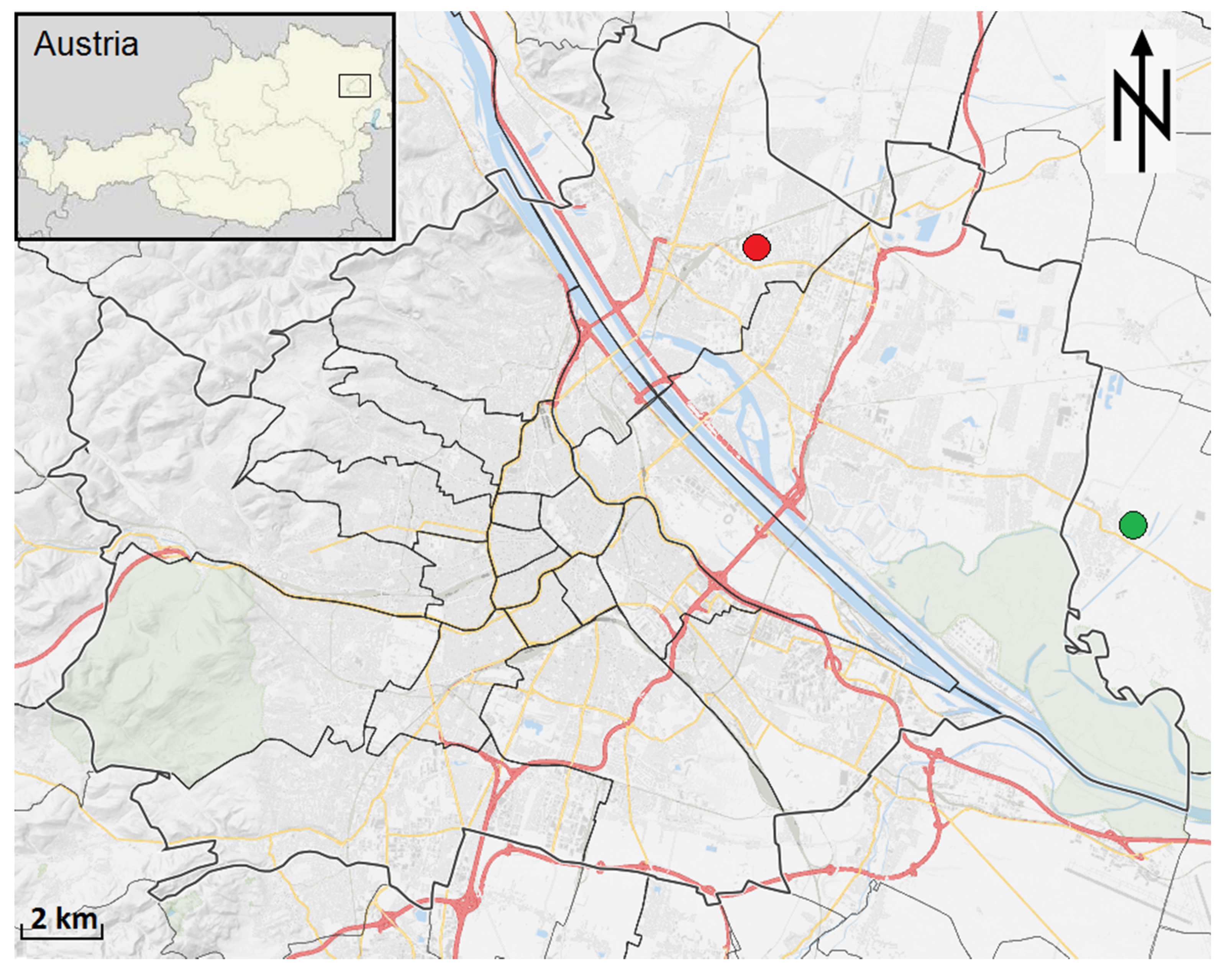
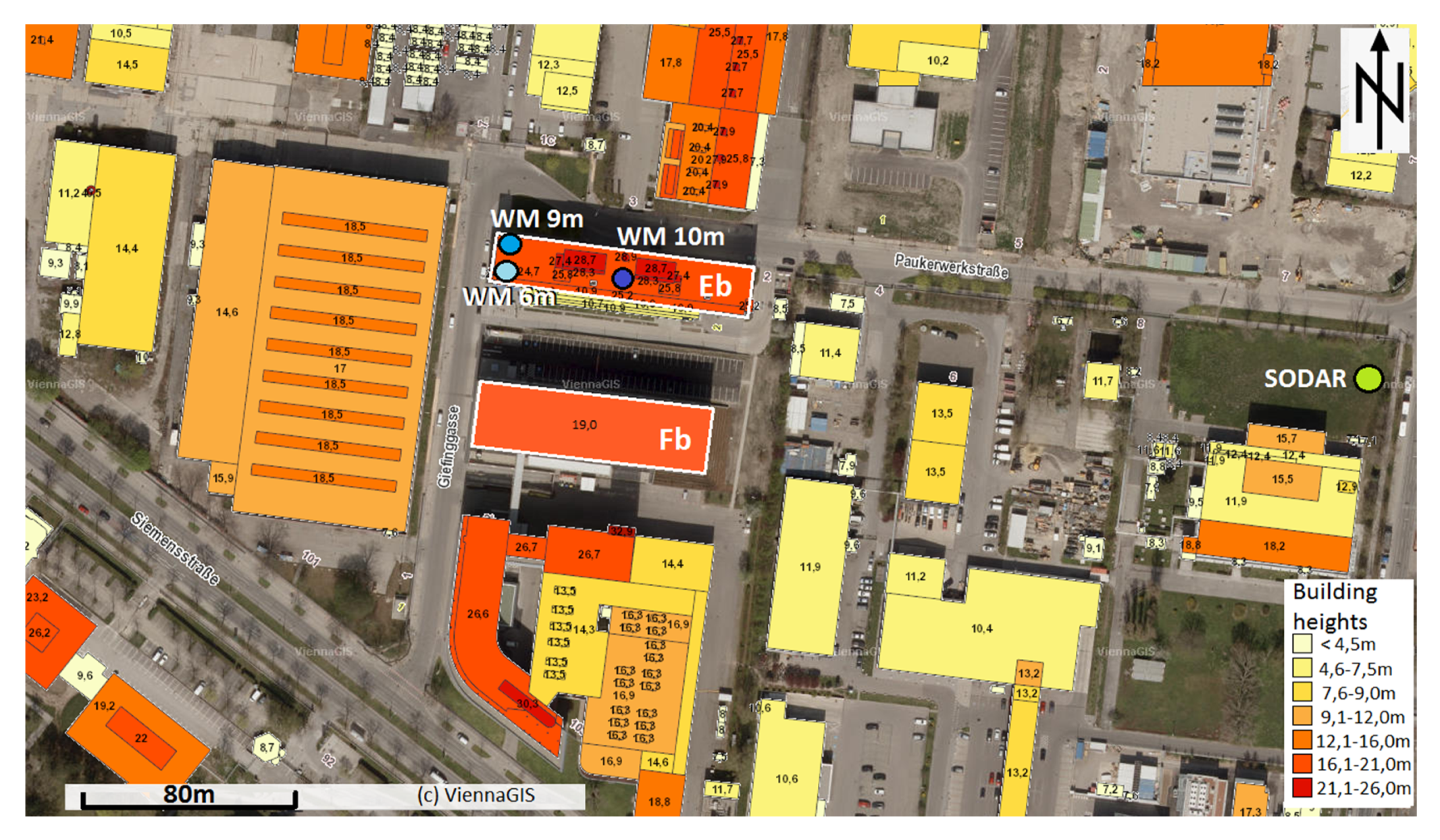
2.1. Measurements
2.2. Modeling
2.3. Scenarios
- Scenario A: no construction at the adjacent property (starting situation until December 2016);
- Scenario B: completed building (existing situation since June 2017, building height 19 m);
- Scenario C: a multi-store car park (comparable to the open building shell during construction in January to February 2017);
- Scenario D: north-west to south-east oriented buildings with 24 m height;
- Scenario E: north-west to south-east oriented buildings with 19 m height;
- Scenario F: buildings arranged at right angle to ENERGYbase (10 m distance between buildings);
- Scenario G: buildings arranged at right angle to ENERGYbase (15 m distance between buildings);
- Scenario H: buildings arranged at right angle to ENERGYbase (20 m distance between buildings);
- Scenario I: buildings arranged in parallel to ENERGYbase with 24 m height;
- Scenario J: buildings arranged in parallel to ENERGYbase, southerly buildings with 15 m height, northerly buildings with 19 m height.
3. Results
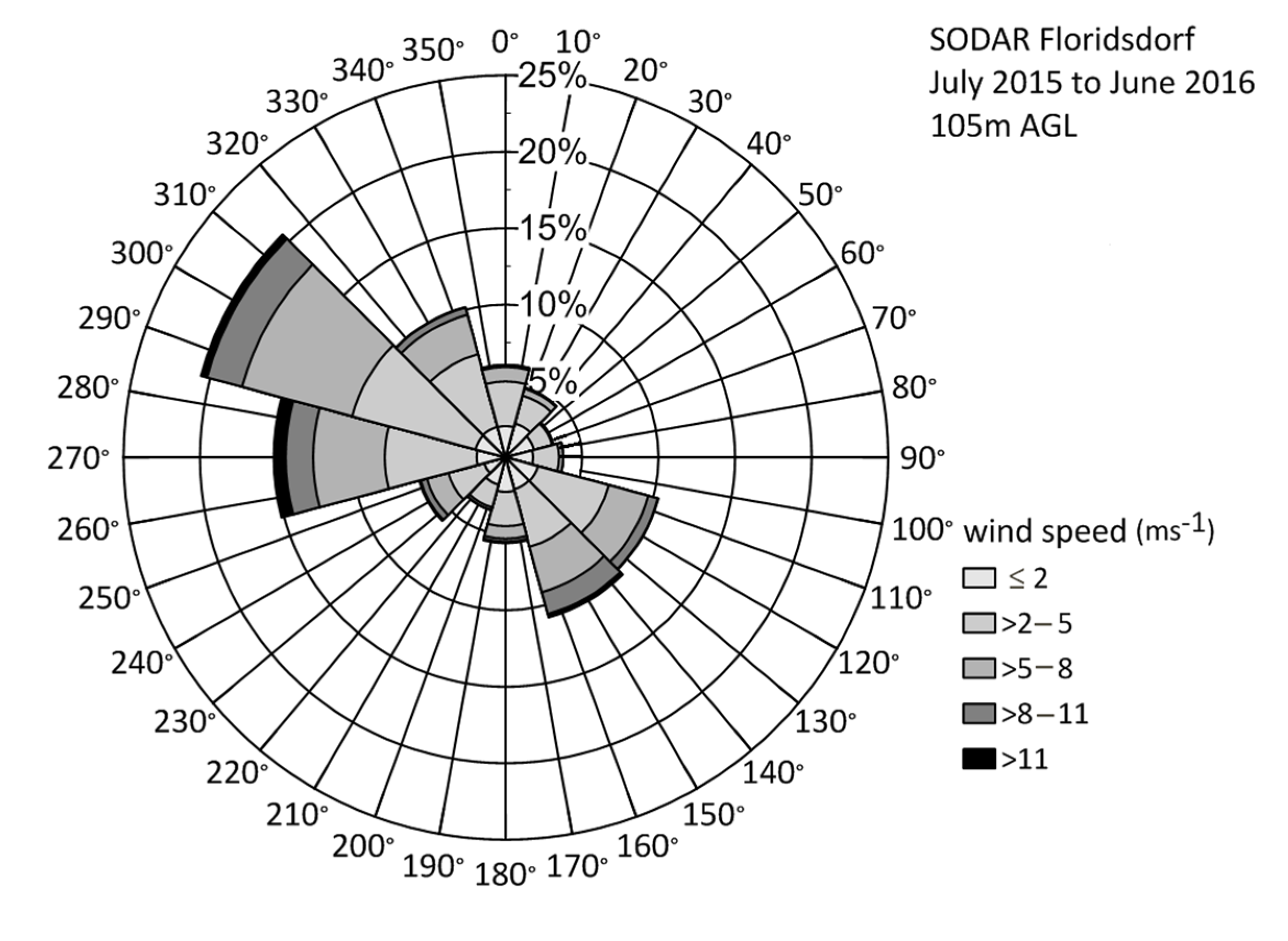
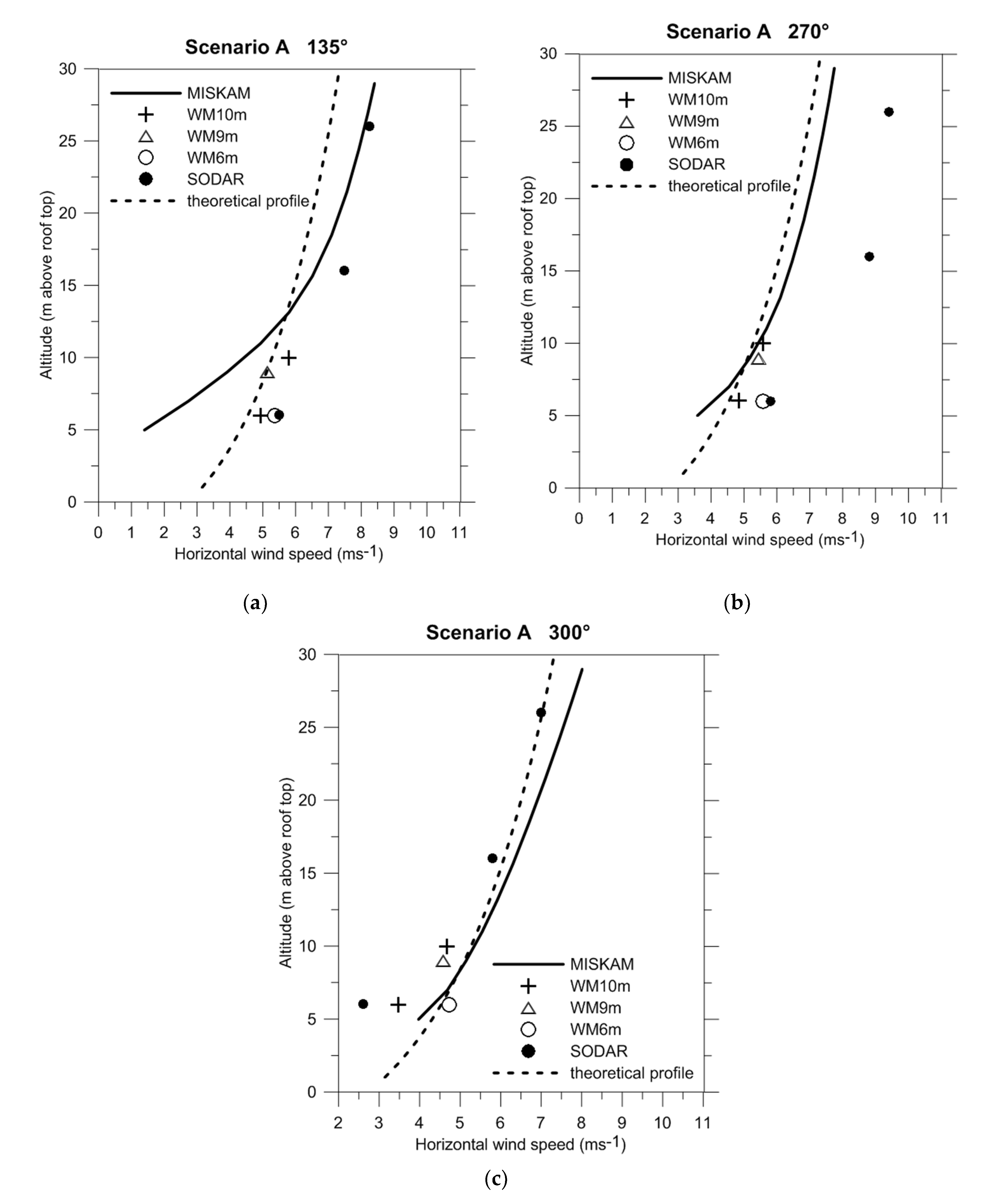
3.1. Measured and Simulated Vertical Wind Profiles within the UCL
3.2. Impact of Changes in Adjacent Building Structures on Wind Conditions at Roof Top
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Meteorological Organization. Initial Guidance to Obtain Representative Meteorological Observations at Urban Sites, Instruments and Observing Methods; Report No. 81, WMO/TD-No.1250; WMO: Geneva, Switzerland, 2006. [Google Scholar]
- Piringer, M.; Joffre, S. (Eds.) The Urban Surface Energy Budget and Mixing Height in EUROPEAN cities: Data, Models and Challenges for Urban Meteorology and Air Quality; Final Report of Working Group 2 of COST-715 Action; Demetra Ltd.: London, UK, 2005; 239p. [Google Scholar]
- Muller, C.; Chapman, L.; Grimmond, C.S.B.; Young, D.T.; Cai, X. Sensors and the City: A review of urban meteorological networks. Int. J. Climatol. 2013, 33, 1585–1600. [Google Scholar] [CrossRef]
- Rafailidis, S. Influence of Building Areal Density and Roof Shape on the Wind Characteristics Above a Town. Bound.-Layer Meteorol. 1997, 85, 255. [Google Scholar] [CrossRef]
- Britter, R.E.; Hanna, S.R. Flow and dispersion in urban areas. Annu. Rev. Fluid Mech. 2003, 35, 469–496. [Google Scholar] [CrossRef]
- Barlow, J.F. Progress in observing and modelling the urban boundary layer. Urban Clim. 2014, 10, 216–240. [Google Scholar] [CrossRef]
- Kastner-Klein, P.; Rotach, M. Mean flow and turbulence Characteristics in an urban roughness sublayer. Bound.-Layer Meteorol. 2004, 111, 55–84. [Google Scholar] [CrossRef]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban areas derived from analysis of urban form. J. Appl. Meteorol. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
- Davenport, A.G.; Grimmond, C.S.B.; Oke, T.R.; Wieringa, J. Estimating the roughness of cities and sheltered country. In Proceedings of the 12th Conference on Applied Climatology, Asheville, NC, USA, 8–11 May 2000; American Meteorological Society: Boston, MA, USA, 2000; pp. 96–99. [Google Scholar]
- Fisher, B.; Joffre, S.; Kukkonen, J.; Piringer, M.; Rotach, M.; Schatzmann, M. (Eds.) Final Report COST Action 715; Demetra Ltd.: London, UK, 2005; pp. 27–46. [Google Scholar]
- Rotach, M.; Batchvarova, E.; Berkowicz, R.; Brechler, J.; Janour, Z.; Karjny, E.; Georgieva, E.; Middleton, D.; Osrodka, L.; Prior, V.; et al. Modification of flow and turbulence structure over urban areas. In Meteorology Applied to Urban Air Pollution Problems; Demetra Ltd.: Sofia, Bulgaria, 2005; pp. 27–46. ISBN 954-9526-30-5. [Google Scholar]
- Hanna, S.; White, J.; Zhou, Y. Observed winds, turbulence, and dispersion in built-up downtown areas of Oklahoma City and Manhattan. Bound.-Layer Meteorol. 2007, 125, 441–468. [Google Scholar] [CrossRef]
- Wood, C.R.; Arnold, S.J.; Balogun, A.A.; Barlow, J.F.; Belcher, S.E.; Britter, R.E.; Cheng, H.; Dobre, A.; Lingard, J.J.N.; Martin, D.; et al. Dispersion Experiments in Central London: The 2007 DAPPLE Project. Bull. Am. Meteorol. Soc. 2009, 90, 955–969. [Google Scholar] [CrossRef]
- Schatzmann, M.; Leitl, B. Validation and application of obstacle-resolving urban dispersion models. Atmos. Environ. 2002, 36, 4811–4821. [Google Scholar] [CrossRef]
- Hertwig, D.; Efthimiou, G.C.; Bartzis, J.G.; Leitl, B. CFD-RANS model validation of turbulent flow in a semi-idealized urban canopy. J. Wind Eng. Ind. Aerodyn. 2012, 111, 61–72. [Google Scholar] [CrossRef]
- Hanna, S.; White, J.; Trolier, J.; Vernot, R.; Brown, M.; Gowardhan, A.; Kaplan, H.; Alexander, Y.; Moussafir, J.; Wang, Y.; et al. Comparisons of JU2003 observations with four diagnostic urban wind flow and Lagrangian particle dispersion models. Atmos. Environ. 2011, 45, 4073–4081. [Google Scholar] [CrossRef]
- Arnold, S.J.; ApSimon, H.; Barlow, J.; Belcher, S.; Bell, M.; Boddy, J.W.; Britter, R.; Cheng, H.; Clark, R.; Colville, R.N.; et al. Introduction to the DAPPLE Air Pollution Project. Sci. Total Environ. 2004, 332, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Dobre, A.; Arnold, S.J.; Smalley, R.J.; Boddy, J.W.D.; Barlow, J.F.; Tomlin, A.S.; Belcher, S.E. Flow field measurements in the proximity of an urban intersection in London, UK. Atmos. Environ. 2005, 39, 4647–4657. [Google Scholar] [CrossRef]
- Eichhorn, J.; Kniffka, A. The Numerical Flow Model MISKAM: State of Development and Evaluation of the Basic Version. Meteorol. Z. 2010, 19, 81–90. [Google Scholar] [CrossRef]
- Yee, E.; Biltoft, C.A. Concentration fluctuation measurements in a plume dispersing through a regular array of obstacles. Bound.-Layer Meteorol. 2004, 111, 363–415. [Google Scholar] [CrossRef]
- Eichhorn, J.; Balczo, M. Flow and dispersal simulations of the Mock Urban Setting Test. In Proceedings of the 12th International Conference on Harmonization within Atmospheric Dispersion Modelling for Regulatory Purposes (HARMO12), Cavtat, Croatia, 6–9 October 2008; pp. 67–72. [Google Scholar]
- Goricsán, I.; Balczó, M.; Czader, K.; Rákai, A.; Tonkó, C. Simulation of flow in an idealised city using various CFD codes. Int. J. Environ. Pollut. 2011, 44, 359. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B. The COST 732 Best Practice Guideline for CFD simulation of flows in the urban environment: A summary. Int. J. Environ. Pollut. 2011, 44, 419–427. [Google Scholar] [CrossRef]
- Britter, R.; Schatzmann, M. (Eds.) Model Evaluation Guidance and Protocol Document; COST Action 732 Quality Assurance and Improvemnet of Microscale Meteorological Models; COST Office: Brussels, Belgium, 2007; 27p, ISBN 3-00-018312-4. [Google Scholar]
- Sarkar, A.; Behera, D.K. Wind Turbine Blade Efficiency and Power Calculation with Electrical Analogy. Int. J. Sci. Res. Publ. 2012, 2, 1–5. [Google Scholar]
- Casini, M. Small Vertical Axis Wind Turbines for Energy Efficiency of Buildings. J. Clean Energy Technol. 2016, 4, 56–65. [Google Scholar] [CrossRef]


| Scenario | 120° | 150° | 270° | 300° | 330° |
|---|---|---|---|---|---|
| A | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| B | 1.02 | 0.95 | 0.97 | 0.92 | 0.93 |
| C | 0.98 | 0.78 | 0.96 | 0.92 | 0.94 |
| D | 0.80 | 0.53 | 0.99 | 0.95 | 0.94 |
| E | 0.81 | 0.71 | 0.96 | 0.91 | 0.91 |
| F | 0.78 | 0.92 | 1.00 | 0.97 | 0.97 |
| G | 0.81 | 0.90 | 0.96 | 0.91 | 0.92 |
| H | 0.74 | 0.90 | 0.95 | 0.91 | 0.92 |
| I | 0.98 | 0.73 | 0.96 | 0.93 | 0.91 |
| J | 1.02 | 0.94 | 0.97 | 0.91 | 0.93 |
| Scenario | 120° | 150° | 270° | 300° | 330° |
|---|---|---|---|---|---|
| A | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| B | 0.99 | 0.92 | 0.94 | 1.03 | 0.94 |
| C | 1.00 | 0.82 | 0.94 | 1.02 | 0.94 |
| D | 0.94 | 0.77 | 1.01 | 1.17 | 0.92 |
| E | 0.91 | 0.82 | 0.96 | 1.11 | 0.86 |
| F | 0.95 | 0.66 | 0.98 | 1.14 | 0.91 |
| G | 0.87 | 0.68 | 0.92 | 1.10 | 0.91 |
| H | 0.81 | 0.75 | 0.92 | 1.11 | 0.90 |
| I | 0.98 | 0.82 | 0.94 | 1.06 | 0.89 |
| J | 1.00 | 0.97 | 0.95 | 1.03 | 0.90 |
| Scenario A | Scenario B | Scenario C | |
|---|---|---|---|
| December 2015–December 2016 | June 2017–October 2017 | January 2017–February 2017 | |
| Mean Wind Speed (m s−1) | |||
| 6 m (WM6m) | 3.0 | 3.2 | 3.2 |
| 9 m (WM9m) | 3.2 | 3.4 | 3.4 |
| 10 m (WM10m) | 3.3 | 3.5 | 3.6 |
| 10 m AGL rural | 3.2 | 3.1 | 3.5 |
| Fraction Factor | |||
| 6 m WM6m) | 0.94 | 1.02 | 0.92 |
| 9 m (WM9m) | 0.99 | 1.08 | 0.96 |
| 10 m (WM10m) | 1.03 | 1.11 | 1.02 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baumann-Stanzer, K.; Stenzel, S.; Rau, G.; Piringer, M.; Feichtinger, F.; Costabloz, T. Monitoring and Modeling Roof-Level Wind Speed in a Changing City. Atmosphere 2020, 11, 87. https://doi.org/10.3390/atmos11010087
Baumann-Stanzer K, Stenzel S, Rau G, Piringer M, Feichtinger F, Costabloz T. Monitoring and Modeling Roof-Level Wind Speed in a Changing City. Atmosphere. 2020; 11(1):87. https://doi.org/10.3390/atmos11010087
Chicago/Turabian StyleBaumann-Stanzer, Kathrin, Sirma Stenzel, Gabriele Rau, Martin Piringer, Felix Feichtinger, and Théophane Costabloz. 2020. "Monitoring and Modeling Roof-Level Wind Speed in a Changing City" Atmosphere 11, no. 1: 87. https://doi.org/10.3390/atmos11010087
APA StyleBaumann-Stanzer, K., Stenzel, S., Rau, G., Piringer, M., Feichtinger, F., & Costabloz, T. (2020). Monitoring and Modeling Roof-Level Wind Speed in a Changing City. Atmosphere, 11(1), 87. https://doi.org/10.3390/atmos11010087





