Abstract
As atmospheric fresh soot particles age, they become coated with other chemical species. This transforms their physicochemical properties and affects their optical characteristics, which is of great importance to air quality, the environment and climate change. One of the predominantly occurring states of soot particles in the ambient environment is the core-shell mixing state. In this study, we used the core-shell model to calculate the optical absorption, scattering and extinction efficiency, absorption proportion and absorption exponent of coated soot particles. We then investigated the effects of different core sizes (D0), incident wavelengths (λ), coating materials and coating thicknesses on these optical characteristics. Absorption efficiency and absorption proportion of soot particles decreased as the coating became thicker, at core sizes of D0 = 20, 50 and 100 nm and λ = 405, 532 and 781 nm, regardless of the type of coating material. As the coating thickness increased, the absorption exponent (β) of inorganic-coated soot particles tended to rise and then fall, while the β value of organic-coated soot particles kept increasing. Our results advance our scientific understanding of the interaction of optical properties with chemical composition, mixing state, and aging processes of soot particles in the atmosphere.
1. Introduction
Fresh soot particles can be as seed particles in the atmospheric aging process, where these secondary species from complex photochemical reactions with volatile organic compounds (VOCs), SO2, and NOx can be coated onto soot particles depending on the aging conditions [1,2]. Previous studies have demonstrated that the optical absorption of soot particles can increase after being coated with organic species [3,4]. For example, Cui et al. (2016) found that the aerosol light absorption at 678 nm increased by 30% after coating materials onto fresh soot particles [5]. Wang et al. (2014) measured the optical properties of atmospheric particles in Xi’an. They showed that the fraction of coated organic compounds onto soot particles increased significantly during heavily polluted periods, and that light absorption at 870 nm increased almost three times due to the coatings of internal mixed soot particles [6]. These studies indicate that coating materials can change the optical properties of soot particles during the chemical aging process and increase their light absorption at different wavelengths compared with fresh soot particles.
The absorption exponent (β) is a physical parameter that describes the absorption capacity of carbon-containing particles as a function of wavelength. Generally, the β value of carbon-containing particles rises as the amount of organic coating increases. Therefore, β can be used as an indicator of the degree of aging of soot particles. Previous studies related to the physical and chemical properties of soot aging processes focused primarily on particle morphology, effective density, light absorption and scattering properties at a specific wavelength. For example, strong absorptive species, such as soot particles, have optical absorption capacities within the ultraviolet-infrared spectrum [7], while the optical absorption capacity of weakly absorbing materials (e.g., brown carbon) is mainly concentrated at short wavelengths of violet. Soot particles with different internal mixing states also present different optical absorption properties [8]. A single-wavelength study can obtain the absorption and scattering properties of particles at a specific wavelength, while multiple wavelengths provide more in-depth information about the interaction between optical properties, mixed state and chemical composition of soot particles.
Besides to experimental measurement, modelling of the optical properties of soot particle aging process has also been performed under a variety of conditions previously. For example, Cheng et al. (2014) investigated the effects of atmospheric water on the optical properties of soot aerosols using a superposition T-matrix method under three different mixing states in the spectral range of 400–1020 nm [9]. They found that different mixing states with atmospheric water (e.g., externally mixed, semi-embedded mixed, and internally mixed) were responsible for the significant changes in the optical properties of soot aerosols. More recently, Doner et al. (2017) modelled the impact of necking and overlapping on the radiative properties of coated soot aggregates by using the Discrete Dipole Approximation (DDA) method [10]. They found that the calculated extinction, absorption, and scattering properties increased as overlapping and necking increased at four different wavelengths in the visible and near-infrared.
It has been well understood that the morphology of freshly emitted soot particles can be described as aggregates or chain-like structure, which consisted of hundreds of spherical primary particles with a certain degree of overlapping and necking between neighboring primary particles [11,12]. In some applications, coated soot aggregates are simply assumed to be single core-shell spheres and are calculated using the Mie method [13,14]. The basic assumption of the core-shell model is to approximate the soot particle as a concentric core-shell system or a homogeneous sphere. It should be noted that the core-shell model might be oversimplified and could lead to some inaccurate results in some conditions. For example, Liu et al., (2016) found that the core-shell model significantly overestimates the absorption enhancement by coating in the visible and the near-infrared compared to the Discrete Dipole Approximation (DDA) results of the coated soot particle [15]. Despite this, most climate models still employ the Mie method to calculate the radiative properties of coated soot particles primarily due to the simplicity of such treatments [11,16].
The core-shell mixing state (fresh soot as the core) is one of the predominantly occurring states of soot particles in the atmosphere [17]. In this study, we used the core-shell theory model to simulate the optical properties of soot particles under different atmospheric aging conditions. The variation pattern of optical efficiency under various conditions is also discussed. We also investigated the effects of different coating materials, core size and coating thickness on absorption proportion and absorption exponent of soot particles. Together, our results provide a fundamental understanding of the interaction of optical properties with chemical composition, mixing state and aging processing of soot particles in the atmosphere.
2. Methods
2.1. The Core-Shell Model
The core-shell model, also known as the double-sphere model, assumes that the spherical core is insoluble and solid. Spherical coatings, such as inorganic or organic species, are assumed to be uniformly coated onto the core. As shown in Figure 1, the core diameter is D0, and the refractive index (RI) of the core is m1 = n1 − k1i. The diameter of the coated particle is Di, and the RI of the coating material is m2 = n2 − k2i. Note that n and k refer to the real and imaginary part of RI, and the above parameters are used as input for core-shell Mie calculation.
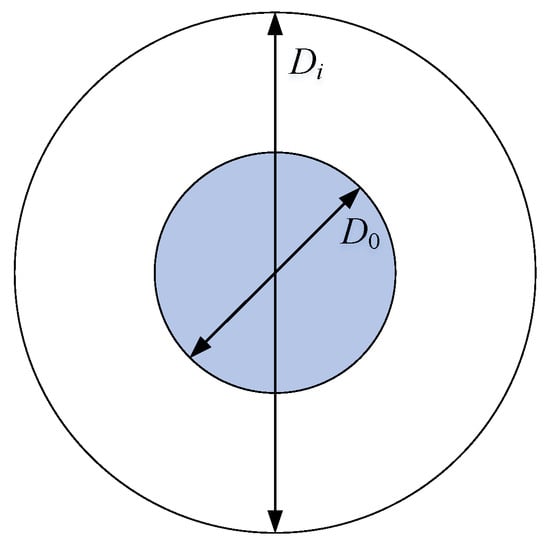
Figure 1.
Core-shell model showing diameter of the core (D0) and the coated particle (Di).
According to the forward-scattering theory [18], the extinction (Qext) and scattering (Qsca) efficiency of a double-layer sphere particle can be expressed as:
The coated particle size parameter (y) can be expressed as y = πDi/λ, where λ is the incident wavelength. The Mie coefficients of an and bn can be expressed as [18]:
In Equations (3) and (4), , and are Riccati–Bessel equations; and are spherical Bessel equations; and is the spherical Hankel equation.
, , and can be expressed as:
where x is the core size parameter with the expression of x = πD0/λ, m = m1/m2. The absorption efficiency Qabs can be expressed as:
In this study, the Mie calculations were conducted using the existing MATLAB (version 2016) code developed by Mätzler (2002) [19]. To verify our modelling results, we simulated the extinction cross-section (Cext) for a single water-coated soot sphere under different coating thickness and compared it with the modelling results from Liu et al., (2012) [20]. Specifically, the refractive indices of soot and water used in Liu et al., (2012) are msoot = 1.75 − 0.435i and mwater = 1.33 − 0i at incident wavelength of 628 nm, and the core diameter of soot (D0) is 30 nm [20]. Here, we extracted the DMiLay result of the first-panel Figure 2 from Liu et al., (2012), and a similar case was modelled using the same parameters as core-shell model input [20]. Note that coating thicknesses q in Liu et al., (2012) is converted to D0/Di for comparison, which is q = (Di − D0)/D0. The comparison result is shown in Figure S1, and both results were almost overlapped, which confirmed the reliability of the core-shell model used in this study to some extent.

Figure 2.
(a) Changes in absorption efficiency (Qabs), (b) scattering efficiency (Qsca) and (c) extinction efficiency (Qext) with soot particle core size D0 at λ = 405, 532 and 781 nm (without coating material).
2.2. The Derivation of Absorption Exponent β
According to the literature [21], the absorption cross-section of a carbon-containing aerosol particle in the atmosphere has the following relationship with wavelength:
In Equation (10), β is the particle absorption exponent, which is related to the particle size and its RI.
For a single particle at a specific incident wavelength (λ), the absorption cross-section Cabs,λ can be expressed as:
where D is the particle size, and Qabs,λ is the absorption efficiency at a given incident wavelength λ.
According to Equation (10), there is
According to Equation (11), the absorption cross-section (Cabs,λ) of a single particle at multiple wavelengths can be calculated by the core-shell model, and then the particle absorption exponent β can be obtained through the fitting of Equation (12). Figure S2 shows how the absorption cross-section of uncoated soot varies against the incident wavelength for a selected case, and the fitted parameter of absorption exponent (β) can be obtained.
3. Results and Discussion
Considering real atmospheric conditions, incident wavelengths of 405 nm (purple), 532 nm (green) and 781 nm (red) were selected in this study to cover the violet–infrared range, since the visible spectrum contains the major part of energy of the solar radiation. Also, according to the Mie theory, a particle scatters light more efficiently when the particle size and the incident wavelength are comparable. This means that the particle size range within accumulation mode is more efficient in scattering the solar radiation. Besides, these wavelengths are highly relevant to some commercial instruments for aerosol optical properties. For example, PASS-3 (three-wavelength photoacoustic soot spectrometer, Droplet Measurement Technologies Inc., CO 80503, USA) can measure aerosol light absorption at 405, 532 and 781 nm [22,23]. This is another reason for choosing these wavelengths, which might be helpful for comparison with experimental measurements in the future.
The organic aerosol, ammonium sulfate, water as well as sea salt were typically observed as coatings onto soot particle in the real atmosphere. They been extensively investigated using transmission electron microscopy (TEM) and numerically modelling method in the previous studies. For example, Adachi and Buseck (2008) found that more than half of all particles contained soot coated by organic matter and sulfates in plumes of Mexico City [24]. Adachi et al., (2014) further found that a large amount of soot particles were internally mixed with non-volatile ammonium sulfate or other materials at a remote mountain site in Japan [25]. Soot particle could also be coated with sea salt aerosol in the marine environment, as evidenced by the observed internal mixtures of NaCl with soot aggregates in the Aerosol Characterization Experiment-2 (ACE-2) over the North Atlantic Ocean [26]. Scarnato et al., (2013) further investigated the morphology and mixing state of bare BC and BC internally mixed with sodium chloride (NaCl) using electron microscopy and a discrete dipole approximation model [27].
In this study, four compositions (H2O, (NH4)2SO4, NaCl and weakly absorbing organic matter) were selected as the coating species of the soot particle to represent various aging conditions. The refractive indices of each material at different wavelengths are shown in Table 1. Note that the organic coating mentioned in this study has weak light-absorption property, which is generally similar to the “brown carbon”. Brown carbon is defined as a light-absorbing carbonaceous material, which can absorb solar radiation, especially at ultraviolet (UV) and shorter visible wavelengths, and contribute to the radiation balance and photochemical reactions in the atmosphere [28,29]. Note also that the RI value for brown carbon is of high uncertainty, and it may vary from different VOC precursors or oxidation conditions. For simplification, we used a set of fixed RI values at three wavelengths for organic aerosol in this study, which are experimentally derived from toluene/NOx chamber experiments [23].

Table 1.
Refractive index of core and coating material used for model calculation.
3.1. Absorption Efficiency Qabs
Figure 2a shows the absorption efficiency Qabs of uncoated soot at different incident wavelengths, which were calculated from the core-shell model. Regardless of the incident wavelength λ, Qabs increased sharply and then decreased slightly with the increase of core diameter D0.
Figure 3 shows the variation in Qabs with Di/D0 (an indicator of coating thickness) under different incident wavelengths (λ) and core sizes (D0). This represents the aging process of fresh soot particles with initial size of D0 under various coating materials. Note that the ranges of Di/D0 modelled in this study (1~10) is to cover a wide coating conditions, which is overall higher than that observed in some typical chamber experiments (e.g., 1~3 in the literature [4]). For an incident wavelength of 405 nm among different D0 shown in Figure 3a–c, Qabs of organic-coated soot was generally higher than the other three inorganic-coated soots, and the gap between both increased with an increase of Di/D0. This could be explained by the weak absorption effect (imaginary part of RI) of the organic coating. The absorption efficiency Qabs of (NH4)2SO4 and NaCl-coated soot particles were almost equivalent, but slightly higher than the water-coated soot particles as Di/D0 increased, particularly for higher core sizes of 50 and 100 nm.
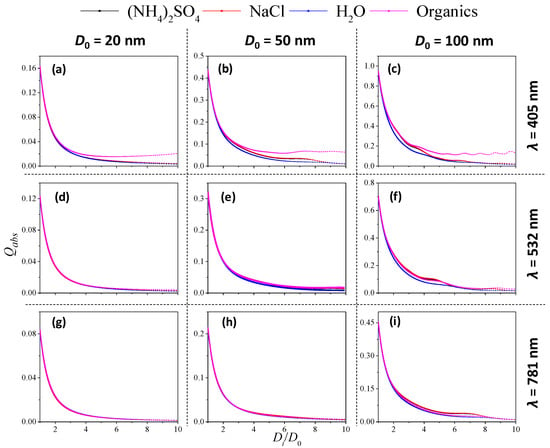
Figure 3.
Variation in absorption efficiency (Qabs) with coating thickness (Di/D0) for various soot-particle coated materials (λ = 405, 532 and 781 nm; soot particle core diameter D0 = 20, 50 and 100 nm). (a–c): (λ = 405 nm; soot particle core diameter D0 = 20, 50 and 100 nm); (d–f): (λ = 532 nm; soot particle core diameter D0 = 20, 50 and 100 nm); (g–i): (λ = 781 nm; soot particle core diameter D0 = 20, 50 and 100 nm).
Figure 3d–i show the variation of Qabs with Di/D0 at incident wavelengths of 532 and 781 nm, respectively. The decay curves of Qabs against Di/D0 almost overlapped for all coating materials; this feature was observed for all core sizes from 20 to 100 nm, suggesting that the coating composition is not sensitive to the absorption efficiency in green and red light. In addition, the absorption efficiency was reduced by more than 95% compared with the soot without coating (Di/D0 = 1).
The absorption cross-section of a single particle (under a selected incident light) is equal to the absorption efficiency multiplying the cross-sectional area, which is described in Equation (11). Although Figure 3 shows that the absorption efficiency decreased significantly as coating thickness increased for all cases, the absorption cross-section still greatly increased. Figure S3 shows a simple example in which the absorption cross-section increased greatly as the coating of the soot particle became thicker.
3.2. Scattering Efficiency Qsca and Extinction Efficiency Qext
Figure 2b,c shows the variation in Qsca and Qext of the uncoated soot particle with D0. At different incident wavelengths, and with an increase of core size, both Qsca and Qext increased sharply and then remained almost stable at the maximum value. Figure 4a–c shows the variation of Qsca against Di/D0 for different coating materials at an incident wavelength of 405 nm. For D0 = 20 nm, Qsca increased with the increase of Di/D0, and the larger real part of the RI of coated soot tended to show a larger scattering efficiency. For D0 = 50 nm, Qsca generally increased with the increase of Di/D0, and Qsca was significantly larger than that of D0 = 20 nm. For D0 = 100 nm, Qsca generally increased first and then decreased with the increase of Di/D0. After Qsca reached the maximum value, the variation of Qsca for different-coated soot was determined by both the RI and coating thickness. In addition, the larger real part of the coating RI tended to show a larger maximum value of Qsca.

Figure 4.
Variation in scattering efficiency (Qsca) with coating thickness (Di/D0) under various soot-particle coated materials (λ = 405, 532 and 781 nm; soot particle core diameter D0 = 20, 50 and 100 nm). (a–c): (λ = 405 nm; soot particle core diameter D0 = 20, 50 and 100 nm); (d–f): (λ = 532 nm; soot particle core diameter D0 = 20, 50 and 100 nm); (g–i): (λ = 781 nm; soot particle core diameter D0 = 20, 50 and 100 nm).
Figure 4d–i show the variation in Qsca with Di/D0 for different-coated soot at λ = 532 and 781 nm, respectively, which displayed a generally similar variation pattern to that at λ = 405 nm. For a given core size (e.g., D0 = 20 nm), Qsca tended to show the highest value at a short incident wavelength of 405 nm, and lowest at a large incident wavelength of 781 nm, regardless of coating material and thickness. The same phenomenon was observed for core sizes of 50 nm and 100 nm.
Figure 5a,d,g show the variation pattern of Qext with Di/D0 for D0 = 20 nm at λ = 405, 532 and 781 nm. Generally, Qext decreased first to the minimum value, and then increased with the rise in Di/D0 for all incident wavelengths. The highest Qext value was observed for NaCl-coated soot, particularly at a large coating thickness (Di/D0 > 5), which is the highest real part of RI among the four coating components. Figure 5a,d,g also shows that the extinction efficiency of soot particles generally grew higher as the incident wavelength increased.
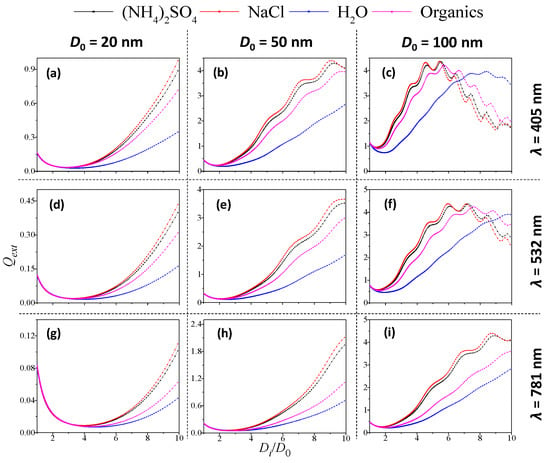
Figure 5.
Variation in extinction efficiency (Qext) with coating thickness (Di/D0) under various soot-particle coated materials (λ = 405, 532 and 781 nm; D0 = 20, 50 and 100 nm). (a–c): (λ = 405 nm; soot particle core diameter D0 = 20, 50 and 100 nm); (d–f): (λ = 532 nm; soot particle core diameter D0 = 20, 50 and 100 nm); (g–i): (λ = 781 nm; soot particle core diameter D0 = 20, 50 and 100 nm).
Figure 5b,c,e,f,h,i show the variation in Qext with Di/D0 for different-coated soot at D0 = 50 and 100 nm, respectively. The Qext values for almost all cases decreased slightly and then greatly increased as Di/D0 grew. Figure 5c,f shows two specific cases for D0 = 100 nm at incident wavelengths of 405 and 781 nm, where the Qext values increased to maximum and then fell. Except for these two cases, the Qext values showed a similar variation pattern for all the remaining cases, similar as observed for D0 = 20 nm. In addition, when the four coating materials were compared, the real part of coating RI determined the Qext level for the coated soot particle and followed the order of NaCl > (NH4)2SO4 > organic > H2O, regardless of core size or incident wavelength.
3.3. Absorption Proportion η of Soot Particles
The absorption proportion η of a soot particle is used as an indicator for the capacity of aerosol light absorption, which is defined as:
Figure 6 shows the variation in the absorption proportion of uncoated soot with a core size D0. As D0 increased, the trend of η decreased continuously: The smaller the incident wavelength, the faster the decay rate of η. In other words, when the uncoated soot particle was at a given size, large incident wavelengths always showed a higher η value than did short incident wavelengths.
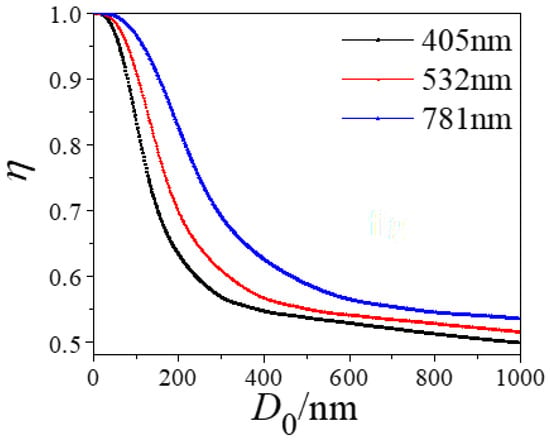
Figure 6.
Changes in absorption proportion η with core diameter D0 for uncoated soot particles under various incident wavelengths.
Figure 7 shows the variation of the η value with Di/D0 under different coating materials. The η values decreased as Di/D0 increased in almost all cases, regardless of core diameter, incident wavelength or coating material. In addition, for all conditions, the decay rate of η exhibited similar behaviour among the four coating materials, being the lowest for water-coated soot and the highest for inorganic-coated soot. This feature may be attributed to the difference in the real and imaginary parts of the RI.
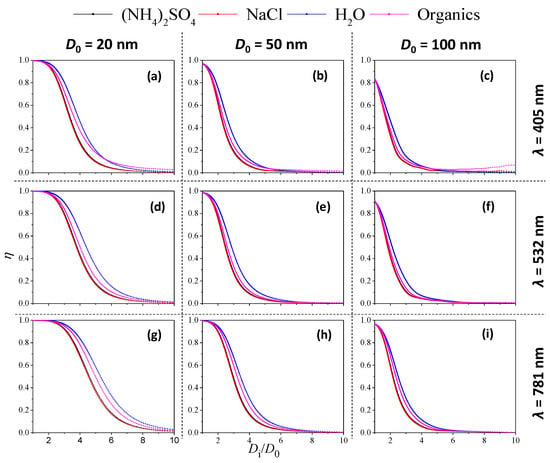
Figure 7.
Variation in absorption proportion η with coating thickness (Di/D0) under various soot-particle coated materials (λ = 405, 532 and 781 nm; soot particle diameter D0 = 20, 50 and 100 nm). (a–c): (λ = 405 nm; soot particle core diameter D0 = 20, 50 and 100 nm); (d–f): (λ = 532 nm; soot particle core diameter D0 = 20, 50 and 100 nm); (g–i): (λ = 781 nm; soot particle core diameter D0 = 20, 50 and 100 nm).
As summarized in Table 1, nsea salt > norganic > nwater, which indicates that scattering is enhanced more by inorganic coating material than by water coating. Therefore, for a given condition (fixed core diameter and incident wavelength), soot particles coated with stronger scattering material (i.e., higher n value of RI) will usually lead to a higher scattering proportion, which corresponds to a lower η value. In addition, there is a clear shift to faster rates of η decay as core diameter increases from 20 to 100 nm, regardless of incident wavelength and coating material. As core diameter increased, the η value approached zero at lower Di/D0.
To further investigate the relationship between η and Di/D0, we performed a model sensitivity test by changing the real and imaginary part of RI for the coating material. Here, we take a core diameter of 50 nm at incident wavelength of 405 nm as an example. Figure 8 shows the variations in η values against Di/D0, with RI values of 1.467 − 0.3i, 1.467 − 0.03i, 1.467 − 0.003i and 1.33 − 0i, respectively. In all cases, the absorption proportion of soot decreased with the increase of Di/D0, approaching a stable level at higher coating thicknesses (e.g., Di/D0 > 6). When the real parts of the RI of the coating material were held at 1.467, η decay slowed under the scenario of a higher imaginary part of RI, which is associated with a higher η value. For example, when the imaginary parts of RI are 0.003, 0.03 and 0.3, the η values at Di/D0 > 6 are ~0.02, ~0.15 and ~0.5, respectively. This behavior is reasonable, because absorption will take a dominant role as coating thickness increases, particularly for coating components with a higher imaginary part of RI.
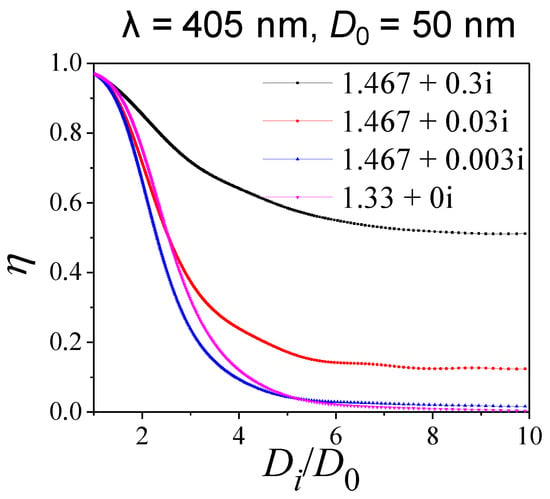
Figure 8.
The changes in absorption proportion η with coating thickness (Di/D0) for various refractive indices of coating material.
3.4. Absorption Exponent β
The absorption exponent β can describe the variation in absorption capacity with wavelength, which can indicate the aging degree of soot particles. Previous studies have shown that the β value of fresh soot ranges from 0.8 to 1.2. Figure S4 shows the relationship between β and D0 of uncoated soot; the β value first increases and then decreases, and the maximum value is 1.14 at D0 of 82 nm. A minimum value of ~0.8 is obtained at a D0 of 160 nm, which is consistent with the descriptions in the literature [34,35].
Figure 9a–c shows the variation of β with Di/D0 at D0 of 30, 40 and 50 nm. Overall, for organic-coated soot particles, β kept increasing as the coating became thicker. However, for inorganic-coated soot, the β value first increased and then decreased as coating thickness increased. This was observed for different D0 values of 30, 40 and 50 nm. For a given core size (D0) and coating thickness (Di/D0), the β value of different coating materials followed the order: organic > NaCl > (NH4)2SO4 > H2O, which may be due to the difference in the real part of the RI.
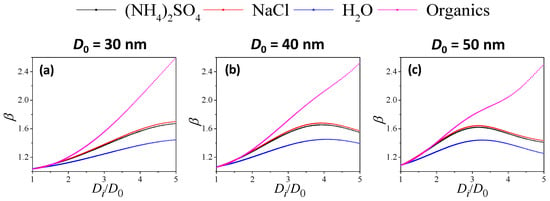
Figure 9.
Variation in absorption exponent β of coated soot particles with coating thickness (Di/D0) for different coating materials ((a–c): core size D0 at 30, 40, 50 nm).
Vehicle emissions are an important consideration for urban air pollution, particularly for diesel cars, as they emit soot particles as well as NOx and VOCs, which will contribute to the formation of secondary organic aerosol coating on fresh soot particles under sunlight [36,37]. From this perspective, we further investigate the variation in β with Di/D0 under organic coating conditions. Figure 10 shows the relationship between β and Di/D0 with D0 of 30, 40 and 50 nm. A linear fitting describing the relationship between β and Di/D0 within core size 30~50 nm is:

Figure 10.
Relationship of absorption exponent β with coating thickness (Di/D0) for organic-coated soot particles (core size D0 at 30, 40, 50 nm).
Within a certain amount of estimation error, the relationship between the absorption exponent β of organic-coated soot and Di/D0 can be approximately parameterized by the Equation (14). This is helpful for predicting soot aging degree under similar scenarios when direct measurement of β is not available. However, it should be qualified more explicitly in the future work, as it depends strongly on the RI of the organic coating.
4. Conclusions
In this work, we used a core-shell model to simulate the optical properties of double-layer spherical soot particles coated with H2O, (NH4)2SO4, NaCl and organic species under different aging conditions. Incident wavelengths of 405, 532 and 781 nm covering ultraviolet-infrared range were selected for model calculation. We investigated the variation in absorption efficiency (Qabs), scattering efficiency (Qsca), extinction efficiency (Qext), absorption proportion (η) and absorption exponent (β) with changes in core size (D0), coating materials, coating thickness (Di/D0) and incident wavelengths (λ). Our conclusions are as follows:
In uncoated conditions as D0 increases, both Qabs and Qext increase sharply and then slightly decrease, while Qsca increases sharply and then stabilizes, regardless of incident wavelengths. In coated conditions as Di/D0 increases, Qabs decreases while Qext generally increases. The type of coating materials, incident wavelengths and core size affect optical efficiency. For example, when the incident wavelength and core size are fixed, the Qsca level of coated soot particles rises as the real part of the refractive index (RI) of the coating increases.
The η of coated soot falls as Di/D0 increases for all core sizes, incident wavelengths and coating materials studied. The η value of the coated soot is mainly controlled by the coating thickness, as well as the real and imaginary parts of the coating species’ RI. For example, when the organic coating is thin, η increases along with a rise in the real part of the RI of the organic coating. However, as the organic coating becomes thicker, the imaginary part of the RI of the organic coating leads to an increase in η.
The β value of soot is also influenced by particle size and RI of the coating material. For soot particles coated with inorganic material, β first increases and then decreases as Di/D0 rises, and coated soot particles with a larger real part of RI tends to show a higher β value. For soot particles coated with organic material, the β value keeps rising as the coating becomes thicker. For organic-coated soot particles with a core size of 30–50 nm, we have determined the relationship between β and Di/D0. This could be used to predict the degree of soot aging, particularly for diesel emissions, in which fresh soot particles are commonly mixed with organic aerosol.
Finally, our results provide some insights into the optical properties of soot-particle aging process. However, it is worth noting that there are still some limitations of this work, as the soot particle aging process was only modelled by a classic core-shell model for a few selected conditions. For future work, it is suggested to apply some advanced models (e.g., Discrete Dipole Approximation (DDA), Rayleigh Debye Gans (RDG) theory, etc.) and compare with the results from core-shell model. This could provide more insights on the scope of application of core-shell model. Besides, the core-shell model should be evaluated against experimental results, particularly from these well-designed and heavily-equipped smog chamber experiments, which could constrain the limitation of the core-shell model and provide more in-depth understanding on aerosol optical properties.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/11/1/86/s1, Figure S1: Changes of extinction cross-section (Cext) with D0/Di for water-coated soot. The refractive indexes of soot and water are msoot = 1.75 − 0.435i and mwater = 1.33 − 0i at wavelength 628 nm. The soot core diameter D0 = 30 nm. The core-shell model result is compared to the data extracted from Figure 2 in Liu et al., (2012), Figure S2: Changes in absorption cross-section Cabs,λ with λ for fresh soot particles under selected conditions (D0 = 30 nm, λ = 405, 532 and 781 nm). This fitting curve shows an example for deriving the absorption exponent β using the core-shell model, Figure S3: Changes in absorption cross-section Cabs,λ with coating thickness (Di/D0) for coated soot particles under selected conditions (D0 = 20 nm, λ = 405 nm, coated by (NH4)2SO4), Figure S4: Variation in absorption exponent β against core diameter (D0) for fresh soot particles without coating material.
Author Contributions
Conceptualization, K.L. and M.Y.; formal analysis, K.L., M.Y. and C.G.; methodology, M.Y. and X.Z.; project administration, K.L. and M.Y.; resources, K.L. and M.Y.; supervision, K.L.; writing—original draft, K.L.; writing—review & editing, K.L., M.Y., J.S., C.G., W.Y. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
There is no financial funding for this work.
Acknowledgments
We would like to thank Hai Yu and Kathryn A. Kovac for the support of technical editing of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo, S.; Hu, M.; Lin, Y.; Gomez-Hernandez, M.; Zamora, M.L.; Peng, J.; Collins, D.R.; Zhang, R. OH-initiated oxidation of m-xylene on black carbon aging. Environ. Sci. Technol. 2016, 50, 8605–8612. [Google Scholar] [CrossRef] [PubMed]
- Schnitzler, E.G.; Dutt, A.; Charbonneau, A.M.; Olfert, J.S.; Jäger, W. Soot aggregate restructuring due to coatings of secondary organic aerosol derived from aromatic precursors. Environ. Sci. Technol. 2014, 48, 14309–14316. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, J.P.; Spackman, J.R.; Fahey, D.W.; Gao, R.S.; Lohmann, U.; Stier, P.; Watts, L.A.; Thomson, D.S.; Lack, D.A.; Pfister, L. Coatings and their enhancement of black carbon light absorption in the tropical atmosphere. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Peng, J.; Hu, M.; Guo, S.; Du, Z.; Zheng, J.; Shang, D.; Levy Zamora, M.; Zeng, L.; Shao, M.; Wu, Y.; et al. Markedly enhanced absorption and direct radiative forcing of black carbon under polluted urban environments. Proc. Natl. Acad. Sci. USA 2016, 113, 4266–4271. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Wang, X.; Yang, L.; Chen, B.; Chen, J.; Andersson, A.; Gustafsson, Ö. Radiative absorption enhancement from coatings on black carbon aerosols. Sci. Total Environ. 2016, 551, 51–56. [Google Scholar] [CrossRef]
- Wang, Q.; Huang, R.; Cao, J.; Han, Y.; Wang, G.; Li, G.; Wang, Y.; Dai, W.; Zhang, R.; Zhou, Y. Mixing state of black carbon aerosol in a heavily polluted urban area of China: Implications for light absorption enhancement. Aerosol Sci. Technol. 2014, 48, 689–697. [Google Scholar] [CrossRef]
- Bond, T.C.; Bergstrom, R.W. Light absorption by carbonaceous particles: An investigative review. Aerosol Sci. Technol. 2006, 40, 27–67. [Google Scholar] [CrossRef]
- Lack, D.A.; Langridge, J.M.; Bahreini, R.; Cappa, C.D.; Middlebrook, A.M.; Schwarz, J.P. Brown carbon and internal mixing in biomass burning particles. Proc. Natl. Acad. Sci. USA 2012, 109, 14802–14807. [Google Scholar] [CrossRef]
- Cheng, T.; Gu, X.; Wu, Y.; Chen, H. Effects of atmospheric water on the optical properties of soot aerosols with different mixing states. J. Quant. Spectrosc. Radiat. Transf. 2014, 147, 196–206. [Google Scholar] [CrossRef]
- Doner, N.; Liu, F.; Yon, J. Impact of necking and overlapping on radiative properties of coated soot aggregates. Aerosol Sci. Technol. 2017, 51, 532–542. [Google Scholar] [CrossRef]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- Li, W.; Shao, L.; Zhang, D.; Ro, C.; Hu, M.; Bi, X.; Geng, H.; Matsuki, A.; Niu, H.; Chen, J. A review of single aerosol particle studies in the atmosphere of East Asia: Morphology, mixing state, source, and heterogeneous reactions. J. Clean. Prod. 2016, 112, 1330–1349. [Google Scholar] [CrossRef]
- Shiraiwa, M.; Kondo, Y.; Iwamoto, T.; Kita, K. Amplification of Light Absorption of Black Carbon by Organic Coating. Aerosol Sci. Technol. 2010, 44, 46–54. [Google Scholar] [CrossRef]
- Abo Riziq, A.; Trainic, M.; Erlick, C.; Segre, E.; Rudich, Y. Extinction efficiencies of coated absorbing aerosols measured by cavity ring down aerosol spectrometry. Atmos. Chem. Phys. 2008, 8, 1823–1833. [Google Scholar] [CrossRef]
- Liu, F.; Yon, J.; Bescond, A. On the radiative properties of soot aggregates—Part 2: Effects of coating. J. Quant. Spectrosc. Radiat. Transf. 2016, 172, 134–145. [Google Scholar] [CrossRef]
- Bauer, S.E.; Menon, S.; Koch, D.; Bond, T.C.; Tsigaridis, K. A global modeling study on carbonaceous aerosol microphysical characteristics and radiative effects. Atmos. Chem. Phys. 2010, 10, 7439–7456. [Google Scholar] [CrossRef]
- Riemer, N.; Vogel, H.; Vogel, B. Soot aging time scales in polluted regions during day and night. Atmos. Chem. Phys. 2004, 4, 1885–1893. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Mätzler, C. MATLAB Functions for Mie Scattering and Absorption, Version 2. IAP Res. Rep. 2002, 8, 9. [Google Scholar]
- Liu, C.; Panetta, R.L.; Yang, P. The Influence of Water Coating on the Optical Scattering Properties of Fractal Soot Aggregates. Aerosol Sci. Technol. 2012, 46, 31–43. [Google Scholar] [CrossRef]
- Massabò, D.; Caponi, L.; Bernardoni, V.; Bove, M.C.; Brotto, P.; Calzolai, G.; Cassola, F.; Chiari, M.; Fedi, M.E.; Fermo, P. Multi-wavelength optical determination of black and brown carbon in atmospheric aerosols. Atmos. Environ. 2015, 108, 1–12. [Google Scholar] [CrossRef]
- Guo, X.; Nakayama, T.; Yamada, H.; Inomata, S.; Tonokura, K.; Matsumi, Y. Measurement of the light absorbing properties of diesel exhaust particles using a three-wavelength photoacoustic spectrometer. Atmos. Environ. 2014, 94, 428–437. [Google Scholar] [CrossRef]
- Nakayama, T.; Sato, K.; Matsumi, Y.; Imamura, T.; Yamazaki, A.; Uchiyama, A. Wavelength and NOx dependent complex refractive index of SOAs generated from the photooxidation of toluene. Atmos. Chem. Phys. 2013, 13, 531–545. [Google Scholar] [CrossRef]
- Adachi, K.; Buseck, P.R. Internally mixed soot, sulfates, and organic matter in aerosol particles from Mexico City. Atmos. Chem. Phys. 2008, 8, 6469–6481. [Google Scholar] [CrossRef]
- Adachi, K.; Zaizen, Y.; Kajino, M.; Igarashi, Y. Mixing state of regionally transported soot particles and the coating effect on their size and shape at a mountain site in Japan. J. Geophys. Res. Atmos. 2014, 119, 5386–5396. [Google Scholar] [CrossRef]
- Li, J.; Anderson, J.; Buseck, P. TEM study of aerosol particles from clean and polluted marine boundary layers over the North Atlantic. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Scarnato, B.V.; Vahidinia, S.; Richard, D.T.; Kirchstetter, T.W. Effects of internal mixing and aggregate morphology on optical properties of black carbon using a discrete dipole approximation model. Atmos. Chem. Phys. 2013, 13, 5089–5101. [Google Scholar] [CrossRef]
- Andreae, M.O.; Gelencsér, A. Black carbon or brown carbon? The nature of light-absorbing carbonaceous aerosols. Atmos. Chem. Phys. 2006, 6, 3131–3148. [Google Scholar] [CrossRef]
- Alexander, D.T.; Crozier, P.A.; Anderson, J.R. Brown carbon spheres in East Asian outflow and their optical properties. Science 2008, 321, 833–836. [Google Scholar] [CrossRef]
- Smyth, K.C.; Shaddix, C.R. The elusive history of m ~= 1.57 − 0.56i for the refractive index of soot. Combust. Flame 1996, 107, 314–320. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, Y.; Sun, Y.; Gao, X.; Cen, K. Analysis of Absorption and Scattering Properties of Water Host Haze Droplet with Insoluble Solid Inclusion. Chin. J. Lasers 2015, 234–241. [Google Scholar] [CrossRef]
- Lang-Yona, N.; Abo-Riziq, A.; Erlick, C.; Segre, E.; Trainic, M.; Rudich, Y. Interaction of internally mixed aerosols with light. Phys. Chem. Chem. Phys. 2010, 12, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Bulatov, V.; Fisher, M.; Schechter, I. Aerosol analysis by cavity-ring-down laser spectroscopy. Anal. Chim. Acta 2002, 466, 1–9. [Google Scholar] [CrossRef]
- Kirchstetter, T.W.; Novakov, T.; Hobbs, P.V. Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Schnaiter, M.; Linke, C.; Möhler, O.; Naumann, K.H.; Saathoff, H.; Wagner, R.; Schurath, U.; Wehner, B. Absorption amplification of black carbon internally mixed with secondary organic aerosol. J. Geophys. Res. Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Liu, D.; Whitehead, J.; Alfarra, M.R.; Reyes-Villegas, E.; Spracklen, D.V.; Reddington, C.L.; Kong, S.; Williams, P.I.; Ting, Y.; Haslett, S. Black-carbon absorption enhancement in the atmosphere determined by particle mixing state. Nat. Geosci. 2017, 10, 184. [Google Scholar] [CrossRef]
- Li, K.; Chen, L.; Han, K.; Lv, B.; Bao, K.; Wu, X.; Gao, X.; Cen, K. Smog chamber study on aging of combustion soot in isoprene/SO2/NOx system: Changes of mass, size, effective density, morphology and mixing state. Atmos. Res. 2017, 184, 139–148. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).