Abstract
Climate change threatens the hydrological equilibrium with severe consequences for living beings. In that respect, considerable differences in drought features are expected, especially for mountain-Andean regions, which seem to be prone to climate change. Therefore, an urgent need for evaluation of such climate conditions arises; especially the effects at catchment scales, due to its implications over the hydrological services. However, to study future climate impacts at the catchment scale, the use of dynamically downscaled data in developing countries is a luxury due to the computational constraints. This study performed spatiotemporal future long-term projections of droughts in the upper part of the Paute River basin, located in the southern Andes of Ecuador. Using 10 km dynamically downscaled data from four global climate models, the standardized precipitation and evapotranspiration index (SPEI) index was used for drought characterization in the base period (1981–2005) and future period (2011–2070) for RCP 4.5 and RCP 8.5 of CMIP5 project. Fitting a generalized-extreme-value (GEV) distribution, the change ratio of the magnitude, duration, and severity between the future and present was evaluated for return periods 10, 50, and 100 years. The results show that magnitude and duration dramatically decrease in the near future for the climate scenarios under analysis; these features presented a declining effect from the near to the far future. Additionally, the severity shows a general increment with respect to the base period, which is intensified with longer return periods; however, the severity shows a decrement for specific areas in the far future of RCP 4.5 and near future of RCP 8.5. This research adds knowledge to the evaluation of droughts in complex terrain in tropical regions, where the representation of convection is the main limitation of global climate models (GCMs). The results provide useful information for decision-makers supporting mitigating measures in future decades.
1. Introduction
A drought is defined as the reduction of the amount of precipitation received in a region during a specific period [1,2,3]. Among natural threats, droughts are considered the most complex and the most expensive (due to the high social costs associated), but the least understood [4]. According to [2], droughts can be classified into four groups according to which part of the hydrological cycle is affected, e.g., meteorological drought, hydrological drought, agricultural drought, and socioeconomic drought [5,6,7], which can be characterized using drought indices with varying degrees of success. In addition to the spatiotemporal complexity of droughts, new trends in extreme climate events due to climatic change conditions are expected. Thus, the assessment of future drought projections at the basin scale, where several societal aspects are more vulnerable, is an urgent need for adequate water management and informed decisions.
In the 20th century, the average temperature on the planet’s surface increased [8,9]. Although future temperature increases are still uncertain, several studies with global climate models (GCMs) using the representative concentration pathways (RCP) converge on the conclusion that an increase of temperature is highly probable [10,11,12]. As a consequence, overall, the increasing evaporation will enhance the atmospheric humidity and precipitation [13]. These conditions reflect the mean state of the atmosphere on climate change (CC); however, the variation of extremes is even more critical. In addition, the atmospheric conditions may be controlled by other factors such as the concentration of aerosols, energy fluxes, and land-use change [14]. In turn, changes in the hydrological cycle in the present and in the future due to global warming is of great interest, especially those related to extreme events, i.e., droughts and floods [11,14,15]. Many aspects of droughts are expected to change, as the frequency, intensity, and duration of CC conditions increase [16]; thus, the use of indices is critical to the monitoring and forecasting of this phenomena.
Drought indices are indicators of environmental and hydro-meteorological variables related to a phenomenon (for example, precipitation, flow, frost, and evapotranspiration, among others) [17]. Several drought indices have been developed in the last decades [1]. Among others, the Palmer severity index (PDSI) [18], crop moisture index (CMI) [19], rain anomaly index (RAI) [20], standardized precipitation index (SPI) [21,22], standardized streamflow index (SSI) [23], and standardized precipitation and evapotranspiration index (SPEI) [24,25], can help to characterize droughts both spatially and temporally, despite some limitations [1].
These indices have been used in different parts of the world to characterize past droughts, as well as to forecast and characterize future droughts on different spatiotemporal scales. For instance, SPI [26,27,28], SSI [28,29,30,31], SPEI [32,33,34], CMI [35,36,37], and Palmer [38,39,40] have been used extensively worldwide. These indices use different hydrometeorological variables as inputs, e.g., SPI and RAI use only precipitation data; SSI uses flow data; SPEI uses precipitation and ETo; CMI uses soil moisture data; the Palmer index uses ETo and soil moisture information. In the Andean region, drought studies have used SPI, SSI, and SPEI indexes frequently [41,42,43,44]. In addition, the drought index (DI) developed by [45] has also been used to predict the occurrence and extent of drought events. However, the SPEI drought index might be more adequate to be considered in a warmer climate [24,41], because it takes into consideration the changes to atmospheric-evaporated demand using the monthly hydrologic water balance (Precipitation-ETo).
To evaluate the changes in extreme drought events many authors use the generalized extreme value (GEV) distribution. For example, [46] used GEV to analyze the maximum and minimum regional values of the drought index in the Mediterranean, and [47] employed GEV to analyze the minimum flows in Europe. In [48], GEV was used to characterize and analyze drought changes through the probability density function of some features in South Korea. GEV is widely used in America. For instance, [49] conducted a GEV analysis in California (USA) to estimate return periods and expected frequency from the 2014 drought and the cumulative 2012–2014 droughts using PDSI; while [50] used GEV and other probability distributions to obtain the best regional probability distribution to produce meteorological drought return period maps; whereas [51] used different types of probability distributions between GEV and two-parameter gamma to select best models to estimate standardized drought indices in a tropical-subtropical region of Brazil.
Mountains provide water for half of the world’s population [52]. The impact of CC in mountain regions is well-documented [53,54]. CC causes glaciers to retreat, affecting the catchments response time [55], in addition to the intensification of extreme events, i.e., droughts and floods. Studying the impact of droughts in the Andean highlands where paramo ecosystem occupies ca. 3 million hectares [56,57] is of great importance because a reduction in rainfall will result in an alteration in the ecosystem services provided, e.g., the supply and regulation of water used for various purposes [56,58,59,60]. Therefore, the instauration of future policies for water management in the face of climate change should rely on a deeper understanding of this phenomenon, which impacts heavily depend on local drivers, taking a risk perspective approach. Ecuador, as a developing country, is especially vulnerable to CC effects and the intensification of climatic variability. However, the impact of droughts is of especial interest because the energy matrix is about 65% dependent on hydroelectricity, in addition to an economy significantly dependent on agriculture [61]. Thus, the study of droughts in the future climate is of utmost importance.
The use of GCMs is, to date, the best approach to study droughts future trends in a changing climate. However, the performance of GCMs in representing precipitation in the tropics is still restricted, mainly due to limitations in the representation of convective precipitation. One approach to improve the regional and local representation of climate is the application of dynamical downscaling (DD) to GCM results. Dynamical downscaling represents the climate in high-resolution by solving the Navier–Stokes complex system of non-linear differential equations for fluids. On one hand, the difficulty to obtain climate results from these equations is related to the numerical resolution, which demands high computational capacities. Another difficulty, sometimes underestimated, is the setting of adequate sub-grid parameterizations such as cumulus convection, the planetary boundary layer, and cloud microphysics, among others [62]. Thus, a sensitivity analysis is necessary to evaluate the set of adequate parameterizations prior to the generation of present and future climate. To date, the attribution of plausible sub-grid models to specific climate and land-use regions is a topic of arduous research [62,63,64].
Despite the improvement of GCM results by DD, the projections of climate are limited by a considerable cascade of uncertainties [62,65]. In relation to intra-model uncertainty, there are 25 GCMs in the coupled model intercomparison project phase 3 (CMIP3) (https://pcmdi.llnl.gov/ipcc/model_documentation/ipcc_model_documentation.html), whereas there are 56 GCMs in the coupled model intercomparison project phase 5 (CMIP5) (https://portal.enes.org/data/enes-model-data/cmip5/resolution). As a result of the increment of centers producing climate results, the intra-model uncertainty has increased [66]. One approach to analyze the results is the generation of a GCM ensemble. Another approach is to select the GCMs that best represent the climate of observed data and either make a band of projections or to generate an ensemble likewise. Other uncertainty sources are related to (i) the future scenario projected among RCP 2.5, 4.5, 6, and 8.5, (ii) the regional climate model used for DD, and (iii) the DD results bias correction methods. The methodology implemented in the present study tries to tackle these limitations.
The Ecuadorian Environmental Agency, MAE in Spanish, in order to develop the Third National Communication on Climatic Change, TCN in Spanish, led an important effort to provide future scenarios of CC, by downscaling CMIP5 GCM results using the Weather Research and Forecasting models, WRF, at 10 km resolution country-wide. The base period selected was 1981 to 2005, and the future period 2011 to 2100. In the first place, a selection of GCMs was based on several statistical criteria [67], finally obtaining CSIRO-Mk3-6.0, GISS-E2-R, IPSL-CM5A-MR, and MIROC-ESM. Then GCM results from these models were used as boundary conditions to drive WRF runs in present and future periods. A detailed account of the methodology is explained in Armenta et al [67].
Therefore, the objective of this study is to perform a spatiotemporal analysis of droughts (magnitude, severity, and duration) through the SPEI drought index in the upper part of the Paute river basin. This region is located in the southern part of the Ecuadorian Andes, which is a water provider for 123,000 families, serving several irrigation and hydroelectric projects. The projections are evaluated from 2011–2070, considering RCPs 4.5 and 8.5 scenarios using GCM results dynamically downscaled to 10 km resolution. The results will provide a better understanding of the droughts in the highlands of Ecuador, helping water managers to take timely decisions.
2. Materials and Methods
2.1. Study Area
The study area includes four sub-basins, e.g., Machángara, Tomebamba, Yanuncay, and Tarqui, in the upper part of the Paute river basin (1602 km2), located in the southern Ecuadorian Andes (Figure 1). This region is essential to the water supply for the city of Cuenca, which is the third most important city in Ecuador [68] with a population of 660,000 inhabitants. The altitude in the study area varies between 2440 and 4400 m above sea level. The upper and middle parts of the basins are covered by patches of Polylepis reticulata, tussock grasses, ground rosettes, cushion plants, and ground rosettes, and the lower part of the basins is covered by pastures, agricultural lands, and urban areas [58,69,70]. According to [71], the study area has two precipitation types: Bimodal type II corresponding to upper and middle part of the basins, and Bimodal type I in the lower part; both of these presented rainfall peaks in April and October; however, Bimodal type II presented a lesser pronounced dry season in June–August, with important anomalies in July due to the intensification of the easterlies and the eastward orientation of the western part of the Paute basin, producing enhanced orographic precipitation [72].
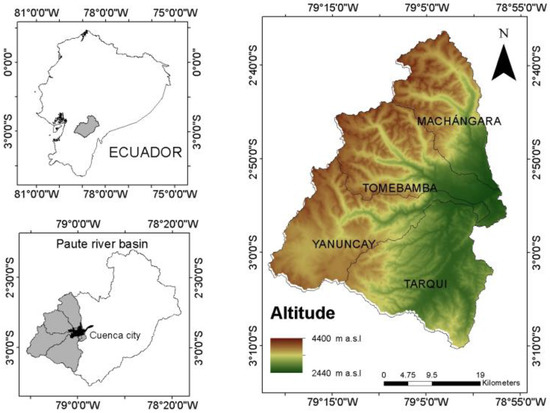
Figure 1.
Study area location.
Despite the importance of this region, few studies about droughts have been developed [45,73,74] in the Machángara river sub-basin, mainly focusing on forecast and risk evaluation of water scarcity. Therefore, spatiotemporal analysis of droughts could help better understand this area, and the implementation of adaptation and mitigation strategies.
2.2. Climate Data
GCMs are used to assess the impacts and risks of climate change and droughts [75]. However, the outputs of GCMs vary widely within the same RCP scenario. The use of a GCM ensemble is a common practice in climate science research to account for intra-model uncertainty [76]. For the TCN project, 4 GCMs were selected through the evaluation of the CMIP5 GCM, showing a better representation of climate features of Ecuador. GCMs were evaluated against ground observations during the base period 1981–2005 [67]. The main features of these models are shown in Table 1. After the GCM selection, the WRF model version 3.6.1 was used to dynamically downscale climate results to 10 km resolution. This resolution is a balance between local climate representation ability and computational power demand to downscale 4 GCMs for the whole country. In this work, the ensemble results of the downscaled GCMs were used, which will be referred to as DGCMs.

Table 1.
List of the 4 global climate models (GCMs) considered for the model ensemble.
To ensemble the results, the reliability ensemble averaging (REA) method [77,78] was implemented for precipitation and temperature. REA combines the outputs of the DGCMs using two criteria: A performance criterion, based on the ability of different models to represent various aspects of the current climate, and a convergence criterion based on simulated changes through models for the same emissions scenario. For more details, the reader should refer to [77]. To account for future intra-scenarios uncertainty, projections for RCP 4.5, which supposes a precise stabilization of the carbon dioxide emissions, and RCP 8.5, which implies the continuity of high carbon dioxide emissions rates, were used from 2011 to 2070.
2.3. Bias Correction of Ensemble Outputs
A bias correction procedure, similar to the one applied in [79] was performed to adjust precipitation and temperature outputs of the DGCM data. Due to the scarcity and uneven distribution of rainfall and temperature stations in the study area, satellite estimates of precipitation and temperature were used as a reference for bias correction. Downscaled precipitation of TRMM 3B43 V7 product at 5-km spatial resolution (PRKTC) [80] was used to bias correct DGCM precipitation data. This product was derived trough a two-step downscaling procedure of satellite images, which were merged with in situ precipitation data and other satellite products (e.g., cloud top temperature, cloud fraction, normalized vegetation index, and soil moisture). Further details of the PRKTC product are available in [80]. MODIS land surface temperature estimates (MOD11A2 V6) at 1 km spatial resolution and 8-day temporal resolution were used as the reference temperature for bias correction of DGCM temperature data. This product was downloaded from NASA and USGS Land Processes Distributed Active Archive Center (LP DAAC) (https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod11a2). To unify the spatial resolution of all satellite products, PRKTC and MOD11A2 V6 estimates were re-gridded to the resolution of the DGCM (~10 km) through the nearest neighbor interpolation method. Monthly PRKTC and MOD11A2 V6 data during 2001–2005 corresponding to the same period of the DGCM models were used to derive monthly-adjusted coefficients for both variables. Finally, DGCM estimates were calibrated multiplying the monthly-adjusted coefficients by the DGCM estimates in the base and future period.
2.4. Temperature and Precipitation Variation
The analysis of the variation of temperature and precipitation over time was made with the average values in the base period (1981–2005) and two future periods (2011–2040 and 2041–2070). The comparison was made with maps of the base period and future periods, using the average value pixel-wise in each period. The comparison between periods was made with the statistical stability over time of the data, and, thus, tests of stationarity were made to the base period [81,82,83].
2.5. Precipitation and Evapotranspiration Index (SPEI)
For characterizing droughts, the SPEI index was used. It could be considered a meteorological-hydrological index because it includes the changes in evaporated atmospheric demand using the monthly hydrologic water balance (precipitation–reference evapotranspiration). SPEI is obtained in three steps: (i) calculation of the reference evapotranspiration (ETo), (ii) calculation of the water balance, e.g., D = Precipitation–ETo, and (iii) adjustment of the water balance to the probability log-logistic distribution and further standardization of the distribution [24]. There are different methods to estimate the ETo, depending on the availability of meteorological data [84,85,86], for instance, Penman–Monteith [84], Hargreaves [87], and Thornthwaite [88], among others. The best estimates of ETo is by Penman–Monteith method; however, the main limitation is the difficulty to obtain several meteorological parameters such as air humidity, temperature, radiation, atmospheric pressure, and wind speed [24].
In this study, the Thornthwaite method was used to calculate the ETo. The monthly water balance was used with the log-logistic probability distribution, then it was normalized following the approximation of Abramowitz and Stegun [89] to obtain SPEI index. SPEI can be calculated for different time scales (1, 3, 6, 12, or more months) [25,85]. Specifically, for the purposes set herein, the SPEI3 is used, which is calculated as the sum of the water balance for three consecutive months. The classification of the drought and moisture categories based on the SPEI index is shown in Table 2 [24]. The SPEI index is calculated pixel-wise for the base and future periods to identify spatial and temporal drought changes in the study area. For the validation of SPEI3, the categories’ frequencies, derived from bias correction of DGCM in the base period, were compared to frequencies derived from data of precipitation and temperature of three meteorological ground stations (Labrado, Chanlud, and Aeropuerto) provided by the National Institute of Meteorology and Hydrology of Ecuador (INAMHI).

Table 2.
Classification of standardized precipitation and evapotranspiration index (SPEI) index.
2.6. Drought Characterization
Following [90], values less or equal to −1 of drought occurrence were assumed for SPEI3 (Figure 2). The threshold level is based on the run-length concept and frequency analysis. Three parameters were used to characterize the drought time series:
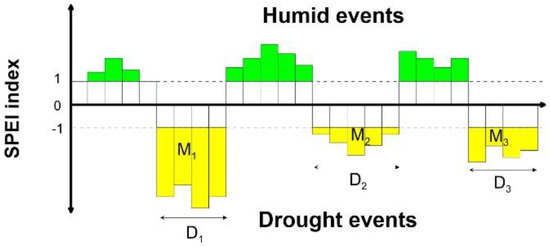
Figure 2.
Scheme of drought characterization. M = Magnitude, D = Duration, Severity = M/D.
- Magnitude: The accumulated sum of all values in drought event
- Duration: Duration of a drought event.
- Severity: Ratio between magnitude and duration.
It is well documented that extreme events will be enhanced by climate change [91]. Thus, it is essential to evaluate future trends in droughts and their features such as magnitude, duration, and severity. In this work, the generalized extreme value distribution (GEV) was used to analyze the changes in extreme values of droughts for the duration, magnitude, and severity for several return periods. The GEV distribution of three parameters is defined by a location (µ), showing where the origin is located; the scale (σ) determines the statistical dispersion of the probability distribution; and the shape (ξ) parameter specifies the type of distribution: Type I (ξ → 0) Gumbel, Type II (ξ > 0) Frechet, and Type III (ξ < 0) Weibull [92]. The weighted moment method was used to estimate the parameters of GEV distribution. This method was chosen because of its stability and robustness in small size samples [93]. The Kolmogorov–Smirnov (KS) test was used to validate the quality of fit. This test measures the degree of agreement between the data set distribution and a theoretical distribution (the significant p-value was greater or equal to 0.05) [94]. The spatial changes of the three drought characteristics were calculated by a change ratio, Rc, calculated by the ratio between the future feature value and the base period feature value for a given scenario and return period. The spatial variations of Rc for the duration, magnitude, and severity were calculated pixelwise in the study area, where the fit was significant for several return periods frequently used in the literature, e.g., 10, 50, and 100 years [90,95,96,97]. This process was performed for the scenarios RCP 4.5 and RCP 8.5 in the two future periods (Future 1: 2011–2040, Future 2: 2041–2070). A map containing the [p] values is presented in Appendix A.
3. Results and Discussion
3.1. Precipitation and Temperature Variation
Figure 3a shows the behavior of the precipitation in the base and future periods. During the entire period, the two scenarios (RCP 4.5 and RCP 8.5) show an increase in their trend. However, the scenario RCP 8.5 shows a higher increase in monthly precipitation in Future 2. Figure 3b shows the trend of temperature; it has a rise in both scenarios. During the first two future decades, the two scenarios have similar behavior; however, since 2031, the RCP 8.5 shows a higher trend than the RCP 4.5. It should be noted that the trend stabilizes since 2061 for the RCP 4.5 scenario.
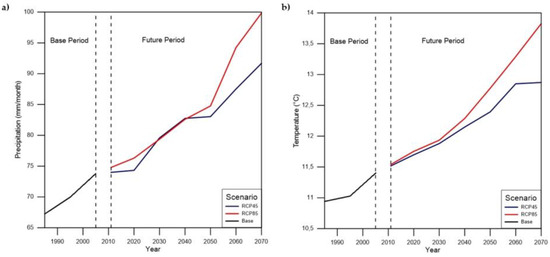
Figure 3.
Variation in the base period and future periods of (a) Precipitation; (b) Temperature.
Figure 4a shows the maps of precipitation changes in the study area. Spatially the precipitation increases from one period to another (Base period: 1981–2005, Future period 1: 2011–2040, Future period 2: 2041–2070). The precipitation for the scenario RCP 8.5 is higher than precipitation for the scenario RCP 4.5. Besides, during Future 2 more precipitation is expected, especially in the Machángara and Tomebamba rivers sub-basins. Regarding temperature variations, Figure 4b displays that the temperature increases slightly from period to period, and the scenario RCP 8.5 shows more increment than scenario RCP 4.5.
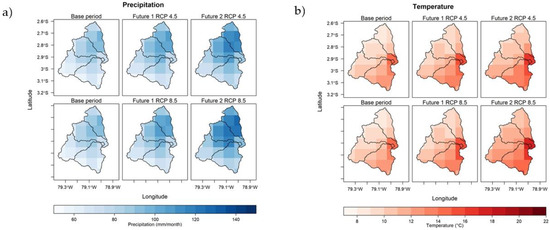
Figure 4.
(a) Precipitation and (b) temperature variation maps of the base period and future periods.
These results are similar to the results found in [98,99], in which a similar tendency of the temperature in the future has been shown. Moreover, the results of temperature variation are very similar to the study of [100].
3.2. Drought Characterization and Analysis
The comparison of moderate, severe, and extreme droughts frequencies between DGCM corrected data and the observed data of the three meteorological stations is shown in Figure 5. This figure indicates that the frequencies are very similar; therefore, the DGCM corrected data was used for the space-time analysis of droughts in the future.
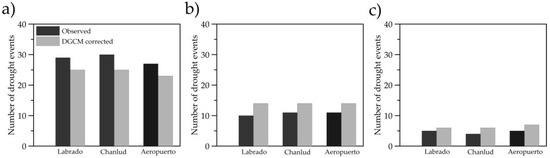
Figure 5.
Frequencies of drought categories: (a) moderate drought, (b) severe drought, and (c) extreme drought.
Figure 6a shows the change ratio of the severity, magnitude, and duration of droughts for RCP 4.5 for Future 1 with respect to the base period. The magnitude and duration show a marked decrease with respect to the base period. Nonetheless, in general, as the return-period increases, the rate of this declination becomes smaller. The adjusted GEV distributions for durations do not follow the extreme shapes distributions clearly, as is revealed by the p-value (Appendix A). This entails implicitly significant uncertainties that could affect the inferences related to this drought variable; however, a general overview of the duration (taking into account the pixels that comply with the significant p-value) shows a decrease of it when the return period increases. The severity for RCP 4.5 for Future 1 has an increase respecting to the base period. The last implies that, although duration and magnitude decreases, the former feature has a more pronounced declination than the latter one. Nonetheless, there are pixels that do not reflect the severity behavior (i.e., the relation between magnitude and duration). This disagreement can be mostly explained by problems of the GEV distributions, which in some cases were not fitted properly. The previous discussion is one of the mentioned consequences of the implicit uncertainty involving the distributions of the duration, which is also a concerning issue to keep in mind for the remaining scenarios and futures of analysis.
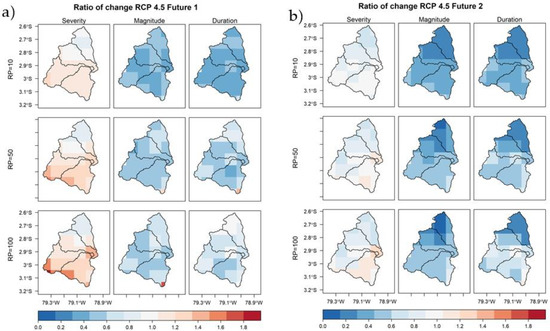
Figure 6.
Ratio change of drought features of scenario RCP 4.5 with respect to the base period (1981–2005): (a) Future 1 (2011–2040) and (b) Future 2 (2041–2070).
The change ratio of drought features for the scenario RCP 4.5 in Future 2 is shown in Figure 6b. The magnitude and duration have severe decreasing patterns, which are more intense than Future 1 of the same scenario. Furthermore, in contrast to what happened for Future 1, the severity shows a decreasing effect. This implies that the decreasing rate of change for magnitudes are more pronounced than durations—in respect to the base period—while the opposite occurs for the first future (although the fitted-distributions for durations also show problems according to Appendix A). In this RCP 4.5 scenario, the greenhouse-gas concentrations reach their peak in 2040 (i.e., Future 1), after which it starts to stabilize (i.e., Future 2). It is well known that these emissions entail an increase in the quantities and frequencies of the precipitations events [13]. Therefore, a probable consequence of such rainfall alterations would be the reduction of magnitudes and durations of droughts for the mountain areas [76,99,101]. Nonetheless, the switch of severity—from positive to negative—would probably be related to an alteration of the rain frequency more than to its quantity for the first period (i.e., an increase in the rainfall frequencies would have a more intense effect on the duration than on the magnitude of droughts). The opposite effect occurs during the gas stabilization emissions (i.e., the second future). For that period, significant changes in the magnitudes and durations of droughts are still present. However, the differences in magnitudes are more intense than for durations, as indicated by the severity. This suggests that rainfall amounts will have a greater effect on drought magnitudes, than duration. It is worth mentioning that climate processes behind the discussed effects are very complex by nature. So, the discussion about the mechanism of change of droughts related to rainfall alterations have to be understood as probable explanations, which need a more comprehensive analysis.
Figure 7 shows the ratio of change for magnitude, duration, and severity under the RCP 8.5 climate scenario (for both futures). On the one hand, Figure 7a,b show again that the magnitude and duration have a sharp decrease relative to the base period. Interestingly, the rate of change for magnitudes and durations seems to be smaller for larger return-periods. The last is a clear symptom that the probability function of extremes changes its magnitudes and shapes in different climate scenarios (i.e., tail-shapes). As a consequence, interpolations and extrapolations have different trends for any return-period. On the other hand, the severity switches its behavior from a decreasing to increasing pattern—from the first to the second period. This is the opposite of the effect shown in the RCP 4.5 scenario; but it is probably a response to the interactions between quantities and frequencies of precipitation events, as explained before. The contrasting effect on the severity switching for both scenarios could be considered counterintuitive at first glance, keeping in mind that for the RCP 8.5 a hypothetical increment of greenhouse-gas is permanent (which is a rather different hypothesis than the one made for the RCP 4.5) [102]. Nonetheless, these differences in severity switching would mean that, although magnitudes and durations have similar decreasing patterns for both scenarios, the interactions between them (explaining the differences in severities) are rather different. Furthermore, these severity switching differences could encode other more complex climate interactions between the drought variables and other climate variables.
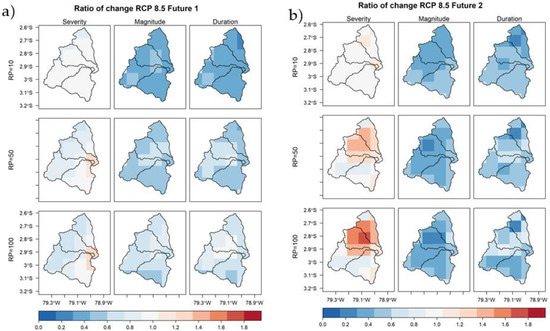
Figure 7.
Ratio change of drought features of scenario RCP 8.5 with respect to the base period (1981–2005): (a) Future 1 (2011–2040) and (b) Future 2 (2041–2070).
In the Andes of Ecuador [103] it was found that the temperature will increase in the future, resulting in drought events of greater magnitude. However, these drought events will be short-lived. With respect to precipitation, Ref. [103] shows that the increase in rainfall would produce decreasing trends in the magnitude of drought events. Both conclusions are in agreement with the findings of this paper. Therefore, such trends of drought may be characteristic of the Andean region of Ecuador. However, further studies at a country-wise scale are necessary. When comparing these results with studies developed in the Central and Southern Andes mountains [99,104,105], it is observed that future projections also show an increase in temperature, which could have an influence on the magnitude of future drought events. In relation to more specific features of droughts, [76] conducted a study in the highlands of Bolivia, Chile, and Argentina for the period 2011–2040, finding that drought will be shorter, which may be due to the increase in precipitation as indicated in [99]. However, the severity will increase [99]. A seasonal analysis could be carried out in future studies to know how the behavior of drought events will be during the different months [99]. Due to the contrasting response of specific regions to CC, trends in droughts differ across the world. For instance, [90] used the SPEI index and the RCP 8.5 scenario, showing that the severity of the droughts in South Korea would be stronger. Interestingly, [106] conducted a study in the highlands and mountain regions of the Czech Republic using the SPEI index for RCP 4.5 and RCP 8.5, indicating that severe droughts will be the new norm. Finally, the results reveal that, although magnitudes and durations of droughts have significative changes, the climate mechanisms relating them could be different for distinct climate scenarios. This presents new opportunities for research studies dealing with the interactions between rainfall and droughts alterations in the future, hypothesizing climate change conditions. Furthermore, the behavior of droughts here presented, as a response to climate change, could be seen as complementary knowledge for similar mountain regions, as reported in [76,99,101]; or, in relative contrast to what will happen to other regions [90,106].
4. Conclusions
Applying a probability distribution function of extreme values for the SPEI index in three return periods (10, 50, and 100 years), the magnitude, duration, and severity of droughts were characterized in the base (1981–2005) and future (2011–2040 and 2041–2070) periods for RCP 4.5 and 8.5. A temporal and spatial analysis was performed in the upper part of the Paute river basin through the change ratio of drought features. The results show that, under climate change, the characteristics of droughts will be altered. Interestingly, magnitudes and durations would suffer a dramatic decrease in the scenarios here considered. On the other hand, the severity of droughts also shows a decrement pattern under the RCP 4.5 scenario (for the period 2011–2040), and for the RCP 8.5 scenario (for the period 2041–2070). Nonetheless, for the remaining scenarios and periods, the severity shows a general increment that intensifies for longer return periods. Interestingly, both effects of severity are present for different scenarios and future periods. These would imply that, even when a general decreasing effect exists for magnitude and durations, the climate mechanism behind those effects could be very different for distinct climate scenarios. Therefore, this study brings new opportunities for further research. Furthermore, since the mountain areas have complex climate conditions, a climate analysis on this spatial scale would serve as complementary or contrasting knowledge of similar analysis for other areas and for different spatial scales. The main limitations of the present study are related to the well-known cascade of uncertainties of climate projections. However, the GCM selection and further downscaling and bias correction of results help to diminish the uncertainty to a certain degree. Future studies will be focused on a higher resolution as well as on identifying intra-annual future droughts features variations. The robustness of the results provides useful information for decision-makers for further implementation of droughts impact prevention measures and risk mitigation for future decades of this century.
Author Contributions
Conceptualization, A.A.; methodology, M.M.; D.M., D.Z., M.M., and L.M.; software, D.Z., L.C., D.M., J.C., M.M., and L.M.; formal analysis, A.A. and D.M.; data curation, J.C.; writing—original draft preparation, D.Z.; writing—review and editing, A.A. and D.Z.; supervision, A.A.; project administration, A.A.; funding acquisition, A.A.
Funding
This research was funded by the University of Cuenca through its Research Department (DIUC) via the projects “Evaluación de métodos de generación de escenarios para la simulación del riesgo de fallo en el suministro de agua en épocas de estiaje. Caso de estudio en un sistema de recursos hídricos multipropósito” and “Evaluación del riesgo de sequias en cuencas andinas reguladas influenciadas por la variabilidad climática y cambio climático. Caso de estudio en la cuenca del río Machángara”. The authors also thank to the Ecuadorian Corporation for the Development of Research and Academia (CEDIA) and DIUC through the project “Evaluación de los efectos de las actividades socioeconómicas en el cambio del uso del suelo y del cambio climático en las amenazas a inundaciones y sequías en la cuenca del río Tomebamba” for its financial support.
Acknowledgments
The authors would like to thank the MAE and INAMHI for the information provided. We are grateful to Daniela Ballari for provide the downscaled TRMM 3B43 V7 dataset.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
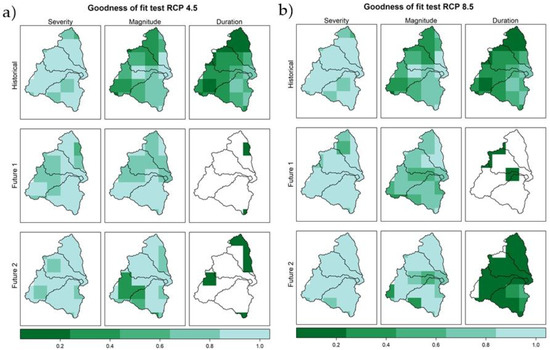
Figure A1.
p-values of the goodness of fit test for GEV distribution in (a) RCP 4.5 and (b) 8.5 (base period and Future 1 and 2). White color indicates zones where the p-value is less to 0.05.
References
- Mishra, A.K.; Singh, V.P. Review paper A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought as a Natural Hazard: Concepts and Definitions. In Drought: A Global Assessment; Routledge: London, UK, 2000; p. 16. [Google Scholar]
- Mishra, A.K.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess. 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Leng, G.; Tang, Q.; Rayburg, S. Climate change impacts on meteorological, agricultural and hydrological droughts in China. Glob. Planet. Chang. 2015, 126, 23–34. [Google Scholar] [CrossRef]
- Keyantash, J. The Quantification of Drought: An Evaluation of Drought Indices. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Huang, S.; Pollack, H.N.; Shen, P.Y. Temperature trends over the past five centuries reconstructed from borehole temperatures. Nature 2000, 403, 756–758. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Sato, M.; Ruedy, R.; Lo, K.; Lea, D.W.; Medina-Elizade, M. Global temperature change. Proc. Natl. Acad. Sci. USA 2006, 103, 14288–14293. [Google Scholar] [CrossRef]
- Houghton, J.T.; Ding, Y.; Griggs, D.J.; Noguer, M.; van der Linden, P.J.; Dai, X.; Maskell, K.; Johnson, C.A. Climate Change 2001: The Scientific Basis; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Hirabayashi, Y.; Kanae, S.; Emori, S.; Oki, T.; Kimoto, M. Global projections of changing risks of floods and droughts in a changing climate. Hydrol. Sci. J. 2008, 53, 754–772. [Google Scholar] [CrossRef]
- Nazarenko, L.; Schmidt, G.A.; Miller, R.L.; Tausnev, N.; Kelley, M.; Ruedy, R.; Russell, G.L.; Aleinov, I.; Bauer, M.; Bauer, S.; et al. Future climate change under RCP emission scenarios with GISS ModelE2. J. Adv. Model. Earth Syst. 2015, 244–268. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Water Vapor Feedback and Global Warming. Annu. Rev. Energy Environ. 2002, 25, 441–475. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Projected changes in drought occurrence under future global warming from multi-model, multi-scenario, IPCC AR4 simulations. Clim. Dyn. 2008, 31, 79–105. [Google Scholar] [CrossRef]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- Park, C.K.; Byun, H.R.; Deo, R.; Lee, B.R. Drought prediction till 2100 under RCP 8.5 climate change scenarios for Korea. J. Hydrol. 2015, 526, 221–230. [Google Scholar] [CrossRef]
- Brito, S.S.B.; Cunha, A.P.M.A.; Cunningham, C.C.; Alvalá, R.C.; Marengo, J.A.; Carvalho, M.A. Frequency, duration and severity of drought in the Semiarid Northeast Brazil region. Int. J. Climatol. 2018, 38, 517–529. [Google Scholar] [CrossRef]
- Palmer, W. Meteorological Drought; Paper 45; US Weather Bureau: Washington, DC, USA, 1965. [Google Scholar]
- Palmer, W.C. Keeping Track of Crop Moisture Conditions, Nationwide: The New Crop Moisture Index. Weatherwise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Van Rooy, M.P. A rainfall anomaly index independent of time and space. Notos 1965, 14, 43. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. Drought monitoring with multiple time scales. In Proceedings of the 9th Conference on Applied Climatology, Dallas, TX, USA, 15–20 January 1995; pp. 233–236. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate computation of a streamflow drought index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 3023, 3001–3023. [Google Scholar] [CrossRef]
- Meresa, H.K.; Osuch, M.; Romanowicz, R. Hydro-meteorological drought projections into the 21-st century for selected polish catchments. Water 2016, 8. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Barker, L.J.; Hannaford, J.; Chiverton, A.; Svensson, C. From meteorological to hydrological drought using standardised indicators. Hydrol. Earth Syst. Sci. 2016, 2483–2505. [Google Scholar] [CrossRef]
- Turco, M.; Levin, N.; Tessler, N.; Saaroni, H. Recent changes and relations among drought, vegetation and wildfires in the Eastern Mediterranean: The case of Israel. Glob. Planet. Chang. 2017, 151, 28–35. [Google Scholar] [CrossRef]
- Huang, S.; Huang, Q.; Chang, J.; Leng, G. Linkages between hydrological drought, climate indices and human activities: A case study in the Columbia River basin. Int. J. Climatol. 2016, 36, 280–290. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Yao, H.; Gao, L.; Chen, Y.; Liu, M. Non-linear relationship of hydrological drought responding to meteorological drought and impact of a large reservoir. J. Hydrol. 2017, 551, 495–507. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J. Drought hazard assessment in typical corn cultivated areas of China at present and potential climate change. Nat. Hazards 2016, 81, 1323–1331. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, Q.; Zhao, X.; Wu, P.; Pan, W.; Gao, X.; Sun, M. Temporal and spatial evolution of the standardized precipitation evapotranspiration index (SPEI) in the Loess Plateau under climate change from 2001 to 2050. Sci. Total Environ. 2017, 595, 191–200. [Google Scholar] [CrossRef]
- Venkataraman, K.; Tummuri, S.; Medina, A.; Perry, J. 21st century drought outlook for major climate divisions of Texas based on CMIP5 multimodel ensemble: Implications for water resource management. J. Hydrol. 2016, 534, 300–316. [Google Scholar] [CrossRef]
- Pablos, M.; Martínez-Fernández, J.; Sánchez, N.; González-Zamora, Á. Temporal and spatial comparison of agricultural drought indices from moderate resolution satellite soil moisture data over northwest Spain. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Sánchez, N.; Piles, M.; Pablos, M.; Wardlow, B.; Tadesse, T.; Svoboda, M.; Hispano, I.; De Investigaciones, L.; Ciale, A.; Duero, S. Preliminary Assessment of an Integrated Smos and Modis Application for Global Agricultural Drought Monitoring. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Li, R.; Tsunekawa, A.; Tsubo, M. Index-based assessment of agricultural drought in a semi-arid region of Inner Mongolia, China. J. Arid Land 2014, 6, 3–15. [Google Scholar] [CrossRef]
- Gong, Z.; Zhao, S.; Gu, J. Correlation analysis between vegetation coverage and climate drought conditions in North China during 2001–2013. J. Geogr. Sci. 2017, 27, 143–160. [Google Scholar] [CrossRef]
- Ge, Y.; Cai, X.; Zhu, T.; Ringler, C. Drought frequency change: An assessment in northern India plains. Agric. Water Manag. 2016, 176, 111–121. [Google Scholar] [CrossRef]
- Fok, H.S.; He, Q.; Chun, K.P.; Zhou, Z.; Chu, T. Application of ENSO and drought indices for water level reconstruction and prediction: A case study in the lower Mekong River estuary. Water 2018, 10. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Chura, O.; López-Moreno, J.I.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Aguilar, E.; Moran-Tejeda, E.; Trujillo, F.; Martínez, R.; Nieto, J.J. Spatio-temporal variability of droughts in Bolivia: 1955–2012. Int. J. Climatol. 2015, 35, 3024–3040. [Google Scholar] [CrossRef]
- Penalba, O.C.; Rivera, J.A. Regional aspects of future precipitation and meteorological drought characteristics over Southern South America projected by a CMIP5 multi-model ensemble. Int. J. Climatol. 2016, 36, 974–986. [Google Scholar] [CrossRef]
- Ivits, E.; Horion, S.; Fensholt, R.; Cherlet, M. Global ecosystem response types derived from the standardized precipitation evapotranspiration index and FPAR3g series. Remote Sens. 2014, 6, 4266–4288. [Google Scholar] [CrossRef]
- Rivera, J.A.; Penalba, O.C.; Villalba, R.; Araneo, D.C. Spatio-temporal patterns of the 2010-2015 extreme hydrological drought across the Central Andes, Argentina. Water 2017, 9, 652. [Google Scholar] [CrossRef]
- Avilés, A.; Célleri, R.; Paredes, J.; Solera, A. Evaluation of Markov Chain Based Drought Forecasts in an Andean Regulated River Basin Using the Skill Scores RPS and GMSS. Water Resour. Manag. 2015, 29, 1949–1963. [Google Scholar] [CrossRef]
- Sousa, P.M.; Trigo, R.M.; Aizpurua, P.; Nieto, R.; Gimeno, L.; Garcia-Herrera, R. Trends and extremes of drought indices throughout the 20th century in the Mediterranean. Nat. Hazards Earth Syst. Sci. 2011, 11, 33–51. [Google Scholar] [CrossRef]
- Feyen, L.; Dankers, R. Impact of global warming on streamflow drought in Europe. J. Geophys. Res. Atmos. 2009, 114, 1–17. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, C.J. A multimodel assessment of the climate change effect on the drought severity-duration-frequency relationship. Hydrol. Process. 2013, 27, 2800–2813. [Google Scholar] [CrossRef]
- Robeson, S.M. Revisiting the recent California drought as an extreme value. Geophys. Res. Lett. 2015, 42, 6771–6779. [Google Scholar] [CrossRef]
- Núñez, J.H.; Verbist, K.; Wallis, J.R.; Schaefer, M.G.; Morales, L.; Cornelis, W.M. Regional frequency analysis for mapping drought events in north-central Chile. J. Hydrol. 2011, 405, 352–366. [Google Scholar] [CrossRef]
- Blain, G.C.; de Avila, A.M.H.; Pereira, V.R. Using the normality assumption to calculate probability-based standardized drought indices: Selection criteria with emphases on typical events. Int. J. Climatol. 2018, 38, e418–e436. [Google Scholar] [CrossRef]
- Mountain Partnership. Mountains as the Water Towers of the World: A Call for Action on the Sustainable Development Goals; FAO: Rome, Italy, 2014. [Google Scholar]
- Buytaert, W.; Bievre, B. De Water for cities: The impact of climate change and demographic growth in the tropical Andes. Water Resour. Res. 2012, 48, 1–13. [Google Scholar] [CrossRef]
- Buytaert, W.; Célleri, R.; Timbe, L. Predicting climate change impacts on water resources in the tropical Andes: Effects of GCM uncertainty. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef]
- Vuille, M.; Francou, B.; Wagnon, P.; Juen, I.; Kaser, G.; Mark, B.G.; Bradley, R.S. Climate change and tropical Andean glaciers: Past, present and future. Earth Sci. Rev. 2008, 89, 79–96. [Google Scholar] [CrossRef]
- Buytaert, W.; Iñiguez, V.; Bièvre, B. De The effects of afforestation and cultivation on water yield in the Andean páramo. For. Ecol. Manag. 2007, 251, 22–30. [Google Scholar] [CrossRef]
- Llambí, L.D.; Soto-W., A.; Borja, P.; Ochoa, B.; Celleri, R.; Bievre, B. De Páramos Andinos: Ecologia, Hidrología y Suelos de Páramos; IAvH, FONAG, USAID, Instito de Monta-a, ICAE, GEF, UNEP, CONDENSAN: Quito, Ecuador, 2012; p. 292. [Google Scholar]
- Buytaert, W.; Célleri, R.; De Bièvre, B.; Cisneros, F.; Wyseure, G.; Deckers, J.; Hofstede, R. Human impact on the hydrology of the Andean páramos. Earth Sci. Rev. 2006, 79, 53–72. [Google Scholar] [CrossRef]
- Buytaert, W.; Cuesta-Camacho, F.; Tobón, C. Potential impacts of climate change on the environmental services of humid tropical alpine regions. Glob. Ecol. Biogeogr. 2011, 20, 19–33. [Google Scholar] [CrossRef]
- Buytaert, W.; Wyseure, G.; De Bièvre, B.; Deckers, J. The effect of land-use changes on the hydrological behaviour of Histic Andosols in south Ecuador. Hydrol. Process. 2005, 19, 3985–3997. [Google Scholar] [CrossRef]
- Ministerio del Ambiente del Ecuador. Tercera Comunicación Nacional del Ecuador sobre Cambio Climático; Ministerio del Ambiente del Ecuador: Quito, Ecuador, 2017. [Google Scholar]
- Hong, S.Y.; Kanamitsu, M. Dynamical downscaling: Fundamental issues from an NWP point of view and recommendations. Asia Pac. J. Atmos. Sci. 2014, 50, 83–104. [Google Scholar] [CrossRef]
- Hahmann, A.N. Representing Spatial Subgrid-Scale Precipitation Variability in a GCM. J. Hydrometeorol. 2003, 4, 891–900. [Google Scholar] [CrossRef]
- Mölg, T.; Kaser, G. A new approach to resolving climate-cryosphere relations: Downscaling climate dynamics to glacier-scale mass and energy balance without statistical scale linking. J. Geophys. Res. Atmos. 2011, 116, 1–13. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Tebaldi, C.; Mearns, L.O.; Nychka, D.; Smith, R.L. Regional probabilities of precipitation change: A Bayesian analysis of multimodel simulations. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Armenta, G.; Villa, J.; Jácome, P.S. Proyecciones Climáticas de Precipitación y Temperatura Para Ecuador, Bajo Distintos Escenarios De Cambio Climático; Ministerio del Ambiente: Quito, Ecuador, 2016. [Google Scholar]
- Célleri, R.; Campozano, L.; Avilés, A. Integrated water resources management in an Andean mountain basin: The case of the Machángara river. In Nexus Outlook: Assessing Resource Use Challenges in the Water, Energy and Food Nexus; Al-Saidi, M., Ribbe, L., Eds.; Nexus academic Publishers: Punjab, Pakistan, 2016; pp. 80–97. [Google Scholar]
- Hansen, B.C.S.; Rodbell, D.T.; Seltzer, G.O.; León, B.; Young, K.R.; Abbott, M. Late-glacial and Holocene vegetational history from two sites in the western Cordillera of southwestern Ecuador. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2003, 194, 79–108. [Google Scholar] [CrossRef]
- Vanacker, V.; Govers, G.; Barros, S.; Poesen, J.; Deckers, J. The effect of short-term socio-economic and demographic change on landuse dynamics and its corresponding geomorphic response with relation to water erosion in a tropical mountainous catchment, Ecuador. Landsc. Ecol. 2003, 18, 1–15. [Google Scholar] [CrossRef]
- Celleri, R.; Willems, P.; Buytaert, W.; Feyen, J. Space-time rainfall variability in the Paute basin, Ecuadorian Ande. Hydrol. Process. 2007, 21, 12. [Google Scholar] [CrossRef]
- Campozano, L.; Célleri, R.; Trachte, K.; Bendix, J.; Samaniego, E. Rainfall and Cloud Dynamics in the Andes: A Southern Ecuador Case Study. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef]
- Avilés, A.; Célleri, R.; Solera, A.; Paredes, J. Probabilistic Forecasting of Drought Events Using Markov Chain- and Bayesian Network-Based Models: A Case Study of an Andean Regulated River Basin. Water 2016, 8, 37. [Google Scholar] [CrossRef]
- Avilés, A.; Solera Solera, A.; Paredes-Arquiola, J.; Pedro-Monzonís, M. Integrated Methodological Framework for Assessing the Risk of Failure in Water Supply Incorporating Drought Forecasts. Case Study: Andean Regulated River Basin. Water Resour. Manag. 2018, 32. [Google Scholar] [CrossRef]
- Blenkinsop, S.; Fowler, H.J. Changes in European drought characteristics projected by the PRUDENCE regional climate models. Int. J. Climatol. 2007, 27, 1595–1610. [Google Scholar] [CrossRef]
- Penalba, O.C.; Rivera, J.A. Future Changes in Drought Characteristics over Southern South America Projected by a CMIP5 Multi-Model Ensemble. Am. J. Clim. Chang. 2013, 2, 173–182. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Calculation of average, uncertainty range, and reliability of regional climate changes from AOGCM simulations via the “Reliability Ensemble Averaging” (REA) method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Tebaldi, C.; Knutti, R. The use of the multi-model ensemble in probabilistic climate projections. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 2053–2075. [Google Scholar] [CrossRef]
- Mahmud, M.R.; Hashim, M.; Matsuyama, H.; Numata, S.; Hosaka, T. Spatial downscaling of satellite precipitation data in humid tropics using a site-specific seasonal coefficient. Water 2018, 10, 409. [Google Scholar] [CrossRef]
- Ulloa, J.; Ballari, D.; Campozano, L.; Samaniego, E. Two-Step Downscaling of Trmm 3b43 V7 Precipitation in Contrasting Climatic Regions With Sparse Monitoring: The Case of Ecuador in Tropical South America. Remote Sens. 2017, 9, 758. [Google Scholar] [CrossRef]
- Chen, H.L.; Rao, A.R. Testing Hydrologic Time Series for Stationarity. J. Hydrol. Eng. 2002, 7, 129–136. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Ondo, J.C.; Gachon, P.; Bobée, B. Frequency analysis of a sequence of dependent and/or non-stationary hydro-meteorological observations: A review. J. Hydrol. 2006, 329, 534–552. [Google Scholar] [CrossRef]
- Dickey, B.Y.D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Potop, V.; Možný, M. The Application a New Drought Index -Standardized Precipitation Evapotranspiration Index in the Czech Republic. In Mikroklima a Mezoklima Krajinných Struktur a Antropogenních Prostředí; Czech Bioclimatic Society, Czech Hydrometeorological Institute: Prague, Czech Republic, 2011. [Google Scholar]
- Vicente-Serrano, S.M.; Lanjeri, S.; López-Moreno, J.I. Comparison of different procedures to map reference evapotranspiration using geographical information systems and regression-based techniques. Int. J. Climatol. 2007, 27, 1103–1118. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. American Geographical Society An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. Available online: http://www.jstor.org/stable/210739 (accessed on 11 August 2016). [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables (National Bureau of Standards Applied Mathematics Series No. 55). J. Appl. Mech. 1965, 32, 239. [Google Scholar] [CrossRef]
- Kim, B.S.; Chang, I.G.; Sung, J.H.; Han, H.J. Projection in Future Drought Hazard of South Korea Based on RCP Climate Change Scenario 8.5 Using SPEI. Adv. Meteorol. 2016, 2016, 1–23. [Google Scholar] [CrossRef]
- Katz, R.W.; Brown, B.G. Extreme events in a changing climate: Variability is more important than averages. Clim. Chang. 1992, 21, 289–302. [Google Scholar] [CrossRef]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions using Linear Combinations of order Statistics. J. R. Stat. Soc. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Massey, F. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Rodríguez, R.; Navarro, X.; Casas, M.C.; Ribalaygua, J.; Russo, B.; Pouget, L.; Redaño, A. Influence of climate change on IDF curves for the metropolitan area of Barcelona (Spain). Int. J. Climatol. 2014, 34, 643–654. [Google Scholar] [CrossRef]
- Gregersen, I.B.; Madsen, H.; Arnbjerg-Nielsen, K. Estimation of climate factors for future extreme rainfall: Comparing observations and RCM simulations. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 10–16 September 2011; pp. 10–16. [Google Scholar]
- Casas, M.C.; Codina, B.; Redano, A.; Lorente, J. A methodology to classify extreme rainfall events in the western mediterranean area. Theor. Appl. Climatol. 2004, 77, 139–150. [Google Scholar] [CrossRef]
- Chou, S.C.; Lyra, A.; Mourão, C.; Dereczynski, C.; Pilotto, I.; Gomes, J.; Bustamante, J.; Tavares, P.; Silva, A.; Rodrigues, D.; et al. Assessment of Climate Change over South America under RCP 4.5 and 8.5 Downscaling Scenarios. Am. J. Clim. Chang. 2011, 3, 512–527. [Google Scholar] [CrossRef]
- Demaria, E.M.C.; Maurer, E.P.; Thrasher, B.; Vicuña, S.; Meza, F.J. Climate change impacts on an alpine watershed in Chile: Do new model projections change the story? J. Hydrol. 2013, 502, 128–138. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q.; Huang, W.; Ho, C.H.; Li, R.; Tang, Z. Projected climate regime shift under future global warming from multi-model, multi-scenario CMIP5 simulations. Glob. Planet. Chang. 2014, 112, 41–52. [Google Scholar] [CrossRef]
- Touma, D.; Ashfaq, M.; Nayak, M.A.; Kao, S.C.; Diffenbaugh, N.S. A multi-model and multi-index evaluation of drought characteristics in the 21st century. J. Hydrol. 2015, 526, 196–207. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Cáceres, N.; Ayala, O.; Rosero, D.; Lane, M. What does the future hold? Historical climate analysis and projection of future climatic scenarios for the andean canton of Pedro Moncayo, Ecuador. Rev. Geogr. Am. Cent. 2018, 3, 297–318. [Google Scholar] [CrossRef]
- Ragettli, S.; Immerzeel, W.W.; Pellicciotti, F. Contrasting climate change impact on river flows from high-altitude catchments in the Himalayan and Andes Mountains. Proc. Natl. Acad. Sci. USA 2016, 113, 9222–9227. [Google Scholar] [CrossRef]
- Zazulie, N.; Rusticucci, M.; Raga, G.B. Regional climate of the Subtropical Central Andes using high-resolution CMIP5 models. Part II: Future projections for the twenty-first century. Clim. Dyn. 2018, 51, 2913–2925. [Google Scholar] [CrossRef]
- Potopová, V.; Štěpánek, P.; Zahradníček, P.; Farda, A.; Türkott, L.; Soukup, J. Projected changes in the evolution of drought on various timescales over the Czech Republic according to Euro-CORDEX models. Int. J. Climatol. 2018, 38, e939–e954. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).